Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 May;86(5):3204–3210. doi: 10.1016/S0006-3495(04)74368-4

Theoretical Analysis of Twist/Bend Ratio and Mechanical Moduli of Bacterial Flagellar Hook and Filament

Terence C Flynn *, Jianpeng Ma *,†,‡
PMCID: PMC1304185  PMID: 15111433

Abstract

Certain motile bacteria employ rotating flagella for propulsion. The relative flexibility of two key components of the flagellum, filament and hook, is partially responsible for the mechanistic workings of this motor. A new computational method, the quantized elastic deformational model, was employed in this article to calculate the dimensionless twist/bend ratio (EI/GJ) of the filament and hook, providing a quantitative means to compare their relative stiffness. Both ratios were much <1.0, an average of 0.0440 for the filament and 0.0512 for the hook, indicating that within each structure bending is favored over twisting. These two ratios, along with previous experimental measurements, allowed us to propose a theoretical Young's modulus (E) between 106 and 107 dyn/cm2 for the hook. This value is orders of magnitude smaller than experimentally determined Young's moduli of the filament, hence in agreement with empirical evidence linking compliance in the flagellum mainly to the hook.

INTRODUCTION

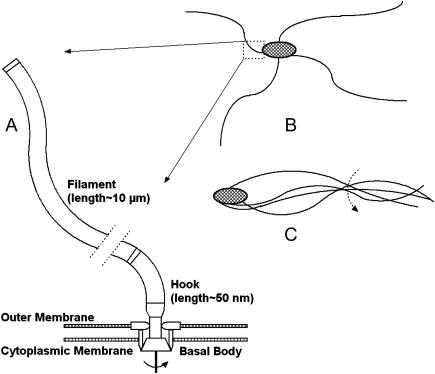
Rotating flagella propel motile bacteria, such as Escherichia coli and Salmonella typhimurium (Berg and Anderson, 1973; Silverman and Simon, 1974). Each individual flagellum consists of three key segments/components: the flagellar basal body, the filament, and the hook that connects the two (Fig. 1 A) (Berry and Armitage, 1999). The basal body is a rotary motor, traversing the bacterial membrane, which generates torque by means of a transmembrane ion gradient (Glagolev and Skulachev, 1978; Larsen et al., 1974; Manson et al., 1977), similar to ATP synthase (Abrahams et al., 1994; Boyer, 1997; Ma et al., 2002). The filament is essentially a long rigid rod, ∼200 Å in diameter and up to 10 μm (100,000 Å) in length, which serves as a propeller (Berry and Armitage, 1999). The filament is able to adopt many polymorphic conformations, including left-handed and right-handed supercoils, depending on various environmental conditions (Kamiya et al., 1979; Macnab and Ornston, 1977; Mimori et al., 1995; Morgan et al., 1995). In contrast to the stiff filament, the hook is a shorter flexible linking segment that may function as a universal joint, transmitting the torque generated by the motor upwards to the filament, and also allowing the filament to spin off-axis and bundle with adjacent filaments (Fig. 1) (Berg and Anderson, 1973; Berry and Armitage, 1999; Morgan et al., 1993).

FIGURE 1.

FIGURE 1

Open in a new tab

(A) Schematic representation indicating relative orientation of three components of the bacterial flagellum: basal body, responsible for torque generation; filament, essentially a long rigid rod; and hook, a flexible linking region. The figure is not drawn to scale; hence, representative lengths of filament and hook are noted. Dotted lines interrupting the filament represent a long section removed for figure clarity. (B and C) Cartoon portrayals of a flagellated bacteria, depicting how bending at the hook may allow bundling of adjacent filaments, leading to in-phase rotation.

Over 95% of the mass of the flagellum resides solely in the filament (Morgan et al., 1995). Electron microscopy has provided the most detailed structures of the S. typhimurium filament to date (Fig. 2 A) (Mimori et al., 1995; Morgan et al., 1995; Yonekura et al., 2003). The filament is helical, and has ∼11 monomers for every two turns of the one-start helix. Alternately, the filament can be depicted as 11 protofilaments arranged around a hollow central channel ∼30 Å in diameter (Samatey et al., 2001). It has been estimated that 20,000 flagellin monomers associate to form a 10-μm (100,000 Å) long filament (O'Brien and Bennett, 1972). Wild-type flagellin from S. typhimurium is a ∼51 kDa protein with 494 residues, consisting of four domains, D0, D1, D2, and D3, named in accordance with their radial positions from the inside of the filament to the outside. D0, D1, and D2 comprise the core of the filament, whereas D3 protrudes from the filament's surface (Mimori et al. 1995; Samatey et al. 2001).

FIGURE 2.

FIGURE 2

Open in a new tab

Electron microscopy density sections, ∼300 Å in length, of the flagellar filament (A) (Mimori et al., 1995) and hook (B) (D. Thomas, T. Shaikh, and D. DeRosier, private communications). The surface of the filament is characterized by protrusions (domain D3), whereas that of the hook is demarcated by a series of grooves. Note that the density sections used in the simulations were over three times as long.

The structure of the S. typhimurium hook has also been determined by electron microscopy (Fig. 2 B) (Morgan et al., 1993). These hooks are cylindrical with inner and outer diameters of 30 Å and 180 Å, respectively. In contrast to the filament, each monomer of the hook, FlgE, has only three domains D1, D2, and D3, none of which protrudes from its surface, which is instead demarcated by a series of deep grooves, similar to the thread of a screw. However, the general helical nature of the hook and filament are similar.

The differential mechanical properties, such as Young's modulus E and shear modulus G, of the hook and filament are essential to the function of the flagellum and are directly linked to structural differences between the two. They have been examined using a variety of experimental methods, ranging from quasielastic scattering of laser light to optical tweezers (Table 1) (Berg, 1976; Block et al., 1989, 1991; Fujime et al., 1972; Hoshikawa, 1983; Hoshikawa and Kamiya, 1985; Powers, 2002; Trachtenberg and Hammel, 1992). The measured Young's modulus E and shear modulus G of the filament are in the range of 1010–1012 and 1011–1012 dyn/cm2, respectively. The shear modulus G of the hook was also determined to be 108 dyn/cm2. These values suggested the filament to be orders of magnitude stiffer than the hook. Specifically, Block and colleagues (Block et al., 1989, 1991) determined that the torsional/twisting compliance of the flagellum resides mainly in the hook, leading them to speculate that this compliance could allow multiple filaments to bundle in parallel and rotate in phase (Fig. 1 C). The differential moduli of the filament and hook provide an ingenious mechanism that is the key to unified motion in these bacteria. This motion would not be possible if the entire flagellum were composed of only one protein with an identical set of mechanical properties.

TABLE 1.

Mechanical properties of flagellar hook and filament determined by various methods

Filament
Hook
Author Year E (dyn/cm2) G (dyn/cm2) E (dyn/cm2) G (dyn/cm2)
Fujime 1972 1011 – – –
Fujime* 1972 1010 – – –
Hoshikawa 1985 – 1011–1012 – –
Block 1991 – – – 108
Trachtenberg 1992 1011–1012 – – –
Flynn† 2004 – – 106–107 –
Open in a new tab
*

Recalculated by Hoshikawa and Kamiya (1985) based on updated filament dimensions.

†

Theoretical value calculated by QEDM in this work.

The field of mechanics defines stiffness as a property that specifies the resistance of a structure to deformation under a given load. Flexural and torsional stiffness gauge the resistance of a structure to bending and twisting, respectively (Etnier, 2001; Niklas, 1991; Roark, 1989; Vogel, 1992). Flexural stiffness, or flexural rigidity, is given by EI, where E is Young's modulus and I is the second moment of inertia. Torsional stiffness, or torsional rigidity, is given by GJ, where G is the shear modulus, sometimes denoted as μ, and J is the polar second moment of inertia. I and J describe the cross-sectional area of a structure, and are influenced by its size and shape (Feynman et al., 1964). A standard means to compare the relative resistance of a structure to bending versus twisting is to employ the dimensionless “twist/bend ratio,” given by EI/GJ (Niklas, 1991; Vogel, 1992). EI/GJ ratios >1.0 are indicative of structures that twist relatively more easily than they bend, whereas values <1.0 typify structures that prefer to bend rather than twist. For example, a solid steel circular cylinder has a value of ∼1.3 (Vogel, 1992).

In this article we employ a new computational method, the quantized elastic deformational model (QEDM) (Ming et al., 2002a; Tama et al., 2002), to calculate the dimensionless twist/bend ratio of both the filament and hook, thereby providing a quantitative means to compare their stiffness. QEDM is able to extract motional and mechanical data from low-resolution protein structures, such as electron density maps. The protein is modeled as an elastic object and the mass density distribution is equated to the electron density distribution of the protein. Here, QEDM is used to determine the vibrational normal modes of ∼1000-Å-long electron density map sections of S. typhimurium filament and hook. The eigenvalues of the first bending and twisting modes of a structure are directly related to the flexural and torsional stiffness, respectively (see Methods) (Meirovitch, 2001).

RESULTS

QEDM analysis of hook and filament

Electron density maps of S. typhimurium hook (D. Thomas, T. Shaikh, and D. DeRosier, private communications) and filament (Mimori et al., 1995) ∼1000 Å in length at resolutions of 10 Å and 9 Å, respectively, were discretized into 8000 Voronoi cells. QEDM analysis was then performed for the hook and filament at several cutoff distances, rc, between 35 and 55 Å (see Table 2 and Methods). These cutoffs are larger than the 13-Å cutoff that is typically employed in QEDM, due to the enormous size of the filament and hook, and the coarse-grained nature of the model (Beuron et al., 2003; Doruker et al., 2002; Kong et al., 2003; Ming et al., 2002b). This cutoff determines the number of interacting “pairs” in the system and hence the resulting eigenvalues of the calculated modes. An array of cutoffs was used for each structure because the cutoff employed for one structure cannot be directly equated to that of another (e.g., a cutoff of 45 Å in the hook does not correlate with a 45-Å cutoff in the filament), as a result of the inherent difference of density distribution between the two structures (see “Radial distributions of the hook and filament”). The first six eigenvalues calculated via QEDM were found to have magnitudes of zero, when cutoffs in this range were employed. Similarly, the first six frequencies of a standard normal mode analysis are also zero, and represent full-body translations and rotations about the x, y, and z axes. Consequently, we can assume that the cutoff range is accurate.

TABLE 2.

Twist/bend ratios (EI/GJ) calculated by QEDM

Filament
Hook
Eigenvalues
Eigenvalues
QEDM cutoff (Å) Mode 7 Mode 9 EI/GJ Mode 7 Mode 9 EI/GJ
35 1.177 × 10−3 TIP effect* – 1.074 × 10−3 6.728 × 10−3 0.0378
40 2.376 × 10−3 1.346 × 10−2 0.0418 3.406 × 10−3 1.770 × 10−2 0.0455
45 4.511 × 10−3 2.516 × 10−2 0.0424 9.004 × 10−3 4.056 × 10−2 0.0525
50 8.356 × 10−3 4.470 × 10−2 0.0442 2.003 × 10−2 8.167 × 10−2 0.0580
55 1.524 × 10−2 7.565 × 10−2 0.0477 3.504 × 10−2 1.331 × 10−1 0.0622
Average – – 0.0440 – – 0.0512
Open in a new tab
*

Ma (2004)

Computed versus experimental twist/bend ratios

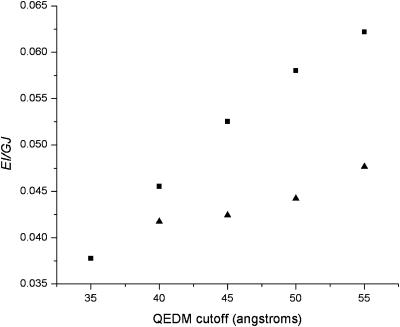
The eigenvalues of the first bending (mode 7) and twisting (mode 9) modes from QEDM analysis were used to compute the dimensionless twist/bend ratios (EI/GJ) of the hook and filament according to Eq. 12 (see Methods). The first bending and twisting modes were determined by visualizing the motions using Quanta (www.msi.com). The average values of QEDM-computed twist/bend ratios of the hook and filament are 0.0512 and 0.0440, respectively (Table 2 and Fig. 3). Such low values of twist/bend ratios signify that both structures bend more readily than they twist (i.e., EI is much smaller than GJ in both hook and filament). Consequently, the twist/bend ratios alone provided no striking information about the relative stiffness of the two structures, and must be analyzed in the context of experimental results.

FIGURE 3.

FIGURE 3

Open in a new tab

Plot of QEDM-calculated twist/bend ratios (EI/GJ) versus the range of QEDM cutoffs employed for the flagellar filament (▴ data points) and hook (▪ data points). The low values of EI/GJ signify that both structures bend more readily than they twist. The differential convergence rate of the ratios of the two structures is due to their inherent differences in density distributions (see Fig. 4).

For the filament, a range of experimentally determined E and G values are available in the literature (Table 1). Using these values, the twist/bend ratios of the filament can be obtained by dividing the experimental E and G filament values in Table 1, then multiplying by a factor of 0.5 to account for I/J. 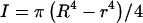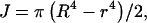The cross-sectional equations for I and J differ only by a factor of two in the denominator for the hollow cylindrical structures of both hook and filament, Inline graphic and Inline graphic where R and r represent the outer and inner radii, respectively (Roark, 1989). This yielded a range of 0.005–5.00 for filament twist/bend ratios. Note that these ratios cover three orders of magnitude due to the difficulty involved in accurately measuring the mechanical properties of biological structures at the nanometer level. The QEDM-obtained filament twist/bend ratios listed in Table 2 fall within the range of experimentally determined filament twist/bend ratios (0.005–5.00), thus supporting the computational method employed in this work.

In contrast, an experimentally determined hook twist/bend ratio could not be obtained because Young's modulus E of the hook has never been directly determined in experiments. However, Block and colleagues did obtain an experimental value of the hook shear modulus G, 108 dyn/cm2 (Block et al., 1991). If the maximum and minimum values of the QEDM-computed hook twist/bend ratios from Table 2 are employed in conjunction with Block's value of the shear modulus G above, it is trivial to calculate a theoretical Young's modulus E for the hook, which is found to be on the order of 106–107 dyn/cm2. This calculated value is several orders of magnitude smaller than the lowest experimentally determined Young's modulus for the filament (Table 1).

Radial distributions of the hook and filament

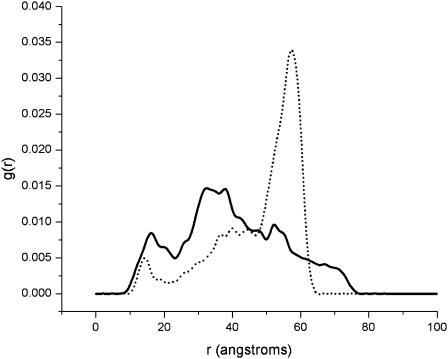
An important issue that must be addressed is the rate of convergence of the QEDM-calculated twist/bend ratios for the hook and filament. It appears that the ratios for the filament converged slightly quicker over the range of QEDM cutoff distances than for the hook (Fig. 3). This differential convergence rate of the ratios of the two structures is believed to be the direct result of their inherently different density distributions. The radial distribution function, g(r), for each structure was calculated and plotted in Fig. 4. QEDM relies on a set of finite Voronoi cells to represent the original density map (see Methods); thus the radial distributions computed are not exactly identical to those of the initial density maps (see Fig. 4 in Mimori et al., 1995 for the filament), but the general features of the curves are similar. A comparison of the radial distribution curves of the hook and filament revealed that the density for the filament is evenly dispersed over two peaks (domains D0, D1, and D2) lying in a radial range of 10–50 Å, whereas that of the hook is clustered primarily around a radial distance of 55 Å (Fig. 4). The net effect of these differences is that the filament has a more densely packed, rigid core than the hook, thus imparting a higher degree of stiffness to the filament. The more evenly distributed density of the core region of the filament also accounts for the quicker convergence of the twist/bend ratios for the filament over the range of QEDM cutoff distances as seen in Fig. 3.

FIGURE 4.

FIGURE 4

Open in a new tab

Plot of radial distribution function (g(r)) versus radial distance for the filament (solid line) and hook (dotted line). The density of the filament is evenly dispersed over two peaks (domains D0, D1, and D2), whereas that of the hook is clustered primarily around a radial distance of 55 Å. Consequently, the filament has a more densely packed, rigid core than the hook, imparting it with a higher degree of stiffness.

CONCLUDING DISCUSSION

The dimensionless twist/bend ratios (EI/GJ) for both the hook and filament were calculated from the eigenvalues of the QEDM-obtained bending and twisting modes at several cutoff distances, over a range of 35–55 Å (Table 2). Primary inspection of these ratios, an average of 0.0440 for the filament and 0.0512 for the hook, implies that in each of these structures bending is favored over twisting (since EI/GJ < 1.0). However, it is important to realize that this ratio does not rule out the possibility that one structure is far stiffer in both bending and twisting than a comparative structure, thereby yielding twist/bend ratios of similar magnitudes. This is the likely scenario in the current work, where the filament is stiffer than the hook in both bending and twisting. The filament twist/bend ratios calculated by QEDM fall within the range of twist/bend ratios (0.005–5.00) computed from experimentally measured Young's modulus E and shear modulus G values. In contrast, an experimental value of Young's modulus for the hook has not yet been determined. However, employing the twist/bend ratios of the hook calculated by QEDM and the experimental hook shear modulus found by Block and colleagues (Block et al., 1991), allowed us to propose a Young's modulus between 106 and 107 dyn/cm2 for the hook. This number is orders of magnitude smaller than the values of the experimental Young's modulus of the filament (Table 1), hence in agreement with empirical evidence linking compliance in the flagellum mainly to the hook (Block et al., 1989, 1991). Consequently, this computational analysis provides quantitative support to experimental evidence that the filament is indeed more rigid than the hook. The dual flexibility of the hook in both bending and torsion allows it to serve as the ideal universal joint, transmitting the rotary motion upwards to the stiffer filament while allowing adjacent filaments to bundle and rotate off-axis, resulting in unified filament motion.

In conclusion, the theoretical nature of Young's modulus calculated for the hook in this study should be stressed. Although the QEDM-obtained hook twist/bend ratios did not converge as quickly as they did for the filament, it is likely due to the inherent difference of density distribution of the two structures, rather than a simulation artifact. The theoretical value of Young's modulus should serve as a guide for further experimental studies.

METHODS

Quantized elastic deformational model

QEDM is a method capable of determining the conformational flexibility of a biological molecule without the atomic structure or coordinates (Ming et al., 2002a; Tama et al., 2002). QEDM draws on two techniques: vector quantization (Gray, 1984; Makhoul et al., 1985) and the anisotropic network model (ANM) (Atilgan et al., 2001; Tirion, 1996). Vector quantization discretizes any three-dimensional electron density map into a set of finite Voronoi cells, which portray the shape and density distribution of the initial map. The deformational motions of the molecule are determined by ANM, which assumes that the dynamics of a folded protein can be approximated as an elastic network formed by the Cα atoms of the backbone. ANM is essentially a normal mode analysis (Brooks et al., 1995) that utilizes a simplified potential function given by

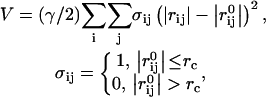graphic file with name M3.gif (1)

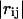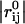where γ represents the strength of the potential, and is assumed to be the equivalent for all pairs, rc is the cutoff distance, and Inline graphic and Inline graphic are the instantaneous and equilibrium values of the pairwise distance between the ith and jth Cα atoms, respectively (Tirion, 1996). σij is the Heaviside step function, which details the cutoff effect of the interaction (Hildebrand, 1976). Comparable to a standard normal mode analysis, the direction of motion in each deformational mode is given by a 3N-dimensional eigenvector calculated through diagonalization of the second derivative Hessian matrix of the total potential function (Brooks et al., 1995). For nonlinear, three-dimensional systems there are 3N-6 modes, because the first six modes are zero-frequency modes.

QEDM was used to analyze both the hook and filament. A 10-Å resolution electron density map of a 960-Å-long section of S. typhimurium hook was provided by D. Thomas, T. Shaikh, and D. DeRosier, private communications). The 9-Å resolution map of a 303-Å-long section of filament, also from S. typhimurium, was obtained from Koji Yonekura and Keiichi Namba (Mimori et al., 1995). A 1000-Å section of filament was constructed from the 303-Å section using the programs EMAN (version 1.2; ncmi.bcm.tmc.edu) and IRIS Explorer (release 5.0; www.nag.co.uk). In both cases, 8000 Voronoi cells were used to discretize the density. The number of Voronoi cells can be set to either correspond with the number of Cα atoms in the structure or be much less than this number, yielding a coarse-grained model, as is the case in this work (Doruker et al., 2002; Ming et al., 2002a,b). Additional calculations were performed on densities discretized into 4000 Voronoi cells (data not shown). The resulting modes were identical to those calculated for the 8000 Voronoi cell case, indicating that resolution was not a factor. γ was set to 1.0 for all of the simulations because its value does not affect the distribution of the motions (Atilgan et al., 2001; Ming et al., 2002a,b). Solving for the eigenvalues and eigenvectors in each simulation required ∼100 h of computing time on a Silicon Graphics Iris Indigo (Mountain View, CA).

Relating frequency of vibration to flexural and torsional rigidity

The equation for vibration of a beam, of length L, in bending is given by

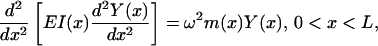graphic file with name M6.gif (2)

where EI(x) is the flexural stiffness/rigidity, in which E is Young's modulus and I(x) the cross-sectional area moment of inertia, Y(x) represents the bending profile, ω is the vibration frequency, and m(x) is the mass per unit length (Meirovitch, 2001). For a uniform beam, EI(x) and m(x) are considered constant and Eq. 2 reduces to

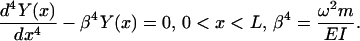graphic file with name M7.gif (3)

The solution of this fourth order differential equation is

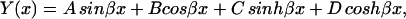graphic file with name M8.gif (4)

where A, B, C, and D are constants to be evaluated dependent upon the boundary conditions of the system (Meirovitch, 2001). In the case of a beam with free ends, the boundary conditions are 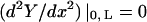Inline graphic (no bending moment at the ends of the beam) and 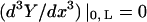Inline graphic (no shearing force at the ends of the beam), yielding the first relationship of interest

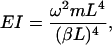graphic file with name M11.gif (5)

where (βL) = 1.506π for the first bending mode.

Similarly, the equation for torsion in a shaft, of length L, is given by

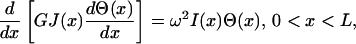graphic file with name M12.gif (6)

where GJ(x) is the torsional stiffness/rigidity, in which G is the shear modulus and J(x) the area moment of inertia of the shaft, Θ(x) is the twist angle, and ω is the vibration frequency (Meirovitch, 2001). For a uniform shaft, GJ(x) and I(x) are taken to be constant, rendering the following equation

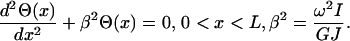graphic file with name M13.gif (7)

The solution to this second order differential equation is

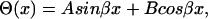graphic file with name M14.gif (8)

where A and B are constants that depend on given boundary conditions (Meirovitch, 2001). In the case of a shaft with free ends the boundary conditions are 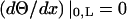Inline graphic (no torque at the ends of the shaft). Leading to the second relationship of interest,

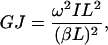graphic file with name M16.gif (9)

where (βL) = π for the first torsion mode. For a solid rod 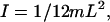Inline graphic where m and L are the total mass and length of the rod, respectively (Feynman et al., 1964). Substituting the values for I and βL into Eq. 9 yields

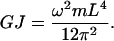graphic file with name M18.gif (10)

The last equality that must be considered is the relationship between frequencies and eigenvalues. QEDM outputs a set of displacement coordinates and eigenvalues, λ, for each calculated mode, 1–N. From ANM, 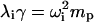Inline graphic (Atilgan et al., 2001), where λi is the eigenvalue of the ith mode, γ is the strength of the potential, ωi is the frequency of the ith mode, and mp is the point mass. Total mass, m, in Eqs. 5 and 10 is equal to the product of point mass, mp, times the number of points, np (i.e., Voronoi cells for QEDM). Substituting these quantities into Eqs. 5 and 10 yields

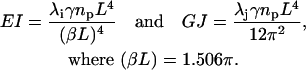graphic file with name M20.gif (11)

Dimensionless twist/bend ratio

Taking the ratio of EI/GJ from Eq. 11 generates the desired relationship

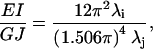graphic file with name M21.gif (12)

in which λi and λj represent the ith and jth eigenvalues for the first bending (mode 7) and torsional (mode 9) modes, respectively.

Acknowledgments

The authors would like to thank D. Thomas, T. Shaikh, D. DeRosier, K. Yonekura, and K. Namba for providing the electron density maps of the hook and filament, M. Baker for assistance with EMAN, and D. Ming and Y. Kong for helpful discussions.

This research was supported in part by grants to J.M. from the American Heart Association (AHA-TX0160107Y), the Robert A. Welch Foundation (Q-1512), the National Institutes of Health (R01-GM067801), and a National Science Foundation Career Award (MCB-0237796). J.M. is a recipient of the Award for Distinguished Young Scholars Abroad from the National Natural Science Foundation of China.

References

  1. Abrahams, J. P., A. G. Leslie, R. Lutter, and J. E. Walker. 1994. Structure at 2.8 Å resolution of F1-ATPase from bovine heart mitochondria. Nature. 370:621–628. [DOI] [PubMed] [Google Scholar]
  2. Atilgan, A. R., S. R. Durell, R. L. Jernigan, M. C. Demirel, O. Keskin, and I. Bahar. 2001. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 80:505–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Berg, H. C. 1976. Does the flagellar rotary motor step? In Cell Motility. R. Goldman, T. Pollard, and J. Rosenbaum, editors. Cold Spring Harbor Laboratory, New York. 47–56.
  4. Berg, H. C., and R. A. Anderson. 1973. Bacteria swim by rotating their flagellar filaments. Nature. 245:380–382. [DOI] [PubMed] [Google Scholar]
  5. Berry, R. M., and J. P. Armitage. 1999. The bacterial flagella motor. Adv. Microb. Physiol. 41:291–337. [DOI] [PubMed] [Google Scholar]
  6. Beuron, F., T. C. Flynn, J. Ma, H. Kondo, X. Zhang, and P. S. Freemont. 2003. Motions and negative cooperativity between p97 domains revealed by cryo-electron microscopy and quantized elastic deformational model. J. Mol. Biol. 327:619–629. [DOI] [PubMed] [Google Scholar]
  7. Block, S. M., D. F. Blair, and H. C. Berg. 1989. Compliance of bacterial flagella measured with optical tweezers. Nature. 338:514–518. [DOI] [PubMed] [Google Scholar]
  8. Block, S. M., D. F. Blair, and H. C. Berg. 1991. Compliance of bacterial polyhooks measured with optical tweezers. Cytometry. 12:492–496. [DOI] [PubMed] [Google Scholar]
  9. Boyer, P. D. 1997. The ATP synthase: a splendid molecular machine. Annu. Rev. Biochem. 66:717–749. [DOI] [PubMed] [Google Scholar]
  10. Brooks, B. R., D. Janezic, and M. Karplus. 1995. Harmonic analysis of large systems. I. Methodology. J. Comput. Chem. 16:1522–1542. [Google Scholar]
  11. Doruker, P., R. L. Jernigan, and I. Bahar. 2002. Dynamics of large proteins through hierarchical levels of coarse-grained structures. J. Comput. Chem. 23:119–127. [DOI] [PubMed] [Google Scholar]
  12. Etnier, S. 2001. Flexural and torsional stiffness in multi-jointed biological beams. Biol. Bull. 200:1–8. [DOI] [PubMed] [Google Scholar]
  13. Feynman, R. P., R. B. Leighton, and M. Sands. 1964. The Feynman Lectures on Physics. Addison-Wesley, Reading, MA.
  14. Fujime, S., M. Maruyama, and S. Asakura. 1972. Flexural rigidity of bacterial flagella studied by quasielastic scattering of laser light. J. Mol. Biol. 68:347–359. [DOI] [PubMed] [Google Scholar]
  15. Glagolev, A. N., and V. P. Skulachev. 1978. The proton pump is a molecular engine of motile bacteria. Nature. 272:280–282. [DOI] [PubMed] [Google Scholar]
  16. Gray, R. M. 1984. Vector quantization. IEEE ASSP Mag. 1:4–29. [Google Scholar]
  17. Hildebrand, F. B. 1976. Advanced Calculus for Applications. Prentice-Hall, Inc., Englewood Cliffs, NJ.
  18. Hoshikawa, H. 1983. Elastic properties of bacterial flagellar filaments. I. Free rotation case. Biophys. Chem. 17:105–109. [DOI] [PubMed] [Google Scholar]
  19. Hoshikawa, H., and R. Kamiya. 1985. Elastic properties of bacterial flagellar filaments. II. Determination of the modulus of rigidity. Biophys. Chem. 22:159–166. [DOI] [PubMed] [Google Scholar]
  20. Kamiya, R., S. Asakura, K. Wakabayashi, and K. Namba. 1979. Transition of bacterial flagella from helical to straight forms with different subunit arrangements. J. Mol. Biol. 131:725–742. [DOI] [PubMed] [Google Scholar]
  21. Kong, Y., D. Ming, Y. Wu, J. K. Stoops, Z. H. Zhou, and J. Ma. 2003. Conformational flexibility of pyruvate dehydrogenase complexes: a computational analysis by quantized elastic deformational model. J. Mol. Biol. 330:129–135. [DOI] [PubMed] [Google Scholar]
  22. Larsen, S. H., J. Adler, J. J. Gargus, and R. W. Hogg. 1974. Chemomechanical coupling without ATP: the source of energy for motility and chemotaxis in bacteria. Proc. Natl. Acad. Sci. USA. 71:1239–1243. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Ma, J. 2004. New advances in normal mode analysis of supermolecular complexes and applications to structural refinement. Curr. Protein Pept. Sci. 5:119–123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Ma, J., T. C. Flynn, Q. Cui, A. G. Leslie, J. E. Walker, and M. Karplus. 2002. A dynamic analysis of the rotation mechanism for conformational change in F1-ATPase. Struct. 10:921–931. [DOI] [PubMed] [Google Scholar]
  25. Macnab, R. M., and M. K. Ornston. 1977. Normal-to-curly flagellar transitions and their role in bacterial tumbling. Stabilization of an alternative quaternary structure by mechanical force. J. Mol. Biol. 112:1–30. [DOI] [PubMed] [Google Scholar]
  26. Makhoul, J., S. Roucos, and H. Gish. 1985. Vector quantization in speech coding. Proc. IEEE 73:1551–1588. [Google Scholar]
  27. Manson, M. D., P. Tedesco, H. C. Berg, F. M. Harold, and C. Van der Drift. 1977. A protonmotive force drives bacterial flagella. Proc. Natl. Acad. Sci. USA. 74:3060–3064. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Meirovitch, L. 2001. Fundamentals of Vibrations. McGraw-Hill, New York.
  29. Mimori, Y., I. Yamashita, K. Murata, Y. Fujiyoshi, K. Yonekura, C. Toyoshima, and K. Namba. 1995. The structure of the R-type straight flagellar filament of Salmonella at 9 Å resolution by electron cryomicroscopy. J. Mol. Biol. 249:69–87. [DOI] [PubMed] [Google Scholar]
  30. Ming, D., Y. Kong, M. A. Lambert, Z. Huang, and J. Ma. 2002a. How to describe protein motion without amino acid sequence and atomic coordinates. Proc. Natl. Acad. Sci. USA. 99:8620–8625. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Ming, D., Y. Kong, S. J. Wakil, J. Brink, and J. Ma. 2002b. Domain movements in human fatty acid synthase by quantized elastic deformational model. Proc. Natl. Acad. Sci. USA. 99:7895–7899. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Morgan, D. G., R. M. Macnab, N. R. Francis, and D. J. DeRosier. 1993. Domain organization of the subunit of the Salmonella typhimurium flagellar hook. J. Mol. Biol. 229:79–84. [DOI] [PubMed] [Google Scholar]
  33. Morgan, D. G., C. Owen, L. A. Melanson, and D. J. DeRosier. 1995. Structure of bacterial flagellar filaments at 11 Å resolution: packing of the alpha-helices. J. Mol. Biol. 249:88–110. [DOI] [PubMed] [Google Scholar]
  34. Niklas, K. J. 1991. The elastic moduli and mechanics of Populus tremuloides (Salicaceae) petioles in bending and torsion. Am. J. Bot. 78:989–996. [Google Scholar]
  35. O'Brien, E. J., and P. M. Bennett. 1972. Structure of straight flagella from a mutant Salmonella. J. Mol. Biol. 70:133–152. [DOI] [PubMed] [Google Scholar]
  36. Powers, T. R. 2002. Role of body rotation in bacterial flagellar bundling. Phys. Rev. E. 65:040903. [DOI] [PubMed] [Google Scholar]
  37. Roark, R. J. 1989. Formulas for Stress and Strain. McGraw-Hill, Inc., New York.
  38. Samatey, F. A., K. Imada, S. Nagashima, F. Vonderviszt, T. Kumasaka, M. Yamamoto, and K. Namba. 2001. Structure of the bacterial flagellar protofilament and implications for a switch for supercoiling. Nature. 410:331–337. [DOI] [PubMed] [Google Scholar]
  39. Silverman, M., and M. Simon. 1974. Flagellar rotation and the mechanism of bacterial motility. Nature. 249:73–74. [DOI] [PubMed] [Google Scholar]
  40. Tama, F., W. Wriggers, and C. L. Brooks,, III. 2002. Exploring global distortions of biological macromolecules and assemblies from low-resolution structural information and elastic network theory. J. Mol. Biol. 321:297–305. [DOI] [PubMed] [Google Scholar]
  41. Tirion, M. M. 1996. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys. Rev. Lett. 77:1905–1908. [DOI] [PubMed] [Google Scholar]
  42. Trachtenberg, S., and I. Hammel. 1992. The rigidity of bacterial flagellar filaments and its relation to filament polymorphism. J. Struct. Biol. 109:18–27. [DOI] [PubMed] [Google Scholar]
  43. Vogel, S. 1992. Twist-to-bend ratios and cross-sectional shapes of petioles and stems. J. Exp. Bot. 43:1527–1532. [Google Scholar]
  44. Yonekura, K., S. Maki-Yonekura, and K. Namba. 2003. Complete atomic model of the bacterial flagellar filament by electron cryomicroscopy. Nature. 424:643–650. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES