Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 May;86(5):3260–3268. doi: 10.1016/S0006-3495(04)74374-X

Tissue Electroporation: Quantification and Analysis of Heterogeneous Transport in Multicellular Environments

Paul J Canatella 1, Matthew M Black 1, David M Bonnichsen 1, Conor McKenna 1, Mark R Prausnitz 1
PMCID: PMC1304191  PMID: 15111439

Abstract

Although electroporation is gaining increased attention as a technology to enhance clinical chemotherapy and gene therapy of tissues, direct measurements of electroporation-mediated transport in multicellular environments are lacking. In this study, we used multicellular tumor spheroids of DU145 prostate cancer cells as a model tissue to measure the levels and distribution of molecular uptake in a multicellular environment as a function of electrical and other parameters. These measurements, and subsequent analysis, were used to test the hypothesis that cells in a multicellular environment respond to electroporation in a heterogeneous manner that differs from isolated cells in suspension due to differences in cell state, local solute concentration, and local electric field. In support of the hypothesis, molecular uptake was consistently lower for cells within spheroids than cells in dilute suspension and was spatially heterogeneous, with progressively less uptake observed for cells located deeper within spheroid interiors. Reduced uptake and heterogeneity can be explained quantitatively by accounting for the effects of cell size on transmembrane voltage and cell volume, limited extracellular solute reservoir, heterogeneous field strength due to influence of neighboring cells, and diffusional lag times.

INTRODUCTION

Electroporation transiently disrupts cell membranes and thereby permits intracellular delivery of molecules. This phenomenon has been widely exploited as a means to load cells with exogenous molecules, such as DNA (Chang et al., 1992; Nickoloff, 1995). More recently, electroporation of tissue has been demonstrated for applications such as targeted delivery of chemotherapeutics to tumors, efficient gene transfection of cells in vivo, and increased skin permeability for transdermal drug delivery (Jaroszeski et al., 1999, 2000; Prausnitz, 1999; Mir, 2001).

Although these applications of tissue electroporation are compelling, success has been limited by the lack of understanding the differences between electroporation of suspended cells and intact tissues. In simple systems, such as isolated cells in suspension, molecular transport into cells has been shown to generally increase at larger transmembrane voltages, longer pulses, and larger numbers of pulses above an electroporation threshold (Chang et al., 1992; Nickoloff, 1995; Canatella et al., 2001).

A few decades of study have provided rigorous theoretical models of electroporation at the membrane level (Weaver and Chizmadzhev, 1996) and largely phenomenological understanding at the cellular level (Teissie et al., 1999), but relatively little mechanistic work has been done at the tissue level. Most studies involving living tissue have emphasized endpoint measurements downstream from the electroporation event, such as levels of gene expression or suppression of tumor growth. It is therefore the goal of this study to provide direct measurements of electroporation-mediated transport in multicellular tissue-like environments and to identify mechanistic differences between transport in these environments and isolated cell suspensions.

Because there are different physical barriers and heterogeneous geometries within tissue, transport in multicellular environments is expected to have unique characteristics. We therefore propose to test the hypothesis that cells in a multicellular environment respond to electroporation in a heterogeneous manner that differs from isolated cells in suspension due to differences in cell state, local solute concentration, and local electric field. As a model tissue, we have used multicellular tumor spheroids, which contain densely and heterogeneously packed cells surrounded by extracellular matrix often used to mimic microregions within tumors (Sutherland, 1988).

EXPERIMENTAL METHODS

To study electroporation in a multicellular environment, we prepared multicellular spheroids of DU145 prostate cancer cells in siliconized (Sigmacote SL-2; Sigma, St. Louis, MO) spinner culture flasks (F7609; Techne, Cambridge, UK) (Essand et al., 1995) in a 5% CO2 environment in RPMI-1640 medium containing 10% (v/v) heat-inactivated fetal bovine serum, 100 units/ml penicillin, 100 μg/ml streptomycin, and 250 μg/ml amphotericin B (Sigma). Cultures were magnetically stirred at 50 rpm during growth. Beginning 48 h after initiating a culture, the media was partially changed three times per week to replenish nutrients.

Spheroids of different size ranges were separated by size using a series of gravity-fed nylon meshes (Small Parts Inc., Miami Lakes, FL), centrifuged (1000 × g, 6 min; Beckman Coulter, Fullerton, CA), washed using phosphate-buffered saline (PBS), suspended in RPMI-1640 with HEPES (Cellgro, Mediatech, Herndon, VA) and 10−4 M calcein (a membrane-impermeable fluorescent green dye; Molecular Probes, Eugene, OR) and incubated for 10 min before electroporation, unless otherwise noted.

Spheroid suspensions (0.8 ml) were placed in 4-mm gap cuvettes (Genetronics, San Diego, CA), exposed to exponential-decay (BTX, Genetronics) or rectangular-wave pulses (CytoPulse Sciences, Columbia, MD) (Canatella et al., 2001) and then incubated at 37°C for 10 min before washing with PBS (1000 × g, 3 min; Eppendorf, Hamburg, Germany). For flow cytometry analysis, which requires isolated cells, spheroids were dissociated using two different methods that retain information about the radial position previously occupied by dissociated cells within the spheroid.

One method to identify the radial position previously occupied by a dissociated cell involves radially dependent staining with a diffusion-limited dye, as described by Durand (1982). After a 10-s incubation of intact spheroids with 10 μM of a blue fluorescent dye (i.e., Hoechst 33342 or calcein blue-AM, Molecular Probes) followed by centrifuging three times in PBS to wash (1000 × g, 3 min), spheroids were completely dissociated in dye-free media containing 0.25% trypsin at 37°C for 10 min. This caused bright labeling of cells on the spheroid's external surface and progressively less intense labeling of cells located deeper inward. Because this method provides efficient sample recovery, it was used in most experiments in this study.

Another method to identify the radial position of cells involves sequential removal of concentric cell layers and collection of these layers as separate fractions. Using a selective automated dissociation apparatus described by Freyer and Schor (1989) in which trypsin “peels” off the outermost cell layer of spheroids, dissociated cells were removed through a filtered flow system and collected over time in fractions according to radial position. In our apparatus, spheroids were placed in a flask stirred at 140 rpm, maintained at 37°C, and continuously fed with 0.25% trypsin at a rate of 10 ml/min (Manostat, Barrington, IL). Effluent from the flask was collected as 30-ml fractions in 50-ml conical tubes prefilled with 20 ml of culture medium to inactivate the trypsin in collected samples. Because sample recovery is inefficient using this process, it was used in this study only when physical separation of cells dissociated from different radial locations was required.

After cells were electroporated and dissociated (by one of the two methods listed above), they were centrifuged in PBS three times (1000 × g, 3 min) and resuspended in PBS with 10 μg/ml of propidium iodide (a fluorescent red nonviable cell stain, Molecular Probes) to label nonviable cells. Flow cytometry (FACSVantage SE; Becton Dickinson, Franklin Lakes, NJ) was then used to determine the number of molecules in each of at least 30,000 cells per sample, as described by Canatella et al. (2001). Briefly, using 488-nm excitation (Innova Enterprise II; Coherent, Palo Alto, CA), light scatter and red fluorescence from propidium iodide (677-nm longpass filter) were used to identify viable cells, and green fluorescence intensity (530/30-nm bandpass filter) was used to quantify the number of internalized calcein molecules with the aid of calibration beads (Flow Cytometry Standards, Fishers, IN). As described by Durand (1983), cell position within the spheroid was determined by measuring blue fluorescence intensity (excitation at 351 nm and emission using a 424/44-nm bandpass filter), with greatest blue fluorescence intensity associated with cells from the spheroid periphery.

RESULTS AND DISCUSSION

Cells in multicellular spheroids behave differently from isolated cells

This study tested the hypothesis that cells in a multicellular environment respond to electroporation in a heterogeneous manner that differs from isolated cells in suspension. We first used flow cytometry to assess whether uptake of a fluorescent marker compound (calcein) into multicellular spheroids differed from that in suspended cells, and then provide additional analysis to explain observed differences.

Reduced uptake for cells in multicellular spheroids

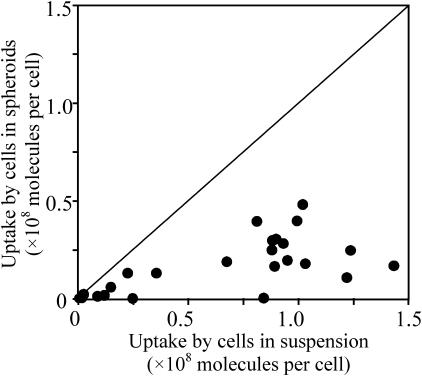
To demonstrate the effect of electroporating cells in a multicellular environment, Fig. 1 shows the number of calcein molecules taken up by average individual cells in spheroids versus the average number taken up by isolated cells under the same electroporation conditions. In these experiments, the electroporation condition varied from 0.1 to 0.9 kV/cm, 1–40-ms pulse length, and 1–4 pulses (20-s spacing). Over the broad range of conditions tested, cells within spheroids consistently took up fewer molecules.

FIGURE 1.

FIGURE 1

Open in a new tab

Comparison of electroporation-mediated uptake of calcein molecules in multicellular spheroids versus isolated cells in suspensions at the same bulk electroporation conditions. Spheroid uptake responses were less than predicted values for single cells. Uptake by cells within spheroids was determined using 400-μm diameter spheroids. Uptake by cells in suspension was determined using the validated empirical correlation described by Canatella and Prausnitz (2001). Uptake by cells within spheroids was consistently less than cells in suspension. Data points each represent the average uptake by 20,000 cells from a single sample (n = 1), each at a different electroporation condition.

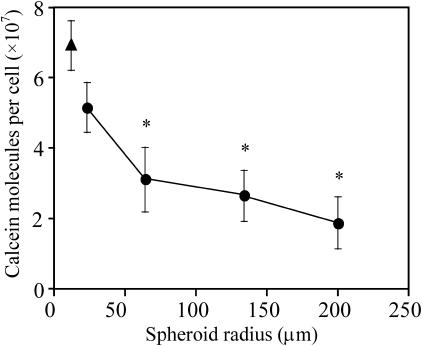
Different sized spheroids were also electroporated to further demonstrate the influence of a multicellular environment on electroporation's effects. As shown in Fig. 2, the cells in the spheroids generally took up fewer molecules than isolated cells (t-test, p < 0.05). Moreover, larger spheroids took up still fewer molecules than smaller spheroids (ANOVA, p = 0.06). This provides further evidence that a multicellular environment decreases the effects of electroporation and that the presence of more cells around a given cell (i.e., as in larger spheroids) decreases the effect even further.

FIGURE 2.

FIGURE 2

Open in a new tab

Effect of spheroid radius on molecular uptake. Single cells (▴) or multicellular spheroids of different sizes (•) were electroporated with a single, 38-ms exponential-decay pulse at 0.45 kV/cm bulk field strength. The asterisks indicate that uptake from the three largest spheroid sizes were significantly less than for single cells (t-test, p < 0.05). Average is mean ± SE; n ≥ 3.

Heterogeneous uptake as a function of radial depth within spheroids

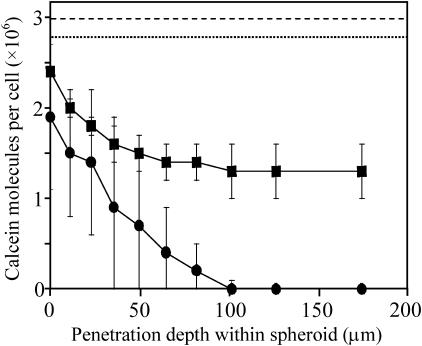
We next sought to determine if the reduced effects of electroporation are seen uniformly throughout the spheroid or if there might be spatial heterogeneity. Fig. 3 shows representative results for how uptake of calcein depends on cell location within a spheroid. For the two electroporation conditions shown, there is a strong radial dependence of uptake, with less uptake seen for cells located deeper within a spheroid's interior (t-test, interior versus periphery, p < 0.05). The dashed lines at the top of Fig. 3 indicate levels of uptake observed for isolated cells electroporated under the same two conditions. Combined, these data show that at all positions within the multicellular spheroid, uptake was lower than in isolated cells (t-test, p < 0.05).

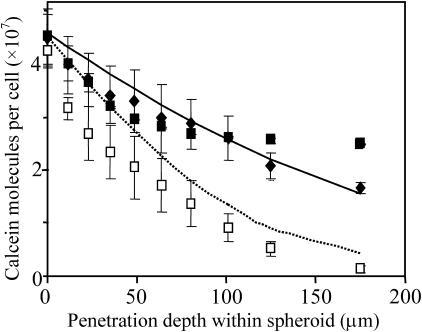
FIGURE 3.

FIGURE 3

Open in a new tab

Effect of radial position of cells within spheroids on molecular uptake using two different electroporation protocols that cause approximately the same level of uptake in isolated cells in suspension. Electroporation conditions used were one exponential-decay pulse of 7 ms, 0.5 kV/cm (•, dotted line) and four rectangle-wave pulses of 0.05 ms, 2.5 kV/cm, 20-s interpulse spacing (▪, dashed line). The points represent experimental data from spheroids that were 200 μm in radius. The dashed lines represent uptake levels for isolated cells in suspension, based on the correlation described by Canatella and Prausnitz (2001). Average is mean ± SE; n ≥ 3.

The electroporation conditions shown in Fig. 3 were selected because they cause similar levels of uptake in isolated cells, but cause very different responses in spheroids. The first condition (▪) used four short (0.05 ms) pulses of strong field strength (2.5 kV/cm) with 20-s spacings and achieved significant levels of uptake throughout the spheroid, although interior cells took up fewer molecules. The second condition (•) used a single long (7 ms) pulse of weaker field strength (0.5 kV/cm). Interestingly, uptake in spheroids electroporated under the second condition was generally lower and cells located >50-μm deep within the interior exhibited no significant molecular uptake (t-test, p > 0.1).

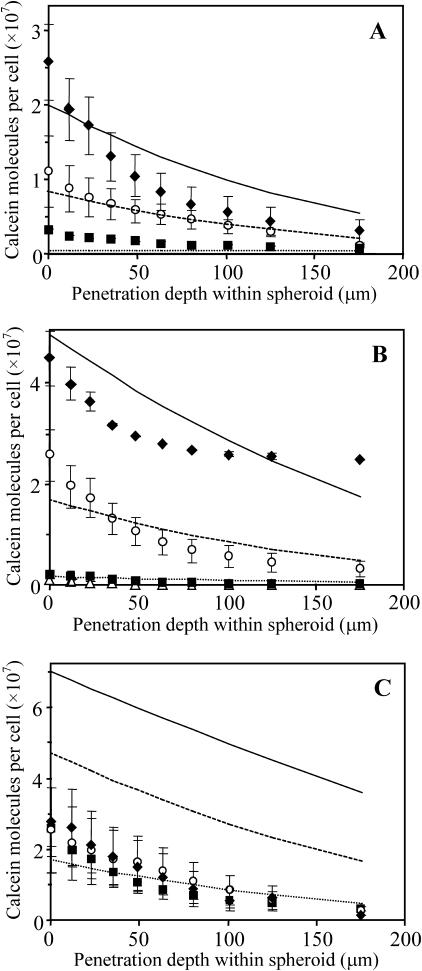
A more comprehensive study of the effects of radial position and electroporation parameters is shown in Fig. 4. A range of different field strengths (Fig. 4 A, 0.2–0.5 kV/cm), pulse lengths (Fig. 4 B, 1–40 ms), and numbers of pulses (Fig. 4 C, 1–4, 20 s spacing) were studied. Similar to electroporation of isolated cells (Canatella, et al, 2001; Canatella and Prausnitz, 2001), molecular uptake into spheroid cells increased with increasing field strength and pulse length at each penetration depth (ANOVA, p < 0.01). However, the number of pulses did not have a significant effect over the range studied (ANOVA, p > 0.1), which differs from observations made in isolated cells (Canatella, et al, 2001; Canatella and Prausnitz, 2001).

FIGURE 4.

FIGURE 4

Open in a new tab

Effect of field strength, pulse length, and number of pulses on electroporation-mediated uptake as a function of radial position of cells within multicellular spheroids. Conditions used were (A) one 22-ms pulse with field strengths of 0.2 (▪), 0.4 (○), and 0.5 (♦) kV/cm; (B) one 0.5-kV/cm pulse with pulse lengths of 1 (Δ), 7 (▪), 20 (○), and 40 (♦) ms; and (C) one (▪), two (○), and four (♦) 20-ms, 0.5-kV/cm pulses. The points represent experimental data from spheroids. The lines represent predictions from the model developed in this study to account for changes in cell state (Eq. 1), local solute concentration (Eqs. 2–6), and local electric field (Eqs. 7–9) within spheroids (see text). Average is mean ± SE; n ≥ 3.

Why cells in multicellular spheroids behave differently from isolated cells

Our data support the first part of the proposed hypothesis: that cells in a multicellular environment respond to electroporation in a heterogeneous manner that differs from isolated cells in suspension. This leads us to question why this difference exists. Characteristic features that require explanation are observations that 1), the multicellular environment reduces molecular uptake; 2), these effects are enhanced even further by location deeper within spheroids; and 3), cells in spheroids exhibit a different dependence on electrical conditions than isolated cells. We propose that these observations can be explained by differences in cell state, local solute concentration, and local electric field within multicellular environments. These are critical parameters because they address the solute being transported, the cell into which transport occurs, and the electric field that mediates the transport.

Effect of cell state

Differences between cells within multicellular spheroids and those in isolated suspension may be due in part to differences between the cells themselves. To decouple effects of a cell being located in a multicellular environment at the time of electroporation and the effects of a cell having been grown in that environment before electroporation, we physically dissociated spheroids either before or after electroporation.

Fig. 5 shows these results. A control experiment involving electroporation of a suspension of isolated cells is shown in Fig. 5 A. Under the same bulk electroporation conditions, intact spheroids were electroporated and subsequently dissociated and separated into cells from the spheroid periphery (Fig. 5 B) and interior (Fig. 5 C). As expected, there is a radial dependence of uptake, where interior cells have less uptake than those from the periphery. In this experiment, uptake by peripheral cells was not statistically different from isolated cells (t-test, p > 0.10).

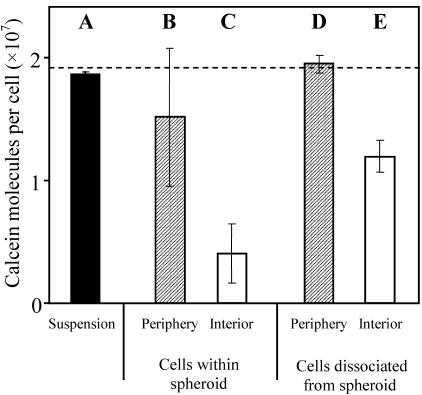
FIGURE 5.

FIGURE 5

Open in a new tab

Effect on uptake caused by the multicellular environment within a spheroid before and during electroporation. (A) Isolated cells electroporated in suspension. Intact spheroids electroporated and analyzed as cells from the periphery (B) and interior (C) of the spheroid. Cells harvested from the periphery (D) or interior (E) of dissociated spheroids and electroporated as isolated cells in suspension. One 19-ms exponential-decay pulse of 0.46 kV/cm was used. Average is mean ± SE; n = 3.

As a third experiment, spheroids were initially dissociated and separated into peripheral and interior cells, and subsequently electroporated as isolated cell suspensions. In this way, cells grown in a multicellular environment could be electroporated as isolated cells. Again, cells originally from the periphery (Fig. 5 D) were indistinguishable from control cells (t-test, p > 0.1). However, cells originally from the interior (Fig. 5 E) had significantly less uptake than cells originally from the periphery (Fig. 5 D) (t-test, p = 0.08) and from cells grown in isolated suspension (Fig. 5 A) (t-test, p < 0.1). This indicates that because the cells had been grown deep within a multicellular environment, they responded to electroporation differently. There is also a difference between interior cells electroporated while still within a spheroid (Fig. 5 C) and those electroporated after being dissociated (Fig. 5 E) (t-test, p = 0.1), which suggests that a cell's presence within a multicellular environment during electroporation also affects molecular uptake.

The observation that interior cells behave differently, even after dissociation from spheroids, suggests a difference in cell state. It has been reported in other studies that cells from the interior of a spheroid can function differently from peripheral cells (Sutherland and Durand, 1984) and that interior cells can be as much as 30% smaller, probably due to reduced interior nutrient levels caused by long diffusional distances from the spheroid surface (Sutherland, 1988). To determine if interior cells from our spheroids were smaller, we examined flow cytometry forward scatter data and found that volumes of the most interior cells were only 54% of periphery cell volumes, following the common expectation that light scatter is proportional to cell volume (Bouvier et al., 2001; Shapiro, 2003) (data not shown). Therefore, interior cell radii were up to 19% smaller than peripheral cells (for a spherical cell shape, which was confirmed by confocal microscopy on intact and dissociated spheroids; data not shown). Assuming a linear relationship between cell radius and position within the spheroid (which is consistent with flow cytometry data), this observation can be expressed as

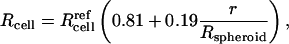graphic file with name M1.gif (1)

where Rcell is cell radius and 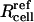Inline graphic is the reference radius of a “normal” cell (i.e., 11 μm; Canatella et al., 2001) and r is the radial position within a spheroid of radius Rspheroid. The consequences of this observation are discussed below.

Effects of local solute concentration

To provide additional insight, we considered that a multicellular environment might cause changes in the local solute (i.e., calcein) concentration surrounding interior versus peripheral cells. Because uptake by electroporation is known to depend directly on extracellular solute concentration (Chang et al., 1992; Neumann et al., 1989), this could be an important consideration.

A first possibility is that the extracellular concentration within spheroids could be time-dependent. Unlike isolated cell suspensions, where cells are typically added into a well-mixed solution, for spheroids there is a diffusional time lag for solutes to penetrate into their interior. Fig. 6 addresses this issue by electroporating spheroids 10 s, 10 min, or 30 min after initial incubation in calcein solution. For incubation times of 10 and 30 min, there was no difference in the uptake profiles (two-way ANOVA, p > 0.1). However, for a 10-s incubation, uptake was significantly reduced as a function of position within the spheroid (two-way ANOVA, p < 0.01), although there was no difference in uptake observed at the spheroid surface (t-test, p > 0.1). This is probably because the extracellular solute concentration inside the spheroid is transiently below equilibrium with that outside.

FIGURE 6.

FIGURE 6

Open in a new tab

Effect of preelectroporation incubation time on electroporation-mediated uptake as a function of radial position of cells within multicellular spheroids. Duration of spheroid incubation in calcein solution was 10 (□), 600 (▪), and 1800 s (♦). One exponential-decay pulse of 0.48 kV/cm and 38 ms was used. The points represent experimental data from spheroids. The lines represent predictions from the model developed in this study that accounts for changes in cell state (Eq. 1), local solute concentration (Eqs. 2–6), and local electric field (Eqs. 7–9) within spheroids (see text). Average is mean ± SE.

To validate this expectation, we used a mathematical model for non-steady-state diffusion to predict the diffusional lag time required to achieve constant calcein concentration throughout the spheroid. Diffusion of calcein through the extracellular region of nonelectroporated spheroids was modeled in spherical coordinates with three boundary conditions: solute concentration is 1), initially zero within the spheroid; 2), equal at the spheroid surface and in the surrounding bath; and 3), bounded at all times within the spheroid (Crank, 1975), as

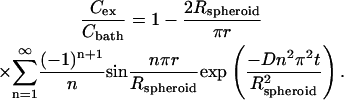graphic file with name M3.gif (2)

Cex is the extracellular solute concentration (which is a function of r), Cbath is the external bath concentration, t is time, and D is the solute diffusivity in dilute aqueous solution, 3.5 × 10−6 cm2/s (Prausnitz et al., 1996), neglecting effects of tortuosity. In this study, predictions were made using the first 10 terms in the infinite series.

Equation 2 predicts that it takes 33 s for the concentration at the interior of a representative spheroid (Rspheroid = 200 μm) to reach 90% of that outside. This is consistent with Fig. 6, which shows reduced uptake after a 10-s incubation, but no dependence on incubation time at the longer incubation times. Because all of the other data presented in this study used a preelectroporation incubation time of 10 min, transiently reduced extracellular calcein concentration cannot explain the observed reduction in uptake as a function of radial position.

We therefore considered a second aspect of the local solute concentration: unlike in dilute cell suspension, where an effectively unlimited reservoir of extracellular calcein is available for uptake, the finite extracellular volume within a multicellular spheroid limits the number of molecules that can be taken up by cells. A simplified analysis of this situation assumes that cells in the periphery can access an extracellular bath equivalent to cells in dilute suspension, whereas cells in the interior can only take up molecules in the extracellular space that immediately surrounds them. An additional assumption is that the ratio of intracellular/extracellular solute concentration is the same throughout the spheroid (i.e., the fractional approach to equilibrium is the same),

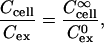graphic file with name M4.gif (3)

where Ccell is the intracellular solute concentration, 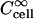Inline graphic is the intracellular solute concentration measured for cells within an infinitely large extracellular bath under the same electroporation conditions, Cex is the post-electroporation extracellular solute concentration, and 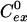Inline graphic is the preelectroporation extracellular solute concentration determined as a function of radial position using Eq. 2.

This expression can be combined with a mass balance on the solute

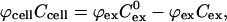graphic file with name M7.gif (4)

where ϕcell and ϕex are the volume fractions occupied by the cells and extracellular space, respectively, and ϕex is ∼0.35 (Nederman et al., 1984). The resulting solution yields

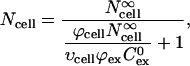graphic file with name M8.gif (5)

where Ncell is the number of molecules delivered into cells within a spheroid, 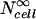Inline graphic is the number of molecules delivered into cells within an infinitely large extracellular bath under the same electroporation conditions, and υcell is cell volume determined as a function of radial position using Eq. 1.

An additional effect on solute uptake comes from the earlier observation that interior cells can be smaller. As a result, at the same intracellular concentration, smaller cells contain fewer molecules. Assuming that the number of molecules per cell scales linearly with cell volume, we can account for this effect using

graphic file with name M10.gif (6)

where the superscript ref corresponds to a reference cell outside a spheroid. Because the effects of limited extracellular volume and reduced intracellular volume as a function of radial position should be independent, the net effect of these geometrical factors can be accounted for using Eq. 6, where 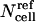Inline graphic is determined using Eq. 5 and the dependence of time and radial position are accounted for using Eqs. 1 and 2.

Effects of local electric field

An additional effect introduced by the multicellular environment is perturbation of the electric field by neighboring cells. These effects have been modeled by Miklavcic and colleagues (Susil et al., 1998; Pavlin et al., 2002) and can be analyzed by accounting for two effects. First, one must account for the different conductivities of spheroids and the bathing medium when calculating the average electric field strength within a spheroid, Uspheroid, as (Pavlin et al., 2002)

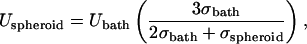graphic file with name M12.gif (7)
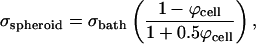graphic file with name M13.gif (8)

where Ubath is the electric field strength in the bath far away from the spheroid and σspheroid and σbath are the effective conductivities of the spheroid and bath, respectively. Using values of ϕcell = 0.65 (Nederman et al., 1984), σbath = 1.29 S/m (Lide, 2003) and, thus, σspheroid = 0.34 S/m (Eq. 8), this analysis yields Uspheroid = 1.33 Ubath (Eq. 7).

To account for local perturbations to the electric field caused by neighboring cells, the maximum applied transmembrane voltage, ψcell, must be calculated for cells within the spheroid. Susil et al. (1998) have performed finite element modeling to determine the local electric field experienced by a cell as a function of cell-to-cell spacing; for closely spaced cells found in spheroids, ψcell = Uspheroid Rcell. Additional analysis of the electric field distribution within spherical multicellular structures showed no variation in applied transmembrane potential as a function of position within the spheroid (Pavlin et al., 2002). Combining these results with Eq. 7 yields

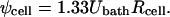graphic file with name M14.gif (9)

In contrast, for cells in dilute suspension, ψcell = 1.5 Ubath Rcell (Chang et al., 1992), which shows that the applied transmembrane voltage experienced by cells within multicellular spheroids is 11% less than isolated cells as a net result of the competing effects of 1), increased electric field due to decreased conductivity within spheroids and 2), decreased electric field caused by close cell-to-cell spacing. Recognizing that cell radius is a function of position within a spheroid, Eq. 9 should be combined with Eq. 1 to fully account for the influences on applied transmembrane voltage.

Validation of quantitative analysis

To determine if the behavior of molecular uptake within spheroids observed experimentally can be accounted for by our analysis of differences in cell state, local solute concentration, and local electric field within multicellular environments, we have used a statistical correlation validated for isolated cells and quantitatively modified it for spheroids using the expressions developed above. This isolated-cell correlation was developed based on nonlinear regression of experimental data for uptake of calcein by DU145 prostate cancer cells at >300 different electroporation conditions (Canatella and Prausnitz, 2001), and is therefore directly applicable to the present study as

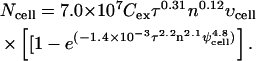graphic file with name M15.gif (10)

In this expression, Ncell is the average number of molecules delivered into a cell, Cex is the extracellular solute concentration (M), τ is the effective pulse length (ms), n is the number of pulses, υcell is the cell volume (μm3), and ψcell is the maximum applied transmembrane potential (V).

To make quantitative predictions of molecular uptake in spheroids, Eq. 10 was combined with the analysis developed in this study as follows. To account for the finite extracellular volume within spheroids, Eq. 5 was used. Then, Eq. 10 was employed to determine 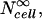Inline graphic where υcell was corrected to reflect the position-dependence of cell volume using Eq. 1. Cex was corrected to account for the time-dependence of extracellular solute concentration using Eq. 2, and ψcell was corrected to account for the effects of neighboring cells and position-dependent cell size using Eq. 9 combined with Eq. 1.

The predictions from this analysis are shown in Figs. 4 and 6. General agreement between the trends of the predictions and the experimental data points suggest that these predictions may be useful as guides.

In light of the above analysis, it is interesting to revisit Fig. 3, where two different electroporation conditions had similar effects on isolated cells, but very different effects on spheroids. The reduced uptake in spheroids can be at least partially explained by the lower electric field strength throughout the spheroid. The radial dependence of uptake can be at least partially explained by the still-further-reduced applied transmembrane voltage and intracellular volume of interior cells due to their smaller size. Finally, the stronger radial dependence of uptake for spheroids electroporated at weaker field strength, for which cells deep within the interior exhibited no uptake at all, is probably due to the applied transmembrane voltage being just above threshold on the periphery and then reduced below threshold in the interior. Although limited extracellular volume could also play a role, our calculations suggest that this effect was not significant at the conditions used in Fig. 3 (calculation not shown).

It is also interesting to revisit Fig. 5, where isolated cells previously grown within spheroids (Fig. 5 E) exhibited less uptake than isolated cells grown in conventional monolayer culture (Fig. 5 A). Equation 10 is applicable to both scenarios and predicts uptake by “normal” isolated cells (Rcell = 11 μm) to be 1.9 × 107 molecules/cell, in good agreement with Fig. 5 A (t-test, p > 0.10). For cells grown deep within spheroids and thus having a reduced radius of 9.6 μm, the prediction becomes 0.7 × 107 molecules/cell, which is statistically indistinguishable from the uptake measured in Fig. 5 E (t-test, p > 0.10). This indicates that accounting only for changes directly caused by reduced cell radius can explain the lower molecular uptake by the interior cells after dissociation from the spheroid. Other features of the cell state might also play a role, but have not been investigated here.

Implications for electroporation applications

The preceding analysis shows that electroporation of cells in multicellular environments differs from cells in dilute suspension. These differences should be accounted for when electroporating cells within tissues. Although electroporation in vivo is more complex, the following observations may assist applications of tissue electroporation.

Time dependence

As shown in Fig. 6 and Eq. 2, time is required for molecules to diffuse from the surface of a multicellular spheroid through the extracellular spaces to bathe interior cells with solute. In vivo, a similar time lag would be expected due to transport by convection in blood vessels and diffusion within tissues from the site of injection. This suggests that delaying electroporation pulse(s) until some time after injection should yield greater molecular uptake. Partly for this reason, clinical electroporation-assisted chemotherapy protocols often employ delays of a few minutes (Heller et al., 1999).

Limited extracellular volume

The limited extracellular reservoir of molecules surrounding densely packed cells can reduce intracellular uptake when intracellular concentrations approach extracellular concentrations (Eq. 5). When this occurs, multiple pulses separated by long spaces can provide time to replenish depleted extracellular spaces with solute from neighboring tissue or incoming blood flow. Clinical multiple-pulse protocols employ 1-s interpulse delays (Heller et al., 1999), which is probably too short to replenish typical tissue treatment volumes on the order of 1 cm3.

Reduced electric field

In high-density multicellular environments, the presence of neighboring cells can reduce the local electric field by as much as one-third relative to the local electric field experienced by an isolated cell. In this study, the presence of a highly conductive saline solution surrounding the less-conductive spheroid locally increased the electric field within the spheroid (Eq. 7). These two competing effects decreased the electric field within spheroids by a net of 11% relative to isolated cells. However, for cells in a tissue that is not bathed in a reservoir of conductive medium, the second of these effects would not occur, suggesting a one-third reduction in field strength for densely packed cells in tissue. Electroporation protocols developed in vitro might need to account for this by using higher bulk field strengths within tissues.

Dependence on cell size

The dependence of electroporation's effects on radial position of cells within spheroids could be explained largely by the position-dependent variation in cell size. Smaller cells took up fewer molecules because their intracellular volume was smaller and the transmembrane voltage induced in a cell decreases with decreasing cell radius. Thus, for the same bulk electric field, the smaller cells found within the spheroid interior experienced weaker electroporation than larger cells found on the spheroid periphery.

Although the observed distribution of cell size variation may be unique to spheroids, cell-to-cell variation in transmembrane voltage is likely to be found in tissues due to 1), differences in cell size; 2), differences in orientation of nonspherical cells relative to the electric field; and 3), local variations in the electric field due to heterogeneous tissue electrical properties or edge effects of electrodes. This suggests that long (e.g., ms) pulses at an applied transmembrane voltage just above electroporation threshold, which are believed to be optimal for cell suspensions (Canatella and Prausnitz, 2001), may be inferior to short (e.g., μs) pulses at higher voltage in multicellular environments. This is because low-voltage electroporation is extremely sensitive to voltage: a slightly smaller applied transmembrane voltage can dip below threshold, whereas a slightly larger voltage can kill cells. In contrast, the effects of short, high-voltage pulses are less sensitive to voltage (Canatella et al., 2001), which is advantageous for tissue electroporation. Possibly for this reason, short, high voltage pulses are commonly used in clinical electroporation of tumors (Heller et al., 1999).

CONCLUSIONS

This study tested the hypothesis that cells in a multicellular environment respond to electroporation in a heterogeneous manner that differs from isolated cells in suspension due to differences in cell state, local solute concentration, and local electric field. In support of the hypothesis, electroporation of multicellular spheroids yielded less uptake than isolated cells over a broad range of electroporation conditions. Moreover, uptake levels were heterogeneous, where uptake progressively decreased for cells located deeper within a spheroid's interior. Overall reduced levels of uptake were explained by a locally reduced electric field strength within spheroids due to spatially heterogeneous electrical properties and a reduced extracellular reservoir of solute within spheroids due to dense packing of cells. The dependence of uptake on radial position within spheroids was explained by an extracellular solute concentration gradient during transient diffusional lag times and the observation that cell size decreased for cells located deeper within spheroids, which in turn led to smaller cell volumes and smaller transmembrane voltages.

These unique features of the multicellular environment were quantitatively accounted for and generally validated using experimental data. These observations suggest that tissue electroporation could be enhanced by using larger field strengths than used for cell suspensions, applying short pulses at relatively large field strengths, delaying application of pulses until some time after injection of solutes, and possibly applying multiple pulses with long interpulse delays.

Acknowledgments

We thank Steve Woodard for help with flow cytometry and confocal microscopy, Joan Karr and John Petros for helpful discussions, and CytoPulse Sciences for providing a PA-4000 pulser.

This work was supported in part by the National Science Foundation and Emory/Georgia Tech Biomedical Technology Research Center.

Dr. Canatella's present address is Unilever Research and Development, Edgewater, NJ 07020.

References

  1. Bouvier, T., M. Troussellier, A. Anzil, C. Courties, and P. Servais. 2001. Using light scatter signal to estimate bacterial biovolume by flow cytometry. Cytometry. 40:188–194. [DOI] [PubMed] [Google Scholar]
  2. Canatella, P. J., J. F. Karr, J. A. Petros, and M. R. Prausnitz. 2001. Quantitative study of electroporation-mediated molecular uptake and cell viability. Biophys. J. 80:755–764. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Canatella, P. J., and M. R. Prausnitz. 2001. Prediction and optimization of gene transfection and drug delivery by electroporation. Gene Ther. 8:1464–1469. [DOI] [PubMed] [Google Scholar]
  4. Chang, D. C., B. M. Chassy, J. A. Saunders, and A. E. Sowers, editors. 1992. Guide to Electroporation and Electrofusion. Academic Press, New York.
  5. Crank, J. 1975. The Mathematics of Diffusion, 2nd Ed. Clarendon Press, Oxford, UK.
  6. Durand, R. E. 1982. Use of Hoechst 33342 for cell selection from multicell systems. J. Histol. Cytol. 30:117–122. [DOI] [PubMed] [Google Scholar]
  7. Durand, R. E. 1983. Oxygen enhancement ratio in V79 spheroids. Radiat. Res. 96:322–334. [PubMed] [Google Scholar]
  8. Essand, M., C. Grovnik, T. Hartman, and J. Carlsson. 1995. Radioimmunotherapy of prostatic adenocarcinomas: effects of 131I-labelled E4 antibodies on cells at different depth in DU 145 spheroids. Int. J. Cancer. 63:387–394. [DOI] [PubMed] [Google Scholar]
  9. Freyer, J. P., and P. L. Schor. 1989. Automated selective dissociation of cells from different regions of multicellular spheroids. In Vitro Cell. Dev. Biol. 25:9–19. [DOI] [PubMed] [Google Scholar]
  10. Heller, R., R. Gilbert, and M. J. Jaroszeski. 1999. Clinical applications of electrochemotherapy. Adv. Drug Del. Rev. 35:119–129. [DOI] [PubMed] [Google Scholar]
  11. Jaroszeski, M. J., R. Gilbert, C. Nicolau, and R. Heller. 1999. In vivo gene delivery by electroporation. Adv. Drug Del. Rev. 35:131–137. [DOI] [PubMed] [Google Scholar]
  12. Jaroszeski, M. J., R. Gilbert, C. Nicolau, and R. Heller, editors. 2000. Electrochemotherapy, Electrogenetherapy, and Transdermal Drug Delivery. Humana Press, Totowa, NJ.
  13. Lide, D. R., editor. 2003. CRC Handbook of Chemistry and Physics. CRC Press, Boca Raton, FL.
  14. Mir, L. M. 2001. Therapeutic perspectives of in vivo cell electropermeabilization. Bioelectrochemistry. 53:1–10. [DOI] [PubMed] [Google Scholar]
  15. Nederman, T., B. Norling, B. Glimelius, J. Carlsson, and U. Brunk. 1984. Demonstration of an extracellular matrix in multicellular tumor spheroids. Cancer Res. 44:3090–3097. [PubMed] [Google Scholar]
  16. Neumann, E., A. E. Sowers, and C. A. Jordan, editors. 1989. Electroporation and Electrofusion in Cell Biology. Plenum Press, New York.
  17. Nickoloff, J. A., editor. 1995. Animal Cell Electroporation and Electrofusion Protocols. Humana Press, Totowa, NJ.
  18. Pavlin, M., N. Pavselj, and D. Miklavcic. 2002. Dependence of induced transmembrane potential on cell density, arrangement, and cell position inside a cell system. IEEE Trans. Biomed. Eng. 49:605–612. [DOI] [PubMed] [Google Scholar]
  19. Prausnitz, M. R., C. S. Lee, C. H. Liu, J. C. Pang, T.-P. Singh, R. Langer, and J. C. Weaver. 1996. Transdermal transport efficiency during skin electroporation and iontophoresis. J. Control. Rel. 38:205–217. [Google Scholar]
  20. Prausnitz, M. R. 1999. A practical assessment of transdermal drug delivery by skin electroporation. Adv. Drug Deliv. Rev. 35:61–76. [DOI] [PubMed] [Google Scholar]
  21. Shapiro, H. M. 2003. Practical Flow Cytometry. Wiley-Liss, New York.
  22. Susil, R., D. Semrov, and D. Miklavcic. 1998. Electric field-induced transmembrane potential depends on cell density and organization. Electro-Magnetobiol. 17:391–399. [Google Scholar]
  23. Sutherland, R. M. 1988. Cell and environment interactions in tumor microregions: the multicell spheroid model. Science. 240:177–184. [DOI] [PubMed] [Google Scholar]
  24. Sutherland, R. M., and R. E. Durand. 1984. Growth and cellular characteristics of multicell spheroids. Recent Results Cancer Res. 95:24–49. [DOI] [PubMed] [Google Scholar]
  25. Teissie, J., N. Eynard, B. Gabriel, and M. P. Rols. 1999. Electropermeabilization of cell membranes. Adv. Drug Deliv. Rev. 35:3–19. [DOI] [PubMed] [Google Scholar]
  26. Weaver, J. C., and Y. A. Chizmadzhev. 1996. Theory of electroporation: a review. Bioelectrochem. Bioenerget. 41:135–160. [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES