Revisiting Voltage-Dependent Relief of Block in Ion Channels: A Mechanism Independent of Punchthrough

Abstract

Voltage dependence of block was investigated in a simple model for permeation in a multiion pore. Internal blocker could bind to three states of the open channel that differed in the locations and number of permeant ion bound; blocker dissociation occurs exclusively to the internal solution, and the blocker does not itself enter the electric field. By changing the relative stability of blocker binding to these three states, block displayed voltage dependence with relief of block at high potentials. Similar patterns of block could also be generated in more detailed models of ion permeation. These results illustrate that the observation of relief of block at high potentials is not a sufficient criterion for establishing that a blocker is permeant in a channel that has a complex permeation cycle.

INTRODUCTION

Mechanistic studies of ion permeation have relied heavily on the use of inhibitors as reporter molecules. One class of inhibitors, known as blockers, physically occludes conduction by binding within the vestibule and preventing permeant ions from accessing the selectivity filter. Many channel blockers are charged molecules and display affinities that vary with the membrane potential (Hille, 2001). With most voltage-dependent blockers, affinity changes exponentially with voltage, as predicted if the blocker enters the electric field but does not traverse the entire pore (Woodhull, 1973). However there are numerous instances (including methylammonium, Na⁺, and Cs⁺ block of K⁺ channels (Adelman and French, 1978; French and Wells, 1977; French and Shoukimas, 1985; Hille, 1975; Nimigean and Miller, 2002), acetylcholine (ACh) block of the ACh receptor (Sine and Steinbach, 1984), quaternary ammonium block of Na⁺ channels (Huang et al., 2000; Huang and Moczydlowski, 2001) and polyamine block of cyclic nucleotide-activated channels; Guo and Lu, 2000) in which the voltage dependence is more complex. In these cases, voltage dependence is multiphasic with an apparent relief of block at high potentials. The observation of multiphasic voltage dependence is generally considered evidence that the blocker is slightly permeant, and that at extreme potentials it can “punch” through the pore.

A wealth of functional and structural evidence indicates that many channel pores undergo changes in occupancy, either in number or positions of bound permeant ions, during the conduction cycle (Dutzler et al., 2003; Hess and Tsien, 1984; Hodgkin and Keynes, 1955; Morais-Cabral et al., 2001; Neyton and Miller, 1988a,b; Pusch et al., 1995; Zhou et al., 2001; Zhou and MacKinnon, 2003). In this study we reexamine the phenomenon of voltage-dependent block in the context of several simple models for ion conduction. In these models, relief of block at extreme potentials can occur simply as a consequence of blocker binding to multiple open states even when the blocker cannot itself transit the pore.

Methods

Kinetic schemes were evaluated using MATLAB 6.5.1, with rate constants as follows:

Scheme III

Ion association: AE¹, BF: 1×10⁹ M⁻¹ s⁻¹; AC, X1X3: 1×10⁸ M⁻¹ s⁻¹. Ion dissociation: EA¹, FB: 1×10⁹ s⁻¹; CA, X3X1: 3.2×10⁷ s⁻¹. Blocker association: BX2, AX1¹, CX3¹: 1×10⁸ M⁻¹ s⁻¹. Blocker dissociation: X2B, X1A¹, X3C¹: 1×10⁶ s⁻¹. Shuffling transitions: AB, EF¹, X1X2¹: 1×10⁸ s⁻¹; BA, FE¹, X2X1¹: 3.2×10⁷ s⁻¹; CF, FC: 1×10⁹ s⁻¹.

Scheme IV

Ion association: AE¹, BF, CG¹, DH: 1×10⁹ M⁻¹ s⁻¹; AC, BD², EG, FH², X1X3, X2X4²: 1×10⁸ M⁻¹ s⁻¹. Ion dissociation: EA¹, FB, GC¹, HD: 1×10⁹ s⁻¹; CA, DB² GE, HF², X3X1, X4X2²: 3.2×10⁷ s⁻¹. Blocker association: AX1¹, BX2, CX3¹, DX4: 1×10⁸ M⁻¹ s⁻¹. Blocker dissociation: X1A¹, X2B, X3C¹, X4D: 1×10⁶ s⁻¹. Shuffling transitions: AB, CD², EF¹, GH^1,2, X1X2¹, X3X4^1,2: 1×10⁸ s⁻¹; BA, DC², FE¹, HG^1,2, X2X1¹, X4X3^1,2: 3.2×10⁷ s⁻¹; CF, FC: 1×10⁹ s⁻¹.

Scheme V

Ion association: AB, CD, EF, GH, X1X2, X3X4: 1×10⁸ M⁻¹ s⁻¹; AE, BF, CG¹, DH¹: 1×10⁹ M⁻¹ s⁻¹. Ion dissociation: BA, DC, FE, HG, X2X1, X4X3: 3.2×10⁷ s⁻¹; EA, FB, GC¹, HD¹: 1×10⁹ s⁻¹. Blocker association: AX1, BX2, CX3¹, DX4¹: 1×10⁸ M⁻¹ s⁻¹. Blocker dissociation: X1A, X2B, X3C¹, X4D¹: 1×10⁶ s⁻¹. Shuffling transitions: BC, FG¹, X2X3¹: 3.2×10⁷ s⁻¹; CB, GF¹, X3X2¹: 3.2×10⁷ s⁻¹; CE, DF: 1×10⁹ s⁻¹; EC, FD: 3.2×10⁹ s⁻¹.

Repulsion was added by modifying the rate constants indicated with superscripts 1 and 2 by multiplicative factors equal to the square root of the appropriate repulsion factor (a repulsion factor of 100 in Scheme III, for example, yielded rates for the EF and FE transitions that were 10-fold faster and slower than the equivalent rates in the absence of repulsion (AB and BA, respectively)). 1 indicates the repulsion factor for the interaction between ions in the internal vestibule and internal selectivity filter site, 2 is that for the interaction between ions in the external vestibule and external selectivity filter site. Scheme IV was evaluated with a value of 100 for 2.

In transitions involving the selectivity filter, voltage dependence is partitioned as follows: Schemes III and IV: from inner vestibule into selectivity filter, 0.25; movement between the two selectivity filter sites, 0.5; and exit from the filter into the outer cavity, 0.25.

Scheme V: from inner vestibule into selectivity filter, 0.5; from outer vestibule into selectivity filter, 0.5. In voltage-dependent transitions, voltage dependence is partitioned evenly between forward and backward rates.

For Fig. 5, blocker and K⁺ entry into the cavity each have voltage dependence, and the same fraction of the field is traversed by both ions; values are as indicated in the figure legend. In these cases, the fraction of the voltage drop between the two vestibules was reduced to account for the drop from bulk solution into the inner vestibule, but the ratios of voltage drops between binding sites across selectivity filter (1:2:1) was maintained.

FIGURE 5.

Effect of adding voltage dependence to blocker binding. Scheme III (with repulsion) was used to evaluate the effect of adding voltage dependence to the blocker binding step. K_1/2 values were examined as the percentage of membrane potential crossed by the blocker was increased from 0 to 5, 10, and 15% (solid, dashed, dot-dash, and dotted curves, respectively).

BACKGROUND

Woodhull model of voltage dependence

For charged compounds that act as blockers, voltage dependence is typically described with the Woodhull model shown in Scheme I (Woodhull, 1973). Here inhibition results from a simple binding reaction in which the charged blocker X binds to an open channel O at a site located within the electric field producing a blocked channel B.

If dissociation to the trans side is negligible, the reaction reduces to that shown in Scheme II (Fig. 1 A). In this case, the total binding energy at an applied voltage V, ΔG°(V), is simply the sum of the intrinsic binding energy in the absence of voltage, ΔG°(0 mV), and that provided by a charged molecule in an electric field, so that

(1)

where z is the valence of the blocker, F is Faraday's constant, and δ is the fraction of the potential, V, traversed in reaching the binding site. Accordingly, the observed K_1/2 varies with membrane potential V according to

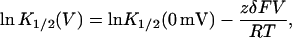(2)

where K_1/2(0 mV) reflects the voltage-independent binding constant, and R and T have their usual meanings. When a positively charged rapid blocker inhibits a simple Ohmic channel from the internal solution according to Scheme II, the fraction of raw current remaining decreases with depolarizing potentials (Fig. 1 B, solid and dashed curves). Blocker affinity rises exponentially as the potential is increased (Fig. 1 C, dashed line), since the binding energy resulting from the membrane potential is linearly related to the magnitude of the membrane potential.

FIGURE 1.

Woodhull model of channel block. (A) State diagrams depicting block with punchthrough (Scheme I) and simple nonpermeant channel block (Scheme II). In both cases, internal blocker (X_i) binds to an open channel (O) generating a blocked state (B). In Scheme I, blocker can also dissociate to the outside (X_o), but because the concentration of blocker on the outside is low, this reaction is effectively irreversible. (B) Inhibition of current through an Ohmic channel (solid line) by 10 mM blocker as predicted by blocking Schemes I and II. (C) K_1/2 of block as a function of voltage in Schemes I and II. In both B and C, the dotted and dashed curves show inhibition predicted by Schemes I and II, respectively, and were generated using a value of 10 mM blocker, with a blocker K_D(0 mV) of 10 mM and zδ of 0.1; in Scheme I, dissociation to the outside is 200-fold slower than that to the inside solution.

For a permeant blocker as depicted in Scheme I, release to the trans solution is enhanced as the potential is increased. The emergence of a second pathway for dissociation results in decreased block at the single-channel level at extreme potentials (Fig. 1 B, dotted curve). The apparent affinity is reduced at high potentials, with an observable reversal of voltage dependence (Fig. 1 C, dotted line).

The explanation of relief of inhibition at high potentials being caused by permeant block is so appealing that its observation is typically taken as a diagnostic indication for such a mechanism. However, as we show below, this phenomenon can theoretically result even when a blocking molecule does not go through the channel.

RESULTS

In this study we use a kinetic model to illustrate a general mechanism that accounts for relief of block with impermeant blockers. Such models have well-documented inadequacies that can extend to their application to conduction and blockade (Miller, 1999; Nonner et al., 1999). Here we use them simply to provide an intuitive understanding of the general features that underlie this behavior.

Conduction and block in a simple eight-state model

Fig. 2 shows a basic model for ion conduction and blockade generated from those recently developed for permeation through potassium channels (Berneche and Roux, 2003; Morais-Cabral et al., 2001; Nimigean and Miller, 2002). This model contains four binding sites along the permeation pathway. Two sites are within the selectivity filter proper, and two are located at the inner and outer vestibules. Occupancy of sites within the filter is governed by the following rules: firstly, the two sites cannot be occupied simultaneously, and secondly, the filter must always contain an ion.

FIGURE 2.

Schematic diagram of a model for ion conduction and nonpermeant block. Sites within the selectivity filter are shown as closed boxes, and the internal and external vestibules are depicted by the open boxes on the left and right, respectively. Permeant ions are represented as closed circles and blocker is depicted by the letter “X”. Allowed transitions are shown with arrows.

During conduction, ions move from the outer to inner solution by cycling through the model in the order: state A→C→F→(B or E)→A. An ion in the extracellular solution first binds to a site within the outer vestibule (A→C). In a concerted transition (C→F), this ion enters the outer site of the selectivity filter while a second ion in the inner selectivity filter site moves into the inner vestibule. The ion in the inner vestibule dissociates to the inner solution and the ion in the filter moves within the selectivity filter to the inner site; the sequence of these two events (either F→E→A or F→B→A) depends on the relative magnitudes of the rate constants associated with these transitions. Blocker can bind to the inner cavity from any state in which the cavity is empty (A, B, or C), but cannot enter the selectivity filter, and therefore does not traverse the channel. In Figs. 3–5 below, the blocker has a K_D of 10 mM (defined in the B↔X2 transition).

FIGURE 3.

Basic conduction and block in Scheme III. (A) Voltage dependence of the relative occupancies of the five conducting states (A, B, C, E, F) in the absence of blocker. (B) Current predicted by Scheme III in symmetric 200-mM permeant ion under control conditions (solid curve) and in the presence of 10 mM internal blocker (dashed curve). (C) Effect of voltage on K_1/2, determined from curves shown in Fig. 3 B using Eq. 3. The blocker binding step itself is voltage-independent; rate constants for all transitions are given in the Methods section.

Voltage dependence is apportioned to the individual transitions so that the entire voltage drop occurs across the selectivity filter proper, and both vestibules are isopotential with their adjacent bulk solutions. Transitions into and out of the filter each have half the voltage dependence of movement between the two selectivity filter sites; thus the A↔B and F↔C transitions have identical voltage dependences.

Fig. 3 shows how the occupancy of the conducting states (Fig. 3 A) and the predicted current (Fig. 3 B, solid curve) vary with voltage when the model is evaluated with symmetric 200 mM permeant ion in the absence of blocker. The current plateau at extreme potentials indicates that voltage-independent transitions become rate-limiting. At negative voltages, conduction is limited by ion binding to the extracellular vestibule (A→C transition); the channels accumulate in states A and E (Fig. 3 A), with their relative distribution determined by the concentration of internal permeant ion. At positive potentials, the voltage-independent C→A step of ion unbinding from the external solution is limiting. State F is only sparsely populated because the F→C transition is very fast at positive potentials, and channels distribute between states B and C depending on the concentration of internal permeant ion.

After generating analogous I-V curves in the presence of inhibitor (Fig. 3 B, dotted lines), the apparent affinity of the blocker, K_1/2, can be determined from the fractional remaining single-channel current, i/i_o, according to the equation

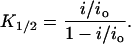(3)

In each case below, computing the K_1/2 directly from the relative fraction of channels in the blocked states produces qualitatively similar results to those obtained using Eq. 3.

Although no voltage dependence has been ascribed to the blocker-binding step, inhibition is slightly voltage-dependent (Fig. 3 C) over the range of 0–200 mV. This reflects the change in distribution among the five conducting states with voltage. At positive potentials the principle occupied states (B and C) each bind the blocker. At negative potentials, although the channels are largely in state A, states E and F are also noticeably populated; since blocker cannot bind to these latter states directly, their presence reduces the measured K_1/2 by mass action. The relative distributions of these states change between roughly 0 and 200 mV yielding a voltage-dependent K_1/2 over this range of potentials.

The introduction of repulsion

The basic model described above fails to take into account mutual destabilization resulting from ions bound at two adjacent sites, for instance, when ions are bound simultaneously within the inner vestibule and in the inner selectivity filter site. Figs. 4 and 5 demonstrate the consequences of introducing such repulsion into Scheme III. The extent of the destabilization is quantified in subsequent discussion by a repulsion factor, the magnitude of which reflects the overall change in the equilibrium constant. For example, with a repulsion factor of 100, the individual forward (e.g., A→E) and reverse rate constants are decreased and increased, respectively, by factors of 10 (see Methods). Repulsion between two adjacent ions is independent of the species of the ions; the repulsive effect of a blocker bound in the cavity is identical to that of a permeant ion bound in the same location. Three states in Scheme III—E, X1, and X3—are destabilized by repulsion.

FIGURE 4.

Conduction and block in Scheme III, with the addition of repulsion. (A) Relative occupancies of conducting states in the absence of blocker; state E is too sparsely occupied to be apparent on this scale. (B) Current generated by Scheme III in the absence and presence of 42 mM blocker (solid and dashed curves, respectively), in symmetric 200-mM permeant ion. Simulations in A and B were generated assuming a repulsion factor of 100. (C) Variation of K_1/2 with voltage calculated with Eq. 3 from curves like those shown in Fig. 4 B. Curves were generated with the following repulsion factors: dotted, 1 (no repulsion); dot-dash, 3; dashed, 10; and solid, 100. Except for the addition of repulsion, rate constants were identical to those used to generate Fig. 3, and are given in Methods. No voltage dependence was ascribed to the blocker-binding transition.

The introduction of repulsion has a relatively modest effect on conduction in the absence of blocker. Fig. 4 A shows the distribution of channel among the five open states in the absence of blocker, now with a repulsion factor of 100 introduced to the A↔E and E↔F transitions. The destabilization of state E dramatically lowers its occupancy, and correspondingly increases the population of state A. Since the A→C transition is rate-limiting at negative voltages, this shift results in a small increase in the amplitude of inward current (Fig. 4 B, solid curve).

The introduction of repulsion has a dramatic impact on blockade, both at the level of single-channel current (Fig. 4 B, dashed curve) and the observed inhibition constant K_1/2 (Fig. 4 C, solid curve). In the presence of blocker, the slope of the single-channel I-V curve undergoes noticeable changes, transiently flattening near 0 mV. Moreover, although the K_1/2 is still voltage-independent at extreme potentials, it varies in a nonmonotonic fashion at intermediate voltages. During the falling phase, the voltage dependence is reasonably high; analysis of the limiting slope of this segment using the Woodhull model yields a zδ ∼0.5. After reaching a minimum, K_1/2 actually increases with voltage; this rising phase represents, by definition, relief of block.

Fig. 4, A and B, and the solid curve in Fig. 4 C were generated using a value of 100 for the repulsion factor. As described below, this value is roughly that expected from calculations based on the high-resolution crystal structures of KcsA. However, the relief of block does not rely on having this level of repulsion. The dashed and dot-dashed curves in Fig. 4 C were constructed with repulsion factors of 10 and 3, respectively, and illustrate the same basic features, including relief of block.

The observed relief of block has a very simple origin. As discussed above, the addition of repulsion has little effect on the distribution of the channel among conducting states in the absence of blocker (Figs. 3 A and 4 A). However, the introduction of repulsion has a profound effect on the way these states interact with blocker. In the absence of repulsion, all three states—A, B, and C—have the same affinity for blocker; in the presence of repulsion, the affinity of state B is unchanged, but states A and C have reduced blocker affinity, since in both latter states the inner filter site is occupied by a permeant ion. The multiphasic nature of the K_1/2 value simply reflects the voltage-dependent distribution of the three states. At extreme negative and positive potentials, states A and C, respectively, with reduced blocker affinity, are most prevalent. Over the intermediate potentials where state B is dominant, the K_1/2 value approaches its value in the absence of repulsion (Fig. 4 C, dotted curve). As voltage is progressively increased from negative to positive potentials, the apparent affinity gradually shifts to reflect the relative proportion of channels in the high-affinity state B compared to the lower-affinity states A and C. Accordingly, the magnitude and breadth of the dip can be adjusted by altering the relative stabilities of the three states (data not shown).

Effect of additional voltage dependence

The data generated in Figs. 3 and 4 assumed that the blocker binding site was isopotential with the bulk solution. Fig. 5 shows the effect of introducing voltage dependence to binding at the inner cavity.

As the voltage dependence of binding increases with zδ ranging from 0.05 to 0.15, the overall shape of the voltage dependence of K_1/2 has features reminiscent of those seen when zδ is 0 (solid curve). In each case voltage dependence is multiphasic, although as the voltage dependence of blocker binding increases, relief of block becomes less prominent. K_1/2 values no longer plateau at extreme potentials, but instead the voltage dependence reaches a limiting value given by the voltage dependence of the binding reaction. As expected, the curves intersect at 0 mV, reflecting the voltage-independent binding K_1/2.

Extension to more detailed permeation models

The data above illustrate that it is possible to observe multiphasic voltage dependence in the absence of punchthrough in one particularly simple conduction model; Fig. 6 shows that the same phenomenon can be observed in other more general conduction schemes. Scheme IV (Fig. 6 A) expands on Scheme III by explicitly considering triple occupancy of the pore, thereby increasing the symmetry of the model. A second repulsion factor is added to reflect mutual destabilization occurring between ions bound simultaneously in the outer vestibule and the outer selectivity filter site. Scheme V (Fig. 6 B) relaxes the requirement of Schemes III and IV that the selectivity filter contain an ion at all times. In this case, the channel contains three ion binding sites, one within the selectivity filter and two flanking sites in the inner and outer vestibules. There are no concerted ion movements in this model, and movement of an ion bound within the selectivity filter to one of the vestibules leaves the selectivity filter site vacant. In this model, the pore can empty completely of permeant ions, and repulsion occurs between ions located simultaneously in the inner cavity site and the selectivity filter. In both Schemes IV and V, blocker binds to the inner vestibule site but cannot enter the selectivity filter or traverse the pore, and the inner vestibules are isopotential with the internal solution so blocker entry is itself voltage-independent.

FIGURE 6.

Relief of block in two detailed models of ion conduction. A, C, and E show Scheme IV, and B, D, and F show Scheme V. (A and B) Diagrams depicting the cycles of conduction and block in Schemes IV and V. Scheme IV has two sites within the selectivity filter (completed boxes), whereas Scheme V has only one. Internal and external vestibules are depicted by open boxes on the left and right, respectively. Permeant ions are depicted by black circles and blocking molecules are represented by the letter “X”. (C and D) Single channel I-V curves in the absence and presence of blocker (solid and dashed curves). Eight and 30 mM blocker were used when generating the blocked curves for Schemes IV and V, respectively. (E and F) Variation of K_1/2 with voltage.

For both Schemes IV and V, the K_1/2 of blockade was determined from the effect of blocker on single-channel current (Fig. 6, C and D, Eq. 1) generated using rate constants provided in the Methods section. As observed above in Scheme III, block in Schemes IV and V also displays multiphasic voltage dependence (Fig. 6, E and F). These additional cases illustrate that the multiphasic voltage dependence without punchthrough observed in Scheme III is not simply a consequence of the particular details of that simple scheme, but instead reflects a general pattern that can be generated even in detailed models of ion conduction.

DISCUSSION

This study of blockade in a relatively simple model for conduction through a multiion pore illustrates two important principles regarding voltage-dependent blocker affinities. First, it reinforces the notion that block can be voltage-dependent even when the blocker does not enter the electric field. Second, it demonstrates that relief of block at high potentials can occur even when a blocker is itself impermeant.

General characteristics of the model

Both of these features arise as a simple consequence of having multiple open states with two properties: the relative occupancy among the open states varies with voltage, and the states have different affinities for the blocker. In the models we show above, blocker binds directly to each of the predominant conducting states, and nonmonotonic voltage dependence comes principally from the fact that these states have different affinities. In more complex models of ion permeation, multiphasic voltage dependence could also theoretically arise as a consequence of voltage-dependent changes in the fraction of channels accessible to blocker.

In Scheme III, the voltage-dependent profiles of the different open states result primarily from the voltage-independent transition between states A and C. Channels accumulate in states A and C at negative potentials and positive potentials, respectively, and in state B at intermediate voltages.

In models of ion conduction, each open state has a unique pattern of bound permeant ion. Since each pattern may easily result in at least subtle alterations of the energy landscape, the open states may have different blocker affinities. Although different affinities could arise from voltage-dependent conformational changes, we use a simple repulsion mechanism in the models presented here to illustrate the effect of the open channels having varying blocker affinity. The dimensions and properties of known channel structures provide a basis for evaluating the possible magnitude of this effect. In the KcsA structure, for instance, a quaternary ammonium analog binds in the vestibule roughly 8 Å from a permeant ion in the selectivity filter (Zhou et al., 2001). With two ions binding at a distance of 10 Å in a medium of dielectric constant 10, the electrostatic repulsion would be roughly 3.3 kcal/mol. This value correlates well with the repulsion energy used in generating the data in Figs. 4 and 5. The simulations in Fig. 4 assumed a repulsion factor of 100 for the overall reaction, corresponding to a net destabilization of the doubly liganded state of 2.7 kcal/mol; the same basic effect was seen with even less destabilization (Fig. 4 C; a repulsion factor of 10 corresponds to 1.3 kcal/mol).

As an aside, we note that the shapes of the I-V curves generated by our models are more similar to those observed when large organic molecules block cation channels (Guo and Lu, 2000; Huang et al., 2000) than with alkali cation block of K⁺ channels (French and Shoukimas, 1985; French and Wells, 1977). In the latter case, the I-V curve has a characteristic N shape in which the raw current reaches a local maximum, decreases with voltage until a local minimum is reached, and then continues to increase at higher potentials. In contrast, the blocked current curve changes monotonically in Schemes III–V above. This difference may simply reflect distinct locations of the binding sites: alkali cations might penetrate deeper into the selectivity filter, and would thus cross a larger fraction of the membrane voltage. N-shaped I-V curves are easily modeled by punchthrough mechanisms as in Scheme I (Begenisich and Cahalan, 1980a,b); we do not know whether such curves could also be generated with an impermeant blocker in Schemes III–V given the correct choice of conduction scheme and rate constants.

Voltage dependence of block

Structural data from open channels show that in a number of cases, including K⁺ channels and the ACh receptor, blockers bind within large aqueous vestibules (Unwin, 1995; Zhou et al., 2001). Electrostatic calculations indicate that the vast majority of membrane potential drops across the selectivity filter, with little or no voltage difference between the vestibule and bulk solution (Berneche and Roux, 2003; Jiang et al., 2002). Thus if these blockers are voltage-dependent, it is likely the voltage dependence arises from a secondary source and not because they themselves enter the electric field.

Adelman and French used the idea that voltage dependence arises in part from a coupling of blocker binding with movement of permeant ions within the channel to explain the anomalously high voltage dependence of Cs⁺ block of K⁺ channels (Adelman and French, 1978). Recent studies of tetraethylammonium block of the Shaker and K_IR channels conclude that such coupling accounts for the majority of voltage dependence in those cases (Spassova and Lu, 1998, 1999; Thompson and Begenisich, 2003). In the model presented here, voltage dependence arises primarily as a consequence of the selective destabilization of several inhibited states. Blocker binding is not linked in a concerted fashion with ion movement in the pore, but rather reflects the voltage-dependent steady-state distribution of conducting states.

Relief of block

The observation of relief of block at high potentials has generally been considered sufficient to confirm that a blocker is permeant. This criterion has been used to establish that polyamines and quaternary ammonium compounds permeate cyclic nucleotide-activated channels (Guo and Lu, 2000) and Na⁺ channels, respectively (Huang et al., 2000; Huang and Moczydlowski, 2001) and that punches through a mutant of cystic fibrosis transmembrane conductance regulator (Gong and Linsdell, 2003). Our model predicts relief of block with a blocker that does not traverse the pore, illustrating that simply observing this phenomenon is not a sufficient criterion for establishing that a blocker can go through the channel, and suggesting an alternate explanation for at least some of the cases listed above. The most obvious candidates for the non-punchthrough mechanism are large organic blockers that display nonmonotonic block in channels with conduction pathways known to be quite narrow, for instance, methylammonium inhibition of K⁺ channels (Hille, 1975).

If blockers were constrained to act either as described by Scheme I or Scheme III, then a permeant blocker could in theory be distinguished based on the behavior at limiting positive potentials. At very positive potentials, the affinity for a blocker that punches though continues to decrease; in contrast, with an impermeant blocker shown in Scheme III, blocker affinity will either plateau or increase at high potentials, depending on the intrinsic voltage dependence of blocker entry. We note that in cyclic nucleotide-gated channels, polyamine block displays a triphasic voltage dependence remarkably reminiscent of the curves shown in Fig. 5 (Guo and Lu, 2000). Although those data were interpreted in the context of a complex model for permeant block, our observations here indicate that the polyamines may in fact be impermeant.

Our results with the models above indicate that it will often be difficult to distinguish unambiguously whether a blocker is truly permeant based on electrophysiological recordings alone. In some cases blockers are sufficiently permeant to carry measurable ionic currents in solutions devoid of other cations (for example, Na⁺ and Cs⁺ in K⁺ channels; French and Wells, 1977; Heginbotham and MacKinnon, 1993). It is also possible that their permeability in the presence of other cations could be assessed from detailed investigation of the reversal potential. This would be observed as a deviation from the Nernst potential when the blocker is added together with a single permeant ion. Although we expect such deviations will be slight, they may be detectable: in the Na⁺ channel, Begenisich and Cahalan (1980a) have observed an effect of Cs⁺ on the reversal potential measured under biionic conditions in solutions of Na⁺ and K⁺. Ultimately, however, establishing that a blocker is permeant may rely on the direct measurement of the physical transfer of blocker from one side of the membrane to the other using flame photometry, ion-sensitive electrodes, or radiolabeled compounds.