Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Jun;86(6):3783–3793. doi: 10.1529/biophysj.103.036681

Investigation of Temperature-Induced Phase Transitions in DOPC and DPPC Phospholipid Bilayers Using Temperature-Controlled Scanning Force Microscopy

Z V Leonenko *, E Finot †, H Ma ‡, T E S Dahms ‡, D T Cramb *
PMCID: PMC1304279  PMID: 15189874

Abstract

Under physiological conditions, multicomponent biological membranes undergo structural changes which help define how the membrane functions. An understanding of biomembrane structure-function relations can be based on knowledge of the physical and chemical properties of pure phospholipid bilayers. Here, we have investigated phase transitions in dipalmitoylphosphatidylcholine (DPPC) and dioleoylphosphatidylcholine (DOPC) bilayers. We demonstrated the existence of several phase transitions in DPPC and DOPC mica-supported bilayers by both atomic force microscopy imaging and force measurements. Supported DPPC bilayers show a broad Lβ–Lα transition. In addition to the main transition we observed structural changes both above and below main transition temperature, which include increase in bilayer coverage and changes in bilayer height. Force measurements provide valuable information on bilayer thickness and phase transitions and are in good agreement with atomic force microscopy imaging data. A De Gennes model was used to characterize the repulsive steric forces as the origin of supported bilayer elastic properties. Both electrostatic and steric forces contribute to the repulsive part of the force plot.

INTRODUCTION

The physical and chemical properties of biological membranes are of critical importance for understanding specific membrane function. Supported phospholipid bilayers (SPBs) are accepted models for complex biological membranes (see McConnell et al., 1986; Stelze and Sackmann, 1989; Sonnleitner et al., 1999; Kalb et al., 1990; Schmidt et al., 1992; Ramsden and Schneider, 1993; Pearce et al., 1992; Nielsen et al., 1999). SPBs also hold promise for nanosensor development. They could serve as a template for the incorporation of proteins and receptors and reduce nonspecific interactions.

SPBs are composed of phospholipids adsorbed to a planar solid support. The complex structural dynamics of the bilayers are governed by temperature-dependent parameters such as average interfacial area per lipid, thickness of bilayer, and disorder of hydrophobic tails. The SPB can exist in several lamellar phases: gel phase; liquid crystalline or fluid phase; subgel phase; and ripple phase (Tenchov et al., 2001). Often, phase behavior is dominated by the main Lβ–Lα (gel-fluid) transition. A large number of intermediate stable, metastable, and transient lamellar gel structures can be adopted by different lipids (Tenchov et al., 2001). For saturated phosphatidylcholines, such as DPPC, there are four recognized lamellar phases: namely, a liquid-crystalline phase (Lα), and phases with ordered hydrocarbon chain arrangements: ripple phase (Pβ); gel phase (Lβ); and subgel or crystal phase (Lc) (Meyer et al., 2000).

Phase-related bilayer properties have been examined using a variety of experimental techniques (Bizzotto and Nelson, 1998; Nelson and Bizzotto, 1999; Tamm and McConnell, 1985; Kalb et al., 1992; Nollert et al., 1995). Physical properties of lipids such as density and thickness have been studied by differential scanning calorimetry, pressure calorimetry or dilatometry, and densitometry and other methods (Exerowa, 2002; Ebel et al., 2001).

Atomic force microscopy (AFM) has also proven to be a valuable tool for imaging “soft” biological samples (Leonenko et al., 2000; Zasadzinski et al., 1991; Hui et al., 1995; Singh and Keller, 1991; Beckmann et al., 1998), especially in oscillating mode (Han et al., 1996, Han and Lindsay, 1998; Fasolka et al., 2001). The power of AFM lies in the fact that not only can images of high resolution be generated without drying the sample, but that the forces of interaction between AF probe and the surface can be measured precisely, giving information about the mechanical properties of biological samples (Lee et al., 1994; Cappella and Dietler, 1999; Senden et al., 1994; Cleveland et al., 1995; Biggs, 1995; Dufrêne et al., 1998; van der Vegte and Hadziioannou, 1997). On approach of the AFM probe tip to the sample, the force-distance curve can be used to characterize surface properties such as van der Waals and electrostatic forces, and solvation, hydration, and compression-related steric forces. The retraction force curves often show a hysteresis referred to as an adhesion pulloff event, which can be used to estimate the adhesion forces. Much experimental force data are now available in the literature, and theoretical models have been developed for the analysis of forces acting between two solid surfaces (Cappella and Dietler, 1999; Senden et al., 1994; Cleveland et al., 1995; Biggs, 1995; Dufrêne et al., 1998). In contrast, only a few publications address force measurements of soft thin layers such as thiol self-assembled monolayers (van der Vegte and Hadziioannou, 1997; Dimitriadis et al., 2002) and phospholipid bilayers (Franz et al., 2002; Butt and Franz, 2002; Loi et al., 2002). Moreover, none of these have examined the force measurements as a function of temperature.

Temperature-dependent AFM studies may provide valuable information about changes in structural and physical properties of bilayers during phase transitions. A few temperature-dependent AFM studies involving imaging bilayers have been previously reported (Giocondi et al., 2001; Leonenko et al., 2000; Leonenko and Cramb, 2002, 2004; Tokumasu et al., 2002; Xie et al., 2002), but none have involved force measurements as a function of temperature.

In this article we present results on DOPC- and DPPC-supported phospholipid bilayers during heating above TM. Both force measurements and AFM imaging were performed to compare different bilayer phases during phase transitions. The changes in force curves as functions of temperature and loading rate were analyzed.

EXPERIMENTAL TECHNIQUES

Materials

Dioleoylphosphatidylcholine (DOPC, lyophilized or in chloroform solution; Sigma, Oakville, ON), 1,2-dipalmitoyl phosphatidylcholine (DPPC; Avanti Polar Lipids, Alabaster, AL) were used without further purification. Phosphate buffer (pH 6.8) and distilled nanopure water were used in the preparation of all vesicles. Freshly cleaved ASTMV-2 quality, scratch-free ruby mica (Asheville-Schoonmaker Mica, Newport News, VA) was used as the solid support.

Methods

Supported planar bilayers were prepared for AFM imaging by vesicle fusion method (Leonenko et al., 2000, Brian and McConnell, 1984). All vesicles were prepared as previously reported (Leonenko et al., 2000). Briefly, an appropriate aliquot of phospholipid chloroform solution was measured into a small vessel and the chloroform removed using a stream of dry nitrogen. The dry phospholipid was then suspended in phosphate buffer or pure water to its final concentration and stirred for 30 min. The solution was sonicated (Model 1200, Branson, Danbury, CT) at room temperature for 10 min. Between the sonication periods, the solution was stirred at room temperature for 15 min. For this method, the solutions were cycled ∼10 times until they appeared to be clear. Aliquots of the vesicle solution were deposited on freshly cleaved pure mica. After a controlled period of time the mica was gently rinsed with nanopure water.

Surfaces were imaged with an atomic force microscope (Pico SPM, Molecular Imaging, Tempe, AZ) equipped with an AFMS-165 scanner. The nominal spring constants of Au-Cr-coated Maclevers (Molecular Imaging) used were ∼0.6 N/m. The tip radius of curvature is quoted as being typically 25 nm. The scan rate was fixed to 20 μm/s. The standard MAC mode fluid cell (Molecular Imaging) was used throughout. All imaging and force measurements were performed in a liquid cell under nanopure water. The height scale was calibrated using colloidal gold spheres of well-defined size (diameter 5 and 14 nm; Vesenka et al., 1993).

Temperature-dependent experiments were executed using the AFM temperature controller and hot MAC Mode Stage (Molecular Imaging). The temperature was varied from 22 to 65°C, within 0.1°C in accuracy with a 1°C/min ramp. The atomic force microscope was also used as a force apparatus. Force measurements were performed on DPPC and DOPC bilayers formed from water solutions. The experiment consists in monitoring the interaction between the AFM tip and the substrate by sensing the cantilever deflection, Zc, as a function of the piezo elongation, Zp, as the tip is moved toward and away from the substrate. It is a well-known fact that the force interactions depend on the velocity of the surface approach (Cappella and Dietler, 1999), especially for soft viscoelastic materials. All measurements were performed over five velocities: 0.5, 5, 50, 500, and 2500 nm per second. A statistical analysis has revealed that 10 measurements at different locations of the same area are required to determine parameters such as the adhesion and the long-range forces with 10% accuracy. Force curves were monitored as a function of temperature and lateral position of the cantilever.

As the tip-sample separation cannot be independently measured, we developed a systematic procedure for calculating the sensitivity of the apparatus. This measurement assumes that the tip and the mica surface are brought into a nondeformable contact in the higher loading region. Raw data (Zc versus Zp) are then converted into force F versus surface-tip separation D using Hooke's law. F = k Zc, where k is the spring constant of the cantilever, and the geometric relationship is D = Zc–Zp for incremental changes.

RESULTS AND DISCUSSION

Imaging bilayer phase transitions

DPPC bilayer

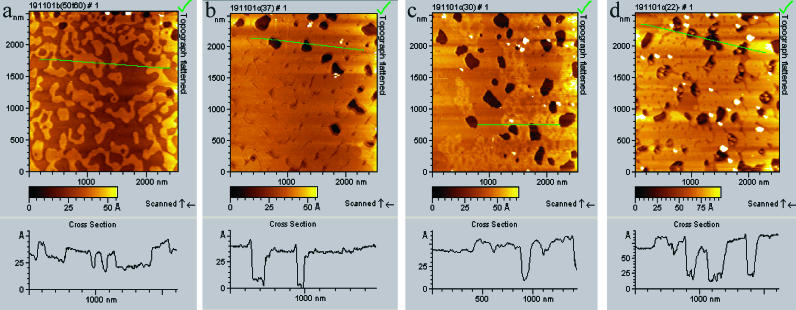
A DPPC-supported bilayer was imaged while heating from room temperature to 65°C and also while cooling back to room temperature. The bilayer was formed by applying a vesicle solution in buffer onto a freshly cleaved mica surface. After incubation, the cell was rinsed and filled with water for imaging. The topography images (Fig. 1) show a well-defined gel phase, Lβ, for the DPPC bilayer at T = 22°C. Phase contrast images (data not shown) confirm that the dark areas correspond to mica and the bright areas to the bilayer, which has an effective thickness of 4.8 ± 0.3 nm and a surface coverage of 89%. Several phase transitions are then observed as a function of increasing temperature. During heating of the DPPC bilayer, a broad main transition was observed at 42–52°C (Fig. 1, b and c) leading to the formation of lower domains. The coexistence of two domains (4.2 ± 0.4 nm and 3.3 ± 0.3 nm) was observed during this temperature interval (Fig. 1 b). As the temperature is increased further, the amount of surface covered by the higher domains (4.2 nm) decreases and then completely disappears at 52°C, showing a thin bilayer that includes some defects (Fig. 1 c). Note that during this dynamic process the coverage of lower domains had increased to 97% (Fig. 1 c), and eventually to 100% (image not shown). This corresponds to the increase in area per lipid from 47.9 Å2 (initial area/lipid at 20°C from Nagle and Tristam-Nagle, 2000) to 53.8 Å2, which is lower than experimental data (at 50°C reported by Nagle and Tristam-Nagle, 2000) of 64 Å2. Such a discrepancy might originate from the effect of the bilayer support in our AFM measurements, which could hinder complete expansion of the bilayer. Since there is no lipid in the solution above the bilayer, we assume all changes are accounted for by expansion of the bilayer itself. A further increase in temperature, 53–60°C, leads to another apparent transition within the fluid phase (Fig. 1 d). This transition is characterized by the formation of even lower domains (0.8–1.0-nm lower; the exact thickness of bilayer was not measurable because of defect absence) and a further increase in surface coverage (closing of all defects; Fig. 1 e). This transition was complete at 60°C, and the thin bilayer has totally covered the surface at this point. The absolute increase in surface coverage due to this transition was not measurable, because of an insufficient number of surface defects.

FIGURE 1.

FIGURE 1

Open in a new tab

AFM topography images showing the phase transition in DPPC bilayer in liquid cell upon heating and cooling back to room temperature. (a) Heating DPPC bilayer to room temperature, 22°C; (b) heating to 50°C; (c) heating to 52°C; (d) heating to 54°C; (e) heating to 60°C; (f) cooling back to 54°C; (g) cooling back to 51°C; (h) cooling back to 49°C; and (i) cooling back to room temperature, 22°C.

The first 42–52°C transition is attributed to the main Lβ–Lα transition, and the second transition, between 53 and 60°C, possibly corresponds to the formation of the fluid-disordered phase, perhaps with interdigitated or partly interdigitated lipid chains. No further changes were observed above 60°C.

Slowly cooling the system back showed that the two higher temperature transitions at 42–52°C and 53−60°C are reversible and that the bilayer can be restored to its initial thickness of 4.8 nm (Fig. 1, g–i).

Previous studies have established the Lβ–Lα phase-transition temperature for DPPC at 41°C (Biltonen and Lichtenberg, 1993). The presence of the mica support changes and significantly broadens the temperature of the main Lβ–Lα phase transition compared with that observed using differential scanning calorimetry (DSC). Interestingly, Yang and Appleyard (2000) employed DSC to examine the effect of a mica-supported DPPC bilayer. The SPB was prepared by coating microscopic shards of mica with DPPC via vesicle fusion. In their study, three peaks in the range 41–46°C for the thermogram of supported DPPC were observed. They attribute the two higher temperature peaks to phase transitions in separate leaflets. This would lead to three or possibly four domains of bilayer thickness at intermediate temperatures, unless one leaflet melts completely before the other starts to melt (leading to two domains). During main transition we observed coexistence of only two domains, which we attribute to gel- and liquid-phase DPPC. It is well-known that the phase transition (measured using DSC) of small unilamellar vesicles (SUVs) is broader than that measured for multilamellar vesicles (MLVs; Biltonen and Lichtenberg, 1993). This is rationalized as stronger bilayer coupling and cooperativity in the case of the MLVs. We previously investigated DPPC SUVs (Carnini et al., 2004) and found the width of the DSC peak to be 4°C as compared to 1°C for MLVs. Thus, the TM width of 10°C observed using AFM might be due, in part, to the single bilayer nature of the SPB. Also, the broadening of the phase transition that we observe may be due, in part, to the mica support—which may serve to inhibit the migration of the liquid-phase areas together and thus reduce the cooperativity of the transition.

Significantly, when vesicles were formed in pure water (i.e., a fully hydrated bilayer; see Fig. 2), we observed an additional subtransition below TM. The initial thickness of the fully hydrated gel-phase bilayer at room temperature was slightly larger, at 5.5 ± 0.2 nm. The additional subtransition was observed only during the cooling process, at 35–36°C (Fig. 2), and not during heating. This subtransition was not observed for a DPPC bilayer when the vesicle solution was formed in buffer. Fig. 2 shows the main transition at 52–42°C (Fig. 2 a), and growth of higher gel domain is complete at 40°C (Fig. 2 b). An additional subtransition starts at 35–36°C (Fig. 2 c), and continues down to room temperature. For fully hydrated DPPC bilayers, the thickness of the fluid-phase (at T = 52°C) and the gel-phase (at T = 22°C) bilayers were measured as 3.6 ± 0.3 nm and 5.5 ± 0.2 nm, respectively. During the main transition 42°–52°C, the bilayer thickness changes from 3.6 nm to 4.4 ± 0.2 nm. During the additional subtransition, which occurs between 35 and 36°C, the bilayer thickness increases further from 4.4 ± 0.2 nm to 5.5 ± 0.2 nm.

FIGURE 2.

FIGURE 2

Open in a new tab

AFM topography images showing the phase transition in fully hydrated DPPC bilayer during cooling back from 60°C to room temperature. Bilayer was formed from water solution by applying 30 μL of 0.5 mg/mL onto freshly cleaved pure mica for 5 min, then the cell was rinsed and covered with nanopure water. (a) Cooling back to 50°C; (b) to 36°C; (c) to 30°C; and (d) to 22°C.

During the subtransition, growing domains appear to be round and randomly distributed. We have no evidence that this is the formation of ripple phase. The height difference (∼1 Å) in the bilayer may correspond to decoupled phase transitions in the two leaflets. We assume that the arrangement of water molecules at the interface plays an important role for the subtransition and may contribute to the structural heterogeneity across the supported bilayer. This may be less pronounced for the bilayer formed from buffer.

DOPC bilayer

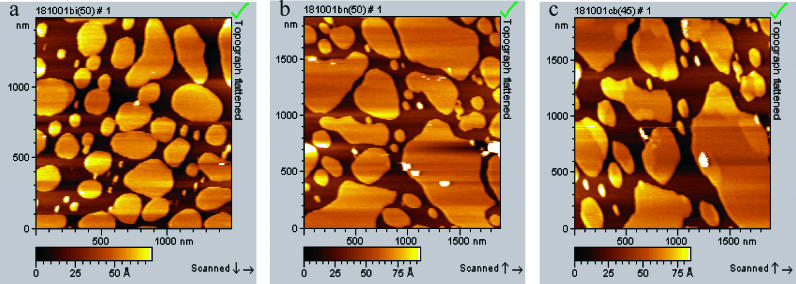
A DOPC bilayer was used to investigate the change in morphology of the fluid phase with temperature. Fig. 3 shows DOPC bilayer patches, formed from buffer solution, of various lateral sizes from 50 nm up to 250 nm and with an effective thickness of 5.5 ± 0.1 nm (room temperature, not shown). Fig. 3, a and b, show the bilayer at 50°C. From this figure the expansion of the bilayer patches is evident. For the Lα-DOPC bilayer the change begins in the range 37–40°C, and is accompanied by a 44% increase in bilayer surface coverage, and bilayer thinning from 5.5 ± 0.1 to 4.6 ± 0.1 nm (average of 100 cross-section measurements). This corresponds to a total volume increase of 17.9%. The bilayer swelling observed may be a characteristic of a liquid-ordered to liquid-disordered transition (Dietrich et al., 2001). The distance between the tails of the bilayer increases progressively in proportion with the surface coverage. At 50°C, the SPB patches changed in size and shape during a 25-min scan. This is in contrast to room temperature, where the SPB patches did not change during a scan lasting one hour. Fig. 3 c shows the bilayer after it has cooled down to 45°C. In this figure, there is evidence of domains with different thicknesses. A DOPC bilayer formed from water solution (image not shown) shows similar changes with temperature, although the thickness of the bilayer was slightly different (see Table 3).

FIGURE 3.

FIGURE 3

Open in a new tab

AFM topography images showing the expansion of DOPC fluid-phase bilayer during heating. DOPC bilayer was formed from buffer solution by applying 70 μL of 0.5 mg/mL onto freshly cleaved pure mica for 30 min, then the cell was rinsed and covered with nanopure water. The images shown are after: (a) heating to 50°C; (b) 1 h scanning at 50°C; and (c) cooling to 45°C.

TABLE 3.

Comparison between the length L measured by force analysis, the indentation corresponding to an applied force of 1 nN, and the height given by AFM for a fully hydrated DOPC bilayer

DOPC Thickness of bilayer, estimated from theoretical fit, L, in nm Indentation for 1 nN, in nm Thickness of bilayer, measured by AFM cross section, in nm Thickness of bilayer, literature data, in nm
T = 60°C 1.5 4.0 2.1 —
T = 36°C 2.7 4.3 3.1 —
T = 22°C 4.1 6.1 4.0 3.7
Open in a new tab

Thickness of DOPC bilayer from literature data are shown for comparison. Literature values are taken from Petrache et al. (2000) and Nagel and Tristam-Nagel (2000).

Forces between the bilayer and the silicon nitride tip as a function of temperature

DPPC bilayer

Adhesion forces

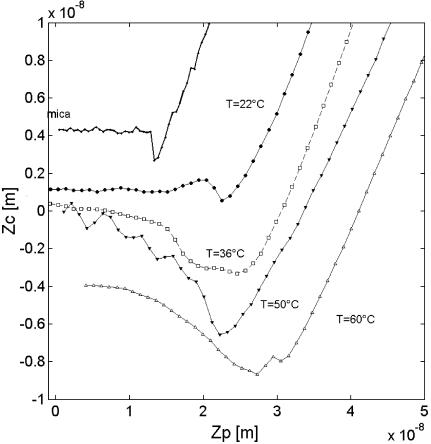
Surface force profiles between the silicon nitride tip and a DPPC bilayer were measured as a function of temperature. Raw data of the cantilever deflection corresponding to the retraction of the tip from the bilayer, after contact with the tip, are shown in Fig. 4. The data corresponding to the mica surface immersed in water are presented for comparison. Mica was characterized by an abrupt jump out of contact of 1.5 nN. This adhesion force was found independent of temperature to within 5% error. The adhesion force acting on the DPPC bilayer at 22°C does not differ drastically from the mica substrate and is only slightly reduced to 1 nN. The adhesion event originates from van der Waals forces, which can be thought of in terms of the Hamaker constant. A bilayer adsorbed on mica is known to reduce the overall Hamaker constant (Israelachvili, 1992).

FIGURE 4.

FIGURE 4

Open in a new tab

Cantilever deflection Zc as a function of the piezo translation Zp during the retraction of the tip from the DPPC layer for four temperatures. The curve monitored on mica is independent of temperature, and is shown for comparison.

Temperature increase leads to a gradual change of the force profile. The force required for detaching the tip from the bilayer increases from 3 nN at 36°C up to 10 nN at 50°C. This is observed from Fig. 4 as an increased change in cantilever deflection (Zc) as a function of piezo translation (Zp) during retraction. In addition, the jump out of the contact is not abrupt, compared with a solid-like surface (i.e., mica or Lβ-DPPC). The distance the tip travels before it separates from the surface increases with increase of temperature. As van der Waals forces are known to vary only slightly with temperature, the change in the profile is likely due to tip-bilayer interactions that depend on bilayer phase.

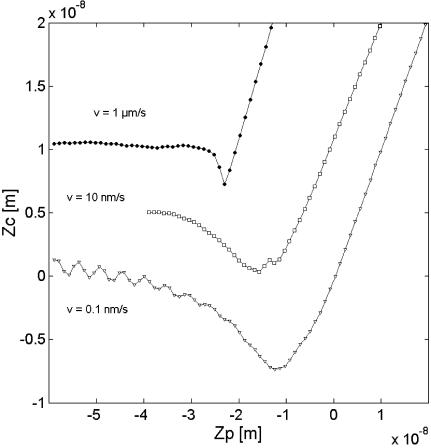
The fluid nature of the DPPC at T > 50°C was demonstrated in Imaging Bilayer Phase Transition. It is possible that the tip actually starts to perturb a small patch of lipid from the bilayer during retraction at 50°C. However, there is not enough energy/force available to completely overcome the bilayer self-adhesion. Thus, there remains a jump out of contact. To examine this assertion, the forces were measured as a function of the scan rate, v, of the piezo motion. A slower scan rate could lead to more tip-lipid interactions and subsequently an increase in detachment force. Thus, a greater force may represent a greater number of lipid molecules interacting with the tip.

No significant change in the tip-bilayer adhesion force on DPPC layer was recorded for v varying from 0.5 up to 2500 nm/s when temperature was held below 40°C. This suggests that the following changes above TM are not due to memory effects. Fig. 5 shows an increase in the forces between DPPC bilayer and the tip at 60°C with decreasing v. For a high speed, v = 1 μm/s, the force profile looks like one observed on a solid-like gel-phase bilayer at T = 22°C with an abrupt jump out of contact. With decreasing v, the time of contact, τ, between the tip and the bilayer increases. The value τ can be found through dividing the vertical distance of contact (given on the piezo axis; see Fig. 5) by v. For τ longer than ∼2 s, the increase in force may be explained by an increase in number of lipids interacting with the tip. The mechanism may involve tail rearrangement during tip-bilayer contact, which leads to the increase of the contact area and formation of a lipid meniscus between the tip and the mica (Schneider et al., 2000). The characteristics of this meniscus may strongly depend on the tip radius, the surface chemistry of the tip, the mobility of the tails, and the surface tension of the solvent in the vicinity of the tip. Since we observed no evidence of lipids permanently coating the AFM tip, the tip-lipid affinity appears to be too low for complete extraction of any bilayer patches.

FIGURE 5.

FIGURE 5

Open in a new tab

Cantilever deflection Zc as a function of the piezo translation Zp during the retraction of the tip from DPPC layer for three scan rates v at a temperature T = 60°C.

Statistical analysis of adhesion forces

It has been demonstrated that the force of a unit interaction between an AFM tip and a surface can be determined from a statistical analysis of a series of detachment force measurements. For a statistical analysis based on adhesive force originating from a discrete number n of individual interactions or bonds, Fs has been used. The total force distribution follows Poisson statistics, with mean force Fadh = nFs and variance 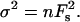Inline graphic The force of one bond, Fs, is therefore given by the square of the variance of the force divided by the mean adhesion force Fadh. The value n is the ratio between Fadh and Fs. This analysis has the advantage that the knowledge of the mean radius of curvature is not required (Williams et al., 1996) and gives information on the nature of the bilayer.

A fluid bilayer is typically ascribed to a high number of tip-sample bonds for T > 40°C. The force of a single bond is increased in a fluid phase. In addition, in a fluid phase, n increases with decreasing the v. Table 1 presents the standard deviation of the adhesion force in the gel phase and the fluid phase for three values of v. It is also shown that the adhesion in the fluid phase is more reproducible than in the gel phase. This means that the number of bonds, n, involved is higher in the fluid phase. It has been shown previously that the force required to remove a single lipid from a bilayer is of the order 30–140 pN (Marrink et al., 1998, Evans et al., 1995), depending on the lipid and on the technique employed. The lowest values that we measure are at least twice this range, suggesting that we do not observe single lipid events. Instead, our unit bonds must represent patches containing more than three lipids. This is in agreement with the ensemble model, which suggests that lipids in a large membrane can move collectively (Alakoskela and Kinnunen, 2001). Again, the detachment force between patch and tip must be smaller than the extraction force of the entire patch, otherwise we would see evidence of tip coating. This is consistent with our previous work (Leonenko et al., 2000, 2002; Leonenko and Cramb, 2002), where continuous imaging of bilayers displayed no resolution degradation or changes in force curves that would result from uncontrollable lipid coating of the AFM tip.

TABLE 1.

Experimental adhesion force Fadh and its standard error σ on DPPC and DOPC membrane; calculation of the number of bindings n and the mean force of a single bond Fs

Fadh (nN) σ (nN) Fs (nN) n
DPPC T = 22°C (v = 10 nm/s) 1 0.6 0.3 3
T = 60°C (v = 1000 nm/s) 3 1.5 0.75 4
T = 60°C (v = 10 nm/s) 5 2.0 0.8 6
T = 60°C (v = 0.1 nm/s) 7 2.6 0.7 10
DOPC T = 22°C (v = 10 nm/s) 3 1.2 0.5 6
T = 60°C (v = 10 nm/s) 4 1.3 0.4 10
Open in a new tab
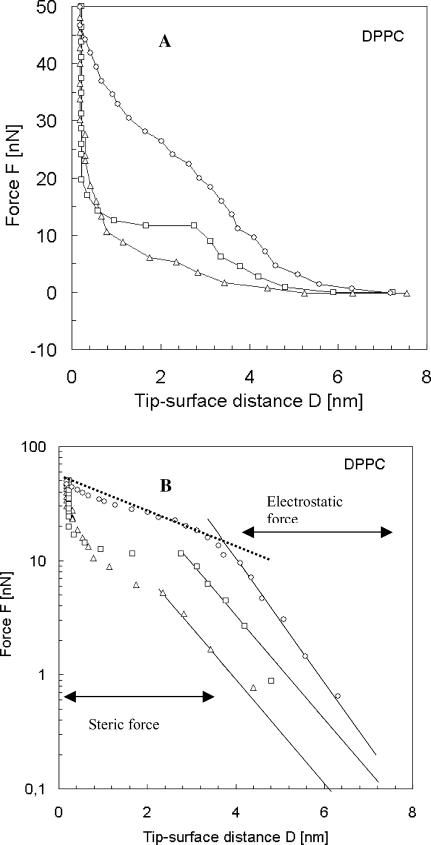
Repulsive forces

Fig. 6 A shows the three patterns of the force versus the tip-sample separation measured on DPPC bilayer in the temperature range between 20 and 60°C. At a separation larger than 7 nm from the surface, no force is acting on the probe. At the distance close to 7 nm, a repulsive force between the probe and the sample is present. The logarithmic representation (Fig. 6 B) helps to determine the nature of the repulsive regime. Three exponential regimes clearly exist, one at long range from 3 to 7 nm, another at short range between 0.3 nm and 3 nm, and the third steep one in close contact with mica. The long range can be explained by an electrostatic origin, due to the effective surface charge, which originates from water shielding. The approximate expression of the electrostatic force (also called double-layer force) is given by Butt (1991) as

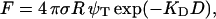graphic file with name M2.gif (1)

where R is the tip radius, σ is the surface charge, ψT is the tip potential, D is the tip-surface distance, and KD is the inverse of the Debye length. KD can be estimated to 0.25 nm−1. The long-range force does not seem to be affected by temperature, as the three curves in the log-plot are almost parallel in Fig. 6 B.

FIGURE 6.

FIGURE 6

Open in a new tab

(A) Evolution of the repulsive force F acting on the tip as a function of the distance D between the AFM tip and the DPPC bilayer deposited on mica. Forces were monitored during the approach of the tip onto the sample for three temperatures (▵, T = 22°C; □, T = 36°C; and ○, T = 65°C). (B) Experimental data represented by asterisks were fitted using Eq. 1. The theoretical fits are shown in solid line for the electrostatic force (Eq. 1) and dashed line for the steric force (Eq. 2). The logarithmic representation helps in determination of the range of reliability of the equation and therefore the evaluation of the thickness of the bilayer.

The second exponential part is attributed to the steric forces and deformation of the bilayer. The repulsive force in the short-range regime at the contact of the bilayer cannot be treated using common elastic mechanical models such as Hertz's theory, or any other models based on continuum mechanics. With our AFM experiments we are examining very small, discrete areas where nanoindentation is induced not only by macroscopic compression of the bilayer but also by nanoscale structural changes in the bilayer. Therefore, here we should use a molecular approach, including interactions involved in steric forces (Franz et al., 2002).

The exponential increase of the repulsive force likely originates from tail steric repulsion induced by the AFM tip compressing the bilayer. The tails in the bilayer will resist compression, because compression will increase the local concentration of the alkyl segments, increasing the free energy of the system. The steric forces of compression act on the bilayer until the loading force is close to the yield force, when the tip breaks through the bilayer. The breakthrough force decreases as the temperature increases, and DPPC bilayer at elevated temperatures shows similar instability in the force plot as fluid-phase DOPC bilayer and DOTAP bilayer (Loi et al., 2002).

The steric force per unit of area that the bilayer exerts on the tip can been modeled using the formalism developed in the work of de Gennes (1987). This model has been further developed by Cappella and Dietler (1999), where interaction between two polymer surfaces was considered. We considered the interaction of the AFM probe and the bilayer, which gives the formula for the steric repulsion force as

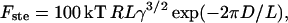graphic file with name M3.gif (2)

where k is the Boltzmann constant, R is the tip radius of curvature, T is the temperature, γ is the tail density (the inverse of the area per lipid), D is the distance between the AFM tip and mica surface, and L is the uncompressed bilayer thickness. Similar to the equation for two interacting polymer surfaces (Cappella and Dietler, 1999), this formula is valid in the range of distances, where 0.2 < D/L < 0.9. The fit of the experimental data using Eq. 2 is plotted as a dotted line in Fig. 6 B.

Since the tip radius is not well defined, it is difficult to estimate the tail density from the fit, but the transition between the two exponential regimes can be a good way to measure the thickness of the bilayer L. At 22°C, a transition occurs at D = 4 nm corresponding to a thickness L = D/0.9 = 4.5 nm which agrees with what is known from the literature (4.7 nm). Contrary to the electrostatic force, the magnitude and the range of the steric force decrease with increasing the temperature. The steric force in a fluid phase, at elevated temperatures, is reduced by 50% compared to a gel phase (see Fig. 6). This can be explained by the reduction of the tail density with the temperature. The tail density is reduced from 1/50 to 1/67.1, considering area per lipid as 50 A2 at room temperature and 67.1 Å2 at 65°C (Petrache et al., 2000; Nagle and Tristam-Nagle, 2000; Janiak et al., 1979), which makes 25% of the difference and therefore a change of 40% in the force if we use Eq. 2. In a fluid regime, i.e., at T > 50°C, the shape of the steric part of the force-distance curve starts to depart from exponential dependence and is similar to the linear abrupt jump observed for fluid-phase DOTAP bilayer at room temperature (Loi et al., 2002). It appears that Eq. 2 is only valid for the gel-phase DPPC bilayer, where lateral motion of the lipids is lower. The transition distance was used to deduce the length L from Fig. 6 B. Results as a function of temperature are collected on the first row of Table 2. The bilayer thickness decreases as observed in AFM imaging mode.

TABLE 2.

Comparison between the length L measured by force analysis, the indentation corresponding to an applied force of 1 nN, and the height given by AFM for a fully hydrated DPPC bilayer

DPPC Thickness of bilayer, estimated from theoretical fit L, in nm Indentation for 1 nN, in nm Thickness of bilayer, measured by AFM cross section, in nm Thickness of bilayer, literature data, in nm
T = 65°C 2.5 4 2.5 —
T = 50°C 3.3 4 3.6 3.6
T = 36°C 3.6 5 4.4 —
T = 22°C 4.5 5.8 5.5 4.7
Open in a new tab

Thickness of DPPC bilayer from literature data are shown for comparison. Literature values are taken from Petrache et al. (2000) and Nagel and Tristam-Nagel (2000).

It is interesting to compare the force analysis and the height measured by image cross-section. In AFM, the applied force is the lowest possible (below 1 nN) required not to deform the surface. In MAC mode, we apply a force <1 nN on the bilayer surface under water; therefore, in the electrostatic regime, the tip is not in contact with the sample. Nanoindentation for a typical force of 1 nN (shown in Table 2) correlates with the thickness of bilayer obtained from AFM image cross-section, but at room temperature is larger than the bilayer thickness determined by other methods (Petrache et al., 2000; Nagle and Tristam-Nagle, 2000; Janiak et al., 1979). Thus, AFM can overestimate the thickness of the layer since repulsive forces can be detected above the layer. This difference appears to be more marked at room temperature than at elevated temperatures due to the decreased mobility of both lipids and water molecules bound to the bilayer interface. Nevertheless, the difference in height in AFM can be used to gain information on the change in layer thickness, if the applied force remains unchanged over the entire scan time.

DOPC bilayer

Adhesion forces

The DOPC bilayer exhibits adhesion behavior similar to that described for the fluid-phase DPPC bilayer. Adhesion forces remain constant up to T = 36°C with a standard error corresponding to a number of bonds of n = 6, as reported in Table 1. The adhesion increases progressively from 36°C to the higher temperatures, which corresponds to an increase in n from 6 to 12. The adhesion force is strongly dependent on v which is a distinctive feature for the fluid phase. Therefore the sensitivity δn/δν can be used to characterize the fluidity of the bilayer.

Repulsive forces

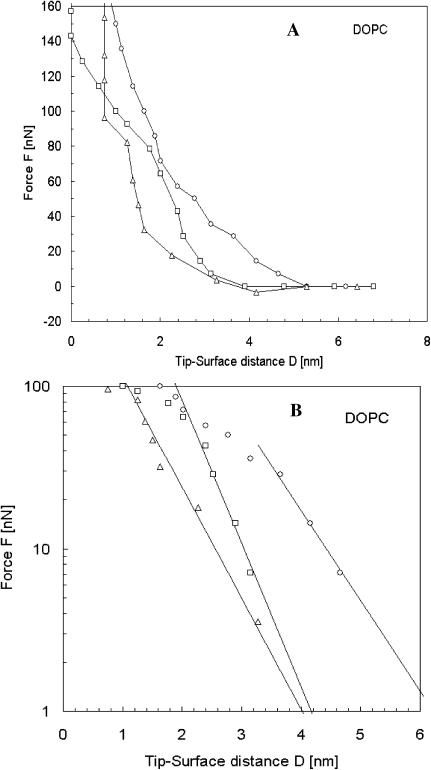
Fig. 7 shows the forces between the fully hydrated DOPC bilayer and the tip during the approach. The same force analysis was performed on DOPC as for DPPC. The electrostatic forces on DOPC are the same order of magnitude as for DPPC. The greatest difference comes from the short-range forces. The thickness of the layer as a function of the temperature is shown in Table 3.

FIGURE 7.

FIGURE 7

Open in a new tab

(A) Evolution of the force acting on the tip as a function of the distance between the tip and mica covered by a DOPC bilayer. Force curves were monitored during the approach of the tip onto the sample for three temperatures (▵, T = 60°C; □, T = 50°C; and ○, T = 22°C). (B) Experimental data represented by symbols were fitted using Eq. 1. The theoretical fit is shown in solid line. The logarithmic representation helps in determination of the range of reliability of the equation and therefore the evaluation of the thickness of the bilayer.

At T = 22°C, the thickness of DPPC and DOPC are close, but with high temperature, the thickness of DOPC is reduced considerably (to 1.5 nm). This likely results from swelling of the bilayer, observed in tapping mode, which should decrease the tail density, and with it the magnitude of the steric force. The increase in the lateral mobility and tilting of lipids at elevated temperatures also decrease repulsive forces considerably, which is in agreement with the measured steric forces in our experiments at higher temperatures.

Comparison of forces for DPPC and DOPC bilayers

When compared, adhesion forces for DPPC and DOPC bilayers show similarity for fluid-phase DPPC bilayer at elevated temperatures and fluid-phase DOPC bilayer at room temperature. The unit force, Fs, for fluid-phase DPPC, is 0.8 nN compared to 0.5 nN for DOPC bilayer (Table 1), and the number of unit bonds is 6 for both fluid-phase DPPC and DOPC bilayers. This correlation permits evaluation of a bilayer fluidity and is in good agreement with imaging data. Therefore, adhesion forces, which depend on physical properties of the bilayer and on force analysis, give important information on the nature of the bilayer. The repulsive part of the force plot, using a steric force model, also provides an important insight into the properties of the bilayer and the ability of lipids to resist compression. Steric forces reduce with the temperature increase for DPPC bilayer and correlate well with low steric forces for DOPC fluid-phase bilayer at room temperature. In general, a fluid-phase bilayer can be characterized by reduced repulsive forces compared to the gel-phase bilayer. The major contribution to this change is provided by changes in steric forces. Lipid compression is much easier in the fluid phase due to the higher disorder of tails, mobility of lipids, and lower tail density.

CONCLUSIONS

Various experimental and theoretical studies have suggested the existence and importance of domains in both biological and model membranes. Nonequilibrium domain formation, which offers a local geometrical environment for membrane processes, may be of considerable importance for the functionality of biological membranes. Here we demonstrated using temperature-controlled atomic force microscopy the existence of several phase transitions in DPPC and DOPC mica-supported bilayers. Data of both topographical imaging and force measurements provide invaluable insight into membrane behavior during phase transitions.

Individual bond forces can be estimated for lipid bilayers as well as changes in binding number which can be used as distinctive features of the increase of bilayer fluidity. A force analysis revealed that the interaction between the tip and the surface was governed by electrostatic forces for longer range and by steric forces at shorter range. Electrostatic repulsion likely originates from an effective charge density at the bilayer-water interface, where zwitterionic headgroups interact with water molecules. Whatever the origin of the effective charge, there is no doubt that the electrostatic force exists since no attractive force was detected during the tip approach. A surface of zero charge should always develop attractive van der Waals forces. In the present study, the electrostatic force is high enough to counterbalance the van der Waals forces.

Steric forces can be used to determine the thickness of the layer adsorbed at the surface and are in good agreement with the image cross-section analysis. With the temperature increase, the steric force departs from a pure exponential law due to the increase of the lateral mobility of the phospholipid tails. The transition between the electrostatic regime and the steric regime for force measurements can be an effective way to estimate the bilayer thickness.

Acknowledgments

The authors thank Dr. W. Han and Dr. S. Wu, Molecular Imaging, Tucson, Arizona, for continuing support and useful discussions.

Financial support from the National Sciences and Engineering Research Council of Canada (D.T.C and T.E.S.D) is gratefully acknowledged.

References

  1. Alakoskela, J.-M., and P. K. J. Kinnunen. 2001. Probing phospholipid main transition by fluorescence spectroscopy and a surface redox reaction. J. Phys. Chem. B. 105:11294–11301. [Google Scholar]
  2. Beckmann, M., P. Nollert, and H.-A. Kolb. 1998. Manipulation and molecular resolution of a phosphatidylcholine-supported planar bilayer by atomic force microscopy. J. Membr. Biol. 161:227–233. [DOI] [PubMed] [Google Scholar]
  3. Biggs, S. 1995. Steric and bridging forces between surfaces bearing adsorbed polymer: an atomic force microscopy study. Langmuir. 11:156–162. [Google Scholar]
  4. Biltonen, R. L., and D. Lichtenberg. 1993. The use of differential scanning calorimetry as a tool to characterize liposome preparation. Chem. Phys. Lipids. 64:129–142. [Google Scholar]
  5. Bizzotto, D., and A. Nelson. 1998. Continuing electrochemical studies of phospholipid monolayers of dioleoyl phosphatidylcholine at the mercury-electrolyte interface. Langmuir. 14:6269–6273. [Google Scholar]
  6. Brian, A. A., and H. M. McConnell. 1984. Allogenic stimulation of cytoxic T cells by supported planar membranes. Proc. Natl. Acad. Sci. USA. 81:6159–6163. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Butt, H. J. 1991. Measuring electrostatic, van der Waals, and hydration forces in electrolyte solutions with an atomic force microscope. Biophys. J. 60:1438–1444. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Butt, H.-J., and V. Franz. 2002. Rupture of molecular thin films observed in atomic force microscopy. I. Theory. Phys. Rev. E. 66:031601. [DOI] [PubMed] [Google Scholar]
  9. Cappella, B., and G. Dietler. 1999. Force-distance curves by atomic force microscopy. Surf. Sci. Rep. 34:1–104. [Google Scholar]
  10. Carnini, A., H. A. Phillips, L. G. Shamrakov, and D. T. Cramb. 2004. Revisiting lipid-general anesthetic interactions. II. Halothane location and changes in lipid bilayer microenvironment monitored by fluorescence. Can. J. Chem. In press.
  11. Cleveland, J. P., T. E. Schäffer, and P. K. Hansma. 1995. Probing oscillatory hydration potentials using thermal-mechanical noise in an atomic-force microscope. Phys. Rev. B. 52:8692–8695. [DOI] [PubMed] [Google Scholar]
  12. De Gennes, P. G. 1987. Polymers at the interface; a simplified view. Adv. Colloid Interface Sci. 27:189–209. [Google Scholar]
  13. Dietrich, C., L. A. Bagatolli, Z. N. Volovyk, N. L. Thompson, M. Levi, K. Jacobson, and E. Gratton. 2001. Lipid rafts reconstituted in model membranes. Biophys. J. 80:1417–1428. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Dimitriadis, E. K., F. Horkay, J. Maresca, B. Kachar, and R. S. Chadwick. 2002. Determination of elastic moduli of thin layers of soft material using the atomic force microscope. Biophys. J. 82:2798–2810. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Dufrêne, Y. F., T. Boland, J. W. Schneider, W. R. Barger, and G. U. Lee. 1998. Characterization of the physical properties of model biomembranes at the nanometer scale with the atomic force microscope. Faraday Discuss. 111:79–94. [DOI] [PubMed] [Google Scholar]
  16. Ebel, H., P. Grabitz, and T. Heimburg. 2001. Enthalpy and volume changes in lipid membranes. I. The proportionality of heat and volume changes in the lipid melting transition and its implication for the elastic constants. J. Phys. Chem. B. 105:7353–7360. [Google Scholar]
  17. Evans, E., K. Ritchie, and R. Merkel. 1995. Sensitive force technique to probe molecular adhesion and structural linkages at biological interfaces. Biophys. J. 68:2580–2587. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Exerowa, D. 2002. Chain-melting phase transition and short-range molecular interactions in phospholipid foam bilayers. Adv. Coll. Interf. Sci. 96:75–100. [DOI] [PubMed] [Google Scholar]
  19. Fasolka, M. J., A. M. Mayes, and S. N. Magonov. 2001. Thermal enhancement of AFM phase contrast for imaging diblock copolymer thin film morphology. Ultramicroscopy. 90:21–31. [DOI] [PubMed] [Google Scholar]
  20. Franz, V., S. Loia, H. Muller, E. Bamberg, and H.-J. Butt. 2002. Tip penetration through lipid bilayers in atomic force microscopy. Coll. Surf. B Biointerf. 23:191–200. [Google Scholar]
  21. Giocondi, M. C., V. Vie, E. Lesniewska, P. E. Milhiet, M. Zinke-Allmang, and C. Le Grimellec. 2001. Phase topology and growth of single domains in lipid bilayers. Langmuir. 17:1653–1659. [Google Scholar]
  22. Han, W., S. M. Lindsay, and T. A. Jing. 1996. Magnetically driven oscillating probe microscope for operation in liquids. Appl. Phys. Lett. 69:1–3. [Google Scholar]
  23. Han, W., and S. M. Lindsay. 1998. Probing molecular ordering at a liquid-solid interface with a magnetically oscillated atomic force microscope. Appl. Phys. Lett. 72:1656–1658. [Google Scholar]
  24. Hui, S. W., R. Viswanathan, J. A. Zasadzinski, and J. N. Israelachvili. 1995. The structure and stability of phospholipid bilayers by atomic force microscopy. Biophys. J. 68:171–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Israelachvili, J. Intermolecular and Surface Forces. 1992. Academic Press, New York.
  26. Janiak, M. J., D. M. Small, and G. G. Shipley. 1979. Temperature and compositional dependence of the structure of hydrated dimyristoyl lecithin. J. Biol. Chem. 254:6068–6078. [PubMed] [Google Scholar]
  27. Kalb, E., J. Engel, and L. K. Tamm. 1990. Binding of proteins to specific target sites in membranes measured by total internal reflection fluorescence microscopy. Biochemistry. 29:1607–1613. [DOI] [PubMed] [Google Scholar]
  28. Kalb, E., S. Frey, and L. K. Tamm. 1992. Formation of planar bilayers by fusion of vesicles to supported phospholipid monolayers. Biochim. Biophys. Acta. 1103:307–316. [DOI] [PubMed] [Google Scholar]
  29. Lee, G. U., D. A. Kidwell, and R. J. Colton. 1994. Sensing discrete streptavidin-biotin interactions with atomic force microscopy. Langmuir. 10:354–357. [Google Scholar]
  30. Leonenko, Z. V., A. Carnini, and D. T. Cramb. 2000. Supported planar bilayer formation by vesicle fusion: the interaction of phospholipid vesicles with surfaces and the effect of gramicidin on bilayer properties using atomic force microscopy. Biochim. Biophys. Acta. 1509:134–147. [DOI] [PubMed] [Google Scholar]
  31. Leonenko, Z., and D. Cramb. 2002. Effects of DNA adsorption on the phase cycling of a supported mixed phospholipid bilayer. Nano Lett. 2:305–309. [Google Scholar]
  32. Leonenko, Z. V., and D. T. Cramb. 2004. Revisiting lipid-general anesthetic interactions. II. Thinned domain formation in supported planar bilayers induced by halothane and ethanol. Can. J. Chem. In press.
  33. Leonenko, Z., D. Merkle, S. P. Lees-Miller, and D. Cramb. 2002. Lipid phase dependence of DNA-cationic phospholipid bilayer interactions examined using atomic force microscopy. Langmuir. 18:4873–4884. [Google Scholar]
  34. Loi, S., G. Sun, V. Franz, and H.-J. Butt. 2002. Rupture of molecular thin films observed in atomic force microscopy. II. Experiment. Phys. Rev. E. 66:031602. [DOI] [PubMed] [Google Scholar]
  35. Marrink, S., O. Berger, P. Tieleman, and F. Jähnig. 1998. Adhesion forces of lipids in a phospholipid membrane studied by molecular dynamics simulations. Biophys. J. 74:931–943. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. McConnell, H. M., T. H. Watts, R. M. Weiss, and A. A. Brian. 1986. Supported planar membranes in studies of cell-cell recognition in the immune system. Biochim. Biophys. Acta. 864:95–106. [DOI] [PubMed] [Google Scholar]
  37. Meyer, H. W., K. Semmler, W. Rettig, W. Pohle, A. S. Ulrich, S. Grage, C. Selle, and P. J. Quinn. 2000. Hydration of DMPC and DPPC at 4°C produces a novel subgel phase with convex-concave bilayer curvature. Chem. Phys. Lipids. 105:149–166. [DOI] [PubMed] [Google Scholar]
  38. Nagle, J. F., and S. Tristam-Nagle. 2000. Structure of lipid bilayers. Biochim. Biophys. Acta. 1469:159–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Nelson, A., and D. Bizzotto. 1999. Chronoamperometric study of TiI reduction at gramicidin-modified phospholipid-coated mercury electrodes. Langmuir. 15:7031–7040. [Google Scholar]
  40. Nielsen, L. K., J. Risbo, T. H. Callisen, and T. Bjornholm. 1999. Lag-burst kinetics in phospholipase A2 hydrolysis of DPPC bilayers visualized by atomic force microscopy. Biochim. Biophys. Acta. 1420:266–271. [DOI] [PubMed] [Google Scholar]
  41. Nollert, P., H. Kiefer, and F. Jahnig. 1995. Lipid vesicle adsorption versus formation of planar bilayers on solid surfaces. Biophys. J. 69:1447–1455. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Pearce, K. H., R. G. Hiskey, and N. L. Thompson. 1992. Surface binding kinetics of prothrombin fragment-1 on planar membranes measured by total internal-reflection fluorescence microscopy. Biochemistry. 31:5983–5995. [DOI] [PubMed] [Google Scholar]
  43. Petrache, H. I., S. W. Dodd, and M. F. Brown. 2000. Area per lipid and acyl length distributions in fluid phosphatidylcholines determined by 2H NMR spectroscopy. Biophys. J. 79:3172–3192. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Ramsden, J. J., and P. Schneider. 1993. Membrane insertion and antibody recognition of a glycosylphosphatidylinositol-anchored protein: an optical study. Biochemistry. 32:523–529. [DOI] [PubMed] [Google Scholar]
  45. Schmidt, A., J. Spinke, T. Bayerl, E. Sackmann, and W. Knoll. 1992. Streptavidin binding to biotinylated lipid layers on solid supports. Biophys. J. 63:1185–1192. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Schneider, J., Y. F. Dufrêne, W. R. Barger, Jr., and G. U. Lee. 2000. Atomic force microscope image contrast mechanisms on supported lipid bilayers. Biophys. J. 79:1107–1118. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Senden, T. J., C. J. Drummond, and P. Kékicheff. 1994. Atomic force microscopy: imaging with electrical double layer interactions. Langmuir. 10:358–362. [Google Scholar]
  48. Singh, S., and D. J. Keller. 1991. Atomic force microscopy of supported planar membrane bilayers. Biophys. J. 60:1401–1410. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Sonnleitner, A., G. J. Schutz, and T. Schmidt. 1999. Free Brownian motion of individual lipid molecules in biomembranes. Biophys. J. 77:2638–2642. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Stelze, M., and E. Sackmann. 1989. Sensitive detection of protein adsorption to supported lipid bilayers by frequency dependent capacity measurements and microelectrophoresis. Biochim. Biophys. Acta. 981:135–142. [DOI] [PubMed] [Google Scholar]
  51. Tamm, L. K., and H. M. McConnell. 1985. Supported phospholipid bilayers. Biophys. J. 47:105–113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Tenchov, B., R. Koynova, and G. Rapp. 2001. New ordered metastable phases between the gel and subgel phases in hydrated phospholipids. Biophys. J. 80:1873–1890. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Tokumasu, F., A. J. Jin, and J. A. Dvorak. 2002. Lipid membrane phase behaviour elucidated in real time by controlled environment atomic force microscopy. J. Electr. Microsc. 51:1–9. [DOI] [PubMed] [Google Scholar]
  54. van der Vegte, E. W., and G. Hadziioannou. 1997. Scanning force microscopy with chemical specificity: an extensive study of chemically specific tip-surface interactions and the chemical imaging of surface functional groups. Langmuir. 13:4357–4368. [Google Scholar]
  55. Vesenka, J., S. Manne, R. Giberson, T. Marsh, and E. Henderson. 1993. Colloid gold particles as an incompressible atomic force microscope imaging standard for assessing the compressibility of biomolecules. Biophys. J. 65:992–997. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Williams, J. M., T. Han, and T. P. Beebe, Jr. 1996. Determination of single-bond forces from contact force variances in atomic force microscopy. Langmuir. 12:1291–1295. [Google Scholar]
  57. Xie, A. F., R. Yamada, A. A. Gewirth, and S. Granick. 2002. Materials science of the gel to fluid phase transition in a supported phospholipid bilayer. Phys. Rev. Lett. 89:6103–6106. [DOI] [PubMed] [Google Scholar]
  58. Yang, J., and J. Appleyard. 2000. The main phase transition of mica-supported phosphatidylcholine membranes. J. Phys. Chem. B. 104:8097–8100. [Google Scholar]
  59. Zasadzinski, J. A., C. A. Helm, M. L. Longo, A. L. Weisenhorn, S. A. Gould, and P. K. Hansma. 1991. Atomic force microscopy of hydrated phosphatidylethanolamine bilayers. Biophys. J. 59:755–760. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES