Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Jun;86(6):3905–3913. doi: 10.1529/biophysj.104.040055

Competing Hydrophobic and Screened-Coulomb Interactions in Hepatitis B Virus Capsid Assembly

Willem K Kegel 1, Paul van der Schoot 1
PMCID: PMC1304292  PMID: 15189887

Abstract

Recent experiments show that, in the range from ∼15 to 45°C, an increase in the temperature promotes the spontaneous assembly into capsids of the Escherichia coli-expressed coat proteins of hepatitis B virus. Within that temperature interval, an increase in ionic strength up to five times that of standard physiological conditions also acts to promote capsid assembly. To explain both observations we propose an interaction of mean force between the protein subunits that is the sum of an attractive hydrophobic interaction, driving the self-assembly, and a repulsive electrostatic interaction, opposing the self-assembly. We find that the binding strength of the capsid subunits increases with temperature virtually independently of the ionic strength, and that, at fixed temperature, the binding strength increases with the square root of ionic strength. Both predictions are in quantitative agreement with experiment. We point out the similarities of capsid assembly in general and the micellization of surfactants. Finally we make plausible that electrostatic repulsion between the native core subunits of a large class of virus suppresses the formation in vivo of empty virus capsids, that is, without the presence of the charge-neutralizing nucleic acid.

INTRODUCTION

For many kinds of virus, the self-assembly of the empty virus core shells (or capsids) from their protein subunits resembles that of surfactant micelles (Debye, 1949), in the sense that one either finds only the protein subunits present in the aqueous solution, or the protein subunits in equilibrium with the fully assembled capsids (Tanford, 1980). For both capsids and micelles, the transition between the assembled and disassembled states is a fairly sharp function of the concentration of dispersed material (see e.g., Bruinsma et al., 2003; Caspar, 1963, 1980; Zlotnick, 1994).

Building on the idea that capsid assembly is subject to the laws of equilibrium thermodynamics, Ceres and Zlotnick (2002) recently calculated the free energy of interaction between Escherichia coli-expressed hepatitis B virus coat proteins assembled into predominantly T = 4 type capsids by fitting an association equilibrium model to their experimental data. These coat proteins, denoted Cp1492, form capsids indistinguishable from the native HBcAg core protein subunits (Zlotnick et al., 1996). At near neutral pH, they found the strength of the attractive interaction between the homodimeric Cp1492 proteins to be quite modest, of the order of a few times the thermal energy per subunit contact. The precise value of the free energy of interaction was found to increase with increasing temperature and with increasing ionic strength, at least within the ranges probed (Ceres and Zlotnick, 2002). The strengthening of the attractive interaction between the subunits with increasing temperature indicates that the in vitro assembly of hepatitis B virus capsids is driven by hydrophobic interactions, which are entropic in nature (Tanford, 1980). To rationalize the effect of the ionic strength, Ceres and Zlotnick (2002) conjecture that the subunits more easily adopt an assembly active conformation at elevated ionic strengths (see also Caspar, 1980).

In this work, we offer an alternative interpretation of the observations of Ceres and Zlotnick, amenable to experimental verification. The basic tenet of our proposal is that the attractive hydrophobic interactions that seem to promote the self-assembly of hepatitis B virus capsids must be counteracted by repulsive electrostatic interactions between the subunits. The latter can be weakened by the addition of inert salt. If we translate this presumption into a coarse-grained potential of mean force acting between the subunits, modeled as structureless, quasimacroscopic objects, we find that it becomes possible to quantitatively describe the scaling of the equilibrium constant of the hepatitis B virus capsid assembly with the temperature, as well as that with the ionic strength. The treatment we adopt allows us to extract information on the properties of the hydrophobic surfaces buried upon assembly of the capsid as well as on the net charge of the water-exposed surface from the available experimental data.

The concept of a potential of mean force that is the sum of attractive and repulsive contributions has proven quite useful in the context of the stability of charged colloids (Israelachvili, 1992; Verwey and Overbeek, 1999), including that of proteins (Broide et al., 1996). For the case of virus coat protein subunits, however, the dominant attractive interactions seem to arise from hydrophobic interactions between parts of the proteins, rather than from the van der Waals interactions that destabilize colloidal dispersions (Curtis et al., 2002; Verwey and Overbeek, 1999). In fact, as already advertised, there seems to be a closer analogy between the assembly of virus capsids and the micellization of surfactant molecules in aqueous solutions than that with the demixing of colloidal particles. Surfactants and capsid subunits both unite polar and less polar moieties within a single molecule, and the phenomena of micellization and capsid assembly both presumably involve the microphase separation of the apolar parts of the molecules due to hydrophobic interactions (Caspar, 1980; Ceres and Zlotnick, 2002; Lauffer, 1966). It might be useful to mention in this context that the self-assembly of ionic amphiphiles can be promoted by the addition of inert ions that screen the electrostatic repulsion between the charged headgroups (Gunnarsson et al., 1980; Tanford, 1980).

The remainder of this article is set up as follows. First, we briefly review the kinds of interaction that could be involved in the hepatitis B virus capsid assembly, and eliminate those that are in all likelihood either too weak or that produce a temperature or ionic strength dependence at odds with the observations of Ceres and Zlotnick. For the driving force we presume that these are well described by a phenomenological hydrophobic interaction potential valid for pairs of macroscopic hydrophobic surfaces (Israelachvili, 1992). We make plausible that if there is a net charge present on the water-exposed portions of the capsid proteins, this produces a repulsive interaction inversely proportional to the root of the ionic strength irrespective of the precise details of the local geometry of the capsid, provided its radius is much larger than the subunit size. By analyzing the linear temperature dependence of the resulting net interaction strength, we find that the leading-order term can be associated with the excess surface enthalpy of the hydrophobic interfaces between subunits buried in the capsid.

Next, we apply our findings to the thermodynamics of the association equilibrium between the free dimer subunits and the fully formed capsids, and formulate the connection between the equilibrium constant and the free energy of subunit assembly. We fit our expression for the latter to the experimental data taken from Ceres and Zlotnick (2002) and find, within the bounds of experimental uncertainty, quantitative agreement. The values of the fitting parameters extracted are the effective surface charge density of the water-exposed surface area of the capsid, and the excess thermodynamic potentials associated with the hydrophobic faces of the capsid proteins that are shielded from the aqueous solvent upon aggregation. In analogy with the critical micelle concentration, we introduce the concept of a critical capsid concentration and show that hepatitis B capsid assembly seems to obey a universal law of mass action. Finally, we end the article with an outline of our main conclusions and with a discussion where we make a testable prediction as to the pH dependence of the equilibrium constant.

FREE ENERGY OF ASSOCIATION

There are many types of interaction that might be involved in the stabilization of hepatitis B virus capsid assemblies, as in fact there are in any type of supramolecular polymer (Ciferri, 2000). Obvious ones are Coulomb interactions between oppositely charged moieties, hydrogen bonds, van der Waals interactions (including specific ion effects, see e.g., Ninham and Yaminsky, 1997), and hydrophobic interactions between apolar patches on the surfaces of the proteins. Of these, only the hydrophobic interactions become potentially stronger with increasing temperature. We furthermore note that all the others are weakened by the addition of inert 1:1 salt (Tanford, 1980). For hepatitis B capsids, the buried contact area between the assembled capsid proteins appears to be largely hydrophobic (Ceres and Zlotnick, 2002). Any putative salt bridges or other types of electrostatic interaction (even at high salt concentration) are unlikely to contribute significantly to the protein binding energy, because the hydrophobic character of the contact area leads to a significant loss of solvation of the groups involved if removed from the aqueous environment in the aggregation process (vanVlijmen et al., 1998). Further support for the importance of hydrophobic interactions in capsid assembly comes from the observation that capsid formation is strongly inhibited by bis-ANS (5, 5′-bis[8-(phenylamino)-1-naphtalenesulfonate]) (Zlotnick et al., 2002). This molecule is known to bind specifically to hydrophobic surface patches.

We are led to conclude that hydrophobic interactions must indeed be the dominant driving force toward the assembly of hepatitis B virus capsids, as was in fact also concluded by Ceres and Zlotnick (2002). A phenomenological potential describing hydrophobic interactions between two identical apolar surfaces in water is (Israelachvili, 1992),

graphic file with name M1.gif (1)

where γ denotes the surface tension between hydrophobic material and aqueous phase, A the contact area, D the separation of the surfaces, and λ a decay length of the order of a few nanometers provided D < λ (at larger separations a longer decay length with a different amplitude takes over; Israelachvili, 1992). Both the surface tension γ and the length λ depend, if only in principle, upon the salt concentration (Toikka et al., 1996). At contact, D should be on the atomic scale, so D/λ ≪ 1, and the issue of λ being ionic strength-dependent or not becomes irrelevant.

Not quite so irrelevant is the ionic strength-dependence of the surface tension γ. As is well known, the surface tension between water and an apolar medium of low dielectric constant increases with increasing salt concentration. This is caused by a surface depletion effect, induced by the interaction of the ions with their own image charges (Onsager and Samaras, 1934). From the recent theory of Levin (2000) we deduce that the surface tension increment due to the presence of a 1:1 electrolyte of molar concentration cs > 0.1 M must at room temperature obey γ–γ(0) ≈ 0.06 + 1.2 cS in units of mN/m. Here, γ(0) denotes the bare surface tension in the absence of salt. Measurements of the surface tension of water against air do indeed give a linear dependence on the ionic strength, albeit not quite in agreement with the theoretical prediction, with γ–γ(0) ≈ 1.6 cS again in units of mN/m for salt concentrations up to one molar (Matubayasi et al., 1999). This suggests that for cS < 1 M, the surface tension increment due to the presence of salt is at most 1.6 mN/m and probably less than that because the effective dielectric constant of the interior of the proteins is likely to be higher than that of air. Perhaps more importantly, corrections due to the finite size of the proteins should fairly strongly diminish the depletion effect and therefore also the surface-tension increment (Messina, 2002). For this reason, we presume that we can ignore the salting-out effect that the electrolyte may have on the dimer subunits through the surface-tension increment it induces. This assumption may fail for salt concentration in excess of ∼1 M. We finally note in this context that it was shown by Ceres and Zlotnick (2002) that the electrolyte is unlikely to impact upon the self-assembly by merely altering the activity of bulk water. If this were the case, the addition of nonionic solutes such as sucrose should have a comparable effect. However, adding sucrose at concentrations in excess of 1 M was incapable of inducing capsid formation (Ceres and Zlotnick, 2002).

In the light of these considerations, we write for the free energy of binding upon assembly of a complete aggregate

graphic file with name M2.gif (2)

with n the mean number of quasiequivalent hydrophobic contacts of a subunit in the capsid, and q ≫ 1 the number of subunits per capsid. Note that of the quantities in Eq. 2, both A and γ ≈ γ(0) may be a function of the temperature. In the following, we ignore any temperature dependence of the contact area.

If the salting-out of the hydrophobic surfaces cannot account for the observed influence of the ionic strength on the stability of the hepatitis B capsids, the question is what does? The answer must, in our view, be that the protein subunits carry a net charge at near neutral pH. Note that the presence of charges stabilizes the proteins, and ipso facto also the capsids, against macroscopic phase separation (i.e., demixing). By the same token, however, the charges on the subunits also destabilize the micro-phase-separated state that the capsids represent, because it makes the subunits repel each other. Consequently, hepatitis B capsid assembly must be enhanced with increasing ionic strength because the presence of salt screens the Coulomb interactions between charges that are separated by more than roughly a Debye screening length. So, we put forward not that the attractive interactions between the subunits are enhanced by the presence of salt, as was suggested in Ceres and Zlotnick (2002), but that the repulsive interactions are diminished.

The problem now is of course how to calculate the effective electrostatic repulsion between the subunits without actually having to explicitly deal with the complexities of the T-shaped structure of the subunits (Conway et al., 1997), as well as that of the fully formed capsid, which is covered with four types of perforating hole ranging in width from ∼1 to 3 nm (Zlotnick et al., 1996). Fortunately, we do not need to because the mean capsid diameter of ∼30 nm is significantly greater than the various length scales of the structure on it. For example, the maximum shell thickness is ∼5 nm at the location of the spikes on the capsids, but it is much smaller than that on most of the shell's surface. This allows us to coarse-grain the charge distribution on the surface of the capsid. We note that the inside and outside surface of the capsid are connected through open passages so the actual distribution of the net charge may in fact be three-dimensional.

Within a Debye-Hückel approximation, the potential of mean force VC acting between two charges located at positions → and →′ on the water-exposed surface of the virus capsid can be written (Verwey and Overbeek, 1999) as

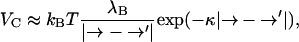graphic file with name M3.gif (3)

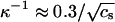where kB denotes Boltzmann's constant, T the absolute temperature, λB = e2/4πɛ0ɛrkBT the Bjerrum length, and Inline graphic the Debye screening length, with e the unit charge, ɛ0 the permittivity of vacuum, ɛr the relative permittivity of the medium (water), and ρS the number density of the 1:1 electrolyte (in units of m−3). Obviously, cS = 10−3 ρS/NA with NA Avogadro's number. At room temperature, λB ≈ 0.7 nm and Inline graphic nm. To explicitly calculate the (nonlocal) free energy GC associated with the Coulomb interaction between the subunits that make up the capsid, we need to perform a summation of Eq. 3 over all pairs of charges on the capsid but exclude those present on the same protein subunit. The calculation is greatly facilitated if we presume that the (net) charge is uniformly distributed over a spherical shell of mean radius R and thickness d ≪ R. Let there be z (net) unit charges on each of the q-dimer subunits. Straightforward algebra then gives

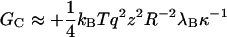graphic file with name M6.gif (4)

to leading order in d/R ≪ 1, and provided κR > 1. On account of the large size of the hepatitis B virus capsids, this latter condition is met when cS > 4 mM. Notice the strong impact of the ionic strength on GC through the 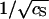Inline graphic-dependence of the Debye length κ−1. It is in our view precisely this term that makes the self-assembly of hepatitis B virus capsids so sensitive to the ionic strength. Quite similar expressions have been derived in the context of the self-assembly of charged micelles (Gunnarsson et al., 1980; Tanford, 1980), and in that of end-charged dendrimers (Lyulin et al., 2003).

It is of interest to note that the above expression approximately applies even if κd > 1, and one is probing the detailed structure of the capsid ignored in our calculation. That this must be so can be made plausible as follows. At high salt concentration, one would only expect charged patches on neighboring subunits to interact significantly. Presuming that such patches can be represented by more or less flat, parallel surfaces, we have for the potential of mean force (Israelachvili, 1992)

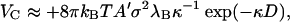graphic file with name M8.gif (5)

with A′ the surface area of interaction, σ the net surface density of charges, and 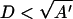Inline graphic again the separation of the surfaces. In analogy to our analysis of the hydrophobic interaction, we thus write

graphic file with name M10.gif (6)

at least for κD ≪ 1. Because the patches involved in the electrostatic interactions are unlikely to be the same ones as those that interact through hydrophobic interactions, the areas A and A′ as well as the (effective) number of contact neighbors n and n′ need not be identical. It is easy to verify that, apart for a (geometrical) constant, Eqs. 6 and 4 are indeed identical, for σ = z/n′A′ and the total surface area involved in Coulomb interactions may be defined as n′qA′.

On the basis of the above considerations, we propose the following Ansatz for the free energy of interaction associated with the assembly of a complete hepatitis B virus capsid,

graphic file with name M11.gif (7)

which we expect to apply for concentrations of salt below, say, 1 M. In Eq. 7, we recognize in the first term the hydrophobic attraction that drives the self-assembly of capsid, proportional to the total hydrophobic area AH ≈ 2nqA buried in the formation of the capsid and shielded from contact with the solvent. Counteracting the effects of the hydrophobic attraction is an electrostatic repulsion proportional to the exposed charged surface area, so AC ≈ n′qA′ if we absorb an uninteresting dimensionless geometrical constant in the effective area AC. Our approach is not identical to but is similar in spirit to that of Odijk (1994), who studied the impact of hydrophobic interactions on the second and third virial coefficient of charged, rod-like biopolymers.

If we perform a Taylor expansion of γ around an arbitrary reference temperature, T0, we obtain

graphic file with name M12.gif (8)

for absolute temperatures T that are not too far removed from T0, i.e., for |T−T0|≪T0. The quantity s(T0) ≡ −(∂γ/∂T)T0 is the (bare) surface excess entropy of the hydrophobic surface in contact with water at the temperature T = T0. It turns out that the quantity s is less than 0 for a whole range of hydrophobic interfaces over a fairly large temperature domain, implying that the hydrophobic attraction between the subunits should indeed increase with increasing temperature, as expected (Claesson et al., 1986; Israelachvili, 1992; Villers and Platten, 1988). The repulsive, Coulomb part of Eq. 7 increases much more slowly with temperature, as we shall see in the next section. As a consequence, the dependence of the strength of the interactions between subunits on temperature is fully determined by the value of s(T0).

THE EQUILIBRIUM CONSTANT

The hepatitis B virus capsid of interest consists of 120 dimer subunits making up a spherical capsid shell of icosahedral symmetry and a triangulation number T = 4. (Only a small fraction of the capsids have a triangulation number T = 3 (Ceres and Zlotnick, 2002).) Let the dimers be denoted by A1 and the fully formed capsid by Aq, where q = 120 for the hepatitis B capsid. To an excellent approximation, the self-assembly of the capsids can be described by an equilibrium reaction qA1 ↔ Aq, because partially formed capsids are only present in exceedingly low relative amounts (Ceres and Zlotnick, 2002; Zlotnick, 1994). Thermodynamic equilibrium demands that qμ1 = μq, with μ1 chemical potential of the dimers and μq that of the complete capsids. Assuming the dispersion to be dilute, the chemical potential of each component i can be written as 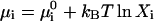Inline graphic, where 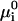Inline graphic denotes a standard chemical potential and Xi the mole fraction of component i. In the dilute limit, we may approximate Xi ≈ ci/55.6 with ci the concentration of component i in M. (The molarity of pure water at room temperature is close to 55.6 M.) For the equilibrium concentration of capsids, we thus obtain

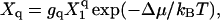graphic file with name M15.gif (9)

with gq the number of distinguishable ways in which the capsid can be realized (the degeneracy), and

graphic file with name M16.gif (10)

Due to the highly ordered, crystal-like structure of the capsid one would sensibly expect gq to be equal to unity (Zlotnick, 1994). The second, approximate equality in Eq. 10, involving the binding free energy G, holds if it greatly exceeds a thermal energy per subunit; hence, if G ≫ q kBT. In that case, the effective free energy change due to the bonding into the capsid structure predominates, and we need not consider potential contributions from large-scale elastic deformation or breathing modes (Morse and Milner, 1995), nor from a possible conformational change of the protein dimers upon assembly. There appears to be little evidence for the latter (Wingfield et al., 1995), albeit that it cannot be ruled out altogether (Ceres and Zlotnick, 2002).

We stress that there should be no quantum-mechanical contributions in Eqs. 9 and 10 arising from rotational or any other degrees of freedom, including those associated with the so-called cratic entropy, for in the coarse-grained description the solvent degrees of freedom have effectively been integrated out, as have those of the counterions. This means that the smallest length is set by the solvent size, not by the thermal wavelength. (For a discussion of this point, see e.g., Reiss et al., 1996.)

The dimensionless equilibrium constant, K, is related to the above quantities by

graphic file with name M17.gif (11)

and to the dimension-bearing equilibrium constant Kcapsid, defined in Ceres and Zlotnick (2002), according to ln K ≈ ln Kcapsid + (q–1)ln 55.6 = ln Kcapsid + 478.2. Inserting Eq. 7 into Eq. 11, and expanding it to linear order in the temperature relative to a reference temperature T0, we obtain

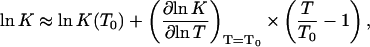graphic file with name M18.gif (12)

with

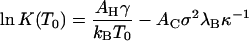graphic file with name M19.gif (13)

and

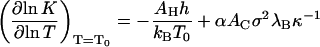graphic file with name M20.gif (14)

both evaluated at T = T0. Here, we have for simplicity presumed that the interactions areas, AC and AH, as well as the surface charge density, σ, are invariants of the temperature. (This may be valid over a limited range of conditions only.) The quantity α ≡ ½ + ½ (∂ln ɛr/∂ln T)T = T0 is a measure for the sensitivity of the Coulomb interactions between the subunits and temperature changes, and h(T0) = γ(T0) + T0s(T0) denotes the (bare) excess surface enthalpy of the hydrophobic surface at the reference temperature T = T0. For bulk water, α ≈ −0.14 (Weast et al., 1984), suggesting that the reference value of the association constant at T = T0, Eq. 13, must be a much stronger function of the ionic strength than its differential increment with temperature, Eq. 14. As we shall see, this is borne out by the measurements of Ceres and Zlotnick (2002).

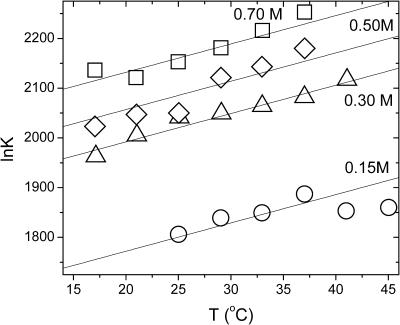
The equilibrium constants of the hepatitis B capsid assembly obtained by Ceres and Zlotnick (2002) for a range of temperatures and salt concentrations are plotted in Fig. 1. The model predicts that if we plot ln K versus temperature T we should get a straight line with a slope 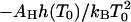Inline graphic, at least if we ignore the expected weak dependence on the ionic strength and set α = 0 in Eq. 14. (Below we show that this is justifiable.) Applying a least-squares linear fitting procedure to the data of Fig. 1 did not produce any indication of a systematic dependence of the slopes on the salt concentration within the experimental uncertainty, confirming our expectation. For this reason, we average the values for the fitted slopes. Our theoretical fits are also shown in the Fig. 1, where we see a single slope with a tangent of 5.7 ± 2.4 K−1 fits all the data reasonably well. This implies that for the hepatitis B capsid, 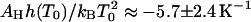Inline graphic. If we arbitrarily set the reference temperature at T0 = 273.15 K, and if we make use of the estimated buried hydrophobic surface area of AH ≈ 120 × 1.3 × 10−17 = 1.56 × 10−15 m2 (Ceres and Zlotnick, 2002), we get for the bare excess surface enthalpy a value of h(T0) ≈ −3.8 mN/m, equivalent to about −13 kBT per subunit. (Note that our binding enthalpy and that defined in Ceres and Zlotnick, 2002, differ in sign by construction.)

FIGURE 1.

FIGURE 1

Open in a new tab

The logarithm of the equilibrium constant, ln K, as a function of temperature, T, at various salt concentrations as indicated in the figure. Symbols are data from Ceres and Zlotnick (2002). Lines are linear fits with a fixed slope of +(5.7 ± 2.4) K−1. The extrapolated values of ln K at T = T0 = 273 K are plotted in Fig. 2.

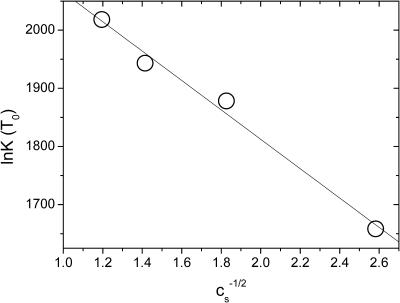
At the reference temperature T0, we have ln K(T0) ≈ AHγ(T0)/kBT0 − ACσ2 λBκ−1(T0). Hence, if we plot the experimentally obtained values for ln K(T0) as a function of Inline graphic, we should get a straight curve with negative slope. Fig. 2 confirms that this is the case. The slope of the curve is a measure for the surface charge density, whereas γ(T0) follows from the intercept at Inline graphic for which the electrostatic interactions are completely screened by the presence of an infinite amount of salt. From the intercept of the linear fit to the data of Fig. 2, we extract AHγ(T0)/kBT0 ≈ 2317 ± 35. Note that this value is to be compared (and indeed comparable) to the values of the “enthalpy per contact” as reported by Ceres and Zlotnick (2002). Insertion of the estimate AH ≈ 1.56 × 10−15 m2 (Ceres and Zlotnick, 2002) produces a bare surface tension of γ(T0) ≈ +5.5 mN/m, and an excess surface entropy of s(T0) = (h(T0) − γ(T0))/T0 ≈ −0.03 mN/mK. The latter finding is consistent with the hydrophobic interaction data of Claesson et al. (1986), which point at typical values for s of the order of −0.01 mN/mK for T ≈ 303 K. The value we find for the surface tension γ is roughly an order-of-magnitude smaller than that of ∼50 mN/m between water and oil, but comparable to that between water and hexanol (Villers and Platten, 1988). Apparently, the hydrophobic surfaces on the subunits are only weakly hydrophobic, a conclusion that may in fact also be drawn from the slightly negative value of the bare surface excess enthalpy that we found by fitting our theory to the data.

FIGURE 2.

FIGURE 2

Open in a new tab

The logarithm of the equilibrium constant, ln K, at the temperature T = T0 = 273 K as a function of the inverse square-root of the salt concentration 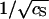Inline graphic. The slope of the fitted line is −(253 ± 19) and its intercept is +(2317 ± 35). See the main text for an interpretation of these values.

From the fitted line to the data of Fig. 2, we find for the quantity ACσ2 ≈ (253 ± 19)/2.1 × 10−19 ≈ (1.2 ± 0.1) × 1021 m−2. If we naively replace AC by the estimated surface area of the capsids, equal to ∼2.8 × 10−15 m2, we get for the effective surface charge density at near-neutral pH a value of σ ≈ 6.7 × 1017 m−2, or ∼0.7 charge per nm2. This is close to the limit where one would expect charge renormalization to take place (Trizac et al., 2003), and corresponds to ∼15 net charges per dimer subunit or to 7–8 net charges per protein molecule. Whether this is realistic or not is difficult to ascertain at this point, considering that (as far as we are aware) no acid-base titration data are available in the literature. Also, theoretical acid-base titration curves, such as available for foot-and-mouth disease virus capsids (vanVlijmen et al., 1998), seem to be lacking for hepatitis B virus capsids. Note that, ideally, one would determine the net charge of the capsid, e.g., in an electrophoresis or conductivity experiment, and use that to calculate the total area exposed to the water, AC. It is at least reassuring that the number of charges that we find is significantly smaller than the total number of chargeable groups on Cp1492, being 15 negative plus 11 positive charges as an upper bound (Reddy et al., 2001).

With all the model parameters fixed, we are now in the position to assess the internal consistency of our treatment by evaluating the relative contribution of the Coulomb interaction to the quantity ∂ln K/∂ln T evaluated at T = T0 given in Eq. 14. Inserting the found values for the various model parameters, we obtain for the ratio 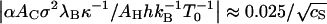Inline graphic. This shows that the electrostatic contribution to the slope of Fig. 1 is <6% for 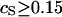Inline graphic M. This is consistent with the observations, and justifies our neglect of this contribution a posteriori.

We now make connection with the theory of micellization (Israelachvili, 1992; Tanford, 1980), allowing us to predict the equivalent of the so-called critical micelle concentration, the critical capsid concentration that we denote by c*. We (arbitrarily) define c* as that overall concentration of protein subunits at which half of them is absorbed into assemblies. Combining Eq. 11 with the law of conservation of mass, c = c1 + qcq, where c denotes the molar concentration of subunits in the solution, gives

graphic file with name M27.gif (15)

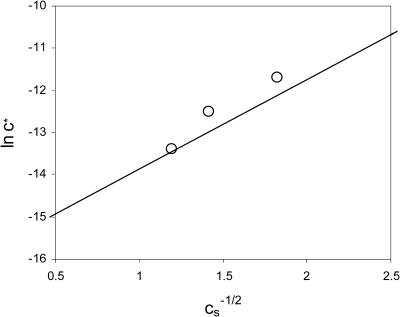
Here, c* is the critical capsid concentration in M, and ln K is given by Eq. 12. Since according to our theory the equilibrium constant is a sensitive function of the ionic strength, so should be the critical capsid concentration c*. It shifts to lower values with increasing salt concentration in agreement with the data of Ceres and Zlotnick (2002), as is shown in Fig. 3. A similar phenomenon can also be observed in micelles of charged surfactants (Gunnarsson et al., 1980).

FIGURE 3.

FIGURE 3

Open in a new tab

The logarithm of the critical capsid concentration, ln c*, versus the inverse square-root of the salt concentration, 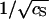Inline graphic. The straight line gives our theoretical fit to the measured equilibrium constants of Ceres and Zlotnick (2002). The circles are estimates from the experimental association curves given in Fig. 1 B of Ceres and Zlotnick (2002).

With the critical capsid concentration defined, it is now straightforward to show that the fraction material absorbed in capsids, f ≡ qcq/c, is a universal function of c/c*, or, in other words, that f = f(c/c*) is independent of the temperature, the ionic strength and, in fact, the pH. From Eqs. 9, 10, and 15, it follows that

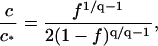graphic file with name M28.gif (16)

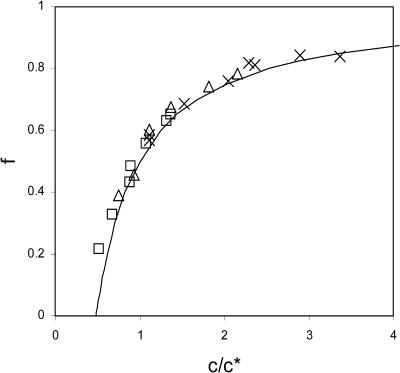
where q is again the aggregation number. In Fig. 4 we have plotted f as a function of c/c* for the data given in Fig. 1 B of Ceres and Zlotnick (2002) for the three ionic strengths 0.3, 0.5, and 0.7 M, showing that our analysis is indeed pertinent and that there is indeed a close resemblance between capsid assembly and micellization.

FIGURE 4.

FIGURE 4

Open in a new tab

The fraction of material assembled into capsids, f, versus the overall concentration of dimer subunits c, scaled to the critical capsid concentration c*. The symbols represent the data from Ceres and Zlotnick (2002) for samples at a temperature of 25°C. Crosses, cS = 0.7 M; triangles, cS = 0.5 M; and squares, cS = 0.3 M. The drawn line is the universal aggregation curve, given by Eq. 16.

It is important to point out that if q ≫ 1, Eq. 16 simplifies to f ≈ 1 − c*/2c for c ≥ c*/2 and f ≈ 0 for c < c*/2, i.e., the crossover from the monomeric to the polymeric regime becomes quite sharp as in fact is also evident from Fig. 4. The aggregation curve is therefore relatively insensitive to the relative amounts of T = 3 (with q = 90) and T = 4 capsids (with q = 120). In the limit q → ∞, the polymerization or capsidization transition becomes infinitely sharp, and equivalent to a phase transition reminiscent of the Bose-Einstein condensation of ideal bosons (Cuesta and Sear, 2002).

DISCUSSION AND CONCLUSIONS

Zlotnick and co-workers have convincingly shown that the assembly of hepatitis B capsids can be understood in terms of a chemical equilibrium that is regulated by a combination of mass action, and the intrinsic propensity of the capsid core proteins to aggregate (Ceres and Zlotnick, 2002; Zlotnick, 1994). In this work, we believe to have made plausible that this propensity to aggregate is due to hydrophobic interactions, as in fact seems to be the case for many types of capsid (Ceres and Zlotnick, 2002), but that it is counteracted by screened Coulomb interactions between charged moieties on the dimer subunits.

Our suggestion that the stability of the capsids is intimately linked with the presence of charges on them implies that the capsid assembly must be pH-dependent, if only in principle. The reason is that to a lowest order of approximation the surface charge density is a function of the pH according to

graphic file with name M29.gif (17)

at least if all the ionizable groups behave independently. (However, this may be too crude an approximation. See e.g., Boström et al., 2003.) Here, σa and σb denote the maximum surface charge densities of acidic and basic groups. Eq. 17 is a consequence of the well-known Henderson-Hasselbalch equation (Stryer, 1980), where we have for simplicity lumped all acidic groups and all basic groups together, and assign an effective pKa for the former and an effective pKb for the latter. A tentative estimate for both pK values and both surface charge densities may be obtained from the primary sequence of the hepatitis B monomer subunit protein (Reddy et al., 2001) by presuming that all acidic and basic peptide residues are water-exposed. This allows one to estimate the pH for which σ ≈ 0 and the capsid is approximately charge-neutral, that is, estimate its isoionic value denoted as pI. We find that pI ≈ 6–7 for the Cp1492 hepatitis B virus capsid proteins studied by Ceres and Zlotnick (2002). This implies that the surface charge density should increase with increasing pH above its neutral value, leading to a reduced stability of the virus capsids.

There is in fact experimental evidence to support this prediction, albeit not on the Cp1492 protein, but on a closely related variant of the hepatitis B virus protein known as HBeAg. Like the Cp1492 protein, HBeAg does not carry the C-terminal protamine domain present in the core protein HBcAg, but it does have a N-terminal extension not present on the Cp1492 protein (Wingfield et al., 1995). The HBeAg protein dimers readily form capsids too, albeit mainly of the T = 3 type, which with a dimer aggregation number of q = 90 are somewhat smaller in size than the T = 4 species formed by the HBcAg and Cp1492 proteins. Wingfield and collaborators found that for a particular choice of ionic strength and HBeAg protein concentration, the amount of protein absorbed into capsids strongly decreases from >80% to practically nil when increasing the pH from 7 to 9.5 (Wingfield et al., 1995). This strongly suggests that a charging up of the capsids does indeed destabilize them, as predicted. See Eqs. 12–16.

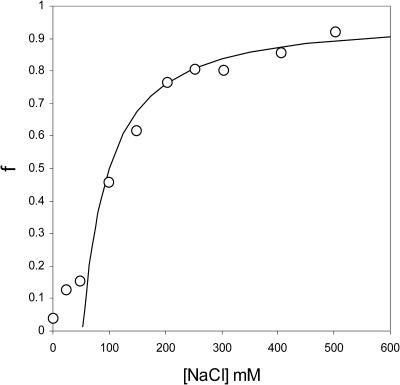
Wingfield and collaborators also find, in accordance with our analysis, that the degree of association increases with increasing ionic strength (Wingfield et al., 1995), confirming once again the importance of electrostatic interactions to the self-assembly of capsids. The ionic strength data of Wingfield et al. (1995) can in fact be described almost quantitatively by the theory presented in this article, as Fig. 5 shows. Plotted is the fraction HBeAg proteins incorporated into capsids versus the concentration of sodium chloride at a fixed concentration of the protein. The fitting to the data is straightforward, once we realize that the shift of the critical capsid concentration with the concentration of 1:1 electrolyte obeys

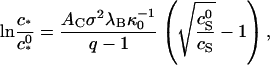graphic file with name M30.gif (18)

where 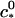Inline graphic is a reference critical capsid concentration at the salt concentration 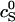Inline graphic and the corresponding Debye length 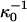Inline graphic. The experiments were done in 50 mM Tris-HCl buffer at pH = 7 (Wingfield et al., 1995), implying that cS ≈ 0.05 + [NaCl] with [NaCl] the concentration of sodium chloride in M. (At neutral pH, almost all of the Tris is dissociated.) The buffer only significantly impacts upon the fitted capsid aggregation curve for salt concentrations below about 0.1 M.

FIGURE 5.

FIGURE 5

Open in a new tab

Fraction of material assembled into capsids, f, as a function of the concentration of NaCl in units of mM. The symbols represent the data of Wingfield et al. (1995) on aqueous solutions of HBeAg dimer proteins that assemble into T = 3 capsids with an aggregation number of q = 90. Concentration of protein 0.5 g/l at pH = 7.0 and at near room-temperature. The drawn line is theoretical fit using Eqs. 16 and 18.

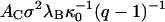We read off from Fig. 5 that for the given concentration of 0.5 g/l of HBeAg protein, f = 1/2 for Inline graphic ≈ 0.15 M. The steepness of the capsidization curve is now determined by the quantity Inline graphic, which by fitting to the data of Fig. 5 we find to be equal to ∼3.2. If we presume that all the capsids are of the T = 3 type, we find that this implies that there must be ∼11 net charges per HBeAg dimer, which is somewhat less than we found for the Cp1492 dimers. The slight discrepancy between theory and experiment at very low [NaCl] may be due to the influence of a net charge density that can only be presumed to be a constant at sufficiently high ionic strengths (Boström et al., 2003).

It is, in the light of our findings, tempting to speculate that the potentially large number of positive charges on the arginine-rich protamine domains of the viral HBcAg subunits strongly suppresses their assembly into capsids at near neutral pH. It may well be that the binding of negatively charged nucleic acids to the protamine domains causes the Coulomb repulsion between the core proteins to be sufficiently reduced to assist the assembly of the complete virus particles under physiological conditions (see also Hatton et al., 1992; Zlotnick et al., 1997). This, then, would provide a physical mechanism to prevent the formation of empty virus capsids in vivo. As many different globular viruses share a protamine domain (Bringas, 1997), this conclusion may extend to a large class of virus.

Another consequence of our findings is that viral assembly and viral disassembly (or uncoating) depends on the local physical environment. Indeed, ionic strength, pH, and temperature together determine the effective interaction between virus subunits and thereby, loosely speaking, whether the assembled or the uncoated state of the virus is stable. Different environments (in particular, pH) in different organelles in biological cells may switch one of either state on or off. This, in turn, could enable viruses to release their genetic material at the desired location only.

Acknowledgments

We thank Ineke Braakman (Utrecht University) and Jan Groenewold (Delft University of Technology) for discussions and for critically reading the manuscript.

References

  1. Boström, M., D. R. M. Williams, and B. W. Ninham. 2003. Specific ion effects: the role of co-ions in biology. Europhys. Lett. 63:610–615. [Google Scholar]
  2. Bringas, R. 1997. Folding and assembly of hepatitis B virus core protein: a new model proposal. J. Struct. Biol. 118:189–196. [DOI] [PubMed] [Google Scholar]
  3. Broide, M. L., T. M. Tominc, and M. D. Saxowsky. 1996. Using phase transitions to investigate the effect of salts on protein interactions. Phys. Rev. E. 53:6325–6335. [DOI] [PubMed] [Google Scholar]
  4. Bruinsma, R. F., W. M. Gelbart, D. Reguera, J. Rudnick, and R. Zandi. 2003. Viral self-assembly as a thermodynamic process. Phys. Rev. Lett. 90:248101. [DOI] [PubMed] [Google Scholar]
  5. Caspar, D. L. D. 1963. Assembly and stability of the Tobacco Mosaic virus particle. Adv. Protein Chem. 18:37–121. [DOI] [PubMed] [Google Scholar]
  6. Caspar, D. L. D. 1980. Movement and self-control in protein assemblies—quasiequivalence revisited. Biophys. J. 32:103–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Ceres, P., and A. Zlotnick. 2002. Weak protein-protein interactions are sufficient to drive assembly of hepatitis B virus capsids. Biochemistry. 41:11525–11531. [DOI] [PubMed] [Google Scholar]
  8. Ciferri, A. 2000. Supramolecular Polymers. Marcel Dekker, New York, NY.
  9. Claesson, P. M., R. Kjellander, P. Stenius, and H. K. Christenson. 1986. Direct measurement of temperature-dependent interactions between non-ionic surfactant layers. J. Chem. Soc. Faraday Trans. I. 82:2735–2746. [Google Scholar]
  10. Conway, J. F., N. Cheng, A. Zlotnick, P. T. Wingfield, S. J. Stahl, and A. C. Steven. 1997. Visualization of a 4-helix bundle in the hepatitis B virus capsid by cryo-electron microscopy. Nature. 386:91–94. [DOI] [PubMed] [Google Scholar]
  11. Cuesta, J. A., and R. P. Sear. 2002. Phase transition analogous to Bose-Einstein condensation in systems of noninteracting surfactant aggregates. Phys. Rev. E. 65:031406. [DOI] [PubMed] [Google Scholar]
  12. Curtis, R. A., C. Steinbrecher, M. Heinemann, H. W. Black, and J. M. Prausnitz. 2002. Hydrophobic forces between protein molecules in aqueous solutions of concentrated electrolyte. Biophys. Chem. 98:249–265. [DOI] [PubMed] [Google Scholar]
  13. Debye, P. J. W. 1949. Light scattering in soap solutions. Ann. N. Y. Acad. Sci. 51:575–592. [Google Scholar]
  14. Gunnarsson, G., B. Jönsson, and H. Wennerström. 1980. Surfactant association into micelles. An electrostatic approach. J. Phys. Chem. 84:3114–3121. [Google Scholar]
  15. Hatton, T., S. Zhou, and D. N. Standring. 1992. RNA- and DNA-binding activities in hepatitis B virus capsid protein: a model for their roles in viral replication. J. Virol. 66:5232–5241. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Israelachvili, J. 1992. Intermolecular and Surface Forces. Academic Press, San Diego, CA.
  17. Lauffer, M. A. 1966. Polymerization-depolymerization of Tobacco Mosaic Virus protein. VII. A model. Biochemistry. 5:2440–2446. [DOI] [PubMed] [Google Scholar]
  18. Levin, Y. 2000. Interfacial tension of electrolyte solutions. J. Chem. Phys. 113:9722–9726. [Google Scholar]
  19. Lyulin, S. V., L. J. Evers, P. van der Schoot, A. A. Darinskii, A. V. Lyulin, and M. A. J. Michels. 2004. Effect of solvent quality and electrostatic interactions on the size and structure of dendrimers—Brownian dynamics simulation and mean-field theory. Macromolecules. 37:3049–3063. [Google Scholar]
  20. Matubayasi, N., H. Matsuo, K. Yamamoto, S. Yamaguchi, and A. Matuzawa. 1999. Thermodynamic quantities of surface formation of aqueous electrolyte solutions*1. I. Aqueous solutions of NaCl, MgCl2, and LaCl3. J. Colloid Interface Sci. 209:398–402. [DOI] [PubMed] [Google Scholar]
  21. Messina, R. 2002. Image charges in spherical geometry: application to colloidal systems. J. Chem. Phys. 117:11062–11074. [Google Scholar]
  22. Morse, D. C., and S. T. Milner. 1995. Statistical mechanics of closed fluid membranes. Phys. Rev. E. 52:5918–5945. [DOI] [PubMed] [Google Scholar]
  23. Ninham, B. W., and V. Yaminsky. 1997. Ion binding and ion specificity: the Hofmeister effect and Onsager and Lifshitz theories. Langmuir. 13:2097–2108. [Google Scholar]
  24. Odijk, T. 1994. Long-range attraction in polyelectrolyte solutions. Macromolecules. 27:4998–5003. [Google Scholar]
  25. Onsager, L., and N. N. T. Samaras. 1934. The surface tension of Debye-Hückel electrolytes. J. Chem. Phys. 2:528–536. [Google Scholar]
  26. Reddy, V. S., P. Natarajan, B. Okerberg, K. Li, K. Damodaran, R. T. Morton, C. L. Brooks, III, and J. E. Johnson. 2001. Virus particle explorer (VIPER), a website for virus capsid structures and their computational analyses. J. Virol. 75:11943–11947. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Reiss, H., W. K. Kegel, and J. Groenewold. 1996. Length scale for configurational entropy in microemulsions. Ber. Bunsenges. Phys. Chem. 100:279–295. [Google Scholar]
  28. Stryer, L. 1980. Biochemistry. W. H. Freeman and Company, New York.
  29. Tanford, C. 1980. The Hydrophobic Effect. Wiley, London, UK.
  30. Toikka, G., R. A. Hayes, and J. Ralston. 1996. Surface forces between spherical ZnS particles in aqueous electrolyte. Langmuir. 12:3783–3788. [Google Scholar]
  31. Trizac, E., L. Bocavet, M. Auboy, and H. H. v. Grünberg. 2003. Alexander's prescription for colloidal charge renormalization. Langmuir. 19:4027–4033. [Google Scholar]
  32. vanVlijmen, H. W. T., S. Curry, M. Schaefer, and M. Karplus. 1998. Titration calculations of foot-and-mouth disease virus capsids and their stabilities as a function of pH. J. Mol. Biol. 275:295–308. [DOI] [PubMed] [Google Scholar]
  33. Verwey, E. J. W., and J. T. G. Overbeek. 1999. Theory of Stability of Lyophobic Colloids. Dover Press, Minneola, NY.
  34. Villers, D., and J. K. Platten. 1988. Temperature dependence of the Interfacial tension between water and long-chain alcohols. J. Phys. Chem. 92:4023–4024. [Google Scholar]
  35. Weast, R. C., M. J. Astle, and W. H. Beyer. 1984. Handbook of Chemistry and Physics. CRC Press, Boca Raton, FL.
  36. Wingfield, P. T., S. J. Stahl, R. W. Williams, and A. C. Steven. 1995. Hepatitis core antigen produced in Escherichia coli: subunit composition, conformational analysis, and in vitro capsid assembly. Biochemistry. 34:4919–4932. [DOI] [PubMed] [Google Scholar]
  37. Zlotnick, A. 1994. To build a virus capsid: an equilibrium model of the self assembly of polyhedral protein complexes. J. Mol. Biol. 241:59–67. [DOI] [PubMed] [Google Scholar]
  38. Zlotnick, A., P. Ceres, S. Singh, and J. M. Johnson. 2002. A small molecule inhibits and misdirects assembly of hepatitis B virus capsids. J. Virol. 76:4848–4854. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Zlotnick, A., N. Cheng, J. F. Conway, F. P. Booy, A. S. Steven, S. J. Stahl, and P. T. Wingfield. 1996. Dimorphism of hepatitis B virus capsids is strongly influenced by the C-terminus of the capsid protein. Biochemistry. 35:7412–7421. [DOI] [PubMed] [Google Scholar]
  40. Zlotnick, A., N. Cheng, S. J. Stahl, J. F. Conway, A. C. Steven, and P. T. Wingfield. 1997. Localization of the C-terminus of the assembly domain of hepatitis B virus capsid protein: implications for morphogenesis and organization of encapsidated RNA. Proc. Natl. Acad. Sci. USA. 94:9556–9561. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES