Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Jun;86(6):3914–3922. doi: 10.1529/biophysj.103.034595

Studies of χ(2)/χ(3) Tensors in Submicron-Scaled Bio-Tissues by Polarization Harmonics Optical Microscopy

Shi-Wei Chu *, Szu-Yu Chen *, Gia-Wei Chern *, Tsung-Han Tsai *, Yung-Chih Chen †, Bai-Ling Lin †, Chi-Kuang Sun *
PMCID: PMC1304293  PMID: 15189888

Abstract

Optical second- and third-harmonic generations have attracted a lot of attention in the biomedical imaging research field recently due to their intrinsic sectioning ability and noninvasiveness. Combined with near-infrared excitation sources, their deep-penetration ability makes these imaging modalities suitable for tissue characterization. In this article, we demonstrate a polarization harmonics optical microscopy, or P-HOM, to study the nonlinear optical anisotropy of the nanometer-scaled myosin and actin filaments inside myofibrils. By using tight focusing we can avoid the phase-matching condition due to micron-scaled, high-order structures in skeletal muscle fibers, and obtain the submicron-scaled polarization dependencies of second/third-harmonic generation intensities on the inclination angle between the long axes of the filaments and the polarization direction of the linear polarized fundamental excitation laser light. From these dependencies, detailed information on the tensor elements of the second/third-order nonlinear susceptibilities contributed from the myosin/actin filaments inside myofibrils can thus be analyzed and obtained, reflecting the detailed arrangements and structures of the constructing biomolecules. By acquiring a whole, nonlinearly sectioned image with a submicron spatial resolution, we can also compare the polarization dependency and calculate the nonlinear susceptibilities over a large area of the tissue at the same time—which not only provides statistical information but will be especially useful with complex specimen geometry.

INTRODUCTION

Second-harmonic generation (SHG) and third-harmonic generation (THG) have been emerging as important imaging modalities in nonlinear optical microscopy in recent years. In contrast to laser-induced fluorescence, harmonic generations (HGs) are known to leave no energy deposition upon the material with which they interact due to their energy conservation characteristics; that is, the emitted HG photon energy is the same as the annihilated excitation photon energy. This energy-conservation characteristic provides the optical “noninvasive” nature desirable for microscopy applications, especially for in vivo biological imaging (Guo et al., 1997; Peleg et al., 1999; Chu et al., 2001). Different from the incoherent mechanisms involved in fluorescence processes where no polarization dependency with the excitation lasers is preserved when the molecular rotation time is much faster than the fluorescence time, HGs (especially SHG) exhibit highly specific polarization relationships during the interaction between the excitation and the harmonic generated photons determined by the local arrangements of the constituent molecules. By changing the angle between the known excitation light polarization and the underlying molecule orientation, the polarizations of the emitted HGs can thus be used to determine the detailed nonlinear properties of biological tissues, which reflect the detailed arrangements and structures of the constructing biomolecules. Different from simple polarization microscopy (Empedocles et al., 1999), which is commonly used to determine the linear optical anisotropy of samples by using two polarizers orthogonal to each other, polarization harmonics optical microscopy, i.e., P-HOM, allows detection at arbitrary combinations of excitation and signal polarizations and can thus extract point group symmetry of the nanocrystalline structures inside the sample. Moreover, due to its nonlinear nature, the generated SHG intensity depends on the square of the incident light intensity, whereas the generated THG intensity depends on the cube of the incident light intensity. Therefore, different from the sophisticated pol-scope (Liu et al., 2000) and similar to multiphoton-induced fluorescence process (Denk et al., 1990), this nonlinear dependency allows localized excitation and provides intrinsic optical sectioning as well as submicron spatial selectivity in our developed technique. The near-infrared light source used for P-HOM also provides deep penetration into biological tissues and thus we can probe the nonlinear anisotropy inside bio-tissues without complex physical sectioning and fixing processes.

Since SHG does not occur in optically centrosymmetric media, SHG microscopy was first demonstrated for the studies of SHG photonic crystals (Gannaway and Sheppard, 1978), surfaces/interfaces (Shen, 1989), and field distribution in semiconductors (Sun et al., 2000, 2001), and was then applied to biological study including membrane potentials (Peleg et al., 1999; Moreaux et al., 2000), tissue polarity (Freund et al., 1986; Guo, et al., 1997), cellular structure (Campagnola et al., 2002), and biocrystalline structures (Chu et al., 2002). On the other hand, due to the optical dispersion property in biological tissues, THG was proven to be generated from regions with optical inhomogeneity and was applied to image general cellular and subcellular structures (Barad et al., 1997; Müller et al., 1998; Chu et al., 2001; Sun et al., 2003a,b). We have previously demonstrated the simultaneous acquisition of SHG and THG imaging modalities in plant and animal tissues for morphological and functional studies (Chu et al., 2002; Sun et al., 2003a,b).

The contrast in harmonics optical microscopy (HOM), especially SHG, reflects local arrangements and the crystallization degrees of underlying biomolecules and can thus be used to study the structural symmetry of the molecule arrangements and local intra- and intercellular matrices of tissues. It has been shown that with appropriate input laser polarization control and output SHG polarization detection, the absolute molecular orientations (Shen, 1989) and crystallization degree (Campagnola et al., 2002) can be obtained from the second-order nonlinear susceptibility. THG has also been found to exhibit strong polarization dependence on the orientation of nanoscopic aggregation domains in conjugated polymer films (Schaller et al., 2002). However, there are very few articles addressing issues on the analysis of tensor elements of the nonlinear HG susceptibilities in submicron-scaled biocrystalline structures, which is of fundamental importance. In this article, we use the P-HOM technique to study and analyze the contributing tensor elements of the nonlinear optical susceptibilities, including both second- and third-harmonic generations. We demonstrated, for the first time, the explicit determination of all nonvanishing tensor elements of the second-order nonlinear optical susceptibility χ(2) for SHG in submicron-scaled myofilaments inside mouse skeletal muscle tissues by analyzing the polarization relation between the incident fundamental and emitted SHG signals. The same technique was then utilized to investigate the third-order susceptibility χ(3) for THG in the same mouse skeletal muscle tissues. Although there are ambiguities in the determination of χ(3) nonlinear optical coefficients, specific relations can still be obtained based on the simple experimental observations.

MATERIALS AND METHODS

Our homebuilt laser scanning P-HOM (Chu et al., 2003) is adapted from an Olympus (Olympus Optical, Tokyo, Japan) FV300 scanning system combined with an Olympus BX51 upright microscope in which all optics are modified to allow the passage of ∼1200–1350-nm infrared light. A homebuilt Cr:Forsterite laser, which operates at 1230 nm with a repetition rate of 110 MHz and a pulse width of 100 fs (350-mW average output), was used as the light source (Liu et al., 2001) to allow both SHG/THG to fall within the visible spectrum and provide high penetration into biological tissues (Bouma et al., 1996). The linearly s-polarized laser output was first shaped and collimated by a telescope to avoid power loss at XY galvanometer mirror scanners and to fit the aperture of the focusing objective. The collimated beam was then coupled into the Olympus FV300 scanning system connected to the Olympus BX51 microscope with an aperture fitting tube lens. Real-time scanning was accomplished through the high-speed galvanometer mirrors inside the FV300. The excitation laser pulse was focused on the desired location inside the live specimen by scanning with a spot size close to diffraction limit, with a high numerical-aperture (NA) objective (LUMPlanFl/IR 60×/water/NA 0.90, Olympus). Skeletal muscle dissections are placed on a free rotating/moving stage beneath the focusing objective for controlling the relative angle between the muscle fiber and electric field direction of the linearly polarized incident light. We have also tried to place a half-wave plate in front of the FV300 to control the polarization direction without moving the sample. However, due to the substantial ellipticity introduced in the galvanometer mirrors and dichroic beamsplitter inside FV300, the output light after the objective became elliptically polarized if non-s-polarized light was sent into FV300. To retain the linear polarization of the laser light on the studied biosample, we fixed the laser polarization as s-polarization before FV300 and measured the polarization effects on HG intensity by rotating the sample around the optical propagation axis. The forward-propagated HGs are collected using a high-NA (1.4) oil-immersion condenser. By using the NA 0.9 long-working-distance objective and the NA 1.4 achromatic collection lens, the diffraction-limited spatial resolution, which also indicates the spatial selectivity of our system, can be improved to 400 nm and 500 nm in radial directions with THG and SHG microscopy, respectively, using 1230-nm excitation wavelength. For HG intensity mapping, two photomultiplier tubes (PMTs, R928P, Hamamatsu Photonics, Hamamatsu City, Japan), which are synchronized with the galvanometer mirrors, are used to respectively record the filtered SHG and THG intensities point-by-point to form two-dimensional sectioned images. A polarizer (10LP-VIS, Newport Corporation, Irvine, CA) was inserted into the optical path in front of the PMTs to analyze the polarization state of the emitted SHG/THG radiation. Mouse muscle tissues were dissected from the leg of a 1-year-old freshly sacrificed mouse and preserved in formalin. Before experiment, the mouse muscle tissues were mounted on a glass slide under a 150-μm-thick cover glass with direction of the parallel arranged muscle fibers lying on the plane of the glass slide.

THEORETICAL ANALYSIS OF HARMONIC GENERATIONS IN MUSCLE

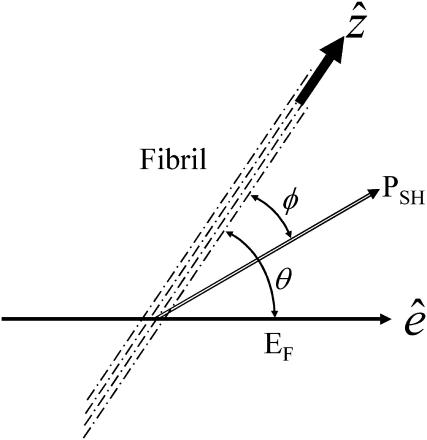
A skeletal muscle consists of bundles of muscle fibers called fascicules. Each fascicule consists, in turn, of a bundle of elongated muscle fiber cells. Within the muscle cell are longitudinal units, the myofibrils, which are made up of myosin and actin myofilaments. The myofilaments are organized in a specific manner that gives the muscle fiber a cross-striated appearance. The functionally significant repeating (with ∼2-μm period) unit of the myofibril is the sarcomere, which is the segment of the myofibril between two Z-lines, containing one section of A-band and one section of I-band. Inside a myofibril, the orderly arranged myofilaments provide the necessary nanocrystalline effect that determines the polarization dependency of the measured harmonic generations. We assign the parallel long axes of myosin/actin filaments as z axis (Fig. 1), which is the same as the long axes of parallel-aligned muscle fibers and myofibrils. The spatial arrangement of the helical myosin/actin filaments constituting the myofibrils, inside a skeletal muscle fiber, has a hexagonal symmetry in the plane perpendicular to z axis (for the detailed description of muscle fiber structure, please refer to Ross et al., 1989, Fig. 10.3). Since our spatial selectivity is smaller than the size of a myofibril (∼1-μm), it should be the spatial symmetry of the local arrangement of the underlying myosin and actin filaments (∼8–20-nm-thick), which is hexagonal, that determines the susceptibility tensor of the studied harmonic generations. By taking a scanning image, we are measuring 512 × 512 spatial points. Since our analysis is based on the scanned images, the nonlinear susceptibility we measured here is therefore the ensemble average of local arrangements of the myosin and actin filaments inside different spatial points with a submicron size. With parallel-aligned myosin and actin filaments, and loosely arranged nanohexagonal cells without orientation uniformity in the plane perpendicular to the z axis, the spatial symmetry of the ensemble-averaged myofilaments examined in an optical scale becomes cylindrical rather than hexagonal.

FIGURE 1.

FIGURE 1

Open in a new tab

Schematic drawing showing the relative directions of the assigned parameters for HG calculation.

Second-harmonic generation

The nonvanishing effective nonlinear SHG tensor coefficients 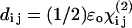Inline graphic in a hexagonal symmetry medium are d31, d33, d15, and d14 (Butcher and Cotter, 1990). We naturally assume the symmetry axis as the parallel long axes of myosin/actin filaments (i.e., z axis). If Kleinman's symmetry holds, then d15 = d31 and d14 = 0, which is the same as the SHG tensor coefficients with cylindrical symmetry; and we shall follow this parameter setting in the subsequent analysis due to the cylindrical nature of muscle tissue (Uttenweiler et al., 1998). The most general vector expression for the second-order nonlinear polarization P(2) under cylindrical symmetry assumption is, from Stoller et al. (2002),

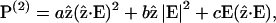graphic file with name M2.gif (1)

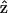where Inline graphic represents the unit vector along the symmetry z-axis, 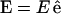Inline graphic is the incident electric field with fundamental light frequency, and 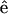Inline graphic is the polarization unit vector. In our SHG measurement, the incident fundamental field is linearly polarized. The letters a, b, and c are parameters related to effective second-order SHG coefficient tensors. Their relations to the dij coefficients are d31 = b, d15 = c/2, and d33 = (a + b + c) (Stoller et al., 2002). 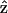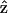Without helicity in myosin/actin filaments, b and c should be vanished since +Inline graphic and −Inline graphic would be symmetric in this case.

Due to the symmetry in the plane perpendicular to the z axis, in our experiment, we choose the optical propagation direction 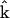Inline graphic perpendicular to the myosin/actin filament axis 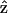Inline graphic (and incident field polarization 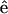Inline graphic). In this case, we can control the incident field polarization E in both ordinary and extraordinary axes, which are perpendicular or parallel to the filament axis 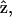Inline graphic respectively. We also decompose the induced second-order polarization into components parallel and perpendicular to the filament axis as

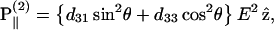graphic file with name M12.gif (2)
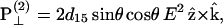graphic file with name M13.gif (3)

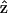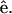where θ is the angle between Inline graphic and Inline graphic From the above expression, the 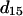Inline graphic coefficient only contributes to the perpendicular component 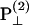Inline graphic with an angular dependence of sin2 θ. On the other hand, both d31 and d33 contribute to the parallel component 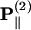Inline graphic. Their angular dependence can be understood as follows. The magnitudes of the input field projected onto the directions parallel and perpendicular to the filament axis are proportional to cos θ and sin θ, respectively. The parallel component will contribute to second-order polarization via d33 coefficient, resulting in a second-order polarization also in the direction parallel to 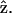Inline graphic As a result, the corresponding second-order polarization has a cos2 θ. dependency. Similar argument leads to the sin2 θ dependence for d31 coefficient. On the other hand, the second-order polarization 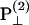Inline graphicis contributed from the interaction between input field projections parallel and perpendicular to 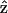Inline graphic through d15 and thus has a sin θ cos θ dependency. Given the nonlinear polarization, the second-harmonic intensity ISHG is proportional to 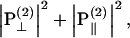Inline graphic and from Eqs. 2 and 3, we have

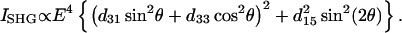graphic file with name M23.gif (4)

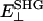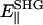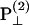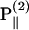The polarization of the second-harmonic field, which is a combination of second-harmonic electric fields Inline graphicand Inline graphic induced by Inline graphicand Inline graphic, respectively, has an inclination angle φ relative to the filament axis. This angle can be obtained from the angle of 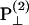Inline graphic relative to 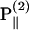Inline graphic as

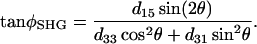graphic file with name M30.gif (5)

A schematic plot explaining the parameter assignment is given in Fig. 1.

Third-harmonic generation

The third-order susceptibilities for a hexagonal molecule has 41 nonzero elements and 19 independent elements (Butcher and Cotter, 1990; Boyd, 1992). If we further simplify the independent elements by assuming cylindrical symmetry, the third-order polarization can be expressed as

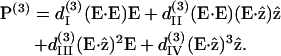graphic file with name M31.gif (6)

There are only four independent effective third-order coefficients d(3). These four coefficients are related to the elements of third-order susceptibility tensor χ(3) as

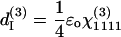graphic file with name M32.gif (7a)
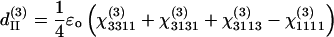graphic file with name M33.gif (7b)
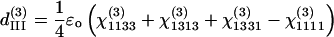graphic file with name M34.gif (7c)
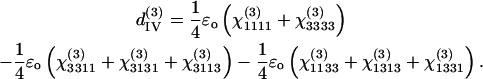graphic file with name M35.gif (7d)

Similar to the case of SHG, we also decompose the induced third-order polarization P(3) into those parallel and perpendicular to the filament axis, corresponding to the extraordinary and ordinary waves, respectively, as

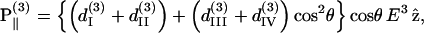graphic file with name M36.gif (8)
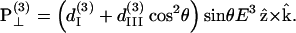graphic file with name M37.gif (9)

The third-harmonic intensity and polarization angle can be obtained using a method similar to that described above, giving

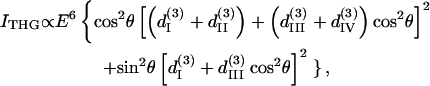graphic file with name M38.gif (10)

and

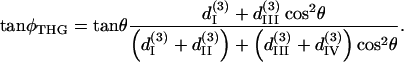graphic file with name M39.gif (11)

EXPERIMENTAL RESULTS AND DISCUSSION

Fig. 2, A and B, show the simultaneously acquired SHG and THG signal intensity dependencies on the angle θ between myosin/actin filaments orientation 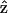Inline graphic and the incident fundamental polarization 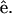Inline graphic No polarizer was placed between the detection PMTs and the sample. The rotation axis was adjusted to the center of the image so that the same sectioning region in a muscle fiber can be monitored. The arrow in Fig. 2 A indicates the fundamental polarization direction 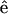Inline graphic. The strong SHG emission from a submicron-sized volume inside a muscle fiber can be attributed to the semicrystallized organization of myosin and actin filaments inside a myofibril (Chu et al., 2002) as previously discussed, since second-order nonlinear processes are only allowed in non-centrosymmetric media. In Fig. 2 A, an individual sarcomere with a cross-striated appearance that is composed of an A-band and an I-band with a ∼2-μm period can be observed where bright SHG stripes come from the A-bands due to the densely packed myosin/actin filaments inside (Campagnola et al., 2002), demonstrating the excellent resolving power of this technique. It is interesting and straightforward to find that the maximum of SHG emission intensity does not occur with the myosin/actin filaments being parallel or perpendicular to the fundamental polarization, but instead where a global and a local intensity minima can be found. Moreover, there are two maxima and two minima within a 180° rotation of the sample. We will discuss these results and compare them with theories later. On the other hand, THG can be observed from Fig. 2 B to be generated from the interface between a muscle fiber and the surrounding fixing solvent as well as from the muscular I-bands, which are composed of parallel-aligned, thinner actin filaments (8-nm thickness) and whose positions are just complementary to that of A-band with strong SHG emission. Unlike SHG, THG is allowed in all materials and should be easily detected in case there is no absorption at the third-harmonic wavelength. However, under a strong focusing condition such as in our experiment, all the THG generated before the focus will be reabsorbed coherently after the focus, due to the Gouy phase shift effect. Therefore, in practice, net THG emission is limited to an interface between two bulk materials that differ in dispersion or in third-order nonlinear susceptibility (Schins et al., 2002). This is the reason why we can observe strong THG emission at the interface between muscle fibers and the environment. Since the A-bands of a myofibril are filled with thick myosin and thin actin filaments with little dispersion differences, no perceptible THG radiates from the A-bands. But for the I-bands, which are mainly constituted by actin filaments and exhibit lots of hollow spaces between these thin filaments, the large refractive index contrast at a nanometer scale inside breaks the Gouy phase shift effect and produces appreciable THG signals. The maximum of THG intensity occurs as the fundamental polarization being parallel to the myosin/actin filaments, whereas the minimum occurs because they are perpendicular to each other. By acquiring a whole nonlinear image section rather than using a single-point detection methodology, we can compare the polarization dependency and calculate the nonlinear susceptibility over a large area of the tissue at the same time, which not only provides a statistical average of the studied nonlinearity but will also be useful with complex specimen geometry.

FIGURE 2.

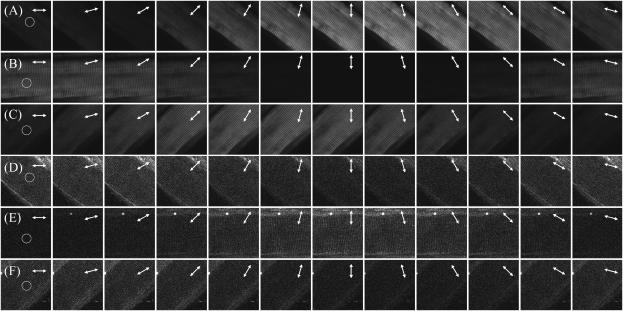
FIGURE 2

Open in a new tab

Optically sectioned image series of (A) SHG and (B) THG signals showing the obvious alternation of these nonlinear signal intensities as the angle between the myosin/actin filaments and fundamental polarization (shown with ↕) varies. Image size, 60 × 60 μm2.

The polarization of the emitted SHG/THG can be determined by inserting a polarizer into the collection path and the results are shown in Fig. 3. The arrows in Fig. 3 represent the optical axis of the polarizer and only the HGs signals with polarization parallel to this optical axis can be detected. Fig. 3, A–C, and D–F, give the SHG and THG signal changes, respectively, as the polarizer rotates. Perfect polarization linearity can be found with SHG signals, whereas THG radiation from muscle exhibits some ellipticity.

FIGURE 3.

FIGURE 3

Open in a new tab

Determination of forward propagated (A–C) SHG and (D–F) THG polarization by inserting a polarizer in the collection path. The arrows in each image indicate the optical axis of the polarizer at the time of acquiring and the fundamental polarization is ↕ throughout the experiment. The circles in each figure point out the area where we use for calculation.

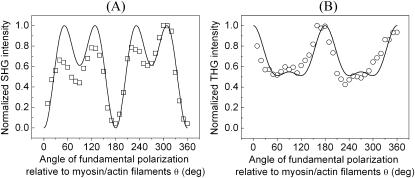
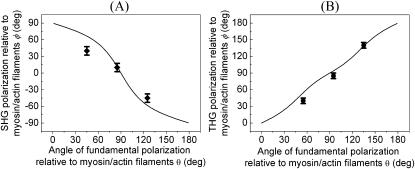
The complete SHG/THG signal intensity dependencies on myosin/actin filaments orientation relative to the incident fundamental polarizations throughout the 360° rotation are given in Fig. 4 (open squares and circles). Fig. 4, A and B, show the SHG and THG intensity dependency separately as well as the simulation results (solid lines) as a function of the angle θ between the fibril axis 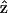Inline graphic and input field polarization 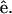Inline graphic The physical origin of the relatively complex polarization dependency is the nature of the “non-centrosymmetric” cylindrical symmetry (cylindrical symmetry without a σh mirror reflection plane) in muscle fibers. The nonlinear optical response of materials with such symmetry is certainly highly dependent on the relative magnitude of the individual nonlinear matrix element, as we shall discuss below. No polarizer was inserted in the emission path during the measurements of Fig. 4. After inserting the polarizer, the polarization orientation of the emitted HG signals can be determined and the results are given in Fig. 5 as a function of the angle θ. The data points in Fig. 5 A and 5 B are independently deduced from Fig. 3, A–C, and Fig. 3, D–F. For SHG calculation, Eq. 4 and 5 are applied respectively to compute the intensity (solid line in Fig. 4 A) and polarization orientation (solid line in Fig. 5 A) dependency on θ, the angle of fundamental polarization relative to the myosin/actin filaments. Under the parameter assignment as 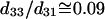Inline graphic and d15/d31 = 1.15, the calculated fitting curve agrees well with the experimental data, and the root mean-square (RMS) of the fitting errors are 0.428 and 0.48 for SHG intensity and polarization orientation, respectively. Under the condition that the RMS of fitting error be <0.43 and 0.48 for SHG intensity and polarization separately, the solution range for d15/d31 is limited to 1.15 ± 0.01 and is 0.09 ± 0.03 for d33/d31 (see black area in Fig. 6 A). If the limitation of intensity fitting error is relaxed to be <0.5, the solution set for the second-order nonlinear susceptibility matrix elements will expand to the light shaded area in Fig. 6 A. Therefore, the second-order nonlinear susceptibility tensor for SHG from the myosin/actin filament ensemble inside a myofibril can be written down as

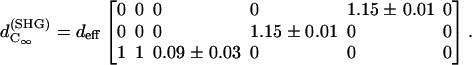graphic file with name M46.gif (12)

FIGURE 4.

FIGURE 4

Open in a new tab

The experimental data showing the (A) SHG (shown in □) and (B) THG (shown in ○) intensity modifications as a function of the angle between fundamental polarization and myosin/actin filaments (θ) along with the calculated fitting (solid line in both figures).

FIGURE 5.

FIGURE 5

Open in a new tab

The experimental data showing the (A) SHG (shown in ♦ with error bar) and (B) THG (shown in • with error bar) polarization variations as a function of the angle between fundamental polarization and myosin/actin filaments (θ) along with the calculated fitting (solid line in both figures).

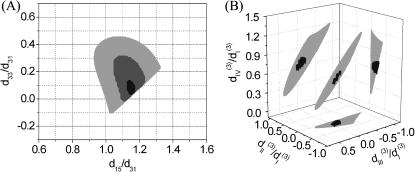
FIGURE 6.

FIGURE 6

Open in a new tab

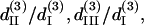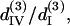(A) The solution set for d15/d31 and d33/d31 depending on the allowed error range. The solid, shaded, and light shaded areas represent that fitting errors for SHG intensity are <0.43, 0.45, and 0.5, respectively, whereas the errors for polarization orientation are all <0.48. (B) The solution set for Inline graphic and Inline graphic depending on the allowed error range. When the fitting error for THG intensity is <0.43 and for THG polarization orientation is <0.32, all the possible solutions are plotted in the black area. When the constraint of THG intensity fitting error is relaxed to be <0.5, the resulting expanded solution set is plotted in light shading.

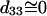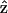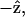The Inline graphic result implies that it is difficult to produce an axial second-order polarization with an optical field parallel to the myosin/actin filaments and that the radiated SHG are contributed mainly from d31 = dzxx and d15 = dxzx. Note that the nonzero d31 and d15 suggest the chirality in myosin and actin filaments inside a myofibril. Since chirality implies asymmetry between Inline graphic and Inline graphic if the filaments are not asymmetric, its optical properties should be invariant under 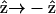Inline graphic transformation. However, from Eq. 1, the second-order nonlinear polarization P(2) changes sign under such a transformation unless all coefficients a = b = c = 0. Therefore, the nonzero coefficients (thus nonzero d31 and d15) imply a favored direction for 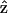Inline graphic of the filaments due to chirality. This suggestion complies with a previous conjecture, which states that the nonlinear optical properties in several biological materials (e.g., collagen matrix and muscle) are induced or enhanced by the chirality in their structure (Verbiest et al., 1998; Kim et al., 2000), and also agrees with the histological observation by electron microscopy. The 1.15 ± 0.01 ratio of d15/d31 also slightly deviates from the result of Kleinman's symmetry, which states that d15 = d31 when fundamental and SHG frequencies both are much lower than the molecular resonant frequency. Our 1230-nm laser and the resulted 615-nm SHG are in fact not that far from the molecular resonant frequency of muscle (∼430- and 550-nm, Marquez et al., 1998) and may be accounted for by the slight deviation from the Kleinman's symmetry. This minor deviation indicates that the Kleinman's symmetry should hold for an excitation wavelength much longer than 1230 nm to avoid resonant enhancement in the SHG frequency. It is interesting to notice that with the fundamental light propagating along the muscle fiber 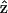Inline graphic direction, there should be no active components contributing to the SHG generation according to Eq. 9. We have also arranged our experiments according to this geometry and no significant SHG can be observed. The linearity of the SHG indicates that the depolarization effect of our high-NA objective is insignificant. Since 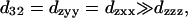Inline graphic when the laser polarization is aligned with 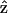Inline graphic(the molecular axis), the contribution of the depolarized light (with polarization component other than 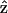Inline graphic) should be dominant, which is not the case in our experiment. This should be attributed to the fundamental Gaussian beam we utilized in our experiments and the high sectioning capability provided by the optical nonlinear processes where signals occurring around the focus dominate the observed image. The phase front and electric field distribution of a tightly focused Gaussian beam at focus is flat under paraxial approximation when using a relatively low-NA (<1.0) objective.

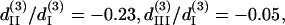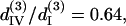For THG fitting, the following relations have been used in Eq. 10 and 11: Inline graphic and Inline graphic whose resulted curve of the THG intensity and angular dependency on θ fits well to experiments (Figs. 4 B and 5 B) with an RMS error of 0.426 for intensity and 0.316 for polarization orientation. Although the calculated results agree well with the experimental data, there is still a great degree of freedom in choosing the relative values of the third-order coefficients. Under the condition that the RMS of fitting error be <0.43 and 0.32 for THG intensity (Fig. 4 B) and polarization orientation (Fig. 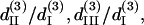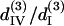5 B), respectively, only a small solution set for Inline graphic and Inline graphicis allowed and this solution set is plotted in Fig. 6 B (black area). If the constraint is loosened to allow the RMS of fitting error to be as large as 0.5 for THG intensity while keeping the polarization orientation constraint as 0.32, the permissible solution set will expand slightly, but all the possible solutions still fall within a three-dimensional area with a volume <2 (see the shaded area of Fig. 6 B). Although other measurements, such as oblique incidence on the muscle tissue, should be performed to fix the relations between these four effective parameters, we have successfully restricted all the possible combinations of these parameters (i.e., the contributing matrix elements) to a limited space depending on the acceptable fitting error.

In summary, we have demonstrated that, by studying the polarization relationship between the coherently generated harmonic signals and the fundamental excitations within the submicron-scaled foci by using the P-HOM, all nonvanishing elements of second-order nonlinear optical susceptibility χ(2) in the submicron-scaled matrices formed by myosin and actin filaments inside myofibrils of skeletal muscle tissue can be explicitly determined. With the use of tightly focused P-HOM, we can avoid the phase-matching condition due to high-order micron-scaled structures in skeletal muscle fibers and obtain the submicron-scaled polarization dependency of second-harmonic generation intensity on the inclination angle between the filaments' long axes and the polarization direction of the linear polarized fundamental excitation laser light. From these dependencies, detailed information on the tensor elements of the second-order nonlinear susceptibilities can thus be analyzed and obtained. By acquiring a whole nonlinearly sectioned image with a submicron spatial resolution we also compare the polarization dependency and calculate the nonlinear susceptibilities over a large area of the tissue at the same time, which will not only provide the desired statistical average of the nonlinearity but will be especially useful with complex specimen geometry. The intrinsic optical sectioning and deep penetration capabilities of this technique also permit the determination of nonlinear susceptibility deep inside thick biological tissues. The same technique was also utilized to investigate the third-order susceptibility χ(3) for THG. Although there are ambiguities in the determination of χ(3) nonlinear optical coefficients, certain relations were found that explain well the experimental observations. The solution set for the contributing matrix elements 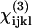Inline graphic is restricted to a limited small space, which provides a useful guide for further determination of these elements.

Acknowledgments

The authors gratefully acknowledge financial support under the National Health Research Institute (NHRI-EX92-9201EI), the National Science Council (NSC-91-2215-E-002-021), and the National Taiwan University Center for Genomic Medicine of Taiwan, Republic of China. S.-W.C. gratefully acknowledges generous support from MediaTek Corporation.

References

  1. Barad, Y., E. Eisenberg, M. Horowitz, and Y. Silberberg. 1997. Nonlinear scanning laser microscopy by third harmonic generation. Appl. Phys. Lett. 70:922–924. [Google Scholar]
  2. Bouma, B. E., G. J. Tearney, I. P. Bilinsky, B. Golubovic, and J. G. Fujimoto. 1996. Self-phase-modulated Kerr-lens mode-locked Cr:Forsterite laser source for optical coherence tomography. Opt. Lett. 21:1839–1841. [DOI] [PubMed] [Google Scholar]
  3. Boyd, R. W. 1992. Nonlinear Optics. Academic Press, San Diego, CA.
  4. Butcher, P. N., and D. Cotter. 1990. The Elements of Nonlinear Optics. Cambridge University Press, London, UK.
  5. Campagnola, P. J., A. C. Millard, M. Terasaki, P. E. Hoppe, C. J. Malone, and W. A. Mohler. 2002. Three-dimensional high-resolution second-harmonic generation imaging of endogenous structural proteins in biological tissues. Biophys. J. 81:493–508. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Chu, S.-W., I.-H. Chen, T.-M. Liu, P.-C. Cheng, C.-K. Sun, and B.-L. Lin. 2001. Multi-modal nonlinear spectral microscopy based on a femtosecond Cr:Forsterite laser. Opt. Lett. 26:1909–1911. [DOI] [PubMed] [Google Scholar]
  7. Chu, S.-W., I.-H. Chen, T.-M. Liu, C.-K. Sun, S.-P. Lee, B.-L. Lin, P.-C. Cheng, M.-X. Kuo, D.-J. Lin, and H.-L. Liu. 2002. Nonlinear bio-photonic crystal effects revealed with multi-modal nonlinear microscopy. J. Microsc. 208:190–200. [DOI] [PubMed] [Google Scholar]
  8. Chu, S.-W., T.-M. Liu, I.-H. Chen, and C.-K. Sun. 2003. Real-time second-harmonic-generation microscopy based on a 2-GHz repetition rate Ti:sapphire laser. Opt. Express. 11:933–938. [DOI] [PubMed] [Google Scholar]
  9. Denk, W., J. H. Strickler, and W. W. Webb. 1990. Two-photon laser scanning fluorescence microscopy. Science. 248:73–76. [DOI] [PubMed] [Google Scholar]
  10. Freund, I., M. Deutsch, and A. Sprecher. 1986. Connective tissue polarity: optical second-harmonic microscopy, crossed-beam summation, and small-angle scattering in rat-tail tendon. Biophys. J. 50:693–712. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Empedocles, S. A., R. Neuhauser, and M. G. Bawendi. 1999. Three-dimensional orientation measurements of symmetric single chromophores using polarization microscopy. Nature. 399:126–130. [Google Scholar]
  12. Gannaway, J. N., and C. J. R. Sheppard. 1978. Second-harmonic imaging in the scanning optical microscope. Opt. Quantum Electron. 10:435–439. [Google Scholar]
  13. Guo, Y., P. P. Ho, A. Tirksliunas, F. Liu, and R. R. Alfano. 1997. Optical harmonic generation from animal tissues by the use of picosecond and femtosecond laser pulses. Opt. Lett. 22:1323–1325. [DOI] [PubMed] [Google Scholar]
  14. Kim, B.-M., J. Eichler, K. M. Reiser, A. M. Rubenchik, and L. B. Da Silva. 2000. Collagen structure and nonlinear susceptibility: effects of heat, glycation, and enzymatic cleavage on second harmonic signal intensity. Laser Surg. Med. 27:329–335. [DOI] [PubMed] [Google Scholar]
  15. Liu, L., R. Oldenbourg, J. R. Trimarchi, and D. L. Keefe. 2000. A reliable, noninvasive technique for spindle imaging and enucleation of mammalian oocytes. Nat. Biotechnol. 18:223–225. [DOI] [PubMed] [Google Scholar]
  16. Liu, T.-M., S.-W. Chu, C.-K. Sun, B.-L. Lin, P.-C. Cheng, and I. Johnson. 2001. Multiphoton confocal microscopy using a femtosecond Cr:Forsterite laser. Scanning. 23:249–254. [DOI] [PubMed] [Google Scholar]
  17. Marquez, G., L. V. Wang, S.-P. Lin, J. A. Schwartz, and S. L. Thomsen. 1998. Anisotropy in the absorption and scattering spectra of chicken breast tissue. Appl. Opt. 37:798–804. [DOI] [PubMed] [Google Scholar]
  18. Moreaux, L., O. Sandre, M. Blanchard-Desce, and J. Mertz. 2000. Membrane imaging by simultaneous second-harmonic generation and two-photon microscopy. Opt. Lett. 25:320–322. [DOI] [PubMed] [Google Scholar]
  19. Müller, M., J. Squier, K. R. Wilson, and G. J. Brakenhoff. 1998. 3D microscopy of transparent objects using third-harmonic generation. J. Microsc. 191:266–274. [DOI] [PubMed] [Google Scholar]
  20. Peleg, G., A. Lewis, M. Linial, and L. M. Loew. 1999. Nonlinear optical measurement of membrane potential around single molecules at selected cellular sites. Proc. Natl. Acad. Sci. USA. 96:6700–6704. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Ross, M. H., E. J. Reith, and L. J. Romrell. 1989. Histology: a Text and Atlas. Williams & Wilkins, Baltimore, MD.
  22. Schaller, R. D., P. T. Snee, J. C. Johnson, L. F. Lee, K. R. Wilson, L. H. Haber, R. J. Saykally, T.-Q. Nguyen, and B. J. Schwartz. 2002. Nanoscopic interchain aggregate domain formation in conjugated polymer films studied by third harmonic generation near-field scanning optical microscopy. J. Chem. Phys. 117:6688–6698. [Google Scholar]
  23. Schins, J. M., T. Schrama, J. Squier, G. J. Brakenhoff, and M. Müller. 2002. Determination of material properties by use of third-harmonic generation microscopy. J. Opt. Soc. Am. B. 19:1627–1634. [Google Scholar]
  24. Shen, Y. R. 1989. Surface properties probed by second harmonic and sum frequency generation. Nature. 337:519–525. [Google Scholar]
  25. Stoller, P., K. M. Reiser, P. M. Celliers, and A. M. Rubenchik. 2002. Polarization-modulated second harmonic generation in collagen. Biophys. J. 82:3330–3342. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Sun, C.-K., C.-C. Chen, S.-W. Chu, T.-H. Tsai, Y.-C. Chen, and B.-L. Lin. 2003a. Multi-harmonic generation biopsy of skin. Opt. Lett. 28:2488–2490. [DOI] [PubMed] [Google Scholar]
  27. Sun, C.-K., S.-W. Chu, S.-P. Tai, S. Keller, U. K. Mishra, and S. P. DenBaars. 2000. Scanning second-harmonic-generation and third-harmonic-generation microscopy of GaN. Appl. Phys. Lett. 77:2331–2333. [Google Scholar]
  28. Sun, C.-K., S.-W. Chu, S.-P. Tai, S. Keller, A. Abare, U. K. Mishra, and S. P. DenBaars. 2001. Mapping piezoelectric-field distribution in gallium nitride with scanning second-harmonic generation microscopy. Scanning. 23:182–192. [DOI] [PubMed] [Google Scholar]
  29. Sun, C.-K., S.-W. Chu, S.-Y. Chen, T.-H. Tsai, T.-M. Liu, C.-Y. Lin, and H.-J. Tsai. 2003b. Harmonic generation microscopy for developmental biology. J. Struct. Biol. In press. [DOI] [PubMed]
  30. Uttenweiler, D., C. Weber, and R. H. A. Fink. 1998. Mathematical modeling and fluorescence imaging to study the Ca2+-turnover in skinned muscle fibers. Biophys. J. 74:1640–1653. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Verbiest, T., S. V. Elshocht, M. Kauranen, L. Hellemans, J. Snauwaert, C. Nuckolls, T. J. Katz, and A. Persoons. 1998. Strong enhancement of nonlinear optical properties through supramolecular chirality. Science. 282:913–915. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES