Photobleaching-Corrected FRET Efficiency Imaging of Live Cells

Abstract

Fluorescent resonance energy transfer (FRET) imaging techniques can be used to visualize protein-protein interactions in real-time with subcellular resolution. Imaging of sensitized fluorescence of the acceptor, elicited during excitation of the donor, is becoming the most popular method for live FRET (3-cube imaging) because it is fast, nondestructive, and applicable to existing widefield or confocal microscopes. Most sensitized emission-based FRET indices respond nonlinearly to changes in the degree of molecular interaction and depend on the optical parameters of the imaging system. This makes it difficult to evaluate and compare FRET imaging data between laboratories. Furthermore, photobleaching poses a problem for FRET imaging in timelapse experiments and three-dimensional reconstructions. We present a 3-cube FRET imaging method, E-FRET, which overcomes both of these obstacles. E-FRET bridges the gap between the donor recovery after acceptor photobleaching technique (which allows absolute measurements of FRET efficiency, E, but is not suitable for living cells), and the sensitized-emission FRET indices (which reflect FRET in living cells but lack the quantitation and clarity of E). With E-FRET, we visualize FRET in terms of true FRET efficiency images (E), which correlate linearly with the degree of donor interaction. We have defined procedures to incorporate photobleaching correction into E-FRET imaging. We demonstrate the benefits of E-FRET with photobleaching correction for timelapse and three-dimensional imaging of protein-protein interactions in the immunological synapse in living T-cells.

INTRODUCTION

Recent development of variants of the green fluorescent protein has provided genetically encoded tags for specific fluorescent labeling of proteins. This has spurred great interest in the development of fluorescence resonance energy transfer (FRET) imaging techniques to visualize protein interactions in living cells with subcellular resolution (Mitra et al., 1996; Heim and Tsien, 1996). FRET is a short-range (<10 nm) effect whereby excitation of the donor fluorophore is transferred to the acceptor. When the donor and acceptor are attached to macromolecules, FRET shows that the molecules are in close apposition, presumably interacting. FRET results in several characteristic changes in local sample fluorescence, which can be spatially resolved in the form of FRET images. Firstly, fluorescence of donor is quenched. This can be measured by the recovery of donor fluorescence after photobleaching of the acceptor (donor dequenching; Szaba et al., 1992; Bastiaens and Jovin, 1996). Secondly, fluorescence of the acceptor (if it is a fluorophore) is induced upon donor excitation. This is the basis of sensitized emission imaging methods (Uster and Pagano, 1986). Thirdly, the lifetime and polarization of donor fluorescence are modulated by FRET. These can be resolved by fluorescence lifetime imaging microscopy (FLIM; Bastiaens and Squire, 1999; Kusumi et al., 1991).

The goal of FRET imaging is to visualize and quantitate molecular interactions in biologically relevant terms. Such measurements should be independent of the local concentrations of donor and acceptor molecules. Donor dequenching measurements are the most straightforward in that they report FRET directly in terms of well-defined FRET efficiency values (E). The other methods monitor FRET in the form of user-defined FRET indices. Unfortunately, irreversible destruction of acceptor makes the donor-dequenching method incompatible with timelapse imaging in living cells. FLIM has been successfully implemented for live cell studies, although it requires highly specialized instrumentation and expertise.

Sensitized-emission imaging is becoming the most popular approach to nondestructive, live FRET imaging, as it can be implemented on widefield and confocal microscopes. Thus, the sensitized fluorescence of acceptor is detected through an optical FRET filter set selecting acceptor emission during donor excitation (I_DA image). In practice, the I_DA image is contaminated by directly excited fluorescence of acceptor and by the tail of the donor emission spectrum. To account for this bleedthrough or crosstalk and to render the FRET index independent of fluorescence intensity, two additional images are acquired: acceptor fluorescence during acceptor excitation (I_AA) and donor fluorescence during donor excitation (I_DD). Given that the crosstalk coefficients of acceptor and donor in the FRET filter set, a and d, respectively, are constant and assuming that no other crosstalk components are present, sensitized emission, F_c, can be calculated by linear unmixing of the I_DA intensity (Tron et al., 1984; Youvan et al., 1997; Gordon et al., 1998).

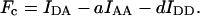(1)

F_c per se is still dependent on fluorophore concentration, which has led over the years to the implementation of many ratiometric FRET indices.

The typical makeup of an index used to detect FRET from the sensitized emission is a ratio designed such that its value should increase with FRET. The numerator of the ratio contains the I_DA intensity and modifications to correct for crosstalk. The particulars of crosstalk correction constitute one source of differences between FRET indices. The denominator is even more contentious since it not only provides for a way to render the whole index independent of fluorescence intensity, but also defines the correlation of the FRET index in terms of the particular parameters of the experiment. Therefore, the various published FRET indices can be grouped according to which fluorescence—donor (group 1), acceptor (group 2), or both (group 3)—denominate the FRET index. This way of classification of FRET indices is helpful because it reduces the superficial abundance of FRET indices to several representatives (Table 1 and Methods).

TABLE 1.

Relation of FRET indices to E_max and degrees of molecular interaction

Method (assuming b = c = 0)	Relation to Emax, χD, χA	Type 1 experiment (k = const):	Type 3 experiment (k ≠ const):		Reference
		Follows degree of interaction?	Follows donor occupancy?	Follows acceptor occupancy?
Sensitized fluorescence
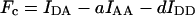
	RDDGEmaxχD[Dtotal]	No	No	No	Youvan et al. (1997)
Group 1 ratios
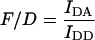
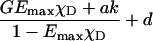		Yes,*NL	No	No	Miyawaki et al. (1997)
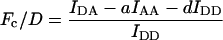
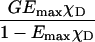		Yes,*NL	Yes,*NL	No	Vanderklish et al. (2000)
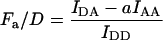
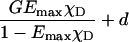		Yes,*NL	Yes,*NL	No	Zal et al. (2002)
Group 2 ratios
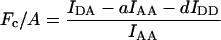
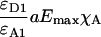		Yes,*L	No	Yes,*L	Jiang and Sorkin (2002)
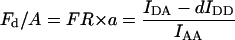
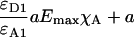		Yes,*L	No	Yes,*L	Erickson et al. (2001)
Group 3 ratios
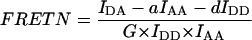
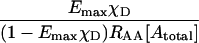		No	No	No	Gordon et al. (1998)
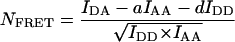
	GEmaxχD/((1–EmaxχD)k)1/2	Yes,*NL	No	No	Xia and Liu (2001)
E-FRET method
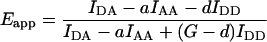
	EmaxχD	Yes,*L	Yes,*L	No	This article
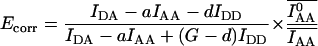
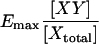		Yes, L	Yes, L	No
or

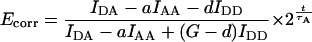
Published formulae were translated to symbols used in this article. The dependence of each index on E_max, χ_D, and χ_A was derived in Appendix. See Appendix: Glossary for definition of acronyms and symbols.

^*Only if imaging-induced photobleaching is negligible.

Most FRET indices generally fulfill the goal of detecting FRET, but they are difficult to interpret in terms of the degree of molecular interaction. They are also sensitive to imaging-induced sample photobleaching, which is a major limitation for timelapse and three-dimensional imaging of FRET. Moreover, FRET indices depend on the optical parameters of the imaging system in use, preventing quantitative evaluation, comparison, and standardization of FRET imaging data between laboratories.

Repeated imaging of fluorescence is almost invariably accompanied by gradual photobleaching of fluorophores. This inadvertent photobleaching is usually slow, unlike the intentional acceptor photobleaching for the donor-dequenching method, but nevertheless it gradually affects the correspondence between the fluorescence intensity of donor and/or acceptor and the concentrations of the corresponding carrier molecules X and Y. If photobleaching occurs, a decrease in any FRET index published to date does not necessarily indicate the dissociation of the XY complex.

The fundamental, instrument-independent measure of FRET is the FRET efficiency, E. This is defined as the proportion of the excited states of the donor that become transferred to the acceptor. Measurements of E for samples undergoing dynamic interactions result in the apparent FRET efficiency, E_app, which is the product of the specific efficiency of the complex, E_max (if only one species is formed), and χ_D, the degree of donor-acceptor complex [DA] formation with respect to fluorescent donor [D_total].

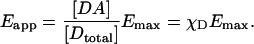(2)

Thus, E_app is biologically relevant because it is proportional to the degree of complex formation with respect to the donor-labeled molecule X (but only if the sample is not subject to photobleaching during the experiment). E_max is typically determined in vitro from samples of donor and acceptor that are complexed homogenously, stoichiometrically, and completely with each other. If E_max is known, the spatiotemporal distribution of χ_D in subcellular compartments can be explicitly determined from FRET images, if these are obtained in terms of E_app.

In this study, we describe a nondestructive, 3-cube method, termed E-FRET, to measure E_app on a pixel-by-pixel basis. This is possible thanks to a novel way of calibrating the imaging system for the relationship between E and sensitized emission. Furthermore, we demonstrate practical computational approaches to correct E_app for photobleaching, both in timelapse and three-dimensional experiments. This is done by calculating E_corr, which is the FRET efficiency that would be apparent if there was no photobleaching. This extends the time frame of live FRET imaging, improves quantitation of the FRET data, and facilitates their interpretation in terms of the degree of molecular interaction with respect to the donor-labeled molecules.

METHODS

DNA constructs and cells

We divide FRET constructs into three classes, depending on how well donor and acceptor concentrations correlate throughout the cell. In Type 1 experiments, donor and acceptor are attached to the same carrier molecule so that their concentrations are correlated. Such constructs are used to detect conformational changes that increase or reduce the FRET signal. In Type 2 experiments, donor and acceptor are joined by a linker that can be enzymatically digested. Donor and acceptor concentrations are correlated before the linker is digested, but may distribute differently in the cell thereafter; for example, if the FRET construct is targeted to cell membranes. In such cases, Type 2 experiments require full crosstalk correction typical of Type 3 experiments; otherwise they can be treated as Type 1. Type 3, or intermolecular FRET, is the most general category, whereby donor and acceptor are attached to different macromolecules; hence their concentrations are not correlated.

Type 1 constructs CFP-lck-YFP and YFP-CFP were designed to undergo constitutive energy transfer with low and high efficiency, respectively. CFP and YFP-Q69K (Miyawaki et al., 1999) cDNA (from pECFP-N1 and in-house mutated pEYFP-N1, Clontech, Palo Alto, CA) were inserted after the unique domain and at the end of mouse p56lck cDNA, respectively. EYFP and ECFP were joined by a 10-amino-acid linker. The constructs were transfected into the A18 T-cell hybridoma (Zal et al., 2002). The FRET efficiency for CFP-lck-YFP was E = 10% and for YFP-CFP E = 33%, as determined from donor recovery after acceptor photobleaching. E was independent of the level of expression, the activation state of the cells, or intracellular compartmentalization. For Type 3 experiments we used the A18.ZC.4Y cells coexpressing the CD3ζ-CFP and CD4-YFP fusion proteins or CD4-CFP and CD4-YFP. Formation of intercellular contacts was induced by mixing A18.ZC.4Y cells with C5-peptide-loaded LK35 B cell tumor as described before (Zal et al., 2002). The CD4-CFP and CD4-YFP pair was cotransfected in the CD4-negative A18 cells by nucleoporation (Amaxa Biosystems, Cologne, Germany). After 24 h, CD4 was cross-linked by the GK1.5-biotin antibody (Southern Biology Associates, Birmingham, AL) and streptavidin-allophycocyanin (Molecular Probes, Eugene, OR). FRET was measured in the areas of clustering identified by the allophycocyanin fluorescence. Autofluorescence could be almost eliminated in lymphocytes by growing cells overnight in the riboflavin-low, HEPES-buffered 199 medium with Hanks salts (GIBCO, Invitrogen, Carlsbad, CA), supplemented with 5% FCS, 50 μM β-mercaptoethanol, 2 mM L-glutamine, and without antibiotics.

Microscopy

Two widefield microscope systems were used for this work. The DeltaVision system consisted of an Olympus IX70 (Olympus, Melville, NY) microscope equipped with a 100-W mercury lamp, Photometrics CH350L (Roper, Tucson, AZ) cooled charge-coupled device (CCD) camera, and the SoftWorx 2.0 acquisition and analysis software (Applied Precision Instruments, Issaquah, WA). The optical filters (Chroma, Rockingham, VT) were 436/10 nm, 470/30 nm (CFP excitation and emission) and 500/20 nm, 535/30 nm (YFP excitation and emission). The JP4 multi-bandpass dichroic mirror was stationary. Different combinations of excitation and emission filters were introduced into the light-path of the microscope by filter wheels.

The second microscope system was specifically designed for fast FRET imaging to reduce errors due to cellular motility. This system was based on simultaneous acquisition of donor emission and acceptor emission during donor excitation by two CoolSnapHQ cameras (Roper, Tucson, AZ) attached to a Zeiss 200-M microscope through a beamsplitter (custom 510LPXR, Chroma, Rockingham, VT) and stationary emission filters. Rapid wavelength switching between donor and acceptor excitation was performed with a DG4 galvo illuminator customized with a 300W xenon lamp (Sutter, Novato, CA). YFP excitation for sensitized-emission imaging was attenuated to 20% by appropriate positioning of the exit mirror and was left at 100% for donor recovery measurements. The system was managed by Slidebook software (3I Corporation, Denver, CO). The optical filters were 430/25 nm, 470/30 nm (CFP excitation and emission) and 510/20 nm, 550/50 nm (YFP excitation and emission), and the JP4 dichroic mirror. Cameras were typically run in 2 × 2 binning mode with software flatfield correction and estimated noise of <2%. Images were automatically aligned with subpixel resolution through the frequency-based algorithm of the Slidebook software. Background was removed based on the average reading in a cell-devoid area of each image.

Crosstalk calibration

Crosstalk or bleedthrough of fluorescence between the donor and acceptor's emission spectra must be removed or rendered constant for specific detection of the FRET signal. The principle of crosstalk removal through the linear spectral unmixing algorithm (Gordon et al., 1998; Youvan et al., 1997) is valid for fluorophores which do not exhibit changes of the emission spectrum due to environmental factors other than FRET. In particular, the intensity of each crosstalk component remains in constant proportion to the main fluorescence of each fluorophore. Crosstalk coefficients are calculated by the image math, i.e., on a pixel-by-pixel basis. Cells expressing a range of levels of donor or acceptor are used to verify that crosstalk coefficients are indeed constant across the range of concentrations and subcellular compartmentalization. Thus, acceptor-only and donor-only cells are imaged using the donor excitation-donor emission (I_DD), donor excitation-acceptor emission (I_DA), and acceptor excitation-acceptor emission (I_AA) filter combinations. Coefficients a and b for acceptor bleedthrough in the I_DA and I_DD filter sets and c and d for donor bleedthrough in the I_AA and I_DA filter sets, respectively, are defined below.

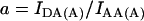(3)

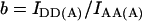(4)

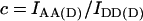(5)

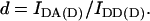(6)

I represents the pixel-by-pixel image intensity, minus background, using the combination of excitation and emission filters indicated by the lower index, for samples containing only donor or acceptor, as indicated in parentheses. Finally, if the crosstalk coefficients are constant across cells in the field of view, their averages are calculated from several areas encompassing single cells. This cancels high frequency noise and increases precision. Bleedthrough parameters for ECFP and EYFP on the DeltaVision system were a = 0.21 ± 0.01, d = 0.95 ± 0.05, b = c = 0. For the dual-camera 3I system, a = 0.0154 ± 0.0011 (a = 0.077 at 20% YFP excitation), d = 0.647 ± 0.023, and b = c = 0. The difference between the microscopes in the a-coefficient was mostly due to the mercury vs. xenon illumination, whereas d was lower in the dual-camera system thanks to the optimized filters and the beamsplitter between cameras.

Bleedthrough coefficients were constant for ECFP and EYFP within living cells, as demonstrated previously (Zal et al., 2002). If the crosstalk coefficients do not appear constant, possible causes of crosstalk calibration errors have to be considered. These include cell autofluorescence, the lack of flatfield correction, and incorrect background subtraction, as well as detector nonlinearity and/or low dynamic range of signal digitization.

Existing methods

Group 1 FRET indices (donor-denominated) have been formulated as the F_c/D ratio of the I_DA intensity, with both donor and acceptor bleedthrough subtracted, to the donor fluorescence (Kam et al., 1995, Gordon et al., 1998). Alternatively, only the acceptor bleedthrough is subtracted from I_DA and ratioed to the donor image, rendering the donor bleedthrough constant (F_a/D) (Zal et al., 2002). Group 2 indices (acceptor-denominated) are exemplified by the F_c/A ratio of the crosstalk-subtracted I_DA image to the acceptor image (Jiang and Sorkin, 2002). This is similar to the FR ratio for effective FRET efficiency (Erickson et al., 2001). Group 3 indices are donor- and acceptor-denominated. At a high local concentration of donor and acceptor, FRET can be caused by diffusion-driven random collision (Gordon et al., 1998). To compensate for this effect, these workers proposed using the ratio of sensitized emission to the product of donor and acceptor fluorescence (FRETN). Another group 3 formula, the ratio of the sensitized fluorescence to the square-root of the product of donor fluorescence and acceptor fluorescence, was put forward recently (N_FRET; Xia and Liu, 2001).

Basic E-FRET formulae

Our first goal was to standardize FRET imaging by calculating E from the 3-cube intensities I_DA, I_DD, and I_AA. This would allow us to replace arbitrary, instrument-dependent FRET indices with E, and thus to relate 3-cube FRET imaging to donor recovery after acceptor photobleaching or FLIM measurements. The apparent FRET efficiency of a sample, E_app, is given by the relative increase of donor fluorescence after complete acceptor photobleaching, which is the basis for the donor-dequenching method,

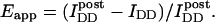(7)

To calculate E_app from the I_DA, I_DD, and I_AA intensities, we define the parameter G as the ratio of the sensitized emission F_c to the corresponding amount of donor recovery in the I_DD channel after acceptor photobleaching,

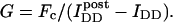(8)

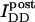is the intensity of donor fluorescence after acceptor photobleaching. G is similar to the parameter defined theoretically before (Gordon et al., 1998). The proof that G as defined by Eq. 8 is constant, and the method to determine G experimentally, is provided in the following section. Combining Eqs. 7 and 8 allows us to eliminate :

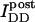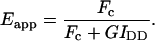(9)

The sensitized fluorescence F_c is calculated by subtraction of the major crosstalk components from I_DA and the minor crosstalk components from I_DD and I_AA, using previously calibrated crosstalk coefficients a, b, c, and d, defined in Eqs. 3–6:

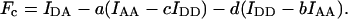(10)

If the minor crosstalk components are negligible, b = c = 0, F_c is given by the more familiar Eq. 1. Introducing F_c from Eq. 10 or Eq. 1 (for b = c = 0) we arrive at the general E-FRET formulae, which allow calculation of E_app from terms measured by 3-cube imaging:

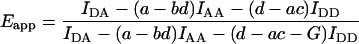(11)

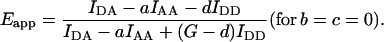(12)

FRET data from 3-cube imaging are frequently visualized in terms of the F_c/I_DD ratio. A form of the E-FRET formula, which is useful for calculating E_app from the F_c/I_DD ratio, is given as

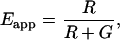(13)

where R = F_c/I_DD (Table 1). The E-FRET formula Eq. 11, Eq. 12, or Eq. 13 is applied on a pixel-by-pixel basis through image math. The result is an image with pixel values between 0 and 1, which is programmed in the software to be presented in a color-encoded scale.

Determination of the G parameter

The parameter G is crucial to calculation of FRET efficiency because it relates the level of sensitized emission to the drop in donor fluorescence attributable to FRET. To prove that G, as defined in Eq. 8, is a constant parameter for a given imaging system and fluorophores, we consider the following. The intensity of sensitized emission F_c is proportional to the concentration of the donor-acceptor complex [DA], the intensity of illumination reaching the sample through the donor excitation filter ν_D, the absorption coefficient of donor ɛ_D, the specific FRET efficiency of the complex E_max, the quantum yield of acceptor Q_A, the throughput of the acceptor emission light-path L_A, the quantum sensitivity of the camera for acceptor emission S_A, and the exposure time for the I_DA image t_DA. The amount of donor fluorescence recovery after acceptor photobleaching is proportional to [DA], ν_D, ɛ_D, E_max, the quantum yield of donor Q_D, the throughput of the emission light-path including the donor emission filter L_D, the quantum sensitivity of the camera for donor emission S_D, and the exposure time for the I_DD image, t_DD. The value ν_D is the same for imaging through the I_DD and I_DA filter sets, when using a fixed multi-bandpass dichroic beamsplitter and no neutral density filters. Therefore

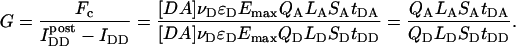(14)

As evident from Eq. 14, G is constant for a given choice of fluorophores (Q_D and Q_A) and the imaging setup (L_D, L_A, S_D, and S_A) and independent of underlying FRET efficiency, essentially as described before (Gordon et al., 1998). Thus, G can be calibrated using a reference FRET sample with a different E_max than in the experiment as long as exposure timings remain proportional and the same donor and acceptor fluorophores are used.

A relatively simple and direct way to measure G merges donor recovery after acceptor photobleaching with sensitized-emission imaging. Cells expressing the constitutive FRET constructs CFP-lck-YFP or YFP-CFP are fixed and imaged using all three filter combinations to record the I_DD, I_DA, and I_AA images. Then the acceptor is photobleached by extended illumination through the acceptor excitation filter. Photobleaching destroys fluorophores asymptotically, hence incompletely. Therefore cells are imaged again using all three filter set combinations to capture the and 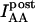images. Substituting F_c in Eq. 8 and allowing for the incomplete photobleaching of acceptor gives the formula for experimental determination of G:

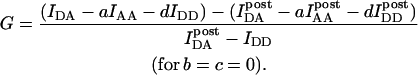(15)

To increase precision, average fluorescence intensities of user-drawn regions-of-interest (ROI) are used. We used whole cells, for which the particular ROI shape is not critical. For ECFP and EYFP on the DeltaVision system, we measured G = 5.1 ± 0.15 and for the dual-camera 3I system G = 3.5 ± 0.1.

Methods for correction of E for photobleaching

Our second goal was to introduce correction for photobleaching, which degrades measurements in timelapse and three-dimensional experiments. The main problems to consider are: 1), the different photosensitivities of donor and acceptor; 2), the effect of sensitized photobleaching (Mekler et al., 1997); and 3), changes in cell morphology and/or focal position. Depending on the setup of the imaging experiment we will define internal and external correction for photobleaching.

E_corr: photobleaching-corrected FRET efficiency

Photobleaching breaks the correspondence between fluorescence intensity of the fluorophore and the concentration of carrier molecules X and Y. Thus, the degree of fluorescent complex formation with respect to total donor χ_D = [DA]/[D_total] is no longer equivalent to the degree of complex formation with respect to the donor-carrying molecule X: [XY]/[X_total]. ([DA] ≤ [XY] are the concentrations of fluorescent XY complexes and all XY complexes, respectively, and [D_total] ≤ [X_total] are the total concentrations of fluorescent X molecules and all X molecules, respectively.) To introduce imaging-induced photobleaching into the E-FRET formula we will define E_corr, which would be apparent if there was no photobleaching, i.e., with respect to the carrier molecule X:

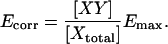(16)

The distinction E_corr in Eq. 16 and E_app in Eq. 2 is that the latter refers to the fluorescent tags, which are affected by photobleaching, whereas the former refers to the carrier molecules themselves, which are the true interest of the biologist. Given stoichiometric and complete labeling of carrier X by donor and carrier Y by acceptor, and no prior exposure of the sample to photobleaching, the starting conditions are 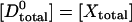and .

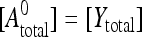Internal correction

One of the derivative effects of FRET is the accelerated bleaching of acceptor and decreased bleaching of donor in the sites of interaction. Sensitized photobleaching of acceptor is caused by the energy transferred from the donor during donor excitation. On the other hand, the energy transfer decreases the lifetime of the donor's excited state, hence the rate of donor photobleaching. Due to these effects, donor and acceptor are photobleached with spatially and temporally variable rates 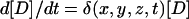and 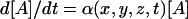, respectively. The rate coefficients δ and α are dependent on the local E_app and on the rate of exchange of the carrier molecules between the areas of low and high interactions. If there is a fast equilibrium between free and complexed X and Y, i.e., if the half-life of the complex is shorter than the imaging interval, diffusional mixing will ensure uniform photobleaching within the topologically enclosed compartment. This compartment can be the whole cell or an intracellular structure. In such cases, mathematically accurate photobleaching correction is straightforward. Approximate correction is possible in the remaining situations.

Let us first consider an experimental setup where photobleaching due to imaging is slower than the rates of complex formation and dissociation. Due to equilibration by diffusion, the photobleaching rate coefficients δ(t) and α(t) will fluctuate with time, depending on the average E_app. Total fluorescent donor at time t is given by 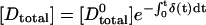, and total fluorescent acceptor is 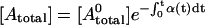. At equilibrium, the fraction of DA complexes in which both donor and acceptor are still fluorescent at time t is given by 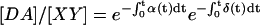. Therefore 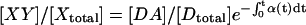. Introducing these terms into Eq. 16 and noting E_app in Eq. 2, we arrive at the formula describing correction of E_app for photobleaching:

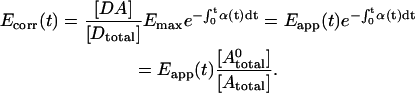(17)

It is apparent that deviation of E_app from E_corr in experiments where donor-acceptor interaction kinetics are faster than the rates of photobleaching is caused only by acceptor photobleaching. Thus, E_corr is calculated for each time point by multiplying the apparent FRET efficiency E_app, given by Eq. 11, Eq. 12, or Eq. 13, by the ratio of the total acceptor fluorescence at the beginning of imaging, 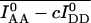to the total acceptor fluorescence at time t, 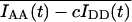(both corrected for crosstalk if c > 0). The readings are taken over whole cells or ROIs corresponding to subcellular compartments within which FRET is measured, as

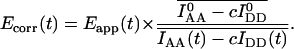(18)

Simplified correction is possible if acceptor photobleaching adheres to first-order kinetics (i.e., is time-independent) and the minor bleedthrough coefficient c is zero:

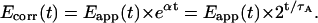(19)

In this case, photobleaching correction is based on the acceptor half-life, τ_A. Acceptor half-life is derived from fitting the exponential curve I_AA 2^−t/τ to the total I_AA intensity in a cell or subcellular compartment, using the time course of acceptor images. Time t is the running total illumination time and can be expressed in terms of the time point number instead. Eq. 19 is less sensitive to random fluctuations than Eq. 18 thanks to the interpolation and should be used for experiments where acceptor photobleaching can be approximated with a single exponential. Appropriate image math operations to implement calculation of E_corr according to Eq. 18 or Eq. 19 were programmed into the image processing software (3I Corporation) utilizing the direct-fit or exponential-fit photobleaching correction algorithms, respectively.

Approximated correction for slow interactions

Approximated correction will typically be required where the frequency of image capture is greater than the half-life of the complex or if diffusion is restricted. Acceptor photobleaching will be faster in the areas of increased E_app due to insufficiently fast exchange with the pool of free fluorophores. Nevertheless, if the overall FRET efficiency is low, then most of the acceptor loss can be attributed to direct excitation with the I_AA filter set, rather than to FRET sensitization (see below). Donor will photodestruct slower in sites of complex formation, but this effect is largely cancelled for low E_app by the ratiometric nature of E, Eq. 17. Therefore, good photobleaching correction is possible based on the total instead of a strictly local rate of acceptor photobleaching.

Next, we estimate the maximum error incurred with such correction and ask how deeply acceptor can be photobleached for the desired precision, set at 10% of E_corr. Let α_free be the rate of acceptor photobleaching due only to direct illumination of acceptor, i.e., in areas of noninteraction, or in a sample containing acceptor alone. The value α_free sets the limit of error for the true rate of acceptor photobleaching in areas of interaction. The rate of direct acceptor photobleaching caused by illumination with wavelengths λ₁ and λ₂, used for donor and acceptor excitation, depends on the respective illumination intensities ν₁ and ν₂, the length of exposures t₁, t₂, and the absorbance coefficients of acceptor ɛ_A1, ɛ_A2 at λ₁ and λ₂. The rate of sensitized acceptor photobleaching is proportional to ν₁ɛ_D1t₁E_maxχ_A, where ɛ_D1 is the absorbance coefficient of donor at the donor excitation wavelength, and χ_A = [DA]/[A]_total is the local degree of complex formation with respect to acceptor. Thus, the local rate of acceptor photobleaching α in an interacting sample is

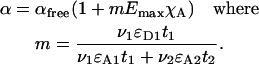(20)

Therefore, the limit of error caused by using α_free instead of α for photobleaching correction is

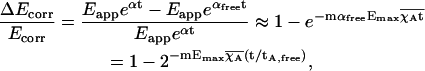(21)

where τ_A,free is the half-life of free acceptor in the control sample. Let us assume continuous interaction with maximum acceptor occupancy χ_A = 1 and E_max = 25%. For our imaging system, the timing t₁ = t₂ and the intensity of exposures ν₁ ≈ ν₂, when using similar bandwidth for excitation, no neutral filtering, and a xenon source. For CFP and YFP, ɛ_D1 = 26,000 M⁻¹ cm⁻¹, ɛ_A1 = 2520 M⁻¹ cm⁻¹, and ɛ_A2 = 65,520 M⁻¹ cm⁻¹ (λ₁ = 430/25 nm, λ₂ = 510/20 nm), hence m ≈ 0.38. Thus the error of correction will remain <10% of E_corr until >67% of acceptor is photobleached (1.6τ_A,free).

A more general estimate is possible for imaging systems using different light sources and/or filters. Typically, imaging of FRET is set up such that intensities of images remain within the same order of magnitude. Thus, ν₁ɛ_D1t₁Q_D = ∼ν₂ɛ_A2t₂Q_A. Therefore, for fluorophores with quantum yields of similar magnitude, m ≤ 1. In the worst case scenario of m = 1, photobleaching correction is possible, with accuracy >10% of E_corr, until up to 35% of the acceptor is destroyed. In practice, correction is calculated using the average rate of acceptor photobleaching in the sample or cell compartment according to Eq. 18 or Eq. 19, which will introduce significantly less error.

External correction

Experiments involving changing focal planes (three-dimensional, four-dimensional) or extensive cell movement are not amenable to the internal correction because the overall acceptor intensity does not reflect the progress of acceptor photobleaching. In such cases external correction is applied using the half-life of acceptor in a reference sample subjected to the same sequence of exposures as intended for the experiment. The reference sample may be noninteracting or acceptor-only but closer approximation is obtained from a sample with E_app matching the basal E_app during the experiment. The value τ_A in the reference sample is applied to the experimental data according to Eq. 19. If the rate of acceptor photobleaching does not adhere to the simple exponential model, the external compensation multipliers 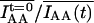(assuming c = 0) are determined for each time point using the reference sample and applied according to Eq. 18 for corresponding time points of the experiment. The distinct benefit of external compensation is such that the acceptor half-life τ_A or the compensation multipliers can be measured using short timelapse intervals and can then be applied to experimental data with longer timelapse intervals and/or changing focal planes (but not the x–y coordinates). The maximum error due to sensitized photobleaching, and the limit of allowable acceptor photobleaching for external correction are the same as estimated above for stable interactions. It is important to note that any error due to the rate of acceptor photobleaching determined in a noninteracting sample instead of the actual rate in experiment results only in undercorrection and will not cause false-positives.

Mathematical modeling

Mathematical simulation of the responses of FRET indices (listed in Existing Methods, above) and the basic E-FRET formula Eq. 12 to varying concentration of donor and acceptor was performed to establish how well they correlate with the degrees of interaction. First, we derived general equations linking each FRET index to the degree of interaction with respect to donor χ_D = [DA]/[D_total], or to the degree of interaction with respect to acceptor χ_A = [DA]/[A_total]. [DA] is the concentration of donor-acceptor complex, and [D_total], [A_total] are the total concentrations of donor and acceptor, respectively. Derivation of equations for the simulation is described in the Appendix and collected in Table 1. The equations were programmed into a spreadsheet software program (Excel 2000, Microsoft, Redmond, WA). Graphs of the responses by each formula were generated by varying the concentration of donor, acceptor, or both, assuming a high affinity interaction and no photobleaching. Concentrations were normalized to facilitate comparison of trends. For modeling purposes we set parameters typical for CFP and YFP with mercury illumination: the crosstalk of donor and acceptor fluorescence into the FRET filter set are d = 0.9 and a = 0.25, respectively, the detection sensitivity per mol for the I_AA filter set being R_AA = 1.5 R_DD of the sensitivity of the I_DD filter set, and the ratio of sensitized emission to the decrease of the donor fluorescence G = 4. The specific FRET efficiency of the complex was set at E_max = 40%. Parameters E_max, G, a, and d are instrument- and fluorophore-specific and different values of these parameters affect scaling but do not change the trends and general relationships between curves.

RESULTS

To illustrate the benefits of the E-FRET method for imaging of molecular interactions in living cells, it is important to use it both for internal FRET constructs as well as for interactions between independent molecules. We distinguish three types of FRET experiments with respect to the degree of fluorophore correlation. Type 1 experiments encompass constructs where donor and acceptor are attached to the same carrier, such that FRET efficiency is modulated by conformational changes. This ensures correlation between the fluorophores and normally warrants simplified, 2-cube FRET imaging (except when photobleaching is encountered). Type 2 constructs incorporate a digestible linker between the fluorophores. The suitability of 2-cube imaging for Type 2 constructs depends on subcellular compartmentalization of donor and acceptor after their separation by the proteolytic activity. Lastly, Type 3 experiments are the most general, and, arguably, the most interesting category, where donor and acceptor are on different carrier molecules. Their concentrations are not correlated, which necessitates explicit crosstalk correction, hence 3-cube imaging. Here, we use the interaction between the CD3ζ-CFP chain of T-cell receptor and CD4-YFP co-receptor during the recognition of antigenic peptide-MHC-II complexes by T-lymphocytes. Quantitative monitoring of the interaction in timelapse and three-dimensions is important to understand the function of the immunological synapse formed between T-cells and antigen-presenting cells (Gascoigne and Zal, 2004; Zal et al., 2002). First, we show that combination of two FRET methods: sensitized-emission imaging and the donor recovery after acceptor photobleaching allows us to measure the G parameter, which is crucial for E-FRET calculations. We show that G is constant for a given imaging system and that it can be calibrated using a reference FRET construct, as described in Methods. Subsequently, we show that E-values obtained by the E-FRET method are equivalent to E measured by the donor-dequenching technique. We then demonstrate the advantage of E-FRET with photobleaching correction for timelapse and three-dimensional imaging of antigen recognition by T-lymphocytes. Lastly, we compare the E-FRET method to existing FRET indices for their ability to correlate with the degree of molecular interaction.

Calibration of the G-factor and calculation of E

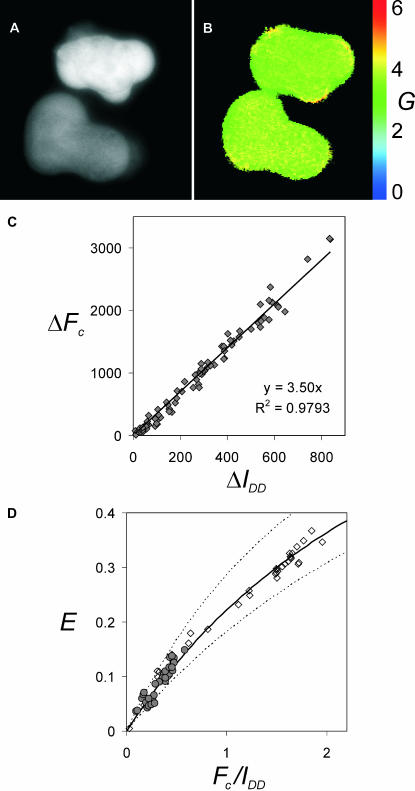
Calculation of FRET efficiency (E) from 3-cube imaging data requires knowledge of the correlation factor G between the sensitized emission and the concomitant drop in donor fluorescence. G should be constant for a given choice of donor, acceptor, and imaging parameters, and independent of E_app, as shown on theoretical grounds by Gordon and co-workers (1998) and here by Eq. 14. To verify experimentally that G is constant for our imaging system, we photobleached YFP in cells expressing varying levels of the YFP-CFP construct and visualized G on a pixel-by-pixel basis. The average G was indeed constant for different concentrations of YFP-CFP (exemplified by two cells in Fig. 1, A and B), whereas some pixel-to-pixel variation could be attributed to the camera noise and specimen stability during the time required for photobleaching. Next, we plotted the absolute values of the change in sensitized emission versus the absolute values of the increase of donor fluorescence after partial (∼50–60%) and complete (∼95%) photobleaching (Fig. 1 C). These were co-linear, demonstrating the validity of Eq. 15, with the slope G = 3.50 (for ECFP, EYFP on the dual-camera microscope, see Methods).

FIGURE 1.

Calibration of G and validation of E-FRET calculation. The G factor was determined on a pixel-by-pixel basis using cells expressing varying levels of the YFP-CFP construct. (A) Two cells are shown with a twofold difference in fluorescence intensity (YFP channel). (B) The same area shown in terms of the G factor calculated by Eq. 15 after photobleaching of YFP by 3-min illumination (95% decrease in YFP intensity). The average value for the upper cell was G = 3.42 and for the lower cell G = 3.47. Standard deviations were SD = 0.15 and SD = 0.13, respectively. (C) G determined from the slope of the correlation between the drop in sensitized emission and CFP recovery, after complete and partial photobleaching of YFP in the YFP-CFP construct. (D) The apparent FRET efficiency E_app was determined by the donor-recovery method for cells expressing YFP-CFP (open diamonds) and for cross-linking of CD4 in cells coexpressing CD4-CFP and CD4-YFP (shaded circles). The solid line represents the results of the E-FRET calculation using the values of the F_c/D index recorded before acceptor photobleaching and G = 3.50, demonstrating good agreement of the E-FRET method with the donor-recovery method for independent experiments. Dashed lines are for G = 2.5 (upper line) and G = 4.5 (lower line).

The formula deriving FRET efficiency from the 3-cube intensity values predicts a hyperbolic relationship between E and the F_c/D FRET index, Eq. 13. We computed E_app according to the E-FRET formula Eq. 13 for cells or subcellular regions with different F_c/D values and compared it with E_app determined by donor recovery after acceptor photobleaching in the same samples. These showed good agreement (open diamond and solid line, Fig. 1 D). To further validate this method for a Type 3 experiment, we used cells coexpressing variable levels of the transmembrane T-cell glycoprotein CD4-CFP and CD4-YFP. Cross-linking of CD4 by biotinylated antibody and streptavidin resulted in capping and internalization of CD4 (data not shown) and varying degrees of FRET. E measured in the caps by the donor-recovery method remained in good agreement with E computed by the E-FRET formula using G determined with the YFP-CFP construct (shaded circle, Fig. 1 D). Hence, once G is calibrated, it can be used for calculating E_app in experimental samples by Eq. 11, Eq. 12, or Eq. 13. In conclusion, the E-FRET method allows determination of FRET efficiency from the intensities measured by 3-cube imaging, which is suitable for visualization of E on a pixel-by-pixel basis.

Imaging-induced photobleaching affects FRET measurements

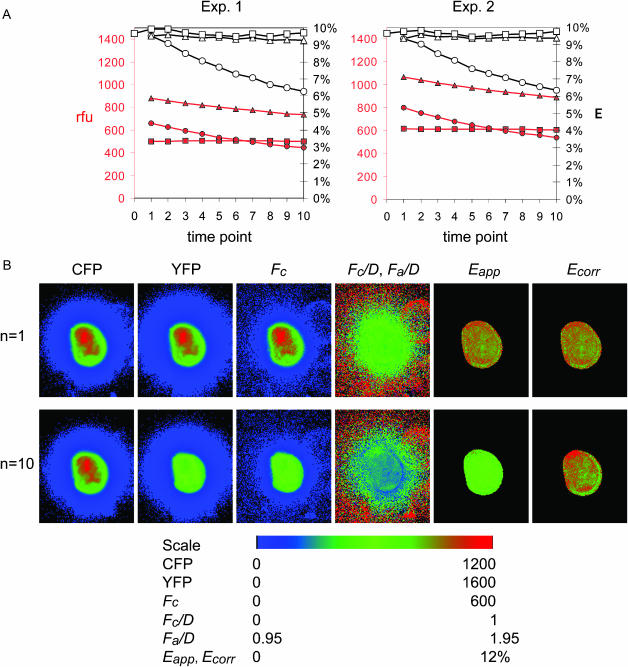
Imaging-induced photobleaching is detrimental to prolonged FRET experiments. We therefore considered how photobleaching of donor and acceptor affect the apparent FRET efficiency E_app, and incorporated appropriate correction procedures. This allowed us to calculate the corrected FRET efficiency E_corr, which would be apparent if the sample was not photobleached (see Methods, Eq. 18 or Eq. 19). To evaluate the performance of photobleaching compensation under experimental conditions, we set up timelapse imaging of cells expressing the Type 1 fusion construct CFP-lck-YFP, which undergoes constitutive energy transfer with E_max = 10%. Fig. 2 A shows that prolonged imaging returned a decreasing E_app reading over time. Next, we introduced internal compensation according to Eq. 18 or Eq. 19. Both resulted in stable values of E_corr, as expected for a constitutive FRET construct (Fig. 2 A). Closer inspection of the data demonstrates that the E_corr values calculated by Eq. 19 are consistently slightly higher than E_corr calculated by Eq. 18. This is because Eq. 19 corrects up to E_corr as if no exposures of the sample were yet taken, whereas Eq. 18 corrects up to the amount of acceptor after the first exposure. Normally, the difference should be small and not significant, although Eq. 19 is advantageous for single exponential photobleaching.

FIGURE 2.

Photobleaching correction during timelapse FRET imaging in Type 1 experiment. Cells expressing CFP-lck-YFP were imaged by taking 1 s exposures per time point to acquire the I_DD, I_DA, and I_AA images. (A) Single-cell averaged image intensities, minus background, are shown in red (I_DD, shaded squares; I_DA, shaded triangles; and I_AA, shaded circles). The value E_app was calculated according to Eq. 12 (open circles). Photobleaching-corrected FRET efficiency E_corr was calculated according to Eq. 19 (open squares), and using Eq. 18 (open triangles). Two experiments are demonstrated. (B) FRET efficiency imaging and photobleaching correction on pixel-by-pixel basis. Images of a cell from A are shown. The top row consists of images taken at the first time point: I_DD (CFP), I_AA (YFP), sensitized fluorescence (F_c, Eq. 1), the FRET ratios F_c/D and F_a/D, E_app, and E_corr using Eq. 19, defined in Table 1. The lower row shows corresponding images of the same cell at the time point n = 10.

To assess the performance of photobleaching compensation on a pixel-by-pixel basis, we used Eq. 19 on a series of timelapse images of cells expressing CFP-lck-YFP. Fig. 2 B illustrates the first and the 10th time point of the experiment. At the 10th time point the noncorrected image of the F_c/D ratio and E_app were noticeably decreased. Images of E_corr at exposure 1 and exposure 10 show that E_corr remained stable, as expected for the constitutive FRET construct, demonstrating the utility of the correction method.

Photobleaching compensation for Type 3 experiments

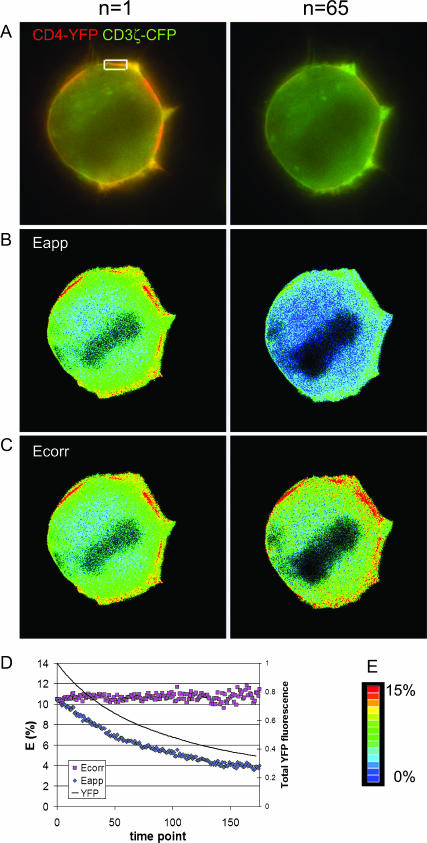
Type 3 experiments are the most general category of FRET experiments, whereby donor and acceptor are attached to separate macromolecules. Type 3 experiments introduce temporal variability of local E due to the dynamics of protein interactions within the cell, making it difficult to quantitatively demonstrate the effect of photobleaching correction independent of biological responses. To illustrate the benefits of FRET efficiency correction applied to timelapse and three-dimensional imaging of a Type 3 experiment, we used the interaction between the CD3ζ chain of T-cell receptor and CD4 co-receptor during antigen recognition in the immunological synapse of T-lymphocytes. Fig. 3 shows results of a timelapse experiment, where we imaged FRET between CFP attached to CD3ζ and YFP attached to CD4, both coexpressed in the A18.ZC.4Y T-cell hybrid (Zal et al., 2002). The A18.ZC.4Y cells were mixed with an excess of antigen-loaded antigen-presenting cells (LK35 B cell tumor) and allowed to form the intercellular contact areas, or immunological synapses. Both CD3ζ-CFP and CD4-YFP were recruited to the synapses, and interacted as described before (Zal et al. 2002). We observed gradual loss of YFP fluorescence, Fig. 3 A, which was accompanied by decreasing E_app in regions of clustering of CD3ζ and CD4 in the cell membrane, Fig. 3 B. Internal correction was then applied based on the total whole-cell YFP signal and the first-order rate of acceptor photobleaching as per Eq. 19. As seen in Fig. 3 C, E_corr corrected for the loss of FRET due to the imaging-induced photobleaching. An increased pixel noise is evident in the E_corr image at n = 65 (Fig. 3 C) as compared with the time point n = 1. This is consistent with the general loss of fluorescence signal, hence a decreasing signal/noise ratio of the raw data (see the error propagation analysis below). The entire imaging sequence was analyzed for the average FRET efficiency in one contact area, selected with the white box in Fig. 3 A. The result is shown in Fig. 3 D. The overall trend of the average remained constant, despite the worsening signal/noise ratio.

FIGURE 3.

Imaging of photobleaching-corrected FRET efficiency in Type 3 timelapse experiment. The A18.ZC.4Y cells expressing CD3ζ-CFP and CD4-YFP were mixed with an excess of antigen-loaded antigen-presenting cells (LK35 B cell tumor), and allowed to form the intercellular contact areas for 30 min. Cells were then kept at room temperature to prevent gross changes in the cell shape during imaging. One-hundred-seventy-five time points were acquired and analyzed for FRET efficiency. The whole sequence took <3 min to acquire and we did not see any gross changes in the interaction between CD3ζ and CD4 at room temperature during this time. CFP (green) and YFP (red) fluorescence are shown merged after the first and 65th exposure cycle (A). E_app calculated according to Eq. 12 (no photobleaching correction) is shown in B. Internal correction of E_app was applied based on the total whole-cell YFP signal and first-order rate of acceptor photobleaching as per Eq. 19 (C). The lookup color table is below (E). The normalized total YFP fluorescence is shown in D, dark line (the starting whole-cell average YFP signal was 996.6 on a 12-bit scale), E_app (shaded diamonds), and E_corr (shaded squares).

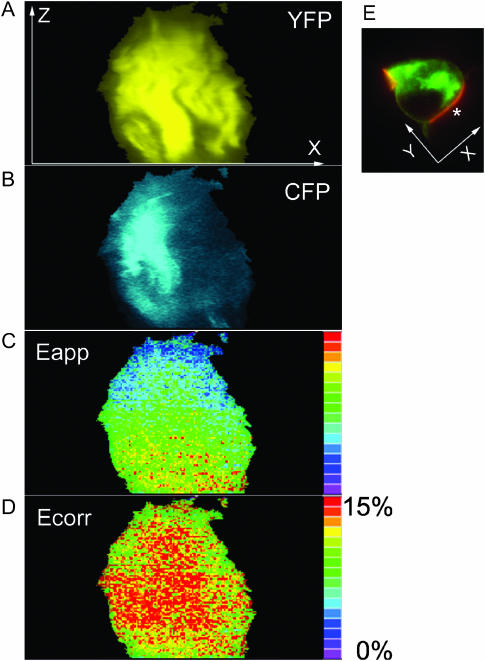
To demonstrate the use of E_corr in a three-dimensional experiment, we imaged a single contact area, marked by an asterisk in Fig. 4 E. The effect of gradually decreasing FRET was observed along the z axis from the bottom to the top of the cell (i.e., along the direction of the z scan), which is consistent with progressive photobleaching of YFP during the sequence. Fig. 4 D shows E_corr in the same contact area, demonstrating more symmetrical distribution of FRET thanks to removal of the photobleaching trend. We conclude that E_corr allows quantitative visualization of molecular proximity in living cells in timelapse and three-dimensional experiments, which would otherwise be masked by imaging-induced photobleaching.

FIGURE 4.

E-FRET imaging with photobleaching correction in a three-dimensional FRET experiment. We acquired a series of 137 planes of a single contact area between the A18.ZC.4Y cell and antigen-loaded LK35 B cell, using the 100× NA 1.45 objective, timed as in Fig. 3. A and B show side (x–z) views of YFP and CFP fluorescence, respectively, in the contact area marked in E. C and D show, respectively, FRET efficiency between CD3ζ-CFP and CD4-YFP without and with photobleaching correction.

Error propagation analysis

The precision of the E-FRET calculation depends on the precision of three input intensities and three calibrated parameters: I_DD, I_DA, I_AA, a, d, G, assuming a = d = φ. Error propagation analysis in response to a 10% error applied to each of the inputs, shown in Table 2, indicates that the I_DD and I_DA intensities, and to a lesser extent, the d coefficient, have the major impact. The E-FRET formulae are relatively tolerant to the error of G at low FRET efficiencies (<30%). When the actual input errors (specified in the Methods) were taken into account, the maximum per-pixel accumulated error of E_app was relatively constant: from ±2.4% to ±2.6% (Table 2).

TABLE 2.

Error propagation analysis for the E-FRET formula

Variable or parameter	ΔEapp [%] (Absolute error of Eapp in response to 10% input error)
	Eapp = 0%	Eapp = 10%	Eapp = 30%
IDD	1.7	2.2	2.8
IDA	2.7	3.0	3.3
IAA	0.89	0.72	0.43
a	0.89	0.72	0.43
d	1.9	1.5	0.92
G	0	0.82	2.0
Actual per-pixel error*	2.4	2.5	2.6
Actual pixel noise†	1.4	1.2	1.1

Error propagation analysis was performed on Eq. 12 and Eq. 13 by introducing a 10% disturbance into each variable (I_DD, I_DA, I_AA) or parameter (a, d, G) of the formulae. The resulting deviation of E_app is shown for three levels of E_app as indicated. The unit of error is the percent of energy transfer. The starting parameters were a = 0.077, d = 0.647, G = 3.50, I_DD = 750, I_AA = 3000, I_DA = 716.1 (for E_app = 0%), I_DA = 1008 (for E_app = 10%), and I_DA = 1845 (for E_app = 30%). Intensities are expressed in the relative camera response units. These values represent typical readings during actual experiments except for the input errors.

^*The actual per-pixel accumulated error of E_app was calculated based on 2 × 2 binning and input errors specified in the Methods for the dual-camera system.

^†The actual pixel-to-pixel noise is contributed only by the variables (I_DD, I_DA, I_AA).

When one is interested in monitoring the spatiotemporal changes of E it is more relevant to consider the pixel-to-pixel noise, rather than the absolute error of E. Pixel noise is not affected by errors of constant parameters a, d, and G, but only by experimental variables (I_DD, I_DA, I_AA). The pixel-to-pixel noise was still relatively constant: from ±1.4% to ±1.1% for low and high FRET efficiencies (Table 2). This has important implications for the signal/noise ratio. Photobleaching correction (E_corr) boosts E_app along with the noise. With the underlying pixel-to-pixel noise of E_app remaining relatively constant, the pixel-to-pixel noise of E_corr increases with increasing correction, hence the signal/noise ratio of E_corr degrades (as seen in Fig. 3 C, n = 1 and n = 65). An effective improvement in the signal/noise ratio is obtained by measuring E_corr over a multipixel ROI (Fig. 3, A and D), which increases the statistical significance of E_corr. The only situation when the calculations of E_app and E_corr (as well as other group 1 indices) become unstable mathematically is when donor intensity drops close to the camera noise.

Comparison with other ratiometric sensitized-emission methods

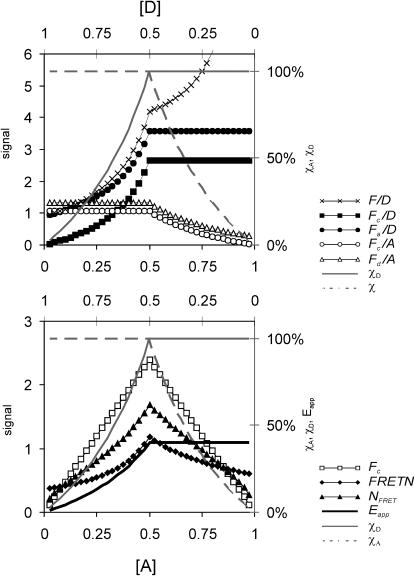
We used mathematical modeling under a variety of simulated experimental conditions to compare E_app calculated by the E-FRET formula with several representative FRET indices from each denominator group (defined in Methods and Table 1). We solved each of the formulae with respect to the degree of donor occupancy by acceptor χ_D or the degree of acceptor occupancy by donor χ_A (collected in Table 1 and explained in the Methods and Appendix). Responses were plotted along χ_D and χ_A over a range of donor and acceptor concentrations, such that any correlations or the lack of correlation with χ_D and/or χ_A could be recognized and demonstrated visually. The results of the analysis for both Type 1 experiments (donor and acceptor on the same molecule) and Type 3 experiments (donor and acceptor on different molecules) are summarized in Table 1. For brevity, we show only the simulation of a Type 3 experiment, where we reciprocally varied concentrations of donor and acceptor (Fig. 5). This simulation demonstrates that, regardless of the variable concentrations of donor and acceptor, group 1 indices F_c/D, F_a/D, as well as E_app, have the same trend as χ_D whereas group 2 indices F_c/A and F_d/A follow χ_A. In contrast, neither FRETN nor N_FRET (group 3) correlate consistently with either donor or acceptor occupancy throughout the whole range of their ratios. For example, increasing the acceptor concentration, while decreasing the donor concentration, causes FRETN to decline but χ_D remains constant. Likewise, increasing the donor concentration while decreasing acceptor concentration causes FRETN to decline, while χ_A stays constant. Additional simulations (not shown) demonstrate that FRETN correlates with χ_D only if the concentration of acceptor is constant and with χ_A only if donor concentration is constant. Similarly, N_FRET is concentration-dependent for Type 3 experiments, although less so than FRETN due to the square-root in the denominator of N_FRET. The only case when N_FRET retains correlation with χ_D (and χ_A) is in the special case of Type 1 experiments but in such a case the simpler F/D ratio is also suitable (not shown). F/D loses correlation with either degree of interaction for Type 3 experiments due to the incomplete crosstalk correction for acceptor (donor crosstalk is rendered constant by ratioing to the donor fluorescence).

FIGURE 5.

Modeling of the responses of FRET methods to variable concentration of donor and acceptor attached to different carriers (Type 3 experiment). In this simulation, donor and acceptor concentrations change reciprocally (acceptor concentration increasing and donor concentration decreasing) and a high affinity interaction between the donor-labeled and the acceptor-labeled species is assumed. Responses of several representative FRET indices from each denominator group (nomenclature and formulae defined in Table 1) were calculated and plotted along the degree of donor interaction χ_D (thin gray line, right y axis) and degree of acceptor interaction χ_A (broken gray line, right y axis), such that any correlation could be recognized visually. The following indices were included for comparison with E_app (solid black line, right y axis). Group 1, donor-denominated ratios: F/D (no crosstalk subtraction, x-marks), F_c/D (both donor and acceptor bleedthrough subtracted, ▪), F_a/D (only acceptor bleedthrough subtracted, •). Group 2, acceptor-denominated ratios: F_c/A (full crosstalk subtraction, ○), F_d/A (only donor crosstalk subtracted, equivalent to FR × a (Erickson et al., 2001), ▵). Group 3, donor-acceptor denominated indices: FRETN (♦), and N_FRET (▴). Nonratioed sensitized emission F_c is included for comparison (□). Increasing the acceptor concentration while decreasing the donor concentration causes increasing χ_D, up to χ_D = 1 when donor and acceptor concentrations are equal ([D] = [A] = 0.5). When acceptor concentration exceeds donor concentration, donor is saturated and χ_D = 1. Similarly, χ_A increases with donor concentration when [D] < [A] up to χ_A = 1, then remains saturated at [D] > [A]. Note that only F_c/D, F_a/D (top graph), and E_app (bottom graph) maintain the same tendencies as χ_D, whereas F_c/A and F_d/A correlate with χ_A. In contrast, F_c, F/D, FRETN, and N_FRET do not correlate consistently with the degrees of interaction for Type 3 experiments.

Closer examination shows that F_c/A and F_d/A are linearly proportional to the degree of acceptor interaction, whereas F_c/D and F_a/D follow the degree of donor interaction, but in a disproportional manner. This behavior of F_c/D and F_a/D is due to the quenching of donor fluorescence, which forms the denominator of F_c/D and F_a/D. This effect complicates the interpretation of relative changes of the F_c/D and F_a/D ratios in terms of the relative changes of the degree of donor interaction. At this point, we conclude that:

1. E_app computed by the E-FRET method is linearly proportional to the degree of donor interaction.

2. Group 1 indices F_c/D and F_a/D reflect the degree of donor interaction nonlinearly.

3. Group 2 indices F_c/A and F_d/A are proportional to the acceptor occupancy.

4. Group 3 indices FRETN and N_FRET are not indicative of the degrees of molecular interactions in Type 3 experiments.

Overall, only E_app (and E_corr if photobleaching correction is desired) fulfills two goals of FRET imaging: proportionality to the degree of molecular interaction (with respect to donor) and the independence of the optical parameters of the imaging system.

DISCUSSION

FRET efficiency imaging

Because imaging of FRET based on the sensitized emission of acceptor does not immediately allow calculation of the apparent FRET efficiency E_app, various indices and ratios have been used to visualize FRET. We use the E_app symbol instead of E to distinguish it from the specific transfer efficiency of pure interacting complex (E_max). Here we define and demonstrate a practical method to visualize sensitized-emission imaging data in terms of E_app. Our method, designated E-FRET, allows visualization of FRET similarly to the donor-recovery method, but without the inherent drawbacks. Furthermore, we approach another problem plaguing timelapse and three-dimensional imaging of FRET, which is the degradation of measurements due to gradual photobleaching of the sample. E-FRET provides for appropriate correction such that the corrected FRET efficiency E_corr can be calculated as if photobleaching did not occur. All calculations are based on 3-cube imaging allowing easy adaptation to existing microscopes. E_app and E_corr allow easy evaluation of the relative magnitude of the FRET effect and facilitate comparison of FRET data between laboratories, independent of the instrumentation involved.

E-FRET unifies ratiometric FRET methods with the donor recovery after acceptor photobleaching method. The distinct advantage of the methodology presented here rests in experimental calibration of the G parameter, which is necessary for calculating FRET efficiency from sensitized-emission imaging. G was introduced to link sensitized emission of acceptor with the concomitant quenching of donor (Gordon et al., 1998). We found that calculation of G from physical constants allowed only a rough estimate due to the large error margin inherent in the determination of quantum yields in cells, and in the determination of the spectral transmission characteristics of the imaging path of the microscope (Zal et al., 2002). Instead we calibrate G directly as the ratio of sensitized emission in a reference sample to the donor recovery after acceptor photobleaching. We demonstrate that the FRET construct for G calibration need not be the same as for the experiment and may have different E_max, which does not need to be known. Determination of G for a particular imaging system does not require any additional equipment other than what is typically necessary for 3-cube imaging. Once calibrated, G is applicable to subsequent calculations of E_app and E_corr for experiments relying on the same donor and acceptor fluorophores as long as timing of exposures in all channels is kept proportional. An analogous approach should be directly applicable to measure G as the ratio of the change of sensitized emission to donor recovery after enzymatic digestion of a Type 2 FRET construct (data not shown). This will allow determination of G for photo-stable acceptors.

G estimated from optical parameters of the imaging system (Eq. 14) and the formula given by Eq. 13 allowed us in a previous study to convert, for the first time, readings of the F_a/D index to FRET efficiency values (Zal et al., 2002). A formula for the E_app equivalent (E_D) was presented recently (Hoppe et al., 2002) but required back-calculation of instrumental parameters based on external determination of E_max. E_D relied on two parameters: γ, which is the ratio of the acceptor extinction coefficient to the donor at donor excitation and ξ, which is a proportionality constant, similar in concept but different from G in that G = γ/ξ. Both γ and ξ had to be calculated from the known stoichiometry of interaction and the specific FRET efficiency of the interaction E_C (equivalent to E_max), which was obtained from lifetime measurements. Such measurements are usually impractical without access to FLIM instrumentation or biochemical purification of the complex. In our photobleaching calibration method, knowledge of E_max is not necessary and G can be calibrated without additional instrumentation. The FR ratio was proposed for computation of effective FRET efficiency defined with respect to acceptor as E_maxχ_A (Erickson et al., 2001). FR is different from the classic definition of FRET efficiency, although it is useful for monitoring χ_A.

Linear crosstalk correction is an integral part of E-FRET calculations and is built into the corresponding formulae based on previous work (Youvan et al., 1997). Elangovan and co-workers observed nonlinear bleedthrough between CFP and dsRED1 or Alexa488 and Cy3 which prompted tabulated crosstalk correction depending on fluorescence intensity (Elangovan et al., 2003). It is not clear whether factors intrinsic to fluorophores or related to the detection devices caused this effect. Therefore the constancy of bleedthrough factors has to be tested for new donor-acceptor pairs and imaging systems. In this respect it is important to note that the bleedthrough coefficients for ECFP and EYFP were indeed remarkably constant across a wide range of concentrations in cells, in different intracellular compartments, and under clustering conditions (data not shown; but see Zal et al., 2002), when measured using CCD cameras with flatfield correction and intraimage background subtraction.

Comparison of E-FRET with other FRET methods

A remarkable variety of formulae have been proposed for reporting FRET based on sensitized-emission imaging (Berney and Danuser, 2003). The reasons behind the proposal of differing indices are at least twofold. The first is the need for simplicity: Type 1 (internal FRET) and some Type 2 (digestible linker) experiments require only two-image ratioing to achieve the simplest possible, concentration-independent, FRET index. In contrast, Type 3 (heterologous) and some Type 2 experiments require explicit crosstalk subtraction demanding three-image calculations. The second reason behind the proliferation of FRET methods is due to conflicting criteria for interpreting changes in FRET in Type 3 experiments. For Type 3 experiments, the general question asked by the experimenter, whether donor-labeled species X and acceptor-labeled Y physically interact, can be broken into more specific and quantitative problems: 1), if and where a significant proportion of X is in the proximity of Y, and 2), if and where a significant proportion of Y is in proximity of X, 3), is this proximity a biologically relevant molecular interaction or a random collision? Questions 1 and 2 are not equivalent for Type 3 experiments. For instance, if Y is present in excess over X, a high affinity interaction of the two will give 100% interaction with respect to X and a low degree of interaction with respect to Y, and vice versa. From this point of view we distinguished three categories of FRET ratio indices to compare with E-FRET with respect to correlation with the degrees of molecular interaction. Group 1 indices are denominated by donor fluorescence, group 2 indices are denominated by acceptor fluorescence, and group 3 indices are denominated by both donor and acceptor.

Comparison of E-FRET with other FRET ratios through mathematical modeling of Type 3 experiments demonstrated that group 1 ratios F_c/D and F_a/D as well as the E-FRET formula reflect the donor occupancy by acceptor. Therefore these measures should be used for experiments where acceptor is available at or above stoichiometric concentration over donor, such that it is the affinity of interaction, not the acceptor availability which is limiting. Group 2 ratios F_c/A and F_d/A correlate with the acceptor occupancy by donor and thus are preferable for experiments where the acceptor-labeled species is limiting. Unfortunately, this also limits the intensity of sensitized emission, making group 2 ratios error-prone (data not shown). Group 3 indices FRETN and N_FRET were concentration-dependent and did not consistently correlate with either degree of interaction.

There are two main advantages of E_app over the group 1 FRET indices that correlate with donor occupancy. Unlike the F_c/D or F_a/D ratios, E_app is independent of the optical configuration of the imaging system, allowing for direct comparison of data between laboratories. Secondly, E_app is linearly proportional to the degree of donor occupancy by acceptor, which allows interpretation of an n-fold change in E_app as an n-fold change in the degree of complex formation by donor. Ultimately, if the specific FRET efficiency of the interacting complex, E_max, can be established, and if only one species of complex forms, the degree of interaction between donor-labeled molecules X and acceptor-labeled Y, with respect to X, can be directly calculated as

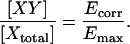(22)

E_max can be estimated from within the imaging data as the extrapolated maximum observable E_corr (or E_app) for sites of high affinity interaction. Alternatively, E_max can be measured by FLIM (Hoppe et al., 2002), or in vitro if a purified donor-acceptor complex can be procured.

Nonspecific FRET and Group 3 indices

The main reason behind the proposal of group 3 indices FRETN (Gordon et al., 1998) and N_FRET (Xia and Liu, 2001) was to prevent detection of FRET caused by nonspecific proximity due to diffusion-driven collision at high concentrations. Unfortunately, attempting to combine a measure of specificity with the detection of FRET itself resulted in concentration-dependent FRET indices which do not correlate with the degrees of complex formation with respect either to donor or acceptor. To correct for the apparent over-normalization in FRETN, Xia and Liu proposed to calculate N_FRET, which differs in that the square-root was applied to the denominator of FRETN (Xia and Liu, 2001). Our analysis shows that this did not eliminate the concentration dependence of N_FRET for Type 3 experiments. The only case when N_FRET correlated with the occupancy of donor by acceptor, independent of their concentration, was for Type 1 experiments (not shown). Thus FRETN and N_FRET are not suitable for monitoring the degree of molecular interaction in Type 3 experiments, although FRETN is useful in that it correlates with the affinity constant for interactions reaching the state of equilibrium (Gordon et al., 1998, Sorkin et al., 2000).

There is no doubt that FRET due to specific versus nonspecific interactions must be distinguished. Nevertheless, it should be noted that close proximity due to localized concentration, but without formation of high affinity complexes, can be biologically relevant—for example, for signal transduction or enzymatic reactions. Therefore we tend to view the specificity of FRET in terms of the underlying affinities of interaction. Kenworthy and Edidin distinguished between the specific FRET and the random collision-driven FRET signals by establishing whether FRET efficiency measured by the donor-recovery method is concentration-dependent (Kenworthy and Edidin, 1998). An increase in FRET efficiency detected only at high concentrations of acceptor indicated that the underlying molecular interaction is nonspecific (or of low affinity). If, on the other hand, the FRET signal remained high even at low donor and acceptor concentrations, this indicated a specific, i.e., high affinity interaction. We propose that the same strategy is followed for E-FRET imaging. The detection of molecular proximity by measuring E_app or E_corr should be considered separately from the assessment of the biological specificity of the proximity, which requires secondary analysis. The latter can be done by comparing experimental samples with appropriate negative controls, as well as by evaluating E_app against the acceptor concentration and acceptor/donor ratios (Zal et al., 2002). Such analysis is outside the scope of this work, which deals with how to detect and visualize proximity between donor and acceptor-labeled macromolecules in terms of FRET efficiency, irrespective of the cause of the proximity.

Photobleaching correction for timelapse and three-dimensional FRET experiments

Gradual photobleaching of fluorophores degrades the dynamic range of FRET responses and interferes with timelapse and three-dimensional FRET imaging. Visualizing FRET in terms of true FRET efficiency E_app allowed us to devise methods for calculation of photobleaching-corrected FRET efficiency E_corr. This is the hypothetical efficiency that would have been observed if not for the photobleaching. Several interconnected photobleaching effects had to be considered. Donor and acceptor fluorophores may differ widely in their resistance to photobleaching. For example, EYFP is more sensitive to photobleaching than ECFP (Tsien, 1998). Furthermore, donor in complex with acceptor photobleaches more slowly than free donor due to the decreased excited state lifetime. Likewise, acceptors in an interacting experimental sample are photobleached in two ways: by direct excitation, and indirectly, by FRET sensitization during donor excitation (Mekler et al., 1997). Our analysis indicates that the effect of donor photobleaching is small compared to the impact of acceptor photobleaching, and is largely cancelled by the ratio nature of E_app. Thus, in essence, photobleaching correction involves stretching the dynamic range of E_app by normalizing to the acceptor fluorescence at the beginning of the experiment.

The impact of sensitized acceptor photobleaching depends on the kinetics of complex formation. If the rate of acceptor photobleaching is slower than the rates of complex association and dissociation, then the acceptor bleaches uniformly in a given compartment due to exchange with the free pool. The ensuing correction is based on the internal rate of acceptor photobleaching, determined from the series of acceptor images, and is mathematically accurate. On the other hand, if the complexes are stable compared with the rate of acceptor photobleaching, acceptor in the sites of interaction will undergo slightly faster photobleaching and the correction based on total acceptor photobleaching will be approximate. Nevertheless, we show that in 3-cube imaging the relative impact of sensitized acceptor photobleaching is small compared to direct photobleaching. Therefore, the approximation is good: for most imaging systems, over one-third of acceptor can be photobleached with the correction error remaining at <10% of E_corr.

We offer two complementary practical approaches to photobleaching correction. Internal correction is designed for those imaging experiments where the total acceptor fluorescence is a good reflection of acceptor photobleaching. These would typically be single focal plane timelapse sequences on a timescale sufficiently short to disregard gross morphological changes and turnover of fluorescent proteins in the cell. External correction works well for three-dimensional and timelapse experiments involving morphological changes, as long as the accumulated exposure is the same for all elements of the image, i.e., cells do not migrate in and out of the field of view and the illumination intensity is uniform.

Photobleaching correction for Type 1 FRET experiments

Type 1 experiments offer the advantage of simplified 2-cube imaging (or a camera split with a constant excitation wavelength), but this is not sufficient for photobleaching correction. Calculating E_corr for Type 1 experiments necessitates a departure from the convenience of 2-cube imaging since it requires acquisition of acceptor images as well, i.e., 3-cube imaging. Nevertheless, it may be necessary if significant photobleaching is observed during the experiment.

Practical limitations

The most important practical limitation of photobleaching correction comes from the propagation of pixel noise in images losing their intensity due to photobleaching. This pixel-to-pixel noise, which in our system was estimated ±2.6% of energy transfer (Table 2 legend), is amplified by photobleaching correction. The impact of increasing signal/noise will depend greatly on the general conditions of the experiment and is vastly lessened by averaging E across a region of interest. Error propagation analysis indicated that the major potential sources of error are the precision of the I_DA intensity, followed by the I_DD intensity, and the d bleedthrough coefficient (Table 2). The I_AA intensity and the a and G parameters had a lesser impact. Ensuring good signal/noise ratio at the beginning of the experiment through utilization of low noise CCD electronics and effective use of the dynamic range of the camera(s) will allow prolonged E-FRET imaging with photobleaching correction. In practice, we were able to continue photobleaching correction until >50% of acceptors were destroyed.

Accurate determination of the distance between fluorophores in the interacting complex, hence by inference between the carrier macromolecules, depends on determination of E_max. Distance calculations based on E_app or E_corr lead to underestimated distances. Although E-FRET methodology greatly improves quantitation of 3-cube imaging data, there still exist additional variables in the setting of a live FRET imaging experiment, which dictate careful interpretation of the distances derived from E_app or E_corr. The first variable is the orientational parameter 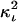(usually assumed to be a constant equal to two-thirds for unobstructed rotation of at least one fluorophore). It is usually impossible or impractical to know 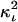in the local cell microenvironment (Matko and Edidin, 1997). The other unknown is the existence of alternative donor-acceptor complexes if more than one conformation can be assumed by the carrier macromolecules. For these reasons, imaging of FRET efficiency in single cells so far stops short of measuring absolute distances between fluorescent tags in situ. This is an area for much needed progress.

In conclusion, the E-FRET method provides for unified presentation of FRET imaging data in units of FRET efficiency and independent of instrumental parameters. This allows quantitative comparison of FRET images between laboratories and facilitates interpretation of the data in terms of the changes in the degree of donor interaction with acceptor. Photobleaching correction should benefit all sensitized emission-based FRET studies involving repeated and prolonged exposure of samples to the excitation light, i.e., timelapse studies in live cells, and three-dimensional visualization of FRET in live or fixed specimens.

APPENDIX: GLOSSARY

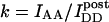is the ratio of acceptor fluorescence to donor fluorescence under the conditions of no interaction (E_app = 0). k is the constant for Type 1 (intramolecular) FRET experiments (if no photobleaching takes place) but is variable for Type 3 (intermolecular) FRET experiments.

E_max is the specific FRET efficiency for stoichiometric and complete interaction.

E_app is the apparent FRET efficiency (donor recovery after acceptor photobleaching would measure this).

E_corr is the photobleaching-corrected FRET efficiency.

χ_D, χ_A are the degrees of complex formation with respect to donor, Eq. 2, or acceptor χ_A = [DA]/[A_total], respectively, counting only fluorescent molecules (affected by photobleaching).

is degree of complex formation with respect to the donor-labeled species X, Eq. 16, counting all molecules, including those that were photobleached (not affected by photobleaching).

I_DD, I_DA, and I_AA are the pixel or ROI intensities, after background subtraction, using, respectively, the donor excitation-donor emission, donor excitation-acceptor emission, and acceptor excitation-acceptor emission filter sets.

G is the ratio of sensitized emission in the I_DA filter set before photobleaching (F_c) to donor recovery in the I_DD filter set after acceptor photobleaching.

ɛ_D1, ɛ_A1 are absorbance coefficients at donor excitation wavelength of donor or acceptor, respectively.

R_DD, R_AA are responses of the detector with the I_DD filter set to unit concentration of donor and the detector with the I_AA filter set to unit concentration of acceptor, respectively.

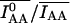is the photobleaching correction factor: ratio of total acceptor fluorescence in the compartment at the beginning of experiment to total acceptor fluorescence in the compartment at the current exposure.

t is the experiment time or exposure number.

τ_A is the half-life of acceptor during the experiment, in units of t.

L, NL is linearly or nonlinearly.

a, b, c, d are crosstalk constants (Eqs. 3–6).