Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Jun;86(6):3940–3950. doi: 10.1529/biophysj.103.035048

High Field/High Frequency Saturation Transfer Electron Paramagnetic Resonance Spectroscopy: Increased Sensitivity to Very Slow Rotational Motions

Eric J Hustedt 1, Albert H Beth 1
PMCID: PMC1304295  PMID: 15189890

Abstract

Saturation transfer electron paramagnetic resonance (ST-EPR) spectroscopy has been employed to characterize the very slow microsecond to millisecond rotational dynamics of a wide range of nitroxide spin-labeled proteins and other macromolecules in the past three decades. The vast majority of this previous work has been carried out on spectrometers that operate at X-band (∼9 GHz) microwave frequency with a few investigations reported at Q-band (∼34 GHz). EPR spectrometers that operate in the 94–250-GHz range and that are capable of making conventional linear EPR measurements on small aqueous samples have now been developed. This work addresses potential advantages of utilizing these same high frequencies for ST-EPR studies that seek to quantitatively analyze the very slow rotational dynamics of spin-labeled macromolecules. For example, the uniaxial rotational diffusion (URD) model has been shown to be particularly applicable to the study of the rotational dynamics of integral membrane proteins. Computational algorithms have been employed to define the sensitivity of ST-EPR signals at 94, 140, and 250 GHz to the correlation time for URD, to the amplitude of constrained URD, and to the orientation of the spin label relative to the URD axis. The calculations presented in this work demonstrate that these higher microwave frequencies provide substantial increases in sensitivity to the correlation time for URD, to small constraints in URD, and to the geometry of the spin label relative to the URD axis as compared with measurements made at X-band. Moreover, the calculations at these higher frequencies indicate sensitivity to rotational motions in the 1–100-ms time window, particularly at 250 GHz, thereby extending the slow motion limit for ST-EPR by two orders of magnitude relative to X- and Q-bands.

INTRODUCTION

Saturation transfer electron paramagnetic resonance (ST-EPR) spectroscopy, a technique developed by Hyde and Dalton (1972), has been utilized to characterize the global rotational dynamics of a wide range of soluble and membrane bound proteins and other macromolecules over the past three decades (for recent reviews see Beth and Robinson, 1989; Hemminga and de Jager, 1989; Beth and Hustedt, 2003; Marsh et al., 2003). Using nitroxide spin labels and conventional X-band (∼9 GHz) EPR spectrometers, ST-EPR provides high sensitivity to the correlation times for rotational motions in the microsecond to millisecond time window (Thomas et al., 1976). This time window, which is outside the picosecond to microsecond sensitivity window of conventional linear EPR (McCalley et al., 1972), is of considerable interest since it spans the correlation time range that is characteristic of the global rotational motions of a large number of intrinsic membrane proteins (see Beth and Hustedt, 2003). Moreover, it overlaps the timescales for many enzyme catalyzed reactions (kcat's), for a wide range of cellular membrane transport processes, and for the initial phases of transmembrane signaling events in cells. As the database of high resolution static structures of proteins continues to expand, investigations aimed at understanding the dynamics of functionally relevant structural transitions of proteins (functional dynamics) are becoming more numerous. It is now evident that many proteins undergo significant structural rearrangements in carrying out their biological functions. With the advent of site-directed spin-labeling methods (SDSL; see Hubbell et al., 1996, 2000; Feix and Klug, 1998; Columbus and Hubbell, 2002) for placing a probe at selected sites in proteins, ST-EPR offers unique opportunities for studies aimed at quantifying the relatively slow functional dynamics of proteins and, therefore, for understanding the molecular bases for a wide range of structural rearrangements.

Some of the challenges in characterizing the global rotational dynamics of intrinsic membrane proteins or the functional dynamics of proteins are that the motions are often highly anisotropic, they often occur on the microsecond to second(s) timescale, and they can be constrained in angular amplitude. ST-EPR spectra have been shown to be sensitive to the correlation time for rotational motions in the fast end of this timescale, to the anisotropic nature of the motion, and to restrictions on the amplitude of motion (see Beth and Robinson, 1989; Howard et al., 1993; Blackman et al., 2001; Hustedt and Beth, 2001; Beth and Hustedt, 2003). However, the lineshape effects from different motional processes can look remarkably similar, particularly at X-band and lower microwave frequencies, due to the nearly axial character of the spectra. At higher magnetic fields and resonant frequencies, the spectra are dominated by the anisotropic g-tensor, they are distinctively nonaxial, they are spread over a wider range of resonant field values, and they hold the potential for providing much more detailed information on the anisotropy of motion (Hustedt and Beth, 2001; Beth and Hustedt, 2003).

The vast majority of the ST-EPR studies that have been carried out to date have utilized X-band spectrometers due in large part to the wide-spread availability of instruments that operate in the 8–10-GHz microwave frequency range. Moreover, these instruments are easy to house and to operate, and they are capable of making routine and reproducible ST-EPR measurements on dilute (e.g., micromolar to millimolar) biological samples. Some ST-EPR studies have been carried out at Q-band (e.g., Johnson and Hyde, 1981; Johnson et al., 1982a,b; Blackman et al., 2001). The increased spectral dispersion at Q-band relative to X-band and lower frequencies results in increased sensitivity to the anisotropy of motion (Johnson et al., 1982a; Hustedt and Beth, 2001) and increased sensitivity to constraints on the amplitude of motion (Hustedt and Beth, 2001). In the past decade, spectrometers that operate at higher fields and at higher microwave frequencies in the 94–250-GHz range have been developed, and these instruments have been utilized to record conventional linear EPR spectra on a wide range of biological samples (e.g., Earle et al., 1994; Smirnov et al., 1995; Hustedt et al., 1997; Barnes and Freed, 1998; Gaffney and Marsh, 1998; Barnes et al., 1999; Budil et al., 2000; Bar et al., 2001; Mangels et al., 2001; Rohrer et al., 2001). These studies have shown that the higher microwave frequencies provide important advantages relative to the lower frequency measurements including separation of overlapping spectra with slightly different g-values (e.g., Smirnov et al., 1998), unique determination of all of the principal elements of the A- and g-tensors, and the ability to shift the range of sensitivity to faster rotational motions and to suppress the contributions of slower rotational motions on the linear EPR timescale (e.g., Barnes et al., 1999; Freed, 2000). Despite the success and the advantages of high frequency conventional EPR for characterizing the picosecond to microsecond dynamics of spin-labeled proteins, no experimental ST-EPR studies of microsecond to millisecond dynamics at microwave frequencies in the 94–250-GHz range have been reported.

One of the major determinants of sensitivity of ST-EPR signals to very slow rotational motions is the magnitude of the change in resonance condition with a change in orientation of the spin label relative to the external magnetic field (i.e., |∂Hres/∂Ω|; Thomas et al., 1976; Fajer and Marsh, 1983; Beth and Robinson, 1989; Beth and Hustedt, 2003). At those positions of the spectrum where |∂Hres/∂Ω| is large, high spectral sensitivity to the correlation time for rotational motion has been observed experimentally and predicted theoretically for many different motional models. The width of each of the nuclear manifolds from nitroxide spin labels increases at the higher fields due to the anisotropic g-tensor interactions. Consequently, there is a field dependent increase in ‖∂Hres/∂Ω| for each nuclear manifold at the higher magnetic fields (see Beth and Robinson, 1989; Beth and Hustedt, 2003). Based upon the previous literature, one would predict that the increased spectral width of the manifolds would lead to larger changes in lineshapes as a function of rotational correlation time and that the wider manifolds would be sensitive to longer correlation times. These potential advantages and the desirability of developing methods that are sensitive to rotational motions in the millisecond or longer correlation time range prompted this work.

The calculations that are presented here demonstrate that ST-EPR spectra at the higher microwave frequencies will provide some important additional information relative to those obtained at X-band. First, as predicted, there is a monotonic shift in sensitivity to longer correlation times as a function of microwave frequency. Second, the spectra become much more sensitive to the anisotropic characteristics of the motion at the higher microwave frequencies. Third, the spectra are more sensitive to small constraints to rotational diffusion at the higher microwave frequencies. These latter two advantages are important for correctly interpreting the complex dynamics of systems that are undergoing anisotropic rotational diffusion and/or constrained rotational diffusion. The calculations presented here demonstrate the potential utility of high field/high frequency for ST-EPR studies of very slow rotational motions, and they provide strong motivation for carrying out experimental work to verify these predictions.

METHODS

ST-EPR spectra for the unconstrained uniaxial rotational diffusion (URD) model were calculated with an algorithm that utilizes the transition rate matrix (TRM; Thomas and McConnell, 1974) approach for treating rotational dynamics as described in previous work (Hustedt and Beth, 1995). Zeeman overmodulation effects were treated explicitly in the algorithm that was employed for unconstrained URD (algorithm II; Hustedt and Beth, 1995). ST-EPR spectra for the constrained URD model were calculated using a square well restriction, and Zeeman overmodulation effects were approximated as described by Hustedt and Beth (2001). The principal elements of the A- and g-tensors that were employed in all calculations were determined from [15N,2H]-maleimide spin-labeled glyceraldehyde-3-phosphate dehydrogenase (GAPDH) in previous work (Beth et al., 1981). These included Axx = 10.62 G; Ayy = 10.38 G; Azz = 50.15 G; gxx = 2.0091; gyy = 2.0061; and gzz = 2.0022. The value for T1e was set to 5 μs, unless otherwise noted, based upon saturation recovery measurements at X-band (A. H. Beth and B. H. Robinson, unpublished) and T2e was set to 40 ns to match the experimental ST-EPR linewidth observed from spin-labeled glyceraldehyde-3-phosphate dehydrogenase (Beth et al., 1981). These values are all representative of the values observed from other [15N,2H] spin-labeled proteins including bovine serum albumin (Hustedt et al., 1993), epidermal growth factor (Stein et al., 2002), and anion exchange protein (Hustedt and Beth, 1995, 2001). All spectra for unconstrained URD were calculated using a 5-G Zeeman field modulation amplitude and a microwave observer field of 0.2 G in the rotating frame. Spectra for constrained URD were also calculated with an effective modulation amplitude of 5 G (Robinson, 1983) and a microwave observer field of 0.2 G. The spectra chosen for display are the second-harmonic, out-of-phase absorption signals, denoted 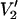Inline graphic (Thomas et al., 1976), using a 50-kHz reference modulation frequency and 100-kHz detection unless otherwise noted.

All calculations were performed on a 2.5-GHz Pentium IV CPU computer. The calculations were judged to be converged when inclusion of additional angular grids in the transition rate matrix resulted in no further change in lineshape. At 9.8, 34, and 60 GHz, N = 128 was sufficient for convergence; at 94 and 140 GHz, N = 256 was sufficient; and at 250 GHz, N = 512 was sufficient. Spectra at 9.8, 34, 60, 94, and 140 GHz were calculated at 201 field values and spectra at 250 GHz were calculated at 401 field values. The FORTRAN source code used in the calculations is available from the authors.

RESULTS

Sensitivity of V2′ signals to τ as a function of microwave frequency

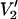The calculated Inline graphic ST-EPR spectra in Fig. 1 show the range of lineshape changes that are predicted to occur as a function of the correlation time for URD for τ‖ from 1 μs to 100 ms at microwave frequencies of 9.8, 94, 140, and 250 GHz. These spectra, which are all calculated using the same URD model with the spin label z axis tilted by 54.7° relative to the diffusion axis (Fig. 2, θ = 54.7° and φ = 0°), demonstrate two important points. First, the magnitude of the overall change in lineshape increases monotonically as a function of increasing microwave frequency. Second, there is increasing sensitivity to longer correlation times as the microwave frequency is increased. Both of these points are illustrated graphically in Fig. 3 where the total area under the Inline graphic lineshape is plotted versus τ‖ at different microwave frequencies. Unlike the linear V1 EPR signal, the integrated intensity of the 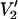Inline graphic signal increases with increasing correlation time and is a simple measure of the dynamics reflected in the complex lineshape.

FIGURE 1.

FIGURE 1

Open in a new tab

Calculated 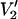Inline graphic signals at 9.8, 94, 140, and 250 GHz. The five spectra in each column were calculated for the same URD model with the spin label z axis tilted by 54.7° relative to the diffusion axis (θ = 54.7° and φ = 0°) at correlation times of 1 μs, 10 μs, 100 μs, 1 ms, and 100 ms. All spectra are shown normalized to the same amplitude and are scaled to the same width for display. Actual widths are 100 G at 9.8 GHz, 200 G at 94 GHz, 250 G at 140 GHz, and 400 G at 250 GHz. Values for all other input parameters, given in Methods, included υm = 50 kHz; hm = 5 G; h1 = 0.2 G; T1e = 5 μs; T2e = 40 ns; gxx = 2.0091; gyy = 2.0061; gzz = 2.0022; Axx = 10.62 G; Ayy = 10.38 G; and Azz = 50.15 G.

FIGURE 2.

FIGURE 2

Open in a new tab

Definition of the polar angles between the spin label reference frame and the URD axis of rotational diffusion.

FIGURE 3.

FIGURE 3

Open in a new tab

Parameterized data from 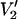Inline graphic signals calculated at 9.8, 34, 60, 94, 140, and 250 GHz. The data are plotted as the integral of 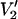Inline graphic at τ‖ divided by the integral of 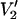Inline graphic at τ‖ = 1 μs vs. τ‖ in seconds. The URD model and all input parameters were the same as for the data presented in Fig. 1.

An important result that is demonstrated in Fig. 3 is that ST-EPR spectra are predicted to be very sensitive to motions in the 1–100-ms time range at 250 GHz. This very slow motional range, which is characteristic of the timescales for many important biological events, has been difficult to address using currently available methods (see Beth and Hustedt, 2003). As also shown in Fig. 3, sensitivity to correlation times in the 1–10-μs time window is comparable at all of the microwave frequencies in the 9.8–250-GHz range. These calculations indicate that the higher frequencies provide useful sensitivity to the longer correlation times without any loss of sensitivity to the faster correlation times.

Many additional calculations of ST-EPR spectra have been carried out for other URD models including alignment of the nitroxide z axis with the URD axis (θ = 0° and φ = 0°), alignment of the nitroxide x axis with the URD axis (θ = 90° and φ = 0°), and alignment of the nitroxide y axis with the URD axis (θ = 90° and φ = 90°) as a function of correlation time. Representative calculations for τ‖ = 1 μs are shown in Fig. 4. For all of the motional models examined, the same relative sensitivity to rotational motions is observed including increased sensitivity to very slow motions in the 1–100-ms time range at the higher microwave frequencies.

FIGURE 4.

FIGURE 4

Open in a new tab

Calculated 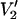Inline graphic signals for three different URD models at 9.8, 94, 140, and 250 GHz. In each panel, the three spectra are superimposed for URD with τ‖ = 1 μs and θ = 0° and φ = 0° (solid line); θ = 90° and φ = 0° (dashed line); and θ = 90° and φ = 90° (dotted line). All other input parameters were the same as in Fig. 1.

Sensitivity of V2′ signals to the orientation of the spin label relative to the URD axis as a function of microwave frequency

Experimental and theoretical work has shown that the 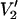Inline graphic ST-EPR signal at 9.8 GHz is sensitive to anisotropic rotational diffusion and to the orientation of the spin label reference frame relative to the diffusion tensor (for extensive discussions see Hyde and Dalton, 1979; Robinson and Dalton, 1980, 1981; Beth and Robinson, 1989; Beth and Hustedt, 2003). Previous work has also shown that 34 GHz provides a useful increase in sensitivity of the 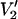Inline graphic signal to the anisotropy of rotational motion relative to 9.8 GHz due to the increased spectral anisotropy arising from the g-tensor interactions (e.g., Johnson et al., 1982a; Blackman et al., 2001; Beth and Hustedt, 2003). The limited number of calculations that have previously been carried out at 94 GHz have indicated that substantial additional increases in sensitivity to the anisotropy of rotational motion might be obtained at higher field/higher frequency operation (Hustedt and Beth, 2001; Beth and Hustedt, 2003).

The data in Fig. 4 reinforce these previous observations and extend them to investigate the sensitivity of 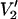Inline graphic signals at 140 and 250 GHz to anisotropic motion. These calculations show the remarkably different lineshapes that are predicted for three different geometries of spin label reference frame relative to the URD axis (τ‖ = 1 μs, θ = 0°, and φ = 0°; τ‖ = 1 μs, θ = 90°, and φ = 0°; τ‖ = 1 μs, θ = 90°, and φ = 90°) at 94, 140, and 250 GHz relative to the modest differences in lineshapes for these same three geometries at 9.8 GHz. A major uncertainty in ST-EPR studies of very slow rotational dynamics has been how to relate apparent or effective rotational correlation times to the true rotational correlation times for the spin-labeled macromolecule. This uncertainty arises from the necessity of analyzing experimental data in terms of a rotational diffusion model. At 9.8 GHz, different rotational diffusion models can fit the experimental data with nearly identical statistics (e.g., Hustedt and Beth, 1995). Each model will yield a different value, or different values, for the rotational correlation times (Beth and Robinson, 1989; Beth and Hustedt, 2003).

The spectra in Fig. 4 demonstrate that the 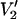Inline graphic spectra at the higher microwave frequencies have characteristic lineshapes that are indicative of the diffusion model. This point is readily appreciated by comparing the data in Fig. 1 where the major tilt angle is 54.7°, and hence the spectral lineshapes closely resemble those for isotropic rotational diffusion (Robinson and Dalton, 1980) with those at the corresponding microwave frequency in Fig. 4. At 9.8 GHz, there are only subtle differences between the spectral shapes for the three URD models in Fig. 4 and those at some other correlation time in Fig. 1. Conversely, at 94, 140, and 250 GHz, none of the spectra at different correlation times in Fig. 1 look similar to the three spectra at the corresponding microwave frequency in Fig. 4. This high sensitivity to the axis of motional averaging at the higher microwave frequencies as well as to the correlation time for motional averaging should prove useful in studies of complex local and global rotational motions in the very slow motion regime.

Sensitivity of V2′ Signals to constrained URD as a function of microwave frequency

Fig. 5 shows the 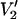Inline graphic signals that are predicted to occur for different widths (Δ) of a square well restriction on the amplitude of URD at 9.8 (top left), 94 (top right), 140 (lower left), and 250 GHz (lower right). The parameterized data in Fig. 6 demonstrate that the higher microwave frequencies provide a substantial increase in sensitivity to small values of Δ relative to 9.8 GHz (i.e., |∂integral|/∂Δ is larger at the higher frequencies for Δ < 15°). However, ST-EPR spectra at the higher frequencies are actually less sensitive than 9.8 GHz to large values of Δ. The data in Fig. 5 show that as Δ is decreased, there is a monotonic change in the 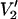Inline graphic lineshape that mimic the changes that occur as a result of slowing of unconstrained URD (Fig. 1). However, it may be possible in many instances to analyze experimental data obtained at multiple microwave frequencies to uniquely determine Δ and τ‖ as described in the Discussion section.

FIGURE 5.

FIGURE 5

Open in a new tab

Effects of a square well potential on calculated 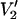Inline graphic lineshapes at 9.8, 94, 140, and 250 GHz. The eight spectra in each panel were calculated for a URD model with τ‖ = 1 μs and the spin label z axis tilted by 54.7° relative to the diffusion axis for Δ-values of 1°, 5°, 15°, 30°, 45°, 60°, 75°, and 90°. The spectra at all four microwave frequencies monotonically decrease in amplitude as Δ decreases. All other input parameters were the same as in Fig. 1.

FIGURE 6.

FIGURE 6

Open in a new tab

Parameterized data from the 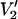Inline graphic signals shown in Fig. 4. The data are plotted as the integral of 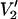Inline graphic at Δ divided by the integral of 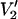Inline graphic at Δ = 1° vs. Δ (the full width of the square well potential in degrees).

The data in Fig. 5 were calculated using a single URD model with τ‖ set to 1 μs and the nitroxide z axis tilted by 54.7° relative to the diffusion axis. Although spectral sensitivity to Δ is highly dependent on the orientation of the spin label relative to the URD axis at 9.8 GHz as shown in previous work (Hustedt and Beth, 2001), the increased spectral dispersion at microwave frequencies of 94, 140, and 250 GHz minimizes this dependence (data not shown). However, the magnitude of change in 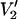Inline graphic lineshape as a function of Δ is monotonically diminished at all four microwave frequencies as the correlation time for URD becomes longer (data not shown). The loss of sensitivity is the direct result of approaching the no motion limit for the 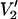Inline graphic signal at the longer correlation times. As this limit is approached, a restriction in amplitude of URD simply produces no further spectral effects (see Fig. 5 and the accompanying discussion in Hustedt and Beth, 2001). The converse is also true; as Δ approaches 0°, the spectra become insensitive to τ‖. The higher microwave frequencies shift these dependencies slightly, but the overall conclusions remain the same as for 9.8 and 34 GHz (Hustedt and Beth, 2001).

Dependence of V2′ signals on T1e and on υm

Previous work at 9.8 and 34 GHz has shown that the shape of the 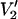Inline graphic signal and the sensitivity of this signal to rotational motion depend subtly on T1e (e.g., Hyde and Dalton, 1972, 1979; Thomas et al., 1976). Several measurements of T1e have been made on spin-labeled proteins in the 1–34-GHz range and over a wide range of rotational correlation times using saturation recovery EPR (e.g., Percival and Hyde, 1976; Robinson et al., 1994; J. S. Hyde, Medical College of Wisconsin, private communication, 2003). However, experimentally determined T1e values for solution samples of nitroxide spin labels in the 94–250-GHz range have not been reported to date. Therefore, additional calculations have been carried out using shorter (1 μs) and longer (25 μs) values of T1e for comparison with the data reported in Figs. 1 and 3–6, all of which were calculated using a T1e of 5 μs. The data at 250 GHz shown in Fig. 7 summarize a large number of calculations that have been carried out at 94, 140, and 250 GHz. Specifically, the 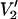Inline graphic signal amplitude and lineshape are dependent on T1e just as they are at 9.8 GHz (see Thomas et al., 1976; Hyde and Dalton, 1979). However, the overall sensitivity of this ST-EPR signal to τ‖ is not significantly altered by T1e over this range of values. We have also investigated the dependence of the 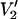Inline graphic signal on T1n (data not shown). These calculations have shown that the lineshapes are largely insensitive to the value of T1n when the nitrogen nuclear relaxation time is 100 ns or longer. This conclusion is independent of rotational correlation time in the 1-μs–0.1-s range and the microwave frequency in the 9.8–250-GHz range. At X-band, T1n for a 15N nitroxide is ∼1 μs at a correlation time of 1 μs and increases slightly with increasing correlation time for rotational diffusion in the 1-μs–1-ms time range (see Robinson et al., 1994). Though extensive solution studies of nitroxide, T1n's have not been reported at the higher microwave frequencies to date; it is not anticipated that they will shorten at the higher frequencies nor that they will significantly affect the ST-EPR spectra.

FIGURE 7.

FIGURE 7

Open in a new tab

Effect of T1e on the 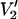Inline graphic signal at 250 GHz. The parameterized data were derived from calculations carried out for a URD model with the nitroxide z axis tilted by 54.7° (θ = 54.7° and φ = 0°) with respect to the diffusion axis at the indicated values of τ‖ with T1e = 1 μs (▪), 5 μs (▴), and 25 μs (•). The data are plotted as [(integral 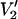Inline graphic (τ‖) − integral 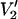Inline graphic (τ‖ = 1 μs))/(integral 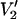Inline graphic (τ‖ = 100 ms) − integral 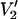Inline graphic (τ‖ = 1 μs))] vs. τ‖ in seconds.

The 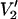Inline graphic ST-EPR signal at microwave frequencies in the 1–34-GHz range is very sensitive to the amplitude and frequency of the Zeeman-field modulation (Hyde and Dalton, 1972; Thomas et al., 1976; Robinson, 1983; Beth and Robinson, 1989). The modulation frequency, in particular, has been shown to be a useful experimental parameter at the lower microwave frequencies for shifting the window of sensitivity to rotational motions (reviewed in Beth and Robinson, 1989) and for gaining insights into the presence of multiple motional species (Hustedt and Beth, 1995; Blackman et al., 2001; Stein et al., 2002). The data in Fig. 8 demonstrate the substantial changes in lineshape that are observed at different modulation frequencies in the 10–100-kHz range. The data in Fig. 9 show graphically how modulation frequencies in the 10–100-kHz range produce useful shifts in the window of motional sensitivity at 250-GHz microwave frequency. In particular, lineshapes calculated using 100-kHz Zeeman modulation (solid squares) changed more rapidly with correlation time at the fast end of the range shown and more slowly at the slow end of the range in comparison to the lineshapes for 10-kHz Zeeman modulation (solid circles). Additional calculations at 94 and 140 GHz gave very similar results (data not shown).

FIGURE 8.

FIGURE 8

Open in a new tab

Effect of υm on calculated 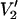Inline graphic lineshapes at 250 GHz. The four spectra shown were calculated for a URD model with the nitroxide z axis tilted by 54.7° with respect to the diffusion axis, τ‖ = 100 μs, and υm = 100, 50, 25, and 10 kHz from top to bottom, respectively. All other input parameters were the same as given in Fig. 1.

FIGURE 9.

FIGURE 9

Open in a new tab

Parameterized data for the effect of υm on the 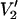Inline graphic signal at 250 GHz. The parameterized data were derived from the calculations shown in Fig. 7 plus additional spectra calculated at the indicated correlation times. The data are plotted as [(integral 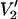Inline graphic (τ‖) − integral 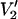Inline graphic (τ‖ = 1 μs))/(integral 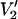Inline graphic (τ‖ = 100 ms) − integral 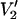Inline graphic (τ‖ = 1 μs))] vs. τ‖ in seconds for υm = 100 kHz (▪), 50 kHz (▴), and 10 kHz (•). The data at 25 kHz in Fig. 7 have been omitted from this plot to aid in visualization. The curve at 25 kHz is bounded by those at 10 and 50 kHz (not shown).

DISCUSSION

High field/high frequency linear EPR is becoming an important tool for spin-labeling studies of protein structure and microsecond to picosecond dynamics. The advantages of increased resolution of spectral features due to the anisotropic g-tensor, the shift in the window of motional sensitivity to faster rotational correlation times, and the increased sensitivity for small samples have all been well documented in the literature. Although the success of high field/high frequency operation in conventional linear EPR studies is well documented, and spectrometers that operate in the 94–250-GHz range are increasingly available, the potential advantages of these higher frequencies for ST-EPR studies of very slow rotational dynamics have not been explored. The current computational studies have been undertaken to determine potential advantages of these higher frequencies and, in so doing, to provide motivation for adapting and optimizing high field/high frequency instruments for making experimental ST-EPR measurements on small aqueous samples. The results from this computational study are very compelling, particularly with regard to observing and quantifying the very slow, constrained motions of macromolecules. Given the emerging general interest in measuring and understanding the functional dynamics of proteins that have been labeled at selected sites by the methods of site-directed spin labeling, a renewed look at the capabilities of ST-EPR, including utilization of the many technical advances in instrumentation that have occurred in the past three decades, is warranted.

Sensitivity to rotational/reorientational dynamics over 11 orders of magnitude in correlation time

Conventional EPR spectroscopy using nitroxide spin labels can be utilized to measure rotational dynamics in the 10-ps–1-μs time window at X-band (McCalley et al., 1972). Higher field/higher frequency extends the range of motional sensitivity to even shorter correlation times. At 250 GHz, it is possible to observe motions as fast as 1 ps (see Budil et al., 1993; Borbat et al., 2001). In contrast, ST-EPR spectroscopy at X-band provides sensitivity to motions in the microsecond to millisecond time range (Thomas et al., 1976). The parameterized data presented in Fig. 3 indicate that ST-EPR at 250 GHz should extend the slow motion limit upwards from 1 ms to 0.1 s. Thus, using both conventional and ST-EPR at frequencies of 9.8 and 250 GHz, it should be possible to measure the rotational dynamics of a nitroxide spin label over 11 orders of magnitude in correlation time. This is a remarkable range of sensitivity that spans most of the time range of interest in spin-labeling studies of global and local rotational dynamics in proteins. Given that each of these measurements can be made with the same spin-labeled sample using different sample geometries and volumes without the necessity of changing reporter probes, EPR and ST-EPR offer distinct advantages in terms of ease of sample preparation and characterization relative to many other techniques.

Sensitivity to the characteristics of rotational motion

A vast literature in the past three decades has addressed the sensitivity of conventional EPR to the characteristics of the rotational diffusion exhibited by spin-labeled macromolecules (for representative reviews see Freed, 1976, 2000; Seelig, 1976; Griffith and Jost, 1976; Robinson et al., 1985; for recent examples see Barnes and Freed, 1998; Barnes et al., 1999; Budil et al., 2000). Previous work has also shown that ST-EPR spectra in the 9.8–34-GHz range exhibit sensitivity to anisotropic global rotational diffusion in the microsecond to millisecond correlation time range (for representative reviews see Beth and Robinson, 1989; Beth and Hustedt, 2003), to constrained URD (Hustedt and Beth, 2001), and to motion in a cone relative to a director axis (Howard et al., 1993). Despite this sensitivity, it has remained challenging to analyze experimental ST-EPR data at the lower microwave frequencies from complex systems undergoing multiple modes of anisotropic and/or constrained rotational motion since many combinations of correlation times, probe orientations, and restricting potentials can give rise to remarkably similar spectra (see Beth and Hustedt, 2003).

The results of the calculations in Fig. 4 show that ST-EPR spectra at higher field/higher frequency are remarkably sensitive to the axis of rotational motion. Even at 94 GHz, the g-tensor anisotropy dominates the spectrum giving rise to distinct, resolved spectral features when the external magnetic field is aligned along any one of the three principal axes of the spin label (see Fig. 4). Consequently, rotational processes that couple different orientations of the spin label give rise to spectral effects in distinct regions of the spectrum. This spreading of sensitivity to distinct motional processes into different regions of the spectrum should provide greatly increased capabilities for rigorously testing different motional models and, consequently, for determining accurate values for rotational correlation times in real experimental systems undergoing anisotropic rotational diffusion.

Sensitivity to constrained uniaxial rotational diffusion

The calculated 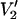Inline graphic spectra in Fig. 5 and the parameterized data in Fig. 6 show that there is a monotonic increase in sensitivity to small values of Δ (i.e., Δ < 15°) for constrained URD in going from 9.8 to 250 GHz. Interestingly, there is actually a loss in sensitivity to large values of Δ (i.e., Δ > 30°) at the higher microwave frequencies. It should be noted, however, that these calculations were all carried out using a 5-G (peak-to-peak) Zeeman field modulation amplitude, the same value that is normally utilized at X-band. It may well be that one could gain additional sensitivity to large values of Δ at the higher frequencies by going to a higher modulation amplitude. The higher modulation amplitude would couple a wider range of orientation states thereby potentially increasing sensitivity to large values of Δ.

The increased sensitivity to small values of Δ is helpful if one is interested in quantitating a very strong constraint to rotational diffusion. However, it is also reason for some caution in most spin-labeling applications since the local small amplitude, high frequency structural fluctuations of the protein backbone or of the spin label relative to the backbone can give rise to spectral diffusion that would appear as much faster overall rotational motion. The issue of binding “tightness” of spin label probes in ST-EPR at X-band has been addressed previously (see Hyde and Dalton, 1979). Although this has not routinely been a major concern at the lower frequencies, it may be a reason for caution at the higher frequencies. One avenue that should be pursued is to explore the development of new spin label reagents that have internal structural rigidity (including planar ring systems with no possibility for chair/boat interconversions) and that react with two sites on the protein. Reagents that would bridge i, i + 2 positions on a β-strand or i, i + 3 positions on a α-helix, for example, might prove to be useful additions to the current selection of spin label reagents for site-directed spin-labeling applications that address the very slow local or global dynamics of proteins.

Global analysis of experimental ST-EPR data

In the past decade, computational algorithms for ST-EPR lineshapes have been incorporated into nonlinear least-squares minimization routines and utilized to link the analysis and fitting of multiple experimental data sets (Hustedt et al., 1993; Hustedt and Beth, 1995; Blackman et al., 2001; Stein et al., 2002). This data analysis approach, called global analysis, was initially developed for analyzing experimental data sets in optical spectroscopy (reviewed in Beechem et al., 1991; Beechem, 1992). The advantage of global analysis of experimental data sets, collected under different conditions, is that it is often possible to separate complex experiments into their individual components much more reliably than can be done by analyzing any single experiment in isolation. There is a detailed discussion of this approach in fluorescence spectroscopy where data can be collected as a function of excitation/emission wavelengths, temperature, pressure, or any other chosen independent variable (see Beechem et al., 1991).

Beth and Robinson (1989) showed that ST-EPR data obtained from a two component sample at different Zeeman modulation frequencies in the 1–100-kHz range could be simultaneously analyzed to successfully determine the correlation times and the mol fractions of two isotropic motion species. Subsequent work has shown that the modulation frequency is a suitable independent experimental variable for global analysis of ST-EPR data obtained from complex experimental systems with multiple motional species present (e.g., Blackman et al., 2001; Stein et al., 2002). Figs. 8 and 9 show how the spectral lineshapes and the window of motional sensitivity can be altered by choice of modulation frequency at 250 GHz microwave frequency. The same trends are observed at 9.8, 34, 60, 94, and 140 GHz (data not shown).

The parameterized data shown in Fig. 3 indicate that the microwave frequency can serve as another very effective independent experimental variable for global analysis of experimental ST-EPR data. When the data in Fig. 3 are replotted as in Fig. 10, the magnitude of the shift of motional sensitivity as a function of microwave frequency is readily appreciated. The high sensitivity of the 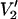Inline graphic signal to diffusion model at the higher frequencies shown in Fig. 4, along with the ability to shift the window of motional sensitivity with modulation frequency and/or microwave frequency, should greatly enhance the capabilities of computational approaches when used in combination with global analysis for uniquely interpreting the experimental data from complex systems.

FIGURE 10.

FIGURE 10

Open in a new tab

Parameterized data showing the magnitude of change in 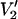Inline graphic as a function of τ‖ at six different microwave frequencies. All calculations were carried out using the model described in Fig. 3. The data are plotted as [(integral 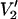Inline graphic (τ‖) − integral 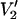Inline graphic (τ‖ = 1 μs))/(integral 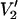Inline graphic (τ‖ = 100 ms) − integral 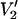Inline graphic (τ‖ = 1 μs))] vs. τ‖ in seconds at microwave frequencies of 9.8 (solid hexagons), 34 (▾), 60 (▴), 94 (♦), 140 (▪), and 250 GHz (•).

In addition to analyzing data from complex systems undergoing anisotropic rotational diffusion and with more than one motional species present, it should be possible to differentiate between the effects of global anisotropic motion and the effects of a restoring potential on experimental data. Even though τ‖ and Δ produce similar spectral effects on the 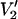Inline graphic signal, their effects can be differentiated as a function of microwave frequency. This differential sensitivity should prove effective in enabling a detailed analysis of data from systems where there is constrained motion (e.g., internal very slow functional dynamics of domains) in the presence of global very slow motion of the protein.

The current studies and most previous studies of rotational dynamics of spin-labeled proteins have utilized the 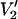Inline graphic signal exclusively. However, many other EPR signals collected at a partially saturating microwave power, including the first harmonic out-of-phase dispersion (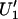Inline graphic; Hyde and Dalton, 1972, 1979; Thomas et al., 1976), also provide sensitivity to very slow rotational motions (e.g., Perkins et al., 1976). No attempts have been made to date to include these additional signals in the global analysis of experimental data due in large part to the low signal/noise of dispersion signals at the lower microwave frequencies when using conventional microwave cavities, as well as the time and effort that are required to individually collect data both in-phase and out-of-phase at different harmonics of the Zeeman modulation frequency. Recent advances in parallel digital detection of EPR signals including time-locked subsampling (TLSS; Hyde et al., 1998) permits the simultaneous detection of absorption and dispersion signals both in-phase and out-of-phase at all harmonics of the Zeeman modulation. This technical advance should provide a rich data set for application of global analysis methods in the fitting and interpretation of ST-EPR data.

Technical challenges

The calculations presented in this work indicate that ST-EPR studies at high field/high frequency will provide an important complement to conventional X-band measurements for elucidating the complex, very slow dynamics of spin-labeled proteins or other macromolecules. However, there are technical challenges that must be addressed before experimental high field/high frequency ST-EPR measurements at 94, 140, or 250 GHz are possible. First, sufficient microwave power must be available to induce at least partial saturation of the spin system. Even though T1e values for nitroxide spin-labeled proteins at these higher frequencies have not been measured experimentally, current theory and extrapolation from measurements at lower frequencies suggest that T1e will get longer as the microwave frequency increases (Robinson et al., 1994; J. S. Hyde, Medical College of Wisconsin, personal communication, 2003). Even if T1e increases to 25 μs at 250 GHz, on the order of 0.15-G microwave field in the rotating frame will still be necessary for obtaining high sensitivity to rotational dynamics and adequate signal/noise for ST-EPR. Second, Zeeeman field modulation amplitudes on the order of 5 G in the 1–100-kHz range that are homogeneous over the active dimensions of the sample are desirable. Third, phase sensitive detection with high phase stability at the first and second harmonics of the reference modulation frequency or, alternatively, digital parallel detection both in-phase and out-of-phase at the first and second harmonics are necessary. Though none of these requirements appear insurmountable, current instruments that have been designed for conventional EPR experiments at low power will require some modifications for ST-EPR applications.

All of the calculations presented in this work utilized input parameters that are appropriate for [15N,2H] nitroxide spin labels. The computational algorithms employed can also be utilized to calculate lineshapes using input parameters from [14N,2H] or normal isotope [14N,1H] spin labels. Though extensive calculations have not been carried out at 94, 140, or 250 GHz to date using input parameters that are appropriate for [14N,1H] spin labels, the calculations that have been performed suggest that the same increases in sensitivity to very slow rotational motions, to small values of Δ, and to the anisotropy of rotational motion that are described for the high resolution [15N,2H] probes are predicted for [14N] spin labels (data not shown). Although all of the calculations presented are based on URD models, it is predicted that the same increases in sensitivity to very slow rotational motions, to the width of restricting potentials, and to the anisotropy of motion will be observed for generalized isotropic and anisotropic motional models as well. Testing of this latter prediction will have to await extension of the computational algorithms utilized in this work to include rotational motion about orthogonal molecular axes or to direct experimental testing using well-defined model systems once spectrometers are available for making ST-EPR measurements at high field/high frequency.

Acknowledgments

The authors thank Drs. Charles Cobb, Hassane Mchaourab, and David Piston for critiquing the manuscript before submission.

This work was supported by National Institutes of Health grant R37 HL34737 to A.H.B.

References

  1. Bar, G., M. Bennati, H. H. Nguyen, J. Ge, J. A. Stubbe, and R. G. Griffin. 2001. High-frequency (140-GHz) time domain EPR and ENDOR spectroscopy: the tyrosyl radical-diiron cofactor in ribonucleotide reductase from yeast. J. Am. Chem. Soc. 123:3569–3576. [DOI] [PubMed] [Google Scholar]
  2. Barnes, J. P., and J. H. Freed. 1998. Dynamics and ordering in mixed model membranes of dimyristorylphosphatidylcholine and dimyristorylphosphatidylserine: a 250-GHz electron spin resonance study using cholestane. Biophys. J. 75:2532–2546. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Barnes, J. P., Z. Liang, H. S. Mchaourab, J. H. Freed, and W. L. Hubbell. 1999. A multifrequency electron spin resonance study of T4 lysozyme dynamics. Biophys. J. 76:3298–3306. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Beechem, J. M. 1992. Global analysis of biochemical and biophysical data. Methods Enzymol. 210:37–54. [DOI] [PubMed] [Google Scholar]
  5. Beechem, J. M., E. Gratton, M. Ameloot, J. R. Knutson, and L. Brand. 1991. The global analysis of fluorescence intensity and anisotropy decay data: second-generation theory and programs. In Topics in Fluorescence Spectroscopy, Vol. 2: Principles. J. R. Lakowicz, editor. Plenum Press, New York. 241–305.
  6. Beth, A. H., K. Balasubramanian, R. T. Wilder, S. D. Venkataramu, B. H. Robinson, L. R. Dalton, D. E. Pearson, and J. H. Park. 1981. Structural and motional changes in glyceraldehyde 3-phosphate dehydrogenase upon binding to the band 3 protein of the red blood cell membrane examined with [15N,2H] maleimide spin label and EPR. Proc. Natl. Acad. Sci. USA. 78:4955–4959. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Beth, A. H., and E. J. Hustedt. 2004. Saturation transfer EPR: rotational dynamics of membrane proteins. In “Biomedical ESR”. S. S. Eaton, G. R. Eaton, and L. J. Berliner, editors. Kluwer Academic/Plenum Publishing, New York. In press.
  8. Beth, A. H., and B. H. Robinson. 1989. Nitrogen-15 and deuterium substituted spin labels for studies of very slow rotational motion. In Biological Magnetic Resonance, Vol. 8, Spin Labeling - Theory and Applications. L. J. Berliner and J. Reuben, editors. Plenum Press, New York. 179–253.
  9. Blackman, S. M., E. J. Hustedt, C. E. Cobb, and A. H. Beth. 2001. Flexibility of the cytoplasmic domain of the anion exchange protein, band 3, in human erythrocytes. Biophys. J. 81:3363–3376. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Borbat, P. P., A. J. Costa-Filho, K. A. Earle, J. K. Moscicki, and J. H. Freed. 2001. Electron spin resonance in studies of membranes and proteins. Science. 291:266–269. [DOI] [PubMed] [Google Scholar]
  11. Budil, D. E., K. Earle, and J. H. Freed. 1993. Full determination of the rotational diffusion tensor by electron paramagnetic resonance at 250 GHz. J. Phys. Chem. 97:1294–1303. [Google Scholar]
  12. Budil, D. E., S. V. Kolaczkowski, A. Perry, C. Varaprasad, F. Johnson, and P. R. Strauss. 2000. Dynamics and ordering in a spin-labeled oligonucleotide observed by 220 GHz electron paramagnetic resonance. Biophys. J. 78:430–438. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Columbus, L., and W. L. Hubbell. 2002. A new spin on protein dynamics. Trends Biochem. Sci. 27:288–295. [DOI] [PubMed] [Google Scholar]
  14. Earle, K. A., J. K. Moscicki, M. Ge, D. E. Budil, and J. H. Freed. 1994. 250-GHz electron spin resonance studies of polarity gradients along the aliphatic chains in phospholipid membranes. Biophys. J. 66:1213–1221. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Fajer, P., and D. Marsh. 1983. Sensitivity of saturation transfer ESR spectra to anisotropic rotation. Application to membrane systems. J. Magn. Reson. 51:446–459. [Google Scholar]
  16. Feix, J. B., and C. S. Klug. 1998. Site-directed spin labeling of membrane proteins and peptide-membrane interactions. In Biological Magnetic Resonance, Vol. 14: Spin Labeling: The Next Millennium. L. J. Berliner, editor. Plenum Press, New York. 251–281.
  17. Freed, J. H. 1976. Theory of slow tumbling ESR spectra for nitroxides. In Spin Labeling: Theory and Applications. L. J. Berliner, editor. Academic Press, New York. 53–132.
  18. Freed, J. H. 2000. New technologies in electron spin resonance. Annu. Rev. Phys. Chem. 51:655–689. [DOI] [PubMed] [Google Scholar]
  19. Gaffney, B. J., and D. Marsh. 1998. High-frequency, spin-label EPR of nonaxial lipid ordering and motion in cholesterol-containing membranes. Proc. Natl. Acad. Sci. USA. 95:12940–12943. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Griffith, O. H., and P. C. Jost. 1976. Lipid spin labels in biological membranes. In Spin Labeling: Theory and Applications. L. J. Berliner, editor. Academic Press, New York. 453–523.
  21. Hemminga, M. A., and P. A. de Jager. 1989. Saturation transfer spectroscopy of spin labels. Techniques and interpretation of spectra. In Biological Magnetic Resonance, Vol. 8. Spin Labeling Theory and Applications. L. J. Berliner and J. Reuben, editors. Plenum Press, New York. 131–178.
  22. Howard, E. C., K. M. Lindahl, C. F. Polnaszek, and D. D. Thomas. 1993. Simulation of saturation transfer electron paramagnetic resonance spectra for rotational motion with restricted angular amplitude. Biophys. J. 64:581–593. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hubbell, W. L., D. S. Cafiso, and C. Altenbach. 2000. Identifying conformational changes with site-directed spin labeling. Nat. Struct. Biol. 7:735–739. [DOI] [PubMed] [Google Scholar]
  24. Hubbell, W. L., H. S. Mchaourab, C. Altenbach, and M. A. Lietzow. 1996. Watching proteins move using site-directed spin labeling. Structure. 4:779–783. [DOI] [PubMed] [Google Scholar]
  25. Hustedt, E. J., and A. H. Beth. 1995. Analysis of saturation transfer electron paramagnetic resonance spectra of a spin-labeled integral membrane protein, band 3, in terms of the uniaxial rotational diffusion model. Biophys. J. 69:1409–1423. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Hustedt, E. J., and A. H. Beth. 2001. Simulation of saturation transfer electron paramagnetic resonance spectra for a restricted uniaxial rotational diffusion model. Biophys. J. 81:3156–3165. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Hustedt, E. J., C. E. Cobb, A. H. Beth, and J. M. Beechem. 1993. Measurement of rotational dynamics by the simultaneous non-linear analysis of optical and EPR data. Biophys. J. 64:614–621. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Hustedt, E. J., A. I. Smirnov, C. F. Laub, C. E. Cobb, and A. H. Beth. 1997. Molecular distances from dipolar coupled spin labels: the global analysis of multifrequency cw-EPR data. Biophys. J. 74:1861–1877. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Hyde, J. S., and L. R. Dalton. 1972. Very slow tumbling spin labels: adiabatic rapid passage. Chem. Phys. Lett. 16:568–572. [Google Scholar]
  30. Hyde, J. S., and L. R. Dalton. 1979. Saturation transfer spectroscopy. In “Spin Labeling II: Theory and Applications”. L. J. Berliner, editor. Academic Press, New York. 1–70.
  31. Hyde, J. S., H. S. Mchaourab, T. G. Camenisch, J. J. Ratke, R. W. Cox, and W. Froncisz. 1998. Electron paramagnetic resonance detection by time-locked subsampling. Rev. Sci. Instrum. 69:2622–2628. [Google Scholar]
  32. Johnson, M. E., and J. S. Hyde. 1981. 35-GHz (Q-band) saturation transfer electron paramagnetic resonance studies of rotational diffusion. Biochemistry. 20:2875–2880. [DOI] [PubMed] [Google Scholar]
  33. Johnson, M. E., L. Lee, and L. W.-M. Fung. 1982a. Models for slow anisotropic rotational diffusion in saturation transfer electron paramagnetic resonance at 9 and 35 GHz. Biochemistry. 21:4459–4467. [DOI] [PubMed] [Google Scholar]
  34. Johnson, M. E., P. Thiyagarajan, B. Bates, and B. L. Currie. 1982b. A comparison of resolution enhancement methods in saturation transfer EPR. 15N isotopically substituted spin labels and 35 GHz high-frequency operation. Biophys. J. 37:553–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Mangels, M. L., A. C. Harper, A. I. Smirnov, K. P. Howard, and G. A. Lorigan. 2001. Investigating magnetically aligned phospholipids bilayers with EPR spectroscopy at 94 GHz. J. Magn. Reson. 151:253–259. [DOI] [PubMed] [Google Scholar]
  36. Marsh, D., L. Horvath, T. Pali, and V. A. Livshits. 2004. Saturation transfer spectroscopy of biological membranes In “Biomedical ESR”. S. S. Eaton, G. R. Eaton, and L. J. Berliner, editors. Kluwer Academic/Plenum Publishing, New York. In press.
  37. McCalley, R. C., E. J. Shimshick, and H. M. McConnell. 1972. The effect of slow rotational motion on paramagnetic resonance spectra. Chem. Phys. Lett. 13:115–119. [Google Scholar]
  38. Percival, P. W., and J. S. Hyde. 1976. Saturation-recovery measurements of the spin-lattice relaxation times of some nitroxides in solution. J. Magn. Reson. 23:249–257. [Google Scholar]
  39. Perkins, R. C., T. Lionel, B. H. Robinson, L. A. Dalton, and L. R. Dalton. 1976. Saturation transfer spectroscopy: signals sensitive to very slow molecular reorientation. Chem. Phys. 16:393–404. [Google Scholar]
  40. Robinson, B. H. 1983. Effects of overmodulation on saturation transfer EPR signals. J. Chem. Phys. 78:2268–2273. [Google Scholar]
  41. Robinson, B. H., and L. R. Dalton. 1980. Anisotropic rotational diffusion studied by passage saturation transfer electron paramagnetic resonance. J. Chem. Phys. 72:1312–1324. [Google Scholar]
  42. Robinson, B. H., and L. R. Dalton. 1981. Approximate methods for the fast computation of EPR and ST-EPR spectra. V. Application of the perturbation approach to the problem of anisotropic motion. Chem. Phys. 54:253–259. [Google Scholar]
  43. Robinson, B. H., D. A. Haas, and C. Mailer. 1994. Molecular dynamics in liquids: spin-lattice relaxation of nitroxide spin labels. Science. 263:490–493. [DOI] [PubMed] [Google Scholar]
  44. Robinson, B. H., H. Thomann, A. H. Beth, P. Fajer, and L. R. Dalton. 1985. EPR and Advanced EPR Studies of Biological Systems. L. R. Dalton, editor. CRC Press, Boca Raton, FL.
  45. Rohrer, M., T. F. Prisner, O. Brugmann, H. Kass, and M. Spoerner. 2001. Structure of the metal-water complex in Ras x GDP studied by high-field EPR spectroscopy and 31P NMR spectroscopy. Biochemistry. 40:1884–1889. [DOI] [PubMed] [Google Scholar]
  46. Seelig, J. 1976. Anisotropic motion in liquid crystalline structures. In Spin Labeling: Theory and Applications. L. J. Berliner, editor. Academic Press, New York. 373–409.
  47. Smirnov, A. I., R. L. Belford, and R. B. Clarkson. 1998. Comparative spin label spectra at X-band and W-band. In Spin Labeling: The Next Millenium. L. J. Berliner, editor. Plenum Press, New York. 83–107.
  48. Smirnov, A. I., T. I. Smirnova, and P. D. Morse. 1995. Very high frequency electron paramagnetic resonance of 2,2,6,6-tetramethyl-1-piperidinyloxy in 1,2-dipalmitoyl-sn-glycero-3-phosphaticylcholine liposomes: partitioning and molecular dynamics. Biophys. J. 68:2350–2360. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Stein, R. A., E. J. Hustedt, J. V. Staros, and A. H. Beth. 2002. Rotational dynamics of the epidermal growth factor receptor. Biophys. J. 41:1957–1964. [DOI] [PubMed] [Google Scholar]
  50. Thomas, D. D., L. R. Dalton, and J. S. Hyde. 1976. Rotational diffusion studied by passage saturation transfer electron paramagnetic resonance. J. Chem. Phys. 65:3006–3024. [Google Scholar]
  51. Thomas, D. D., and H. M. McConnell. 1974. Calculation of paramagnetic resonance spectra sensitive to very slow rotational motion. Chem. Phys. Lett. 25:470–475. [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES