Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Jun;86(6):4049–4058. doi: 10.1529/biophysj.103.033043

The Fast Tumble Signal in Bacterial Chemotaxis

Shahid Khan *, Sanjay Jain †, Gordon P Reid ‡, David R Trentham ‡
PMCID: PMC1304305  PMID: 15189900

Abstract

We have analyzed repellent signal processing in Escherichia coli by flash photorelease of leucine from photolabile precursors. We found that 1), response amplitudes of free-swimming cell populations increased with leucine jump concentration, with an apparent Hill coefficient of 1.3 and a half-maximal dose of 14.4 μM; 2), at a 0–0.5 mM leucine concentration jump sufficient to obtain a saturation motile response, the swimming cell response time of ∼0.05 s was several-fold more rapid than the motor response time of 0.39 ± 0.18 s measured by following the rotation of cells tethered by a single flagellum to quartz coverslips; and 3), the motor response time of individual cells was correlated with rotation bias but not cell size. These results provide information on amplification, rate-limiting step, and flagellar bundle mechanics during repellent signal processing. The difference between the half-maximal dose for the excitation response and the corresponding value reported for adaptation provides an estimate of the increase in the rate of formation of CheYP, the phosphorylated form of the signal protein CheY. The estimated increase gives a lower limit receptor kinase coupling ratio of 6.0. The magnitude and form of the motor response time distribution argue for it being determined by the poststimulus switching probability rather than CheYP turnover, diffusion, or binding. The temporal difference between the tethered and swimming cell response times to repellents can be quantitatively accounted for and suggests that one flagellum is sufficient to cause a measurable change of direction in which a bacterium swims.

INTRODUCTION

The motility of Escherichia coli is a succession of swimming runs alternating with brief tumbling events that reorient the bacteria. To a good approximation, the bacteria swim when the four or so flagella per cell form a counterclockwise (CCW) rotating bundle that pushes the cell forward. Reorientation occurs when flagella switch from CCW to clockwise (CW) rotation. Tumbles or twiddles are sharp reorientation events, identified in classical studies (Berg and Brown, 1972). The rotation behavior of individual motors may be observed by tethering cells by a single flagellum to a static surface. E. coli are attracted or repelled by a wide range of compounds. Positive concentration jumps of attractant stimuli increase CCW rotation, thereby prolonging swimming runs to minutes, depending on stimulus strength. Repellent stimuli have the opposite effect (reviewed by Bren and Eisenbach, 2000).

The biochemistry and structural biology of the chemotactic phosphorelay is now understood in some detail (reviewed by Falke et al., 1997; Stock et al., 2000). The rotation bias of flagellar motors is mb = tCCW/(tCW + tCCW) where tCCW and tCW are the mean counterclockwise and clockwise intervals respectively. The value mb is controlled by phosphorylated levels of the chemotaxis signal protein CheY. The methyl-accepting chemotaxis proteins, MCPs, the phosphorylating histidine kinase, CheA, and a coupling protein, CheW, form receptor signaling complexes. Increased occupancy of the receptors by attractants or repellents inhibits or activates CheA, respectively. The excitation process, namely the initial mb change, is rapid (<1 s). CheA phosphorylates the MCP methylesterase CheB in addition to CheY. Adaptation via change in MCP methylation has a compensatory effect on CheA activity, restoring mb to its prestimulus value.

The excitation response to repellent has been difficult to characterize. Excitation and adaptation responses are more rapid for a repellent than an attractant (Khan et al., 1995; Springer et al., 1979). In addition, many repellents act by perturbing cytoplasmic pH (Kihara and Macnab, 1981), thus making determination of the dose-response relation difficult. Leucine is the most potent and well-understood example of a repellent. Repulsion toward leucine, mediated by the major MCP Tsr, does not involve periplasmic binding proteins, changes in cytoplasmic pH, or membrane perturbation (Eisenbach et al., 1990; Kihara and Macnab, 1981; Tso and Adler, 1974). Tsr is the predominant MCP in E. coli strain RP2361 due to deletion of the gene for Tar, the other major MCP (Feng et al., 1997). The leucine tumble response is mediated predominantly by the Tsr receptor. Leucine triggers an attractant response in a Δtsr strain, and a null response in a double mutant in which the tar lesion in strain RP2361 is combined with the Δtsr mutation (see Khan and Trentham, 2004). Here, we report on the excitation behavior of RP2361 free-swimming and tethered cells to photolysis of two caged compounds that released L-leucine rapidly compared to the excitation process when exposed to a pulse of near-ultraviolet irradiation (Scheme 1).

Figure 6.

Figure 6

Open in a new tab

MATERIALS AND METHODS

Strain, media, and chemicals

E. coli strain RP2361 (Δtar) 386-2.Strr (Khan et al., 1993) was a gift from Dr. J. S. Parkinson. Streptomycin (Sigma Chemical, St. Louis, MO) was used at 50 μg/ml final concentration. The bacteria were grown in Luria broth to midexponential phase as previously described (Khan et al., 1993). Motility buffer was 50 mM 2-(4-morpholino)ethanesulfonic acid, pH 6.0, 10 mM potassium chloride, 0.1 mM EDTA, 5 mM lithium lactate, 125 μM L-methionine, 5 mM dithiothreitol. For some experiments where rapidity of the biological response after photolysis was not an issue we used the pH 7.0 phosphate buffer solution specified by Jasuja et al. (1999a).

Synthesis and properties of caged leucines

N-1-(2-Nitrophenyl)ethoxycarbonyl-L-leucine (NPEC-Leu) was synthesized and purified in 20% overall yield essentially as described for the corresponding caged serine (Khan et al., 1993). A modification was introduced at the step involving the extraction of by-product. The extracting ether solution also contained significant caged leucine and so was backextracted with an aqueous solution saturated with NaCl. Purity of the NPEC-Leu was established from its 1H-NMR spectrum (using a JEOL FX90Q spectrometer, JEOL-USA, Peabody, MA) and by thin layer chromatography using ninhydrin to show any leucine contamination. The absorption spectrum and photochemical properties were treated as being identical to those of the analogous caged serine (Khan et al., 1993).

O-2,6-Dinitrobenzyl-L-leucine (DNB-Leu) was synthesized and purified in approaching 100% yield as described for the β-2,6-dinitrobenzyl ester of L-aspartic acid (Jasuja et al., 1999a) using N-tBOC-L-leucine as starting material. The product quantum yield was 0.21 and the rate of release of leucine on laser flash photolysis at 22°C and pH 7 in 50 mM potassium phosphate and 1 mM dithiothreitol was 2300 s−1 as inferred from the rate of decay of the aci-nitro intermediate (Jasuja et al., 1999a). Amino acid analysis indicated the DNB-Leu was contaminated with 0.085% leucine. DNB-Leu is susceptible to base catalyzed hydrolysis; the rate was not measured but assumed to be similar to that of the α-2,6-dinitrobenzyl ester of L-glutamate which hydrolyzes at a rate of 0.12 h−1 at 22°C and pH 7 in 100 mM potassium phosphate.

Microscopy

A Nikon Optiphot microscope was used for imaging the bacteria (Nikon USA, Melville, NY). Swimming bacteria were imaged under dark-field illumination (10× CF-Fluor or 40× ELWD objectives). A chamber was constructed by pressing a glass coverslip onto a ring of grease (Apiezon Products, Manchester, UK) mixed with 10-μm marker beads (Bang Laboratories, Fishers, IN). The depth of field provided by the low power objective and the shallow chamber ensured that tumbling bacteria remained in focus. Bacteria were tethered in a laminar flow-cell, imaged, and digitized as described by Jasuja et al. (1999a). Fresh medium was flowed in between flashes and the cells were allowed to adapt to the medium change before the next flash. Extents of caged leucine photolysis were determined from the fluorescence of HPTS (8-hydroxypyrene-1,3,6-tris-sulfonic acid generated by photolysis of caged HPTS (Jasuja et al., 1999a).

Data acquisition and analysis

A high-speed charge-coupled device camera (HSC-180, Motion Analysis, Santa Rosa, CA) was used for image acquisition. The video signal from the camera was input directly into the SUN Sparc-II computer via a VP320 digitizer (Motion Analysis) and analyzed using ExpertVision software (Motion Analysis). Data collection was initiated by pushing the Event1 marker button on the VP320. After a preset delay, the digitizer produced a transistor-transistor-logic pulse that was transmitted via a custom-made trigger box and a stimulator (Grass Instruments, West Warwick, RI) to open a mechanical shutter for an epi-illumination flash or to trigger a flash lamp. The transistor-transistor-logic pulse was converted into an audio signal as required for marking videotapes.

Video data of free-swimming E. coli were digitized at 30 frames per second. Rapid responses at the highest photoreleased L-leucine concentrations were also digitized at 60 frames/s. Swimming cell responses were expressed as the population rate of change of direction (rcd) (frame-to-frame mean ± SD). The population linear speed (spd) was also monitored. Population rcd and spd as well as the algorithm for frame-by-frame computation of these quantities have been described (Khan et al., 1993). Subsaturation response amplitudes (Δrcd) were determined by averaging over successive 10 frame windows at 30 frames/s as detailed in Jasuja et al. (1999b). For saturation responses marked by an initial spike (see Results), the window was moved so as to exclude the spike. Standard deviations as well as the mean Δrcd were computed (see Jasuja et al., 1999b). The Marquardt-Levenberg algorithm was applied to the coupled set of equations for the excitation reactions to obtain two-parameter least-squares fits to the Δrcd data using Sigmaplot version 8.0 (SPSS, Chicago, IL).

Tethered cell responses were digitized at 30 frames/s resolution (Jasuja et al., 1999a). The tethered cell excitation response time, Inline graphic was defined as the time interval from photolysis to the first reversal, with the cell rotating CCW at the instant of flash photolysis. For each cell these times (mean ± SD) were determined from multiple flash sequences by frame-by-frame analysis of files, performed offline, digitized directly into the computer. For determination of the dependence of Inline graphic on mb, the prestimulus mb for a 10-s interval preceding the flash was determined from videotaped records. A PC DOS-based version of ExpertVision and a VP110 digitizer (Motion Analysis) were used for analysis of the videotapes.

RESULTS

Responses of free-swimming E. coli to L-leucine photorelease

NPEC-Leu was used for most photorelease assays since this compound is stable at room temperature. The assays were carried out at pH 6.0 to ensure that photolysis kinetics did not limit the motile response. Detectible changes in the population rcd were evident upon photorelease of 3 μM L-leucine. Saturation tumble responses were obtained when the photoreleased L-leucine concentration was 250 μM or greater (Fig. 1). Visual examination of video records showed that cells tumbled for >2 s, then gradually regained normal motility.

FIGURE 1.

FIGURE 1

Open in a new tab

Responses of free-swimming cells of Δtar mutant E. coli strain RP2361 to photorelease of L-leucine at pH 6.0 and 22°C. 1000–1500 cell paths were averaged for each L-leucine concentration jump. Under these conditions, the prestimulus population rcd for strain RP2361 was 555 ± 46° s−1 (frame-to-frame mean ± SD, indicated by solid and dotted lines, respectively). The dashed line denotes the rcd recorded for tumbly mutant populations. The arrows mark the time of the photolysis flash.

An initial spike of ∼0.1 s with rcd values exceeding those measured for constantly tumbling mutants was routinely observed at ≥0.25 mM concentration jumps. This feature may represent synchronized violent bundle breakup, which would not occur when individual cell records from unstimulated tumbly mutant populations are averaged. Earlier records of saturation-repellent responses to protons revealed similar excursions of the population rcd to values greater than documented for tumbly mutants (see Fig. 7 in Khan et al., 1993; Figs. 2 and 4 A in Khan et al., 1995), but these were not as pronounced as those seen here for leucine.

FIGURE 2.

FIGURE 2

Open in a new tab

Response amplitudes as a function of photoreleased leucine concentration. The curve represents the best fit to the data (mean ± SD) calculated from the Hill equation (see text) for C = 1.3 ± 0.5, L1/2 = 14.4 ± 0.5 μM, and Δrcdmax = 362 ± 34° s−1.

FIGURE 4.

FIGURE 4

Open in a new tab

(A) Responses of individual tethered cells. The variation among individual cells is greater than the variation in the response times of a single cell to multiple photolyzing flashes. In addition to the 16 reversing cells depicted in Fig. 3, responses were measured for four more cells from the same experiment, that showed a single, brief (<0.25 s) CW interval in the 10-s interval preceding the flash. Cells 1 and 12 belong to the group; the other two cells failed to respond. (B) Time until motor reversal as a function of prestimulus motor bias (N = 20 cells, two cells with prestimulus mb = 1, Inline graphic = 0.9 s). The solid line denotes the least-squares fit. The dotted lines show 95% confidence intervals. (C) Peak and declining phase (solid bars) of the histogram of motor excitation times obtained for a 0–0.5 mM leucine jump (N = 73 events; combined data of A and B) fit by a function of form exp(−pt), where p = 2.8 s−1. The function was scaled to fit the data histogram.

We used DNB-Leu to check that photolysis reactions were not rate-limiting. Prestimulus leucine contamination resulting from any caged compound breakdown was kept to a minimum by using high flash intensities and low caged compound concentrations. Tumble responses of similar magnitude and kinetics were obtained for both compounds (not shown). Since the by-products of NPEC-Leu and DNB-Leu photolysis are hydroxide ions and protons, respectively (Scheme 1), this experimental check also showed that the pH 6.0 medium used had adequate buffering capacity to prevent pH changes of a magnitude sufficient to trigger motile responses.

As observed earlier for protons acting as repellent (Khan et al., 1993), swimming cell response times decreased with stimulus strength. At saturation the response time was ∼50 ms (Fig. 1), indistinguishable from that due to protons. The response time did not decrease when the digitization rate was increased to 60 frames/s, showing that the 50-ms saturation response was limited by biological factors rather than the digitization rate.

The response amplitudes were fit to the leucine jump concentration by the Hill equation (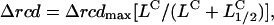Inline graphic where L is the dose concentration and L1/2 the half-maximal dose, C the Hill coefficient, and Δrcdmax the maximum increase in the population rcd (Fig. 2). The best fit gave L1/2 = 14.4 ± 0.5 μM, C = 1.3 ± 0.5, and Δrcdmax = 362 ± 34° s−1.

Swimming cells respond more rapidly than tethered cells

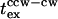The tethered cell excitation time (Inline graphic) measures a single motor response. The value Inline graphic measured by iontophoretic application for two repellents, benzoate and nickel chloride, was ∼0.2 s (Block et al., 1982; Segall et al., 1982), fourfold greater than the response of swimming cells to leucine. Perturbation of the cytoplasmic pH is the basis for repulsion to benzoate, whereas the mechanism of the response to metal ions is not known. It is possible that the 0.2-s times reflect a feature peculiar to the action of these compounds, for example the time required for permeation of benzoate into the cytoplasm. Alternatively, these longer times might have been an artifact of the iontophoresis method (Khan, 2000). We therefore investigated this issue by comparing tethered and swimming cell responses obtained using the same cultures and the same stimulus (0–0.5 mM leucine jump) applied by flash photolysis of NPEC-leucine (Fig. 3).

FIGURE 3.

FIGURE 3

Open in a new tab

Saturation response kinetics of swimming versus tethered cell (N = 47 events, 16 cells) populations obtained from the same cultures. The frame-to-frame difference (δrcd), rather than absolute rcd values are plotted for comparison with the tethered cell data. The Inline graphic histogram has 40 ms bins. 0.5 mM L-leucine was photoreleased at zero time in each case.

Twenty tethered cells that were capable of reversing were each subjected to three flashes. Sixteen of these cells exhibited one or more CW intervals of duration >0.25 s in the 10-s time period preceding flash photolysis. The mean 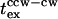Inline graphic was 0.33 ± 0.10 s for these 16 cells. However, the response time for swimming cells was 50 ms. Thus, swimming cells respond more rapidly than tethered cells. This difference could explain the discrepancy in response times found in the literature. A similar Inline graphic (∼0.2–0.3 s) is consistent with signal processing being limited by a downstream reaction common to all repellents tested thus far (Block et al., 1982; Segall et al., 1982; this study).

Motor excitation time depends upon its rotational bias

Mean 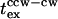Inline graphic values varied from cell to cell (Fig. 4 A). The four cells out of 20 that had a single, brief (<0.25 s) CW interval in the 10 s preceding flash photolysis did not respond, or had long response times. Similarly, exclusively CCW-rotating cells, a significant (>20%) fraction of the tethered cell population, did not reverse when subjected to jumps of photoreleased leucine or only did so after an abnormal length of time. This result suggested that a possible cause of the heterogeneity in the Inline graphic distribution was due to variable mb. To test this effect we quantified prestimulus mb values for 20 cells stimulated in a separate experiment. For this purpose, a simultaneous videotaped record was made for each flash sequence. Bias values were obtained for a 10-s period before flash photolysis from the videotape record either by computer-assisted or manual analysis (see Materials and Methods). Even though we could only explore a limited bias range with the RP2361 strain, the results show that Inline graphic was linearly dependent upon mb (Fig. 4 B).

The apparent bell shape of the distribution shown in Fig. 3 changes to a distribution with a significant tail once data from all cells is considered (Fig. 4 C), rather than a selected subset of the most CW-biased, and hence responsive, cells. The distribution mean is increased to 0.39 ± 0.18 s. A single exponential fit with a rate constant of 2.8 s−1 provides a reasonable fit to the histogram for intervals beyond 0.2 s (solid bars). This suggests that Inline graphic is limited by a Poisson process, with another process determining how quickly a tethered cell can respond to account for the paucity of early excitation reversal events (Fig. 4 C, shaded bars). This paucity implies that another process, possibly limited by the load, determines how quickly the motor can respond—a point taken up in the Discussion.

A model for tumble signal processing

We sought to exploit our data to explain: 1), amplification during repellent signaling; 2), the nature of the rate-limiting step in the repellent response; and 3), the basis for the difference between the response times of cells tethered by a single flagellum and those of swimming cells.

Amplification during repellent signaling

We first related the half-maximal dose for the amplitude of the excitation response (Inline graphic) with that obtained in adaptation time experiments (Fig. 5 A). We assumed that the latter correspond to KD, the biochemical ligand-receptor dissociation constant. The measured rcd values were related to the KD by the following set of equations:

  1. The fraction of CheA molecules activated was calculated based on the assumption that CheA is associated with the MCPs as complexes with fixed stoichiometry and that each complex behaves independently. This fraction is proportional to the change in receptor occupancy, ΔRocc.

  2. The peak poststimulus CheYP concentration, YP, before adaptation was computed from the equation 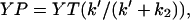Inline graphic where YT is total intracellular CheY concentration, k′ the poststimulus rate constant for CheY phosphorylation, and k2 the rate constant for CheYP dephosphorylation. The value k′ is k1(1−ΔRocc) + Ak1(ΔRocc) = k1(1 + (A−1)ΔRocc), where k1 is the prestimulus rate of CheYP formation and A is the CheA activation factor.

  3. The poststimulus mb was computed from the equation Inline graphic where KM is the CheYP-motor dissociation constant and H the Hill coefficient for the YP dependence of the mb change. The equations have five fixed (k1, k2, KD, KM, and YT) and two floating (A and H) parameters. Fixed parameters were chosen to be k1 = 1.7 s−1, k2 = 4 s−1 (Kim et al., 2001), KD = 1.5 mM (Tso and Adler, 1974), KM = 4 μM (Sagi et al., 2003), and YT = 10 μM. The best fit to the coupled equations (Materials and Methods) gave A = 81 ± 27 and H = 3.4 ± 1.0.

A determines the difference between the half-maximal dose for the YP change and the KD as the k′ increase is proportional to the product of A and ΔRocc for large A, with A independent of ΔRocc The sharpness of the mb change (i.e., the form of the stimulus response relation) is determined by H. The best-fit H value was lower than the reported value of 10.5 (Cluzel et al., 2000). This underestimate was expected since our measurements were made on populations rather than single cells. The fit was not sensitive to the absolute parameter values of YP, YT, and KM chosen, as long as the ratios (YP/YT, YP/KM) remained constant. The mb actually depends upon free rather than total YP. However, more detailed calculations (not described) showed that the difference may be compensated by increasing YT. Therefore, rather than introduce additional parameters for intracellular concentrations of the YP binding targets, we set YT approximately twofold lower than published values (Zhao et al., 1996).

FIGURE 5.

FIGURE 5

Open in a new tab

(A) Predicted changes in intracellular parameters to L-leucine concentration jumps (L mM) obtained upon fit of the observed response amplitudes shown in Fig. 2 using the following equations: ΔRocc (dotted line) = L/(L+ KD). Normalized CheYP turnover (thin solid line) = (k′ + k2)/kmax and YP/YT (thick solid line) = k′/(k′ + k2) where k′ is k1(1 + (A−1)ΔRocc) and kmax is CheYP turnover when L is 50 mM. Predicted poststimulus mb (dashed line) = 1 − YPH/(YPH + Inline graphic). Observed poststimulus rcd values were converted to poststimulus mb (circles) using prestimulus mb−Δmb, where Δmb = m(Δrcd). Prestimulus mb = 0.77, ∼10% higher, whereas m = 0.0016, ∼33% greater, than the values expected from the empirical relation determined by Khan et al. (1993). The relation is valid for rcd values <1000° s−1, so higher rcd values (shaded circles) were not used for the fit. The fit gave A = 81 ± 27 and H = 3.4 ± 1.0. (B) Fit (line) to the Fig 4 B data (open circles) when Inline graphic were determined by the poststimulus tCCW, given vmax = 0.83 s−1. Poststimulus mb were calculated from prestimulus mb employing KD, KM, YT, A, and H values used for, or obtained from, A and a two-state model of the flagellar switch. (Inset: solid line is the isoenergetic state; dotted line is the nonisoenergetic state.) (C) Predicted probability density of swimming versus tethered cell response with time. Each motor is assumed to switch independently from CCW to CW rotation with a probability density pΔt, with p taken to be 2.8 s−1. Thus, the probability density (B(t) s−1) for tethered cell reversal is pe−pt (solid line). A swimming cell, initially with a CCW rotating bundle, is assumed to change swim trajectory when r out of its f flagella switch to CW rotation. Probability densities for this change to occur are plotted for f = 4 and r = 1 (4pe−4pt, dashed line) or 2 (12p(e−3pt−e−4pt), dotted line), respectively (see text). Solid and dashed vertical bars denote times when B(t) = B(0)/2 for the two cell populations.

The value k1 is limited by CheA autophosphorylation. The rate of transfer of the γ-phosphate of ATP to activated CheA has been reported to be 23 ± 3 s−1 (Levit et al., 1999). If k1 for strain RP2361 is assumed to be 1.7 s−1, based on the work with ΔtsrΔcheZ mutants (Kim et al., 2001), the maximal increase in the ratio, (k′/k1), will be (23/1.7) = 13.5. A = n(k′/k1), where n is the coupling ratio, the fractional increase in the activated CheA population over ΔRocc. The value n is a measure of signal amplification and is equal to A/(k′/k1) = 6 ± 2.

Nature of the rate-limiting step in the repellent response

A priori, motor response could be limited by buildup and diffusion of intracellular CheYP, or by CheYP binding to sites on the motor and/or the motor switch transition from CCW to CW configuration. As detailed below, the experimentally determined values for Inline graphic indicate that the last possibility is the correct one.

Build-up of intracellular CheYP occurred in ∼50 ms for a saturating repellent response to protons as measured by fluorescence resonance energy transfer (FRET) between YFP-CheY and CFP-FliM (Sourjik and Berg, 2002b). Analysis of the response kinetics suggested that activation in vivo was comparable to that obtained in vitro. The 0–0.5-mM leucine concentration jump provides a close to saturation stimulus. Poststimulus CheYP turnover estimated for a jump of this magnitude (Fig. 5 A) is 38 s−1, twice as rapid as the rate measured by FRET. It is likely that the latter rate is limited by CheYP diffusion from receptor clusters to the motor and/or CheYP-motor association. The time for diffusion of CheYP from receptors to motor in a cell of length x would be x2/6D s, where x is mean distance between receptors to the motor and D is the CheYP diffusion coefficient. In the extreme case, all the receptors are localized to one pole and the motors are confined to the opposite pole; this time is 0.13 s for x = 1.4 μm, the mean length for the tethered E. coli population used, and a lower limit D-value of 2.5 μm2 s−1. This interval is a factor-of-three less than 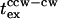Inline graphic. The diffusion time is probably closer to (0.13/4) = 0.03 s, since the actual mean receptor-motor separation would be one-half the mean cell length, given that motors are positioned randomly in the cell membrane. A diffusion-limited CheYP-motor association rate of 21 s−1 may be estimated from the rate constant of 3 × 106 M−1 s−1 used in modeling the flagellar motor switch (Duke et al., 2001) and a poststimulus CheYP concentration of 7 μM calculated for a 0–0.5-mM leucine jump (Fig. 5 A). Both CheYP diffusion and motor association are too rapid to account for the observed Inline graphic of 0.39 ± 0.18 s.

The Inline graphic is comparable in timescale to the poststimulus tccw. The latter cannot be measured directly due to onset of adaptation. However, we estimated the predicted maximal reversal frequency, vmax, obtained at mb = 0.5 and compared it with the value (0.85 s−1) reported for E. coli (Scharf et al., 1998). To obtain vmax we assumed that a fixed, single activation energy barrier governs transitions between the CW and CCW states and that mb changes result from symmetric changes in the ground state energies (Khan and Macnab, 1980; Turner et al., 1999; see also this article, Fig. 5 B, inset). 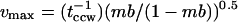The Inline graphic distribution will then be Poisson, consistent with our observation (Fig. 4 C), and Inline graphic s−1 for a 0–0.5-mM leucine jump, where Inline graphic (Fig. 4 C). Poststimulus mb = 0.08, given a prestimulus mb of 0.77 (Fig. 5 A). The value vmax will then be 2.8 × (0.08/0.92)0.5 = 0.83 s−1, in good agreement with the reported value.

The idea that Inline graphic is determined by tccw explains the former's dependence on prestimulus mb (Fig. 4 B). Poststimulus mb were computed from different prestimulus mb values for the 0–0.5-mM leucine jump with the parameters used for, or obtained from, Fig. 5 A. Predicted tccw values were then computed for vmax = 0.83 s−1, from the equation 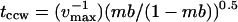Inline graphic (Fig. 5 B, solid line). The plot confirmed the qualitative trend of the mb dependence of 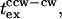Inline graphic even though quantitative agreement was modest. Better fits could be achieved by use of a more sophisticated scheme for modeling the intracellular phosphorelay and/or more switching reaction energetics; these measures were not warranted at this time.

Basis for the difference between the response times of cells tethered by a single flagellum and those of swimming cells

The swimming cell response reflects the cooperative output of multiple motors. In addition, motors operate in a different load regime when powering single tethered cells compared to flagella. A dependence on load was not discerned over the range encountered in the tethered cell population analyzed in Fig. 4 B. The 20 cells had a mean length l of 1.4 ± 0.3 μm, with l varying 0.9–1.8 μm. The corresponding difference in frictional coefficient, proportional to l3/P where P is an axial ratio-dependent term relatively insensitive to l (Garcia de la Torre and Bloomfeld, 1981), was 7.3; but there was no correlation between cell length and excitation time over this range ((corr. coeff)2 = 0.03 for a Log-Log plot of l vs. Inline graphic). These data were consistent with the report that tccw is insensitive to load (Fahrner et al., 2003).

We now propose a statistical model for tethered and swimming cell response time differences (Fig. 3) based on the stochastic nature of tccw given that multiple flagella determine bundle behavior and Inline graphic is determined by tccw. We assessed whether the observed difference could be explained by switching statistics and, in turn, provide an estimate of the number of flagella that need to reverse to affect swimming behavior. Let the bundle consist of f flagella motors, all rotating CCW for swimming cells. Probability density (probability/time) functions (B(t) s−1) for different numbers of CW rotating motors, r, were then obtained based on the following assumptions: 1), the swim trajectory changes when r out of f motors rotate CW; 2), tccw changes instantaneously to its poststimulus value when a pulse is applied at t = 0; 3), once a motor reverses to the CW state it remains in that state for the duration of the excitation response; and 4), the probability that a motor reverses in the small time interval between t and t + Δt, pΔt, is the same for all motors in a given cell. Hence the probability that it has reversed by time t is 1−e−pt. The bundle disrupts between t and t + Δt if r−1 motors reverse between 0 and t, and another motor reverses between t and t + Δt.

Then B(t) Δt = [probability that up to time t any r−1 out of f motors reverse] × [probability that between t and t + Δt one out of the remaining f−(r−1) motors reverses] = [fCr−1(1−e−pt)r−1(e−pt)f−(r−1)] × [(f−(r−1))pΔt], where fCr−1 is the number of ways of choosing r−1 motors out of f, (1−e−pt)r−1 is the probability that each of these r−1 motors reverse in the first t seconds, and (e−pt)f−(r−1) is the probability that in this time the remaining f−(r−1) motors do not. The probability that more than one motor reverses in the time interval Δt is small and is neglected. B(t) is no longer a simple exponential if two or more motors are needed to switch for the rcd change.

B(t) is plotted for f = 4, since there are 3.2 ± 1.7 flagella per E. coli cell (Turner et al., 2000), and r = 1 and 2 (Fig. 5 C). The smaller the value of r, the more rapid the change in rcd. The value r = 1 gives a significantly closer match to the data for response times of swimming cells (dashed line, Fig. 5 C), a result consistent with available knowledge. Motor reversal initiates polymorphic transitions; changes in the sense of the filament helix from left- to right-handed accompany the CCW to CW motor reversal and propagate through the filament as a kink in ∼0.1 s (Macnab and Ornston, 1977). Even if one event does not lead to a violent breakup of the filament bundle, the CW-rotating flagellum will likely separate from the bundle to change the trajectory of the swimming cell, as seen for E. coli with fluorophore-tagged filaments (Turner et al., 2000).

DISCUSSION

Our results lead to insights regarding amplification during tumble signal generation, the nature of the rate-limiting step during tumble signal processing, and the motile response of swimming cells and the output of a single flagellar motor.

CheA activation from a multimeric receptor cluster can explain the observed amplification

There is increasing evidence that receptor-CheA stoichiometry in ternary receptor complexes is not equimolar. In vitro CheA activity increased upon association with CW-locked Tsr signal fragments with a Hill coefficient of 5.2 (Ames and Parkinson, 1994). CheA activity of membrane-bound receptor complex preparations has been studied as a function of chemoattractant concentration. Such studies reveal that the ligand affinity varies with receptor methylation state. A Hill coefficient of 6.8 for the ligand concentration dependence of CheA activity was measured for the most methylated Tsr species (Li and Weis, 2000). Upper limit receptor/CheA mole ratios of 6.7 to 5.2, depending upon the methylated Tar receptor species, have been estimated (Bornhorst and Falke, 2003). The highest CheA activity reported thus far has been for isolated complexes where the receptor to CheA ratio was shown by immunoelectron microscopy to be 7 (Francis et al., 2002). Finally, x-ray crystallographic (Kim et al., 2002) and genetic (Ames et al., 2002) evidence indicates that receptors are organized as trimer teams with one CheA per receptor trimer.

Here, we have related the difference evident from temporal behavioral assays between the half-maximal dose for repellent excitation response amplitudes (Sourjik and Berg, 2002a; see also this article) and adaptation times (Berg and Tedesco, 1975) to the extent of CheA activation. The calculated activation factor A is greater than expected on the basis of the in vitro measurements and may be used, in turn, to estimate the receptor/CheA coupling ratio. Our estimated value of n is 6 ± 2. Thus, the in vivo data provide support for the high receptor/CheA stoichiometry obtained in vitro.

The accuracy of our estimate is limited particularly by uncertainty in the value assumed for the KD. Adaptation times have been shown to correspond to a dissociation constant for a number of chemoeffectors (Clarke and Koshland, 1979) as well as the half-maximal dose obtained from spatial migration assays (Berg and Tedesco, 1975). The dissociation constant for leucine has not been measured. The leucine half-maximal dose values measured in spatial migration (Khan and Trentham, 2004; Tso and Adler, 1974) and adaptation (Berg and Tedesco, 1975) assays vary over a sixfold range. This large spread could be due to variation in the heterogenous mix of receptor methylation states, caused by physiological or strain differences. We chose the lowest reported value (1.5 mM) to demonstrate that n > 1, where n would be fourfold (i.e., >6) if the highest reported value (9.8 mM) were chosen. Estimates of other parameter values probably err by a factor of 2; but it would be surprising if the random errors thus introduced all acted to lower n. We conclude that n > 1.

The value n could, most simply, correspond physically to the receptor/CheA mole ratio of the receptor complex. If CheA was maximally activated by ligand binding to any one receptor binding site in a receptor complex found in vitro (Francis et al., 2002), this could result in an n-fold greater fractional increase in CheA activity per unit increase in ligand occupancy. Nonlinear effects due to multiple ligand occupancy of the receptor complexes would not become significant before ΔRocc = 0.25, a level at which most of the CheY would exist as CheYP (Fig. 5 A).

Motor switching reactions limit repellent signal processing

The problem with identification of the rate-limiting step during chemotactic signal processing has been that several intermediate steps occur on the 10–100-ms timescale. These include CheYP turnover, diffusion of CheYP through the cytoplasm, and binding to the motor. Our finding that the Inline graphic for individual tethered cell motors varies and can be as high as 0.9 s for extreme CCW-biased motors (Fig. 4) therefore rules out these reactions as rate-limiting for the motor response.

There must be, in addition, a process that, when convoluted with the Poisson Inline graphic distribution (Fig. 4 C), accounts for the delay that causes a paucity of early events. One contributing factor is that the reversal of a cell tethered by a filament lags behind its associated motor reversal. Compliance in the tether winds it up by an angle dependent upon tether length and cell size, typically half a revolution (Block et al., 1989). Upon CCW to CW motor reversal, the torque on the woundup tether, equal to the torque on the tethered cell, will continue to drive the cell half a revolution CCW. The tethered cells analyzed in our study were chosen with 10 Hz or lower rotation speeds so that their rotation direction could be identified at the 30 frame/s digitization rates used. The mean speed was 5.4 ± 1.6 Hz. Thus, unwinding of the filament tether would introduce a mean delay of 93 ± 30 ms. A factor-of-two variation resulting from variable tether length as well as rotation speed would account for the rise phase, centered at 140 ± 50 ms, of the histogram. Delay would be inconsequential for swimming cells since flagellar bundles rotate at ∼100 Hz (Turner et al., 2000). Alternatively, there could be a load-dependent limit to how rapidly the motor itself can reverse. Stronger rotor-stator attachments might be made in the high-torque, low-speed regime characteristic of tethered cell rotation, rather than at the high flagellar rotation speeds obtained during swimming. Detachment and reattachment of the stator complexes needed for reversal of rotation would then take longer in tethered cells. To distinguish between these possibilities we need to know more about CheYP binding to the motor and individual motor excitation time distributions at low external load, possible through analysis of the rotation of beads attached to flagellar stubs (Berry and Berg, 1997).

The relation between cell motile response and single motor output

The motile response of the free-swimming cell is the principal parameter relevant to bacterial chemotaxis. The difference between the reversals of tethered cell and the cell “tumble” response is expected. First, motor response time will be at least 1.6 times more rapid for filament versus tethered cell rotation (0.39 ± 0.18 s), because the lower load enables access to a more complete tccw distribution {(ln2)/2.8 = 0.24 s}(from data analysis of Fig. 4 C). Second, the probability that any one out of multiple flagella reverse must be greater than the reversal probability of the single flagellum responsible for tethered cell rotation assuming that there are no strong filament interactions holding the flagellar bundle together. The difference will be fourfold if reversal of a single flagellum out of four is sufficient for initiation of a tumble response, as measured by the rcd (Fig. 5 C). These two factors together account quantitatively for >80% of the almost eightfold more rapid response obtained with swimming cells; i.e., 0.05 vs. 0.39 s. Thus, the “fast” tumble response reflects the mean response times of swimming cells and motor-switching stochastics rather than rate-limiting delivery of CheYP to the motor. The agreement between the swimming cell response time and the FRET measurement of CheY-FliM association half-time noted by Sourjik and Berg (2002b) is a fortuitous coincidence. It may have arisen from evolutionary pressure for the behavioral response to be approximately as fast as the intracellular signal transduction reactions.

The situation may be different for the smooth-swim response to attractant stimuli where consolidation of a stable CCW-rotating bundle, requiring reversal of all CW-rotating flagella, may determine the response. The response times of swimming and tethered cells could therefore be similar for attractant signals. Preliminary data suggest that this is indeed the case (Jasuja et al., 1999a).

Acknowledgments

We thank Catherine Kim and Meghan Gleason for technical assistance and Areejit Samal for help with figures.

Supported by National Institutes of Health grant R01-GM43919 (to S.K.) and a grant from the Department of Science and Technology, Government of India (to S.J.).

APPENDIX: GLOSSARY OF ABBREVIATIONS USED

Table 1.

CW Clockwise
CCW Counterclockwise
tCCW(s) Mean counterclockwise interval
tCW(s) Mean clockwise interval
mb Motor rotation bias
rcd (° s−1) Rate of change of direction
Δrcd Difference between the response peak and prestimulus rcd
δrcd The rcd difference from frame-to-frame
Inline graphic(s) Tethered cell excitation time
YP(μM) CheYP concentration
C Hill coefficient for dependence of Δrcd on leucine concentration
H Hill coefficient for dependence of mb on YP
ΔRocc Tsr leucine occupancy
Inline graphic (mM) Half-maximal leucine dose for Δrcd change
KD (mM) Tsr-leucine dissociation constant
KM (μM) CheYP motor dissociation constant
k′(s−1) Poststimulus rate constant for CheY phosphorylation
k1 (s−1) Prestimulus rate constant for CheYP formation
k2 (s−1) Rate constant for CheYP dephosphorylation
vmax (s−1) Maximum reversal frequency
B(t)(s−1) Probability density for poststimulus reversal of r motors
A CheA activation factor
n Receptor CheA coupling ratio
f Number of flagellar motors
r Number of CW rotating motors
Open in a new tab

David R. Trentham's present address is The Randall Centre, King's College London, Guy's Hospital Campus, London SE1 1UL, UK.

Sanjay Jain is on leave from the Indian Institute of Science, Bangalore 560012, India.

References

  1. Ames, P., and J. S. Parkinson. 1994. Constitutively signaling fragments of Tsr, the Escherichia coli serine chemoreceptor. J. Bacteriol. 176:6340–6348. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Ames, P., C. A. Studdert, R. H. Reiser, and J. S. Parkinson. 2002. Collaborative signaling by mixed chemoreceptor teams in Escherichia coli. Proc. Natl. Acad. Sci. USA. 99:7060–7065. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Berg, H. C., and D. A. Brown. 1972. Chemotaxis in Escherichia coli analysed by three-dimensional tracking. Nature. 239:500–504. [DOI] [PubMed] [Google Scholar]
  4. Berg, H. C., and P. M. Tedesco. 1975. Transient response to chemotactic stimuli in Escherichia coli. Proc. Natl. Acad. Sci. USA. 72:3235–3239. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Berry, R. M., and H. C. Berg. 1997. Absence of a barrier to backwards rotation of the bacterial flagellar motor demonstrated with optical tweezers. Proc. Natl. Acad. Sci. USA. 94:14433–14437. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Block, S. M., J. E. Segall, and H. C. Berg. 1982. Impulse responses in bacterial chemotaxis. Cell. 31:215–226. [DOI] [PubMed] [Google Scholar]
  7. Block, S. M., D. F. Blair, and H. C. Berg. 1989. Compliance of bacterial flagella measured with optical tweezers. Nature. 338:514–518. [DOI] [PubMed] [Google Scholar]
  8. Bornhorst, J. A., and J. J. Falke. 2003. Quantitative analysis of aspartate receptor signaling complex reveals that the homogeneous two-state model is inadequate: development of a heterogeneous two-state model. J. Mol. Biol. 326:1597–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Bren, A., and M. Eisenbach. 2000. How signals are heard during bacterial chemotaxis: protein-protein interactions in sensory signal propagation. J. Bacteriol. 182:6865–6873. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Clarke, S., and D. E. Koshland, Jr. 1979. Membrane receptors for aspartate and serine in bacterial chemotaxis. J. Biol. Chem. 254:9695–9702. [PubMed] [Google Scholar]
  11. Cluzel, P., M. Surette, and S. Leibler. 2000. An ultrasensitive bacterial motor revealed by monitoring signaling proteins in single cells. Science. 287:1652–1655. [DOI] [PubMed] [Google Scholar]
  12. Duke, T. A., N. L. Novere, and D. Bray. 2001. Conformational spread in a ring of proteins: a stochastic approach to allostery. J. Mol. Biol. 308:541–553. [DOI] [PubMed] [Google Scholar]
  13. Eisenbach, M., C. Constantinou, H. Aloni, and M. Shinitzky. 1990. Repellents for Escherichia coli operate neither by changing membrane fluidity nor by being sensed by periplasmic receptors during chemotaxis. J. Bacteriol. 172:5218–5224. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Fahrner, K. A., W. S. Ryu, and H. C. Berg. 2003. Biomechanics: bacterial flagellar switching under load. Nature. 424:938. [DOI] [PubMed] [Google Scholar]
  15. Falke, J. J., R. B. Bass, S. L. Butler, S. A. Chervitz, and M. A. Danielson. 1997. The two-component signaling pathway of bacterial chemotaxis: a molecular view of signal transduction by receptors, kinases, and adaptation enzymes. Annu. Rev. Cell Dev. Biol. 13:457–512. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Feng, X., J. W. Baumgartner, and G. L. Hazelbauer. 1997. High- and low-abundance chemoreceptors in Escherichia coli: differential activities associated with closely related cytoplasmic domains. J. Bacteriol. 179:6714–6720. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Francis, N. R., M. N. Levit, T. R. Shaikh, L. A. Melanson, J. B. Stock, and D. J. DeRosier. 2002. Subunit organization in a soluble complex of Tar, CheW, and CheA by electron microscopy. J. Biol. Chem. 277:36755–36759. [DOI] [PubMed] [Google Scholar]
  18. Garcia de la Torre, J. G., and V. A. Bloomfield. 1981. Hydrodynamic properties of complex, rigid, biological macromolecules: theory and applications. Q. Rev. Biophys. 14:81–139. [DOI] [PubMed] [Google Scholar]
  19. Jasuja, R., J. Keyoung, G. P. Reid, D. R. Trentham, and S. Khan. 1999a. Chemotactic responses of Escherichia coli to small jumps of photoreleased L-aspartate. Biophys. J. 76:1706–1719. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Jasuja, R., Y. Lin, D. R. Trentham, and S. Khan. 1999b. Response tuning in bacterial chemotaxis. Proc. Natl. Acad. Sci. USA. 96:11346–11351. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Khan, S. 2000. On bacterial tactic response times and latencies. Biophys. J. 78:2186–2187. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Khan, S., F. Castellano, J. L. Spudich, J. A. McCray, R. S. Goody, G. P. Reid, and D. R. Trentham. 1993. Excitatory signaling in bacteria probed by caged chemoeffectors. Biophys. J. 65:2368–2382. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Khan, S., and R. M. Macnab. 1980. The steady-state counterclockwise/clockwise ratio of bacterial flagellar motors is regulated by protonmotive force. J. Mol. Biol. 138:563–597. [DOI] [PubMed] [Google Scholar]
  24. Khan, S., J. L. Spudich, J. A. McCray, and D. R. Trentham. 1995. Chemotactic signal integration in bacteria. Proc. Natl. Acad. Sci. USA. 92:9757–9761. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Khan, S., and D. R. Trentham. 2004. Biphasic chemotactic excitation in Escherichia coli to L-leucine. J. Bacteriol. 186:588–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kihara, M., and R. M. Macnab. 1981. Cytoplasmic pH mediates pH taxis and weak-acid repellent taxis of bacteria. J. Bacteriol. 145:1209–1221. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kim, C., M. Jackson, R. Lux, and S. Khan. 2001. Determinants of chemotactic signal amplification in Escherichia coli. J. Mol. Biol. 307:119–135. [DOI] [PubMed] [Google Scholar]
  28. Kim, S. H., W. Wang, and K. K. Kim. 2002. Dynamic and clustering model of bacterial chemotaxis receptors: structural basis for signaling and high sensitivity. Proc. Natl. Acad. Sci. USA. 99:11611–11615. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Levit, M. N., Y. Liu, and J. B. Stock. 1999. Mechanism of CheA protein kinase activation in receptor signaling complexes. Biochemistry. 38:6651–6658. [DOI] [PubMed] [Google Scholar]
  30. Li, G., and R. M. Weis. 2000. Covalent modification regulates ligand binding to receptor complexes in the chemosensory system of Escherichia coli. Cell. 100:357–365. [DOI] [PubMed] [Google Scholar]
  31. Macnab, R. M., and M. K. Ornston. 1977. Normal-to-curly flagellar transitions and their role in bacterial tumbling. Stabilization of an alternative quaternary structure by mechanical force. J. Mol. Biol. 112:1–30. [DOI] [PubMed] [Google Scholar]
  32. Sagi, Y., S. Khan, and M. Eisenbach. 2003. Binding of the chemotaxis response regulator CheY to the isolated, intact switch complex of the bacterial flagellar motor: lack of cooperativity. J. Biol. Chem. 278:25867–25871. [DOI] [PubMed] [Google Scholar]
  33. Scharf, B. E., K. A. Fahrner, L. Turner, and H. C. Berg. 1998. Control of direction of flagellar rotation in bacterial chemotaxis. Proc. Natl. Acad. Sci. USA. 95:201–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Segall, J. E., M. D. Manson, and H. C. Berg. 1982. Signal processing times in bacterial chemotaxis. Nature. 296:855–857. [DOI] [PubMed] [Google Scholar]
  35. Sourjik, V., and H. C. Berg. 2002a. Receptor sensitivity in bacterial chemotaxis. Proc. Natl. Acad. Sci. USA. 99:123–127. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Sourjik, V., and H. C. Berg. 2002b. Binding of the Escherichia coli response regulator CheY to its target measured in vivo by fluorescence resonance energy transfer. Proc. Natl. Acad. Sci. USA. 99:12669–12674. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Springer, M. S., M. F. Goy, and J. Adler. 1979. Protein methylation in behavioural control mechanisms and in signal transduction. Nature. 280:279–284. [DOI] [PubMed] [Google Scholar]
  38. Stock, A. M., V. L. Robinson, and P. N. Goudreau. 2000. Two-component signal transduction. Annu. Rev. Biochem. 69:183–215. [DOI] [PubMed] [Google Scholar]
  39. Tso, W. W., and J. Adler. 1974. Negative chemotaxis in Escherichia coli. J. Bacteriol. 118:560–576. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Turner, L., W. S. Ryu, and H. C. Berg. 2000. Real-time imaging of fluorescent flagellar filaments. J. Bacteriol. 182:2793–2801. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Turner, L., A. D. Samuel, A. S. Stern, and H. C. Berg. 1999. Temperature dependence of switching of the bacterial flagellar motor by the protein CheY(13DK106YW). Biophys. J. 77:597–603. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Zhao, R., C. D. Amsler, P. Matsumura, and S. Khan. 1996. FliG and FliM distribution in the Salmonella typhimurium cell and flagellar basal bodies. J. Bacteriol. 178:258–265. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES