Water Movement during Ligand Unbinding from Receptor Site

Abstract

An 1-ns unbinding trajectory of retinol from the bovine serum retinol-binding protein has been obtained from molecular dynamics simulations. The behavior of water during ligand unbinding has never been studied in detail. I described a new method for defining a binding site, located the water molecules involved in the binding site, and examined their movements during unbinding. I found that there were only small changes in the binding site. During unbinding, the number of water molecules inside the binding site decreased, with some water molecules exhibiting movements similar in magnitude to bulk water, and there were rearrangements of the hydrogen bonds. This work represents the first detailed study of the behavior of water during an unbinding process.

INTRODUCTION

Ligand-receptor interaction is the first step to many basic processes of life, e.g., enzyme catalysis, neurotransmitter and hormone action, and antibody-antigen recognition. To elucidate the detailed mechanisms of ligand-receptor interactions, experiments such as crystallography, nuclear magnetic resonance, and electron microscopy are invaluable. Nevertheless, they only provide limited information about the dynamics of the ligand-receptor complex and the solvent molecules, which are crucial to understanding the binding process. Furthermore, it is difficult to isolate the factors that contribute to binding, and quantitate their relative importances. Simulations complement theory and experiments by making it possible to study each factor in depth and to obtain structural and dynamical details simultaneously at picosecond resolutions.

One of the early simulation studies of the mechanism of ligand-receptor interaction was by Kern et al. (1994), who performed a molecular dynamics (MD) simulation of 300 ps on adenylate kinase complexed to its transition-state inhibitor in water. They identified secondary structure transitions and domain closures, and thus the induced fit movement of the enzyme. They also concluded that reliable results were achievable only if water was explicitly included in the simulation.

Rognan et al. (1994) performed MD simulations on a different ligand-receptor complex system, the Class I MHC HLA-B 2075 protein bound to three different artificial peptides and two natural peptides in explicit water. The trajectory lasted 150 ps, and they found a higher stability of the MHC-ligand complexes with the artificial peptides than with the natural peptides. These results agreed with the experimental results of a semiquantitative assay, which showed that the artificial ligands bind with an affinity constant of 0.5 μM, whereas the natural homologs bind with an affinity constant of 40 μM. This study demonstrates that MD simulations can be used to study ligand-receptor interactions on a semiquantitative basis.

Subsequently, steered molecular dynamics was developed to simulate ligand unbinding from the receptor (Leech et al., 1996), and this method has been applied to various ligand-receptor systems successfully (Grubmüller et al., 1996; Izrailev et al., 1997; Marrink et al., 1998; Kosztin et al., 1999). Steered molecular dynamics requires the predetermination of the unbinding trajectory. Previous work used molecular complexes where the unbinding trajectory is determined from experiments, or where various putative unbinding trajectories are used for the simulation. To overcome this problem, I developed the mutual repulsion method (Chau, 2001) to allow the ligand to explore its own unbinding trajectory. This study shows that the free energy change of unbinding can be estimated, and also demonstrates the effect of hydrophobic interaction. However, no work to date has thoroughly investigated the change in structure and dynamics of the receptor site and water when the ligand unbinds. This research attempts to define the change in properties of the binding site and the water molecules around it.

METHODS

Molecular dynamics simulation

Atomic coordinates of the holo bovine serum retinol-binding protein were obtained from the Brookhaven Protein Databank (Zanotti et al., 1993; PDB code: 1HBP). The model used for the protein and retinol is the GROMOS87 potential (van Gunsteren and Berendsen, 1987). With conservation of crystallographically determined water molecules, the protein was solvated in truncated octahedral boxes filled with 5537 SPC/E water molecules (Berendsen et al., 1987). Four sodium ions were added to ensure total electronic neutrality.

All minimizations and simulations were performed using version 2 of DL_POLY (Forester and Smith, 1996). The solvated structure was minimized, and simulations were started with an NVT run at 30 K, taking initial velocities from a Maxwellian distribution. The temperature was gradually increased to 310 K over a period of 100 ps, using a Nosé-Hoover thermostat (Nosé, 1984; Hoover, 1985) with a time constant of 0.1 ps. SHAKE was used to constrain bond lengths (Ryckaert et al., 1977). The time step was 1 fs. A cutoff of 10 Å was used with simple truncation. The simulations were then continued for 400 ps in an NPT ensemble using the Nosé-Hoover thermostat and the Melchionna barostat (Melchionna et al., 1993). The last 200 ps of this NPT simulation was used to determine the optimal box size for a pressure of 10⁵ Pa (1 atm). This box size was then used for a subsequent 100-ps NVT simulation to equilibrate the system, followed by a mutual repulsion (Chau, 2001) run of 1 ns. Mutual repulsion reached maximal value at 800 ps, and thereafter the simulation was continued for another 200 ps without further increasing the repulsion. This was because the simulation box was not very large, and pushing the retinol further away from the protein meant that the ligand would come too near the other side of the protein. Both my simulation and previous experiments showed that the free energy change was purely entropic. The experimental entropy change ΔS = −364 J mol⁻¹ K⁻¹ (Noy and Xu, 1990); this value compares favorably with my simulation result of ΔS = −580 ± 30 J mol⁻¹ K⁻¹. Configurational data were output every 20 fs during this 1 ns, but, unless otherwise stated, only one configuration per 10 ps was used in all analyses described in this article.

Definition of binding site

The volume of the binding site was evaluated by first approximating it to a polyhedron. In this work, the C_α atoms of 68 amino acids around the binding site were selected as the limiting vertices of the polyhedron (a list of these amino acids can be found in the Appendix).

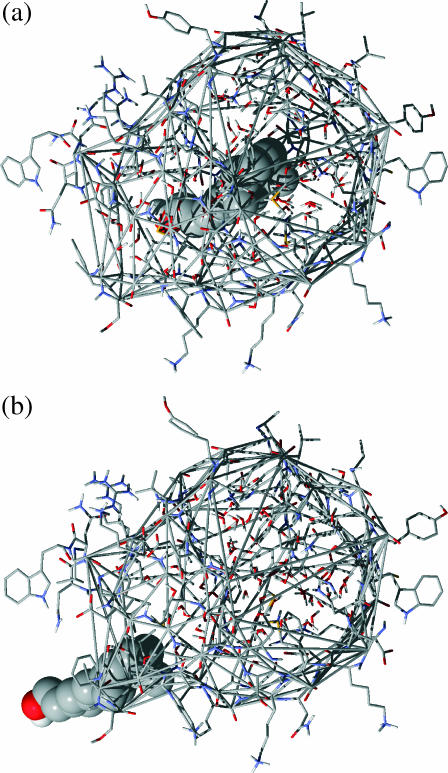
These vertices formed a quasiconvex hull, so triangles were constructed from the polyhedron vertices using a convex hull program (Clarkson et al., 1993). Each triangular face was then mathematically defined. A point P which was inside the binding site was chosen, and triangular pyramids were constructed from P to every triangular face, whose three vertices had position vectors a₁, a₂, and a₃. The volume of the triangular pyramid was calculated by multiplying the vector cross product (a₂−a₁) × (a₃−a₁) with the normal distance between the plane of the triangle and point P. Since the binding-site polyhedron is not exactly a convex hull, P was chosen so that the angular area of the triangles summed to 4π, to ensure that the volumes were calculated exactly (the author thanks S. Ling Chan for pointing this out and supplying the correction program). Fig. 1 shows the quasiconvex hull around the binding-site amino acids in the beginning and at the end of the simulation.

FIGURE 1.

Diagrams showing the construction of the quasiconvex hull to define the binding site. The amino acids around the binding site are shown in wireframe, retinol in space-filling model, and the quasiconvex hull is defined by thin shaded double lines. Water molecules enclosed by the binding-site polyhedron are also shown in wireframe. (a) The binding site in the beginning of the mutual repulsion simulation. (b) The binding site at the end of the simulation.

Water molecules and hydrogen bonds

The number of water molecules inside the binding site was determined by counting the water molecules inside the polyhedron.

The number of hydrogen bonds inside the binding site was determined by counting all hydrogen bonds involving water, whether they be between water molecules, or between amino acids and water molecules. I used the hydrogen bond definition in Chau et al. (1996). For a donor-acceptor pair B−A⋯H−D, where A is the acceptor atom, D the donor atom, B the atom immediately bonded to A, and H the hydrogen atom involved in the hydrogen bond, the conditions for a hydrogen bond include all of the following: 1), that the distance between A and D be <3.5 Å; 2), that the distance between A and H be <2.5 Å; 3), that the angle subtended by atoms A, H, and D ∠AHD, conventionally known as θ, be between 130° and 180°; and 4), that the angle subtended by atoms B, A, and H ∠BAH, conventionally known as φ, be between 90° and 180°. Note that for acceptor atoms which are bonded to two atoms, such as the nitrogen on histidines, B is a dummy atom created by taking the mean position of the two atoms bonded to nitrogen.

There is a direct correlation between the energy and the geometry of the hydrogen bond in liquid water, and the results obtained from the energetic and geometric definitions of the hydrogen bond are mutually consistent (Geiger et al., 1979; Rossky and Karplus, 1979; Rossky and Zichi, 1982). Previous work (Chau et al., 1996) has shown that, within limits, changing the geometric definition of a hydrogen bond does not qualitatively alter the results, so I did not attempt an analysis using a different definition.

Selection of water molecules inside the binding site

A reference point, P, which was definitely inside the binding site, was generated. Its position vector was p.

Let the position of the oxygen atom be point T, with position vector t. Determine the point S where the vector t−p hits a triangular face of the polyhedron, this triangular face being determined by its three vertices Q₁, Q₂, and Q₃. The position vector of that point on the Q₁Q₂Q₃ plane, s, is defined by

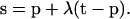(1)

If 0 < λ < 1, the point T is on the other side of the Q₁Q₂Q₃ plane of P. Ifλ < 0, then points P and T are on the same side of the Q₁Q₂Q₃ plane. If λ > 1, point T is also on the same side of the Q₁Q₂Q₃ plane.

We now have to determine whether S is inside the triangle defined by Q₁, Q₂, and Q₃. Let q be the position vector of Q₁, q₁ be the vector from vertex Q₁ to Q₂, and q₂ be the vector from vertex Q₁ to Q₃. Then if point S is inside the triangle, its position vector s can be expressed as

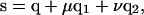(2)

where

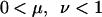(3)

and

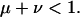(4)

Otherwise, point S is not inside the triangle Q₁Q₂Q₃.

The purpose of this process is to repeat each point with all faces, and count the number of times vector t−p cuts these faces. If this vector cuts these faces an odd number of times, the water is outside. Otherwise the water is inside. This procedure was carried out on all water molecules.

Calculation of distance traveled and distance ratio

The net distance traveled by any water molecule is the magnitude of the vector from its initial position to its final position, at the end of the 1-ns unbinding simulation.

The actual distance traveled is evaluated by adding up the distance traveled by the water molecule every picosecond, and then accumulating all 1000 of each leg. The distance ratio is the actual distance divided by the net distance, and is a measure of whether the water was undergoing directional motion or nondirectional motion. The higher the distance ratio, the less directional the motion of the water molecule. The distance ratio of the water molecules in this work varied from <50 to >2000. For reference, the distance ratio of ice Ih at 10 K is 1480 ± 1030 (SD), and of water at 310 K is 87 ± 47.

Determination of movement characteristics

If the position vector of the oxygen atom of a water molecule is r_i at the i^th ps, and r_i+1 at the i + 1^th ps, then we can calculate each step

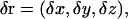where (δx, δy, δz) are the values in Cartesian coordinates. If the movement of the oxygen atom is random, then the mean values of δx, δy, and δz will be zero, and the distribution will be Gaussian.

RESULTS

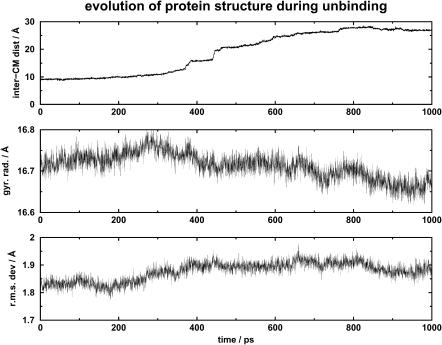
Fig. 2 shows the evolution of the distance between the centers of mass of retinol and of the retinol-binding protein (top panel), the radius of gyration of the protein (middle panel), and the root mean-square difference between the simulated protein structure and the protein structure from the liganded form of the bovine serum retinol-binding protein 1HBP (bottom panel) over the whole 850-ps unbinding simulation. Overall, the protein structure was not perturbed. This finding is consistent with results from experiment (Zanotti et al., 1993).

FIGURE 2.

Diagram showing the change of the radius of gyration of the protein, and the root mean-square difference between the simulated protein structure and the protein structure from the liganded form of the bovine serum retinol-binding protein 1HBP, as the ligand unbinds from the receptor.

Volume of binding site

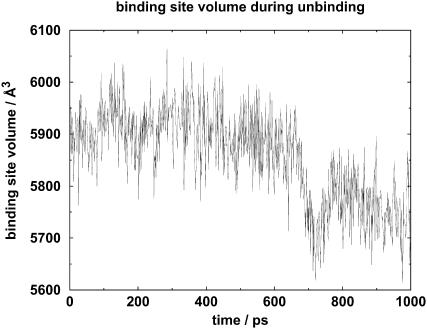
The change of volume of the binding site is shown in Fig. 3. The binding-site volume was ∼5900 ų in the initial 500 ps. It then decreased to below 5700 ų at ∼700 ps. During the last 300 ps, the volume increased to ∼5800 ų and then decreased to ∼5700 ų.

FIGURE 3.

Diagram showing the volume of the binding site during the course of unbinding.

Using a previously developed method (Chan and Purisima, 1998), I calculated the volume occupied by retinol, which was ∼270 ų. Thus the volume of the ligand was approximately the same as the decrease in the volume of the binding site. The volume of the protein was 20,600 ų ± 90 ų before ligand unbinding, but during the last 50 ps of the 1-ns simulation, the volume was 20,500 ų ± 50 ų. There was thus no detectable volume change of the protein.

This means that there was a net increase of 270 ų of the protein-ligand system, ΔV = +270 ų ± 90 ų. We can use this to estimate the difference between experimental and simulation values of entropy change, performed at NPT and NVT ensembles, respectively. Matubayasi et al. (1994) has shown that

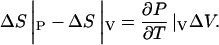Using the values for SPC water, we can evaluate that the contribution of a volume increase of 270 ų ± 90 ų is ∼354 J mol⁻¹ K⁻¹ ± 118 J mol⁻¹ K⁻¹. Note that this is only an approximate estimate of the correction for the two different ensembles.

Number of water molecules

The number of water molecules inside the binding site during the unbinding simulation is shown in Fig. 4. During the first 200 ps, there were ∼77 water molecules inside the binding site. Over time, the number of water molecules decreased to ∼73. Thus, at least within the timescale of the simulation, there was net loss of water from the binding site, and the unbinding of retinol would leave a space of ∼270 ų. How would the water molecules rearrange themselves to accommodate the changes?

FIGURE 4.

Diagram showing the number of water molecules inside the binding site during the course of unbinding.

Number of hydrogen bonds

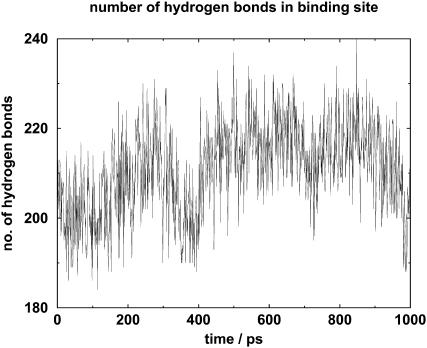
In this analysis, a hydrogen bond is a bond either between two water molecules, both of which are in the binding site, or between an amino acid of the binding site and a water molecule inside the binding site. Note that the hydrogen bonds formed between binding-site water molecules and other nonbinding-site molecules are not counted, so one cannot divide the number of hydrogen bonds by the number of water molecules to evaluate the average number of hydrogen bonds per binding-site water molecule. The number of such hydrogen bonds is shown in Fig. 5.

FIGURE 5.

Diagram showing the number of hydrogen bonds inside the binding site during the course of unbinding. These hydrogen bonds are formed either between the water molecules, or between the water molecules and amino acids of the binding site.

In the initial 300 ps, the number of hydrogen bonds increased from ∼200 to 220, but it decreased to ∼200 from 300 ps to 400 ps. From 400 ps to 500 ps, there was an increase to ∼220. Thereafter, the number of hydrogen bonds stayed at ∼220, except for a slight decrease to 210 at 700 ps. Between 850 ps and 1 ns, the number of hydrogen bonds decreased to ∼200.

Thus there was an initial increase in hydrogen bond numbers of ∼10%, followed in the last 150 ps by a decrease to the initial value.

It thus appears that there was a general decrease of binding-site volume, the number of water molecules inside the binding site, and the number of hydrogen bonds during the last 300 ps of the unbinding simulation.

Movement of water molecules

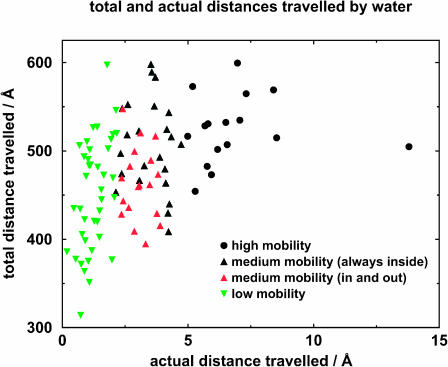
Although at any one point in time there are 73–77 water molecules inside the binding site, some water molecules move into it and some move out of it. In total, 97 water molecules were located which had at least been inside the binding site for some time. Thereafter I shall call these water molecules the “binding-site water molecules,” and detailed analysis was performed on their movement. In the following discussion, each water molecule will be identified uniquely by a number which has been assigned by the simulation program. Fig. 6 shows the net distance traversed by the water molecules of the binding site. Based on the analysis results, the binding-site water molecules are divided into three classes, as shown in Fig. 7. Their behavior is described below.

FIGURE 6.

Net distance traveled by water molecules inside the binding site.

FIGURE 7.

Net and actual distances traveled by water molecules. The medium-mobility water molecules are divided into two groups: those which are always inside the binding site and those which move in and out of the binding site.

Water molecules of high mobility

Of the 97 binding-site water molecules, 16 of them moved by >5 Å during unbinding. Their distance ratios ranged from 60 to 110; typically they were <100; they also made comparatively fewer hydrogen bonds. They possessed mobility similar to that of bulk phase water. Of these 16, five of them left the binding site, and 11 went into the space left vacated by the leaving retinol molecule.

Of the latter 11 molecules, only one of these water molecules spent a small proportion of the time just outside the binding site; the other 10 are entirely within the binding site throughout the unbinding process. A typical example of such a molecule is water 15,206, which moved by 7.07 Å during the simulation, from its original position on the side of the binding site, toward its central axis, to occupy space vacated by retinol. Fig. 8 a shows its position at five points in time.

FIGURE 8.

(a) Position of water 15,206 at 0 ps, 200 ps, 400 ps, 600 ps, 800 ps, and 1 ns of the unbinding process. The protein structure is shown in shaded wireframe, the trajectory described by the center of mass of retinol is shown in yellow, and the water 15,206 at five different positions is shown in red space-filling model. From the angle of view of the diagram, the water molecule moves from the periphery to the center, toward the right-hand side of the diagram. It should be noted that from this angle of view the position of the water at 0 ps overlaps that at 200 ps. (b) Diagram showing the hydrogen-bonding partners of water 15,206. The numbers on the left show the atom number of the other atom making the hydrogen bond; the letter d after the number denotes that the atom in question acts as the donor (with the oxygen of water 15,206 as acceptor); the letter a after the number means that the atom in question acts as the acceptor (with the hydrogen of water 15,206 as donor).

The hydrogen bonds formed between water 15,206 and binding-site amino acids and other water molecules are shown in Fig. 8 b. In the initial stages of unbinding, most of the hydrogen bonds were with two other water molecules: water 15,206 acted as the hydrogen bond acceptor to water 15,242 (via hydrogen 15,243 or 15,244), and as hydrogen bond donor to water 15,557 (via oxygen 15,557). Gradually, the hydrogen bond to water 15,242 was broken, and water 15,206 became a hydrogen bond acceptor to water 15,419 (via hydrogen 15,420), then water 8096 (via hydrogen 8097) and then water 8072 (via hydrogen 8074). The hydrogen bond to water 15,557 was less and less often observed after ∼600 ps, with water 8096 and water 10,097 acting more often as the hydrogen bond acceptor to water 15,206. Water 9926 started to form hydrogen bonds with water 15,206 after ∼200 ps, and was firmly established in approximately the last 150 ps of the unbinding. Water 15,206 also made hydrogen bonds to many other water molecules as it moved from the periphery of the binding site to the central part of the binding site.

Of the five water molecules which left the binding site, water 9893 left the binding site through the “rear” entrance, but the other four water molecules left the binding site through its mouth.

Water molecules of low mobility

At the other extreme, 40 of the binding-site water molecules moved by <∼2 Å during the unbinding process. The distance ratio of the movement of these water molecules ranged from 191 to >2000, and generally was of the order of a few hundred, meaning the motion was less directional in nature. Some water molecules possessed mobility approaching that of ice. These water molecules were usually tightly associated with the protein, and they made a comparatively higher number of hydrogen bonds.

An example of such a low-mobility water molecule is water molecule 15,251, which moved by a net distance of only 0.92 Å during the whole simulation, with a distance ratio of 434. Fig. 9 a shows its position in five points in time. The hydrogen bonds formed between water 15,251 and binding-site amino acids and other water molecules are shown in Fig. 9 b. Two main hydrogen bonds where water 15,251 acted as the acceptor were with Arg⁶⁰ (with the donor being the main chain amide bond hydrogen 582) and with water 15,659 (with the donor being hydrogen 15,660). Water 15,251 also acted as hydrogen bond donor to water 10,001. These three hydrogen bonds were present almost all the time. In addition, intermittently, water 15,251 acted as hydrogen bond donor to the main chain carbonyl oxygen of Asp³⁹ (oxygen 401) and the same atom of Asn⁴⁰ (oxygen 410). This situation is very different from the situation of water 15,206, which made hydrogen bonds with a large number of amino acids and/or water molecules, but each for a short period of time. The difference in the positions of the water oxygen at the i + 1^th ps and at the i^th ps is evaluated, and displayed for all three coordinates axes in Fig. 9 c. The distribution approximates to a Gaussian distribution, which is consistent with water 15,251 displaying characteristics of random motion.

FIGURE 9.

(a) Position of water 15,251 at 0 ps, 200 ps, 400 ps, 600 ps, 800 ps, and 1 ns of the unbinding process. The figure legend is the same as Fig. 8 a, except that the positions of water 15,251 are shown in red space-filling model. They overlap each other, because the water molecule hardly moves. (b) Diagram showing the hydrogen-bonding partners of water 15,251. The numbers on the left show the atom number of the other atom making the hydrogen bond; the letter d after the number denotes that the atom in question acts as the donor (with the oxygen of water 15,251 as acceptor); the letter a after the number means that the atom in question acts as the acceptor (with the hydrogen of water 15,251 as donor). (c) The relative frequency of displacement of water molecule 15,251 at successive picoseconds. The distribution approximates to a Gaussian distribution, which is consistent with this water molecule displaying random motion.

Water molecules of medium mobility

Between the two extremes, nearly half the water molecules moved by a net distance between 2 Å and 5 Å. In this group of water molecules, 23 were always inside the binding site, and participated in the rearrangement of water structure inside the binding site. Their distance ratios ranged from 97 to 229, so they did not move as much as the binding-site high-movement water molecules described in the previous paragraph.

The other 18 molecules spent at least some time outside the binding site. Usually these water molecules are on the edge of the binding site, interleaved between amino acids, and moved in and out with no apparent specific direction. Their distance ratios ranged from 107 to 228. Some of them, e.g., waters 8381 and 2216, were only inside the binding site for, respectively, 1 ps and 6 ps, out of 1 ns of simulation time.

Previous work showed that the unbinding of retinol was largely independent of protein motion (Chau and Howe, 2002). In this work, visual inspection of the movement of retinol and of water showed that there was some degree of correlation between ligand unbinding and water movement (data not shown). As retinol left the binding site, some water molecules moved to take up the space vacated by the departing ligand. The pseudocharges stopped increasing after 800 ps and the separation between the centers of mass of retinol and the protein stopped changing after that time, but there were still changes in the hydration of the binding site after that time.

This water movement analysis has shown that, during the unbinding of retinol from its binding protein, approximately one-half the binding-site water molecules moved very little. Fewer than one-fifth of these water molecules either left the site or occupied the space vacated by the leaving retinol, and the rest of these water molecules moved moderately to rearrange the water structure inside the binding site. A large part of these rearrangements took place when the ligand was leaving, but they continued after retinol had stopped moving. Intuitively, one could visualize the process as the ligand vacating space behind, which was filled up by water molecules. Water rearrangement was a slower process than ligand unbinding, so the former continued after retinol had cleared the binding site. If one were to repeat this simulation at a lower unbinding speed, one would expect this rearrangement process to become more simultaneous with unbinding. One would not, however, expect a different unbinding path to have a major effect on the water rearrangement.

DISCUSSION

Ligand-receptor interaction is the first step to most processes in biology, whether it be the recognition of a hormone or a neurotransmitter by its receptor, or the interaction between immunological molecules and antigens. In this research, structural studies resulting from crystallography, NMR, and neutron diffraction are, of course, of great importance. However, these studies do not give us much dynamic information about the processes involved, especially the role of water. Simulations complement experiments by allowing scientists to investigate the behavior of water in greater detail.

Methods have been developed in the past to unbind a ligand from its receptor (Ermak and McCammon, 1978; Leech et al., 1996), and these methods have been applied to various ligand-receptor systems successfully (Northrup et al., 1984, 1988; Grubmüller et al., 1996; Izrailev et al., 1997; Marrink et al., 1998; Kozstin et al., 1999). However, none of the work has investigated the behavior of water in detail. This work uses a trajectory obtained using a novel simulation method for unbinding ligands (Chau, 2001), and has elucidated some points of general interest.

Even for a protein that binds a hydrophobic ligand, the binding site of bovine serum retinol-binding protein was lined with water molecules. Many of these water molecules appeared not to exhibit much movement, and could well be essential to the structural integrity of the protein. In this work, I did not observe any increase in water molecules inside the binding site after the ligand had left; indeed, there was a decrease in the number of water molecules. I also showed that, on ligand unbinding, the binding site of the protein decreased slightly in volume. This decrease was approximately equal to the volume of the departing ligand. This decrease in binding-site volume on ligand unbinding was also observed in previous work (Lensink et al., 2002).

Using a new way of defining a binding site, I demonstrated that this entailed a rearrangement of the structure of water inside the binding site: during the middle part of the unbinding process, there was a 10% increase in the number of hydrogen bonds, either between the water molecules, or between the water molecules and the protein. This increase in hydrogen bonds was concomitant with a decrease in the number of water molecules. Approximately one-fifth of the water molecules exhibited movements similar in magnitude to bulk water to occupy the space left behind by retinol. This was then followed by a general decrease of binding-site volume, number of water molecules inside the binding site, and the number of hydrogen bonds. Case studies on two water molecules show that high-mobility water molecules made hydrogen bonds of short time duration with a large number of other hydrogen-bonding groups, but low-mobility water molecules appeared to be “locked” in hydrogen bonds with a small number of hydrogen-bonding groups, although each hydrogen bond was of long duration.

Since the binding site did not change much during the unbinding process, it was not difficult to define it manually. However, if the binding site were to alter its shape or volume dramatically during unbinding, an automated procedure for determining the binding site would be useful.

This work represents the first detailed study of the behavior of binding-site water molecules when a ligand unbinds from a receptor. It would be interesting to extend this work to longer timescales and to other ligand-receptor complexes, to see if a general principle of water movement could be deduced.

APPENDIX

The C_α atoms of the following amino acids around the binding site are selected as the limiting vertices of the polyhedron:

TABLE 1.

Trp24	Tyr25	Ala26	Ala28	Lys29	Lys30	Asp31	Pro32	Glu33	Gly34	Phe36	Leu37
Gln38	Ile41	Val42	Ala43	Glu44	Phe45	Ser46	Met53	Ser54	Ala55	Thr56	Ala57
Lys58	Gly59	Leu63	Val69	Ala71	Asp72	Met73	Val74	Gly75	Thr76	Phe77	Phe86
Lys87	Met88	Lys89	Tyr90	Trp91	Gly92	Ala94	Ser95	Phe96	Leu97	Gln98	Lys99
Gly100	Asn101	Asp102	Asp103	His104	Trp105	Ile106	Val116	Gln117	Tyr118	Ser119	Cys120
Arg121	Asp131	Ser132	Tyr133	Ser134	Phe135	Val136	Phe137