The Stability and Dynamics of the Human Calcitonin Amyloid Peptide DFNKF

Abstract

The stability and dynamics of the human calcitonin-derived peptide DFNKF (hCT_15–19) are studied using molecular dynamics (MD) simulations. Experimentally, this peptide is highly amyloidogenic and forms fibrils similar to the full length calcitonin. Previous comparative MD studies have found that the parallel β-stranded sheet is a stable organization of the DFNKF protofibril. Here, we probe the stability and dynamics of the small parallel DFNKF oligomers. The results show that even small DFNKF oligomers, such as trimers and tetramers, are stable for a sufficient time in the MD simulations, indicating that the crucial nucleus seed size for amyloid formation can be quite small. The simulations also show that the stability of DFNKF oligomers increases with their sizes. The small but stable seed may reflect the experimental rapid formation of the DFNKF fibrils. Further, a noncooperative process of parallel β-sheet formation from the out-of-register trimer is observed in the simulations. In general, the residues of DFNKF peptides near the N-/C-termini are more flexible, whereas the interior residues are more stable. Simulations of mutants and capped peptides show that both interstrand hydrophobic and electrostatic interactions play important roles in stabilizing the DFNKF parallel oligomers. This study provides insights into amyloid formation.

INTRODUCTION

The amino acid sequences of naturally occurring proteins determine their unique 3D structures that are essential for biological functions. Yet, proteins can also misfold to form insoluble amyloid fibrils. These fibrils are highly ordered protein depositions shown to be involved in severe diseases including Alzheimer's, Parkinson's, Huntington's, prion, and type II diabetes (Dobson, 1999, 2003; Harper and Lansbury, 1997; Rochet and Lansbury, 2000; Wanker, 2000). Amyloidogenic proteins do not share sequence or structural homology. Nevertheless, x-ray diffraction data show that they have a similar semiordered cross-β-fibril organization (Serpell, 2000). Detailed atomic information of the 3D structure of the amyloid is lacking. Since amyloid fibrils are noncrystalline and insoluble, the structure cannot be obtained by conventional methods such as x-ray crystallography and solution NMR. Although solid-state NMR and molecular simulations provide options for understanding the structures of amyloid fibrils, they are still difficult and challenging (Ma and Nussinov, 2002b; Petkova et al., 2002). There are still many open questions regarding these highly ordered amyloid fibrils. For example, what is the driving force of amyloid aggregation? In protein folding, the hydrophobic effect is usually regarded as the driving force; however, some hydrophilic peptides can also form ordered amyloids (Balbirnie et al., 2001; Reches et al., 2002). Second, which interactions stabilize the ordered structure of the amyloid fibrils? In particular, what are the roles of side-chain interactions in the formation of an amyloid fibril? Are there particular residues that play key roles in amyloid formation? Furthermore, what is the minimal size of the amyloid seed and its stability? How sensitive is amyloid formation to small sequence changes?

These challenging problems are being addressed by both experimental and computational approaches. Experiments have established that a hexamer (NFGAIL) of the human islet amyloid polypeptide (hIAPP) and even a smaller pentamer (FGAIL) are sufficient for amyloid formation (Tenidis et al., 2000). Molecular dynamics (MD) simulations indicate that the most stable conformation of the ordered aggregates of NFGAIL is an antiparallel orientation within the sheets and parallel organization between sheets (Zanuy et al., 2003). Furthermore, several fragments in the Syrian hamster prion protein (ShPrP) have been shown to form amyloids. For the AGAAAAGA fragment (Gasset et al., 1992), explicit water MD simulations of the oligomers (Ma and Nussinov, 2002a) indicate that they are stable in an antiparallel arrangement when the size is from six to eight peptides. The heptapeptide GNNQQNY derived from the yeast prion Sup-35 illustrates similar amyloid properties as the full length Sup-35 (Balbirnie et al., 2001). This heptapeptide has been well studied by MD simulations in an implicit water model with a total simulation time of 20 μs (Gsponer et al., 2003). The simulations generated an in-register parallel association of GNNQQNY β-strands, consistent with x-ray diffraction and Fourier transform infrared (FTIR) spectroscopy. The parallel β-sheet arrangement is favored in energy over the antiparallel due to side-chain interactions mainly from hydrogen bonds between the amide groups and the tyrosine aromatic rings π-stacking. Recently, a parallel β-strand structure of full length Alzheimer's β-amyloid (Aβ_1–40) has been observed by solid-state NMR techniques (Petkova et al., 2002). Roughly at the same time, Ma and Nussinov (2002b) used MD simulations to examine the stabilities of different possible oligomers formed by fragments of the Aβ. They independently proposed a very similar bent structure for Aβ_10–35 with a double layered sheet (Ma and Nussinov, 2002b; Petkova et al., 2002). Moreover, multiple long timescale MD simulations have been used to study the assembly of Aβ_16–22. These suggested that an α-helical conformation may be an intermediate in the assembly. Similar results were obtained from circular dichroism by monitoring the secondary structure changes of Aβ_1–40 and Aβ_1–42 during the amyloid formation (Kirkitadze et al., 2001).

Recently, Gazit et al. (Reches et al., 2002) found that a short pentapeptide containing aromatic and charged residues (DFNKF) from human calcitonin (hCT) can form highly ordered amyloid fibrils. hCT is a 32-amino acid peptide hormone, important in the calcium-phosphorous metabolism (Arvinte et al., 1993; Zaidi et al., 2002). hCT tends to aggregate, and its amyloid depositions are associated with medullary carcinoma of the thyroid (Arvinte et al., 1993). The DFNKF fragment was chosen due to the pH effects on the fibril formation of hCT (Kanaori and Nosaka, 1995) and the proposed role of aromatic residues in the fibrillation (Azriel and Gazit, 2001; Gazit, 2002a,b). These results showed some striking features: i), Early studies generally concluded that the hydrophobic effect plays an important role in the fibril formation. Nevertheless, this hydrophilic/charged peptide can also form highly ordered amyloid fibrils. ii), Few cases were reported for amyloid formation by pentapeptide and tetrapeptide. Short fragments that can form ordered fibrils imply that amyloid formation with full-length proteins may be dominated by some specific residues/segments. The unexpected high rate of amyloid formation (E. Gazit, Tel Aviv University, 2004, personal communication) by DFNKF indicates that the nucleating seed may be relatively small, albeit stable. Very recently, solid-state NMR data on the DFNKF peptide using isotope labeling on two Phe positions have been published (Naito et al., 2004). The authors showed that a mixture of 70% antiparallel structure (the first Phe forms a hydrogen bond with Lys) and 30% other structure (the first Phe forms a hydrogen bond with Asn) can have a best fit to the solid-state NMR data. It is also interesting to point out that the authors suggested that the full length calcitonin peptide forms a mixture of antiparallel and parallel β-sheets at acidic condition.

Unlike other larger amyloid-forming fragments, the small size of DFNKF peptide allows us to study the stability and dynamics of the potential amyloid nuclei by using computational approaches. Earlier studies (our unpublished results) have tested the stabilities of various two- and three-sheet arrangements, with parallel/antiparallel sheets and strands. After tests of 24 models with over 82 ns explicit water simulations, these studies have found that the single layer β-sheet with parallel strands is a stable organization for the DFNKF. Furthermore, replica-exchange molecular simulations, sampling a wide range of conformational space of DFNKF oligomers at temperatures ranging from 300 K to 600 K, also showed that the parallel structure of DFNKF tetramer is the lower energy conformer (our unpublished results). Parallel organization has been suggested for an assortment of different amyloid fibrils (Balbirnie et al., 2001; Bouchard et al., 2000; Petkova et al., 2002). However, no stable antiparallel DFNKF β-sheet structure had been found in the MD simulations. Further attempts in our group are currently ongoing to search for stable antiparallel β-sheets using enhanced MD simulation protocols.

Currently, there are increasing indications that small oligomers are the toxic agents in amyloidogenic diseases (Hardy and Selkoe, 2002; Kayed et al., 2003). Here, we employ all-atom MD simulations to explore the stabilities and dynamics of potential small oligomer seeds of DFNKF peptides, with the size increasing from dimer to tetramer. The results show that the stabilities of parallel DFNKF oligomers increase with the number of strands. Small DFNKF oligomers such as trimer and tetramer are stable in the parallel organization for a sufficient time in the 350-K MD simulations, indicating that the seed size for the DFNKF amyloid aggregation can be quite small. The direct observation of the dynamic registration of parallel DFNKF oligomers from the out-of-register conformation in the trimer simulations implies that an extended strand may serve as a β-sheet template, assisting in amyloid formation. Characterization of the formation of the in-register parallel structure shows that it follows a noncooperative process. Sequence variant studies including mutations and capping show that the side-chain–side-chain interactions are important in preserving the parallel DFNKF arrangements. In particular, the Asn side-chain–side-chain hydrogen bonds between two neighboring chains were found to be particularly important in retaining the parallel DFNKF integrity. The N-/C-terminal residues (Asp and Phe) as well as the backbone hydrogen bonds near the N-/C-terminus were observed to be more flexible than the residues in the interior of the strands.

COMPUTATIONAL METHODS

All MD simulations were performed using the CHARMM molecular simulation software with CHARMM-22 all-atom force field (MacKerell et al., 1998). Simulations were performed using an NVT ensemble with periodic boundary conditions. The DFNKF oligomers and mutants studied here were solvated with explicit TIP3 water molecules in a cubic box. The lengths of the cubic box used for the DFNKF monomer, dimer, trimer, and tetramer simulations are 30 Å, 30 Å, 35 Å, and 40 Å, respectively. A 10-ns simulation was carried out for each system at 350 K. This simulation temperature is slightly higher than room temperature and may aid in avoiding kinetic traps and allow us to probe the stabilities and dynamics of DFNKF oligomers more quickly in the limited simulation time. The Adopted Basis Newton-Raphson (ABNR) energy minimizations were performed for all systems before the MD simulations. A 1-fs time step was used in the numerical integration. A group based distance cutoff was applied at 10 Å and 11 Å when generating the list of pairs. The force switching function was used to smooth the electrostatic potential energy, whereas the van der Waals shift function was used to smooth the van der Waals potential energy starting at 8 Å (Steinbach and Brooks, 1994). The nonbonded neighboring list was updated every 20 steps.

To probe the dynamical structure characteristics during the simulations, some quantities were computed. We calculated the C_α-RMSD, the residue-wise distances d_ij(t), the scalar product of end-to-end vectors cos(θ)_ij, the fraction of native contact (Q_nat), the population of the β-strand and of the α-helix, the end-to-end distance, and the radius of gyration (R_g). The C_α-RMSDs were calculated from the minimal deviations of the C_α atoms of the trajectories away from the energy minimized structure with parallel organizations by superimposing the conformations. The residue-wise distances d_ij(t) were calculated from the distances between the C_α atom of residue i and the C_α atom of residue j at different simulation time t. The scalar product of end-to-end vectors, 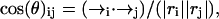for a pair chain i and j, were calculated to monitor the relative orientations of chains i and j (Klimov and Thirumalai, 2003). When cos(θ)_ij is close to 1.0, chains i and j adopt a parallel-like organization. In contrast, when cos(θ)_ij is close to −1.0, chains i and j adopt an antiparallel-like organization. The native contacts included backbone hydrogen bonds and side-chain contacts (Rao and Caflisch, 2003). The backbone hydrogen bond was calculated based on the definition of hydrogen bonds used in STRIDE (Frishman and Argos, 1995). A native side-chain contact is considered when the distance between the geometrical center is smaller than 6.7 Å. The energy minimized structures with parallel organization were used to construct the native contacts. The fraction of native contacts was calculated as the fraction of contacts common to both the current conformation and the native structure (here, the energy minimized structures with parallel packing were used). The end-to-end distance was calculated between the nitrogen atom in the ammonium group and the carbon atom in the carboxyl group. The radius of gyration (R_g) for the oligomers and peptide was computed using all the heavy atoms (Massi et al., 2001).

To probe possible minima of the DFNKF monomer and dimer that may exist in the simulation, the free energy landscape was determined from the histogram analysis (Zhou et al., 2001) by calculating the normalized probability, P(X) = exp(−βW(X))/Z, where X is any set of reaction coordinates. The relative free energy (or the so-called potential of mean force) can be described as W(X₂) − W(X₁) = −RT log(P(X₂)/P(X₁)). The free energy landscape was expressed as a function of various reaction coordinates including the end-to-end distance, the radius of gyration, the cos(θ)_ij, and the average of the five residue-wise distances.

RESULTS AND DISCUSSION

Notations used in this study

For clarity and convenience, the notations used in this study to denote an individual residue and its corresponding chain are as follows:

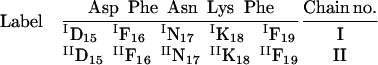Here, the dimer notations are used as an illustration. Each residue in each oligomer is indicated by one subscript and one superscript number and is abbreviated by its one letter code. Since the DFNKF peptide is taken from residues 15–19 of the hCT, the sequence numbers are kept the same as those in the hCT. They are shown as subscript numbers along with their one letter code. To distinguish between the same residues in different chains, their chain numbers are denoted in the superscript of the one letter code. Based on these notations, each residue in each chain has its own notation. For example, the Phe at the C-terminal of the second chain is denoted as ^IIF₁₉. On the other hand, the Phe next to Asp in the second chain is indicated by ^IIF₁₆.

Relative stability of DFNKF oligomers

It is currently accepted that amyloid fibril formation follows a nucleated assembly mechanism and proceeds via a conformational change (Jarrett et al., 1993; Jarrett and Lansbury, 1993; Lomakin et al., 1997; Serio et al., 2000; Tenidis et al., 2000). The early events in the nucleus formation involve a series of association steps. These are not favorable thermodynamically since the interstrand interactions (enthalpy) cannot compensate for the loss of the entropy after the association. Once the crucial nucleus is formed, further steps of association are thermodynamically favored. The addition of smaller monomers to the larger nucleus has a lower entropic cost, and the monomers can interact with the growing nucleus at multiple sites, resulting in rapid amyloid formation. Therefore, studying the stability and dynamics of DFNKF oligomers that are potential nuclei is essential to understand the assembly mechanism.

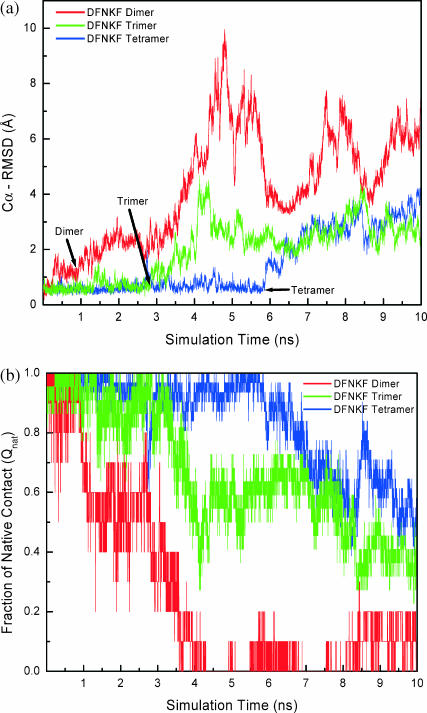
The time series of the C_α-root mean-square deviation (C_α-RMSD) and the fraction of native contacts (Q_nat) of different sizes of DFNKF oligomers have indicated their relative stabilities (Fig. 1). The C_α-RMSD and the Q_nat were calculated at 350 K based on the corresponding energy minimized structures because the native structures were not available. At the early stage of the simulations, all three simulated DFNKF oligomers fluctuated around their energy minimized structures with small C_α-RMSD and large Q_nat. Subsequently, the C_α-RMSD increased (and Q_nat decreased) in all three simulations, and they no longer came back to the energy minimized basins during the course of simulations. However, the dissociation (increase of C_α-RMSD and decrease of Q_nat) of the three DFNKF oligomers initiated at different time stages (with different lag phases). The magnitude of the DFNKF dimer C_α-RMSD increased sharply after ∼1.0 ns and reached the maximal value of 9.7 Å roughly at t ∼ 4.8 ns. Similarly, at t ∼ 4.8 ns, the calculated Q_nat of the dimer was zero, indicating that the dimer has no native-like characteristics at this stage. Nevertheless, the dimer did not dissociate completely. A small fraction of the native contacts was observed during the rest of the simulation. In contrast to the large C_α-RMSD fluctuation of the dimer, the tetramer maintained its parallel integrity with remarkably low values of C_α-RMSD until t ∼ 6.0 ns, after which it increased gradually. For the trimer, the magnitudes of the C_α-RMSD and Q_nat were between dimer and tetramer.

FIGURE 1.

Structural characteristics (C_α-RMSD and fraction of native contacts) of DFNKF oligomers calculated by MD simulations at 350 K. (a) The C_α-root mean-square deviations (C_α-RMSD) of the DFNKF oligomers as a function of time. The C_α-RMSDs were calculated from the energy minimized structures based on the C_α atoms. The time of initial decomposition of the parallel β-strands of each oligomer observed is indicated by the arrow. (b) The time-dependent native contact fraction (Q_nat) of the DFNKF oligomers. The native contacts were defined based on the energy minimized structures in terms of the backbone hydrogen bonds and side-chain native contacts. A sharp increase in the C_α-RMSD and a quick decrease of Q_nat of DFNKF dimer indicate a relative instability. In contrast, a slow increase in C_α-RMSD and Q_nat of the DFNKF tetramer indicates that the tetramer is relatively more stable than the dimer and trimer.

To estimate the relative stabilities of DFNKF oligomers in a more quantitative manner, two criteria were defined for stable parallel β-strands. The DFNKF oligomer is considered as a stable and parallel structure when its C_α-RMSD is lower than 2.5 Å and at the same time its Q_nat is higher or equal to 0.70. Based on these two criteria, the population times of stable and parallel structures were estimated to be 1.30 ns, 3.71 ns, and 6.98 ns, for parallel DFNKF dimer, trimer, and tetramer, respectively. It can be clearly seen that the stabilities of the parallel oligomers were dramatically increased from dimer to tetramer. Overall, the DFNKF oligomers were stabilized with the increase in the number of strands. Moreover, in a 10-ns MD simulation at 300 K (data not shown), the DFNKF tetramer was found to maintain a remarkably stable parallel structure during the entire simulation. These observations suggest that even small oligomers, parallel trimer or tetramer, can act as stable seeds in prompting amyloid fibril formation. Thus, the size of the critical nucleus for enhancing amyloid fibrillization can be quite small. Previous MD simulations of the aggregation mechanism of Aβ_16–22 amyloid peptide in explicit water (Klimov and Thirumalai, 2003) and the GNNQQNY peptide with the implicit water model (Gsponer et al., 2003) also observed that even a small number of peptides (three) can form in-register structures. These results also support our observations that three or four peptides are stable enough to act as the nucleus for amyloid formation.

The parallel DFNKF oligomers are mainly stabilized by backbone hydrogen bonds, salt bridges, side-chain hydrogen bonds, and π-π-interactions between neighboring chains. The interchain interactions, through which the parallel DFNKF β-sheet is organized, will be described elsewhere in detail (Haspel et al., unpublished results). Here, we briefly discuss the roles of the more significant interchain interactions stabilizing the parallel DFNKF oligomers. We focus on how the parallel DFNKF oligomers are stabilized by these interactions as their sizes increase. The examination of how an individual interchain interaction affects the stabilities of parallel DFNKF oligomers is discussed in the sequence variation section.

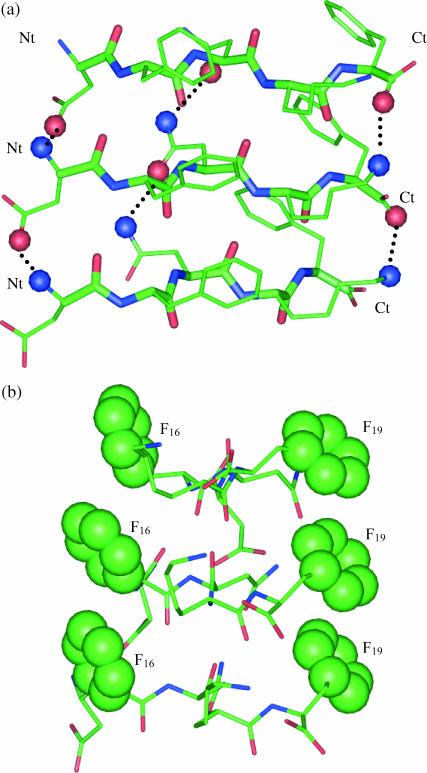
Undoubtedly, backbone hydrogen bonds play an important role in organizing either the parallel or the antiparallel DFNKF β-sheet. In addition, the side-chain/side-chain and side-chain/N- and side-chain/C-terminal interactions also play important roles in stabilizing the parallel strands (shown in Fig. 2 a). The side chain of Asp forms salt bridges with the ammonium group of the N-terminus of the neighboring chain. Similarly, the longer Lys side chain also forms salt bridges with the carboxyl group at the C-terminus of its adjacent chain. However, these salt bridge stabilizations only exist in the shortened peptides. In the full length peptide, these residues do not have the ability to form these salt bridges. Furthermore, the Asn–Asn side-chain hydrogen bond also forms between neighboring chains. These hydrogen bonding networks hold the parallel DFNKF strands together. In addition to the electrostatic interactions, the hydrophobic π-π-stacking of the Phe aromatic rings also plays an important role in stabilizing these parallel strands. π-π-stacking is well known to play central roles in molecular recognition and self-assembly (Shetty et al., 1996; Sun and Bernstein, 1996). Furthermore, the higher occurrence of aromatic residues in amyloid-related peptides relative to their lower occurrence in proteins (Gazit, 2002b) suggested that π-π-stacking may play an important role in amyloid formation. In particular, in the DFNKF peptide, the aromatic residues constitute 40% of the residues of the whole chain. Similar side-chain interactions were pointed out to be very important in a previous study generating the in-register parallel packing of GNNQQNY β-strands (Gsponer et al., 2003). β-helices may form with different residue types; however, the aligned residues in successive ladders are consistently observed to have similar chemical properties. β-helices have been discussed as a possible fold for amyloids (Wetzel, 2002). Although the short peptides DFNKF studied here cannot form β-helices, nevertheless, their homotypic side-chain stacking in parallel β-sheet are similar to β-helices.

FIGURE 2.

Interchain interaction network stabilizing the parallel DFNKF oligomers. The DFNKF trimer is used here for demonstration. (a) Side-chain electrostatic interactions. The side-chain–side-chain hydrogen bonds and side-chain–N-/C-termini salt bridges include Asn–Asn, Asp– (N-termini), and Lys–COO⁻ (C-termini). The oxygen and nitrogen atoms on side chains forming the interchain hydrogen bonds are shown in red and blue balls, respectively. (b) Side-chain aromatic π-stacking. The end-to-end vectors of the DFNKF chains are perpendicular to the paper. The Phe aromatic rings are shown as large balls. It can be seen that the aromatic rings that stack onto each other are located at the two sides of the DFNFK β-sheet plane.

Clearly, every single chain within the parallel DFNKF oligomers is stabilized by its neighboring chains. When a chain is located at the edge of the oligomers, it is only stabilized by its one neighboring chain. In contrast, when the chain is between two chains, it is stabilized by interchain interactions from its two neighboring chains. This explains why the parallel DFNKF oligomer becomes more stable as the number of chains increases. A dimer does not have any chain located between two other chains. The looser interactions result in a less stable structure. In contrast, a larger tetramer has two chains stabilized by two other chains leading to a more stable structure.

Dynamics of parallel DFNKF oligomers

Knowledge of the dynamical behavior of the DFNKF oligomers is expected to provide insights into the role of individual residues in stabilizing the DFNKF oligomers. Understanding the structural fluctuation of amyloid fibrils may provide hints for designing drugs to decompose the amyloid fibril targeted at the flexible portion. Here, we probed the dynamical behavior of parallel DFNKF oligomers. Although it does not provide a complete amyloid assembly mechanism, it generates useful information toward the understanding of the amyloid assembly mechanism.

DFNKF monomer conformation and dynamics

To understand the dynamics and stability of the DFNKF oligomers, we first characterized the structure and the dynamical behavior of the DFNKF monomer. The dynamical characteristics of the DFNKF monomer are essential, especially since it serves as a reference in the understanding of the conformational changes in the oligomer simulations. To characterize the conformers of the DFNKF monomer, a 12-ns MD trajectory is generated at 350 K with the same simulation conditions used in the DFNKF oligomer simulations. To avoid the bias imposed on the initial structure, the first 2-ns trajectories were discarded with a total of 10 ns used in the analysis.

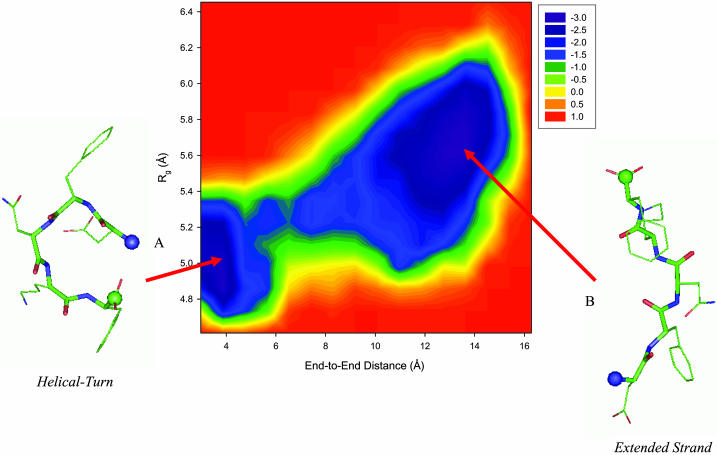
To characterize the conformation of the DFNKF monomer, the free energy landscape as a function of the end-to-end distance and the radius of gyration was calculated (Fig. 3). The energy unit is shown in RT (T = 350 K). The end-to-end distance of DFNKF was defined by the distance between the nitrogen atom of the N-terminal ammonium group and the carbon atom of the C-terminal carboxyl group. The radius of gyration was calculated using all the heavy atoms. There are two main basins in Fig. 3. The structures in basin A are the helical-turn/random coil-like states with shorter end-to-end distances and smaller radii of gyration. Those conformations own a higher helical propensity. In contrast, the structures in basin B are extended β-strand-like states with end-to-end distances of ∼13 Å. In this simulation, the DFNKF visited basins A and B several times, indicating that the system has reached equilibrium. There is an energy barrier separating basins A and B. The barrier height is slightly higher than the thermal energy. Since there are two populated conformers of the DFNKF monomer that coexist in solution, the process of cross-β-amyloid fibril formation, which finally converts the non-β-stranded monomers to the β-stranded conformation, may undergo a conformation change (e.g., from basin A → B).

FIGURE 3.

Free energy profile of the DFNKF monomer as a function of the end-to-end distance and the radius of gyration at 350 K. The energy scale is in RT instead of kcal/mol. Two main basins (minima, shown in purple) are identified. (A) Helical turn-like conformation. This structure has a shorter end-to-end distance and a smaller radius of gyration with higher helical propensity. (B) Extended β-strand-like conformation. The conformation of this state is extended with an end-to-end distance of ∼13 Å. Secondary structure analysis based on the ψ- and φ-angles shows that the conformations within this basin have higher β-strand content. Representative structures of these two basins are shown along with the free energy landscape. The backbone atoms are shown as thick sticks, whereas the side-chain atoms are presented as thin sticks. The N- and C-termini are denoted by blue and green balls, respectively.

DFNKF dimer dynamics and energy landscape

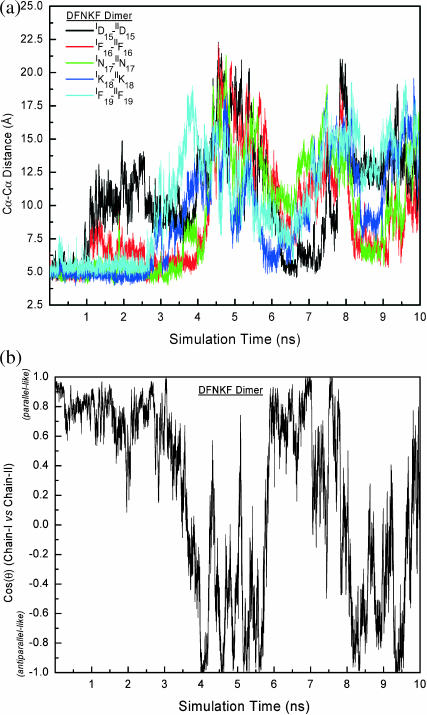
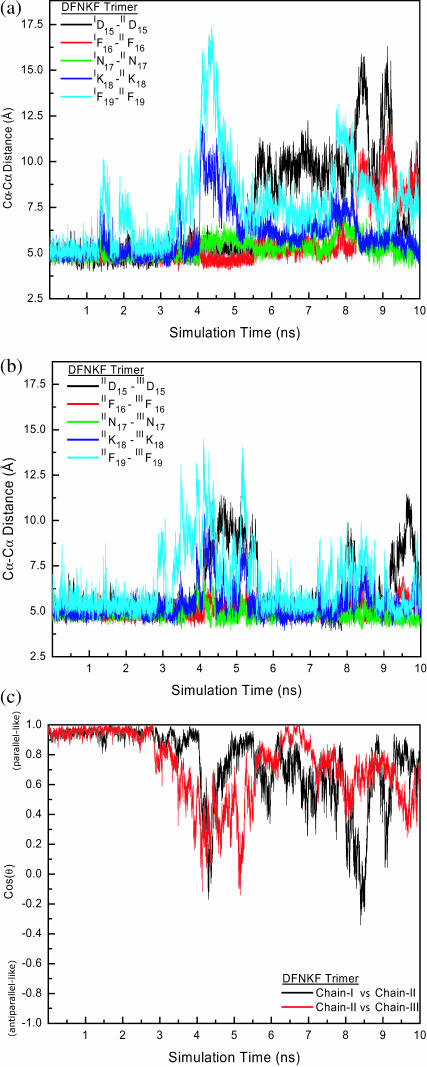
The dynamics of the DFNKF dimers were characterized. To characterize the dynamical structures of DFNKF oligomers away from the parallel structure, the interchain residue distance d_ij(t) and the cross angles (cos(θ)) between chains were calculated. Fig. 4 a shows the five residue-wise distances and the cross angle between chains of the DFNKF dimer as a function of simulation time. Only the homogeneous residue-pair interactions between chains (in parallel arrangement) were calculated. In this figure, the ^ID₁₅-^IID₁₅ C_α-distance increases at t ∼ 1 ns, whereas the other residue-pair distances are kept around their in-register parallel distances until t ∼ 2.5 ns. At t ∼ 5 ns, all residue-wise distances reach their maximal values approximately at the same time. On the other hand, the DFNKF dimer rearranges to the antiparallel-like structure (see Fig. 4 b; the cos(θ) ∼ −1); however, the structures are not in-register antiparallel arrangements. Instead, one of the chains forms a helical turn-like structure with similar structures shown in basin A (in Fig. 3). Subsequently, all residue-wise distances reach another minimum with a parallel-like association at ∼6.5 ns. The DFNKF dimer structure reorganizes from parallel-like to antiparallel-like structures and from antiparallel-like to parallel-like structures in an oscillatory way, but at some time periods the fraction of native contacts is very low.

FIGURE 4.

Structural characteristics (pairwise residue C_α-C_α distances and cross angle between chains) of the DFNKF dimer. (a) The pairwise residue C_α-C_α distances change with time. The C_α-C_α distances are calculated based on C_α atom distances between a residue pair. The charged (Asp and Lys) and C-terminus residues (^IF₁₉ and ^IIF₁₉) are more flexible at the early events of the simulation. The five pair-residue distances plotted here reach the maximum roughly at the same time (t ∼ 5 ns) and return to their minima together at ∼6.5 ns showing that some periodic events occur during the simulation. (b) The time dependence of cos(θ), the cross angle between chain-I and chain-II. The definition of cos(θ) is described in Computational Methods. The oscillation between parallel and antiparallel arrangement is observed.

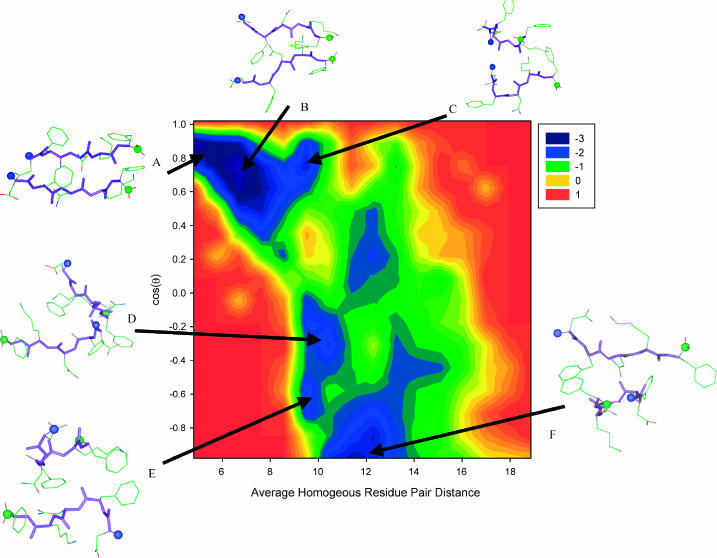
To understand the conformational change of the DFNKF dimer, the free energy landscape of the DFNKF dimer at 350 K is plotted (Fig. 5) in terms of the cos(θ) between chains and the average homogeneous residue pair distance (the average distance of five residue pairs used in Fig. 4 a). Several basins (local minima) were characterized: (A) the parallel in-register dimer; (B) parallel dimer with a larger separation between interchain N-/N-termini; (C) parallel dimer, but the separations between the chains are larger; (D) interchain N- and C-termini residues associated with an antiparallel arrangement; (E) one chain in a helical turn-like structure associates with another partially extended chain; and (F) a structure similar to structure E, however, with a more extended strand. The helical turn-like structures identified in basins E and F are similar to the helical turn-like structure characterized in the DFNKF monomer simulations (Fig. 3). The free energy landscape can provide information regarding the DFNKF aggregation pathway and the corresponding barriers. For convenience, the energy scale is shown in RT instead of kcal/mol. These six basins can be further classified as two larger basins. Since there is no clear energy barrier between basins A, B, and C, these three basins can be classified as one basin only (denoted as basin I). Similarly, basins D, E, and F can also be classified as a single basin (denoted as basin II). Conformers within the same larger basins (I and II) can freely convert to each other at RT (T = 350 K). In this simulation, the free energy landscape suggests that the helical turn-like structure (basins E and F) can potentially convert to the parallel β-stranded dimer (basins A and B) via an intermediate state (basin D) having an antiparallel-like arrangement at 350 K. The largest energy barrier occurs between basins I and II retarding the free interconverting dimers between basins I and II. In this barrier region, the structure adopts a perpendicular interchain arrangement (cos(θ) ∼ 0.0 and average residue-wise distance ∼9 Å). The energy landscape of the DFNKF dimer was established based only on a 10-ns MD simulation at 350 K. Although it provides a protocol for the DFNKF dimer aggregation, the conformational space sampled is limited. A broad conformational sampling of the DFNKF oligomer aggregate using replica-exchange molecular dynamics (REMD) simulation, an effective conformation sampling method, is expected to provide further details of the DFNKF aggregation mechanism (Tsai et al., unpublished results).

FIGURE 5.

The free energy landscape of the DFNKF dimer as a function of cos(θ) and the average distance of five pair-residue distances used in Fig. 4 a at 350 K. Several basins (local minima) are identified: (A) the parallel in-register DFNKF dimer; (B) the parallel DFNKF dimer with larger ^ID₁₅-^IID₁₅ separation; (C) the parallel DFNKF dimer with larger interchain separation; (D) the antiparallel DFNKF dimer with one associated N-/C-terminus residue pair; (E) the DFNKF dimer with one chain forming a helical turn-like structure and another chain is partially extended; and (F) the DFNKF dimer with one extended chain and one helical turn-like structure. The backbone atoms are shown as thick sticks and the side-chain atoms are shown as thin sticks. The N-terminus is denoted by blue balls and the C-terminus is indicated by green balls. The energy scale is shown in RT.

DFNKF trimer simulation: direct observation of the formation of parallel β-sheet

Fig. 6 shows the residue-wise distances and cos(θ) between chains of the DFNKF trimer. In the early events of the simulation (t = from 0 ns to ∼3.0 ns), the DFNKF trimer kept its parallel in-register integrity. Subsequently, the partial DFNKF trimer structure fluctuated away from the parallel in-register arrangements indicated by the larger C_α-C_α distances. At ∼4.5 ns, the twist angles between chains (in Fig. 6 c) are ∼90° as well as the larger separations between ^IF₁₉-^IIF₁₉, ^IIF₁₉-^IIIF₁₉, ^IK₁₈-^IIK₁₈, ^IIK₁₈-^IIIK₁₈, and ^IID₁₅-^IIID₁₅, which indicate that the DFNKF trimer loses its parallel integrity at this period. However, during from t ∼ 5.5 ns to t ∼ 7.0 ns, the chain-II and chain-III register back to the parallel arrangement denoted by the five smaller pairwise C_α-C_α distances as well as the calculated smaller cross angles at this time period. In contrast, the interchain structural characteristics between chain-I and chain-II fluctuate during from t ∼ 5.5 ns to t ∼ 7.0 ns, especially for the N-/C-terminal residues. By the end of the simulation, the orientation of chain-I with respect to chain-II has a larger deviation from their parallel structure.

FIGURE 6.

Structural characteristics (pairwise residue C_α-C_α distances and cross angle between chains) of the DFNKF trimer. (a) The pairwise residue C_α-C_α distances between chain-I and chain-II. (b) The pairwise residue C_α-C_α distances between chain-II and chain-III. (c). The time dependence of cos(θ), the cross angle between the chains. The definition of cos(θ) is given in Computational Methods. Only the cross angles between chain-I versus chain-II and chain-II versus chain-III are shown. The DFNKF trimer stays at the in-register parallel structure until ∼2.5 ns. After 2.5 ns, the structural characteristics between chain-I and chain-II lose their parallel structural character. In contrast, the structure between chain-II and chain-III is in parallel during the simulation time between ∼5.5 ns and ∼7.0 ns. Chain-II, whose conformational space is restrained by chain-I and chain-II, has less conformational entropy, providing a β-sheet template for the chain-III registration. In general, the charged and C-terminal residues are more flexible.

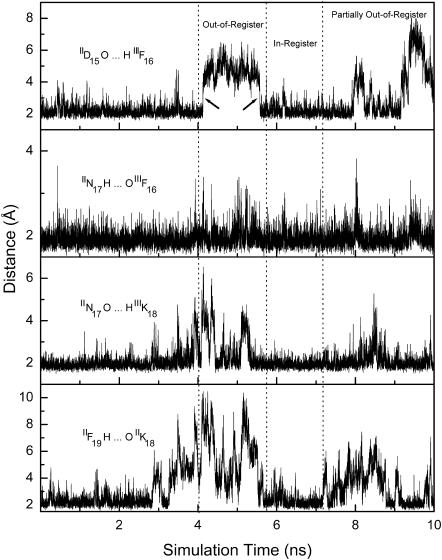
The dynamical registration of the parallel in-register structure of chains-II and -III in the trimer from the out-of-register structure was further characterized by the formation of interchain backbone hydrogen bonds. Fig. 7 shows the distances of four interchain (between chain-II and chain-III) hydrogen bonding atom pairs as a function of simulation time. Because the simulation started from the parallel structure, these hydrogen bonds were formed with hydrogen-oxygen distances of ∼2.0 Å at the early stages of the simulation. From ∼4.1 ns to ∼5.6 ns, the structures of chains-II and -III were out-of-register with hydrogen bond distances away from the optimal values. Subsequently, chains-II and -III underwent an aggregation process, and all distances reached parallel in-register structures during the simulation time from ∼5.6 ns to ∼7.2 ns. After ∼7.2 ns, partially out-of-register structures were formed.

FIGURE 7.

Structural characteristics (four backbone hydrogen atom pair distances) of chains-II and -III within the DFNKF trimer. The H and O represent the amide hydrogen and carbonyl oxygen. From ∼5.6 ns to ∼7.2 ns, the formation of in-register from the out-of-register structure can be observed. The four backbone hydrogen bonds are formed within this time period. The formation of the in-register structure is not a cooperative process (see text for discussion).

The processes of registration and unregistration reveal several interesting features of the DFNKF aggregation. i), The registration process is noncooperative. The formation of ^IIN₁₇ O…H ^IIIK₁₈ and ^IIF₁₉ H…O ^IIIK₁₈ hydrogen bonds was continuous with a gradual decrease in the distance between native hydrogen bonding atoms. In contrast, the ^IID₁₅ O…H ^IIIF₁₆ hydrogen bond formed quickly with a sudden decrease in the corresponding native hydrogen bonding atoms as indicated by the arrows shown in Fig. 7. Similar behavior was also observed for the breaking of the ^IID₁₅ O…H ^IIIF₁₆ hydrogen bond (also indicated by an arrow in Fig. 7). ii), The ^IIN₁₇ H…O ^IIIF₁₆ hydrogen bond is relatively more stable than other backbone hydrogen bonds. This hydrogen bond was rarely broken in the simulation, and it appears to play an important role in stabilizing the parallel organization of the DFNKF peptides. iii), The unregistration proceeded with the breaking of the ^IIF₁₉ H…O ^IIIK₁₈ hydrogen bond near the C-terminus. In the region of the partially out-of-register structures, the ^IIF₁₉ H…O ^IIIK₁₈ hydrogen bond near the N-terminus as well as the ^IID₁₅ O…H ^IIIF₁₆ hydrogen bond was relatively unstable. Nevertheless, the ^IIN₁₇ H…O ^IIIF₁₆ and ^IIN₁₇ O…H ^IIIK₁₈ hydrogen bonds at the interior of the strands still remained in the partially out-of-register region, indicating that hydrogen bonds near the termini are relatively unstable. Within the same simulation time, the parallel in-register structure was not observed in the DFNKF dimer simulations when the system left the in-register structure. This might be due to the lower entropic origin of chain-II, whose interlocking by chain-I and chain-III may provide a β-strand template, assisting chain-III to register in a parallel fashion more easily (Fig. 7, from t ∼ 5.6 ns to t ∼ 7.2 ns).

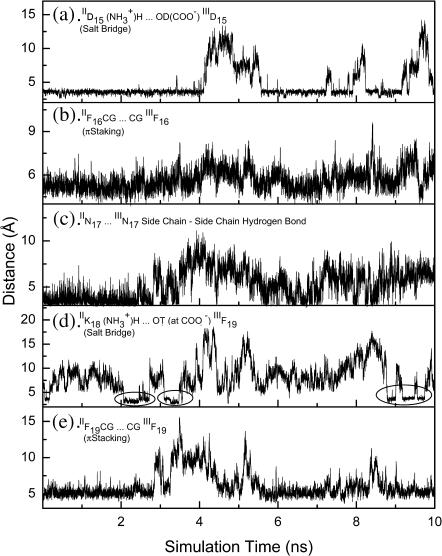
The side chain–side chain interactions between chains-II and -III within the trimer are also very interesting. Fig. 8 shows five selected side chain–side chain distances within the simulation time. They include two salt bridges near the C- and N-termini, two aromatic interactions, and one side chain–side chain hydrogen bond. For the salt bridge interactions, the average distance between all possible hydrogen bond donors (e.g., two oxygen atoms at the carboxylate group) and acceptors (e.g., three hydrogen atoms at the 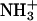group) was used. Similar treatments were used to handle the Asn–Asn side-chain hydrogen bonds. Thus, the minimal distances for the salt bridge interactions and Asn–Asn side-chain hydrogen bond are longer than the hydrogen bond distances shown in Fig. 7. The C_γ-C_γ (for the Phe residues) distances were chosen to represent the relative π-π-interactions. The behavior of these three kinds of side-chain–side-chain interactions are remarkably different. The ^IIF₁₆–^IIIF₁₆ was well packed during the simulation as evidenced by the lower C_γ-C_γ fluctuation. On the other hand, the ^IIF₁₉–^IIIF₁₉ packing has a larger C_γ-C_γ fluctuation. However, the fluctuation decreased after ∼5.8 ns until the end of the simulation. The Asn–Asn side-chain hydrogen bond frequently broke and quickly reformed within very short time periods. In contrast to the Asn–Asn side-chain hydrogen bond behavior, the salt bridge interaction is very strong and stable once it is formed. Nevertheless, when it is broken, it takes a longer time to reform. This is clearly seen in Fig. 8 a for the ^IID₁₅…^IIID₁₅ salt bridge interaction. Similar behavior, but to a lesser extent, was observed for the salt bridge at the C-terminus (Fig. 8 d). For clarity, the durations of the formation of this salt bridge are marked by circles (Fig. 8 d).

FIGURE 8.

Structural characteristics (five selected side-chain–side-chain distances) of chains-II and -III within the DFNKF trimer. (a) Salt bridge interaction at the N-terminus between 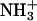on ^IID₁₅ and COO⁻ on the ^IIID₁₅ side chain. The distance shown here is averaged over the six possible from H to O distances. (b) π-π-Interaction occurring at the F₁₅ between chains-II and -III. The C_γ-C_γ distance is used to present the π-π-interactions. (c) Asn–Asn side-chain hydrogen bond. The distance presented here is also averaged over the distances from the Asn side-chain oxygen atom (hydrogen bond donor, at chain-II) to the two hydrogen atoms (hydrogen bond acceptors, at chain-III). (d) Salt bridge interaction at the C-terminus between 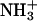on the ^IIK₁₈ side chain and COO⁻ on the ^IIIF₁₉ C-terminus. The distance shown here is averaged over the six possible from H to O distances. (e) π-π-Interaction occurring at the F₁₉ between chains-II and -III. The C_γ-C_γ distance is used to present the π-π-interaction.

In general, the charged residues (Lys, Asp, and Phe₁₉) and N-/C-terminal residues (Asp and Phe₁₉) were more flexible than the remaining residues in the DFNKF trimer simulation. Here, the C-terminal residue Phe₁₉ is regarded as a charged residue since it carries a charge due to its C-terminal position. These observations might be due to two reasons: 1), The charged residues, Asp, Lys, and Phe₁₉ are more soluble. Thus, they also have favorable interactions with water. When they are solvated by water molecules, the residue-wise interactions are screened and might lead to larger separations. 2), The D₁₅-D₁₅ and F₁₉-F₁₉ interactions are easier to break since the N- and C-termini residues are easily attacked by water molecules (Zhou et al., 2001). The intrinsic instability of N- and C-termini residue pairs in the β-strands as well as the charged ^IK₁₈-^IIK₁₈ pair may provide hints for rational drug design. Target molecules that promote the solubility of N-/C-terminal residues might decompose the cross-β-amyloid fibril more easily.

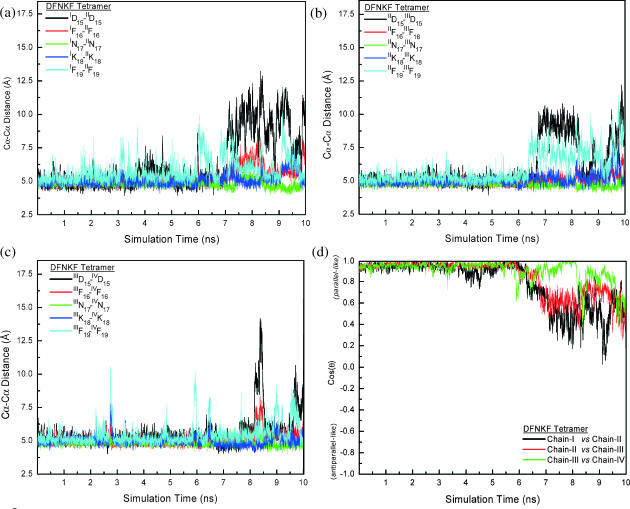
DFNKF tetramer dynamics profile

The residue-wise distances and cos(θ) between the chains of the DFNKF tetramer are shown in Fig. 9. To facilitate a comparison, the same scale is used as in Fig. 6 (DFNKF trimer). It is clear that the DFNKF tetramer has a smaller fluctuation as compared to the DFNKF trimer. Until t ∼ 6 ns, the entire DFNKF tetramer structure is maintained in its parallel in-register packing. After t ∼ 6 ns, the ^ID₁₅-^IID₁₅, ^IID₁₅-^IIID₁₅, ^IF₁₉-^IIF₁₉, and ^IIF₁₉-^IIIF₁₉ distances start fluctuating with larger magnitudes. Nevertheless, the association between chain-III and chain-IV was almost maintained in their parallel in-register packing during the entire simulation. Even though both chains-I and -IV are located at the edges of β-sheet, their stabilities are different. The initial structure is not a perfect symmetry, resulting in uneven interactions of chains-I and -II. Similar results are also observed for trimer simulation. In contrast to the dimer and trimer simulations, the Lys residues in the tetramer were less flexible. However, the limited simulations do not allow us to assess whether Asn and Phe₁₆ dominate the stability. Further simulations and mutant experiments in vitro are needed.

FIGURE 9.

Structural characteristics (pairwise residue C_α-C_α distances and cross angle between chains) of the DFNKF tetramer. (a) The pairwise residue C_α-C_α distances between chain-I and chain-II. (b) The pairwise residue C_α-C_α distances between chain-II and chain-III. (c) The pairwise residue C_α-C_α distances between chain-III and chain-IV. (d) The time dependence of cos(θ), the cross angle between the chains. The definition of cos(θ) is shown in Computational Methods. Only the cross angles between chain-I versus chain-II, chain-II versus chain-III, and chain-III versus chain-IV are shown. For comparison, the same scale is used as in the plots of the DFNKF trimer in Fig. 6. The fluctuations of the DFNKF tetramer are smaller compared to the DFNKF trimer results in Fig. 6. The structural characteristics of chain-III versus chain-IV are nearly in-register and parallel during the whole simulation. The Asp at the N-terminal and Phe residues at the C-terminal are relatively more flexible than other residues, similar to the observations in the dimer and trimer simulations.

Effects of sequence variation on the stability of DFNKF tetramers

Previous studies (our unpublished results) have pointed out that side-chain interactions play significant roles in stabilizing the parallel DFNKF oligomers. These include i), salt bridge interactions between the Lys and the C-terminus and between the Asp and the N-terminus; ii), side-chain hydrogen bonds between Asn and its adjacent strands; and iii), π-stacking between aromatic Phe residues. The effects of these interactions on the stability of nine-stranded DFNKF systems were examined by mutant studies in previous studies (our unpublished results). Here, we examined the effects of these interactions on the stability of the smaller DFNKF tetramers, with longer timescale MD simulations (10 ns). In addition to the mutant studies of the DFNKF tetramers, capping studies were used to mimic as much as possible the properties of the DFNKF tetramers when the peptides are part of the longer calcitonin sequence and at the same time to screen the salt bridge interactions of the chain termini. For the capping studies, the DFNKF tetramer was capped with a normal Nme and Ace, resulting in a blocked peptide sequence Ace-DFNKF-Nme, where Ace is acetylate and Nme is N-methylamide. In addition, three mutants, DFAKF (designed to probe the role of Asn side-chain hydrogen bond), DANKF (to examine the role of Phe₁₆), and DFNKA (to examine the role of Phe₁₉), were also studied. Each mutant was studied as a tetramer.

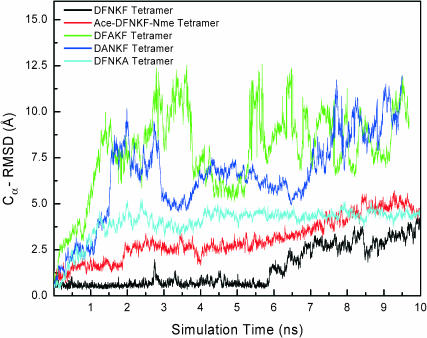
Fig. 10 shows the C_α-RMSD of these DFNKF mutants from their corresponding energy minimized structures with parallel organization. The results for the DFNKF are also plotted in Fig. 10 for comparison. It is clear that the C_α-RMSDs of all DFNKF mutants as well as the Ace-DFNKF-Nme are larger than the original DFNKF tetramer, indicating that the side-chain interactions we noted above are important and affect the stabilities of the parallel DFNKF oligomers. When the Asn was mutated to Ala, it lost its integrity quickly as evidenced by the remarkably large C_α-RMSD. The Asn side-chain–side-chain hydrogen bonds (discussed in the dynamics analysis above), even though easily broken, are also easy to reform, and may play an important role in maintaining the parallel DFNKF integrity. Similarly, previous studies also indicated that the glutamines can form a side-chain hydrogen bond network along the fibril axis to stabilize the parallel packing (Bevivino and Loll, 2001).

FIGURE 10.

The C_α-RMSD of four DFNKF sequence variants and original DFNKF tetramer as a function of time. The four sequence variants included one capped variant, Ace-DFNKF-Nme tetramer, and three mutants, DFAKF, DANKF, and DFNKA tetramers. The initial structures for all calculations were in the parallel arrangements. The C_α-RMSDs were calculated from the corresponding energy minimized structures in parallel manners. The C_α-RMSD of the original DFNKF tetramer is also plotted for comparison. The C_α-RMSDs are the indicators of the relative stabilities of the DFNKF sequence variants from the original DFNKF. The Ace-DFNKF-Nme and DFNKA tetramers are slightly less stable than the original DFNKF tetramer. Comparing the C_α-RMSDs of the DFAKF and DANKF with the original DFNKF indicated that these mutants are relatively unstable.

For the DANKF and DFNKA simulations, the C_α-RMSDs of DFNKA tetramers are slightly larger than the original DFNKF tetramer, indicating that this mutant might be only slightly unstable as compared to the original DFNKF tetramer. In contrast, the C_α-RMSD of the DANKF tetramers is much higher than the wild-type DFNKF tetramer. The parallel integrity of the DANKF tetramers is quickly lost in the simulations. The role of salt bridge interactions are studied by blocking the termini using Ace and Nme. Here, the stronger salt bridge interactions are screened and are replaced by weaker hydrogen bonds. The C_α-RMSDs of Ace-DFNKF-Nme tetramers are also larger than in the original DFNKF tetramer, indicating that salt bridges do affect the stability of the DFNKF amyloid and showing that the simulations for such a short peptide may make deduction for the full length hCT. Thus, the parallel DFNKF tetramer is stabilized by these two salt bridge interactions. To conclude, the DFNKF salt bridges, side-chain–side-chain hydrogen bonds, and π-stacking do contribute to keep the parallel arrangement of the DFNKF oligomers. In particular, the Asn side chain–side chain hydrogen bond plays a significant role in preserving the parallel integrity of DFNKF oligomers. These mutations, which remove specific salt bridges, hydrogen bonds, or hydrophobic interactions, may inhibit the formation of amyloid fibrils.

CONCLUSIONS AND FUTURE WORK

Increasing evidence indicates that small amyloid oligomers may cause the neurotoxicity (Hardy and Selkoe, 2002; Kayed et al., 2003). These observations suggest that it is essential to study the stability and dynamics of small amyloid oligomers in detail. In this study, we have explored the stabilities and dynamics of the DFNKF oligomers, which are amyloid-forming peptides derived from the human calcitonin peptide. DFNKF oligomers with parallel arrangement were found to become more stable as the number of strands increases. The DFNKF trimer and tetramer are stable in the parallel arrangement for a sufficient time in the MD simulations, indicating that the size of the crucial nucleus seed for the DFNKF amyloid formation can be quite small. This may explain the rapid formation of the DFNKF amyloid fibrils in experiment, which to date apparently has not been observed for other amyloid peptides. The simulation results also show that the β-strand acts as a β-sheet template in prompting other conformers to register in parallel. The process of registration is noncooperative. In general, residues near the N-/C-termini are found to be more flexible, whereas interior residues are relatively more stable. The sequence variant studies indicate that the side chain–side chain interactions including salt bridges, hydrogen bonds, and hydrophobic interactions in the parallel DFNKF oligomers are very important. In particular, the Asn side-chain hydrogen bond was found to be crucial in stabilizing the parallel DFNKF structure.

Here, we employ conventional MD to study small DFNKF oligomers. Although it provides significant insights into the oligomers' stabilities and dynamics, due to the limitations of current computer power and simulation methods, the mechanism of amyloid fibril formation cannot be explored in detail. In an attempt to better address the conformational sampling problem, our group is currently employing a more powerful sampling method, the replica-exchange molecular dynamics (Gnanakaran and Garcia, 2003; Sugita and Okamoto, 2000), to more completely sample the conformational energy surface of the DFNKF oligomers. This should provide more detailed information of the DFNKF aggregation mechanism and energy landscape.