Molecular Dynamics Simulations of the Lipid Bilayer Edge

Abstract

Phospholipid bilayers have been intensively studied by molecular dynamics (MD) simulation in recent years. The properties of bilayer edges are important in determining the structure and stability of pores formed in vesicles and biomembranes. In this work, we use molecular dynamics simulation to investigate the structure, dynamics, and line tension of the edges of bilayer ribbons composed of pure dimyristoylphosphatidylcholine (DMPC) or palmitoyl-oleoylphosphatidylethanolamine (POPE). As expected, we observe a significant reorganization of lipids at and near the edges. The treatment of electrostatic effects is shown to have a qualitative impact on the structure and stability of the edge, and significant differences are observed in the dynamics and structure of edges formed by DMPC and palmitoyl-oleoylphosphatidylethanolamine. From the pressure anisotropy in the simulation box, we calculate a line tension of ∼10–30 pN for the DMPC edge, in qualitative agreement with experimental estimates for similar lipids.

INTRODUCTION

Many physical and biochemical properties of lipid bilayers are important to the bilayer's fundamental role as the basis of biological membranes. These properties are now commonly investigated by atomistic molecular dynamics (MD) simulation (for general reviews of atomistic simulation of lipid bilayers, see Scott, 2002; Saiz and Klein, 2002; Feller, 2000; Forrest and Sansom, 2000; Tieleman et al., 1997; Tobias et al., 1997). Some of these properties include elastic moduli for bending and stretching (Ayton et al., 2002; Marrink and Mark, 2001; Lindahl and Edholm, 2000), diffusion constants (Moore et al., 2001; Lindahl and Edholm, 2001), electrostatic and dielectric properties (Stern and Feller, 2003; Pandit and Berkowitz, 2002), intrinsic permeability to ions and small molecules (Wilson and Pohorille, 1996; Bassolino-Klimas et al., 1995; Marrink and Berendsen, 1994), influence on solvating water (Aman et al., 2003; Rog et al., 2002), mechanisms of fusion (Ohta-Iino et al., 2001; Tieleman and Bentz, 2002; Marrink and Tieleman, 2002), and influences on membrane-associated macromolecules (Bond and Sansom, 2003; Colombo et al., 2003; Im and Roux, 2002; Capener and Sansom, 2002; Grossfield and Woolf, 2002; Gullingsrud et al., 2001; Bachar and Becker, 2000). Simulation has been useful for providing detailed insight into how complex molecular interactions lead to experimentally observable behavior.

Free edges are infrequently observed in bilayer or membrane systems. At equilibrium, edges will typically be eliminated from bilayer systems either through the assembly of extended lamellar sheets or of closed-shell vesicle structures. Nonetheless, several motivations exist for studying the bilayer edge. Edge defects are formed transiently by mechanical or electrical impulses (e.g., osmotic stress or electroporation) as a means of introducing DNA or other material into living cells. Spontaneously formed pore edges have been proposed to play roles in bilayer fusion (Noguchi and Takasu, 2001; Müller et al., 2002) and transleaflet “flip-flop” lipid diffusion (Raphael et al., 2001). Edges are presumably present during the initial stages of lipid assembly into lamellar or vesicle structures (Leng et al., 2002). The typical instability of the edge can be characterized by a positive free energy per unit length (or line tension) that experiment and theory place on the order of 10⁻¹¹ N. Early experiments relied on indirect measurements such as vesicle leakage rates (Taupin et al., 1975), the shapes of open-ended bilayer tubes (Harbich and Helfrich, 1979), or the voltage-dependent rate of electroporation (Chernomordik et al., 1985) to calculate the line tension. With the achievement of video imaging of giant vesicles (Menger and Angelova, 1998; Sandre et al., 1999), line tensions have been measured somewhat more directly through aspiration of pore-containing vesicles into a pipette (in which case the dynamics of the vesicle could be related to the dynamics of water efflux through the pore) (Zhelev and Needham, 1993; Moroz and Nelson, 1997) and through the direct observation of pore resealing dynamics (Karatekin et al., 2003). The edge can be stabilized by the addition of a variety of “edge-active agents” (Fromherz et al., 1986) that can reduce or eliminate the line tension, as observed experimentally, e.g., in the formation of stable bicelle disks used in macromolecular NMR (Glover et al., 2001) and in the formation of stable channels by some ceramides (Siskind and Colombini, 2000).

From early accounts (Litster, 1975) onward, the microscopic structure of the edge has been envisioned as a rounded, hemicylindrical rim of hydrophilic headgroups that protects the hydrophobic bilayer interior from contact with water. In the absence of experimental methods for the study of such a transient structure, few attempts have been made to add more detail to this picture. Computer simulations of pore formation in a lattice-based model of a diblock-copolymer bilayer have been reported (Müller and Schick, 1996), showing that, except for very small pore sizes, the expected reconstructed hydrophilic edge picture was valid and that a line tension could be obtained by relating bilayer surface tension to the pore size for sufficiently large pores. Very small pores, with lifetimes on the order of 15 ns, were observed during atomistic simulation of the self-assembly of the phospholipid dipalmitoylphosphatidylcholine (DPPC) into a bilayer (Marrink et al., 2001); these had the character of point defects rather than one-dimensional edges. The formation of small pores in the bilayer, through mechanical tension or applied electric field, has recently been modeled at the atomistic level (Tieleman et al., 2003) showing that headgroups do line the aqueous interior of the pore. A phenomenological theoretical study (May, 2000) has modeled the edge by treating lipids as incompressible yet elastically deformable objects whose energy depends on chain extension length as well as headgroup packing density curvature. This calculation yielded the line tension of the edge as a function of a lipid shape parameter (in good general agreement with experimental estimates) as well as a description of the optimal shape profile of the membrane rim.

In attempting to model a bilayer edge, one might begin with a bilayer disk structure or a bilayer containing a large pore; in either case, the radius of curvature of the edge in the bilayer plane (or equivalently, the magnitude of the Gaussian curvature of the lipid-water interface, positive for a disk and negative for a pore) depends on the size of the system simulated. In this investigation, we have chosen instead to simulate a system with zero mean curvature along the direction of the edge, a continuous bilayer ribbon, or rather a 2D array of ribbons in which the ribbon edges continue across periodic boundaries in a unique direction that we will call z. Apart from the avoiding the uncertainty of the dependence of edge properties on curvature (an interesting question, but one requiring a series of simulations), this arrangement facilitates the calculation of the line tension from the anisotropy of pressure in z versus x and y. Lipid bilayer ribbons studied were composed either of dimyristoylphosphatidylcholine (DMPC) or palmitoyl-oleoylphosphatidylethanolamine (POPE).

In these simulations, the migration of headgroups around the DMPC edge to form a rounded, reconstructed structure appears complete within 2 ns, whereas for POPE the process is significantly slower and continued throughout a 14-ns simulation. Edge structure and line tension are significantly influenced by long-ranged electrostatic forces. The line tensions calculated for DMPC ribbons simulated using the particle mesh Ewald (PME) algorithm (Darden et al., 1993; Essmann et al., 1995) ranged between 12 and 35 pN (within qualitative agreement with experimental estimates for several lipids) but rose by an order of magnitude when an electrostatic truncation method was used. The edge profile of the DMPC ribbon in the simulation displayed bulges at the edges when electrostatic forces were treated fully but not when truncation was used. The effects of electrostatics and lipid structure differences offer some insight into the general principles governing line tension and edge structure.

METHODS

The molecular dynamics simulations were carried out using GROMACS (version 3.1.3, single precision; Berendsen et al., 1995; Lindahl et al., 2001). Most simulations were performed on a Beowulf-type cluster of dual-processor 1.4-GHz 1600 MP Athlon Linux nodes (Linuxlabs, Atlanta, GA), using either one or six processors; some final calculations were performed using an Intel 3.0-GHz dual processor system (Penguin Computing, San Francisco, CA). The VMD package (Humphrey et al., 1996) was used for visualization and molecular graphics.

The starting configurations were adapted as described below from the fluid phase DMPC and POPE bilayer coordinates made available by the Tieleman group at the University of Calgary at http://moose.bio.ucalgary.ca/Downloads/files/dmpc_npat.pdb and http://moose.bio.ucalgary.ca/Downloads/files/pope.pdb (Tieleman and Berendsen, 1998).

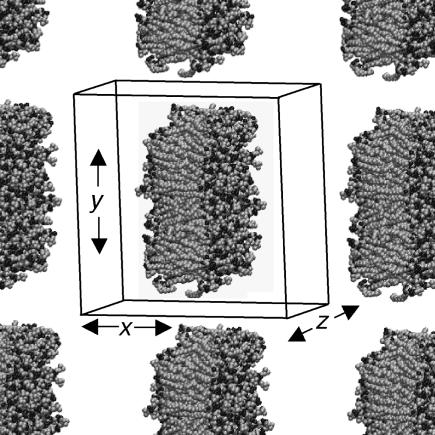
To generate a ribbon-like configuration from the intact DMPC bilayer, we first double the system size by appending its replica in the x direction using the GROMACS genconf utility, yielding a rectangular bilayer patch of 256 lipids with 7310 waters. Lipids whose phosphorus atom coordinates lied in a 3.4-nm band in the y direction were removed, leaving behind a ribbon of 183 lipids with two free edges, separated from its replica by open space. The x and z coordinates of the system were then switched so that the edges would run along the z axis (which will be necessary for proper pressure equilibration in GROMACS). The simulation box dimension in the x direction (now normal to the bilayer) was increased to prevent steric interaction of the ribbon with its replica in case it rotates around the z axis. The empty spaces in the simulation box were filled with water using the genbox utility; a number of waters inserted within the bilayer interior by this utility were then removed. The starting configuration of the DMPC bilayer ribbon in the context of neighboring periodic repeats, with waters omitted, is shown in Fig. 1. The same procedure, with only details changed, was used to prepare all ribbon simulations to run. Details are listed in Table 1.

FIGURE 1.

Starting geometry of 183-DMPC ribbon system. The lipid component of the system, with primary simulation box boundary and partial periodic repeats in the x-y plane, is shown. The bilayer structure is continuous in the z direction.

TABLE 1.

Overview of simulation runs

Run	Box dimensions (x, y, z), nm*	No. of lipids	No. of H2O	Description	Treatment of electrostatic interaction	Simulation time (total)
1	(6.176, 6.176, 6.661)	128 DMPC	3,655	Intact bilayer	PME	5 ns
2	(12.280, 12.280, 6.140)	183 DMPC	24,308	Ribbon	Cutoff	19.5 ns
3	(12.280, 12.280, 6.140)	183 DMPC	24,308	Ribbon	PME	8 ns
4	(6.114, 22.028, 6.176)	256 DMPC	17,702	Ribbon	Cutoff first 0.5 ns then PME	5 ns
5	(8.300, 22.028, 6.176)	256 DMPC	27,299	Ribbon	Cutoff first 0.5 ns then PME	7 ns
6	(12.497, 16.0, 6.141)	183 DMPC	33,213	Ribbon	PME	4 ns
(Lipid configuration from end of run 3)
7	(8.453, 12.694, 9.486)	340 POPE	20,867	Ribbon	Cutoff first 6 ns then PME	14.4 ns

^*Box size is the size of initial configuration. The box sizes in the x and y (and for intact bilayer simulation, z, as well) direction fluctuate by a small amount during the simulation.

Force fields and topologies made available by the Tieleman group at http://moose.bio.ucalgary.ca/Downloads were also used. The DMPC force field uses the DPPC parameters of Berger et al. (1997), with two methylene groups removed from each tail chain. The POPE force field uses these same interactions for the saturated tail united atom methylene and methyl groups, whereas parameters for the cis-double bond and partial charges are derived from the GROMOS force field (van Gunsteren et al., 1996) following Tieleman and Berendsen (1998). The flexible simple point charge (SPC) water potential (Berendsen et al., 1981) was used for solvent.

The integration time step was chosen as 2 fs. All bonds were constrained to a fixed length during position updates via the LINCS algorithm (Hess et al., 1997). The center of mass motion removal was performed every 5000 steps to avoid drifting the system. In this work, we have used two methods for treating electrostatic forces. In some simulations, a dual-stage cutoff or truncation was used, with the first shell at 0.9 nm and the second shell at 1.8 nm; forces between charge sites whose distance falls between the two shells are updated only every 10 time steps. For a complete treatment of electrostatic forces in the periodic system, the particle mesh Ewald method (Darden et al., 1993; Essmann et al., 1995) was used, with a real-space cutoff of 0.9 nm, a maximal spacing of 0.12 nm for the Fourier transform grid, and fourth-order interpolation.

To keep temperature and pressure stable around the room temperature (300 K) and 1 atm, we used the Berendsen coupling algorithm (Berendsen et al., 1984). Temperature scaling of solvent and lipid degrees of freedom were performed independently, both with a time constant of 100 fs. The pressure coupling scheme is dictated by the geometry of the ribbon system. The length of the box along the z axis (parallel to the edge) is fixed, whereas the box dimensions in x and y are scaled jointly; the time constant for scaling is set to 500 fs, with an assumed compressibility of 4.5×10⁻⁵ bar⁻¹. Through this semiisotropic pressure coupling scheme, a positive line tension is supported along the edge while the system's volume is allowed to equilibrate to 1 atm pressure. In analogy to the calculation of surface tension during simulations of interfacial systems (Hill, 1986; Zhang et al., 1995), the line tension Λ is derived from the diagonal elements P_ii of the pressure tensor, which are calculated by GROMACS. The work of extending the system along the z direction by an increment dL_z, while fixing the x and y directions, can be equated to the sum of the work of changing the system's volume and the work of changing the total length of the ribbon edge:

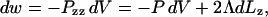(1)

where P is the bulk pressure and P_zz is the diagonal element of the pressure tensor along the edge direction. (The factor of two multiplying the line tension arises from the presence of two edges.) The bulk pressure in this geometry is represented by the pressure perpendicular to the edge, (P_xx + P_yy). As dV/dL_z = L_xL_y, differentiation and rearrangement of Eq. 1 gives the line tension:

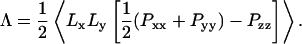(2)

No surface tension term appears in this equation because the area of the bilayer ribbon is not constrained by the box dimensions; the bilayer can therefore be considered to be at zero surface tension.

Simulations of intact bilayers, performed for comparison purposes, use more conventional semiisotropic scaling (with zero applied surface tension) in which the box dimensions parallel to the bilayer plane are jointly coupled to a pressure bath and the normal dimension is coupled separately (i.e., NP_nγT ensemble; Zhang et al., 1995).

During the ribbon simulations, the ribbon can and does drift translationally in x and y and rotate in the x-y plane. To analyze the cross sectional structure of the ribbon independently of these motions, an intraribbon set of coordinates (x′, y′) was defined such that its origin is at the center of mass of the phosphorous atom coordinates, whereas the primary axes of inertia of the structure (defined by the set of phosphorus atoms projected onto a single x-y plane) lie along x′ and y′. In other words, x′ always represents the bilayer normal, whereas y′ represents the direction parallel to the bilayer but normal to the edge.

RESULTS

Migration of headgroups

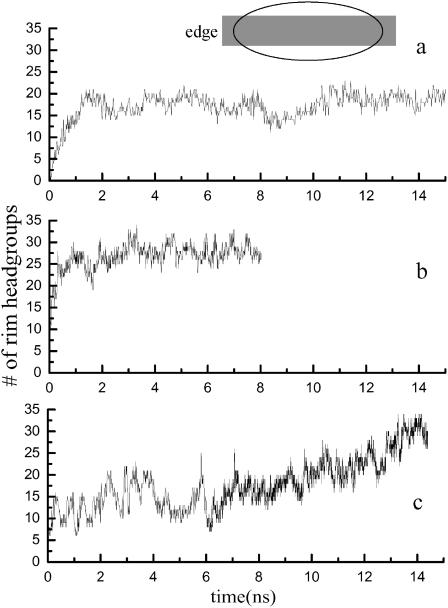
As the initial configuration involves a large area of hydrocarbon tail exposure to water, it is not surprising that the equilibration of the system involves the migration of polar headgroups around the edge to intervene between solvent and the solvophobic bilayer interior, as has been observed in simulations of small pores (Tieleman et al., 2003). Fig. 2 shows the number of headgroup phosphorus atoms in a slice of the edge region, defined in the ribbon internal coordinates as from x′ = −10 Å to 10 Å, as a function of time. A constant number of headgroups in the rim region is a sign that the system has reached at least a metastable state. For DMPC, the number of headgroups in the edge region reaches a roughly constant value within 2 ns, regardless of the method used to treat the electrostatic interactions or the width of the ribbon. However, for POPE, this process is very much slower; equilibrium was apparently not established over the 10-ns duration of the simulation. For this reason, we focus primarily on DMPC in the analysis of our results.

FIGURE 2.

Time course of lipid headgroup migration. Variation in the number of headgroup phosphorus atoms at the bilayer edge, defined as shown in the cartoon as the region from −1.0 nm to 1.0 nm in the x′ direction. (a) Run 2 (from Table 1): DMPC with truncation. (b) Run 3: DMPC with PME. (c) Run 7: POPE.

General morphology of the bilayer edge

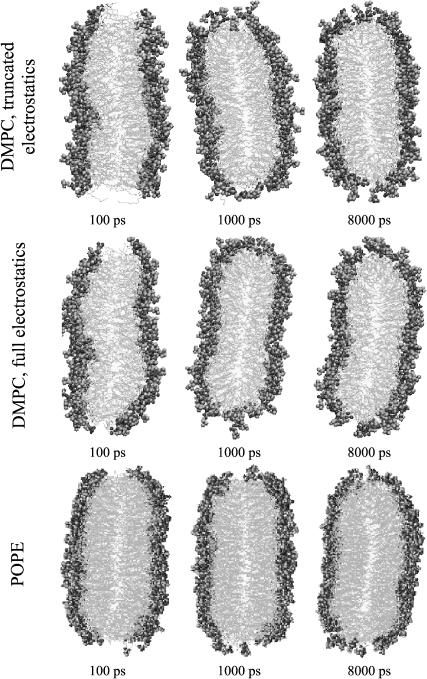
Fig. 3 shows a series of snapshots in the x′-y′ plane (with solvent omitted for clarity) of DMPC ribbons modeled using both electrostatic cutoffs and PME, and of the POPE ribbon. At the early stage of the reorganization of the DMPC edge, we see some of the hydrocarbon tails of edge lipids extending into the solvent, especially in the case of the cutoff simulation. Most of these tail chains returned to the bilayer interior within 500 ps, as more and more headgroups begin to occupy the edge region. After 2 ns, this process seems to reach equilibrium. However, we observe that the packing of lipid headgroups in the edge region is still sparser than in the middle, even after 8 ns.

FIGURE 3.

Evolution of cross-sectional structure of edge: simulation snapshots. (Top) Run 2, (middle) run 3, and (bottom) run 6 from Table 1.

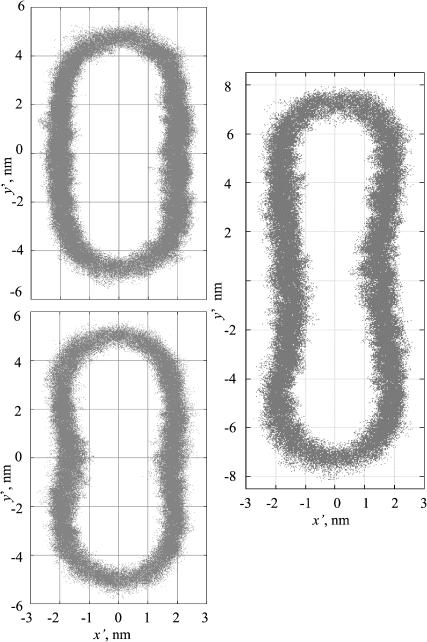
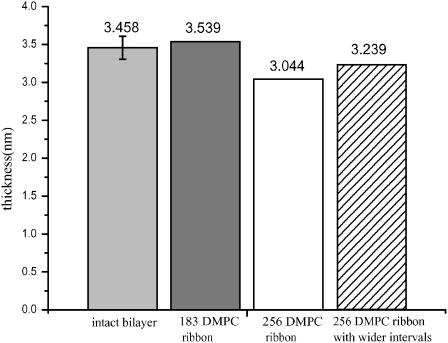
To better visualize the time-averaged cross sectional structure of the ribbon and its edges, we have generated scatter plots of the x′ and y′ coordinates of all lipid headgroups' phosphorus atoms, sampled at 10-ps intervals after the initial 3-ns equilibration of the trajectory (Fig. 4). When truncation is used for the electrostatic interactions, the midsection of the ribbon appears as a flat bilayer, whereas the edge adopts a semielliptical profile. In contrast, when full electrostatics are used via the PME algorithm, a thickening of the bilayer ribbon near the edges (or, conversely, a pinching of the ribbon in the center) becomes apparent. This effect appears also for a wider ribbon (256 DMPC) in which the bulging edges are separated by a wider region of locally almost flat bilayer. In comparing the thickness of these ribbons near their middle (defined as the distance between the peaks in the probability density histogram for the phosphorus atom position in the normal direction, and plotted in Fig. 5) the larger ribbon is clearly thinner in its midsection (and thicker in the bulge near the edge) than an intact DMPC bilayer simulated under equivalent conditions.

FIGURE 4.

Ribbon shape profiles. Scatter plots of phosphorus atom positions generated from entire trajectories (after 3 ns equilibration), indicating the position of the headgroups. (Top left) Run 2, (bottom left) run 3, and (right) run 4.

FIGURE 5.

Mean bilayer thickness in different simulation runs. Thickness is defined as the distance between peaks in the probability distribution of phosphorus sites in the x′ direction (or z direction for the intact bilayer.) From left to right, values are derived from runs 1, 3, 4, and 5.

The area per headgroup at the bilayer edge is not easy to define, as it requires the definition of the surface area of a curved, diffuse interface with no clear demarcation from the bilayer interior. To give a reasonable estimate, we fit the edge regions of these scatter plots to a semiellipse. The position of the center of the ellipse on the y′ axis (y₀′ and −y₀′), as well as the two diameters of the ellipse, are varied to minimize the average mean-square radial distance of the position of the lipid phosphorus site to the elliptical function. The area per headgroup is then defined as the perimeter of the ellipse, multiplied by the z dimension of the box to give an edge surface area, divided by the number of P atoms with |y′| > y₀′. For the flat interior sections of the bilayer ribbon and for intact bilayers, the area per headgroup is defined in the normal way. From Table 2, it is evident that the use of full electrostatics generally increases the area per headgroup (as found previously, e.g., by Patra et al., 2003) and that headgroups at the edge have roughly 50% greater area to occupy.

TABLE 2.

Area per lipid of DMPC from different system and different part of ribbon

		DMPC: area per lipid (Å2)
System		Truncation	PME
Intact bilayer	(128DMPC)	58.9	60.4
Ribbon center	(183 DMPC)	61.2	66.0 (run 3)
			66.1 (run 6)
	(256 DMPC)	68.9	70.3 (run 4)
			67.7 (run 5)
Ribbon edge	(183 DMPC)	99.4	100.7 (run 3)
			95.5 (run 6)
	(256 DMPC)	108.8	103.6 (run 4)
			97.5 (run 5)

Tail conformational statistics

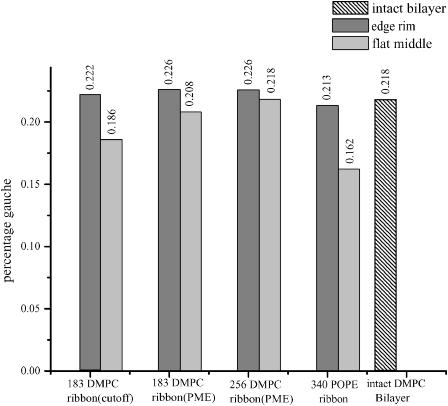
As any order parameter defined relative to the bilayer normal is not particularly appropriate for describing structure at a rounded edge, we concentrate on an internal measure, the fraction of gauche dihedral angles (defined here to be between 40° and 90°) along the saturated hydrocarbon tails, to attempt to quantify the edge's influence on tailgroup packing. As shown in Fig. 6, in DMPC simulations performed using truncation, gauche defects are 20% more common at the edges of the ribbon than in its midsection, but in the more experimentally relevant simulation using the PME method the effect measured in two different simulations was an increase between 3% and 10%. For POPE, the fraction of kinks in the saturated tails was higher by 30% at the ribbon edge than in the midsection; this may be a consequence of incomplete equilibration, however, as a high gauche percentage was also observed during the initial equilibration period of the DMPC ribbon (data not shown.)

FIGURE 6.

Percentage of gauche dihedral angles in lipid tails. All torsional angles around single bonds in lipid tails are counted.

Line tension

The line tensions of the ribbon edges, obtained using Eq. 1 from the average pressure anisotropy in the system, are presented in Table 3 along with some experimental values obtained for various lipid bilayer systems. The determination of the line tension with high precision is difficult. The pressure fluctuations in a finite condensed phase system are very large (on the order of 100 atm) but very rapid, yielding a precision of roughly ±30% based on the block averaging method (Allen and Tildesley, 1987) for runs of several nanoseconds. However, these large, rapid fluctuations may obscure smaller, slower fluctuations whose contributions to the line tension would not then be included in the error bars. In particular, a slow but noticeable decrease in the average line tension was observed over the course of the POPE simulation, consistent with the ongoing reconstruction that would be expected to stabilize the edge. The most striking result is that the effect of electrostatic truncation on the calculated line tension is enormous, giving results an order of magnitude above those obtained using the PME algorithm. The influences of box size and ribbon width on measured DMPC line tensions are less clear. Increasing the closest approach between bilayer periodic image edges from ∼2.2 nm (run 3) to ∼6 nm (run 6) gave a 30% reduction in line tension, which may or may not be statistically significant. In runs 4 and 5 with a wider ribbon, increasing the spacing between ribbons normal to the bilayer from ∼2 nm to ∼4 nm yielded a reduction in line tension by a factor of 3.

TABLE 3.

Lipid bilayer line tension: comparison of computational and experimental results

System	Line tension (pN)	Reference	Methods
183 DMPC ribbon (run 3)	24 ± 7	This work	Molecular dynamics
256 DMPC ribbon (run 4)	35 ± 10		simulation
256 DMPC ribbon (run 5)	12 ± 9
183 DMCP ribbon (run 6)	17 ± 6
340 POPE ribbon (run 7)	57 ± 10
183 DMPC ribbon (run 2) (truncated electrostatics)	410 ± 40
DOPC	6.9 ± 0.4	Karatekin et al. (2003)	Vesicle pore closure
DOPC (different commercial source of material)	20.7 ± 3.5		dynamics
SOPC	9.2 ± 0.7	Zhelev and Needham (1993)	Micropipette aspiration
SOPC with 50 mol % cholesterol	30.5 ± 1.2
SOPC with 50 mol % cholesterol	26	Moroz and Nelson (1996)	Reinterpretation of results of Zhelev and Needham
DOPC	25	Genco et al. (1993)	Electroporation
DPsPC	30
DLPC/DPsPC mixtures	21–28
Egg lecithin	21
Egg lecithin	42	Fromherz et al. (1986)	Vesicle size distributions
Egg lecithin	8.6 ± 0.4	Chernomordik et al. (1985)	Electroporation
Escherichia coli PE	16 ± 0.6
Egg lecithin	20	Harbich and Helfrich (1979)	Observation of open
			cylindrical vesicles
DPPC	6.5	Taupin et al. (1975)	Vesicle response to osmotic stress

Equilibrium dynamics

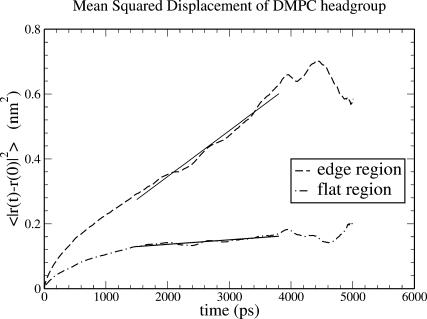
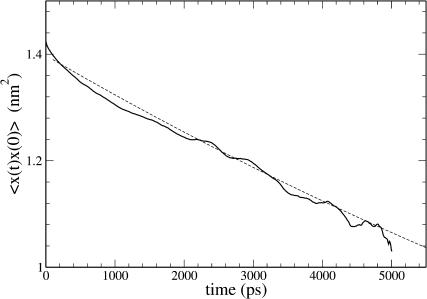
The mean-square displacement of lipid headgroups (measured at the position of the phosphorus atom) in the interior bilayer section of the ribbon is compared to that at the edge in Fig. 7. In each case, displacement of the headgroup phosphorus atom in one of the bilayer internal coordinates is graphed; for the interior flat part of the ribbon, motion in the y′ dimension across the ribbon, and for the edge, motion in the x′ dimension normal to the bilayer plane. The diffusion constant derived from the limiting slope of the mean-square displacement at the edge (7.1×10⁻⁷ cm² s⁻¹) is 10-fold higher than that obtained in the normal bilayer environment (7.0×10⁻⁸ cm² s⁻¹, in reasonable agreement with simulation results by Moore et al., 2001). These are not strictly appropriate quantities to compare; flip-flop motion at the edge is on a curved surface and is bounded by the bilayer thickness, whereas diffusion parallel to the edge within the bilayer is on a flat surface and unbounded; but nonetheless the result suggests a significant enhancement in the rate of motion across the surface for lipids at the edge. Another measure of dynamics at the edge is from a positional correlation function, 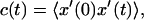evaluated for lipids at the edge as shown in Fig. 8. Since x′ changes sign from one leaflet to the other, this function will decay to 0 as lipids lose correlation with their original leaflet through random flip-flop events. From fitting the initial slope of c(t) to an exponential decay, we estimate a correlation time of 18 ns for headgroup angular fluctuations around the bilayer edge.

FIGURE 7.

Effect of environment on mean-square displacement (MSD) of the DMPC headgroup phosphorus site. (Dashed curve) MSD in the x′ (transleaflet) direction of lipids at the edge. (Dot-dash curve) MSD in the y′ direction (perpendicular to the edge) for lipids in the flat center of the ribbon. Solid curves are linear least-square fits over the time range 1.5–3.8 ns. Diffusion constants D are derived from the slopes of these fits through the Einstein formula for one-dimensional diffusion, 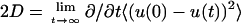where u = x′ or y′. Data obtained from simulation run 3.

FIGURE 8.

Time correlation function of the headgroup flip-flop coordinate. For lipid phosphorus atoms in the DMPC edge region, the time correlation function where x′ is the displacement from the bilayer center plane. The solid curve shows simulation data; the dashed curve shows fit to simple exponential decay, with a time constant of 18.4 ns.

DISCUSSION

Influence of electrostatics treatment on DMPC edge properties

The truncation of Coulomb interactions has been identified as a source of artifacts in biomolecular simulation in general and in lipid bilayer simulation in particular (Tu et al., 1996; Patra et al., 2003). In this study, a comparison of results obtained using truncation with those obtained using a superior, infinite-range method (particle mesh Ewald summation) illuminates some of the forces that determine the stability and structure of the bilayer edge.

The most dramatic result pertains to the line tension, or free energy per unit length of the edge, which is an order of magnitude greater when truncation is used (Table 3). Qualitatively, this most likely reflects the partial destabilization of the planar bilayer arising from long-ranged repulsions between headgroups, whose average net polarization is normal to the bilayer plane. These repulsions will be important at distances comparable to the thickness of the bilayer, but will be effectively canceled out by attractions to the dipoles on the opposite leaflet at distances much larger than the bilayer thickness. The breaking of the bilayer and the curvature of the interface at the rim partially relieve this repulsive energy.

To further investigate the effect of electrostatics treatment on line tension, we have performed four short (50 ps) simulations using PME or cutoffs on lipid ribbon starting configurations equilibrated with either method. This duration of simulation is long enough to obtain an order-of-magnitude estimate of the line tension but short enough that the initial structure is largely unaltered. The choice of electrostatics treatment used during the short simulation had a much greater effect than did the starting structure. (Simulations using PME gave line tensions of 5 and 2 × 10⁻¹¹ N, whereas simulations using cutoffs gave line tensions of 3 and 4 × 10⁻¹⁰ N for starting structures obtained from PME and cutoff simulations respectively.) From this we can conclude that the predominant effect of electrostatics treatment on line tension is direct, consistent with the dipolar repulsion model described above. Structural differences between model bilayers equilibrated with PME and cutoffs may be a secondary influence on line tension.

Another important effect of electrostatics treatment is the appearance of a slight thickening or bulging in the cross sectional profile of the edge when full electrostatics were used. Why might this be the case? The edge by geometric necessity has a higher area per headgroup than the flat bilayer (by a factor of two, assuming a hemicylindrical edge with a radius half the bilayer thickness, and constant lipid volume; in these simulations, by a factor of 1.6), meaning that the exposure to solvent of the hydrophobic tails is greater at the edge. Bulging or thickening at the edge lowers the area per headgroup by increasing the radius of curvature, at the expense of increasing the number of lipids in the perturbed edge environment. As we have already suggested, long-ranged dipolar repulsions lower the cost of breaking the planarity of the bilayer, so this distortion may be facilitated by extended electrostatic interactions. Furthermore, the area per headgroup is already higher (and the bilayer is thinner) when PME is employed, so the increase in exposed hydrophobic surface at the edge that drives the thickening is also somewhat greater. If our arguments based simply on long-ranged dipolar repulsions are correct, the addition of these interactions into a phenomenological model like that of May (2000) should yield a bulging edge instead of the entirely convex cross section that was observed with only local interactions included.

System size scaling

The observed effects of increasing the ribbon width on the edge structure are difficult to interpret. We assume that in the limit of a very broad ribbon the middle bilayer region would have properties of an unperturbed continuous bilayer. In this simulation, the middle bilayer region is thinner than in a continuous bilayer simulated with periodic boundary conditions and semiisotropic pressure scaling with no surface tension applied, and becomes even thinner when the width of the ribbon is increased by 40% (from 183 DMPC to 256 DMPC, at a constant ribbon length). A further complicating observation is that in a separate simulation with 256 DMPC, in which the spacing between ribbons was increased, the thickness increased somewhat.

We have considered several possible explanations. One is that this thinning is a real effect that would appear in a much wider ribbon, and that the bilayer only gradually reaches an unperturbed thickness several nanometers away from the edge. Another is that the difference in thickness is a nonequilibrium effect or random fluctuation that is slow to relax on the simulation timescale (Marrink and Mark, 2001), and that our calculated value is not converged. Finally, this result may arise from boundary conditions; as has been proposed by Feller and Pastor (1996) but not conclusively corroborated by further studies (Lindahl and Edholm, 2000; Marrink and Mark, 2001), the constraint that the bilayer be continuous across periodic boundaries in two dimensions might place the unperturbed intact bilayer under some effective lateral pressure, in which case the center of the ribbon (which is only subject to this constraint in the z dimension) may more closely reflect a tension-free bilayer than does the intact bilayer with full periodic boundary conditions.

Flip-flop dynamics

Transleaflet or flip-flop motion is typically considered to be an exceedingly slow process (Kornberg and McConnell, 1971) with a timescale on the order of seconds or more, as it requires the disruption of the bilayer structure and removal of the polar headgroup from the water interface. At the DMPC edge, simulation results show (Fig. 7) that translation in the flip-flop direction is significantly more rapid than is lateral diffusion in an intact bilayer; this may be the result of the lower headgroup packing density at the edge (Table 2). It is tempting to assign a leaflet residence timescale for lipids at the edge by assuming a simple exponential decay in the correlation of the position with respect to the bilayer normal (Fig. 8). This may not be a valid assumption; the initial decay in the correlation function of Fig. 8 may simply reflect local fluctuations in the headgroup position, whereas actual flip-flop motion may occur at a slower timescale due to tail entanglements or other effects. In fact, over the course of 5 ns simulation (after allowing 3 ns for initial edge reconstruction and equilibration), we observe that many lipids at the edge made significant excursions toward and away from the center line of the bilayer, but only one of ∼70 edge lipids completed a clear flip-flop from one leaflet to the other, significantly fewer than an 18-ns flip-flop time would predict.

Nevertheless, even a single flip-flop event in 5 ns represents an enormous acceleration of the flip-flop rate observed experimentally in intact, unstressed bilayers. The implication for the role of pores or edges in flip-flop dynamics is that in the presence of an edge, the experimentally observed bulk flip-flop rate will probably be limited by the rate at which lipids diffuse toward and away from the edge in DMPC and not by the actual flip-flop process at the edge. It is not surprising that the presence of an edge should greatly increase the rate of transleaflet motion; the influence of pores on flip-flop behavior in bilayers under tension has been investigated with this idea in mind (Raphael et al., 2001).

Effects of lipid structure: comparison of DMPC with POPE

The timescale of edge reconstruction in POPE (as shown in Fig. 2) is at least several times longer than for DMPC. Although the substitution of phosphatidylethanolamine for phosphatidylcholine in lipid headgroups has been shown experimentally to give to a modest decrease in probe molecule diffusion constants (Ladha et al., 1996), as have substituting longer tail tail-chains (Müller and Galla, 1987) and introducing cis-double bonds (Vaz et al., 1985), the combined effects of these substitutions would not be expected to give a 10-fold decrease in lateral diffusion constant at equilibrium. The most probable explanation for the pronounced difference in this study is that reconstruction of the edge (unlike lateral diffusion) involves a net increase in the spacing between headgroups, requiring a greater activation energy for the migration of PE headgroups (which allow hydrogen bonding between the hydrogens of the primary amine and the phosphate oxygens) than for PC headgroups.

The line tension calculated for POPE is significantly greater than that obtained for DMPC. Although we do not place too much weight on the former value, as it was calculated during an incompletely equilibrated trajectory, the disruption of close PE headgroup associations would indeed be expected to further reduce the stability of the free edge.

Line tension: comparison with experiment and general discussion

As long as a full treatment of electrostatic effects is used, the line tension values obtained from simulation are reasonable in comparison to the experimental values listed in Table 3, which were determined by a range of methods for several different lipid systems. The prediction of line tension by this simulation method for the molecular dynamics run durations used in this study is not as precise as one might desire; the error bars reflecting statistical uncertainty due to the system's rapid pressure fluctuations are rather large. The discrepancies among the four DMPC runs (3–6 in Table 1), of different ribbon widths and interribbon spacings, do not admit a consensus value for the line tension. Whether these discrepancies arise from finite size effects or from random fluctuations that are slow to relax on the simulation lengthscale (and so are not represented in the statistical uncertainty ranges) is unclear. Comparisons of runs 2 and 4 with runs 6 and 5 suggest a trend in which increasing the amount of solvent surrounding the ribbon decreases the calculated line tension. Such a trend would be expected to result from repulsions between the ribbon and its periodic images, which would artificially inflate the line tension at small interribbon distances by increasing P_xx and P_yy in Eq. 2.

SUMMARY AND CONCLUSIONS

We have studied the behavior of lipids at the bilayer edge through simulations in a ribbon geometry. We observe that a significant reorganization of the DMPC edge, migration of polar headgroups to form a roughly hemicylindrical cap, occurs within 2 ns. However, this process is much slower in a POPE ribbon, perhaps as a result of the stronger associations between phosphatidylethanolamine headgroups. A thickening or bulging of the bilayer near the DMPC edge is observed when long-ranged electrostatic forces are included in the calculation, but not when Coulomb forces are truncated. The edge microenvironment leads to a 50% increase in area per lipid headgroup and a roughly order-of-magnitude increase in headgroup mobility for DMPC, but a much smaller increase in the percentage of gauche defects in the lipid tails. Flip-flop motion at the edge is greatly enhanced compared to its experimentally determined rate in the intact bilayer, occurring on a timescale of ∼18 ns rather than seconds or more. The line tensions (i.e., reversible work of formation of an edge) calculated from these simulations, in the range of 10s of piconewtons, are in reasonable agreement with estimates derived from various experiments, but suffer from large statistical uncertainties and possible finite size effects. Given that experimental methods of determining line tension are generally difficult, indirect, and highly sensitive to the effects of impurities segregating toward the edge and lowering the line tension (Karatekin et al., 2003), we conclude that with improved simulation statistics and further investigation of finite size effects, atomistic simulation will be a useful tool to predict and interpret the relationship between lipid molecular structure and this fundamental material property of bilayers and membranes.