Abstract
This article presents a general statistical mechanical approach to describe self-folding together with the hybridization between a pair of finite length DNA or RNA molecules. The model takes into account the entire ensemble of single- and double-stranded species in solution and their mole fractions at different temperatures. The folding and hybridization models deal with matched pairs, mismatches, symmetric and asymmetric interior loops, bulges, and single-base stacking that might exist at duplex ends or at the ends of helices. All possible conformations of the single- and double-stranded species are explored. Only intermolecular basepairs are considered in duplexes at this stage.
In particular we focus on the role of stacking between neighboring nucleotide residues of single unfolded strands as an important source of enthalpy change on helix formation which has not been modeled computationally thus far. Changes in the states of the single strands with temperature are shown to lead to a larger heat effect at higher temperature. An important consequence of this is that predictions of enthalpies, which are based on databases of nearest-neighbor energy parameters determined for molecules or duplexes with lower melting temperatures compared with the melting temperatures of the oligos for which they are used as a predictive tool, will be underestimated.
INTRODUCTION
Now that the Human Genome Project has provided us with a catalog of tens of thousands of genes in a variety of organisms, an important problem is to develop appropriate tools to understand and use this information. In particular, biological processes such as DNA replication, transcription, translation, mutation, and repair are of great importance. These processes form the basis of recently developed biological techniques, such as DNA and RNA chip technologies (Seetharaman et al., 2001; Shoemaker et al., 2001), PCR, sequencing by hybridization, and gene diagnostics, including SNP detection. These technologies require accurate prediction of hybridization thermodynamics to matched versus mismatched sites. The statistical thermodynamic theory of DNA/RNA hybridization has been well understood for a number of years (Zimm, 1960; Poland, 1974). However, despite the fact that a half century has passed since the discovery of the structure of the DNA double helix, major questions still remain regarding its thermodynamic behavior and stability. Thus, the parameters that determine the cooperativity of melting have been difficult to measure and also, it has been difficult to test some basic theoretical assumptions such as the justification of the Jacobson-Stockmayer loop-weighting function, the nearest-neighbor model for the interaction between nucleotides, and the role of heat capacity changes, 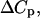 volume changes, ΔV, and compressibility changes,
volume changes, ΔV, and compressibility changes, 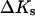 that accompany nucleic acid conformational transitions.
that accompany nucleic acid conformational transitions.
We have observed that in current theoretical treatments of DNA or RNA melting, little attention has been paid to the effects of concentrations of different conformational species in the solution to the overall equilibrium (Applequist and Damle, 1963). It is well known that melting of oligomeric DNA or RNA molecules is typically complicated by coupled equilibria between the different conformational species. Thus, the melting transitions of mono-molecular hairpins would be expected to be concentration independent, whereas double- or multiple-stranded complexes should melt at higher temperatures when strand concentration is increased. Over the past two decades, the structure and the conformational flexibility of several specially designed and synthesized oligonucleotides have been characterized (Breslauer et al., 1975; Albergo et al., 1981; Gralla and Crothers, 1973; Early et al., 1981). The goal of such studies has been to develop an understanding of the molecular forces that control the various sequence and solvent specific conformational forms found within DNA and RNA polymers.
Melting experiments have been the most useful way to measure the stabilities of RNA and DNA structures under different conditions. Thermodynamic parameters are easy to extract from UV absorbance versus temperature curves of simple RNA or DNA secondary structures, duplexes or hairpins, that melt in a single, two-state transition. Comparisons of RNAs and DNAs with different basepairs, loop sequences, bulges, etc. have yielded an extremely useful database from which the stabilities of larger structures can be estimated (Freier et al., 1983; Sugimoto et al., 1987; Hickey and Turner, 1985; Puglisi and Tinoco, 1989; Blake, 1972). The idea behind the experiments on such short model oligomers is that small but specific structural changes, such as loops, bulges, dangling ends, etc., can be detected by changes in the chemical potential.
The estimation of these parameters is based on nearest-neighbor approximations for inter-residue interactions (Borer et al., 1974). The major assumption is that the stability of a basepair is dependent only on the identity of adjacent basepairs because the major interactions involved in transformation between different conformations of the polynucleotide sequence are stacking and hydrogen bonding. Both are short-range interactions. SantaLucia has published a detailed article comparing the nearest-neighbor parameters from seven different laboratories based on data from natural polymers, synthetic polymers, oligonucleotide dumbbells, and oligonucleotide duplexes (SantaLucia, 1998). The analysis shows that the data are in very good agreement.
There have been several major improvements in the calculation of the partition function for a single-stranded species based on the McCaskill algorithm (McCaskill, 1990; Hofacker et al., 1994; Matzura and Wennborg, 1996) or estimation of the free energy based on free energy minimization and the corresponding sub-ensemble around the minimum free energy conformation (Sankoff et al., 1983; Zuker and Sankoff, 1984; Zuker and Stiegler, 1981; Zuker, 1989a; Williams and Tinoco, 1986; Waterman, 1983; Waterman and Byers, 1985; Zuker, 1989b). For more details about current energy rules and free energy minimization, see the article by Zuker et al. (1999). In this work, our primary applications are to relatively small oligonucleotide sequences, which makes appropriate the use of certain simplifications. For dimer formations, we have ignored the possibility of intramolecular basepairs. For single-stranded species, we have used the minimum free energy computed using the “nafold” program in the “mfold” package by Zuker et al. (1999). A new and more robust software package is being prepared to replace the initial development programs used for calculations in this work. This new software uses our own version of partition function calculations for single-stranded species (McCaskill, 1990; Hofacker et al., 1994).
Our primary aim in this article is to develop the statistical mechanical formalism appropriate to hybridization processes between finite length DNA and RNA sequences that takes into account the whole ensemble of single- and double-strand species in solution and the exchange of material between them. In particular, we focus also on the role of stacking between neighboring nucleotide residues of single strands as an important source of enthalpy change on helix formation (Poerschke et al., 1973). Thus, each oligomer has a stacked-unstacked transition that is superimposed upon the helix-coil transition. Therefore we should expect that the measured enthalpy for the helix-single strand transition will be less at low temperatures where the nearest-neighbor nucleotide residues in the single strands are partially stacked than at very high temperatures where the nearest-neighbor nucleotide residues are totally unstacked. Currently, the thermodynamic analysis of hybridization processes is based on Poland's method and its modifications (Poland, 1974; Fixman and Freire, 1977; Poland, 1981). This method can deal only with nearest-neighbor stacking between two strands of RNA or DNA. It can also handle symmetric internal loops caused by strand separation. However, Poland's method does not take into account the terminal mismatch stacking and no intrastrand basepairs are allowed. On the other hand, the folding model that we will develop here deals with matches, mismatches, symmetric and asymmetric interior loops, bulges, and single-base stacking that might exist at the ends. In addition, our model takes into account the whole ensemble of single- and double-stranded species in solution and the exchange of material between them. This leads to a statistical thermodynamic description of both self-folding and hybridization of RNA or DNA sequences. The only drawback is that whereas the time complexity of the Poland algorithm is 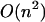 and its improvement based on the Fixman and Freire approximation is O(n), ours is
and its improvement based on the Fixman and Freire approximation is O(n), ours is 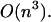 However, when a limitation for loop length is applied, we go from
However, when a limitation for loop length is applied, we go from 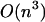 to
to 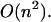 We also have developed a set of computer programs that aid in the analysis of RNA or DNA melting with multiple unfolding transitions. The programs can simulate both UV hyperchromicity and scanning calorimetry melting curves by summing computed pairing probabilities multiplied by measured extinction coefficients and by numerical differentiation of the computed Gibbs free energy, respectively.
We also have developed a set of computer programs that aid in the analysis of RNA or DNA melting with multiple unfolding transitions. The programs can simulate both UV hyperchromicity and scanning calorimetry melting curves by summing computed pairing probabilities multiplied by measured extinction coefficients and by numerical differentiation of the computed Gibbs free energy, respectively.
METHODS
Statistical ensemble of species
An initial mass of 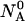 and
and 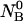 molecules of polynucleotide sequences A and B are added to a physiological solution at a given volume V and temperature T. It is assumed that the solution is sufficiently dilute so that the average distance between the molecules,
molecules of polynucleotide sequences A and B are added to a physiological solution at a given volume V and temperature T. It is assumed that the solution is sufficiently dilute so that the average distance between the molecules, 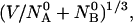 is greater than the intermolecular distance necessary for each molecule to explore all possible conformations without overlapping with other molecules and bigger than the range of forces acting between the molecules. The molecules
is greater than the intermolecular distance necessary for each molecule to explore all possible conformations without overlapping with other molecules and bigger than the range of forces acting between the molecules. The molecules 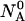 and
and 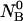 are allowed to form chemical species in terms of hybridizations between all possible pairs; two homo-dimers, AA and BB, and the single hetero-dimer, AB. Based on the above assumptions, the solution can be described as an ensemble of ideally mixed species such as single-folded strands
are allowed to form chemical species in terms of hybridizations between all possible pairs; two homo-dimers, AA and BB, and the single hetero-dimer, AB. Based on the above assumptions, the solution can be described as an ensemble of ideally mixed species such as single-folded strands 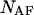 and
and 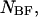 single-unfolded strands
single-unfolded strands 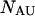 and
and 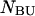 as well as the double-stranded hybridized forms of all possible pair combinations between the polynucleotide sequences
as well as the double-stranded hybridized forms of all possible pair combinations between the polynucleotide sequences 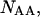
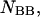 and
and 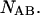 The species are characterized by their corresponding ensembles of possible conformational states. Letting
The species are characterized by their corresponding ensembles of possible conformational states. Letting 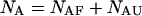 and
and 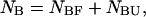 the partition function for such a system at a given temperature T, volume V, and all possible distributions of the initial material
the partition function for such a system at a given temperature T, volume V, and all possible distributions of the initial material 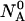 and
and 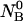 between the corresponding species
between the corresponding species 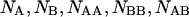 is computed as (Kubo, 1965):
is computed as (Kubo, 1965):
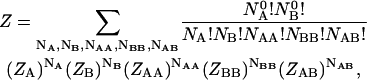 |
(1) |
where the 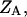
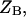
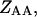
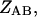 and
and 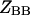 are the partition functions for the corresponding species. The partition functions of the single-stranded species have the forms:
are the partition functions for the corresponding species. The partition functions of the single-stranded species have the forms:
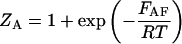 |
(2) |
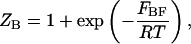 |
(3) |
where 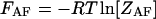 and
and 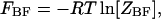 and
and 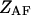 and
and 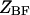 are the partition functions of the corresponding self-folded species AF and BF. The “1” in Eqs. 2 and 3 pertains to the fact that by definition, a folded state must contain at least one basepair, whereas
are the partition functions of the corresponding self-folded species AF and BF. The “1” in Eqs. 2 and 3 pertains to the fact that by definition, a folded state must contain at least one basepair, whereas 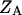 and
and 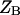 include the unfolded states. The free energies
include the unfolded states. The free energies 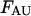 and
and 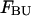 of the unfolded species AU and BU have been set to 0.
of the unfolded species AU and BU have been set to 0.
Taking into account that the free energy of a closed system at constant temperature, volume and pressure tends toward a minimum (Landau and Lifshitz, 1969) the equilibrium distributions of 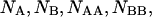 and
and  are determined by the minimization of the free energy under the constraints that
are determined by the minimization of the free energy under the constraints that
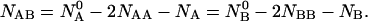 |
(4) |
The minimum of the free energy can be easily determined if we take into account that the sum in Eq. 1 is dominated by its largest term, determined by setting to zero the first variation with respect to the concentrations of the species. As a result we obtain:
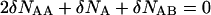 |
(5) |
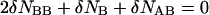 |
(6) |
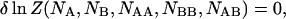 |
(7) |
where
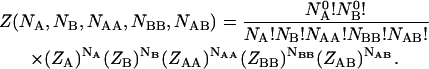 |
(8) |
The above variational equations lead to the following relations that control the exchange of material between the different species:
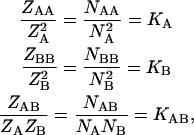 |
(9) |
where 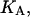
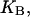 and
and 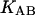 denote the corresponding chemical equilibrium constants.
denote the corresponding chemical equilibrium constants.
These relations lead to the following system of nonlinear equations for the species concentrations:
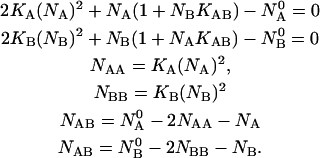 |
(10) |
Given the 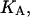
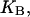
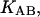
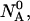 and
and 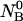 the first two equations can be solved with respect to
the first two equations can be solved with respect to 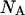 and
and 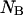 using, for example, Newton's method for solving two nonlinear functions. Replacing
using, for example, Newton's method for solving two nonlinear functions. Replacing 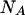 and
and 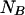 in the rest of the equations,
in the rest of the equations, 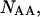
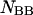 and
and 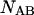 are determined straightforwardly. Finally, taking into account that
are determined straightforwardly. Finally, taking into account that  and
and 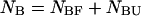 we have:
we have:
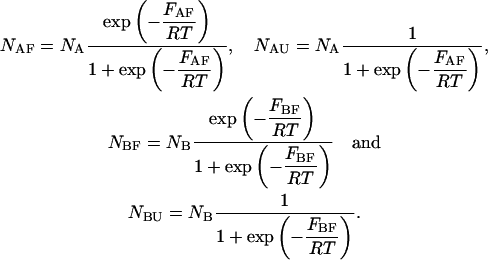 |
(11) |
The chemical potentials of the species can be obtained by differentiating the free energy 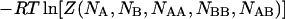 with respect to the concentrations of their corresponding molecules. Thus we have:
with respect to the concentrations of their corresponding molecules. Thus we have:
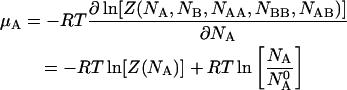 |
(12) |
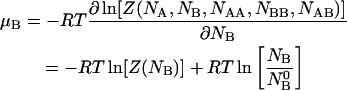 |
(13) |
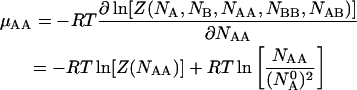 |
(14) |
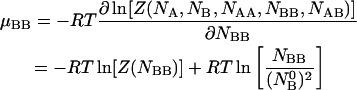 |
(15) |
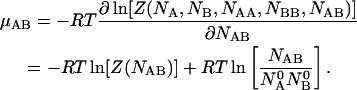 |
(16) |
Finally, the free energy of the whole ensemble of species can be represented in the form (Landau and Lifshitz, 1969):
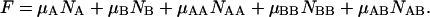 |
(17) |
Extinction coefficients and melting curves
The transition between folded and unfolded structures, as well as the partial forms of their conformational intermediates, can be monitored as a function of the temperature by any physical property that is dependent on the number and type of basepairs formed. Fortunately, the absorption spectra as well as thermodynamics are physical properties that are consistent with the nearest-neighbor models (Puglisi and Tinoco, 1989; Blake, 1972; Petersheim and Turner, 1983). In other words, given nearest neighbors must have identical values of their absorptions or melting free energies regardless of their position in the interior or at the ends of the sequence. Thus, the property being monitored as a function of the temperature is proportional to the fraction of basepairs that are stacked as a nucleic acid molecule or duplex is melted. In this article we do not restrict ourselves to the case of two-state transitions where there are only two types of conformational species as the temperature changes: fully folded and fully unfolded. Rather, we consider the ensemble of all possible intermediate states, thus yielding the most detailed possible picture of the melting process between the folded and unfolded states of the single and double-stranded forms. The task we are going to solve can be formulated as follows in the next paragraph.
As a result of interconversions between the single and double-stranded forms at each temperature, there is an equilibrium between the different conformational species; single-stranded A, single-stranded B, double-stranded AA, double-stranded BB, and double-stranded AB. Each of these forms is characterized with an ensemble of conformational states where each conformation is characterized by the fraction of its basepairs and their location along the sequences that are melted at any given temperature. Thus, along the sequence(s) we have alternating loops, single-stranded regions, and double-stranded regions. The locations and the lengths of these portions depend on their relative Boltzmann statistical weights. We set the double-stranded forms as our zero level from which the contribution of the melted single-stranded forms should be counted. This assumption is rather convenient; experiments have shown that the contribution from the double-stranded forms is ∼75% from that of the melted single forms (Bloomfield et al., 2000). With this approximation, the absorption of the ensemble of all possible conformational species, taking into account their interconversions and their own ensemble of conformational changes, can be represented in the following form:
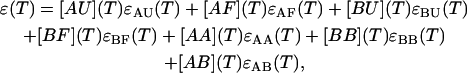 |
(18) |
where ɛ(T) is the extinction of the ensemble of all possible species as a function of temperature, T; 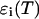 for i running among all the different species represent the species extinctions as a function of temperature; and [AU](T), [AF](T), [BU](T), [BF](T), [AA](T), [BB](T), and [AB](T) represent the mole fractions of the corresponding species as a function of the temperature which are calculated as described above. We will focus now on the extinctions of the species
for i running among all the different species represent the species extinctions as a function of temperature; and [AU](T), [AF](T), [BU](T), [BF](T), [AA](T), [BB](T), and [AB](T) represent the mole fractions of the corresponding species as a function of the temperature which are calculated as described above. We will focus now on the extinctions of the species 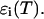 First we should take into account that the extinction is determined by the contribution of the melted or mismatch loop regions along the constituent sequences of the double-stranded species (Bloomfield et al., 2000). At each given temperature there is an ensemble of conformations with a narrow or broad distribution of such loops. The contribution of each of them is proportional to its relative Boltzmann statistical weight. It follows from here that the extinction for the AB species, for example, can be represented in the form
First we should take into account that the extinction is determined by the contribution of the melted or mismatch loop regions along the constituent sequences of the double-stranded species (Bloomfield et al., 2000). At each given temperature there is an ensemble of conformations with a narrow or broad distribution of such loops. The contribution of each of them is proportional to its relative Boltzmann statistical weight. It follows from here that the extinction for the AB species, for example, can be represented in the form 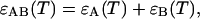 where the contributions from sequences A and B are as follows
where the contributions from sequences A and B are as follows
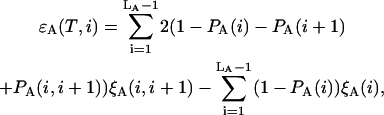 |
(19) |
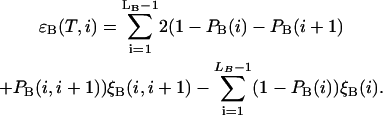 |
(20) |
Here 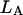 and
and 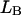 stand for the lengths of the nucleic acid A and B, and ξ is for extinction coefficients of single bases (one argument) or (by a slight abuse of notation) for dinucleotides (two arguments).
stand for the lengths of the nucleic acid A and B, and ξ is for extinction coefficients of single bases (one argument) or (by a slight abuse of notation) for dinucleotides (two arguments). 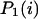 and
and 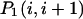 are the probabilities that an arbitrary single {i}, {i + 1} or double {i, i + 1} nearest-neighbor positions along the sequence 1 forms basepairs with the sequence 2 and vice versa. Using these probabilities we can express the probabilities that two closest along the sequence A or B nucleotides with positions i and i + 1 are melted (giving a contribution ξ(i, i + 1) to the total absorbance) as
are the probabilities that an arbitrary single {i}, {i + 1} or double {i, i + 1} nearest-neighbor positions along the sequence 1 forms basepairs with the sequence 2 and vice versa. Using these probabilities we can express the probabilities that two closest along the sequence A or B nucleotides with positions i and i + 1 are melted (giving a contribution ξ(i, i + 1) to the total absorbance) as 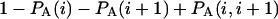 and
and 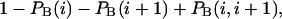 respectively.
respectively.
Heat capacity and melting
With increasing temperature, the overwhelming majority of the single and double-stranded species conformations tend toward their corresponding unfolded states, as reflected by the large enthalpy and entropy gain associated with base pairing disruption and loop formation. The relative changes of the species concentration, which reflect the structural changes of the melting process, have a nonlinear character as shown by the mass equations derived above. This makes the analysis of the melting process rather complicated. Differential scanning calorimetry (DSC) is a widely used tool for investigating the conformational changes in the melting process (Breslauer et al., 1992; Sturtevant, 1987). It measures the difference in heat or the heat capacity required to raise the temperature of the solution. The advantage of this method is that thermodynamic parameters such as enthalpy, H, entropy, S and free energy, F = E − TS + PV, which can be obtained in this way, do not depend on a theoretical model for the underlying conformational changes occurring in the melting material. Usually in the melting experiments the change in V is negligible, so the term PV is constant and the free energy is estimated from F = E − TS, and the enthalpy H is equivalent to the internal energy E. From statistical thermodynamics it is well known that the heat capacity, 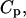 is derived from the second derivative of the free energy, F, with respect to the temperature T.
is derived from the second derivative of the free energy, F, with respect to the temperature T.
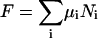 |
(21) |
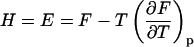 |
(22) |
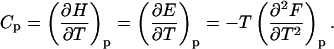 |
(23) |
The summation over i includes all possible different species in the solution. One still has to make the above calculations for varying temperatures over the desired range. To compute H and 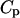 for a particular temperature
for a particular temperature 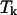 an approach based on the derivation made by the “Vienna group” is used (Hofacker et al., 1994). A least-squares parabola is fitted to F at 2m + 1 points:
an approach based on the derivation made by the “Vienna group” is used (Hofacker et al., 1994). A least-squares parabola is fitted to F at 2m + 1 points: 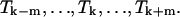 The second derivative of this polynomial is the estimate used for the second derivative of F with respect to a temperature
The second derivative of this polynomial is the estimate used for the second derivative of F with respect to a temperature 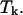
Recursive calculation
Partition function
In any statistical thermodynamic model, all the thermodynamic information is contained in the partition function under consideration
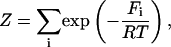 |
(24) |
where 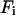 is the free energy of the
is the free energy of the 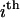 state of the system. In our model, we wish to calculate the species partition functions,
state of the system. In our model, we wish to calculate the species partition functions, 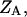
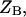
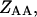
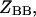
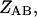
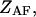 and
and 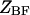 that determine the thermodynamic properties of the single-stranded species
that determine the thermodynamic properties of the single-stranded species 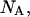
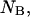 and the double-stranded species
and the double-stranded species 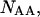
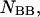 and
and 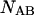 of the polynucleotide molecules A and B.
of the polynucleotide molecules A and B.
The polynucleotide sequences of the double-stranded forms are described as follows. The sequence for A is represented by 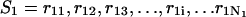 and sequence B is represented by
and sequence B is represented by 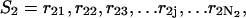 where
where 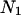 and
and 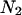 stand for their corresponding lengths and
stand for their corresponding lengths and 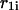 and
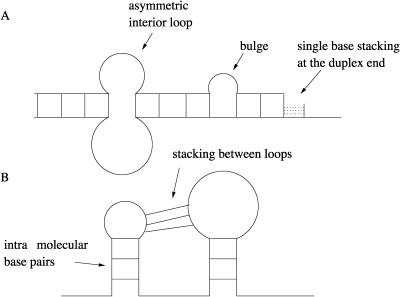
and 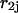 are the sequence coordinates of the corresponding nucleotides of sequences 1 and 2. In this article we will use some simplification concerning possible conformational states of the hybrid form AB. Thus, hybridization will account only for stacked pairs, interior loops, bulges, and, at the ends, dangling bases. At this stage, we do not consider intramolecular basepairs. Stacking between the loop regions of sequence 1 and sequence 2 are also not considered (Fig. 1).
are the sequence coordinates of the corresponding nucleotides of sequences 1 and 2. In this article we will use some simplification concerning possible conformational states of the hybrid form AB. Thus, hybridization will account only for stacked pairs, interior loops, bulges, and, at the ends, dangling bases. At this stage, we do not consider intramolecular basepairs. Stacking between the loop regions of sequence 1 and sequence 2 are also not considered (Fig. 1).
FIGURE 1.
Diagram A illustrates the contributions of stacked pairs, symmetric and asymmetric interior loops, bulges, and, at the ends, dangling bases to the duplex stability. Diagram B illustrates what type of contributions are not taken into consideration in this work. Thus, at this stage, we do not consider intramolecular basepairs, and stacking between the loop regions is also not considered.
As described by Mathews et al. (1999), Doktycz et al. (1990), Blommers et al. (1989), LeBlanc and Morden (1991), Zieba et al. (1991), and Zuker et al. (1999), the energy rules allow us to ascribe to each stacked pair an energy dependent only on pairs under consideration and their nearest neighbors. The recursion calculation is based on the condition that there are at least two nucleotides along sequences 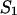 and
and 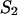 that are in contact. A contact, or basepair, is denoted by
that are in contact. A contact, or basepair, is denoted by 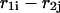 for
for 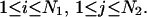 Sequence enumeration is always from 5′ to 3′. The contact
Sequence enumeration is always from 5′ to 3′. The contact 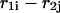 includes an initiation free-energy term necessary to bring the two sequences together
includes an initiation free-energy term necessary to bring the two sequences together 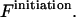 Each nucleotide pair,
Each nucleotide pair, 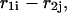 formally divides the hybridized form
formally divides the hybridized form 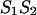 of sequences 1 and 2 into two parts; left, L and right, R, in such way that the free energy,
of sequences 1 and 2 into two parts; left, L and right, R, in such way that the free energy, 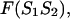 of
of 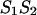 is a sum of the free energies of the left
is a sum of the free energies of the left 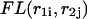 and right
and right 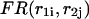 parts plus the initiation free energy
parts plus the initiation free energy 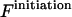 which is assumed to be the same for all possible pairs
which is assumed to be the same for all possible pairs 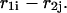 Thus,
Thus,
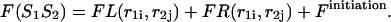 |
(25) |
This additive property of the energy rules based on nearest neighbor approximation forms the basis of the recursion calculations of the partition function 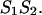 The additivity of the free energy leads to a multiplication of the partition functions of the left, ZL and right, ZR, parts. Therefore, the recursions for the partition functions of the left and right parts are:
The additivity of the free energy leads to a multiplication of the partition functions of the left, ZL and right, ZR, parts. Therefore, the recursions for the partition functions of the left and right parts are:
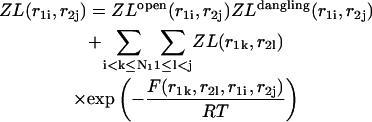 |
(26) |
 |
(27) |
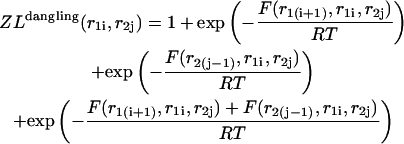 |
(28) |
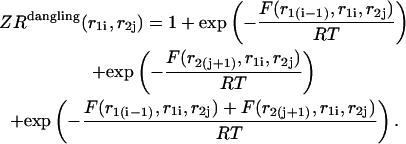 |
(29) |
Here 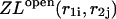 and
and 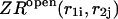 correspond to cases where only the
correspond to cases where only the 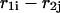 pair is formed in the left and right parts, respectively; whereas
pair is formed in the left and right parts, respectively; whereas 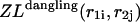 and
and 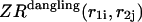 correspond to the dangling free energies of the tails of sequence 1 and 2. The dangling free energies take into account the ensemble of all possible stackings between the nucleotides adjacent to the
correspond to the dangling free energies of the tails of sequence 1 and 2. The dangling free energies take into account the ensemble of all possible stackings between the nucleotides adjacent to the 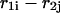 pair. When
pair. When 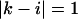 and
and 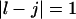 the free energy
the free energy 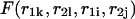 represents a stacked pair that belongs to a secondary structure, when
represents a stacked pair that belongs to a secondary structure, when 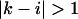 and
and 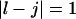 or
or 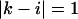 and
and 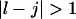 we have a bulge. In general when
we have a bulge. In general when 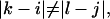 the free energy,
the free energy, 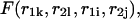 represents an asymmetric internal loop, whereas
represents an asymmetric internal loop, whereas 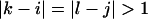 leads to a symmetric loop. For a detailed description of the free energies of bulges, symmetric and asymmetric internal loops, and dangling ends, we refer the reader to the articles by Zuker et al. (1999) and (Mathews et al., 1999). Based on the multiplication property of the partition functions for the left and the right parts of the
leads to a symmetric loop. For a detailed description of the free energies of bulges, symmetric and asymmetric internal loops, and dangling ends, we refer the reader to the articles by Zuker et al. (1999) and (Mathews et al., 1999). Based on the multiplication property of the partition functions for the left and the right parts of the 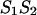 hybridization form for the total partition function we have:
hybridization form for the total partition function we have:
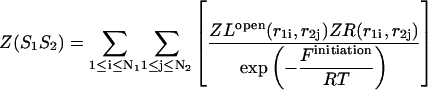 |
(30) |
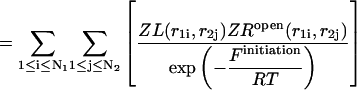 |
(31) |
Pair probabilities
The calculated partition functions will allow us to derive the probabilities of various conformations. Our main interest here is to calculate the probabilities 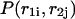 and
and 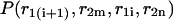 of a single
of a single 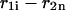 and double
and double 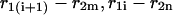 pair formation, where
pair formation, where 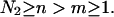 These probabilities play a major role in hybridization or melting processes.
These probabilities play a major role in hybridization or melting processes.
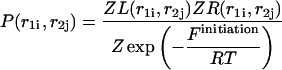 |
(32) |
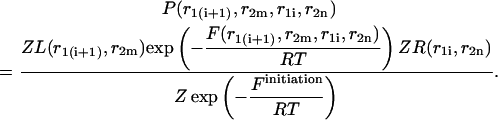 |
(33) |
It is now easy to calculate the probabilities 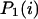 and
and 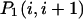 that an arbitrary single {i}, {i + 1} or double {i, i + 1} nearest-neighbor positions along the sequence 1 forms basepairs with the sequence 2 and vice versa. We have:
that an arbitrary single {i}, {i + 1} or double {i, i + 1} nearest-neighbor positions along the sequence 1 forms basepairs with the sequence 2 and vice versa. We have:
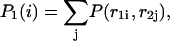 |
(34) |
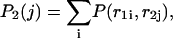 |
(35) |
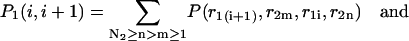 |
(36) |
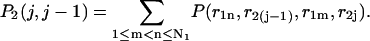 |
(37) |
In particular the equilibrium fraction of bases paired θ can be calculated from
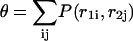 |
(38) |
RESULTS AND DISCUSSIONS
Table 1 presents the experimental and predicted thermodynamic parameters such as enthalpy 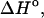 entropy
entropy 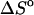 and the melting temperature,
and the melting temperature, 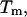 for a number of oligonucleotides taken from the literature (Allawi and SantaLucia, 1997). There are two main groups of sequences in Table 1; those in which the transition equilibrium involves only two states, i.e., duplex (as complete as possible if mismatches occur) and random coils, and those in which the transition equilibrium involves more than two states. Sequences from the two-state group are designed to have a melting temperature,
for a number of oligonucleotides taken from the literature (Allawi and SantaLucia, 1997). There are two main groups of sequences in Table 1; those in which the transition equilibrium involves only two states, i.e., duplex (as complete as possible if mismatches occur) and random coils, and those in which the transition equilibrium involves more than two states. Sequences from the two-state group are designed to have a melting temperature, 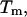 between 30°C and 60°C and to minimize the possibility of forming stable alternative secondary structures such as slipped duplexes or hairpins. Non-two-state sequences are designed to form both duplex and hairpin species. In addition, sequences are designed with uniform distribution of the 11 different G·T mismatch containing nearest neighbors. The data set for internal G·T mismatches does not contain sequences that have terminal G·T mismatches. As a result, there are only 10 uniquely determined parameters as linear combinations of 11 G·T nearest-neighbor dimers (Allawi and SantaLucia, 1997). This special design is a very good test for the nearest-neighbor model according to which the terminal nearest neighbors make the same contribution as internal neighbors.
between 30°C and 60°C and to minimize the possibility of forming stable alternative secondary structures such as slipped duplexes or hairpins. Non-two-state sequences are designed to form both duplex and hairpin species. In addition, sequences are designed with uniform distribution of the 11 different G·T mismatch containing nearest neighbors. The data set for internal G·T mismatches does not contain sequences that have terminal G·T mismatches. As a result, there are only 10 uniquely determined parameters as linear combinations of 11 G·T nearest-neighbor dimers (Allawi and SantaLucia, 1997). This special design is a very good test for the nearest-neighbor model according to which the terminal nearest neighbors make the same contribution as internal neighbors.
TABLE 1.
Experimental and predicted thermodynamic parameters of oligonucleotides
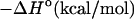 |
 |
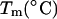 |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SEQUENCES | exp* | A† | B‡ | exp | A | B | exp | A | B | |||
| CAAAGAAAG | 46.7 | 46.1 | 46.1 | 137.0 | 136.6 | 160 | 27.6 | 24.5 | 21 | |||
| GTTTTTTTC | — | — | — | — | — | — | — | — | — | |||
| CAAATAAAG | 55.6 | 48.4 | 51.1 | 165 | 142 | 166.9 | 30.2 | 28.5 | 26 | |||
| GTTTGTTTC | — | — | — | — | — | — | — | — | — | |||
| CGTGTCTCC | 52 | 52.4 | 53.3 | 142.4 | 142.8 | 161.6 | 50 | 52.1 | 49 | |||
| GCACGGAGG | — | — | — | — | — | — | — | — | — | |||
| CGAGTGTCC | 62.5 | 59.5 | 60.7 | 174.1 | 164.8 | 183.5 | 51.6 | 51.8 | 51 | |||
| GCTCGCAGG | — | — | — | — | — | — | — | — | — | |||
| GGACTCTCG | 57.9 | 50.5 | 51.6 | 162.7 | 138.4 | 157.8 | 46.9 | 49.1 | 45 | |||
| CCTGGGAGC | — | — | — | — | — | — | — | — | — | |||
| GGACTGACG | 62.6 | 58.5 | 59.6 | 174.9 | 162.2 | 180.4 | 51 | 50.9 | 51 | |||
| CCTGGCTGC | — | — | — | — | — | — | — | — | — | |||
| GGAGTCACG | 65.4 | 52.4 | 53.6 | 182.4 | 142.8 | 162 | 52.6 | 52.1 | 50 | |||
| CCTCGGTGC | — | — | — | — | — | — | — | — | — | |||
| GACCGTGCAC | 53.4 | 55.2 | 55.7 | 148.9 | 153.5 | 170.4 | 46 | 48.2 | 49 | |||
| CTGGTGCGTG | — | — | — | — | — | — | — | — | — | |||
| GACGTTGGAC | 60.4 | 54.3 | 54.8 | 169.3 | 150 | 166.2 | 49.1 | 49.5 | 49 | |||
| CTGCGGCCTG | — | — | — | — | — | — | — | — | — | |||
| GACGTTAGGC | 46 | 51.3 | 51 | 123.5 | 140.2 | 153.4 | 51.1 | 50.5 | 51 | |||
| CTGCGGTCCG | — | — | — | — | — | — | — | — | — | |||
| GGAGTGCTCC | 65.7 | 58 | 61.1 | 187.1 | 163.6 | 188.7 | 46.5 | 45.7 | 47 | |||
| CATGAGGCTAC | 69.9 | 67.2 | 66.1 | 197.6 | 189.6 | 200.3 | 50.6 | 50.1 | 49.0 | |||
| GTACTTCGATG | — | — | — | — | — | — | — | — | — | |||
| CATGTGACTAC | 64.2 | 65.6 | 62.1 | 182.1 | 188 | 191.2 | 47.2 | 44.8 | 45.0 | |||
| GTACATTGATG | — | — | — | — | — | — | — | — | — | |||
| CCATCGCTACC | 79.8 | 71.6 | 73.2 | 223.8 | 199.4 | 218 | 56.6 | 55.7 | 55.0 | |||
| GGTAGTGATGG | — | — | — | — | — | — | — | — | — | |||
| CCATTGCTACC | 75.7 | 67.3 | 70.1 | 214.8 | 189.3 | 213.6 | 51.5 | 51 | 50.0 | |||
| GGTAATGATGG | — | — | — | — | — | — | — | — | — | |||
| GATCATTGTAC | 69.3 | 65.9 | 65.1 | 198.1 | 189.6 | 200.2 | 46.9 | 43.8 | 44.0 | |||
| GTAGTGACATG | — | — | — | — | — | — | — | — | — | |||
| GATCTTTGTAC | 67.6 | 64.0 | 63.3 | 194.5 | 184.9 | 196.2 | 44.6 | 41.8 | 43.0 | |||
| CTAGAGACATG | — | — | — | — | — | — | — | — | — | |||
| GTAGCGTCATG | 76.6 | 72.0 | 71.2 | 215.5 | 202.6 | 213.0 | 54.7 | 52.8 | 55.0 | |||
| CATCGTAGTAG | — | — | — | — | — | — | — | — | — | |||
| GTAGTGACATG | 68.3 | 65.6 | 64.4 | 194.7 | 188.0 | 199.5 | 47.3 | 44.8 | 45.0 | |||
| CATCATTCTAG | — | — | — | — | — | — | — | — | — | |||
| CCATGCGTAACG | 71.2 | 70.0 | 72.1 | 200.7 | 195.6 | 215.0 | 52.1 | 54.1 | 53.0 | |||
| GGTATGCGTTGC | — | — | — | — | — | — | — | — | — | |||
| CGAGACGTTTCG | 61.0 | 65.4 | 67.6 | 174.1 | 186.8 | 205.0 | 43.7 | 45.7 | 45.0 | |||
| CGAGCATGTTCG | 59.8 | 68.4 | 70.5 | 169.6 | 194.2 | 215.5 | 45.3 | 48.7 | 47.0 | |||
| CGCGAATTTGCG | 79.3 | 74.4 | 83.4 | 224.1 | 208.8 | 256.4 | 53.9 | 54.5 | 55.0 | |||
| CGTGACGTTACG | 73.3 | 68.0 | 70.4 | 210.0 | 192.6 | 212.8 | 47.7 | 49.3 | 49.0 | |||
| CGTGTCGATACG | 73.8 | 70.0 | 72.1 | 210.9 | 198.4 | 216.6 | 48.8 | 49.9 | 50.0 | |||
| CGTTACGTGACG | 64.9 | 68.0 | 70.4 | 184.0 | 192.6 | 211.8 | 47.8 | 49.3 | 50.0 | |||
| CTCGGATCTGAG | 75.0 | 69.2 | 71.7 | 214.5 | 198.4 | 220.7 | 48.8 | 46.2 | 50.0 | |||
| CTCTCATGGGAG | 50.4 | 55.0 | 50.3 | 141.5 | 154.4 | 200 | 41.9 | 45.3 | 52.0 | |||
| CTCTGATCGGAG | 60.3 | 69.2 | 70.4 | 170.3 | 198.4 | 214.7 | 46.7 | 46.2 | 51.0 | |||
| CTGTCATGGCAG | 59.2 | 58.8 | 61.8 | 164.2 | 163.2 | 188.8 | 51.4 | 50.8 | 56 | |||
| CTGTGATCGCAG | 67.0 | 73.0 | 74.9 | 188.2 | 207.2 | 224.8 | 51.4 | 50.6 | 53.0 | |||
| CTTGGATCTAAG | 64.0 | 60.6 | 60.0 | 187.3 | 178.2 | 189.3 | 38.1 | 35.2 | 39.0 | |||
| CAACTTGATATTAATA | 91.3 | 98.5 | 98.9 | 264.0 | 286.4 | 295.1 | 47.1 | 50.1 | 55.0 | |||
| GTTGAATTATAATTAT | — | — | — | — | — | — | — | — | — | |||
| CAACTTGATATTAATA | 92.6 | 102.8 | 103.3 | 266.0 | 296.5 | 304.9 | 49.4 | 53.4 | 59.0 | |||
| GTTGAGCTATAATTAT | — | — | — | — | — | — | — | — | — | |||
| CAACTTGATATTAATA | 95.5 | 100.1 | 100.4 | 274.0 | 287.7 | 296.5 | 50.5 | 54.0 | 62.0 | |||
| GTTGAACTATAGTTAT | — | — | — | — | — | — | — | — | — | |||
| CGTCTGTCC | 56.5 | 58.5 | 59.5 | 156.5 | 162.2 | 179.3 | 50.1 | 50.9 | 50.0 | |||
| GCAGGCAGG | — | — | — | — | — | — | — | — | — | |||
| GATCTGTGTAC | 70.6 | 66.3 | 65.4 | 202.5 | 190.7 | 200.8 | 46.7 | 44.1 | 46.0 | |||
| CTAGATACATG | — | — | — | — | — | — | — | — | — | |||
| CGAGTCGATTCG | 69.6 | 67.4 | 69.7 | 199.7 | 192.6 | 211.4 | 46.1 | 46.4 | 48.0 | |||
| CTTGCATGTAAG | 56.7 | 64.4 | 64.5 | 162.9 | 187.0 | 199.4 | 39.5 | 40.5 | 41.0 | |||
| CGTGTCTAGATACG | 78.3 | 82.2 | 84.9 | 222.6 | 234.4 | 252.6 | 51.7 | 52.1 | 53.0 | |||
| GACGTGAGGC | 35.6 | 59.5 | 59.1 | 94.0 | 166.0 | 178.3 | 43.8 | 50.8 | 51.0 | |||
| CTGCGTTCCG | — | — | — | — | — | — | — | — | — | |||
| CGTTGCGTAACG | 58.7 | 73.3 | 79.5 | 163.1 | 203.4 | 243.3 | 49.2 | 57.5 | 56.0 | |||
| CTCGCATGTGAG | 64.6 | 73.0 | 73.6 | 181.9 | 207.2 | 221.3 | 49.7 | 50.6 | 54.0 | |||
| CTGGCATGTCAG | 67.8 | 58.8 | 58.8 | 191.2 | 163.2 | 176.7 | 50.7 | 50.8 | 52.0 | |||
| CTGGGATCTCAG | 73.8 | 55.0 | 54.6 | 213.4 | 154.4 | 168.2 | 45.6 | 45.3 | 47.0 | |||
| GCGTACGCATGCG | 80.9 | 97.3 | 98.3 | 220.0 | 264.4 | 280.5 | 66.3 | 71.0 | 69.0 | |||
| CGCATGTGTACGC | — | — | — | — | — | — | — | — | — | |||
Experimental data are from the article of SantaLucia (Allawi and SantaLucia, 1997). Standard errors for experimental entropy 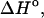 enthalpy
enthalpy 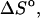 and the melting temperature
and the melting temperature 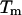 are 8%, 8%, and 2°C, respectively.
are 8%, 8%, and 2°C, respectively.
Predictions based on two-state model (Allawi and SantaLucia, 1997).
Predictions based on the partition function calculations described in this article.
Our calculations are based on the following main assumptions:
The different species that can be formed by two sequences A and B in solution, such as single-stranded folded (AF, BF) or unfolded (AU, BU) and double-stranded hybridization in terms of two equivalent (AA, BB) or two different (AB) sequences can be described as an ensemble of ideally mixed species. This assumption is rather obvious as a result of the experimental requirement for low concentrations of the sequences.
The free energies of the unfolded sequences at 37°C are used as a reference state in our calculations. This assumption is of special importance because databases of thermodynamic parameters reported at a given temperature are often used to predict hybridization properties at different temperatures as part of various diagnostic and therapeutic protocols (Owczarzy et al., 1997). The usual assumption is that because of the enthalpy-entropy compensation,
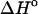 and
and 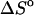 per basepair or stack for double-stranded helixes and single-stranded helixes, respectively, can be considered as temperature independent for most practically important temperature ranges. However, when
per basepair or stack for double-stranded helixes and single-stranded helixes, respectively, can be considered as temperature independent for most practically important temperature ranges. However, when 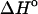 and
and 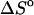 represent the difference between the double helix and the single-stranded sequences, adjustments should be made for stacking present in the single-stranded sequences before and after the double helix is formed. Without taking into account the temperature dependence (and probable dependence of some other factors) of the reference state, the deviation between the calculated and experimentally determined values for
represent the difference between the double helix and the single-stranded sequences, adjustments should be made for stacking present in the single-stranded sequences before and after the double helix is formed. Without taking into account the temperature dependence (and probable dependence of some other factors) of the reference state, the deviation between the calculated and experimentally determined values for 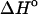 and
and 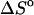 can be quite large. The reference state refers to unfolded single strand sequences in which stacking between nearest neighbor nucleotides are present.
can be quite large. The reference state refers to unfolded single strand sequences in which stacking between nearest neighbor nucleotides are present.We do not take into account intramolecular basepairs in duplexes. This is rather good approximation for short sequences.
Conformational transformation between different structural species is as follows. Single-stranded unfolded sequences can hybridize to form the double helix species or can form internal basepair contacts to form single-stranded hairpins. However, single-stranded hairpins cannot hybridize with each other to form double helixes. They have to unfold first. This assumption is rather strong in general, but for sequences for which the equilibrium transformation involves only two states, it is a good approximation. Work on the more general case is in progress in our lab. We have to note that this assumption does not restrict the general expression for the partition function presented in (1) above.
In Table 1, the experimental data show good agreement both with the calculations by our group and that of SantaLucia. It is important to note that the calculations of the SantaLucia group are based on the approximation that folded species do not explore all possible conformations in their folded state but are represented by the conformations with minimum energy. In our calculations we do explore all possible conformations of the folded species within the limitations specified above. In both the SantaLucia and our groups, the entropy loss by the single-stranded unfolded sequences in forming the first basepair of the double helix is taken into account by an experimentally determined initiation parameter. Since the conformation of denatured single strands is unknown, this is a reasonable approximation. The enthalpy and entropy contribution per basepair relative to the unfolded sequences are taken from experiments at 37°C. As a result, the entropy values of our calculations are consistently greater than those of the SantaLucia group. The differences are relatively small which should be expected because of the way the sequences are designed. Nevertheless, our calculations show that there is a variability around the minimum energy conformations of the folded species, and of course this variability will increase with the sequence length. Of particular interest are the last six sequences in Table 1 which melt with non-two-state thermodynamics regardless of the way they are designed. For two of them NTS-1, (5′-CGTTGCGTAACG-3′)2 and NTS-2, 5′-GCGTACGCATGCG-3′/3′-CGCATGTGTACGC-5′ (Plum et al., 1995), the non-two-state melting is in contrast with the good agreement between the experimentally determined van't Hoff enthalpies derived from 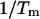 versus
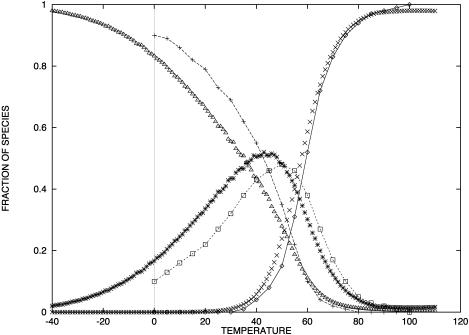
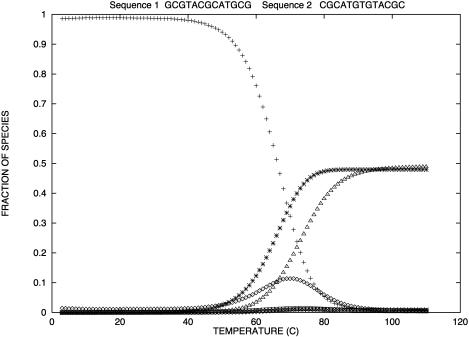
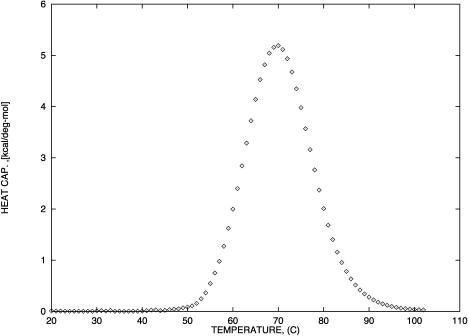
versus 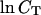 plots and from the fits of individual melting curves. Melting simulation of NTS-1 from SantaLucia and our group and NTS-2 from our group are represented in Figs. 2–4, respectively.
plots and from the fits of individual melting curves. Melting simulation of NTS-1 from SantaLucia and our group and NTS-2 from our group are represented in Figs. 2–4, respectively.
FIGURE 2.
Predicted fraction of species from our group and that of SantaLucia (Allawi and SantaLucia, 1997) formed by CGTTGCGTAACG versus temperature at total strand concentration of 1 × 10−4 M. (⋄) Random coil (SantaLucia); (+) duplex(SantaLucia); (□) hairpin (SantaLucia); (×) random coil (Dimitrov and Zuker); ▵ duplex (Dimitrov and Zuker); (*) hairpin (Dimitrov and Zuker).
FIGURE 3.
Predicted fraction of species versus temperature for NTS-2 5′-GCGTACGCATGCG-3′/3′-CGCATGTGTACGC-5′ from our group. Conditions: strand concentrations, 2 × 10−4 M; 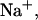 1000 mM;
1000 mM; 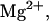 0 mM. (⋄) 11 (duplex); (+) 12 (duplex); (□) 2 (hairpin); (×) 1 (hairpin); (▵) 1 (random coil); (*) 2 (random coil); (♡) 22 (duplex).
0 mM. (⋄) 11 (duplex); (+) 12 (duplex); (□) 2 (hairpin); (×) 1 (hairpin); (▵) 1 (random coil); (*) 2 (random coil); (♡) 22 (duplex).
FIGURE 4.
Predicted heat capacity versus temperature for NTS-2 5′-GCGTACGCATGCG-3′/3′-CGCATGTGTACGC-5′. Conditions: strand concentrations, 2 × 10−4 M; 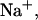 1000 mM;
1000 mM; 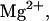 0 mM.
0 mM.
In Fig. 2, both SantaLucia's and our simulations are in good agreement and clearly show a significant population of hairpins at temperatures near the duplex 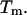 Similarly (Fig. 3), our simulations show the presence of the duplex from sequence 2, CGCATGTGTACGC, near the melting temperature for the NTS-2 duplex, GCGTACGCATGCG/CGCATGTGTACGC.
Similarly (Fig. 3), our simulations show the presence of the duplex from sequence 2, CGCATGTGTACGC, near the melting temperature for the NTS-2 duplex, GCGTACGCATGCG/CGCATGTGTACGC.
Fig. 4 shows the calculated heat capacity for the NTS-2 duplex. It is consistent with the agreement between the UV melting data and calorimetric data from the experimental results of Plum et al. (1995) and SantaLucia. Our calculations show that heat capacity is almost perfectly symmetric as one would expect from a two-state melting process. Thus, it is well known that the van't Hoff enthalpy change, 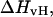 calculated from the temperature dependence of the equilibrium constant from spectroscopic data equals the total calorimetric enthalpy change,
calculated from the temperature dependence of the equilibrium constant from spectroscopic data equals the total calorimetric enthalpy change, 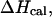 only if the melting reaction follows a two-state transition between free and bound molecules and if the change in the spectroscopic signal used to calculate the equilibrium constant reflects the entire population of free and bound molecules. Otherwise,
only if the melting reaction follows a two-state transition between free and bound molecules and if the change in the spectroscopic signal used to calculate the equilibrium constant reflects the entire population of free and bound molecules. Otherwise, 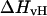 and
and 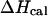 are different. Therefore, when
are different. Therefore, when 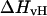 and
and 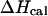 are equal, this can be taken to indicate a two-state transition. However, our mole fraction calculations show that the apparent two-state shape for the heat capacity follows from the fact that the maximum of the CGCATGTGTACGC duplex fraction is centered at the melting temperature of the NTS-2 duplex. As a result, the melting of CGCATGTGTACGC duplex is superimposed on that of the NTS-2 duplex which leads to almost symmetric shape of the heat capacity curve. Our simulations show clearly the advantage of the general statistical mechanical approach which explores all possible conformations of single hairpins and double helixes as well as the conformational transformations among them. In such way, we avoid confusions from the assumption of two-state melting based on the agreement between the van't Hoff and the total enthalpy change during the melting process.
are equal, this can be taken to indicate a two-state transition. However, our mole fraction calculations show that the apparent two-state shape for the heat capacity follows from the fact that the maximum of the CGCATGTGTACGC duplex fraction is centered at the melting temperature of the NTS-2 duplex. As a result, the melting of CGCATGTGTACGC duplex is superimposed on that of the NTS-2 duplex which leads to almost symmetric shape of the heat capacity curve. Our simulations show clearly the advantage of the general statistical mechanical approach which explores all possible conformations of single hairpins and double helixes as well as the conformational transformations among them. In such way, we avoid confusions from the assumption of two-state melting based on the agreement between the van't Hoff and the total enthalpy change during the melting process.
Next we analyze the role of stacking between neighboring nucleotide residues of single strands as an important source of enthalpy change on helix formation. Thus, each oligomer has a stacked-unstacked transition that is superimposed upon the helix-coil transition. Therefore we should expect that the measured enthalpy for the helix-single strands transition will be less at low temperatures where the nearest-neighbor nucleotide residues in the single strands are partially stacked than at very high temperature where the nearest-neighbor nucleotide residues are totally unstacked. On the other hand, in both our group and the SantaLucia group, the difference in heat capacities  between the unfolded and folded states of the species is taken to be zero. The calculated enthalpy contributions and the melting temperatures (Table 1) between the SantaLucia group and our group, as should be expected, based on the same
between the unfolded and folded states of the species is taken to be zero. The calculated enthalpy contributions and the melting temperatures (Table 1) between the SantaLucia group and our group, as should be expected, based on the same 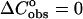 approximation), are in very good agreement. However, the existence of heat capacity
approximation), are in very good agreement. However, the existence of heat capacity 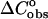 differences between the unfolded and folded states has been demonstrated experimentally in a few groups (Holbrook et al., 1999; Freier et al., 1981; Chalikian et al., 1999). Thus, in the work of Holbrook et al. (1999), it has been found that the contributions to the
differences between the unfolded and folded states has been demonstrated experimentally in a few groups (Holbrook et al., 1999; Freier et al., 1981; Chalikian et al., 1999). Thus, in the work of Holbrook et al. (1999), it has been found that the contributions to the 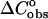 coming from changes in nonpolar and polar surfaces in single helix formation and the docking of the single strand helixes in hybridization and self-folding processes largely offset each other. As a result, the observed heat capacity changes in double-strand helix formation must arise primarily from temperature-dependent coupled processes in the unfolded strands. From the analysis of DSC and UV thermal-scan data, the values of enthalpies of ordering and folding of the single strands together with their relative fractional extents at a given temperature allowed the authors in combination with the observed DSC and isothermal titration calorimetry (ITC) enthalpies to extract the
coming from changes in nonpolar and polar surfaces in single helix formation and the docking of the single strand helixes in hybridization and self-folding processes largely offset each other. As a result, the observed heat capacity changes in double-strand helix formation must arise primarily from temperature-dependent coupled processes in the unfolded strands. From the analysis of DSC and UV thermal-scan data, the values of enthalpies of ordering and folding of the single strands together with their relative fractional extents at a given temperature allowed the authors in combination with the observed DSC and isothermal titration calorimetry (ITC) enthalpies to extract the 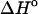 for double helix formation. Changes in the states of the single strands with temperature are shown to lead to a larger heat effect at higher temperature. Our calculations together with the experimental ITC data on the enthalpies of association of two 14 bp complementary sequences 5′-GCGTCATACAGTGC-3′ and 5′-GCACTGTATGACGC-3′ taken from the work of Holbrook et al. (1999) are shown in Fig. 5.
for double helix formation. Changes in the states of the single strands with temperature are shown to lead to a larger heat effect at higher temperature. Our calculations together with the experimental ITC data on the enthalpies of association of two 14 bp complementary sequences 5′-GCGTCATACAGTGC-3′ and 5′-GCACTGTATGACGC-3′ taken from the work of Holbrook et al. (1999) are shown in Fig. 5.
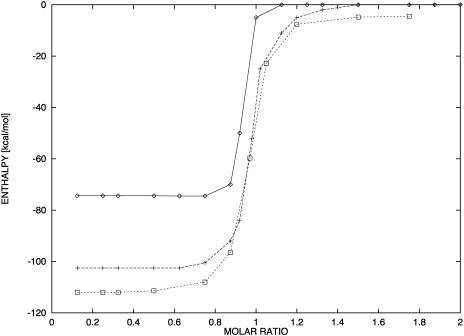
FIGURE 5.
Comparison of predicted and experimental integrated ITC 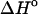 of duplex formation at 293 K, 312 K, and 310 K. Conditions: 120 mM
of duplex formation at 293 K, 312 K, and 310 K. Conditions: 120 mM 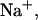 concentration in the calorimetric cell 4.98 μM and 50.8 μM in the injection syringe (Holbrook et al., 1999). (⋄) T = 292.8 K (exp); (+) T = 312.4 K (exp); (□) T = 310.15 K (predicted).
concentration in the calorimetric cell 4.98 μM and 50.8 μM in the injection syringe (Holbrook et al., 1999). (⋄) T = 292.8 K (exp); (+) T = 312.4 K (exp); (□) T = 310.15 K (predicted).
The data in Fig. 5 represent experimental and calculated enthalpies at 292.8 K, 310 K, and 312.4 K in 120 mM 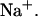 The results indicate that
The results indicate that 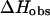 decreases strongly with increasing temperature. In the past few years, a series of experimental and theoretical papers were published on the differences between the DNA and RNA polymer and oligonucleotide nearest-neighbor thermodynamics. These differences led to the notion that there is a length dependency in DNA thermodynamics. An important paper of SantaLucia (1998) showed that most probably, this length dependence is only for the salt effect but not for the nearest-neighbor propagation energies. Thus, increasing sequence lengths lead to increasing melting temperatures as a result of the increase of the total number of basepair contacts whereas the nearest neighbor propagation energies, to a good approximation, do not change. Moreover, the melting temperature can be increased by increasing the number of energy rich basepair contacts without increasing the sequence length. Thus, the difference between the predicted and experimentally determined enthalpies is a direct consequence of the change in the melting temperature and as a result the changes in the heat effect from the stacking in the unfolded single strand sequences rather than the sequence length itself. The above analysis indicates that predictions of enthalpies based on databases of nearest-neighbor energy parameters determined for sequences with lower melting temperatures compared with the melting temperature of the sequences for which they are used as a predictive tool will be underestimated. In the work of SantaLucia, all sequences are designed to have a melting temperature between 30°C and 60°C, whereas the database of nearest-neighbor parameters which they used is determined at 37°C. Our calculations demonstrate that the predicted enthalpies for the sequences in the work of SantaLucia are in good agreement with their experimental data because the sequences are designed to melt near the database melting temperature.
decreases strongly with increasing temperature. In the past few years, a series of experimental and theoretical papers were published on the differences between the DNA and RNA polymer and oligonucleotide nearest-neighbor thermodynamics. These differences led to the notion that there is a length dependency in DNA thermodynamics. An important paper of SantaLucia (1998) showed that most probably, this length dependence is only for the salt effect but not for the nearest-neighbor propagation energies. Thus, increasing sequence lengths lead to increasing melting temperatures as a result of the increase of the total number of basepair contacts whereas the nearest neighbor propagation energies, to a good approximation, do not change. Moreover, the melting temperature can be increased by increasing the number of energy rich basepair contacts without increasing the sequence length. Thus, the difference between the predicted and experimentally determined enthalpies is a direct consequence of the change in the melting temperature and as a result the changes in the heat effect from the stacking in the unfolded single strand sequences rather than the sequence length itself. The above analysis indicates that predictions of enthalpies based on databases of nearest-neighbor energy parameters determined for sequences with lower melting temperatures compared with the melting temperature of the sequences for which they are used as a predictive tool will be underestimated. In the work of SantaLucia, all sequences are designed to have a melting temperature between 30°C and 60°C, whereas the database of nearest-neighbor parameters which they used is determined at 37°C. Our calculations demonstrate that the predicted enthalpies for the sequences in the work of SantaLucia are in good agreement with their experimental data because the sequences are designed to melt near the database melting temperature.
In conclusion, we present here a general statistical mechanical approach appropriate to describe the hybridization processes between finite length DNA and RNA sequences that takes into account the whole ensemble of single and double strand species in the solution and their fractional extents at different temperatures. The folding models for both duplexes and self-folding of single strands developed here deals with matches, mismatches, symmetric and asymmetric interior loops, bulges and single base stacking that might exist at the ends and explores all possible conformations of the single and double strand species. The advantage of such a general approach is most clearly demonstrated in the cases where the melting of the different species are superimposed onto each other, leading to an agreement between the van't Hoff and the total enthalpy change during the melting process. As a result, it is not clear whether such a melting process is two-state or a multi-state that involves intermediates. In particular, we focused also on the role of stacking between neighboring nucleotide residues of single unfolded strands as an important source of enthalpy change on helix formation which has not been distinguished thus far. Changes in the states of the single strands with temperature are shown to lead to a larger heat effect at higher temperature. An important consequence of this is that predictions of enthalpies based on databases of nearest-neighbor energy parameters determined for sequences with lower melting temperatures compared with the melting temperature of the sequences for which they are used as a predictive tool, will be underestimated. Lastly, this article demonstrates the need for an accurate statistical mechanical description of the single-stranded unfolded sequences that can still preserve some nearest-neighbor stacking contacts. The development of such a method is in progress in our laboratory. Further information about the programs used in this article can be found at http://www.bioinfo.rpi.edu/applications/hybrid/.
Acknowledgments
We thank Professor Douglas H. (Doug) Turner for stimulating discussions and valuable comments on the manuscript in advance of publication.
This work has been supported by a grant to M. Zuker, number GM54250, from the National Institutes of Health.
References
- Albergo, D., L. A. Marky, K. J. Breslauer, and D. H. Turner. 1981. Thermodynamics of (dG-dC)3 double-helix formation in water and deuterium oxide. Biochemistry. 20:1409–1413. [DOI] [PubMed] [Google Scholar]
- Allawi, H. T., and J. SantaLucia, Jr. 1997. Thermodynamics and NMR of internal G·T mismatches in DNA. Biochemistry. 97:10581–10594. [DOI] [PubMed] [Google Scholar]
- Applequist, J., and V. Damle. 1963. Theory of effects of concentration and chain length on helix-coil equilibria in two-stranded nucleic acids. J. Chem. Phys. 39:2719–2721. [DOI] [PubMed] [Google Scholar]
- Blake, R. D. 1972. Thermodynamics of Oligo(A)N·2Poly(U)∞ from the dependence of the temperature of the helix-coil transition on oligomer concentrations. Biopolymers. 11:913–933. [DOI] [PubMed] [Google Scholar]
- Blommers, M. J., J. A. Walters, C. A. Haasnoot, J. M. Aelen, G. A. van der Marel, J. H. van Boom, and C. W. Hilbers. 1989. Effects of base sequence on the loop folding in DNA hairpins. Biochemistry. 28:7491–7498. [DOI] [PubMed] [Google Scholar]
- Bloomfield, V. A., D. M. Crothers, and I. Tinoco, Jr. 2000. Nucleic Acids. Structure, Properties and Functions. University Science Books, Sausalito, CA.
- Borer, P. N., B. Dengler, I. Tinoco, Jr., and O. C. Uhlenbeck. 1974. Stability of ribonucleic acid double-stranded helices. J. Mol. Biol. 86:843–853. [DOI] [PubMed] [Google Scholar]
- Breslauer, K. J., E. Freire, and M. Straume. 1992. Calorimetry: a tool for DNA and ligand-DNA studies. Methods Enzymol. 211:533–567. [DOI] [PubMed] [Google Scholar]
- Breslauer, K. J., J. M. Sturtevant, and I. Tinoco, Jr. 1975. Calorimetric and spectroscopic investigation of the helix-to-coil transition of a ribo-oligonucleotide: rA7U7. J. Mol. Biol. 99:549–565. [DOI] [PubMed] [Google Scholar]
- Chalikian, T. V., J. Volker, G. E. Plum, and K. J. Breslauer. 1999. A more unified picture for the thermodynamics of nucleic acid duplex melting: a characterization by calorimetric and volumetric techniques. Proc. Natl. Acad. Sci. USA. 96:7853–7858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doktycz, M. J., T. M. Paner, M. Amaratunga, and A. S. Benight. 1990. Thermodynamic stability of the 5′ dangling-ended DNA hairpins formed from sequences 5′-(XY)2GGATAC(T)4GTATCC-3′, where X,Y=A,T,G,C. Biopolymers. 30:829–845. [DOI] [PubMed] [Google Scholar]
- Early, T. A., D. R. Kearns, W. Hillen, and R. D. Wells. 1981. A 300-MHz proton nuclear magnetic resonance investigation of deoxyribonucleic acid restriction fragments: dynamic properties. Biochemistry. 20:3764–3769. [DOI] [PubMed] [Google Scholar]
- Fixman, M., and J. J. Freire. 1977. Theory of DNA melting curves. Biopolymers. 16:2693–2704. [DOI] [PubMed] [Google Scholar]
- Freier, S. M., D. Alkema, A. Sinclair, T. Neilson, and D. H. Turner. 1983. Contribution of dangling end stacking and terminal base-pair formation to the stabilities of XGGCCp, XCCGGp, XGGCCYp, and XCCGGYp helixes. Biochemistry. 22:6198–6206. [DOI] [PubMed] [Google Scholar]
- Freier, S. M., K. O. Hill, T. G. Dewey, L. A. Marky, K. J. Breslauer, and D. H. Turner. 1981. Solvent effects on the kinetics and thermodynamics of stacking in poly (cytidylic acid). Biochemistry. 20:1419–1426. [DOI] [PubMed] [Google Scholar]
- Gralla, J., and D. M. Crothers. 1973. Free energy of imperfect nucleic acid helices. II. Small hairpin loops. J. Mol. Biol. 73:497–511. [DOI] [PubMed] [Google Scholar]
- Hickey, D. R., and D. H. Turner. 1985. Solvent effects on the stability of A7U7p. Biochemistry. 24:2086–2094. [DOI] [PubMed] [Google Scholar]
- Hofacker, I. L., W. Fontana, P. F. Stadler, S. Bonhöffer, M. Tacker, and P. Schuster. 1994. Fast folding and comparison of RNA secondary structures. Monatsh. Chem. 125:167–188. [Google Scholar]
- Holbrook, J. A., M. W. Capp, R. M. Saecker, and M. T. Record. 1999. Enthalpy and heat capacity changes for formation of an oligomeric DNA duplex: interpretation in terms of coupled processes of formation and association of single-stranded helices. Biochemistry. 38:8409–8422. [DOI] [PubMed] [Google Scholar]
- Kubo, R. 1965. Statistical Mechanics. An advanced course with problems and solutions. North-Holland Publishing Company. Amsterdam, the Netherlands.
- Landau, L. D., and E. M. Lifshitz. 1969. Statistical Physics. Pergamon, Oxford, UK.
- LeBlanc, D. A., and K. M. Morden. 1991. Thermodynamic characterization of deoxyribooligonucleotide duplexes containing bulges. Biochemistry. 30:4042–4047. [DOI] [PubMed] [Google Scholar]
- Mathews, D. H., J. Sabina, M. Zuker, and D. H. Turner. 1999. Expanded sequence dependence of thermodynamic parameters improves prediction of RNA secondary structure. J. Mol. Biol. 87:911–940. [DOI] [PubMed] [Google Scholar]
- Matzura, O., and A. Wennborg. 1996. RNAdraw: an integrated program for RNA secondary structure calculation and analysis under 32-bit Microsoft Windows. Comput. Appl. Biosci. 12:247–249. [DOI] [PubMed] [Google Scholar]
- McCaskill, J. S. 1990. The equilibrium partition function and base pair binding probabilities for RNA secondary structure. Biopolymers. 29:1105–1119. [DOI] [PubMed] [Google Scholar]
- Owczarzy, R., P. M. Vallone, F. J. Gallo, T. M. Paner, M. J. Lane, and A. S. Benight. 1997. Predicting sequence-dependent melting stability of short duplex DNA oligomers. Biopolymers. 44:217–239. [DOI] [PubMed] [Google Scholar]
- Petersheim, M., and D. H. Turner. 1983. Base-stacking and base-pairing contribution to helix stability: Thermodynamic of double-helix formation with CCGG, CCGGp, CCGGAp, CCGGUp, and ACCGGUp. Biochemistry. 22:256–263. [DOI] [PubMed] [Google Scholar]
- Plum, G. E., A. P. Grollman, F. Johnson, and K. J. Breslauer. 1995. Influence of the oxidatively damaged adduct 8-oxodeoxyguanosine on the conformation, energetics, and thermodynamic stability of a DNA duplex. Biochemistry. 34:16148–16160. [DOI] [PubMed] [Google Scholar]
- Poerschke, D., O. C. Uhlenbeck, and F. H. Martin. 1973. Thermodynamics and kinetics of the helix-coil transition of oligomers containing GC basepairs. Biopolymers. 12:1313–1335. [Google Scholar]
- Poland, D. 1974. Recursion relation generation of probability profiles for specific-sequence macromolecules with long-range correlations. Biopolymers. 13:1859–1871. [DOI] [PubMed] [Google Scholar]
- Poland, D. 1981. Cooperative Equilibria in Physical Biochemistry. Clarendon Press. Oxford, UK.
- Puglisi, J. D., and I. Tinoco, Jr. 1989. Absorbance melting curves of RNA. Methods Enzymol. 180:304–325. [DOI] [PubMed] [Google Scholar]
- Sankoff, D., J. B. Kruskal, S. Mainville, and R. J. Cedergren. 1983. Fast algorithms to determine RNA secondary structures containing multiple loops. In Time Warps, String Edits, and Macromolecules: The Theory and Practice of Sequence Comparison. D. Sankoff and J. B. Kruskal, editors. Addison-Wesley, Reading, MA. 93–120.
- SantaLucia, J., Jr. 1998. A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl. Acad. Sci. USA. 95:1460–1465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seetharaman, S., M. Zivarats, N. Sudarsan, and R. R. Braker. 2001. Immobilized RNA switches for the analysis of complex chemical and biological mixture. Nat. Biotechnol. 19:336–341. [DOI] [PubMed] [Google Scholar]
- Shoemaker, D. D., E. E. Schadt, C. D. Armour, Y. D. He, P. Garrett-Engele, P. D. McDonagh, and P. M. Loer. 2001. Experimental annotation of the human genome using microarray technology. Nature. 409:922–927. [DOI] [PubMed] [Google Scholar]
- Sturtevant, J. M. 1987. Biochemical applications of differential scanning calorimetry. Annu. Rev. Phys. Chem. 38:463–488. [Google Scholar]
- Sugimoto, N., R. Kierzek, and D. H. Turner. 1987. Sequence dependence for the energetics of dangling ends terminal base pairs in ribonucleic acid. Biochemistry. 26:4554–4558. [DOI] [PubMed] [Google Scholar]
- Waterman, M. S. 1983. Sequence alignment in the neighborhood of the optimum with general application to dynamic programming. Proc. Natl. Acad. Sci. USA. 80:3123–3124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waterman, M. S., and T. H. Byers. 1985. A dynamic programming algorithm to find all solutions in a neighborhood of the optimum. Math. Biosci. 77:179–188. [Google Scholar]
- Williams, A. L., and I. Tinoco, Jr. 1986. A dynamic programing algorithm for finding alternate RNA secondary structures. Nucleic Acids Res. 14:299–315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zieba, K., T. M. Chu, D. W. Kupke, and L. A. Marky. 1991. Differential hydration of dA-dT base pairing and dA and dT bulges in deoxyoligonucleotides. Biochemistry. 30:8018–8026. [DOI] [PubMed] [Google Scholar]
- Zimm, B. H. 1960. “Theory of melting” of the helical form in double chains of the DNA type. J. Chem. Phys. 33:1349–1356. [Google Scholar]
- Zuker, M. 1989a. Computer prediction of RNA structure. Methods Enzymol. 180:262–288. [DOI] [PubMed] [Google Scholar]
- Zuker, M. 1989b. On finding all suboptimal foldings of an RNA molecule. Science. 244:48–52. [DOI] [PubMed] [Google Scholar]
- Zuker, M., and D. Sankoff. 1984. RNA secondary structures and their prediction. Bull. Math. Biol. 46:591–621. [Google Scholar]
- Zuker, M., and P. Stiegler. 1981. Optimal computer folding of large RNA sequences using thermodynamics and auxiliary information. Nucleic Acids Res. 9:133–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuker, M., D. H. Mathews, and D. H. Turner. 1999. Algorithms and thermodynamics for RNA secondary structure prediction: a practical guide. In RNA Biochemistry and Biotechnology. J. Barciszewski, and B. F. C. Clark, editors. NATO ASI Series. Kluwer Academic Publishers. Dordrecht, the Netherlands. 11–43.