On the Theory of Noncovalent Binding

Abstract

It is widely accepted that the binding constant of a receptor and ligand can be written as a two-body integral involving the interaction energy of the receptor and the ligand. Interestingly, however, three different theories of binding in the literature dictate three distinct integrals. The present study uses theory, as well as simulations of binding experiments, to test the validity of the three integrals. When binding is measured by a signal that detects the ligand in the binding site, the most accurate results are obtained by an integral of the Boltzmann factor, where the bound complex is defined in terms of an exclusive binding region. A novel prediction of this approach, that expanding a ligand can increase its binding constant, is borne out by the simulations. The simulations also show that abnormal binding isotherms can be obtained when the region over which the signal is detected deviates markedly from the exclusion zone. Interestingly, the binding constant measured by equilibrium dialysis, rather than by monitoring a localized signal, can yield a binding constant that differs from that obtained from a signal measurement, and that is matched best by the integral of the Mayer factor.

INTRODUCTION

The noncovalent binding of molecules in solution is of fundamental importance in biology, playing a key role in such basic processes as metabolism, regulation, and immunity. Noncovalent binding is of interest in chemistry too, where it may be exploited in chemical detection, separations, and the self-assembly of supramolecular structures. Thus, it is perhaps unexpected that the fundamental theory of noncovalent association is still in question. It is widely accepted that, given the potential of mean force acting between two molecules, the binding constant can be evaluated as an integral over the position of one molecule relative to the other; but at least three different forms of this integral have been espoused in recent publications (see below). The present article addresses this problem by a combination of theory and simulation.

It is useful to begin by reviewing the standpoint of the experimentalist, because it is experiment that provides the evidence for binding and yields the measured affinity that theory attempts to explain or predict. Perhaps the most common method of measuring a binding constant is to monitor a signal that is thought to be proportional to the concentration of the noncovalent complex; that is, by obtaining a binding isotherm. The signal may be spectroscopic, calorimetric, or—as in the measurement of enzyme inhibition by a bound ligand—functional. The value of the binding constant is then determined by fitting a theoretical curve to the experimental data. (Measuring the signal for a single concentration of R and L is rarely adequate because the signal's upper and lower baselines must be determined for a given value of the signal to be interpreted in terms of the extent of binding.) The theoretical form of the binding isotherm is obtained by considering the association of a receptor R and a ligand L to form the complex RL. The equilibrium constant for this reaction, the binding constant, may be written as

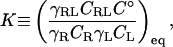(1)

where C_X and γ_X indicate, respectively, the concentration and activity coefficient of species X, C° is the standard concentration expressed in the same units as the other concentrations, and the subscript eq indicates a quantity evaluated under equilibrium conditions. It is often assumed that the activity coefficients are near 1, so these terms are frequently not written explicitly. (Note that K is free of units when C° is correctly included in its definition.) The binding isotherm gives the fraction of the receptor with bound ligand, r, as

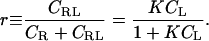(2)

With luck, an experimental isotherm will match this theoretical curve-fitting, in which case the binding constant K can be extracted via curve-fitting. If the experimental isotherm diverges significantly from the theoretical ideal, then it is appropriate to ask whether equilibrium dimerization is truly occurring and whether the signal being monitored is suitable.

In another experimental technique, equilibrium dialysis, a macromolecule at known concentration is trapped within a dialysis bag that is permeable to a smaller ligand. The ligand is allowed to equilibrate across the membrane, and the concentrations of ligand inside and outside the bag are measured. The excess concentration of ligand inside the bag is attributed to binding and hence is equated with the concentration of the complex, enabling evaluation of K. The value of K can be obtained from a full-fledged binding isotherm or, at least in principle, from a single measurement at a well-chosen ligand concentration.

The theoretician's challenge is to account for measured affinity data and ultimately to predict binding affinities to useful accuracy. The first requisite for accomplishing this is an energy model that accurately and efficiently provides the energy of the system as a function of its configuration. Developing such a model is highly nontrivial and will continue to be a subject of research in many labs, but it is not the focus of the present study. We address instead the second requisite, a theory or formula that says how to use an energy model to compute a binding affinity that can legitimately be compared with experiment. Three major competing theories are considered.

In one theory, K is evaluated as the integral of the Mayer factor over all space (Hill, 1986) (equivalent to the second virial coefficient),

(3)

where W is the potential of mean force between the two molecules. Thus, Groot focuses on the compressibility of a mixture of receptors and ligands to show that the binding constant is the integral over all space of the receptor-ligand correlation function, and notes that this quantity goes to the Mayer integral in the limit where receptor-receptor and ligand-ligand interactions are negligible (Groot, 1992). Dill reaches the same result via analysis of the equilibrium dialysis experiment (Stigter and Dill, 1996). An appealing feature of the Mayer integral is that there is little difficulty in defining what is meant by the complex: the integral extends over all space, yet is finite because the Mayer factor goes to zero at long range (which applies so long as the potential of mean force decays with the receptor-ligand distance r_RL more sharply than 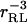). On the other hand, this theory yields the somewhat odd result that K_Mayer falls as the steric bulk of the receptor and ligand increase, because the Mayer factor equals −1 in the region where the ligand overlaps the receptor. Indeed, the binding constant can become negative if the overlap region is large enough. This result seems wrong, at least when affinity is measured via a signal as discussed above, because increasing the extent of steric overlap by itself should not reduce the fraction of receptor with ligand in the binding site. However, in the context of equilibrium dialysis, the result may be correct: increasing the amount of steric overlap will indeed reduce the number of ligands in the dialysis bag and thus decrease the apparent affinity of the receptor for the ligand. In fact, it has been pointed out that the equilibrium dialysis experiment could yield a negative binding constant (van Holde, 1971). One might say that the equilibrium dialysis experiment provides a global assessment of the interactions—both attractive and repulsive—of the receptor with the ligand, whereas the signal technique provides a local assessment of the affinity of a specific region of the receptor for the ligand.

An alternative theoretical approach involves viewing the bound complex, the free receptor, and the free ligand, as three distinct chemical species. From this perspective, the binding constant should be computed as the ratio of the partition function of the complex to the product of the partition functions of the free molecules. This approach is widely used to compute covalent binding constants, as exemplified by the treatment of the reaction 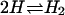in many physical chemistry textbooks, and there is no obvious reason why it should not be applicable to noncovalent binding as well. Assuming classical statistical thermodynamics where the spacing of quantized energy levels is assumed to be much smaller than thermal energy, as was also done for the other two theories of binding considered in this article, the binding constant in this approach is simply the integral of the Boltzmann factor for the potential of mean force of the receptor and ligand (Chandler, 1979; Shoup and Szabo, 1982; Jorgensen, 1989; Gilson et al., 1997):

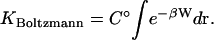(4)

(The Appendix reviews how this expression can be obtained for the reaction 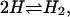starting from the usual translational, rotational, and vibrational partition functions.) However, this approach poses a problem that is particularly noticeable in the case of noncovalent binding: the Boltzmann factor does not go to zero as W goes to zero at long range, so K_Boltzmann is at risk of becoming infinite. Thus, to apply this formula, one must define the domain of integration, in effect establishing the receptor-ligand distance at which the receptor and ligand no longer form a complex. When the potential of mean force has a deep and circumscribed energy well, any definition of the complex that encompasses the energy well and does not extend much further will give reasonable results (Gilson et al., 1997). However, for a weak and/or long-ranged interaction potential, the definition of the complex matters and it is difficult to decide where to draw the line. Thus, for the association of two amides in water, the binding constant computed with this formula was found to vary 1200-fold as the integration range varied by 2 Å (Jorgensen, 1989). Two relatively clear definitions of the complex have been proposed. One suggests that, when binding is detected via a signal, the Boltzmann integral should range over those conformations in which the signal is detected (Gilson et al., 1997; Luo and Sharp, 2002). Another suggests that the integral extend outward from the base of the energy well to the −1 kT isopotential contour, so that the ligand is considered “bound” when its attraction to the receptor exceeds thermal energy (Luo and Sharp, 2002). However, neither of these suggestions has been validated by comprehensive theory or by comparison with simulated binding experiments. It may also be tempting to argue that the very idea of a ligand-receptor complex is an artificial construct. Thus, the Boltzmann integral has been incorporated into theories of ion-pairing to explain deviations from Debye-Hückel theory (Bjerrum, 1926; Prue, 1969; Justice and Justice, 1976). In this context, the distance at which two ions cease being a “pair” can be chosen based upon theoretical convenience (Justice and Justice, 1976). However, for pairwise noncovalent binding, the definition of the bound complex cannot be arbitrary because even a weak binding interaction can generate a perfectly reasonable isotherm that fits the chemical equilibrium model and thus yields a single distinct value of the binding constant. Thus, it would appear, as previously pointed out (Groot, 1992), that nature knows how to define the complex, even if we do not.

A third theoretical approach, pioneered by Andersen (1973) and further developed by Hoye and Olaussen (1980), and Wertheim (1984), explicitly accounts for a solution of ligands and receptors, rather than limiting attention to a single ligand and receptor as in the two theories discussed above. Central to this theory is an exclusive, or saturating, energy model; that is, one where a receptor and ligand do not attract other receptors or ligands once they have paired off. Exclusivity is essential for dimerization: if each receptor could bind multiple ligands and each ligand could bind multiple receptors, then one would see polymerization or even a phase change, rather than dimerization. In what will here be called the Andersen theory, cluster expansions are used to show that an exclusive interaction potential leads to formation of ligand-receptor dimers, and that the concentration of dimers is related to the concentrations of free ligands and free receptors by a binding equilibrium. The binding constant is computed by separating the interaction potential into two parts: a short-ranged, repulsive part W_R and a softer, longer-ranged, attractive part W_A. The binding constant is then given by

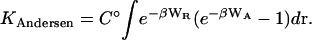(5)

(Hoye and Olaussen use this same approach, but their formula for K has the form of the Mayer integral because their RL interaction potential includes no steric contribution.) This formula appears to have two practical advantages. First, because the term 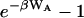goes to zero at long range, there seems to be no need for the geometric definition of the complex that is required to obtain a finite value of K_Boltzmann. Second, the term 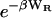brings the integrand to zero in the steric overlap region, so steric overlap does not affect the binding constant. Thus, the Andersen formula combines some of the advantages of the Mayer and Boltzmann formulae above. On the other hand, there is a new ambiguity because it is not always clear how W is to be separated into W_R and W_A. It also is not clear how to handle an attractive potential with a long-ranged component that extends beyond the zone in which binding is exclusive. Finally, this theory, like the Mayer theory, predicts that the binding constant goes to zero as the depth of the attractive energy well goes to zero, even though it is clearly possible to observe “complexes,” as defined by a spectroscopic signal, even if the attractive potential goes to zero. Accordingly, Jackson and co-workers note that the number of ligand-receptor complexes from this theory will not correspond exactly to the number obtained by a count of ligand-receptor pairs that are within bonding distance (Jackson et al., 1988).

In summary, pairwise noncovalent binding is more subtle than it initially might appear, and there is still no generally accepted theory for this fundamental phenomenon. From a practical standpoint, although the differences among the three theories diminish for small, tight-binding molecules, there are receptor-ligand systems that bind weakly enough for the theories to differ significantly, so the question of which theory to use is important if one wishes to develop quantitative models of weak binding. This article therefore seeks to further elucidate the theoretical basis of pairwise noncovalent binding. The central approach is to compare theory with simulations designed to mimic actual experimental measurements. Two types of experiments are considered: 1) spectroscopic detection of binding to generate an isotherm that is fitted to a theoretical isotherm, and 2) equilibrium dialysis. To our knowledge, this article represents the first direct comparison of the three theories discussed above.

The article is organized as follows. The Theory section presents a novel combinatorial theory of binding which shows that exclusive binary associations lead directly to the standard binding isotherms associated with Eq. 1 and indicates that, when binding is measured via a signal, the binding constant is an integral of the Boltzmann factor (K_Boltzmann), whereas when binding is measured by equilibrium dialysis, the binding constant is the integral of the Mayer factor (K_Mayer). Methods describes Monte Carlo simulations used to test the theories of binding discussed above, and Results and Discussion compares the simulation results with theory.

THEORY

The theory of Andersen (1973), Hoye and Olaussen (1980), and Wertheim (1984) hinges on a recognition of the importance, for pairwise binding, of exclusivity in the interaction between the receptor and the ligand. Pairwise exclusivity is a requirement for the formation of dimers, as opposed to higher order multimers or even a phase transition, as concentration increases. Exclusivity also provides an intuitively satisfying explanation of the fact that the binding constant can be written as an integral involving only one ligand and one receptor, rather than requiring an integral over all ligands and receptors because exclusivity implies that, when a ligand and a receptor interact attractively, they are effectively isolated from the other molecules in the system. However, this theoretical approach has not been used to directly address the actual methods used to measure binding affinity; i.e., measurement via a spectroscopic signal or equilibrium dialysis.

Here, we describe a simplified theory built on the basic insight that binary binding requires an exclusive, attractive interaction between two molecular species. When a signal is used to measure binding, the theory yields a standard binding isotherm with a binding constant that equals the integral of the Boltzmann factor. When equilibrium dialysis is used to measure binding, however, the Mayer factor is obtained.

Measurement of binding via a spectroscopic signal

Consider a one-dimensional box of length L that contains N_R receptors and N_L ligands, with concentrations C_R = N_R/L and C_L = N_L/L, respectively. Only pairwise interactions are considered to exist. The molecules can have two orientations; that is, each molecule can be viewed as having an arrow that points in either the positive or negative direction. Each receptor has a steric part of length R_H which entirely excludes ligand, and an attractive part of length R_A that can be occupied by at most one ligand; hence, this part is called the exclusion zone. When a ligand is in a receptor's exclusion zone, the ligand-receptor interaction energy is either 0 or ε, where ε < 0, depending upon the relative orientations of the receptor and the ligand. We first consider the case where the ligand-receptor energy is ε only when the ligand and receptor are oriented toward each other. Ligand-ligand interactions are treated as point-like and the receptors are treated as fixed in position and orientation, a model that is appropriate when the receptors are dilute. The receptors' contribution to the partition function is constant and can therefore be set aside. The system is diagrammed in Fig. 1.

FIGURE 1.

Diagram of one-dimensional system treated in the Theory section. Three receptors are shown as elongated rectangles with a black steric exclusion zone and a clear exclusion zone, and an arrow to indicate orientation; two are oriented to the right, and one to the left. Three ligands are also shown as hatched rectangles of finite size, although the theory treats them as particles of zero size. Two ligands are oriented to the left and one to the right, and one is bound to the leftmost receptor.

The partition function can be written as a sum of the contributions made by states with different numbers n = [1, min(N_L, N_R)] of ligands bound to receptors,

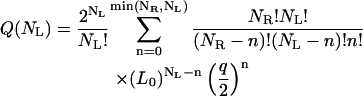(6)

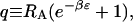(7)

where L₀ is the free volume accessible to the ligands L₀ = L − N_R(R_H + R_A), q is the partition function of one ligand in the energy well of one receptor, and factors of the de Broglie wave length that will cancel in the final results have been omitted. The partition function in Eq. 6 can be rewritten in the compact form

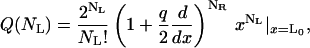(8)

which can then be used to obtain the following expression for the semigrand canonical partition function in L,

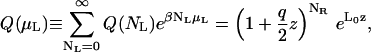(9)

where μ_L is the chemical potential of the ligand, and z is the activity, 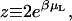the factor of 2 resulting from the two possible orientations of the ligand can adopt. Note that the concentration of the free, point-like ligand in a reservoir in equilibrium with this system will be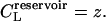

This system is monitored by a signal that turns on when a ligand is in a receptor's exclusion zone, independent of their relative orientation; thus, the signal is generated even if the ligand does not interact favorably with the receptor. This model corresponds to a signal, such as fluorescent resonance energy transfer, which is insensitive to conformational details. If the signal produced by one ligand in one exclusion zone is s₀, then the signal per unit length s (signal density) is proportional to the concentration of ligands in exclusion zones. From Eq. 9,

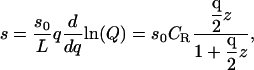(10)

and the limiting signal density at high ligand concentration is

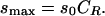(11)

Thus, an experimentalist monitoring the signal density as a function of the activity of ligand, z, would find the fractional occupancy of receptors by ligands, r, to be

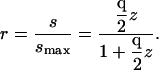(12)

This expression has the functional form expected for a binary binding isotherm (Eq. 2) and thus permits the apparent binding constant K to be identified with Boltzmann integral q/2:

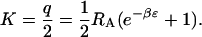(13)

Here, the factor of ½ results from the ligand's loss of orientational freedom upon binding, and corresponds to the factor of 1/8 π² in three-dimensional binding theory (Gilson et al., 1997).

In a real system, there is no guarantee that the conformations in which the signal is generated will coincide exactly with the exclusion zone. To examine the consequences of a mismatch between these two regions, we now consider the case in which signal is detected only when the ligand interacts favorably with a receptor: it must be within an exclusion zone and oriented correctly. In this case, the signal density becomes

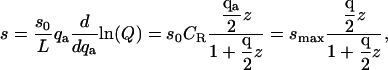(14)

where 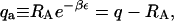and the maximal signal density s_max is given by

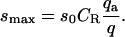(15)

Interestingly, although the signal now registers only a fraction of the ligands within exclusion zones, the apparent binding constant is unchanged at q/2, the integral of the Boltzmann factor over the entire exclusion zone. However, the apparent strength of the signal is reduced by the factor q_a/q; i.e., by the probability that a ligand in the exclusion zone is oriented so as to generate signal. Other modifications of the signal clearly will yield analogous results so long as the signal is confined to the exclusion zone.

The present analysis shows that exclusive binding suffices to reproduce the standard binding isotherm and furthermore identifies the binding constant with the integral of the Boltzmann factor over the exclusion zone. This result supports the validity of viewing the bound complex as a separate chemical species with its own chemical potential that is computable as a Boltzmann integral. Moreover, the apparent chemical potential of the complex equals the integral of the Boltzmann factor over the exclusion zone, so long as the signal used to detect binding turns on for every ligand position in the exclusion zone. However, it is not necessary for the signal to turn on for every orientation of the ligand. The simulations described in Results show furthermore that if the signal does not yield the expected value of the affinity, the full isotherm will show a marked deviation from ideality.

Although the present model is set in one dimension, it can be extended in a straightforward way to higher dimensions, where it still yields the result that the binding constant is the integral of the Boltzmann factor for the ligand in the exclusion zone,

(16)

where W is the receptor-ligand potential of mean force, and r is the position of the ligand with respect to the receptor; the factor of 1/N is a normalization constant for the rotational degrees of freedom that equals 2 for the one dimensional case, 2π for two dimensions, and 8π² for the three dimensional case; and the factor of standard concentration, C° = 1 mol/liter = 1 molecule/1660 ų, has been added for completeness (Gilson et al., 1997).

Proposed definition of the exclusion zone

The chief weakness of the theory presented above is that its exclusion regions are artificially simple. In reality, a ligand moving away from the energy minimum and out into solution might continue to feel an attractive potential even as it left room for a second ligand to occupy the binding site. We suggest that it is natural to define the exclusion zone—i.e., the domain over which the Boltzmann constant should be integrated—as the region that includes the local energy minimum associated with the binding site and that is extended until the two molecules, R₁ and L₁, move far enough apart that a second receptor or ligand, R₂ or L₂, can interact more strongly with either L₁ or R₁, respectively. If the integral is carried out in a coordinate system rooted in R₁, then the integral extends over all positions, orientations, and conformations of L₁ for which the R₁−L₁ interaction is stronger than any R₁−L₂ or L₁−R₂ interaction. This definition makes sense intuitively because once another ligand, say, has room to interact more strongly with R₁ than L₁, it is the second ligand that will qualify as bound, so the integral for L₁ should terminate at that limit.

Measurement of binding by equilibrium dialysis

In equilibrium dialysis, the concentration of receptor-ligand complexes is measured as the difference between the total concentration of ligand in the dialysis bag and the concentration of ligand in a receptor-free reservoir at equilibrium with the system. The combinatorial theory of binding introduced above may be applied to this experiment as follows. The concentration of ligand in the reservoir, 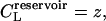as noted above; and Eq. 9 can be used to derive the total concentration of ligand in the bag C_L, the concentration of ligand-receptor complexes C_RL, and the concentration of free receptor 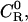as

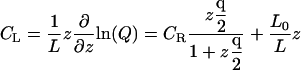(17)

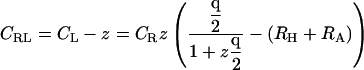(18)

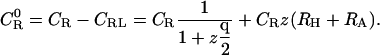Hence,

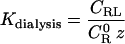(19)

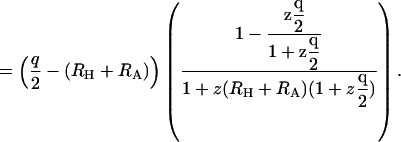(20)

The quantity (q/2) − (R_H+R_A) is K_Mayer for the R−L interaction potential in this system, and the quantity by which K_Mayer is multiplied in Eq. 20 goes to 1 as the ligand is dilute; that is when the activity of the ligand, z, goes to zero. This result suggests that the binding constant derived from an equilibrium dialysis experiment differs from that obtained by monitoring a signal, and that it asymptotically approaches the Mayer integral as ligand becomes dilute. These results are consistent with the simulation results described below.

BINDING SIMULATIONS

Metropolis Monte Carlo simulations of rigid model receptors R and ligands L are used here to test theories of binding. The R−L interaction potentials are designed so that only one ligand at a time can interact strongly with a given receptor, except as otherwise noted; this prevents the formation of aggregates larger than dimers (Andersen, 1973; Hoye and Olaussen, 1980; Wertheim, 1984). Most of the simulations are carried out in two dimensions with simple interaction potentials that consist of hard-core R−R and L−L interactions and an R−L interaction that combines a hard-core interaction with a local energy well. Several additional simulations are done for a three-dimensional system that includes a 6–12 Lennard-Jones potential in the R−R, R−L, and L−L interactions, along with a smoothly varying r⁻³ interaction with a distance cutoff. The simulations model the measurement of binding by a signal and by equilibrium dialysis.

For signal-based measurements, a signal is considered to turn on when the ligand occupies a specified zone in or near the receptor's binding site, and the average signal strength is computed for various ligand concentrations. The resulting graphs of signal strength as a function of ligand concentration are fitted to a standard binding isotherm to extract an “experimental value” of the binding constant K_isotherm. The activity of L is controlled by dividing the simulation region into two parts. Receptors are allowed to occupy only the main part, but the ligands are allowed to equilibrate between the main part and a reservoir region in which the ligands are treated as ideal gas particles, ensuring that their activity coefficient in this region is unity. The activity of L is adjusted by adjusting the total number of ligands, and in some cases by imposing a uniform potential field in the reservoir region. The activity coefficients of the receptors and the receptor-ligand complexes are expected to be about equal and thus to cancel, to good approximation. This expectation was validated by computing several binding constants under very dilute conditions that gave good agreement with binding constants obtained under the conditions described above.

To speed the calculations, some simulations include only a single receptor fixed in position. The validity of this approach was demonstrated by comparisons with two-dimensional simulations for four mobile receptors. One set of simulations involved four mobile receptors in a box of size 40 u × 40 u. For well depths −0.1 and −0.5 kcal/mol, isotherms were generated by carrying out simulations in which the total number of ligands started at 240 and decreased in steps of 12, with 4 × 10⁶ Monte Carlo steps per particle; for well depths of −1.0 and −2.0 kcal/mol, the total number of ligands decreased from 160 in steps of 8, with 5 × 10⁶ Monte Carlo steps per particle. The other simulations involved a single receptor fixed at the center of a box of size 20 u × 20 u. For well depths −0.1 and −0.5 kcal/mol, the total number of ligands decreased from 60 in steps of 3, with 3 × 10⁶ Monte Carlo steps per particle; for well depths of −1.0 and −2.0 kcal/mol, the total number of ligands decreased from 40 in steps of 2, with 5 × 10⁶ Monte Carlo steps per particle. The signal strength was plotted versus the activity of L and binding constants were extracted from these isotherms by data fitting. As shown in Table 1, the binding constants from the single-receptor simulations agree well with those from the multiple-receptor simulations.

TABLE 1.

Comparison of binding constants from binding isotherms for simulations with one fixed receptor (K_isotherm(1)) and with four mobile receptors (K_isotherm(4)), for Potential A and Potential B described in Two-Dimensional Simulations

	Potential A		Potential B
ɛ	Kisotherm(1)	Kisotherm(4)	Kisotherm(1)	Kisotherm(4)
−0.1	8.8	8.9	10.5	9.9
−0.5	11.2	10.9	13.4	12.2
−1.0	17.9	17.0	21.2	18.8
−2.0	74.8	63.0	85.2	67.9

ɛ: depth of the potential energy well (kcal/mol).

For simulations of equilibrium dialysis, the system is divided into a “dialysis bag” containing both R and L, and a reservoir that only L can enter and in which L retains its L−L interactions. The equilibrated concentrations of L inside and outside the bag are used to compute the number of bound complexes and hence the binding constant. The dialysis bag contains two receptors, and 10 ligands are allowed to equilibrate between this region and the ligand reservoir of equal size outside the dialysis bag, where L−L interactions in the reservoir are the same as in the dialysis bag. The number of Monte Carlo steps is 5 × 10⁷ per particle and the dialysis bags range in size from 20 u × 20 u to 120 u × 120 u. A single simulation suffices to calculate a binding constant by this method, and simulations over the range of ligand concentrations agree with each other to within ∼10%. The reported results are for the most dilute systems.

All energies are expressed in kcal/mol, but the distance units (u) used here are arbitrary, especially for the two-dimensional simulations. For the three-dimensional simulations, the distance units can be assigned specific values so that binding constants can be computed with respect to the standard concentration of 1 mol/liter.

Two-dimensional simulations

Square-well ligand-receptor interaction potentials

Here the R−R and L−L pairs interact as pure hard disks with radii of 3 u and 1.5 u. The R−L pair has a hard-disk interaction which turns on below a R−L distance of 4.5 u, and which is modified by a wedge-shaped binding site. Simulations are reported for well depths ε of −0.1 to −4.0 kcal/mol . Two forms of binding site are considered, as diagrammed in Fig. 2:

• Potential A. When the R−L axis is within ±α, where α = 30°, of a receptor axis defining the binding site, the interaction energy E ≤ 0 instead of being repulsive. It is zero except when the center-to-center distance r_RL satisfies 1.5 u < r_RL < 2.5 u, in which case E = ε < 0.

• Potential B. When the R−L axis is within ±α, where α = 19.5°, of a receptor axis defining the binding site, the interaction energy E ≤ 0 instead of being repulsive. The ligand also possesses an axis, and the interaction energy E = ε < 0 only when 2.5 u < r_RL < 4.5 u and the orientation of the ligand is within ±90° of the binding site axis.

FIGURE 2.

Diagram of Potential A (left) and Potential B between receptor and ligand, as a function of position of the center of the disk-shaped ligand. Steric zones are dark and attractive zones are demarcated by arcs. For Potential B, the ligand feels the attractive potential only when it is oriented to within ±90° of the axis of the binding site.

Except as otherwise noted, the binding signal is considered to be detected when the ligand lies within the angular region of the wedge-shaped binding site defined by α and has 1 u < r_RL < 4 u for Potential A and 2 u < r_RL < 5 u for Potential B. For Potential B, where the ligand possesses an orientational degree of freedom, the signal is independent of the ligand's orientation except as otherwise noted. Note that the R−L interaction potential is such that at most one ligand can occupy either of these signal zones, so the signal zones conform closely to the exclusion zones. To examine the consequence of a signal zone that deviates markedly from the exclusion zone, results are also presented for Potential A with a signal zone having the same angular range, but the smaller radial range 2 u < r_RL < 3 u. It is worth emphasizing that the signal zones play no role in the equilibrium dialysis simulations.

Funnel-like ligand-receptor interaction potentials

As discussed in Results, the square-well potentials are too simple to allow some questions to be addressed. Therefore, additional simulations are reported with funnel-like receptor-ligand potentials constructed as nested square-wells. The receptor-ligand interaction is pure hard-sphere except when the ligand lies within a wedge-shaped binding site defined around a receptor axis. The interaction energy is as follows: 0 if the ligand lies in the ±30° wedge unless it lies in a deeper part of the well; −2 if 1.5 u < r_RL < 2.5 u unless it lies in a deeper part of the well; −4 if 1.7 u < r_RL < 2.3 u and |θ| < 9° unless the ligand lies in the deepest part of the well; and −6 if 1.97 u < r_RL < 2.03 u and |θ| < 1°, where θ is the angular position of the ligand relative to the binding site axis. Two sizes of ligand are considered, a small ligand with radius 0.1 u, and a large ligand with radius 3 u. It should be emphasized that the radius of the ligand does not influence the spatial extent of the energy well seen by the ligand within the wedge-shaped binding site. It only affects the purely repulsive receptor-ligand interactions outside this angular zone and, importantly, interactions with other ligands. Therefore, the Boltzmann integral for the small ligand over the exclusion zone of the large ligand essentially equals the Boltzmann integral of the large ligand over the same region, and vice versa. It should also be noted that the exclusion zone of the small ligand, which corresponds approximately to the −6 kcal/mol part of the energy well, is much smaller than that of the large ligand, which includes the entire energy well.

Several different signal zones are considered for the funnel-like energy wells. Initially, the signal zones correspond closely to the exclusion zones of the respective ligands. (See Proposed Definition of the Exclusion Zone.) Further simulations are then done for the large ligand using the small ligand's signal zone, and vice versa. Finally, simulations of the large ligand are carried out with a signal zone having the same angular extent as the exclusion zone, but extending over only 0 u < r_RL < 1.7 u.

Three-dimensional simulations

Simulations of three-dimensional systems in which receptors and ligands interact with van der Waals and dipole-dipole-like forces are included as a more realistic test of the theories considered here. The R−R, L−L, and R−L interactions are hard-core in nature for distances <5.0, 3.0, and 4.0 u, respectively, but the hard-core interactions are supplemented with a Lennard-Jones interaction 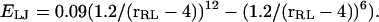The R−L interaction is modified by a wedge-like cutout to form a binding site with a ±45° aperture extending as close as 1.0 u to the center of the receptor. Thus, the R−L interaction is hard-core at a distance closer than 1 u in the binding site, but beyond this offset the ligand feels a Lennard-Jones interaction 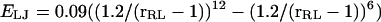and a dipole-dipole-like potential that depends on the angle θ_RL between the R−L axis and the binding-site axis:

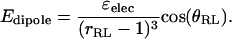(21)

Here ε_elec determines the strength of the interaction, and simulations are reported for values of −4.1, −5.1, and −7.7 kcal–u³/mol. This interaction is cut off by setting E_dipole to 0 for R_RL > 6.5 u. These potentials are of interest because the interactions are smoothly varying and include a nonexclusive attractive component, notably the trench-like Lennard-Jones energy well that surrounds the receptor. The exclusion zone, as defined in Proposed Definition of the Exclusion Zone, corresponds approximately to the region where 1 u < r_RL < 5 u within the wedge-like cutout.

The binding isotherm simulations are run in a 20 u × 20 u × 20 u box containing one receptor and from 0 to 100 ligands, in steps of five ligands. The main simulation box is in equilibrium with a 20 u × 20 u × 5 u reservoir that does not admit receptors and where the ligands are treated as ideal gas particles. In some cases, the chemical potential of ligands in the reservoir is modified by imposition of a uniform potential in the range of −5 to 0 kcal/mol. Simulations are equilibrated with 10⁶ Monte Carlo steps per molecule in the system, and data are gathered with 10⁷ steps per molecule. A signal is considered to be detected when the ligand-receptor distance is between 1 u and 6 u, and when the angular position of the ligand is within the binding site's angular boundaries.

The equilibrium dialysis simulations use a dialysis bag of dimensions 50 u × 50 u × 50 u that contains two receptors, and 10 ligands are equilibrated between the bag and a reservoir of equal size in which the ligands interact as in the bag. The simulations are run for 5 × 10⁸ Monte Carlo steps per particle.

Data fitting

Binding constants are extracted from simulated isotherms by fitting computed signal strengths to the standard binding isotherm. The program Mathematica is used to minimize the root mean-square deviation between the data and the ideal curve. In accord with experimental practice, a separate upper asymptote is fitted to each isotherm. The curve-fitting uses data from 5% to 90% of the apparent saturation value, except for a few of the weakest binding cases where the fit extends to 80% saturation because it is difficult to reach sufficiently high concentrations.

Evaluation of binding integrals

The simulations described above provide the “experimental” binding constants to which the theories discussed in the Introduction are compared. The theoretical binding constants are computed by integration of the Mayer factor, the Boltzmann factor, and the Andersen integrand, for the various R−L interaction potentials. The Mayer and Andersen integrals are evaluated analytically for the two-dimensional systems. For Potential A, the Andersen integral is the Mayer factor multiplied by the area of the energy well,

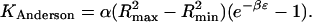(22)

For Potential B, the form is the same but because the potential goes to 0 for half of the possible ligand orientations, a factor of ½ appears,

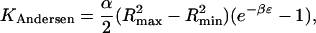(23)

where R_min and R_max are the minimum and maximum extent of the attractive well. The Mayer integrals are the same except that the area of the area of hard-core interaction is subtracted,

(24)

where R is the hard-core diameter of the R−L interaction. Similar formulae apply to the funnel-shaped interaction potentials.

For the three-dimensional systems, the Mayer integral is evaluated numerically by positioning the ligand on a polar grid around the receptor. The distance r_RL is sampled from 1 to 8 u in 560 steps; cos θ is sampled from −1 to 1 in 80 steps; and φ is sampled from 0 to 2π in 128 steps. The Andersen integral is not evaluated for the three-dimensional systems because it is not clear how to separate the smoothly varying interaction potential into repulsive and attractive parts as required by the theory; see Introduction.

The integration domain for the Boltzmann integral proposed in Proposed Definition of the Exclusion Zone is based upon three-body interactions and is evaluated numerically. The integrals are done by considering two ligands, L₁ and L₂, in the presence of a receptor, R₁, which is kept fixed. The Boltzmann factor is integrated over the coordinates of L₁, whereas L₂ competes with L₁ for binding at the energy minimum. In principle, a second receptor, R₂, also competes with R₁, but the geometry of the molecules is such that, as R₁ and L₁ are separated, a second ligand L₂ will always slip in and compete with L₁ before R₂ can fit in and compete with R₁. Therefore, only a second ligand is considered in the present calculation. The two ligands interact either by hard steric interactions (two-dimensional systems) or Lennard-Jones interactions (three-dimensional systems). The integral over the coordinates of Ligand 1 is started at the center of the energy well and is extended until L₁ is far enough away from the receptor that L₂ can enter the energy well and find a conformation of lower energy. More specifically, L₁ is initially placed at the center of the energy well of interest and its position is sampled on expanding circular shells (spherical shells for three-dimensional systems) around this point. For each position of L₁, L₂ samples all positions previously occupied by L₁. If L₂ can find a point that is unobstructed by L₁ and that has a lower (more stable) energy of interaction with the receptor than that of L₁, then L₂ is considered to be bound instead of L₁; otherwise, L₁ is considered to be bound, and the Boltzmann factor for its interaction with the receptor is computed and is added to the running binding integral. This integral effectively terminates when L₁ is far enough away from the energy well that L₂ can always find a position at lower energy than L₁. When the L−L interaction is smoothly varying, L₂ is considered to be obstructed by L₁ when the L−L interaction is >10 kcal/mol. Note that a grid point is considered to contribute to the binding constant if L₁ can adopt any orientation that endows it with lower energy than L₂, can attain in any orientation on any grid point previously occupied by L₁.

For Potential A in two dimensions, the ligand positions are sampled at distances from 0 to 3 u away from the center of the energy well in 120 steps, with θ varying between 0 and 2π in 120 steps. For Potential B, the sampling is the same except that the orientation of the ligand is also sampled from 0 to 2π in 12 steps. For the funnel-shaped energy wells in two dimensions, the positions of the small ligand are sampled in 500 radial steps of size 0.0004 u centered on the energy well at r_RL = 2.0 u, and 500 steps in θ of size 2π/500. The positions of the large ligand are sampled with the same θ steps but the radial steps are 0.0004 u for r_min < 0.05, 0.004 for < 0.05 u < r_min < 0.3, and 0.01 for 0.3 u < r_min < 3 u, where r_min is the distance from the center of the energy well. For the three-dimensional systems, ligand positions are sampled at distances from 0 to 4 u away from the energy minimum in 80 steps; cos θ is sampled from −1 to 1 in 20 steps; and the azimuthal angle is sampled from 0 to 2π in 60 steps.

RESULTS

Signal-based measurement of binding in two dimensions

Square-well potentials

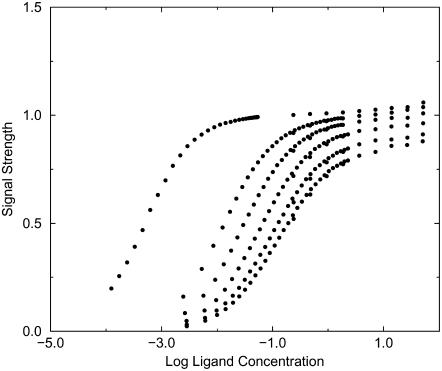
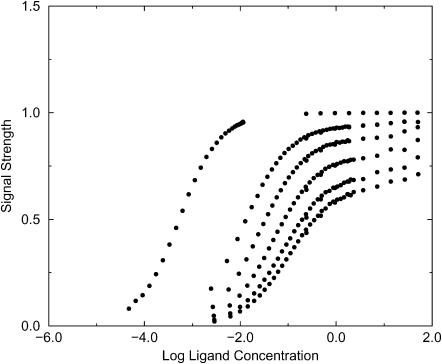
When the signal used to monitor binding conforms approximately to the exclusion zone defined in Evaluation of Binding Integrals, the binding isotherms from the simulations conform quite well to ideal isotherms as shown in Figs. 3 and 4. The isotherms in these figures can be treated as experimental data and used to extract binding constants via curve-fitting. These experimental binding constants can then be used to test the theories discussed in the Introduction. The results for the two-dimensional simulations, shown in Tables 2 and 3, clearly indicate that the Boltzmann integral over the exclusion zone, K_Boltzmann,ex, yields the most accurate results, whereas the Mayer integral is the least accurate; however, the agreement among the three theories improves for strong binding, as expected from the form of the integrals. It is also of interest to examine K_Boltzmann,kT, the Boltzmann integral over the region where the receptor-ligand interaction potential is <−kT. For these simplified potentials K_Boltzmann,kT = K_Boltzmann,ex, except when ε > −kT, in which case, erroneously, K_Boltzmann,kT = 0.

FIGURE 3.

Simulated binding isotherms for Potential A with well-depths −4, −2, −1.5, −1, −0.5, and −0.1 kcal/mol.

FIGURE 4.

Simulated binding isotherms for Potential B with well-depths −4, −2, −1.5, −1, −0.5, and −0.1 kcal/mol.

TABLE 2.

Comparison of binding constants extracted from simulated isotherms with theoretical binding constants for Potential A

		Theoretical integrals
ɛ	Kisotherm	KBoltzmann,ex	KMayer	KAndersen
−0.1	8.8	8.3	−52.4	0.4
−0.2	9.3	8.8	−51.9	0.9
−0.3	9.8	9.3	−51.4	1.4
−0.4	10.4	10.0	−50.7	2.0
−0.5	11.2	10.7	−50.0	2.8
−0.6	12.0	11.6	−49.1	3.7
−0.7	13.3	12.7	−48.0	4.7
−0.8	14.5	13.9	−46.8	6.0
−0.9	16.0	15.4	−45.3	7.5
−1	17.9	17.1	−43.6	9.2
−1.1	20.2	19.2	−41.5	11.3
−1.2	23.0	21.6	−39.1	13.7
−1.3	26.1	24.5	−36.2	16.6
−1.4	29.9	27.9	−32.8	20.0
−1.5	34.4	31.9	−28.8	24.0
−1.6	39.6	36.7	−24.1	28.7
−1.7	46.5	42.3	−18.5	34.3
−1.8	54.3	48.9	−11.9	40.9
−1.9	63.4	56.7	−4.1	48.7
−2	74.8	65.9	5.1	57.9
−4	1780	1690	1630	1680

ε: depth of energy well in kcal/mol.

TABLE 3.

Comparison of binding constants extracted from simulated isotherms with theoretical binding constants for Potential B

		Theoretical integrals
ɛ	Kisotherm	KBoltzmann,ex	KMayer	KAndersen
−0.1	10.5	7.6	−56.3	0.4
−0.2	11.0	8.1	−55.8	0.9
−0.3	11.7	8.7	−55.2	1.5
−0.4	12.5	9.4	−54.5	2.3
−0.5	13.4	10.2	−53.7	3.1
−0.6	14.6	11.2	−52.7	4.1
−0.7	15.7	12.4	−51.5	5.3
−0.8	17.3	13.8	−50.1	6.6
−0.9	19.0	15.4	−48.5	8.3
−1	21.2	17.3	−46.5	10.2
−1.1	23.6	19.6	−44.3	12.5
−1.2	26.4	22.3	−41.6	15.2
−1.3	30.2	25.5	−38.4	18.4
−1.4	34.4	29.3	−34.6	22.1
−1.5	39.7	33.7	−30.2	26.6
−1.6	45.5	38.9	−24.9	31.8
−1.7	52.9	45.2	−18.7	38.0
−1.8	61.9	52.5	−11.4	45.3
−1.9	72.1	61.1	−2.8	54.0
−2	85.2	71.4	7.4	64.2
−4	1990	1870	1810	1860

ɛ: depth of energy well in kcal/mol.

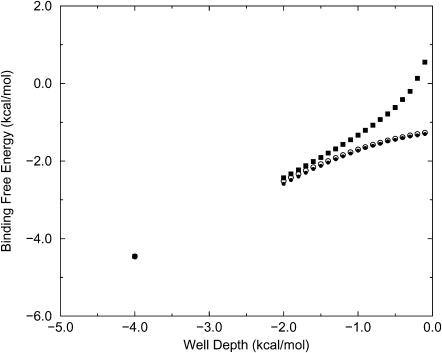
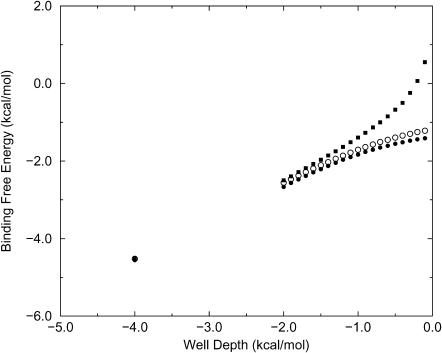
The binding constants K can be converted into binding free energies by the expression ΔG = −RT ln K, and Figs. 5 and 6 graph these energies as a function of the well depth for the two-dimensional simulations. The agreement between K_Boltzmann and the simulated binding constants is again apparent, as is the systematic deviation of K_Andersen from the simulation results for weak binding. (Binding free energies are not shown for the Mayer formula because ΔG is mathematically undefined when K < 0.) In considering the relationship between well-depth and binding free energy, it should be kept in mind that the present binding free energies are not referred to an accepted standard concentration because there is no standard for a two-dimensional system; because C° is not included explicitly, the standard concentration is, in effect, 1 molecule/u². If a different standard were applied, however, all the binding free energies would merely be shifted by a single offset.

FIGURE 5.

Calculated binding free energy versus well-depth (kcal/mol) for Potential A (data in Table 2). •, simulation; ○, Boltzmann formula; ▪, Andersen model.

FIGURE 6.

Same as previous figure but for Potential B (data in Table 3).

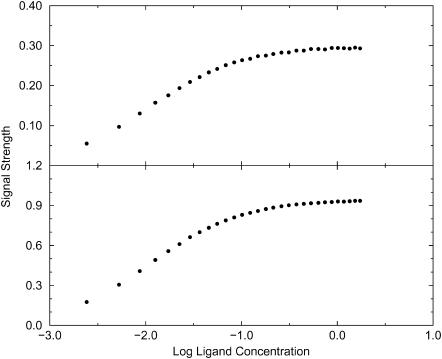
When the signal used to detect binding deviates markedly from the exclusion zone, nonideal and potentially misleading binding isotherms can be obtained. For example, the top graph in Fig. 7, which clearly is not an ideal binding isotherm, is obtained if the signal is assumed to turn on only when the ligand lies in a 2–3 u distance range from the receptor. For comparison, the normal isotherm obtained with the larger original signal zone is presented in the bottom graph. Note that the value of 17.9 extracted from the normal isotherm corresponds closely with the Boltzmann integral over the exclusion zone, 17.1.

FIGURE 7.

Simulated binding isotherms for Potential A with well-depth −1 kcal/mol. (Top) Signal detected for 2 u < r_RL < 3 u. (Bottom) Signal detected for 1 u < r_RL < 4 u.

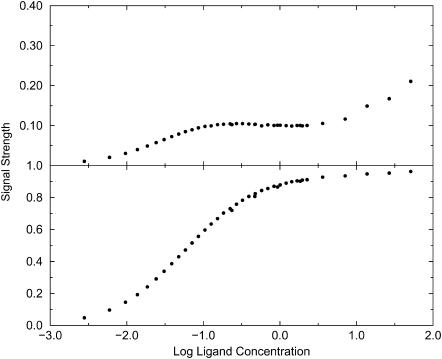
It is also of interest to examine the consequences of a signal that depends upon the orientation of the ligand relative to the receptor. The analysis in the Theory section suggests that a signal that extends over the entire exclusion zone but that turns on only when the ligand is oriented correctly still yields a binding constant equal to the integral of the Boltzmann factor over the exclusion zone and all orientations. This prediction is borne out by the simulations, as illustrated in Fig. 8, which refers to Potential B. The top isotherm is obtained when the signal turns on only when the ligand is oriented to within ±30° of the receptor-ligand vector, whereas the bottom isotherm is obtained when the signal turns on for any orientation of the ligand. The shapes of the two isotherms are essentially identical; the only difference is in the level at which the signal saturates, as predicted by the theory; see Eq. 15. As a consequence, data fitting yields the same binding constant in both cases.

FIGURE 8.

Simulated binding isotherms for Potential B with well-depth −2 kcal/mol. Both isotherms use a signal zone extending from 2 to 5 u in r_RL. (Top) Signal is detected only when the ligand is oriented to within ±30° of the binding site's axis. (Bottom) Signal is detected irrespective of orientation of ligand.

Funnel-like potentials

The receptor-ligand systems just discussed are too simple to allow thorough evaluation of the theory in Proposed Definition of the Exclusion Zone because the attractive parts of the ligand-receptor binding potentials are square wells whose spatial extents approximately match the exclusion zones. The results, therefore, leave open the possibility that a Boltzmann integral over the entire energy well may in general be as accurate as a Boltzmann integral over the exclusion zone. Also, the theory leads to the novel and testable prediction that a large ligand binds a receptor more strongly than a small ligand purely as a consequence of its greater size and hence larger exclusion zone, but this prediction is not tested by the simulations presented so far. Additional simulations for funnel-like receptor-ligand interaction potentials enable these issues to be addressed.

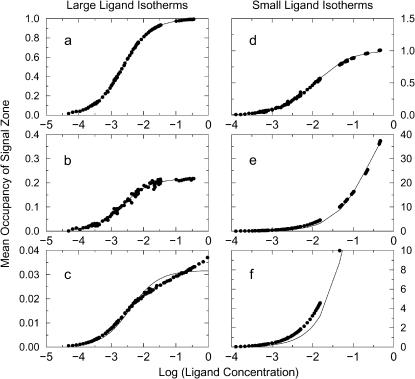
When the signal zones correspond closely to the exclusion zones, the simulations yield classical binding isotherms in which the signal saturates at a level corresponding to one ligand in the exclusion zone, as shown in Fig. 9, a and d. The binding constants extracted from these isotherms are 85 and 432 for the large and small ligands, respectively. Thus, remarkably, the binding constants extracted from these data by curve-fitting differ, although both ligands possess the same attractive ligand-receptor interaction potential. This result confirms our conjecture that the size of the ligand-ligand exclusion zone influences the apparent binding constant. However, it may still be of concern that the difference between these binding constants for the two ligands may be an artifact of the difference in the extent of the signal zones, since the signal zones match the exclusion zones and therefore are of different size for the two ligands. This possibility is examined by repeating the simulations with different signal zones, as now described.

FIGURE 9.

Simulated and fitted binding isotherms for funnel-shaped potentials with large ligand (left-hand graphs) and small ligand (right-hand graphs). Ordinate shows mean occupancy of the signal zone. (a) Large ligand with signal zone equal to corresponding exclusion zone. (b) Large ligand with signal zone equal to exclusion zone of small ligand. (c) Large ligand with signal zone extending from 0 to 1.7 u and hence excluding the energy minimum. (d) Small ligand with signal zone equal to corresponding exclusion zone. (e) Small ligand with signal zone equal to exclusion zone of large ligand. (f) Detail of isotherm shown in e.

First, simulations of the small ligand were carried out in which the signal zone was extended to match that which had been used for the large ligand. Note that this larger region corresponds closely to the overall energy well and hence to the region in which the attractive receptor-ligand potential is stronger than the thermal energy, kT. These simulations yield an isotherm whose shape deviates noticeably from ideal and whose maximal signal corresponds to occupancy of the signal zone by >30 ligands (Fig. 9, e and f). Although it is clearly risky to extract a binding affinity from this abnormal isotherm, one may nonetheless do so. The result is a pseudobinding affinity of 4 which paradoxically is weaker than the value of 85 obtained with the original small signal zone, even though a larger part of the energy well is now included in the signal zone. The reason is that including shallower parts of the well in the signal zone causes the isotherm to saturate only at high concentration. The contribution to the isotherm of the classical and relatively tight binding of ligand in the central −6 kcal/mol part of the well is lost in the much larger signal of the more numerous ligands that come to occupy the shallower part of the energy well at higher concentrations. Second, for the large ligand, the extent of the signal zone was reduced to the exclusion zone of the small ligand. Interestingly, the shape of the resulting isotherm (Fig. 9 b) still matches the ideal. Even more intriguing, curve-fitting to the new isotherm yields a binding affinity of 434, which is essentially the same as that obtained when the signal extended over the entire exclusion zone of the large ligand. It should be noted, however, that the saturating signal for the isotherm, ∼0.2, is now much lower than that obtained with the full exclusion zone for the large ligand, for obvious reasons, and the data are noisier because the mean occupancy is not as well converged as before. It is also worth making clear that it is possible to select a signal zone for the large ligand that will yield an abnormal binding isotherm. Thus, the isotherm obtained when the signal zone is restricted to 0 u < r_RL < 1.7 u and thus does not encompass the deepest part of the well has an abnormal shape, as shown in Fig. 9 c, and yields an experimental binding constant of 255, approximately one-half of the correct value from the normal isotherm Fig. 9 a.

Table 4 compares the affinities extracted from the ideal isotherms presented above with those calculated by various theories. The experimental binding constants K_isotherm agree well with Boltzmann integrals over the exclusion zones of the respective ligands K_Boltzmann,ex, but integrating the Boltzmann factor over the entire funnel-shaped energy-well, which implies integrating out to the –kT energy contour, yields a binding constant of K_Boltzmann,kT that is off by about a factor of 4 for the small ligand. The Mayer and Andersen integrals are close to K_Boltzmann,kT and thus are likewise markedly in error for the small ligand.

TABLE 4.

Comparison of simulated and theoretical binding constants for funnel-like potentials in two dimensions for large and small ligands

Ligand	Kisotherm	KBoltzmann,ex	KMayer	KAndersen	KBoltzmann,kT
Large	432	430	358	410	411
Small	85	86	387	410	411

K_isotherm is obtained by fitting to the normal isotherms obtained with signal zones that match the respective exclusion zones. K_Boltzmann,ex: integral of Boltzmann factor for ligand-receptor interaction over the exclusion zone. K_Boltzmann,kT: integral of Boltzmann factor for ligand-receptor interaction over the region in which the receptor-ligand interaction potential is <−kT kcal/mol.

Signal-based measurement of binding in three dimensions

Three-dimensional simulations are included to confirm the generality of key results from the artificial but more tractable two-dimensional simulations. The results, summarized in Table 5, confirm that the Boltzmann integral over the exclusion zone, K_Boltzmann,ex, agrees far better than the Mayer integral with the binding constants K_isotherm extracted from the simulated isotherms. Also, although the integral of the Boltzmann factor to the −kT energy contour is much more accurate than the Mayer integral, it is less accurate than the Boltzmann integral over the exclusion zone, especially for the weakest potential. Finally, integrals of the Boltzmann factor out to the 6.5 u cutoff of the ligand-receptor potential, K_{Boltzmann,cut}, markedly overestimate the affinities from the simulations because they extend outside the wedge-shaped binding site and include a spherical shell around the entire ligand for which the interaction potential is favorable due to the Lennard-Jones part of the receptor-ligand interaction potential. Values of K_Andersen are not provided here because it was not clear how to divide the smoothly varying R−L potential, which includes a nonexclusive Lennard-Jones attraction, into the repulsive and attractive potentials, W_R and W_A, that are required by the theory, as discussed in the Introduction.

TABLE 5.

Comparison of binding constants extracted from simulated isotherms and simulated equilibrium dialysis with theoretical binding constants for three-dimensional simulations

	Simulations		Theoretical integrals
ɛ	Kisotherm	Kdialysis	KBoltzmann,ex	KBoltzmann,kT	KBoltzmann,cut	KMayer
−4.1	78.8	−467	59.8	26.5	1690	−457
−5.1	117	−418	104	70.9	1740	−412
−7.7	1470	844	1410	1350	3020	867

ɛ_elec: parameter determining strength of r⁻³ interaction (Eq. 21). K_{Boltzmann,cut}: integral of the Boltzmann factor to the 6.5u cutoff of the ligand-receptor potential. See previous tables and text for other symbols.

The binding constants in Table 5 in effect use a standard concentration of 1 molecule/u³, but it is possible to refer the results to the standard concentration of 1 mol/liter by assigning a real distance to the distance unit u. The results, shown in Table 6, indicate that the stronger binding cases considered here have dissociation constants in a range that is of experimental interest for weakly binding systems.

TABLE 6.

Computed dissociation constants (K_Boltzmann,ex⁻¹) for three-dimensional systems at standard concentration 1 mol/liter, as a function of the length in Å assigned to the distance unit u, for three values of ε_elec (kcal/mol)

	εelec
u (Å)	−4.1	−5.1	−7.7
1	27.8 M	16.0 M	3.14 M
4	0.434 M	0.250 M	49.1 mM
10	27.8 mM	16.0 mM	3.14 mM

Note that the receptor-ligand interaction includes a Lennard-Jones term along with the “electrostatic” part, so ε_elec is not proportional to the depth of the energy well.

Equilibrium dialysis

In equilibrium dialysis, the extent of binding is determined from the net concentration of ligands in a dialysis bag containing receptors. This contrasts with measurement via a localized signal, where binding is assessed based upon the number of ligands that are near the receptor. Simulations of equilibrium dialysis, summarized in Tables 5 and 7, show that binding constants from the two methods can differ significantly, and that the binding constants from equilibrium dialysis correspond most closely to the Mayer integral, in accord with previous theory (Stigter and Dill, 1996). The negative binding constants in the tables imply that the steric bulk of the receptors displace more ligand than the binding sites attract, a possibility that was previously foreseen (van Holde, 1971).

TABLE 7.

Comparison of binding constants extracted from equilibrium dialysis simulations with results from the Mayer formula, for the two-dimensional systems

	Potential A			Potential B
ɛ	Kdialysis	Kisotherm	KMayer	Kdialysis	Kisotherm	KMayer
−0.1	−50.2	8.83	−52.4	−53.0	10.5	−56.3
−0.2	−49.6	9.25	−51.9	−53.3	11.0	−55.8
−0.3	−49.2	9.77	−51.4	−51.3	11.7	−55.2
−0.4	−47.6	10.4	−50.7	−52.3	12.5	−54.5
−0.5	−49.0	11.2	−50.0	−51.0	13.4	−53.7
−0.6	−46.7	12.0	−49.1	−49.6	14.6	−52.7
−0.7	−46.1	13.3	−48.0	−50.9	15.7	−51.5
−0.8	−45.0	14.5	−46.8	−46.8	17.3	−50.1
−0.9	−42.9	16.0	−45.3	−47.2	19.0	−48.5
−1.0	−41.6	17.9	−43.6	−45.5	21.2	−46.6
−1.1	−39.2	20.2	−41.5	−41.8	23.6	−44.3
−1.2	−37.6	23.0	−39.1	−37.4	26.4	−41.6
−1.3	−34.7	26.1	−36.2	−38.0	30.2	−38.4
−1.4	−32.6	29.9	−32.8	−33.5	34.4	−34.6
−1.5	−28.0	34.4	−28.8	−29.8	39.7	−30.2
−1.6	−20.5	39.6	−24.1	−25.2	45.5	−24.9
−1.7	−16.7	46.5	−18.5	−18.2	52.9	−18.7
−1.8	−12.0	54.3	−11.9	−11.8	61.9	−11.4
−1.9	−4.5	63.4	−4.1	−4.3	72.1	−2.8
−2.0	4.7	74.8	5.1	5.7	85.2	7.5
−4.0	1670	1780	1630	1840	1990	1810

ɛ: depth of energy well in kcal/mol.

DISCUSSION AND CONCLUSIONS

This study provides a consistent theoretical picture of noncovalent association that is applicable to computational models and the interpretation of experimental data. Central to this work is the use of simulations that mimic the methods by which binding constants are actually measured and that can therefore be used to assess and compare the accuracy of various theories. The simulations, further supported by theory developed here, elucidate the applicability of several different theories of binding.

The simulations reproduce the long-recognized fact that, when a poorly chosen signal is used to measure binding, the experiment can yield an isotherm that deviates markedly from ideality and yields a value of the binding constant that is at best suspect. The present analysis suggests that an ideal isotherm is reliably obtained when the signal zone comprises those positions of a ligand that prevent any other ligand from interacting more strongly with the receptor; i.e., when the signal is detected when the ligand lies in the exclusion zone defined in Proposed Definition of the Exclusion Zone. However, some variations in the signal zone are permissible, and the minimal requirement seems to be that the signal must report occupancy of the entire deep part of the energy well without reporting on binding of more than one ligand at a time.

A central result of the present study is that the binding constant extracted from an ideal isotherm agrees extremely well with the integral of the Boltzmann factor over the exclusion zone. It should be emphasized that integrating the Boltzmann factor over the signal zone is not a reliable approach, even when the signal provides a good isotherm. Thus, for the funnel-shaped potentials, limiting the large ligand's signal zone to the −6 kcal/mol part of the energy well yields a good isotherm (Fig. 9 b), but integrating over this small region yields a binding constant of ∼90 instead of the correct value of ∼430. The problem of relying on the signal zone to define the range of integration is thrown into particularly sharp relief by the fact that a signal might be detected for only an infinitesimal range of ligand positions, or it could alternatively be extremely long-ranged. The corresponding Boltzmann integrals range between 0 and infinity, although altering the range of the signal clearly does not change the true binding affinity. (Also, abnormal isotherms are expected from a miniscule or highly extended signal zone, as just discussed.) One might also seek to compute the binding constant as a Boltzmann integral over all ligand positions for which the ligand-receptor potential is <–kT. However, the present results show that this approach can be considerably less accurate than integrating over the exclusion zone.

The idea that the binding constant equals the Boltzmann integral over the exclusion zone leads to a novel prediction that the observed affinity of a large ligand will be greater than that of a small ligand if both ligands have the same receptor-ligand interaction potential, because the larger ligand has a larger exclusion zone. It is satisfying that this phenomenon is observed in the simulations with funnel-shaped potentials which are specificially designed to test this prediction. Some intuition regarding this result can be gained by recognizing that expansion of the integration range for the small ligand beyond its exclusion zone implies integrating over a region that can be occupied by many of the small ligands, so the integral should not be expected to correspond to the binding constant for 1:1 ligand-receptor binding.

The simulations also show that the formulae of Andersen, Hoye and Olaussen, and Wertheim, yields binding constants that are somewhat less accurate than those given by the Boltzmann integral over the exclusion zone. For signal-based measurements of binding, the Mayer integral is even less accurate. However, binding constants measured by equilibrium dialysis are matched well by the Mayer integral because it uniquely accounts for the exclusion of ligand from the dialysis bag by the steric bulk of the receptor. Interestingly, the equilibrium dialysis experiment can yield an affinity different from that obtained by a signal-based measurement. Indeed, unlike a measurement based upon a short-ranged signal, equilibrium dialysis can in principle yield a negative binding constant, as previously noted (van Holde, 1971). A broader issue in the application of either the Mayer or the Andersen formula has to do with the fact that these integrals range over all of space. As a consequence, for a receptor with multiple binding sites, they will incorrectly yield a single binding constant that includes attractive contributions from all of the binding sites. It thus appears that these formulae do not eliminate the need to provide some geometric definition of the bound complex for a given binding site.

One may readily delineate the cases in which the Mayer and Boltzmann integrals will differ markedly. The essence of the problem is captured by a simplified receptor-ligand system with interaction energy W = 0 except within an interaction region of volume V comprising an attractive exclusion zone and a repulsive steric overlap zone. We are then interested in cases where the ratio of the Mayer and Boltzmann integrals deviates from 1, as

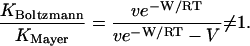(25)

This occurs when

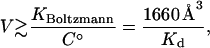(26)

where K_d is the dissociation constant measured with a local signal and referred to a standard concentration C° = 1 molecule/1660 ų. For example, deviations will occur for a protein that binds ligand with a (signal-based) dissociation constant of 10 μM when the steric volume is ≥1.7 × 10⁸ų, which corresponds to a linear dimension of several hundred Angstroms. Thus, significant deviations can occur for large receptors with weak binding sites. In contrast, the Andersen formula will rarely yield significant errors because it does not integrate the Mayer factor over the region of steric overlap.

APPENDIX

This addendum shows that the commonly used approach to computing covalent binding affinities via the rigid rotor-harmonic oscillator approximation (see, e.g., Chapter 9 of McQuarrie, 1973) yields a binding constant equal to the Boltzmann integral (Eq. 4), in the classical limit, and thus further validates the use of a Boltzmann integral for noncovalent pairwise binding. Consider the association of a monatomic receptor R and ligand L of respective masses M_R and M_L to form a covalent dimer D. The product of the moments of inertia of the dimer equal I = b²μ, where 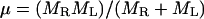is the reduced mass. The covalent bond between the monomers is approximated by a quadratic potential with force constant ω, equilibrium distance b, and well-depth E₀, relative to the monomers:

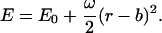(27)

In the classical limit where the gap between vibrational energy levels is much smaller than kT, the partition functions and binding constant become

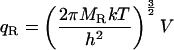(28)

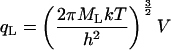(29)

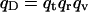(30)

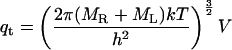(31)

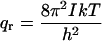(32)

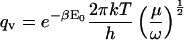(33)

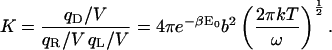(34)

This expression for K is equivalent to that from K_Boltzmann if the integration domain is approximated as ranging over bond lengths of 0–∞,

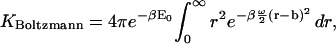(35)

where the factor of 4π results from the integral over the angular degrees of freedom of the ligand relative to the receptor.