Abstract
Pneumolysin (PLY), an important protein virulence factor of the human bacterial pathogen Streptococcus pneumoniae, could be a candidate for inclusion in a new anti-streptococcal vaccine. PLY solution species from monomer via multimeric intermediates to ring-shaped oligomers were studied with time-dependent sedimentation velocity in the analytical ultracentrifuge (AUC). Hydrodynamic bead modeling was used to interpret the data obtained. PLY remained mostly monomeric in solution; intermediate PLY multimers were detected in small quantities. Current understanding of PLY molecular mechanism is guided by a model built on the basis of its homology with perfringolysin O (PFO) for which there is an atomic structure. PFO, a virulence factor of the organism Clostridium perfringens, has almost the same molecular mass as PLY and shares 48% sequence identity and 60% sequence similarity with PLY. We report a comparative low-resolution structural study of PLY and PFO using AUC and small-angle x-ray scattering (SAXS). AUC data demonstrate that both proteins in solution are mostly monodisperse but PLY is a monomer whereas PFO is mostly dimeric. Ab initio dummy atom and dummy residue models for PFO and PLY were restored from the distance distribution function derived from experimental small-angle x-ray scattering curves. In solution, PLY is elongated, consistent with the shape predicted by its high-resolution homology model. The PFO dimer is also an elongated particle whose shape and volume are consistent with a staggered antiparallel dimer.
INTRODUCTION
The cholesterol-binding toxins (CBTs) are a family of membrane-attacking cytolysins produced by a number of Gram-positive bacteria (Tweten, 1995). All CBTs are characterized by high similarity in their primary structure and near identity in the so-called tryptophan-rich (Trp-rich) loop comprising 11 amino acids (in the case of PLY ECTGLAWEWWR) close to the C-terminal of the polypeptide chain (Morgan et al., 1996). This structural motif is connected to the functional activity of the CBTs: to bind cholesterol and to assemble on the membrane surface; in this way a transmembrane pore is formed, which is thought to mediate cell lysis (Gilbert, 2002). Modification of the single cysteine in the Trp-rich loop with small thiol compounds (such as dithio(bis)nitrobenzoate) prevents toxins from binding to membranes and/or self-associating (Gilbert et al., 1999a). Reductive cleavage of the disulfide restores activity and constitutes the basis of a characteristic property (thiol-activation) often ascribed to the CBT family (Palmer, 2001).
Two comprehensively studied CBTs are perfringolysin (PFO) from Clostridium perfringens and pneumolysin (PLY) from Streptococcus pneumoniae. These toxins share 60% amino acid sequence similarity and 48% identity (Mitchell, 1999) and have almost the same mass and polypeptide chain length (52.7 kDa and 471 residues for PLY; 55.8 kDa and 500 residues for PFO). This is the basis upon which a homology model for PLY was built using the PFO high-resolution structure as a template (Rossjohn et al., 1998).
The high-resolution structure of PFO is elongated (with dimensions 110 Å × 55 Å × 30 Å), mostly planar and slightly twisted in the middle. The structure comprises four domains with predominantly β-sheet secondary structure (Rossjohn et al., 1997). Although biophysical characterization of PFO has led to greater understanding of the mechanism of its interaction with membranes and a model for the structural changes that occur during membrane insertion (Shepard et al., 1998; Hotze et al., 2002; Ramachandran et al., 2002; Heuck et al., 2000), the behavior of PFO in solution remains not fully understood.
Crystals of PLY have been obtained (Kelly and Jedrzejas, 2000) and the structure solution by molecular replacement using the PFO atomic structure model is in progress. At this stage there seem to be significant differences between the PLY and PFO structures (M. J. Jedrzejas, personal communication). Thus, currently there is no satisfactory high- or low-resolution model of the PLY molecule in solution available, only low-resolution images from electron microscopy (EM) and cryo-electron microscopy for PLY monomers, deconvoluted from ring-shaped oligomers (Morgan et al., 1995; Gilbert et al., 1999b). It is important to determine the structure of PLY (in crystal and solution form) because PLY is a candidate for inclusion in improved vaccines against a number of pneumococcal infections resulting in human diseases such as pneumonia, otitis media, meningitis, and bacteremia (Cundell et al., 1995; Paton, 1996, 1998).
The damaging action of PLY as a cytolysin involves pore formation on the host cell membrane surface. Closed rings of 30–50 PLY subunits (350–450 Å in diameter) and arc-shaped incomplete ring structures are observed in electron micrographs of cells exposed to PLY (Morgan et al., 1995). The first step in PLY oligomerization is the appearance of a dimer (Gilbert et al., 1998, 1999a) but the subsequent stages in the ring-assembly process remain unknown. Connected to this process is a question about the driving force in PLY oligomer growth. In other words, is it only PLY monomers that participate in the growth of large oligomers or do intermediate, smaller oligomers (e.g., tetramers, hexamers, etc.) combine to form the observed rings and arcs? This question can be answered without the presence of membrane because PLY is also able to form “indefinite” ring-shaped oligomers in solution, which appear to be helix-like structures (Gilbert et al., 1999b).
Sedimentation velocity data analyzed with a recently derived method for determining continuous size distributions (mass or sedimentation coefficient) of polydisperse macromolecules in solution provide information about heterogeneity within solute systems (Schuck, 2000; Perugini et al., 2000). Applying this approach to a series of sedimentation velocity runs extending over a period of 149 h, we were able to observe the development of PLY oligomer populations in bulk solution excluding very heavy particles (e.g., PLY oligomer helices) that immediately sediment in the centrifugal field.
Despite the fact that in preliminary AUC experiments PLY was determined to be mostly a monomer in solution (Morgan et al., 1993), in subsequent solution studies the toxin was derivatized with thionitrobenzoate (TNB) (Gilbert et al., 1999a) to avoid any oligomer formation. In studies of the PLY-TNB conjugate the assumption has been made that derivatized toxin is structurally unchanged (Gilbert et al., 1998, 1999a; Nöllmann et al., 2004). In this work we aim to determine the low-resolution solution shape of PLY and PLY-TNB in the form of dummy atom/dummy residue models restored from SAXS data for the proteins in solution. This approach to structure determination is comprehensively illustrated in a number of recent studies (Ackerman et al., 2003; Sokolova et al., 2001; Bernocco et al., 2003; Svergun et al., 2000; Funari et al., 2000; Vachette et al., 2002; Gruber et al., 2001; Zou et al., 2003).
In summary: we focus on several aspects of the solution behavior of PFO and PLY: i), the time-dependent appearance of PLY intermediate oligomers; ii), the predominant solution species for PFO and PLY; and iii), the shape of PFO and PLY in solution to establish the validity of the PLY homology model based on the PFO high-resolution structure.
MATERIALS AND METHODS
Materials
All chemicals were from Sigma (St. Louis, MO).
Protein purification
PLY was overexpressed and purified according to an improved version of the protocol developed by Mitchell et al. (1989) later modified by Gilbert et al. (1998). Protein fractions were examined on a 10% SDS PAGE gel and assayed for hemolytic activity according to a standard protocol (Walker et al., 1987). The concentration of pure PLY was determined by absorbance spectroscopy at 278 nm using an extinction coefficient (ɛ) of 1.36 cm2mg−1 (Morgan et al., 1994). Finally PLY was stored in PBS buffer (8 mM Na2HPO4, 1.5 mM KH2PO4, 2.7 mM KCl, 137 mM NaCl, pH 7.48). To prevent self-association after eluting, pure PLY was immediately derivatized at its only cysteine residue (Cys-428) via Ellman's reaction with dithio(bis)nitrobenzoate to form PLY-TNB following a well-established procedure (Wang et al., 1986; Gilbert et al., 1999a). The quality of the derivatization process was judged from the ratio of absorbances at 278 nm and 337 nm (A278:A337), which was 3.5:1 indicative of Health Sciences Center, Oklahoma City <10% underivatized PLY present in solution.
Histidine-tagged PFO (PFO-HIS) in buffer A (10 mM MES, 300 mM NaCl, 1 mM EDTA, 10% glycerol, 5 mM DTT, pH 6.5) was a kind gift from Professor R. Tweeten (University of Oklahoma, Health Sciences Center, Oklahoma City, OK) purified according to a protocol described by Shepard et al. (1998). For some of the sedimentation velocity and sedimentation equilibrium experiments (which could be affected by the presence of glycerol) buffer A was exchanged with buffer B (6.5 mM Na2HPO4, 3.5 mM KH2PO4, 2.7 mM KCl, 300 mM NaCl, pH 6.5) via extensive dialysis.
Recombinant PFO (without the histidine tag) was cloned to PKK233-2-2 with ampicillin and tetracycline resistance. Supernatant, harvested from the Escherichia coli culture according to the protocol described by Shepard et al. (1998). Purification of PFO was carried out in the same way as PLY. Purified fractions of PFO were examined on a 10% SDS PAGE gel and assayed for hemolytic activity as for PLY. PFO concentration was measured spectrophotometrically at 280 nm (ɛ = 84,000 M−1 cm−1; Shepard et al., 1998). Purified protein was stored in buffer A at −20°C.
Analytical ultracentrifugation
Sedimentation velocity (SV) and sedimentation equilibrium (SE) experiments were performed on a Beckman Coulter (Palo Alto, CA) Optima XL-I analytical ultracentrifuge using both absorbance (at 278 for PLY and 280 nm for PFO, as well as at 337 nm for PLY-TNB) and interference optics. The experimental temperature for all AUC runs performed was 4°C. Partial specific volumes ( ) for PLY and PFO were calculated from their amino acid compositions, using the program SEDNTERP (Laue et al., 1992) and extrapolated to the experimental temperature following the method of Durchschlag (1986). The density and viscosity of PBS-type buffers at the experimental temperature was also calculated using SEDNTERP. The density of buffer A at 4°C was also determined experimentally using a density/specific gravity meter DA-510 (Kyoto Electronics Manufacturing, Kyoto, Japan). The viscosity of buffer A was measured using an Ubbelohde viscometer (Bradbury, 1970) in a water bath at a carefully controlled constant temperature of 4°C.
) for PLY and PFO were calculated from their amino acid compositions, using the program SEDNTERP (Laue et al., 1992) and extrapolated to the experimental temperature following the method of Durchschlag (1986). The density and viscosity of PBS-type buffers at the experimental temperature was also calculated using SEDNTERP. The density of buffer A at 4°C was also determined experimentally using a density/specific gravity meter DA-510 (Kyoto Electronics Manufacturing, Kyoto, Japan). The viscosity of buffer A was measured using an Ubbelohde viscometer (Bradbury, 1970) in a water bath at a carefully controlled constant temperature of 4°C.
SV experiments were performed at 48,000 rpm for PLY/PLY-TNB in PBS and for PFO-HIS in buffer B, and at 60,000 rpm for PFO/PFO-HIS in buffer A. The distribution of sedimenting material in AUC was modeled as a distribution of Lamm equation solutions (Schuck, 2000) where the measured boundary a(r,t) was modeled as an integral over differential concentration distribution c(s)
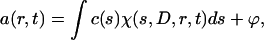 |
(1) |
where ϕ is noise component, r is distance from the center of rotation, t is time. The expression χ(s, D, r, t) denotes the solution of the Lamm equation for a single species (Lamm, 1929) by finite element methods (Schuck, 1998). Implemented in the program SEDFIT (Schuck, 1998) integral Eq. 1 is solved numerically by discretization into a grid of 200 sedimentation coefficients and calculating the best-fit concentrations for each plausible species in a linear least-squares fit. Experimental data were fitted using a maximum entropy regularization parameter of p = 0.95. This model was applied to describe the heterogeneity of the material moving in the AUC cell. Also, SV profiles were treated as comprising discrete independent species for the exact determination of sedimentation coefficients (s) for the species observed. Sedimentation coefficients were extrapolated to zero concentration and converted to standard conditions: those that would be measured in water at 20°C. The concentration (c0) of each species fitted in SEDFIT (using the independent species model) derived from both absorbance and interference scans was used for the determination of the “fringe extinction coefficient” (N) for these particular proteins in the buffers used. This parameter can be expressed as follows:
 |
(2) |
Equilibrium in SE experiments was attained after 38 h. The speeds of rotation were selected so that the value for the parameter σ (the reduced apparent molecular weight) (Yphantis, 1960) was between 2 and 4 for each plausible oligomeric species. Thus, SE traces for PLY-TNB and PFO-HIS (in buffer B) were obtained at 15,000 rpm, 20,000 rpm, and 24,500 rpm; PFO-HIS/PFO samples in buffer A were examined at 11,500 rpm, 15,000 rpm, 18,000 rpm, 22,000 rpm, and 24,500 rpm. True optical baselines were obtained after a further 6 h of rotation at 48,000 rpm. The concentration of samples in the SE experiments ranged between 2.4 μM and 6.4 μM for PLY/PLY-TNB, and between 1.5 μM and 15 μM for PFO/PFO-HIS. SE data were fitted globally using both the Beckman XL-A/XL-I software (Fullerton, CA) implemented in Microcal ORIGIN 6.0 and the NONLIN program (Johnson et al., 1981) (WINDOWS version). The “fringe extinction coefficient” N derived from SV data (Eq. 2) was used to convert the association constant in inverse fringe units to a dissociation constant in molar units, e.g., the dimer-monomer dissociation constant in molar units can be calculated from the association constant expressed in inverse fringe units ( ) as follows:
) as follows:
 |
(3) |
where ɛ is the protein extinction coefficient (M−1cm−1) and l is the optical pathlength (cm). The concentration of dimer in a sample (cdimer) can thus be determined:
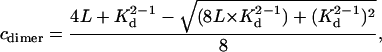 |
(4) |
where L is the molar loading concentration of monomer.
Hydrodynamic bead modeling
To describe the shape of the different PLY oligomers detected in SV experiments a very low-resolution bead model of the PLY monomer was constructed based on the cryo-EM structure described by Gilbert et al. (1999b). This model was used as a building block to construct ring-shaped oligomers formed with 30, 40, and 50 monomers to cover the range of sizes observed with EM (Morgan et al., 1994). Bead models were designed with the program AtoB (Byron, 2000, 1997). Then, plausible PLY oligomeric intermediates were built by removal of monomers from the rings to yield oligomers of lower stoichiometry, from a 32-mer down to a single monomer. This procedure was performed using the program MacBeads (written by Dr. Dan Thomas, then at the National Centre for Macromolecular Hydrodynamics (NCMH), University of Leicester; obtainable on request from the NCMH (see http://www.nottingham.ac.uk/ncmh/unit/software.html)). The sedimentation coefficient for anhydrous bead assemblies was calculated using the program HYDRO (Garcia de la Torre et al., 1994) and a typical hydration of 0.4 gwater/gprotein was used to convert s to a hydrated value, which is more representative of the experimental situation. The program HYDROPRO (Garcia de la Torre et al., 2000) was used to calculate sedimentation coefficients for dummy atom models (DAMs) generated from SAXS data, following the approach described by Ackerman et al. (2003).
SAXS data collection and treatment
All protein samples were extensively dialyzed against their reference buffers before their use in scattering experiments. Freshly purified PLY was kept at low concentration (0.2 mg/ml) at 4°C to slow down the oligomerization process and was then concentrated immediately before SAXS measurements. Concentrated PLY was then microfuged (20,800 g) for 40 min at 4°C and afterwards placed in the beam in a mica-windowed cell. PLY-TNB was also centrifuged to remove possible aggregates formed by nonderivatized PLY.
X-ray scattering experiments on PFO-HIS were carried out on Beamline 2.1 at the Synchrotron Radiation Source (Daresbury, UK) with beam currents of between 80 and 170 mA, an electron energy of 2 GeV, and a wavelength of 1.54 Å. Two camera lengths (d) were used in the experiments: 1.25 m to cover a momentum transfer range of 0.03 < s < 0.6 Å−1 and 3.25 m for 0.01 < s < 0.2 Å−1, where s = (4πsinθ)/λ and 2θ is the scattering angle. The detector was calibrated using a sample of wet rat tail collagen. For the short camera length the PFO-HIS concentration was 16 mg/ml whereas for the long camera length the sample concentration was 1.6 mg/ml. Experimental data were collected and averaged as 45 × 60 second frames for d = 1.25 m and 30 × 60 second frames for d = 3.25 m. The data were normalized for buffer scattering and detector response using the program XOTOKO (Boulin et al., 1986).
SAXS data for PLY/PLY-TNB samples were collected on the X33 camera at the European Molecular Biology Laboratory (EMBL), Hamburg Outstation, Hamburg, Germany, on the storage ring DORIS III of the Deutsches Elektronen Synchrotron. The experimental procedure was similar to that described above for PFO-HIS. Scattering curves were recorded at a wavelength of 1.5 Å at a sample-detector distance 2.2 m covering the momentum transfer range 0.01 < s < 0.35 Å−1. Sample concentrations were 7 mg/ml and 4 mg/ml for PLY-TNB and 10 mg/ml and 2 mg/ml for PLY. Data were normalized to the intensity of the incident beam and corrected for detector response, buffer scattering, and scaled for concentration using the program PRIMUS (Konarev et al., 2003). To check for radiation damage and aggregation during all SAXS experiments performed, the data in the first and last frame were compared. The distance distribution function P(r) was calculated with the program GNOM (Semenyuk and Svergun, 1991; Svergun, 1992).
Shape modeling
The low-resolution shapes of the proteins studied were restored as dummy atom models (DAMs) using the program DAMMIN in both slow (packing radius of 3.5 Å) and fast (packing radius of 6.5 Å) modes (Svergun, 1999) and dummy residue models (DRMs) using the program GASBOR (version 20) (Svergun et al., 2001). The resolution of the dummy models was determined as 2π/smax where smax is the reciprocal spacing of the highest-resolution data point used in the restoration process (Perkins, 1988). DRMs and DAMs were generated in fast mode 20 times from single scattering data sets and corresponding P(r) functions to establish a degree of similarity for models generated and then averaged to find the most common shape. All 20 models were superimposed using the program SUPCOMB (Kozin and Svergun, 2001). The models were averaged using a computer program developed in-house (PDB-AVERAGE (M. Nöllmann, unpublished)) that maps the Gaussian electron density of the structures (Duncan and Olson, 1993) into a cubic lattice (with a total length greater than the maximum model dimension and a lattice parameter of 0.5 Å), and then randomly populates the regions of highest electron density with new beads using a Monte Carlo approach (Hesselbo and Stinchcombe, 1995). In practice, threshold values were chosen somewhere between 20 and 40% of the total Gaussian electron density, i.e., dummy atoms with electron densities less than the chosen range were eliminated. During this procedure the Porod volume of the DAMs was maintained close to the volume of the originally generated models. Finally, the averaged low-resolution model was superimposed with the crystal structure using a neural network approach with the program SITUS (Wriggers and Chacon, 2001). Low-resolution models for PFO were superimposed with a high-resolution dimer model constructed from the PFO monomer crystal structure (Protein Data Bank accession code 1PFO) arbitrarily built using the molecular graphics software SWISS PDB-VIEWER (Guex and Peitsch, 1997), (http:/www.expasy.ch/sprbv/mainpage.html). The low-resolution averaged PLY model was superimposed with the PLY homology model (Rossjohn et al., 1998).
RESULTS
Time-dependent distribution of PLY oligomeric species
Nonderivatized PLY in solution was initially investigated to reveal the appearance of oligomers with time. Six consecutive SV runs were performed to observe trends in the development of PLY oligomers in solution over a 149 h period. Throughout the time course the dominant species was PLY monomer with s20,w = 3.42 Svedbergs (S) (Fig. 1, a and b). This value agrees well with previous AUC studies (Morgan et al., 1993) as well as with s calculated for the PLY low-resolution bead model (Fig. 1 c; Table 1). However, there is a fall (12%) in the concentration of monomer between the first and last SV runs (Fig. 1 a, insert) determined by integration of the peak at 3.42 S on the c(s) distribution. This loss of PLY monomer is not due to the formation of intermediate oligomeric species as these are present at tiny concentrations (Fig. 1 b) but can be easily interpreted as macro-oligomer formation in progress. We have previously observed the formation of indefinite, helical oligomers (Morgan et al., 1994; Gilbert et al., 1999b): these rapidly sediment out of the bulk solution. Moreover, protein aggregates were visible to the naked eye 24 h after sample preparation and sedimented under “ambient” gravity. Obviously, these particles could not be observed in the AUC cell. Apart from monomers, a very small contribution by heavier species was detected. To reveal their presence, the c(s) pattern was magnified ∼100 times (Fig. 1 b). Very small peaks with apparent s increasingly above that of the monomeric species were observed as time went on. The same overall result was obtained when the same PLY sample was spun in the AUC at 20,000 rpm, however, the resolution of species was poorer (data not shown).
FIGURE 1.
SV data revealing the appearance of PLY oligomers with time in PBS buffer. (a) c(s) distribution for SV data obtained at 4°C, 48,000 rpm: 3 h (solid line), 26 h (dotted line), 149 h (dashed line) after sample preparation. In all cases the sample loading concentration was 7 μM (monomeric molar units). (Inset) c(s) analysis of primary data over a narrower s-range, revealing a drop in the main (∼3.4 S) peak over time. The difference in c(s) scale compared with the main panel arises as a result of integration over a narrower s-range. (b) By expanding the c(s) scale the progressive appearance of very small amounts of oligomers can be observed. (c) Bead models and calculated sedimentation coefficients for PLY. The calculations were performed with the program HYDRO (Garcia de la Torre et al, 1994); a typical protein hydration (0.4 gwater/gprot) was used. The error on s represents the range of values calculated for oligomers “isolated” from rings comprising 30, 40, and 50 PLY monomers (i.e., different curvature in the arcs).
TABLE 1.
Apparent sedimentation coefficients of PLY oligomeric species observed during a 149 h period
| Time (h)
|
|||||||
|---|---|---|---|---|---|---|---|
| 3
|
26
|
51
|
75
|
120
|
149
|
||
| PLY oligomer | Calculated s20,w (S)* | Experimental s20,w(S) | |||||
| Monomer | 3.6 | 3.42 | 3.42 | 3.42 | 3.43 | 3.43 | 3.42 |
| Dimer | 5.6 ± 0.02 | – | 5.37 | 5.2 | – | – | 5.37 |
| Trimer | 7.1 ± 0.03 | 6.2 | 7 | 7.2 | 6.5 | 6.2 | 7 |
| Tetramer | 9.0 ± 0.80 | – | 8.8 | – | 8.3 | 8.3 | – |
| Hexamer | 10.1 ± 0.05 | – | – | 9.9 | 9.4 | 9.9 | 9.4 |
| Octamer | 11.5 ± 0.06 | – | – | – | 12.2 | – | – |
| 12-mer | 13.7 ± 0.06 | – | – | – | – | – | 13.3 |
| 16-mer | 15.4 ± 0.02 | – | – | – | – | 14.8 | – |
| Semicircle | 17.2 ± 0.70 | – | – | – | 18.2 | 17.4 | 17.4 |
| 32-mer | 20.5 | – | – | – | – | – | – |
| Ring | 21.9 | ||||||
| 23.7 ± 1.2 | – | – | – | 26.0 | – | – | |
| 30.7 | |||||||
Error in calculated s20,w indicates the range of sedimentation coefficients calculated for oligomers “isolated” from rings comprising 30, 40, and 50 PLY monomers (see Materials and Method section and Fig. 1 c).
To interpret the stoichiometry of the observed oligomers, a low-resolution bead modeling approach was used to construct plausible oligomers (see Materials and Methods). To build a PLY monomer model each domain of the high-resolution homology model (Rossjohn et al., 1998) was represented as a single bead (Morgan et al., 1994). The four beads were positioned in agreement with the domain structure for PLY observed with cryo-EM (Gilbert et al., 1999b) domain 4 was rotated by 45° relative to the long axis of PLY defined by domains 2 and 1; in oligomeric models the monomer was oriented with domain 3 inside the ring. The models of PLY monomer and ring-shaped oligomer as well as some plausible intermediate oligomers together with corresponding calculated sedimentation coefficients are shown in Fig. 1 c. Thus, accepting some uncertainty in the sedimentation coefficients arising from the low-resolution shape representation and nominal hydration used for the calculations, the experimentally observed species could be collated with the bead models. This analysis is presented in detail in Table 1. Importantly, the calculated sedimentation coefficient for the four-bead PLY monomer model was in good agreement with the experimentally determined values. In summary, PLY particles in solution moving under ultracentifugal force appear to be mostly monomeric over a period of ∼1 week. AUC can detect only quite small amounts of higher mass PLY oligomers; most of them are consecutive oligomeric states from dimer to hexamer, other higher oligomers were hardly detected although the centrifugal force used was appropriate for their detection. Thus the formation of heavy ring-shaped oligomers/helices (Morgan et al., 1994; Gilbert et al., 1999b) seems to be a rapid process but could equally arise from a slow but highly cooperative process.
PLY is predominantly monomeric; PFO is predominantly dimeric in solution
Samples of PLY-TNB were also examined for heterogeneity using the c(s) size distribution approach. One dominant species was evident as a single peak centered around an apparent sedimentation coefficient ( ) of 3.5 S and direct fitting of SV boundaries gave sedimentation coefficient values of 3.5–3.6 S for different detection systems (absorbance at 280 nm, absorbance at 337 nm, and interference) (Fig. 2, a and b). These results were almost identical with the PLY data (within the experimental error limits).
) of 3.5 S and direct fitting of SV boundaries gave sedimentation coefficient values of 3.5–3.6 S for different detection systems (absorbance at 280 nm, absorbance at 337 nm, and interference) (Fig. 2, a and b). These results were almost identical with the PLY data (within the experimental error limits).
FIGURE 2.
Comparative SV characterization of PLY and PFO. (a) Size distribution (c(s)) analysis of the SV data converted to standard conditions for PLY samples in PBS (peak 1). PLY absorbance data at 280 nm, loading concentration (in monomer molar units), c = 15.7 μM (solid line); PLY-TNB absorbance at 280 nm, c = 12 μM (dashed line), and its absorbance at 337 nm, c = 42.4 μM (dashed-dotted line). For PFO samples (peak 2) in buffer A, absorbance data at 280 nm (PFO-HIS, c = 12.3 μM, solid line; and PFO, c = 11.5 μM, dotted line). (b) Extrapolation to zero concentration of sedimentation coefficients for PLY (interference data, □); PLY-TNB (interference data, ○; absorbance at 337 nm, ▵); PFO-HIS (interference data, ⋄; PFO absorbance data at 280 nm, ×).
PFO is highly homologous to PLY and has almost the same molecular mass. A single c(s) peak was observed for PFO-HIS at a significantly higher 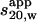 (4.9 S) than for PLY (or PLY-TNB) (3.5 S); therefore PFO-HIS seems to be a tight dimer (this is also supported by SE experiments (see below)). Sedimenting boundaries for all PFO-HIS samples studied were analyzed with SEDFIT (Schuck, 1998) using an upper limit in the analysis of s20,w = 35 S, but no higher oligomers were detected in solution. Dimerization of PFO-HIS was revealed more clearly by removing preservative agents such as glycerol and dithiothreitol (DTT) from the buffer and replacing MES buffer by PBS (as for PLY samples). Under these conditions the c(s) distribution had two easily distinguishable peaks centered at 3.7 S and 5 S with strong concentration dependence: a 5 S peak predominated for the higher concentration PFO-HIS whereas a single peak at 3.8 S was obtained for the most dilute sample (Fig. 3 a). Importantly, the peak positions are almost independent of protein concentration, therefore the dimerization process seems to be slow on the timescale of the SV experiment (Schuck, 2003).
(4.9 S) than for PLY (or PLY-TNB) (3.5 S); therefore PFO-HIS seems to be a tight dimer (this is also supported by SE experiments (see below)). Sedimenting boundaries for all PFO-HIS samples studied were analyzed with SEDFIT (Schuck, 1998) using an upper limit in the analysis of s20,w = 35 S, but no higher oligomers were detected in solution. Dimerization of PFO-HIS was revealed more clearly by removing preservative agents such as glycerol and dithiothreitol (DTT) from the buffer and replacing MES buffer by PBS (as for PLY samples). Under these conditions the c(s) distribution had two easily distinguishable peaks centered at 3.7 S and 5 S with strong concentration dependence: a 5 S peak predominated for the higher concentration PFO-HIS whereas a single peak at 3.8 S was obtained for the most dilute sample (Fig. 3 a). Importantly, the peak positions are almost independent of protein concentration, therefore the dimerization process seems to be slow on the timescale of the SV experiment (Schuck, 2003).
FIGURE 3.
SV results for PFO-HIS in buffer B. (a) Size distribution (c(s)); interference data obtained for monomeric loading concentrations of 8.9 μM (solid line), 7.3 μM (dashed line), 5.4 μM (dotted line), 2.5 μM (dashed-dotted line). (b) The concentration dependence of s: “monomer” (□), “dimer” (○). The solid line marks the sedimentation coefficient calculated for the PFO monomer from its crystal structure; dotted lines are the extrapolation of s20,w to zero concentration for the two species.
Linear extrapolation to zero concentration of the SV data treated as independent discrete species gives values for the PFO-HIS “monomer” sedimentation coefficient under standard conditions of 3.6 ± 0.2 S and for its “dimer” the value of 5.0 ± 0.3 S. The error is the uncertainty of the linear extrapolation shown in Fig. 3 b. The “monomer” value is in excellent agreement with the sedimentation coefficient calculated for the PFO high-resolution structure using the program HYDROPRO (Garcia de la Torre et al., 2000) (3.6 S) (Fig. 3 b; Table 2), whereas the dimer value is very similar to that calculated for a “side-to-side” model constructed for PFO dimer (5.4 S). The fact that the observed experimental s is less then that calculated for the “side-to-side” dimer model could be the result of some elongation of the dimer due to, for example, some staggering in the dimeric form or additional hydration in the dimeric form, which is very unlikely. The sedimentation coefficients of PFO and PFO-HIS in buffer A are comparable with each other (Fig. 2, a and b). Both appear to be dimeric under these conditions. Hence the histidine tag does not induce the dimerization of PFO monomers, although, according to our SE data (below), it appears to decrease the Kd by nearly two orders of magnitude (Table 2).
TABLE 2.
Summary of AUC results for PLY and PFO
Experimental 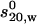 (S) (S)
|
|||||||
|---|---|---|---|---|---|---|---|
| Sample | s20,w (S) Calculated using HYDROPRO | Monomer | Dimer | Mmonomer (kDa), calculated* | Mw (kDa) single-species model | 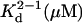 |
|
| PFO-HIS | Buffer A | – | 4.9 ± 0.1† | 110.0 ± 3† | 0.2 ± 0.05† | ||
| Buffer B | 3.61 | 3.6 ± 0.1† | 5.0 ± 0.3† | 56.4 | 99.0 ± 1† | 9.1 ± 0.5† | |
| PFO, buffer A | – | 4.8 ± 0.1‡ | 55.8 | 96.3 ± 3† | 10.0 ± 0.5† | ||
| PLY | 3.5 ± 0.1† | – | – | – | |||
| PLY-TNB | 280 nm/interference | 3.45 | 3.6 ± 0.1† | – | 52.8 | 52.0 ± 1‡ | – |
| Absorbance at 337 nm | 3.7 ± 0.1 | – | 54.1 ± 5 | – | |||
From amino acid sequence.
Interference data.
Absorbance data at 280 nm.
The stoichiometry of PLY and PFO particles in solution was verified using sedimentation equilibrium (SE) analysis. SE data for PLY-TNB were fitted globally with a single species model (Fig. 4 a). The resultant molecular mass agrees well with the mass calculated from its amino acid sequence (Table 2). Thus, PLY-TNB is predominantly monomeric in solution at the concentration studied. Importantly, the molecular weights obtained from absorbance data acquired at 280 nm (detecting all PLY molecules in the PLY-TNB sample) as well as at 337 nm (detecting only PLY-TNB) were very similar (within the error limits) (Table 2). The increased error on the mass determined at 337 nm resulted from the low absorption signal of PLY-TNB.
FIGURE 4.
SE data fits for PLY, PFO, and their covalently modified variants. (a) PLY-TNB (c = 6.6 μM) absorbance at 280 nm (□) and at 337 (○), at a rotor speed of 20,000 rpm and a temperature of 4°C. The data were fitted with a single-species model; residuals of the fits are in the uppermost panels. (b) Interference data for: PFO-HIS (□) in buffer A (c = 4.0 μM, 3.5 μM, 3.0 μM, left to right); PFO (○) in buffer A (c = 5.7 μM, 2.8 μM, 1.4 μM) at a rotor speed of 18,000 rpm and a temperature of 4°C, and PFO-HIS in buffer B (▵) (c = 4.0 μM, 2.7 μM, 1.7 μM) at a rotor speed of 20,000 rpm and a temperature of 4°C. The data were fitted with a monomer-dimer model; residuals of the fits are in the panels above each data set.
PFO-HIS in buffer A has a weight average molecular weight of 110.3 ± 3 kDa (interference detection), which is comparable with the mass calculated from its primary structure (113 kDa) for a dimer. SE data for PFO samples were fitted globally with a monomer-dimer association model (Fig. 4 b). A decrease in the root-mean-square deviation (rmsd) values between the experimental SE curves and the fit was obtained (0.02 as opposed to 0.03 for the single species model for interference data). Slight variation in the stability of PFO dimer was observed depending upon both the presence/absence of histidine tag on the protein as well as preservative agents in the buffer (glycerol and DTT) (Table 2). These results confirm the dimeric nature of PFO, with a constant of dissociation of ∼10 μM His-tagged in buffer B (which lacks glycerol and DTT) or without the His-tag in buffer A (which includes glycerol and DTT). Apparently, PFO-HIS in buffer A is more stable as a dimer; therefore, this sample was used for further SAXS measurements owing to its greater solution homogenity.
SAXS data treatment and ab initio shape modeling
SAXS curves are presented in Fig. 5 a. There is a noticeable difference between the scattering curves for PLY/PLY-TNB and for PFO-HIS: the curve for PLY is almost featureless whereas the PFO curve has several strong features. There is also a slight difference between the scattering curves for PLY and PLY-TNB (Fig. 5 a). Further treatment of the SAXS data was conducted using indirect transformation of the reciprocal space scattering data into a real space P(r) versus r function (Svergun, 1992). The distance distribution function P(r) for all three proteins studied indicates an elongated shape by the presence of an extended shoulder in the P(r) function at distances greater than the radius of gyration (Rg) (Fig. 5 b). The maximal dimension (Dmax) and radius of gyration (Rg) values for PLY and PFO samples in solution exceed the Dmax value calculated for the PLY homology model/PFO crystal structure. For PFO these experimental parameters are as follows: Rg = 43 Å and Dmax = 138 Å compared with those calculated from its crystal structure (Rg = 33.7 Å and Dmax = 110 Å). A “side-to-side” PFO dimer should have a slightly higher maximal dimension (for our arbitrarily built side-to-side PFO dimer this parameter was 125 Å); whereas an “end-to-end” PFO dimer will be twice as long (∼220 Å). Thus, the PFO dimer in solution is probably in a side-to-side conformation and is slightly staggered. For PLY/PLY-TNB the difference between the experimental and calculated values was not as significant: experimental Rg values were 38 Å and 39 Å, respectively, and Dmax values were 125 Å and 135 Å, respectively, compared with an Rg of 36 Å and Dmax of 110 Å calculated for the PLY homology model. PLY in solution is more similar to the homology model based on the PFO high-resolution structure whereas PLY-TNB is a larger particle whose structure is more elongated.
FIGURE 5.
SAXS data treatment. (a) Scattering curves (logarithm of intensities of scattered x rays (I(s))) as a function of scattering vector, s, for PLY (c = 10 mg/ml), PLY-TNB (c = 7 mg/ml), and PFO-HIS (c = 16 mg/ml). Experimental data (shaded circles); envelope scattering generated by the program DAMMIN (Svergun, 1999) in slow mode (solid line). (b) Distance distribution function P(r) for PLY-WT (□), PLY-TNB (○), and PFO-HIS (▵).
Low-resolution structures (DAMs and DRMs) were restored ab initio from the experimental data with a resolution of 23 Å for all proteins examined. Thus, PFO-HIS has approximate dimensions of 137 Å × 55 Å × 47 Å, PLY 118 Å × 45 Å × 24 Å, and PLY-TNB 130 Å × 35 Å × 17 Å. The dimensions of the PFO-HIS DAM/DRM are consistent with an antiparallel PFO dimer model. This, in turn, is consistent with the SE results reported above. The  of PFO-HIS (in buffer A, which was used for SAXS studies) is 0.2 μM, therefore at the monomer concentration used in the SAXS study (286 μM) the system comprised 96% (140.2 μM) dimeric and only 4% (5.3 μM) monomeric PFO-HIS. Thus, the scattering curve is overwhelmingly dominated by contributions from dimeric species.
of PFO-HIS (in buffer A, which was used for SAXS studies) is 0.2 μM, therefore at the monomer concentration used in the SAXS study (286 μM) the system comprised 96% (140.2 μM) dimeric and only 4% (5.3 μM) monomeric PFO-HIS. Thus, the scattering curve is overwhelmingly dominated by contributions from dimeric species.
In Fig. 6 averaged DAMs for PLY and PFO are presented superimposed on the PLY homology model and an arbitrarily constructed antiparallel staggered PFO dimer model, respectively. Dummy residue modeling using the program GASBOR (Petoukhov et al., 2002) gave very similar shapes (data are not shown). Twenty DAMs were generated from a single data set for each protein sample and the similarity of the models was verified using the normalized spatial discrepancy (NSD) index (Kozin and Svergun, 2001). By definition, the NSD tends to 0 for ideally superimposed similar objects and it exceeds 1 if the objects systematically differ from each other; therefore the models could be assumed to be similar for NSD values <1. In our case the mean NSD value for one arbitrarily chosen DAM superimposed on each of the remaining 19 models was 0.63 for PFO, 0.71 for PLY-TNB, and 0.6 for PLY.
FIGURE 6.
Three orthogonal views of the averaged DAMs superimposed with the relevant high-resolution structures: (a) PFO DAM and constructed antiparallel staggered dimer model; (b) PLY-TNB DAM and PLY homology model; (c) PLY DAM and PLY homology model.
To confirm that the shapes of the averaged PFO and PLY DAMs were consistent with the hydrodynamic data obtained from SV studies we calculated their sedimentation coefficients using the program HYDROPRO (Garcia de la Torre et al., 2000), which calculates hydrodynamic parameters for shell models that it constructs from user input files of model coordinates. To ensure that the primary hydrodynamic model was filled with overlapping spheres we selected a radius for the atomic elements (the AER) greater than the radius of the dummy atoms that are hexagonally packed in the DAM and thus do not overlap and do not properly fill the model volume (see Ackerman et al., 2003 and Scott et al., 2002 for earlier examples of this approach). To determine the amount of bound water for each protein DAM the anhydrous protein volume (VA = M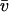 /NA, where M is the protein mass and NA is Avogadro's number) was subtracted from the Porod volume (the volume of the hydrated protein) of the DAM. The effective hydration of the PFO-HIS and PLY DAMs in HYDROPRO was typical of proteins (0.36 gwater/gprotein and 0.34 gwater/gprotein, respectively) whereas that calculated for PLY-TNB was higher (0.6 gwater/gprotein). The sedimentation coefficient calculated with HYDROPRO for the PFO-HIS DAM (5.1 S) agrees well with the experimentally measured value (4.9 S) (Table 3); s calculated for the PLY DAM (3.14 S) was also in reasonable agreement with the experimental data (3.5 S) whereas for the PLY-TNB DAM it was lower (2.94 S) because of the large hydration of the DAM.
/NA, where M is the protein mass and NA is Avogadro's number) was subtracted from the Porod volume (the volume of the hydrated protein) of the DAM. The effective hydration of the PFO-HIS and PLY DAMs in HYDROPRO was typical of proteins (0.36 gwater/gprotein and 0.34 gwater/gprotein, respectively) whereas that calculated for PLY-TNB was higher (0.6 gwater/gprotein). The sedimentation coefficient calculated with HYDROPRO for the PFO-HIS DAM (5.1 S) agrees well with the experimentally measured value (4.9 S) (Table 3); s calculated for the PLY DAM (3.14 S) was also in reasonable agreement with the experimental data (3.5 S) whereas for the PLY-TNB DAM it was lower (2.94 S) because of the large hydration of the DAM.
TABLE 3.
Summary of shape parameters derived from SAXS data
| Parameters derived from scattering data
|
Parameters of DAMs
|
Parameters of HYDROPRO models
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Vanh* (nm3) |
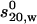 (S) (S) |
Dmax (nm) | Rg (nm) | VPorod (nm3) | δ (gwater/gprot) | Vaveraged model (nm3) | AER† (Å) | s (S) | Vfilling model (nm3) | δ (gwater/gprot) | |
| PFO (dimer) | 136.6 | 4.9 ± 0.1 | 13.7 | 4.2 ± 0.1 | 204.4 | 0.36 | 186.4 | 6.5 | 5.11 | 204.1 | 0.34 |
| PLY | 64.4 | 3.5 ± 0.1 | 12.5 | 3.8 ± 0.1 | 96.2 | 0.36 | 66.4 | 6.5 | 3.14 | 96.2 | 0.36 |
| PLY-TNB | 64.4 | 3.6 ± 0.1 | 13.5 | 3.9 ± 0.1 | 129.4 | 0.70 | 136.8 | 6.5 | 2.94 | 129.4 | 0.70 |
Calculated from molecular mass and partial specific volume (both parameters derived from amino acid sequence).
AER is radius for atomic elements of filled model.
DISCUSSION
The main objective of this work was the evaluation of the size and shape of PLY and PFO particles in solution to find out: i), whether the PLY high-resolution homology model built on the basis of its homology with PFO is representative of PLY in solution; and ii), whether the solution and crystal shapes of PFO are coincidental. In the course of our investigations the additional interesting features of the two protein systems were revealed.
PLY solution behavior
PLY and PLY-TNB are mostly monomeric in solution at the concentrations studied here. This largely confirms the preliminary AUC study conducted by Morgan et al. (1993) where SV and SE data for PLY in solution were interpreted as representative of monomer alone. The time course SV study presented in this article shows that PLY remaining in bulk solution during ultracentrifugation is also mostly monomeric. According to the size-distribution analysis results presented here there is little point in considering intermediate oligomers formed during the aggregation process because of the negligible amount detected. However, as a possible way to clarify this problem in the future, the PLY oligomerization process could be slowed down or fixed at distinct stages. Thus, in this experimental setup PLY behavior in solution can be realistically considered as a two-species system: monomer and ring-shaped oligomer (including the helical form). From our data we are unable to conclude whether the ring-shaped oligomers form by sequential addition of monomers to a growing oligomer or via the coalescence of intermediate oligomers (e.g., dimers, hexamers, etc.).
PFO dimerization
The AUC results demonstrating that PFO is predominantly dimeric in solution are consistent with earlier findings that PFO crystals had an asymmetric unit of 180 Å length and volume of 153 nm3 (Feil et al., 1996; Sugahara et al., 1996) and were interpreted to contain a dimer. These dimensions are similar to those of our PFO DAM: the length (Dmax) is 137 Å and volume is 200 nm3. The DAM volume appears to be larger than that determined for the crystallographic asymmetric unit because DAMs include bound water. The difference in length could be indicative of a difference in conformation of the PFO dimer in solution and in the crystalline state.
Our results on PFO dimerization are not in contradiction with the kinetic analysis of the fluorescence-detected transition from water-soluble monomer to membrane-inserted oligomer and other multiple fluorescence studies of the membrane anchoring mechanism of PFO accompanied by structural transition from α-helixes to antiparallel β-strands inside the protein (Ramachandran et al., 2002; Hotze et al., 2002; Heuck et al., 2000, 2001; Rossjohn et al., 1999; Shatursky et al., 1999) where PFO was considered to be a monomer. We have shown the 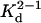 of PFO-HIS is 0.2 μM (in buffer containing glycerol and DTT) and that in our experiments PFO is predominantly dimeric in solution. Fluorescence spectroscopy measurements by Tweten and collegues (Shepard et al., 1998; Heuck et al., 2000) were conducted at low protein concentrations, where the amount of dimer would constitute <20% (mol %) of the system. On the basis of our findings the existing model for the mechanism of PFO interaction with cell membranes could possibly be extended.
of PFO-HIS is 0.2 μM (in buffer containing glycerol and DTT) and that in our experiments PFO is predominantly dimeric in solution. Fluorescence spectroscopy measurements by Tweten and collegues (Shepard et al., 1998; Heuck et al., 2000) were conducted at low protein concentrations, where the amount of dimer would constitute <20% (mol %) of the system. On the basis of our findings the existing model for the mechanism of PFO interaction with cell membranes could possibly be extended.
Ab initio modeling, averaging, and superimposition of high- and low-resolution structures
Three-dimensional dummy models are restored from one-dimensional scattering curves, therefore as a solution they are not unique, i.e., DAMs/DRMs derived from the same data set are usually not identical (Funari et al., 2000; Svergun and Koch, 2002; Zou et al., 2003). Here we have developed a method for the creation of the most representative shape from the array of DAMs/DRMs generated from a single scattering curve. The averaging procedure is an important part of the overall data treatment because it allows us to summarize objectively a series of DAMs/DRMs based on a single scattering curve. For example, we concluded that the dimerization of PFO was more likely to be antiparallel after averaging all 20 DAMs/DRMs restored from the PFO scattering pattern. In addition we have observed that the featurelessness of the PLY scattering curve resulted in a higher heterogeneity of DAMs/DRMs so it was possible to standardize the shape of PLY in solution only as a result of the averaging procedure. As a general feature, the L-shaped structures derived from the PLY/PLY-TNB scattering curves look similar to the low-resolution image of the PLY monomer obtained from the oligomer electron density map (Gilbert et al., 1999b), and to the high-resolution PLY homology model. Nevertheless, some differences exist between the homology model and our DAMs/DRMs. In fact, in answer to the first question (i) raised at the start of the Discussion section, PLY in solution appears to be longer than predicted by the homology model. Derivatization with TNB appears to further elongate and thin the structure in regions corresponding to domains 2 and 4 of the homology model. Interestingly, the twist in the middle of the PLY homology model (Rossjohn et al., 1997) was also observed in our low-resolution models in all 20 DAMs/DRMs generated. Structures for PFO and PLY in solution appear to be elongated and flattened with anisometry ∼1:8 for PLY-TNB, 1:5 for PLY, and 1:3 for PFO-HIS; which gives a less stable shape reconstruction (Volkov and Svergun, 2003) with a high enough value of NSD, particularly for PLY-TNB. Unlike PLY, the PFO-HIS curve contained several easily distinguishable features that resulted in good reproducibility of the dummy models. We have observed a characteristic twist in the middle of the PFO solution structure found also in its crystal structure (Rossjohn et al., 1997). Moreover, the PFO solution particles were twisted in such a way as to make the superimposition with the high-resolution dimer model difficult. It was necessary to slightly stagger the dimer to contain it within the envelope defined by the average DAM. As a consequence of the observed dimerization of PFO we are unable to answer satisfactorily to the second question (ii) raised above.
Different oligomeric configurations in solution for two highly homologous CBTs (PLY and PFO) may be related to the mechanism of release of the toxins by the bacteria responsible for the synthesis of the proteins. PFO is synthesized with a typical secretion signal and is actively secreted by C. perfringens from intact bacteria (Rossjohn et al., 1999). The toxin therefore has to cross the cytoplasmic membrane and it may be that a dimer form of the protein is necessary for this process. In contrast, the majority of PLY is released from S. pneumoniae when the organism undergoes autolysis (Morgan et al., 1996). The protein does not have a typical secretion signal and presumably does not cross the membrane of the cell. The differences in solution behavior may also point to differences in the mechanism of prepore/pore complex formation. There are several models of pore formation that range from assembly of the high molecular weight pore by addition of monomers inserted into the membrane to assembly of the complete ring as a prepore followed by insertion into the membrane. It is possible that the extent of oligomerization that occurs by these mechanisms is different between the different CBTs and that these differences are reflected in the solution behavior of the proteins. Such differences may also explain the difficulties experienced in trying to crystallize PLY in comparison to PFO.
Acknowledgments
The authors are grateful to Dr. Rodney Tweten for the kind gift of PFO-HIS samples as well as for helpful discussions during this project and to Graeme Cowan for developing the PFO clone. Special thanks to Dr. Günter Grossmann (SRS, Daresbury Laboratory, UK) and the team of Dr. Dmitri Svergun (EMBL Outstation, Hamburg, Germany) for help in SAXS data collection and primary data treatment. The EMBL Outstation (Hamburg, Germany) and SRS (Daresbury, UK) are also acknowledged for the beam time granted for this study.
A.S.S. acknowledges the Wellcome Trust for financial support (grant 05606/Z/99/Z to O.B, T.J.M, and others). M.N. is grateful to the Wellcome Trust for support in the form of a studentship.
References
- Ackerman, C. J., M. M. Harnett, W. Harnett, S. M. Kelly, D. I. Svergun, and O. Byron. 2003. 19 Å solution structure of the filarial nematode immunomodulatory protein, ES-62. Biophys. J. 84:489–500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernocco, S., B. M. Steiglitz, D. I. Svergun, M. V. Petoukhov, F. Ruggiero, S. Ricard-Blum, C. Ebel, C. Geourjon, G. Deleage, B. Font, D. Eichenberger, D. S. Greenspan, and D. J. Hulmes. 2003. Low resolution structure determination shows procollagen C-proteinase enhancer to be an elongated multidomain glycoprotein. J. Biol. Chem. 278:7199–7205. [DOI] [PubMed] [Google Scholar]
- Boulin, C., R. Kempf, M. H. J. Koch, and S. M. McLaughlin. 1986. Data appraisal, evaluation and display for synchrotron radiation experiments: hardware and software. Nucl. Instrum. and Methods 249:399–407. [Google Scholar]
- Bradbury, J. H. 1970. Viscosity. In The Physical Principles & Techniques of Protein Chemistry: Part B. Academic Press, New York, NY and London, UK. 99–145.
- Byron, O. 1997. Construction of hydrodynamic bead models from high-resolution x-ray crystallographic or nuclear magnetic resonance data. Biophys. J. 72:408–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Byron, O. 2000. Hydrodynamic bead modeling of biological macromolecules. Methods Enzymol. 321:278–304. [DOI] [PubMed] [Google Scholar]
- Cundell, D., H. R. Masure, and E. I. Tuomanen. 1995. The molecular basis of pneumococcal infections: a hypothesis. Clin. Infect. Dis. 21:S204–S212. [DOI] [PubMed] [Google Scholar]
- Duncan, B. S., and A. J. Olson. 1993. Shape analysis of molecular surfaces. Biopolymers. 33:231–238. [DOI] [PubMed] [Google Scholar]
- Durchschlag, H. 1986. Specific volumes of biological macromolecules and some other molecules of biological interest. In Thermodynamic Data for Biochemistry and Biotechnology. H-J. Hinz, editor. Springer-Verlag, Berlin, Germany; Heidelberg, Germany; New York, NY; Tokyo, Japan. 45–128.
- Feil, S. C., J. Rossjohn, K. Rohde, R. K. Tweten, and M. W. Parker. 1996. Crystallization and preliminary X-ray analysis of a thiol-activated cytolysin. FEBS Lett. 397:290–292. [DOI] [PubMed] [Google Scholar]
- Funari, S. S., G. Rapp, M. Perbandt, K. Dierks, M. Vallazza, C. Betzel, V. A. Erdmann, and D. I. Svergun. 2000. Structure of free Thermus flavus 5 S rRNA at 1.3 nm resolution from synchrotron X-ray solution scattering. J. Biol. Chem. 275:31283–31288. [DOI] [PubMed] [Google Scholar]
- Garcia de la Torre, J., M. L. Huertas, and B. Carrasco. 2000. Calculation of hydrodynamic properties of globular proteins from their atomic-level structure. Biophys. J. 78:719–730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia de la Torre, J., S. Navarro, M. C. Lopez Martinez, F. G. Diaz, and J. J. Lopez Cascales. 1994. HYDRO: a computer program for the prediction of hydrodynamic properties of macromolecules. Biophys. J. 67:530–531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert, R. J. C. 2002. Pore-forming toxins. Cell. Mol. Life Sci. 59:832–844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert, R. J. C., R. K. Heenan, P. A. Timmins, N. A. Gingles, T. J. Mitchell, A. J. Rowe, J. Rossjohn, M. W. Parker, P. W. Andrew, and O. Byron. 1999a. Studies on the structure and mechanism of a bacterial protein toxin by analytical ultracentrifugation and small-angle neutron scattering. J. Mol. Biol. 293:1145–1160. [DOI] [PubMed] [Google Scholar]
- Gilbert, R. J. C., J. L. Jimenez, S. Chen, I. J. Tickle, J. Rossjohn, M. Parker, P. W. Andrew, and H. R. Saibil. 1999b. Two structural transitions in membrane pore formation by pneumolysin the pore-forming toxin of Streptococcus pneumoniae. Cell. 97:647–655. [DOI] [PubMed] [Google Scholar]
- Gilbert, R. J. C., J. Rossjohn, M. W. Parker, R. K. Tweten, P. J. Morgan, T. J. Mitchell, N. Errington, A. J. Rowe, P. W. Andrew, and O. Byron. 1998. Self-interaction of pneumolysin the pore-forming protein toxin of Streptococcus pneumoniae. J. Mol. Biol. 284:1223–1237. [DOI] [PubMed] [Google Scholar]
- Gruber, G., D. I. Svergun, U. Coskun, T. Lemker, M. H. Koch, H. Schagger, and V. Muller. 2001. Structural insights into the A1 ATPase from the archaeon, Methanosarcina mazei Go1. Biochemistry. 40:1890–1896. [DOI] [PubMed] [Google Scholar]
- Guex, N., and M. C. Peitsch. 1997. SWISS-MODEL and the Swiss-PdbViewer: an environment for comparative protein modeling. Electrophoresis. 18:2714–2723. [DOI] [PubMed] [Google Scholar]
- Hesselbo, B., and R. B. Stinchcombe. 1995. Monte-Carlo simulation and global optimization without parameters. Phys. Rev. Lett. 74:2151–2155. [DOI] [PubMed] [Google Scholar]
- Heuck, A. P., E. M. Hotze, R. K. Tweten, and A. E. Johnson. 2000. Mechanism of membrane insertion of a multimeric beta-barrel protein: perfringolysin O creates a pore using ordered and coupled conformational changes. Mol. Cell. 6:1233–1242. [DOI] [PubMed] [Google Scholar]
- Heuck, A. P., R. K. Tweten, and A. E. Johnson. 2001. Beta-barrel pore-forming toxins: intriguing dimorphic proteins. Biochemistry. 40:9065–9073. [DOI] [PubMed] [Google Scholar]
- Hotze, E. M., A. P. Heuck, D. M. Czajkowsky, Z. Shao, A. E. Johnson, and R. K. Tweten. 2002. Monomer-monomer interactions drive the prepore to pore conversion of a beta-barrel-forming cholesterol-dependent cytolysin. J. Biol. Chem. 277:11597–11605. [DOI] [PubMed] [Google Scholar]
- Johnson, M., J. J. Correia, D. A. Yphantis, and H. Halvorsen. 1981. Analysis of data from the analytical ultracentrifuge by nonlinear least square techniques. Biophys. J. 36:575–588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly, S. J., and M. J. Jedrzejas. 2000. Crystallization and preliminary X-ray diffraction analysis of a functional form of pneumolysin a virulence factor from Streptococcus pneumoniae. Acta Crystallogr. D56:1452–1455. [DOI] [PubMed] [Google Scholar]
- Konarev, P. V., V. V. Volkov, A. V. Sokolova, M. H. J. Koch, and D. I. Svergun. 2003. PRIMUS: a Windows-PC based system for small-angle scattering data analysis. J. Appl. Crystallog. S6:1277–1282. [Google Scholar]
- Kozin, M. B., and D. I. Svergun. 2001. Automated matching of high- and low-resolution structural models. J. Appl. Crystallog. 34:33–41. [Google Scholar]
- Lamm, O. 1929. Die Differentialgleichung der Ultrazentrifugierung. Ark. Mat. Astr. Fys. 21B:1–4. [Google Scholar]
- Laue, T. M., B. D. Shah, T. M. Ridgeway, and S. Pelletier. 1992. Computer-aided interpretation of analytical sedimentation data for proteins. In Analytical Ultracentrifugation in Biochemistry and Polymer Science. Redwood Press Ltd, Melksham, UK. 90–125.
- Mitchell, T. J. 1999. Pneumolysin: structure, function and role in desease. In The Comprehensive Sourcebook of Bacterial Protein Toxins. J. E. Alouf and J. H. Freer, editors. Academic Press, London, UK. 476–94.
- Mitchell, T. J., J. A. Walker, F. K. Saunders, P. W. Andrew, and G. J. Boulnois. 1989. Expression of the pneumolysin gene in Escherichia coli: rapid purification and biological properties. Biochim. Biophys. Acta. 1007:67–72. [DOI] [PubMed] [Google Scholar]
- Morgan, P. J., P. W. Andrew, and T. J. Mitchell. 1996. Thiol-activated cytolysins. Rev. Med. Microbiol. 7:221–229. [Google Scholar]
- Morgan, P. J., S. C. Hyman, O. Byron, P. W. Andrew, T. J. Mitchell, and A. J. Rowe. 1994. Modeling the bacterial protein toxin pneumolysin in its monomeric and oligomeric form. J. Biol. Chem. 269:25315–25320. [PubMed] [Google Scholar]
- Morgan, P. J., S. C. Hyman, A. J. Rowe, T. J. Mitchell, P. W. Andrew, and H. R. Saibil. 1995. Subunit organisation and symmetry of pore-forming oligomeric pneumolysin. FEBS Lett. 371:77–80. [DOI] [PubMed] [Google Scholar]
- Morgan, P. J., P. G. Varley, A. J. Rowe, P. W. Andrew, and T. J. Mitchell. 1993. Characterisation of the solution properties and conformation of pneumolysin the membrane-damaging toxin of Sreptococcus pneumoniae. Biochem. J. 296:671–674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nöllmann, M., R. J. Gilbert, T. J. Mitchell, M. Sferrazza, and O. Byron. 2004. The role of cholesterol in the activity of pneumolysin a bacterial toxin. Biophys. J. 86: 3141–3157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer, M. 2001. The family of thiol-activated cholesterol-binding cytolysins. Toxicon. 39:1681–1689. [DOI] [PubMed] [Google Scholar]
- Paton, J. C. 1996. The contribution of pneumolysin to the pathgenicity of Streptococcus pneumoniae. Trends Microbiol. 4:103–106. [DOI] [PubMed] [Google Scholar]
- Paton, J. C. 1998. Novel pneumococcal surface proteins: role in virulence and vaccine potential. Trends Microbiol. 6:85–87. [DOI] [PubMed] [Google Scholar]
- Perkins, S. J. 1988. X-ray and neutron solution scattering. In Modern Physical Methods in Biochemistry. A. Neuberger, editor. Elsevier Science Publishers B.V., Amsterdam, The Netherlands. 143–251.
- Perugini, M. A., P. Schuck, and G. J. Howlett. 2000. Self-association of human apolipoprotein E3 and E4 in the presence and absence of phospholipid. J. Biol. Chem. 275:36758–36765. [DOI] [PubMed] [Google Scholar]
- Petoukhov, M. V., N. A. Eady, K. A. Brown, and D. I. Svergun. 2002. Addition of missing loops and domains to protein models by x-ray solution scattering. Biophys. J. 83:3113–3125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramachandran, R., A. P. Heuck, R. K. Tweten, and A. E. Johnson. 2002. Structural insights into the membrane-anchoring mechanism of a cholesterol-dependent cytolysin. Nat. Struct. Biol. 9:823–827. [DOI] [PubMed] [Google Scholar]
- Rossjohn, J., S. C. Feil, W. J. McKinstry, R. K. Tweten, and M. W. Parker. 1997. Structure of a cholesterol-binding thiol-activated cytolysin and a model of its membrane form. Cell. 89:685–692. [DOI] [PubMed] [Google Scholar]
- Rossjohn, J., R. J. C. Gilbert, D. Crane, P. J. Morgan, T. J. Mitchell, A. J. Rowe, P. W. Andrew, J. C. Paton, R. K. Tweten, and M. W. Parker. 1998. The molecular mechanism of pneumolysin a virulence factor from Streptococcus pneumoniae. J. Mol. Biol. 284:449–461. [DOI] [PubMed] [Google Scholar]
- Rossjohn, J., R. K. Tweten, J. I. Rood, and M. W. Parker. 1999. Perfringolysin O. In The Comprehensive Sourcebook of Bacterial Protein Toxins. J. E. Alouf and J. H. Freer, editors. Academic Press, London, UK. 496–510.
- Schuck, P. 1998. Sedimentation analysis of noninteracting and self-associating solutes using numerical solutions to the Lamm equation. Biophys. J. 75:1503–1512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuck, P. 2000. Size-distribution analysis of macromolecules by sedimentation velocity ultracentrifugation and Lamm equation modeling. Biophys. J. 78:1606–1619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuck, P. 2003. On the analysis of protein self-association by sedimentation velocity analytical ultracentrifugation. Anal. Biochem. 320:104–124. [DOI] [PubMed] [Google Scholar]
- Scott, D. J., J. G. Grossmann, J. R. Tame, O. Byron, K. S. Wilson, and B. R. Otto. 2002. Low resolution solution structure of the Apo form of Escherichia coli haemoglobin protease Hbp. J. Mol. Biol. 315:1179–1187. [DOI] [PubMed] [Google Scholar]
- Semenyuk, A. V., and D. I. Svergun. 1991. GNOM: a program package for small-angle scattering data processing. J. Appl. Crystallog. 24:537–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shatursky, O., A. P. Heuck, L. A. Shepard, J. Rossjohn, M. W. Parker, A. E. Johnson, and R. K. Tweten. 1999. The mechanism of membrane insertion for a cholesterol-dependent cytolysin: a novel paradigm for pore-forming toxins. Cell. 99:293–299. [DOI] [PubMed] [Google Scholar]
- Shepard, L. A., A. P. Heuck, B. D. Hamman, J. Rossjohn, M. W. Parker, K. R. Ryan, A. E. Johnson, and R. K. Tweten. 1998. Identification of a membrane-spanning domain of the thiol-activated pore-forming toxin Clostridium perfringens perfringolysin O: an alpha-helical to beta-sheet transition identified by fluorescence spectroscopy. Biochemistry. 37:14563–14574. [DOI] [PubMed] [Google Scholar]
- Sokolova, A., M. Malfois, J. Caldentey, D. I. Svergun, M. H. Koch, D. H. Bamford, and R. Tuma. 2001. Solution structure of bacteriophage PRD1 vertex complex. J. Biol. Chem. 276:46187–46195. [DOI] [PubMed] [Google Scholar]
- Sugahara, M., N. Sekino-Suzuki, Y. Ohno-Iwashita, and K. Miki. 1996. Crystallization and preliminary X-ray diffraction of θ toxin (perfringolysin O) a pore-forming cytolysin of Clostridium perfringens. J. Cryst. Growth. 168:288–291. [Google Scholar]
- Svergun, D. I. 1992. Determination of regularisation parameter in direct-transform methods using perceptual criteria. J. Appl. Crystallog. 25:495–503. [Google Scholar]
- Svergun, D. I. 1999. Restoring low resolution structure of biological macromolecules from solution scattering using simulated annealing. Biophys. J. 76:2879–2886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Svergun, D. I., A. Becirevic, H. Schrempf, M. H. Koch, and G. Gruber. 2000. Solution structure and conformational changes of the Streptomyces chitin-binding protein (CHB1). Biochemistry. 39:10677–10683. [DOI] [PubMed] [Google Scholar]
- Svergun, D. I., and M. H. Koch. 2002. Advances in structure analysis using small-angle scattering in solution. Curr. Opin. Struct. Biol. 12:657–660. [DOI] [PubMed] [Google Scholar]
- Svergun, D. I., M. V. Petoukhov, and M. H. Koch. 2001. Determination of domain structure of proteins from X-ray solution scattering. Biophys. J. 80:2946–2953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tweten, R. K. 1995. Pore-forming toxins of the Gram positive bacteria. In Virulence Mechanisms of Bacterial Pathogens. J. A. Rothe, C. A. Bolin, K. A. Brogden, C. Minion, and M. J. Wannemuehler, editors. American Society for Microbiology, Washington, DC. 207–30.
- Vachette, P., E. Dainese, V. B. Vasyliev, P. Di Muro, M. Beltramini, D. I. Svergun, V. De Filippis, and B. Salvato. 2002. A key structural role for active site type 3 copper ions in human ceruloplasmin. J. Biol. Chem. 277:40823–40831. [DOI] [PubMed] [Google Scholar]
- Volkov, V. V., and D. I. Svergun. 2003. Uniqueness of ab initio shape determination in small-angle scattering. J. Appl. Crystallog. 36:860–864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker, J. A., R. L. Allen, P. Falmagne, M. K. Johnson, and G. J. Boulnois. 1987. Molecular cloning characterization and complete nucleotide sequence of the gene for pneumolysin the sulfhydril-activated toxin of Streptococcus pneumoniae. Infect. Immun. 55:1184–1189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, P.-F., D. M. Veine, S. H. Ahn, and C. H. Williams, Jr. 1986. A stable mixed disulfide between thioredoxin reductase and its substrate thioredoxin: preparation and characterisation. Biochemistry. 35:4812–4819. [DOI] [PubMed] [Google Scholar]
- Wriggers, W., and P. Chacon. 2001. Using Situs for the registration of protein structures with low-resolution bead models from X-ray solution scattering. J Appl Crystallog. 34:773–776. [Google Scholar]
- Yphantis, D. A. 1960. Equilibrium ultracentrifugation of dilute solutions. Biochemistry. 3:297–317. [DOI] [PubMed] [Google Scholar]
- Zou, P., M. Gautel, A. Geerlof, M. Wilmanns, M. H. Koch, and D. I. Svergun. 2003. Solution scattering suggests cross-linking function of telethonin in the complex with titin. J. Biol. Chem. 278:2636–2644. [DOI] [PubMed] [Google Scholar]








