Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Jul;87(1):582–595. doi: 10.1529/biophysj.104.041046

A New Method of Identifying the Site of Tyrosyl Radicals in Proteins

Dimitri A Svistunenko 1, Chris E Cooper 1
PMCID: PMC1304380  PMID: 15240491

Abstract

Protein-bound tyrosyl radicals catalyze many important enzymatic reactions. They can also initiate oxidative damage to cells. Here we report a new method of computer simulation of tyrosyl radical electron paramagnetic resonance spectra. The method enables the determination of the rotational conformation of the phenoxyl ring in a radical with unprecedented accuracy (∼2°). When coupled with a new online database, all tyrosine residues in a protein can be screened for that particular conformation. For the first time we show relationships between the spin density on atom C1 (ρC1) and the principal g-factors measured by electron paramagnetic resonance spectroscopy (ρC1 on gx is shown to be linear). The new method enables the accurate determination of ρC1 in all known tyrosyl radicals, evaluates the likelihood of a hydrogen bond, and determines the possibility of a ρC1 distribution in the radicals. This information, together with the accurately determined rotational conformation, is frequently sufficient to allow for an unambiguous identification of the site of radical formation. The possibility of a similar relationship between ρC and gx in other radicals, e.g., tryptophanyl, is discussed.

INTRODUCTION

Many proteins make use of free radicals as part of their catalytic mechanism (Frey, 2001). Reactions catalyzed include electron transfer (e.g., photosynthetic reaction center), biosynthesis (e.g. ribonucleotide reductase, i.e., RNR; prostaglandin H synthase, i.e., PGHS; and horseradish peroxidase), the generation of reactive intermediates in host defense (e.g., myeloperoxidase, lactoperoxidase), or the removal of reactive oxygen species (e.g., catalase). The uncontrolled formation of protein-bound free radicals is increasingly being seen as playing a role in the etiology of a range of diseases, e.g., rhabdomyolysis or subarachnoid hemorrhage (Reeder et al., 2002).

Tyrosine (Tyr) is undoubtedly the most frequently reported site of free radical formation in proteins. Some tyrosyl radicals are associated with the enzymatic activity. Others are formed transiently during enzyme turnover or inhibition. Tyrosyl radicals have been found in RNR from different sources (Allard et al., 1996; Reichard and Ehrenberg, 1983; Sahlin et al., 1982); in ovine and human PGHS (Dorlet et al., 2002; Hsi et al., 1994); in Mycobacterium tuberculosis catalase-peroxidase treated with peroxyacetic acid (Chouchane et al., 2002); in Dactylium dendroides galactose oxidase (Babcock et al., 1992; Whittaker et al., 1996a); in Phanerochaete chrysosporium glyoxal oxidase (Whittaker et al., 1996b); in bovine catalase treated with H2O2 (Ivancich et al., 1996); in human hemoglobin (Hb), soybean leghemoglobin (Lb), horse and sperm whale myoglobins (Mb) treated with H2O2 (Davies and Puppo, 1992; Gunther et al., 2000, 1998; Svistunenko et al., 2002); and in photosystem II (PSII) (Hoganson and Babcock, 1992; Tommos et al., 1995).

The method of choice for detecting free radicals in proteins is electron paramagnetic resonance (EPR) spectroscopy. However, the assignment of an EPR spectrum to a tyrosyl radical is not always straightforward, since tyrosyl radicals in different proteins show very different EPR spectra. Furthermore, even when an EPR spectrum is definitively assigned to a tyrosyl radical, the question remains: which tyrosine is responsible for the radical? Conventionally, mutation of different tyrosine residues is used to answer this question. However, although site-directed mutagenesis can rule out residues for which the mutation has no effect on the observed EPR spectrum, perturbation of an EPR spectrum is not unequivocal evidence that the radical is in the mutation site. For example, the mutated amino acid may be involved in the primary chemistry of radical formation which is then being transferred to the final stable site. In such case the mutation will perturb the EPR spectrum even though the observed radical is far away from the mutation. This appears to be the case, for example, with sperm whale Mb treated with hydrogen peroxide where the Tyr103 to Phe103 mutation removes the observed tyrosyl radical, yet the radical is likely to be on Tyr151 (Svistunenko et al., 2002).

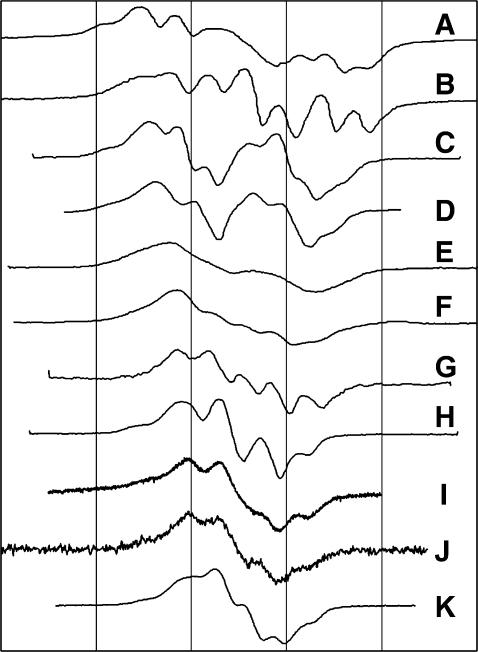
The variability of the EPR spectra of the tyrosyl radicals in different proteins (Fig. 1) is traditionally associated with the ability of the phenolic group in tyrosine to rotate around the Cβ−C1 bond (Fig. 2).

FIGURE 1.

FIGURE 1

Open in a new tab

The X-band EPR spectra of Tyr radicals in different proteins. (A) P. denitrificans CcO+H2O2 (MacMillan et al., 1999); (B) horse metMb+H2O2 (Miki et al., 1989); (C) mouse TA3 cells RNR (Sahlin et al., 1987); (D) E. coli RNR (Hoganson and Babcock, 1992); (E) ovine PGHS, wide doublet (Kulmacz et al., 1990); (F) ovine PGHS, narrow singlet (Dorlet et al., 2002); (G) soybean metLb+H2O2 (Davies and Puppo, 1992); (H) S. typhimurium RNR (Allard et al., 1996); (I) A. thaliana photosystem II Inline graphic radical (Svistunenko et al., 2002); (J) metHb+H2O2 (Svistunenko et al., 2002); and (K) bovine catalase+peroxyacetic acid (Ivancich et al., 1996). The spectra were plotted on a common magnetic field axis as described in Software and Methods. The gridlines are drawn at a 20-Gauss interval.

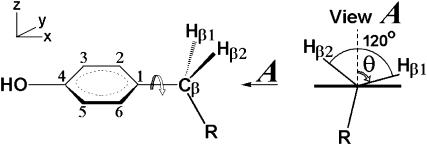
FIGURE 2.

FIGURE 2

Open in a new tab

A definition of the ring rotation angle in tyrosine. The ring rotation angle θ in tyrosine is defined in this article for view A. It is the angle for proton β1; it is positive when measured clockwise from the upward perpendicular to the ring plane when the Cβ−R bond is below the horizontally oriented ring plane.

When a radical is formed on a Tyr, the oxygen proton is lost. The EPR spectrum is therefore defined by the hyperfine interaction of the unpaired electron with the four ring protons and with the β-protons of the methylene group. The hyperfine interaction with the β-protons depends on the rotation angle θ (Fig. 2), according to the McConnell relation (McConnell and Cheshunt, 1958),

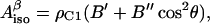graphic file with name M1.gif (1)

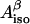where Inline graphic is the isotropic hyperfine splitting constant, ρC1 is the spin density on atom C1, and B′ and B″ are constants, with B′ being commonly neglected in practical applications and B″ being equal to 58 G (Fessenden and Schuler, 1963). The 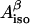Inline graphic-values for both β-protons can be determined via a simulation of the experimental X-band (∼9 GHz) EPR spectrum. The two unknowns, ρC1 and θ, can then be found from a system involving the use of Eq. 1 written for the two protons. Knowing the value of θ for a tyrosyl radical is important for identification of the responsible tyrosine residue, because this angle can be directly measured for any tyrosine, if the three-dimensional structure of the protein is known.

Thus, tyrosyl radicals with different rotational conformations of the phenoxyl ring will have EPR spectra with different patterns of hyperfine structure. This rationalization of the variability of the EPR lineshapes (Fig. 1) has been generally validated in a number of publications by computer simulation of the experimental X-band EPR spectra of tyrosyl radicals (Sahlin et al., 1982; DeGray et al., 1992; Hoganson and Babcock, 1992; Schmidt et al., 1996; Allard et al., 1996; Ivancich et al., 1996, 2001a,b; Himo et al., 1997; Shi et al., 2000; Gunther et al., 2000; Di Bilio et al., 2001; Warncke and Perry, 2001; Svistunenko et al., 2002). Unfortunately, it is usually necessary to specify ∼30 parameters to simulate a tyrosyl radical EPR spectrum. Although many agree that most of these parameters are conserved, i.e., constants for all tyrosyl radicals, there are still 12 nonconserved parameters which have to be specified individually for every type of tyrosyl radical. This considerable number of degrees of freedom unavoidably results in a low accuracy in the parameters determined. The extent of these errors results in a significant degree of ambiguity over the conclusions this type of study can possibly hope to achieve.

When analyzing the simulation parameters previously reported for different tyrosyl radicals we found that no single set of the rotation-independent parameters could be successfully used to simulate all known tyrosyl radical spectra when only the β-protons' splitting constants are allowed to vary. In other words, the variability of the lineshapes of the X-band EPR spectra of tyrosyl radicals cannot be exclusively explained by different angles of rotation of the phenoxyl group.

We therefore report here a completely new approach to the simulation of the tyrosyl radical EPR spectra. We have developed an algorithm enabling us to determine all simulation parameters, using only two input variables: the unpaired spin density on atom C1 and the phenoxyl ring rotation angle. These two input variables, being clear physical and geometrical values and not mathematical constructs, can only be varied within known limited intervals. Thus, we have managed to shrink the 30-dimensional space of tyrosyl radicals existence to a tiny two-dimensional plane with clearcut borders at all four sides. The fact of the tyrosyl radical spectra dependence on ρC1 and on the angle of the phenoxyl ring rotation is already well established. The importance of our results is in our new finding that every spectrum is completely defined by just these two values. All nonconserved parameters necessary for the simulation of the spectrum can be derived (calculated) from the spin density and the rotation angle. This has only become possible because we have found new empirical relationships between the parameters previously considered independent; the most important of these is the relationship between ρC1 and the g-factor components.

By using the algorithm, it is possible to define whether a tyrosyl radical is responsible for the observed EPR spectrum and, if so, the most likely site harboring the radical can be identified on the protein. Additionally, the use of the algorithm allows us for the first time to predict an EPR spectrum, i.e., to simulate a lineshape that has not been experimentally determined yet.

SOFTWARE AND METHODS

Software used

UN-SCAN-IT Automated Digitizing System, Version 5.0 (Silk Scientific Corporation, http://www.silkscientific.com/) was used to digitize scanned EPR spectra published in the literature. The program simpow6 (Mark Nilges, Illinois EPR Research Center, http://ierc.scs.uiuc.edu/∼nilges/software.html) was used for the EPR spectra simulation. Swiss-PdbViewer 3.7 (http://ca.expasy.org/spdbv/text/disclaim.htm) was used to analyze the three-dimensional structure of the proteins and to measure the dihedral angles that were used to calculate θ.

All spreadsheet-calculators (see Supplementary Material for these tools) were created in Microsoft Excel 2000:

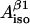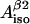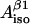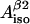  • theta_in_tyr.xls—file-calculator for finding θ and ρC1 for any pair of values Inline graphic and Inline graphic (four solutions) or to calculate Inline graphic and Inline graphic for fixed θ- and ρC1-values (single solution).

  • g_and_k.xls—file-calculator for finding gx, gy, and gy from K, or to calculate gy, gy, and K from gx.

  • algorithm.xls—calculates all parameters necessary for a simulation of a tyrosyl radical EPR spectrum while using two input parameters, ρC1 (the spin density on atom C1; range of values 0.320–0.440) and the phenoxyl ring rotation angle θ (range of values −90° to +90°).

  • al_XB.xls and al_HF.xls (at least one pair of these files per each radical)—for calculating the simulation parameters for concrete X-band and high field (HF) EPR spectra of a Tyr radical; these are the abbreviated (low graphics) versions of the algorithm.xls file with the values of ρC1 and θ already typed in for every radical spectrum, so that the full set of the simulation parameters is readily available for every spectrum presented in the article.

Plotting Fig. 1

The X-band EPR spectra of tyrosyl radicals in different proteins, published by different authors, were scanned and digitized using UN-SCAN-IT. The magnetic field axis, common for all spectra, is not shown since the absolute value of the resonance field is different for each spectrum due to different microwave frequencies used. All spectra are aligned horizontally by an arbitrary chosen g-factor (2.005), the exact position of which on each spectrum was determined after the simulations of these spectra were performed.

Determination of the ring rotation angle θ from the dihedral angles

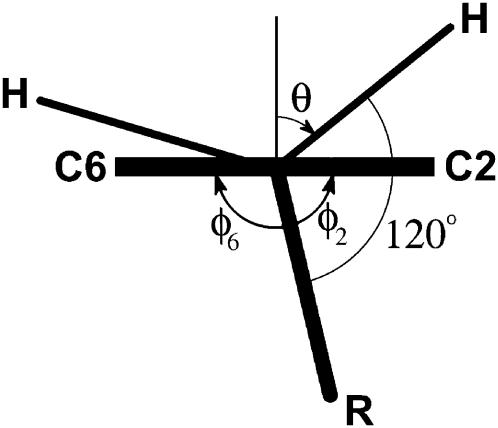
Protons are not resolved in the x-ray crystallographic data, so angle θ can only be determined indirectly from the dihedral angle formed by the ring plane and the R−Cβ−C1 plane (Fig. 3).

FIGURE 3.

FIGURE 3

Open in a new tab

The ring rotation angle θ can be found from directly measurable dihedral angles φ2 defined by R–Cβ–C1–C2 and φ6 defined by R–Cβ–C1–C6 (note that φ2 and φ6 have opposite signs).

From the figure, θ° = 90° − (120° − φ2) = φ2 − 30°. Since φ2 is only approximately equal to (180−φ6), because the ring atoms never form an ideal plane, we used an average value instead of φ2. Thus,

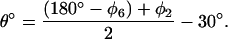graphic file with name M8.gif

The angles φ2 and φ6 are dihedral angles and can be measured by the appropriate Swiss-PbdViewer tool. For more details see the home page of our Rotation Angle database (http://privatewww.essex.ac.uk/∼svist/lev1/tyrdb/home.shtml). This database is a collection of data on the value of angle θ in tyrosine residues in various proteins.

Plotting the spectra in Table 1

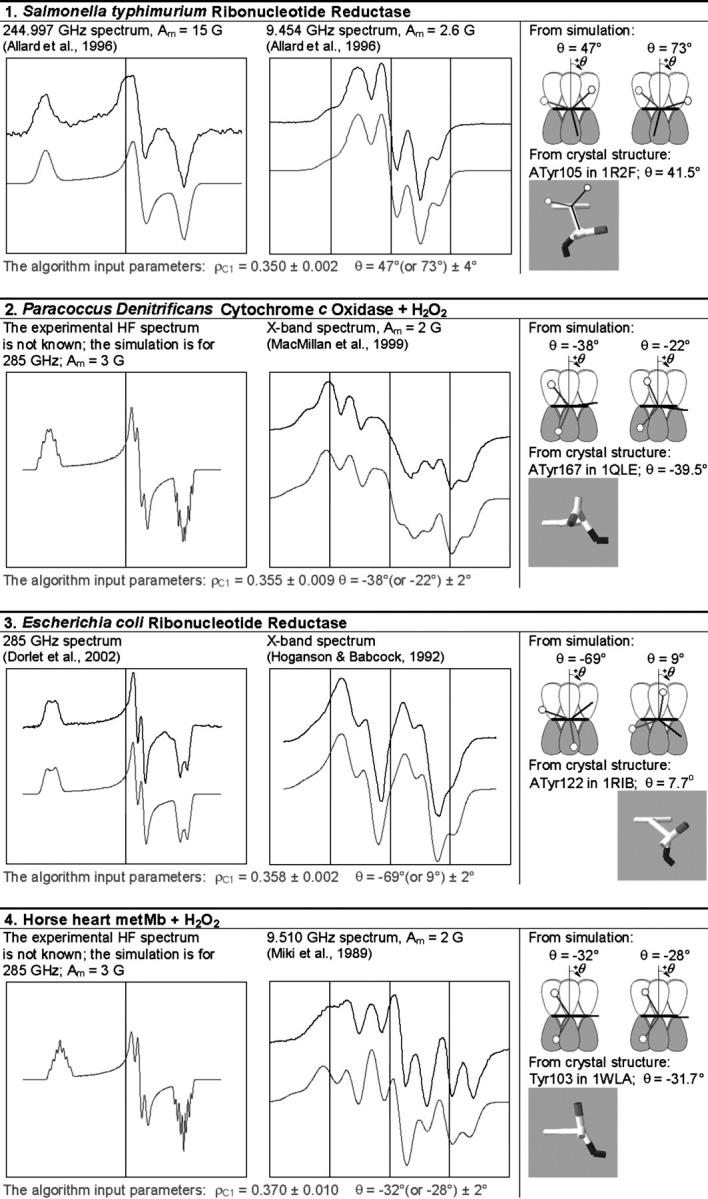
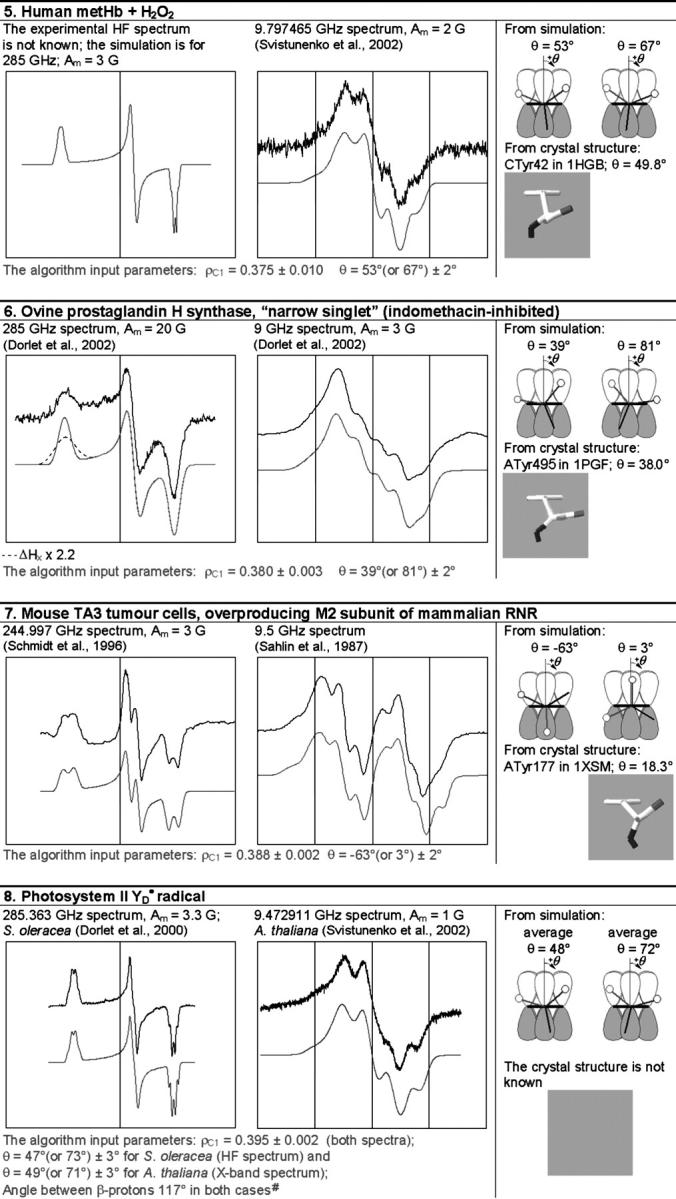
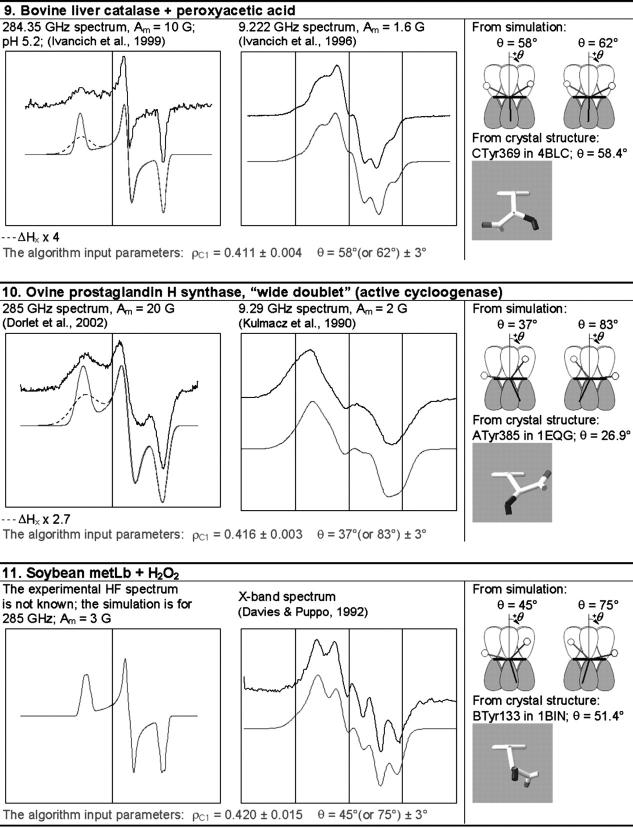
TABLE 1.

The simulation of the HF and X-band EPR spectra of tyrosyl radical in different proteins

graphic file with name biophysj00041046T01AtoD_HT.jpg
graphic file with name biophysj00041046T01EtoH_HT.jpg
graphic file with name biophysj00041046T01ItoK_HT.jpg
Open in a new tab

In each box, the simulated spectrum is shown below the experimental one. All experimental spectra are taken from the literature. When experimental spectrum is not available, only the simulated one is present. In three cases (6, 9, and 10), the dashed trace corresponds to the spectrum simulated for a greater than the algorithm predicts x-component of the linewidth, all other parameters being generated by the algorithm. The optimal values of the algorithm input parameters ρC1 and θ, used to calculate the simulation parameters (see Supplementary Material, Simulation Data), are indicated under the spectra. The radicals in the table are arranged by ascending ρC1. For each radical, the two optimal θ-angles, equivalent in terms of providing the simulation parameters, are compared with the θ-angle found from the crystal structure, the latter shown under the corresponding optimal angle. The tyrosine number and the Protein Data Bank (http://www.rcsb.org/pdb/) file, e.g., 1R2F for S. typhimurium RNR (Eriksson et al., 1998), are indicated. Other structure files quoted in the table were first presented in the articles: 1QLE (Harrenga and Michel, 1999), 1RIB (Nordlund and Eklund, 1993), 1WLA (Maurus et al., 1997), 1HGB (Liddington et al., 1992), 1PGF (Loll et al., 1996), 1XSM (Kauppi et al., 1996), 4BLC (Ko et al., 1999), 1EQG (Selinsky et al., 2001), and 1BIN (Hargrove et al., 1997). The details of 1), how the errors in optimal ρC1 and θ were determined; 2), how the spectra were plotted on a common magnetic field axis; and 3), how the θ-values were found from the crystal structure, are all described in Software and Methods.

#The algorithm (available in Supplementary Material as the file calculator algorithm.xls) allows us to vary the angle between the projections of the bonds Cβ−Hβ1 and Cβ−Hβ2 to the y–z plane (default value is 120°). The photosynthetic Inline graphic radical is the only occasion when we exercised this option.

All experimental and simulated X-band spectra are presented in a 80-G wide field window centered at the g-factor value of 2.00500 (the absolute values of the field being different for different spectra, and not shown). All the HF spectra are also plotted on a regular magnetic field scale, although not only the absolute values of the field but the field ranges as well are different for different spectra. The standard for the HF spectra presentation is chosen therefore as follows: the left edge of the field window for every HF spectrum corresponds to the g-factor of 2.01100, and the right edge corresponds to the g-factor of 1.99900. Consequently the middle of the window corresponds approximately, although with a good accuracy, to the g-factor of 2.005. Thus, the HF and the X-band windows are set with the center corresponding to the same g-factor, 2.005.

Determination of the errors in ρC1 and θ (Table 1 and Fig. 7)

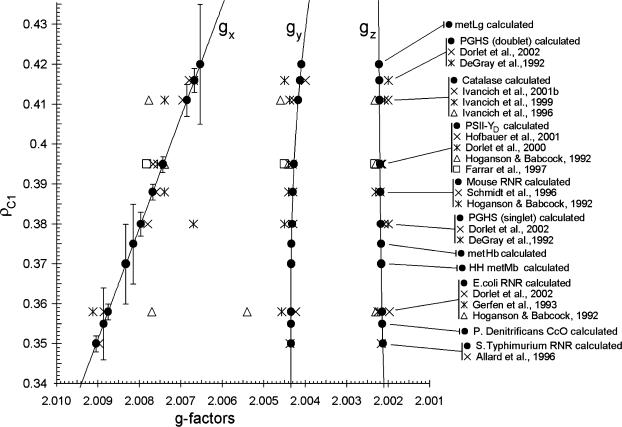
FIGURE 7.

FIGURE 7

Open in a new tab

The ρ-g chart for the 11 tyrosyl radicals studied (•). The value of the spin density on atom C1 (ρC1) for each tyrosyl radical was found as the optimal input parameter of the algorithm for the EPR spectrum simulation (Table 1); the principal values of the g-factor were generated by the algorithm. The errors in ρC1 are indicated at the gx components (note significantly higher error for the radicals with unknown HF spectrum). The continuous lines are generated by the algorithm. The literature data on the principal g-factors of the Tyr radicals are also shown with the ρC1-value for each radical formally assumed the same as the value found in this work (compare with Fig. 6).

The errors in determination of the optimal values of ρC1 and θ (Table 1) were found during the simulation of the spectra, when either ρC1 or θ was varied around its optimal value, whereas the other parameter (θ or ρC1, respectively) was kept at its optimal value. The error in ρC1 was determined when the deviation in this parameter resulted in a HF spectrum noticeably different from the experimental HF spectrum. Similarly, the error in θ was determined when this parameter was varied around its optimal value and the changes in the simulated X-band spectrum were monitored. For the tyrosyl radicals with unknown HF spectra (in leghemoglobin, hemoglobin, myoglobin, and cytochrome c oxidase), the error in ρC1 was found while varying this value and monitoring the changes in the X-band simulated spectrum. Since the X-band spectra are less sensitive to the g-factor changes than the HF spectra, the errors in ρC1 determined for these four cases are significantly greater than when determined by monitoring the HF simulated spectrum.

RESULTS

How can we develop an algorithm that can be used to calculate all the parameters necessary for simulation of an EPR spectrum of a tyrosyl radical? To simulate a tyrosyl radical EPR spectrum, one needs to specify ∼30 parameters (this number could slightly vary depending on the simulation software used). Most of these parameters are conserved; they are thought to be the same for all different tyrosyl radicals. However, different articles quote slightly different values for these conserved parameters (see Supplementary Material, Algorithm description.pdf, Table S1). This brings up a problem: the conserved parameters, used to simulate a tyrosyl radical spectrum, often do not work as well when used unchanged (as conserved) in a simulation of another tyrosyl radical spectrum; the simulation results in a spectrum noticeably different from the experimental one. To solve this problem, our algorithm provides for the first time values of the conserved simulation parameters that work equally well for all simulations. These values (see Supplementary Material, Algorithm description.pdf, Eqs. S1 and S2) are the same in all our simulations of tyrosyl radical spectra measured at all frequencies (see below).

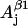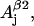The nonconserved parameters are those that might be different for different tyrosyl radicals. There are 12 of those—three spatial components of four physical values: hyperfine splitting constants for the two β-protons Inline graphic and Inline graphic g-factor gj, and individual linewidth ΔHj (j = x, y, z). It is generally accepted that the hyperfine splitting constant tensors for the β-protons are axial: 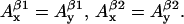Inline graphic This decreases the total number of nonconserved parameters from 12 to 10. Thus, different lineshapes of tyrosyl radicals in different protein system are caused by the differences in the 10 (of the 30 total) simulation parameters. To simulate a tyrosyl radical EPR spectrum means to find a point in a 10-dimensional search space.

It is reasonable to suggest that not all of these 10 nonconserved parameters are independent and that, in fact, some can be expressed as functions of the others. If we knew what these truly independent parameters were, and how the other parameters could be derived from the independent ones, this would then decrease the dimension of the search space and would significantly facilitate the simulation process. The accuracy of such a simulation would also be significantly higher, since the random error would be resulted from adding up the random errors of fewer variables.

The details of the theory behind the algorithm are given in Supplementary Material, Algorithm description.pdf. Below, we are giving a briefly summary of the algorithm. First, we have introduced a variable K,

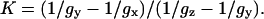graphic file with name M12.gif (2)

The usefulness of K is that it can be measured with a high accuracy directly from a high field (HF) EPR spectrum, without actually knowing the values of the g-factors, since the definition in Eq. 2 is equivalent to the ratio of the distances between components x and y and between components y and z: (Hy−Hx)/(Hz−Hy).

We have measured K directly from all available HF spectra and showed that, for different radicals, the three g-factors can be represented as smooth continuous empirical functions of K. Thus we have added one new variable (K) to our set of 10 parameters, but have formulated three more equations. This brings down the number of independent variables from ten to eight.

In a similar way we demonstrate that the individual linewidth components ΔHj (j = x, y, z) can be represented, like the g-factors, as functions of K (the graphical representations of these dependences are given in Supplementary Material, Algorithm description.pdf):

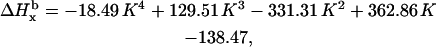graphic file with name M13.gif
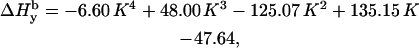graphic file with name M14.gif
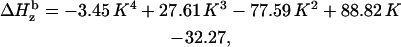graphic file with name M15.gif

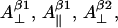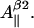
where subscript b indicates that these are the basic linewidth components, independent of the spectrometer settings (the value of the modulation amplitude should be added to these values). Addition of these three equations to the system results in a further reduction of the number of independent variables by three; there are five variables now: K, Inline graphic and Inline graphic

Using highly precise data for the axial hyperfine splitting constants for the β-protons in the photosynthetic radical in three different organisms (Rigby et al., 1994), we have formulated an empirical dependence of the 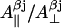Inline graphic ratio on the rotation angle θ (the graphical representation of this dependences is given in Supplementary Material, Algorithm description.pdf):

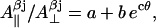graphic file with name M19.gif

where a = 1.12, b = 9.37 10−6, and c = 0.162 degree−1.

Writing this dependence for the two β-protons enables us to add two more independent equations to our system of dependences, although only adding one new independent variable θ. Therefore, we effectively have, at this step, four independent variables.

Finally, the McConnell relation written for the two protons would add two more independent equations and three new variables: 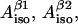Inline graphic and ρC1 (angle θβ2 for the second β-proton is not a new independent variable since it is considered to be equal to θβ1+120° where θβ1 is a variable already employed; θβ1 equals to θ from the previous paragraph). Effectively, the number of independent variables is increased by one (there are now five variables). However, the isotropic hyperfine splitting constants are not really independent variables; they can be explicitly expressed over the parallel and perpendicular components:

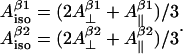graphic file with name M21.gif (3)

Thus we have just added two more equations without adding any new variables, which decreases the number of independent variables by two, down to the final number of three.

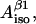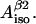Now, it is completely our choice which of the variables we are going to set as independent. For convenience we select K, Inline graphic and Inline graphic We can now calculate all 10 nonconserved simulation parameters from these three input variables.

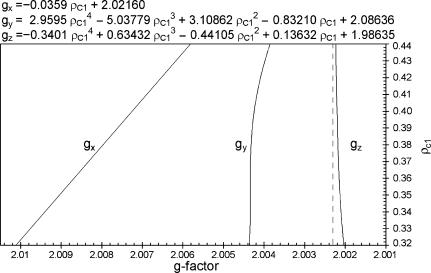
The initial version of our algorithm described above decreases the dimension of the search space in finding the right simulation parameters from 10 to 3. We have successfully used this version to simulate all previously published tyrosyl radical EPR spectra. However, one unexpected, and exciting, result led to a significant improvement in the algorithm. The dependence between ρC1 and gx turned out to be practically linear (see Supplementary Material, Algorithm description.pdf, Fig. S10). Therefore it follows that, instead of K, the values of gx, gy, and gz can now be expressed over ρC1 (Fig. 4). This is the first time that a relationship between the g-factor and the spin density has been reported. As ρC1 increases, the three g-factors become closer to each other approximating the g-factor of a free electron. This behavior of the g-factor anisotropic components is similar to that we have previously described in the ferric heme proteins, when the three components tend to a single isotropic g-value of a free radical as the unpaired spin density shifts from the heme to the ligand (Svistunenko et al., 2000).

FIGURE 4.

FIGURE 4

Open in a new tab

The ρ-g chart for tyrosyl radicals in proteins. The chart shows the empirical dependences derived in the Supplementary Material, Algorithm description.pdf, of the g-factor components on the spin density on the C1 atom. The g-factor axis is given in a reverse order, increasing from the right to the left. The g-factor of a free electron (2.002319) is shown as a dotted vertical line.

We have incorporated the first of the dependences (Eq. 4) into the latest version of our algorithm

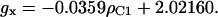graphic file with name M24.gif (4)

Adding this linear dependence between ρC1 and gx to the system of dependences brings the number of truly independent variables down to two. As before, it is our choice which two parameters we consider independent. The version of the algorithm presented in this article uses the spin density ρC1 and the ring rotation angle θ.

Thus, our revised algorithm is capable of calculating all 10 nonconserved parameters using only two input variables: ρC1 and θ. The algorithm, as a calculating tool, is available in the form of an Excel file-calculator algorithm.xls (see Supplementary Material).

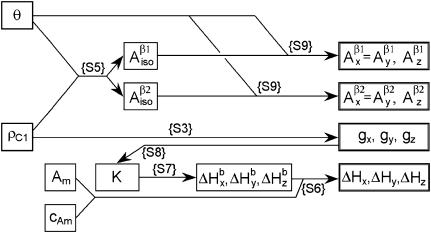
Fig. 5 illustrates how all the nonconserved simulation parameters, 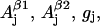Inline graphic and ΔHj (j = x, y, z), can now be derived from just two input parameters, ρC1 and θ. Consequently, the best simulation can be found far more readily, as the whole search space is diminished from ten to two dimensions. Importantly, the two input parameters, as they have a very clear physical meaning, can only be varied within certain limits: the phenoxyl group rotation angle θ makes the full cycle every half of the 2π revolution and is therefore defined on the interval of (−90°; +90°), whereas ρC1 in all so-far known tyrosyl radicals varies within a narrow interval of 0.350–0.420, according to our results (shown below).

FIGURE 5.

FIGURE 5

Open in a new tab

The schematic representation of the algorithm for finding the simulation parameters for a tyrosyl radical EPR spectrum (see Supplementary Material, Algorithm description.pdf). The simulation parameters shown in the four boxes on the right are calculated according to the indicated formulas given in Algorithm description.pdf. The values of the input parameters θ and ρC1 define the isotropic hyperfine splitting constant for the methylene β-protons. The x-, y-, and z-components of these constants are found from the isotropic value and from the value of θ. The ρC1-value alone defines the three components of the g-factor. The linewidth components ΔHj are found from the basic linewidth values 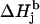Inline graphic and from the value of the modulation amplitude Am used; a small constant cAm that accounts for inaccuracy in the modulation field calibration might be added to Am. The basic linewidth components 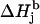Inline graphic (intrinsic radical properties independent of the spectrometer used) are direct functions of the parameter K which is, in turn, a direct function of the three g-factors. All calculations can be preformed using the file calculator algorithm.xls, available as Supplementary Material online.

We have used our algorithm to simulate the lineshapes of all tyrosyl radical spectra we have been able to find in the literature, measured by both X-band and HF EPR spectroscopy (Table 1). For every radical, the same pair of optimal ρC1- and θ-values was used to generate the simulation parameters for both HF and X-band spectra. Our method of simulation is thus a way to accurately find these two physical characteristics. Once there is a deviation from the optimal value in an input parameter, say ρC1, the algorithm would generate a different set of 10 nonconserved output (simulation) parameters; the resulting simulated spectrum based on such values will be different (worse) than the optimal simulated spectrum.

For a particular value of ρC1 there are two possible values of θ in the range of (−90°; +90°) that result in generation of identical sets of simulation parameters (see Supplementary Material, theta_in_tyr.xls, for details). EPR spectroscopy alone is unable to tell which of the two angles corresponds to the actual conformation of the radical. Therefore, if we want to find out which Tyr residue is responsible for the radical in a particular protein, we will have to compare the rotational conformations of all Tyr residues with each of two possible θ-angles. We have created an online database (http://privatewww.essex.ac.uk/∼svist/lev1/tyrdb/home.shtml) that can help in performing this task. It is possible by using the database to display the list of Tyr residues in a protein, to set a target value θtarget, and to sort all residues by the difference |θ−θtarget|. The top of the sorted table of records shows the residues with the closest rotational conformation to the radical's rotational conformation as determined by our algorithm.

By having only two degrees of freedom in the simulation of the EPR spectrum, we find ourselves in a position to be able to predict an EPR spectrum that has not actually been measured before. There are four instances in Table 1 when the HF experimental spectrum is not known. The optimal ρC1- and θ-values were found from the X-band simulations and simply used to simulate (and thus predict) the HF spectra (Table 1).

For the catalase radical and for both PGHS radicals, the optimal simulation of the HF spectrum was only attained when the width of the x-component was markedly increased as compared with the algorithm-generated parameter (note the dashed traces for the HF spectra for the three radicals, Table 1). This is associated with a gx-distribution in the radicals (variable population of radicals with differing values of gx), caused by a distribution of the H-bond strength (Ivancich et al., 1999). Since we show that gx and ρC1 are related (Eq. 4), it follows that ρC1 is also distributed in these particular radicals.

DISCUSSION

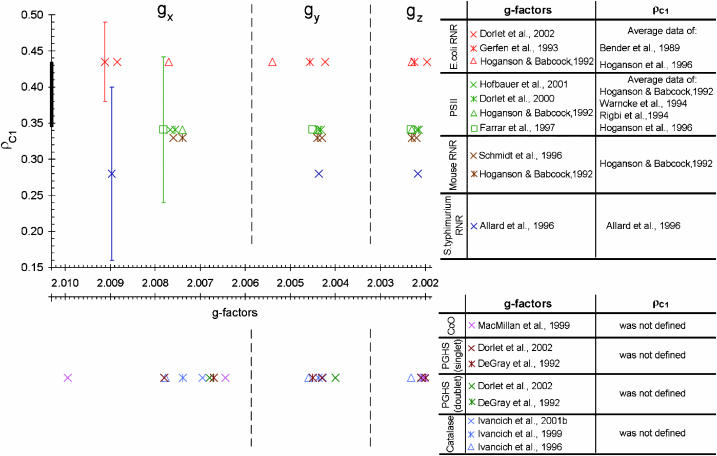
We have developed a semiempirical algorithm that enables us to determine accurately ρC1 for all known tyrosyl radicals, evaluates the likelihood of a hydrogen bond, and determines the possibility of a ρC1 distribution in the radicals. We call our algorithm semiempirical because it does more than simply interpolate existing literature data. For example, if someone wanted to establish a pure empirical relationship between ρC1 and the g-factors they might attempt to plot the available values of these parameters (see Supplementary Material, Algorithm description.pdf, for Tables S3 and S5) on one plane. The result would be as shown in Fig. 6. Obviously, it is not possible to average these rough data and to construct continuous and smooth empirical dependences between ρC1 and the g-factors. Not surprisingly, no relationship has been previously reported between these parameters.

FIGURE 6.

FIGURE 6

Open in a new tab

The literature data on the three g-factors and the spin density on the C1 atom in different tyrosyl radicals. The thick segment of the ρC1 axis indicates the size of Fig. 7 if plotted on this scale. The dotted vertical lines approximately indicate the gx, gy, and gz areas. The data quoted can be found tabulated in Supplementary Material, Algorithm description.pdf, Tables S3 and S5.

When a lack of accuracy in the literature data does not allow us to find continuous and smooth relationships between parameters, we must hypothesize about what these relationships actually are. While observing the condition that our hypothetical relationships should lie within available experimental errors, we justify our hypothesis by successful simulation of all known lineshapes of tyrosyl radical EPR spectra. The same graph as shown in Fig. 6, but plotted according to our algorithm is demonstrated in Fig. 7. This figure shows that the g-factors we calculate are in good correspondence with those previously reported. At the same time, the values of ρC1 we find for different tyrosyl radicals turn out to be within the range of 0.350–0.420 (ΔρC1 = 0.07), which is a fivefold narrower interval than that known from the literature (0.14–0.49, ΔρC1 = 0.35; see Fig. 6; see also Supplementary Material, Algorithm description.pdf, Table S5). More than that, we are able to specify ρC1 for every radical within an error of 0.005. A high accuracy in ρC1 is important, because it ensures a correspondingly high accuracy in finding the rotation angle, which, in turn, allows identification of the Tyr residue in the protein—the ultimate goal of such studies, successfully achieved in our work.

The scientific novelty of our results is in the fact that we make a leap from Fig. 6 to Fig. 7. Not only does our method find all parameters necessary for the simulation of tyrosyl radical EPR spectra, it also establishes a new empirical relationship between the spin density on atom C1 and the g-factors (Fig. 4); we look forward to an independent quantum mechanical justification of these relationships.

The value of gx can be used to assess the electrostatic environment of tyrosyl radicals. In particular, if gx is shifted to lower values it indicates the possibility of a hydrogen bond (Ivancich et al., 1999). Since we have established the linear dependence between ρC1 and gx (Eq. 4) the possibility of a hydrogen bond is now associated with the spin density on C1. Fig. 7 shows that the radicals in a hydrophobic environment, such as in S. typhimurium and E. coli RNR and in CcO, are in the bottom of the ρ-g chart (low values of ρC1), whereas the radicals known to have a hydrogen bond due to the proximity of a protonated oxygen atom to the phenoxyl oxygen (both PGHS radicals, the 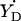Inline graphic radical in PSII, and the radicals in bovine catalase and mouse RNR) are all in the middle and the top of the chart. We suggest that all radicals with ρC1 > 0.38 are H-bonded, and that the higher the ρC1-value, the stronger the bonding.

When the experimental HF spectrum shows the width of the gx component is significantly broader than the algorithm predicts (catalase radical and both PGHS radicals, Table 1), this points to a distribution of gx (and, consequently, ρC1) in the population of the radicals. Such distribution is associated with the distribution of the strength of the H-bond (Ivancich et al., 1999). Interestingly, the fact of H-bond strength distribution does not seem to be associated with the strength itself: gx is clearly not distributed in the mouse RNR radical and in PSII-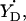Inline graphic yet the ρC1-values for these radicals (and the strength of the H-bond) are between those for the PGHS narrow singlet and the catalase radical, both having distributed gx-values.

For decades, researchers have been using the McConnell empirical relation for finding rotational conformation of tyrosyl radicals and ρC1 from the isotropic hyperfine splitting constants for the β-protons. Such an approach is much less accurate than the one we suggest. Traditionally, a researcher has to make the following few steps to find ρC1 and θ: 1), to make a hypothesis about four axial values of the hyperfine splitting constants A (two values for each of the two protons); 2), to show that the simulation is satisfactory; 3), to average the anisotropic A-values; and 4), to use those averaged, isotropic values in the McConnell equations written for two protons. Such a system of two equations then has to be solved, and the two unknowns, the rotation angle and the spin density, can be found. The low accuracy of ρC1 found by this approach is explicitly illustrated in Fig. 6. Besides, this approach results in two solutions for ρC1, one of which has to be selected and the other discarded, so additional arguments have to be considered to make this choice (see Supplementary Material, Algorithm description.pdf, and the file calculator theta_in_tyr.xls for details). In our method we solve an inverse problem: we suggest a way of finding the anisotropic hyperfine splitting components from the rotation angle. We have formulated this empirical approach on the basis of highly accurate data obtained on the photosynthetic radical found in different rotational conformations in three different organisms (Rigby et al., 1994) (see Table S2, Fig. S3, and Eq. S9 in Algorithm description.pdf). This has allowed us to make a hypothesis about a single value (instead of four), the rotation angle, and to find the four values of the hyperfine splitting constants for two protons.

A relationship between ρC1 and the three g-factors, similar to that we have described in Eq. 4, may exist for other protein radicals. For example, the tryptophanyl radical (the second most common protein radical) also has two β-methylene protons for which the hyperfine splitting constants would depend on the rotation angle of the indole ring in the same way (according to the McConnell relation) as the constants depend on the phenoxyl ring rotation in tyrosyl radicals. We can speculate that the gx-value of a tryptophanyl radical is related to the spin density on atom C3 (the ring carbon to which Cβ is attached; analog of C1 in Tyr) in a way similar to Eq. 4. Such a hypothesis, however should be undertaken with caution since the indole ring, unlike phenoxyl ring, does not have the axial symmetry associated with the x axis. So, although it is reasonable to suggest that a relationship similar to Eq. 4 would be valid for tryptophanyl radicals (the higher the ρC3, the lower the gx), such a relationship might be not linear.

Is there any experimental data to support our structural assignments? X-ray crystallography looks at the structure of a tyrosine in a crystal, whereas EPR looks at frozen solution structures of tyrosine radicals. Adding/subtracting an electron, or going to the crystal state, might perturb the rotation angle. Although being aware of these caveats, it is nevertheless instructive to compare the angles determined by EPR with those obtained from the published protein structure to see if there are cases where we have good agreement. EPR methods alone always yield two possible values for the phenoxyl ring rotation angle (Table 1). When there is a consensus about the location of the radical in proteins (S. typhimurium, E. coli, mouse RNR, and ovine PGHS wide doublet), one of the two optimal θ-values is always in a good agreement with the value found from the crystal structure for the corresponding Tyr residues, indicating consistency in the values of the rotation angle found by the two different methods (Table 1). When the location of the radical is not known, or there is only a tentative assignment in the literature, we suggest a method of creation of a shortlist of tyrosine residues in the protein with a rotational conformation close to either of the two optimal θ-values (Svistunenko et al., 2003).

For example, the optimal θ-value for the tyrosyl radical in HH Mb (−32° or −28°) allows us to unambiguously identify the residue as Tyr103 (θ = −31.7°, Table 1) since the only other tyrosine (Tyr146) is characterized by θ = −57.5°, which is markedly different from either of the optimal θ-values. Our identification of Tyr103 as the site of the radical in the HH metMb/H2O2 system is in agreement with earlier assignment of this radical, also based on an analysis of the EPR spectral lineshape (Gunther et al., 2000). The (presumably identical) radical that can be spin-trapped in the HH Mb/H2O2 system by 2-methyl-2-nitrosopropane (Fenwick and English, 1996) or by 3,5-dibromo-4-nitrosobenzene sulfonate (Harris et al., 2002) was also demonstrated to be located on Tyr103 by the use of mass spectrometry (Fenwick and English, 1996) and by a combination of EPR, electrophoretic purification, and mass spectrometry (Harris et al., 2002).

The radical in Lg was hypothesized to be located on Tyr133, the closest tyrosine to the heme (Davies and Puppo, 1992). Indeed, the value of angle θ in this residue, when averaged over two identical chains, is 52.0°, as can be found from structure file 1BIN (Hargrove et al., 1997). This value is only 7° different from the angle of 45° obtained from our simulation (Table 1). Two other tyrosine residues in this protein, Tyr25 and Tyr30, are less probable candidates, in that the corresponding averaged angles for these residues are 8.5° and 28.7°, respectively—which are 36.5° and 16.3° different from the angle of 45°. Thus, by the closeness of angle θ in the three tyrosine residues to the angle found from the simulation—7° for Tyr133, 16.3° for Tyr30, and 36.5° for Tyr25—the first residue, Tyr133, is indeed the most likely site to host the radical (Table 1), whereas the other two tyrosine residues present in Lg are far less probable candidates.

No residue assignment has been given so far to the radical in human metHb. Our analysis of a total of 12 Tyr residues in Hb (structure file 1HGB; Liddington et al., 1992) have shown that Tyr42 in the α-subunits is the most probable site of the free radical location since angle θ = 53° obtained from the simulation is only 3.5° different from the value of this angle averaged over two homologous α-subunits (θ = 56.5°). Two other sites, Tyr130 and Tyr35 in the β-subunits, should be considered as “next most probable” since the values of their angle averaged over the two homologous β-subunits are 7.8° and 8.8° different from the value of 53° obtained from the simulation.

In bigger proteins with a large number of Tyr residues the analysis can be more laborious. Nevertheless, a residue responsible for the radical can sometimes still be singled out. For example, the radical in P. denitrificans CcO was tentatively assigned to the active site Tyr280 (MacMillan et al., 1999). Our recent data showed, however, that the rotational conformation of Tyr280 is inconsistent with the radical being on this residue (Svistunenko et al., 2003). Instead, our analysis points to Tyr167 (Table 1) as the most probable site (of a total of 37 tyrosine residues present in P. denitrificans CcO) that could host the observed radical (Svistunenko et al., 2003). Tyr167 is a highly conserved residue and is close to the active site. Interestingly, our algorithm shows that the homologous residue in the bovine CcO (Tyr129) can be responsible (Svistunenko et al., 2003) for the EPR spectrum observed in this enzyme and previously assigned to a tryptophan residue (Rigby et al., 2000). We find it particularly intriguing that our algorithm predicts the rotational conformation of a hypothetical tyrosyl radical in the bovine CcO very close to the rotational conformation of Tyr129—the residue, homologous to Tyr167 in the P. denitrificans CcO, to which we have assigned the radical in this enzyme quite confidently. Clearly, more studies are required to resolve the contradiction between previous interpretations and our assignment of the radical in bovine CcO.

CONCLUSIONS

We propose a universal algorithm for finding all parameters necessary for the simulation of a tyrosyl radical EPR spectrum. The algorithm bluntly specifies the values for all conserved simulation parameters (the same set for all radicals) and calculates the 10 nonconserved parameters while employing only two input variables: the spin density on atom C1 and the phenoxyl ring rotation angle. Our method makes it possible for the first time to perform a global simulation of all known lineshapes when using a common algorithm.

The algorithm is largely based on our finding that the principal g-values of a tyrosyl radical can be presented as polynomial functions of ρC1, the dependence of gx on ρC1 being linear. This has a particular practical importance, since gx can be measured directly by HF EPR.

Our algorithm makes it easy to determine whether an observed EPR spectrum arises from a tyrosyl radical and whether the radical has an H-bond. The recipe is simple: take an HF spectrum and measure the gx-value; find ρC1 by using Eq. 4; and use this value as the input parameter in the algorithm and vary the other parameter, angle θ, to achieve a good fit to the experimental X-band spectrum. If the HF spectrum is not available, both parameters, θ and ρC1, will have to be varied, although ρC1 should only be varied within a narrow interval of 0.34–0.43. If ρC1 > 0.38, the radical is likely to be H-bonded, and if the gx-component in the experimental HF spectrum is markedly broader than in the simulated spectrum, the strength of the H-bond (as well as ρC1) is distributed. If a spectrum cannot be simulated using this method, it is highly unlikely that it originates from a tyrosyl radical.

A simulation based on our algorithm results in finding the values of ρC1 and θ with unprecedented accuracy. Our new online database, dedicated to ranking all Tyr residues in proteins by angle θ, significantly helps in finding the residue responsible for the radical. In many cases an unambiguous assignment of the tyrosyl radical can be performed. Where this is not the case, our method generates a shortlist of most likely “tyrosine candidate sites,” ready to be tested one-by-one by alternative methods—e.g., site-directed mutagenesis.

SUPPLEMENTARY MATERIAL

The following supplementary materials are available in a single archive file by visiting BJ Online at http://www.biophysj.org: the document Algorithm Description.pdf (Figs. S1–S10, Tables S1–S6, Eqs. S1–S19); Excel file calculators (algorithm.xls, theta_in_tyr.xls, g_, and_k.xls); and the folder Simulation Data.

Supplementary Material

[Supplemental Material]
biophysj_87_1_582__index.html (740B, html)

Acknowledgments

This work was supported by the Wellcome Trust.

References

  1. Allard, P., A. L. Barra, K. K. Andersson, P. P. Schmidt, M. Atta, and A. Gräslund. 1996. Characterization of a new tyrosyl free radical in Salmonella typhimurium ribonucleotide reductase with EPR at 9.45 and 245 GHz. J. Am. Chem. Soc. 118:895–896. [Google Scholar]
  2. Babcock, G. T., M. K. El-Deeb, P. O. Sandusky, M. M. Whittaker, and J. W. Whittaker. 1992. Electron-paramagnetic resonance and electron nuclear double-resonance spectroscopies of the radical site in galactose-oxidase and of thioether-substituted phenol model compounds. J. Am. Chem. Soc. 114:3727–3734. [Google Scholar]
  3. Bender, C. J., M. Sahlin, G. T. Babcock, B. A. Barry, T. K. Chandrashekar, S. P. Salowe, J. Stubbe, B. Lindström, L. Petersson, A. Ehrenberg, and B.-M. Sjöberg. 1989. An ENDOR study of the tyrosyl free radical in ribonucleotide reductase from Escherichia coli. J. Am. Chem. Soc. 111:8076–8083. [Google Scholar]
  4. Chouchane, S., S. Girotto, S. Yu, and R. S. Magliozzo. 2002. Identification and characterization of tyrosyl radical formation in Mycobacterium tuberculosis catalase-peroxidase (KatG). J. Biol. Chem. 277:42633–42638. [DOI] [PubMed] [Google Scholar]
  5. Davies, M. J., and A. Puppo. 1992. Direct detection of a globin-derived radical in leghemoglobin treated with peroxides. Biochem. J. 281:197–201. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. DeGray, J. A., G. Lassmann, J. F. Curtis, T. A. Kennedy, L. J. Marnett, T. E. Eling, and R. P. Mason. 1992. Spectral analysis of the protein-derived tyrosyl radicals from prostaglandin H synthase. J. Biol. Chem. 267:23583–23588. [PubMed] [Google Scholar]
  7. Di Bilio, A. J., B. R. Crane, W. A. Wehbi, C. N. Kiser, M. M. Abu-Omar, R. M. Carlos, J. H. Richards, J. R. Winkler, and H. B. Gray. 2001. Properties of photogenerated tryptophan and tyrosyl radicals in structurally characterized proteins containing rhenium(I) tricarbonyl diimines. J. Am. Chem. Soc. 123:3181–3182. [DOI] [PubMed] [Google Scholar]
  8. Dorlet, P., A. W. Rutherford, and S. Un. 2000. Orientation of the tyrosyl D, pheophytin anion, and semiquinone 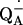Inline graphic radicals in photosystem II determined by high-field electron paramagnetic resonance. Biochemistry. 39:7826–7834. [DOI] [PubMed] [Google Scholar]
  9. Dorlet, P., S. A. Seibold, G. T. Babcock, G. J. Gerfen, W. L. Smith, A. L. Tsai, and S. Un. 2002. High-field EPR study of tyrosyl radicals in prostaglandin H2 synthase-1. Biochemistry. 41:6107–6114. [DOI] [PubMed] [Google Scholar]
  10. Eriksson, M., A. Jordan, and H. Eklund. 1998. Structure of Salmonella typhimurium nrdF ribonucleotide reductase in its oxidized and reduced forms. Biochemistry. 37:13359–13369. [DOI] [PubMed] [Google Scholar]
  11. Farrar, C. T., G. J. Gerfen, R. G. Griffin, D. A. Force, and R. D. Britt. 1997. Electronic structure of the YD tyrosyl radical in photosystem II: a high-frequency electron paramagnetic resonance spectroscopic and density functional theoretical study. J. Phys. Chem. B. 101:6634–6641. [Google Scholar]
  12. Fenwick, C. W., and A. M. English. 1996. Trapping and LC-MS identification of protein radicals formed in the horse heart metmyoglobin-H2O2 reaction. J. Am. Chem. Soc. 118:12236–12237. [Google Scholar]
  13. Fessenden, R. W., and R. H. Schuler. 1963. Electron spin resonance studies of transient alkyl radicals. J. Chem. Phys. 39:2147–2195. [Google Scholar]
  14. Frey, P. A. 2001. Radical mechanisms of enzymatic catalysis. Annu. Rev. Biochem. 70:121–148. [DOI] [PubMed] [Google Scholar]
  15. Gerfen, G. J., B. F. Bellew, S. Un, J. M. Bollinger, J.-A. Stubbe, R. G. Griffin, and D. J. Singel. 1993. High-frequency (139.5 GHz) EPR spectroscopy of the tyrosyl radical in Escherichia coli ribonucleotide reductase. J. Am. Chem. Soc. 115:6420–6421. [Google Scholar]
  16. Gunther, M. R., B. E. Sturgeon, and R. P. Mason. 2000. A long-lived tyrosyl radical from the reaction between horse metmyoglobin and hydrogen peroxide. Free Radic. Biol. Med. 28:709–719. [DOI] [PubMed] [Google Scholar]
  17. Gunther, M. R., R. A. Tschirret-Guth, H. E. Witkowska, Y. C. Fann, D. P. Barr, P. R. Ortiz de Montellano, and R. P. Mason. 1998. Site-specific spin trapping of tyrosine radicals in the oxidation of metmyoglobin by hydrogen peroxide. Biochem. J. 330:1293–1299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Hargrove, M. S., J. K. Barry, E. A. Brucker, M. B. Berry, G. N. Phillips, Jr., J. S. Olson, R. Arredondo-Peter, J. M. Dean, R. V. Klucas, and G. Sarath. 1997. Characterization of recombinant soybean leghemoglobin a and apolar distal histidine mutants. J. Mol. Biol. 266:1032–1042. [DOI] [PubMed] [Google Scholar]
  19. Harrenga, A., and H. Michel. 1999. The cytochrome c oxidase from Paracoccus denitrificans does not change the metal center ligation upon reduction. J. Biol. Chem. 274:33296–33299. [DOI] [PubMed] [Google Scholar]
  20. Harris, M. N., S. W. Burchiel, P. G. Winyard, J. R. Engen, C. D. Mobarak, and G. S. Timmins. 2002. Determining the site of spin trapping of the equine myoglobin radical by combined use of EPR, electrophoretic purification, and mass spectrometry. Chem. Res. Toxicol. 15:1589–1594. [DOI] [PubMed] [Google Scholar]
  21. Himo, F., A. Gräslund, and L. A. Eriksson. 1997. Density functional calculations on model tyrosyl radicals. Biophys. J. 72:1556–1567. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Hofbauer, W., A. Zouni, R. Bittl, J. Kern, P. Orth, F. Lendzian, P. Fromme, H. T. Witt, and W. Lubitz. 2001. Photosystem II single crystals studied by EPR spectroscopy at 94 GHz: the tyrosine radical YD?. Proc. Natl. Acad. Sci. USA. 98:6623–6628. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hoganson, C. W., and G. T. Babcock. 1992. Protein-tyrosyl radical interactions in photosystem II studied by electron spin resonance and electron nuclear double resonance spectroscopy: comparison with ribonucleotide reductase and in vitro tyrosine. Biochemistry. 31:11874–11880. [DOI] [PubMed] [Google Scholar]
  24. Hoganson, C. W., M. Sahlin, B.-M. Sjöberg, and G. T. Babcock. 1996. Electron magnetic resonance of the tyrosyl radical in ribonucleotide reductase from Escherichia coli. J. Am. Chem. Soc. 118:4672–4679. [Google Scholar]
  25. Hsi, L. C., C. W. Hoganson, G. T. Babcock, and W. L. Smith. 1994. Characterization of a tyrosyl radical in prostaglandin endoperoxide synthase-2. Biochem. Biophys. Res. Commun. 202:1592–1598. [DOI] [PubMed] [Google Scholar]
  26. Ivancich, A., P. Dorlet, D. B. Goodin, and S. Un. 2001a. Multifrequency high-field EPR study of the tryptophanyl and tyrosyl radical intermediates in wild-type and the W191G mutant of cytochrome c peroxidase. J. Am. Chem. Soc. 123:5050–5058. [DOI] [PubMed] [Google Scholar]
  27. Ivancich, A., G. Mazza, and A. Desbois. 2001b. Comparative electron paramagnetic resonance study of radical intermediates in turnip peroxidase isozymes. Biochemistry. 40:6860–6866. [DOI] [PubMed] [Google Scholar]
  28. Ivancich, A., H. M. Jouve, and J. Gaillard. 1996. EPR evidence for a tyrosyl radical intermediate in bovine liver catalase. J. Am. Chem. Soc. 118:12852–12853. [Google Scholar]
  29. Ivancich, A., T. A. Mattioli, and S. Un. 1999. Effect of protein microenvironment on tyrosyl radicals. A high-field (285 GHz) EPR, resonance Raman, and hybrid density functional study. J. Am. Chem. Soc. 121:5743–5753. [Google Scholar]
  30. Kauppi, B., B. B. Nielsen, S. Ramaswamy, I. K. Larsen, M. Thelander, L. Thelander, and H. Eklund. 1996. The three-dimensional structure of mammalian ribonucleotide reductase protein R2 reveals a more-accessible iron-radical site than Escherichia coli R2. J. Mol. Biol. 262:706–720. [DOI] [PubMed] [Google Scholar]
  31. Ko, T. P., J. Day, A. J. Malkin, and A. McPherson. 1999. Structure of orthorhombic crystals of beef liver catalase. Acta Crystallogr. D Biol. Crystallogr. 55:1383–1394. [DOI] [PubMed] [Google Scholar]
  32. Kulmacz, R. J., Y. Ren, A. L. Tsai, and G. Palmer. 1990. Prostaglandin H synthase: spectroscopic studies of the interaction with hydroperoxides and with indomethacin. Biochemistry. 29:8760–8771. [DOI] [PubMed] [Google Scholar]
  33. Liddington, R., Z. Derewenda, E. Dodson, R. Hubbard, and G. Dodson. 1992. High resolution crystal structures and comparisons of T-state deoxyhaemoglobin and two liganded T-state haemoglobins: T(α-oxy)haemoglobin and T(met)haemoglobin. J. Mol. Biol. 228:551–579. [DOI] [PubMed] [Google Scholar]
  34. Loll, P. J., D. Picot, O. Ekabo, and R. M. Garavito. 1996. Synthesis and use of iodinated nonsteroidal antiinflammatory drug analogs as crystallographic probes of the prostaglandin H2 synthase cyclooxygenase active site. Biochemistry. 35:7330–7340. [DOI] [PubMed] [Google Scholar]
  35. MacMillan, F., A. Kannt, J. Behr, T. Prisner, and H. Michel. 1999. Direct evidence for a tyrosine radical in the reaction of cytochrome c oxidase with hydrogen peroxide. Biochemistry. 38:9179–9184. [DOI] [PubMed] [Google Scholar]
  36. Maurus, R., C. M. Overall, R. Bogumil, Y. Luo, A. G. Mauk, M. Smith, and G. D. Brayer. 1997. A myoglobin variant with a polar substitution in a conserved hydrophobic cluster in the heme binding pocket. Biochim. Biophys. Acta. 1341:1–13. [DOI] [PubMed] [Google Scholar]
  37. McConnell, H. M., and D. B. Cheshunt. 1958. Theory of isotropic hyperfine interaction in π-electron radicals. J. Chem. Phys. 28:107–117. [Google Scholar]
  38. Miki, H., K. Harada, I. Yamazaki, M. Tamura, and H. Watanabe. 1989. Electron-spin resonance spectrum of Tyr151 free radicals formed in reactions of sperm whale metmyoglobin with ethyl hydroperoxide and potassium irridate. Arch. Biochem. Biophys. 275:354–362. [DOI] [PubMed] [Google Scholar]
  39. Nordlund, P., and H. Eklund. 1993. Structure and function of the Escherichia coli ribonucleotide reductase protein R2. J. Mol. Biol. 232:123–164. [DOI] [PubMed] [Google Scholar]
  40. Reeder, B. J., M. A. Sharpe, A. D. Kay, M. Kerr, K. Moore, and M. T. Wilson. 2002. Toxicity of myoglobin and haemoglobin: oxidative stress in patients with rhabdomyolysis and subarachnoid haemorrhage. Biochem. Soc. Trans. 30:745–748. [DOI] [PubMed] [Google Scholar]
  41. Reichard, P., and A. Ehrenberg. 1983. Ribonucleotide reductase—a radical enzyme. Science. 221:514–519. [DOI] [PubMed] [Google Scholar]
  42. Rigby, S. E., S. Junemann, P. R. Rich, and P. Heathcote. 2000. Reaction of bovine cytochrome c oxidase with hydrogen peroxide produces a tryptophan cation radical and a porphyrin cation radical. Biochemistry. 39:5921–5928. [DOI] [PubMed] [Google Scholar]
  43. Rigby, S. E., J. H. Nugent, and P. J. O'Malley. 1994. The dark stable tyrosine radical of photosystem II studied in three species using ENDOR and EPR spectroscopies. Biochemistry. 33:1734–1742. [DOI] [PubMed] [Google Scholar]
  44. Sahlin, M., A. Gräslund, A. Ehrenberg, and B.-M. Sjöberg. 1982. Structure of the tyrosyl radical in bacteriophage T4-induced ribonucleotide reductase. J. Biol. Chem. 257:366–369. [PubMed] [Google Scholar]
  45. Sahlin, M., L. Petersson, A. Gräslund, A. Ehrenberg, B. M. Sjöberg, and L. Thelander. 1987. Magnetic interaction between the tyrosyl free radical and the antiferromagnetically coupled iron center in ribonucleotide reductase. Biochemistry. 26:5541–5548. [DOI] [PubMed] [Google Scholar]
  46. Schmidt, P. P., K. K. Andersson, A.-L. Barra, L. Thelander, and A. Gräslund. 1996. High-field EPR studies of mouse ribonucleotide reductase indicate hydrogen-bonding of the tyrosyl radical. J. Biol. Chem. 271:23615–23618. [DOI] [PubMed] [Google Scholar]
  47. Selinsky, B. S., K. Gupta, C. T. Sharkey, and P. J. Loll. 2001. Structural analysis of NSAID binding by prostaglandin H2 synthase: time-dependent and time-independent inhibitors elicit identical enzyme conformations. Biochemistry. 40:5172–5180. [DOI] [PubMed] [Google Scholar]
  48. Shi, W., C. W. Hoganson, M. Espe, C. J. Bender, G. T. Babcock, G. Palmer, R. J. Kulmacz, and A. Tsai. 2000. Electron paramagnetic resonance and electron nuclear double resonance spectroscopic identification and characterization of the tyrosyl radicals in prostaglandin H synthase 1. Biochemistry. 39:4112–4121. [DOI] [PubMed] [Google Scholar]
  49. Svistunenko, D. A., J. Dunne, M. Fryer, P. Nicholls, B. J. Reeder, M. T. Wilson, M. G. Bigotti, F. Cutruzzola, and C. E. Cooper. 2002. Comparative study of tyrosine radicals in hemoglobin and myoglobins treated with hydrogen peroxide. Biophys. J. 83:2845–2855. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Svistunenko, D. A., M. A. Sharpe, P. Nicholls, C. Blenkinsop, N. A. Davies, J. Dunne, M. T. Wilson, and C. E. Cooper. 2000. The pH dependence of naturally occurring low-spin forms of methaemoglobin and metmyoglobin: an EPR study. Biochem. J. 351:595–605. [PMC free article] [PubMed] [Google Scholar]
  51. Svistunenko, D. A., M. T. Wilson, and C. E. Cooper. 2003. Tryptophan or tyrosine? On the nature of the amino acid radical formed following hydrogen peroxide treatment of cytochrome c oxidase. Biochim. Biophys. Acta. in press. [DOI] [PubMed]
  52. Tommos, C., X.-S. Tang, K. Warncke, C. W. Hoganson, S. Styring, J. McCracken, B. A. Diner, and G. T. Babcock. 1995. Spin-density distribution, conformation, and hydrogen bonding of the redox-active tyrosine Yz in photosystem II from multiple-electron magnetic-resonance spectroscopies: implications for photosynthetic oxygen evolution. J. Am. Chem. Soc. 117:10325–10335. [Google Scholar]
  53. Warncke, K., G. T. Babcock, and J. McCracken. 1994. Structure of the YD tyrosine radical in photosystem II as revealed by 2H electron spin echo envelope modulation (ESEEM) spectroscopic analysis of hydrogen hyperfine interactions. J. Am. Chem. Soc. 116:7332–7340. [Google Scholar]
  54. Warncke, K., and M. S. Perry. 2001. Redox state dependence of rotamer distributions in tyrosine and neutral tyrosyl radicals. Biochim. Biophys. Acta. 1545:1–5. [DOI] [PubMed] [Google Scholar]
  55. Whittaker, M. M., W. R. Duncan, and J. W. Whittaker. 1996a. Synthesis, structure, and properties of a model for galactose oxidase. Inorg. Chem. 35:382–386. [DOI] [PubMed] [Google Scholar]
  56. Whittaker, M. M., P. J. Kersten, N. Nakamura, J. Sandersloehr, E. S. Schweizer, and J. W. Whittaker. 1996b. Glyoxal oxidase from Phanerochaete chrysosporium is a new radical-copper oxidase. J. Biol. Chem. 271:681–687. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplemental Material]
biophysj_87_1_582__index.html (740B, html)
biophysj_87_1_582__svistunenko_online_materials.zip (1.7MB, zip)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES