Determination of Cell Capacitance Using the Exact Empirical Solution of ∂Y/∂C_m and Its Phase Angle

Abstract

Measures of membrane capacitance offer insight into a variety of cellular processes. Unfortunately, popular methodologies rely on model simplifications that sensitize them to interference from inevitable changes in resistive components of the traditional cell-clamp model. Here I report on a novel method to measure membrane capacitance that disposes of the usual simplifications and assumptions, yet is immune to such interference and works on the millisecond timescale. It is based on the exact empirical determination of the elusive partial derivative, ∂Y/∂C_m, which heretofore had been approximated. Furthermore, I illustrate how this method extends to the vesicle fusion problem by permitting the determination of ∂Y_v/∂C_v, thereby providing estimates of fusion pore conductance and vesicle capacitance. Finally, I provide simulation examples and physiological examples of how the method can be used to study processes that are routinely interrogated by measures of membrane capacitance.

INTRODUCTION

Biological cells are typically modeled as simple parallel combinations of an electrical resistance and capacitance. Measures of membrane capacitance (C_m) based on this model under voltage clamp provide an informative view of such varied processes as fertilization (Jaffe and Schlichter, 1985), ionic channel gating (Fernandez et al., 1982), synaptic vesicle fusion (Neher and Marty, 1982), gap junctional coupling (Santos-Sacchi, 1991a), and receptor cell activity (Zhao and Santos-Sacchi, 1999).

A powerful feature of capacitance measures is the ability to monitor interactions between membrane-bound compartments, e.g., fusion of vesicles with the plasma membrane or cell coupling via gap junctions (Neher and Marty, 1982; Joshi and Fernandez, 1988; Santos-Sacchi, 1991a; Zhao and Santos-Sacchi, 1998), because these measures provide an estimate of membrane surface area (Fricke, 1925; Cole, 1971). Indeed, electrical measures of vesicular fusion (Alvarez De Toledo et al., 1993) have played a significant role in the development of one of the most controversial issues facing neurobiology today, namely, the occurrence of kiss-and-run synaptic vesicle transmitter release (Gandhi and Stevens, 2003; Aravanis et al., 2003). Single-frequency admittance analysis of membrane fusion, pioneered by Neher and Marty (1982), has been used by a number of investigators to gauge the time course of vesicular membrane fusion by monitoring the changes in the conductance of the fusion pore that initiates membrane fusion (Breckenridge and Almers, 1987; Alvarez De Toledo et al., 1993; Debus and Lindau, 2000; Klyachko and Jackson, 2002). Estimates of the pore's initial conductance hover near single-channel conductance values (Breckenridge and Almers, 1987; Lollike et al., 1995).

Arguably the most widely used method to measure membrane capacitance (C_m) is the phase-angle method, variously termed, but all employing approaches to extract the current at a particular phase angle arising from small changes in C_m (Neher and Marty, 1982; Gillis, 1995). Such AC methods ostensibly provide excellent time resolution and sensitivity. Multifrequency approaches, which we and others have used (Fernandez et al., 1982; Santos-Sacchi, 1989; Zhao and Santos-Sacchi, 1999), are less in vogue, but offer potential protection from changes in admittance that can plague single-sine methods. Implementations of step, single-, and dual-sine techniques are available in a few software packages (jClamp, www.SciSoftCo.com; pClamp, www.Axon.com; Pulse Control, www.Instrutech.com, chroma.med.miami.edu/cap).

One of the key problems that challenges the validity of C_m measures, and thus our understanding of those cellular processes that are interrogated by C_m measurements, is the interference of those measures by changes in either patch electrode resistance (R_s) or cell membrane resistance (R_m), the latter often a natural corollary of those cellular processes (Gillis, 1995; Debus et al., 1995). An extensively discussed topic of the single-sine camp concerns the determination of the proper phase angle to utilize in measuring small changes in membrane capacitance. There are various mechanisms to determine an appropriate phase angle, but all estimates of capacitance employ simplifying assumptions and requirements, usually devised to limit the effects of uncontrollable R_s and R_m changes on C_m measures. Indeed, the traditional methodology of single-sine admittance analysis suffers from a number of assumptions and simplifications, especially those methods used to extract vesicle capacitance and conductance, and the fusion pore conductance. These assumptions cannot be met in all cases, and this quandary is clearly indicated by the posthoc manipulations of data that are often required (Lindau, 1991; Ratinov et al., 1998). In detailing these assumptions, I refer to the traditional electrical circuit models that are used to evaluate admittance data (Fig. 1). A nearly universal assumption is that R_m ≫ R_s; additionally, for fusion vesicle analysis, R_v ≫ R_p, and in some cases R_v = ∞. Below I illustrate through circuit analysis and modeling how these assumptions can lead to errors, and provide a method, based on the exact empirical identification of the partial derivatives ∂Y/∂C_m and ∂Y_v/∂C_v, that offers solutions without compromising assumptions. The approach is referred to as the eCm method.

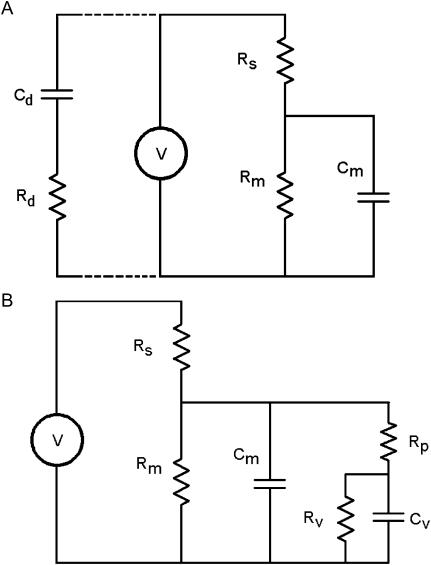
FIGURE 1.

Circuit models. (A) The standard patch-clamp-cell model. Voltage (V) is set across the electrode (R_s) and cell membrane resistance (R_m)—capacitance (C_m). The series components between headstage and ground, R_d and C_d, model the whole-cell capacitance compensation circuitry when connected. (B) A vesicle is fused with the plasma membrane. C_v is vesicle capacitance, R_p is fusion pore resistance, and R_v is vesicle resistance.

Theory

The phase of the capacitive current components evoked by a sinusoidal command voltage (V) across the simple models presented in Fig. 1 can be used to arrive at measures of the capacitive components themselves. Once the capacitive component values are obtained, the resistive component values are easily deduced. This can be appreciated from the following evaluation, which first deals with the model without a fusion vesicle and without capacitance compensation components (Fig. 1 A).

Two standard conditions must be met for successful use of the methods detailed here: 1), the patch-clamp system transfer function (which derives from all equipment that contributes to shaping the output current) must be corrected for. This is a trivial matter, where a pure resistor, say 1 MΩ, is used at the input of the headstage to determine the correction phase and magnitude at each frequency (see Gillis, 1995 for details); and 2), the pipette stray capacitance must be neutralized before establishing whole-cell configuration.

Absent vesicle fusion

The current measurable under voltage clamp (Fig. 1) is that through R_s, namely, I_Rs. According to Ohm's law, I_Rs is defined as the product of the clamp voltage (V) and input admittance (Y) of the circuit,

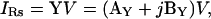(1)

where A_Y and B_Y are the real and imaginary components of the admittance. Closer inspection of the circuit reveals that I_Rs is the sum of a resistive and a capacitive component induced by only that portion (V_m) of the clamp voltage (V), which drops across the cell membrane (R_m ‖ C_m),

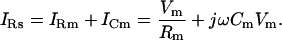(2)

These equations show that I_Rs can be represented as a frequency (ω = 2πf) dependent complex number,

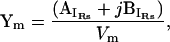(3)

where Y_m is the membrane admittance, A_Irs is the real component, and B_Irs is the imaginary component of I_Rs. Plainly, this signifies that the phase relationship between capacitive (I_Cm) and resistive (I_Rm) membrane current components is 90°. It is important to realize that the magnitude of the series resistance (R_s), or its existence (i.e., R_s = 0), is irrelevant, and will not affect the phase relationship between I_Cm and I_Rm. Of course, for R_s > 0, the phase of I_Rs, relative to that of V, will vary as a result of any circuit parameter change, because the phase of I_Rs is dependent on that of V_m,

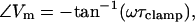(4)

where τ_clamp, the actual clamp time constant, is

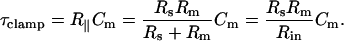(5)

Viewed relative to the phase of the command voltage (V), the capacitive current phase angle, Φ, will always reside at

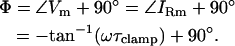(6)

Thus, in the absence of R_s (R_s = 0), the angles of V_m and V are identical, and Φ will be orthogonal to the angle of V. However, as pointed out by Neher and Marty (1982), the introduction of R_s causes Φ to shift away from orthogonality with respect to the applied command voltage (V). The phase shift, θ, in the angle of I_Rs that accompanies changes in the circuit parameters is defined as

(7)

and thus

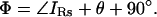(8)

Although it is apparent from Eq. 2 that the magnitude of the current at Φ, namely, I_Cm, can be used to extract C_m

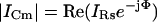(9)

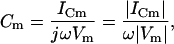(10)

neither absolute angle, θ nor Φ, can be determined from direct manipulation of the empirically obtained input admittance at any one frequency. Thus, in the face of changing circuit parameters, estimating C_m by directly measuring raw current at Φ appears unfeasible. Nevertheless, inspection of the current at Φ can be achieved by operating on the imaginary component of I_Rs, whose phase follows those phase shifts that result from parameter changes.

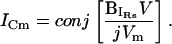(11)

Thus, the imaginary component of Y (or I_Rs) can be used to find C_m. To obtain direct estimates of C_m from 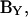one needs to correct 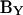with a noncomplex gain factor (H_c) that accounts for the relationship between inevitable changes in R_s, R_m, and C_m that occur during the course of an experiment.

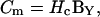(12)

where, after substitution and rearrangement,

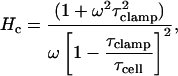(13)

and

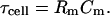(14)

Note that τ_cell is the membrane time constant, and most importantly,

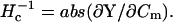(15)

Thus, to extract C_m from 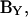we must precisely evaluate the partial derivative, ∂Y/∂C_m. This is one of the enigmas facing cell capacitance aficionados.

There are two methods that are routinely used to provide estimates of ∂Y/∂C_m and its phase angle; both involve dithering of circuit parameters, and typically require hardware modifications and/or manipulations (Fidler and Fernandez, 1989; Joshi and Fernandez, 1988; Neher and Marty, 1982). Series resistance dithering and capacitance compensation dithering each have shortcomings that have been discussed in detail (Joshi and Fernandez, 1988). Ultimately, these shortcomings stem from the untoward effects of series resistance, because as 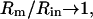the circuit of Fig. 1 A approaches a simple parallel R_m C_m configuration, and the estimates ultimately provide precise solutions. Regrettably, we are rarely so lucky during our experimental manipulations of cells to guarantee such relationships (Debus et al., 1995). Can this problem be resolved? That is, can the true magnitude and phase angle of ∂Y/∂C_m be obtained, so that estimates of C_m are impervious to cell and clamp parameter changes? Furthermore, can this be accomplished without hardware additions and manipulations? Actually, it is a simple task, requiring, in addition to measures of 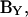the determination of the partial derivative, ∂Y/∂ω or correspondingly, ∂I_Rs/∂ω. As we shall see, such a determination ensures accurate measures of membrane capacitance.

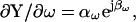(16)

where the magnitude (α_ω) and phase (β_ω) are

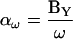(17)

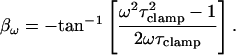(18)

Significantly, β_ω, the phase angle of ∂I_Rs/∂ω and ∂Y/∂ω, is identical to that of ∂Y/∂C_m, and also to the angle of ∂Y/∂R_m + 90°. This can be appreciated immediately by inspection of the partial derivatives.

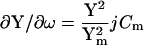(19)

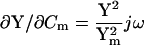(20)

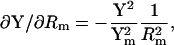(21)

where

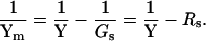(22)

It is this equivalence between the angles of ∂Y/∂ω and ∂Y/∂C_m that forms the basis of the new eCm method of capacitance measurement that I report here. Given the angle, β_ω, and the real and imaginary components of Y, the two time constants, τ_clamp and τ_cell, can be found. Each has two solutions, one of which will be realizable (positive) depending on the circuit parameters. For subsequent calculations the positive values must be used.

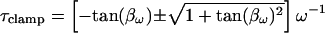(23)

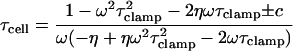(24)

where

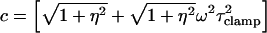(25a)

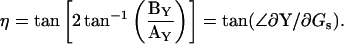(25b)

Finally, with τ_clamp and τ_cell in hand, H_c (Eqs. 13 and 15) can be obtained, thus revealing the exact solution for all clamp parameters, R_s, R_m, and C_m.

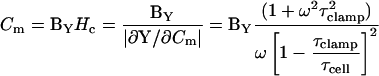(26)

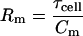(27)

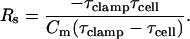(28)

For completeness, the pertinent partial derivatives are provided in polar form (all parameters obtainable through a combination of measurement (that of Y and β_ω; see following) and calculation (as above)),

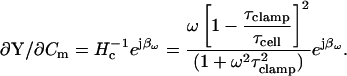(29)

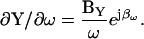(30)

The exact determination of β_ω

Several practical approaches to obtain β_ω via frequency manipulations are available. Ordinarily, the empirical determination of an angle of a partial derivative with respect to angular frequency, such as β_ω, is found by introducing a second voltage sinusoid (ω₁), in addition to the primary, ω_0, at an infinitesimal interval of dω, which must be approximated with Δω. The angle of the resulting difference current will closely approximate β_ω. However, the determination of β_ω using digital techniques necessitates that the two frequencies be no closer than the minimum frequency interval, ω_min. This interval is determined by the number of points (npts) of the stimulus (ω_min = 1/(dt npts), where dt = sample clock) (see Oppenheim and Schafer, 1975). Unfortunately, the rather large size of ω_min offered by a stimulus composed of, say, 128 points at 4 μs clock, will provide for a poor approximation of dω by Δω (f_min would be 1953.1 Hz). Of course, npts can be increased such that ω_min would be very small and permit a reasonable approximation of β_ω, but time resolution suffers. If high time resolution is not an issue, or if discrete determinations (as in “pause and dither” approaches) are acceptable, then determining the angle of the difference current at the primary frequency (ω₀) and secondary frequency (ω₁) at a very small interval will give β_ω.

Alternatively, a nondiscrete hardware implementation of this technique could easily allow dω to be approached; furthermore, the magnitude of the second frequency could be quite small, because only the phase would be required. In fact, the stimulus could very well resemble a single sinusoid, thus limiting the cell's stimulus exposure.

Notwithstanding these approaches to the determination of β_ω, our overriding intent is to obtain a method for C_m measurement without additional hardware or hardware manipulations, and to correct for parameter changes on a point-by-point (real time) basis. To this end, it is fortuitous that the need for an infinitesimal interval, dω, can be circumvented by acknowledging that for the linear component model of Fig. 1 a, R_s or R_m may be considered frequency independent. That is, we may use either of the derivations of R_s or R_m provided by Pusch and Neher, 1988 (their Eqs. 5 and 6 reproduced below); also see Lindau and Neher (1988) to obtain an exact solution of β_ω at ω₀.

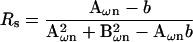(31)

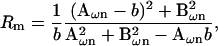(32)

where b = 1 / (R_s + R_m) and n = 0,1.

Equating R_s (or R_m, either of which produce the exact same result) determined at two angular frequencies, ω₀ and ω₁, provides two solutions for b (b₀, b₁; solutions not shown), and therefore two solutions for τ_clamp at ω₀ (obtained by utilizing Pusch and Neher's (1988) solution for C_m; their Eq. 7),

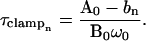(33)

Notably, however, either solution of 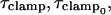or 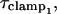when used to derive the angle of ∂Y/∂ω, i.e., β_ω0, from Eq. 18 produces only one, unique result, namely

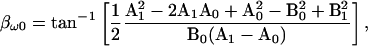(34)

where the subscripts denote the real (A) and imaginary (B) admittance components at any two angular frequencies, ω₀ and ω₁. It should be pointed out that whereas two frequencies are required to obtain β_ω, the value itself is derived from ∂Y/∂ω₀, whose location is exactly at ω₀.

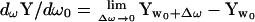(35)

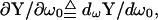(36)

that is, all three pieces of information, B_Y, A_Y, and β_ω that are used to measure C_m theoretically derive from single (ω₀), not dual, frequency inspection.

Present vesicle fusion

The fusion of independent membrane-bound compartments (vesicle to the plasma membrane or gap junctional coupling between two cells) can be evaluated with input capacitance measures, and modeled to obtain component values of the applicable circuit (Fig. 1 B) (Zhao and Santos-Sacchi, 1998; Bigiani and Roper, 1995; Santos-Sacchi, 1991a). Below, I focus on vesicular fusion. If experiments are performed using the cell-attached mode it must be determined that the cell's input admittance is far greater than the patch admittance. Additionally, data must be corrected posthoc after determination of stray pipette capacitance (perhaps using the Sylgard bead-sealing technique (Sakmann and Neher, 1995)), which may be greater than patch capacitance. Thus, the application of this method under cell-attached mode is not straightforward. Nevertheless, in that case, or if vesicle fusion is monitored under whole-cell mode, the following applies; the subscript m denotes either patch or whole-cell characteristics. The input admittance before (Y_b) and after (Y_a) vesicle fusion differs.

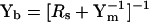(37)

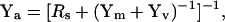(38)

where

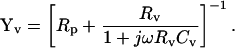(39)

Typically, access to the circuit parameters defining the vesicle admittance (Y_v: R_p, R_v, and C_v; see Fig. 1 B) is obtained experimentally by making an inescapable assumption – that at the onset of fusion R_s, R_m, and C_m remain unchanged. Given the model, without this assumption estimates cannot be obtained with confidence.

The original and still common method to calculate vesicle parameters, including fusion pore conductance, employs capacitance compensation to estimate vesicle admittance (Breckenridge and Almers, 1987; Lindau, 1991; Ales et al., 1999). In this case, membrane admittance before fusion is removed by subtracting the Y_m baseline determined by capacitance compensation dithering (Neher and Marty, 1982); the subsequent change in admittance after vesicle fusion is used to calculate vesicle components based on a simplified vesicle circuit model of C_v in series with R_p (Breckenridge and Almers, 1987). We can employ the eCm method to arrive at Y_v, in a similar manner. First, Y_m is extracted from Y_b, the exact value of R_s having been obtained by analysis (see above) before fusion.

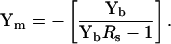(40)

Consequently, the vesicle admittance, Y_v, which includes the fusion pore, can be calculated (by substitution of Eq. 40 into Eq. 38) as a function of admittances measured before and after fusion,

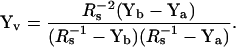(41)

From inspection of the vesicle circuit (Fig. 1 B), it is clear that

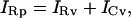(42)

that is, we have the analogous circuit conditions that we analyzed above in the absence of fusion. The parameters R_p, R_v, and C_v simply and, respectively, replace R_s, R_m, and C_m. Using the same analysis logic as above, the magnitude and angle of ∂Y_v/∂C_v is obtained, thus enabling the solution of all vesicle circuit parameters. The following equations detail fusion event analysis.

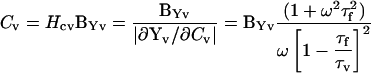(43)

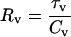(44)

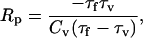(45)

where

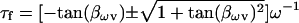(46)

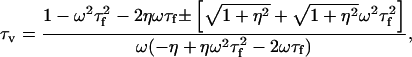(47)

and

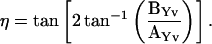(48)

Simulations and biological cell examples

I provide several approaches to evaluate the eCm method of parameter estimation, including mathematical modeling, physical modeling, and tests on biological cells. It is important to realize that tests on biological cells may provide important information on real-world capabilities, but cannot be used to truly verify the validity of an approach. For example, it is impossible to know if a certain time course of C_m change is truly occurring in cells, unless, of course, confirmation is obtained through other measures. However, physical and mathematical model evaluations can confirm validity of an approach, and do provide confidence that the results from biological cells are sound. In the first set of evaluations, MatLab (Natick, MA) was used to model the circuit admittance and implement eCm strictly in the frequency domain. In the following mathematical and physical simulations, measures were made at an f₀ of 390.6 Hz and f₁ of twice that, delivered simultaneously, unless otherwise noted. Amplitudes at each frequency were set equal, at 10–20 mV peak. Fig. 2 presents a simple whole-cell mathematical model simulation where the circuit parameters are stepped to evaluate component interactions on C_m measures; comparisons are made of calculated component values using either the eCm method or other approaches that contain approximations. Clearly, eCm is superior, and is impervious to fluctuations in circuit component values. Fig. 3 presents another mathematical simulation in Matlab where vesicle fusion under whole-cell mode is evaluated, and compared with the standard methodology (Breckenridge and Almers, 1987; Lollike et al., 1995). Both methods are excellent even in the face of substantial R_s changes, but even with changes in vesicle resistance the eCm method produces an exact reconstruction of the model parameter changes. Although these model data highlight the exact nature of the eCm method, more demanding modeling efforts show the method's strengths. For the tests that follow, capacitance measures were obtained with eCm as implemented in the software package jClamp using a time resolution of 2.56 ms (i.e., f₀ of 390.6 Hz), unless otherwise noted.

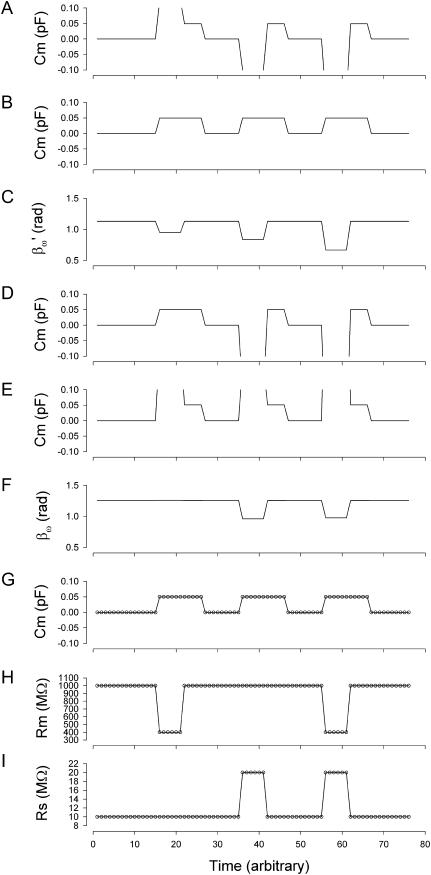
FIGURE 2.

Simulation of capacitance changes in whole-cell mode. The component values of the model (R_s: 10 MΩ, R_m: 1 GΩ, and C_m: 6.5 pF) in Fig. 1 A were modulated out of phase with each other, with a C_m jump of 0.05 pF accompanied by either a 600-MΩ drop in R_m, or a 10-MΩ increase in R_s or all changes occurring simultaneously (see panels G–I). The stimulating frequency f₀ was the same for single-sine and eCm methods, with f₀ at 390.6 Hz and f₁ at twice that. In panels A–C, calculations are based on setting the PSD angle to an estimate (denoted by the prime) of β_ω, the angle of ∂Y/∂G_s − 90°, 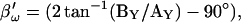to mimic R_s dithering. (A) A true piecewise linear approach was employed using this angle 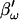in place of β_ω in Eq. 52. Whole-cell capacitance compensation was modeled by connecting and supplying the circuit components R_d and C_d (Fig. 1) with corresponding values of R_s and C_m, but with an overall negative admittance. PSD angle and gain corrections (1/abs(∂Y/∂C_m) were determined from whole-cell conditions at the zero time point and remained fixed throughout. It can be seen that when cell components are changed (G–I) the phase angle changes causing errors in C_m estimation (A). Even though the PSD angle is set to guard against R_s changes, a change from 10 to 20 MΩ (I) is too large to counter; such overpowering effects of parameter changes are well known (Lindau, 1991). However, if capacitance compensation is not employed and point-by-point resetting of new angle and gain factors are made and applied, absolute C_m is obtained without any errors (B). To make point-by-point corrections experimentally, the raw admittance (Y) at each point was taken and the angle of 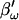was calculated according to Zierler (1992), namely, 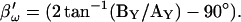The true gain factor, H_c, at each data point was calculated as 1/abs(∂Y/∂C_m). With each new gain and angle, circuit parameters were calculated as in Eq. 52, by extracting the component of Y at that phase angle and multiplying by that gain factor. Each admittance point was so treated to obtain circuit parameters. The reason this procedure works so well is that the value returned by this modified PSD analysis is the imaginary component of Y; thus, this method produces the same results as the eCm method as shown in panel G. This useful single-sine approach, employing the estimate of H_c provided by Gillis (1995), is implemented in jClamp. However, because this is an estimate of the true gain, 1/abs(∂Y/∂C_m), relying on circuit approximations, C_m estimates are not fully immune from circuit parameter changes. In panels D–F, calculations are based on setting the PSD angle to the angle of ∂Y/∂C_m, namely β_ω, to mimic capacitance compensation dithering. (D) The true piecewise linear approach was employed as above in panel A. In this case, using β_ω, the large change in R_m does not affect the phase angle substantially (F), so C_m estimates are accurate and robust. However, R_s changes do interfere with angle and estimate, as expected (Joshi and Fernandez, 1988). Unlike the treatment above (B), panel E shows that applying a point-by-point correction as detailed above to the uncompensated admittance fails to provide error free C_m estimation, because the imaginary component of Y is not returned in this case. Panels G–I show the results of the eCm method, where the calculated absolute values are depicted by the circles. Note an exact correspondence between actual parameter values (solid lines) and calculated estimates (○), with no parameter interactions. Simulation in MatLab.

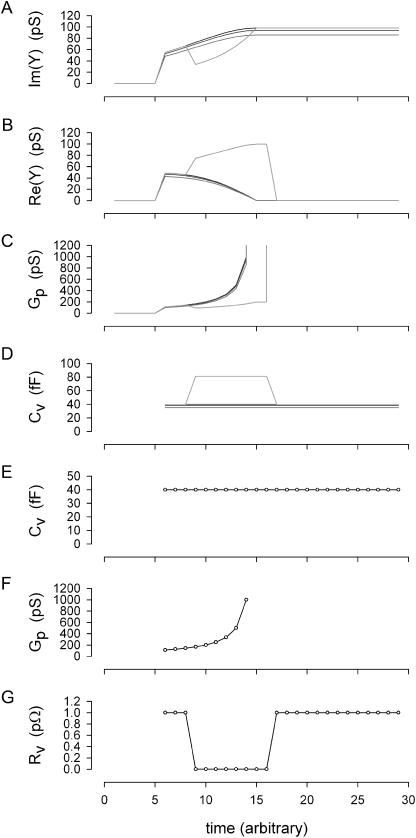
FIGURE 3.

Simulation and analysis of vesicle fusion event. Whole-cell conditions remained constant throughout simulation at R_m: 1 GΩ, and C_m: 6.5 pF, with R_s: 1, 10, and 20 MΩ for dark traces (vesicle resistance, R_v, held constant at 1 pΩ (1e15Ω)). For the shaded trace, R_s was 1 MΩ and vesicle resistance, R_v, was stepped transiently from 1 pΩ to 10 GΩ as shown in panel G. (A, B) Imaginary and real components of admittance determined according to Breckenridge and Almers (1987). (C, D) Vesicle pore conductance and capacitance extracted from admittance using standard methodology (Breckenridge and Almers, 1987; Lollike et al., 1995). Note very good correspondence between components of model even when R_s changes substantially (solid lines in panels E, F), but not when R_v is altered (shaded line). This discrepancy is not unanticipated because the standard methodology sets R_v as infinite (Breckenridge and Almers, 1987; Lollike et al., 1995). (E, F) Vesicle model parameters (solid lines) and estimates made with the eCm method (○). Correspondence is exact under all conditions. At time >5, vesicular fusion was simulated by linearly ramping the fusion pore resistance (R_p; initially infinite) from 9 GΩ (111 pS) to 1 GΩ (1000 pS); the resulting pore conductance is shown in panel F (solid line). Fusion event analysis was implemented at that time.

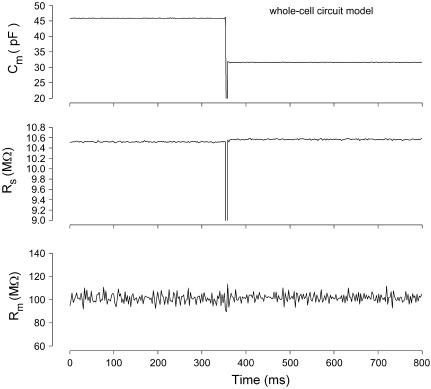
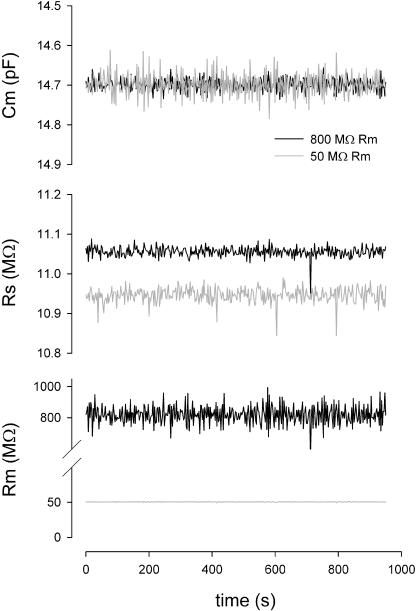
Fig. 4 shows the results of a physical implementation of the simple model in Fig. 1 A under voltage clamp during a large step in capacitance, that was evoked by physically dislodging an additional capacitor that was placed parallel with C_m. Simultaneous measures of R_s and R_m remain essentially unperturbed. To evaluate large changes in R_m, this parallel approach did not work because of associated parasitic capacitances of the large resistances involved. Instead, Fig. 5 shows two separate measures where all circuit and measurement details remained exactly the same except that either a 50-MΩ or 800-MΩ R_m resistor was soldered into place. Again, there are minimal changes in C_m measures. Fig. 6 shows the effects of maladjustments of the amplifier's fast capacitive compensation on parameter estimates. The model cell was measured over 10 seconds at a resolution of 2.56 ms while changes in compensation were made. Stray R_s capacitance of ±0.15 pF had little effect on C_m (±0.4%) or R_m (<±0.01%) parameter estimation. R_s estimates varied ±1.8%.

FIGURE 4.

Effects of large C_m changes on parameter estimates with the eCm method. Nominal initial component values of R_s: 10 MΩ, R_m: 100 MΩ, and C_m: 33 pF ‖ 15 pF. A step decrease in capacitance was accomplished by suddenly removing the parallel 15 pF component. The three panels show the calculated values of the parameters using the eCm method at a sampling rate of 2.56 ms. Note large abrupt drop in capacitance (top) with virtually no effect on measures of R_s and R_m (middle and bottom). Model was voltage clamped with a PC clone, Axon 200 amplifier (Union City, CA) in resistive feedback mode (β = 0.1), 10-kHz Bessel filter, and Axon 1322A A/D D/A board.

FIGURE 5.

Effects of large R_m changes on parameter estimates with the eCm method. Nominal component values of R_s: 10 MΩ, R_m: 50 or 800 MΩ, and C_m: 15 pF. Note minimal interference with C_m and R_s estimates when a 50-MΩ resistor replaced the 800-MΩ resistor, other than changes in noise levels. PC clone, Axon 200 amplifier in capacitive feedback mode, 10-kHz Bessel filter, and Axon 1322A A/D D/A board were used.

FIGURE 6.

Effects of uncompensated stray capacitance on C_m measures with the eCm method. (A) Capacitive currents evoked by voltage step. Model R_s was in headstage but ungrounded. (Top) Fully compensated, (middle) undercompensated, and (bottom) overcompensated. The effect of these extremes was evaluated during parameter estimations after reassembly of the model circuit. (B) The three panels show model cell parameter estimates during manual under- and overcompensation of fast capacitance compensation. C_m was modulated ±0.3%; R_s, ±1.8%; and R_m, < ±0.01%. The increase in C_m occurred during under compensation. Nominal component values of R_s: 10 MΩ, R_m: 300 MΩ, and C_m: 18 pF. C_m noise: 14.6 fF rms; system noise with model 3.75 pA rms, 10-kHz Bessel filter, PC clone, Axon 200 amplifier in capacitive feedback mode, and Axon 1322A A/D D/A board.

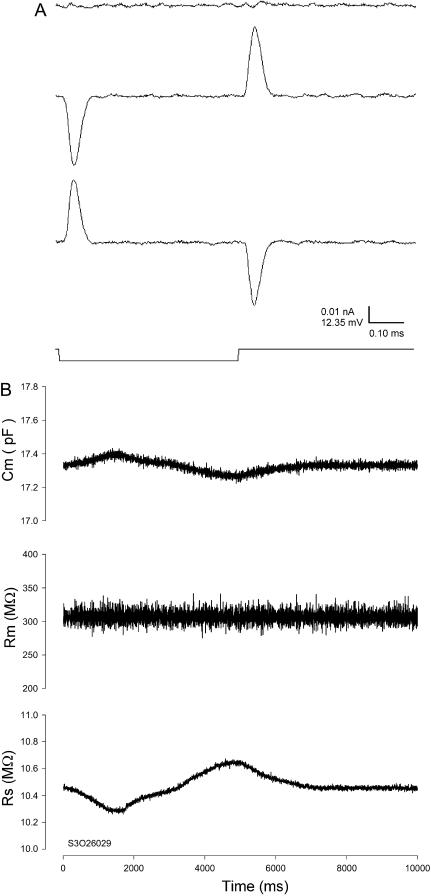
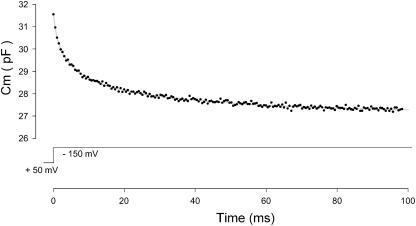
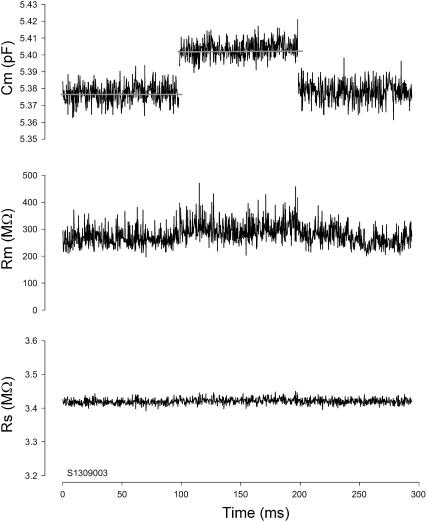
Finally, in Figs. 7 and 8 biological cells are investigated. Fig. 7 shows measures of outer hair cell (OHC) capacitance obtained with jClamp using a time resolution of 512 μs. Detrending of data before analysis was performed (Santos-Sacchi, 2002). The rapid relaxation in capacitance during a step voltage change is due to the shift of the cell's nonlinear Q-V function along the voltage axis (Santos-Sacchi et al., 1998). In that article, we confirmed through alternative measures that the time course of C_m relaxation corresponded to the shift. The shift signifies the very rapid change in the gain of OHC electromotility, a process that likely drives the mammalian cochlear amplifier (Santos-Sacchi, 2003). The solid shaded line is a triple exponential fit to the data. The three time constants are 1.04, 5.96, and 36 ms. This time course is over an order of magnitude faster than has been previously reported (Santos-Sacchi et al., 1998). The substantial noise levels in this trace derive from the huge nonlinear capacitance (>20 pF) and low input resistance (<300 MΩ) of the OHC. For comparison, Fig. 8 shows capacitance measures in a HEK cell transfected with prestin (Meltzer and Santos-Sacchi, 2001), where C_m noise was 5.5 fF (rms; 0.256 ms time resolution (f₀: 390.6 Hz); see discussion on noise effects below). This cell possesses a nonlinear Q_max (by fitting the Q-V curve with a two-state Boltzmann function (Santos-Sacchi, 1991b)) of 63.7 fC, giving rise to a peak voltage-dependent capacitance at −101 mV of 420 fF. The figure shows a 30-fF step in capacitance when voltage was stepped from +50 mV to +30 mV. These data indicate that the sensitivity of the eCm method is well within the range required for fusion event analysis.

FIGURE 7.

Measurement of outer hair cell nonlinear capacitance with the eCm method. The rapid relaxation in capacitance during a step voltage change is due to the shift of the cell's nonlinear Q-V function along the voltage axis (Santos-Sacchi et al., 1998), and was confirmed through alternative measures. Cell was clamped with a PC clone, Axon 200B amplifier, 10-kHz Bessel filter, and Axon 1321A A/D D/A board with conditions described previously (Santos-Sacchi et al., 1998). See text for further details.

FIGURE 8.

Measurement of capacitance step in prestin transfected HEK cell. Under voltage clamp a step voltage from +50 mV to +30 mV evoked a step increase in capacitance of 30 fF. C_m noise: 5.5 fF rms. PC clone, Axon 200B amplifier in resistive feedback mode, 10-kHz Bessel filter, and National Instruments (Austin, TX) PCI-6052E A/D D/A board were used.

DISCUSSION

Three pieces of information are required to determine the circuit parameters, R_s, R_m, and C_m of the traditional patch-clamp-cell model circuit (Fig. 1 A). The typical information obtained in a one-frequency (ω₀) measurement, namely, the real and imaginary components of the admittance, is insufficient. A third piece of information is required, and is usually obtained by exploring beyond ω₀, that is, by utilizing information obtained at frequencies other than ω₀. One popular solution is the “sine+dc” method (Pusch and Neher, 1988; Gillis, 2000), where a third piece of information, the input resistance (R_in = R_s + R_m), is extracted based on a priori knowledge of membrane reversal potential. This is basically a measurement at ω₁ = 0. Alternatively, another non-dc piece of information, the admittance at 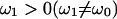can be used to extract R_in (Santos-Sacchi et al., 1998; Santos-Sacchi, 2002). The latter approach benefits from statistical modeling to obtain an optimal result (Barnett and Misler, 1997). In this report, I have uncovered an additional piece of information at ω₀, namely, β_ω, which can be used to determine all circuit parameters. Despite the location of β_ω precisely at ω₀, the method does require two-frequency stimulation, and therefore analogous to the standard dual-sine method, it is reasonable to expect that optimal results could arise from further refinement (Barnett and Misler, 1997). I should also note that because β_ω depends on τ_clamp, an alternative approach would be fitting of current transients induced by step voltage commands. Of course, any method that does not measure β_ω synchronously with the primary frequency component will be unable to correct for changes in cell parameters on a point-by-point basis. This will limit the utility of the technique, and this limitation is inherent in all “pause and dither” techniques. The eCm method benefits from point-by-point correction because gain and angle are redetermined and applied point-by-point at the f₀ rate.

Relation of the eCm method to traditional phase-tracking methods

The eCm method that I have developed here simply estimates absolute C_m by dividing the imaginary component of the input admittance (B_Y) at a single frequency by the absolute value of the partial derivative ∂Y/∂C_m at that same frequency. This method has an unforeseen relation to traditional phase-tracking techniques. The original phase-tracking method was devised to account for and limit the effects of resistive components on C_m measures (Neher and Marty, 1982; Joshi and Fernandez, 1988). It is a method that theoretically strives to determine C_m changes through measurement of changes in input admittance (ΔY) as a function of changes in the circuit parameter, C_m.

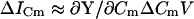(49)

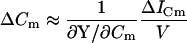(50)

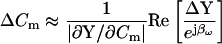(51)

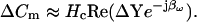(52)

The latter equation is related to the nonsimplified form of Eq. 43 in Gillis (1995) and is addressed in a subsequent article of his (Gillis, 2000). However, heretofore, approximations of both β_ω and H_c have only been possible. The benefits and drawbacks of using particular parameter approximations have been discussed in detail (Joshi and Fernandez, 1988). Thus, phase-tracking paradigms that use estimates of the magnitude and angle of ∂Y/∂C_m are recognized as better suited to systems where R_s is stable and R_m may fluctuate (Joshi and Fernandez, 1988). However, where the resistive components have the converse behavior, the angle of ∂Y/∂G_s − 90°, namely, 2 tan⁻¹ (B_Y/A_Y) − 90° as nicely provided by Zierler (1992), may be a better choice (Joshi and Fernandez, 1988). Unfortunately, where both resistive components simultaneously fluctuate, phase tracking is problematic. Despite these caveats, and even with the correct quantities I now provide, implementation of the phase tracking either by feeding the raw current output of the patch clamp into a hardware lock-in amplifier or a software phase detector (PSD) appears to be an inappropriate implementation of the phase analysis concept (Joshi and Fernandez, 1988; Neher and Marty, 1982; Fidler and Fernandez, 1989). That is, if the analyzed signal is Y, then in contradistinction to Eq. 52,

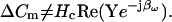(53)

Consequently, the result of evaluating Y (or I_Rs) directly should not provide an accurate picture of changes in C_m (i.e., ΔC_m).

The surprising fact is, however, that implementations using direct evaluations of Y can, under certain conditions, provide very good estimates of absolute C_m.

It should be noted that applying capacitance and series resistance compensation at the onset of an experiment cannot be construed as providing a ΔI_Rs (i.e., ΔY V) output from the amplifier. This is simply a one-time subtraction that would have to be repeated, along with a new angle determination, every time a data point is collected. Additionally, only a two-element model is used by amplifiers for such compensation.

One reason for success with this direct approach would be if R_s were very small, i.e., as R_s approaches zero, 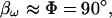and absolute values of I_Cm will be evaluated. Unfortunately, it is unlikely that R_s will be so low (and maintained so low) so as to approach this condition. Notwithstanding this apparent quandary, it is possible to implement phase-tracking paradigms with direct evaluations of Y and still obtain excellent estimates of C_m in the face of very large changes in R_s and R_m. Surprising, the angle returned by series resistance dithering works better than that returned by capacitance compensation dithering.

Series resistance dithering

Dithering of the series resistance, championed by Joshi and Fernandez (1988), is used to return a close approximation of β_ω, namely ∠∂Y/∂G_s − 90°. This approximation, however, when used with a direct analysis of Y, rather than ΔY, and point-by-point (i.e., real time) gain and angle correction is surprisingly exact (see the simulations in Fig. 2 B). The outcome of such an implementation does not suffer from the caveats normally expected with the phase-tracking approach (Joshi and Fernandez, 1988)—namely, large changes in R_m (or R_s) have no effect on the measure of C_m. The reason for this is because the angle of ∂Y/∂G_s is twice the angle of Y (Zierler, 1992), and the PSD measurements are simply returning B_Y,

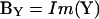(54)

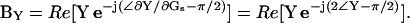(55)

Thus, whereas Eq. 53 fails to provide ΔC_m estimates, simply replacing the angle 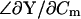with 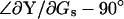results in an exact solution for absolute C_m, as shown previously in Eq. 26,

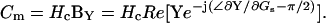(56)

Any complex number can be evaluated at twice its angle to return its real component and at twice its angle −90° to return its imaginary component. Thus, in this case, it turns out that the eCm method is simply being employed.

Capacitance compensation dithering

The initial work of Neher and Marty (1982) utilized capacitance compensation dithering to obtain an angle at which to evaluate, via PSD, changes in C_m. The angle provides an excellent approximation of β_ω when capacitance compensation is in effect. This is shown by inspection of ∂Y/∂C_d and its angle, based on the model of Fig. 1 A, now including the capacitance compensation components C_d and R_d (in series with each other, from headstage to ground).

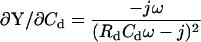(57)

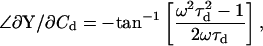(58)

where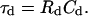

β_ω, the angle of ∂Y/∂C_m, remains unaffected by the addition of the capacitance compensation circuitry,

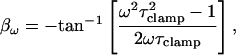(59)

thus indicating that when the clamp time constant (τ_clamp) and compensation time constant (τ_d) are equal, i.e., when compensation is in effect, the angle returned by dithering equals β_ω. Unlike the use of the angle returned by series resistance dithering, the use of this angle to measure C_m with direct evaluations of Y is not as accurate (Fig. 2 E). It should be noted that these analyses only apply to direct measures of Y that are corrected on a point-by-point basis for phase and gain changes, and not necessarily to the traditional use of the angle (Neher and Marty, 1982).

Validity, accuracy, and sensitivity of C_m measurement methods

There are several factors, including model validity, approximations, and noise that contribute to errors in the measurement of capacitance with sinusoidal analysis. Obviously, approximations lead to errors only if they fail; however, because approximations often remove a particular component, e.g., R_s or R_v, from the system of equations, it is impossible to gauge failure during an experiment. Thus, it is prudent to make as few simplifications and approximations as possible. The mathematical and physical modeling that I have presented clearly indicate that the eCm method benefits from this rule.

Noise, on the other hand, is an issue that affects all electrical measures of cell activity regardless of the method's validity. Even for a method that provides a valid measure of some electrical quantity in the absence of noise, the introduction of noise can prove devastating, or at least render it useless for a given task. Not surprisingly, some methods may be able to deal with system noise better than others.

The design of sinusoidal stimulus protocols has enormous impact on C_m measurement sensitivity in the face of real-world noise. Important issues such as stimulus frequency, stimulus magnitude, stray capacitance, and unexpected conductance changes have been discussed in detail (Gillis, 1995; Barnett and Misler, 1997; Thompson et al., 2001; Debus et al., 1995). Careful attention to these issues can lead to incredible sensitivity; for example, with very high-frequency stimulation and very large voltages, very good signal/noise ratios can be obtained, providing noise floors well below 1 fF (Klyachko and Jackson, 2002). One of the consequences of the equivalency between the eCm method and the phase-tracking method as typically employed, is that effects of noise on performance might be expected to be similar for each method. To evaluate issues like this, comparisons were made under varying noise conditions in model simulations.

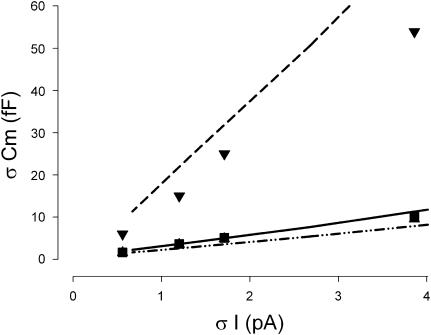
In Fig. 9, a modeling approach is used to compare the effects of Gaussian noise levels on C_m estimate noise among a few common methods of C_m estimation. In this approach, the simple circuit of Fig. 1 A was modeled in the time domain using the RK4 method hardcoded in C within jClamp; the results were then independently analyzed by transient step analysis, single-sine analysis, dual-sine analysis, or the eCm method. Step analysis follows the method outlined in a prior publication (see appendix in Huang and Santos-Sacchi, 1993). Such an analysis is multifrequency, providing extended information similar to that obtained from “chirp” stimuli (Santos-Sacchi, 1991b; Santos-Sacchi, 1989), and wideband noise stimuli (Fernandez et al., 1982). Features of our step method included automatic clocking to reach steady state and utilization of exponential fitting after the initial onset transient, methodology recently reemphasized as important for the robust use of transient analysis for C_m measurement (Thompson et al., 2001). In our original implementation and in jClamp, a correction for errors introduced by the R_s/R_m voltage divider on Q, namely that is employed (Huang and Santos-Sacchi, 1993). To my knowledge, no other implementation accounts for this potential error. Single-sine analysis follows the approximation (for β_ω and H_c) method outlined in the Fig. 2 legend. The dual-sine method (Santos-Sacchi, 1992; Santos-Sacchi et al., 1998), follows the same fast Fourier transform-based determination of the real and imaginary components employed by the eCm method. In both cases estimates derived from both ω₀ and ω₁ are averaged (f₀: 390.6 Hz; f₁: 781.2 Hz). This averaging benefit must be kept in mind when comparing single-sine estimates. All methodologies are standard features in jClamp. In Fig. 9 the relation between measured C_m noise and imposed current noise is examined for each of the methodologies with either a 100-MΩ or 500-MΩ R_m. All methods work well under low-noise conditions, and this simply indicates that the true limitation for C_m estimation is the noise of the system at those frequencies used by the method. Indeed, under real-world conditions where system noise levels are well minimized, step, single-sine and dual-sine techniques can provide roughly equivalent C_m estimate noise levels (within ±10–30%) close to theoretical limits (Gillis, 1995; Barnett and Misler, 1997; Thompson et al., 2001). However, under forced noise levels as in Fig. 9 the eCm and single-sine techniques appear better able to deal with higher noise levels than this step implementation. Because of the exact same implementation of frequency analysis and the absence of approximations for eCm and dual-sine approaches, sensitivities turn out to be essentially equivalent. Had β_ω been determined in another manner, e.g., by the dω approach, the results may have differed. Given the relation between the single-sine phase-tracking approach and the eCm method detailed above, it is not surprising that these two methods are roughly equivalent in handling noise. For each method, slightly better noise levels are achieved when β_ω is fixed during analysis to simulate a “pause and dither” approach; thus, recalculating β_ω for each sample introduces additional noise in the analysis that must be balanced with the increased validity afforded by point-by-point correction. The step analysis is particularly prone to high noise levels; this is especially obvious when low frequency (e.g., 60 Hz) interference is included, and is in marked contrast to sinusoidal approaches that can avoid extraneous spectral interference. The conclusions based on this mathematical modeling effort were essentially confirmed with a physical implementation (see Fig. 9). From these results, it is clear that given a sufficiently low system noise or actually a sufficiently high signal/noise level, the eCm method will have the sensitivity to analyze fusion events, as clearly suggested by the physiological results shown in Fig. 8.

FIGURE 9.

Effect of system noise on C_m estimate noise. Results from either mathematical modeling (lines) or physical modeling (symbols). Three methodologies, step (dashed line, ▾), eCm (dash-dotted line, ▴), and single-sine phase tracking (solid line, ▪) are presented. For the software model, forced Gaussian noise levels were imposed, and the noise of C_m estimates calculated. For the physical model, system noise levels were 3.8 pA rms when the model was attached to the headstage. To obtain lower system noise levels, averaging was performed to produce the plotted noise levels. For the electrical model, a 10-kHz Bessel filter was used, and the frequency components of the remaining noise were likely different from the wideband noise used for the math model. This likely accounts for differences in math and electrical model results. In any case, the data from each model indicate that as system noise decreases, all of the methods become comparable. Nominal component values of R_s: 10 MΩ, R_m: 300 MΩ, and C_m: 18 pF. IBM T40 laptop in battery mode (Armonk, NY), Axon 200 amplifier in capacitive feedback mode, 10-kHz Bessel filter, and Quatech (Hudson, OH) DAQP 308 PCMCIA PC card A/D D/A board were used.

SUMMARY

The new eCm method that I outlined here provides another tool for analysis of cellular processes that can be interrogated by C_m measures. It is a method that works in the absence of usual simplifying assumptions and approximations of the traditional patch-clamp-cell model circuit. In detailing the approach, several new observations have been made. They include: 1), the imaginary component of the input admittance Y, namely, B_Y, can be worked on by ∂Y/∂C_m to obtain absolute values of C_m; 2), the angle of ∂Y/∂C_m, namely, β_ω, is the same as that of ∂Y/∂ω and therefore can be obtained from frequency manipulation alone; 3), given β_ω, the absolute value of ∂Y/∂C_m can be determined; 4), frequency manipulation need not require an infinitesimal dω to extract β_ω; and 5), the traditional phase-tracking technique that evaluates raw amplifier currents, rather than difference currents, at the angle provided by series resistance dithering, works similar to the eCm method by simply returning estimates of B_Y, not ΔI_Cm, and ultimately provides absolute, not delta, C_m estimates. Finally, it might be expected that enhancements of the eCm technique may arise from future implementations in hardware and by statistical optimizations.