Abstract
A dendritic spine is an intracellular compartment in synapses of central neurons. The role of the fast twitching of spines, brought about by a transient rise of internal calcium concentration above that of the parent dendrite, has been hitherto unclear. We propose an explanation of the cause and effect of the twitching and its role in the functioning of the spine as a fast calcium compartment. Our molecular model postulates that rapid spine motility is due to the concerted contraction of calcium-binding proteins. The contraction induces a stream of cytoplasmic fluid in the direction of the dendritic shaft, thus speeding up the time course of spine calcium dynamics, relative to pure diffusion. Simulations indicate that chemical reaction rate theory at the molecular level can explain spine motility. They reveal two time periods in calcium dynamics, as measured recently by other researchers. It appears that rapid motility in dendritic spines increases the efficiency of calcium conduction to the dendrite and speeds up the emptying of the spine. This could play a major role in the induction of synaptic plasticity. A prediction of the model is that alteration of spine motility will modify the time course of calcium in the dendritic spine and could be tested experimentally.
INTRODUCTION
A dendritic spine is a small, ∼1-μm protrusion consisting of a head, where a synaptic contact is made with an afferent fiber, and a stalk, which connects the head to the parent dendrite. Synaptic current is transferred from the spine head with little loss into the parent dendrite, making it unlikely that the spine constitutes an electronic filter, as was predicted in early models. An alternative hypothesis was offered over a decade ago, which suggests that the spine is a unique calcium compartment, allowing [Ca2+] to rise to levels that are much higher than those of the parent dendrite. Indeed, there is a great deal of evidence to suggest that calcium plays a major role in synaptic plasticity, being responsible for long-term potentiation or long-term depression of synaptic currents. Thus the concentration and duration of calcium rise inside the dendritic spine is assumed to determine the nature of spine plasticity. The spine has a unique geometry which varies tremendously from spine to spine. The relation between spine shape and calcium homeostasis is not entirely clear but the rules governing the dynamics of calcium diffusion in the spine have been studied both experimentally and theoretically (Bonhoeffer and Yuste, 2002; Nimchinsky et al., 2002; Shepherd, 1996). Many relevant models (Koch and Zador, 1993; Koch and Segev, 1998; Koch, 1999; Zador et al., 1990; Segev and Rall, 1988; Franks and Sejnowski, 2002) have been proposed to explain calcium diffusion in dendritic spines. These models are based on a phenomenological approach, using some coupling between the diffusion equation and the ambient chemical reactions. The dendritic spine is in fact compartmentalized into subunits where the diffusion process is discretized, whereas ordinary differential equations describe the chemical bonds to buffer protein molecules. Using the same type of model, Volfovsky et al. (1999) studied calcium dynamics for various spines, when the neck length is changing.
A fast twitching movement of the dendritic spine was predicted by Crick (1982), who posed a question about the rules “governing the change of shape of the spine and, in particular the neck of the spine,” and later on “how these rules are implemented in molecular terms.” Fast contractions of dendritic spines (twitching) after an action potential, or a backpropagating action potential, have been reported in Korkotian and Segal (2001), where it was shown that blocking calcium currents in the spine prevents twitching. It was also shown that spontaneous calcium transients are associated with rapid contraction of the spine head. The twitching lasts from a few hundreds of a millisecond up to 2 s. At the end of the calcium flow, the spine relaxes to its original shape.
Proteins are found inside the dendritic spines and their spatial distribution can be measured. In Morales and Fifkova (1989), the number of myosin molecules is ∼100 inside a single spine. We choose the number of proteins between 50 and 100. Note that 1 μm gives 600 proteins in 1 μm3. In a spine head of volume 0.5 μm3 this represents ∼75 molecules. The relevant proteins include actin, which has been shown by Korkotian and Segal (2001) to be directly involved in the biophysical process underlying spine motility. This was done by showing that blocking actin polymerization prevents the twitching. It was shown that dendritic spines contain also a network of myosin molecules (Morales and Fifkova, 1989). The spatial distribution of myosin in the spine has been observed to be uniform, and to have sparse presence in the postsynaptic density.
We propose here an answer to Crick's question about the cause and effect of the twitching and its role in the functioning of the spine as a conductor of calcium. Specifically, we attribute the twitching motion to the contraction of actin-myosin-type proteins when they bind calcium, and include its effect on the dynamics of the calcium ions in the spine. This is the first quantitative theory of the twitching and its role in calcium dynamics in the spine.
MATERIALS AND METHODS
Physical description and mathematical model for calcium simulation in a dendritic spine
We model the spine as a machine powered by the calcium it conducts and we describe its moving parts. We propose that calcium ions set the machine in motion by initiating the contraction of the actin-myosin that they bind at active sites on the proteins. We maintain, by analogy to the muscle, that actin-myosin sites are involved in motility events and elucidate the cause and effect of twitching in the functioning of the spine by adding up the local contractions of the separate calcium-saturated buffer proteins, to achieve a global contraction effect. The contraction of the spine head induces a flow field of the cytoplasmic fluid, which in turn pushes the ions, thus speeding up their movement in the spine.
We chose the rate of contraction according to previous data (Chapter 34 of Kandel et al., 2001). There is, however, insufficient molecular evidence to guarantee that this is the only value that has been observed. It has been reported that a myosin head can contract ∼0.06 μm in a few milliseconds. We choose this rate as a representative value.
Simplifications of the model
We make several simplifications in constructing the model of the spine. We neglect other types of organelles that are also involved in calcium dynamics: the spine apparatus and mitochondria. Furthermore, it is known that calcium stores in the spine release calcium ions when prompted by external calcium ions, under specific conditions. We neglect this effect here to avoid complicating our model. We also restrict the biochemical structure of the spine by singling out the calmodulin, actin-myosin, calcineurin, and one type of calcium pump. All these proteins constrain calcium flow in the dendritic spine by binding calcium ions for random periods of time. The technical assumption in the model is that the motion of actin-myosin proteins is negligible relative to that of calcium ions and that they contract at a fixed rate, as long as they keep four calcium ions bound. Thus contraction begins and ends at random times. Since we are interested in the dynamics of calcium, when the ions are already inside the spine, we avoid the computation of the transient time starting from the action potential and the opening of the voltage-sensitive calcium channels. The specific geometry of the spine needs to be considered to evaluate the time evolution of calcium concentration in the spine. In a simplified model of the spine, its geometry is characterized by the length and diameter of the spine neck and by the radius of the spine head (Fig. 1). Another geometrical feature is the distribution of calcium-dependent buffer molecules that contract when they bind enough calcium.
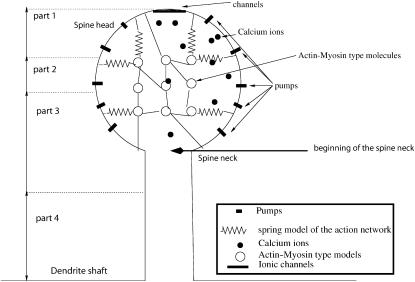
FIGURE 1.
Schematic representation of a dendritic spine. The model of a dendritic spine is composed of a spherical head and a cylindrical neck that connects the head to the dendrite. The head contains an active network of protein molecules of myosin, actin, and calmodulin. Active pumps are located on the surface of the head, and calcium channels are situated on top. The solid black circles represent calcium ions. The springs connecting the circles and the membrane represent the actin network: when a protein contracts it affects the spine volume. The diagram is not drawn to scale. The spine is arbitrarily partitioned into four compartments, as indicated on the left part of the figure: compartment 1, from the top of the head to a distance of R/3; compartment 2, from R/3 to the middle of the head; compartment 3, from the middle of the head to a distance of l/4, where l is the length of the neck; and compartment 4, the bottom l/4 of the neck.
When a dendritic spine twitches, the volume decreases by 10–20% of its initial value, as indicated in Korkotian and Segal (2001). In the present study, we neglect the change in the volume, but we replace it with the flow field that the contraction generates, because it changes the nature of the ionic trajectories. Since we do not calculate concentrations, but rather follow the number of ions in the spine, which is the appropriate variable, the variation in concentration due to contraction can be neglected. Indeed, when inert dye molecules are inserted into the spine, instead of calcium, the number of dye molecules inside the spine is measured, not their concentration. The contraction, however, increases the probability that a trajectory hits the neck, which is assumed fixed, thereby decreasing the mean exit time. The error incurred by neglecting this effect is of the same order of magnitude as that incurred by considering the dendritic spine empty of its organelles.
Our mathematical model for the description of ionic motion in the spine is the Langevin equation. We use it to simulate the collective motion of ions, their binding to buffer proteins, and their release. Two different protein distributions are examined for a fixed spine geometry. To evaluate the effect of spine motility on calcium dynamics, the trajectories of ions are compared with and without the motility. The motility is finally examined when hundreds of calcium ions flow from the top of the spine head.
The Langevin description
We model the spine as a physical device whose components are described by simple physical laws. The ionic motion and interactions with proteins is described at the molecular level. The present model involves certain simplifications. Electrostatic forces between ions are neglected, so that different ionic species can be studied separately. We focus on calcium ions only and assume that an ionic trajectory can be well described by the Langevin equation. We adopt the classical description of the diffusive motion of calcium ions in water by the overdamped Langevin equation (Berry et al., 2000). Thus the random trajectory of the ith calcium ion is the solution of the Langevin equation
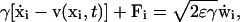 |
(1) |
where v(x, t) is the hydrodynamic flow field, Fi is the electrostatic force exerted on ion i by the other ions, γ is the dynamical viscosity, 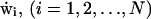 are independent Gaussian white noises, ε = kBT/m, where T is absolute temperature, m is the reduced mass of the ion, kB is Boltzmann's constant, and Einstein's relation for the diffusion constant is
are independent Gaussian white noises, ε = kBT/m, where T is absolute temperature, m is the reduced mass of the ion, kB is Boltzmann's constant, and Einstein's relation for the diffusion constant is
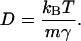 |
Since electrostatic interactions are neglected, we set Fi = 0. When an ion hits the spine membrane it is reflected, unless it happens to hit an empty pump. In the latter case, the ion is assumed to be absorbed by the pump. We assume every ion that reaches the dendritic shaft is absorbed there and its trajectory is terminated.
The dynamics of the forward and backward chemical binding reactions
We approximate a binding site on a protein by a spherical domain of radius Ra and assume that it can only contain one calcium ion at a time. The forward calcium binding reaction is imitated by making the boundary of the sphere absorbing for the trajectories of Eq. 1, as long as the sphere is empty. That is, the moment a trajectory of Eq. 1 hits the sphere, both the trajectory and the sphere are terminated for a random time. After this random time both the sphere and the trajectory reappear, with the trajectory restarting outside the sphere. The reappearance represents the release of the ion from the binding site by thermal activation (this is the backward binding reaction).
The size of the sphere is calibrated to fit the forward binding rate. Specifically, the calibration is done off line in a separate steady-state reaction with a sufficient number of ions, according to the calibration formula
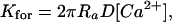 |
(2) |
where [Ca2+] is the stationary calcium concentration, as described in Berry et al. (2000) and Chandrasekhar (1954). In this case ions arrive at an empty binding site in a Poissonian stream (Nadler et al., 2001).
The random time interval between the forward binding and the reappearance is chosen to be exponentially distributed with a rate constant that is the experimentally measured rate of the backward binding reaction, also calculated off line. The exponentially distributed waiting time for the backward reaction is based on Kramers' theory of activated barrier crossing, as described in Berry et al. (2000), Kramers (1940), Matkowsky et al. (1982), and Hänggi et al. (1990). Active pumps are modeled similarly: when an ion falls into a pump, the pump cannot accept another ion until it empties, which requires a given random or deterministic time.
The flow field v(x, t)
The hydrodynamic flow field v(x, t) is induced by the contraction of actin-myosin proteins that bind enough calcium (we assume four calcium ions per protein). Each protein that binds four calcium ions (henceforward called a saturated molecule) contracts at a given rate for a given time. In our model this contraction causes the spine head to shrink at a rate proportional to the number of saturated proteins, thus pushing the fluid it contains toward the dendritic shaft.
More specifically, denoting by Ns(t) the number of saturated proteins, the induced potential flow field v(x, t) can be written as the product of a spatial function G(x) and a time-dependent function, vqNs(t). Here G(x) is computed by using a Green's function, which captures the geometry of the domain, and vq is a constant, computed from the ratio of the contraction length to the contraction time of a molecule. We choose here the simplest approximation, given by G(x) = −k, where k is the unit vector parallel to the direction of the spine neck and pointing away from dendrite (Fig. 1).
Simulation
Calcium ions enter the spine head through NMDA channels after a glutamatergic stimulation. NMDA channels are located on top of the spine head, where we assume that five of them are coactivated. We confine our simulation to this case and do not address the possible entrance of the calcium through the VDCC, which corresponds to another interesting case, initiated by a backpropagation action potential.
The simulation in this work starts when the ions are already inside the spine head, neglecting all the entrance processes through the channels. In the worst case scenario, when the ions enter through the top of the head, they are located at the longest distance from the spine neck and their mean exit time is the longest possible. A simple computation, using R2 = 6Dt, shows that for R = 1 μm and D = 600 μm2/s the order of magnitude of the time the ions equilibrate in the head is milliseconds. So at the timescale of hundreds of milliseconds to seconds, which is the time we are interested in, the initial position of ions is forgotten by the system and does not really influence the timescale of the dynamics.
The calcium ions are initially clustered in the spine head near the channels. We have arbitrarily restricted the simulations by including only two kinds of proteins: the first one imitates the chemical behavior of calmodulin or actin-myosin and is referred to as type 1 protein, and the second kind represents the calcineurin protein, and is referred to as type 2 protein. The proteins in both groups are calcium-dependent, but only the proteins of the first group can produce a contraction, when they bind four calcium ions. More specifically, Troponin C, a part of the troponin complex involved in the actin-myosin contraction, binds up to four calcium ions (see the statement “this molecule is closely related to calmodulin” on page 854 of Alberts et al., 1994). Type 2 proteins have only one binding site for calcium.
The simulation begins after a fixed number of ions has entered the spine through the channels and the ions are initially clustered near the channels at five different sites at the top of the spine head. They are moved according to Eq. 1 inside a domain Ω, which is the interior of the spine, outside the unoccupied binding sites of the proteins.
Trajectories are reflected at the part ∂Ωr of the boundary of Ω, where there are no pumps and they are terminated at the pumps and at the bottom of the neck. That is, we assume that an ion that arrives at the dendrite (at the bottom of the spine neck) cannot return to the spine. When an ion reaches an empty pump, the pump becomes inactivated for a mean time τpumps, which is the time necessary to pump the ion out. We chose the number of pumps to be 0, 4, or 10, and located them symmetrically on the bottom part of the head surface.
When a trajectory reaches the boundary of a binding site, both the trajectory and the binding site are removed from the simulation for a random time, as previously described. At the moment the fourth binding site on a type 1 protein molecule becomes occupied, a quantum of velocity in the direction of the neck is added to the flow field v(x, t). As soon as one ion leaves a binding site on a saturated type 1 protein molecule, this quantum of velocity is subtracted off from the field, as long as the field is not zero.
Range of the parameters in the simulations
The values in Table 1 are based on Volfovsky et al. (1999). The radii δ1 and δ2 are computed from the calibration formula of the forward binding constant, using a concentration of 0.5 μm for calcium, and CaM and 1 μm for calcineurin.
TABLE 1.
| D = 400 μm2/s | Diffusion coefficient of calcium ions |
| Ninit = {100, 300} | Number of calcium ions in spine at time 0 |
| NAM = {50, 60} | Number of type 1 proteins in spine |
| Ncal = {10, 30} | Number of type 2 proteins |
| Npumps = {0, 4, 10} | Number of pumps |
| Nchannel = 5 | Number of channels |
| N(t) = | Number of calcium ions in spine at time t |
| δ1 = 0.01 μm | Radius of a calcium binding site on a type 1 protein |
| δ2 = 0.02 μm | Radius of a calcium binding site on a type 2 protein |
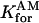 = 50 μm−1/s = 50 μm−1/s |
Forward binding rate of calcium to type 1 proteins |
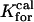 = 50 μm−1/s = 50 μm−1/s |
Forward binding rate of calcium to type 2 proteins |
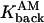 = 500s−1 = 500s−1
|
Rate of calcium dissociation from type 1 proteins |
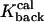 = 25s−1 = 25s−1
|
Rate of calcium dissociation from type 2 proteins |
| R = 0.5 μm | Radius of the head |
| d = {.2, 0.4} | Diameter of the neck |
| l = {.3, .6, 1} | Length of the neck |
| Spumps = 0.01 μm | Size of the active center of the pumps |
| τpumps = 9 ms | Characteristic time of pumps |
RESULTS
Calcium dynamics
To evaluate the effect of the spine rapid motility on the dynamics of calcium concentration, we have followed the time evolution of the trajectories of calcium ions, the number of ions bound by the proteins, the number of ions pumped out, and the number of ions that reached the dendrite. To study the effect of the hydrodynamic push, the simulations were run with and without the push, while preserving all other characteristics of the simulation.
Occupation of the space
The geometric characteristics of ionic trajectories are compared in two different dynamics, with and without the hydrodynamic push. We observe that the ion trajectories are distributed differently in space and the nature of the movement is different in the two cases (Fig. 2). This result is clearly seen in the comparison of graphs in Fig. 2, a and b. In the absence of the hydrodynamic push, the only effect of the proteins is the binding of calcium ions for a finite random time and this does not affect the nature of the trajectories. The trajectories are described as two-dimensional random-walk, which is recurrent (Karlin and Taylor, 1977), so every trajectory fills the entire space, if allowed to proceed indefinitely. When an ion binds to a protein, it is maintained fixed during the random binding time. With the additional hydrodynamic flow, however, recurrence time becomes long, so trajectories fill the space at a much reduced rate. The hydrodynamic flow causes the ions to drift in the direction of the neck and consequently the time they spend in the spine head is considerably reduced. Trajectories are described by a dynamical system with two components—one is a pure Brownian motion, and the other is the hydrodynamic drift.
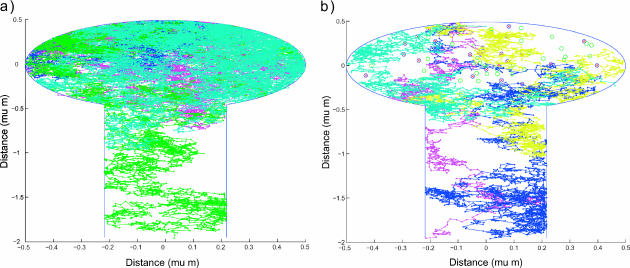
FIGURE 2.
The filling of space by five random trajectories in the spine (a) with no drift, and (b) with drift. Each color corresponds to a trajectory. Proteins are uniformly distributed in the spine head, and are represented by circles and crossed circles, respectively. A trajectory starts at the top of the spine head where channels are located and continues until it is terminated at the dendritic shaft or at an active pump. The parameters for the simulation are δ1 = 0.02 μm, δ2 = 0.01 μm, 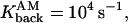
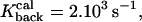 R = 0.5 μm, d/2 = 0.21794 μm, l = 1.5 μm, and Npumps = 10.
R = 0.5 μm, d/2 = 0.21794 μm, l = 1.5 μm, and Npumps = 10.
In addition, qualitatively, the probability of a trajectory to return to the head from the spine neck is reduced if it has to diffuse upstream, against the hydrodynamic drag force. Thus the ionic trajectory stays inside the spine a shorter time in the presence of the hydrodynamic flow, as compared to the time without it. Below, quantitative data concerning the number of calcium binding events for the two types of dynamics will be given. Indeed, to quantify the effect of different dynamics on trajectories, data are produced with enough ion trajectories so that mean values are achieved and thus can be compared.
Two stages of calcium concentration decay
To study calcium dynamics in dendritic spines and the collective effect of binding and unbinding of ions to the proteins, a simulation with 100 calcium ions is presented. When 100 calcium ions enter into the spine head, it increases the spine concentration from 100 to 300 nM (depending on the volume of the spine), which corresponds to the physiological range of increases (Majewska et al., 2000). After the ions start moving, the fraction of the bound ions is responsible for the hydrodynamic component of the velocity applied to the free ions. This fraction is at any moment a random variable, which depends on the initial number of calcium ions. The parameters used for the simulation are Ninit = 100, 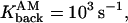
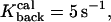 R = 0.5 μm, l = 0.2 μm, d/2 = μm, and Npumps = 10 and proteins are clustered near the postsynaptic density. The radius of the bin that contains the empirical distribution is R/8. The bin is located near the entrance of the channels, at the top of the spine head.
R = 0.5 μm, l = 0.2 μm, d/2 = μm, and Npumps = 10 and proteins are clustered near the postsynaptic density. The radius of the bin that contains the empirical distribution is R/8. The bin is located near the entrance of the channels, at the top of the spine head.
The time course of calcium is divided into two periods
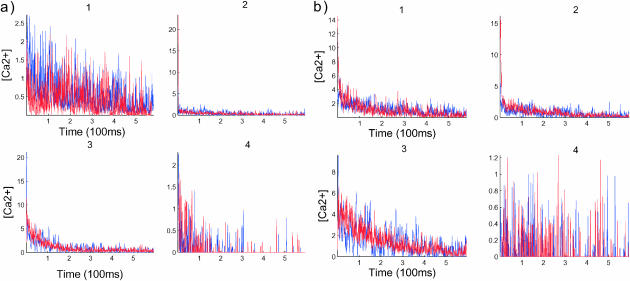
The time course of calcium concentration in the spine is presented in Fig. 3, where two time periods can be clearly identified: a quick decay, starting at the beginning of the simulation and ending at ∼250 ms, and a slower decay that continues to the end of the simulation (Fig. 3 a1).
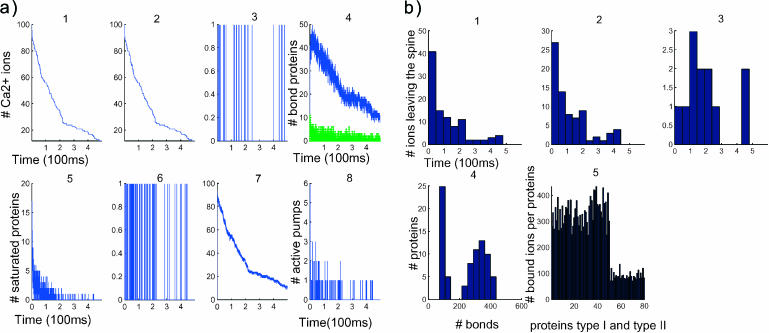
FIGURE 3.
Dynamics of 100 calcium ions in dendritic spine. (a) Time evolution of the concentration and binding. (First row) Concentration versus time (in μs). (Left to right) 1, [Ca2+] in the total spine. 2, [Ca2+] in spine head. 3, Number of ions in the neck. Note that the neck contains only one ion at a time. 4, Number of bound proteins (type 1, blue; type 2, green. Note the stochastic nature of those curves. (Second row, left to right) 5, Number of saturated proteins of type 1 versus time. 6, Arrival times of ions at active pumps: the ions leave one at a time. 7, Number of bound ions versus time. 8, Number of active pumps versus time. (b) Statistical analysis after 100 ions have crossed to the dendrite. (First row, left to right) 1, Calcium efflux from the spine versus time (in μs). 2, Calcium efflux through pumps versus time. 3, Calcium influx into the dendrite versus time. (Second row, left to right) 4, Number of proteins that have bound a given number of ions: only five proteins bound 400 ions during the entire time course of the simulation. 5, The abscissa represents the numbered proteins: 1–50 are the proteins of type 1, 51–80 are type 2. The ordinate represents the number of calcium ions that each protein bound in the simulation.
The decay curve in Fig. 3 a5 shows the number of saturated proteins, which is proportional at any moment to the velocity amplitude. The more the proteins are saturated, the larger the amplitude component of the velocity. Thus ions are directed sooner toward the dendritic shaft. When a simulation starts with 100 ions, only 10% of the proteins get saturated by 40 ions at the beginning and then the number of saturated proteins decays exponentially in time. The first fast time period of Fig. 3 a1 is explained by the large number of saturated proteins in that period, represented in Fig. 3 a5, compared to the number of proteins that are saturated in the second time period.
The average of the hydrodynamic effect can be estimated by the 2.5 proteins saturated for the first 250 ms. Indeed each protein contributes to the speed of a total of 50 nm/ms. The total speed of the push is 0.5 μm/ms. The push speeds up the arrival of ions at the lower part of the spine head, where the pumps are located, relative to arrivals by pure diffusion. Since the sojourn time of ions in the pumps is chosen to be short, the ions leave mainly through the head. Approximately 10% of the ions reach the dendrite at the end of the simulation, ∼15% are left in the spine and 70% leave through the pumps (Fig. 3, b2 and b3). This proportion is controlled by the fast pumping rate, the distribution of proteins, and the size of the narrow neck. In the second period, that starts after 250 ms, the number of saturated proteins is very low. At most, one protein is saturated and the saturation lasts only for a short time. The ions arrive less frequently at the pumps or at the neck. The main driver of the ions in the second period is diffusion, not drift. The accelerated rate of pumping in this simulation (sojourn time of 1 ms) implies that only few pumps are active at a time, as it is shown in Fig. 3 a8. One ion at a time leaves through the pumps, as indicated in Fig. 3 a6. Finally, there is never more than one ion in the neck at a time.
Since the distribution of proteins in the spine is clustered near the postsynaptic density, the maximum number of bonds is reached very early in the simulation. But in this simulation the effect of the push is not sufficiently strong to direct all the ions toward the neck. The 1:4 ratio of the efflux through the pumps, compared to that through the dendrite, may be due to the large number of fast pumps.
Statistical analysis of the number of bound proteins
The statistical analysis of the simulation reveals the number of bonds made between ions and proteins. Fig. 3 b4 indicates that the total number of bonds peaks twice, once when 25 proteins form <80 bonds, and a second time when 12 proteins form 300 bonds. This result can be interpreted by taking into account two main differences. First, there is a factor 5 in the forward binding rate of the two types of proteins, and second, protein of type 1 can bind four calcium ions, whereas protein of type 2 can bind no more than one.
A more accurate description of the number of bonds is provided in Fig. 3 b5, where it is estimated per molecule. The number of bonds per type 1 site (displayed below the 50th) is 350, whereas for type 2 (displayed after the 50th) it is 80. In a first approximation, each protein can be considered to be statistically independent. The amplitude of the fluctuation (standard deviation) in the number of bonds is a function of the protein distribution and the backward binding rate, which is the average time an ion stays bound. The fluctuation of type 1 proteins is 50 with a mean of 350, whereas the fluctuation in type 2 proteins is 15 with a mean of 80.
In summary, two time periods can be discerned in the simulation that includes a drift effect. To understand what parameters control the push and affect the general dynamics of calcium, we consider in the next paragraphs the effect of the protein distributions and compare systematically the evolution of the calcium concentration with and without the push.
Influence of protein distribution on calcium dynamic
To study the effect of the protein distribution on calcium dynamics inside the dendritic spine, two types of proteins distributions are considered: a uniform distribution (UD) in the dendritic spine head, and a postsynaptic distribution (PSD), where the proteins are accumulated in clusters near the calcium channels, at the postsynaptic density. The PSD/UD distributions in the simulation include the contractile proteins, because the mechanical effect is different in each configuration due to the different probability to have the same number of saturated molecules. However, for the same number of saturated proteins, the total push is similar.
The parameters of the simulation are Ninit = 200, 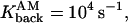
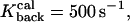 R = 1 μm, l = 0.3 μm, and d/2 = 0.3 μm. There are four pumps, 60 proteins of type 1, and 10 of type 2. In each simulation, the effect of two factors are compared on the evolution of [Ca2+], push versus no push, and PSD versus UD. There are four combinations of these factors.
R = 1 μm, l = 0.3 μm, and d/2 = 0.3 μm. There are four pumps, 60 proteins of type 1, and 10 of type 2. In each simulation, the effect of two factors are compared on the evolution of [Ca2+], push versus no push, and PSD versus UD. There are four combinations of these factors.
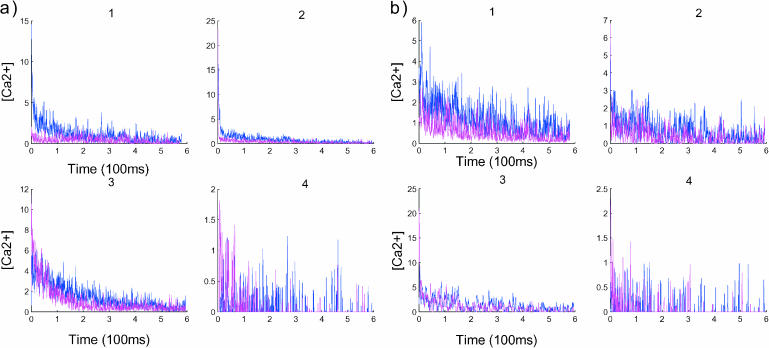
In Fig. 4, the time course of [Ca2+] is presented similarly as in Fig. 3 and the simulation runs for 600 ms. The time-dependent curves with and without the push are displayed in the same graphs, for identical protein distribution. The push effect in the PSD case has a drastic effect between 100 and 400 ms and the number of ions remaining inside the spine is reduced to one-half of the initial number. Such difference is less significant in the uniformly distributed case. The results give a quantitative estimate of the protein distribution effect on calcium dynamics.
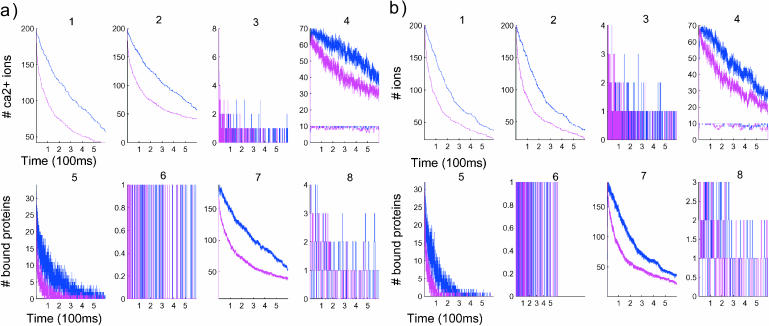
FIGURE 4.
Comparison of the time evolution for postsynaptic (a) and uniform (b) distributions of proteins. Blue curves correspond to a simulation without the push effect, whereas magenta curves correspond to simulations with it. (Panels a and b, first row) Concentration versus time (in μs). (Left to right) 1, [Ca2+] in the total spine. 2, [Ca2+] in spine head. 3, Number of ions in the neck. Note that the neck contains few ions at a time. 4, Number of bound proteins (type 1, blue; type 2, green). Note the stochastic nature of those curves. (Second row, left to right) 5, Number of saturated proteins of type 1 versus time. 6, Arrival times of ions at active pumps: the ions leave one at a time. 7, Number of bound ions versus time. 8, Number of active pumps versus time.
The two time periods of calcium time course appears in the curve representing the number of bound ions in Fig. 4 b7. The concentration of calcium decays faster with the PSD distribution than with the UD. Many more ions are bound initially in the PSD case than with UD (comparison of Fig. 4, part a5 with b5, and Fig. 4, part a4 with b4). Due to the very long binding time (the average binding time is 20 ms) of the second type of proteins, they are continuously saturated during the simulation (lower curves of Fig. 4, a4 and b4). As a consequence the fluctuation in the number of bound ions for protein of type 2 is small, compared with the fluctuation of the first kind. Finally for an initial concentration of 200 calcium ions, the number of ions in the neck is still small—two or three, on average (Fig. 4, a3 and b3).
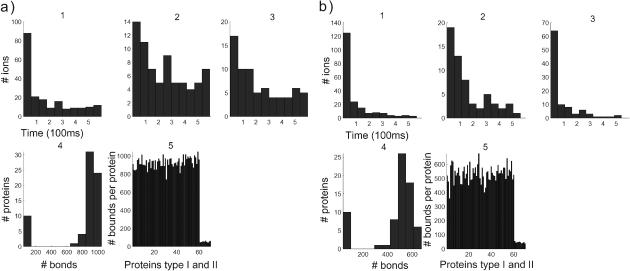
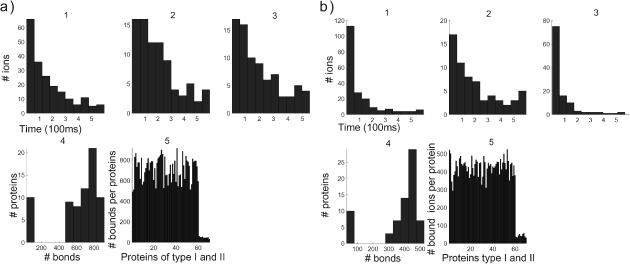
By comparing Fig. 5Fig. 5, parts a5 and b5 or Fig. 6, parts a5 and b5, it appears that the main effect of the push is to direct the ions toward the dendrite. The number of bound proteins (for the first kind) is on the average 500, with a variance of 70, whereas the average is 900 with no push, with a variance of 100. As a consequence, under the push effect, 40% fewer proteins are bound.
FIGURE 5.
Comparison of the time evolution for postsynaptic distribution of proteins (a) with push and (b) without. (Panels a and b, left to right, first row) 1, Calcium efflux from the spine versus time (in μs). 2, Calcium efflux through pumps versus time. 3, Calcium influx into the dendrite versus time. (Second row, left to right) 4, Number of proteins that have bound a given number of ions. 5, The abscissa represents the numbered proteins: 1–60 are the proteins of type 1, 61–80 are type 2. The ordinate represents the number of calcium ions that each protein bound in the simulation.
FIGURE 6.
Comparison of the time evolution for a uniform distribution of proteins (a) with push and (b) without. (Panels a and b, left to right, first row) 1, Calcium efflux from the spine versus time (in μs). 2, Calcium efflux through pumps versus time. 3, Calcium influx into the dendrite versus time. (Second row, left to right) 4, Number of proteins that have bound a given number of ions. 5, The abscissa represents the numbered proteins: 1–60 are the proteins of type 1, 61–80 are type 2. The ordinate represents the number of calcium ions that each protein bound in the simulation.
To compare the effect of the distribution, when no push is applied, the average number of bonds is different: 700 for UD and 850 for PSD. With push, in the PSD case, the average of the number of bonds is maintained higher compared to no push: 400 for UD, 500 for PSD.
To analyze the push effect on calcium dynamics, we compared first Fig. 5, parts a3 and b3. When the distribution of proteins is a PSD, 115 ions get out at the dendritic shaft with push, whereas only 74 exit when no push is applied. The exit time distribution of the ions at the dendritic shaft differs significantly in each cases in the first 100 ms, with a factor 3. Second, in the case of a UD (Fig. 6, a3 and b3), the ratio of ions leaving through the dendrite with push and no push is 100/88, with a main difference, again, in the first 100 ms, of a factor 3.
Compartmentalization analysis
To study more precisely the hydrodynamic effect, we divided the spine into four compartments (Fig. 1) and ran simulations with and without the push. In that case, ions are tracked across compartments. The compartments are defined as follows: compartment 1, from the top of the head to a distance of R/3; compartment 2, from R/3 to the middle of the head; compartment 3, from the middle of the head to a distance of l/4, where l is the length of the neck; and compartment 4, the bottom l/4 of the neck. The histogram of the arrival time of calcium ions in the four compartments is given in Figs. 7 and 8, where simulations are run respectively for proteins in the UD and PSD cases.
FIGURE 7.
Compartmentalization analysis in a spine divided into four compartments. For each graph, the blue curves represent the result with push and the curves in red without push. Panel a shows the dynamics when the proteins are UD, whereas in b, the dynamics are related to PSD. The data are smoothed out by averaging the number of ions in each compartment: for the quantity X(t), we plot 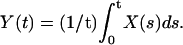 The y axis of the graphs represents the concentration in each compartment. The compartments are defined in Fig. 1.
The y axis of the graphs represents the concentration in each compartment. The compartments are defined in Fig. 1.
FIGURE 8.
Compartmentalization analysis where the postsynaptic distribution is compared to the uniform distribution. Blue curves represents the data for PSD, whereas the red curves are for UD. As predicted, no significant change is noticed when no push is applied for both distributions of b, although a significant difference appears in the first compartment, a1.
In Fig. 7 a1, the two curves evolve similarly for 180 ms (the first period). Due to large fluctuations, the end of this period is not well defined in the UD case. But in Fig. 7 b3, at 200 ms, the fluctuations undergo a transition that reflects the transition between periods. A comparison with Fig. 7 a3 reveals that the transition is different in the UD and PSD cases. In the UD case, there is a deterministic decay of the number of ions before the transition occurs, whereas in the PSD case, the transition is not preceded by a deterministic decay. Finally, by comparing Fig. 7 a4 with its part b4, it appears that the arrival distribution of ions in the fourth part in the UD case is more spread in the first period than that in the PSD case, where the distribution seems more concentrated. After the first period, there is no distinction between the two.
DISCUSSION
How spine motility affects calcium dynamics
In this work, we have developed a model of calcium dynamics based on a Langevin description. This approach allows us to study calcium dynamics from a single to a continuum number of ions and enables us to follow any ion trajectory at any time. To compute the time evolution of spine calcium concentration, we have proposed, at a molecular level, a mathematical model of all the elements that are relevant to the mechanics of moving calcium ions through a dendritic spine. Our approach gives a new explanation to the time decay law of calcium in dendritic spines.
We have shown that the rapid spine movement produces fast clearance of calcium from the dendritic spine and directs it at a specific location between the neck and the dendritic shaft. The main conclusion of the article concerns the quantification of the effect of the hydrodynamic push on calcium dynamics in the spine. In particular, we have shown that not only the push effect is created by the calcium ions, but that the push targets the same calcium ions toward the middle of the spine, where the spine apparatus and relevant proteins are located. The flow due to the push does not allow the calcium ions to stay inside the spine head and to return to the head, once they are inside the neck. The drift increases the efficiency of calcium conduction from the synapse to the dendrite and speeds up the calcium clearance of the spine. The simulation shows that in the absence of the drift effect, the proportion of calcium ions conducted to the dendrite is 2–3 times smaller in the first 100 ms than in its presence.
Relationship to experiments
Recently Majewska et al. (2000) have found a double-exponential decay of the calcium concentration inside the spine. The two decays were reported to be the consequence of the saturation of some buffers, binding kinetics of endogenous buffers, diffusion of buffers, buffer calcium diffusion across the spine neck, and the effect of the pumps (Majewska et al., 2000). Our model also revealed the double-exponential decay of the calcium concentration inside the spine. However, this result found in Majewska et al. (2000) can be reinterpreted in the light of our model, as we have found that it is a consequence of the dynamics created by the push effect.
We observe that the decay, corresponding to a predominantly hydrodynamic effect, starts after the ions enter the spine head. This decay is rapid and its duration is random. It ends when hardly any contractive molecules are saturated. In the second period, ionic motion is mainly driven by pure diffusion and pump extrusion. By using a molecular model, it was possible to reproduce the number of bonds that the population of calcium ions forms when flowing through the spine. This number measures the efficiency of the interaction between the spine and the population of calcium ions. The number of bonds that are formed between calcium ions and proteins inside the spine is recovered in a simulation of the stochastic dynamics of calcium ions there.
For both time periods, the time course of calcium decays exponentially in time. For the second period, identified as purely driven by random movement, the time constant equals the first eigenvalue of the Laplacian on the spine domain, with the adequate boundary conditions. Therefore, this time constant depends mainly on the geometry. Along the spine axis, denoted by x, c(x, t) is the solution of the drift-diffusion equation
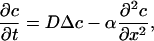 |
where α is the average velocity
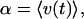 |
which is assumed constant. The solution c can be expressed as
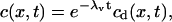 |
where cd(x, t) is the solution of a driftless diffusion equation, the time constant λv is given by
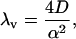 |
and D is the aqueous diffusion constant. To compute numerically some values of λv, we assume that the average velocity induced by the push is 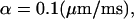 corresponding to a spine contraction of 0.1 μm in 1 ms, which is a rough experimental approximation. Then for D = 400 μm2 s−1 and 〈v0〉 = 0.1 s, we obtain λv = 0.16 s−1. This number matches the time constant λe found experimentally in Majewska et al. (2000), which is λe = 0.14 s−1.
corresponding to a spine contraction of 0.1 μm in 1 ms, which is a rough experimental approximation. Then for D = 400 μm2 s−1 and 〈v0〉 = 0.1 s, we obtain λv = 0.16 s−1. This number matches the time constant λe found experimentally in Majewska et al. (2000), which is λe = 0.14 s−1.
Calcium dynamics and plasticity
Dendritic spines are considered to be the privileged locus, where synaptic changes occur. For example, long-term potentiation starts when a certain number of CaMK-II have been activated by calmodulin (Lisman, 1994). Calmodulin in the active state binds four calcium ions. In spines, the number of CaMK-II is estimated to be low, ∼10. When the threshold of activation is achieved, the message that will finally lead to some biophysical changes is transmitted to the rest of the neuron. Calcium is the first messenger in this cascade, first binding calmodulin. In that particular context, the hydrodynamic effect studied here has two main consequences: the first one is to direct the calcium ions in the direction of the calmodulin; the second produces a coincidence of several bond calmodulin, increasing the probability of going over the threshold where CAM-KII is activated. The hydrodynamic effect makes more probable the induction of plasticity after calcium ions flow in.
Possible experiments and testable hypothesis on the role of fast spine motility in calcium dynamics
As predicted by the present model (Fig. 4), alteration of spine fast motility changes the time course of calcium ions. An uncaging method coupled with a two-photon imaging system should reveal calcium dynamics when spine motility has been pharmacologically blocked and the result should be compared to the predicted curves (Fig. 4). We also found that when spine motility is blocked, the number of bonds made by calcium ions is reduced by 30% (Figs. 5 and 6). As a consequence, the induction of various chemical pathways might be affected, especially if the induction threshold falls into this range. For example, an entry of calcium through NMDA receptors, and not through voltage-sensitive calcium channels (Emptage et al., 1999; Korkotian and Segal, 1998; Yuste et al., 2000) in the spine, induces calcium release from internal stores, producing a local change in the concentration. If the level of calcium entry is critical for such induction, by blocking spine motility, we predict that calcium release from calcium stores will be affected. This process is involved in global calcium regulation in the dendritic spine (Sabatini et al., 2001) and we predict a significant change of calcium concentration in an experiment where a backpropagation action potential is paired with a local excitation. In normal conditions, a supralinear calcium concentration inside the spine is observed (Yuste and Denk, 1995), whereas here, when the fast motility is blocked, we predict that the supralinear summation will be diminished or abolished. Such a result would confirm the role of spine motility in regulating a feedback calcium loop mechanism.
Another prediction of the model concerns the role of calcium dynamics in the induction of synaptic plasticity (Lisman, 1989; Malenka et al., 1989), probably initiated during the first hundreds of milliseconds in the first period (Majewska et al., 2000). If spine fast motility is entirely responsible for the time course of the first period of calcium dynamics, blocking spine fast motility will affect the induction of synaptic plasticity such as long-term depression or long-term potentiation. Therefore, to test this assumption, blocking spine fast motility will delay or abolish the induction of plasticity. However, these experiments still await the development of new specific drugs that will alter only the spine fast motility. Indeed, an alteration of actin-myosin will block nonspecifically too many molecular pathways in the cell.
Acknowledgments
We thank Nathalie Rouach and Menahem Segal for their comments and help during the preparation of this article.
D.H. thanks the Sloan and Swartz foundation for the financial support. Z.S. was partially supported by research grants from the Binational US-Israel Science Foundation and the Foundation for Basic Research, Israel Academy of Science.
References
- Alberts, B., D. Brays, J. Lewis, M. Raff, K. Roberts, and J. D. Watson. 1994. Molecular Biology of the Cell, 3rd ed. Garland Science Publishing, New York.
- Berry, R. S., S. A. Rice, and J. Ross. 2000. Physical Chemistry, 2nd Ed. Oxford University Press, New York.
- Bonhoeffer, T., and R. Yuste. 2002. Spine motility: phenomenology, mechanisms and function. Neuron. 35:1019–1027. [DOI] [PubMed] [Google Scholar]
- Chandrasekhar, S. 1954. Stochostic problems in physics and astronomy. Rev. Mod. Phys. 15:1–89. Also in N. Wax, 1954, Selected Papers on Noise and Stochastic Processes, Dover, NY.
- Crick, F. 1982. Do dendritic spines twitch? Trends Neurosci. 5:44–46. [Google Scholar]
- Emptage, N., T. V. Bliss, and A. Fine. 1999. Single synaptic events evoke NMDA receptor-mediated release of calcium from internal stores in hippocampal dendritic spines. Neuron. 22:115–124. [DOI] [PubMed] [Google Scholar]
- Franks, K. M., and T. J. Sejnowski. 2002. Complexity of calcium signaling in synaptic spines. Bioessays. 24:1130–1144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hänggi, P. H., P. Talkner, and M. Borkovec. 1990. Reaction-rate theory: fifty years after Kramers. Rev. Mod. Phys. 62:251. [Google Scholar]
- Kandel, E. R., J. H. Schwartz, and T. M. Jessel. 2001. Principles of Neural Science, 4th Ed. McGraw-Hill, NY.
- Karlin, S., and H. Taylor. 1977. A First Course in Stochastic Processes, 2nd Ed. Academic Press, New York.
- Koch, C. 1999. Biophysics of Computation. Oxford University Press, New York.
- Koch, C., and I. Segev. 1998. Methods in Neuronal Modeling, 3rd Ed. MIT Press, Cambridge, MA.
- Koch, C., and A. Zador. 1993. The function of dendritic spines: devices subserving biochemical rather than electrical compartmentalization. J. Neurosci. 13:413–422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korkotian, E., and M. Segal. 1998. Fast confocal imaging of calcium released from stores in dendritic spines. Eur. J. Neurosci. 10:2076–2084. [DOI] [PubMed] [Google Scholar]
- Korkotian, E., and M. Segal. 2001. Spike-associated fast twitches of dendritic spines in cultured hippocampal neurons. Neuron. 30:751–758. [DOI] [PubMed] [Google Scholar]
- Kramers, H. A. 1940. Brownian motion in a field of force. Physica. 7:284. [Google Scholar]
- Lisman, J. 1994. The CaM kinase II hypothesis for the storage of synaptic memory. Trends Neurosci. 10:406–412. [DOI] [PubMed] [Google Scholar]
- Lisman, J. 1989. A mechanism for the Hebb and the anti-Hebb processes underlying learning and memory. Proc. Natl. Acad. Sci. USA. 86:9574–9578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majewska, A., E. Brown, J. Ross, and R. Yuste. 2000. Mechanisms of calcium decay kinetics in hippocampal spines: role of spine calcium pumps and calcium diffusion through the spine neck in biochemical compartmentalization. J. Neurosci. 20:1722–1734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malenka, R. C., J. A. Kauer, D. J. Perkel, and R. A. Nicoll. 1989. The impact of postsynaptic calcium on synaptic transmission—its role in long-term potentiation. Trends Neurosci. 12:444–450. [DOI] [PubMed] [Google Scholar]
- Matkowsky, B. J., Z. Schuss, and E. A. Ben-Jacob. 1982. Singular perturbation approach to Kramers' diffusion problem. SIAM J. Appl. Math. 42:835–849. [Google Scholar]
- Morales, M., and E. Fifkova. 1989. Distribution of MAP2 in dendritic spines and its colocalization with actin. An immunogold electron-microscope study. Cell Tissue Res. 256:447–456. [DOI] [PubMed] [Google Scholar]
- Nadler, B., T. Naeh, and Z. Schuss. 2001. The stationary arrival process of independent diffusers from a continuum to an absorbing boundary is Poissonian. SIAM J. Appl. Math. 62:433–447. [Google Scholar]
- Nimchinsky, E. A., B. L. Sabatini, and K. Svoboda. 2002. Structure and function of dendritic spines. Annu. Rev. Physiol. 64:313–353. [DOI] [PubMed] [Google Scholar]
- Sabatini, B. L., M. Maravall, and K. Svoboda. 2001. Ca2+ signaling in dendritic spines. Curr. Opin. Neurobiol. 11:349–356. [DOI] [PubMed] [Google Scholar]
- Segev, I., and W. Rall. 1988. Computational study of an excitable dendritic spine. J. Neurophysiol. 60:499–523. [DOI] [PubMed] [Google Scholar]
- Shepherd, G. M. 1996. The dendritic spine: a multifunctional integrative unit. J. Neurophysiol. 75:2197–2210. [DOI] [PubMed] [Google Scholar]
- Volfovsky, N., H. Parnas, M. Segal, and E. Korkotian. 1999. Geometry of dendritic spines affects calcium dynamics in hippocampal neurons: theory and experiments. J. Neurophysiol. 82:450–454. [DOI] [PubMed] [Google Scholar]
- Yuste, R., and W. Denk. 1995. Dendritic spines as basic functional units of neuronal integration. Nature. 22:682–684. [DOI] [PubMed] [Google Scholar]
- Yuste, R., A. Majewska, and K. Holthoff. 2000. From form to function: calcium compartmentalization in dendritic spines. Nat. Neurosci. 3:653–659. [DOI] [PubMed] [Google Scholar]
- Zador, A., C. Koch, and T. H. Brown. 1990. Biophysical model of a Hebbian synapse. Proc. Natl. Acad. Sci. USA. 87:6718–6722. [DOI] [PMC free article] [PubMed] [Google Scholar]