The Influence of Short-Chain Alcohols on Interfacial Tension, Mechanical Properties, Area/Molecule, and Permeability of Fluid Lipid Bilayers

Abstract

We used micropipette aspiration to directly measure the area compressibility modulus, bending modulus, lysis tension, lysis strain, and area expansion of fluid phase 1-stearoyl, 2-oleoyl phosphatidylcholine (SOPC) lipid bilayers exposed to aqueous solutions of short-chain alcohols at alcohol concentrations ranging from 0.1 to 9.8 M. The order of effectiveness in decreasing mechanical properties and increasing area per molecule was butanol>propanol>ethanol>methanol, although the lysis strain was invariant to alcohol chain-length. Quantitatively, the trend in area compressibility modulus follows Traube's rule of interfacial tension reduction, i.e., for each additional alcohol CH₂ group, the concentration required to reach the same area compressibility modulus was reduced roughly by a factor of 3. We convert our area compressibility data into interfacial tension values to: confirm that Traube's rule is followed for bilayers; show that alcohols decrease the interfacial tension of bilayer-water interfaces less effectively than oil-water interfaces; determine the partition coefficients and standard Gibbs adsorption energy per CH₂ group for adsorption of alcohol into the lipid headgroup region; and predict the increase in area per headgroup as well as the critical radius and line tension of a membrane pore for each concentration and chain-length of alcohol. The area expansion predictions were confirmed by direct measurements of the area expansion of vesicles exposed to flowing alcohol solutions. These measurements were fitted to a membrane kinetic model to find membrane permeability coefficients of short-chain alcohols. Taken together, the evidence presented here supports a view that alcohol partitioning into the bilayer headgroup region, with enhanced partitioning as the chain-length of the alcohol increases, results in chain-length-dependent interfacial tension reduction with concomitant chain-length-dependent reduction in mechanical moduli and membrane thickness.

INTRODUCTION

The interaction of short-chain alcohols with biological membranes forms an important area of exploration because of the role of alcohols in metabolism, membrane fusion, drug delivery, alcohol toxicity, alcohol tolerance, and general anesthesia. Of particular interest is fundamental understanding of the molecular mechanism of action of short-chain alcohols on the lipid portions of biomembranes. To this end, model systems of known lipid composition such as unilamellar vesicles or supported bilayers have served as ideal platforms to elucidate the details of the effect of short-chain alcohols on the physical and thermodynamic properties of lipid membranes.

The emerging paradigm is that short-chain alcohols (given their amphiphilic nature) primarily confine themselves to the hydrophilic headgroup region instead of the hydrocarbon core as demonstrated by nuclear magnetic resonance (NMR; Barry and Gawrisch, 1994), nuclear Overhauser effect spectroscopy (Feller et al., 2002; Holte and Gawrisch, 1997), fluorescence spectroscopy (Rottenberg, 1992), and Fourier-transform infrared studies (Chiou et al., 1992). Their location in the headgroup region disturbs the natural microstructure of the lipid membrane and is apparently responsible for observed increases in membrane fluidity or disorder (Chin and Goldstein, 1977), increases in the membrane lipid lateral mobility (Chen et al., 1996), decreases in the main phase transition temperature (Rowe, 1985), and the formation of an interdigitated gel phase (Slater and Huang, 1988). Past works have also shown that alcohols increase membrane permeability (Komatsu and Okada, 1995, 1997), induce shape transformations of vesicles (Angelova et al., 1999), and influence membrane thermodynamic parameters (Rowe et al., 1998; Trandum et al., 2000; Westh and Trandum, 1999; Westh et al., 2001). Other important physical properties that short-chain alcohols may affect, but which need exploring, are mechanical properties and thickness, which are closely tied to integral membrane protein activities and cell shape. A close relationship between mechanical stress and activities in membrane-embedded proteins has been established with mechanical sensitive ion channels (Sukharev et al., 1997), gramicidin (Goulian et al., 1998), and the meta-I to meta-II transition in rhodopsin (Mitchell and Litman, 1999, 2000). Theoretical works exist relating the structure, function, and surface arrangement of membrane-bounded proteins and enzymes to membrane mechanics and thickness (Cantor 1997a,b; Dan et al., 1994; Dan and Safran, 1998). Shape and stability of cells and liposomes are regulated by mechanics as demonstrated by observed shape deformations of erythrocytes (Evans, 1989) and neutrophils (Tsai et al., 1993) and vesicle budding-fission-fusion events involved in vesicle-mediated material transport (Sackmann, 1994). Certainly, a quantification of the perturbation of these mechanical properties and thickness by short-chain alcohols would be relevant in understanding the general mechanisms behind alcohol's adverse action on biological functions.

Until recently, quantitative studies of the effect of alcohol on membrane mechanics and thickness of fluid-phase membranes were unconsidered in literature. We have recently reported how ethanol can modify the mechanical properties and decrease the membrane thickness (from measuring the area expansion of fluid-phase lipid vesicles with the inherent assumption that lipid chain volume is conserved; Ly et al., 2002). Motivated by this earlier study, we now explore a homologous series of n-alcohols from methanol to butanol to understand the role of acyl chain-length on membrane mechanics and thickness. As before, we applied the micropipette aspiration technique, pioneered by Evans and Needham (for general reviews of the technique see Needham and Zhelev, 1996, 2000), to directly measure these mechanical properties (bending modulus, area compressibility modulus, lysis tension, and lysis strain) and area expansion of individual giant unilamellar vesicles (GUVs) in a series of alcohol/water mixtures over a range of concentrations (∼0.1 to 9.8 M). We chose 1-stearoyl-2-oleoyl-phosphatidylcholine (SOPC) mixed with a minute amount of 1-stearoyl-2-oleoyl-phosphatidylserine (SOPS) as our model membrane because of its similarities to the natural fluidity and thickness of biological membranes. Although each alcohol in our series differs from its neighbor by one CH₂ group, we observed quantifiable variations in mechanical properties and area expansion of SOPC membranes exposed to aqueous solutions containing methanol through butanol. We relate this effect to lowering of interfacial tension by showing that the area compressibility data follows Traube's Rule, which predicts that for each CH₂ group in an alcohol molecule, three-times-lower alcohol concentration will be required to reach the same interfacial tension between a hydrophobic and water/alcohol solution (Traube, 1891). We then convert area compressibility to interfacial tension to verify and show for the first time that bilayers adhere to Traube's rule, determine partitioning and Gibbs free energy of adsorption of each alcohol into the lipid headgroup region, and predict the increase in the area per headgroup and decrease in line tension of a membrane pore due to interfacial tension reduction by each alcohol (methanol through butanol). Previous to this work, the partitioning and Gibbs energy values had not been determined in this way. We used flow-pipette experiments to directly measure the increase in area per headgroup and membrane permeability for bilayers exposed to short-chain alcohols. We believe that this is the first measurement of short-chain alcohol permeability of a model membrane. Finally, we relate line tension reduction (determined by interfacial tension reduction) to the observed lowered breaking strength (lysis tension) of the membrane.

EXPERIMENTAL PROCEDURE

Materials

SOPC and SOPS were purchased in chloroform from Avanti Polar Lipids (Alabaster, AL) and used without further purification. Ethanol (200 Proof) was bought from Gold Shield Chemical (Hayward, CA). Methanol, 1-propanol, and 1-butanol, sucrose, and glucose of high grade were bought from Sigma-Aldrich (St. Louis, MO). Chloroform was purchased from Fisher Scientific (Fairlawn, NJ). Bovine serum albumin (fraction V, low heavy metals) was purchased from Calbiochem (San Diego, CA). Deionized water used was produced by a Barnstead nanopure water system (Dubuque, IA) and had a resistivity of 18.1 MΩ/cm.

Giant vesicle preparation

Our electroformation protocol to grow GUVs of SOPC and SOPS (99.5:0.5 mol %) is similar in nature to other practitioners of this technique (Angelova et al., 1992; Shoemaker and Vanderlick, 2003). We began with painting 50 μl of an SOPC and SOPS (99.5:0.5 mol %) solution in chloroform/methanol (2:1 volume ratio, 0.5 mg/ml) evenly on two parallel platinum wires (diameter 1 mm) held 3 mm apart in an open-center Teflon block. We used a slow-flowing nitrogen stream to quickly evaporate the solvent from the wires, and afterward placed the block under vacuum for at least 2 h to remove any trace solvent. We sealed the open center on both sides with SurfaSil-coated (Pierce, Rockford, IL) coverslips with vacuum grease. We used a side opening on the block to fill the open volume slowly with 100 mM sucrose and applied an AC field (3 volts peak-to-peak) across the wire at 10 Hz for 30 min, 3 Hz for 15 min, 1 Hz for 7 min, and 0.5 Hz for 7 min. GUVs formed on the electrodes, and we gently harvested and used them within a few days.

Micropipette aspiration setup

Our micropipette aspiration setup included an inverted Nikon Diaphot 300 microscope (Nikon, Melville, NY) equipped with a 40× Hoffman modulation contrast objective (Modulation Optics, Greenvale, NY), a high resolution charge-coupled device camera (Dage MTI, Michigan City, IN), a manometer slider with linear encoder (Velmex, Bloomfield, NY), a video overlay box (Polvision, Western Australia), and an S-VHS recorder (Sony SVO-9500MD). Pressure readings from the slider were overlayed onto vesicle images. We controlled the position of the micropipette with a micromanipulator (model MHW-3, Narishige, Japan). Micropipettes were made from pulling capillary glass tubings (Fredrick and Dimmock, Millville, NJ) into thin tapered shafts with a glass puller (David Kopf Instruments, Tujunga, CA). We fractured the tips flat with inner diameters of 6–8 μm with a microforge (Stoelting, Wood Dale, IL) and then coated the tips with SurfaSil (Pierce) to passivate the surface. We filled the pipettes with 100 mM glucose, 0.02% total wt. albumin solution. Albumin was necessary to reduce static charge buildup on the glass surfaces that could prematurely lyse the vesicles.

The sample chamber, used to house the vesicles in alcohol/water mixtures, was constructed out of two Surfasil-coated microscope slides separated by two small rectangular Plexiglas spacers. We filled the ∼1-ml cavity with an alcohol/water mixture containing ≤105 mM glucose. Alcohol and the osmotic imbalance (between the exterior glucose and interior sucrose concentrations) can change the surface area/volume of the vesicles. We desired slightly deflated vesicles for aspiration so less glucose (105–70 mM) was included in the alcohol/water mixtures as the alcohol concentration increased from 0 to 10 M. We added 10 μl solution of electroformed vesicles enclosing 100 mM sucrose into the chamber. On the timescale that we waited to start aspiration of a vesicle, >5 min, the alcohol concentration outside the vesicle had equilibrated with the concentration inside the vesicle, as will be shown in the results. We easily found vesicles lying on the bottom of the chamber due to the density difference between sucrose and glucose. We inserted an aspiration pipette into one of the open sides of the chamber and a flow pipette into the other when we were conducting flow experiments. Evaporation during the experiments was virtually eliminated by enclosing the sample chamber in a modified petri dish containing a thin layer of an alcohol/water mixture with small openings for pipettes and a viewing port for the objective.

Micropipette aspiration experiments

We performed the micropipette aspiration technique to measure the mechanical properties of vesicles in alcohol/water mixtures at room temperature. We aspirated individual vesicles inside a glass micropipette, and the applied suction pressure, ΔP, was related to the induced isotropic membrane tension, τ, as follows (Evans and Needham, 1987),

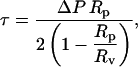(1)

where R_p is the radius of the pipette and R_v is the radius of the vesicle. As we increased the suction pressure, the projection length, L, increased (Fig. 1). The change in projection length, ΔL, is related to the observed or apparent area strain, α, where α = (A−A_o)/A_o, with A_o being the membrane area of the vesicle measured at an initial low tension state and A being the membrane area after pressurization to a higher tension state. Through simple geometric arguments, the relationship reduces to (Evans and Needham, 1987)

(2)

FIGURE 1.

Video micrographs of an SOPC vesicle aspirated inside a micropipette in an aqueous bathing solution without alcohol. An increase, ΔL, in projection length, L, is observed when the applied membrane tension, τ, is increased from (A) 0.3 mN/m to (B) 3.4 mN/m. (C) When the same vesicle, held at 0.3 mN/m, is exposed to a flowing stream of an alcohol/water solution of the same osmolarity as the aqueous bathing solution, an increase, ΔL, in projection length, L, is observed. The transmembrane exchange scheme of alcohol from a flow pipette to a vesicle is shown. The value C_out denotes alcohol concentration inside the flow pipette; C_ads is the total surface density of adsorbed alcohol molecules in the membrane; C_in denotes the alcohol concentration inside the vesicle; and k_on and k_off are the rate constants for adsorption and desorption, respectively.

For aspiration, we chose vesicles with diameters between 20 and 40 μm that were slightly deflated. The excess membrane area aided in forming a small visible projection inside the pipette at an initial low tension. In all experiments, vesicles were prestressed beyond 1 mN/m for 1–2 s to smooth out any folds or tethers in the membrane and relaxed back to a desired low tension. We increased the suction pressures in a stepwise manner and waited ∼5 s after each step to provide good images for later analysis. For convenience, we performed separate micropipette aspiration experiments in the low and high tension regimes although at times we did aspirate vesicles through the full range. We aspirated vesicles from 0.001 to 0.5 mN/m to determine their bending moduli and aspirated other vesicles from 0.5 mN/m until rupture to determine their area compressibility moduli, lysis tensions, and lysis strains at rupture. We video-recorded the aspiration experiments onto tapes and afterward measured the diameters of the vesicles, the projection lengths, and applied pressures with image analysis software (ATI Multimedia Center, Marlborough, MA). We applied the equations discussed below to determine the mechanical properties.

The mechanics of thin materials show that increases in α comes from two modes of deformations of a vesicle under aspiration (Evans and Rawicz, 1990; Rawicz et al., 2000),

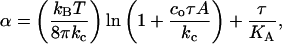(3)

where A is the membrane area, k_c is the bending modulus, K_A is the direct area compressibility modulus, k_B is the Boltzmann's constant, T is absolute temperature, and c_o is a constant (∼0.1) that depends on the type of modes (spherical harmonics or plane waves) used to describe surface undulations. Thermal shape undulations of flaccid vesicles are readily seen under a microscope, and the first term represents the smoothing out of these bending undulations. The second term represents direct stretching of the area per lipid molecule. We ignore any contribution in α from enhanced partitioning of molecules into the membrane as tension increases. A thermodynamic analysis of alcohol partitioning (presented in the Appendix) shows that the increase in surface density of alcohol molecules in the membrane is small and would have negligible effect on the strain during the mechanical pressurization of vesicles until failure.

Experimentally, we calculated the bending modulus from plotting ln(τ) versus α in the tension range of 0.001 to 0.5 mN/m. Presented in Fig. 2 is a typical plot of natural log tension-strain behavior of SOPC vesicles in a 7.4 M methanol/water mixture. In this low tension regime, the logarithmic term dominates and shows that almost all increases in α come from smoothing out thermal undulations, and the bending modulus is simply the product of the slope and k_bT/8π.

FIGURE 2.

Tension-strain measurements for an SOPC vesicle in a 7.4 M methanol/water solution. The points (circles in left curve) from plotting the natural log of the tension, τ, against area strain, α, is linear in the low-tension regime (0.001–0.5 mN/m). The same points (circles in right curve) plotted with τ against α is nearly linear in the high-tension regime (>0.5 mN/m). Subtracting out contribution from smoothing out subvisible thermal shape undulations from α in the high tension regime gives the direct area strain, α_dir, and the replotted points (squares) shifts the line to the left.

We calculated the area compressibility modulus by plotting τ versus α in the high tension regime (τ > 0.5 mN/m). In this regime, the linear term, τ/K_A, dominates as illustrated in Fig. 2 for a vesicle in a 7.4 M methanol/water mixture. By convention, the slope is known as the apparent area compressibility modulus, K_app (Rawicz et al., 2000). This modulus includes a small contribution from the logarithmic term because even at the highest tension, subvisible thermal undulations persist. We determined the direct area compressibility modulus, K_A, by subtracting the logarithmic contribution from α to get the direct area strain, α_dir. The appropriate contribution, Δα(i), for each i^th value of α that we subtracted out is (Rawicz et al., 2000)

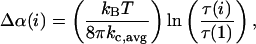(4)

where k_c,avg is the average bending modulus and τ(1) is the initial low tension state, usually experimentally set at ∼1 mN/m. K_A is the revised slope from plotting τ versus α_dir (square points in Fig. 2). In some cases where measured values of k_c,avg were unavailable, we used linear interpolated values, but we note that varying the bending modulus at ∼±20% generally changed the average K_A values by ±5%.

In the micropipette aspiration experiments, we subjected vesicles to a range of incremental alcohol concentrations where significant effects on the bending and area compressibility moduli could be observed. Alcohol concentrations were experimentally measured in volume percentages, but they are presented here in molar concentrations to compare correctly the mechanical properties of SOPC membranes as a function of alcohol chain-length. For the bending modulus experiments, the concentrations (M) and number of experiments performed at each concentration (in parentheses) were: 0 (32), 2.47 (9), 4.94 (7), and 7.41 (11) for methanol; 1.70 (6) and 3.41 (12) for ethanol; 0.39 (6), 0.78 (14), and 1.30 (12) for propanol; and 0.22 (11) and 0.55 (10) for butanol. For the area compressibility modulus experiments, the concentrations (M) and number of experiments performed at each concentration (in parentheses) were: 0 (42), 2.47 (16), 4.94 (15), 7.41 (17), and 9.88 (12) for methanol; 1.70 (10), 2.56 (11), and 3.41 (17) for ethanol; 0.19 (10), 0.39 (10), 0.78 (19), and 1.30 (19) for propanol; and 0.11 (12), 0.33 (13), and 0.55 (6) for butanol.

Flow-membrane area expansion experiments

We performed flow experiments to measure membrane area expansion of vesicles caused from alcohol exposure. We aspirated individual vesicles into a micropipette (7–9 μm in diameter) at a low tension of ∼1 mN/m in a 105 mM glucose mixture. Afterward, we placed a flow pipette (100–150 μm in diameter) directly in front of the aspirated vesicle (see Fig. 1 C) to deliver a constant flow of 105 mM glucose, alcohol/water mixture around the vesicle. We video-recorded the dynamic growth of the projection length until the projection length reached a plateau, the projection broke away from the vesicle, or the vesicle collapsed. We subsequently analyzed the tapes to convert the dynamic growth, ΔL, of the projection length into an apparent area expansion, (ΔA/A_o)_exp, where (ΔA/A_o)_exp = (A–A_o)/A_o, with A_o being the initial surface area of the vesicle before alcohol exposure and A being the surface area after exposure. Values for (ΔA/A_o)_exp are determined through Eq. 2. For vesicles with stable projection growth, we only observed changes in the projection length for (ΔA/A_o)_exp values up to 0.15, and the radius of the outer portion of the vesicle remained relatively unchanged within a resolution limit of ∼0.5 μm.

We made the flow pipettes from drawing capillary glass tubings into constant diameter shafts with the glass puller. We fractured the pipettes for diameters between 100 and 150 μm with the microforge, and the tips were coated with SurfaSil. The flow pipette was connected directly to a syringe with plastic tubing and filled with the desired alcohol/water mixtures. We set the syringe pump (KD Scientific Model 200, New Hope, PA) to drive the flow at a constant velocity of ∼450 μm/s. The flow velocity was measured by observing polystyrene microspheres (Polysciences; ∼3 μm in diameter) flowing out of the pipette.

RESULTS

Methanol, ethanol, and propanol are miscible in water in all proportions whereas butanol has a limited solubility of ∼1 M (Brown et al., 2000; Raina et al., 2001b). For all experiments, the maximum alcohol concentration we used for methanol, ethanol, propanol, and butanol were 9.8 M, 3.4 M, 1.3 M, and 0.55 M, respectively. Below this limit, SOPC vesicles in these alcohol/water mixtures were sufficiently stable for micropipette aspiration. Although alcohols can increase the permeability of the membrane to solutes (Ingram, 1990; Mansure et al., 1994), we did not observe any appearances of swollen or ghost vesicles in alcohol/water mixtures during the experimental timescale of a few hours, meaning that no significant amount of glucose or sucrose transferred across the membrane. (Swollen vesicles would be seen if glucose permeated into the vesicle's interior, concomitantly with water. Ghost vesicles are semitransparent due to the loss index of refraction from mixing of exterior glucose and interior sucrose.)

Bending and area compressibility moduli measurements

Presented in Fig. 3 are the bending moduli obtained for the membranes of SOPC vesicles in alcohol/water/glucose mixtures using micropipette aspiration. There is an obvious dependence on acyl chain-length and concentration of alcohol. This is evident by the separation between the curves and the initial steepness in the curves, respectively. For a given concentration, butanol decreased the bending modulus the most followed by the other alcohols in sequence. The average k_c value decreased from ∼0.8 × 10⁻¹⁹ J to ∼0.4 × 10⁻¹⁹ J (a 50% reduction) as the alcohol concentration reached the high limit in our studied concentration range. Our bending modulus results qualitatively agree with the works of Safinya et al. (1989), who demonstrated that the bending modulus of fluid-phase dimyristoylphosphatidylcholine (DMPC) decreased upon addition of pentanol.

FIGURE 3.

Average bending modulus, k_c, values of SOPC vesicles in alcohol/water mixtures: methanol (diamonds), ethanol (squares), propanol (triangles), and butanol (circles). Bars indicate 1 SD. Differences between control and alcohol-exposed vesicles were statistically significant (P < 0.05) as evaluated by Student's t-test (α = 0.05) except for values at 1.70 M of ethanol and 0.39 M of propanol.

Fig. 4 contains plots of ln(τ) versus α for individual vesicles in four alcohol/water mixtures in the low tension regime of 0.001–0.5 mN/m with individual A_o values set at ∼0.001 mN/m. We chose data in which the bending modulus of each line is representative of the population average value found in Fig. 3. As we demonstrated previously with ethanol, we generally observe that ln(τ) is linearly proportional to α until a crossover tension of ∼0.5 mN/m for all four alcohols. The linearity indicates that the bending modulus and alcohol interactions with the membrane are independent of the amount of membrane fluctuations that were smoothed out in this low tension regime.

FIGURE 4.

Natural log tension, τ, versus apparent area strain, α, plotted for individual SOPC vesicles in various alcohol/water mixtures near the high concentration limit: 7.4 M methanol (diamonds), 3.4 M ethanol (squares), 1.3 M propanol (triangles), and 0.55 M butanol (circles). For clarity, the propanol and butanol curves are slightly displaced from their y-intercepts of −5.8 and −5.6, respectively.

Presented in Fig. 5 are the apparent and true area compressibility moduli values (K_app and K_A) obtained for the membranes of SOPC vesicles in alcohol/water/glucose mixtures using micropipette aspiration. Obtained from the raw data (Fig. 7), K_app represents both direct stretching and the smoothing of bending fluctuations whereas K_A only includes direct stretching of the bilayer. For both of these quantities, there are obvious dependences on acyl chain-length and concentration of the alcohol. For all four alcohols, the average values of K_app decreased from 200 mN/m to ∼100 mN/m (a 50% reduction) and average values of K_A decreased from 230 mN/m to 150 mN/m or less (a 35% reduction) as alcohol concentration reached the high limit. Independent of alcohol type, we observed the difference between K_A and K_app slightly widens as the alcohol concentration increases. This reflects the significant role of the logarithmic term in Eq. 3 as the magnitude of the bending modulus decreases with increasing alcohol concentration. Since K_app and K_A are dependent mechanical properties, we expect all points in Fig. 5 to collapse on the same curve if we plot K_A versus K_app, regardless of which alcohol interacts with the SOPC membrane. This is evident in Fig. 6, and it demonstrates the accuracy and reproducibility of our mechanical measurements.

FIGURE 5.

Average area compressibility modulus, K_A (solid marks) and K_app (open marks), of SOPC vesicles in alcohol/water mixtures. Symbols are methanol (diamonds), ethanol (squares), propanol (triangles), and butanol (circles). Bar indicates 1 SD. For clarity, only one representative error bar of all the measurements is shown (all error bars were equal or less than this one). Differences between control and alcohol-exposed vesicles were statistically significant (P < 0.05) as evaluated by Student's t-test (α = 0.05).

FIGURE 7.

Tension, τ, versus apparent area strain, α, of individual SOPC vesicles in four alcohol/water mixtures near the high limit: 7.4 M methanol (diamonds), 3.4 M ethanol (squares), 1.3 M propanol (triangles), and 0.55 butanol (circles). For clarity, the curves are slightly displaced apart.

FIGURE 6.

Correlation between K_A and K_app values from Fig. 5 at various alcohol/water mixtures: methanol (diamonds), ethanol (squares), propanol (triangles), and butanol (circles).

From the area compressibility data in Fig. 5, it can be seen easily that at any particular K_A value, the concentration of alcohol required to reach that K_A value was reduced by approximately a factor of 3 for each additional CH₂ group. For example, at a K_A value of ∼140 mN/m, the concentrations (M) for methanol, ethanol, propanol, and butanol are 9.88, 3.41, 0.78, and 0.3, respectively. Interestingly, this finding agrees with Traube's rule, a general rule for the expected interfacial energy of a hydrophobic-water/alcohol interface due to alcohol adsorption at the interface (Traube, 1891)—a point that we will discuss in detail in the next section.

Fig. 7 contains plots of τ versus α for individual vesicles in four alcohol/water/glucose mixtures in the high tension regime (τ > 0.5 mN/m) with individual A_o values set at ∼0.5 mN/m. We chose data in which the area compressibility modulus of each line is representative of the population average value found in Fig. 5. The τ versus α for individual vesicles is linear in the high tension regime up to the rupture tension for all four alcohols (see Fig. 7) and is still linear when subvisible thermal undulations were removed from α (data not shown). The linearity indicates that the area compressibility modulus is constant up to the lysis strain of ∼0.04, and within this range of areal strain, the alcohol concentration in the membrane remains relatively unchanged as the membrane is being laterally stretched (as expected from the discussion in the Appendix). The linearity we observed for strains up to 0.04 for all the surface-active alcohols qualitatively agrees with the work of Santore et al. (2002), who showed that surfactant (Pluronic L31) binding to unilamellar polymeric (OE7) vesicles exhibited a linear behavior for strains up to 0.05. However, polymeric vesicles are more stretchable than lipid membranes, and they showed that nonlinearity occurred for strains between 0.05 and 0.20, possibly due to significant exposure of the hydrophobic membrane core and subsequent enhanced adsorption capacity for surfactant molecules.

Flow experiments to observe bilayer area expansion

When aspirated vesicles in an aqueous solution without alcohol were exposed to an alcohol/water/glucose mixture (by a flow pipette), we generally observed that the projection quickly increased within <1 min. The change in projection length, ΔL, was converted to an area expansion, (ΔA/A_o)_exp, where the increase in membrane area from flow is normalized by the initial membrane area without flow (through Eq. 2).

Fig. 8 shows example time evolutions of the increase and decrease in (ΔA/A_o)_exp for SOPC membranes exposed to (and removed from) a flowing stream of methanol, propanol, and butanol. For all alcohol/water mixtures, the major increase and decrease in (ΔA/A_o)_exp occurred within <30 s and the process was reversible.

FIGURE 8.

Single vesicles, weakly aspirated inside a micropipette at ∼1 mN/m in an alcohol-free solution, were exposed to a flow pipette (∼100 μm in diameter) that delivered a constant alcohol/water mixture stream of the same osmolarity as the alcohol-free solution at desired alcohol concentration. The time course of vesicle membrane expansion was tracked and analyzed to obtain the equilibrium expansion and apparent permeability coefficient of alcohol transport across the membrane. The removal of the flow pipette results in membrane retraction, showing the reversible dynamics of alcohol transport across the membrane. Symbols are 4.9 M methanol (diamonds), 0.39 M propanol (triangles), and 0.11 M butanol (circles).

For (ΔA/A_o)_exp below 0.05, we generally observed that the projections reached stable plateaus, indicating that the internal alcohol concentration had equilibrated with the exterior flow alcohol concentration. For (ΔA/A_o)_exp between 0.05 and 0.15, some projections reached stable plateaus whereas others broke away from the vesicle or the vesicle collapsed or flew away. For (ΔA/A_o)_exp above 0.15, we generally did not observe any stable projection growth. These observations show that as the membrane expands rapidly beyond 0.05, there is a higher probability that the projection will pinch and break away from the main body of the vesicle. For vesicles with projections that reach plateaus, we never observed any retraction of the projections. This shows that short-chain alcohols, within the experimental range of concentrations, did not induce membrane pores large enough for external glucose to filter into the vesicle's interior with a co-transport of water. If pores were to form, we would observe vesicle swelling and a retraction of the projection as seen in the works of Longo et al. (1998, 1997) with virus fusion peptide and works of Needham and Zhelev (1995) with lysolipid.

When aspirated vesicles in an aqueous solution without alcohol were exposed to a flow of the same solution, we expected the projection length to remain constant. However, we observed that the projection grew slightly, and the growth appeared proportional with flow velocities between 100 to 500 μm/s. When the flow was removed, the projection returned to its original position. With the flow set at 450 μm/s, a positive applied pressure of 330 ± 18 Pa (or an effective τ of −0.88 ± 0.07 mN/m) was required to cause the projection to return to its original position. Presently we do not know the cause behind the growth and attribute it to general flow effects. We have ruled out folds or small tethers incorporating into the membrane of the aspirated vesicle because we prestressed vesicles above 2 mN/m for 1–2 s and relaxed them to a holding tension of ∼1 mN/m to remove such entities. We have also ruled out flow pressure because the pressure drop across the vesicle for flow around a sphere at low Reynolds number is negligible, <30 Pa (or an effective τ-value below 0.05 mN/m) for the flow velocities we were utilizing. For all the experimental data we present here, we settled on a fast flow velocity of 450 μm/s (much higher than what we used in our previous work on ethanol) to ensure that the local alcohol concentration on the surface of the vesicles was uniform and of similar concentration as in the flow pipette. At this velocity, the flow-induced projection growth was typically small and corresponded to a spike of (ΔA/A_o)_exp of 0.022 ± 0.005 within 1 or 2 s of exposure.

Lysis tension and lysis strain

Presented in Fig. 9, A and B, are the direct lysis area strain, α_dir-lyse, and lysis tension, τ_lyse, of membranes of SOPC vesicles in alcohol/water/glucose mixtures using micropipette aspiration at a fairly fast 0.1 mN/m/s tension ramp. The value τ_lyse is the tensile strength of the membrane at the point of rupture. The apparent lysis strain, α_lyse, is the corresponding fractional increase in membrane area at rupture. The value α_dir-lyse was obtained by subtracting the contribution due to smoothing of thermal shape undulations, Δα(i), from α_lyse using Eq. 4. Hence, α_dir-lyse accounts for direct lateral stretching of the area per lipid molecules in the membrane before membrane failure. The value α_dir-lyse in Fig. 9 A has no clear dependence on acyl chain-length or alcohol concentration, and the value averages ∼0.036 ± 0.006. Fig. 9 A generally shows that the SOPC membrane cannot be stretched beyond 0.05, consistent with previous findings (Evans and Needham, 1987). Consequently, the K_A values dictate the τ_lyse values since τ_lyse is given by K_Aα_dir-lys. Therefore, τ_lys and K_A show the same downward trends as acyl chain-length and concentration of alcohol are increased as evidenced by the striking similarity between Fig. 5 and Fig. 9 B. The τ_lys values are decreased by as much as 50%, once again demonstrating the severe membrane destabilization effect of alcohol.

FIGURE 9.

(A) Average direct lysis area strain, α_dir-lyse, of SOPC vesicles in alcohol/water mixtures obtained after subtracting out from the apparent lysis area strain, α_lyse, the area increases due to smoothing out thermal shape undulations. Differences between control and alcohol-exposed vesicles were statistically significant (P < 0.05) as evaluated by Student's t-test (α = 0.05) except for values at 2.47 M of methanol, 1.30 M of propanol, 0.33 M, and 0.55 M of butanol. (B) Average lysis tension, τ_lyse, values of SOPC vesicles in alcohol/water mixtures. Differences between control and alcohol-exposed vesicles were statistically significant (P < 0.05) as evaluated by Student's t-test (α = 0.05), except for values at 2.47 M and 4.94 M of methanol and 0.11 M of butanol. Symbols are methanol (diamonds), ethanol (squares), propanol (triangles), and butanol (circles). Values are based on 10 vesicles or more. Bars indicate 1 SD.

DISCUSSION

Bilayer interfacial tension, area per headgroup, and membrane thickness

The mechanical aspiration results presented in this study show, via decreases in the bending and area compressibility moduli, that less work is required to smooth out thermal undulations or stretch the area per lipid of a bilayer in an alcohol/water mixture compared to water alone. Certainly, this reflects a change in the intermolecular forces between the lipid membrane and water phase, or stated another way, an alcohol-induced decrease in the interfacial tension of each leaflet of the bilayer where this decrease is a net result of the alcohol's interactions with the membrane, the water's interactions with the membrane, and the alcohol's interactions with water. As noted elsewhere (Jaehnig, 1996; Roux, 1996), the interfacial tension of a bilayer is not an experimentally obtainable quantity, but we previously demonstrated with our work on ethanol that simple theoretical models can be applied to estimate interfacial tension, γ, of a bilayer from the elasticity measurements (Ly et al., 2002). It is worth noting here that no complete theory exists that relates the interfacial tension of a bilayer to its mechanical properties. Rawicz et al. (2000) proposed γ = K_A/6 by modeling a lipid monolayer as an idealized polymer brush where the surface pressure in each monolayer depends on the free energy of chain extension. The well-known Israelachvili-Mitchel-Ninham (IMN) model (Israelachvili et al., 1980) predicted γ = K_A/4, from balancing the attractive interfacial tension of a lipid monolayer with a repulsive term dominated by steric interactions, hydration forces, and electrostatics. Both models show that γ in each monolayer and K_A are related by a constant factor, either 4 or 6. The limitations of the idealized polymer brush in approximating the free energy of chain extension as a Gaussian-harmonic and ignoring interactions from the headgroup, interface, and chemical variations in lipid types have been carefully discussed by Rawicz et al. (2000). Despite these limitations, the model has given useful insights into the origins of bilayer elasticity and thickness, and it has correctly predicted the surface pressure-area isotherm measured for an SOPC monolayer, as well as the area/headgroup of an SOPC molecule in a bilayer. From our elasticity measurements of SOPC membranes in water, the Rawicz's model gives an estimated γ-value of 38 ± 3 mN/m, which predicts an SOPC headgroup area of 58 Ų ± 2 Ų (from a surface pressure-area isotherm which is discussed in more detail below in this section). This headgroup size is more consistent with the deuterium NMR measurement (Koenig et al., 1997) of 61.4 ± 0.2 Ų compared to the IMN estimate of a γ-value of 57 ± 4 mN/m that predicts a headgroup area of 51 Ų ± 2 Ų. For this reason, we prefer to apply the Rawicz's relation of γ = K_A/6 to estimate the interfacial tension values from our area compressibility modulus measurements. However, qualitatively, the use of either model will not change the interpretation of our results presented here in terms of alcohol adsorption to the membrane, and the quantitative values based on the Rawicz's model are approximations, given the simplicity of the model.

Fig. 10 A show the γ-values versus alcohol concentration we obtained from applying the Rawicz's model (γ = K_A/6) to our average K_A data for SOPC membranes. For comparison, γ-values of alkane-water/alcohol interfaces from the data of Bartell and Davis (1941) and Rivera et al. (2003) are plotted alongside. In comparison to the alkane γ-values, the bilayer γ-values decrease much less as alcohol concentration is increased. In addition, the bilayer γ-values do not parallel the alkane lines, showing that modeling a bilayer as alkane-like may lead to an overestimate of the reduction in the bilayer interfacial tension. However, the alkane system as a model for the bilayer captures the general trend of the dependence of acyl chain-length and concentration of alcohol on bilayer interfacial tension. The differences in interfacial tension values between the bilayer and alkane are attributed to physical differences in the interfaces and the amount of alcohol adsorbed (as will be discussed later in quantitative detail).

FIGURE 10.

(A) Interfacial tension, γ, values versus alcohol concentration for the four alcohol/water mixtures: methanol (diamonds), ethanol (squares), propanol (triangles), and butanol (circles). Values at the SOPC bilayer-water interface (solid marks) are from the K_A/6 relation, and values at the alkane-water interface (open marks) are reprinted with permission from Bartell and Davis (1941) (Copyright 1941 American Chemical Society) and Rivera et al. (2003) (Copyright 2003 by the American Physical Society). The single error bar is representative of all error bars. (B) The interfacial tension values are replotted against the log of concentration to show roughly equal spacing of 0.5 for all the curves.

Plotting bilayer γ-values against the log of the alcohol concentration for all the alcohols (as shown in Fig. 10 B) reveals clearly the dependence of γ on the acyl chain-length of the alcohol. The successive curves are displaced by nearly equal intervals of 0.5 for both the bilayer and alkane interfaces. This finding agrees with Traube's rule that for each additional CH₂ group, the concentration required to reach the same interfacial tension was reduced roughly by a factor of 3 (Traube 1891). Langmuir related this difference in concentration to a Gibbs free energy of ∼2.67 kJ/mol to bring one CH₂ group from the bulk aqueous phase to a hydrophobic interface (Langmuir, 1917). Overall, Figs. 10, 5, and 3 show that alcohol decreases the bilayer interfacial tension and concomitantly weakens mechanical cohesion, with the effect more pronounced as acyl chain-length increases.

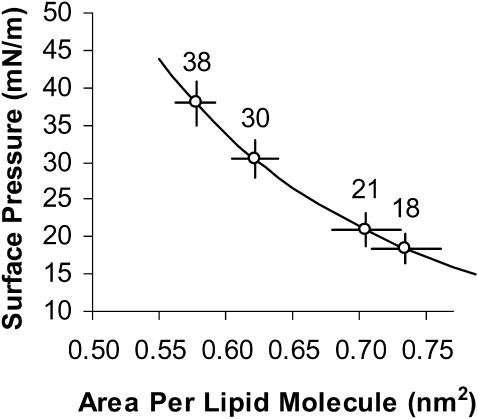
From the difference in γ-values between vesicles exposed to water and vesicles exposed to alcohol/water mixtures, we can predict the increase in area per lipid molecule. This entails the use of a surface pressure-area isotherm. We note that the surface pressure, Π, of each monolayer leaflet in a tension-free vesicle is balanced by its interfacial tension, γ, or Π = γ (Evans and Waugh, 1977). Thus, in Fig. 11, we can overlay our γ-data onto a fit of Π versus area per molecule data for an SOPC monolayer at the air-water interface from the works of Smaby et al. (1994) and obtain estimates for the area-per-molecule values. For all four types of alcohol molecules, we have plotted the γ-values onto the SOPC-water monolayer isotherm to obtain area-per-molecule estimates instead of using an SOPC-alcohol-water monolayer isotherm. We assume in the liquid-expanded state of the SOPC-water monolayer where the effective area per SOPC lipid molecule ranges from 60 to 80 Ų that the headgroup region of the SOPC lipid can accommodate the presence of the alcohol molecules without changing the effective area per lipid molecule. This stems from the fact that the limiting areas of the SOPC lipid and alcohol molecules are ∼40 Ų (Smaby et al., 1994) and 18 Ų (Haydon and Taylor, 1960), respectively; the alcohol/lipid ratio is ∼2 at the high alcohol limits (from Figs. 11 and 13); and the acyl chains of the alcohols are sufficiently short (less than the maximum length of ∼0.63 nm for butanol in the all-trans state) that they reside in the headgroup region (∼0.5 nm) without penetrating inside the hydrocarbon core of the SOPC lipids (Feller et al., 2002; Ueda and Yoshida, 1999). To our knowledge, the SOPC-alcohol-water monolayer isotherms have not been measured. This would be a worthwhile future venture to investigate if the SOPC pressure-area curve, upon addition of alcohols in the subphase, shifts away or crosses the standard curve (no alcohol in the subphase) and to test our assumption that the area per SOPC lipid molecule is approximately the same in either an SOPC-water or SOPC-alcohol-water isotherm for a specific alcohol concentration at a particular surface pressure.

FIGURE 11.

Surface pressure-area per lipid molecule isotherm of an SOPC monolayer at the air-water interface up to its collapse pressure of ∼45 mN/m (reprinted with permission from Smaby et al., 1994; Copyright 1994 American Chemical Society). Plotted onto the line are γ-values for SOPC vesicles in a butanol/water mixture (given in Fig. 10 based on γ = K_A/6). From the x axis, area per molecule is estimated to predict direct area expansion plotted in Fig. 12. Bars indicate 1 SD.

FIGURE 13.

Total alcohol surface density versus concentration for the four alcohol types: methanol (diamonds), ethanol (squares), propanol (triangles), and butanol (circles). Values at the SOPC bilayer-water interface are solid marks whereas values at the alkane-water interface are open marks. For comparison, the surface density of a saturated butanol monolayer is represented by the dashed line.

Using a different method of analysis, independent of the assumption of γ = K_A/6, we can predict the area per SOPC lipid molecule of unilamellar vesicles in specific alcohol/water mixtures. In this method, we convert the pressure-area per molecule isotherm of an SOPC monolayer into an elasticity modulus/area per molecule isotherm. By definition, the elasticity modulus, E, of a monolayer is 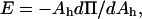where A_h is the area per lipid molecule (Adamson and Gast, 1997), and for comparison to K_A, E must be multiplied by a factor of 2 since a bilayer consists of two monolayers. Rawicz et al. (2000) showed that the measured SOPC isotherm of Smaby et al. (1994) could be fitted accurately to an equation of state of the form 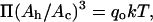where A_c is the limiting lipid area of ∼0.4 nm² and q_o is a constant value of 33 nm⁻². We applied the elastic modulus definition to this equation of state to generate a plot of 2E vs. A_h. When we compare our measured K_A values of SOPC vesicles in alcohol/water mixtures to the derived 2E values, the predictions of area per SOPC lipid molecule are identical to the values estimated by the previous method based on the polymer brush model's general relation of γ = K_A/6. This derives from the fact that, in the area per SOPC molecule range of interest on the Π-A_h isotherm, the value of 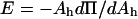is always 3 Π.

We next convert the area/molecule values to direct area expansion, (ΔA/A_o)_dir (the increase in area/molecule normalized by the area/molecule with no alcohol present) and plot (ΔA/A_o)_dir versus alcohol concentration in Fig. 12 A. We see a clear dependence of (ΔA/A_o)_dir on both alcohol concentration and acyl chain-length, with increases in (ΔA/A_o)_dir up to 25%. By assuming lipid chain volume is conserved in fluid membranes, we can relate the increase in area/molecule to a corresponding decrease in membrane thickness. For clarity, we show the results separately in Fig. 12 B based on x-ray diffraction measurement of 4 nm (peak to peak) for the thickness of an SOPC membrane in an aqueous solution with a deformable hydrocarbon core of 3 nm (Rawicz et al., 2000).

FIGURE 12.

(A) Predicted (ΔA/A_o)_dir and measured (ΔA/A_o)_exp-dir direct membrane area expansion of SOPC vesicles from alcohol/water exposure: methanol (diamonds), ethanol (squares), propanol (triangles), and butanol (circles). Predicted values (open marks) came from the line in Fig. 11. Measured values (solid marks) came from flow pipette experiments when area expansion of vesicles reached equilibrium conditions. (B) Assuming constant membrane volume, corresponding decreases in membrane thickness from the predicted and measured direct area expansion were calculated. Measured values are based on six vesicles or more. Bars indicate 1 SD.

Our prediction that the headgroup area per lipid molecule increases with alcohol concentration with an accompanying decrease in membrane thickness implies that the lipid chains become more disordered or “looser” packed with a higher degree of gauche conformations. This correlates positively with reported measurements of enhanced membrane fluidity in the presence of alcohol (Chin and Goldstein, 1977). The increase in area per molecule that we predict may also explain the observed faster lateral diffusion motion of lipids in neural crest cells in the presence of alcohol (Chen et al., 1996). According to the free volume theory (Almeida et al., 1992), an increase in the lipid headgroup area would result in a larger free area for lipid diffusion; hence larger lipid diffusion coefficients are probably caused by the “looser” packing of the bilayer in the presence of ethanol compared to the lamellae without alcohol.

Bilayer area expansion from alcohol flows

Our predictions that the lipid membrane will expand and thin as vesicles are exposed to alcohol/water mixtures were confirmed independently through flow experiments. For simplicity, we assumed the membrane area expansion observed upon exposure to alcohol is the sum of three effects although the effects may not be truly independent from one other:

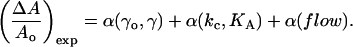(5)

The first term is the increase in area per molecule from a decrease in interfacial tension of the outer and inner leaflets of the bilayer. This term should be compared to the direct area expansion predictions in Fig. 12 A. For vesicles held at a constant tension, the second term accounts for the increase in mechanical deformation (strain) as mechanical properties (bending and area compressibility moduli) change, but this term is neglectfully small. The last term reflects any flow-induced effects on the membrane area, but we note that this term may not necessarily be independent from α(k_c, K_A) if the unknown cause for α(flow) is of a mechanical origin. We ignore any contribution in area expansion from the acyl chains of the alcohols since they are reported to not penetrate into the hydrocarbon core (Chiou et al., 1992). Therefore, to compare our measured flow area expansion numbers, (ΔA/A_o)_exp, to our predicted direct area expansion values, (ΔA/A_o)_dir, we subtracted α(k_c, K_A) and α(flow) of 0.022 from the equilibrium (ΔA/A_o)_exp values to get the direct equilibrium area expansion numbers, (ΔA/A_o)_exp-dir. We estimated α(k_c, K_A) with the equation

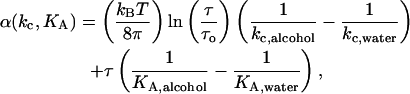(6)

where τ is the holding tension, τ_o is the tension at zero strain (estimated to be ∼0.004 mN/m from where the τ vs. α line typically crosses the y axis in the mechanical properties experiments), k_c,alcohol is the average bending modulus of vesicles in a specific alcohol/water mixture, k_c,water is the average bending modulus of vesicles in an aqueous mixture without alcohol, K_A,alcohol is the average area compressibility modulus of vesicles in a specific alcohol/water mixture, and K_A,water is the average area compressibility modulus of vesicles in an aqueous mixture without alcohol. This deformation contribution is very small and averages <0.005. (Our previous article, Ly, 2002, stated that α(k_c, K_A) or Δ(ΔA/A_0%) values were 0.02, 0.06, 0.06, and 0.09 for vesicles exposed to 5%, 10%, 15%, and 20% (vol:vol) ethanol/water solutions, respectively. Instead, they should read 0.0012, 0.0013, 0.0022, and 0.0045, respectively.)

The direct equilibrium area expansion (ΔA/A_o)_exp-dir values for vesicles with stable projection changes are plotted in Fig. 12 A for comparison with the predicted (ΔA/A_o)_dir values obtained from the relation γ = K_A/6. It can be seen that the values are within experimental error of each other, demonstrating that membrane area expansion indeed is derived from decreases in interfacial tension for vesicles exposed to alcohol/water mixtures.

Surface excess

With the establishment that the homologous series of n-alcohols from methanol to butanol decreases the interfacial tension of the bilayer-water interface, we proceed to apply the fundamental theory of Gibbs adsorption (Adamson and Gast, 1997; Chattoraj and Birdi, 1984) to predict quantitatively the amount of alcohol accumulated at the bilayer-water interface in excess of the bulk, from decreases in interfacial tension. For perspective, surface enrichment of methanol, ethanol, propanol, and butanol at the air-water interface (as predicted by the Gibbs equation from surface tension measurements) are experimentally confirmed by x-ray grazing, neutron reflectivity, and mass spectrometry (Li et al., 1993, 1996; Raina et al., 2001a,b). The Gibbs equation of adsorption in concentrated solution for two immiscible phases is

(7)

where Γ_ex is the surface excess of alcohol molecules, a is the activity coefficient times mole fraction of alcohol in the aqueous phase with the standard state defined by pure alcohol, γ is the interfacial tension, and RT is the thermal energy per mole. We determined the activity coefficients by fitting the two-suffix Margules equations to experimental vapor-liquid equilibrium data of alcohols and water. (We readily found data for methanol and ethanol, but we had difficulties finding n-propanol and n-butanol data at 25°C and settled on n-propanol at 30°C and 2-butanol at 25°C; Chu, 1956; Gmehling et al., 1977.) We evaluated the derivative dγ/da for the SOPC bilayer by successfully fitting γ-values versus activity to exponential functions. The total alcohol surface density values (surface excess density plus surface bulk-phase density) for the bilayer-water interface (and alkane-water interface for comparison; Bartell and Davis, 1941; Rivera et al., 2003) are presented in Fig. 13 as functions of acyl chain-length and concentration of the alcohol. The dashed line represents a saturated butanol monolayer using the estimated surface area of 18 Ų per alcohol molecule (Haydon and Taylor, 1960). (Ethanol and propanol have similar headgroup areas, but methanol has a slightly smaller area of 16 Ų.) As expected from the difference in interfacial tension behavior between the bilayer and alkane interfaces (Fig. 8), we see in Fig. 13 distinct separations of the curves which clearly shows that alcohol adsorbs much less at the interface of the bilayer than the alkane by almost twofold. Presumably, the hydrophobic effect drives alcohol adsorption at the interface to minimize hydrophobic exposure of the interface to water as well as the hydrophobic surface of the alcohols. Since the alkane has a bare hydrophobic interface whereas the bilayer has an interface of mixed hydrophobic (from the upper segments of the lipid hydrocarbon tails) and hydrophilic (from the polar headgroups) characteristics, the driving force for alcohol adsorption at the interface of the alkane would be greater than the bilayer's.

From the total surface density values presented in Fig. 13, we calculated the partition coefficient, K_x, in terms of mole fraction as defined by the equation

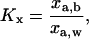(8)

where x_a,b is the mole fraction of alcohol in the bilayer and x_a,w is the mole fraction of alcohol in the water phase (Rowe et al., 1998). In calculating x_a,b as the ratio of the surface density of alcohol over the sum of surface density of alcohol and surface density of lipid molecules (from the estimated area per lipid molecule in Fig. 11), we note that our estimated K_x values would be slightly less than the true values since we do not account for the small amount of alcohols that may reside in the core of the bilayer. Nonetheless, the K_x values of 9.2, 23.8, 99.1, and 237.7 obtained in the limit of dilute concentrations for methanol, ethanol, propanol, and butanol, respectively, are in general agreement with reported values of 7.8, 16.6, 49.3, and 119.0 as measured by centrifugation of alcohol in DMPC liposomes (and converted from molalities unit; Katz and Diamond, 1974). Additionally, our K_x value of 237.7 for butanol is similar to other published values where titration calorimetry measured 170–183 for dipalmitoyl phosphocholine (DPPC; Zhang and Rowe, 1992) and C-13 nuclear magnetic resonance reported 270–800 for DPPC and 186–600 for DMPC (Rowe et al., 1987) in their fluid-phase states. Note that the difference between each number in the series roughly follows Traube's rule of a factor of 3, indicating that alcohol partitioning is at the root of the Traube's rule effect.

Gibbs free energy of adsorption

The adsorption of alcohol at the bilayer-water interface has long been considered to be primarily driven by the hydrophobic effect (Rowe et al., 1998). The main characteristics of the hydrophobic effect are an overall increase in the entropy of the system, an anomalous heat capacity change, and a standard Gibbs free energy of transfer, ΔG_o, that is proportional to the acyl chain-length. Traditionally, ΔG_o has been calculated on the basis of the partition coefficient, K_x, of alcohol in the bilayer and water phase, i.e.,

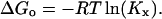(9)

As we will demonstrate, ΔG_o values can be independently (or alternatively) obtained from interfacial tension values. The use of interfacial tension values to calculate ΔG_o has been readily applied in air-liquid (Gillap et al., 1968), liquid-liquid (Apostoluk and Szymanowski, 1998), and Langmuir monolayer studies (Heywang et al., 2001), and to our knowledge, we are the first to apply this concept to a bilayer (presumably because interfacial tension values of a bilayer and micelles are not directly measurable). Many forms of ΔG_o in terms of interfacial tension values are reported in literature, but for comparison with measured ΔG_o values of adsorption of short-chain alcohols to an oil-water interface, we chose the following common form with the standard state defined with respect to an infinitely dilute solution,

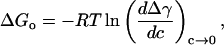(10)

where Δγ = γ_o−γ is the monolayer surface pressure, γ_o is the interfacial tension at c = 0, and c is the alcohol concentration in molarity. Within this context, ΔG_o is defined as the difference in the chemical potential between the interface and bulk water phase at infinite dilution, and it represents the work done by the alcohol molecule to transfer from the bulk water phase to the surface. We cautiously evaluate the derivative dΔγ/dc as c approaches zero, noting that we have few γ-values in the dilute regime (especially for methanol and ethanol) to accurately determine the slopes. We proceed with the calculations to understand qualitatively, if not quantitatively, the role acyl chain-length has on ΔG_o. We find the slopes evaluated for each alcohol from a linear regression were indifferent to the number of γ-values we used, whether the first two or first four.

Presented in Fig. 14 are the estimated ΔG_o values plotted against the number of carbons for the transfer of alcohols from the water phase to the bilayer-water interface along with reported values for transfer to a petroleum ether-water interface from the works of Haydon and Taylor (1960). We see, as expected, that the ΔG_o values of the bilayer are of smaller magnitudes than the values of the petroleum ether (reflective of the physical differences of the two interfaces). The slope of the bilayer line in Fig. 14 reveals the dependence of ΔG_o on carbon number, and its value of 2.9 ± 0.2 kJ/(mol-CH₂) is similar to the value of 3.5 kJ/(mol-CH₂) at the petroleum ether-water interface (Haydon and Taylor, 1960), 3.5 kJ/(mol-CH₂) at other alkane-water interfaces (Chattoraj and Birdi, 1984; Tanford, 1980), and 3.1 kJ/(mol-CH₂) estimated from the partition coefficients of alcohols in DPPC liposomes (Jain et al., 1978). The linear relationship between ΔG_o and number of carbons for the bilayer-water interface and the similar Gibbs free energy per CH₂ to the alkane-water interfaces are consistent with the characteristics of the hydrophobic effect. Our results in concert with the findings of Rowe (1998) who determined the Gibbs free energy value of 3.5 kJ/(mol-CH₂) based on partition coefficients support the accepted view that alcohol adsorption is primarily driven by the hydrophobic effect.

FIGURE 14.

Plot of the standard Gibbs free energy of adsorption of alcohols from an infinitely diluted water phase to an SOPC bilayer-water interface (solid marks) and a petroleum ether-water interface (open marks) (reprinted with permission from Haydon and Taylor, 1960; Copyright 1960 by the Royal Society) against chain length.

Permeability coefficient

From the dynamic growth of the membrane area in our flow experiments, we can obtain permeability coefficients, P (cm/s), of alcohols crossing the membrane. The value P is defined as the ratio of the net flux of solute across a membrane of thickness l over the difference of solute concentration on the two sides of the bilayer. As noted by others (Chanturiya et al., 1999), P-values of alcohols across synthetic lipid membranes have not been measured. To our knowledge, only P-values of short-chain alcohols have been measured in biological systems including human erythrocytes (Brahm, 1983), yeasts (Guijarro and Lagunas, 1984), and bacteria (Schoberth et al., 1996). For perspective, P-values of water (Brahm, 1982; Olbrich et al., 2000), carboxylic acid (Walter and Gutknecht, 1984; Xiang and Anderson, 1998), and other small solutes (Paula et al., 1996; Walter and Gutknecht, 1986) have been extensively studied and modeled in both synthetic and biological membranes to gain a general understanding of membrane permeability in metabolism and drug delivery (since most drug molecules transport passively across the membrane).

Fig. 1 C illustrates the expected kinetic processes involved in the molecular exchange of alcohol molecules across a lipid membrane of a vesicle. The molecular transport involves essentially five steps. Alcohol is carried by convection from the flow pipette to the outer surface of the aspirated vesicle. Alcohol then adsorbs to the headgroup region of the outer leaflet, and this process is characterized by the “on” rate k_on. Coupled to this process is alcohol desorption from the headgroup region, which is denoted by the “off” rate k_off. Alcohol then diffuses across the hydrocarbon core and adsorbs in the headgroup region of the inner leaflet. Desorption from the inner leaflet (k_off) coupled with adsorption (k_on) follows, and alcohol then migrates by diffusion to the center of the aqueous interior of the aspirated vesicle. Equilibrium is achieved when the alcohol concentration inside the vesicle, C_in, is the same as the exterior, C_out. During this transport process, the membrane area of the vesicle expands as the number of adsorbed alcohol molecules, C_ads, both in the outer and inner leaflet increases (due primarily from an induced decrease in bilayer interfacial tension), and this membrane growth can be monitored precisely by micropipette aspiration to determine the kinetic constants k_on and k_off and permeability coefficients P. The set of equations that describes the time evolution of alcohol adsorption to the membrane and alcohol accumulation inside the volume of the vesicle is

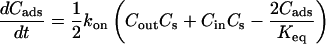(11)

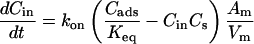(12)

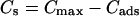(13)

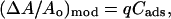(14)

where C_s is the number of open sites for adsorption, C_max is the maximum available open sites for adsorption, A_m is the surface area of the vesicle exposed to alcohol (neglecting the surface area of the projection adjacent to the micropipette's wall and assuming the pool of alcohol inside the pipette should eventually equal C_out), V_m is the volume of the spherical vesicle, K_eq is the equilibrium constant (K_eq = k_on/k_off), t is the time, (ΔA/A_o)_mod is the instantaneous direct area expansion due to alcohol adsorption, and q is a proportional constant. For clarity, Eqs. 11 and 12 are derived in the Appendix.

In formulating these mathematical equations to describe the kinetic transport of alcohol across the membrane, we made and defend here five key assumptions.

1. We assumed that no concentration boundary layer exists on the outside of the vesicle's surface for specific alcohols, thus the concentration of alcohol at the vesicle's surface was the same as the inside of the flow pipette. We show in the Appendix that the mass transfer resistance for alcohol to reach the vesicle's surface from the flow pipette is negligible for methanol, ethanol, and propanol due to the high diffusion coefficients of alcohols in water, justifying this assumption. For butanol, the “on” rate is comparable to the diffusion rate, and a boundary layer concentration is used as discussed in the Appendix.

2. We assume in Eq. 14 (and as evidenced from Fig. 15) that the direct area expansion, (ΔA/A_o)_mod, is proportional to the total surface density of alcohol in the membrane.

3. We assumed that the adsorption/desorption of alcohol molecules from the bulk into the headgroup regions (of both the outer and inner leaflets) can be adequately described by the Langmuir adsorption model. The Langmuir model is valid (Adamson and Gast, 1997; Fogler, 1992) when the surface-adsorbed alcohol molecules in the headgroup region, C_ads (molecules/Ų), and alcohol concentration in the bulk phase, C_bulk (M), fit the following equation:

   (15)

   By plotting C_bulk/C_ads versus C_bulk in Fig. 16 from values in Fig. 13, we find the points indeed fall on a straight line for each alcohol type. This confirms that the simple Langmuir model is sufficient to describe the adsorption/desorption of alcohol molecules into the bilayer, but we note the model cannot distinguish whether the alcohol binding sites in the membrane are nonspecific or specific (alcohol interacting mainly with the phosphate or carbonyl group). Interestingly, the Langmuir model suggests that the process of alcohol adsorption/desorption in the membrane is noncooperative for the range of concentrations we are investigating, but it is plausible that the process may become cooperative at higher concentrations or equivalently, when the area per lipid molecule in the membrane expands beyond a critical value. The K_eq and C_max values from a simple fit of the points in Fig. 16 are reported in Table 1. The C_max values for ethanol, propanol, and butanol are close to the saturated monolayer value of 0.055 molecules/Ų whereas the value for methanol is within order of the saturated monolayer value of 0.063 molecules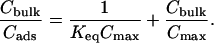/Ų.

4. We assumed that the surface densities of alcohol molecules in both the outer and inner headgroup regions are equally distributed at any time during the kinetic transport such that we can characterize the surface densities of adsorbed molecules as a single parameter C_ads. We show in the Appendix that this assumption is valid since the rate of equilibration by diffusion across the hydrocarbon core is much faster than the experimental timeframe of seconds to minutes. Additionally, if the rate of diffusion is much “slower” than the adsorption/desorption rates, then we would expect an accumulation of alcohol molecules in the outer leaflet and a slow transport of these molecules to the inner leaflet. Hence, one of the leaflets would have expanded quickly whereas the other would have expanded much more slowly. It has been demonstrated previously using lysolipids by Needham and Zhelev (1995) and fusion peptides by Longo (1998; 1997), that when such asymmetry of expansion occurs, glucose-sized pores are generated in the membrane and swelling of the vesicle ensues. We never observed swelling of the vesicles, even during membrane expansion as large as 20%. We concluded then that the use of a single adsorption parameter, C_ads, is valid.

5. We assume that the alcohol concentration inside the vesicle was well mixed, in other words, no concentration gradient of free ethanol existed in the interior volume of the vesicle. We show in the Appendix that by diffusion alone, the timescale to reach a uniform concentration inside a typical vesicle for any difference in concentrations between the inner surface and interior is much shorter than the experimental timescale of seconds to minutes. On occasions, we observed aspirated vesicles with small internal vesicles swirling inside under flow conditions at both short and long times, possibly from coupling with flow-induced lipid motion as observed by Shoemaker and Vanderlick (2003), and we contend then that internal convection would further decrease this timescale.

FIGURE 15.

Plot showing to a first-order approximation a linear relationship between the predicted membrane expansion (from interfacial tension reduction) and alcohol surface density. The predicted membrane expansion values were obtained from Fig. 12 A. The alcohol surface density values came from Fig. 13.

FIGURE 16.

Ratio of bulk alcohol concentration over surface density versus bulk alcohol concentration from values found in Fig. 13. The linearity of the points shows that adsorption/desorption of alcohol molecules into the headgroup regions of the bilayers follow the Langmuir adsorption model.

TABLE 1.

List of parameters (C_max, K_eq, k_off, and k_on) in the Langmuir adsorption model, membrane permeability values of alcohols P, and ratio of membrane area change to surface density constant q

	Methanol	Ethanol	Propanol	Butanol
Cmax (molecules/Å2)	0.15 ± 0.01	0.07 ± 0.01	0.06 ± 0.01	0.05 ± 0.01
Keq (1/M)	0.04 ± 0.01	0.21 ± 0.01	0.90 ± 0.07	2.64 ± 0.26
koff (1/s)	300 ± 100	400 ± 400	800 ± 400	>1000
kon (1/(M × s))	10 ± 5	80 ± 80	700 ± 360	>2600
qestimate (Å2/molecules)	5.3 ± 0.8	4.6 ± 0.7	6.3 ± 0.9	6.5
qfit (Å2/molecules)	5.3 ± 0.6	3.0 ± 1.3	3.4 ± 0.8	4.1 ± 1.1
P (cm/s)	1.2 ± 0.4 × 10−5	3.8 ± 3.0 × 10−5	2.8 ± 1.4 × 10−4	1.2 ± 1.4 × 10−3

Values for k_off, q_fit, and P are averages based on six vesicles or more for vesicles in 4.94 M methanol, 1.70 M ethanol, 2.56 M ethanol, 0.19 M propanol, 0.39 M propanol, and 0.11 M butanol aqueous mixtures. The value q_estimate was determined from the slopes in the studied concentration range from Fig. 15. The q_fit and P-values for ethanol at 1.70 M and 2.56 M and propanol at 0.19 M and 0.39 M showed no concentration dependence so averages of these values are presented here. For butanol, the model predictions of area expansion (ΔA/A_o)_mod with k_off values between 10³ and 10⁵ were indistinguishable within the experimental error of measured membrane expansion (ΔA/A_o)_exp-dir (due to image resolution limitation) so a minimum value of >1000 is reported. The value k_on was computed simply from the relation K_eq = k_on/k_off.

The set of coupled differential equations (Eqs. 11–14) were solved numerically with PolyMath 5.1 (written by Mordechai Shacham, Michael B. Cutlip, and Michael Elly) to obtain (ΔA/A_o)_mod as a function of time and fit to the flow pipette profiles of direct area expansion (ΔA/A_o)_exp-dir versus time for vesicles exposed to the following alcohol/water mixtures: 4.94 M methanol/water, 1.70 M ethanol/water, 2.56 M ethanol/water, 0.19 M propanol/water, 0.39 M propanol/water, and 0.11 M butanol/water. Values of q which relate area expansion to surface density were set initially from data in Fig. 15, obtained from our area compressibility measurements. However, since the data in Fig. 15 are averages over many vesicles, it was necessary to finely adjust the value of q for each fit to duplicate the area expansion plateau value in each flow profile. Thus, although there was slight adjustment, q is not, strictly, a free parameter. Averages of the “fit” q-values show that they indeed are similar to values calculated using Fig. 15 in the same concentration range (Table 1). The only free parameter, k_off, was adjusted to obtain the best fit with experimental data. Before fitting the model, the experimental results were adjusted by removing the flow-induced membrane expansion spike of ∼0.022. Generally, the observed spike value at 1 or 2 s of flow exposure was removed from every data point in the profile, and the time of the spike is set as zero. At time zero, C_ads and C_in were set to zero. The numerical solution of the model can be generally fitted to a double-exponential function of the form (ΔA/A_o)_mod = B−A₁exp(−s₁t)−A₂exp(−s₂t), where A₁, A₂, B, s₁, and s₂ are constants. In the framework of the Langmuir adsorption model, the exponentials reflect the outer flux, J_outer = k_onC_outC_s−k_offC_ads. At time zero, C_s is maximum and C_ads is zero. So the molecular flux, J_outer, is large initially and the first exponential captures this fast alcohol adsorption at short time (milliseconds to seconds). J_outer decreases sharply at long time (seconds to minutes) as C_s decreases, and C_ads increases where this is reflected in the second exponential, giving an equilibration time on the order of seconds. Under well-controlled laminar flow conditions, many of these experimental area expansion values, (ΔA/A_o)_exp-dir, versus time plots follow this predicted double-exponential shape of the model, especially the sets involving propanol and butanol. Example profiles of (ΔA/A_o)_mod, C_in, and the fitting of k_off for a vesicle in a 0.39 M propanol/water mixture are shown in Fig. 17. We find that k_on (reported in Table 1) becomes substantially larger as the chain-length of the alcohol increases, presumably reflecting the increased hydrophobicity with chain-length. Interestingly, our values of k_off are insensitive to chain-length. On first reflection, this result may indicate that k_off is reflecting diffusion across a concentration boundary layer in the vesicle interior since that rate would be invariant to chain-length. However, a comparison of timescales shows that this is unlikely. For example, our k_off values can be used to estimate the rate at which a single alcohol molecule is desorbing from a saturated bilayer (0.001s), in which time an alcohol molecule displaces ∼2 μm or one-tenth of the distance to the center of the vesicle. Hence, it is likely that a boundary layer never forms. Possibly, k_off is limited by a process that is insensitive to alcohol chain-length such as hydrogen bonding to the lipid headgroups.

FIGURE 17.

Direct membrane area expansion versus time of a vesicle exposed to a 0.39 M propanol/water mixture. (A) Experimental area expansion data (ΔA/A_o)_exp-dir (circles) are fitted to a kinetic model (ΔA/A_o)_mod with a k_off value of 1200 s⁻¹ and a q-value of 3.05 Ų/molecules. The second curve below is the model's prediction of the alcohol concentration inside the vesicle, C_in, used for calculating permeability coefficient, P. (B) Curves for different k_off values from the kinetic model's predictions are drawn for comparison. The top line corresponds to 10⁴ followed by 10³, 10², and 10 s⁻¹ with the best-fitted line at ∼1200 s⁻¹.

The transmembrane permeability coefficient, P (cm/s), was calculated by performing a simple mass balance around the interior of the vesicle, i.e.,

(16)

Assuming V_m, A_m, and P are constant over the timescale of the experiment, the solution is

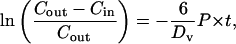(17)

where D_v is the diameter of the vesicle. By plotting 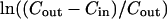versus time with C_in obtained from the previously discussed modeling, the slope reveals the permeability coefficient. An example plot is shown in Fig. 18 and P-values are reported in Table 1. Butanol has the most rapid exchange with a high permeability value of 10⁻³ cm/s, followed by propanol (10⁻⁴ cm/s), ethanol (10⁻⁵ cm/s), and methanol (10⁻⁵ cm/s). These order-of-permeability values correlate with the k_on values seen in Table 1, indicating that the rate of adsorption is a critical determinant of permeation. To the author's best knowledge, this is the first article to report permeability values of short-chain alcohols across model lipid membrane systems. Therefore, it is interesting to compare our values to those obtained in cellular systems. Brahm (1983) shows the permeability of these short-chain alcohols through the red blood cell membrane (in tracer efflux experiments by the continuous flow tube method) to be ∼10⁻³ cm/s. Other investigators have shown that the value of ethanol ranges ∼10⁻⁴ cm/s in Zymomonas mobilis (Schoberth et al., 1996), Saccharomyces cerevisiae (Guijarro and Lagunas, 1984), and rabbit erythrocyte (Jones, 1988). This discrepancy of small-molecule permeability in model membranes versus cell membranes has been observed before. For example, as observed using water as the diffusing species, permeability through model membranes is generally 10-fold smaller than permeability measured in biomembranes which allow small-molecule diffusion through protein-mediated anion transport channels (Gennis, 1989). In addition, Angelova et al. (1999) observed that the timescale of ethanol exchange by simple diffusion in giant vesicles was on the order of minutes (∼5 min) using phase-contrast microscopy. Their vesicle sizes ranged between 40 and 80 μm in diameter, giving an equivalent P-value of 1.5 × 10⁻⁵ cm/s based on Eq. 17. Overall, it appears that our permeability coefficients are reasonable.

FIGURE 18.

From the values of C_in in Fig. 17 A, the permeability coefficient of a vesicle in a 0.39 M propanol/water mixture is computed to be 1.9 × 10⁻⁴ cm/s by multiplying the slope with D_v/6 where D_v = 33 μm is the vesicle's diameter.

Membrane failure and critical pore size

The destabilizing effect of alcohol on the lipid membrane can be thought of in terms of the mechanism of membrane failure, i.e., the formation of hydrophilic pores. Pores are activated stochastically through thermal membrane fluctuations (or purposely through the application of a strong electric field across the membrane, a process known as electroporation, or addition of lytic peptides such as melittin or protegrin in the membrane solution; Longo et al., 1998; Zhelev and Needham, 1993). Our data can be used to estimate the lowering of the line tension, λ, of a pore in the presence of alcohol in addition to the critical radius, r_c, of a stochastically formed pore at ∼4% area strain (the average α_dir-lyse value) above which the membrane will lyse. The free energy required to form a pore of radius r in a membrane is (Litster, 1975)

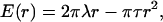(18)

where λ is the energetic cost of forming a pore edge per unit length (line tension) and τ is the applied membrane tension. By taking the derivative of the expression with respect to r and defining a critical radius r_c = λ/τ, Sung and Park (1997) showed that the radial force as a function of radius is

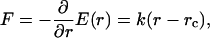(19)

where k = 2πτ. For a stress-free vesicle (τ = 0), the expression shows that pores formed by thermal fluctuations or electroporation will always reseal or heal, and the membrane becomes stable against pore growth. However, for a stressed vesicles at any tension (τ > 0), the membrane will fail from an infinitely growing pore if the pore radius exceeds the critical radius, r > r_c. Otherwise if r < r_c, the pore will seal eventually. To determine λ from our data, we draw upon (with one modification) a simple model by May (2000) that relates line tension to interfacial tension and lipid parameters. His main two assumptions were the pore is a semicylindrical rim with a radius b_o that is flushed with an unperturbed bilayer of thickness 2b_o and the molecular cross-sectional area of the lipid in the micellar region at the hydrocarbon-water interface is estimated to be two times larger than the optimum cross-sectional area of the lipid in the bilayer, namely a_m = 2a₀. May used the IMN model (Israelachvili et al., 1980), also known as the opposing force model (OFM), to estimate a₀ from the molecular free energy of the lipids, 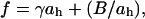where γ is the interfacial tension, B is a lipid headgroup repulsion strength, and a_h is the cross-sectional area of the lipid in the bilayer. For consistency, we applied the lipid free energy form in the Rawicz's model to estimate a₀, where ɛ = 3n_sk_BT/2 is the harmonic chain energy prefactor used to describe the free energy of chain extension in a polymer monolayer, n_s is the number of statistical segments in a chain (n_s ≈ L = 2.25 nm for SOPC), and L and a_c are the length and headgroup area of the chain in the all-trans state. At equilibrium, i.e., df/da_h = 0 and a_h = a_o, thus 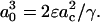The line tension, λ, defined as the excess free energy per unit length of the membrane edge, is calculated from 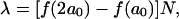where 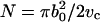is the number of lipids found in the micellar region per unit length, v_c is the total lipid acyl-chain volume, and b₀ = v_c/a₀. Thus, the simple expression for line tension is

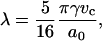(20)

which is very similar to the May's equation based on the IMN model of 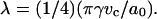We applied this expression to estimate λ-values of SOPC vesicles in alcohol/water mixtures from our estimated γ- and a₀ values found in Figs. 10 A and 11, respectively. The total acyl-chain volume, v_c, of 1019 ų was computed by summing over the individual CH₃, CH₂, and CH segments in the chain tails of an SOPC molecule (Nagle and Tristram-Nagle, 2000).

The estimated λ-value for SOPC in a solution with no alcohol (Fig. 19) is almost an order-of-magnitude higher than experimental values of ∼1 × 10⁻¹¹ N (Zhelev and Needham, 1993) due to the simplicity and approximations made in the model. Therefore, it is more instructive to think of our results in terms of line tension reduction. It is estimated that the line tension was decreased by as much as 50% at the high limits of alcohol species and concentration used here. Therefore, 50% less mechanical tension was required to rupture the membrane through pore growth. Although there is a bit of spread in the λ versus τ_lyse plot (Fig. 19), the r_c value (λ/τ_lys) for each data point is ∼6.5 nm and a line fit to the data gives a slope of 6.5 nm. Since our base line tension value is almost an order of magnitude too high, our pore size should be closer to 1 nm in diameter. This indicates that near 4% area strain, critical pores in the range of 1 nm are forming as a result of an excess free area per lipid molecule. These results support the view that membrane failure typically is a result of thermally driven density fluctuations and highlight the importance of using a consistent ramp rate of the tension since the stochastic nature of this process means that lysis tension will be dependent on ramp rate (Evans et al., 2003; Evans and Ludwig, 2000).

FIGURE 19.

Plot of membrane line tension versus lysis tension. The slope gives a critical radius of 6.5 nm. Symbols are methanol (diamonds), ethanol (squares), propanol (triangles), and butanol (circles).

CONCLUSIONS

The important outcomes of this work are:

1. That lipid bilayers obey Traube's rule of interfacial tension reduction for short-chain alcohols, i.e., for every additional CH₂ group, an alcohol becomes three times more effective in decreasing interfacial tension of the bilayer.

2. Area compressibility moduli, lysis tension, and bending modulus are directly dependent on interfacial tension, thus Traube's rule is a good first-order approximation for their behaviors as well.

3. The partitioning of alcohol into the bilayer-water interface is responsible for the Traube's rule dependence, and thus for every additional CH₂ group, three times more alcohol partitions into the interface.

4. Alcohols more effectively decrease the interfacial tension of alkane-water interfaces in comparison to a bilayer-water interface because more alcohol partitions into those more hydrophobic interfaces.

5. Short-chain alcohols increase the area per molecule in a chain-length-dependent manner that is predicted quantitatively by the decrease in interfacial tension.

6. Membrane permeability to these alcohols is also chain-length-dependent due to more rapid adsorption as the chain-length increases.

7. Substantial decreases in mechanical properties and membrane thickness (e.g., 20%) take place at alcohol concentrations in which major alterations in the metabolism of microorganisms have been observed, supporting the view that membrane mechanics and the influence of membrane mechanics on membrane proteins is a major factor in normal and abnormal cell functions.

APPENDIX

Surface density of alcohol's dependence on applied tension

When vesicles are aspirated during the mechanical tests, it is conceivable that the partitioning or surface density of the alcohols in the membrane may increase with applied tension at a fixed bulk concentration in the bathing solution. This would occur if the alcohol molecules primarily reside in the deformable hydrocarbon core, but as previously presented in the Discussion, alcohol molecules are sufficiently short to reside mostly in the headgroup region. Nonetheless, we can show that even if alcohol molecules could reside in the deformable hydrocarbon core, the increase in applied tension would only minutely affect the alcohol's surface density and consequently have little effect on interfacial tension and area strain. To estimate the amount of enhanced partitioning, we followed the thermodynamic analysis presented by Zhelev (1998) for the adsorption of lysolipid into the membrane. The change in surface density of alcohol molecules will be determined from the dependence of the applied membrane tension on the Gibbs energy of the membrane. The assumption is that only the alcohol molecules in the hydrocarbon core of the membrane (and not the bulk) will experience a change in their Gibbs energy when there is an applied membrane tension. At equilibrium, the chemical potential for the alcohol in the bathing solution and in the membrane are equal,

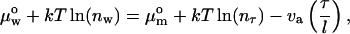(A1)

where n_w is the molar concentration of alcohol in the bathing solution; 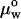and 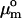are the standard chemical potentials of alcohol in the bathing solution and in the membrane, respectively; v_a is the volume of an alcohol molecule in the membrane (approximated with the hydrocarbon volume (ų) formula of 27.4 + 26.9 n where n is the number of carbon groups—see Tanford, 1980); 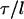is the membrane bulk pressure (Pa); l is the thickness of the hydrocarbon core (estimated to be ∼3 nm); and n_τ is the membrane concentration or surface density of alcohol at tension τ. By considering only alcohol concentrations instead of alcohol activities, this equation ignores any intermolecular interactions between the membrane and alcohol and their dependence on tension.

When τ is increased from zero to a particular value, the Gibbs energy remains constant for the bathing solution since it is independent of the applied stress. Hence, the right side of Eq. A1 would give the dependence of the change of alcohol in the membrane as an exponential function of applied tension,

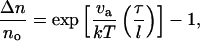(A2)

where n_o is the surface density of alcohol at zero membrane tension. For the tension range that we applied to the vesicles up to the lysis tension, 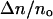appears linear with τ. At the lysis tension limits, we calculated 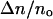values of 4–6% for the short-chain alcohols. Hence, the interfacial tension of the membrane would be slightly lowered, but the effect on the strain would be too small to be measurable.

Alcohol transport across the membrane

We imagine a vesicle bathed in an aqueous solution without alcohol. The surface density of alcohol in the membrane, C_ads, and alcohol concentration in the outer and inner bathing solution would be zero. At time zero, the vesicle is suddenly exposed to a laminar flow of alcohol/water solution of a specific concentration, C_out. A thin concentration boundary layer also known as an “unstirred layer” or “stagnant film” forms around the vesicle. Within this layer, the alcohol concentration changes from C_out* at the surface of the vesicle to C_out at the edge of the boundary layer.

Alcohol molecular exchange between the adjacent bathing solutions and membrane surfaces occurs both at the outer and inner monolayers (see Fig. 1 C). Assuming the Langmuir adsorption model is appropriate and the surface density of alcohol molecules in the membrane, C_ads, is uniform in both monolayers, the rate of exchange at the outer monolayer is

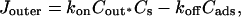(A3)

where C_s is the number of open sites for adsorption. At the inner monolayer, the rate of exchange is

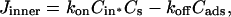(A4)

where C_in* is the bulk alcohol concentration adjacent to the inner monolayer. The rate of accumulation in the membrane, dC_ads/dt, is then the sum of the two fluxes multiplied by the contact area, A_m, between each monolayer of the bilayer and bathing solution:

(A5)

We find the boundary layer (discussed later in the Appendix) to be essentially nonexistent for methanol, ethanol, and propanol, i.e., C_out* = C_out and the bulk alcohol concentration inside the vesicle to be uniform (also discussed later in the Appendix), i.e., C_in* = C_in. With these assumptions and noting that K_eq = k_on/k_off, we get

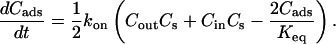(A6)

The rate of accumulation of alcohol inside the vesicle, dC_in/dt, is related to J_inner, i.e.,

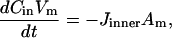(A7)

where V_m is the interior volume of the vesicle.

Concentration uniformity outside vesicle for methanol, ethanol, and propanol

During the alcohol adsorption/desorption in the outer monolayer of the vesicle, the concentration in the boundary layer adjacent to the monolayer, C_out*, is potentially less than the concentration at the edge of the boundary layer, C_out (which is the same concentration inside the flow pipette). The molar flux from edge of the boundary layer to the monolayer surface is

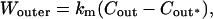(A8)

where k_m is the mass transfer coefficient. At the monolayer surface, the molar flux W_outer is equal to J_outer which reduces to

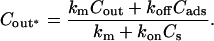(A9)

We calculated the mass transfer coefficient, k_m, values from the mass transfer correlation for laminar flow around a spherical particle,

(A10)

where this relationship is known as the Frössling correlation (Frössling, 1938). Sh is the Sherwood number Re is the Reynolds number 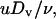and Sc is the Schmidt number 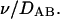Here, u is the velocity of the flow stream, D_v is the diameter of the vesicle, D_AB is the bulk diffusion coefficient of alcohol molecules, and ν is the kinematic viscosity of water.

Equation A9 shows that C_out* is equal to C_out when the quantity k_off × C_ads in the numerator is much smaller than k_m × C_out and the quantity k_on × C_s in the denominator is much smaller than k_m. For a vesicle with a typical 40-μm diameter, k_m increased from 50 to 70 μm/s as the flow velocity u climbed from 0 to 450 μm/s. The maximum values of k_off × C_ads were calculated based on k_off values in Table 1 and the equilibrium C_ads value in Fig. 13 for the alcohol concentration studied. The maximum values of the quantity k_on × C_s were computed by setting C_s = C_max and using C_max and k_on values from Table 1. The numerical values of k_off × C_ads and k_on × C_s are listed in Table 2 and show clearly that the assumption that C_out* = C_out is reasonable for methanol, ethanol, and propanol. For butanol, the relatively large magnitudes of k_on and k_off make the terms k_off × C_ads and k_on × C_s non-negligible. In this case, Eq. A9 was used to calculate C_out* to solve the set of coupled differential equations (Eqs. 11–14) to determine C_ads and C_in as functions of time.

TABLE 2.

Values calculated for order-of-magnitude analysis on Eq. A9

	Methanol	Ethanol		Propanol		Butanol
Cout (M)	4.94	1.70	2.56	0.19	0.39	0.11
km × Cout (mole/(m2 × s) at km = 50 μm/s	0.247	0.085	0.128	0.010	0.020	0.006
km × Cout (mole/(m2 × s) at km = 70 μm/s	0.346	0.119	0.179	0.013	0.027	0.008
koff × Cads(mole/(m2 × s)	0.001	0.001	0.002	0.001	0.002	0.002
kon × Cs (μm/s)	0.26	0.93		6.97		21.60

Timescale for concentration uniformity across membrane

In our derivation of the equations describing the transport of alcohol from the outer solution to the interior of the vesicle, we assumed that the surface density of alcohols in both the outer and inner monolayer were the same. This would be true if the time for the alcohol species to diffuse and equilibrate from the outer monolayer to the inner monolayer was much less than the total time for alcohol equilibration between the outer and inner volume of the vesicle. We estimate this time by modeling the transport of alcohol molecules across the membrane as unsteady state diffusion of a solute in a slab with a no flux boundary at the inner surface, i.e.,

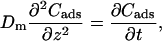(A11)

where z is in the direction perpendicular to the membrane surface and D_m is the effective diffusivity of alcohol through the membrane. The boundary conditions are 1), at the edge of the inner monolayer surface (z = 0) for all t; 2), C_ads = finite value at the edge of the outer monolayer surface (z = l) for t > 0; and 3), C_ads = finite value, but less than C_ads (z = l) at t = 0 for 0 < z < l. The differential equation is solved by separation of variables, and analytical and graphical solutions are readily available in many textbooks (Hines and Maddox, 1985). For any finite value of C_ads (z = l), C_ads (z = 0) approaches C_ads (z = l) when D_m × t/l² ≈ 1.5. For our system, the membrane thickness, l, is ∼4 nm and diffusivity ranges from 10⁻⁸ to 10⁻⁶ cm²/s (Diamond and Katz, 1974; Schoberth et al., 1996). The time to equilibrate would range from 0.2 to 20 μs. This quantity is small compared to the total experiment time of seconds to minutes ensuring that C_ads can be assumed uniform in the membrane.

Timescale for concentration uniformity inside vesicle

As alcohol desorbs from the interior of the membrane, it will be transported by diffusion into the interior aqueous space thus mixing with the interior alcohol/water solution. Convection probably also is occurring, as discussed in the text, but we will only consider diffusion here. If the timescale of mixing is much smaller than the timescale of equilibration of the whole system, which is controlled mainly by the desorption rate, then we can assume that no concentration boundary layer exists in the vesicle's interior. To calculate the time necessary for mixing, we employ the familiar differential equation describing unsteady diffusion of solute inside a sphere, i.e.,

(A12)

The boundary conditions are 1), at r = 0 for all t and 2), C_in = finite value at r = R_v for t > 0; 3) C_in = finite value, but <C_in (r = R_v) at t = 0 for r < R_v. In this model, we assume the only mode of transport inside the vesicle is simple diffusion, neglecting any effect from flow-induced convection. The equation is solved by the separation of variables method. From either the analytical or graphical solution, for any finite value of C_in (r = R_v), C_in (r = 0) approach C_in (r = R_v) when For our particular system with R_v = 20 μm and D_AB = 1 × 10⁻⁵ cm²/s, we find the time for the alcohol concentration to be thoroughly well-mixed inside the vesicle is ∼0.2 s. In comparison, the timescale of equilibration of the whole system is on the order of seconds to minutes. Therefore, we are relatively confident that no concentration boundary layer exists within the vesicle, when diffusion alone is considered.