Ca-Activation and Stretch-Activation in Insect Flight Muscle

Abstract

Asynchronous insect flight muscle is specialized for myogenic oscillatory work, but can also produce isometric tetanic contraction. In skinned insect flight muscle fibers from Lethocerus, with sarcomere length monitored by a striation follower, we determined the relation between isometric force (F₀) at serial increments of [Ca²⁺] and the additional active force recruited at each [Ca²⁺] by a stretch of ∼12 nm per half-sarcomere (F_SA). The isometric force-pCa relation shows that 1.5–2 units of pCa are necessary to raise isometric force from its threshold (pCa ∼6.5) to its maximum (F_0,max). The amplitude of F_SA depends only on the preceding baseline level of isometric force, which must reach at least 0.05 F_0,max to enable stretch-activation. F_SA rises very steeply to its maximum as F₀ reaches ∼0.2 F_0,max, then decreases as F₀ increases so as to produce a constant sum (F₀ + F_SA) = F_max. Thus Ca- and stretch-activation are complementary pathways that trigger a common process of cross-bridge attachment and force production. We suggest that stretch-induced distortion of attached cross-bridges relieves the steric blocking by tropomyosin of additional binding sites on actin, thereby enabling maximum force even at low [Ca²⁺].

INTRODUCTION

Stretch of a calcium-activated muscle triggers a delayed increase of force, a phenomenon called stretch-activation (SA). Stretch-activation is present in skeletal and, especially, in cardiac muscle of vertebrates (Steiger, 1977; Vemuri et al., 1999), but is stronger and longer-lasting in asynchronous fibrillar insect flight muscle (IFM) (Abbott and Steiger, 1977; Pringle, 1978). Three-quarters of all known insect species depend for flight on asynchronous IFM (Josephson et al., 2000b). In these, wingbeat rhythm is not matched to the rate of neural stimulation, which supports oscillatory work at a myogenic rather than neurogenic rhythm. During live insect flight, alternating contractions of antagonistic muscles sustain high power, oscillatory cycling at frequencies from ∼20 Hz in large bugs and beetles to ≥1000 Hz in tiny midges (Pringle, 1978; Josephson et al., 2000a,b).

Stretch-activation has been duplicated in skinned muscle fibers by holding activating calcium at a constant “priming” level (for example, 3 μM free [Ca²⁺]; Tregear et al., 1998), at which isometric force generation is low. With [Ca²⁺] held at priming level, a small stretch (i.e., 1.5% of the fiber length) is followed by a large, delayed rise of active force, persistent over seconds. Reshortening to the original length triggers a delayed reduction of force (shortening deactivation). A stretch superposed on the low force level resulting from shortening deactivation can again trigger SA, recovering the prerelease isometric force (Güth et al., 1981).

Stretch-activation is the most important mode for powering flight in insects that have asynchronous IFM (Jewell and Rüegg, 1966; Abbott and Mannherz, 1970; Josephson et al., 2000b). However, isometric contraction in intact asynchronous IFM tetanized by electrical or nerve stimulation has also been well demonstrated by other studies (Machin and Pringle, 1959; Ikeda and Boettiger, 1965; Heinrich, 1993; Josephson et al., 2000a, 2001). Isometric contraction can be produced in glycerinated Lethocerus IFM fibers by simply raising [Ca²⁺] to ≥0.01 mM in the presence of MgATP (Taylor et al., 1999). The physiological role for isometric contraction in asynchronous IFM is most notable in the use of tetanus (simultaneous prolonged isometric contraction by opposing flight muscles) for shivering thermogenesis, which occurs during the preflight warmup that brings IFM to ∼40°C, as required for flight in bees and most larger insects (Barber and Pringle, 1966; Heinrich, 1993; 1996).

Despite 40 years of investigations, it is still not clear if force development by stretch-activation implies a mechanism different from force development determined by Ca-activation. Moreover, it is controversial whether optimum stretch-activation requires a high Ca-activated tension (pCa ∼4.5; Lund et al., 1987, 1988; Granzier and Wang, 1993), or a minimal Ca-activated tension (Abbott and Mannherz, 1970; Tregear et al., 1998).

Are stretch-activation and Ca-activation additive, complementary, or competitive? What fraction of the total force capability remains to be developed by SA after full isometric activation by Ca²⁺? Does isometric force development after an increase of [Ca²⁺] actually imply latent stretch-activation owing to prestretch of the fiber while relaxed (Jewell and Rüegg, 1966; Granzier and Wang, 1993)?

These questions can be resolved by continuously monitoring sarcomere length during the mechanical force responses. This insures 1), that isometric contraction is not affected by shortening against failing segments of weakened sarcomeres or against excessive end compliance, complications that can induce shortening deactivation and 2), that the size of the half-sarcomere stretch chosen for eliciting SA is maintained constant throughout the experiment, as it must be for determining the dependence of stretch-activation on [Ca²⁺] and isometric force.

In Lethocerus IFM skinned fibers with sarcomere length recording by a striation follower (Huxley et al., 1981), we have determined the relation between isometric force (F₀) at serial increments of [Ca²⁺] and the additional active force (F_SA) recruited at each [Ca²⁺] by a stretch of ∼12 nm per half-sarcomere. Since Mg²⁺ has been reported to depress active force in IFM (White and Donaldson, 1975; M. K. Reedy, unpublished results), experiments were repeated at two [Mg²⁺] to modulate, at the same [Ca²⁺], the isometric force on which SA is superimposed. This provides a baseline for exploring whether SA depends on [Ca²⁺] or on prestretch isometric force. We find that SA can be triggered above a threshold level of Ca-activated force (∼0.05 of maximal isometric force, F_0,max). The amplitude of F_SA depends only on the preceding baseline level of Ca-activated isometric force (F₀). F_SA rises steeply to its maximum as F₀ rises from the threshold level to ∼0.2 F_0,max. As F₀ rises higher, the amplitude of F_SA decreases proportionately, so that the sum (F₀+F_SA) maintains a maximum constant value (F_max). Increasing [Mg²⁺] shifts to the right the dependence of isometric F₀ on pCa, but does not alter the relation between F_SA and F₀. These results indicate that stretch-activation and Ca-activation are complementary in recruiting force-generating cross-bridges. The dependence of SA on a minimum number of Ca-activated cross-bridge attachments suggests that the stretch-induced distortion of cross-bridges acts so as to spread the displacement of tropomyosin over longer segments of actin than those activated by calcium-troponin at low [Ca²⁺]. The mechanism of stretch-activation proposed in this work provides a framework for explaining the ability of IFM to produce oscillatory work.

METHODS

Preparation and mounting of the fibers

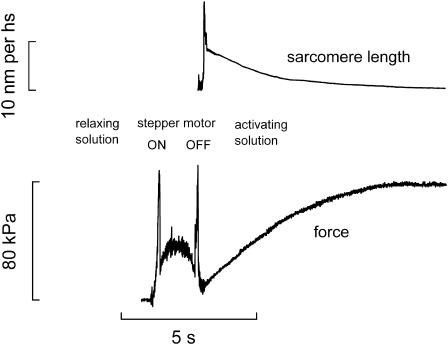
Single fibers were dissected from glycerinated bundles of the dorsal longitudinal muscle of the giant waterbug Lethocerus indicus (Fam. Belostomatidae). The bundles were prepared from dorsal longitudinal muscles permeabilized in a protease-inhibitor cocktail by osmotic-shock treatment, cycling alternately between detergent and glycerol buffers before cryostorage in 75% glycerol relaxing buffer with 5 mM DTT at −80° to −100°C for up to one year before use, as described (Reedy et al., 1988). Fibers, selected for maximum transparency (only ∼30% develop during glycerination the glassy transparency that suits them for the striation follower), were moved from storing solution into relaxing solution. Handcut aluminum T-clips were gently clamped to the ends of a working segment 3–4-mm long. T-clipped fibers were then mounted in the experimental trough containing a drop (∼80 μl) of relaxing solution between the lever arms of a capacitance gauge force transducer (30–40 kHz resonant frequency, Huxley and Lombardi, 1980) and a fast loudspeaker motor (Lombardi and Piazzesi, 1990). The T-clipped ends of the relaxed fiber segment were fixed in air (during timed liftouts of ∼20 s) by capillary tube (I.D. 0.25 mm) application of aqueous rigor solution containing glutaraldehyde (5% v/v) and were then glued to the clips by similar applications of shellac dissolved in ethanol (8.3% w/v; Bershitsky and Tsaturyan, 1995). A rapid solution exchange system held four separate ∼80-μl drops of buffer on a thermoregulated motordriven platform, each drop ∼3-mm deep, optically flattened top and bottom between 3 × 9-mm rectangles of coverslip glass. Horizontal translation by a computer-controlled stepper motor (Linari et al., 1993) changed solutions by moving one drop after another to the fiber, which was kept aligned and unmoving on the optical axis of a striation follower (Huxley et al., 1981). The system allowed immediate and continuous recording of sarcomere length in a selected segment of the fiber in each new solution by the striation follower. As shown in Fig. 1, sarcomere length recording started as soon as the glass floor, supporting any new drop, moved into alignment with the optical axis of the striation follower.

FIGURE 1.

Slow time base records of force (lower trace) and sarcomere length (upper trace) following the transfer to the activating solution (pCa = 4.50, low Mg). The striation follower signal becomes reliable at the end of the movement of the stepper motor which brings the droplet of activating solution to the fiber. Length of the fiber: 3.10 mm; length of the segment under the striation follower, 1.17 mm; initial sarcomere length, 2.61 μm; cross-sectional area, 3500 μm²; temperature, 20.3°C.

Solutions

The composition of the relaxing and activating solutions (Table 1) was calculated, at low and high Mg, with a computer program similar to that described by Brandt et al. (1972), kindly provided by P. W. Brandt. The concentrations of multivalent ionic species are calculated after solving the multiple equilibria of two metals (Ca and Mg) and two ligands (EGTA and ATP), by using the following apparent association constant (log values at pH = 6.8): CaEGTA, 5.9; MgEGTA, 0.5; CaATP, 3.6; MgATP, 4.0. Potassium propionate was used to adjust the ionic strength to 105 mM in all final solutions.

TABLE 1.

Solution compositions

Solution	MOPS (mM)	Na2ATP (mM)	MgAcetate (mM)	EGTA (mM)	NaN3 (mM)	CaCl2 (mM)	Kprop (mM)	Na2CP (mM)	CPK (U/ml)
Relaxing (low Mg)	20	6.6	5.3	5	5	—	15	10	300
Activating (low Mg)	20	6.8	5.3	5	5	5.1	4.4	10	300
Relaxing (high Mg)	20	5.5	6	5	5	—	24.7	10	300
Activating (high Mg)	20	5.6	6	5	5	4.9	14.8	10	300

MOPS, 3-[n-morpholino]propanesulfonic acid; ATP, adenosine triphosphate; EGTA, ethyleneglycol-bis-(b-aminoethyl ether)-n, n, n′, n′-tetraacetic acid; Kprop, potassium propionate; Na₂CP, sodium salt of phosphocreatine; CPK, creatine phosphokinase. Substrate concentration, 5 mM; free [Mg²⁺], 0.3 mM (low Mg), and 1 mM (high Mg). Ionic strength, 105 mM; pH, 6.8 at 20°C.

Experimental protocol

Fiber length was adjusted in relaxing solution so as to have the fiber just taut. Relaxed force was 0.04 ± 0.03 (mean ± SE) F_0,max (where F_0,max is the isometric force developed at saturating [Ca²⁺] in low [Mg²⁺]). Relaxed sarcomere length was measured with a 40× objective at 3–5 regions of the fiber. The variation of sarcomere length along the fibers was at maximum ±0.6% (SE). Average sarcomere length from the five fibers selected for analysis was 2.65 ± 0.02 μm. The changes in the sarcomere length (nm per half-sarcomere, hs) of a selected segment ∼1.0-mm long were continuously monitored by the striation follower. Only the fibers (five) that maintained a good sarcomere length signal throughout the whole experiment were considered for the analysis. In these fibers the shortening accompanying the rise of maximal Ca-activated force was 2.84 ± 1.08 nm/hs and reduced in proportion to the lower force at lower [Ca²⁺].

For each activation, after the isometric force had attained a steady value (F₀), which required from ∼15 s (pCa 3.5) to ∼65 s (pCa 6.7), stretch-activation was induced by applying to the fiber a 0.5-ms step-stretch of 11.8 ± 0.5 nm/hs. This was achieved by adjusting the size of the step produced by the motor to 1.6 ± 0.1% of the fiber length at the beginning of the experiment. In the selected fibers a constant setting for motor stretch remained adequate to produce the desired half-sarcomere stretch for the whole duration of the experiment. Force baseline was measured following development of SA, by applying a large (30–40 nm/hs) step release 1 s after the stretch (Fig. 2 B). After each Ca-activation, lasting from 20 s (pCa 3.5) to 70 s (pCa 6.7), the fiber was transferred back into relaxing solution. A stretch of the same amplitude was imposed on the relaxed fiber at several times during the experiment to determine the passive response to the 12-nm stretch (Fig. 2 A). This was ∼0.2 F_0,max (Fig. 4, row 0). Experiments were done both at 0.3 mM free [Mg²⁺] (low Mg) and 1 mM free [Mg²⁺] (high Mg), taking each fiber through the full pCa range in both cases. The starting [Mg²⁺] level, low or high, chosen for each serial set of [Ca²⁺] increments from pCa = 9 to pCa = 4.5 or 3.5 (low or high Mg²⁺, respectively), was alternated for successive fibers to randomize the cumulative effects of deterioration of the fiber with successive activations. Usually two complete series were obtained, one at high and one at low [Mg²⁺], before the fiber showed impaired mechanical performance, consisting of deterioration in the sarcomere length signal and/or decrease of F₀ at saturating [Ca⁺²] by >20%.

FIGURE 2.

Response of the fiber to the mechanical protocol. (A) In relaxing solution; (B) in activating solution at saturating [Ca²⁺]. In each column, from top to bottom, traces show: fiber length change in % of fiber length (L₀), length change per half-sarcomere of the segment under striation follower and force. The imposed stretch was 1.4% L₀ in both relaxed and activated fiber and the monitored half-sarcomere stretch was ∼14 nm in either condition. Activating solution with pCa 4.5, [Mg²⁺] 0.3 mM. L₀, 3.85 mm; length of the segment under the striation follower, 0.97 mm; sarcomere length, 2.67 μm; cross-sectional area, 3300 μm²; temperature, 20.0°C.

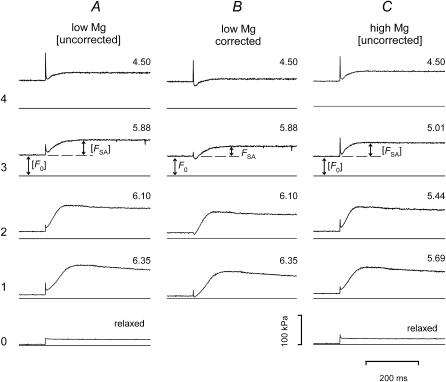
FIGURE 4.

Stretch-activated force responses (F_SA) to 0.5-ms ramp-stretch of ∼12 nm/hs superimposed on steady isometric force (F₀) at each different [Ca²⁺]. Note that the limited time resolution of the records causes inconsistency in the amplitudes for phase-1 elastic responses. Figures on the right of each trace indicate the pCa value. Dashed extension of F₀ indicates the level above which F_SA is measured. Horizontal rows (1–4) are numbered from bottom to top in order of increasing [Ca²⁺]. Row 0 is the response of the relaxed fiber. Bottom line in each panel shows zero force. (A and C) Force responses of the activated fibers are not corrected for the passive response (bracketed labels). In each row records were selected to match F₀ values within ∼5%. (B) Traces obtained from responses of the activated fiber in A after subtraction of the force response in the relaxed fiber. F_0,S was 85 kPa in low Mg and 80 kPa in high Mg. L₀, 3.23 mm; length of the segment under the striation follower, 0.98 mm; initial sarcomere length, 2.65 μm; cross-sectional area, 4100 μm²; temperature, 20.9°C.

Data collection and analysis

Force, motor position, and striation follower signals were recorded with a sampling interval of 0.5 ms via an A/D card (Computerscope EGAA, RC Electronics, Goleta, CA) on a PC. The limited time resolution used in this work does not allow adequate resolution within the phase-1 elastic response (Fig. 2) and accounts for the apparent inconsistency in height of phase-1 spikes in traces in Fig. 4. The responses were measured directly on the PC with the EGAA software. Force and motor position were continuously monitored also on a chart recorder (Multitrace 2 Recorders 5022, Lectromed, Hertfordshire, UK). Data are expressed as mean ± SE.

RESULTS

Isometric force-pCa relation in low and high Mg

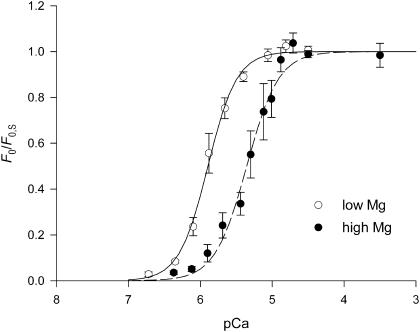
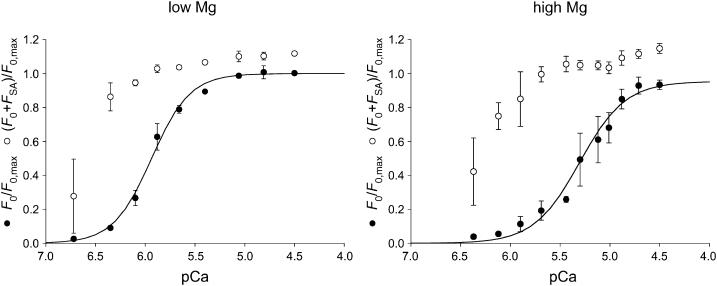
For the same subsaturating [Ca²⁺], F₀ was higher in low Mg than in high Mg, but the maximal isometric force attained at saturating pCa (F_0,S) was only slightly lower (7%) in high Mg: 80 ± 5 kPa (mean ± SE, five fibers) in low Mg and 75 ± 5 kPa in high Mg. However the paired t-test showed that this difference is significant (p < 0.05), therefore both high and low Mg data related to stretch-activation are presented relative to the maximum isometric force, F_0,max, which is the force at saturating pCa (F_0,S) in low Mg.

The force-pCa relations (Fig. 3, low Mg, open circles; high Mg, solid circles) develop roughly the same sigmoidal curvature and slope in either high or low Mg. When the Hill equation is fitted to the data, the parameter n (the Hill coefficient that estimates the steepness of the relation) is 2.17 ± 0.14 and 1.97 ± 0.20 in low and high Mg, respectively, in agreement with values reported from nonflight striated muscle of a marine arthropod (Ashley and Moisescu, 1977). These values are lower than those reported for vertebrate skeletal muscle, where the slope of the force-pCa relation is notably steeper (see Fig. 9 and Discussion). The high Mg relation is shifted toward higher [Ca²⁺] by ∼0.6 units of pCa. pK, the value of pCa at which F₀ = 0.5 F_0,S, is 5.89 ± 0.01 in low Mg and 5.35 ± 0.02 in high Mg, indicating that the inhibition of force induced by a threefold increase in [Mg²⁺] is overcome by a threefold increase in [Ca²⁺]. Note that the effect of Mg²⁺ is at a concentration 2–3 orders-of-magnitude greater than that of Ca²⁺, similar to what was previously reported by Fabiato and Fabiato (1975) for skinned cardiac cells.

FIGURE 3.

Force-pCa relation in low Mg (open circles) and high Mg (solid circles). Steady isometric force F₀ is expressed relative to the isometric force at saturating pCa (F_0,S); vertical bars are SE. F_0,S: in low Mg, 80 ± 5 kPa; in high Mg, 75 ± 5 kPa. Data from five fibers. Low Mg (continuous line) and high Mg (dashed line) are calculated from the Hill equation F₀/F_0,S = 1/(1+10^n(pCa-pK)), where n, the Hill coefficient that expresses the steepness of the relation, and pK, the pCa at which F₀ = 0.5 F_0,S, are the parameters fitted by using a nonlinear least-squares method (SigmaPlot, SPSS Science Software). The best fit parameters are listed in the table

	n	pK
Low Mg	2.17 ± 0.14	5.89 ± 0.01
High Mg	1.97 ± 0.20	5.35 ± 0.02

below.

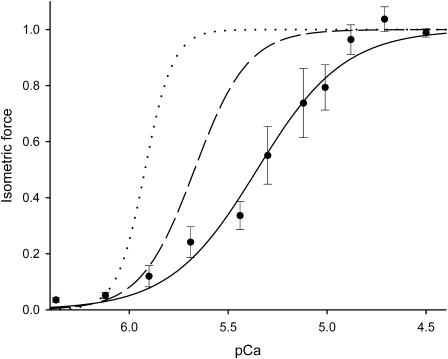
FIGURE 9.

Comparison of force-pCa relations in different species. For each species the force is expressed as relative to the force at saturating pCa. All the relations are obtained with [Mg²⁺] 1 mM. (Solid circles and continuous line) IFM (from Fig. 3, solid circles); (dotted line) skinned rabbit psoas fiber (from Fig. 3B in Brandt et al., 1980); and (dashed line) fast skinned fiber of human vastus lateralis muscle (from Fig. 9B in Linari et al., 2004).

The force response to stretch

As shown in Fig. 2 B, a step-stretch of ∼12 nm/hs superimposed on isometric Ca-activated force elicited a multiphase response consisting of a force rise simultaneous with the step due to the elastic properties of the fiber (phase 1 according to the definition of the force transient proposed by Huxley and Simmons, 1971). This is followed by a rapid fall in force that reaches a minimum within 8 ms (similar to the Huxley and Simmons phase-2 quick recovery), and next by a subsequent rise in force, the stretch-activation (SA), which is reminiscent of Huxley and Simmons phase 3, but exaggerated in extent and duration. These three phases of the response to stretch have also been identified with Huxley and Simmons transient response phases 1–3 in IFM studies by Abbott and Steiger (1977).

Despite limited time resolution, it is clear that the amplitudes of both the phase-1 elastic response and the phase-2 quick recovery increased with rising [Ca²⁺] and the consequently rising level of isometric force on which the step-stretch was superimposed (Fig. 4 A, rows 1–4). Because the time taken by the stretch (∼0.5 ms) is long relative to the high speed of the early components of quick recovery, the phase-1 response is truncated and consequently the active stiffness of the fiber is underestimated. However, a precise determination of stiffness was not among the aims or requirements of this work.

The passive response of the fiber to the 12-nm stretch (Fig. 2 A and Fig. 4 A, row 0) is likely due to the elasticity in parallel with the contractile component (White, 1983), primarily the C-filaments that link myosin filaments to Z-bands in IFM (Granzier and Wang, 1993). Thus the corrected active response to stretch can be obtained by subtraction of the force records of the relaxed fiber from the force records of the activated fiber (as was done to derive panels B from panels A in Fig. 4). All data reported in the graphs in Figs. 5–8 are obtained after subtraction of passive response.

FIGURE 5.

Relations of F₀ (solid circles) and (F₀ + F_SA) (open circles) versus pCa at the two [Mg²⁺]. The ordinate in both graphs is expressed as relative to F_0,max, the isometric force at saturating pCa in low Mg. Data from three fibers. Continuous lines are calculated from Hill equation using the best-fit parameters listed in the table

	n	pK
Low Mg	2.26 ± 0.18	5.94 ± 0.02
High Mg	1.89 ± 0.20	5.31 ± 0.03

below.

FIGURE 6.

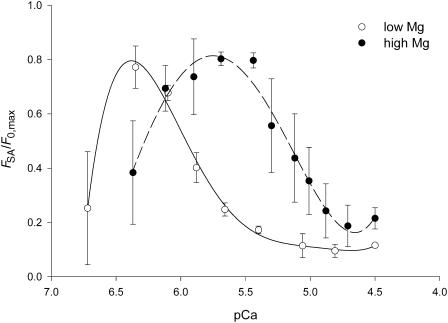
Relation of F_SA versus pCa. Same data as in Fig. 5. The ordinate is normalized to F_0,max. Lines are the polynomial fit to data. Low Mg (open circles and continuous line); high Mg (solid circles and dashed line).

FIGURE 7.

Relations of (F₀+F_SA) (A) and F_SA (B) versus F₀. All data are made relative to F_0,max. Same data and symbols as in Fig. 6. In B, lines are obtained by linear regression analysis to either low Mg (continuous line) or high Mg (dashed line) in the range of F₀/F_0,max >0.09. Parameters (mean ± SE) of the line fits in B are listed in the table

	Slope	Ordinate intercept
Low Mg	−0.75 ± 0.02	0.86 ± 0.01
High Mg	−0.78 ± 0.06	0.92 ± 0.04

below.

FIGURE 8.

Rate of development of F_SA(r) against pCa (A) and F₀ (B). In both graphs, open circles refer to low Mg and solid circles to high Mg. The value of r is measured as the reciprocal of the time from the minimum of force at the end of phase 2 to 63% of F_SA. In B, lines are the best fit on the data (low Mg, continuous line and high Mg, dashed line) of the exponential equation: r = a + b*(1–exp(−(F₀/F_0,max)/c)). As shown in the table

	a (s−1)	b (s−1)	c
Low Mg	−1.79 ± 5.28	38.54 ± 5.16	0.168 ± 0.057
High Mg	−1.40 ± 2.15	39.82 ± 2.03	0.168 ± 0.019

below, a is zero and b and c have similar values independent of [Mg²⁺].

The amplitude of the fall in force during phase 2 was larger at higher [Ca²⁺] and F₀ (Fig. 4 A), so that the minimum level of uncorrected force sank progressively closer to the level of prestretch isometric force. After subtraction of the passive response to stretch, this corrected minimum undershoots the original isometric force (Fig. 4 B), as reported by Thorson and White (1983). Considering the large size of the stretch, it is likely that the low force reached during phase-2 recovery is due not only to a “relaxation” process in the attached myosin heads, but also to detachment of strained heads and their rapid reattachment to sites farther along the actin filament (White, 1983; Piazzesi et al., 1997).

Stretch-activated (phase-3) force slowly decays over hundreds of ms (Fig. 4). The amplitude of stretch-activated force, F_SA, is measured by the difference between the peak force in phase 3 and the isometric force preceding the stretch. Fig. 4, A and C, shows that the amplitude of F_SA decreases, whereas the speed of its development increases, as [Ca²⁺] and F₀ increase. Comparison of records in each row of columns A and C in Fig. 4 shows that similar amplitude and speed of development of F_SA can be obtained at different [Ca²⁺], provided that F₀ at different [Ca²⁺] is adjusted to the same level by changing [Mg²⁺]. As shown by comparison of traces 0A and 0C in Fig. 4, the properties of the relaxed fiber are not affected by [Mg²⁺].

Stretch-activation in relation to [Ca²⁺] and isometric force

A quantitative analysis of the relation of SA to [Ca²⁺] and isometric force is shown in Figs. 5–8. For each fiber all data are plotted relative to the maximum isometric force F_0,max, that is, to the force at saturating pCa in low Mg.

Plots of total force (F₀ + F_SA) versus pCa are shown in Fig. 5 for both low Mg (left panel, open symbols) and high Mg (right panel, open symbols) together with the corresponding isometric force-pCa relations (solid symbols). In either Mg²⁺ concentration, (F₀ + F_SA) begins to increase abruptly, as soon as the [Ca²⁺] is enough to cause the development of a minimum isometric tension (0.05 F_0,max), which defines the threshold for triggering SA. (F₀ + F_SA) attains its maximum value, F_max, at a [Ca²⁺] much lower than that required to raise F₀ to its maximum. F_max always remains ∼10% > F_0,max. The (F₀ + F_SA)-pCa relation is shifted to the right at high Mg, similar to the rightward shift of the F₀-pCa relation. However, a precise definition of the early events in the (F₀ + F_SA)-pCa relation and of its Mg-dependent shift is difficult, due to the abrupt increase of F_SA near the SA triggering threshold.

In Fig. 6 the amplitude of stretch-activated force, F_SA, is plotted versus pCa for the two [Mg²⁺]. F_SA increases steeply to its maximum value within 0.4–0.6 pCa units at the SA triggering threshold. F_SA then decreases to its minimum value of ∼10–20% of F_max at the [Ca²⁺] high enough to produce maximum isometric force. The minimum F_SA at saturating pCa is larger in high Mg (∼0.2 F_0,max) than in low Mg (∼0.1 F_0,max) because in high Mg the maximum isometric force is 7% lower than in low Mg, whereas F_max is the same. In parallel with the effect of [Mg²⁺] on the F₀-pCa relation, high Mg also shifts the maximum value of F_SA toward higher [Ca²⁺] by ∼0.6 units.

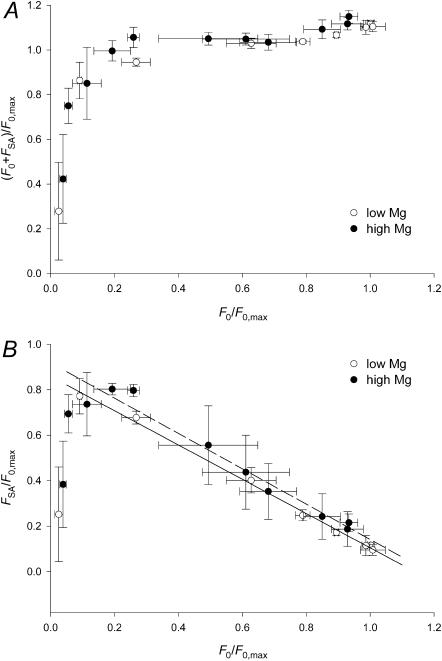
Fig. 7 shows the relations of both (F₀ + F_SA) (A) and F_SA (B) versus F_0, where all values are expressed as a fraction of F_0,max. The dependence of total force (F₀ + F_SA) on F₀ in either the low Mg (open circles) or high Mg (solid circles) regime is the same, independent of [Mg²⁺]. (F₀ + F_SA) rises abruptly as F₀ increases and at ∼0.2 F_0,max has already attained ∼95% of F_max. This is the consequence of the fact that SA is not directly dependent on either [Ca²⁺] or [Mg²⁺] and only depends directly on a minimum level of isometric force preceding the step. Moreover, as F₀ rises above this minimum threshold value, F_SA quickly reaches a maximum and then reduces in proportion to the further increase in F₀. The complementary role of SA and isometric tension between 0.2 F_0,max and F_0,max is made evident in Fig. 7 B by the linear relation between F_SA and F₀. In the range where F₀ increases from 0.2 to 1.0 F_0,max, F_SA reduces proportionally from a maximum of 0.8 F_0,max to a minimum of ∼0.1 F_0,max, independent of the proportions of [Ca²⁺] and [Mg²⁺]. In fact the slope and the ordinate intercept of the linear regression equations fitted to low Mg (open circles) and high Mg data (solid circles) do not differ significantly (see table in Fig. 7 legend). For F₀ <0.05 F_0,max, SA is dramatically impaired, and then, above the threshold level (∼0.05 F_0,max), SA develops explosively. This explosive rise explains the difficulty in precisely defining the relation of F_SA versus pCa when F₀ is <0.2 F_0,max.

The rate of stretch-activated force development

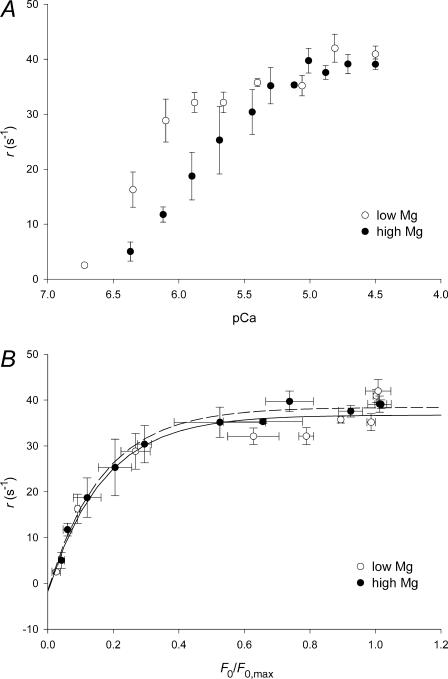
The force traces in Fig. 4 show that the development of stretch-activated force (phase 3) does not occur through a simple exponential process. At low F₀ and large F_SA phase 3 shows a sigmoidal time course. As F₀ increases and F_SA reduces, phase-3 time course becomes faster and more exponential-like. Thus the speed of the stretch-activated force development increases with rising [Ca²⁺]. Fitting the series of responses with the same equation (sigmoidal or sum of two exponentials) failed to give satisfactorily results; however, an estimate of the dependence on [Ca²⁺] of the rate of F_SA development can be obtained by plotting r, the reciprocal of the time from the minimum of force at the end of phase 2 to 63% of F_SA, against pCa (Fig. 8 A). The 63% time point can only give an approximate estimate of the overall rate, because it takes in the first component seen at lower F₀ and [Ca²⁺], but the resulting relations nevertheless turn out to be analytically useful. Thus, at each nonsaturating pCa, r is higher in low Mg, but at saturating pCa, r reaches the same value in both high and low Mg. The relations do not superimpose if the high Mg relation is shifted to the left by the difference between pK values in Fig. 5 (∼0.6 pCa units). After such a shift, the high Mg data points fall to the left of low Mg data points, especially in the region of threshold for SA. However, low Mg and high Mg data almost superimpose when plotted versus F₀ (Fig. 8 B), so we take it as confirming again the dependence of F_SA on F₀ rather than on pCa.

DISCUSSION

From our study of glycerinated IFM from the waterbug Lethocerus, we identify three primary findings not previously detailed or correlated in any study of asynchronous IFM. First, sustained isometric contraction can be elicited at slack fiber length with no imposed stretch, as a sigmoidally rising response to rising [Ca²⁺]. The maximum isometric force in Lethocerus fibers, F_0,max, is ∼80 kPa, which is slightly above the upper force range cited (20–70 kPa; Josephson et al., 2000a) for electrically stimulated tetanus in live asynchronous IFM. Second, this capability for Ca-dependent isometric activation coexists in a complementary relation with the IFM capability for stretch-activated delayed rise of active force. This relation is such that the sum of calcium-activated force (F₀) plus stretch-activated force (F_SA) reaches a maximum total value, F_max (∼10% larger than F_0,max), as soon as rising [Ca²⁺] brings F₀ to ∼0.2 F_0,max. When [Ca²⁺] rises higher still, F_max stays constant, so that F_SA progressively reduces from 80% to 10% of F_0,max, replaced by F₀ as it rises toward its maximum. Third, the capacity to reach maximum stretch-activation rises almost explosively over a much shorter pCa interval (0.4–0.5 pCa units) than does the capacity for maximum F₀, which develops over an interval of ∼1.5 pCa units.

Isometric force and its relation to [Ca²⁺]

The isometric force capability of maximally Ca-activated skinned fibers of IFM in our experiments (∼80 kPa) is comparable to that found by Granzier and Wang (1993). However, they found a similar high level of isometric force only after a prestretch of 5% of the fiber length. Since sarcomere length during isometric force development was not monitored in those experiments, it seems conceivable that, upon isometric Ca-activation of unstretched fibers, initial shortening (greater than the ∼3 nm/hs recorded in our experiments) against attachment compliance or against a weak segment along the fiber could induce shortening deactivation and depress isometric force, requiring a prestretch to recover full force. A similar explanation may apply to the finding by Lund et al. (1987) that a prestretch can markedly increase the Ca-activated ATPase rate.

The slope of the F₀-pCa relation found for Lethocerus IFM in this work, measured by Hill's coefficient n, is ∼2, a value smaller than those (3–6) found in vertebrate skeletal muscle in our laboratory and reported in literature (Fig. 9). This shows that the range of pCa units from threshold to saturation of isometric force is 2.5–5 times wider in Lethocerus IFM than in vertebrate skeletal muscle. The reduced steepness of the isometric force-pCa curve is consistent with the reduced number of Ca⁺² binding sites found in troponin-C isoforms of Lethocerus IFM (Qiu et al., 2003; Agianian et al., 2004). The consequent reduced sensitivity of Lethocerus IFM thin filaments to activation by submaximal [Ca²⁺] under isometric conditions leaves wider opportunity for the stretch-dependent mechanism to elicit maximum force at subsaturating [Ca²⁺].

Effects of Mg

We find that a threefold increase of [Mg²⁺] from 0.3 to 1 mM, with no change in MgATP substrate concentration, causes a decrease of isometric force developed at subsaturating [Ca²⁺]. This agrees with previous findings by White and Donaldson (1975) in IFM and by Ashley and Moisescu (1977) in crustacean muscle that high [Mg²⁺] suppresses active force. However, the force-inhibition of Lethocerus IFM by a threefold rise in [Mg²⁺] is almost completely overcome by a threefold increase in [Ca²⁺]. The result of this competitive inhibition is that the F₀-pCa relation in high Mg is shifted by ∼0.6 units toward higher [Ca²⁺], whereas the F_0,max level of force at saturating [Ca²⁺] is approximately the same in low and high [Mg²⁺] (Fig. 3). It is not clear if the same kind of Ca²⁺-Mg²⁺ competition applies to the rate of stretch-activated force development, r (Fig. 8 A). Both the r-pCa relation and the F₀-pCa relation span 1.5–2 pCa units and are shifted toward higher [Ca²⁺] in high Mg, although the shift of r-pCa relation is less than that of F₀-pCa relation. On the other hand, stretch-activated force development is a complex process and r is a parameter that only roughly describes its speed (see further discussion in Mechanism of Stretch-Activation).

Relation between Ca-activation and stretch-activation

One main finding of this work is that F_max, the maximum force attained by the sum of F₀ and F_SA, is a plateau that stays constant for all [Ca²⁺] above the level necessary for the isometric force to attain 0.2 F_0,max (Figs. 5 and 7 A). The contribution of stretch-activated force is maximum at this point along the F₀-pCa relation (Fig. 6). As [Ca²⁺] and isometric force increase, the contribution of stretch-activated force decreases, until, at pCa 5–4.5, F₀ reaches its maximum and F_SA its minimum (Fig. 5). The diminishing contribution of F_SA to total maximum force is linearly related to the growing contribution from F₀ (Fig. 7 B). Thus the F_max plateau expresses a ceiling of maximum force, corresponding to the recruitment of a maximum number of force-generating cross-bridges, X, of which one fraction, C, becomes force-generating in response to Ca²⁺, whereas the remainder, S = X–C, can be recruited by stretch. As C increases with rising [Ca²⁺], S reduces accordingly, directly limiting the additional force, F_SA, that can be recruited by stretch. Note that SA occurs only above the minimum threshold F₀ value of 0.05 F_0,max, indicating that there is a minimum number of cross-bridges that must be attached to initiate stretch-activation. Then, F_SA quickly attains its maximum contribution of 80% of maximum force over the same pCa interval that brings isometric force to ∼20% of F_max. The saturation of F₀ by rising calcium takes place over a [Ca²⁺] interval of 1.5 pCa units, whereas the explosive rise in F_SA takes place across an interval of only 0.5–0.6 pCa units. The use of two [Mg²⁺] demonstrates that the constant factor for full triggering of F_SA is the level of preceding force, not [Ca²⁺].

Our finding that F_max is ∼10% > F_0,max can be explained by a corresponding increase in the number of crossbridge attachments after stretch. A 12-nm/hs stretch would exceed the axial range over which most isometric cross-bridges can remain attached. Detachment of strained cross-bridges upon stretch is suggested by the decrease in force during the phase-2 quick recovery (Fig. 4 B). Rapid detachment and reattachment after the stretch, thereby establishing a new distribution, has been described in frog skeletal muscle (Piazzesi et al., 1997). A small number of the prestretch cross-bridges remaining attached during stretch may add to the number of cross-bridges newly attached after stretch, to produce a total F_max, 10% > F_0,max. Alternatively, F_max may be higher without change in the number of attached cross-bridges if a small fraction of original cross-bridges remaining attached after the stretch contribute a higher force per cross-bridge to total force. A third possibility exists that the 10% difference between F_max and F_0,max is due to the contribution of a parallel elasticity recruited during activation in addition to that responsible for the passive response that has been subtracted from the active force. This supplementary parallel elasticity could be due to a cytoskeleton structure sensitive to Ca-activation (Bagni et al., 2002). Without stiffness measurements and without definition of the relation between the amount of stretch-activated force and the size of the stretch, it is not possible to discriminate among these possibilities.

Mechanism of stretch-activation

Our finding that a minimum level of active isometric force, and thus a minimum number of Ca-activated cross-bridges, is necessary to elicit stretch-activation weakens the hypotheses that non-cross-bridge strain sensors between thick and thin filaments (White, 1983; Bullard et al., 1988; Reedy et al., 1994) or between thick filaments and Z-band (Thorson and White, 1983; Al-Khayat et al., 2003) are required to recruit force generating cross-bridges in IFM. A second proposal, the match-mismatch model (Wray, 1979), is inconsistent with our findings. That Ca-activated, isometric force can reach 90% of the maximum force, whereas stretch-activated force adds only ∼10% to total force, is inconsistent with the hypothesis that a stretch-induced shift in relative register between helical arrays on myosin and actin filaments transforms an isometric state highly inhibited by lattice mismatch to a state highly enabled by a lattice-matched position. Moreover, a high degree of lattice register has been observed in maximally Ca-activated isometric contractions by EM in IFM quick-frozen for EM tomography (Taylor et al., 1999; Tregear et al., 2004). We propose that the mechanism through which stretch promotes recruitment of cross-bridges in IFM is that the distortion of the Ca-activated cross-bridges by the stretch displaces tropomyosin (Tm) via IFM-specific structural interactions involving the regulatory proteins (Bullard et al., 1988; Agianian et al., 2004), thereby relieving steric blocking by Tm of myosin binding sites on actin, and allowing more cross-bridge attachment.

At low [Ca²⁺] with few cross-bridges attached, Tm blocking of myosin binding sites is considered the main obstacle to the attachment of more cross-bridges (Brandt et al., 1987, 1990). Stretch-induced distortion of the attached cross-bridges can displace longer segments of Tm and open more binding sites than were opened by Ca-troponin. Our experiments indicate that the fraction of Ca-activated cross-bridges required to produce 20% of F_0,max is sufficient to open all of the remaining binding sites to cross-bridge attachment.

The explosive increase in F_SA between 0.05 and 0.2 F_0,max indicates a positive feedback mechanism: the first stretch-promoted attachments produce further displacement of Tm allowing further opening of binding sites that repeat the process as a cascade until saturation of binding sites occurs. This positive feedback mechanism is particularly evident at low F₀, where, as shown by the sigmoidal shape of tension rise during stretch-activation, sequential recruitment takes longer since the initial attachments are fewer. As Ca-activated cross-bridge attachments increase, the number of binding sites simultaneously exposed by stretch-induced displacement of Tm increases, whereas the number of cross-bridges remaining to be recruited by stretch is reduced. Thus the rate of the stretch-activated force development increases, whereas F_SA reduces. The positive feedback mechanism produces a steeply developing saturation of the amplitude of SA (Fig. 7), whereas the rate of SA development increases with the number of cross-bridges present before the stretch (Fig. 8 B). It is possible that the stretch-activation mechanism we propose is present in all asynchronous IFM. This view is strengthened by the finding that two TnC isoforms, shown in Lethocerus IFM to separately enable either stretch-activation or Ca-activation (Agianian et al., 2004), are also found in fruitflies and mosquitoes (Qiu et al., 2003). EM evidence shows that IFM tropomyosin movements in vitro correspond closely to those shown by vertebrate Tm (Cammarato et al., 2004). Although the two isoforms of TnC are not found in other muscles that exhibit stretch-activation, such as vertebrate myocardium, a mechanism based on axial spread of tropomyosin displacement, promoted by stretch-induced distortion of attached cross-bridges, is consistent with present knowledge of the steric blocking mechanism of regulation, in which cross-bridge binding and troponin can work in concert to shift Tm away from the myosin binding sites (Bremel and Weber, 1972; Maytum et al., 1999; Gordon et al., 2000), even on actin monomers far from those bound to myosin heads.

Our finding that stretch-activation is almost fully replaced by Ca-activation at saturating [Ca²⁺] is not in contradiction with previous studies showing that oscillatory work elicited by sinusoidal length changes rises with rising [Ca²⁺] (Jewell and Rüegg, 1966; Blanchard et al., 1999; Irving et al., 2001). Under oscillatory work conditions, deactivation caused by the shortening phase, whatever the [Ca²⁺], very probably induces low force and low number of cross-bridge attachments (Güth et al., 1981), from which the subsequent restretch phase would recover large F_SA, according to the stretch-activation mechanism proposed here. To model in detail the interplay between shortening deactivation and stretch-activation will require future work aimed at determining the dependence on the size of the length change of both shortening deactivation and stretch-activation and the related changes in number of cross-bridges.