The Role of Unstructured Extensions in the Rotational Diffusion Properties of a Globular Protein: The Example of the Titin I27 Module

Abstract

The possibility of predicting the overall shape of a macromolecule in solution from its diffusional properties has gained increasing importance in the structural genomic era. Here we explore and quantify the influence that unstructured and flexible regions have on the motions of a globular protein, a situation that can occur from the presence of such regions in the natural sequence or from additional tags. I27, an immunoglobulin-like module from the muscle protein titin, whose structure and properties are well characterized, was selected for our studies. The backbone dynamics and the overall tumbling of three different constructs of I27 were investigated using ¹⁵N NMR relaxation collected at two ¹⁵N frequencies (60.8 and 81.1 MHz) and fluorescence depolarization spectroscopy after labeling of a reactive cysteine with an extrinsic fluorophore. Our data show that the presence of disordered tags clearly exerts a frictional drag that increases with the length of the tags, thus affecting the module tumbling in solution. We discuss the use and the limitations of current approaches to hydrodynamic calculations, especially when having to take into account local flexibility.

INTRODUCTION

A significant portion of the currently known proteins is made up by a serial assembly of building blocks that form independently folded units (or domains). The possibility of cutting proteins into such smaller units able to retain their three-dimensional (3D) structure and functions has opened new avenues into the study of proteins whose size and/or shape would otherwise be well outside the range of most of the high-resolution techniques. Multidomain proteins may then be approached by characterizing the structure of their isolated domains under the assumption that these will not, to a first approximation, be influenced by sequence or spatially contiguous regions (for reviews see Bork et al., 1996; McEvoy et al., 1997). Once the structures of the individual components have been obtained though, more work is needed to determine how they are assembled in the full-length protein. The mutual domain orientations and the dynamics of the linking regions are critical parts of this analysis to reconstruct the overall shape and structure. It is therefore important to develop tools that allow us to establish a confident way to determine this information.

A few years ago, we started a project aiming at the characterization of the structure of titin, a giant muscle protein containing up to 300 semiindependent domains interspaced sequentially with no linkers in between (Labeit and Kolmerer, 1995). Titin is an essential muscle protein able to form filaments 1-μm long that connect half of the sarcomere from the Z-disk to the M-line (for a recent review see Granzier and Labeit, 2002). The titin filament is thought to determine the length of the muscle fiber as a “molecular ruler” (Labeit et al., 1991) and to have other important regulatory functions. Determination of the properties of titin domains has been of major interest both from the structural and from a more functional perspective. Large interest has in particular been paid to establishing the elastic properties of titin domains as they could have a functional role in explaining passive muscle elasticity (Granzier et al., 2002). For our studies it was important to determine the relative degree of independence and flexibility of individual domains. We addressed these questions by a number of complementary techniques such as small-angle scattering, NMR, and fluorescence studies. One of the practical problems we encountered was that often our constructs would contain unstructured tags, added for purification purposes and not removed. This is a common practice among biochemists and does not seem to prevent or interfere with structure determination by NMR or crystallography. The extensions could however affect the diffusional properties of the specimens thus becoming important when trying to characterize the motions and shape of the proteins.

To shed light on this problem, we decided to carry out an extensive study using one of the best characterized of the titin domains, the 27th module present in the region of the protein localized in the sarcomere I band (I27). This domain has been characterized both by NMR and by fluorescence (Improta et al., 1996; Politou et al., 1995, 1996). We studied the dynamical properties of this domain when isolated and when attached to histidine tags of different lengths. Both NMR relaxation and fluorescence depolarization anisotropy, the two techniques most commonly used for this purpose, were used to obtain a more reliable estimate of the overall rotational correlation times. The experimental results were then compared with hydrodynamic calculations using a rigid-body approach. The effect of disordered main-body residues is discussed together with the limitations of the current methods. Our results pave the way for further studies using longer multidomain titin constructs and are of more general interest for studies that aim at characterizing the dynamical properties of folded domains attached to unstructured regions.

MATERIALS AND METHODS

Sample production

Three I27 constructs were used in this study. The first, I27_SHT (short His-tag), is the original one described in Politou et al. (1996) and contains a Met(His)₆(Ser)₂ tag without the insertion of a cleavage site. The second, I27_LHT (long His-tag) contains the same Met(His)₆(Ser)₂ tag followed by a factor Xa protease cleavage site (IleGluGlyArg↓Gly). This results in the addition of an extra N-terminal Gly to the original I27 sequence after enzymatic removal of the His-tag to produce the third construct I27_NHT (no His-tag). To obtain the I27_LHT construct, the DNA sequence of I27 was subcloned into the pET8c vector and fused amino-terminally with the required tag sequence.

Expression was induced in the Escherichia coli BL21(DE3)pLys S strain (Novagen, Merck KGaA, Darmstadt, Germany) using 0.5 mM isopropyl-d-thiogalactopyranoside (IPTG), when the absorbance at 595 nm was 0.5. The ¹⁵N-labeled samples were obtained by growing cells in minimal media containing (¹⁵NH₄)₂SO₄ (Isotec, Cambridge, MA) as the sole source of nitrogen. The recombinant proteins, either ¹⁵N-labeled or unlabeled, were purified by metal chelate affinity chromatography on Ni²⁺-NTA agarose (Quiagen, Hilden, Germany) as described by Politou et al. (1994), using an imidazole gradient at pH 8. Fractions eluting at 300 mM imidazole contained the protein, as controlled by SDS-PAGE on 15% polyacrylamide gels, and were dialyzed against 20 mM NaH₂PO₄/Na₂HPO₄, pH 7. If necessary, the samples were further purified by size exclusion HPLC (SE-HPLC) using a Beckman System Gold Model 126 with ultraviolet/visible D-166 detector (Beckman Instruments, Fullerton, CA). The separating system consisted of a 6 × 40 mm TSK PROGEL PW_XL precolumn followed by one 78 × 300 mm TSK G4000 PW_XL column and two 78 × 300 mm TSK G3000 PW_XL columns (Toso Biosep, Stuttgart, Germany). The flow rate was 0.35 ml/min, and before injection each sample was centrifiltered on 0.22 μm cellulose acetate microcentrifuge filters (Spin-X, Sigma, St. Louis, MO). After purification, the samples were concentrated with a CentriconYM-3 centrifugal concentrator (Millipore, Billerica, MA) to ∼5 mg/ml for NMR analysis.

To obtain I27_NHT, after the NMR measurements the ¹⁵N-labeled I27_LHT module was diluted to 0.15 mg/ml and then dialyzed into factor Xa cleavage buffer (100 mM NaCl, 50 mM Tris-HCl, 1 mM CaCl₂, pH 8). Removal of the His-tag was then done by incubation with 18 units/ml of factor Xa protease (Novagen) at room temperature for 48 h. Factor Xa was inactivated with 8.7 μM of 4-(amidinophenyl)methanesulfonyl fluoride hydrochloride (Calbiochem, Merck KGaA). The reaction mixture was dialyzed in 20 mM Tris-HCl, 200 mM NaCl, 2 mM β-mercaptoethanol (Ni²⁺-NTA equilibration buffer without NP-40) and applied to the Ni²⁺-NTA agarose column. The ¹⁵N-labeled I27_NHT was recovered in the flow-through fractions as confirmed by SDS-PAGE on 15% polyacrylamide gels. It was then concentrated to ∼1 mg/ml (Centricon YM-3) and then dialyzed in 20 mM NaH₂PO₄/Na₂HPO₄, pH 7. The protein was then further purified by SE-HPLC as described above, and again concentrated (Centricon YM-3) to ∼4 mg/ml for NMR analysis.

Sample concentrations were determined in a Beckman DU 640M spectrophotometer from the absorbance at 280 nm using absorption coefficients computed from the sequence of 0.61, 0.64, and 0.71 ml mg⁻¹ cm⁻¹ for I27_LHT, I27_SHT, and I27_NHT, respectively, after correcting for scattering contribution by subtracting the absorbance at 320 nm. A Kratos Compact 4 MALDI-TOF mass spectrometer (Kratos Analytical, Manchester, UK) was employed to check the molecular masses of the purified modules.

Protein labeling with fluorophores

Because of the weak intrinsic fluorescence of protein chromophores, an extrinsic fluorescent probe, acrylodan [(6-acryloil-2-(dimethylamino)naphthalene)] (Molecular Probes, Eugene, OR), was covalently attached to some I27 preparations for fluorescence anisotropy measurements. The reaction formed a very strong thioether bond with an exposed cysteine (most likely Cys-47, Cys-63 being buried), as confirmed by fluorescence spectroscopy using a Perkin Elmer LS50B spectrofluorimeter (Wellesley, MA).

The labeling reaction was made by adding dropwise over a 10-min period a 10-fold molar excess of the probe dissolved in methanol to a 1 mg/ml protein solution in 20 mM NaH₂PO₄/Na₂HPO₄, at pH 7. The reaction was performed under stirring at 22°C in the dark for 48 h. The excess of fluorescent probe was eliminated first through centrifiltration at 13,000 rpm for 10 min and then by extensive dialysis. The degree of labeling was determined by ultraviolet spectroscopy, correcting the protein absorbance at 280 nm for the contribution of the probe at this wavelength (correction factor 0.31 × A₃₉₁). The labeled proteins were further purified by the same SE-HPLC system as described above, but including a RF-535 fluorescence detector (Shimadzu Italia, Milan, Italy) operating with λ_ex = 391 nm and λ_em = 515 nm. Care was taken to collect only the main fluorescent peak. The samples were then concentrated with a Centricon YM-3 centrifugal concentrator to 0.1–0.2 mg/ml before fluorescence anisotropy experiments.

For the pH-dependence comparison, a single acrylodan-labeled I27_SHT preparation was purified by SE-HPLC in 20 mM NaH₂PO₄/Na₂HPO₄, pH 7, and was then split into two aliquots. One was dialyzed in 20 mM NaCH₃COO at pH 4.5. Both aliquots were then concentrated to 0.1–0.2 mg/ml, and their purity confirmed with SE-HPLC.

Fluorescence anisotropy

Dynamic fluorescence measurements were performed by means of a frequency modulated phase fluorimeter (Digital K2, ISS, Champaign, IL). The excitation was accomplished by the 363.7-nm line of an argon ion laser (Spectra Physics, 2025, Mountain View, CA) operating at 30 mW. The laser intensity was modulated by a radiofrequency generator over a frequency range of 0.6–300 MHz. Digital data acquisition and storage was provided by the ISS-A2D ADC card inserted in a personal computer. For each data set, at least 15 logarithmically spaced frequencies were employed in the range 5–300 MHz with a cross-correlation frequency of 400 Hz. Phase angles and modulation ratios accuracy were of 0.2° and 0.004, respectively. Long-pass filters at 477 nm for the sample and at 435 nm for the reference (Andover, Salem, NH) were employed to cut Rayleigh and Raman scattering. The samples were placed in quartz 10-mm path cells thermostatically maintained at 20 ± 0.2°C by a Haake recirculating bath (Thermo Electron, Karlsruhe, Germany). For further details, see Collini et al. (1995).

For lifetime measurements, the emission polarizer was set at the magic angle position, and a solution of dimethyl-popop (1,4-bis(4-methyl-5-phenyloxazol-2-yl)benzene) in ethanol was used as reference sample of known lifetime (1.45 ns) (Lakowicz, 1999). The phase shift and the demodulation of the fluorescence signal with respect to the incident signal was acquired as a function of the modulation frequency in the range 5–300 MHz. These quantities are related to the fluorescence lifetime by expressions involving the Laplace transform of the fluorescence intensity (Lakowicz, 1983; Lakowicz et al., 1984). Thereby, a fit of phase shifts and demodulations versus modulation frequency gives the parameters of the fluorescence decay. In general, the fluorescence lifetime decay can be analyzed as a sum of discrete exponential components:

(1)

where α_i are the preexponential factors and ϕ_i are the corresponding lifetime values. Data fitting gives the lifetime values and the corresponding fractional intensity normalized to unity defined as follows:

(2)

Fluorescence decay can also be analyzed by employing a lifetime distribution rather than a sum of discrete components:

(3)

where ϕ_i is the lifetime of the i-th fluorescent species and α_i are the preexponential factors, which, here are replaced by Gaussian distribution functions α_i(τ) according to:

(4)

with parameters ϕ_i, the central value of the i-th distribution, and w_i, the corresponding width.

When performing a fluorescence anisotropy decay measurement, vertically polarized excitation light is used and the emission is detected both in the parallel () and in the perpendicular () polarizer configurations. The two components of the fluorescence intensity are related to the fluorescence anisotropy, r(t), by:

(5)

Again, in the frequency domain we measure the difference in phase angles and the demodulation ratios for each component, respectively, defined as:

(6)

which are related to the intensity components, according to Collini et al. (1992):

(7)

where is the Laplace transform of the perpendicular and parallel components of the fluorescence intensity. In this work we have always found that the time decay of r(t) can be fitted by the sum of two exponentials, given by:

(8)

where r₀ is the limiting anisotropy, τ₁ and τ₂ are the two rotational correlation times with relative amplitudes g₁ and g₂ = 1 − g₁. The rotational correlation times were then corrected to standard conditions (H₂O, 20°C) using values of 1.0101 and 1.0087 cPs, extrapolated from the tabulated values at 20°C (Weast, 1986), for the 20 mM NaH₂PO₄/Na₂HPO₄, pH 7, and for the 20 mM NaCH₃COO, pH 4.5 buffers, respectively.

NMR relaxation measurements

Solutions of 0.4 and 0.7 mM in NaH₂PO₄/Na₂HPO₄ at pH 7 were initially used for the NMR relaxation analysis of I27_NHT and I27_LHT, respectively. The I27_LHT sample was then diluted to a concentration of 0.2 mM to test for possible aggregation. The ¹⁵N relaxation data were measured at 25°C both at 600 and 800 MHz. The errors on the T₁ and T₂ measurements were estimated to have an average value of 3%, whereas the error on the nuclear Overhauser effect (NOE) measurements is ∼5%.

The ¹⁵N heteronuclear relaxation rates were interpreted using the program TENSOR2 (Dosset et al., 2000). The internuclear distance r_NH was assumed as 1.02 Å. The effects of cross-relaxation between dipolar and chemical shift anisotropy relaxation interactions on the measurements of hetero-atom T₁ and T₂ relaxation times were suppressed (Kay et al., 1992).

The relaxation of a protonated ¹⁵N nucleus is dominated by the dipolar interaction with its directly attached proton and by chemical shift anisotropy. The relaxation parameters are related to the spectral density function of N-H bond vector by the following equations (Abragam, 1961):

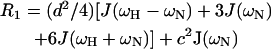(9)

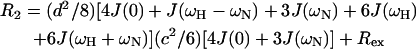(10)

(11)

in which c = ω_NΔσ/√3, μ₀ is the permeability of free space; h is Plank's constant; γ_H and γ_N are the gyromagnetic ratios of the ¹H and ¹⁵N nuclei; ω_H and ω_N are the Larmor frequencies of the ¹H and ¹⁵N nuclei, r_NH is the internuclear ¹H-¹⁵N distance (1.02 Å); Δσ is the chemical shift anisotropy (−160 ppm); J(ω) is the value of the spectral density function at frequency ω. R_ex is a term introduced to account for other pseudo-first-order processes contributing to R₂, such as conformational averaging on the microsecond/millisecond timescale. The three measurable relaxation parameters are insufficient to determine uniquely the values of the spectral density function at five frequencies in Eqs. 9–11 [J(0), J(ω_N), J(ω_H − ω_N), J(ω_H), and J(ω_H + ω_N)] without an assumption about the form of the spectral density function. This problem has been approached in two ways, first by the application of so-called reduced spectral density mapping, in which the values of the spectral density function at three frequencies, ω₀, ω_N, and ω_H, can be determined explicitly from the three measured relaxation parameters (Farrow et al., 1995; Ishima and Nagayama, 1995; Lefevre et al., 1996; Dayie et al., 1996a,b). By assuming that dJ(ω)/dω² is relatively constant between ω = ω_H + ω_N and ω = ω_H − ω_N the linear combinations of J(ω_H − ω_N), J(ω_H), and J(ω_H + ω_N) in the above equations can be replaced with a single equivalent spectral density term, giving simplified expressions for the ¹⁵N relaxation parameters (Farrow et al., 1995):

(12)

(13)

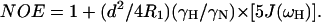(14)

It has been shown that the J(0) and J(ω_N) are correlated linearly (Lefevre et al., 1996). The individual contributions J_i(ω) should obey the linear relationship:

(15)

with α and β the slope and the intercept of the linear fit.

Using the simplest form of the correlation function, a monoexponential decay, the contributions J(ω) may be expressed as Lorentzian functions characterized by a correlation time τ:

(16)

Combining the two equations leads to a third-degree equation in τ:

(17)

Solution of this equation leads to three roots in τ. The first root has no physical meaning, whereas the second and the third correspond to the overall and internal correlation times, respectively, of the various motions contributing to the low-frequency part of the spectral density function.

The alternative approach to interpret the relaxation parameters relies on the assumption of a physical model to describe the spectral density function (Lipari and Szabo, 1982a,b). The spectral density function assuming an anisotropic rotational diffusion is given by:

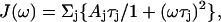(18)

where the symbols are defined as in Woessner (1962).

For the general case, six parameters (D_xx, D_yy, D_zz, θ, φ, ψ) are optimized, where the Euler angles (θ, φ, ψ) define the orientation of the diffusion tensor frame in the chosen molecular frame. In the case of an axial symmetry, D_⊥ = D_xx = D_yy, D_‖ = D_zz, and the three remaining terms of J(ω) are defined by τ_1,2,3 = (6D_⊥)⁻¹, (5D_⊥ + D_‖)⁻¹, (2D_⊥ + 4D_‖)⁻¹ and A_1,2,3 = (3cos²α − 1)²/4, 3sin²αcos²α, (3/4)sin⁴α, where α is the angle between the N-H bond and the unique axis of the diffusion tensor.

Once the orientation and the component of the diffusion tensor are optimized, internal mobility is characterized using the anisotropic diffusion tensor in a hybrid anisotropic diffusion/Lipari-Szabo spectral density function:

(19)

with

For the diffusion tensor and internal mobility analysis, the Cartesian coordinates of I27 were taken from the NMR ensemble (Improta et al., 1996). The rotational correlation times were corrected to standard conditions using a viscosity of 8.976 mPs at 25°C for the NaH₂PO₄/Na₂HPO₄ buffer, deduced from the tabulated value at 20°C, 1.0101 cPs, (Weast, 1986), and assuming a similar change in viscosity with temperature as that of pure water.

NMR B factors

The structures are averaged from the selected ensemble by the newly developed “wheatsheaf” algorithm (D. Thomas and A. Pastore, 2004, unpublished work). This averages the bond lengths, interbond angles, and dihedral angles, and then builds a single representative structure from these averaged values. We find that this initial angle-averaged model usually has very good α- and β-structures, but the proteins tend to fall apart at the loops. This is a consequence of large rotations not being commutative in three dimensions, so the averages are not accurate in regions of high variability. The original spatial arrangement is restored by an iterative Newton-Raphson-style algorithm that adjusts the dihedral angles based on an all-atom versus all-atom comparison of the representative output structure with all of the input structures, which means that the output structure is an average of the input structures in a least-squares sense. We find that the geometry of the averaged output is almost invariably better than that of the input files, and anomalous features occur very rarely.

The so-called temperature factors are calculated by rotationally superposing all the input structures onto the output structure (following the procedure in Diamond, 1988) and then evaluating the variance of the positions of the corresponding atoms in the set of input structures, and scaling it for output.

Hydrodynamic computations

Computation of the rotational correlation time in standard conditions (H₂O, 20°C, η = 1.002 cP) from the NMR atomic structures of I27 was performed employing the program hydropro v. 5a (Garcia de la Torre et al., 2000; Bernado et al., 2002), using an effective atomic radius σ_H = 3.0 Å for the primary models and stick boundary conditions. A Gly residue was manually inserted before Leu-1 in the I27 structure (Improta et al., 1996) to compute the hydrodynamic parameters of I27_NHT. Both the mean structure, calculated as described above, and the individual structures of the NMR bundle were used. The calculations were repeated for the average structure after truncating to their β-carbon positions the subset of residues identified in this study as having T₁ or T₂ backbone values differing more than one standard deviation (Glu-27, Asp-29, His-31, Lys-37, Leu-41, Lys-54, Gln-64, Leu-65, Glu-88, and Leu-89).

Extrapolation to zero bead size was performed for each of the five τ_i using 11 “minibeads” shell models, with radii between 1.95 and 0.95 Å for I27. Clear outliers were removed from the regression analyses and the harmonic mean of the rotational correlation times τ_h was then computed.

The rotational diffusion coefficient D_R of the three constructs was also calculated using the formula described by Halle and Davidovic (2003), which relates it to the protein molecular weight, M_P, that is, D_R (s⁻¹) = 2.78 × 10¹¹/M_P (g mol⁻¹). Molecular weights of 9837, 10,910, and 11,423 were assumed for I27_NHT, I27_SHT, and I27_LHT, respectively.

RESULTS

Fluorescence measurements

Fluorescence measurements were carried out on two I27 constructs, one containing a nine-residue tag (I27_SHT), and the other without it (I27_NHT). The steady-state fluorescence spectra of the I27-acrylodan complexes have an emission maximum at 510 nm (data not shown), suggesting that the probe is relatively exposed to the solvent (Prendergast et al., 1983). For comparison, the emission maxima for bovine serum albumin (Wang et al., 1995; Narazaki et al., 1997; Flora et al., 1998) and β-lactoglobulin (D'Alfonso et al., 2003) are at ∼465 nm and 483 nm, respectively, indicating a more shielded environment. The fluorescence intensity decay of acrylodan cannot be described by a single exponential (Wang et al., 1995; Narazaki et al., 1997; Flora et al., 1998; D'Alfonso et al., 2003), but a good fit was obtained either by analyzing the decay as a sum of two exponentials (ϕ₁ and ϕ₂) or by a Gaussian distribution of lifetimes. As reported in Table 1, similar lifetime values were obtained from the sum-of-two-exponentials analysis for I27_NHT and I27_SHT (both at pH 7 and at pH 4.5). In the Gaussian analysis, the value of the center ϕ_C and its amplitude w usually depend upon the degree of exposure of the probe. As can be seen in Table 1, we found relatively short ϕ_C and w values (on average ∼1.9 ns and ∼0.8 ns), whereas, for example, for β-lactoglobulin these values are 3.5 ns and 1.4 ns, respectively (D'Alfonso et al., 2003). These data further support the idea that in the I27 samples the label is indeed relatively exposed to the solvent. Nevertheless, from the fluorescence lifetime it can be concluded that acrylodan is an acceptable probe to follow the relatively fast overall tumbling of the titin module.

TABLE 1.

Fluorescence lifetimes of acrylodan-I27 complexes

Sample	pH	ϕ1 (ns)	f1	ϕ2 (ns)	f2	ϕC (ns)	w (ns)
I27NHT	7.0	2.43 ± 0.04	0.649 ± 0.006	0.98 ± 0.02	0.351 ± 0.006	1.94 ± 0.02	0.78 ± 0.02
I27SHT	7.0	2.58 ± 0.04	0.557 ± 0.007	0.98 ± 0.01	0.443 ± 0.007	1.82 ± 0.04	0.77 ± 0.02
I27SHT	4.5	2.49 ± 0.04	0.624 ± 0.009	0.93 ± 0.02	0.376 ± 0.009	1.87 ± 0.04	0.80 ± 0.02

In Fig. 1, phase differences (solid symbols) and demodulation ratios (open symbols) are shown versus modulation frequency for the acrylodan-I27_SHT (red squares) and acrylodan-I27_NHT (black circles) samples in 20 mM NaH₂PO₄/Na₂HPO₄, pH 7. The data shown are each the average of at least three distinct measurements. The continuous lines represent data fitting employing Eq. 8. The small but systematic difference observed for the two I27 constructs gives different correlation times as reported in Table 2. The longer correlation times, 5.9 and 6.7 ns for I27_NHT and I27_SHT, respectively, can be ascribed to the overall rotation of the whole I27 module, whereas the shorter ones, 0.9 and 1.2 ns, represent a segmental motion of the region where acrylodan is bound. The presence of the His-tag thus appears to slow down the overall tumbling by ∼14%.

FIGURE 1.

Phase differences (degrees) (solid symbols) and demodulation ratios (open symbols) versus modulation frequency in MHz. Acrylodan-I27_NHT (black), acrylodan-I27_LHT at pH 7 (red), and acrylodan-I27_LHT at pH 4.5 (green). Continuous lines represent data fitting employing Eq. 8 in the text.

TABLE 2.

Parameters derived from the fluorescence anisotropy of acrylodan-I27 complexes

Sample	pH	τ1 (ns)	g1	τ2 (ns)	g2	r0	χ2
I27NHT	7.0	5.85 ± 0.61	0.266 ± 0.009	0.87 ± 0.02	0.074 ± 0.002	0.340	0.5
I27SHT	7.0	6.65 ± 0.20	0.246 ± 0.005	1.16 ± 0.05	0.097 ± 0.008	0.343	0.3
I27SHT	4.5	6.85 ± 0.20	0.258 ± 0.008	1.11 ± 0.10	0.087 ± 0.008	0.345	0.4

In addition, because the original NMR structure of I27 (Improta et al., 1996) was determined at acidic pH (4.5), the effect of pH on the rotational correlation times was investigated for the I27_SHT sample. As can be seen from Fig. 1, nearly superimposable data (red squares and green triangles) were obtained at both pHs, leading to very similar correlation times (Table 1). Thus, our results can be considered pH-independent within the range examined.

NMR relaxation data analysis

NMR ¹⁵N relaxation measurements were carried out on ¹⁵N-labeled samples of I27_NHT and on a construct containing a 14-residue tag, I27_LHT. Complete ¹⁵N relaxation data sets were recorded both at 600 and 800 MHz for the two constructs. The data were compared with those published in Improta et al. (1996) collected on I27_SHT, which were also analyzed again for consistency. The ¹⁵N relaxation data at 25°C and their average values are shown in Fig. 2 and Table 3.

FIGURE 2.

Comparison of the experimental T₁, T₂ relaxation times and heteronuclear ¹H-¹⁵N NOE measurements of the I27 constructs. The values for I27_SHT are taken from Improta et al. (1996). Thirteen T₁ values (Asp-29, His-31, Lys-37, Gly-38, Leu-41, Thr-42, Lys-54, Cys-63, Gln-64, Leu-65, Gly-66, Thr-68, and Leu-89) and 10 T₂ values (Glu-27, Asp-29, His-31, Lys-54, Gln-64, Leu-65, Gly-66, Thr-68, Glu-88, and Leu-89) differ more than one standard deviation from the mean, suggesting different dynamic properties for these residues. Four residues exhibit heteronuclear NOE values more than one standard deviation below the mean (Ile-2, Asp-29, His-31, and Leu-89).

TABLE 3.

Average NMR values including all residues

Module	MHz	T1	T2	15N{1H}-NOE
I27NHT	600	513.7	150.3	0.74
I27SHT	600	571.4	129.7	nd*
I27LHT	600	613.6	115.7	nd
I27NHT	800	668.1	130.1	0.83
I27LHT	800	785.2	110.5	0.82

^*nd, not determined.

I27 is known to be a highly soluble protein with no detectable tendency to aggregate. Nonetheless, to exclude the possibility that the long partially hydrophobic tag of I27_LHT could promote aggregation, we recorded a data set at 14 T, halving the protein concentration. The results obtained superimpose within experimental error on those recorded at higher concentration, confirming that the protein is monodisperse under the experimental conditions tested.

Comparison of the T₁ and T₂ values of the three constructs shows an overall increase of T₁ (600_LHT > 600_SHT > 600_NHT; 800_LHT > 800_NHT) and an opposing decrease of T₂ from I27_NHT to I27_LHT, indicative of different overall correlation times. The measured T₁ and T₂ values vary over a wide range, with amide groups of residues 27–31, 38–42, and 64–68 displaying significantly larger values (Fig. 2, top and middle panels). The residues with T₁, T₂, and NOE values that differ more than one standard deviation from the mean are consistent at both fields.

The data were analyzed by the two most commonly used approaches, the Lipari-Szabo model-free approach (Lipari and Szabo, 1982a,b) in combination with the description of rotational diffusion anisotropy formulated by Woessner (1962), and the reduced spectral density mapping approach (Peng and Wagner, 1992; Lefevre et al., 1996).

Model-free approach analysis

The degree of anisotropy was estimated by calculating the ratio of the three inertia tensor components from the average solution structure, obtained according to the method described in D. Thomas and A. Pastore, unpublished work. The relative lengths of the principal axes of the inertia tensor of I27_NHT are 1.0:0.97:0.42, thus indicating that cylindrical symmetry can be assumed. To reduce the possibility of contributions from internal motions in the analysis, residues whose T₁ and T₂ values differ more than one standard deviation from the mean and whose NOE values exceed a fixed cutoff (here chosen as 0.65 and 0.75 for the data at 600 MHz and at 800 MHz, respectively were excluded from further analysis).

The remaining T₁, T₂, and NOE values were analyzed with respect to isotropic, axially symmetric and fully asymmetric rotational tumbling models (Table 4) (Woessner, 1962; Lipari and Szabo, 1982a,b; Clore et al., 1990; Schurr et al., 1994; Mandel et al., 1995). The rotational tumbling of the three I27 constructs is best characterized using the axially symmetric prolate model, whereas adoption of isotropic or symmetric oblate models led to appreciably larger values. No significant improvement was obtained assuming a fully anisotropic model. The overall correlation times determined for the three constructs differ significantly and progressively increase from the I27_NHT to I27_LHT (Table 4).

TABLE 4.

Prolate axially symmetric (PAS) and fully anisotropic (FA) parameters for the three I27 constructs, corrected to standard conditions (water, 20°C), from the T₁/T₂ data and Lipari-Szabo analysis

I27NHT						I27SHT						I27LHT
*Model MHz (vectors)	(ns)	D|/D⊥	τa (ns)	τb (ns)	τc (ns)	Model MHz (vectors)	(ns)	D|/D⊥	τa (ns)	τb (ns)	τc (ns)	Model MHz (vectors)	(ns)	D|/D⊥	τa (ns)	τb (ns)	τc (ns)
PAS 600 (40)	5.63 ± 0.24	1.51	6.59	6.07	4.93	PAS 600 (37)	6.81 ± 0.25	1.63	8.17	7.45	5.80	PAS 600 (38)	7.66 ± 0.36	1.65	9.31	8.40	6.49
PAS 800 (36)	5.69 ± 0.26	1.57	6.78	6.19	4.90	nd	nd	nd	nd	nd	nd	PAS 800 (36)	8.13 ± 0.24	1.81	10.33	9.11	6.72
			τ1 ≈ τ2 (ns)	τ3 ≈ τ4 (ns)	τ5 (ns)				τ1 ≈ τ2 (ns)	τ3 ≈ τ4 (ns)	τ5 (ns)				τ1 ≈ τ2 (ns)	τ3 ≈ τ4 (ns)	τ5 (ns)
FA 600 (40)	5.63 ± 0.26	1.51	6.02	4.98	6.47	FA‡ 600 (37)	6.81 ± 0.27	1.64	7.73	5.69	8.77	FA 600 (38)	7.64 ± 0.41	1.64	8.35	6.59	9.09
FA 800 (36)	5.69 ± 0.17	1.57	6.10	5.04	6.56	nd	nd	nd	nd	nd	nd	FA 800 (36)	8.08 ± 0.25	1.72	8.95	6.69	9.09
Mean value†	5.66 ± 0.18	6.69	6.13	4.92	Mean value†	6.81 ± 0.25		8.17	7.45	5.80	Mean value†	7.99 ± 0.20		9.10	8.11	6.14

^* or 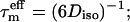for axially symmetric diffusion, D_| = D_z and D_⊥ = D_x = D_y; τ_a = (6D_⊥)⁻¹, τ_b = (5D_⊥ + D_|)⁻¹, τ_c = (2D_⊥ + 4D_|)⁻¹; τ₁ = (4D_x + D_y + D_z)⁻¹; τ₂ = (D_x + 4D_y + D_z)⁻¹; τ₃ = (D_x + D_y + 4D_z)⁻¹; D_iso = trace{D}/3 = (D_x + D_y + D_z)/3; L² = (D_xD_y + D_xD_z + D_yD_z)/3; D_x, D_y, and D_z are the principal values of the diffusion tensor D.

^†From the PAS model values.

^‡nd, not determined.

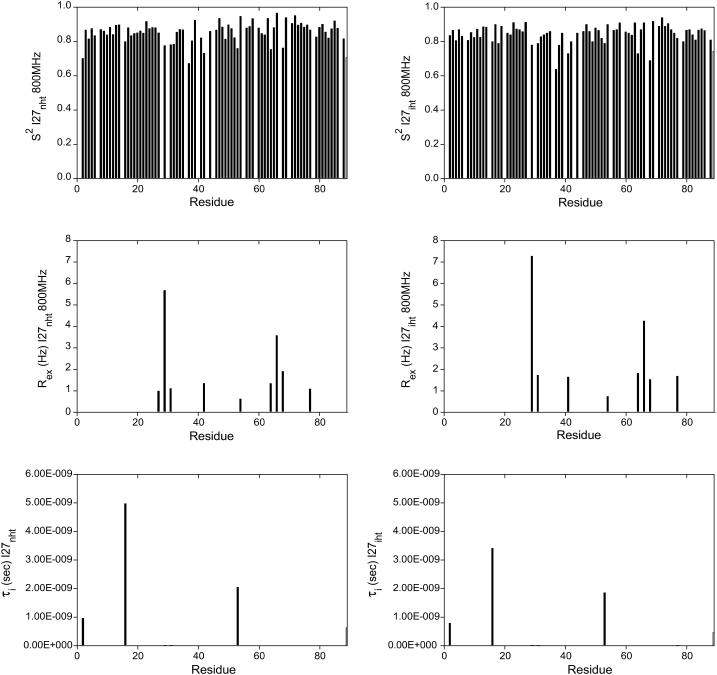
A more detailed analysis was carried out for the two extreme cases I27_NHT and I27_LHT. The results from the two constructs are in qualitative agreement. The calculated dynamics parameters (S², R_ex, and τ_i) versus the polypeptide sequence are shown in Fig. 3. When using the axially symmetric prolate rotational diffusion tensor, the majority of the residues could be fit to model 1, suggesting that the I27 molecule is overall rather rigid. Nine residues required the inclusion of an exchange contribution and could be fit to models 3 and 4. Two residues (Gly-16 and Gly-53) required the extended model (model 5) parameterized by 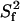and for fast and slow motions, respectively. Only Lys-37 could not be adequately fit by any of the models. The fitting pattern was the same at the two field strengths.

FIGURE 3.

Dynamic parameters for I27_NHT (left panels) and I27_LHT (right panels) assuming axially symmetric rotational diffusion tensor. Order parameters, S², chemical exchange contribution, R_ex, and internal correlation times, τ_i, are plotted versus the residue number. Both distributions were calculated using the program TENSOR 2 (Dosset et al., 2000).

Correlation times (corrected to standard conditions) of 5.40 ± 0.03 ns and 5.42 ± 0.02 ns were obtained for I27_NHT at 600 and 800 MHz, respectively, by fitting the data assuming an isotropic model with the same subset of residues used for determining the anisotropic diffusion tensor.

Comparison of backbone dynamics with NMR-derived B factors

We mapped the S² values onto the 3D structure of I27 (Fig. 4 A). The mean value for the order parameter S² is 0.836 for all residues and 0.85 for all residues in secondary structure elements. The order parameters of residues in loops or at the C-terminus are below the mean values, with residues Gly-16, Asp-29, His-31, Gly-32, Lys-37, Thr-42, Gln-64, Thr-68, and Leu-89 having the lowest values. The nine residues requiring the inclusion of an exchange contribution are mainly located in the loops between the strands BC and EF, whereas Gly-16 and Gly-53, which required the extended model are located in the A′B and DE loops, respectively. The amide of Lys-37, a residue that could not be adequately fit by any of the models, could be involved in the transient formation of a hydrogen bond with the nearby side chain of Gln-39.

FIGURE 4.

(A) Comparison of the B factors as calculated from the RMSD of the NMR bundle (left) with the order parameters (right) as mapped onto the NMR structure of I27 (Improta et al., 1996). The picture was prepared by the program InsightII (Accelrys, San Diego, CA). The B factors were scaled by a factor of 20 and color coded so that red would correspond to residues with high RMSD whereas blue would be those with small RMSD values. Likewise, residues with order parameters <0.8 and >0.9 were colored in red and in blue, respectively. Light red and light blue were used for residues with S² in the 0.81–0.85 and 0.86–0.89 ranges, respectively. (B) Comparison of the order parameters (blue) with the side-chain RMSD values of the family of I27 structures (black) and with the B factors (red).

Because no crystallographic structure of I27 is currently available, no correlation of the order parameters with the experimental crystallographic B factors, a comparison often carried out, is possible. To circumvent this, we compared the residues with order parameters differing from the mean values with B factors computed from the root mean square deviations (RMSDs) of the NMR bundle and with the side-chain RMSDs (Improta et al., 1996) (Fig. 4, A and B). An excellent agreement is observed at the N- and C-termini, and in most of the loops. Interestingly, the long CD loop is less flexible than what we could assume from the B factors, presumably because this region has no regular structure and its conformation was not tightly defined by the NOE restraints.

Spectral density analysis

The dynamic behavior of I27 was also analyzed using the reduced spectral density mapping approach (Farrow et al., 1995; Ishima and Nagayama, 1995; Lefevre et al., 1996; Dayie et al., 1996,b), which allows for the characterization of the frequency motion, overall tumbling rates, and the conformational exchange contributions without the assumption of a specific motional model. The analysis was carried out for I27_NHT and I27_LHT, which represent the two extreme situations of having no tag and the longer tag.

Fig. 5 (left panels) shows the five reduced spectral densities J(0), J(60), J(80), J(600), and J(800), as calculated for I27_NHT versus the protein sequence. Small J(0) values, mostly observed at the N- and C-termini, are indicative of enhanced internal mobility. The higher-frequency spectral density function J(ω_H) shows small variations along the sequence, with the largest values at the N- and C-termini. Unusually large J(0) (J(0) > 2/5 τ_c) and small J(ω_N), indicative of internal motions dominated by conformational exchange processes in the ms-μs timescale, are observed for Asp-29, Lys-54, and Gly-66. A field dependent J(0), which is only observed if conformational exchange contributes to T₂ (Farrow et al., 1995), was also observed for these residues, in agreement with their shorter than average ¹⁵N T₂ values (Fig. 2) and with the requirement of introducing an R_ex exchange term to fit relaxation data better in the model-free analysis (Fig. 3). These residues are in loops, which must therefore experience slow movements in the micro- to millisecond range.

FIGURE 5.

Values of the reduced spectral density functions J(0) (circle at 800 MHz, square at 600 MHz), J(ω_N), and 〈J(ω_H)〉 versus the residue number of I27_NHT (left) and for I27_LHT (right).

Fig. 5 (right panels) shows for comparison the spectral density functions of I27_LHT. The behavior of J(0) values for the corresponding residues in the two proteins are very similar, confirming that the presence of an additional unstructured 14-residue His-tag tail has no effect on the local motions of the protein backbone. However, the J(0) values of I27_LHT, which are very sensitive to the correlation time, appear to be scaled uniformly, reflecting a longer rotational correlation time, again suggesting that the tumbling of the globular domain is influenced by the long disordered His-tag tail.

As mentioned earlier, J(0) and J(ω_N) are expected to correlate linearly (Lefevre et al., 1996). A plot of J(ω_N) versus the corresponding values of J(0) for each NH bond is shown in Fig. 6, together with the theoretical curve that represents the spectral density function values calculated for isotropic Brownian motions for a sphere assuming a rigid tumbling. The deviation from this curve gives us an estimate of the anisotropic nature of the molecule. The N-terminal residue Ile-2, the C-terminal Leu-89, and the residues Asp-29, Lys-54, and Gly-66 were excluded from the calculation because they could bias the results. The spectral densities of the ¹⁵N-¹H vectors are clustered in one domain, i.e., the vectors fall around J(0) ≈ 1.7 ns/rad and J(ω_N) ≈ 0.24 ns/rad with the residues His-31, Thr-42, Gln-64, and Thr-68 located outside this major cluster of points, showing a distinct dynamic behavior relative to the NH vectors of the core. The correlation representative of the NH bonds of Ile-2, Asp-29, Lys-54, Gly-66, and Leu-89 lie off the theoretical curve, indicating the limitation of this model for describing the motions of these residues.

FIGURE 6.

A plot of J(ω_N) as a function of the corresponding J(0) values for each NH bond. NH bonds are represented as open circles. The fit (solid line) was obtained by linear regression. The data were obtained from measurements performed at 800 MHz. The dashed curve corresponds to the theoretical time parametric curve of J(ω_N) vs. J(0).

The average correlation time estimated by this approach for the overall tumbling is τ_c = 6.28 ± 0.19 ns for I27_NHT and τ_c = 8.30 ± 0.25 ns for I27_LHT, after correction to standard conditions. The estimated τ_i values (τ_i = 0.70 ± 0.02 ns for I27_NHT and τ_i = 0.68 ± 0.02 ns for I27_LHT) can be considered as indicative of the presence of complex internal movements in an intermediate timescale around τ_i.

Thus, the reduced spectral density analysis substantiates the findings from the axially symmetric model-free analysis, both for residues exhibiting high flexibility and exchange contributions. Comparison of results obtained by the two methods shows that the τ_c derived from the spectral density mapping approach, although systematically higher, are in good to very good agreement (11% for I27_NHT and 4% for I27_LHT) with those calculated by the axially symmetric model-free analysis. This further confirms that the correct diffusion tensor has been defined in the model-free analysis.

Comparison of the hydrodynamic parameters with those computed from the I27 3D structures

The weighted means of the experimental rotational correlation times obtained from the fluorescence spectroscopy and NMR relaxation approaches are reported in Table 5 (second column). For the tagless I27_NHT module, we can compare this value with the harmonic mean of the five correlation times computed from the 3D structure using HYDROPRO, one of the most widely used programs for hydrodynamic calculations (Garcia de la Torre et al., 2000; Bernado et al., 2002). As can be seen in Table 5 (third column), a value ∼16% larger than the experimental one was obtained for the average structure (to which an N-terminal glycine was manually added). Individual values for each of the 24 members of the original bundle (Improta et al., 1996) were also computed, and corrected for the effect of the extra glycine (+2%). These values ranged from 10% to 18% higher than the experimental value, whereas their mean is just slightly better (+14%) than the average structure (Table 5, fourth and fifth columns). As will be reported elsewhere in more detail (N. Rai, M. Nollmann, B. Spotorno, G. Tassara, F. Byron, and O. Rocco, unpublished work), this overestimation seems to arise from the contribution of the side chains of exposed residues, particularly of the long, hydrophilic kind. We observed that, especially in NMR structures, these residues are often too flexible for their conformation to be determined by experimental data and are often modeled in a fully extended conformation (see Supplementary Material for another detailed example).

TABLE 5.

Summary of the experimental and computed relaxation times (ns)

		Computed
		HYDROPRO
Module	Experimental*	Average model	Mean†	Range†	Reduced‡	H & D§
I27NHT	5.95 ± 0.13	6.91 ± 0.10	6.79 ± 0.12	6.57–7.00	6.41 ± 0.16¶	5.90
					6.12 ± 0.12‖
I27SHT	6.71 ± 0.16	n.a.	n.a.	n.a.	n.a.	6.54
I27LHT	8.11 ± 0.16	n.a.	n.a.	n.a.	n.a.	6.85

^*Weighted mean of the data reported in Tables 2 and 4, and of the spectral density analysis values.

^†Twenty-four conformers (Improta et al., 1996). Raw data were augmented by 2.07% to correct for the contribution of the extra N-terminal glycine not present in these structures.

^‡See text for details.

^§Halle and Davidovic (2003) method.

^¶Average model.

^‖Model 16 (corrected as above).

To correct for this effect, we selected the residues identified in this study as having T₁ or T₂ backbone values differing more than one standard deviation and truncated them to their β-carbon positions in the average structure (Fig. 7, A–C). The computed value for this reduced structure is τ_h = 6.41 ± 0.16 ns, which is closer to but still ∼8% larger than the mean experimental value. Although further truncation of other side chains had negligible effects, it is conceivable that a better selection of residues could be done on the basis of side-chain relaxation experiments not carried out in this study. However, a further improvement to ∼3% (τ_h = 6.12 ± 0.12 ns) was obtained when the reduction was carried out on the conformer having the lowest starting τ_h, model 16 of the bundle (highlighted in green in Fig. 7 A). The most notable differences between this conformer and the average structure are in the conformation of the Glu-27 and Asp-29 side chains, which are less extended in model 16, and at the C-terminal end (Glu-88 and Leu-89), which results in a more compact shape of model 16. As a final test, we reduced the bead radius σ_H of the primary models to 0.28 nm to roughly take into account the possible differential hydration effect on the exposed hydrophobic residues present at both the N- and C-terminal ends of I27_NHT. Values of τ_h = 6.15 ± 0.14 ns and of τ_h = 5.92 ± 0.08 ns for the average model and for model 16 were, respectively, obtained, bringing the agreement within ∼3% and in total accord, respectively.

FIGURE 7.

(A) Superposition of the NMR bundle of I27_SHT (in blue, Improta et al., 1996) on the average structure (in red, this work). Highlighted in dark green is the conformer having the lowest computed τ_h (model 16). The side chains of the residues truncated in the calculation of the hydrodynamic parameters of I27_NHT are displayed on the average structure (orange) and on that of model 16 (light green). The extra glycine present on I27_NHT is not shown, and the histidine tag was not included because it is unstructured. (B and C) Space-filling representations of the average structure and of its truncated version, respectively (coloring scheme as in panel A).

Overall, these results suggest that the computation of the hydrodynamic properties still relies on highly accurate structures and cannot easily take into account flexible regions. Therefore, no attempt was made to compute the hydrodynamic properties of the two I27 constructs with a tag using rigid-body approaches.

Interestingly, when the simplified formula suggested by Halle and Davidovic (2003), who have shown that the rotational diffusion coefficient D_R of globular proteins is inversely proportional to the protein molecular weight, was applied to I27_NHT, a value of D_R = 2.83 × 10⁷s⁻¹ was obtained, corresponding to τ_c = 5.9 ns, in excellent agreement with the mean value reported in Table 5. This value, and those computed for the I27_SHT and I27_LHT constructs, are also reported in Table 5 (last column). By also comparing the latter two with the corresponding weighted means of the experimental data (Table 5, second column), it can be noticed that although the value for I27_SHT is still in very good agreement (−2.5%), that of I27_LHT is strongly underestimated (∼−18%).

DISCUSSION

Although the translational diffusion of a protein in solution is influenced mainly by its overall dimensions, the rotational dynamics are sensitive to fine shape details. Thus, measurement of the rotational correlation time can help to distinguish between alternative models when attempting to predict the overall 3D shape of proteins or protein complexes starting from the high-resolution structure of domains or components. Because of the ease by which compact folding units (modules) can be now routinely expressed and purified in relatively large amounts, the problem of determining the overall structure of large modular proteins that resist crystallization can be tackled by measuring solution properties of stretches of modules, and by comparing them with those that can be computed for proposed 3D arrangements. A similar approach can in principle also be applied to protein complexes. It is therefore important to assess the influence on the solution properties of unstructured and/or highly flexible regions that can be either intrinsic parts of the protein or have been artificially added, for instance, for purification purposes.

In this work, we have presented the results of our studies carried out on a prototypical module, the I27 immunoglobulin-like domain from the gigantic muscle protein titin, using for comparison two independent techniques, fluorescence anisotropy and NMR relaxation. The influence of unstructured tags of different lengths on the rotational dynamics of I27 was assessed by comparison with the untagged module. We had in the past collected conclusive evidence that the nine-residue His-tag used in this study for the I27_SHT construct remains unstructured in solution without interfering with the protein structure or affecting the properties of the flanking regions (Politou et al., 1994, 1995, 1996; Improta et al., 1996). Accordingly, we can exclude that even the longer and partially hydrophobic tag of I27_LHT could interact with the globular domain on the basis of the strong similarity of the chemical shifts of the three constructs (data not shown). On the other hand, we had previously observed that inclusion of the disordered His-tag at the N-terminus of a I27I28 module pair was necessary to fit the experimental small angle scattering data (Improta et al., 1998).

We have now quantified the effect of the additional unstructured residues on the overall rotation tumbling of I27 using two independent techniques. Although fluorescence measurements provide a direct estimate of the overall tumbling rate of a protein, NMR relaxation measurements are the only way to obtain sequence-specific information of the molecular motions. With both techniques we obtain comparable results. An increase of ∼13% in τ_h is observed between I27_NHT and I27_SHT, with a further ∼20% increase of the τ_h of I27_LHT. The presence of a longer disordered tag thus exerts a greater frictional drag, affecting the module tumbling in solution. This suggests that tags should be removed in cases where the hydrodynamic properties of the construct are of interest.

A very important tool to assist the study of multidomain proteins is in principle the possibility of predicting accurately their correlation times from 3D models. We have explored the possibility of applying HYDROPRO, one of the most widely used programs, and the simplified approach recently suggested by Halle and Davidovic (2003), to predict the hydrodynamic properties of I27. Because the method of Halle and Davidovic was empirically calibrated on 16 globular proteins with molecular weight in the range 6500–26,680, we expected that it would fail for the two tagged versions. We observed instead an excellent agreement not only with I27_NHT but also with I27_SHT. In contrast, when using HYDROPRO, we obtained a 16% larger τ_c value already for I27_NHT. Even bigger discrepancies have been noted in the literature when comparing experimental and computed values using rigid-body approaches (e.g., Idowu et al., 2003), but detailed analyses of the underlying reasons of this phenomenon are lacking, to the best of our knowledge. We suggest that the main reason for these discrepancies resides in the way in which long surface side chains are represented. In NMR structures, they tend to be modeled in more extended conformations as compared to their crystallographic counterparts, either because of lack of experimental restraints or because of inherent flexibility. An example of this effect was illustrated by comparing a NMR and a high-resolution x-ray structure of lysozyme, a protein with a similar axial ratio (1.5 vs. 1.6) as I27 (see Supplementary Material). Truncation of the side chains of six exposed arginines in the NMR structure was sufficient to obtain hydrodynamic parameters comparable to those calculated for the crystal structure and in excellent agreement with the experimental data.

In the average NMR structure of I27, whose crystal structure is not available, we truncated at the Cβ level the side chains of the residues identified as having a greater conformational flexibility on the basis of our NMR data, bringing the agreement between experimental and computed data within 8%. A further improvement was obtained by repeating this operation on the conformer having the lowest starting τ_h. The remaining discrepancy could be attributed to the uniform hydration implicit in HYDROPRO and similar rigid-body-based hydrodynamic modeling programs, which is probably not appropriate especially when studying domains isolated from a parent molecule, having an unnatural number of surface-exposed hydrophobic residues. Although it would be tempting to speculate that this analysis could be used to select the “best” conformer out of a bundle of NMR-based structures, we must point out that the removal of flexible side chains was an extreme procedure that was used as a proof of principle. A similar approach was used by Tjandra et al. (1995) in studying the effect of three C-terminal unstructured residues on the rotational tumbling of ubiquitin. As an alternative approach, they generated an ensemble of conformations for the last six residues using Langevin dynamics simulations, and produced from them an average rotational diffusion tensor. The hydrodynamics were studied for both types of structures as a function of hydration using a different bead modeling approach (a bead for each heavy atom, no shell extrapolation, and slip boundary conditions). Similar results were obtained that are in better agreement with the experimental data than when the full x-ray coordinates were used. Although these results support our approach to study the side-chain effects, it would probably be unwise to employ the generation of multiple conformations in conjunction with rigid-body hydrodynamics for long unstructured regions such as the His-tags studied here. More advanced computational tools bridging the gap between molecular dynamics and Brownian dynamics will be needed to fully tackle this issue. Furthermore, it remains to be seen if the amino acid composition of the tag plays a role in the effective frictional properties beyond the pure volumetric effect.

In conclusion, whereas unstructured tags do not seem to interfere with the structure and stability of proteins, they have a noticeable effect on their hydrodynamic properties. They should therefore be used with care when these observables are considered. Despite the major advances in the development of suitable descriptions of the rotational diffusion properties of proteins, the existing computational approaches are still strongly influenced by effects such as the conformation of the side chains and/or by the hydration model assumed. Much work is still needed to develop reliable tools to exploit solution methods to predict the shape of proteins in solution.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.