Abstract
Amphiphilic peptides suspended in aqueous solution display a rich set of aggregation behavior. Molecular-level studies of relatively simple amphiphilic molecules under controlled conditions are an essential step toward a better understanding of self-assembly phenomena of naturally occurring peptides/proteins. Here, we study the influence of molecular architecture and interactions on the self-assembly of model peptides (EAK16s), using both experimental and theoretical approaches. Three different types of EAK16 were studied: EAK16-I, -II, and -IV, which have the same amino acid composition but different amino acid sequences. Atomic force microscopy confirms that EAK16-I and -II form fibrillar assemblies, whereas EAK16-IV forms globular structures. The Fourier transform infrared spectrum of EAK16-IV indicates the possible formation of a β-turn structure, which is not found in EAK16-I and -II. Our theoretical and numerical studies suggest the underlying mechanism behind these observations. We show that the hairpin structure is energetically stable for EAK16-IV, whereas the chain entropy of EAK16-I and -II favors relatively stretched conformations. Our combined experimental and theoretical approaches provide a clear picture of the interplay between single-chain properties, as determined by peptide sequences (or charge distributions), and the emerging structure at the nano (or more coarse-grained) level.
INTRODUCTION
Self-assembly is ubiquitous in nature. Under a variety of conditions, amphiphilic molecules spontaneously assemble into aggregates with tunable size and structure in response to changes in their physical properties. Molecular self-assembly is not only of fundamental interest but also of practical importance: it has emerged as an effective approach for fabricating novel supramolecular structures. Accordingly, considerable effort has been made to take advantage of this ubiquitous phenomenon in nature for various applications (Yeates and Padilla, 2002; Thirumalai et al., 2003; Caplan and Lauffenburger, 2002; Vendruscolo et al., 2003; Fernandez-López et al., 2001; Petka et al., 1998; Holmes et al., 2000; Nowak et al., 2002; Zhang et al., 2002; Hartgerink et al., 2001; Vauthey et al., 2002; Whaley et al., 2000; Lee et al., 2002; Zhang, 2002). Recently, peptide self-assembly has been demonstrated to have potential for diverse biomedical applications, including scaffolding for tissue repair (Holmes et al., 2000; Nowak et al., 2002; Zhang et al., 2002), drug delivery (Hartgerink et al., 2001; Vauthey et al., 2002), and biological surface engineering (Whaley et al., 2000; Lee et al., 2002; Zhang, 2002).
Among many natural and synthetic peptides, the class of “ionically complementary” peptides is of special interest, because they allow the formation of complementary ionic pairs within each chain and/or between different chains. Ionic pairs (from amino acids) in the same chain primarily affect single-chain properties, whereas ionic pairs between different chains stabilize aggregates electrostatically. They not only share some common features of uncharged peptides (e.g., hydrophobicity and hydrogen bonding), but also possess unique charge properties that can sensitively control their aggregation behavior. The simultaneous presence of distinct interactions (e.g., hydrogen bonding, electrostatic, and hydrophobic interactions) in the system leads to rich and subtle molecular self-assembly behavior. Since the discovery of one of these peptides, EAK16-II, by Zhang and his colleagues (1993), extensive effort has been made to understand and take advantage of the self-assembly of this class of peptides. These peptides have been reported to support mammalian cell attachment (Zhang et al., 1994) and have been used as a scaffold for neurite outgrowth and synapse formation (Holmes et al., 2000). They also have been found to form unusually stable β-sheets (Zhang et al., 1994) and macroscopic membranes in the presence of salts (Zhang et al., 1993). A recent study showed that these peptides can form fibrillar assemblies (Hong et al., 2003). The resulting fibrillar nanostructures are similar to those of amyloid fibrils found in conformational diseases, such as Alzheimer's and Parkinson's; thus, these peptides may serve as a model system for studying conformational diseases (Stine et al., 2003; Lomakin et al., 1996; Rochet and Lansbury, 2000).
A number of studies have pointed out the significance of the charge distribution of EAKs in determining their aggregation properties. For example, Hong et al. (2003) recently showed that EAK16-II and EAK16-IV form distinct nanostructures, although they have the same amino acid composition (A, E, and K). The only difference between these peptides is the charge distribution: − − + + − − + + for EAK16-II and − − − − + + + + for EAK16-IV. (Here, the Roman numbers II and IV indicate the number of the same kind of charges grouped together. Similarly, EAK16-I has − + − + − + − +). Note that these charge distributions are realized under typical solvent conditions (e.g., neutral pH) that characterize our EAK systems. According to the observations, EAK16-II forms fibrillar assemblies regardless of pH values, whereas EAK16-IV forms globular assemblies at pH between 6.5 and 7.5, and fibrillar assemblies outside this pH range. Because of the neutralization of ionizable amino acid side groups outside the neutral pH range, Hong et al. proposed that the charge distribution is the determining factor in peptide nanostructure formation.
Other studies also have pointed out the importance of electrostatic interactions in the self-assembling process of peptides (Caplan et al., 2000; López de la Paz et al., 2002). Caplan et al. (2000) reported that the neutralization of an excess charge leads to the self-assembly of β-sheet proteins that would otherwise repel each other, keeping them from forming an aggregate. López de la Paz et al. (2002) showed that the hexapeptides KTVIIE, STVIIE, KTVIIT, etc. form fibrillar nanostructures only when the total net charge of the peptide is ± 1.
Despite the richness of experimental observations, progress on the theoretical side has been slow. The main difficulty arises from the subtle interplay between various intra- and interchain interactions mentioned above, i.e, interactions within a single chain and interactions between different chains, respectively. Recently, however, several groups have studied systems of several to dozens of oligopeptides at atomic resolutions using computer simulations. For example, Hwang et al. (2003) investigated the supramolecular structure of helical ribbons from KFE8, which has a charge distribution + − + −. On the other hand, Gsponer et al. (2003) have performed molecular dynamics (MD) simulations and provided an important insight into the early stages of aggregation of three amyloid-forming heptapeptide chains (GNNQQNY). Although useful, computer simulations at atomic resolution are both expensive and difficult to generalize to other systems. Therefore, one is often forced to simulate only short chains with a limited set of initial conditions (Hwang et al., 2003) or for a very short timescale (∼1 μs instead of seconds; Gsponer et al., 2003).
For the reasons explained above, we take an intermediate approach in this article. Inspired by simulation methods often used in studies of protein folding and DNA, we adopt a simple coarse-grained but physics-oriented model: a charged wormlike-chain (CWLC) model in which a chain has both bending rigidity and electric charge. This model allows us to simulate relatively long individual peptides realistically off-lattice. We can then obtain long trajectories in a conformational space that are a compromise between atomic details and computational limits. Most importantly, with a CWLC, one can efficiently identify key factors such as electrostatic interactions and bending energies that determine the conformational characteristics of individual chains. In particular, we focus on the competition among a few distinct aspects of such ionizable peptides: the bending rigidity of their backbones, the chain entropy (i.e., the entropy associated with chain-conformational degrees of freedom such as bending and rotation of a monomer with respect to others), and the intrachain electrostatic interaction due to charge polarities along the chain. As we shall show below, for a typical range of peptide persistence lengths found in nature, relatively subtle changes in the distribution of charges can change a ground-state conformation completely. This can explain the experimental result that two molecules of the same length, stiffness, and overall charge form completely different nanostructures merely because of a rearrangement of the distribution of charges.
Two experimental techniques were used to study the nanostructures: Atomic force microscopy (AFM) was used to observe the nanostructure formation, whereas Fourier transform infrared (FTIR) spectroscopy was used to identify the secondary structure of the peptides, such as α-helices, β-sheets, and β-turns. The experimental results were then compared with the Monte Carlo (MC) simulations of CWLC s explained above.
EXPERIMENTAL AND THEORETICAL METHODS
Materials
Three types of self-assembling peptides were used: EAK16-I, EAK16-II, and EAK16-IV (C70H121N21O25, 1657 mol wt). The amino acid sequences of these peptides are AEAKAEAKAEAKAEAK (EAK16-I, − + − + − + − +), AEAEAKAKAEAEAKAK (EAK16-II, − − + + − − + +), and AEAEAEAEAKAKAKAK (EAK16-IV, − − − − + + + +) (see Fig. 1). Here, A=Ala, E=Glu, and K=Lys. A has a neutral hydrophobic residue, whereas E and K have negatively and positively charged hydrophilic residues, respectively. The peptides were purchased from Invitrogen (Huntsville, AL) and used without further purification. The N-terminus and C-terminus of these peptides were protected by acetyl and amino groups, respectively, to avoid the end-to-end electrostatic attraction between peptides. Peptide solutions were prepared at the following concentrations in pure water (18 MΩ; Millipore Milli-Q system, Billerica, MA): 0.1 and 1.0 mg/mL for EAK16-I, 0.08, 0.1, 0.3, and 1.0 for EAK16-II, and 0.1, 3.0, and 7.0 mg/mL for EAK16-IV. All peptide samples were stored at 4°C before use. To check the possible effect of impurities, highly purified EAK16-II (Invitrogen, >95%, purified by reverse-phase high-performance liquid chromatography) was also tested to compare with the normal EAK16-II samples.
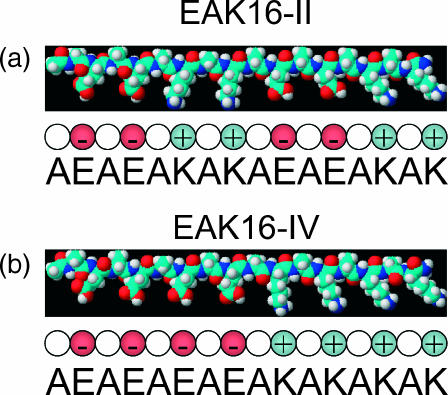
FIGURE 1.
Schematic three-dimensional molecular model drawn with ChemSketch, based on energy minimization: (a) EAK16-II and (b) EAK16-IV. Carbon atoms are cyan, oxygen atoms are red, nitrogen atoms are blue, and hydrogen atoms are white. In this conformation, all of the hydrophobic alanine side chains face in one direction, and all of the lysine and glutamic acid side chains face in the other direction to create two distinct faces. On the polar face, glutamic acid alternates with lysine. Below the molecular models are simplified representations of the peptides with the individual amino acids shown as spherical monomers.
Atomic force microscopy
AFM was used to observe the nanostructure of peptide self-assemblies. The peptides in solution (∼10 μl) were placed on the surface of a freshly cleaved mica sheet that was glued to a steel AFM sample plate. Ten minutes were allowed before washing the peptides with ∼100 μl of pure water to remove unattached peptides. After air-drying for 3 h, AFM imaging was performed at room temperature using the tapping mode on a PicoScanTM AFM (Molecular Imaging, Phoenix, AZ). All images were acquired using a 225-μm silicon single-crystal cantilever (type NCL, Molecular Imaging, Phoenix, AZ) with a typical tip radius of 10 nm and resonance frequency of 165 kHz. Scanners with maximum scan sizes of 35 × 35 and 6 × 6 μm2 were used, and all AFM images had a resolution of 512 × 512 pixels.
Fourier transform infrared spectroscopy
FTIR spectroscopy was applied to determine the secondary structure of peptides. The peptides solution (∼100 μl) was deposited onto a crystal slide of zinc selenide (ZnSe) and dried at room temperature. The FTIR spectrum of the thin film was taken at a wavenumber resolution of 4 cm−1 with a Bio-Rad (Hercules, CA) spectrometer (FTS3000MX, EXCALIBUR series). The baseline was subtracted from the observed absorption intensity and the resulting spectrum was normalized with the maximum intensity within the range of 1600–1700 cm−1, where the characteristic amide I band appeared. By investigating the amide I band, we could identify the secondary structures, including α-helices, β-sheets, and β-turns.
Theoretical models: charged wormlike chain
We model the EAK16 peptides as a CWLC. The chain energy is then a sum of a few distinct contributions:
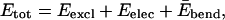 |
(1) |
where Eexcl, Eelec, and 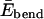 are, respectively, the excluded volume, electrostatic, and bending energy contribution. Here, we adopt the standard Lennard-Jones (LJ) potential ELJ(rij, σ) to describe the excluded volume interaction between two monomers separated by a distance rij, where σ is the interaction range (expected to be roughly the monomer size).
are, respectively, the excluded volume, electrostatic, and bending energy contribution. Here, we adopt the standard Lennard-Jones (LJ) potential ELJ(rij, σ) to describe the excluded volume interaction between two monomers separated by a distance rij, where σ is the interaction range (expected to be roughly the monomer size).
The intrachain electrostatic interaction energy is
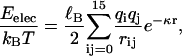 |
(2) |
where ℓB ≡ e2/4πɛkBT is the Bjerrum length (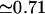 nm at T = 300 K in water), ɛ the dielectric constant of the solvent, qi = ±1 the charge carried by monomer i (in units of the electronic charge e), here a monomer means an amino acid, kB the Boltzmann constant, and rij is the distance between monomers i and j. Finally, the Debye screening length κ−1, a length scale beyond which the electrostatic interaction is exponentially screened, is given by the relation κ2 = 4πℓBI with I the ionic strength (Barrat and Joanny, 1996). The factor 1/2 arises because summing over the i and j indices double counts interactions. Note that two charges a distance ℓB apart have an energy comparable to the thermal energy kBT. We also note that for peptide concentrations used in our experiments (mostly between 0.1 and 1 mg/ml), the Debye screening length κ−1 falls in the range 6.2–19.6 nm, typically exceeding the size 7 nm of EAK16. Intrachain electrostatic interactions are thus not really affected by screening—in what follows, we ignore screening effects. Finally, it should be emphasized that our EAKs are overall electric neutral at and around neutral pH. Hence we do not expect an overall repulsive contribution to chain statistics.
nm at T = 300 K in water), ɛ the dielectric constant of the solvent, qi = ±1 the charge carried by monomer i (in units of the electronic charge e), here a monomer means an amino acid, kB the Boltzmann constant, and rij is the distance between monomers i and j. Finally, the Debye screening length κ−1, a length scale beyond which the electrostatic interaction is exponentially screened, is given by the relation κ2 = 4πℓBI with I the ionic strength (Barrat and Joanny, 1996). The factor 1/2 arises because summing over the i and j indices double counts interactions. Note that two charges a distance ℓB apart have an energy comparable to the thermal energy kBT. We also note that for peptide concentrations used in our experiments (mostly between 0.1 and 1 mg/ml), the Debye screening length κ−1 falls in the range 6.2–19.6 nm, typically exceeding the size 7 nm of EAK16. Intrachain electrostatic interactions are thus not really affected by screening—in what follows, we ignore screening effects. Finally, it should be emphasized that our EAKs are overall electric neutral at and around neutral pH. Hence we do not expect an overall repulsive contribution to chain statistics.
The bending energy  is more subtle and deserves some discussion; in formulating the elastic energy of peptides, one often considers the torsional energies related to the dihedral angles {φ, ψ, ω}, and bond-length and bond-angle strain (Ebond and Ebang). To that end, many different types of potentials have been developed and used (see, for example, Cornell et al., 1995; Van Gunsteren et al., 1996; Jorgensen et al.,1996; MacKerell et al., 1998; Mu et al., 2003). In this work, we map these steric effects onto a single effective harmonic potential
is more subtle and deserves some discussion; in formulating the elastic energy of peptides, one often considers the torsional energies related to the dihedral angles {φ, ψ, ω}, and bond-length and bond-angle strain (Ebond and Ebang). To that end, many different types of potentials have been developed and used (see, for example, Cornell et al., 1995; Van Gunsteren et al., 1996; Jorgensen et al.,1996; MacKerell et al., 1998; Mu et al., 2003). In this work, we map these steric effects onto a single effective harmonic potential
 |
(3) |
where  is an effective persistence length of the backbone and θi is the angle between the two bond vectors
is an effective persistence length of the backbone and θi is the angle between the two bond vectors  and
and 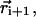 (i.e., a vector tangent to each monomer with magnitude equal to the monomer size). Despite its seemingly dramatic simplification, this equation can be used to study the balance of the competing effects in Eq. 1 that essentially determines single-chain properties. Fig. 2 a shows how one may justify the neglect of atomic details in favor of the coarse-grained chain conformations. Indeed, we shall show that the combination of Eelec and the effective bending energy
(i.e., a vector tangent to each monomer with magnitude equal to the monomer size). Despite its seemingly dramatic simplification, this equation can be used to study the balance of the competing effects in Eq. 1 that essentially determines single-chain properties. Fig. 2 a shows how one may justify the neglect of atomic details in favor of the coarse-grained chain conformations. Indeed, we shall show that the combination of Eelec and the effective bending energy 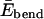 captures all the essential similarities and differences between different types of EAK16 (see Appendix I) in forming nanostructures. Also, note that the WLC has been successfully used in modeling other semiflexible polymers such as DNA, actin, and microtubules at a similarly coarse-grained level (for a review, see, for example, Schlick, 2002). The WLC model has also been used to study protein folding recently (Klimov and Thirumalai, 2002).
captures all the essential similarities and differences between different types of EAK16 (see Appendix I) in forming nanostructures. Also, note that the WLC has been successfully used in modeling other semiflexible polymers such as DNA, actin, and microtubules at a similarly coarse-grained level (for a review, see, for example, Schlick, 2002). The WLC model has also been used to study protein folding recently (Klimov and Thirumalai, 2002).
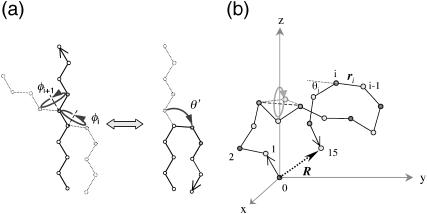
FIGURE 2.
(a) Mapping onto an effective bending energy. A stretched chain can be transformed into a hairpin by successive rotations of dihedral angles φi and φi+1. However, one can achieve a similar conformational change through a rotation of bond angle θ. This implies that we can represent the torsional energy of freely rotating chain model in terms of an effective bending energy to a certain extent. (b) Polymer model used in the simulations. Different symbols represent different charged monomers (shaded circles, neutral; solid diamonds, negatively charged; open diamonds, positively charged monomers). See Computer Simulations for detail.
For these types of calculations, it is often crucial to choose proper parameters (Bright et al., 2001; Millet et al., 2002; Goldenberg, 2003). The persistence length 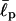 of EAK molecules is not precisely known but is expected to be 1–2 amino acids (aa) long (Carrion-Vazquez et al., 2000; Rief et al., 1998). In our computer simulations, we have used a range of
of EAK molecules is not precisely known but is expected to be 1–2 amino acids (aa) long (Carrion-Vazquez et al., 2000; Rief et al., 1998). In our computer simulations, we have used a range of 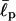 and σ, comparing our simulation data with experiments. This enables us to test the reliability of our simulation results against changes in these parameters. As we shall show, our results nonetheless turn out to be robust over a range of parameters.
and σ, comparing our simulation data with experiments. This enables us to test the reliability of our simulation results against changes in these parameters. As we shall show, our results nonetheless turn out to be robust over a range of parameters.
Computer simulations
We performed Metropolis MC simulations at fixed T to obtain the equilibrium end-to-end distribution G(R, L) of the EAK system. We used an off-lattice, freely jointed chain model that has 15 bonds (16 monomers) of bond length 1 amino acid (aa) = 0.44 nm. At each time step, a monomer rotates randomly between (−Cm × π, Cm × π) about the axis defined by the vector connecting the two nearest monomers where Cm is the constraint of the angle to make the acceptance ratio converge nonlinearly to 50%, while keeping the bond length fixed (Madras and Sokal, 1988) (Fig. 2 b). Note that each trial move changes the chain conformation, and the acceptance of a new conformation is determined by the standard Metropolis algorithm (Metropolis et al., 1953), in which Eq. 1 is used to calculate the chain energy of the CWLC. Each peptide has the following charge distribution at neutral pH: I (− + − + − + − +); II (− − + + − − + +); and IV (− − − − + + + +), where a neutral monomer between two consecutive charged monomers is not shown for simplicity—in reality, the chain has an alternating sequence of charged and neutral monomers.
To sample a wide range of a conformational space in a possibly “rugged” energy landscape, we also used the multicanonical algorithm (Hansmann and Okamoto, 1994; Lemak and Gunn, 2000; Kemp and Chen, 2001). For a readable overview of various algorithms, see Hansmann and Okamoto (1999). Note that this algorithm is similar to but uses a more elaborate technique than the umbrella sampling method (Torrie and Valleau, 1974, 1977; Mezei, 1987; Ferrenberg and Swendsen, 1988; Bartels et al., 1999). To sketch the basic idea, one introduces a weight ω(E) that is inversely proportional to the density of state 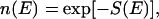 where S(E) is the microcanonical entropy. This will lead to a uniform distribution of energy P(E) ∝ n(E)×ω(E) = constant, and MC simulation samples the energy space uniformly. This is to ensure that the system can overcome any energy barrier. Although we used this technique mainly to obtain global minimum energy conformations of EAK systems, one can calculate any thermodynamic average by reweighting techniques (Kumar et al., 1992, 1995; Bartels et al., 1999; Lemak and Gunn, 2000). Note that one has to implement this averaging procedure by an iterative procedure to calculate the weights properly. In our simulation, the distribution P(E) became flat (as required) after ∼150 iterations. Sampling frequencies and the length of a simulation are adjusted empirically to obtain reliable statistics.
where S(E) is the microcanonical entropy. This will lead to a uniform distribution of energy P(E) ∝ n(E)×ω(E) = constant, and MC simulation samples the energy space uniformly. This is to ensure that the system can overcome any energy barrier. Although we used this technique mainly to obtain global minimum energy conformations of EAK systems, one can calculate any thermodynamic average by reweighting techniques (Kumar et al., 1992, 1995; Bartels et al., 1999; Lemak and Gunn, 2000). Note that one has to implement this averaging procedure by an iterative procedure to calculate the weights properly. In our simulation, the distribution P(E) became flat (as required) after ∼150 iterations. Sampling frequencies and the length of a simulation are adjusted empirically to obtain reliable statistics.
RESULTS AND DISCUSSION
Experiments show that EAK16-IV aggregation differs from that of EAK16-I and -II
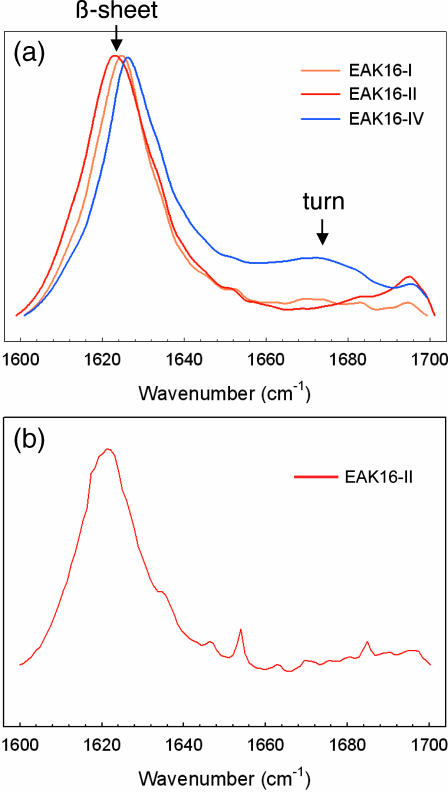
AFM was used to observe the self-assembled nanostructure of peptides. Fig. 3 shows that EAK16-I and -II form fibrillar nanostructures, whereas EAK16-IV forms globular ones. In addition, FTIR spectroscopy was used to study the secondary structure of a peptide because it can identify β-sheets (parallel/antiparallel β-sheets) and turns (such as “hairpins”). FTIR spectra of EAK16s within the wavenumbers of 1600 and 1700 cm−1 are plotted in Fig. 4 a. As shown within these wavenumbers, the amide I band caused by C-O stretching has much information on the secondary structure of peptides. The peak between 1620 and 1640 cm−1 and high-frequency peak ∼1690 cm−1 are attributed to the formation of β-sheet structures, whereas the peaks ∼1650 cm−1 are attributed to the formation of α-helices. Turn structures such as “hairpins” occur at ∼1675 cm−1 (Casal et al., 1988; Dong et al., 1990; Byler and Susi, 1986). Clearly, all three types of EAK16 peptides have a strong peak ∼1620 cm−1, indicating that they have a large β-sheet content. EAK16-I and -II are almost identical, whereas EAK16-IV has a broad peak centered at 1675 cm−1 that is absent in EAK16-I and -II. Generally, this broad peak ∼1670 cm−1 is an indication of turns. One might suspect that this peak is due to the presence of trifluoroacetate (TFA) introduced during the synthesis. However, all three types, EAK16-I, II, and IV, would have shown similar peaks if this peak were associated with TFA, because the peptides were synthesized by the same procedure. Because this peak of EAK16-IV is attributed to a turn structure, these FTIR spectra strongly suggest the possibility of appreciable bending of EAK16-IV molecules.
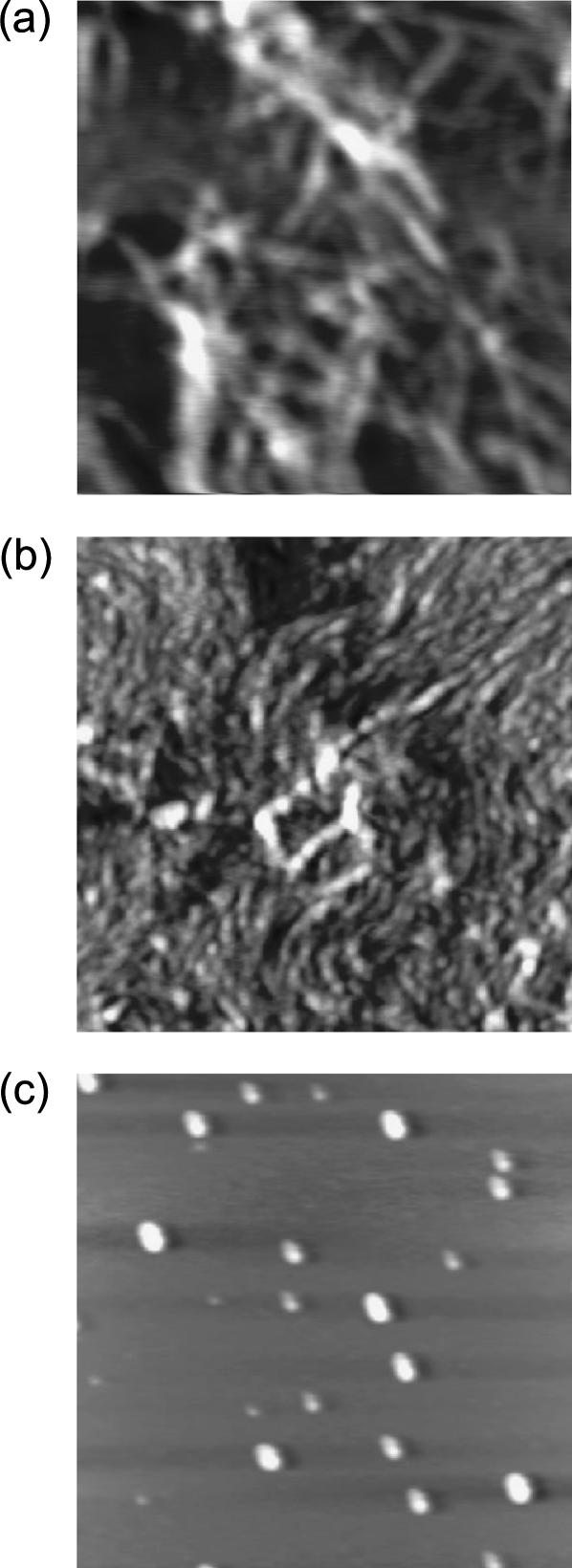
FIGURE 3.
AFM images of EAK16-I (a), -II (b), and -IV (c) at a concentration of 0.1 mg/mL. EAK16-I and -II form fibrillar nanostructures, whereas EAK16-IV forms globular ones. The scan size of the images is 2 × 2 μm2 and z-scale is 5 nm.
FIGURE 4.
(a) FT-IR spectra of EAK16-I, -II, and -IV for peptide concentrations 1.0, 1.0, 3.0 mg/mL, respectively. Distinct from the other two peptides, EAK16-IV has a broad peak centered at ∼1675 cm−1. This particular peak is attributed to the formation of turn structure. (b) FT-IR of EAK16-II at c = 0.08 mg/mL.
Theory and simulations show that the single-chain properties of EAK16-IV differ from that of EAK16-I and -II
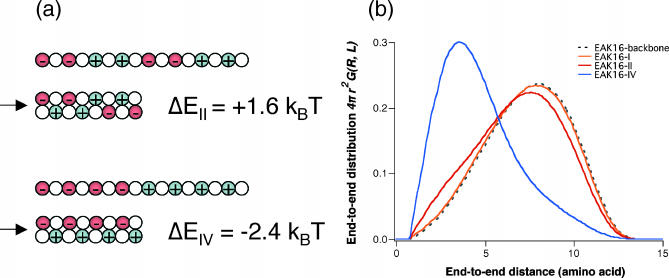
The question is then why EAK16-I and -II show similar behavior whereas IV is different in their aggregation and molecular conformation. As we argued earlier, the only difference, at a single-chain level, between different types of EAK16 is their charge distribution and the resulting polarities. However, the electrostatic interaction alone cannot explain the differences as it would lead to chain collapse in all cases; i.e., we would have seen turns of EAK16-I and -II in FTIR spectra in Fig. 4 a. Thus, there needs to be an effect opposing peptide collapse. As we shall argue, the molecular architecture of EAK16 is such that three important factors—the electrostatic interaction of oppositely charged monomers (Eelec), the effective bending energy of the peptide backbone (Ebend), and the chain entropy—are comparable with each other; thus, the competition among these effects can make dramatic differences in determining the most stable chain conformations. For a fixed chain length (L = 16 amino acids for EAK16), we can show that there exists a range of chain stiffness (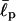 ) where the lowest free-energy state for EAK16-IV is completely different from those of EAK16-I and -II. To see this, let us consider two extreme cases: 1), fully stretched and 2), folded EAK16-II and -IV. Fig. 5 a shows the energy of each of these (calculated using Eqs. 2 and 3 with
) where the lowest free-energy state for EAK16-IV is completely different from those of EAK16-I and -II. To see this, let us consider two extreme cases: 1), fully stretched and 2), folded EAK16-II and -IV. Fig. 5 a shows the energy of each of these (calculated using Eqs. 2 and 3 with 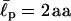 ). This consideration implies that EAK16-II favors a stretched conformation whereas EAK16-IV prefers to be bent: |ΔEelec, II| < ΔEbend < |ΔEelec, IV|, where ΔE is an energy (both bending and electrostatic) with reference to an extended state. See Appendix II for details.
). This consideration implies that EAK16-II favors a stretched conformation whereas EAK16-IV prefers to be bent: |ΔEelec, II| < ΔEbend < |ΔEelec, IV|, where ΔE is an energy (both bending and electrostatic) with reference to an extended state. See Appendix II for details.
FIGURE 5.
(a) Energies in conformational changes from stretched to folded EAK16-II and -IV. For 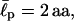 II has to overcome an energy barrier of 1.6 kBT, whereas IV loses 2.4 kBT. Thus, energetically, II prefers to be extended whereas IV prefers to fold. (b) The distribution of the end-to-end distance P(R, L) = 4πR2G(R, L) of CWLC I, II, and IV. The asymmetry in the distribution shows that EAKs with a relatively flexible backbone usually look like “globules” in solution, conformations between fully stretched and completely folded ones. The chain entropy favors this conformation over the other cases, because it has more conformational degrees of freedom (hence more entropy). Each curve was constructed from ∼43 million MC steps. Note how the charge polarities of chain can affect P(R, L) and its peak position. Here,
II has to overcome an energy barrier of 1.6 kBT, whereas IV loses 2.4 kBT. Thus, energetically, II prefers to be extended whereas IV prefers to fold. (b) The distribution of the end-to-end distance P(R, L) = 4πR2G(R, L) of CWLC I, II, and IV. The asymmetry in the distribution shows that EAKs with a relatively flexible backbone usually look like “globules” in solution, conformations between fully stretched and completely folded ones. The chain entropy favors this conformation over the other cases, because it has more conformational degrees of freedom (hence more entropy). Each curve was constructed from ∼43 million MC steps. Note how the charge polarities of chain can affect P(R, L) and its peak position. Here, 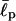 = 2 aa, κ = 0, and σ = 0.9 aa. See also Appendix III.
= 2 aa, κ = 0, and σ = 0.9 aa. See also Appendix III.
A central quantity characterizing single-chain properties is the distribution function G(R, L) of the end-to-end distance 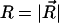 for a given chain length L and persistence length ℓp. Although several accurate approximations of G(R, L) have been developed for homogeneous semiflexible chains (i.e., L ∼ ℓp) over the last few years (Thirumalai and Ha, 1998), G(R, L) for polyampholytes (heterogeneously charged polymers) such as EAK molecules have not been calculated analytically. Therefore, we have performed MC simulations to calculate G(R, L) for a charged WLC that has the same charge sequence as and bending rigidities comparable to those of EAK16-I, -II, and -IV. We also have obtained the minimum-energy conformations of these peptide models from simulations. The results are striking (Fig. 5 b): Because the normalized distribution G(R, L) is a function of distance only, hereafter we use a one-dimensional-projected function P(R, L) ≡ 4πR2 × G(R, L) instead. This is inferred from the relation
for a given chain length L and persistence length ℓp. Although several accurate approximations of G(R, L) have been developed for homogeneous semiflexible chains (i.e., L ∼ ℓp) over the last few years (Thirumalai and Ha, 1998), G(R, L) for polyampholytes (heterogeneously charged polymers) such as EAK molecules have not been calculated analytically. Therefore, we have performed MC simulations to calculate G(R, L) for a charged WLC that has the same charge sequence as and bending rigidities comparable to those of EAK16-I, -II, and -IV. We also have obtained the minimum-energy conformations of these peptide models from simulations. The results are striking (Fig. 5 b): Because the normalized distribution G(R, L) is a function of distance only, hereafter we use a one-dimensional-projected function P(R, L) ≡ 4πR2 × G(R, L) instead. This is inferred from the relation 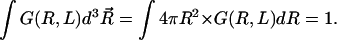 Then, P(R, L)dR is the probability that the two ends of a chain are separated by a distance R.
Then, P(R, L)dR is the probability that the two ends of a chain are separated by a distance R.
First, at room temperature, EAK16-I and -II have very similar end-to-end distributions G(R, L), which are not much different from that of the corresponding uncharged chains (i.e., with the electrostatic interactions turned off). In these two cases, G(R, L) is mainly determined by chain-backbone properties, which dominate electrostatic properties. Second, EAK16-IV shows completely different behavior from the other two: the peak of P(R, L) for IV is located much closer to the origin than in I and II, implying that hairpin is the most stable equilibrium conformation for IV. Note that these characterizations of I, II, and IV are indeed consistent with the FTIR results in Fig. 4 a.
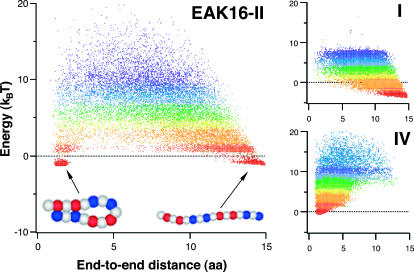
Another key quantity is the lowest-energy conformation, or ground state. The ground state of a typical protein, for example, dominates the equilibrium chain statistics; chain fluctuation around this state can be minimal. However, this may not be the case for oligopeptides such as EAK16 because of their relatively weak intrachain interactions. One then has to explore chain conformations over a wider parameter space. Fig. 6 shows the MC “cloud map” of chain-energy E versus end-to-end distance R obtained using multicanonical methods. As described in the Experimental and Theoretical Methods section, our multicanonical approach enables us to explore a wide range of a conformational space and is advantageous when the energy landscape is rugged. The lowest-energy conformation obtained by this method dominates equilibrium chain statistics at sufficiently low temperatures. As one can see, for a chosen set of parameters (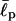 = 2 aa and σ = 0.9 aa), the minimum energy conformation of IV is a slightly twisted hairpin with very small end-to-end distance R (cf. Fig. 5). Therefore, the hairpin is energetically the most stable state. For I, the ground-state conformation is a stretched “worm” because of the relatively weak charge polarity of the chain. On the other hand, II has a more complicated energy profile, with two local minima that correspond to hairpin and “worm” (see Appendix III). Unlike the hairpin structure of EAK16-IV, the extended conformations for EAK16-I and -II are less clearly defined, in that the chain conformation can fluctuate significantly around the stretched conformation without changing the energy significantly.
= 2 aa and σ = 0.9 aa), the minimum energy conformation of IV is a slightly twisted hairpin with very small end-to-end distance R (cf. Fig. 5). Therefore, the hairpin is energetically the most stable state. For I, the ground-state conformation is a stretched “worm” because of the relatively weak charge polarity of the chain. On the other hand, II has a more complicated energy profile, with two local minima that correspond to hairpin and “worm” (see Appendix III). Unlike the hairpin structure of EAK16-IV, the extended conformations for EAK16-I and -II are less clearly defined, in that the chain conformation can fluctuate significantly around the stretched conformation without changing the energy significantly.
FIGURE 6.
Cloud-map representation of the distribution of the end-to-end distance R. The clouds describe a uniform sampling of an energy space by a one-dimensional random walk, i.e., the distribution of dots represents the distribution of R (see text for the detail). The color gradients represent the “temperature” T in the multicanonical sampling. In other words, the distribution of R at a given temperature is described by dots in the same color. Red/blue dots correspond to low/high T, at which the chain conformation is determined mainly by energy entropy. The minimum-energy conformation for type-I is a “worm” whereas, for type-IV, it is a slightly crossed hairpin. (Left) Type-II sequence. The two chains shown below the cloud map are MC generated, typical conformations in the red regions. (Top right) Type-I. (Bottom right) Type-IV.
EAK16-IV assemblies
Based on their experimental results, Hong et al. recently speculated that the strong intramolecular attractive electrostatic interaction between complementary ionic pairs in EAK16-IV may cause it to bend or fold (Hong et al., 2003), thus exposing its hydrophobic face to the solution. This enables these hairpins to self-assemble, above a critical concentration, into aggregates stabilized by the hydrophobic attraction (hydrophobic attraction ∼ kBT per peptide), forming globular structures on account of their single-chain geometry (hairpin). This scenario is supported by our simulation results and the FTIR data. Here, we have two underlying assumptions: a), EAK16-IV has enough space and time to reach its stable conformation, i.e., hairpin, without any intervention from its neighboring chains (through diffusion and collisions, for example). On the other hand, if EAK16-IV peptides are too close from each other, they may form parallel β-sheets before folding due to ionically complementary side chains. b), For average intermolecular distance larger than the chain length L, the interchain electrostatic interaction Φ is much weaker than intrachain interaction (bending and electrostatic) and therefore does not affect the single-chain dynamics appreciably.
To test “a” above experimentally, we have used a very high-concentration sample of EAK16-IV so that the average intermolecular distance dinter becomes comparable to the chain length L. We hoped to see different assembly morphologies due to hindrance in forming hairpins from its neighboring chains. Fig. 7 shows AFM images of EAK16-IV aggregates for two different concentrations 3 mg/mL (dinter = 9.7 nm) and 7 mg/mL (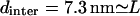 ). Indeed, we do see a change in the morphology from globular to elongated structures, confirming our prediction that the transition should occur near
). Indeed, we do see a change in the morphology from globular to elongated structures, confirming our prediction that the transition should occur near 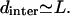
FIGURE 7.
AFM images of EAK16-IV aggregation. Morphology changes from globular to fibrillar in type-IV peptides. (b) c = 3 mg/mL (dinter = 9.7 nm). (a) c = 7 mg/mL (dinter = 7.3 nm). The scan size of the images is 1.5 × 1.5 μm2 and z-scale is 6 nm.
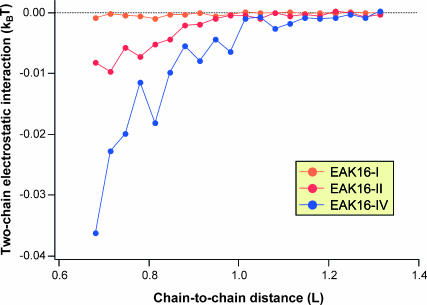
To test “b” above, we have also performed two-chain MC simulations to calculate the average interchain electrostatic energy Φ(x), where x is the distance between the (geometrical) centers of two chains. From Fig. 8, two overall-neutral chains with charge polarities attract each other. As we expected, the interaction energy increases as the chain polarity increases: 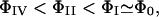 where Φ0 refers to a neutral chain with zero polarity. On the other hand, these interaction energies become significant only when the chains are very close (
where Φ0 refers to a neutral chain with zero polarity. On the other hand, these interaction energies become significant only when the chains are very close (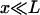 ). When x ≈ L, Φ is almost two orders of magnitude smaller than the thermal energy kBT, thus confirming assertion “b”. Note that although one can reduce the sampling “noise” by performing longer simulations and/or, perhaps, by using multicanonical methods, we do not expect any significant deviation from the results presented here.
). When x ≈ L, Φ is almost two orders of magnitude smaller than the thermal energy kBT, thus confirming assertion “b”. Note that although one can reduce the sampling “noise” by performing longer simulations and/or, perhaps, by using multicanonical methods, we do not expect any significant deviation from the results presented here.
FIGURE 8.
Two-chain electrostatic interaction energy Φ versus center-to-center distance dc2c between chains, in units of kBT and aa, respectively. Three types of charged WLC, EAK16-I, -II, and -IV, were examined, and ∼0.2 billion MC steps and 20,000 chain conformations were sampled for each curve. Note that the interchain interaction is almost two orders of magnitude smaller than the thermal energy kBT. On the other hand, EAK16-I almost behaves like an uncharged peptide.
From the theoretical and experimental evidence presented here, we conclude that individual EAK16-IV peptides fold first into hairpins, exposing their hydrophobic faces, and these hairpins then aggregate into globules that are stabilized by hydrophobic interactions.
EAK16-II assemblies
Although the link between the single molecular properties of EAK16-IV and its nanostructures seems clear, the situation is more tentative for EAK16-II. Recently, Hong et al. (2003) and Fung et al. (2003) showed that EAK16-II forms fibrillar assemblies in pure water at near neutral pH, above a certain critical concentration of peptide. Because the fibrillar aggregates disappeared at the critical concentration, Fung et al. called it a critical aggregation concentration (CAC).
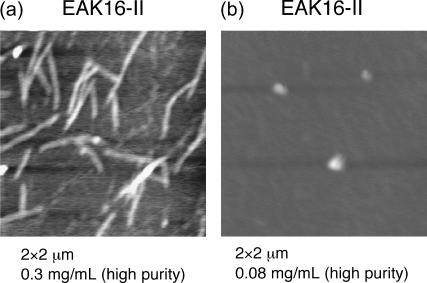
We have performed further investigations on the nanostructure formed by EAK16-II. In particular, we have paid special attention to nanostructure formation at low concentrations, where fibrils disappear. We made significant efforts to minimize the effects of impurities and contamination that could also affect aggregation. In fact, Fung et al. (2003) observed short fibrillar nanostructures with AFM at 0.05 mg/ml (<CAC = 0.1 mg/mL, estimated by surface tension measurements and light scattering). However, this arises from the seeding effect of impurities and contamination on the nucleation and growth, similar to that of amyloid β-protein fibrils (Lomakin et al., 1996). We thus used highly purified EAK16-II samples to minimize this seeding effect. Fig. 9 shows typical AFM images: at c = 0.3 mg/mL, the dominant form of aggregates is fibrillar (Fig. 9 a), whereas, at c = 0.08 mg/mL, small number of globules are seen without any fibrillar aggregates (Fig. 9 b). Further experiments suggest that the transition from fibrils to globules occurs near c* = 0.1 mg/mL, which coincides with the CAC measured by Fung et al. On the other hand, our FTIR for EAK16-II at both below and above c* are virtually identical: our FTIR data do not indicate any turn structures (such as hairpins).
FIGURE 9.
AFM images of EAK16-II aggregation. (a) c = 0.3 mg/mL. (b) c = 0.08 mg/mL. The scan size of the images is 2 × 2 μm2 and z-scale is 2 nm (a) and 7 nm (b).
How do we reconcile the seemingly contradictory AFM and FTIR results? First, EAK16-II has two different ground-state conformations: a hairpin and an extended conformation, with the latter being dominant as can be seen clearly from the cloud map in Fig. 6 (see Appendix IV). Second, the exposed hydrophobic groups of hairpin structures and their geometry imply that the CAC for hairpin structure is much lower than it is for extended structures. These two facts imply that we should consider separately the two types of conformations. At c = 0.08mg/mL, we are evidently below the CAC for extended EAK16-II but above the CAC for folded structures. The molecules in hairpin conformations thus form aggregates, whereas those in β-sheets do not. The AFM can detect the relatively few molecules that have aggregated into globules (Fig. 9). On the other hand, the FTIR spectrum records the distribution of all molecules. A rough estimate from data shows that only one out of 104 molecules is in the hairpin conformation at c = 0.08 mg/mL, with the rest in β-sheets (see Appendix V). Thus, the recorded FTIR shows only the β-sheet contribution (Fig. 4 b).
From single chains to aggregates
The experimental results and the simple theoretical pictures (competing Eelec and Ebend) presented here are strong evidence that the single-chain properties of short peptides play a crucial role in determining the nanostructures formed by self-assembled aggregates. However, more-detailed studies are required to understand the link between single-chain properties and self-assembly, i.e., the aggregation pathway. One way to do this is via simulations of multiple chains.
Recently, Hwang et al. (2003) have investigated the supramolecular structure of helical ribbons formed by dozens of KFE8 peptides using molecular dynamics at an atomic level. We note that KFE8 and EAK8-I have the same coarse-grained structure with the same charge distribution and similar hydrophilic and hydrophobic faces, thus having the stretched conformation as the most stable state. Indeed, this is consistent with the experimental observations of KFE8. Hwang et al. took advantage of this special feature of KFE8 and constructed helical ribbons from specific extended conformations of KFE8. Unfortunately, MD of dozens of longer peptides such as EAK16 is, in general, limited by the computational cost.
Another complementary approach is the MD simulation of a few peptides with atomic details, which will allow one to construct a free-energy surface for the very early steps of aggregation and to study the role of side-chain interactions. One example is the recent study by Gsponer et al. mentioned in the Introduction section (Gsponer et al., 2003), where they simulated three heptapeptides to observe the kinetics of early stage aggregation (∼1 μs). Using our coarse-grained CWLC model, one can perform similar simulations for dozens of longer chains and for longer intermediate timescales. Indeed, several groups are using other simplified models to address intra- and interpeptide interactions in folding and collapse (see, for example, Harrison et al., 1999; Smith and Hall, 2001; Jang et al. 2002; Tiana and Broglia, 2002; Chen et al., 2003).
On the experimental side, several techniques can be used to study the interplay between single peptides and nanostructures. In a direct visualization method, for example, several groups have been able to capture a series of “snapshots” of growing peptide aggregates using AFM (Goldsbury et al., 1999). Although this approach cannot extract molecular details, it can still monitor the dynamics of nanostructure growth.
One alternative technique to investigate the detailed structure of assemblies is nuclear magnetic resonance (NMR) spectroscopy. Because NMR spectroscopy is capable of providing detailed information on specific interatomic distances and torsional angles, the application of NMR techniques to elucidate the nanostructures of peptide is of critical importance (Mikros et al., 2001; Tycko 2000). Although acquiring enough information using NMR spectroscopy is a formidable task, the combination of high-resolution NMR with molecular modeling is anticipated to give detailed information on the nanostructures.
CONCLUSION
We have shown that single-molecule properties have a critical influence on the self-assembly of charged oligopeptides. In particular, we have used a coarse-grained CWLC model and focused on the competition between intrachain electrostatic interactions and the bending energy cost of EAK16 molecules. By including other effects, such as hydrophobicity, we believe our intermediate approach (CWLC) will also be useful in studying the aggregation of several long chains, especially the interplay between their single-chain properties and the emerging nanostructures. Also one can examine how intrachain collapse and interchain aggregation are intertwined in the assembly pathway. The completion of this theoretical program would then lead to an understanding of and control over the self-assembly of naturally occurring proteins.
Acknowledgments
H. Imamura benefited from the computational resources provided by J. Chen.
We acknowledge the financial support from the National Sciences and Engineering Research Council of Canada, (B.Y.H., J.B., and P.C.), the Canadian Foundation for Innovation, and the Canadian Institutes of Health Research (P.C.).
APPENDIX I
In the protein-folding literature, researchers often use the freely rotating chain (FRC) model. In the FRC model, the i-th bond can rotate freely around the (i + 1)-th bond with a fixed bond angle θ. One may introduce a constraint in changing the dihedral angle φ through the torsional energy, for example, in the following form
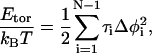 |
where τi is the coefficient of the torsional potential at the i-th monomer. Fig. 2 shows how one can interpret the torsional constraint as an effective bending energy.
APPENDIX II
From the relation |ΔEelec,II| < ΔEbend < ΔEelec,IV, we can extract a reasonable range of 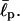 Under this condition, the total energy is positive for EAK16-II (ΔEII > 0) and negative for EAK16-IV (ΔEIV < 0), consistent with the results in Fig. 5 b. Because |ΔEelec,II| = 3.4 kBT, |ΔEelec,IV| = 7.4 kBT, and
Under this condition, the total energy is positive for EAK16-II (ΔEII > 0) and negative for EAK16-IV (ΔEIV < 0), consistent with the results in Fig. 5 b. Because |ΔEelec,II| = 3.4 kBT, |ΔEelec,IV| = 7.4 kBT, and 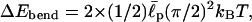 we obtain
we obtain 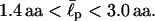 Again this agrees with the known values of
Again this agrees with the known values of 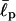 in the literature.
in the literature.
APPENDIX III
We note that the existence of two ground states is moderately sensitive to the effective persistence length 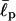 of the chain. When the chain is too flexible (for example,
of the chain. When the chain is too flexible (for example, 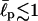 aa), the only ground state is the hairpin because the electrostatic attraction easily dominates the opposing bending energy. In the stiff limit, i.e.,
aa), the only ground state is the hairpin because the electrostatic attraction easily dominates the opposing bending energy. In the stiff limit, i.e., 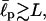 G(R, L) is essentially the same for all three types of oligopeptides and thus the bending energy (together with the chain entropy) solely determines the chain conformations. On the other hand, the cloud maps show more robust behavior for a range of the excluded volume factor σ (0.7–1.2 aa). Finally, under the experimental conditions studied in this article (pure water and peptide concentrations <1 mg/mL), the Debye screening length (Barrat and Joanny, 1996) is larger than the chain length itself, and practically there is no screening (
G(R, L) is essentially the same for all three types of oligopeptides and thus the bending energy (together with the chain entropy) solely determines the chain conformations. On the other hand, the cloud maps show more robust behavior for a range of the excluded volume factor σ (0.7–1.2 aa). Finally, under the experimental conditions studied in this article (pure water and peptide concentrations <1 mg/mL), the Debye screening length (Barrat and Joanny, 1996) is larger than the chain length itself, and practically there is no screening (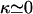 ) within the chain length. Computer simulations also show that charge screening in this system makes no significant differences (data not shown).
) within the chain length. Computer simulations also show that charge screening in this system makes no significant differences (data not shown).
APPENDIX IV
Even for EAK16-II, the peptide can lower its intrachain energy by adjusting the side chains of charged residues by forming a hairpin structure. To fold, however, EAK16-II has to overcome a kinetic barrier first, because hairpins are not the most accessible conformations for EAK16-II, as implied by the MC results of P(R, L). This implies that individual peptides should have enough time available to form hairpins, making many unsuccessful attempts. Otherwise, they would collide into different chains by self-diffusion, forming more stable β-sheets before forming hairpins. In other words, the peptide concentration should be low enough (or, equivalently, the average intermolecular distance is large enough) that the mean folding time of peptide τfold is somewhat shorter than the mean collision or diffusion time τdiff.
A recent study by Jun et al. (2003) enables us to compare τfold and τdiff. Because EAK16-II is long enough (L/ℓp ≈ 8), it may be considered as a flexible chain as regards its folding properties. An upper bound for τfold is then given by the longest relaxation time of the chain τrelax = L2/2D, where L is the chain length and D is the diffusion constant of single amino acid. Now, we define N* as the ratio of 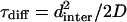 to τfold, where dinter is the average intermolecular distance at c = c*. In other words, N* is the average number of attempts for forming hairpin before peptides collide with each other. Based on the results by Jun et al., we obtain
to τfold, where dinter is the average intermolecular distance at c = c*. In other words, N* is the average number of attempts for forming hairpin before peptides collide with each other. Based on the results by Jun et al., we obtain 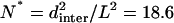 (dinter = 30.2 nm for c* = 0.1 mg/mL, L = 7 nm), i.e., it takes almost 20 unsuccessful attempts for EAK16-II to finally form hairpins at c = c*.
(dinter = 30.2 nm for c* = 0.1 mg/mL, L = 7 nm), i.e., it takes almost 20 unsuccessful attempts for EAK16-II to finally form hairpins at c = c*.
APPENDIX V
With a few assumptions, we can easily see from the AFM images that the majority of peptides are in β-sheets. First of all, we assume that β-sheets form fibrillar nanostructures whereas β-turns form globular ones. We further assume that the peptide concentration on the mica surface is roughly the same as in the solution. Then the number of peptides in β-turns (in the solution) is roughly the ratio of the volume of globular structures in AFM image to the volume of individual EAK16-II molecules. For EAK16-II at the concentration 0.08 mg/mL, we find the number of peptides in β-sheets is 104 times those in β-turns.
On the other hand, the cloud map in Fig. 6 also confirms that the ground state of extended conformation is much more accessible than the ground state of hairpin one. Although both conformations have similar energies, the densities around the two ground states differ by at least a factor of 10, giving a large difference in the number of accessible conformations (one should simulate at higher resolution to obtain a more accurate ratio).
Because such a small fraction of peptides are in a hairpin conformation, their contribution to the FTIR spectrum, which is sensitive to all molecules, is negligible.
S. Jun and Y. Hong contributed equally to this work.
References
- Barrat, J.-L., and J.-F. Joanny. 1996. Theory of polyelectrolyte solution. Adv. Chem. Phys. 94:1–66 (and references therein.). [Google Scholar]
- Bartels, C., M. Schaefer, and M. Karplus. 1999. Multidimensional adaptive umbrella sampling. J. Chem. Phys. 111:8048–8067. [Google Scholar]
- Bright, J. N., T. B. Woolf, and J. H. Hoh. 2001. Predicting properties of intrinsically unstructured proteins. Prog. Biophys. Mol. Biol. 76:131–173. [DOI] [PubMed] [Google Scholar]
- Byler, D. M., and H. Susi. 1986. Examination of the secondary structure of proteins by deconvoluted FTIR spectra. Biopolymers. 25:469–487. [DOI] [PubMed] [Google Scholar]
- Caplan, M. R., P. N. Moore, S. Zhang, R. D. Kamm, and D. A. Lauffenburger. 2000. Self-assembly of a β-sheet protein governed by relief of electrostatic repulsion relative van der Waals attraction. Biomacromolecules. 1:627–631. [DOI] [PubMed] [Google Scholar]
- Caplan, M. R., and D. A. Lauffenburger. 2002. Nature's complex copolymers: engineering design of oligopeptide materials. Ind. Eng. Chem. Res. 41:403–412. [Google Scholar]
- Carrion-vazquez, M., A. F. Oberhauser, T. E. Fisher, P. E. Marszale, H. Li, and J. M. Fernandez. 2000. Mechanical design of proteins-studied by single-molecule force spectroscopy and protein engineering. Prog. Biophys. Mol. Biol. 74:63–91. [DOI] [PubMed] [Google Scholar]
- Casal, H. L., U. Köhler, and H. H. Mantsch. 1988. Structural and conformational changes of β-lactoglobin B: an infrared spectroscopic study of the effect of pH and temperature. Biochim. Biophys. Acta. 957:11–20. [DOI] [PubMed] [Google Scholar]
- Chen, J. Z. Y., A. S. Lemak, J. R. Lepock, and J. P. Kemp. 2003. Minimal model for studying prion-like folding pathways. Proteins. 51:283–288. [DOI] [PubMed] [Google Scholar]
- Cornell, W. D., P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, Jr., D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell, and P. A. Kollman. 1995. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 117:5179–5197. [Google Scholar]
- Dong, A., P. Huang, and W. S. Caughey. 1990. Protein secondary structures in water from the second-derivative amide I infrared spectra. Biochemistry. 29:3303–3308. [DOI] [PubMed] [Google Scholar]
- Fernandez-López, S., H. S. Kim, E. C. Choi, M. Delgado, J. R. Granja, A. Khasanov, K. Kraehenbuehl, G. Long, D. A. Weinberger, K. M. Wilcoxen, and M. R. Ghadiri. 2001. Antibacterial agents based on the cyclic D, L-α-peptide architecture. Nature. 412:452–455. [DOI] [PubMed] [Google Scholar]
- Ferrenberg, A. M., and R. H. Swendsen. 1988. New Monte Carlo technique for studying phase transitions. Phys. Rev. Lett. 61:2635–2638. [DOI] [PubMed] [Google Scholar]
- Fung, S. Y., C. Keyes, J. Duhamel, and P. Chen. 2003. Concentration effect on the aggregation of a self-assembling oligopeptide. Biophys. J. 85:537–548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldenberg, D. P. 2003. Computational simulation of the statistical properties of unfolded proteins. J. Mol. Biol. 326:1615–1633. [DOI] [PubMed] [Google Scholar]
- Goldsbury, C., J. Kistler, U. Aebe, T. Arvinte, and G. J. S. Cooper. 1999. Watching amyloid fibrils grow by time-lapse atomic force microscopy. J. Mol. Biol. 285:33–39. [DOI] [PubMed] [Google Scholar]
- Gsponer, J., U. Haberthür, and A. Caflisch. 2003. The role of side-chain interactions in the early steps of aggregation: molecular dynamics simulations of an amyloid-forming peptide from the yeast prion Sup35. Proc. Natl. Acad. Sci. USA. 100:5154–5157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansmann, U. H. E., and Y. Okamoto. 1994. Comparative study of multicanonical and simulated annealing algorithms in the protein folding problem. Physica A. 212:415–437. [Google Scholar]
- Hansmann, U. H. E., and Y. Okamoto. 1999. New Monte Carlo algorithms for protein folding. Curr. Opin. Struct. Biol. 9:177–183. [DOI] [PubMed] [Google Scholar]
- Harrison, P. M., H. S. Chan, S. B. Prusiner, and F. E. Cohen. 1999. Thermodynamics of model prions and its implications for the problem of prion protein folding. J. Mol. Biol. 286:593–606. [DOI] [PubMed] [Google Scholar]
- Hartgerink, D. J., E. Beniash, and S. I. Stupp. 2001. Self-assembly and mineralization of peptide-amphiphile nanofibers. Science. 294:1684–1687. [DOI] [PubMed] [Google Scholar]
- Holmes, T. C., S. Delacalle, X. Su, A. Rich, and S. Zhang. 2000. Extensive neurite outgrowth and active neuronal synapses on peptide scaffolds. Proc. Natl. Acad. Sci. USA. 97:6728–6733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hong, Y., R. L. Legge, S. Zhang, and P. Chen. 2003. Effect of amino acid sequence and pH on nanofiber formation of the self-assembling peptides EAK16-II and EAK16-IV. Biomacromolecules. 4:1434–1442. [DOI] [PubMed] [Google Scholar]
- Hwang, W., D. M. Marini, R. D. Kamm, and S. Zhang. 2003. Supramolecular structure of helical ribbons self-assembled from a β-sheet peptide. J. Chem. Phys. 118:389–397. [Google Scholar]
- Jang, H., C. K. Hall, and Y. Q. Zhou. 2002. Protein folding pathways and kinetics: molecular dynamics simulations of beta-strand motifs. Biophys. J. 83:819–835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen, W. L., D. S. Maxwell, and J. J. Tirado-Rives. 1996. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 118:11225–11236. [Google Scholar]
- Jun, S., J. Bechhoefer, and B.-Y. Ha. 2003. Diffusion-limited loop formation of semiflexible polymers: Kramers theory and the intertwined time scales of chain relaxation and closing. Europhys. Lett. 64:420–426. [Google Scholar]
- Kemp, J. P., and J. Z. Y. Chen. 2001. Helical structures in proteins. Biomacromolecules. 2:389–401 (and references therein.). [DOI] [PubMed] [Google Scholar]
- Klimov, D. K., and D. Thirumalai. 2002. Stiffness of the distal loop restricts the structural heterogeneity of the transition state ensemble in SH3 domains. J. Mol. Biol. 317:721–737. [DOI] [PubMed] [Google Scholar]
- Kumar, S., D. Bouzida, R. H. Swendsen, P. A. Kollman, and J. M. Rosenberg. 1992. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 13:1011–1021. [Google Scholar]
- Kumar, S., D. Bouzida, P. A. Kollman, R. H. Swendsen, and J. M. Rosenberg. 1995. Multidimensional free-energy calculations using the weighted histogram analysis method. J. Comput. Chem. 16:1339–1350. [Google Scholar]
- Lee, S. W., C. Mao, C. E. Flynn, and A. M. Belcher. 2002. Ordering of quantum dots using genetically engineered viruses. Science. 296:892–895. [DOI] [PubMed] [Google Scholar]
- Lemak, A. S., and J. R. Gunn. 2000. Rotamer-specific potentials of mean force for residue pair interactions. J. Phys. Chem. B. 104:1097–1107. [Google Scholar]
- Lomakin, A., D. S. Chung, G. B. Benedek, D. A. Kirschner, and D. B. Teplow. 1996. On the nucleation and growth of amyloid β-protein fibrils: detection of nuclei and quantitation of rate constants. Proc. Natl. Acad. Sci. USA. 93:1125–1129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- López de la Paz, M., K. Goldie, J. Zurdo, E. Lacroix, and C. M. Dobson. 2002. De novo designed peptide-based amyloid fibrils. Proc. Natl. Acad. Sci. USA 99:16052–16057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKerell, A. D., Jr., D. Bashford, M. Bellott, R. L. Dunbrack, Jr., J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher III, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wirkiewicz-Kuczera, D. Yin, and M. Karplus. 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. Phys. Chem. B. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
- Madras, N., and A. D. Sokal. 1988. The pivot algorithm: a highly efficient Monte-Carlo method for the self-avoiding walk. J. Stat. Phys. 50:109–186. [Google Scholar]
- Metropolis, N., A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller, and E. Teller. 1953. Equation of state calculations by fast computing machines. J. Chem. Phys. 21:1087–1092. [Google Scholar]
- Mezei, M. 1987. Adaptive umbrella sampling: self-consistent determination of the non-Boltzmann bias. J. Comput. Phys. 68:237–248. [Google Scholar]
- Mikros, E., D. Benaki, E. Humpfer, M. Spraul, S. Loukas, C. I. Stassinopoulou, and M. Pelecanou. 2001. High-resolution NMR spectroscopy of the β-amyloid(1–28) fibril typical for Alzheimer's disease. Angew. Chem. Int. Ed. 40:3603–3605. [DOI] [PubMed] [Google Scholar]
- Millet, I. S., S. Doniach, and K. W. Plaxco. 2002. Toward a taxonomy of the denatured state: small angle scattering studies of unfolded proteins. Adv. Protein Chem. 62:241–262. [DOI] [PubMed] [Google Scholar]
- Mu, Y., D. S. Kosov, and G. Stock. 2003. Conformational dynamics of trialanine in water. 2. Comparison of AMBER, CHARMM, GROMOS, and OPLS force fields to NMR and infrared experiments. J. Phys. Chem. B. 107:5064–5073. [Google Scholar]
- Nowak, A. P., V. Breedveld, L. Pakstis, B. Ozbas, D. J. Pine, D. Pochan, and T. J. Deming. 2002. Rapidly recovering hydrogel scaffolds from self-assembling diblock copolypeptide amphilphiles. Nature. 417:424–428. [DOI] [PubMed] [Google Scholar]
- Petka, W. A., J. L. Harden, K. P. McGrath, D. Wirtz, and D. A. Tirrell. 1998. Reversible hydrogels from self-assembling artificial proteins. Science 281:389–392. [DOI] [PubMed] [Google Scholar]
- Rief, M., M. Gautel, A. Schemmel, and H. E. Gaub. 1998. The mechanical stability of immunoglobulin and fibronectin III domains in the muscle protein titin measured by atomic force microscopy. Biophys. J. 74:3008–3014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rochet, J.-C., and P. T. Lansbury, Jr. 2000. Amyloid fibrilligenesis: themes and variations. Curr. Opin. Struct. Biol. 10:60–68. [DOI] [PubMed] [Google Scholar]
- Schlick, T. 2002. Theoretical and computational approaches to biomolecular structure. In Molecular Modeling and Simulation. Springer-Verlag, New York. 199–224.
- Smith, A. V., and C. K. Hall. 2001. Protein refolding versus aggregation: computer simulations on an intermediate-resolution protein model. J. Mol. Biol. 312:187–202. [DOI] [PubMed] [Google Scholar]
- Stine, W. B., Jr., K. N. Dahlgren, G. A. Fraft, and M. J. Ladu. 2003. In vitro characterization of conditions for amyloid-β peptide oligomerization and fibrillogenesis. J. Biol. Chem. 278:11612–11622. [DOI] [PubMed] [Google Scholar]
- Thirumalai, D., and B.-Y. Ha. 1998. Statistical mechanics of semiflexible chains: a mean-field variational approach. In Theoretical and Mathematical Models in Polymer Research, A. Grosberg, editor. Academic Press, San Diego, CA. 1–35.
- Thirumalai, D., D. K. Klimov, and R. I. Dima. 2003. Emerging ideas on the molecular basis of protein and peptide aggregation. Curr. Opin. Struct. Biol. 13:146–159. [DOI] [PubMed] [Google Scholar]
- Tiana, G., and R. A. Broglia. 2002. Design and folding of dimeric proteins. Proteins. 49:82–94. [DOI] [PubMed] [Google Scholar]
- Torrie, G. M., and J. P. Valleau. 1974. Monte Carlo free energy estimates using non-Boltzmann sampling: application to the sub-critical Lennard-Jones fluid. Chem. Phys. Lett. 28:578–581. [Google Scholar]
- Torrie, G. M., and J. P. Valleau. 1977. Nonphysical sampling distributions in Monte Carlo free energy estimation: umbrella sampling. J. Comput. Phys. 23:187–199. [Google Scholar]
- Tycko, R. 2000. Solid-state NMR as a probe of amyloid fibril structure. Curr. Opin. Chem. Biol. 4:500–506. [DOI] [PubMed] [Google Scholar]
- Van Gunsteren, W. F., S. R. Billeter, A. A. Eising, P. H. Hunenberger, P. Kruger, A. E. Mark, W. R. P. Scott, and I. G. Tironi. 1996. Biomolecular Simulation: The GROMOS96 Manual and User Guide. Vdf Hochschulverlag AG an der ETH Zurich, Zurich, Switzerland.
- Vauthey, S., S. Santos, H. Gong, N. Watson, and S. Zhang. 2002. Molecular self-assembly of surfactant-like peptides to form nanotubes and nanovesicles. Proc. Natl. Acad. Sci. USA. 99:5355–5360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vendruscolo, M., J. Zurdo, C. E. MacPhee, and C. M. Dobson. 2003. Protein folding and misfolding: a paradigm of self-assembly and regulation in complex biological systems. Philos. Trans. R. Soc. Lond. A. 361:1205–1222. [DOI] [PubMed] [Google Scholar]
- Whaley, S. R., D. S. English, E. L. Hu, P. F. Barbara, and A. M. Belcher. 2000. Selection of peptides with semiconductor binding specificity for directed nanocrystal assembly. Nature. 405:665–668. [DOI] [PubMed] [Google Scholar]
- Yeates, T., and J. E. Padilla. 2002. Designing supramolecular protein assemblies. Curr. Opin. Struct. Biol. 12:464–470. [DOI] [PubMed] [Google Scholar]
- Zhang, S., T. C. Holmes, C. Lockshin, and A. Rich. 1993. Spontaneous assembly of a self-complementary oligopeptide to form a stable macroscopic membrane. Proc. Natl. Acad. Sci. USA. 90:3334–3338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, S., T. C. Holmes, C. M. Dipersio, R. O. Hynes, X. Su, and A. Rich. 1994. Self-complementary oligopeptide matrices support mammalian cell attachment. Biomaterials. 16:1385–1393. [DOI] [PubMed] [Google Scholar]
- Zhang, S., C. Lockshin, R. Cook, and A. Rich. 1994. Unusually stable β-sheet formation in an ionic self-complementary oligopeptide. Biopolymers. 34:663–672. [DOI] [PubMed] [Google Scholar]
- Zhang, S. 2002. Emerging biological materials through molecular self-assembly. Biotechnol. Adv. 20:321–339. [DOI] [PubMed] [Google Scholar]
- Zhang, S., D. M. Marini, W. Hwang, and S. Santoso. 2002. Design of nanostructured biological materials through self-assembly of peptides and proteins. Curr. Opin. Chem. Biol. 6:865–871. [DOI] [PubMed] [Google Scholar]