Total Internal Reflection with Fluorescence Correlation Spectroscopy: Nonfluorescent Competitors

Abstract

Total internal reflection with fluorescence correlation spectroscopy is a method for measuring the surface association/dissociation rate constants and absolute densities of fluorescent molecules at the interface of a planar substrate and solution. This method can also report the apparent diffusion coefficient and absolute concentration of fluorescent molecules very close to the surface. Theoretical expressions for the fluorescence fluctuation autocorrelation function when both surface association/dissociation kinetics and diffusion through the evanescent wave, in solution, contribute to the fluorescence fluctuations have been published previously. In the work described here, the nature of the autocorrelation function when both surface association/dissociation kinetics and diffusion through the evanescent wave contribute to the fluorescence fluctuations, and when fluorescent and nonfluorescent molecules compete for surface binding sites, is described. The autocorrelation function depends in general on the kinetic association and dissociation rate constants of the fluorescent and nonfluorescent molecules, the surface site density, the concentrations of fluorescent and nonfluorescent molecules in solution, the solution diffusion coefficients of the two chemical species, the depth of the evanescent field, and the size of the observed area on the surface. Both general and approximate expressions are presented.

INTRODUCTION

A variety of biological processes are mediated by interactions between soluble ligands and cell-surface receptors. Examples include immune processes that rely on interactions between soluble antibodies specific for pathogens and antibody receptors on immune cell surfaces (Ravetch and Bolland, 2001; Heyman, 2000); neurological processes in which soluble transmitters such as serotonin stimulate cellular response by binding to specific receptors (Kim and Huganir, 1999; Seal and Amara, 1999); regulation of cellular growth and proliferation by interactions between specific growth factors and their cell-surface receptors (Robinson and Stringer, 2001; Hwa et al., 1999); and blood hemostasis, which is mediated in part by soluble proteins such as fibrinogen that associate with specific receptors on platelet surfaces (Clemetson and Clemetson, 1998; Zwaal et al., 1998).

In a number of cases, it has been hypothesized that cellular signaling processes depend not only on the equilibrium strength of the triggering ligand-receptor interactions, but also on the average lifetimes, or kinetic dissociation rates, of these interactions. Examples include kinetic proofreading to enhance specificity of signal transduction carried out by T-cell receptors (McKeithan, 1995; Rabinowitz et al., 1996); regulation of signaling complex formation by the dissociation kinetics of IgE (Hlavacek et al., 2001) and tumor necrosis factor (Krippner-Heidenreich et al., 2002) from their receptors; the efficacy of ligands interacting with G-protein coupled receptors (Shea et al., 2000); and effects on synaptic transmission mediated by nicotinic acetylcholine receptors at the neuromuscular junction (Wenningmann and Dilger, 2001). To dissect the mechanisms governing the sensitivity, specificity, and regulation of cell signaling, it is necessary to be able to accurately characterize the kinetics of ligand-receptor interactions.

A technique useful for measuring ligand-receptor kinetic rate constants is total internal reflection illumination combined with fluorescence correlation spectroscopy (TIR-FCS). In this method, a small sample volume is defined by the depth of an evanescent field created by an internally reflected laser beam, and a confocal pinhole. The fluorescence fluctuations from the sample volume are monitored and autocorrelated, and the shape of the autocorrelation function yields information about the rates of the processes causing the fluctuations. By fitting experimental autocorrelation data to theoretically predicted expressions appropriate for the system being studied, properties such as kinetic rate constants, diffusion coefficients, and the average number of particles within the detection volume can be determined.

Although both evanescent excitation in fluorescence microscopy (Axelrod, 2001; Thompson and Lagerholm, 1997) and fluorescence correlation spectroscopy (Haustein and Schwille, 2003; Thompson et al., 2002; Rigler and Elson, 2001; Hovius et al., 2000) are fairly well-developed methods, the combination of these two techniques has thus far been limited to only a handful of experimental applications. TIR-FCS was initially demonstrated as a viable method by examining the nonspecific binding of tetramethylrhodamine-labeled immunoglobulin and insulin to serum albumin-coated fused silica (Thompson and Axelrod, 1983). More recently, TIR-FCS has been used to characterize the reversible adsorption kinetics of rhodamine 6G to C-18-modified silica surfaces (Hansen and Harris, 1998a,b), to examine local diffusion coefficients and concentrations of fluorescently labeled, monoclonal IgG in solution very close to substrate-supported phospholipid bilayers (Starr and Thompson, 2002), and to measure mass transport rates of small fluorescent molecules through thin sol-gel films (McCain and Harris, 2003). TIR-FCS is one of several super-resolution fluorescence microscopy methods under current development (Laurence and Weiss, 2003).

We have recently demonstrated that TIR-FCS can accurately report information about the kinetic rate constants for fluorescent ligands in solution that are specifically and reversibly interacting with receptors on surfaces (Lieto et al., 2003). In particular, the method was applied to the reversible interaction of fluorescently labeled IgG with the mouse Fc receptor FcγRII, which was purified and reconstituted into substrate-supported membranes. Because the magnitude of the measured fluorescence fluctuation autocorrelation function is, generally, inversely related to the average number of fluorescent molecules in the observed volume, it was necessary in this work to use a small concentration of fluorescent ligands. To arrange the system so that the total concentration of ligand in solution was on the order of the equilibrium dissociation constant for surface binding, it was necessary to also include a much larger concentration of nonfluorescent ligands. (Working solely with a low concentration of fluorescent ligand would raise the likely possibility of observing primarily ligand interaction with rare, tight, nonspecific binding sites.)

To adequately analyze the data obtained in this initial demonstration of TIR-FCS as a method for measuring specific ligand-receptor kinetic rate constants, we generalized previously developed theories (Starr and Thompson, 2001; Thompson, 1982; Thompson et al., 1981) to find expressions predicting the nature of the TIR-FCS autocorrelation function when both fluorescent and nonfluorescent species compete for surface binding sites. The general expression for the autocorrelation function is presented here, along with a number of approximate expressions applicable to different experimental limits. It is likely that most applications of TIR-FCS to the measure of specific ligand-receptor kinetics will require mixing a small concentration of fluorescent ligands with a much larger concentration of nonfluorescent ligands. The values of the general solution for the autocorrelation function can be compared to the values of the approximate solutions to find the best theoretical form for fitting data given a particular set of experimental conditions.

The theory developed here demonstrates that the autocorrelation function, in general, contains information not only about the kinetic rate constants for the fluorescent ligand but also the kinetic rate constants for the nonfluorescent competitors. Thus, the method should also be applicable to a strategy in which a single fluorescent reporter molecule is used to determine the kinetic association/dissociation rates of nonfluorescent competitors. This arrangement has potential application to the screening of nonfluorescent ligands based on the kinetic, rather than only the equilibrium, properties of ligand-receptor interactions. Practical considerations related to this application will be described in subsequent work.

RESULTS

Definitions

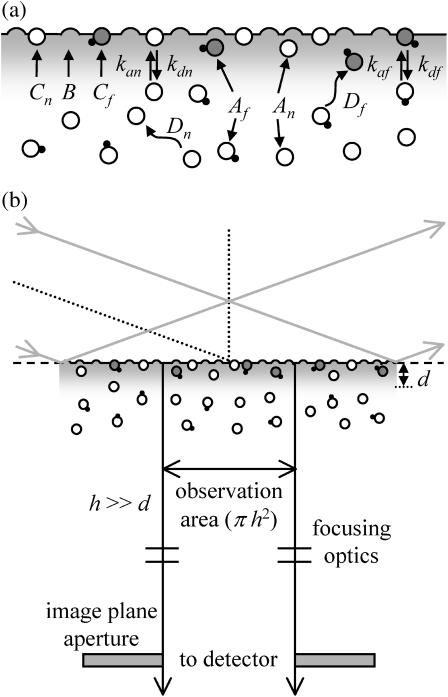
Consider a reversible bimolecular reaction at a surface coupled with diffusion in solution (Fig. 1 a). The surface is denoted by polar coordinates (r, φ), and the distance from the surface to a point in solution is defined as z > 0. A concentration of fluorescent molecules in solution, 〈A_f〉, is in equilibrium with a density of nonfluorescent, unoccupied surface binding sites, 〈B〉, forming fluorescent complexes on the surface of density 〈C_f〉. Nonfluorescent molecules in solution, with concentration 〈A_n〉, compete with the fluorescent molecules for surface binding sites forming a density of nonfluorescent complexes on the surface, 〈C_n〉. The surface association and dissociation rate constants are k_af, k_an, k_df, and k_dn; and the equilibrium association constants describing surface binding are K_f = k_af/k_df and K_n = k_an/k_dn. The average densities of surface-bound fluorescent and nonfluorescent molecules are

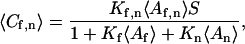(1)

where S = 〈C_f〉 + 〈C_n〉 + 〈B〉 is the total density of surface binding sites. The fluorescent and nonfluorescent molecules diffuse in solution with coefficients D_f and D_n, respectively. In this work, it is assumed that the surface binding sites and surface-bound complexes do not appreciably diffuse in the sample plane.

FIGURE 1.

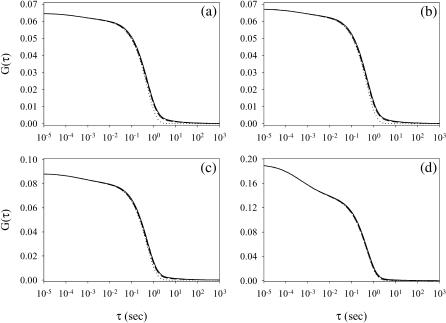
Surface binding mechanism and optical geometry. (a) Fluorescent molecules in solution of concentration 〈A_f〉 diffuse with coefficient D_f and bind to surface sites of density 〈B〉 to form fluorescent complexes of density 〈C_f〉. Nonfluorescent molecules in solution of concentration 〈A_n〉 diffuse with coefficient D_n and compete for the same surface binding sites to form nonfluorescent complexes of density 〈C_n〉. Binding rate constants for association and dissociation are given by k_af, k_df, k_an, and k_dn. Surface binding sites and surface-bound complexes are not laterally mobile along the surface. (b) A laser beam is internally reflected at the interface, creating an evanescent field in the solution with an intensity that decays exponentially with distance from the interface. A small sample volume is defined by the exponential depth, d, in combination with a circular aperture placed at an intermediate image plane of the microscope that defines an area of radius h in the sample plane. In this work, it is assumed that h ≫ d.

The surface is illuminated by the evanescent field created by totally internally reflecting a laser beam at the surface/solution interface (Fig. 1 b). The intensity of the evanescent field decays exponentially as a function of the distance from the interface, with characteristic depth d. Along with the evanescent field, a small, circular aperture placed at an intermediate image plane of the microscope defines an observation volume. The observation area in the sample plane, defined by the image plane aperture, has a radius of h. We assume that h ≫ d; in this case, the fluorescence fluctuation autocorrelation function does not depend on the observation area radius h (Thompson et al., 1981).

At chemical equilibrium, individual molecules diffuse in solution within the observation volume; and bind to and dissociate from sites on the surface. These processes give rise to temporal fluctuations in the fluorescence measured from the observation volume, denoted here by F(t). The temporal fluorescence fluctuation is defined as the difference between the instantaneous fluorescence intensity and its average value; i.e., δF(t) = F(t) − 〈F〉. The normalized fluorescence fluctuation autocorrelation function is

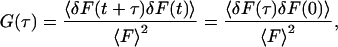(2)

where the second equality holds for ergodic systems.

General expression for the magnitude of the fluorescence fluctuation autocorrelation function

As shown in the Appendix,

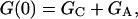(3)

where

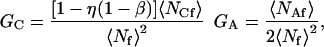(4)

and

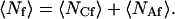(5)

In Eqs. 4 and 5, 〈N_f〉 is the average number of observed fluorescent molecules, 〈N_Cf〉 is the average number of fluorescent molecules on the surface within the observation area, and 〈N_Af〉 is the average number of fluorescent molecules in solution within the observation volume; i.e.,

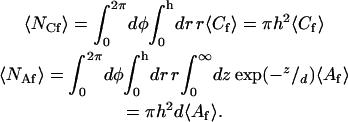(6)

In Eq. 4, η is the fraction of surface-bound molecules that is fluorescent and β is the fraction of surface sites that is unoccupied; i.e., (see Eq. 1)

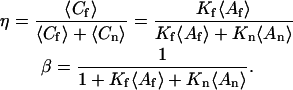(7)

The terms G_C and G_A result from autocorrelations in the fluctuations in concentrations of fluorescent molecules on the surface and in solution, respectively. The factor of two in the denominator of the expression for G_A in Eq. 4 arises from the exponential shape of the evanescent intensity along the z axis and the definition of 〈N_Af〉 given in Eq. 6. The factor [1 − η(1 − β)] in the numerator of the expression for G_C in Eq. 4 arises from the fact that fluctuations in the concentrations of bound species follow binomial rather than Poisson statistics (Thompson, 1982; see also the Appendix). When the average number of observed molecules in solution is much larger than the average number of observed molecules on the surface, G(0) depends only on 〈N_Af〉; i.e., G(0) = [2〈N_Af〉]⁻¹. When the average number of observed molecules on the surface is much larger than the average number of observed molecules in solution, the magnitude of the fluorescence fluctuation autocorrelation function may still depend on both 〈N_Cf〉 and 〈N_Af〉. G(0) loses its dependence on 〈N_Af〉 only if [1 − η(1 − β)]〈N_Cf〉 ≫ 〈N_Af〉, where we note that [1 − η(1 − β)] ≤ 1.

General expression for the fluorescence fluctuation autocorrelation function

As shown in the Appendix, the fluorescence fluctuation autocorrelation function is, in general, given by

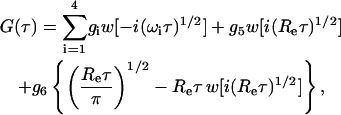(8)

where w(ξ) = exp(−ξ²)erfc(−iξ) (Abramowitz and Stegun, 1974).

The four rates ω_i are given by the solutions to the quartic equation

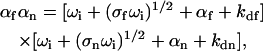(9)

where α_f = k_af〈A_f〉, α_n = k_an〈A_n〉, and

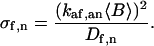(10)

G(τ) has seven characteristic rates: k_df, k_dn, α_f, α_n, σ_f, σ_n, and

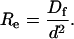(11)

The rates α_f + k_df and α_n + k_dn are the relaxation rates for pseudo first-order reactions and increase with the solution concentrations of fluorescent and nonfluorescent molecules, respectively. The rates σ_f and σ_n are related to rebinding at the surface (Lagerholm and Thompson, 1998; Starr and Thompson, 2001). R_e is the rate for diffusion of fluorescent molecules through the depth of the evanescent intensity. A somewhat unusual property of these expressions is that 〈N_Cf〉 and 〈N_Af〉 are not independent of the characteristic rates; i.e.,

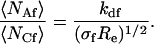(12)

The amplitudes g₁–g₄ in Eq. 8 are

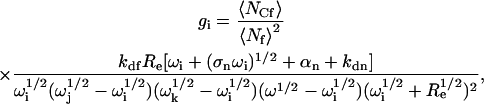(13)

where i ≠ j ≠ k ≠ ℓ. The remaining amplitudes are

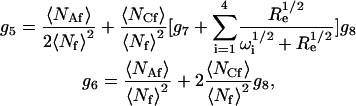(14)

where

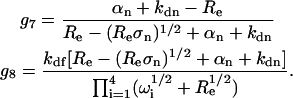(15)

By noting that w(0) = 1, and rewriting β and η in terms of k_df, k_dn, α_f, and α_n (see Eq. 7), one finds that G(0) given by Eqs. 8 and 13–15 equals that shown in Eqs. 3–5.

When nonfluorescent molecules are not present, 〈A_n〉 = 0, α_n = 0, and the four rates ω_i are given by (see Eq. 9)

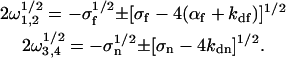(16)

By using these rates in Eqs. 8 and 13–15, one finds the expression for G(τ) when nonfluorescent molecules are not present, which has been previously discussed in detail (Starr and Thompson, 2001; Eqs. 7–11). In this case, η = 1. G_A is given by Eq. 4 but G_C = [β〈N_Cf〉]/[〈N_f〉²].

Limit of no surface binding

When k_af = 0, the fluorescent molecules do not bind to the surface. In this case, 〈N_Cf〉 = 0 (Eqs. 1 and 6) and Eqs. 8, 9, and 13–15 reduce to

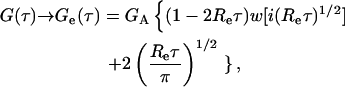(17)

where G_A = [2〈N_Af〉]⁻¹. This expression agrees with previously published results (Starr and Thompson, 2001, 2002). G_e(τ) describes the diffusion of fluorescent molecules through the depth of the evanescent intensity, and decreases monotonically with increasing τ from [2&〈N_Af〉]⁻¹ to zero. The characteristic decay time is 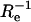and the ratio of the initial slope to the initial value is −R_e. The presence of the nonfluorescent molecules is not detected because cross talk between fluorescent and nonfluorescent molecules occurs only through the surface binding sites for which they compete.

Contributions to G(τ) from surface kinetics

Equations 8–15 give the general form for G(τ), which contains contributions arising from diffusion through the evanescent intensity (e.g., Eq. 17), from surface binding kinetics, and from cross talk between the two processes. The form of G(τ) is significantly simplified in the case where the rate for diffusion through the evanescent intensity, R_e, is much larger than the other six characteristic rates. (Typically, for D ≈ 10⁻⁶ cm² s⁻¹ and d ≈ 0.1 μm, R_e ≈ 10⁴ s⁻¹). In this case, Eqs. 8 and 13–15 reduce to

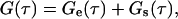(18)

where G_e(τ) is given by Eq. 17, with G_A as shown in Eqs. 4 and 5, and

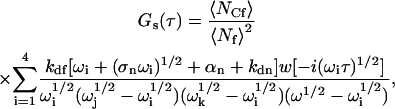(19)

with the four 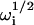given by Eqs. 9 and 10. The function in Eq. 19 does not depend on the rate R_e, and its magnitude, given that w(0) = 1, can be shown in general to equal G_C (Eqs. 4 and 5). Thus, when R_e is by far the largest rate, G(τ) separates into two terms, one that reports information about diffusion through the evanescent intensity and one that reports information about surface association/dissociation kinetics.

Contributions to G(τ) from surface kinetics: reaction limit

For some systems, the rates σ_f and σ_n are much smaller than the intrinsic surface dissociation rates k_df and k_dn, respectively. This limit has previously been called the “reaction limit” (Thompson et al., 1981; Starr and Thompson, 2001) and is associated with the lack of a propensity for rebinding to the surface after dissociation (Lagerholm and Thompson, 1998). For simplicity of data analysis, if the interest is to determine the kinetic rate constants associated with surface association and dissociation, it is advantageous to situate the system in the reaction limit by adjusting the experimental parameters (e.g., by decreasing the total surface site density S or by increasing the solution concentrations 〈A_f〉 and/or 〈A_n〉 so that 〈B〉 is reduced; see Eq. 10).

In the reaction limit where σ_f → 0 and σ_n → 0, the quartic equation specifying the four quantities 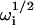(Eq. 9) condenses to the following quadratic equation:

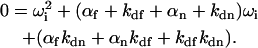(20)

Therefore, 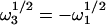and 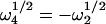. By using the analytical expressions for the four 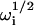from Eq. 20 in Eq. 19, along with the identity w(ξ) + w(−ξ) = 2exp(−ξ²) (Abramowitz and Stegun, 1974), one finds that

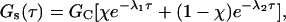(21)

where the rates are given by

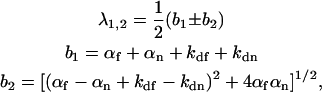(22)

and the amplitudes are defined by Eqs. 4–7 with

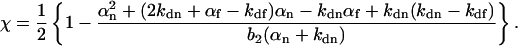(23)

The result in Eqs. 21–23 for the shape (but not the magnitude) of G_s(τ) has been published previously (Thompson, 1982). The remarkable property of these equations is not so much their relative simplicity as compared to Eq. 19, but the result that G_s(τ) contains information about the kinetic association and dissociation rate constants of the nonfluorescent species. Thus, the special characteristics of autocorrelation functions provide information about cross talk between fluorescent and nonfluorescent species that would not be available with many other methods.

In the case that there are no nonfluorescent molecules in solution, α_n = 0, and Eqs. 21–23 reduce to

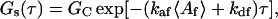(24)

which agrees with previous predictions (Thompson et al., 1981). When the kinetic rate constants for the fluorescent and nonfluorescent species are equivalent, Eqs. 21–23 equal

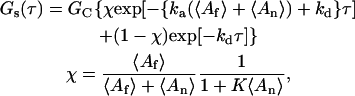(25)

where k_a = k_af = k_an, k_d = k_df = k_dn, and K = K_f = K_n. If, in addition, 〈A_n〉 ≫ 〈A_f〉, χ ≈ 0 and Eq. 25 reduces to its simplest form,

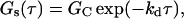(26)

where it should be noted that G(τ) no longer depends on k_a.

Examples of G(τ)

Fig. 2 shows four functions G(τ) calculated from the exact expressions (Eqs. 1, 4–11, and 13–15); from the expressions appropriate for the case in which R_e is the largest rate (Eqs. 1, 4–7, 9–11, and 17–19); and from the reaction-limited approximations (Eqs. 1, 4–7, 17, 18, and 21–23). G(τ) is shown for k_af = k_an = 10⁶ M⁻¹ s⁻¹, k_df = 2 s⁻¹, 〈A_f〉 = 10 nM, D_f = D_n = 50 μm² s⁻¹, S = 800 molecule μm⁻², d = 0.1 μm, and h = 1 μm; and for 〈A_n〉 = 0 (Fig. 2 a), 〈A_n〉= 1 μM and k_dn = 20 s⁻¹ (Fig. 2 b), 〈A_n〉 = 1 μM and k_dn = 2 s⁻¹ (Fig. 2 c), and 〈A_n〉 = 1 μM and k_dn = 0.2 s⁻¹ (Fig. 2 d). In Fig. 2, a–c, the value of G_A is low compared to the value of G_C and G(τ) therefore reflects primarily the surface binding kinetics. In Fig. 2 d, the value of G_A is not negligible, and G(τ) also contains a rapidly decaying component arising from diffusion of the fluorescent ligands through the depth of the evanescent intensity. In all cases, the half-time for decay is approximately equal to 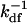. The approximate expressions applicable to the case in which R_e is by far the largest rate (dashed lines) agree well with the general expressions (solid lines). The “reaction limit” approximation is somewhat less accurate for the specific parameter values considered here when there are no nonfluorescent molecules present (Fig. 2 a) or when k_dn ≥ k_df (Fig. 2, b and c). This approximation is more accurate for lower values of σ_f = σ_n (see above and caption to Fig. 2).

FIGURE 2.

Examples of fluorescence fluctuation autocorrelation functions. The predicted values of G(τ) are shown for k_af = k_an = 10⁶ M⁻¹s⁻¹, k_df = 2 s⁻¹, 〈A_f〉= 10 nM, D_f = D_n = 50 μm² s⁻¹, S = 800 molecule μm⁻², d = 0.1 μm, and h = 1 μm. In panel a, 〈A_n〉= 0. In panels b–d, 〈A_n〉= 1 μM. The values of k_dn are (b) 20 s⁻¹, (c) 2 s⁻¹, or (d) 0.2 s⁻¹. Thus, K_f〈A_f〉 = 0.005 and K_n〈A_n〉 is (a) 0, (b) 0.05, (c) 0.5, or (d) 5. The rate R_e is 5000 s⁻¹. The density of free surface sites 〈B〉 in molecule μm⁻² is (a) 796, (b) 758, (c) 532, or (d) 133. The rates σ_f = σ_n in s⁻¹ are (a) 0.0350, (b) 0.0317, (c) 0.0156, or (d) 9.79 × 10⁻⁴. The average number of observed fluorescent molecules in solution, 〈N_Af〉, calculated from Eq. 6, is 1.89. The average number of observed, surface-bound, fluorescent molecules, 〈N_Cf〉, is found from Eqs. 1 and 6, and equals (a) 12.5, (b) 11.9, (c) 8.35, or (d) 2.09. Thus, the values of G_A, as calculated from Eq. 4, are (a) 4.56 × 10⁻³, (b) 4.96 × 10⁻³, (c) 9.02 × 10⁻³, and (d) 0.0596. The average fraction of surface-bound molecules that are fluorescent, η, is found from Eq. 7 as (a) 1, (b) 0.0909, (c) 9.9 × 10⁻³, or (d) 9.99 × 10⁻⁴. The average fraction of surface binding sites that are unoccupied, β (Eq. 7), is (a) 0.995, (b) 0.948, (c) 0.664, or (d) 0.167. The values of G_C, calculated from Eq. 4, are (a) 0.0600, (b) 0.0622, (c) 0.0793, and (d) 0.132. Thus, G(0) is (a) 0.0646, (b) 0.0672, (c) 0.0884, or (d) 0.191. Note that the ratio 〈N_Af〉/〈N_Cf〉agrees with that shown in Eq. 12. G(τ) was calculated from Eqs. 1, 4–11, and 13–15 (solid lines). G(τ) was calculated from Eqs. 1, 4–7, 9–11, and 17–19 (dashed lines). G(τ) was calculated from Eqs. 1, 4–7, 17, 18, and 21–13 (dotted lines).

DISCUSSION

Cellular signaling processes are thought to depend not only on the equilibrium strength of the triggering ligand-receptor interactions, but also on the average lifetimes, or kinetic dissociation rates, of these interactions. To understand the mechanisms governing the sensitivity, specificity, and regulation of cell signaling, it is therefore necessary to be able to accurately characterize the kinetics of ligand-receptor interactions. A technique useful for measuring ligand-receptor kinetic rate constants is total internal reflection illumination combined with fluorescence correlation spectroscopy (TIR-FCS).

In this work, we generalize previously developed theories to find expressions predicting the nature of the TIR-FCS fluorescence fluctuation autocorrelation function when both surface association/dissociation kinetics and diffusion through the evanescent wave in solution contribute to the fluorescence fluctuations, and when both fluorescent and nonfluorescent molecules compete for surface binding sites. Because the magnitude of the measured autocorrelation function is, in general, inversely related to the average number of fluorescent molecules in the observation volume, it is often necessary to mix a small concentration of fluorescent reporter molecules with a larger concentration of nonfluorescent molecules (Lieto et al., 2003).

The general expression for the fluorescence fluctuation autocorrelation function in the presence of nonfluorescent competitors has seven characteristic rates (Eqs. 9–11). The limits of this expression for the cases in which nonfluorescent molecules are not present, and when fluorescent molecules do not bind to the surface, agree with previously published results (Starr and Thompson, 2001). Simplified forms of the autocorrelation function are presented for the situation in which the rate of diffusion through the depth of the evanescent field is much faster than the other rates (Eqs. 17–19), and when the system is in the “reaction limit” (see Eqs. 17, 18, and 21–23). These two simplified forms are compared to the general expression for four different sets of experimental parameters in Fig. 2. A very simple form for G(τ), applicable when, in addition, there is a large excess of nonfluorescent ligands in the sample, has also been found (Eqs. 17, 18, and 26).

TIR-FCS is an attractive method for measuring ligand-receptor kinetics because of the small volumes and required amounts of material. In addition, the planar geometry opens the possibility of using this method in combination with microarrays for high throughput screening based on kinetic dissociation rates. Also, as shown here, when fluorescent and nonfluorescent molecules compete for the surface binding sites, TIR-FCS autocorrelation functions have the unusual characteristic that they contain, in general, information about the kinetic rates for both fluorescent and nonfluorescent molecules. Thus, it may be possible to use a single fluorescent ligand to monitor the kinetics of a variety of competitive or potentially competitive nonfluorescent species. Practical considerations related to the design and implementation of such TIR-FCS screens will be discussed in future work.

APPENDIX: DERIVATION OF THE FLUORESCENCE FLUCTUATION AUTOCORRELATION FUNCTION

Definitions

The fluorescence measured from the observation volume, F(t), is the sum of the fluorescence arising from surface-bound molecules, F_C(t), and the fluorescence arising from molecules in solution, F_A(t). The temporal fluorescence fluctuation, δF(t), is defined as the difference between the instantaneous fluorescence intensity and its average value, 〈F〉; i.e., δF(t) = F(t) − 〈F〉. The normalized fluorescence fluctuation autocorrelation function is defined in Eq. 2. Thus,

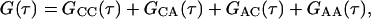(A1)

where

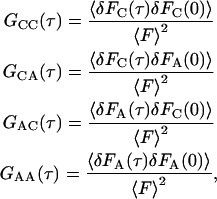(A2)

and F(t) = F_C(t) + F_A(t), 〈F〉 = 〈F_C〉 + 〈F_A〉, δF(t) = δF_C(t) + δF_A(t), δF_C(t) = F_C(t) − 〈F_C〉, and δF_A(t) = F_A(t) − 〈F_A〉. The evanescent intensity has the shape I₀exp(−z/d). Thus,

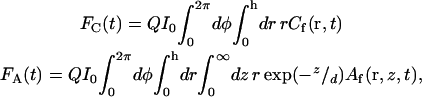(A3)

where Q is a proportionality constant and r = (r, φ) defines the surface/solution interface. The temporally averaged fluorescence intensity is 〈F〉 = QI₀ 〈N_f〉 where 〈N_f〉, the average number of fluorescent molecules in the observation volume, is defined in Eqs. 5 and 6. The solution concentrations and surface densities are written as the sum of their average values and the fluctuations from these values; i.e., C_f,n(r,t) = 〈C_f,n〉 + δC_f,n(r,t), B(r,t) = 〈B〉 + δB(r,t), and A_f,n(r,z,t) = 〈A_f,n〉 + δA_f,n(r,z,t). By using these expressions in Eqs. A2 and A3, one finds that

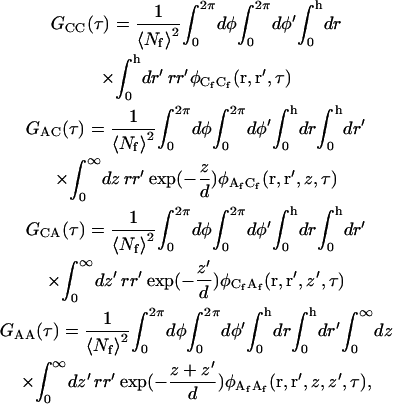(A4)

where the concentration fluctuation autocorrelation functions are defined as

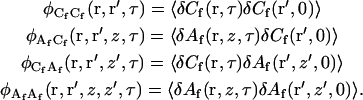(A5)

Differential equations

We assume that the evanescent depth d is at least 10-fold smaller than the radius of the observed area h. In this case, the differential equations describing combined surface reaction and solution diffusion can be written as (Thompson et al., 1981; Lagerholm and Thompson, 1998; Starr and Thompson, 2001)

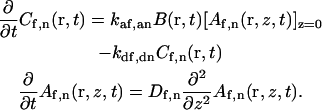(A6)

The total density of binding sites, S = C_f(r,t) + C_n(r,t) + B(r,t), does not fluctuate with time. Thus, δB(r,t) = −δC_f(r,t) −δC_n(r,t). By using this expression, as well as the definitions of the concentrations in terms of their average values and fluctuations from these values (see above) in Eq. A6, and neglecting terms proportional to δC_f,n(r,t)δA_f,n(r,z,t) (Elson and Magde, 1974), one finds that

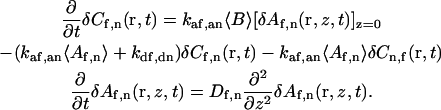(A7)

Multiplying Eq. A7 by either δC_f(r′,0) or δA_f(r′,z′,0) and taking ensemble averages yields eight coupled differential equations:

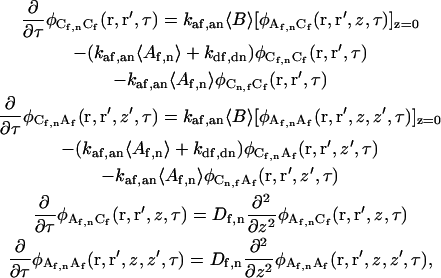(A8)

and four additional correlation functions

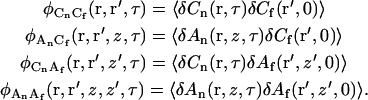(A9)

Boundary conditions

There are eight concentration fluctuation correlation functions (Eqs. A5 and A9) requiring 40 boundary conditions. Thirty-six of the boundary conditions are

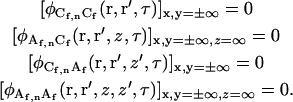(A10)

The remaining four boundary conditions are found from the condition describing the flux at the surface:

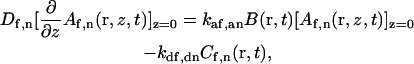(A11)

or (see above)

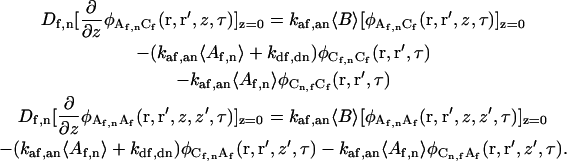(A12)

Initial conditions

In an open volume, fluctuations in the concentrations of molecules of different chemical species are not correlated at the same time. Thus, five of the initial conditions are

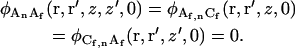(A13)

The fluorescent molecules in solution are correlated at the same time only at the same place. According to Poisson statistics (Elson and Magde, 1974),

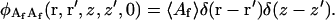(A14)

The fluorescent and nonfluorescent molecules on the surface obey binomial rather than Poisson statistics because the volume is not completely open (Thompson, 1982); i.e., the total number of surface binding sites in the observed area, 〈N_S〉, is constant and equals

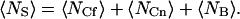(A15)

In Eq. A15, 〈N_Cf〉 is the average number of binding sites in the observed area occupied by fluorescent molecules (Eq. 6), 〈N_Cn〉 is the average number of binding sites in the observed area occupied by nonfluorescent molecules, and 〈N_B〉 is the average number of binding sites in the observed area that are unoccupied at equilibrium:

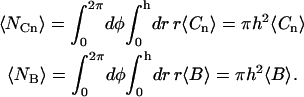(A16)

Because 〈N_S〉 is constant, the surface concentration fluctuations obey binomial statistics (Thompson, 1982), and

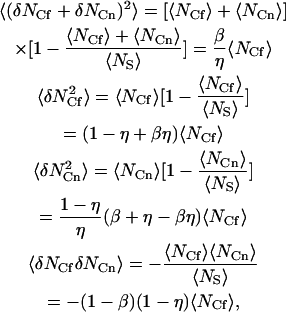(A17)

where the final expression follows from the first three, and the parameters β and η are defined in Eq. 7. Therefore,

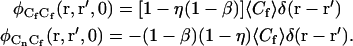(A18)

By using Eqs. A13, A14, and A18 in Eqs. A1, A2, and A4, one finds that G(0) is given by Eqs. 3 and 4 with G_C = G_CC(0) and G_A = G_AA(0). Both G_CA(0) and G_AC(0) are zero.

Concentration fluctuation autocorrelation and cross-correlation functions

The concentration fluctuation correlation functions may be found by using Laplace transforms as previously described (Thompson et al., 1981; Hsieh and Thompson, 1994; Lagerholm and Thompson, 1998; Starr and Thompson, 2001). The result for 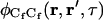is

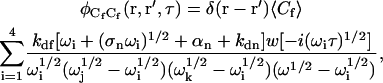(A19)

where the 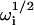are the four roots of the polynomial shown in Eq. 9, α_n is defined in the text, σ_n is defined in Eq. 10, w(ξ) = exp(−ξ²) erfc(−iξ) (Abramowitz and Stegun, 1974), and i ≠ j ≠ k ≠ ℓ. The cross-correlations in concentration fluctuations of the fluorescent species are

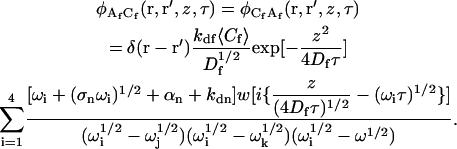(A20)

The autocorrelation of fluctuations in the solution concentration of observed fluorescent molecules is

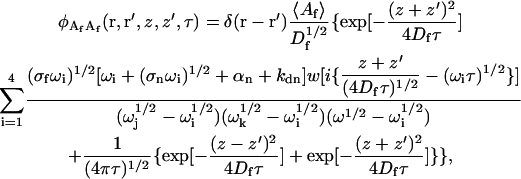(A21)

where σ_f is defined in Eq. 10.

General expression for the fluorescence fluctuation autocorrelation function

G(τ) may be found by using Eqs. A19–A21 in Eq. A4 and then Eq. A1. Completing the integrals (Abramowitz and Stegun, 1974) yields

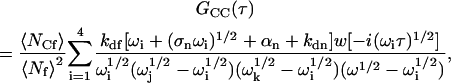(A22)

and

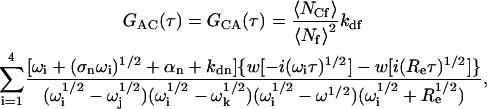(A23)

and

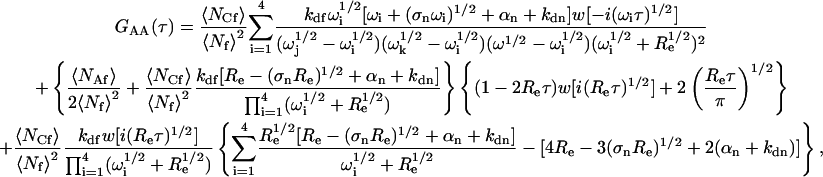(A24)

where R_e is defined in Eq. 11. Summing the terms in Eqs. A22–A24 gives the expression for G(τ) shown in Eqs. 8 and 13–15.