Dynamic Light Scattering Microscopy. A Novel Optical Technique to Image Submicroscopic Motions. I: Theory

Abstract

The theoretical basis of an optical microscope technique to image dynamically scattered light fluctuation decay rates (dynamic light scattering microscopy) is developed. It is shown that relative motions between scattering centers even smaller than the optical resolution of the microscope are sufficient to produce significant phase variations resulting in interference intensity fluctuations in the image plane. The timescale and time dependence for the temporal autocorrelation function of these intensity fluctuations is derived. The spatial correlation distance, which reports the average distance between constructive and destructive interference in the image plane, is calculated and compared with the pixel size, and the distance dependence of the spatial correlation function is derived. The accompanying article in this issue describes an experimental implementation of dynamic light scattering microscopy.

INTRODUCTION

We here describe the theory for a novel imaging technique for optical microscopy based on dynamic light scattering (DLS). Conventional dynamic light scattering (also known as quasielastic light scattering) is a well-established laser-based nonmicroscopic, nonimaging technique commonly used to measure diffusion coefficients of proteins in solution (Pecora, 1964; Cummins et al., 1964). The accompanying article (Dzakpasu and Axelrod, 2004) describes an experimental implementation of this theoretical work, in which DLS is modified for use in a microscope in an imaging mode so that spatial maps can be constructed from the light intensity fluctuation decay rates of scattering centers in the sample.

DLS microscopy is based on the time-dependent interference among electric fields emanating from scattering centers in relative motion and is sensitive to relative motions that are six times smaller than the optical resolution of the microscope. Previously reported applications of DLS in a microscope were limited to a single point (rather than spatial mapping) measurement of diffusion coefficients and flow rates (velocimetry) (Maeda and Fujime, 1972; Mishina et al., 1974, 1975; Cochrane and Earnshaw, 1978; Herbert and Acton, 1979; Nishio et al., 1983, 1985; Blank et al., 1987; Peetermans et al., 1986, 1987a,b,c; Tishler and Carlson, 1993; Wong and Wiltzius, 1993). These works did not address the theoretical question as to how intensity fluctuations can occur from scattering centers mutually close enough to fall within the optical resolution distance of the microscope; that question is addressed here.

We begin with a derivation of the functional form of the scattered electric field at the image plane of a microscope (which is modeled as a simple lens), first from a single scattering center and then from a collection of centers. From the resulting intensity, the temporal and spatial autocorrelation functions are derived. The theory is essentially a combination of scalar diffraction theory for a simple lens and a generalization of the conventional DLS theory as presented by Cummins et al. (1969).

The optical resolution of a microscope specifies the minimum separation of two objects in object space required to form distinctly separated images. If the separation is greater than the resolution distance, then clearly little interference can occur in the image plane. We show here that for scattering centers spaced closer than the optical resolution distance, sufficient phase variations still exist to create intensity fluctuations in the image plane.

As individual scattering centers can enter and/or leave an imaged region monitored by a single pixel in the detector, additional intensity fluctuations are created due to the change in particle number. These intensity fluctuations would occur even for incoherent light scattering (e.g., fluorescence). We derive an expression that includes the effect of intensity fluctuations due to both phase and number variations.

The characteristic decay time of the temporal intensity autocorrelation function guides what is the minimum sample time that should be employed in the detection system. The characteristic decay distance of the spatial autocorrelation function guides what is the maximum pixel size that should be employed in the detection system.

Single scattering center

We first consider the electric field as it scatters from a single particle toward the objective lens, refracts through the lens, and propagates to the image plane. The scattering center is assumed to be much smaller than the wavelength of the incident light λ (the Rayleigh scattering limit); the polarization of the incident light is assumed to be linear and the polarization of the scattered light is assumed to be the same as the incident light. The electric fields are thereby represented as (complex) scalars rather than vectors. All of the light (incident and scattered) is monochromatic so the common factor exp(iωt) is everywhere suppressed.

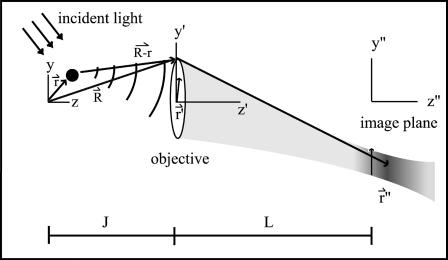
The coordinate systems are depicted in Fig. 1. Scattering center (object) space, objective lens space, and image space coordinates are unprimed, primed, and double-primed, respectively. The optical axis of the microscope is defined as the z axis. The incident light is formed from a collimated laser beam propagating in the y,z plane and passing through a cylindrical lens. This lens focuses in the x-dimension only and leaves the incident light as a thin stripe along the y-direction, although still much larger in every dimension than the optical resolution. Therefore, the illumination electric field amplitude E₀ can be considered constant over a region competent for mutual interference at one detector pixel. The direction of propagation and focusing is such that no direct incident light reaches the objective (i.e., essentially dark field). If k₀ is the incident wave vector and r is the location of a particular scattering center in object space, then the incident electric field E(r) at a single scattering center is

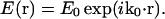(1)

At the position of the objective lens, the scattered light (before propagating through the lens) will produce an electric field E′(r′) with amplitude proportional to both E(r) and some scattering efficiency factor dependent upon the polarizability of the scattering center. However, this scattering efficiency factor is assumed constant among all scattering centers and also isotropic over the range of angles gathered by the lens, so its appearance will be suppressed in the expression for E′(r′),

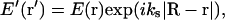(2)

where R is the vector from the origin in r-space to a point on the objective lens represented by two-dimensional vector r′ in the plane of the lens; |R−r| is the distance from the scattering center to that point on the objective; and k_s = |k_s| is the amplitude of the scattered wave vector.

FIGURE 1.

Coordinate systems used in the theory. The object is shown as a discrete black dot, and the point spread intensity in the image region as a blur. The origin in image space is located in the plane of the detector. The origin in object space is chosen at a point on the optical axis such that its focused image is centered at the origin in image space.

The electric field E″(r″,z″) in the image region (with positions denoted in cylindrical coordinates) is given by (Klein, 1970)

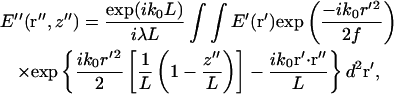(3)

where f is the focal length of the objective lens, k₀ ≡ |k₀| and L is the distance from the objective to the image plane. Assuming a small angle (i.e., small numerical aperture) approximation, the term, 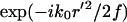, corresponds to the phase shift imposed by the objective lens. The factor 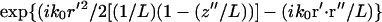describes the phase alteration as the field propagates in the empty space from the objective lens to the image region.

Combining Eqs. 1–3, noting that k_s is oriented in the same direction as R–r with k_s ≈ k₀, and regrouping, we obtain

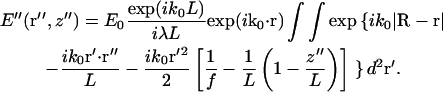(4)

For r ≪ R, we can substitute an approximation for |R−r|:

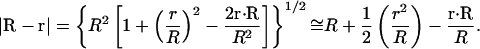(5)

Since 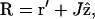where J is the object distance, 1/R can be written in the small aperture approximation (r′ ≪ J) as

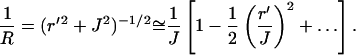(6)

Substituting Eqs. 5 and 6 into Eq. 4, and noting that 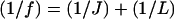, the electric field in the image region becomes

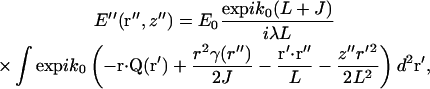(7)

where

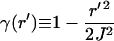(8)

and

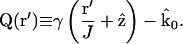(9)

Vector k₀Q is a generalized scattering vector, analogous to q (≡k_s−k₀) in conventional nonimaging DLS. Here, Q additionally takes into account the range of scattering angles gathered by the microscope objective lens.

To simplify Eq. 7 further, we assume that the detector is located in the image plane (z″ = 0). The scattering centers imaged within the same optical resolution area are then very close to the origin in object space so that r ≫ r′ for almost the entire range of the integral. Therefore, the exponent term 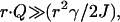implying that the factor 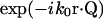in Eq. 7 varies much more rapidly than exp(ik₀r²γ/2J) over the range of the r′, so that the latter factor can be assumed constant and close to unity. Eq. 7 then becomes

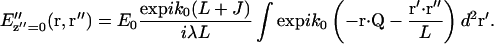(10)

Multiple scattering centers

Each scattering center i located at position r_i produces an electric field at z″ = 0 according to Eq. 10. The total electric field E and the consequent intensity I at the image plane depend on the set of all the r_i positions (i = 1,…N) as follows:

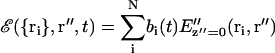(11)

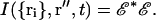(12)

To understand the meaning of the b_i(t) parameters, we define an “equivalent volume” v_pix in object space that contains all of the r-positions that contribute to the intensity observed by a single CCD camera pixel at one position in the image plane. (Of course, the actual region from which scattered light is gathered has graded rather than sharp edges.) We also define an arbitrarily larger volume V that subsumes v_pix and contains the N scattering centers included in the sum in Eq. 11. The occupation number b_i(t) equals unity if scattering center i is in v_pix at time t and zero otherwise. We assume that the positions r_i are statistically independent from each other and randomly time-dependent (e.g., due to Brownian motion). These random motions cause ℰ to fluctuate in both phase and amplitude, and the resulting intensity to fluctuate in amplitude. The temporal and spatial behavior of the intensity fluctuations can be investigated through autocorrelation functions.

Temporal autocorrelation of intensity

The temporal autocorrelation is defined as

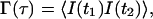(13)

where τ ≡ t₂−t₁, the intensities at the two times are measured at the same r″ position in the image plane, and the ensemble average indicated by the brackets is taken over all possible {r_i} configurations. Because the system is assumed to be in equilibrium, Γ depends only on the time difference τ and not the absolute times. After substituting Eqs. 10–12 into Eq. 13, we get

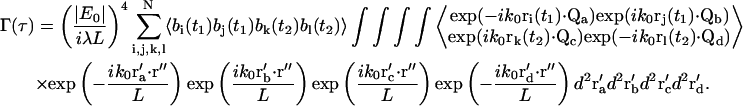(14)

The phase fluctuations (arising from the complex exponential factors) are uncorrelated with number fluctuations (arising from the b factors); this is why the single ensemble average in Eq. 13 can be separated into a product of two ensemble averages (number and phase) in Eq. 14.

The summation in Eq. 14 can be separated according to the relationships among the summation indices i,j,k,l such that

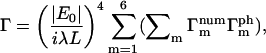(15)

where 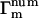and 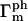are the number and phase fluctuation factors, respectively, and Σ_m represents sums over i,j,k,l restricted as in Table 1.

TABLE 1.

m index	Scattering center indices	Number of unique indices
1	i ≠ j ≠ k ≠ l	4
2	i ≠ j ≠ k = l	2
3	i ≠ j = k = l	1
4	i = j ≠ k = l	0
5	i = k ≠ j = l	0
6	i = j = k = l	0

Phase fluctuation factors

In the first three cases (m = 1,2,3) at least one index is unique from all of the others. In such cases, a factor 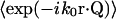with the unique index on the r-vector can be factored out from the overall ensemble average, since the motions of the scattering centers are mutually independent. That factor can be handled as follows (written here for a particular scattering index i),

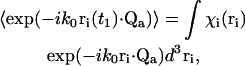(16)

where χ_i is the probability density that the particle is located in the vicinity of position r_i. The scattering centers i are assumed to be uniformly distributed over the volume v_pix imaged by an individual pixel in r-space so that χ_i (r_i) = χ = 1/v_pix. Eq. 16 becomes

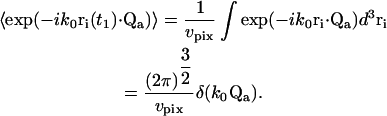(17)

The integral over r′_a in Eq. 14 then becomes

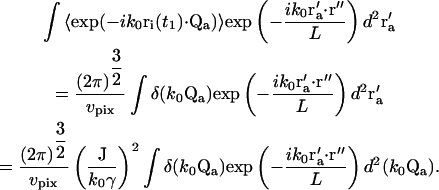(18)

The integral has a nonzero value only when k₀Q_a = 0. From the definition of Q_a in Eq. 9, we can obtain the value of r′_a for which this condition is satisfied:

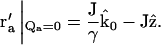(19)

This particular r′_a is located where the extension of the incident beam crosses the plane of the objective lens. Since our experimental setup was designed so that the incident light misses the objective, the integral over r′_a in Eq. 18 (which is limited to the area of the objective) does not include Thus, those terms in the sum of Eq. 15 with at least one unique summation index (i.e., m = 1,2,3) are zero.

The phase term for the m = 4 case from Eq. 15 is

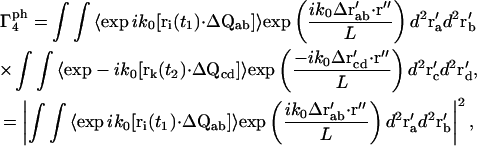(20)

where ΔQ_αβ ≡ Q_β − Q_α and Δr′_αβ ≡ r′_β − r′_α. The terms of the form 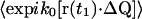are similar to that in Eq. 17, except for the factor ΔQ instead of Q. Therefore, the integral in Eq. 20 can be reduced to

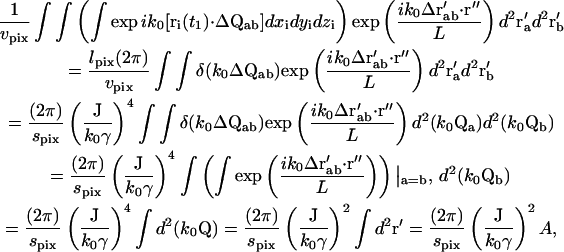(21)

where l_pix is the z-dimension of the observed volume v_pix; s_pix is the area of the observed volume; and A is the area of the objective. Therefore,

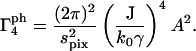(22)

For the m = 5 term in Eq. 15,

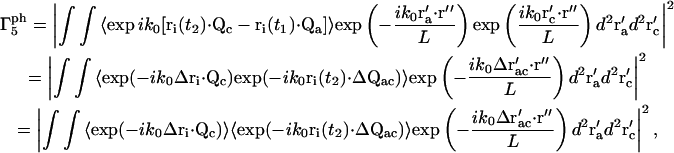(23)

where Δr_i ≡ r_i(t₂) − r_i(t₁). The term 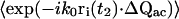reduces to a δ-function, so we obtain

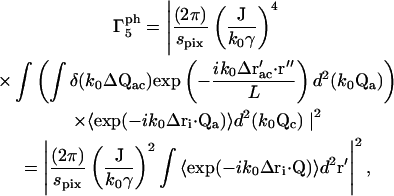(24)

where the subscript c on the r′_c factors has been suppressed. The ensemble average in Eq. 24 can be rewritten as

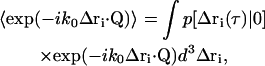(25)

where 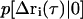is the conditional probability of finding a particle at position Δr_i at time τ given that it was at the origin (Δr_i = 0) at τ = 0. The right side of Eq. 25 is the Fourier transform of ,

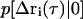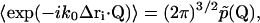(26)

where 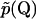is the Fourier transform of 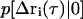into Q-space.

We assume that the scattering centers are undergoing random diffusive motion. Taking the Fourier transform of the diffusion equation 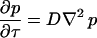from Δr_i-space to Q-space gives

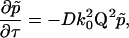(27)

so that

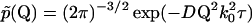(28)

and therefore, in combination with Eq. 26,

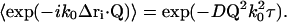(29)

Eq. 24 then becomes

(30)

For the m = 6 term in Eq. 15,

(31)

Number of fluctuation factors

The total volume of the imaged sample is V and the total number of scattering centers in that volume is N. The volume “imaged” by a single pixel is v_pix. The number of particles M(t) (assumed ≪ N) and its expectation value in the volume v_pix can be written

(32)

(33)

The variance of M can be derived from Eqs. 32 and 33:

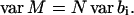(34)

The assumption that 〈b_i〉 ≪ 1 implies that M follows a Poisson distribution so that var M = 〈M〉. Therefore,

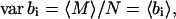(35)

and the temporal autocorrelation function for b_i can be written as

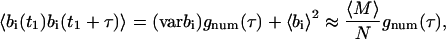(36)

where g_num(τ) is a normalized number fluctuation autocorrelation function such that g(0) = 1 and g(∞) = 0.

We are now set to consider the terms 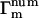that appear in Eq. 15. Since the m = 1,2,3 terms in Eq. 15 are forced to zero by their phase fluctuation factors, we need consider only 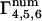. We make the approximations that N ≫ M ≫ 1.

For the m = 4 term of Eq. 15,

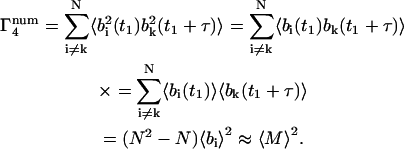(37)

For the m = 5 term,

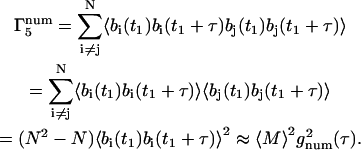(38)

For the m = 6 term,

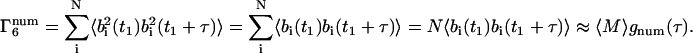(39)

The m = 6 term is smaller than the m = 4 and m = 5 terms by a factor of 1/〈M〉; therefore, it will be neglected. The complete temporal autocorrelation function thereby becomes

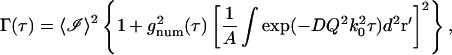(40)

where 〈ℐ〉 is the mean intensity observed at a pixel from the 〈M〉 scattering centers in its view:

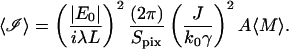(41)

To compare the result given in Eq. 40 with experimentally obtained autocorrelations functions, we construct the normalized temporal autocorrelation function:

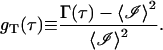(42)

Combining Eqs. 40 and 42 shows that g_T(τ) monotonically decays to zero:

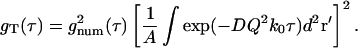(43)

As τ → 0, g_T(τ) → 1. Since g_T(0) is the variance of the intensity fluctuations (normalized to the square of the mean intensity), g_T(0) = 1 means that phase fluctuations have a standard deviation equal to the mean, regardless of the concentration of scattering centers.

Characteristic times and distances

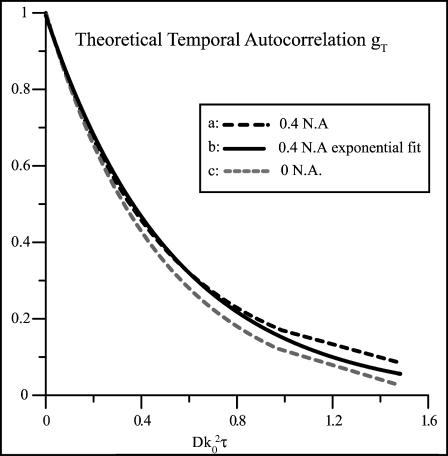
Fig. 2 a shows g_T(τ) (Eq. 43) plotted as a function of the unitless time variable 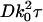, with the indicated integration performed numerically for the particular case where the objective numerical aperture (NA) equals 0.4 (as used in the experimental setup described in the accompanying article). The characteristic decay time 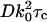, defined as the time required for g_T(τ) to reach its e⁻¹ value, is 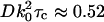for this particular numerical aperture. In that time, the mean distance r_c the particle travels laterally by three-dimensional diffusion is

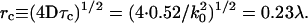(44)

This characteristic distance is approximately a factor of 6 smaller than the resolution of the microscope, which according to the Rayleigh criterion is r_res = 0.61λ/NA = 1.5λ for NA = 0.4. This proves that dynamic light scattering intensity fluctuations of significant amplitude do occur among scattering centers within a resolution distance of each other.

FIGURE 2.

Theoretical temporal autocorrelation function of the scattered light intensity versus unitless time parameter 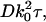as calculated from Eq. 43. Three curves are plotted. (a) The black dashed line curve is obtained from a numerical integration of Eq. 43 for a 0.4-NA objective. (b) The black solid curve is a single exponential decay, fit to the points obtained from the numerical integration. (c) The shaded dashed line is the pure exponential decay obtained from the zero aperture limit.

The actual characteristic time τ_c can be estimated for an aqueous suspension of 200-nm-diameter polystyrene nanospheres as used in some of our experiments. Hydrodynamics predicts D = 2.2 × 10⁻⁸ cm²/s for such spheres. For λ = 632.8 nm, the characteristic time of the temporal intensity autocorrelation function would be τ_c = 2.4 ms. The experimental detection system must be able to observe these fast timescale fluctuations.

Spatial autocorrelation of intensity

We define the spatial correlation region to be the spatial extent of the intensity fluctuations at the image plane. It is measured as the characteristic distance of the spatial autocorrelation function and determines the maximum pixel size allowable for measuring the temporal behavior of the intensity fluctuations. For example, if a pixel is larger than several characteristic spatial correlation regions, then the relative size of the observed fluctuations will be greatly reduced, compromising the signal/noise ratio. Ideally, a pixel should cover less than one spatial correlation region.

We start the calculation of the spatial autocorrelation function in a manner similar to the temporal autocorrelation function (Eq. 14) except here using the intensities at two different positions r″_1,2, recorded at the same time. (Because of the similarity of the mathematical procedures, we will skip most of the details here.) We count only those scattering centers that are actually present in the illuminated region at one snapshot of time, so all the b_i(t) factors can be set equal to unity.

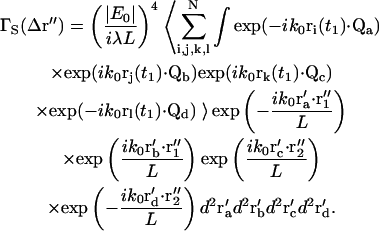(45)

As in the calculation for the temporal autocorrelation function, the spatial autocorrelation function terms corresponding to m = 1,2,3 (see Table 1 after Eq. 15) produce zero values and the m = 4,5,6 terms produce nonzero values. In the these latter terms, an integral appears which can be related to a first-order Bessel function,

(46)

where Δr″ ≡ r″₂−r″₁ and 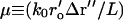and r′_o is the radius of the objective.

The final form of the spatial autocorrelation function becomes

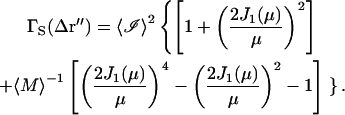(47)

For large 〈M〉, the 〈M〉⁻¹ term is small and is not included in further calculations. The leading term of the spatial autocorrelation function has the same distance dependence as the point spread function of the microscope objective at the image plane (an Airy disk). In analogy with Eq. 42, a normalized form of can be written as

(48)

The characteristic spatial correlation distance is qualitatively the average distance in the image plane from constructive to destructive interference (Jakeman et al., 1970; Cantrell and Fields, 1973). It can be defined quantitatively as the distance l_c in r″-space corresponding to μ = 1. Parameter μ (defined after Eq. 46) can be rewritten in terms of the numerical aperture (NA) and magnification (mag) of the objective (in the low aperture, air immersion case) as

(49)

Thus the spatial correlation distance l_c is

(50)

Variance of intensity fluctuations: mobile fraction

We define the mobile fraction β to be the ratio of the scattered intensity from the mobile scattering centers 〈ℐ〉_mob to the total scattering intensity 〈ℐ〉 in the collection volume of each pixel,

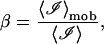(51)

where

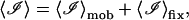(52)

and 〈ℐ〉_fix arises from fixed scattering centers (such as the sample substrate). The mobile fraction β can be estimated from the variance of the intensity fluctuations, which is the difference between the extrapolated values of the temporal autocorrelation function values at τ = 0 and at τ = ∞. Combining the definition of Γ in Eq. 13 with Eq. 52, we get

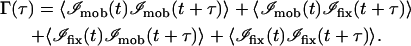(53)

The first term in the above equation can be reduced to 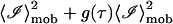where g(0) = 1 and g(∞) = 0. The next two terms are each 〈ℐ〉_mob 〈ℐ〉_fix and the last term is 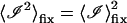since the scattering due to the immobile intensity does not fluctuate. Therefore,

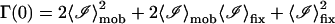(54)

and

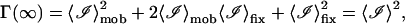(55)

and therefore

(56)

DISCUSSION

We have presented a theoretical basis for measuring the rates of small relative motions among nearby scattering centers in a microscope by use of dynamic light scattering. These relative motions appear as intensity fluctuations due to relative variations in electric field phase, and are large enough to be detected in the image plane. Relative motions of scattering centers even closer than the optical resolution can still produce substantial intensity fluctuations. Therefore, the technique should be adaptable to spatial mapping without sacrificing optical resolution, as described in the accompanying article (Dzakpasu and Axelrod, 2004).

The theory also predicts the spatial scale of the intensity fluctuations. To measure the fluctuations, a detector pixel must not view more than one spatial correlation distance, and this requirement thereby guides the selection of pixel size in a detector.

There are two standard methods of detection for dynamic light scattering: homodyning and heterodyning (Cummins et al., 1969). In the homodyne method, scattered light emanating only from the mobile scattering centers impinges upon the detector whereas in the heterodyne method, light from the source is mixed at the detector with scattered light from the sample. For the same diffusion coefficient in the sample, the heterodyne intensity fluctuation decay rate is only half that of the homodyne rate, since the heterodyne method involves the beating of mobile scattering centers against a static background. The theory described here is a pure homodyne theory. But in fact, the detector invariably receives a large contribution to the scattered light intensity from static components, e.g., collection optics and glass coverslips. This would imply that the calculated diffusion coefficients (as derived from homodyne theory) may underestimate the true diffusion coefficient by up to a factor of 2, depending on the amount of static scattered light from static centers interfering with that from mobile sources. A real sample may contain a continuous range of mobilities from static to highly mobile, which further complicates the interpretation of decay rates.

The theory implies that certain extreme cases could show interesting number fluctuation effects. If the number fluctuations occur on a faster timescale than the phase fluctuations, there would be an appreciable decay of the autocorrelation function before a phase fluctuation occurs. Thus, phase fluctuations can be detected only if they occur on a faster timescale than the number fluctuations. In the limit of one scattering center, the intensity autocorrelation function arises entirely from number fluctuations and will not contain a contribution due to phase fluctuations.