Na/K Pump-Induced [Na]_i Gradients in Rat Ventricular Myocytes Measured with Two-Photon Microscopy

Abstract

Via the Na/Ca and Na/H exchange, intracellular Na concentration ([Na]_i) is important in regulating cardiac Ca and contractility. Functional data suggest that [Na]_i might be heterogeneous in myocytes that are not in steady state, but little direct spatial information is available. Here we used two-photon microscopy of SBFI to spatially resolve [Na]_i in rat ventricular myocytes. In vivo calibration yielded an apparent K_d of 27 ± 2 mM Na. Similar resting [Na]_i was found using two-photon or single-photon ratiometric measurements with SBFI (10.8 ± 0.7 vs. 11.1 ± 0.7mM). To assess longitudinal [Na]_i gradients, Na/K pumps were blocked at one end of the myocyte (locally pipette-applied K-free extracellular solution) and active in the rest of the cell. This led to a marked increase in [Na]_i at sites downstream of the pipette (where Na enters the myocyte and Na/K pumps are blocked). [Na]_i rise was smaller at upstream sites. This resulted in sustained [Na]_i gradients (up to ∼17 mM/120 μm cell length). This implies that Na diffusion in cardiac myocytes is slow with respect to trans-sarcolemmal Na transport rates, although the mechanisms responsible are unclear. A simple diffusion model indicated that such gradients require a Na diffusion coefficient of 10–12 μm²/s, significantly lower than in aqueous solutions.

INTRODUCTION

Intracellular free Na concentration ([Na]_i) plays an important role in modulating the electrical and contractile activity of the heart via the Na/Ca exchanger (NCX) and Na/H exchanger (Bers, 2001). The level of [Na]_i is determined by the balance between Na influx and efflux. Na enters the cell through various pathways, including NCX, Na/H exchanger, and Na channels, whereas the Na/K pump is the main route for Na extrusion.

Several studies have suggested that, in the presence of trans-sarcolemmal fluxes, [Na]_i sensed by the membrane transporters might be different from the bulk [Na]_i, as measured using fluorescent indicators or ion selective microelectrodes (Bielen et al., 1991; Carmeliet, 1992; Wendt-Gallitelli et al., 1993; Lipp and Niggli, 1994; Semb and Sejersted, 1996; Su et al., 1998, 2001; Terracciano, 2001). For such [Na]_i gradients to exist, intracellular Na diffusion has to be slow with respect to the rates of Na transport across the sarcolemma. Su et al. (2001) reported that abrupt Na/K pump inhibition in mouse ventricular myocytes increases the efficacy of a given Ca current to trigger sarcoplasmic reticulum (SR) Ca release. This was interpreted as a prevention of Na extrusion from the junctional cleft (between the SR and sarcolemma) allowing local cleft [Na]_i to rise and favor Ca entry via NCX. Abrupt Na/K pump inhibition was also shown to slow the decline of caffeine-induced Ca transients and NCX current (Terracciano, 2001). Na/K pump reactivation after a period of pump blockade produced a transient peak in the Na/K pump current (Bielen et al., 1991; Fujioka et al., 1998; Su et al., 1998; Despa and Bers, 2003), which was explained by a local, subsarcolemmal [Na]_i depletion due to the rapid Na extrusion via the pump. Using simultaneous measurements of Na/K pump current (I_pump) and global [Na]_i, Despa and Bers (2003) showed that the initial I_pump decay occurred with little change in global [Na]_i and was followed by a second phase when the current decline was paralleled by a decrease in [Na]_i. From the [Na]_i dependence of I_pump measured immediately upon pump activation, before any local [Na]_i depletion could occur (i.e., peak I_pump) and I_pump measured after the rapid decay phase, Despa and Bers (2003) inferred that rapid Na extrusion via the pump could locally decrease [Na]_i near the pump by as much as 3–5 mM. They calculated that such [Na]_i depletion could be induced if Na diffusion near sarcolemma is 10³–10⁴ times slower than experimentally measured in the bulk cytoplasm (Kushmerick and Podolsky, 1969), which is difficult to imagine in a simple physical sense.

Further insight into this is difficult to gain in the absence of direct measurements of the spatial distribution of free [Na]_i. Generally, spatially resolved measurements of intracellular ions are done using confocal microscopy. This is less feasible for Na, because SBFI, the most widely used Na-sensitive fluorescent indicator, is excited in the UV range of the spectrum (340–380 nm) and thus requires special lasers for excitation. An alternative is to use SBFI with two-photon fluorescence microscopy. With this method, the spatial resolution comes from the fact that two-photon excitation is confined to the focal plane. Because there is no out-of-focus absorption, the penetration depth is greatly increased whereas the photobleaching and photodamage outside the focal plane are minimized in two-photon as compared to single-photon excitation. For molecules that require UV excitation, the two-photon fluorescence has the further advantage of avoiding the low throughputs associated with UV microscopy (Williams et al., 1994).

The aim of this article was to investigate whether Na/K pump inhibition/reactivation produces [Na]_i gradients that can be resolved spatially using two-photon microscopy of SBFI in cardiac myocytes. Our data show that 1), quantitative two-photon whole-cell [Na]_i measurements yield similar results to those obtained using single-photon, ratiometric measurements with SBFI, thus validating the two-photon method; 2), local inhibition/activation of the Na/K pumps in a limited part of the cell induces large longitudinal [Na]_i gradients; and 3), such gradients can be theoretically predicted if the effective diffusion coefficient for Na in the cell is significantly lower than previously estimated.

MATERIALS AND METHODS

Myocytes isolation

The procedure for isolation of ventricular myocytes has been described previously (Bassani et al., 1994) and approved by the Loyola University Chicago animal welfare committee. Briefly, rats were anesthetized by intraperitoneal injection of nembutal (∼0.1 mg/g). Hearts were excised quickly, placed on a Langendorff apparatus and perfused for 5 min with nominally Ca-free Tyrode's solution. Then, perfusion proceeded with added collagenase (1 mg/ml) and albumin (0.05%). When the heart became flaccid, the left ventricular tissue was cut into small pieces for further incubation (5 or 10 min) with 0.4 mg/ml collagenase. The tissue was then filtered and Ca concentration in the cell suspension was progressively increased to 1 mM. All experiments were done at room temperature (23–25°C).

Dye loading and single-photon measurements

Isolated myocytes plated on laminin-coated glass coverslips were loaded with 10 μM SBFI-AM (Molecular Probes, Eugene, OR) for 90 min, at room temperature, in the presence of the nonionic surfactant Pluronic F-127 (0.05% w/v). Then, at least 20 min were allowed for the de-esterification of the dye.

SBFI excitation spectra were recorded at 535 ± 20 nm using an epifluorescence microscope equipped with an Optoscan monochromator (Cairn Research, Faversham, UK). The spectra were not corrected for the transmission characteristics of the optical components. The in vitro spectra were recorded in the same solutions as used for in vivo calibration (see below).

Two-photon imaging

Two-photon excitation was done using a mode-locked Ti:sapphire laser (Tsunami) pumped by a Millennia solid-state laser (both from Spectra Physics, Mountain View, CA) and coupled to a laser scanning system (Radiance 2000 MP, Bio-Rad, Hercules, CA). The laser operated at 760-nm center wavelength, 82 MHz repetition rate, and <100 fs pulse width. The laser beam was focused onto the sample placed on the stage of an epifluorescence microscope with a 40× 1.3 NA oil immersion objective. The emitted fluorescence was recorded at 528 ± 25 nm. Two-dimensional images were obtained by scanning the cell at 500 lines/s. Illumination of the sample was restricted to the time of image acquisition. Further details regarding [Na]_i imaging using SBFI and two-photon excitation can be found in the Supplementary Materials.

Solutions and chemicals

The standard Tyrode's solution used in these experiments contained (in mM): 140 NaCl, 4 KCl, 1 MgCl₂, 10 glucose, 5 HEPES, and 1 CaCl₂ (pH = 7.4). The K-free solution used to block the Na/K pump contained (in mM): 140 NaCl, 2 EGTA, 10 HEPES, and 10 glucose (pH = 7.4). The Na/K pump was reactivated in a Na-free solution with the following composition (in mM): 140 TEA, 4 KCl, 2 EGTA, 1 MgCl₂, 10 HEPES, and 10 glucose (pH = 7.4 with TRIS base). The solutions with various [Na]_o used for SBFI calibration were prepared by mixing in different proportions two solutions of equal ionic strength. One solution contained 145 mM Na (30 mM NaCl, 115 mM Na-gluconate) and no K, whereas the other one had 145 mM K (30 mM KCl, 115 mM K-gluconate) and was Na-free. Both calibration buffers also contained 10 mM HEPES, 10 mM glucose and 2 mM EGTA and the pH was adjusted to 7.2 with TRIS base. Gramicidin D and strophanthidin were from Sigma (St Louis, MO).

Statistical analysis

Where appropriate, data are expressed as mean ± SE. Statistical discriminations were performed using Student's unpaired t-test and values of p < 0.05 were considered significant.

RESULTS

Two-photon imaging with SBFI

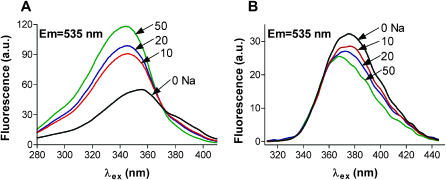
Fig. 1 A shows single-photon excitation spectra of SBFI in buffer solutions with various [Na]. The indicator has an isoexcitation point at ∼370 nm, thus can be used in dual-excitation ratiometric mode. The fluorescence intensity increased markedly with increasing [Na] at 330–350 nm. However, when loaded into cells, the spectral characteristics of SBFI are generally different from those recorded in buffer solutions (Negulescu and Machen, 1990; Borzak et al., 1992; Baartscheer et al., 1997). As Fig. 1 B demonstrates, in rat ventricular myocytes SBFI became practically Na-insensitive at wavelengths <360 nm. The maximum Na sensitivity was at wavelengths ∼380 nm. Thus, we investigated the two-photon excitation of SBFI between 750 and 790 nm. In these conditions, a [Na]_i rise should result in a decrease in the two-photon fluorescence. The Na sensitivity of the signal was similar at all wavelengths investigated, but the signal was higher at 760 nm. Therefore we used 760 nm as the standard excitation wavelength.

FIGURE 1.

Single-photon excitation spectra of SBFI in buffer solutions (A) and in rat ventricular myocytes (B) at various [Na]. Spectra were recorded on the stage of an epifluorescence microscope, at λ_em = 535 ± 20 nm, and were not corrected for the transmission characteristics of the optical components. To obtain the spectra of SBFI when loaded into myocytes, at different [Na]_i, the cells were perfused with divalent-free solutions with various [Na]_o in the presence of 10 μM gramicidin D and 100 μM strophanthidin (see Materials and Methods).

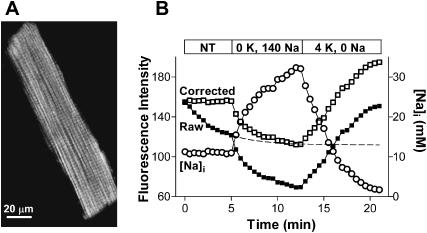
Fig. 2 A shows the two-photon fluorescence image of a myocyte loaded with SBFI-AM. To test whether the two-photon signal is indeed Na-sensitive, after an initial period in Tyrode's solution, myocytes were Na-loaded by blocking the Na/K pump in a K-free solution (Fig. 2 B). Previous data (Despa et al., 2002) indicated that in these conditions [Na]_i rises to ∼40 mM within 5–10 min. Upon Na/K pump inhibition, the intensity of the two-photon fluorescence decreased markedly, consistent with an increase in [Na]_i. When the Na/K pump was reactivated by adding back K, in the absence of external Na, the signal started to increase and reached higher intensities than the initial fluorescence level (Fig. 2 B). This indicates that [Na]_i declined to values below the resting level, in good agreement with our data using single-photon, ratiometric measurements with SBFI (Despa et al., 2002).

FIGURE 2.

Na-sensitivity of the two-photon SBFI signal. (A) Two-photon fluorescence image of a rat ventricular myocyte loaded with SBFI-AM. (B) Changes in the intensity of the two-photon signal upon Na/K pump inhibition (K-free conditions) and reactivation (0 Na, 4 mM K external solution) (solid squares). To correct for the [Na]_i-independent decline in the raw SBFI signal, the points recorded in normal Tyrode's solution were fitted with a monoexponential decay curve (dashed line). The corrected SBFI fluorescence data are indicated by open squares. The corrected signal was then converted into [Na]_i (circles).

In the experiment shown in Fig. 2 B, there was a decrease in the fluorescence intensity in normal Tyrode's solution, when [Na]_i was constant. This was probably due to a combination of photobleaching and leakage of the dye out of the myocyte. Such a [Na]_i-independent decline in the signal was observed in some, but not all experiments. To correct for this rundown, the data points recorded in Tyrode's solution in Fig. 2 B were fitted with a monoexponential decay curve. The corrected signal is also shown in Fig. 2 B. In most of the experiments where signal rundown at constant [Na]_i occurred, myocytes were repeatedly perfused with Na-free solution, where [Na]_i approaches 0, and the correction was done according to the changes in fluorescence intensity at 0 [Na]_i (F₀). The corrected signal was then calibrated in terms of [Na]_i (see below). The changes in [Na]_i upon Na/K pump inhibition/reactivation measured with two-photon SBFI excitation (indicated by circles in Fig. 2 B) compare very well with our previous data using conventional SBFI measurements (Despa et al., 2002). Furthermore, the maximum pump rate and the K_m for intracellular Na derived from the −d[Na]_i/dt in the experiment shown in Fig. 2 B (8.0 mM/min and 10.4 mM, respectively) are similar to what we previously found, using a similar protocol with ratiometric [Na]_i measurements (7.7 ± 1.1 mM/min and 10.2 ± 1.2 mM/min; Despa et al., 2002).

In vivo calibration of the SBFI two-photon signal

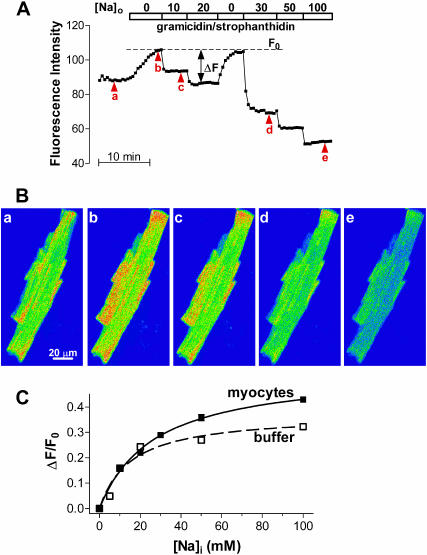
To calibrate the two-photon SBFI signal in terms of [Na]_i, myocytes loaded with SBFI-AM were exposed to solutions containing various [Na]_o in the presence of 10-μM gramicidin D and 100-μM strophanthidin, as previously described (Despa et al., 2002). In these conditions, [Na]_i should equilibrate with [Na]_o and the fluorescence intensity should change accordingly. Indeed, stepwise changes in [Na]_o resulted in marked changes in the SFBI fluorescence, with the intensity decreasing with an increase in [Na]_o (Fig. 3, A and B). Changes in [Na]_i were expressed as ΔF/F₀, where ΔF = F₀−F, F is the measured SBFI fluorescence, and F₀ is the maximum fluorescence (measured at 0 Na, see Fig. 3 A). The advantage of this normalization is that ΔF/F₀ is proportional to changes in [Na]_i.

FIGURE 3.

In vivo calibration of the two-photon SBFI fluorescence signal. (A) Two-photon fluorescence intensity from the entire cell during a calibration experiment. After an equilibration period in normal Tyrode's solution, the myocyte was perfused with divalent-free solutions with various [Na]_o in the presence of 10 μM gramicidin D and 100 μM strophanthidin. (B) Two-photon fluorescence images of the cell at the points indicated by arrowheads in A. (C) Two-photon fluorescence calibration curve in rat ventricular myocytes (—) and in buffer solutions (− − −). The in vivo data represent the mean ΔF/F₀ from 26 myocytes. The in vitro measurements were done in the same solutions as used for in vivo calibration. Data were fitted with a one-site binding equation (ΔF/F₀ = (ΔF/F₀)_max × [Na]_i/(K_d+[Na]_i)) to derive the K_d and (ΔF/F₀)_max.

Fig. 3 C shows the mean ΔF/F₀ as a function of [Na]_i from 26 cells. The points were fitted with a one-site binding equation to derive the apparent dissociation constant of the indicator (K_d) of 27 ± 2 mM. This value is within the range reported for SBFI in various cell types and determined using either single- (Donoso et al., 1992; Baartscheer et al., 1997) or two-photon measurements (Rose et al., 1999). The two-photon calibration curve in buffer solutions (Fig. 3 C) indicated a K_d of 15.4 mM, which is comparable to the value obtained from single-photon measurements in conditions where [Na]+[K] was constant (Haugland, 1996). In all following experiments, two-photon data were converted to [Na]_i using the in vivo calibration curve and the fluorescence at 0 Na measured for each cell. Using this calibration curve, we estimated a resting [Na]_i of 10.8 ± 0.7 mM (n = 23), which is similar to the value we previously found in rat ventricular myocytes (Despa et al., 2002) using traditional (single-photon) ratiometric measurements with SBFI (11.1 ± 0.7 mM).

Local Na/K pump inhibition/reactivation induces [Na]_i gradients

Two-photon microscopy of SBFI was then utilized to determine whether local Na/K pump inhibition and/or reactivation could induce [Na]_i gradients. Rather than focusing on radial [Na]_i gradients, which might be confined to a narrow subsarcolemmal space and thus very hard to detect, we tried to induce and measure longitudinal [Na]_i gradients. For this, the cells were placed in the laminar flow of the perfusion inlet so that the bath solution flowed parallel to the longitudinal axis of the myocyte (Figs. 4 and 5 A). Then, a small glass pipette was positioned near the cell. Experiments with fluorescein included in the pipette demonstrated that solution flowed through the tip of the pipette only when applying pressure on the pipette and that this solution flow was limited to the area downstream of the pipette (Fig. 4). This allowed us to independently manipulate the activity of the Na/K pumps downstream and upstream of the pipette. If the Na/K pumps are inhibited in one part of the cell and Na enters, whereas they are actively extruding Na in the other part, a standing [Na]_i gradient could develop. Diffusion tends to dissipate this gradient to keep [Na]_i homogeneous in the cell. Thus, detectable [Na]_i gradients are expected to develop only if Na diffusion is slow with respect to the sarcolemmal Na transport rates.

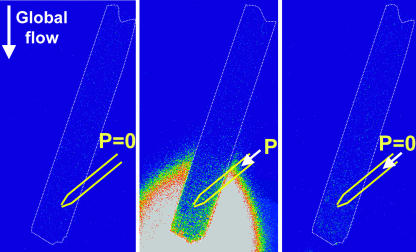
FIGURE 4.

The use of a glass pipette to locally exchange the external solution sensed by the part of the cell downstream of the pipette. The cell was positioned in the laminar bath flow (arrow indicating global flow), with the longitudinal axis almost parallel to the flow. A glass pipette, filled with solution containing 1 μM fluorescein, was positioned near the cell (marked by the white dashed line). Fluorescein was excited at 488 nm and the emitted fluorescence measured at 528 nm. No signal was detected in the absence of pressure on the glass pipette (P = 0), indicating the absence of solution flow from the pipette, i.e., the whole cell senses the bath solution (left). When applying pressure on the pipette (P), the part of the cell downstream of the pipette is exposed to the fluorescent pipette solution, as indicated by the bright fluorescein signal (middle). As soon as the pressure ceases, the solution flow from the pipette stops as well (right).

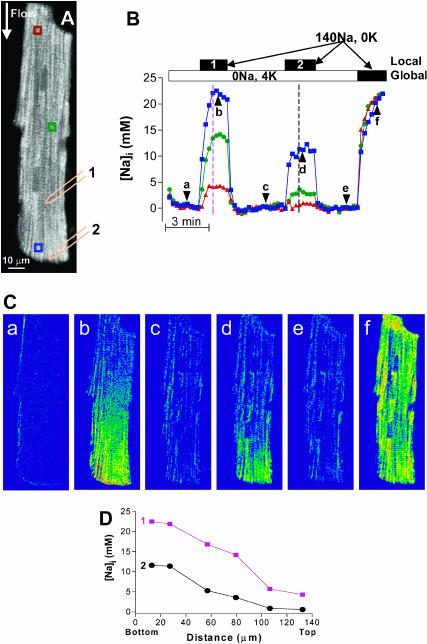
FIGURE 5.

Local Na/K pump inhibition results in [Na]_i gradients. (A) Na/K pumps were blocked in the area downstream of the glass pipette, placed either in position 1 or 2, with K-free solution flowing through the tip of the pipette. The area upstream of the pipette was exposed to the bath solution, which flows parallel to the longitudinal axis of the myocyte. Initially, the bath solution contained 0 Na, 4 mM K. An the end of the experiment, this was changed to the K-free solution. (B) [Na]_i in the three regions indicated in A. The solid bars indicate the application of K-free, 140 mM Na solution via the pipette (Local 1, Local 2) placed in position 1 or 2 (indicated in A) or in the bath solution (Global). (C) ΔF/F₀ images of the cell at the moments marked by arrowheads in B. (D) [Na]_i distribution along the longitudinal axis of the cell during the two episodes of local Na/K pump blockade at the times indicated by the dashed lines in B.

In the experiment shown in Fig. 5, Na/K pumps were blocked downstream of the pipette by locally applying K-free, Na-containing solution, via the pipette (Fig. 5 A). The rest of the cell was initially perfused with 0 Na, 4 mM K solution. Changes in [Na]_i in the three areas indicated in Fig. 5 A are plotted in Fig. 5 B and the ΔF/F₀ images taken at selected times (indicated by arrows in Fig. 5 B) are shown in Fig. 5 C. The cell was equilibrated in the bath solution (0 Na, 4 K) for several minutes before starting the recording. As expected, [Na]_i decreased to values close to 0 throughout the cell (Fig. 5, B and Ba). Then, K-free, Na-containing solution was applied locally via the pipette placed in position 1 (Fig. 5 A). Thus, Na passively entered the cell in the area downstream of the pipette and diffused upstream inside the cell, where it was extruded by the Na/K pumps. Fig. 5, B and Cb, show that this resulted in a marked increase in [Na]_i at the downstream site (where Na influx occurs and the pumps are blocked) and a smaller rise at the sites further away (upstream) from the pipette, where [Na]_i increased because of intracellular diffusion. When the solution flow from the pipette was stopped, [Na]_i declined rapidly to values close to 0 in the entire cell (Fig. 5, B and Cc). Next, a smaller fraction of the Na/K pumps was blocked, by placing the patch pipette near the lower end of the cell (position 2 in Fig. 5 A). This still induced a considerable rise in [Na]_i near the pipette tip, whereas the increase at the center of the cell was minimal and there was practically no effect at the top end of the cell (Fig. 5, B and Cd). Again, when the solution flow through the tip of the pipette was stopped, [Na]_i returned rapidly near 0 (Fig. 5, B and Ce). Finally, Na/K pumps were blocked in the whole cell by switching the bath solution to K-free, 140 mM Na solution. In this case, [Na]_i rose uniformly within the cell (Fig. 5, B and Cf).

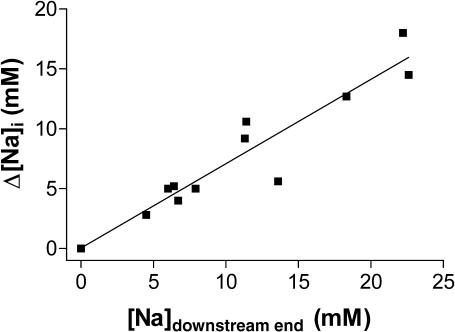
Fig. 5 D shows the [Na]_i-profile along the longitudinal axis of the myocyte during the two episodes of local Na/K pump blockade (as indicated in Fig. 5 B). In both instances, considerable [Na]_i gradients occurred during the local pump inhibition, which were rapidly dissipated upon the release of pump blockade. A larger gradient was created during the first local Na/K pump inhibition, probably because the larger proportion of pumps blocked allowed for a higher increase in [Na]_i at the sites downstream of the glass pipette. Fig. 6 summarizes the results from eight myocytes, with different fractions of Na/K pumps blocked (i.e., different positions of the glass pipette). The fraction of the cell exposed to K-free solution is mainly reflected in the rise in [Na]_i at the downstream end of the myocytes ([Na]_{downstream end}). Fig. 6 shows that the difference in [Na]_i between the downstream and the upstream end of the cells (Δ[Na]_i) increased linearly with [Na]_{downstream end}.

FIGURE 6.

The difference in [Na]_i between the downstream and the upstream end of the myocyte as a function of [Na]_i near the lower end of the cell. Data were obtained in experiments similar to Fig. 5, in eight myocytes, with different positions of the glass pipette, and thus different fractions of pumps blocked. This is mainly reflected in the rise in [Na]_i at the downstream end of the myocyte.

Theoretical model for Na diffusion along the longitudinal axis of the cell

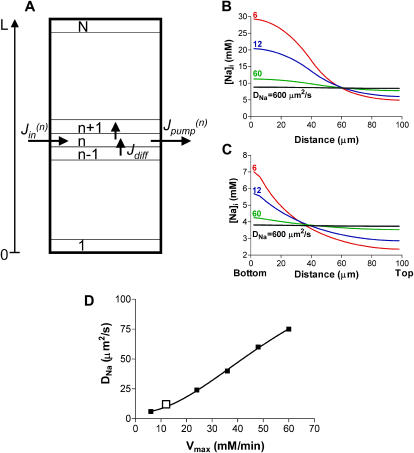
The experiments shown in Figs. 5 and 6 suggest that in cardiac cells Na diffusion is slow enough with respect to the sarcolemmal Na transport rates to allow for [Na]_i gradients. To determine the diffusion coefficient for Na (D_Na) that would allow the existence of such [Na]_i gradients, we developed a simple one-dimensional model for the diffusion of Na in the cell (see Appendix). Briefly, the cell was divided into small compartments along the longitudinal axis (Fig. 7 A). The change in [Na]_i in each compartment is determined by the rate of Na extrusion via the Na/K pump, the passive trans-sarcolemmal Na influx and Na diffusion into/from the adjacent compartments (Fig. 7 A). The trans-sarcolemmal flux values were directly measured in our prior work (Despa et al., 2002). The type of experiment shown in Fig. 5 was mimicked by considering the Na/K pumps blocked in the first M compartments from the lower end of the cell and active in the rest of the compartments. Na influx occurs only in the bottom M compartments.

FIGURE 7.

Simulations of [Na]_i distribution along the longitudinal axis of the myocyte during local Na/K pump inhibition. (A) Schematic representation of the cell model used for simulations. A cylindrical cell (R = 10 μm, L = 100 μm) was divided into N (25 in most simulations) compartments along the longitudinal axis and we solved the equations system for [Na]_i in each compartment. (B and C) The expected longitudinal [Na]_i profile at various values for D_Na when Na/K pumps are blocked in the first 10 and last two compartments from the lower end of the myocyte, respectively. (D) The D_Na that would produce a longitudinal [Na]_i profile similar to the trace for D_Na = 12 μm²/s in B, for various values of Na/K pump V_max. Simulations were done for the case where Na/K pumps were blocked in the bottom 10 compartments. The V_max:D_Na pair used for B is indicated by the open square.

Simulations were done with the Na/K pumps blocked either in the lower 10 compartments (40 μm, assuming a 100-μm-long cell divided into 25 compartments, Fig. 7 B), approximating the situation during local application of K-free solution via the pipette placed in position 1 in the experiment shown in Fig. 5, or in only two compartments (8 μm, Fig. 7 C), simulating the case of the patch pipette placed in position 2. Fig. 7, B and C, shows how the expected [Na]_i profile along the longitudinal axis of the myocyte will depend on D_Na, at steady state, in the two cases. Experimental data indicate that in frog skeletal muscle cells D_Na = 600 μm²/s, i.e., approximately one-half the value measured in aqueous solutions (Kushmerick and Podolsky, 1969). However, for this D_Na, the model suggests a uniform distribution of [Na]_i within the myocyte, in both cases (Fig. 7, B and C). [Na]_i gradients start to be predicted for a D_Na which is ∼10 times lower. The model simulates [Na]_i profiles similar to our experimental data (Fig. 5 D) for a D_Na of 10–12 μm²/s, i.e., 50–60 times lower than measured in skeletal muscle.

The D_Na estimated here depends strongly on the values used for the transmembrane Na fluxes (Fig. 7 D). The simulations in Fig. 7, B and C, were done assuming the maximum pump current density as ∼1 pA/pF (pump rate of 12 mM/min), the K_m for internal Na that we have measured (10.2 mM, Despa et al., 2002), and the passive Na influx such that [Na]_i is at steady state at the resting value of 11 mM (Despa et al., 2002). Fig. 7 D shows how the D_Na that would support our experimental data varies with the maximum Na/K pump rate used in the model. The larger the pump rate, the less restricted Na diffusion has to be to allow for similar subcellular differences in [Na]_i. Nevertheless, even for a five-times-higher pump V_max, D_Na would still have to be approximately eight times lower than 600 μm²/s to explain our data. The model assumes that there are no pumps or Na entry pathways on the “faces” of the cylindrical cell. As expected, including those resulted in a larger difference in [Na]_i between the two ends of the cell. For the simulations shown in Fig. 7 B with D_Na = 12 μm²/s, this difference increased by ∼4 mM. Thus, with Na transport on the faces of the cylindrical cell, the best fit with our data was obtained for a D_Na of ∼15 μm²/s. This does not change our conclusion that D_Na in cardiac myocytes has to be several times lower than 600 μm²/s.

DISCUSSION

Two-photon microscopy of SBFI in rat ventricular myocytes

In this article, we show that two-photon fluorescence microscopy of SBFI can be used to spatially resolve [Na]_i in cardiac myocytes. Although this technique is increasingly used to study subcellular Ca, pH, and redox state (Rubart et al., 2003; Hanson et al., 2002; Huang et al., 2002), its applications for measuring [Na]_i are limited (Niggli and Blatter, 1997; Rose et al., 1999; Rose and Konnerth, 2001). We found that the fluorescent signal generated by the two-photon excitation of SBFI at 760 nm can be readily calibrated in terms of [Na]_i. The apparent K_d of the indicator loaded into rat ventricular myocytes is comparable to the values reported in various cell types using conventional, single-photon microfluorometry (Donoso et al., 1992; Baartscheer et al., 1997) as well as to the value determined by Rose et al. (1999) in neurons using two-photon measurements. Resting [Na]_i obtained here (10.8 ± 0.7 mM) compares well to the values we and others previously reported for rat ventricular myocytes, using either single-photon ratiometric measurements with SBFI (Despa et al., 2002; Levi et al., 1994; Donoso et al., 1992) or ion-selective microelectrodes (Shattock and Bers, 1989). Furthermore, the changes in [Na]_i upon Na/K pump blockade in K-free conditions followed by pump reactivation measured with this method are similar to our previous results using wide-field dual-excitation SBFI measurements. All these lines of evidence support the reliability of the two-photon method for [Na]_i measurements in cardiac myocytes.

Spatially resolved measurements of free [Na]_i have not become routine, partly because SBFI requires excitation by special UV lasers to be used with traditional confocal microscopy. Sodium Green, the only other Na-sensitive fluorescent indicator, loses most of the Na-dependent fluorescence response due to interactions with intracellular proteins (Haugland, 1996) and therefore its use has been limited (Isenberg et al., 2003). Spatial measurements of [Na]_i have also been done using electron probe x-ray microanalysis (Wendt-Gallitelli et al., 1993; Silverman et al., 2002). However, this method measures total rather than free [Na]_i. Therefore, the use of two-photon microscopy of SBFI to monitor the spatial distribution of [Na]_i in cardiac cells may provide further insight into subcellular [Na]_i regulation and its impact on excitation-contraction coupling.

Na/K pump activity and intracellular [Na]_i gradients

Using two-photon microscopy, we showed that large [Na]_i gradients can be generated in rat ventricular myocytes where Na/K pumps are blocked in one part of the cell and active in the rest of the myocyte. Thus, we were able to demonstrate, by direct measurements of the spatial distribution of free [Na]_i, that rapid Na extrusion via the Na/K pump can result in [Na]_i gradients, as suggested by less direct methods (Bielen et al., 1991; Fujioka et al., 1998; Su et al., 1998; Despa and Bers, 2003). However, our experimental conditions were optimal for the occurrence of such gradients, where Na entered into one part of the cell (with Na/K pumps blocked) and was extruded in the other part of the cell (with 4 K, 0 Na solution). The question remains whether such [Na]_i gradients could exist under more physiological conditions and to what extent local changes in [Na]_i produced by one transporter might affect [Na]_i sensed by other transporters.

There is evidence suggesting that the Na/K pump and NCX interact via local changes in [Na]_i in myocytes (Fujioka et al., 1998; Su et al., 1998; Terracciano, 2001). Although there are no data regarding the relative localization of these proteins in cardiac cells, the Na/K pump and NCX are colocalized in smooth muscle (Moore et al., 1993). Furthermore, the Na/K pump and NCX function are both preferentially concentrated in the t-tubules of rat ventricular myocytes, to the same relative percent (Despa et al., 2003). It is less clear though whether Na entering the cells via Na channels (I_Na) during the upstroke of the action potential could locally increase [Na]_i sensed by the Na/K pump or NCX. Silverman et al. (2002) found that activation of Na channels has little effect on the Na/K pump current in guinea-pig ventricular myocytes. However, other reports (Lipp and Niggli, 1994; Su et al., 2001) suggest that I_Na increases local subsarcolemmal [Na]_i, thus affecting excitation-contraction coupling via NCX, and this interaction is modulated by the activity of the Na/K pump. Weber et al. (2003) estimated experimentally that in physiological conditions I_Na might increase local [Na]_i sensed by NCX by ∼1 mM early during the action potential and then this local increase in [Na]_i decays with a time constant of ∼15 ms.

The existence of [Na]_i gradients implies restricted diffusion with respect to the trans-sarcolemmal Na transport rates. Using a simple, one-dimensional model for the diffusion of Na along the longitudinal axis of the myocyte, we found that for such gradients to exist, D_Na has to be 50–100 times lower than the value experimentally determined in muscle cells (Kushmerick and Podolsky, 1969), i.e., 100–200 times lower than in aqueous solutions. We have previously estimated (Despa and Bers, 2003) that rapid Na/K pump activation after a period of pump blockade may result in a local, subsarcolemmal [Na]_i depletion if D_Na near the sarcolemma is 10³–10⁴ times lower than in aqueous solutions. That is a more drastic reduction in D_Na than necessary to explain the data reported here. However, it is possible that Na diffusion is more severely restricted near the sarcolemma than in the bulk cytosol, due to the high density of polar moieties in the subsarcolemmal space.

The D_Na estimated here was obtained assuming a maximum pump rate of 12 mM/min (corresponding to a current density of ∼1 pA/pF). Because the predicted D_Na depends strongly on the values used for the transmembrane Na fluxes (see Fig. 7 D), a higher D_Na would explain our experimental data if the pump V_max is in reality larger. Nevertheless, D_Na still has to be several times lower than 600 μm²/s to explain our experimental data. The reasons for the unexpectedly slow diffusion of cytosolic Na are unclear at present. The intracellular Na buffering is weak (Despa and Bers, 2003) and probably cannot explain such a reduction in Na diffusion. Another explanation is that Na might be taken up into the mitochondria. This could slow diffusion, but should not affect the steady-state [Na]_i gradients that we observed. That is, mitochondrial Na uptake could slow the development of the gradients but not the final standing level. The tortuosity of the cytosol, due to the presence of t-tubules and mitochondria, will increase the effective distance Na has to travel from one compartment to the other and thus might reduce the apparent D_Na.

In summary, we have shown that two-photon fluorescence microscopy of SBFI can be used to monitor reliably the spatial [Na]_i distribution in cardiac cells and that local Na/K pump inhibition/reactivation can generate substantial subcellular [Na]_i gradients in rat ventricular myocytes. This implies that Na diffusion in cardiac myocytes is slow with respect to the trans-sarcolemmal Na transport rate. A simple diffusion model indicates that our data are most consistent with a diffusion coefficient for Na of 10–12 μm²/s, i.e., more than one order-of-magnitude lower than experimentally determined in the cytoplasm of muscle cells. The mechanisms responsible for this slow Na diffusion are currently under investigation.

SUPPLEMENTARY MATERIALS

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

APPENDIX

The cell was considered a long circular cylinder, with radius r and length L, and divided into N compartments along the longitudinal axis, of thickness ΔL= L/N (Fig. 7 A). In each compartment, [Na]_i is determined by the passive Na influx across the sarcolemma, the pump-mediated Na extrusion, and Na diffusion to/from the adjacent compartments. Thus, the change in [Na]_i in the compartment n per unit time (ΔC_n/Δt) is given by

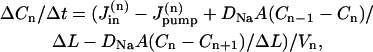(A1)

where D_Na is the diffusion coefficient for Na, A = πr² is the cross-sectional area of the cell, V_n = V_cell/N(= πr² L/N) is the volume of compartment n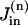, and and 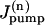are the rates of the passive Na influx and Na extrusion via the Na/K pump in the compartment n, respectively (in mol/time). 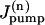is a function of C_n,

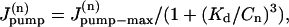where 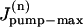is the rate of maximum Na extrusion via the pump in compartment n and K_d (10.2 mM, Despa et al., 2002) is the [Na]_i for half-maximal stimulation of the pump. Assuming that Na/K pumps are uniformly distributed in the sarcolemma, 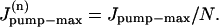A value of 6.4 fmol/s was used for the whole cell J_pump-max (or 12 mM/min for a 32 pL cell, assuming the whole-cell maximum pump current density is ∼1 pA/pF and the surface/volume ratio is 6.7 pF/pL_cell; Bers, 2001).

The passive Na influx was taken as a function of the trans-sarcolemmal Na gradient,

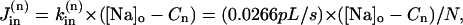where the rate constant 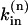is determined from the condition of zero net Na fluxes across the sarcolemma in each compartment at [Na]_i = 11 mM, the resting [Na]_i in rat ventricular myocytes (present data and Despa et al., 2002).

The equations system (A1) was integrated numerically with an integration step of 50 μs. For all simulations shown in Fig. 7, we considered a typical cell with R = 10 μm and L = 100 μm divided into N = 25 compartments as these were sufficient for convergence. To simulate [Na]_i during an experiment similar to Fig. 5, the initial conditions were set to 0 Na in all compartments, 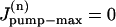in the first M compartments from the lower end of the cell (thus simulating Na/K pump inhibition in K-free solution applied via the pipette) and 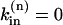in the rest of the cell (the compartments upstream of the patch pipette, perfused with 0 Na, 4 mM K solution).