Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Aug;87(2):754–763. doi: 10.1529/biophysj.104.040279

Molecular Dynamics Simulations of Micelle Formation around Dimeric Glycophorin A Transmembrane Helices

Rosemary Braun *, Donald M Engelman †, Klaus Schulten *
PMCID: PMC1304485  PMID: 15298884

Abstract

Insertion and formation of membrane proteins involves the interaction of protein helices with one another in lipid environments. Researchers have studied glycophorin A (GpA) transmembrane helices embedded in sodium dodecyl sulfate (SDS) micelles to identify contacts significant for helix dimerization. However, a detailed picture of the conformation and dynamics of the GpA-SDS system cannot be obtained solely through experiment. Molecular dynamics simulations of SDS and a GpA dimer can provide an atomic-level picture of SDS aggregation and helix association. We report 2.5-ns simulations of GpA wild-type and mutants in a preformed micelle as well as a 32-ns simulation showing the formation of a complete micelle around wild-type GpA from an initially random placement of SDS molecules in an aqueous environment. In the latter case, an initial instability of GpA helices in water is reversed after the helices become surrounded by SDS. The properties of the spontaneously formed micelle surrounding the GpA are indistinguishable from those of the preformed micelle surrounding the GpA dimer.

INTRODUCTION

A detailed description of the interaction of protein helices with one another in lipid environments is essential to an understanding of the insertion and formation of membrane proteins (Lemmon and Engelman, 1992). The assembly and oligomerization of transmembrane α-helices is known to play a critical role in immune system activity (Kurosaki and Ravetch, 1989; Lanier et al., 1991), fatal cancers (Bargmann et al., 1986; Weiner et al., 1989; Hynes and Stern, 1994), and other biological processes (Lemmon and Engelman, 1992). Genome sequencing studies reveal that 20–30% of open reading frames encode membrane proteins (Wallin and von Heijne, 1998), indicating their biological significance. Transmembrane helices embedded in micelles provide a small system in which helix-helix and helix-lipid interaction may be studied (Lemmon et al., 1992).

Micelles are spherical lipid aggregates in which the hydrophobic tails are at the core and the polar headgroups lie on the surface. Because of their small size and short correlation time, micelles are a convenient mimic for the membrane environment in high-resolution NMR studies (e.g., Lee et al., 2003). In polyacrylamide gel electrophoresis (PAGE) studies, formation of detergent micelles around proteins allows for electrophoretic separation based on the molecular weight of the protein (Lemmon et al., 1992). Although the presence of detergent often disrupts the formation of quaternary structure (Fisher et al., 2003), some membrane proteins are still found to aggregate in the presence of surfactants.

The transmembrane helix of human glycophorin A (GpA) is known to form a stable homodimer under a variety of conditions and has thus been used for many years as a system by which to study the association of transmembrane helices (Lemmon et al., 1992; Fleming and van Grondelle, 1997; Russ and Engelman, 1999; Fisher et al., 1999; Fleming and Engelman, 2001; Fisher et al., 2003). Additionally, while the dissociation rate of the two helices is known to increase with higher detergent concentrations (Fisher et al., 2003, 1999), this effect appears to saturate in the case of high sodium dodecyl sulfate (SDS) concentrations permitting the study of GpA dimerization even in the presence of high (100 mM) SDS concentration (Fisher et al., 2003).

One can study membrane protein formation and aggregation by examining the electrophoretic mobility of dimerizing proteins subject to point mutations. GpA mutants which do not dimerize in the presence of detergent will show a mobility twice that of the dimerizing wild-type GpA in SDS-PAGE assays. It has been observed that GpA transmembrane helices do not dimerize in SDS micelles when strongly polar substitutions are made (Lemmon et al., 1992), and that the mobility in SDS-PAGE experiments on the resulting monomer is also affected. These findings suggest that the mutations alter the interaction of the protein with the detergent micelle, possibly resulting in a structure that differs from a transmicellar α-helix due to helix distortions and interaction with the polar micelle surface. In contrast, mutations in which residues were replaced with nonpolar or weakly polar (G, S, T, Y) amino acids affected dimerization only when applied to specific points in the sequence. Notably, any substitution to G83 of GpA would disrupt dimerization of GpA helices completely; dimerization was also found to be sensitive to any mutations occurring approximately every four residues along the sequence from G83 (Lemmon et al., 1992), and to leucines and isoleucines at the N-terminus. These observations suggest that the positions affecting GpA dimerization are those at the helix-helix interface and play a role in helix-helix packing.

A large body of work has already established the utility of computational models for an enhanced understanding of biophysical processes. Simulations of lipids in different phases are common (Heller et al., 1993) and the function of membrane proteins is routinely studied today in the context of explicit lipid bilayers (e.g., Tieleman et al., 1999; Bernèche and Roux, 2000; Baudry et al., 2001; Tajkhorshid et al., 2002; Cohen and Schulten, 2004).

However, due to limitations in computational power, a study of the dynamics of helix association and the dynamics of lipid aggregation has only recently become feasible. Simplified coarse-grained models (Smit et al., 1993) have been employed, but have the drawback of not providing the atomic-level detail that might be crucial in the present case for capturing the lipid-protein interaction. Contemporary advances in hardware speed and algorithmic efficiency have made recent work involving finer-grained approaches (e.g., Bogusz et al., 2001; Marrink et al., 2000; Shelley et al., 2001) possible.

In this article, we present the results of all-atom molecular dynamics simulations of the GpA wild-type and its disruptive G83A mutant beginning with SDS in the micellar phase. We also present results depicting long-timescale (32 ns) all-atom (65,000 atoms) studies of micelle formation around GpA starting from an initial random SDS distribution, the first such study of spontaneous lipid organization in the presence of protein.

METHODOLOGY

Simulations of GpA and its G83A mutant were carried out in a preformed micelle to investigate the impact of a point mutation on the micelle-enclosed GpA. To understand the dynamics of micelle formation, a simulation starting from a random placement of SDS molecules was also carried out.

The effect of point mutations on the dimerization of GpA helices has been studied extensively by both gel electrophoresis (Lemmon et al., 1992) and ultracentrifugation (Fleming and Engelman, 2001), and the dimerization was found to be highly sequence-dependent. Notably, the mutation of G83 was found to disrupt the dimer consistently; a G83A mutation was found to result in a 3 kcal/mol reduction in the energy of dimerization (Lemmon et al., 1992).

Free molecular dynamics simulation of wild-type GpA and its G83A mutant were carried out using coordinates from the wild-type NMR structure reported in MacKenzie et al. (1996). The protein dimer is presented in Fig. 1. The structure for G83A was created from the wild-type structure by replacing the residue in both helices (circular dichroism experiments—Lemmon et al., 1992—have verified that G83A retains its helical structure) and performing energy minimization.

FIGURE 1.

FIGURE 1

Open in a new tab

NMR structure of GpA helix homodimer. One helical segment is shown as a tube, colored by residue type (nonpolar in gray, polar in green, basic in blue) and surrounded by a transparent representation of the solvent-accessible surface; the other helical segment is shown in solid vdW representation, colored by atom type. The amino acid sequence is also given.

A pre-equilibrated micelle structure of 60 SDS molecules provided by MacKerell (1995) was superimposed on the NMR structure and sterically clashing SDS molecules were removed, resulting in a micelle of 55 SDS molecules surrounding the GpA helix dimers. The micelle-enclosed GpA was minimized and solvated using the explicit TIP3P water model in a cube of water measuring 70 Å on each side, resulting in a system of ∼33,000 atoms and an effective SDS concentration of 270 mM.

Both the wild-type and mutant systems were subject to free molecular dynamics lasting 2.5 ns with periodic boundary conditions and full particle-mesh Ewald electrostatics (Essmann et al., 1995) using NAMD2 (Kalé et al., 1999) with the CHARMM27 force field (MacKerell et al., 1998).

In a second series of simulations the formation of an SDS micelle around a GpA dimer was investigated. As in the case of the other simulations, the wild-type GpA coordinates from the NMR structure were used as a starting point. Fifty-five SDS molecules with conformations taken from the equilibrated micelle were placed at random along with a centrally located GpA helix dimer in a 90 Å cube of TIP3P water. This configuration corresponds to a water/detergent ratio of 375:1 and a detergent concentration of 125 mM. (For comparison, at 300 K the critical micelle concentration, i.e., cmc, in absence of added salts is 8.3 mM, Quina et al., 1995; the cmc with protein present is estimated to be 1 mM, Fisher et al., 2003; and the SDS concentration used in SDS-PAGE studies of GpA is as high as 100 mM, Fisher et al., 1999.) The resulting system, comprising ∼65,000 atoms as shown in Fig. 2, was minimized and subjected to free molecular dynamics lasting 24 ns.

FIGURE 2.

FIGURE 2

Open in a new tab

Simulated spontaneous aggregation shown at 0 ns (top) and 24 ns (bottom). The unit cell is shown as a box, with water molecules depicted as points, SDS molecules shown in licorice representation, and the protein in cartoon representation. The system shown comprises 65,000 atoms.

To accelerate micelle formation, 27 additional SDS molecules were added with random placement to the structure as it was at 18 ns, thus increasing the detergent concentration by 49% and resulting in a total of 82 SDS molecules. Overlapping water molecules were removed, yielding a water/surfactant ratio of 250:1. Free molecular dynamics was carried out for an additional 8 ns.

All simulations were carried out with periodic boundary conditions and full PME electrostatics using NAMD2 (Kalé et al., 1999), the all-atom CHARMM27 force field, and a 2-fs timestep. For the 65,000 atom systems, 128 processors of a 750 AlphaServer ES45 computer cluster at the Pittsburgh Supercomputer Center generate 1 ns simulation in ∼9.5 h; 48 2.1-GHz processors of an in-house Beowulf cluster generate 1 ns in just over a day.

RESULTS

The 2.5-ns simulations of GpA wild-type and its G83A mutant in the preformed micelle are found in agreement with experimental observations, which indicate a stable wild-type dimer and nondimerizing behavior for mutant G83A. For the wild-type, the protein backbone root mean-square deviation (RMSD) stabilized at 1.9 Å after 750 ps; by comparison, the protein backbone RMSD for G83A continued to increase past 3.5 Å after 2.5 ns of simulation, indicating that the system was not in an equilibrium configuration (Fig. 3 a). The bulk of this deviation is attributable to an ongoing rotation of the GpA helices with respect to one another (Fig. 3, b and d), exceeding 24° when the simulation was stopped after 2.5 ns (Fig. 3 b). The center-of-mass distance between the helices was a separation of ∼1 Å, with the closest approach between the helices remaining between Gly79 and Val80, although this distance also increased by over 1 Å (Table 1). Naturally, this distortion of the dimer results in a loss of helix-helix contacts (Fig. 4, a–b).

FIGURE 3.

FIGURE 3

Open in a new tab

Simulations of preformed micelle surrounding GpA. Properties for wild-type GpA (solid line) and G83A mutant (dashed line) are presented. The conformational change revealed by the simulation of the mutant is readily discernible from backbone RMSD (a) and helix-helix orientation angle (b) values, which continue to increase beyond 2.5 ns. The micelle retains its integrity over the course of both simulations, fluidly accommodating the change in GpA mutant conformation without significant change in radius (c). The significant change in the G83A helix-helix angle is depicted in d with the GpA dimer shown in cartoon representation along three axes. In d, light cylinders indicate the initial helix positions and dark cylinders indicate the helix positions at 2.5 ns; the initial and final positions are aligned along one helix, marked by a black dot, to unambiguously show the angle change.

TABLE 1.

GpA helix orientation

Ω (deg) CM (Å) Closest approach (res, Å)
WT, initial (MacKenzie et al., 1996) 37 9.2 Val80-Gly79, 3.5
G83A, 2.5 ns 61 10.2 Val80-Gly79, 5.1
WT, 24 ns 44 ± 2 9.4 ± 0.3 Val80-Gly79, 3.5 ± 0.2
WT, bilayer (Petrache et al., 2000) 39–46 ± 3 8.1–9.4 ± 0.3 —
Open in a new tab

Listed are helix orientation parameters at the beginning and the end of simulation: center-of-mass separation (CM), helix-crossing angle (Ω), and protein segment and distance of closest backbone approach. The initial positions of the GpA helices are from the NMR structure (MacKenzie et al., 1996); values for the G83A mutant are taken from the final time step of the 2.5-ns simulation; figures for the final position of the wild-type are determined by averaging over the last 2 ns of the simulation that included formation of the SDS micelle (see Fig. 2). For reference, the range of values from GpA simulations in phosphocholine bilayers (Petrache et al., 2000) are also shown.

FIGURE 4.

FIGURE 4

Open in a new tab

Helix contacts by residue for wild-type GpA after 2.5-ns equilibration in a preformed micelle (a); GpA G83A mutant in preformed micelle after 2.5 ns (b); and wild-type GpA after spontaneous micelle formation at 24 ns (c). The Cα-to-Cα distance for each pair is shown as a square colored by linear grayscale between 0.0 and 10.0 Å, and white when ≥10.0 Å.

The micelle retained its integrity over the course of both simulations. The micelle expanded slightly from an initial radius of gyration of 14.4 Å to 16.1 Å for both the wild-type and G83A simulations. The average RMS distance of the SDS headgroup sulfurs from the micelle center of mass increased slightly (<10%) from an initial value of 19.7 Å, but remained stable over the course of the simulation (Fig. 3 c). This indicates that the change in angle of the G83A dimer is accommodated by the fluidity (MacKerell, 1995) of the micelle hydrocarbon interior (with longer simulation times, a catastrophic distortion of the micellar system may be observed).

A total of 32 ns of free molecular dynamics provides an atomic-level description of micelle formation around the GpA wild-type dimer. The hydrophobic GpA helices, surrounded by water at the outset of the simulation, were seen to be initially unstable. A peak in the transmembrane helix backbone RMSD of 2.5 Å at ∼5 ns (Fig. 5) corresponds to a significant bending of one of the GpA helices close to the C-terminus (Fig. 5, inset). By 9.5 ns, GpA was surrounded by a partial SDS micelle, and the bent helix straightened again; the protein then appeared stable for the remainder of the simulation with a backbone RMSD of 1.78 Å from the initial structure.

FIGURE 5.

FIGURE 5

Open in a new tab

RMSD of GpA transmembrane region backbone during the early phase of micelle formation. The RMSD settles at 1.78 Å from the starting structure after 9.5 ns. The peak in the 5-ns region results from a significant bend in one of the helices, as shown in the insets: the structures at 5.5 ns and 22 ns are shown in tube representation superimposed on the initial structure in cartoon representation. The helix bend relaxes over the course of the simulation as GpA becomes surrounded by surfactant.

A contribution to the backbone RMSD also comes from a change in the helix crossing angle, from 37° in the starting NMR structure to 44° over the course of the simulation. The center-of-mass distance between the two helices changed only very slightly, from 9.2 Å in the initial structure to 9.4 Å (Table 1). These values are comparable to those seen in GpA simulations carried out in a variety of lipid bilayers (Petrache et al., 2000), suggesting that the curvature of the micelle employed here has an impact on the helix orientation parameters that is not readily distinguishable from effects caused by the choice of bilayer lipids (Petrache et al., 2000; Bond and Sansom, 2003). The transmembrane helix backbone atoms have the closest approach (3.5 Å) at Gly79 and Val80 in both the NMR structure and at the end of the simulation; the change in helix-helix angle is caused by a rotation around the helix-helix interface at these residues. This is in agreement with the experimental observation (Lemmon et al., 1992) that Gly79 plays a critical role in GpA dimerization and supports the hypotheses that a small side chain is necessary for a close approach of the interacting helices (Lemmon et al., 1992) and that hydrogen bonds between Gly79, Val80, and Gly83 of the two helices enhances the stability of the dimer (Curran and Engelman, 2003). The closest side-chain contacts occur for both the NMR structure and the simulated structure between Leu75 and Ile76, mutations of which are known to adversely affect GpA dimerization. The helix-helix distances by residue for the equilibrated structure in a preformed micelle and the protein at the end of the spontaneous micelle formation simulation are comparable as shown in Fig. 4, a and c.

Over the course of the simulation, the initially randomly placed SDS molecules aggregated into small micelle-like clusters, which in turn combined to form successively larger clusters. After the first 18 ns, a large cluster comprising 24 SDS molecules partially surrounded the GpA dimer as the largest cluster within the 90 Å water box (Fig. 6 b). The system was simulated for an additional 6 ns with no significant change in either the protein or the main SDS aggregate.

FIGURE 6.

FIGURE 6

Open in a new tab

SDS configuration at the end of the equilibration of the preformed micelle (a); with initial random placement after 18 ns (b); and after 24 ns (c). Micelle is shown as a transparent surface with SDS molecules indicated in licorice representation; headgroups are highlighted in gold. The GpA dimer is shown in cartoon representation. A cluster of SDS molecules partially surrounds GpA after 18 ns; at 24 ns, a micelle of 44 SDS molecules surrounds GpA, similar to the preformed micelle of 55 SDS molecules.

To speed micelle formation, the concentration of SDS was increased by half and the entire system was then once more subject to free molecular dynamics. The resulting structure, as seen in Fig. 6 c, exhibits a micelle which almost entirely surrounds the GpA dimer.

The resulting micelle has an aggregation number of ∼44, slightly smaller than the aggregation number of 55 for the preformed micelle (see Fig. 6 a), but significantly smaller than experimental micelles surrounding GpA, which have an aggregation number of 81 (Fisher et al., 2003). Longer simulation times would likely result in a higher aggregation number. The radius of gyration of the spontaneously formed micelle, 15.8 Å, is slightly smaller than that of the preformed equilibrated structure (Table 2). Visual inspection of the trajectory using VMD (Humphrey et al., 1996) confirms that the micelle is stable, with no SDS molecule dissociating and diffusing away from the central cluster. Fig. 8 a depicts the distances of SDS sulfurs from the center of GpA for 2.5 ns of the simulation, illustrating that sulfur atoms which enter the region 17–22 Å for longer than 100 ps do not diffuse away; SDS sulfur atoms starting closer to GpA move outward as the SDS molecules reorient.

TABLE 2.

Micelle structural properties

System Nagg rsulf rgyr rpar
Experiment (Itri and Amaral, 1991) 62 22.3 Å 15.4 Å 16.7 Å
Preformed (MacKerell, 1995) 60 20–25 Å 16.02 Å 15–20 Å
Preformed with GpA, initial 55 ∼19 Å 14.42 Å —
Preformed with GpA, 2.4 ns 55 ∼23 Å 16.05 Å ∼18 Å
Spontaneously formed with GpA, 26 ns ∼44 ∼23 Å 15.87 Å ∼18 Å
Open in a new tab

Provided are aggregation numbers (Nagg), sulfur radii (rsulf), radii of gyration (rgyr), and paraffinic radii (rpar) for the experimental SDS micelle structure; preformed micelle without SDS; preformed micelle with GpA before equilibration (minimized structure); preformed micelle with GpA after 2.5-ns equilibration; and spontaneously formed micelle after 26 ns of simulation.

FIGURE 8.

FIGURE 8

Open in a new tab

(a) Distances of SDS sulfur atoms from GpA center of mass between 19 ns and 21.5 ns. Atoms which enter the region between 17 Å and 22 Å at any point and remain in that region longer than 0.1 ns are shown as thick lines. (b) Average MSD of SDS molecules. Data for five individual molecules are shown as a thick black line; a linear fit to the data is also plotted, and has a slope of 77 Å2/ns. For comparison, the average MSD of five SDS molecules which form part of an early cluster is shown as a dotted line. (c) Aggregation number for the micelle surrounding GpA. SDS molecules were considered to be part of the micelle when within 4 Å of GpA and two other SDS molecules; the count is shown as a jagged line. The smooth curve represents the expected aggregation number based on N(t|t0) as given by Eq. 2.

The structure of the spontaneously organized micelle may be further analyzed by examining the density distribution of SDS carbons and sulfurs as well as water molecules as a function of distance from the micelle center of mass in comparison with the equilibrated structure and the initial random placement. In Fig. 7, a–c, snapshots of density distributions of SDS carbons, sulfurs, and water oxygens are plotted as a function of distance from the micelle center of mass. Fig. 7 a depicts the densities for the preformed micelle with GpA wild-type after 2.4 ns; the carbon density decreases and water density increases in the region around 18 Å, compared with an experimentally determined paraffinic radius of 16.3 Å for an “empty” SDS micelle (Itri and Amaral, 1991). The peak in the sulfur density occurs in the vicinity of 23 Å, compared with an experimentally determined radius of 22.3 Å. The close figures for sulfur radii with the enlarged paraffinic radius suggest that the bulk of GpA is accommodated through internal reordering of the micelle rather than overall expansion.

FIGURE 7.

FIGURE 7

Open in a new tab

Density distributions in a preformed micelle with GpA wild-type after 2.4-ns equilibration (a); initial random distribution with GpA wild-type (b); and spontaneously formed micelle after 24 ns (c). Densities for SDS carbons are plotted as •; water oxygens are plotted as □; SDS sulfurs are plotted as ▴. Sulfur densities have been multiplied by 10 for clarity.

In Fig. 7 b, the densities for the initial random placement are depicted. The densities of SDS carbon and sulfur are flat across the graph, as expected. The water density is lower and noisier toward the center, where the GpA protein is located. The final structure after the spontaneous micelle aggregation (Fig. 7 c) has a density profile nearly identical to that of the preformed micelle. As with the preformed micelle, the paraffinic radius is ∼18 Å, and the sulfur peak occurs at ∼23 Å. The peak carbon density is in the range of 0.025 Å−3 between 12 Å and 15 Å, with the lower aggregation number of the spontaneously formed micelle contributing to an overall decrease in carbon density. Likewise, the sulfur density distributions are nearly identical.

The long simulation time permitted the measurement of the diffusion of SDS in water. For the purpose of determining the diffusion coefficient of a single SDS molecule, five SDS molecules that remained unattached to others were monitored over the course of the 24-ns simulation. Using the well-known relationship

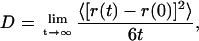graphic file with name M1.gif (1)

a linear fit to the average mean-square deviation (Fig. 8 b) of the five uncoupled SDS molecules gives a diffusion coefficient D = 1.2 × 10−6 cm2/s, which is within the range of values for molecules of its mass. Because small clusters of 2–4 SDS molecules were not reliably stable over the course of the simulation (either due to dissociation or by incorporating into other clusters), and because the diffusion of larger, stable clusters is slow to negligible, diffusion as a function of aggregation number is hard to determine reliably from our simulations. Comparisons of explicit-atom simulations, such as the ones carried out here, with coarser-grained models (Yoon et al., 1993) suggest that the diffusion observed in all-atom simulations is slower and closer to experimental rates than the diffusion observed in coarser-grained models; however, the low viscosity of the TIP3P water model employed in the present simulations likely results in a twofold overestimate of the diffusion coefficient.

Fig. 8 c shows the aggregation number for the main micelle, defined here as the number of SDS molecules within 4 Å of both the protein and two other SDS molecules. A simple diffusion model in which the micelle is treated as an absorptive sphere may be used to model the aggregation (see Appendix), from which one obtains the number N(t|t0) of lipids aggregated at time t,

graphic file with name M2.gif (2)

where a is the radius of the reactive sphere, t0 is the initial time, and N0 = (4π/3) a3 × concentration is the number of SDS molecules initially within the radius a. Using D = 1.2 × 10−6 cm2/s as determined above and c = 10−4 Å−3 one can match N(t|t0) as predicted by Eq. 2 to the aggregation data (Fig. 8 c). The match shown was achieved for t0 = 7 ns and a reaction radius a = 35 Å which is ∼10 Å larger than the sulfur radius of the micelle, possibly due to the length of SDS molecules (10–15 Å). In Fig. 8 a, it can be seen that a region of lower sulfur density develops between the outermost micelle sulfur atoms and ∼35 Å. The initiation time t0 = 7 ns is to be interpreted as the time when an initial cluster has been formed and further aggregation takes place.

Micelle formation at time t < t0 may be understood in the following way. In the first 1.5 ns of the simulation, the aggregation number in Fig. 8 c reflects the approximately five SDS molecules meeting the aggregation criteria (as stated above) in the initial random placement. Nearby SDS molecules accrete rapidly between 1.5 ns and 3.5 ns, forming an initial lipid cluster in contact with the protein comprising 15–16 SDS molecules. For the next 5–6 ns, the cluster remains stable, with free SDS diffusing into the area of lower concentration left by the initial accretion. The leveling at 15 ns occurs with nearly all SDS molecules aggregated into clusters throughout the simulation volume; another sharp increase occurs at 18 ns, when more free SDS is introduced at random.

CONCLUSIONS

Full atom molecular dynamics has been used to investigate helix association and micelle formation. Beginning with the SDS molecules in the micellar phase, it is observed that GpA surrounded by a micelle forms a stable system. Although G83A results in a change to the helix-helix interaction which is disruptive to dimerization, the fluid interior of the micelle accommodates the change in GpA conformation over 2.5 ns.

Simulations beginning with random SDS placement reveal that at concentrations of 0.12–0.19 M, SDS aggregates into a micelle in 20–30 ns, with individual SDS molecules diffusing with D = 1.2 × 10−6 cm2/s. GpA, which is unstable in an aqueous environment, is seen to stabilize after partial micelle aggregation surrounding it. The characteristics of the preformed micelle, including the headgroup radius, paraffinic radius, radius of gyration, and density distributions, are all indistinguishable from those of the spontaneously aggregated micelle.

The simulations also demonstrate that it is feasible to simulate the formation of micelles and possibly other lipid–water phases through all-atom molecular dynamics. Although coarse-grained models of lipids and water have great potential for simulating the formation of larger-scale structures over longer timescales, the all-atom simulations reported here are needed in cases where atomic-level interactions between proteins and lipids or detergents are essential. The necessary ∼65,000 atom simulations are indeed possible today, requiring a few weeks of computational time on a commodity cluster.

Acknowledgments

This work was supported by a grant from the National Institutes of Health NIH PHS 2 P41 RR05969. The authors also acknowledge computer time provided at the National Science Foundation centers by National Resource Allocations Committee grant MCA93S028.

APPENDIX

In this section we derive a mathematical expression for micelle formation described by a simple diffusion model of aggregating lipids. We assume that there exists a stationary micelle of radius a with which the diffusing lipid molecules collide and to which they then remain bound. For the sake of simplicity, the micelle radius is assumed to be fixed; this should not matter as long as the micelle is small compared to the length scale 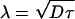Inline graphic where D is the diffusion coefficient of the lipids (here 12 Å2/ns) and τ is the mean time of micelle formation (here ∼20 ns). For the chosen parameters this quantity is λ = 6 nm such that a variation of the micelle size, ∼1 nm, is rather insignificant. We also assume that micelle formation can be described by a radially symmetric model.

To describe diffusion and aggregation of the lipids we consider first a single lipid molecule starting diffusion at t = t0 at a distance r0 from the micelle center. The probability of finding such a lipid at a distance r at time t is given by a radially symmetric probability function p(r, t|r0, t0) that obeys the diffusion equation

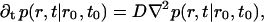graphic file with name M4.gif (A1)

and the initial condition

graphic file with name M5.gif (A2)

The prefactor on the r.h.s. normalizes the initial probability to unity.

The aggregation of the micelle is accounted for by the boundary condition

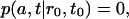graphic file with name M6.gif (A3)

which implies that once a freely diffusing lipid encounters the sphere with radius a it becomes part of the micelle and is no longer counted as freely diffusing.

One can verify that the solution of the above equations A1, A2, and A3 is

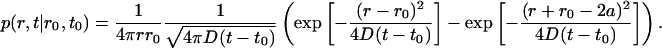graphic file with name M7.gif (A4)

The rate of micelle formation is defined through

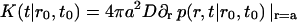graphic file with name M8.gif (A5)

and, in the present case, is

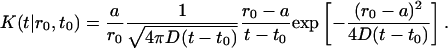graphic file with name M9.gif (A6)

The fraction of lipids aggregated at time t is then

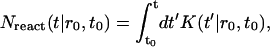graphic file with name M10.gif (A7)

and is found to be

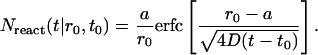graphic file with name M11.gif (A8)

We now account for the fact that there are many lipids at the initial concentration c diffusing and aggregating. By integrating Eq. A8 over all r0 outside the micellar radius a, we can find the number of lipids expected to have aggregated at a given time t:

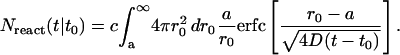graphic file with name M12.gif (A9)

This expression is evaluated as follows. We first note that the substitution 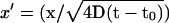Inline graphic leads to

graphic file with name M14.gif (A10)

Using x″ = x′ − a′, this can be written as

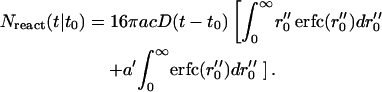graphic file with name M15.gif (A11)

Integrating the first term by parts yields

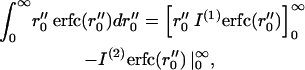graphic file with name M16.gif (A12)

where we introduce the notation (Abramowitz and Stegun, 1965)

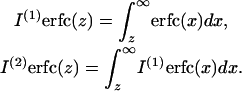graphic file with name M17.gif (A13)

Noting 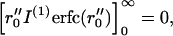Inline graphic the aggregation number Nreact (t|t0) can be written:

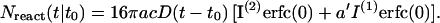graphic file with name M19.gif (A14)

Recalling 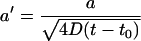Inline graphic and employing the explicit expressions for repeated integrals of erfc given in Abramowitz and Stegun (1965), it can be verified that this integration yields

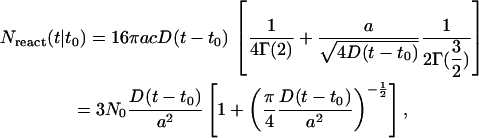graphic file with name M21.gif (A15)

where

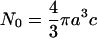graphic file with name M22.gif (A16)

is the initial number of SDS molecules within the radius a for the concentration c. Nreact(t|t0) can be written

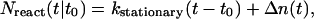graphic file with name M23.gif (A17)

where

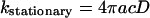graphic file with name M24.gif (A18)

is the well known stationary bimolecular reaction rate and where Δn(t) ≥ 0, i.e.,

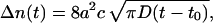graphic file with name M25.gif (A19)

describes deviation from the stationary reaction rate.

References

  1. Abramowitz, M., and I. A. Stegun. 1965. Handbook of Mathematical Functions. Dover, New York.
  2. Bargmann, C. I., M. C. Hung, and R. A. Weinberg. 1986. Multiple independent activations of the Neu oncogene by a point mutation altering the transmembrane domain of p185. Cell. 45:649–657. [DOI] [PubMed] [Google Scholar]
  3. Baudry, J., E. Tajkhorshid, F. Molnar, J. Phillips, and K. Schulten. 2001. Molecular dynamics study of bacteriorhodopsin and the purple membrane. J. Phys. Chem. B. 105:905–918. [Google Scholar]
  4. Bernèche, S., and B. Roux. 2000. Molecular dynamics of the KcsA K+ channel in a bilayer membrane. Biophys. J. 78:2900–2917. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bogusz, S., R. M. Venable, and R. W. Pastor. 2001. Molecular dynamics simulations of octyl glucoside micelles: dynamic properties. J. Phys. Chem. B. 105:8312–8321. [Google Scholar]
  6. Bond, P. J., and M. S. P. Sansom. 2003. Membrane protein dynamics versus environment: simulations of OmpA in a micelle and in a bilayer. J. Mol. Biol. 329:1035–1053. [DOI] [PubMed] [Google Scholar]
  7. Cohen, J., and K. Schulten. 2004. Mechanism of anionic conduction across ClC. Biophys. J. 86:836–845. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Curran, A. R., and D. M. Engelman. 2003. Sequence motifs, polar interactions and conformational changes in helical membrane proteins. Curr. Op. Struct. Biol. 13:412–417. [DOI] [PubMed] [Google Scholar]
  9. Essmann, U., L. Perera, M. L. Berkowitz, T. Darden, H. Lee, and L. G. Pedersen. 1995. A smooth particle mesh Ewald method. J. Chem. Phys. 103:8577–8593. [Google Scholar]
  10. Fisher, L. E., D. M. Engelman, and J. N. Sturgis. 1999. Detergents modulate dimerization, but not helicity, of the glycophorin A transmembrane domain. J. Mol. Biol. 293:639–651. [DOI] [PubMed] [Google Scholar]
  11. Fisher, L. E., D. M. Engelman, and J. N. Sturgis. 2003. Effect of detergents on the association of the glycophorin A transmembrane helix. Biophys. J. 85:3097–3105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Fleming, G. R., and R. van Grondelle. 1997. Femtosecond spectroscopy of photosynthetic light-harvesting systems. Curr. Op. Struct. Biol. 7:738–748. [DOI] [PubMed] [Google Scholar]
  13. Fleming, K., and D. Engelman. 2001. Specificity in transmembrane helix-helix interactions can define a hierarchy of stability for sequence variants. Proc. Natl. Acad. Sci. USA. 98:14340–14344. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Heller, H., M. Schaefer, and K. Schulten. 1993. Molecular dynamics simulation of a bilayer of 200 lipids in the gel and in the liquid crystal-phases. J. Phys. Chem. 97:8343–8360. [Google Scholar]
  15. Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD—visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
  16. Hynes, N. E., and D. F. Stern. 1994. The biology of erbB-2/neu/HER2 and its role in cancer. Biochim. Biophys. Acta. 1198:165–184. [DOI] [PubMed] [Google Scholar]
  17. Itri, R., and L. Q. Amaral. 1991. Distance distribution function of sodium dodecyl sulfate micelles by x-ray scattering. J. Phys. Chem. 9:423–427. [Google Scholar]
  18. Kalé, L., R. Skeel, M. Bhandarkar, R. Brunner, A. Gursoy, N. Krawetz, J. Phillips, A. Shinozaki, K. Varadarajan, and K. Schulten. 1999. NAMD2: greater scalability for parallel molecular dynamics. J. Comp. Phys. 151:283–312. [Google Scholar]
  19. Kurosaki, T., and J. V. Ravetch. 1989. A single amino acid in the glycosyl phosphatidylinositol attachment domain determines the membrane topology of FcgRIII. Nature. 342:805–807. [DOI] [PubMed] [Google Scholar]
  20. Lanier, L. L., G. Yu, and J. H. Phillips. 1991. Analysis of Fc γ RIII (CD16) membrane expression and association with CD3 ζ and Fc ε RI-γ by site-directed mutation. J. Immunol. 146:1571–1576. [PubMed] [Google Scholar]
  21. Lee, K. H., S. Y. Shin, J. Hone, S. T. Yang, J. I. Kim, K. S. Hahm, and Y. Kim. 2003. Solution structure of termite-derived antimicrobial peptide, spinigerin, as determined in SDS micelle by NMR spectroscopy. Biochem. Biophys. Res. Commun. 309:591–597. [DOI] [PubMed] [Google Scholar]
  22. Lemmon, M. A., and D. M. Engelman. 1992. Helix-helix interactions inside lipid bilayers. Curr. Op. Struct. Biol. 2:511–518. [Google Scholar]
  23. Lemmon, M. A., J. M. Flanagan, H. R. Treutlein, J. Zhang, and D. M. Engelman. 1992. Sequence specificity in the dimerization of transmembrane α-helices. Biochemistry. 31:12719–12725. [DOI] [PubMed] [Google Scholar]
  24. MacKenzie, K., J. Prestegard, and D. M. Engelman. 1996. Leucine sidechain rotamers in a glycophorin A transmembrane peptide as revealed by three bond carbon-carbon couplings and 13C chemical shift. J. Biomol. NMR. 7:256–260. [DOI] [PubMed] [Google Scholar]
  25. MacKerell, A., Jr. 1995. Molecular dynamics simulation analysis of a sodium dodecyl sulfate micelle in aqueous solution: decreased fluidity of the micelle hydrocarbon interior. J. Phys. Chem. 99:1846–1855. [Google Scholar]
  26. MacKerell, A. D., Jr., D. Bashford, M. Bellott, R. L. Dunbrack, Jr., J. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, I. W. E. Reiher, B. Roux, M. Schlenkrich, J. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin, and M. Karplus. 1998. All-hydrogen empirical potential for molecular modeling and dynamics studies of proteins using the CHARMM22 force field. J. Phys. Chem. B. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
  27. Marrink, S., D. Tieleman, and A. E. Mark. 2000. Molecular dynamics simulation of the kinetics of spontaneous micelle formation. J. Phys. Chem. B. 104:12165–12173. [Google Scholar]
  28. Petrache, H. I., A. Grossfield, K. R. MacKenzie, D. M. Engelman, and T. B. Woolf. 2000. Modulation of glycophorin A transmembrane helix interactions by lipid bilayers: molecular dynamics calculations. J. Mol. Biol. 302:727–746. [DOI] [PubMed] [Google Scholar]
  29. Quina, F. H., P. M. Nassar, J. B. S. Bonilha, and B. L. Bales. 1995. Growth of sodium dodecyl sulfate micelles with detergent concentration. J. Phys. Chem. 99:17028–17031. [Google Scholar]
  30. Russ, W. P., and D. M. Engelman. 1999. TOXCAT: a measure of transmembrane helix association in a biological membrane. Proc. Natl. Acad. Sci. USA. 96:863–868. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Shelley, J. C., M. Y. Shelley, R. C. Reeder, S. Bandyopadhyay, and M. L. Klein. 2001. A coarse-grain model for phospholipid simulations. J. Phys. Chem. B. 105:4464–4470. [Google Scholar]
  32. Smit, B., K. Esselink, P. A. J. Hilbers, N. M. V. Os, L. A. M. Rupert, and I. Szleifer. 1993. Computer simulations of surfactant self-assembly. Langmuir. 9:9–11. [Google Scholar]
  33. Tajkhorshid, E., P. Nollert, M. Ø. Jensen, L. J. W. Miercke, J. O'Connell, R. M. Stroud, and K. Schulten. 2002. Control of the selectivity of the aquaporin water channel family by global orientational tuning. Science. 296:525–530. [DOI] [PubMed] [Google Scholar]
  34. Tieleman, D. P., H. J. C. Berendsen, and M. S. P. Sansom. 1999. An alamethicin channel in a lipid bilayer: molecular dynamics simulations. Biophys. J. 76:1757–1769. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Wallin, E., and G. von Heijne. 1998. Genome-wide analysis of integral membrane proteins from eubacterial, archaen, and eukaryotic organisms. Protein Sci. 7:1029–1038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Weiner, D. B., J. Liu, J. A. Cohen, W. V. Williams, and M. I. Greene. 1989. A point mutation in the neu oncogene mimics ligand induction of receptor aggregation. Nature. 339:230–231. [DOI] [PubMed] [Google Scholar]
  37. Yoon, D. Y., G. D. Smith, and T. Matsuda. 1993. A comparison of a united atom and an explicit atom model in simulations of polymethylene. J. Chem. Phys. 98:10037–10043. [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES