Abstract
Steroid hormones such as progesterone, testosterone, and estradiol are derived from cholesterol, a major constituent of biomembranes. Although the hormones might be expected to associate with the bilayer in a fashion similar to that of cholesterol, their biological action in regulating transcription of target genes involves transbilayer transfer by free diffusion, which is not observed for cholesterol. We used a novel combination of a continuum-solvent model and the downhill simplex search method for the calculation of the free energy of interaction of these hormones with lipid membranes, and compared these values to that of cholesterol-membrane interaction. The hormones were represented in atomic detail and the membrane as a structureless hydrophobic slab embedded in implicit water. A deep free-energy minimum of ∼−15 kcal/mol was obtained for cholesterol at its most favorable location in the membrane, whereas the most favorable locations for the hormones were associated with shallower minima of −5.0 kcal/mol or higher. The free-energy difference, which is predominantly due to the substitution of cholesterol's hydrophobic tail with polar groups, explains the different manner in which cholesterol and the hormones interact with the membrane. Further calculations were conducted to estimate the rate of transfer of the hormones from the aqueous phase into hexane, and from hexane back into the aqueous phase. The calculated rates agreed reasonably well with measurements in closely related systems. Based on these calculations, we suggest putative pathways for the free diffusion of the hormones across biomembranes. Overall, the calculations imply that the hormones may rapidly cross biomembrane barriers. Implications for gastrointestinal absorption and transfer across the blood-brain barrier and for therapeutic uses are discussed.
INTRODUCTION
In mammals, the gonads produce three major groups of steroid hormones: androgens, estrogens, and progestins; among them, the most common are testosterone, estradiol, and progesterone, respectively (Kawata, 1995). Their participation in bone maturation, central nervous system activity, immune-system regulation (testosterone and estradiol), conception, and intrauterine fetal development (progesterone), as well as many other physiological processes, emphasizes their crucial role in the regulation and development of the human body (Falkenstein et al., 2000).
Steroid hormones also have various therapeutic uses. For example, reduction in circulating levels of both male and female sex hormones (androgens and estrogens) during menopause is often treated with hormone replacement therapy, which was proven to be beneficial in reducing the risk of osteoporosis and neurodegenerative diseases such as Alzheimer's (Goldstein and Sites, 2002).
The biological effects of steroid hormones occur by means of two main mechanisms: the genomic and nongenomic. The first is termed “genomic” since the hormones regulate the transcription of target genes, a process that may last several hours. Modulation of this mechanism occurs through inhibition of transcription and translation. In the nongenomic mechanism, steroid hormones exert actions that are incompatible with the former mechanism. These actions are rapid (seconds to minutes) and are insensitive to inhibitors of transcription and translation. The hormones may produce these effects through changes in membrane fluidity or, alternatively, by binding to—and regulation of—membrane receptors, e.g., GABAA receptors in the brain (Brann et al., 1995; Falkenstein et al., 2000).
After secretion by the endocrine glands, the hormones are transported to the target tissues via the blood, where their major fraction is bound to the serum proteins β-globulin and albumin. According to the genomic mechanism, the lipophilic character of the hormones enables them to dissociate spontaneously from the carriers and enter the target cell by transbilayer passive diffusion. Inside the cell, the hormones bind to intracellular receptors that shuttle between the nucleus and the cytoplasm in an inactive state (Lundberg, 1979). Binding to the hormones induces conformational changes and reorganization to active hormone-receptor complexes (Guiochon-Mantel et al., 1996). Subsequently, the complexes migrate to the nucleus, where they bind to hormone-responsive elements on the DNA and regulate synthesis of new proteins that are required for the hormone's action (Chen and Farese, 1999; Beato and Klug, 2000).
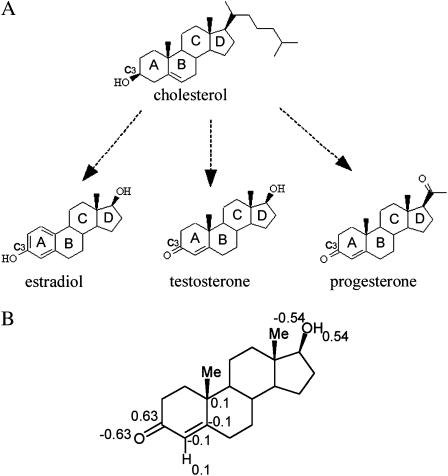
Synthesis of steroid hormones relies mostly on exogenous cholesterol, a major constituent of eukaryotic membranes. The chemical structures of cholesterol and three steroid hormones are depicted in Fig. 1 A. Both cholesterol and the hormones share a backbone of four rigid, planar, fused rings. However, the chemical substituents of the hormones make them more polar than cholesterol. Cholesterol is known to associate strongly with the membrane and modulate its fluidity (Goldstein and Sites, 2002). Both experiments (Golden et al., 1998; Yeagle, 1985) and calculations (Gabdouline et al., 1996; Robinson et al., 1995; Smondyrev and Berkowitz, 1999; Tu et al., 1998; Kessel et al., 2001a) have shown that the most preferable cholesterol-membrane configuration is obtained when cholesterol's hydrophobic core is buried inside the hydrocarbon region of the bilayer, whereas the hydroxyl group protrudes into the polar headgroup region. Since steroid hormones are derived from cholesterol and share an identical backbone, they might be expected to associate with the membrane in a similar way. However, their action through the genomic mechanism involves transbilayer diffusion across the cell membrane rather than permanent association with the membrane.
FIGURE 1.
(A) The two-dimensional structures of cholesterol, estradiol, testosterone, and progesterone. The molecules are presented in similar orientations and the four backbone rings are marked A–D. (B) The partial charges that were assigned to the polar groups of testosterone. The carbonyl was assigned with charges of C (+0.63) and O (−0.63). The hydroxyl group was assigned with O (−0.54) and H (+0.54). Aromatic CH groups were assigned with C (−0.1) and H (+0.1).
Watanabe et al. (1991) investigated the transport of steroid hormones in a system consisting of a hexane-source phase, an aqueous phase, and a hexane-receiving phase. They measured the partition coefficient of the hormones between the water and hexane phases and the rates of hormone transfer between these phases. They also showed that although most of the hormones were bound to serum proteins in the aqueous phase, only unbound hormones transferred between the two solvents.
In the present study, we analyzed cholesterol and the steroid hormones with regard to their association with the membrane. The continuum-solvent model was used to calculate the free energy of interaction between these molecules and the membrane. Downhill simplex optimization was used to determine the most favorable location and orientation of each of these molecules in the membrane. Further calculations were carried out to estimate the average transfer rate of a single hormone molecule from the aqueous phase into a hexane phase and back to the aqueous phase at the other end of the hexane phase, and these were in agreement with experimental results. Based on these calculations, we suggest putative pathways for the free diffusion of steroid hormones across biomembranes.
METHODOLOGY
Three-dimensional structures
Three-dimensional structures of the steroid hormones were taken from the Cambridge Catalogue (Crystallographic Data Center, Cambridge, UK). Several conformations are available for each hormone, depending on the crystallization conditions, but superimposition showed that the root mean-square deviations between them are negligible (RMS < 0.1 Å). This is most likely due to the rigidity of their four-ring backbone. Furthermore, comparison of the three different hormones showed that their four-ring backbones superimpose very well on each other and that they all superimpose well on cholesterol's backbone.
Partitioning of steroid hormones between aqueous and hexane phases
The polarity of the membrane's hydrocarbon core is similar to that of hexane (Sitkoff et al., 1996). Thus, we studied the transfer of the hormones between bulk water and hexane. The free energy associated with this process will be referred to as the solvation free energy (ΔGsol). It can be decomposed into a sum of differences in the electrostatic free energy (ΔGele), resulting from changes in the solvent dielectric constant, and in the nonpolar free energy (ΔGnp) that accounts for van der Waals and solvent-structure effects (Honig and Nicholls, 1995; Kessel and Ben-Tal, 2002),
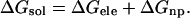 |
(1) |
The continuum-solvent model
ΔGsol was calculated using the continuum-solvent model (Gilson, 1995; Honig and Nicholls, 1995; Nakamura, 1996; Warshel and Papazyan, 1998). We followed the procedure that was used by Sitkoff et al. (1996) to calculate the water-to-liquid alkane transfer free energy of small molecules. The boundary between the hormone and the solvent (water or hexane) was set at the contact area between the van der Waals surface of the hormone and a solvent probe with a 1.4 Å radius (Sharp et al., 1991). The hormone interior and the hexane solvent were assigned a dielectric constant of 2, whereas a value of 80 was assigned to the dielectric constant of the aqueous phase. The system was mapped onto a lattice of 1133 grid points, with a resolution of three points per Å, and the electrostatic potential at each grid point was obtained from finite-difference solutions to the Poisson equation (Honig et al., 1993). ΔGele was obtained by integration over the potential multiplied by the charge distribution in space.
ΔGnp = γA+b was calculated as a linear function of the water-accessible surface area of the hormones upon partitioning between hexane and water (A), with a surface tension coefficient of γ = 0.0278 kcal/(mol Å2) and an intercept b = −1.71 kcal/mol (Sitkoff et al., 1996). The value of A was calculated using the SURFV program (Sridharan et al., 1992).
Assignment of partial charges
Atomic radii and partial charges were defined at the coordinates of each nucleus. The radii and most of the charges were taken from PARSE—a parameter set that was derived to reproduce gas phase-to-water (Sitkoff et al., 1994) and liquid alkanes-to-water (Sitkoff et al., 1996) transfer free energy of small organic molecules. However, the partial charges of the hydroxyl groups, as on ring D of testosterone and ring A of estradiol (Fig. 1 A), and the carbonyl groups, as on ring A of progesterone, are missing in PARSE. Partial charges were assigned to these groups following the same procedure used to derive the original liquid alkanes-to-water PARSE parameters (Sitkoff et al., 1996). In short, we assigned equal and opposite charges to the pairs of atoms that comprise these functional groups. The magnitude of the charge was determined such that the free energy of water-to-hexane transfer of the hormones best matched the experimental results of partitioning between these two solvents. We relied on the measured partitioning of the hormones between water and hexane (Watanabe et al., 1991).
Partitioning of steroid hormones between the aqueous phase and the lipid bilayer
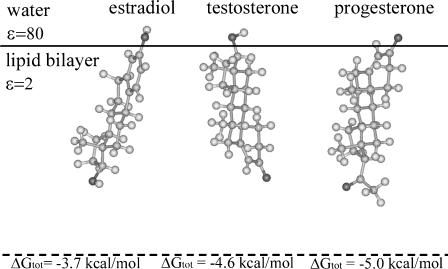
Unlike water-hexane partitioning, where the hormones are fully immersed in each of the two solvents, water-membrane partitioning is dominated by the interface between the two phases. The hormone partitions into the membrane in the location and orientation, together referred to as configuration, that produces the lowest value of ΔGsol (Fig. 2). This is typically obtained when the interactions of the hydrophobic groups with the hydrocarbon region of the membrane are maximal, whereas the contacts between polar groups and that region are minimal. Thus, we used the simplex algorithm, described in the following section, to search for optimal hormone-membrane configurations.
FIGURE 2.
The hormones in their most favorable location and orientation in the membrane slab model. The hormones are represented using a ball-and-stick model, created using InsightII (Accelrys, San Diego, CA). The solid horizontal line marks the boundary between the hydrocarbon region of the membrane, which was assigned a low dielectric constant of ɛ = 2, and the aqueous phase (ɛ = 80). The membrane midplane is shown as a dashed line. The total free energy value associated with each configuration is plotted.
The total free energy (ΔGtot) of the hormone-membrane system is composed of ΔGsol and the immobilization free energy (ΔGimm) (Kessel and Ben-Tal, 2002),
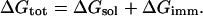 |
(2) |
ΔGimm is the free-energy penalty resulting from the restriction of external translational and rotational motions of the hormones upon association with the membrane. We used an estimate of ΔGimm ≈ 1.3 kcal/mol (Ben-Tal et al., 2000).
Downhill simplex method
The most stable hormone-membrane configuration, associated with the most negative ΔGtot value, was determined using the downhill simplex method (Nelder and Mead, 1965). It is a nonlinear, unconstrained optimization algorithm. Since the minimization does not require the use of derivatives, it is suitable for the continuum-solvent model calculations, for they are impractical to compute derivatives.
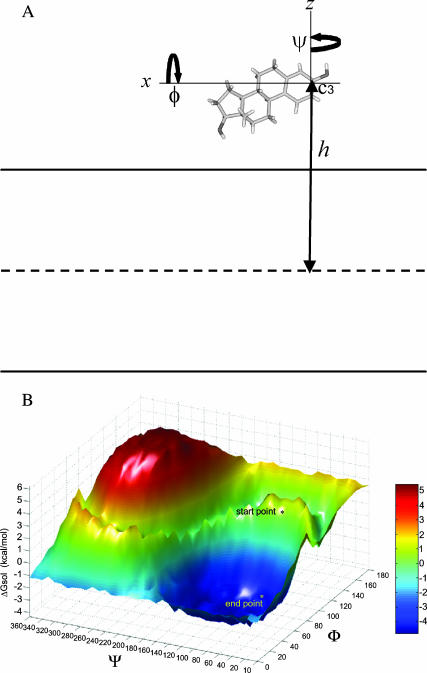
In general, the simplex search does not overcome local minima, and thus we used ∼30 different initial hormone-membrane configurations in each series of runs. Our assumption was that the use of multiple starting points would increase the chances of finding the configuration associated with the lowest free energy. Each configuration was defined by its penetration depth (h) and two rotation angles (ϕ, ψ), as illustrated in Fig. 3 A. These 30 configurations were manually selected, so that the hormone was partially immersed in the bilayer. When converging to an orientation with a local minimum, the search proceeded with initial configurations generated by small rotations and translations around that orientation. Each search proceeded with ∼80 steps (different configurations), until it converged to a local minimum. A convergence criterion of 0.1 kcal/mol was used. Overall, ∼2400 configurations were sampled for each steroid hormone, and the results provided us with the most favorable hormone-membrane configuration, associated with the most negative ΔGtot value.
FIGURE 3.
Simplex optimization method. (A) Estradiol orientation with respect to the membrane is defined by the distance between the C3 carbon atom of the hormone and the membrane midplane (h), and the two rotation angles ϕ and Ψ. (Estradiol is blown out of proportion with respect to the membrane.) (B) A free-energy surface, describing different orientations of estradiol with respect to the bilayer; each configuration is defined by h, which was held constant here, and the rotation angles ϕ and ψ. The input to simplex was an initial configuration (start point; ΔGsol = −0.1 kcal/mol). Simplex then converged to the nearest local minimum (end point; ΔGsol = −4.8 kcal/mol).
Transfer-rate calculations
Since the hormones' sizes are smaller than the membrane's width, translocation across the bilayer involves configurations in which the hormone is fully buried in the lipid bilayer. As mentioned earlier, the dielectric characteristics of the hydrocarbon core of the membrane are similar to those of hexane. We therefore first studied two processes: 1), transfer from water to hexane and 2), transfer from hexane to water. The transfer rate k of each process was calculated using
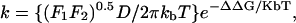 |
(3) |
where kb is the Boltzmann constant, T is the absolute temperature, and D is the diffusion coefficient of a steroid hormone in a uniform medium (Schulten et al., 1981; Wilson and Pohorille, 1996). F1 and F2 are the force constants (i.e., the second derivatives of the free energy as a function of the steroid-hexane distance, h) in the orientations separated by the free-energy barriers (Kessel et al., 2001b). The value ΔΔG is the difference in the solvation free energy of the system (Eq. 1) above the barrier (ΔGa) and below it (ΔGb):
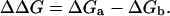 |
(4) |
The water-to-hexane rate
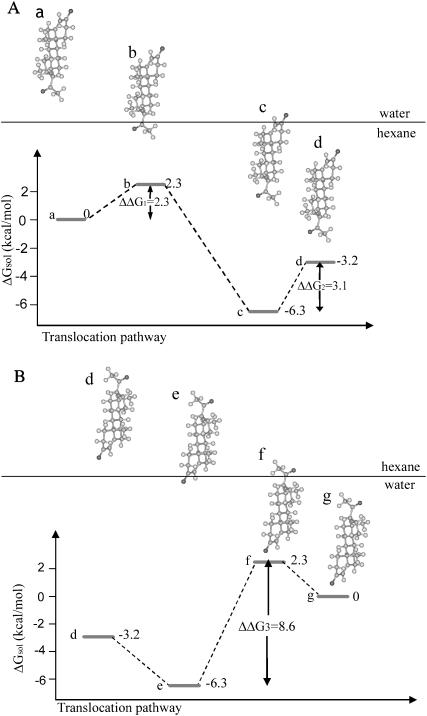
The transfer of a steroid hormone from water into liquid hexane involves two free-energy barriers. In the example of Fig. 4 A, the adsorption of progesterone onto the interface between the aqueous and hexane phases involves insertion of a carbonyl group into the hexane (a–b), which is associated with the first free-energy barrier (ΔΔG1). Subsequently, full insertion of progesterone into the hexane phase requires insertion of a second carbonyl group (c–d) and is associated with a second barrier (ΔΔG2). For each barrier, the average migration time τ was calculated as
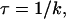 |
(5) |
where k was calculated using Eq. 3. The total migration time τtotal is the sum of the migration times across the two barriers, and the average transfer rate of the whole process is 1/τtotal.
FIGURE 4.
(A) A putative pathway for the transfer of progesterone from bulk water into a hexane phase. The first free-energy barrier (ΔΔG1), observed between configurations a and b, is associated with the transfer of a carbonyl group between the two media. The subsequent transition, between the configurations b and c, involves a free-energy gain due to the transfer of progesterone's hydrophobic core into the hexane phase. The complete burial of the hormone inside bulk hexane (transition from c to d) involves a second free-energy barrier (ΔΔG2) due to the transfer of the second carbonyl group from water to hexane. (B) A putative pathway for the transfer of progesterone from the hexane phase into bulk water. The transition from configuration d to e involves a free-energy gain due to the transfer of a carbonyl group from the hexane phase into water. The following step (transition between configurations e and f) involves a free-energy barrier (ΔΔG3) due to the penalty associated with pulling progesterone's hydrophobic core out of the hexane phase into water. The final transition of progesterone into water (from configuration f–g) involves a free-energy gain due to the transfer of the second carbonyl group from the hexane phase into water. Progesterone is represented using a ball-and-stick model, created using InsightII (Accelrys, San Diego, CA). The boundary between the aqueous and hexane phases is represented as a horizontal line.
The diffusion coefficient of a steroid hormone in an aqueous phase was taken as D ≈ 107 Å2/s, based on the measured values of the hormone's diffusion coefficient through sol-gel glass (Sieminska et al., 1997).
The hexane-to-water transfer rate
The transfer of a steroid hormone from the hexane phase into bulk water (e.g., Fig. 4 B) involves a single free-energy barrier (ΔΔG3), resulting from the transfer of the hormone's hydrophobic core from liquid hexane to the aqueous phase (e–f). Experimental studies that measure D in an organic medium take into account the solvation of the hormone's polar groups in the medium. Since this effect is already included in our calculated ΔΔG (Eq. 4), the use of these measured values in Eq. 3 would overcount the solvation effect. Instead, we used a value of D ≈ 109 Å2/s that was obtained from measurements (Pfeiffer et al., 1989) and calculations (Essmann and Berkowitz, 1999) of the lateral motion of phosphatidylcholine in dipalmitoylphosphatidylcholine (DPPC) bilayers, which does not take solvation effects into account.
Transfer across the membrane
The translocation of a single steroid hormone molecule across the membrane involves transfer from the aqueous phase (e.g., the blood stream) into the hydrocarbon region of the membrane and then back to the aqueous phase at the other end (e.g., the cytosol). The process involves three free-energy barriers (Figs. 5 and 6). The total rates of transfer of the hormones across the membrane were estimated based on the calculated rate of transfer across each of the three barriers.
FIGURE 5.
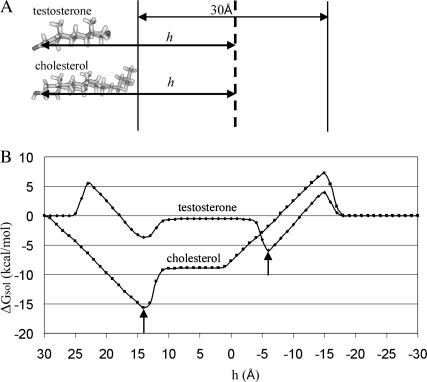
(A) A hypothetical translocation pathway of cholesterol and testosterone across the lipid bilayer. Cholesterol was positioned in its most favorable orientation in the membrane. Testosterone's orientation was determined by superimposing the hormone on cholesterol. The two vertical lines mark the boundary between the aqueous phase and the hydrocarbon region of the membrane. The distance h between the molecules and the membrane midplane (vertical dashed line) was defined as in Fig. 3 A. Cholesterol and testosterone were represented using ball-and-stick models, created using InsightII (Accelrys, San Diego, CA). (B) Solvation free-energy profiles of cholesterol and testosterone along the hypothetical pathways (the horizontal axis h decreases from left to right). The arrows mark the energetically most favorable locations of cholesterol and testosterone in the bilayer in this orientation. It is noticeable that the transfer from bulk water (h = 25 Å) to the lipid bilayer (h = 10 Å) occurs along a characteristic length of 15 Å. A similar length is observed in transfer from the hydrocarbon region back into bulk water.
FIGURE 6.
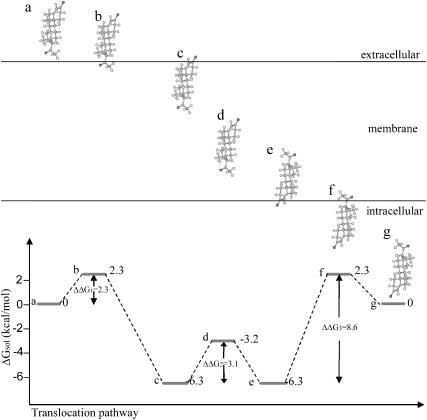
A hypothetical pathway for the passive diffusion of progesterone across the lipid bilayer. Progesterone, represented using a ball-and-stick model, was oriented in its most favorable orientation in the membrane (Fig. 2). The first step (configurations a–b) involves the free-energy barrier ΔΔG1, which results from the transfer of a carbonyl group from water to the hydrocarbon region of the membrane. The second step (configurations b–c) involves a free-energy decrease due to the partitioning of progesterone's hydrophobic core into the hydrocarbon region of the membrane. The third step (configurations c–d) involves the free-energy barrier ΔΔG2, which results from the transfer of the second carbonyl group from water to the hydrocarbon region of the membrane. When fully embedded inside the bilayer (d) progesterone may freely rotate without changing its solvation free energy; progesterone's exit from the other end of the membrane is facilitated by 180° rotation and translation to configuration e. The transition involves a free-energy decrease due to the favorable transfer of a carbonyl group from the membrane into the aqueous phase. The following step (configurations e–f) involves a free-energy barrier (ΔΔG3) due to the penalty associated with the transfer of progesterone's hydrophobic core from the membrane to the aqueous phase. The ultimate step (configurations f–g) involves a free-energy decrease due to the favorable transfer of a carbonyl group from the membrane to the aqueous phase.
RESULTS
We carried out calculations to deal with thermodynamic and kinetic aspects of the interactions of cholesterol and the three steroid hormones with lipid bilayers. The polarity of hexane is very similar to that of the hydrocarbon region of the membrane, and we therefore studied the partitioning and average rate of transfer of cholesterol and the hormones between these phases.
Derivation of atomic partial charges
We calculated the values of ΔGsol associated with the water-to-hexane transfer of the three hormones as a means to derive partial charges for chemical groups that were missing in PARSE. Using the original PARSE radii and optimal partial charges of Fig. 1 B, i.e., assigning partial charges of C (+0.63) and O (−0.63) to the carbonyl group and O (−0.54) and H (+0.54) to the hydroxyl group, the measured free-energy values were reproduced to within <0.3 kcal/mol accuracy (Table 1).
TABLE 1.
The water-to-hexane transfer free energy of steroid hormones (Eq. 1)
| Molecule | ΔGnp* (kcal/mol) | ΔGele† (kcal/mol) | ΔGsol‡ (kcal/mol) | ΔG§ (kcal/mol) |
|---|---|---|---|---|
| Progesterone | −12.7 | 9.5 | −3.2 | −3.3 |
| Testosterone | −11.6 | 10.7 | −0.9 | −0.8 |
| Estradiol | −11.2 | 11.5 | 0.3 | −0.1 |
The nonpolar free energy component.
The electrostatic free energy component.
The solvation free energy (Eq. 1).
The experimental water-to-hexane transfer free energy derived using ΔG = −RTln K, where T = 298 K is the absolute temperature, and K is the partition coefficient measured by Watanabe et al. (1991).
The hormones differ in their affinity to the hexane phase: progesterone is the most hydrophobic of the three and had the highest affinity to the hexane phase, whereas testosterone and estradiol partitioned approximately equally between bulk water and hexane (Table 1). The difference of ∼3 kcal/mol in the ΔGsol value obtained for the three hormones was due to changes in the magnitude of both the electrostatic and nonpolar contributions; along the series progesterone-testosterone-estradiol, the value of ΔGele increased in magnitude, whereas that of ΔGnp decreased. The increase in the value of ΔGele along this series correlates with the replacement of the functional groups from carbonyl to hydroxyl, suggesting that the latter is more polar. Indeed, calculations that were carried out with testosterone using only some of the partial charges (assigning the rest of the atoms with charges of zero) showed that the hydroxyl group contributes ∼5.6 kcal/mol to ΔGele, whereas the carbonyl group contributes ∼5.0 kcal/mol (data not shown). This may seem odd, in view of the magnitude of the partial charges that were assigned to these groups. The reason for this apparent discrepancy is the smaller atomic radius assigned to the hydroxyl's hydrogen atom in PARSE compared to that of the carbonyl's carbon.
Simplex search for favorable hormone-membrane configurations
The simplex algorithm was used to search for optimal hormone-membrane configurations. We conducted the search by manually selecting ∼30 initial orientations for each steroid hormone, as described in Methodology, above.
To verify whether simplex converged to the global minimum, we carried out an exhaustive search in configuration space of the estradiol-membrane system. Fig. 3 illustrates the solvation free-energy surface obtained for this hormone at h = −14 Å, which is the distance associated with the minimum found by simplex. The surface represents the solvation free energy as a function of the rotation angles ϕ and Ψ in increments of 10° in the ranges 0°–180° and 0°–360°, respectively, and includes a single, wide minimum.
Simplex search started from an initial orientation, associated with ΔGsol = −0.1 kcal/mol, and converged to the nearest local minimum of ΔGsol = −4.8 kcal/mol. A consecutive simplex search, starting from that local minimum, converged to the global minimum of ΔGsol = −5.0 kcal/mol, which was also found in the exhaustive search. The similarity between the ΔGsol minima that were produced by the simplex and exhaustive searches demonstrates the potency of the simplex search strategy for this optimization problem.
The simplex calculations involved starting from 30 different initial hormone-membrane configurations, each of which converged to a local minimum after ∼80 configurations. Overall, it involved continuum solvent model calculations for ∼30 × 80 = 2400 configurations. For comparison, the exhaustive search, using a 1 Å step in the interval [3 Å, 15 Å] along the membrane normal and 10° steps in the intervals [0°, 180°] and [0°, 360°] in the rotation angles (ϕ and ψ), involved continuum solvent model calculations for 13 × 18 × 36 = 8424 configurations.
Water/lipid-bilayer partitioning
The most favorable hormone-membrane configurations, obtained using the simplex search, and the total free-energy values associated with them (Eq. 2) are depicted in Fig. 2. The three hormones partitioned into the water-membrane interface, and were oriented with their principal axes approximately vertical to the membrane plane. The hydrophobic core of each hormone and the less polar of its two polar groups were buried inside the membrane, whereas the other polar group partially protruded into the water-membrane interface region. This orientation is comparable to that of cholesterol, which associates with the membrane with its hydrophobic core at the hydrocarbon lipid region and its hydroxyl group protruding into the interface (Kessel et al., 2001a; Fig. 5, this article).
Table 2 shows a free-energy decomposition of the values associated with the most stable hormone-membrane and cholesterol-membrane configurations. It is evident from the table that cholesterol is an outlier; its association with the membrane involved a favorable ΔGnp contribution, which was larger than that obtained for the hormones, and had essentially no ΔGele penalty. Thus, it is strongly linked to the membrane with an extremely negative ΔGtot value. The value ΔGtot of the hormones was mainly influenced by the ΔGnp term, which overcompensates for the penalties resulting from the ΔGele and ΔGimm free-energy terms. Although the hormones partition into the water-membrane interface, they differ in their partitioning tendencies.
TABLE 2.
Free energy of association with the lipid bilayer (Eq. 2)
| Molecule | ΔGnp* (kcal/mol) | ΔGele† (kcal/mol) | ΔGimm‡ (kcal/mol) | ΔGtot§ (kcal/mol) |
|---|---|---|---|---|
| Cholesterol | −15.9 | 0.3 | 1.3 | −14.3 |
| Progesterone | −11.8 | 5.5 | 1.3 | −5.0 |
| Testosterone | −11.0 | 5.1 | 1.3 | −4.6 |
| Estradiol | −10.5 | 5.5 | 1.3 | −3.7 |
The nonpolar free energy term.
The electrostatic free energy term.
The immobilization free energy.
The total free energy.
It is encouraging to note the calculated ΔGtot = −5.0 kcal/mol value obtained for progesterone was close to the value of −3.1 kcal/mol, which was derived from measurements of the partition of this hormone between an aqueous suspending medium and phospholipids in the smooth endoplasmic reticulum (Sato et al., 1979).
Rate of transfer from water to hexane
A hypothetical pathway for the transfer of progesterone between the aqueous and hexane phases is presented in Fig. 4 A. The pathway involves two free-energy barriers, each of which is associated with the electrostatic free-energy penalty due to the transfer of a carbonyl group from water to hexane. Qualitatively similar pathways were obtained for estradiol and testosterone, and the rates of transfer of the three hormones along this hypothetical pathway were calculated using Eq. 3. The force constants F1 and F2 were essentially the same in all the cases that were studied here; F1 ≈ F2 ≈ 0.5 kcal/(mol Å2). A diffusion constant of D = 107 Å2/s, corresponding to hormone diffusion in sol-gel glass, was used.
The calculated water-to-hexane transfer rates of the hormones, in comparison to the measured values, are shown in Table 3. The calculated rates (units of 1/s; Eq. 3) were converted into units of cm/s, corresponding to the measured values, by the use of the characteristic distance of 15 Å associated with the transfer of testosterone (and the other hormones) between hexane and water (Fig. 5). The calculated values are larger than the measured values by a factor of 2–3. Both calculations and measurements similarly rank the hormones according to the transfer rate: progesterone with the highest transfer rate, followed by testosterone and estradiol with the lowest transfer rate. It is noteworthy that the good agreement between the calculated and measured values is probably fortuitous (see Error Estimate, below).
TABLE 3.
The rate of transfer of the steroid hormones from water to hexane
| Molecule | ΔΔG1* (kcal/mol) | ΔΔG2† (kcal/mol) | Kcal‡ (cm/s) | Kexp§ (cm/s) |
|---|---|---|---|---|
| Progesterone | 2.3 | 3.1 | 8.9 × 10−4 | 5.5 × 10−4 |
| Testosterone | 3.7 | 3.0 | 3.2 × 10−4 | 0.96 × 10−4 |
| Estradiol | 3.0 | 5.3 | 0.28 × 10−4 | 0.14 × 10−4 |
The first free energy barrier (Fig. 4 A).
The second free energy barrier (Fig. 4 A).
The calculated rate of transfer of the hormones along a distance of 15 Å (Fig. 5).
Experimental transfer rate from buffer phosphate to hexane (Watanabe et al., 1991).
Rate of transfer from hexane to water
A hypothetical pathway for the hexane-to-water transfer of progesterone is presented in Fig. 4 B. The transition is characterized by a single, large, solvation free-energy barrier that is associated with the hydrophobically unfavorable transfer of the hydrophobic core of the hormone from the liquid hexane to the aqueous phase. Again, qualitatively similar pathways were obtained for estradiol and testosterone, and the rates of transfer of the three hormones along this hypothetical pathway were calculated using Eq. 3. A diffusion constant of D = 109 Å2/s, corresponding to hormone diffusion in nonpolar solvents, was used.
The calculated transfer rates of the hormones between the two phases are shown in Table 4, and are essentially the same. This was expected, since the transition is controlled by the free-energy barrier due to the hexane-to-water transfer of the hydrophobic core of the hormones, which is the same for the three hormones. However, there are still minor differences in the transfer rates. Progesterone, having the highest free-energy barrier (ΔΔG3 = 8.6 kcal/mol), transfers more slowly than testosterone and the latter has a lower transfer rate compared to estradiol, which has the lowest free-energy barrier (ΔΔG3 = 8.0 kcal/mol).
TABLE 4.
The hexane-to-water transfer rate of steroid hormones
| Molecule | ΔΔG* (kcal/mol) | Kcalc† (cm/s) | Kexp‡ (cm/s) |
|---|---|---|---|
| Progesterone | 8.6 | 0.12 × 10−4 | 0.02 × 10−4 |
| Testosterone | 8.3 | 0.19 × 10−4 | 1.5 × 10−4 |
| Estradiol | 8.0 | 0.32 × 10−4 | 7.4 × 10−4 |
The free energy barrier (Fig. 4 B).
Calculated transfer rate along a distance of 15 Å (Fig. 5).
Experimental transfer rate from hexane to buffer phosphate (Watanabe et al., 1991).
Table 4 also shows a comparison of the calculations to experimental results. The calculated transfer rate obtained for progesterone is approximately six times larger than the measured one, and in contrast, the calculated transfer rates obtained for testosterone and estradiol are ∼10–20-fold smaller than the measured values. The trends observed in the calculated and measured values are similar, but this may be fortuitous, since the differences are small compared to the computation error.
Translocation of cholesterol and testosterone across the lipid bilayer
The interaction of the steroid hormones with the membrane is fundamentally different to that of cholesterol. This is demonstrated by the difference in the solvation free-energy curves (Fig. 5 B) that were obtained for the transbilayer transfer of cholesterol and testosterone along the hypothetical pathway of Fig. 5 A. The most favorable cholesterol-membrane configuration was taken from our recent studies (Kessel et al., 2001a). An equivalent orientation of testosterone was obtained by superimposing it on cholesterol as described in Methodology, above. Using these orientations, we repeated the calculations for the membrane translocation of cholesterol and carried out similar calculations with testosterone to obtain the solvation free-energy curves of Fig. 5 B.
The translocation process (Fig. 5) begins at h = 30 Å, where cholesterol's hydrophobic tail is in contact with the bilayer and testosterone is fully embedded in the aqueous phase, with its hydroxyl group facing the membrane. Insertion of cholesterol's hydrophobic tail leads to a deep ΔGsol minimum of ∼−15 kcal/mol at h = 14 Å, mainly affected by a decrease in the ΔGnp component (Table 2). In this position, cholesterol's hydrophobic tail is within the membrane, whereas its hydroxyl group is in the water phase. When cholesterol is fully embedded in the bilayer (11 Å < h < 1 Å) a constant ΔGsol value is obtained. The main free-energy barrier for the transfer of cholesterol back into water (h = 14 Å) results from the nonpolar free-energy penalty, due to the transfer of cholesterol's hydrophobic core from the hydrocarbon region of the lipid bilayer into the aqueous phase.
Testosterone's free-energy profile is more complicated. It involves three free-energy barriers and two minima. The first barrier (h = 23 Å) results from an increase in ΔGele, due to the insertion of the hydroxyl group into the bilayer. The following minimum (h = 14 Å) is obtained when the hydrophobic core protrudes into the membrane, whereas the carbonyl group remains in water. Full insertion of testosterone leads to a second barrier, followed by a constant ΔGsol value (10 Å < h < −3 Å). The minimum solvation free energy (∼−5.9 kcal/mol) is achieved when both the carbonyl and the hydrophobic core are immersed in the bilayer, whereas the hydroxyl group protrudes into the water phase.
Transfer of steroid hormones across the membrane bilayer
Our suggested pathway for the transbilayer movement of steroid hormones is presented in Fig. 6; it is assumed that the hormones cross the membrane in their most favorable orientations (Fig. 2). The membrane translocation can be viewed (approximately) as a combination of two processes: a transfer from water to hexane (Fig. 4 A) followed by a transfer from hexane to water (Fig. 4 B). The entire process involves three free-energy barriers: the first two (ΔΔG1 and ΔΔG2) are essentially identical to the ones obtained for the transfer of the hormones from water-to-hexane, and the third (ΔΔG3) to the hexane-to-water transfer.
Comparison between the transfer rates of the two processes (Tables 3 and 4) reveals that the transfer of progesterone and testosterone from the hydrocarbon region of the membrane into the aqueous phase is the rate-limiting step for the free diffusion across the membrane, and that the height of the hydration free-energy barrier associated with it (ΔΔG3) determines the transfer rate (Fig. 6). In contrast, in the case of estradiol, both transfer rates are similar. Very similar ΔΔG3 values were obtained for each of the three hormones (Table 4), and therefore the rates of transfer of the three hormones across our model membrane are also similar (Table 5). The calculated rates are very similar to the values that were measured in Caco-2 cells (Faassen et al., 2003) but, as discussed in the following section, the agreement is probably fortuitous.
TABLE 5.
Transfer of steroid hormones across biomembranes
| Molecule | ΔGsol* (kcal/mol ) | Kcalc† (cm/s) | Kexp‡ (cm/s) |
|---|---|---|---|
| Progesterone | −3.2 | 2.4 × 10−5 | 2.4 × 10−5 |
| Testosterone | −0.9 | 3.7 × 10−5 | 2.5 × 10−5 |
| Estradiol | 0.3 | 3.0 × 10−5 | 1.7 × 10−5 |
The water-to-hexane transfer free energy of the hormones (Eq. 1).
The calculated transfer rate across a membrane of width of 30 Å.
Experimental transfer rates, measured across Caco-2 cells (Faassen et al., 2003).
Error estimate
We repeated the calculations of Fig. 2 and Table 2 using different grid sizes (1133, 1293, and 1453) and scales (3 and 4 grid points/Å). The calculations showed that the reported ΔGsol values are correct to within an error of ±0.2 kcal/mol. (In this context it is noteworthy that the free energy of water-to-hexane transfer of the hormones, which were used to derive the atomic partial charges of the unique hydroxyl and carbonyl groups of the hormones, were reproduced within an accuracy of ±0.3 kcal/mol; see Table 1.) Such an error may result in a maximum of an ∼twofold difference in the magnitude of the transfer rate.
The high precision of the calculations is due to the simplified model that we used; the neglect of the polar headgroups region of the bilayer and any specific interactions that the hormones may have with the bilayer in our model may result in an error of ∼1 kcal/mol in the value of ΔGtot, as discussed below.
The calculated rate of hormone transfer across the membrane depends on ΔΔG rather than on ΔG (i.e., on differences in the free energy of transfer of the hormones from the aqueous phase into different configurations in the bilayer; Eq. 3), and many of the effects that are missing in our model are likely to be cancelled out. Such effects are also likely to be cancelled out when comparing the interactions of different hormones (or cholesterol) with the lipid bilayer.
Another source of error in the calculated transfer rate is our estimate of the diffusion coefficient, D. The diffusion coefficient in bulk water was approximated by the measured values of hormone's diffusion coefficient in porous sol-gel glass (D ≈ 107 Å2/s; Sieminska et al., 1997). However, the mobility of the hormones in this medium is probably different to that observed for bulk water, which may lead to an order-of-magnitude change in the value of D, which corresponds to a factor of ∼3 in the value of k (Eq. 3). Taking all these uncertainties together, we estimate that the calculated value of k should be accurate to within approximately one or two orders of magnitude.
DISCUSSION
A combination of continuum-solvent model calculations and simplex optimization was used here to study thermodynamic and kinetic aspects of the interaction of cholesterol and steroid hormones with lipid bilayers. The potency of this novel methodology for the study was demonstrated in Fig. 3 B, where the simplex search resulted in a hormone-membrane configuration that is very close to the absolute minimum, both space- and energy-wise. In the following, we discuss the limitations of the theoretical model, and the implications of the results.
The principal limitation of this study is the lack of proteins, both inside and outside the membrane. In particular, we omitted the interactions between the hormones and carrier proteins such as albumin and globulin in the serum. In general, the effective rate of hormone internalization reflects its rate of dissociation from the extracellular carrier, its free diffusion across the lipid bilayer, and its rate of association with an intracellular carrier. Of these three processes, only one—the free diffusion across the membrane—is accounted for (in an approximated way) in our model. However, studies of the transport of testosterone and estradiol across the blood-brain barrier showed that their transfer rate was not influenced by binding to albumin, the main hormones' carrier in the serum (Pardridge and Mietus, 1980). Similarly, the transfer rate of testosterone and estradiol from hexane to water was similar to that from hexane to bovine serum, where the hormones associate with the carrier proteins (Watanabe et al., 1991).
Steroid hormones use free diffusion to enter target cells. However, certain tissues contain the energy-dependent drug-efflux pump P-gp as a protective barrier that transports substrates against their concentration gradient (Uhr et al., 2002). P-gp is expressed in organs that are involved in detoxification processes; intestinal and colon epithelium, blood-brain and blood-testis barriers, pancreas, liver, kidney, adrenal gland, ovaries, and placenta (Fromm, 2002; Uhr et al., 2002; Young et al., 2003). In these cases, our model, which does not take into account the P-gp TM pump, can only be used to calculate (approximately) the rate of hormone transfer into the cell.
The P-gp pump is not expressed in erythrocytes and the stratum corneum, i.e., the outer layer of the skin (Alberts et al., 2002; Bouwstra and Honeywell-Nguyen, 2002). Thus, in these tissues, steroid hormones use free diffusion as their major route of transfer (Koefoed and Brahm, 1994; Sitruk-Ware, 1995). For example, experiments of the permeability of human red cell membranes to steroid sex hormones show a fast transition of the hormones through the lipid phase of the membrane (Koefoed and Brahm, 1994). In addition, transdermal application of steroid hormones, used for hormone replacement therapy at menopause, depends on the diffusion of these lipophilic substrates across the stratum corneum (Sitruk-Ware, 1995). The free diffusion process approximated by our model can be used to describe the transfer of steroid hormones across these tissues.
A second major limitation of the model is the structureless representation of the lipid bilayer as a slab of a hexane-like phase, which is embedded in (implicit) water. The obscure representation of the membrane omits any effect that cholesterol and the hormones may have on the structures of the lipid chains. It also neglects any specific interactions between these molecules and the lipids, as well as membrane defects (Wilson and Pohorille, 1996). Moreover, the polar headgroup region of the bilayer is completely omitted in the slab model, which is based on a stepwise transition in the polarity profile of the membrane. The dielectric constant of the headgroup region is estimated to be between 25 and 40 (Ashcroft et al., 1981). (Note that this is a much higher estimate of ∼200 that was obtained based on molecular-dynamics simulations of DPPC membranes; see Stern, 2003.) Thus, the headgroup region can best be regarded as part of the aqueous phase in the model.
A third limitation is the neglect of effects due to changes in the conformations of cholesterol and the hormones upon interaction with the membrane. This assumption is probably reasonable due to the rigidity of the four-ringed backbone of these molecules. Changes in the conformation of cholesterol's hydrophobic tail are likely to have very little effect, since they are unlikely to change the solvation free energy. Importantly, interactions between the hormone molecules and the formation of oligomers were not considered in the model. Thus, the results should be compared to experiments that were carried out in low concentrations of cholesterol and hormones. In this context, it is noteworthy that NMR studies of bile acids (cholesterol's derivatives, chemically similar to steroid hormones) showed that they flip across the bilayer in their monomeric form (Carbal et al., 1987).
Continuum solvent models have been used to investigate various types of problems (Gilson, 1995; Honig and Nicholls, 1995; Nakamura, 1996; Warshel and Papazyan, 1998), including the calculation of binding energy (Froloff et al., 1997), calculation of pKa shifts (Georgescu et al., 2002), the refining of predicted loop structures (Petrey and Honig, 2004), and the analysis of the effects of mutations (e.g., Dong et al., 2003). Overall, these studies have demonstrated the sensitivity of the calculations to the parameters used: that is, the value of the internal dielectric constant, the partial atomic charges and radii, and the definition of the boundary between the interior and exterior regions (e.g., van der Waals versus molecular surface).
The study presented here involved calculations of desolvation free energy, and we used a well-established protocol and the PARSE parameter set (Sitkoff et al., 1994; 1996) to this effect. PARSE has been derived to reproduce the partitioning of solutes between water and a low-dielectric environment. In our previous studies of the association of various peptides and small molecules, calculations based on PARSE have yielded values that were in very good agreement with experimental data (reviewed in Kessel and Ben-Tal, 2002). This is presumably the reason why, despite the crudeness of the model that was used here, many of the results agree well with the experimental data. This serves as further support for our working hypothesis; namely that the main component of the free energy of transfer of the hormones (and other molecules) across lipid bilayers comes from desolvation effects, which were accurately taken into account in the calculations (Table 1). Since desolvation is the main free-energy determinant in the interaction of cholesterol and the hormones with the lipid bilayer, it is safe to assume that the effects that are missing in the model may add up to an error of ∼20–30% of the value of ΔGtot, i.e., ∼1 kcal/mol.
Our previous investigations showed that the model reproduced the most favorable location and orientation of cholesterol in the lipid bilayer (Kessel et al., 2001a). The current study demonstrated that the same is true for the steroid hormones; the most favorable location of estradiol at the membrane-water interface (Fig. 2) is in good agreement with the location that was estimated by Golden et al. (1998), based on x-ray diffraction studies of model 1-palmitoyl-2-oleoyl-sn-glycerol-3-phosphocholine (POPC) membranes with a trace amount of cholesterol. Golden and co-workers also measured a buffer-membrane partition coefficient of 2900, corresponding to transfer free energy of −4.7 kcal/mol. This value is comparable to the calculated value of ΔGtot = −3.7 kcal/mol (Table 2; Fig. 2).
Our studies suggest a free-energy-based explanation of the different manner in which cholesterol and steroid hormones interact with biomembranes: the free energy of membrane association of cholesterol is three-to-fourfold larger in magnitude than that of the hormones (Fig. 5 B; Table 2). The deep solvation free-energy minimum of ΔGsol = −15 kcal/mol, which was obtained for cholesterol, explains why cholesterol is, in essence, constitutively bound to the membrane. In contrast, the relatively shallow solvation free-energy minimum of −5.0 < ΔGsol < −3.7 kcal/mol obtained for the steroid hormones in their most favorable locations in the membrane, enables them to diffuse freely across the bilayer within biologically reasonable times.
Overall, the calculated rates of transfer of the hormones from water to the hexane phase (Table 3) and back (Table 4) are within a factor of ∼10 of the experimental data of Watanabe et al. (1991). In fact, the agreement is better than that which one would expect from such a crude model (see Error Estimate, above).
The calculated free-energy barriers from hexane to water (Table 4) are relatively large, since they were determined between two extreme configurations without the consideration of any changes in hormone orientation upon transfer to bulk water. Therefore, the calculated rates of transfer of the hormones from hexane to water are expected to be lower than the measured ones. Testosterone and estradiol follow this rule (Table 4), but progesterone is an exception. However, in view of the chemical similarity between the three hormones, the ∼20-fold difference in the measured transfer rate of progesterone versus those that were measured for testosterone and estradiol, suggests that the former value may be erroneous.
Surprisingly, despite the ∼10-fold difference between the calculated and measured transfer rates of the hormones from water to hexane and back, the calculated rate of transfer of the hormones across the model lipid bilayer is essentially the same as the measured rates obtained in experiments using Caco-2 cells (Faassen et al., 2003). Given the crudeness of the model, the agreement is presumably due to a fortuitous cancellation of errors.
The free energy of transfer of a molecule between water and nonpolar solvents, such as octanol, often correlates with the rate of transfer of the molecule across biological membranes (Bodor and Buchwald, 1999; Norinder and Haeberlein, 2002); lipophilic molecules usually cross membrane barriers faster than polar molecules. In fact, this correlation is often used in the pharmaceutical industry to predict the membrane permeability of drug molecules (Bodor and Buchwald, 1999; Norinder and Haeberlein, 2002). Our study shows a few exceptions to this rule. Cholesterol, which is far more lipophilic than the hormones (Table 2), associates tightly with the bilayer and does not cross it at all. Moreover, despite significant differences in the polarity of the hormones, as reflected in the differences in the values of the transfer free energy, the calculated rates of transfer of the three hormones across the membrane are essentially the same (Table 5).
This is mainly due to the fact that the rate of transfer of the hormones across the membrane is determined by the height of the free-energy barrier associated with the transfer from the hydrocarbon region of the membrane into the aqueous phase (Fig. 6; ΔΔG3). The magnitude of this value is essentially the same for all the three hormones, since they share a very similar structure: a four-ring backbone, which is hydrophobic, with a polar group at each end. Cholesterol is unique in that it has a polar group attached to one end and a hydrophobic tail attached to the other. Thus, when considering the transfer rate, the spatial hydrophilic/hydrophobic relationship seems to be more important than the actual identity of the groups at the tips of the hormone. This is in contrast to binding to a receptor, where the chemical nature of these groups is important.
Overall, both the calculated and experimental transfer rates show that the free diffusion of steroid hormones across biomembranes is rapid; K ≈ 3 × 10−5 cm/s, which corresponds to an average diffusion time of ∼0.01 s over a membrane barrier of 30 Å width. This is important when considering the fact that steroid hormones cross a number of barriers on their way to various target tissues. For example, orally administered steroid hormones must translocate across the intestinal epithelial cells before reaching the blood stream. Indeed, these hormones are known to have high gastrointestinal absorption, facilitated by free diffusion across the intestinal epithelial cells (Harman and Limbird, 1996; Faassen et al., 2003). Similarly, steroid hormones diffuse freely across the blood-brain barrier to regulate brain function, e.g., behavioral effects, human sexuality, aggression, cognition, and emotion (Runinow and Schmidt, 1996).
In conclusion, a novel combination of the continuum-solvent model and the simplex search method was used here to analyze the different tendencies of cholesterol and steroid hormones with respect to the lipid bilayer. A clear structure-function relationship was observed: the difference in the chemical groups between cholesterol and steroid hormones influences their ability to cross biomembranes. In addition, the different polar groups among the hormones influence their affinity to lipid bilayers and subsequently their transfer rates across the cell membrane.
Acknowledgments
We are grateful to the Bioinformatics Service Unit of the George S. Wise Faculty of Life Sciences at Tel Aviv University for providing computation facilities.
This work was supported by the Magnet “Pharmalogica” Consortium of the Israel Ministry of Trade and Industry.
References
- Alberts, B., A. Johnson, J. Lewis, M. Raff, K. Roberts, and P. Walter. 2002. Molecular Biology of the Cell. Garland Science, New York.
- Ashcroft, R. G., H. G. Coster, and J. R. Smith. 1981. The molecular organisation of bimolecular lipid membranes. The dielectric structure of the hydrophilic/ hydrophobic interface. Biochim. Biophys. Acta. 643:191–204. [DOI] [PubMed] [Google Scholar]
- Bouwstra, J. A., and P. L. Honeywell-Nguyen. 2002. Skin structure and mode of action of vesicles. Adv. Drug Deliv. Rev. 54:S41–S55. [DOI] [PubMed] [Google Scholar]
- Beato, M., and J. Klug. 2000. Steroid hormone receptors: an update. Hum. Reprod. Update. 6:225–236. [DOI] [PubMed] [Google Scholar]
- Ben-Tal, N., B. Honig, C. K. Bagdassarian, and A. Ben-Shaul. 2000. Association entropy in adsorption processes. Biophys. J. 79:1180–1187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bodor, N., and P. Buchwald. 1999. Recent advances in the brain targeting of neuropharmaceuticals by chemical delivery systems. Adv. Drug Deliv. Rev. 36:229–254. [DOI] [PubMed] [Google Scholar]
- Brann, D. W., L. B. Hendry, and V. B. Mahesh. 1995. Emerging diversities in the mechanism of action of steroid hormones. J. Steroid Biochem. Mol. Biol. 52:113–133. [DOI] [PubMed] [Google Scholar]
- Carbal, D. J., D. M. Small, and J. A. Hamilton. 1987. Transbilayer movement of bile acids in model membranes. Biochemistry. 26:1801–1804. [DOI] [PubMed] [Google Scholar]
- Chen, H. C., and R. V. Farese. 1999. Steroid hormones: interactions with membrane-bound receptors. Curr. Biol. 9:R478–R481. [DOI] [PubMed] [Google Scholar]
- Dong, F., M. Vijayakumar, and H.-X. Zhou. 2003. Comparison of calculation and experiment implicates significant electrostatic contributions to the binding stability of barnase and barstar. Biophys. J. 85:49–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Essmann, U., and M. L. Berkowitz. 1999. Dynamical properties of phospholipid bilayers from computer simulations. Biophys. J. 76:2081–2089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faassen, F., J. Kelder, J. Lenders, R. Onderwater, and V. Herman. 2003. Physicochemical properties and transport across Caco-2 cells. Pharm. Res. 20:177–185. [DOI] [PubMed] [Google Scholar]
- Falkenstein, E., H. C. Tillmann, M. Christ, M. Feuring, and M. Wehling. 2000. Multiple actions of steroid hormones—a focus on rapid, nongenomic effects. Pharmacol. Rev. 52:513–556. [PubMed] [Google Scholar]
- Fromm, M. F. 2002. The influence of MDR1 polymorphisms on P-glycoprotein expression and function in humans. Adv. Drug Deliv. Rev. 54:1295–1310. [DOI] [PubMed] [Google Scholar]
- Froloff, N., A. Windermuth, and B. Honig. 1997. On the calculation of binding free energies using continuum methods: application to MHC class I protein–peptide interactions. Protein Sci. 6:1293–1301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabdouline, R. R., G. Vanderkooi, and C. Zheng. 1996. Comparisons of structures of dimyristoylphosphatidylcholine in the presence and absence of cholesterol by molecular dynamics simulations. J. Phys. Chem. 96:15942–15946. [Google Scholar]
- Georgescu, R. E., E. G. Alexov, and M. R. Gunner. 2002. Combining conformational flexibility and continuum electrostatics for calculating pKas in proteins. Biophys. J. 83:1731–1748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilson, M. K. 1995. Theory of electrostatic interactions in macromolecules. Curr. Opin. Struct. Biol. 5:216–223. [DOI] [PubMed] [Google Scholar]
- Golden, G. A., R. T. Rubin, and R. P. Mason. 1998. Steroid hormones partition to distinct sites in a model membrane bilayer: direct demonstration by small-angle x-ray diffraction. Biochim. Biophys. Acta. 1368:161–166. [DOI] [PubMed] [Google Scholar]
- Goldstein, J. S., and C. K. Sites. 2002. Selective modulation of sex steroids. Ageing Res. Rev. 1:17–28. [DOI] [PubMed] [Google Scholar]
- Guiochon-Mantel, A., K. Delabre, P. Lescop, and E. Milgrom. 1996. The Ernst Schering Poster Award. Intracellular traffic of steroid hormone receptors. J. Steroid Biochem. Mol. Biol. 56:3–9. [DOI] [PubMed] [Google Scholar]
- Harman, J. G., and L. E. Limbird. 1996. Goodman & Gilman's The Pharmacological Basis of Therapeutics. McGraw Hill, New York.
- Honig, B., and A. Nicholls. 1995. Classical electrostatics in biology and chemistry. Science. 268:1144–1149. [DOI] [PubMed] [Google Scholar]
- Honig, B., K. Sharp, and A. S. Yang. 1993. Macroscopic models of aqueous solutions: biological and chemical applications. J. Phys. Chem. 97:1101–1109. [Google Scholar]
- Kawata, M. 1995. Roles of steroid hormones and their receptors in structural organization in the nervous system. Neurosci. Res. 24:1–46. [DOI] [PubMed] [Google Scholar]
- Kessel, A., and N. Ben-Tal. 2002. Free energy determinants of peptide association with lipid bilayers. In Current Topics in Membranes: Peptide-Lipid Interactions. S. A. Simon and T. J. Mcintosh, editors. Academic Press, San Diego, CA.
- Kessel, A., N. Ben-Tal, and S. May. 2001a. Interactions of cholesterol with lipid bilayers: the preferred configuration and fluctuations. Biophys. J. 81:643–658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kessel, A., B. Musafia, and N. Ben-Tal. 2001b. Continuum solvent model studies of the interactions of an anticonvulsant drug with a lipid bilayer. Biophys. J. 80:2536–2545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koefoed, P., and J. Brahm. 1994. The permeability of the human red cell membrane to steroid sex hormones. Biochim. Biophys. Acta. 1195:55–62. [DOI] [PubMed] [Google Scholar]
- Lundberg, B. 1979. The solubilization of some steroids by phosphatidylcholine and phosphatidylcholine-cholesterol vesicles. Chem. Phys. Lipids. 24:257–263. [DOI] [PubMed] [Google Scholar]
- Nakamura, H. 1996. Roles of electrostatic interactions in proteins. Q. Rev. Biophys. 29:1–90. [DOI] [PubMed] [Google Scholar]
- Nelder, J. A., and R. Mead. 1965. A simplex method for function minimization. Comp. J. 7:308–313. [Google Scholar]
- Norinder, U., and M. Haeberlein. 2002. Computational approaches to the prediction of the blood-brain distribution. Adv. Drug Deliv. Rev. 54:291–313. [DOI] [PubMed] [Google Scholar]
- Pardridge, W. M., and L. J. Mietus. 1980. Transport of thyroid and steroid hormones through the blood-brain barrier of newborn rabbit: primary role of protein-bound hormone. Endocrinology. 107:1705–1710. [DOI] [PubMed] [Google Scholar]
- Petrey, D., and B. Honig. 2004. Comparing protein models to native structures: implications for protein model refinement. Biophys. J. 86:87a (Abstr.) [Google Scholar]
- Pfeiffer, W., T. H. Henkel, E. Sackmann, W. Knoll, and D. Richter. 1989. Local dynamics of lipid bilayers studied by incoherent quasi-elastic neutron scattering. Europhys. Lett. 8:201–206. [Google Scholar]
- Robinson, A. J., W. G. Richards, P. J. Thomas, and M. M. Hann. 1995. Behavior of cholesterol and its effect on headgroup and chain conformations in lipid bilayers: a molecular dynamics study. Biophys. J. 68:167–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Runinow, D. R., and P. J. Schmidt. 1996. Androgens, brain and behavior. Am. J. Psychiatry. 153:974–984. [DOI] [PubMed] [Google Scholar]
- Sato, B., R. A. Huseby, K. Matsumoto, and L. T. Samuels. 1979. Molecular nature of interaction of steroids with biomembranes related to androgen biosynthesis. J. Steroid Biochem. 11:1353–1359. [DOI] [PubMed] [Google Scholar]
- Schulten, K., Z. Schulten, and A. Szabo. 1981. Dynamics of reactions involving diffusive barrier crossing. J. Chem. Phys. 74:4426–4432. [Google Scholar]
- Sharp, K. A., A. Nicholls, R. F. Fine, and B. Honig. 1991. Reconciling the magnitude of the microscopic and macroscopic hydrophobic effects. Science. 252:106–109. [DOI] [PubMed] [Google Scholar]
- Sieminska, L., M. Ferguson, T. W. Zerda, and E. Couch. 1997. Diffusion of steroids in porous sol-gel glass: application in slow drug delivery. J. Sol-Gel Sci. Technol. 8:1105–1109. [Google Scholar]
- Sitkoff, D., N. Ben-Tal, and B. Honig. 1996. Calculation of alkane to water solvation free energies using continuum solvent models. J. Phys. Chem. 100:2744–2752. [Google Scholar]
- Sitkoff, D., K. Sharp, and B. Honig. 1994. Accurate calculations of hydration free energies using macroscopic solvent models. J. Phys. Chem. 98:1978–1988. [Google Scholar]
- Sitruk-Ware, R. 1995. Transdermal application of steroid hormones for contraception. J. Steroid Biochim. Mol. Biol. 53:247–251. [DOI] [PubMed] [Google Scholar]
- Smondyrev, A. M., and M. L. Berkowitz. 1999. Structure of dipalmitoylphosphatidylcholine/cholesterol bilayer at low and high cholesterol concentrations: molecular dynamics simulations. Biophys. J. 77:2075–2089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sridharan, S. A., A. Nicholls, and B. Honig. 1992. A new vertex algorithm to calculate solvent accessible surface area. Biophys. J. 61:A174. [Google Scholar]
- Stern, H. A. 2003. Calculations of the dielectric permittivity profile for a nonuniform system: application to a lipid bilayer simulation. J. Chem. Phys. 118:3401–3412. [Google Scholar]
- Tu, K., M. L. Klein, and D. J. Tobias. 1998. Constant-pressure molecular dynamics investigation of cholesterol effects in a dipalmitoylphosphatidylcholine bilayer. Biophys. J. 75:2147–2156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uhr, M., F. Holsboer, and M. B. Muller. 2002. Penetration of endogenous steroid hormones corticosterone, cortisol, aldosterone and progesterone into the brain is enhanced in mice deficient for both mdr1a and mdr1b P-glycoproteins. J. Neuroendocrinol. 14:753–759. [DOI] [PubMed] [Google Scholar]
- Warshel, A., and A. Papazyan. 1998. Electrostatic effects in macromolecules: fundamental concepts and practical modeling. Curr. Opin. Struct. Biol. 8:211–217. [DOI] [PubMed] [Google Scholar]
- Watanabe, S., T. Tani, and M. Seno. 1991. Transport of steroid hormones facilitated by serum proteins. Biochim. Biophys. Acta. 1073:275–284. [DOI] [PubMed] [Google Scholar]
- Wilson, M. A., and A. Pohorille. 1996. Mechanism of unassisted ion transport across membrane bilayers. J. Am. Chem. Soc. 118:6580–6587. [DOI] [PubMed] [Google Scholar]
- Yeagle, P. L. 1985. cholesterol and the cell membrane. Biochim. Biophys. Acta. 822:267–287. [DOI] [PubMed] [Google Scholar]
- Young, A. M., C. E. Allen, and A. L. Audus. 2003. Efflux transporters of the human placenta. Adv. Drug Deliv. Rev. 55:125–132. [DOI] [PubMed] [Google Scholar]