Exploring the Counterion Atmosphere around DNA: What Can Be Learned from Molecular Dynamics Simulations?

Abstract

The counterion distribution around a DNA dodecamer (5′-CGCGAATTCGCG-3′) is analyzed using both standard and novel techniques based on state of the art molecular dynamics simulations. Specifically, we have explored the population of Na⁺ in the minor groove of DNA duplex, and whether or not a string of Na⁺ can replace the spine of hydration in the narrow AATT minor groove. The results suggest that the insertion of Na⁺ in the minor groove is a very rare event, but that when once the ion finds specific sites deep inside the groove it can reside there for very long periods of time. According to our simulation the presence of Na⁺ inside the groove does not have a dramatic influence in the structure or dynamics of the duplex DNA. The ability of current MD simulations to obtain equilibrated pictures of the counterion atmosphere around DNA is critically discussed.

INTRODUCTION

DNA is a highly charged polyanion whose structure, flexibility, and biological function is heavily influenced by the large cloud of negative potential generated around the double helix by the charged phosphate groups. Such a large charge concentration generates strong intramolecular repulsions that are reduced by the screening effect of the polar solvent (typically water and counterions) surrounding nucleic acids under biological conditions. Thus, little of the structure, dynamic, and biological properties of nucleic can be understood without considering the ionic atmosphere surrounding the structure (Jayaram and Beveridge, 1996; Manning, 1978, 1979; Subirana and Soler-Lopez, 2003; Williams and Maher, 2000; Ennifar et al., 2003).

The stabilizing counterion environment of DNA can be generated by proteins, for example histones, by small bioorganic molecules like spermine, or by inorganic monovalent and divalent cations. In opposition with other nucleic acids, where the presence of “structural” ions is well established (see discussion in Orozco et al., 2003; Reblova et al., 2003a,b; Auffinger et al., 2003), the traditional picture portrays naked DNA as a macromolecule that under physiological conditions is surrounded by a cloud of small cations concentrated around the phosphates of the DNA, compensating most of their negative charges (Jayaram and Beveridge, 1996; Manning, 1978, 1979; Subirana and Soler-Lopez, 2003; Williams and Maher, 2000).

The view of counterions as small particles in fast and free movement around DNA agreed with most early x-ray data, which in general did not show small ions in fixed positions around nucleic acids (Drew et al., 1981). This picture of the counterion atmosphere around DNA was challenged in the late 1990s by Beveridge and co-workers (Jayaram and Beveridge, 1996; Young et al., 1997) who performed four short (1.5 ns) Ewald-based isothermal-isobaric (NPT) molecular dynamics (MD) simulations of a (d(CGCGAATTCGCG) (Drew et al., 1981) duplex in water, each begun with a minimum amount of Na⁺ placed in different starting positions around the duplex. The analysis of the four simulations showed that at least one Na⁺ ion could be partially incorporated into the spine of hydration in the minor groove of the central AATT step, providing a nice explanation of the unusual properties of the minor groove in A-tracks. Clearly, Beveridge's results did not demonstrate that one Na⁺ is permanently inserted in the minor groove, but suggested that a nonnegligible amount of Na⁺ could compete dynamically with water for residence in the minor groove.

Beveridge's suggestions fueled new and more accurate experimental work in this area. Thus, since his 1996–1997 articles, the placement of small monovalent ions (Na⁺, K⁺, Rb⁺, Cs⁺, Tl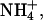⁺, …) around DNA has been studied by a large variety of techniques, including fiber and atomic resolution x-ray diffraction, quantitative electrophoresis data, and different types of NMR experiments (for recent reviews see Egli, 2002; Hud and Polak, 2001; McFail-Isom et al., 1999; Subirana and Soler-Lopez, 2003; Tereshko et al., 2001; Williams and Maher, 2000). However, the picture derived from this massive amount of experimental work, especially with reference to Na⁺, remains unclear. Early x-ray diffraction data by Drew and Dickerson (Drew et al., 1981) showed the existence of a highly structured spine of water in the central minor groove (AATT) of the B-type d(CGCGAATTCGCG) dodecamer, but no sign of the existence of Na⁺ inserted in this water spine. In more recent works, William's group using atomic resolution x-ray data for the same duplex suggested that some of the positions in the spine could be partially occupied by Na⁺ counterions (McFail-Isom et al., 1999; Shui et al., 1998a; Williams and Maher, 2000), leading to a narrowing of the minor groove in the AATT segment. Additional work by the same group suggested that K⁺ and even small quantities of Tl⁺ could also be inserted in the central AATT spine of hydration (Howerton et al., 2001; McFail-Isom et al., 1999; Shui et al., 1998b; Williams and Maher, 2000) Egli and co-workers, using single wavelength anomalous diffraction x-ray experiments (Egli, 2002; Tereshko et al., 1999, 2001) also concluded that monovalent cations (such as Rb⁺) could be bound in the minor groove of the d(CGCGAATTCGCG) duplex. However, other high-resolution x-ray experiments did not support the existence of cations in the minor groove of B-DNA. For example, Dickerson's group revisited the dodecamer d(CGCGAATTCGCG) at high resolution finding no evidence of Na⁺ in the minor groove (Chiu et al., 1999). In another recent study (Soler-Lopez et al., 1999) Subirana and co-workers solved at a very high resolution (0.89 Å) the structure of the 9-mer duplex d(GCGAATTCG) crystallized in the presence of Arg⁺, Na⁺, and Mg²⁺, and none of these ions were found in the central AATT minor groove.

Overall, what is clear from the controversy between crystallographers is the intrinsic shortcoming of this technique as a tool to distinguish between small cations like Na⁺ and water even when very high (better than 1.1 Å) resolution data is available (Egli, 2002; Subirana and Soler-Lopez, 2003; Tereshko et al., 2001; Ennifar et al., 2003). Although more reliable information can be obtained by using other heavier cations like Rb⁺, Cs⁺, or Tl⁺, it is not clear that those ions will be placed in the same positions as the more biologically relevant Na⁺ (Denisov and Halle, 2000; Howerton et al., 2001). Furthermore, we cannot ignore the fact that the search for very high-resolution data is leading to the use of very drastic experimental conditions that might lead to artifactual structures (Subirana and Soler-Lopez, 2003).

Other experimental techniques have been used to investigate the presence of small cations like Na⁺ in the minor groove of A-tracks in B-DNA. Quantitative electrophoresis experiments (Stellwagen et al., 2001) have suggested preferential interaction of Na⁺ with A-tracks, particularly those containing the A_nT_n motif. Fiber diffraction experiments (Chandrasekaran et al., 1995) have been used to argue against the presence of Na⁺ in the minor groove of a poly(dA)·poly(dT) duplex. On the other hand, recent data collected using ultrafast time-resolved stokes-shift spectroscopy suggest strong binding of Na⁺ to DNA, even in sequences without A-tracks (Gearheart et al., 2003). Finally, NMR spectroscopy has been also used to analyze cation-DNA interactions. Feigon's group has demonstrated partial occupancy of the minor groove of an A-track B-DNA minor groove by 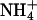(Hud et al., 1999). Recently, Denisov and Halle using ²³Na magnetic relaxation dispersion experiments concluded that the proportion of Na⁺ in the minor groove of A-track B-DNA is very small (∼5%), and the same is true for K⁺, Rb⁺, and Cs⁺, the population of 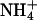being slightly larger (Denisov and Halle, 2000). Overall, Denisov and Halle concluded that the presence of Na⁺ in the minor groove of B-DNA does not have any impact in the structure of the duplex (Denisov and Halle, 2000).

The ionic distribution around DNA has also been examined in theoretical studies. Early Monte Carlo (Beveridge et al., 1991; Jayaram and Beveridge, 1996; Jayaram et al., 1990; Mills et al., 1992) and molecular dynamics simulations (Chuprina et al., 1991; Jayaram and Beveridge, 1996; Laughton et al., 1995; Miaskiewicz et al., 1993; Swaminathan et al., 1991) provided a general picture of the water and counterion environment of DNA, but the limited accuracy and sampling of the methods available at that time limited the reliability of the results obtained. The situation changed in the mid-nineties when new force fields, and accurate methods to deal with highly charged systems, were implemented in molecular dynamics algorithms. Since then theoretical methods, particularly MD algorithms, have become very powerful tools to study nucleic acid structures (for recent reviews see Auffinger and Westhof, 1998; Beveridge and McConnell, 2000; Cheatham and Kollman, 2000; Cheatham and Young, 2000; Orozco et al., 2003, 2004), making the analysis of fine details such as the dynamics of Na⁺ around the double helix a reasonable undertaking.

As described above, Beveridge's group (Jayaram and Beveridge, 1996; Young et al., 1997) was the first to analyze in detail the Na⁺ environment around DNA using state of the art MD simulations. Since then, a large number of improved simulations of the counterion environment around B-DNA have been published. Thus, Feig and Pettitt (1999) performed 10-ns trajectories of Dickerson's dodecamer in the presence of 0.8 M extra NaCl. Ions were placed randomly at the beginning of the simulation, and AMBER-94 force field was used (Cornell et al., 1995). They found Na⁺ with residence times up to 2 ns near (closer than 5.5 Å) to the DNA, and observed sodium cations in the minor groove (AATT segment) with occupancies ∼20% and residence times in the range 20–200 ps. Recently, Beveridge's group (McConnell and Beveridge, 2000) has reinvestigated the counterion atmosphere around Dickerson's dodecamer, finding >15-ns trajectories only a small population (5–10%) of Na⁺ within the minor groove, and no correlation between the width of the groove and the presence of Na⁺ within it. Stefl and Koca (2000) simulated a d(AT)₅ duplex starting from A and B conformations, finding convergence of the DNA to the B form in just 0.5 ns, but a much slower transition for the counterion atmosphere. For the B trajectory (5 ns) Na⁺ were found within the minor groove with residence times ∼1–2 ns. Korolev et al. (2002) simulated a DNA fiber created from the duplex d(ATGCAGTCAG)·d(TGACTGCATC) finding (in 6-ns trajectories) that the phosphates were the regions with greatest Na⁺ density, but that some counterions were located in the minor groove (ratio water/sodium 50:1), with residence times in the range 10–100 ps. Wilson and co-workers (Hamelberg et al., 2000) published a 10-ns trajectory of Dickerson's dodecamer in water. No explanation on the procedure used to place ions at the beginning was provided, but they reported that during the equilibration period one Na⁺ entered the minor groove and stayed there for 6 ns, i.e., 60% of the trajectory. It was reported that insertion of the Na⁺ into the AATT part of the minor groove led to its narrowing. Similar simulations performed by the same group (Hamelberg et al., 2001) for the duplex d(TATAGGCCTATA) showed a much lower population of Na⁺ in the wider minor groove for the central sequence GGCC, supporting the relationship between groove width and ion population in the groove. Very recently, Mocci and Saba (2003) published 8-ns trajectories of three oligonucleotides: d(C(AT)₄G), d(CA₄T₄G), and d(CT₄A₄G), supporting the presence of Na⁺ inside the minor groove only for A-tracks. The ions were placed initially in the regions of more electronegative potential, and after the equilibration period residence times up to 3 ns were found for Na⁺ located in the minor groove of the first two oligonucleotides only. Unfortunately, the Mocci and Saba results are not supported by other recent MD simulation by Lankas et al. (2002), which did not found clear evidence of Na⁺ intrusion in the groove along 17-ns trajectories of polypurine and alternating tracks.

Clearly, MD has been the leading theoretical technique for the analysis of the counterion environment around duplex DNA. The general picture is of a wide and diffuse Na⁺ distribution, the cation being able to enter into the minor groove and stay there for some period of time. However, even with current MD simulations many issues remain unclear. For example, the residence times of Na⁺ within the groove are in a very wide range: 10–6000 ps (see above), but accurate ²⁵Na NMR data suggests that Na⁺ insertion into the groove is a rare event compared with the entry of water (1:1000), but that once the Na⁺ reaches the minor groove it may have a residence time of up to 50 ns, compared with 1 ns for waters in the same position (Denisov and Halle, 2000). Another issue that remains contentious is the structural impact of the presence of Na⁺ in the minor groove. Some authors suggest a direct relationship between groove narrowing and the Na⁺ population of the groove, whereas others deny this. More generally, it is unclear from current MD simulations what the conformational changes are related to the interchange Na⁺/H₂O in the minor groove of A-rich DNA duplexes.

In this article we reinvestigate Na⁺-DNA interactions in Dickerson's dodecamer using a variety of MD-based techniques. Our purpose is not only to describe the counterion environment around DNA, but also to determine what the limits of current MD simulations are for the analysis of rare events involving nucleic acids. To this end we describe not only the results of some relatively conventional simulations, but also the application of some novel methodologies.

METHODS

In common with many other authors (see Introduction), we selected Dickerson's dodecamer (d(CGCGAATTCGCG; Drew et al., 1981) as a model of B-DNA containing a short A-track in the middle of the structure. Three types of calculations were performed on these systems: i), standard unrestricted MD calculations, ii), hybrid Monte Carlo-MD simulations, and iii), “demon-based” MD simulations. All simulations were performed using the AMBER 6.0 suite of programs. The AMBER-99 force field (Cheatham et al., 1999; Cornell et al., 1995) was used in combination with the TIP3P water model (Jorgensen et al., 1983).

Unrestricted molecular dynamics simulations

We began by carrying out 10-ns unrestrained MD simulations in an attempt to determine the equilibrium distribution of Na⁺ around the DNA. Starting structures for the DNA were taken from Protein Data Bank (PDB) entry 355D (Shui et al., 1998a), stripped of ion and solvent coordinates (although see below), and then immersed in a box containing ∼4350 TIP3P water molecules (Jorgensen et al., 1983). Two families of calculations were performed. In the first family (L simulations) only 22 Na⁺ were added to obtain a neutral system. In the second family (H simulations) 15 extra Na⁺ and Cl⁻ were included to simulate a 200-mM NaCl environment (this concentration refers to the extra salt added, excluding the Na⁺ necessary to neutralize DNA). Each family contained a number of individual simulations, differing in the original placement of Na⁺ ions. First (IIII simulations), four ions were placed in the AATT minor groove following Williams and co-workers (Shui et al., 1998a). Second, the four positions in the minor groove were initially filled with water molecules (WWWW simulations). With the exception of the Na⁺ placed within the minor groove in the IIII simulations in the crystallographically determined positions, all other ions were initially placed in the regions of more favored electrostatic potential using standard XLEAP defaults (Case et al., 1999). In summary, four unrestrained MD simulations are reported: L-WWWW, L-IIII, H-WWWW, and H-IIII. Note that the notation refers only to the initial placement of the ions/waters in the minor groove, but that all water and ions were free to move during the simulations.

All starting structures were equilibrated using our standard multistage equilibration process (Shields et al., 1997, 1998) followed by unrestrained equilibration of 1.5 ns. Analyses were performed on data generated through additional 8.5 ns of unrestrained MD simulation at constant pressure and temperature (P = 1 atm.; T = 298 K). SHAKE (Ryckaert et al., 1977) was used to constrain all the bonds at equilibrium values, which allowed us to use a 2-fs step of integration of Newton's equations. To avoid “flying ice cube” effects the velocity of the center of mass of the system was removed every 0.1 ns. Periodic boundary conditions and the particle-mesh-Ewald method (Darden et al., 1993) were used to model long-range electrostatic effects.

Monte Carlo-molecular dynamics simulations

The results from the unrestrained MD simulations suggested to us that the timescale for the interchange of Na⁺ and water within the minor groove could be too long to obtain good statistics for this process from 10-ns trajectories (see below). Furthermore, unrestrained MD trajectories did not allow us to study very rare configurations (e.g., the minor groove filled with Na⁺). Thus, to gain a more complete view of the counterion environment in the AATT minor groove we developed a hybrid Monte Carlo-molecular dynamics algorithm (MC-MD). This strategy, described for the first time here, involves the following steps:

1. Start with a configuration of water/Na⁺ in the minor groove (we started with IIII and William's crystal structure of DNA; PDB entry 355D). Then, equilibrate solvent for 0.5 ns to allow it to adapt to the DNA structure, which, along with those ions/waters in the minor groove, is held fixed with a harmonic restraint of 100 kcal/mol Ų.

2. Run a Monte Carlo step, where one randomly selected particle (ion or water) at one of the binding sites in the minor groove is interchanged with one randomly selected complementary particle (i.e., I←→W and W←→I). For example, one ion placed originally within the minor groove is mutated into a water, and simultaneously a randomly selected water is transformed into Na⁺.

3. Run 15 ps of MD simulation restraining the heavy atoms of the DNA and of those particles in the minor groove binding sites (100 kcal/mol Ų harmonic restrictions). The first 5 ps are considered equilibration (we find that 5 ps is enough for local solvent rearrangement around the inserted particle), and the potential energy of the system (excluding constraints) is collected every 10 fs for the remaining 10 ps. Note that during all this time the solvent and counterions outside the groove are free to move.

4. Repeat step ii and iii until a good sampling of all the 16 possible states (IIII, WIII,…, WWIW,…, WWWW) is obtained.

The process was repeated to give a total of 40 ns of restrained MD of solvent around William's crystal structure of DNA. Careful monitoring of the trajectories indicated good convergence in averaged energy values for each family after the first 10 ns of MC-MD simulation. It is worth noting that we are not using Metropolis criteria, but we collect all energy values, i.e., we are performing a systematic exploration of the configurational space. We find that the need to reorient the solvent after particle interchanges makes standard Metropolis-based MC-MD methods for this unsuccessful (rejection rate of 100%).

Except for the use of restraints to maintain the DNA and the binding sites, the technical details of MD simulations reported here are identical to those of unrestrained MD trajectories outlined above.

Demon-based molecular dynamics

This method (D-MD) was created to analyze the process of particle interchange accompanying a Na⁺ leaving a binding site in the AATT minor groove. The idea of the approach is to favor an unlikely transition (see below) by introducing an “information bias.” The method, inspired by Maxwell's demon, favors trajectories leading to the escape of Na⁺ from the binding site of the groove without introducing artifactual energy terms. The method works as follows:

1. Select a snapshot from an unrestricted MD trajectory, where one Na⁺ is present at one binding site of the AATT minor groove (we used configurations selected after ∼5 ns of the H-IIII trajectory).

2. Generate four replicas of the snapshot by random rotation of the velocity vectors of the Na⁺ (modulus remains constant). The remaining velocities are unaltered.

3. Run independent unrestrained MD trajectories for 15 ps. The first 5 ps are considered equilibration. Twenty-five structures collected from the last 10 ps of each replica are selected.

4. Analyze the 100 (“child”) structures and select the structure showing the Na⁺ most displaced to the exterior of the groove.

5. If the selected “child” structure shows the Na⁺ more exterior to the groove than the “parent” structure it is used as origin of a new generation (step ii) and the process is repeated. Otherwise, new replicas of the “parent” structure are generated and the process is repeated.

Typically the above cycle was repeated 50 times (i.e., 50 generations). The entire process was repeated eight times starting from different configurations (i.e., results in this section correspond to 24 ns of MD simulation). Note that, as in Maxwell's demon, our “engine” to favor transition is not force, but information.

Technical details

All MD simulations were carried out using the “sander” module of AMBER 6.1. MC- and D-MD were performed with the aid of specific scripts coupled to “sander” (Case et al., 1999). Analysis of the trajectories was performed using the tools in the AMBER package as well as with “in-house” software. Molecular interaction potentials were computed using van der Waals-corrected Poisson-Boltzmann potentials as implemented in the cMIP program (Gelpi et al., 2001, 2003). MD-averaged structures were obtained by Cartesian averaging of the last 5 ns of each trajectory followed by restricted optimization (H-atoms only). The differential flexibility of DNA under various ionic environments was analyzed using absolute (γ) and relative (κ) similarity indexes (Cubero et al., 2001; Orozco et al., 2003; Rueda et al., 2003; see Eqs. 1 and 2). Entropies were determined using Schlitter's and Andricioaei-Karplus methods and Harris's extrapolation technique (Andricioaei and Karplus, 2001; Harris et al., 2001; Orozco et al., 2003; Schlitter, 1993). Helical analysis of the DNA was performed using the 3DNA program (Lu and Olson, 2003), and solvent accessible surfaces were computed using NACCESS (Hubbard and Thornton, 1993).

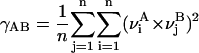(1)

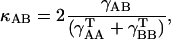(2)

(where ν are principal component (the essential movement) vectors, A and B stand for two different trajectories of equal length (with trajectories fitted to a common frame of reference), and the self-similarity indexes and are obtained by using Eq. 1 on two nonoverlapping portions of equal time length from a single simulation. The index n is always taken as 10, a number of eigenvalues that typically explains ∼80% of the variance of the trajectory.

RESULTS AND DISCUSSION

Unrestricted MD simulations

The four 10-ns MD simulations provide stable trajectories that, as in previous simulations of the same system, reproduce experimental information reasonably well. Thus, there is a good convergence in the general structure of the DNA irrespective of the ionic strength, and of the initial placement of ions. However, a more detailed comparison of the simulations clearly demonstrates that 10 ns is not long enough to obtain a converged representation of the Na⁺ environment around the DNA (see Fig. 1). When four sodium ions are placed in the AATT minor groove in the initial configuration (IIII simulations), three escape very fast, but the fourth remains bound (defined as being within 2.9 Å of an O2, N2, or N3 atom), for both H and L simulations, over the entire trajectory. In contrast, when the minor groove was fully occupied by waters in the starting configuration (both L- and H-WWWW simulations) the trajectories reveal 1 Na⁺ within the AATT minor groove only 1–2% of the time, and no multiple occupancy at all (see Fig. 1). Similar results are obtained if the analysis is extended to the entire minor groove. In this case ∼4–9% of the trajectory reveals 1 Na⁺ within the minor groove in WWWW simulations, whereas for IIII simulations the minor groove contains 1 Na⁺ 92–98% of the time and 2 Na⁺ ions 2–8% of the time. Patterns of hydration mirror those of ion distribution (see Fig. 1). Thus, in WWWW simulations the AATT minor groove is occupied by 6–10 water molecules for ∼72–78% of the trajectory, and for only 22–28% of the time are there 5 or less waters. In contrast, in IIII simulations the AATT minor groove is highly hydrated (6–10 waters) only ∼10% of the time. As before, if the entire minor groove is considered, the same trends are found: ∼85% of the time >20 water molecules are located deep inside the groove (<2.5 Å from O2, N2, or N3) when one analyzes the WWWW trajectories, whereas the corresponding figure from analysis of the IIII trajectories is only 35–60% (see Fig. 1).

FIGURE 1.

Percentage of occupancy along the trajectory of Na⁺ (top) and waters (bottom) inside the minor groove of the entire duplex and the AATT segment.

Despite the disparities in the simulation results, some clear conclusions can be reached. There is a binding site deep inside the minor groove of this dodecamer, where an Na⁺ can reside for very large periods of time, thus reducing the amount of water in the groove. This site is probably the same as that populated in Wilson's trajectory (Hamelberg et al., 2000; see footnote), and probably the same as that assigned experimentally to a 50- ns residence time from NMR data (Denisov and Halle, 2000). Our simulations also make it clear that it is very difficult for a Na⁺ diffusing around the DNA outside the groove to reach this binding site, which supports the NMR-derived conclusion that waters are able to enter this region 1000 times more efficiently than Na⁺. No significant differences are found between simulations performed with a minimum amount of Na⁺, and those performed in the presence of an extra 200 mM NaCl.

Note that other authors have found shorter residence times for Na+ inside the groove: 3 ns (Mocci and Saba, 2003) or 6 ns (Hamelberg et al., 2000), which indicate the stochastic character of the Na+ movement. However, none of the authors has been able to obtain reversible interchanges of Na+ from the high-affinity centers at the bottom of the groove and the exterior.

From the above we see that the initial placement of ions in the simulation has a dramatic effect on the time-averaged picture of the ionic environment deep inside the DNA minor groove over a 10-ns timescale, especially in the central AATT track. Is this sensitivity to the initial conditions also observed in other regions surrounding the DNA? To determine this, we computed the distribution of sodium ions in different layers (defined using radial distances to the nearest DNA heteroatom) around the duplex (see Fig. 2). Clearly, more Na⁺ are found for simulations at higher ionic strength, but the differences are small for inner layers (for example a difference of 0.2–0.4 ions exists between L and H simulations in the 3-Å layer), which is in agreement with the analysis above that no dramatic changes are observed between L and H simulations in the population of sodium cations in the minor groove. Rather, as expected, the distribution of Na⁺ in inner layers is more dependent on the original placement of ions. For example 0.4–0.7 more cations are in the 3-Å layer in IIII simulations compared to the WWWW ones. Clearly, this difference arises from the presence of one Na⁺ deep inside AATT minor groove, because in outer layers the distribution of Na⁺ is the same in WWWW and IIII simulations.

FIGURE 2.

Population of Na⁺ and waters located in different layers around the DNA (excluding the extremes). Standard deviations are noted as error bars for each histogram block. Distances are in Å.

The analysis of the Na⁺ population by layer as a function of time shows the dynamic nature of the Na⁺-DNA interaction. In all the cases the standard deviations in the average number or sodiums per layer are in the range from 1.2 (for the 3-Å layer) to 2 (for the 5-Å layer), indicating a high mobility of ions between the different layers. Analysis of the time evolution of the sodium distributions (see Fig. 3) shows the existence of short-period fluctuations in the Na⁺ population on the subnanosecond timescale, convolved with long-period fluctuations that appear on the 1–2-ns timescale. These fluctuation periods are therefore a reflection of the residence times of most Na⁺ around DNA (probably those routinely found in most MD simulations), but clearly not of the Na⁺ located at the high residence time site within the AATT minor groove, that we estimate at >10 ns.

FIGURE 3.

Time evolution of the number of Na⁺ located at <5 Å from the DNA (excluding the extremes) for the four trajectories considered here. From top to bottom, L-WWWW, L-IIII, H-WWWW, H-IIII.

When the analysis is repeated for water molecules, numbers are larger and accordingly it becomes difficult to determine the significance of small differences. In any case, we find that in general there are no consistent differences between L and H simulations. All the WWWW simulations show a greater number of waters in the different layers around the DNA compared with the IIII simulations, but the differences are very small (<1 water for inner layers and up to 6 waters for the outer layer) considering the number of waters in each layer (see Fig. 2).

The results above provide a picture of DNA-ion interactions where long-residence time binding sites exist for Na⁺ inside the AATT minor groove, but these sites are not easily accessible from the exterior, i.e., periods of long occupancy by Na⁺ will probably be followed by very long periods of water occupancy (Denisov and Halle, 2000). But clearly, 4 × 10-ns long MD simulations cannot reproduce this process. After ∼20 million integrations of Newton's equation, memory of the initial configuration remains and there are still many regions of the space around the DNA that have not been sampled by Na⁺. For example, if the space around DNA is divided into grids of cubic cells (cell volume 1 ų), and the occupancy of Na⁺ and water in each cell (grid point) is computed, a 100% occupancy by water is found in all the cases (i.e., all grid points are visited at least once by water), whereas only from ∼50% (L simulations) to 75% (H simulations) occupancy by sodium cations is seen. Clearly, much longer simulations are necessary to determine, from unrestricted MD calculations, the true equilibrated population of Na⁺ situated deep within the AATT minor groove of B-DNA. However, the inability of our WWWW and IIII trajectories to converge to a common representation of the Na⁺ environment in the minor groove provides us with an excellent tool to analyze if and how the conformational characteristics of this DNA depend on whether Na⁺ is or is not within the AATT minor groove.

As noted above, all trajectories stay fairly close to the crystal structure of the dodecamer. Thus, the root mean square deviation (RMSD) between the different trajectories and William's crystal structure (PDB code 355D) are 1.8–1.9 Å in all the cases (see Table 1). No noticeable differences exist between the trajectories in their ability to reproduce the crystal structure. The average RMSD between the four MD-averaged structures and their corresponding trajectories are in the range 1.3–1.8 Å (values in the diagonal of Table 2), with the IIII trajectories showing the larger RMSDs from their corresponding averaged structures. Interestingly, the RMSD range 1.3–1.8 Å is exactly the same found in cross-comparisons; i.e., average RMSDs between one trajectory and the MD-averaged structure obtained from a different trajectory (off diagonal terms in Table 2). Helical analysis provides very similar values for the four trajectories, the small differences found being clearly smaller than the intrinsic noise of the simulations (see Table 3). In summary, the four trajectories collected here provide a very similar picture of the general DNA structure in solution, and do not support the hypothesis that moderate changes in ionic strength or in the initial placement of ions leads to dramatic changes in the general structure of the duplex. However, a gross analysis in terms of RMSDs cannot reveal if more subtle changes might exist related to the general ionic strength, or to the presence of ions in the AATT minor groove.

TABLE 1.

RMSD (in Å) between the different MD-averaged structures and MD trajectories and the crystal structure (PDB-355D)

	L-WWWW	L-IIIII	H-WWWW	H-IIII
Trajectory	1.8 ± 0.3	1.8 ± 0.4	1.8 ± 0.3	1.9 ± 0.4
Average	1.6	1.5	1.6	1.5

For trajectories, averaged values are displayed with their corresponding standard deviations (also in Å). All values are measurements over the central 10 bases of the dodecamer.

TABLE 2.

Average RMSDs (in Å) between the different MD-averaged structures (rows) and the trajectories (columns)

	L-WWWW	L-IIIII	H-WWWW	H-IIII
L-WWWW	1.3 ± 0.3	1.4 ± 0.2	1.4 ± 0.3	1.4 ± 0.2
L-IIIII	1.4 ± 0.2	1.6 ± 0.2	1.2 ± 0.2	1.6 ± 0.2
H-WWWW	1.4 ± 0.3	1.7 ± 0.2	1.3 ± 0.2	1.8 ± 0.2
H-IIII	1.4 ± 0.2	1.7 ± 0.2	1.3 ± 0.3	1.8 ± 0.2

The standard deviations in the averages (also in Å) are shown.

TABLE 3.

Average values of key helical parameters of the AATT section of the DNA duplex obtained using 3DNA (see Methods)

Simulation	Rise (Å)	Roll (°)	Twist(°)
L-WWWW	3.4 ± 0.3	1.4 ± 5.0	34.5 ± 4.1
L-IIIII	3.4 ± 0.3	1.0 ± 4.9	34.7 ± 4.7
H-WWWW	3.4 ± 0.3	1.5 ± 5.4	34.0 ± 4.2
H-IIII	3.5 ± 0.3	0.8 ± 4.7	34.0 ± 4.2
Crystal (355D)	3.3 ± 0.1	−0.4 ± 1.7	35.2 ± 0.3

Standard deviations in the averages are also shown.

To study in detail any changes in the AATT minor groove related to the presence of ions, we computed the groove width using refined P-P distances (Lu et al., 2003), and the solvent accessible surface (Hubbard and Thornton, 1993) of the nucleobases. Results (Tables 4 and 5) clearly ruled out any systematic change in the width or accessibility of the groove related to the presence of Na⁺ at the bottom of the groove, even in its close vicinity (AATT track and AT step). The small average differences between WWWW and IIII simulations in the width of the groove are not significant from a statistical point of view (Table 4). The same is clear when individual steps are investigated (Table 4). The only noticeable difference between WWWW and IIII simulations lies in the magnitude of the minor groove width fluctuations that in general are smaller for the IIII simulations than for the WWWW ones. As expected, results obtained for L and H simulations are identical both in terms of groove width and accessibility.

TABLE 4.

Minimum refined P-P distances along the minor groove in the central AATT track

	d(AATT)2	d(AA)·d(TT)	d(AT)·d(AT)	d(TT)·d(AA)
L-WWWW	10.9 ± 0.6	10.6 ± 0.9	10.0 ± 0.8	10.6 ± 0.8
L-IIIII	10.8 ± 0.6	10.3 ± 0.7	10.1 ± 0.6	11.0 ± 1.1
H-WWWW	11.0 ± 0.8	10.8 ± 1.0	10.5 ± 1.1	11.0 ± 1.2
H-IIII	10.6 ± 0.6	10.5 ± 0.7	10.0 ± 0.5	10.3 ± 0.7

Average values (in Å) for the entire track and for each step are reported. Refined distances were computed using standard defaults in 3DNA. The standard deviations in the averages are also shown in Å.

TABLE 5.

Solvent accessible surface associated with the bases of DNA for the entire DNA (excluding extremes), the central AATT fragment, and the AT step where the Na⁺ is eventually located

	SAStotal	SASAATT	SASAT
L-WWWW	3590 ± 26	1437 ± 18	714 ± 13
L-IIIII	3600 ± 24	1444 ± 16	713 ± 11
H-WWWW	3582 ± 29	1440 ± 19	714 ± 12
H-IIII	3586 ± 22	1438 ± 17	715 ± 11

All values are in Ų.

To further investigate any possible relationship between the characteristics of the AATT minor groove and the presence of ions deep in the groove we computed Molecular interaction potentials (MIPs) for the average structure of the four trajectories. Note that the MIP measures the interaction energy of the DNA with a probe molecule (Na⁺ in this work), and is very sensitive to small conformational changes that might not be easily detected in distance or solvent accessible surface (SAS) analysis. However (see Fig. 4), even this sensitive technique fails to show any difference in the properties of the minor groove when one Na⁺ is deeply inserted at the bottom of the groove (L-IIIII and H-IIII simulations), or when the groove is entirely occupied by water (L-WWWW and H-WWWW trajectories). In summary, in our hands MD simulations do not support the hypothesis that the presence of Na⁺ deep inside the groove narrows it, increasing its negative electrostatic potential.

FIGURE 4.

Classical molecular interaction between a Na⁺ and the MD-averaged structures obtained from the four trajectories considered here. Contours of −3 kcal/mol are represented.

The results above strongly suggest that the presence of Na⁺ inside the minor groove has a very minor effect on the geometry and recognition properties of DNA. However, the impact on the flexibility of the DNA remains to be investigated. For this purpose we analyzed (see Methods) the essential dynamics of the DNA in the four simulations. In all the cases the most important movements of DNA correspond to twisting and bending movements, as usual in simulations of nucleic acids. Results obtained using the entire DNA structure (see Table 6) show that the essential movements of the helix are the same in the different trajectories (κ indexes between 0.92 and 1.00; see Eqs. 1 and 2), demonstrating that the presence or absence of Na⁺ inside the groove does not change the essential dynamics of DNA. This conservation in the nature of essential movements is found again when the analysis is performed considering only the AATT track of the central AT step.

TABLE 6.

Relative similarity indexes (κ; Eq. 2) between the 10 principal components in the four MD simulations for the entire DNA (excluding extremes), the central AATT segment, and the central AT step

	L-WWWW	L-IIIII	H-WWWW	H-IIII
L-WWWW	1.00	1.00	0.96	0.97
	1.00	0.98	0.98	0.90
	1.00	0.92	1.00	0.95
L-IIIII		1.00	1.00	0.96
		1.00	0.96	1.00
		1.00	0.91	0.99
H-WWWW			1.00	0.91
			1.00	0.88
			1.00	0.94
H-IIII				1.00
				1.00
				1.00

The entire DNA, excluding extremes (top numbers within each group); the central AATT segment (middle numbers); and the central AT step (bottom numbers).

The frequencies of the first modes are always the same (in the range of 12–14 cm⁻¹) for all the simulations. The fluctuations of the RMSD are similar for all the trajectories (see Table 1). Furthermore, entropy analysis confirms (see Table 7) the lack of systematic differences in the global order of DNA induced by the presence/absence of Na⁺ in the interior of the AATT minor groove. In summary, we did not find any evidence that the presence of Na⁺ inside the minor groove leads to any change in the global flexibility of the duplex. However, this does not a priori preclude the existence of local changes in the flexibility near the site of sodium binding. SAS fluctuations in Table 5 are slightly larger for the AATT track when no Na⁺ is bound in the minor groove (WWWW simulations) than when one is present. Fluctuations in interphosphate distances along the minor groove in the AT site are also slightly larger in WWWW simulations than in the IIII ones (see Table 4). Entropy analysis localized in the AATT and AT regions shows slightly larger entropies for WWWW simulations than IIII simulations. In summary, there are many subtle signals suggesting that the presence of sodium deep inside the groove slightly restricts the flexibility of the minor groove, leading to a small and local reduction in the flexibility of the duplex. We must emphasize, however, that the differences found are in most cases very small, and better statistical analysis is necessary to confirm that the presence of Na⁺ slightly rigidifies the minor groove near the binding site.

TABLE 7.

DNA entropy determined using Schlitter and Andricioaei-Karplus methods for the four DNA structures sampled here

	SSchlitter	SKarplus
L-WWWW	2.22	2.07
	0.89	0.82
	0.44	0.41
L-IIIII	2.23	2.07
	0.88	0.81
	0.43	0.40
H-WWWW	2.29	2.14
	0.93	0.85
	0.46	0.43
H-IIII	2.24	2.09
	0.88	0.81
	0.44	0.40

In all the cases, the extrapolation (t = ∞) technique developed by Harris et al. (2001) (see Methods) was used. All values are in kcal/mol K. SEs in the fitted values are always ∼0.1 kcal/mol K. Results for the entire DNA (top numbers within each group); results for the AATT track (middle numbers); and results for the central AT step (bottom numbers).

In summary, our unrestricted MD simulations suggest that binding sites for Na⁺ exist at the bottom of the minor groove in this sequence. These sites are very difficult to reach, but once populated the ion can reside for >10 ns. The presence of the Na⁺ at the bottom of the groove does not produce significant alterations in the structure (as suggested by Beveridge's calculations in reference McConnell and Beveridge, 2000), but might reduce slightly the local flexibility of the duplex, especially at the minor groove level. The long residence time of Na⁺ at the bottom of the groove, combined with the apparently very extended period of time needed for the Na⁺ to reach the bottom of the groove makes good sampling of the process of Na⁺ exchange between the bottom of the groove and the exterior of the DNA through 10-ns MD trajectories very unlikely (Orozco et al., 2004), supporting ²³Na magnetic relaxation dispersion experiments (Denisov and Halle, 2000) and raising doubts as to the ability of currently achievable MD simulation timescales to investigate water/Na⁺ interchange in the groove. It is, however, possible to use such unrestrained MD simulations to investigate the interchange of Na⁺ between the surroundings of DNA and the exterior region, because this happens on the nanosecond timescale, or the formation of weak Na⁺-DNA interactions in the vicinity of the minor groove, a process that can occur on the subnanosecond timescale (Korolev et al., 2002).

The lack of convergence of WWWW and IIII simulations was useful because it allowed us to carefully characterize the DNA both in the presence and absence of Na⁺ at the bottom of the minor groove. However, the same behavior prevented us from reaching any quantitative conclusions regarding the relative weight of the structures containing Na⁺ inside the groove. Analysis of the WWWW trajectories suggests a population of structures containing Na⁺ in the groove below 10%, giving support to the results of Beveridge's group (McConnell and Beveridge, 2000). However, these “bound” configurations correspond to weakly bound Na⁺ and not to Na⁺ placed in binding sites with very long residence times. The results of previous MD simulations performed by other authors (Hamelberg et al., 2000; McConnell and Beveridge, 2000; Mocci and Saba, 2003) suggest that if our IIII simulations were extended for much longer periods the Na⁺ would finally leave the minor groove, because apparently configurations with the minor groove filled with waters are more popular than those with Na⁺. However, we must emphasize that this is only an assumption based on previous MD simulations (see Introduction), but not a direct conclusion from the unrestricted MD calculations reported here. Clearly, other types of calculations are needed to investigate the affinity of Na⁺ and water for the minor groove.

Monte Carlo-molecular dynamics simulations

MC-MD (see Methods) was used to determine the relative stability of DNA structures with either 4 waters or 4 sodium ions filling the four high-affinity binding sites of the AATT minor groove. These non-Metropolis MC-MD calculations are useful because they allow us to study even very unlikely ionic states. However they must be analyzed with much caution for two reasons. Firstly in these simulations the DNA is restrained to remain close to William's conformation (PDB-355D), and the DNA is therefore unable to relax its conformation in response to the different ionic states, or to try to recover the internal symmetry broken by the crystal lattice. This is deliberate because it is primarily a study of how ions respond to the observed DNA crystal structure rather than vice versa. Second, we cannot ignore that the energy differences observed are obtained by subtracting very large numbers, resulting in large statistical errors. To solve the problem associated with the statistical noise in the calculation of the differences between large energy values we performed a detailed statistical analysis, which showed us that to obtain converged average energies we needed to run very long MC-MD simulations including short equilibrations of solvent (see Methods) after each permutation. Results reported in Table 8 correspond to averages obtained by analyzing >10⁵ snapshots characterizing each state (and a total of ∼40 ns of MD simulation). Calculations performed with just one-third of these points yields the same average energies. This, and the small SEs associated with the averages (∼0.2 kcal/mol; Table 8), gives us confidence that average values are well converged and can be used, with the caveats noted above, for at least a qualitative analysis of the stability of the different ionic states of the AATT minor groove.

TABLE 8.

Average relative energy (to the WWWW state) and the corresponding standard deviations of the different states defined by filling the four binding sites with waters or sodium ions

Configuration	No. of samples	Average energy relative to WWWW	SE in 〈E〉
WWWW	208,000	0	0.2
WIWW	191,100	4	0.2
WWIW	190,000	5	0.2
IWWI	201,000	5	0.2
IWWW	197,700	7	0.2
WWWI	201,000	7	0.2
IWIW	192,000	8	0.2
WIWI	200,000	10	0.2
WWII	203,000	16	0.2
IIWI	202,000	20	0.2
IIWW	195,000	20	0.2
WIIW	187,000	21	0.2
IWII	202,000	25	0.2
IIIW	190,000	30	0.2
WIII	201,000	36	0.2
IIII	191,000	50	0.2

States are ordered according to their relative stability. The number of points used for the average of each state is shown (see text). Both average energies and their associated SEs are in kcal/mol.

Clearly, the state where the four binding sites are filled with waters is the most stable configuration, and that containing 4 Na⁺ at the bottom of the groove is very unlikely to exist (Table 8). In general, there is a continuous decrease in stability as the number of binding sites in the AATT minor groove is filled with Na⁺. But this general trend has some exceptions, because, for example, state IWWI seems slightly more stable than states IWWW and WWWI. Symmetry expected from the DNA sequence is not always preserved; see, for example, energies of WWII and IIWW states, reflecting the intrinsic errors of MC-MD calculations and the sizeable internal asymmetry of the crystal structure (>1 Å RMSD between the two halves of the structure). States containing 1 Na⁺ in the minor groove are 4–7 kcal/mol less stable than that containing four waters at the binding sites. As noted above, the numbers in Table 8 must be analyzed with caution, but the energy differences are large enough to guarantee that the importance of configurations containing Na⁺ at the bottom of the groove should be small. Thus, the combination of unrestrained MD and MD-MC simulations supports a general model where the four binding sites existing in the AATT minor groove are much more likely to be occupied by waters than by Na⁺. However, in the rare event that one Na⁺ occupies one of these binding sites, it can stay there for long periods of time, frozen in a kinetic trap.

Demon-based molecular dynamics

The final step in our work was to analyze structural changes accompanying Na⁺ release from the bottom of the groove. As discussed above, this cannot be studied using unrestricted MD simulations, because no spontaneous release was detected during our simulations. We therefore decided to perform a new type of “information-biased” MD simulation that favors trajectories leading to the escape of Na⁺ without adding any explicit force to the system Hamiltonian (see Methods).

As noted in Methods, each demon-MD run involves ∼3 ns of MD simulation, and ∼50 selection steps (generations), which favor the propagation of simulations where the Na⁺ escapes from the groove. This process was repeated eight times, but only in two of the pseudotrajectories did we find exit routes for Na⁺. The difficulty of simulating the release of Na⁺ from the bottom of the groove even with the information bias confirms that the ion is tightly trapped in the interior of the minor groove. Analysis of the two productive trajectories illustrates that the escape of Na⁺ is a complex process that actually happens over a short timescale (see Fig. 5), because once the Na⁺ leaves the long-residence time binding site it escapes easily from the interior of the groove. However, this fast process must await a rare fluctuation of the walls of the minor groove allowing the Na⁺ to find its route to the exterior (see Fig. 5).

FIGURE 5.

Evolution of the interphosphate minor groove distance, the solvent accessible surface of the AATT track, and the escape coordinate (the sum of the distances between ion and the O₂, N₃ atoms of the AT segment) with the number of generations of demon-MD simulations.

CONCLUSIONS

We have performed a large number and variety of MD-based simulations to analyze in detail the possible existence of Na⁺ inside the minor groove of the AATT minor groove in B-DNA, and its structural consequences. With the obvious cautions related to the use of nonpolarizable classical force fields, and to the limited extent of trajectories, our results suggest that there are binding sites at the bottom of the groove where 1 Na⁺ can stay for >10 ns. Over our simulations these binding sites are not spontaneously occupied by Na⁺ placed initially in the exterior of the DNA, raising doubts as to the ability of 10-ns long MD simulations to analyze the interchange of sodium between these specific binding sites and the surroundings. However, MD simulation seems well suited to study other rearrangements of Na⁺ around DNA, including the interchange of Na⁺ between low-affinity positions inside the groove and the exterior.

After analyzing 4 × 10-ns trajectories we could not find any significant change in the structure of DNA related to the presence of 1 Na⁺ placed at the bottom of the AATT minor groove. The only possible alteration found is in the flexibility of the minor groove near the binding site, which in the presence of Na⁺ might become slightly more rigid. The difference in flexibility is, however, small, and is not likely to be of major biological relevance.

MC-MD simulations suggest that the impact of configurations containing Na⁺ inserted in the binding positions suggested by Williams and Maher (2000) is small, because configurations containing 4 waters are more stable than those containing any ion. Configurations with many sodium ions inserted in the bottom of the groove are very unlikely to exist.

Finally, demon-MD simulations confirm that the release of Na⁺ from the binding sites in the groove to exterior is a difficult process, because it needs a concentration of kinetic energy in both the ion and the walls of the groove.

In summary, our simulations provide a complex picture of the Na⁺ environment of DNA, which agrees surprisingly well with that derived from recent magnetic relaxation experiments (Denisov and Halle, 2000). According to our calculations thermodynamic considerations do not favor the presence of Na⁺ in specific binding sites in the interior of the minor groove. However, in the rare situation that Na⁺ reaches one of these positions it can be kinetically trapped for long periods of time, >10 ± 1.5 ns according to our simulations.