Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Aug;87(2):812–821. doi: 10.1529/biophysj.104.041269

Hydration of Enzyme in Nonaqueous Media Is Consistent with Solvent Dependence of Its Activity

Lu Yang 1, Jonathan S Dordick 1, Shekhar Garde 1
PMCID: PMC1304491  PMID: 15298890

Abstract

Water plays an important role in enzyme structure and function in aqueous media. That role becomes even more important when one focuses on enzymes in low water media. Here we present results from molecular dynamics simulations of surfactant-solubilized subtilisin BPN′ in three organic solvents (octane, tetrahydrofuran, and acetonitrile) and in pure water. Trajectories from simulations are analyzed with a focus on enzyme structure, flexibility, and the details of enzyme hydration. The overall enzyme and backbone structures, as well as individual residue flexibility, do not show significant differences between water and the three organic solvents over a timescale of several nanoseconds currently accessible to large-scale molecular dynamics simulations. The key factor that distinguishes molecular-level details in different media is the partitioning of hydration water between the enzyme and the bulk solvent. The enzyme surface and the active site region are well hydrated in aqueous medium, whereas with increasing polarity of the organic solvent (octane → tetrahydrofuran → acetonitrile) the hydration water is stripped from the enzyme surface. Water stripping is accompanied by the penetration of tetrahydrofuran and acetonitrile molecules into crevices on the enzyme surface and especially into the active site. More polar organic solvents (tetrahydrofuran and acetonitrile) replace mobile and weakly bound water molecules in the active site and leave primarily the tightly bound water in that region. In contrast, the lack of water stripping in octane allows efficient hydration of the active site uniformly by mobile and weakly bound water and some structural water similar to that in aqueous solution. These differences in the active site hydration are consistent with the inverse dependence of enzymatic activity on organic solvent polarity and indicate that the behavior of hydration water on the enzyme surface and in the active site is an important determinant of biological function especially in low water media.

INTRODUCTION

Water plays an important role in biological structure and function. For example, hydrophobic interactions that result from the peculiar structuring of water near hydrophobic amino acids provide thermodynamic stability to folded protein structures in aqueous solution (Dill, 1990; Kauzmann, 1959; Tanford, 1973). In addition to water's role as a solvent, water molecules can mediate enzymatic catalysis either directly by taking part in the reaction or indirectly through providing a solvation medium for reactants, transition state, and products (Craik et al., 1985; Fersht, 1999; Hartmann et al., 1998; Heine et al., 2001; Kraut, 1977; Warshel et al., 1989). The role of water in biomolecular structure, function, and interactions remains critical even in low water media. A particularly relevant example is that of enzyme structure and function in organic media, which has received a great deal of attention in the past two decades (Affleck et al., 1992; Carrea and Riva, 2000; Dordick, 1992; Halling, 2000; Klibanov, 2001; Ru et al., 2000; Wang et al., 1997; Wangikar et al., 1997; Zaks and Klibanov, 1985, 1988). The motivation for fundamental studies in the field of nonaqueous enzymology stems partly from a variety of potential applications. For example, by manipulating the microenvironment of an enzyme, through solvent or biocatalyst engineering, it has become possible to modulate enzyme activity, tailor biocatalyst selectivity, and alter enzyme stability (Carrea and Riva, 2000; Dordick, 1992; Klibanov, 2001; Novick and Dordick, 2000; Schmid et al., 2001; Wang et al., 1997).

Traditionally, at least two methods have been used to incorporate proteins into low water organic media. Lyophilized protein powders have been dispersed into organic solvents creating a suspension of particles comprising aggregates of many protein molecules (Dabulis and Klibanov, 1993; Dordick, 1992). Alternatively, proteins have been extracted from aqueous solution into organic solvents through the use of surfactant molecules at concentrations well below their critical micelle concentration (Paradkar and Dordick, 1994a; Wangikar et al., 1997). Proteins, thus extracted, are present as single molecules in organic solutions with their charged amino acid residues ion pairing with oppositely charged surfactant headgroups (Paradkar and Dordick, 1994a). Because the concentration of surfactants is sufficiently low, reversed micelles are not formed, and the protein surface has a considerable exposure to the organic solvent phase.

Although structural investigations of proteins either suspended or solubilized into organic solutions are generally difficult, activity assays provide an indirect probe of protein structure and function. One might expect that the lack of hydrophobic interactions in a bulk nonpolar solvent such as octane (OCT) would lead to protein unfolding and therefore to a complete loss of activity. In contrast, experiments show that proteins are able to maintain their structure in many organic solvents and remain catalytically active (Dordick, 1992; Halling, 2000; Klibanov, 1997). In the absence of a highly polar aqueous medium, which can stabilize somewhat open partially unfolded states, folded protein structures are kinetically stabilized in nonpolar organic solvents (Partridge et al., 1999). Indeed, if a significant conformational unfolding is induced by heating the protein to high temperatures in organic solutions, the process is irreversible due to the absence of hydrophobic driving forces (Wangikar et al., 1997).

Several experimental studies on the activity of enzymes in organic solutions under ambient conditions have highlighted the sensitivity of enzyme activity to the water content of solution. At low water contents, the addition of water leads to an increase in protein activity. At a high enough water content in a predominately nonaqueous environment, the protein activity drops, likely due to structural changes induced by partial denaturation in water-organic solvent mixtures (de Sampaio et al., 1996; Dordick, 1992). However, most applications of nonaqueous enzymology employ water contents below this threshold value. In addition, the protein activity is also sensitive to the type of organic solvent employed. For example, transesterification of N-acetyl-L-phenylalanine ethyl ester (APEE) by Aerosol-OT (AOT)-solubilized subtilisin BPN′ shows activity in n-octane that is as high as 10% of the enzyme's hydrolytic activity in water. However, as the polarity of the organic solvent is increased (e.g., octane → tetrahydrofuran (THF) → acetonitrile (ACN)), the enzymatic activity drops dramatically (Wangikar et al., 1997). Similar dependence of activity on the polarity of the solvent has been reported for other enzymes that were either solubilized by surfactants or simply suspended in organic media (de Sampaio et al., 1996; Kwon et al., 1999; Paradkar and Dordick, 1994a).

Our goal here is to understand the molecular basis of this solvent dependence. It has been suggested that a key determinant of enzymatic activity is the amount of hydration water (or the so-called biological water) that is available for solvation of the enzyme (Carrea and Riva, 2000; Pal et al., 2002; Partridge et al., 1998; Zaks and Klibanov, 1988). This solvation water can affect catalytic activity by changing enzyme flexibility as well as by affecting specific details of the active site hydration. The observed decrease in enzyme activity with increasing solvent polarity reflects the tendency of organic solvents to strip water molecules from the enzyme surface with the extent of water stripping increasing with the polarity of the organic solvent. Although the amount of biological water is closely related to the overall water content as well as the solvent polarity, its quantification is difficult (Gorman and Dordick, 1992; Lee et al., 1998; Wangikar et al., 1997). Halling et al. have shown that the thermodynamic activity of water in a bulk organic solvent correlates well with the enzyme activity and, therefore, is a qualitative indicator of amount of water available for the hydration of enzyme (Bell et al., 1995; Halling, 1994; Partridge et al., 1998). Although the correlation between the thermodynamic activity of water and the amount of hydration water is a good one, it does not always capture the true partitioning of water molecules between enzyme and the bulk organic solvent (Bell et al., 1997). In addition, details of the hydration of enzyme surface, interior, or the active site region for a given level of hydration are difficult to obtain from experiments alone. Obtaining such details will be critical for further elucidating the enzyme structure and function in a variety of low water media.

Here we present results from molecular dynamics (MD) simulations of surfactant-solubilized enzyme subtilisin BPN′ in three different organic media, n-octane, tetrahydrofuran, and acetonitrile, and in bulk water. The inclusion of surfactants and other system components makes the simulation system realistic and, therefore, relevant and complementary to the experimental studies of surfactant-solubilized enzymes in organic media (Paradkar and Dordick, 1994a; Wangikar et al., 1997). The large size of these systems represented at atomistic detail (∼35,000 atoms), however, limits the simulation times to several nanoseconds. As a result, large-scale enzyme structure fluctuations cannot be monitored through such simulations. Nonetheless, the solvent (water and organic solvent) degrees of freedom do relax over much shorter timescales allowing us to probe the details of enzyme hydration in various organic media at a given overall water content (Garcia and Hummer, 2000). We investigate the competitive solvation of the enzyme and its active site by hydration water and organic solvent and quantify the amount and behavior of biological water in different organic media. Differences in the details of enzyme hydration combined with information on enzyme structure and flexibility provide a molecular level picture of enzymes in nonaqueous media. These calculations present a qualitative connection between the active site hydration and enzyme activity in nonaqueous media that highlights the importance of hydration to protein function in nonaqueous media.

DETAILS OF MOLECULAR DYNAMICS SIMULATIONS

Molecular dynamics simulations performed here mimic the details of experiments presented by Wangikar et al. (1997). To best represent the surfactant-solubilized enzyme in solvent, our simulations included the enzyme subtilisin BPN′, enzyme bound water, surfactant AOT, counterions required for electroneutrality, and solvent molecules (Fig. 1). Four different solvent media were considered: octane, tetrahydrofuran, acetonitrile, and water. Coordinates of all heavy atoms of the enzyme and bound water were taken from the enzyme's crystal structure in water (pdb code 1A2Q; Pantoliano et al., 1989). The nonnatural amino acid residue at the location 221 in the crystal structure was replaced with serine present in the wild-type protein. There is some ambiguity regarding the protonation states of ionizable amino acids of the enzyme in organic solutions. It is known, however, that the pH of the aqueous solution from which enzymes are extracted influences the enzyme activity in organic solvents, referred to as the “pH memory” phenomenon (Zaks and Klibanov, 1985). It is therefore believed that the ionizable amino acids maintain their charge states when transferred from water to organic solutions. Following this idea, His residues were deprotonated, whereas Lys, Arg, Glu, and Asp residues were charged corresponding to the experimental pH value of 7.8 (Wangikar et al., 1997).

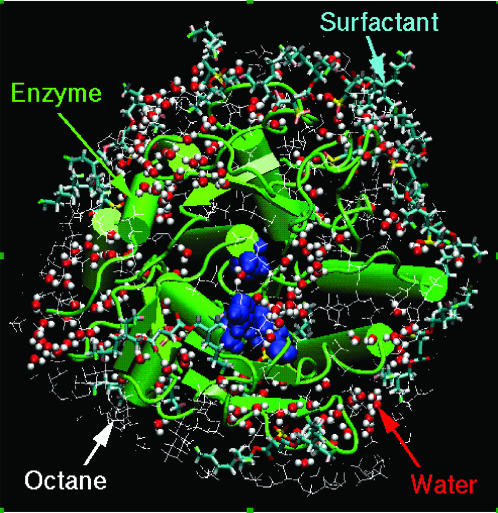
FIGURE 1.

FIGURE 1

Open in a new tab

MD snapshot of the surfactant-solubilized subtilisin BPN′ in OCT: the enzyme (green), water molecules (red and white), surfactant AOT (cyan), and some of the surrounding OCT (white wireframe) molecules are shown. The cubic simulation box is bigger than the image shown, and the space surrounding the enzyme is filled with solvent; only a layer of solvent molecules is shown, however, for visual clarity. The active site residues are highlighted (blue spacefill).

At well below the critical micelle concentration of AOT, subtilisin is extracted from water into organic solvent via ion pairing with AOT molecules, presumably at the enzyme's Lys and Arg residues (Paradkar and Dordick, 1994a,b; Wangikar et al., 1997). There are a total of 13 Lys and Arg residues in subtilisin; therefore, 13 AOT molecules were placed with their sulfate (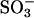Inline graphic) headgroup in the ion-pairing configurations with Lys and Arg residues. When the enzyme is extracted from an aqueous solution, it carries with itself a certain number of bound water molecules. Ideally, we would like to perform several simulations with a different total number of water molecules and study partitioning of that water between enzyme vicinity and the bulk organic solvent. Such calculations are, however, computationally prohibitive. Instead, we chose two different levels of overall water content that bracket the region of interest. We included 186 water molecules that are present in the crystal structure of the enzyme to simulate a low level of hydration. This number is significantly lower than that required to form a monolayer of hydration water (∼846) surrounding the enzyme as indicated by simulations of the enzyme in bulk water. We also performed simulations that included a total of 846 water molecules representing a higher level of overall water content. Results from these simulations are qualitatively similar to those with 186 water molecules and, therefore, much of the discussion in the following sections focuses on the details of those results. Eleven sodium counterions were added to neutralize the overall system. The initial locations of sodium ions were chosen by the ADDIONS utility of AMBER6.0 (Pearlman et al., 1995), which placed them in the enzyme vicinity at electrostatically favorable locations. This enzyme-AOT-counterion-water complex was then solvated in different solvents using condensed solvent boxes obtained from separate MD simulations of pure solvents. The number of solvent molecules were included such that, after equilibration, a completely filled cubic periodic box was sufficiently large (∼70 Å) to minimize enzyme-enzyme interactions in neighboring boxes. Thus, 949 OCT, 2074 THF, 2371 ACN, and 9394 water molecules were included in the four separate simulations. (For system that includes water as the solvent medium, we performed simulations with and without the surfactant molecules. We found that the surfactant molecules detach from the enzyme surface over a nanosecond timescale, leading to the solvation of the enzyme identical to that in bulk water. That is, the small concentration of surfactants appears to have a minimal effect on the enzyme hydration in aqueous medium.) The total number of atoms in all simulations was at least 30,000.

Partial charges and other force field parameters were taken primarily from Cornell et al. (1995). For molecules not present in this force field, parameters were based on those reported in alternative sources (Ennari et al., 1999; Grabuleda et al., 2000; Huige and Altona, 1995) and are listed in Tables 1–9 along with the accompanying figures in the Supplementary Material. The detailed form of the Hamiltonian is given in Cornell et al. (1995). An all atom TIP3P model was used to represent water molecules (Jorgensen et al., 1983). Sodium and calcium ions were represented using parameters from Straatsma and Berendsen (1988). Constant temperature and pressure MD simulations were performed using AMBER6.0 (Pearlman et al., 1995). Periodic boundary conditions were applied and electrostatic interactions were calculated using the particle mesh Ewald (PME) method (Darden et al., 1993) with a grid spacing of ∼1.0 Å. Bonds involving hydrogens were constrained using the SHAKE algorithm (Ryckaert et al., 1977) with a relative geometric tolerance for coordinate resetting of 0.0005 Å. Berendsen's coupling algorithms were used to maintain a constant temperature of 300 K and pressure of 1 atm (Berendsen et al., 1984). A time step of 2 fs was used in all simulations. Equilibration runs were carried out for 1.0 ns followed by production runs of at least 3.6 ns. The equilibration time of 1 ns used here is longer than that used typically in liquid simulations and is clearly long enough for relaxation and equilibration of water and organic solvent degrees of freedom as discussed later. For these large-scale systems with ∼35,000 atoms, a simulation of 1 ns required ∼20 days of CPU time on a Compaq XP1000 Alpha processor. Coordinates were stored every picosecond for further analysis.

RESULTS AND DISCUSSION

Overall enzyme structure and flexibility in aqueous and nonaqueous media

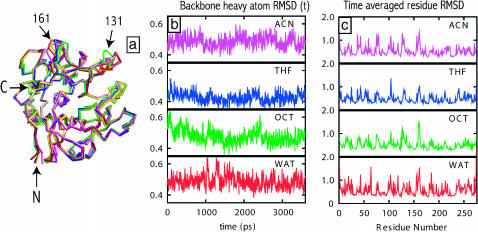
Enzyme structure and flexibility are important determinants of catalytic activity. Therefore, we first studied the effect of different solvent media on the structure and flexibility of subtilisin. Our simulations were initiated using the crystal structure of the enzyme, which relaxes during the simulation. To get an idea of the representative enzyme structure in a given medium, we overlapped and then averaged the time-dependent enzyme structures from a simulation trajectory in that medium. Fig. 2 a shows these representative structures of the enzyme in different solvents superimposed onto the crystal structure. Localized structural differences are observed near the N-termini of enzymes, at the beginning of the helix 133–144, and in the loop region (near Ser-161). These differences are located away from the active site region, confined primarily to the residues on the surface of the enzyme where higher flexibility is expected. Indeed, similar observations were made by Schmitke et al. (1998) through comparisons of free and cinnamoyl-subtilisin structures in water and anhydrous acetonitrile media. Differences in the enzyme's average structures in different media are quantified by calculating root mean square displacement (RMSD) between them (see Table 1). The RMSD values between time-averaged structures are relatively small, less than 1 Å, indicating the lack of any significant structural differences in the enzyme backbone in different media over a timescale of several nanoseconds. The lack of major conformational differences in the enzyme structure reported here is also consistent with previous crystallographic (Fitzpatrick et al., 1993; Schmitke et al., 1997, 1998) as well as MD simulation studies (Hartsough and Merz, 1992; Toba and Merz, 1997).

FIGURE 2.

FIGURE 2

Open in a new tab

Analysis of the enzyme flexibility from MD simulation trajectories: (a) time-averaged backbone structures of subtilisin in water (red), OCT (green), THF (blue), and ACN (magenta) superimposed onto the backbone of crystal structure of subtilisin in water (yellow), (b) instantaneous RMSD of the enzyme backbone in a given solvent from the time-averaged structure in the same solvent, and (c) time-averaged RMSD of residue heavy atoms with respect to their location in the average enzyme structure.

TABLE 1.

Backbone RMSD between time-averaged enzyme structures in different solvents

Crystal WAT OCT THF ACN
Crystal 0 0.62 0.96 0.59 0.67
WAT 0.62 0 0.95 0.56 0.56
OCT 0.96 0.95 0 0.78 0.94
THF 0.59 0.56 0.78 0 0.54
ACN 0.67 0.56 0.94 0.54 0
Open in a new tab

RMSD values between these structures and the crystal structure in water are also included. RMSD values are in Å units.

Thermal fluctuations lead to fluctuations in subtilisin structure during the course of MD simulation. The extent of this structural flexibility is quantified by the backbone RMSD of instantaneous structures of the enzyme from its time-averaged structure. The time dependence of these RMSD values in different solvents is shown in Fig. 2 b. The RMSD values are less than 1 Å, again indicating the absence of large conformational fluctuations from the average structure. Average RMSD values of individual residues from their equilibrium positions (Fig. 2 c) show a similar behavior. We find that the RMSD values range from 0.2 to 2 Å with their average value somewhat below 1 Å in all solvents. These values are akin to the B-factors or temperature factors typically reported in the enzyme crystal structure files. Indeed, locations of the peaks in the RMSD profiles (corresponding to residues on the enzyme surface) correlate well with temperature factors reported in the crystal structure (Pantoliano et al., 1989).

In principle, the overall flexibility of the enzyme characterized by its fluctuations about the equilibrium structure is one of the contributors to the observed enzymatic activity. Although we do not observe large and statistically significant differences in the conformation or flexibility of the enzyme in water and in the three organic solvents, differences in the dynamics of the active site residues can be seen (see Hydration of the Enzyme and Its Active Site). Our observations do not rule out the possible role of large conformational or flexibility changes in enzyme activity. The computational expense of performing atomistic simulations of such large systems (∼35,000 atoms) simply prohibits observations of low frequency and large conformational fluctuations over the simulation timescales. Other important processes such as solvation of the enzyme or solvent dynamics (structural rearrangements and penetration) do indeed occur on much faster timescales, which are accessible to MD simulations as shown below.

Enzyme solvation in different media

Water stripping by solvents

The behavior of water molecules in the vicinity of the enzyme will depend on the nature of the surrounding organic medium. The locations of water molecules in the starting structure in MD simulations were taken from the crystal structure of subtilisin in water. When this structure is placed in aqueous or nonaqueous environments, we expect a change in the locations of water molecules as well as exchange of some water molecules with the molecules in the solvent medium. Such molecular-scale relaxation processes occur over subnanosecond timescales (Garcia and Hummer, 2000). Therefore, we study the equilibrium partitioning of water molecules between the enzyme and its vicinal region and the bulk solution region, which will provide an overall picture of the solvent dependent enzyme hydration.

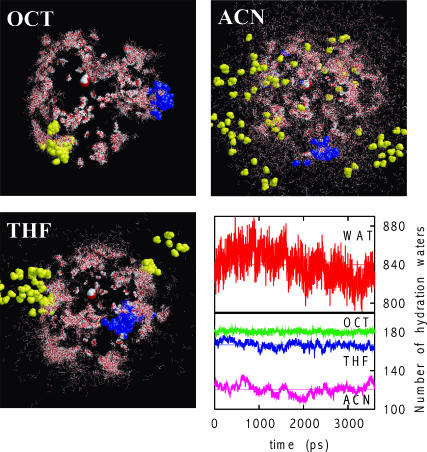
Fig. 3 shows locations of water molecules surrounding the enzyme in OCT, THF, and ACN obtained from the superimposition of ninety equally spaced snapshots from 3.6-ns long MD trajectories. Rigid body rotations and translations were applied to these frames such that enzyme backbones (not shown) are superimposed. The patterns of hydration are strikingly different: whereas most water molecules in OCT remain close to the enzyme, water molecules are stripped off from the enzyme surface in THF, and to a much greater extent in ACN. A preliminary analysis of the dynamics of water molecules was performed. In particular, we calculated the time-dependent RMSD of each water molecule in the system and used the Einstein relation to estimate a value of the translational diffusivity (Allen and Tildesley, 1987). Based on this analysis (i.e., the estimated value of the diffusivity), water molecules can be classified roughly into three categories: tightly bound water molecules that are bound to a specific site of the enzyme, weakly bound water molecules that show interrupted movements between energy minima, and mobile water molecules that show large, bulk water-like, movements. Whereas several numbers of each type of water molecules are observed in three solvents, only one example of each of these three types of water molecules is highlighted in Fig. 3 for visual clarity. Tightly bound water molecules, shown in the red and white spacefill representation are primarily in the enzyme interior. Weakly bound water molecules (blue spacefill) show interrupted motion on the enzyme surface, whereas the relatively mobile water molecules (yellow spacefill) move freely either on certain regions on the enzyme surface (as in OCT) or are stripped off from the surface entirely (as in ACN).

FIGURE 3.

FIGURE 3

Open in a new tab

Water dynamics in organic media (OCT, THF, and ACN) obtained from MD simulations. Water molecules (wireframe red and white) in 90 equally spaced configurations are shown; rigid body rotations and translations were applied such that enzyme backbones (not shown) are superimposed in these snapshots. Based on their dynamics, water molecules can be classified into three categories: tightly bound (red spacefill), weakly bound (blue spacefill), and mobile (yellow spacefill). Only one example (out of many) of each of these three types of water molecules is highlighted in the figure. Although water molecules that are stripped away from the enzyme are always mobile, mobile water molecules can also be found on the enzyme surface (top left). The bottom right panel shows the number of water molecules within 4 Å of the enzyme, the so-called biological water, in different solvents as a function of time. Horizontal lines show the time-averaged values.

Due to the different extents of solvent stripping, at a given overall water content, the amount of biological water available for the enzyme will differ significantly in these media. Such solvent dependent thermodynamic partitioning of water molecules is indeed observed clearly in Fig. 3 (bottom right), which shows the number of water molecules within 4 Å from the enzyme. Close to all of the 186 original water molecules are available for the hydration of enzyme in OCT, whereas 15–20 water molecules are stripped off in THF. The number of water molecules available to the enzyme in ACN is much lower, ∼120 on average. By the same definition, the number of available water in the bulk aqueous solution is, of course, much higher, close to 840 on average. This water stripping behavior is in good agreement with previous experimental observations (Gorman and Dordick, 1992; Schulze and Klibanov, 1991; Wangikar et al., 1997; Zaks and Klibanov, 1988).

Solvent penetration into enzyme

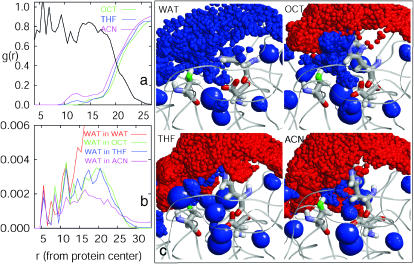
The number of water molecules (equal to 186) included in the simulation is not nearly sufficient to form a complete monolayer surrounding the enzyme. Water molecules therefore hydrate the ionic and polar sites in a patchwork-like fashion leading to a considerable exposure of the enzyme surface to the organic solvent molecules. Fig. 4 a shows spherically averaged densities of heavy atoms of organic solvent molecules OCT, THF, and ACN as a function of distance from the center of the enzyme. A spherically averaged density profile of enzyme heavy atoms from its center is also shown for reference. To some extent, such spherical averaging washes out details of solvation, such as the locations on the enzyme surface where solvent penetration takes place. Nevertheless, the following specific observations can be made. No organic solvent molecules are present in the enzyme interior (r < 9 Å) as shown by zero solvent density in that region. Nonzero solvent densities are, however, observed for r > 9 Å, indicating penetration of the enzyme surface and filling of crevices on the surface by organic solvents to different extents. The catalytic triad of subtilisin is located at distances between 9 Å and 14 Å from its center, which is precisely the region where substantial penetration is observed in Fig. 4 a. Specific details of the active site solvation are discussed in the next subsection. Overall, we find that ACN molecules are able to penetrate the farthest into the enzyme, followed by THF, and then OCT, which penetrates little. This observation complements the water stripping tendency of these solvents observed above. In addition to polarity, the ability of the penetration of the solvent will also depend to some extent on the overall size of the solvent molecules. Thus, the penetration of ACN molecules into crevices on the enzyme surface is likely aided by its relatively smaller size.

FIGURE 4.

FIGURE 4

Open in a new tab

Solvent penetration and the active site hydration in different solvents. (a) Spherically averaged number densities of organic solvent heavy atoms normalized by their bulk density, g(r) = ρ(r)/ρbulk, as a function of distance, r, from the enzyme center. The appropriately scaled density of the enzyme heavy atoms (black line) is shown for reference. (b) Spherically averaged number densities of water molecules (ρwater(r), in units of molecules/Å3) as a function of distance (in Å units) from the enzyme center. c shows the detailed three-dimensional density maps of different molecules in the vicinity of the active site. The enzyme backbone is shown by ribbons, whereas the catalytic triad residues, Asp-32, His-64, and Ser-221, are identified separately in a wireframe representation. The oxygen atom of Ser-221 is colored green to distinguish it from the vicinal density map. The ensemble-averaged densities of water (blue) and organic solvent (red) are shown by spheres of radii proportional to the local density at a grid point. Thus, the large blue spheres indicate tightly bound structural water molecules, whereas uniformly spread smaller blue spheres indicate the weakly bound or mobile water molecules in the active site region.

Hydration of the enzyme and its active site

Spherically averaged densities of water oxygens in different organic solvents as a function of distance from the enzyme center are shown in Fig. 4 b. These density profiles provide information complementary to the solvent penetration data described above. Water density in the enzyme-water system is also shown for reference. For r < 9 Å, i.e., in the enzyme interior, two relatively sharp water density peaks are observed, which indicate primarily structuralwater molecules that are bound tightly to specific sites in the enzyme. For example, the first peak at 5.7 Å from the center corresponds to a water molecule at the bottom of the active site pocket with hydrogen bonding interactions with Asp-32, Ile-31 backbone carbonyl, Asn-123, and the backbone amide group of Ser-125. Three different water molecules within or near the active site contribute to the presence of the second peak around 8.0 Å. Although there is no significant difference in water peak heights in different media at shorter separations, a trend emerges in these profiles at longer separations. For example, in the active site region (9 Å < r < 14 Å), the water density in the enzyme-water system is higher than that in OCT and THF systems and much higher than that in the ACN system. In the interfacial region (14 Å < r < 27 Å), the water density in the bulk water system is significantly higher than in all organic media indicating a well hydrated state of the enzyme in aqueous solution. Water densities in this region appear similar in THF and OCT and are somewhat lower in ACN. This trend in water density in organic solvents reverses beyond 27 Å, which is consistent with the water stripping tendency of polar organic solvents. Similar results are observed in our simulations in which 846 water molecules were included, except that water densities are numerically higher corresponding to a larger level of overall hydration (not shown). It is difficult, however, to quantify an exact distribution of water molecules in the vicinity of the active site pocket from the spherically averaged density profiles presented here. We therefore focus specifically on the active site region below.

Previous simulation studies of biomolecular hydration have characterized the hydration of specific regions of biomolecules by calculating local density of water molecules in those regions (Cheng and Rossky, 1998; Garcia et al., 1997). Although local densities can be calculated by placing a cubic grid in that region, the numerical values of densities are dependent on the size of the bin. For example, the use of a larger bin size (≈1 Å) averages density in a larger volume thereby providing a coarse-grained picture of hydration. In contrast, the use of smaller bin sizes resolves density variations better but, at the same time, enhances local density values due to smaller bin volumes involved. We used bin widths of 1.0, 0.5, and 0.25 Å in our calculations that provided results consistent with each other. We found, however, that calculations using bin width of 0.25 Å provided the clearest picture of the active site solvation. We represented local densities or, alternatively, the average number of water molecules observed in a given bin by spheres of proportional sizes. Significantly high numerical values of local densities were all represented by the spheres of the same largest size, whereas locations with very low densities were not shown for visual clarity. Water and solvent densities are shown only in the vicinity of the active site; including a larger region only obscures the interesting details of hydration shown in Fig. 4. Although the above representation focuses on the time-averaged equilibrium density profiles of molecules, qualitative dynamic information can be inferred from these profiles as well. For example, a tightly bound water molecule gives a constant large localized density at its location, which is represented by a large blue sphere, whereas dynamic water molecules give a uniformly distributed density pattern of smaller blue spheres.

The spatial density profiles in Fig. 4 highlight key differences in the character of enzyme hydration in different media. In the enzyme-water system (top left), a large fraction of the space is occupied by weakly bound or mobile water molecules (uniformly spread smaller blue spheres); in addition, a small number of tightly bound structural water molecules (larger blue spheres) are also present. The locations of structural water molecules are found to be below the enzyme surface slightly away from the solvent water. The uniform spread of weakly bound or mobile water throughout the region indicates that the active site is well hydrated in aqueous solution. The density map in OCT similarly shows mobile or weakly bound water molecules throughout the active site region sandwiched between the enzyme and an envelope of OCT molecules surrounding the enzyme. In contrast, in polar organic solvent environments, the number of water density spheres is considerably reduced indicating a lower degree of the active site hydration. In the active site region in THF, we observe penetration of THF molecules as shown by the red spheres. The integration of water density profiles from the active site center indicates that THF penetration leads to an average loss of approximately only two hydration water molecules from this region compared to that in OCT. The density distribution of the water molecules remaining in the active site region in THF is, however, remarkably different from that in OCT. Whereas the hydration water molecules in OCT are more uniformly distributed and, therefore, weakly bound or mobile, those in THF are considerably more localized as indicated by localized larger water density spheres (Fig. 4 c, bottom left). In ACN medium, the higher penetration of ACN molecules in the active site leads to a considerable loss of hydration water from that region as seen in Fig. 4 c (bottom right). A similar penetration of the active site and concomitant replacement of the active site water by ACN molecules has been observed previously in crystallographic experiments (Schmitke et al., 1998).

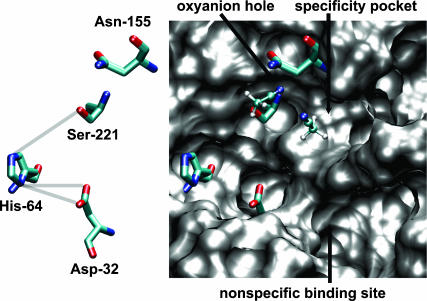
The catalytic mechanism of subtilisin, a serine protease, has been studied previously (Wells and Estell, 1988). Four structural features important for enzymatic activity have been identified, namely, the catalytic triad (Ser-221, His-64, and Asp-32), an oxyanion hole (Asn-155 and Ser-221), the specificity pocket, and the nonspecific binding site. Site directed mutagenesis studies point toward a synergestic catalytic mechanism that involves the attack by the Ser-221 oxygen on the carbonyl carbon of the peptide in the rate determining acylation step (Wells and Estell, 1988). A network of low-barrier hydrogen bonds between the nitrogen of His-64 and the hydrogen of Ser-221 (HB1), and that between Asp-32 oxygen and hydrogen of His-64 (HB2), is known to form. Dissimilar solvation of the active site in different solvents can therefore contribute to different subtilisin activities (Schmitke et al., 1998). Our simulations are performed for the free enzyme without the substrate present. In the substrate binding step, some water or organic solvent molecules from the active site region will need to be removed for efficient binding. Further, catalysis requires that the oxyanion hole be available and that either the catalytic water in the hydrolysis reaction in water or a nucleophile (e.g., an alcohol molecule) in the deacylation step of the transesterification reaction in organic solvents needs to be present in the correct location. In water and in OCT, the active site is hydrated primarily by dynamic water molecules, whereas tightly bound water molecules are present in THF and ACN in that region, which could obstruct substrate binding. Specifically, a more tightly bound water molecule is present near the oxyanion hole in THF, which gets replaced by an ACN molecule in the ACN medium. Fig. 5 indeed shows two ACN molecules that penetrate into the specificity pocket (with the CH3 end pointed in) and near the catalytic water/oxyanion hole region of the active site. The locations where the two ACN molecules bind are identical to those observed in previous crystallography experiments (Schmitke et al., 1998). The removal of the tightly bound ACN from the specificity pocket (Fig. 5) will require extra energy to allow substrate binding. Further, replacement of the ACN molecule at the catalytic water location is required during the deacylation step possibly contributing to the observed differences in subtilisin activities.

FIGURE 5.

FIGURE 5

Open in a new tab

Representative MD snapshot of the active site of subtilisin in ACN. The catalytic triad and Asn-155 of the oxyanion hole are shown with sticks, and the ACN molecules are shown with balls-and-sticks (carbon, light green; oxygen, red; nitrogen, blue; and hydrogen, white). The van der Waals surface (generated by VMD; Humphrey et al., 1996) of the protein in the active site region is shown in gray.

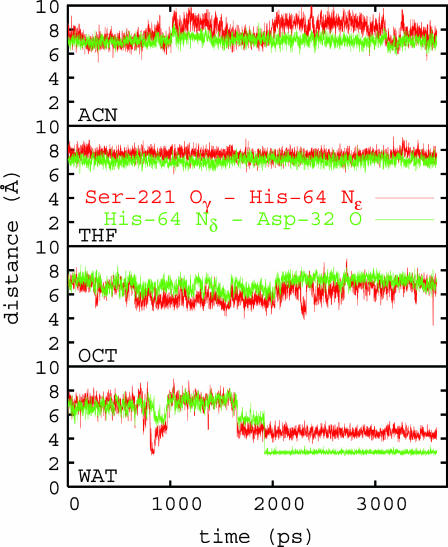
Distances between heavy atoms involved in hydrogen bonds HB1 and HB2, referred to above, are shown in Fig. 6. In water, the formation of favorable hydrogen bonds occurs within a nanosecond timescale as shown by shorter heavy atom distances (≈2–4 Å). Hydrogen bond formation is not observed to the same extent in organic solvents over the simulation timescale. HB distances are shorter in OCT, however, compared to that in THF and ACN. The time dependence of HB distances shows significant fluctuations in water, OCT, and ACN, indicating the higher flexibility of residues involved in the H-bond network in those media compared to THF. These observations again are related to the characteristic patterns of hydration of the active site region shown in Fig. 4 and specifically to the presence of tightly bound water molecule in THF and ACN near Asp-32 and His-64.

FIGURE 6.

FIGURE 6

Open in a new tab

The time-dependent distances between heavy atoms involved in hydrogen bonds HB1 and HB2; from Ser-221 Oγatom to His-64 Nε atom (red) and from His-64 Nδ to Asp-32 O (green) in different organic solvents and in water.

Experiments show that the catalytic activity of sublitisin is highest in water and decreases as the reaction medium is changed from water to OCT, to THF, and to ACN. In OCT, the kcat/Km for transesterification of N-acetyl-L-phenylalanine ethyl ester is 370 M−1s−1, within one order of magnitude of the enzyme's hydrolytic activity in water (kcat/Km ∼ 3500 M−1s−1). This value decreases to 0.36 M−1s−1 in THF and is almost undetectable in ACN (Wangikar et al., 1997). The characteristics of the active site hydration in different solvent environments reported above correlate well with the observed enzymatic activity of surfactant-solubilized subtilisin in those media. Overall, the analysis of MD simulations presented here suggests that the nature of the active site hydration and solvent penetration may play an important role in enzyme function. In particular, the hydration of the active site region with weakly bound and mobile water molecules may be essential for maintaining the enzyme function. The stripping of mobile or weakly bound water molecules from the active site region and their replacement by organic solvent molecules, or the presence of only the most tightly bound water molecules in the active site region, will present obstruction for substrate binding and subsequent catalysis steps.

CONCLUSIONS

We studied the effect of different organic solvent molecules on enzyme hydration and solvent binding in the active site through MD simulations, which provide a detailed molecular picture of enzyme in aqueous and different nonaqueous media. We find that the overall enzyme structure and its flexibility over a timescale of several nanoseconds do not show significant differences in water and in different organic media. In the absence of large conformational changes over this timescale, the key factor that distinguishes molecular-level details in different media is the partitioning of the hydration water between the enzyme and the bulk solvent. The enzyme surface as well as its active site are well hydrated in aqueous solution. However, that hydration water is removed from the enzyme to different extents by organic solvents depending on their polarity. In OCT, the active site is hydrated uniformly by weakly bound and mobile water molecules, whereas in ACN much of the hydration water is extracted from the enzyme accompanied by the penetration and binding of the ACN molecules in the active site. Interestingly, in THF, although only a small number of water molecules are stripped off, the hydration water molecules appear more localized as a result of THF penetration into the active site, likely leading to a much lower enzyme activity in THF compared to that in OCT. Experiments show the inverse dependence of enzyme activity on the polarity of the organic medium employed (Wangikar et al., 1997). Although classical MD calculations of free enzyme are not sufficient to make direct quantitative connections with those experimental results, they highlight the important role of the details of enzyme hydration in determining its catalytic activity.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

Acknowledgments

We gratefully acknowledge partial financial support of the National Science Foundation (CAREER award CTS-0134023 to S.G. and BES-9811352 and BES-0227783 to J.S.D.). We also acknowledge financial support of the National Science Foundation Nanoscale Science and Engineering Center for Directed Assembly of Nanostructures (DMR-0117792). L.Y. thanks the Biochemical Engineering Fellowship provided by the Department of Chemical Engineering at Rensselaer Polytechnic Institute.

References

  1. Affleck, R., Z. F. Xu, V. Suzawa, K. Focht, D. S. Clark, and J. S. Dordick. 1992. Enzymatic catalysis and dynamics in low-water environments. Proc. Natl. Acad. Sci. USA. 89:1100–1104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Allen, M. P., and D. J. Tildesley. 1987. Computer Simulation of Liquids. Clarendon Press, Oxford, UK.
  3. Bell, G., P. J. Halling, B. D. Moore, J. Partridge, and D. G. Rees. 1995. Biocatalyst behaviour in low-water systems. Trends Biotechnol. 13:468–473. [Google Scholar]
  4. Bell, G., A. E. M. Janssen, and P. J. Halling. 1997. Water activity fails to predict critical hydration level for enzyme activity in polar organic solvents: interconversion of water concentrations and activities. Enzyme Microb. Technol. 20:471–477. [Google Scholar]
  5. Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, A. DiNola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
  6. Carrea, G., and S. Riva. 2000. Properties and synthetic applications of enzymes in organic solvents. Angew. Chem. Int. Ed. 39:2226–2254. [PubMed] [Google Scholar]
  7. Cheng, Y. K., and P. J. Rossky. 1998. Surface topography dependence of biomolecular hydrophobic hydration. Nature. 392:696–699. [DOI] [PubMed] [Google Scholar]
  8. Cornell, W. D., P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell, and P. A. Kollman. 1995. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 117:5179–5197. [Google Scholar]
  9. Craik, C. S., C. Largman, T. Fletcher, S. Roczniak, P. J. Barr, R. Fletterick, and W. Rutter. 1985. Redesigning trypsin: alteration of substrate-specificity. Science. 228:291–297. [DOI] [PubMed] [Google Scholar]
  10. Dabulis, K., and A. M. Klibanov. 1993. Dramatic enhancement of enzymatic-activity in organic-solvents by lyoprotectants. Biotechnol. Bioeng. 41:566–571. [DOI] [PubMed] [Google Scholar]
  11. Darden, T., D. York, and L. Pedersen. 1993. Particle mesh Ewald: an N·log(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
  12. de Sampaio, T. C., R. B. Melo, T. F. Moura, S. Michel, and S. Barreiros. 1996. Solvent effects on the catalytic activity of subtilisin suspended in organic solvents. Biotechnol. Bioeng. 50:257–264. [DOI] [PubMed] [Google Scholar]
  13. Dill, K. A. 1990. Dominant forces in protein folding. Biochemistry. 29:7133–7155. [DOI] [PubMed] [Google Scholar]
  14. Dordick, J. S. 1992. Designing enzymes for use in organic solvents. Biotechnol. Prog. 8:259–267. [DOI] [PubMed] [Google Scholar]
  15. Ennari, J., M. Elomaa, and F. Sundholm. 1999. Modelling a polyelectrolyte system in water to estimate the ion-conductivity. Polymer. 40:5035–5041. [Google Scholar]
  16. Fersht, A. 1999. Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding. W. H. Freeman, New York.
  17. Fitzpatrick, P. A., A. C. U. Steinmetz, D. Ringe, and A. M. Klibanov. 1993. Enzyme crystal structure in a neat organic solvent. Proc. Natl. Acad. Sci. USA. 90:8653–8657. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Garcia, A. E., and G. Hummer. 2000. Water penetration and escape in proteins. Proteins. 38:261–271. [PubMed] [Google Scholar]
  19. Garcia, A. E., G. Hummer, and D. M. Soumpasis. 1997. Hydration of an alpha-helical peptide: comparison of theory and molecular dynamics simulation. Proteins. 27:471–480. [PubMed] [Google Scholar]
  20. Gorman, L. A. S., and J. S. Dordick. 1992. Organic-solvents strip water off enzymes. Biotechnol. Bioeng. 39:392–397. [DOI] [PubMed] [Google Scholar]
  21. Grabuleda, X., C. Jaime, and P. A. Kollman. 2000. Molecular dynamics simulation studies of liquid acetonitrile: new six-site model. J. Comput. Chem. 21:901–908. [Google Scholar]
  22. Halling, P. J. 1994. Thermodynamic predictions for biocatalysis in nonconventional media: theory, tests, and recommendations for experimental design and analysis. Enzyme Microb. Technol. 16:178–206. [DOI] [PubMed] [Google Scholar]
  23. Halling, P. J. 2000. Biocatalysis in low-water media: understanding effects of reaction conditions. Curr. Opin. Chem. Biol. 4:74–80. [DOI] [PubMed] [Google Scholar]
  24. Hartmann, M., K. M. Merz, R. van Eldik, and T. Clark. 1998. The important role of active site water in the catalytic mechanism of human carbonic anhydrase ii – a semiempirical MO approach to the hydration of CO2. J. Mol. Model. 4:355–365. [Google Scholar]
  25. Hartsough, D. S., and K. M. Merz. 1992. Protein flexibility in aqueous and nonaqueous solutions. J. Am. Chem. Soc. 114:10113–10116. [Google Scholar]
  26. Heine, A., G. DeSantis, J. G. Luz, M. Mitchell, C. H. Wong, and I. A. Wilson. 2001. Observation of covalent intermediates in an enzyme mechanism at atomic resolution. Science. 294:369–374. [DOI] [PubMed] [Google Scholar]
  27. Huige, C. J. M., and C. Altona. 1995. Force-field parameters for sulfates and sulfamates based on ab-initio calculations: extensions of AMBER and CHARMm fields. J. Comput. Chem. 16:56–79. [Google Scholar]
  28. Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD—visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
  29. Jorgensen, W. L., J. Chandrashekhar, J. D. Madura, R. W. Impey, and M. L. Klein. 1983. Comparison of simple liquid potentials for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
  30. Kauzmann, W. 1959. Some factors in the interpretation of protein denaturation. Adv. Prot. Chem. 14:1–63. [DOI] [PubMed] [Google Scholar]
  31. Klibanov, A. M. 1997. Why are enzymes less active in organic solvents than in water? Trends Biotechnol. 15:97–101. [DOI] [PubMed] [Google Scholar]
  32. Klibanov, A. M. 2001. Improving enzymes by using them in organic solvents. Nature. 409:241–246. [DOI] [PubMed] [Google Scholar]
  33. Kraut, J. 1977. Serine proteases: structure and mechanism of catalysis. Annu. Rev. Biochem. 46:331–358. [DOI] [PubMed] [Google Scholar]
  34. Kwon, O. H., Y. Imanishi, and Y. Ito. 1999. Catalytic activity and conformation of chemically modified subtilisin Carlsberg in organic media. Biotechnol. Bioeng. 66:265–270. [DOI] [PubMed] [Google Scholar]
  35. Lee, C. S., M. T. Ru, M. Haake, J. S. Dordick, J. A. Reimer, and D. S. Clark. 1998. Multinuclear NMR study of enzyme hydration in an organic solvent. Biotechnol. Bioeng. 57:686–693. [PubMed] [Google Scholar]
  36. Novick, S. J., and J. S. Dordick. 2000. Investigating the effects of polymer chemistry on activity of biocatalytic plastic materials. Biotechnol. Bioeng. 68:665–671. [DOI] [PubMed] [Google Scholar]
  37. Pal, S. K., J. Peon, and A. H. Zewail. 2002. Biological water at the protein surface: dynamical solvation probed directly with femtosecond resolution. Proc. Natl. Acad. Sci. USA. 99:1763–1768. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Pantoliano, M. W., M. Whitlow, J. F. Wood, S. W. Dodd, K. D. Hardman, M. L. Rollence, and P. N. Bryan. 1989. Large increases in general stability for subtilisin BPN′ through incremental changes in the free-energy of unfolding. Biochemistry. 28:7205–7213. [DOI] [PubMed] [Google Scholar]
  39. Paradkar, V. M., and J. S. Dordick. 1994a. Aqueous-like activity of alpha-chymotrypsin dissolved in nearly anhydrous organic-solvents. J. Am. Chem. Soc. 116:5009–5010. [Google Scholar]
  40. Paradkar, V. M., and J. S. Dordick. 1994b. Mechanism of extraction of chymotrypsin into isooctane at very low concentrations of aerosol ot in the absence of reversed micelles. Biotechnol. Bioeng. 43:529–540. [DOI] [PubMed] [Google Scholar]
  41. Partridge, J., P. R. Dennison, B. D. Moore, and P. J. Halling. 1998. Activity and mobility of subtilisin in low water organic media: hydration is more important than solvent dielectric. Biochim. Biophys. Acta. 1386:79–89. [DOI] [PubMed] [Google Scholar]
  42. Partridge, J., B. D. Moore, and P. J. Halling. 1999. Alpha-chymotrypsin stability in aqueous-acetonitrile mixtures: is the native enzyme thermodynamically or kinetically stable under low water conditions? J. Mol. Catal. B-Enzym. 6:11–20. [Google Scholar]
  43. Pearlman, D. A., D. A. Case, J. W. Caldwell, W. S. Ross, T. E. Cheatham, S. Debolt, D. Ferguson, G. Seibel, and P. Kollman. 1995. AMBER, a package of computer-programs for applying molecular mechanics, normal-mode analysis, molecular-dynamics and free-energy calculations to simulate the structural and energetic properties of molecules. Comp. Phys. Commun. 91:1–41. [Google Scholar]
  44. Ru, M. T., S. Y. Hirokane, A. S. Lo, J. S. Dordick, J. A. Reimer, and D. S. Clark. 2000. On the salt-induced activation of lyophilized enzymes in organic solvents: effect of salt kosmotropicity on enzyme activity. J. Am. Chem. Soc. 122:1565–1571. [Google Scholar]
  45. Ryckaert, J. P., G. Ciccotti, and H. J. C. Berendsen. 1977. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comp. Phys. 23:327–341. [Google Scholar]
  46. Schmid, A., J. S. Dordick, B. Hauer, A. Kiener, M. Wubbolts, and B. Witholt. 2001. Industrial biocatalysis today and tomorrow. Nature. 409:258–267. [DOI] [PubMed] [Google Scholar]
  47. Schmitke, J. L., L. J. Stern, and A. M. Klibanov. 1997. The crystal structure of subtilisin carlsberg in anhydrous dioxane and its comparison with those in water and acetonitrile. Proc. Natl. Acad. Sci. USA. 94:4250–4255. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Schmitke, J. L., L. J. Stern, and A. M. Klibanov. 1998. Comparison of x-ray crystal structures of an acyl-enzyme intermediate of subtilisin carlsberg formed in anhydrous acetonitrile and in water. Proc. Natl. Acad. Sci. USA. 95:12918–12923. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Schulze, B., and A. M. Klibanov. 1991. Inactivation and stabilization of subtilisins in neat organic-solvents. Biotechnol. Bioeng. 38:1001–1006. [DOI] [PubMed] [Google Scholar]
  50. Straatsma, T. P., and H. J. C. Berendsen. 1988. Free energy of ionic hydration: analysis of a thermodynamic integration technique to evaluate free energy differences by molecular dynamics simulations. J. Chem. Phys. 89:5876–5886. [Google Scholar]
  51. Tanford, C. 1973. The Hydrophobic Effect: Formation of Micelles and Biological Membranes. John Wiley, New York.
  52. Toba, S., and K. M. Merz. 1997. The concept of solvent compatibility and its impact on protein stability and activity enhancement in nonaqueous solvents. J. Am. Chem. Soc. 119:9939–9948. [Google Scholar]
  53. Wang, P., M. V. Sergeeva, L. Lim, and J. S. Dordick. 1997. Biocatalytic plastics as active and stable materials for biotransformations. Nat. Biotechnol. 15:789–793. [DOI] [PubMed] [Google Scholar]
  54. Wangikar, P. P., P. C. Michels, D. S. Clark, and J. S. Dordick. 1997. Structure and function of subtilisin BPN′ solubilized in organic solvents. J. Am. Chem. Soc. 119:70–76. [Google Scholar]
  55. Warshel, A., G. Narayszabo, F. Sussman, and J. K. Hwang. 1989. How do serine proteases really work? Biochemistry. 28:3629–3637. [DOI] [PubMed] [Google Scholar]
  56. Wells, J. A., and D. A. Estell. 1988. Subtilisin - an enzyme designed to be engineered. Trends Biochem. Sci. 13:291–297. [DOI] [PubMed] [Google Scholar]
  57. Zaks, A., and A. M. Klibanov. 1985. Enzyme-catalyzed processes in organic-solvents. Proc. Natl. Acad. Sci. USA. 82:3192–3196. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Zaks, A., and A. M. Klibanov. 1988. Water activity. J. Biol. Chem. 263:8017–8021. [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES