Hill Coefficient for Estimating the Magnitude of Cooperativity in Gating Transitions of Voltage-Dependent Ion Channels

Abstract

A frequently used measure for the extent of cooperativity in ligand binding by an allosteric protein is the Hill coefficient, obtained by fitting data of initial reaction velocity (or fractional binding saturation) as a function of substrate concentration to the Hill equation. Here, it is demonstrated that the simple two-state Boltzmann equation that is widely used to fit voltage-activation data of voltage-dependent ion channels is analogous to the Hill equation. A general empiric definition for a Hill coefficient (n_H) for channel gating transitions that is analogous to the logarithmic potential sensitivity function of Almers is derived. This definition provides a novel framework for interpreting the meaning of the Hill coefficient. In considering three particular and simple gating schemes for a voltage-activated cation channel, the relation of the Hill coefficient to the magnitude and nature of cooperative interactions along the reaction coordinate of channel gating is demonstrated. A possible functional explanation for the low value of the Hill coefficient for gating transitions of the Shaker voltage-activated K⁺ channel is suggested. The analogy between the Hill coefficients for ligand binding and for channel gating transitions further points to a unified conceptual framework in analyzing enzymes and channels behavior.

INTRODUCTION

Voltage-activated Na⁺, K⁺, and Ca²⁺ channels are multisubunits/protomers allosteric proteins that undergo voltage-induced conformational transitions between closed and open states (Almers, 1978; Sigworth, 1994; Yellen, 1998; Bezanilla, 2000). The voltage sensitivity of these channels arises from voltage-induced displacement of charges across the membrane electric field, a phenomenon first noted by Hodgkin and Huxley (1952). These voltage-sensing charges were later found to be alternating basic amino acids that are uniquely arranged at the S₄ transmembrane helix, a motif common to all voltage-activated cation channels (Noda et al., 1984; Stuhmer et al., 1989; Papazian et al., 1991; Liman et al., 1991). In the Shaker voltage-dependent K⁺ channel, for example, the gating charge corresponds to nearly 12–14 electron charge units traversing the membrane electric field (Schoppa et al., 1992; Seoh et al., 1996; Aggarwal and MacKinnon, 1996). Similar number of gating charges move across the membrane electric field when skeletal muscle Na⁺ channels are opened (Hirschberg et al., 1995). Additional contributions to the voltage sensitivity of these channels may arise, however, from cooperative interactions along the activation pathways of such channels (Papazian et al., 1991; McCormack et al., 1991; Schoppa et al., 1992; Tytgat and Hess, 1992; Zagotta et al., 1994; Smith-Maxwell et al., 1998a). Such interactions give rise to cooperativity in channel gating transitions. In the following, cooperativity in channel function is interpreted in a simple, intuitive, and traditional way. We ask how the switch of one subunit from the closed to the open state affects the gating transitions of its neighboring subunits (may be more than one transition for each subunit). In other words, considering cooperativity in channel gating addresses the coupling between the channel's subunits. The extreme case is the two-state model in which all four subunits of the channel switch in a concerted manner—all at once—from the closed to the open state. Alternatively, subunits switching from closed to the open state may occur in an independent fashion, in which channel subunits do not “sense” the conformational state(s) of their adjacent subunits. Cooperative interactions along the reaction coordinate of channel gating may originate from intersubunit interactions in sequential KNF-type (Koshland et al., 1966) transitions of the channel, from MWC-type (Monod et al., 1965) concerted transition(s) along the channel activation pathway or from combination of both (for detailed discussion, see Sigworth, 1994; Zagotta et al., 1994). An estimate of the magnitude of these interactions is the effective gating charge (Z), obtained by fitting the voltage-activation data of a channel to a two-state Boltzmann equation, derived assuming equilibrium of the channel between the closed and open states. As already pointed out, the essence of Z is intuitively reminiscent of the Hill coefficient used to describe the magnitude of cooperativity in ligand binding allosteric systems (Almers, 1978; Islas and Sigworth, 1999).

In what follows, is a rigorous demonstration that the two-state voltage-dependent Boltzmann equation is analogous to the original Hill equation. A framework to understand the meaning of the Hill coefficient for channel gating transitions is suggested. Using three particular and simple gating schemes for channel activation, the relation of n_H to the magnitude and nature of cooperativity in channel gating transitions is demonstrated.

RESULTS AND DISCUSSION

Hill coefficient (n_H) for assessing cooperativity in channel gating transitions

Gating transitions of voltage-activated cation channels are usually studied by measuring voltage-activation relations of the channel. In such measurements, the transition of the channel from the closed to the opened state(s) is induced by changes in the membrane voltage and the elicited ionic currents resulting from ions flow through the open channels are recorded. The probability of the channel to be open and its dependence on voltage is then inferred by plotting the normalized tail current amplitude as a function of voltage (G–V curve). Whereas the total gating charge per channel may be determined by measuring the slope of the G–V curve at very low open probabilities (Almers, 1978), the magnitude of cooperative interactions along the channel activation pathway may be assessed by the slope of such a relation at moderate-range open probabilities (Smith-Maxwell et al., 1998b). An estimate for the slope of the G–V curve at these latter values is frequently obtained by fitting activation data to a Boltzmann equation, derived assuming a simple two-state model for channel activation. According to this model, the equilibrium between the closed (C) and open (O) states of the channel is voltage-dependent (K(V)) and is given by

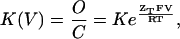(1)

where K is the chemical equilibrium constant for channel gating in the absence of voltage (at 0 mV), Z_T is the total gating charge of the channel that moves across the membrane electrical field upon depolarization, and all the other constants have their usual thermodynamic meaning. This equation can be transformed into a different form as

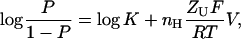(2)

where P is the probability of the channel being open (P = (O/(O+C))), n_H is the number of channel subunits (or protomers), and Z_U is the unitary gating charge associated with one subunit (Z_T = n_H Z_U). Written in this form, it is worth noting the similarity of the equation to the Hill equation that is extensively used to estimate the magnitude of cooperativity in multisubunits' allosteric enzymes (Hill, 1910),

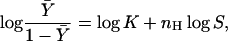(3)

where 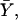the fractional binding saturation function, is the fraction of sites occupied with the substrate (S), n_H is the Hill coefficient, and K is the apparent binding constant of the substrate to the enzyme. This equation was derived assuming an infinitely cooperative case, i.e., where n substrate molecules bind simultaneously to the enzyme. In practice, however, by fitting experimental binding data with the Hill equation, a value between 1 and the total number of binding sites (n) is frequently observed for n_H. n_H, therefore, is an index of cooperativity in ligand binding. Whereas n_H = n reflects cooperative and concerted ligand binding to the enzyme, n_H = 1 reflects noncooperative (independent) sequential binding. Although the last statement is true in the case of many allosteric enzymes, the relation of n_H to cooperativity in ligand binding is not always correct, as n_H depends on the specific details of the ligation reaction (see below).

The analogy between the Hill equation and the Hill form of the Boltzmann equation is not surprising, bearing in mind the underlying assumption of the Boltzmann equation of one concerted transition of all channel subunits (or protomers) from the closed to open state. The similarity between the two equations is not just in structure but also in essence; conformational transitions within a protein may be driven by changes in chemical potential (logS, in the case of ligand-binding systems) or by changes in electrical potential (Z_UFV/RT, in the case of voltage-gated ion channels). Given that the unitary gating charge of the channel is known, fitting channel activation data to the Hill form of the Boltzmann equation may yield a value for the Hill coefficient for channel gating transitions. In a simple way, this allows for comparison of the magnitude of steady-state cooperativity in channel gating transitions between different subtypes of the same channel or between different cation channels, irrespective of differences in the nominal gating charge of the channels. Hill coefficient values for gating transitions of ion channels may be also compared to those derived for other allosteric enzymes like hemoglobin, aspartate transcarbamylase and the GroEL chaperonin. It should be stressed, however, that although it is a common practice to compare Hill values of different proteins, such comparisons, as will be evident later on, are more informative when comparing channels that gate according to similar activation mechanisms. Fitting the Shaker K⁺ channel activation data to the Hill form of the Boltzmann equation (assuming a unitary gating charge of 3) yields a value slightly above 1 for the Hill coefficient (data not shown) (Yifrach and Mackinnon, 2002). Taking into account the tetrameric organization of K⁺ channels (MacKinnon, 1991), this low n_H value obtained for the Shaker K⁺ channel may reflect the fact that the activation pathway of this channel involves many independent subunit transitions (Zagotta et al., 1994; Schoppa and Sigworth, 1998). A possible functional explanation for this low Hill value for the Shaker K⁺ channel will be discussed later.

n_H depends on the Adair-like model parameters

The form of the Hill equation for channel gating transitions (Eq. 2) is based on the assumption that no intermediate states exist along the channel gating reaction, or in other words, that all four channel's subunits switch at once from the closed to fully open state. This, of course, is far from reality for almost all channels studied thus far. Gating reactions of ion channels are much more complicated than predicted by a two-state scheme, requiring many closed and (sometimes) open states (Sigworth, 1994; Zagotta et al., 1994; Bezanilla, 2000). For a channel that gates according to a multistates activation scheme, how reliable is it then to estimate the magnitude of cooperativity in gating transitions using a two-state Hill equation? A similar reservation was made by Adair with respect to the use of the Hill equation to assess the extent of cooperativity in oxygen binding to hemoglobin (Adair et al., 1925). It should be stressed, however, that plotting a channel's open-probability data according to the Hill form of the Boltzmann equation is a legitimate procedure. It is instead the interpretation of the Hill coefficient that requires detailed analysis. Accordingly, and in analogy to ligand binding allosteric systems (Levitzki, 1978), expressions for n_H that depend on the Adair-like constants for particular channel gating schemes can be derived. This allows more precise understanding of the meaning of the Hill coefficient.

A general definition for a Hill coefficient for gating transitions may be derived from Eq. 2 as follows:

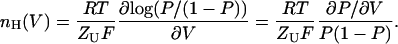(4)

This definition of n_H(V) is analogous to the logarithmic potential sensitivity function of Almers (1978; see Eq. 32 therein), derived for the general case of sequential transitions along a channel's activation pathway. The analogy is interesting when considered from historical perspective. In Almers' original derivation, the total channel gating charge (q_T) was multiplied by a fractional number that is dependent on the number and nature of intermediate states along the gating reaction (Almers, 1978). This number is, in any sense, a scaled Hill-like number. Only several years later, upon cloning of the first voltage-activated channels, was the tetrameric organization of these channels realized (Noda et al., 1984; Tanabe et al., 1987; MacKinnon, 1991). This fact, combined with more accurate determination of the total gating charge per channel (Schoppa et al., 1992; Seoh et al., 1996; Aggarwal and MacKinnon, 1996), allowed, by inference, determination of the unitary gating charge per subunit (Z_U). Incorporating Z_U in Eq. 2 gives n_H its common traditional view, i.e., number of subunits/protomers (normally, 1 ≤ n_H ≤ n).

The general definition of the Hill equation given here (Eq. 4) is also reminiscent of the equation derived by Sigg and Bezanilla describing the dependence of the mean activation charge, 〈q_A〉 (the actual gating charge that is energetically coupled to channel opening), on gating charge displacement (Sigg and Bezanilla, 1997). In that study, the following expression for 〈q_A〉 was derived following a detailed and thorough statistical mechanics analysis,

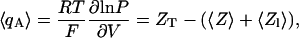(5)

where 〈Z〉 and 〈Z_l〉 are the equilibrium gating charge displacement and the latent gating charge (the effective charge movement during transitions among open states), respectively. It can be easily seen that Eqs. 4 and 5 may be combined to yield the following expression for n_H,

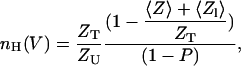(6)

which can be reduced to the following expression for a channel for which 〈Z_l〉 = 0,

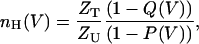(7)

where Q(V) and P(V) are equivalent to the normalized, experimentally determined open probability and charge movement curves, respectively. Equations 5–7, in the context of the Hill analysis developed here, highlight the importance of performing gating currents measurements (Q(V) curves) to gain mechanistic insight regarding the voltage sensitivity of ion channels (Seoh et al., 1996; Sigg and Bezanilla, 1997; Islas and Sigworth, 1999). The magnitude and direction of displacement of the Q(V) curve along the voltage axis with respect to the P(V) curve can be compared. In the simplest case, the two curves will coincide in the case of two-state gating model for which n_H = Z_T/Z_U for the entire voltage range. For the Shaker voltage-gated K⁺ channel that gates according to an activation pathway involving many closed states and one open state (Zagotta et al., 1994; Schoppa and Sigworth, 1998), the Q(V) curve is shifted to the left along the voltage axis with respect to the P(V) curve. This observation combined with results demonstrating that the latent gating charge for this channel is very low (Islas and Sigworth, 1999) may explain the low value of n_H obtained at moderate-range open probabilities for which (1–Q(V))/(1–P(V)) is always smaller than 1. For this case, n_H will equal n, the total number of channel subunits, only at an Almers' range of very low open probabilities achieved at extremely negative voltages. For the general case, analysis using Eq. 5 above (or Eq. 6 within the context of the present analysis) may yield additional insight into the meaning of n_H (Sigg and Bezanilla, 1997).

The definition for the Hill coefficient for channel gating transitions (Eq. 4) makes intuitive sense—n_H is a scaled slope of an open probability function (∂P/∂V) relative to the slope of a reference open probability function (ZF/RT)(P(1–P)), derived for a gating scheme that assumes independent subunit transitions. It can be shown that for an independent gating scheme of the sort the slope of the open probability function with respect to voltage (∂P/∂V) is equal to the scaled multiplication of the probabilities of the channel to be closed and to be opened (P(1–P)(ZF/RT)). For the scheme above, C and O are the respective subunit conformations in the closed and open states and K(V) is the equilibrium constant for subunit transitions. It is also assumed that both the CO and OO states are conductive. Thus, a Hill coefficient value of 1 will be obtained for n_H if the slope of the open probability function (∂P/∂V) is equal to that of the independent, noncooperative case. Deviations of the Hill value from 1 may indicate the existence of cooperativity in channel gating transitions—a reflection of coupling between the channel's subunits. Using this empirical definition of cooperativity in channel gating transitions, one may derive explicit expressions for n_H for different channel gating schemes (different P schemes).

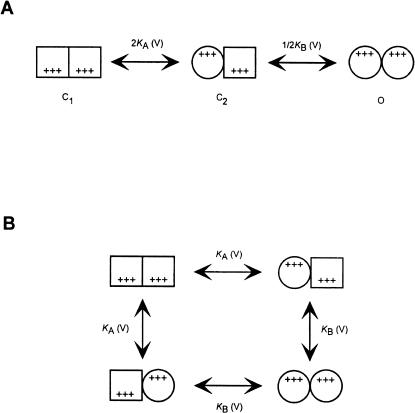
n_H for a KNF-type gating model

Consider, for example, the following simple gating scheme for a homodimeric channel undergoing two sequential KNF-type subunit (or protomer) transitions (Koshland et al., 1966), as shown in Fig. 1 A. In this gating scheme, it is assumed that the channel is open only when both subunits are in the open state (O state). Using the principle of microscopic reversibility and Boltzmann-type transitions for channel subunits/protomers (Eq. 1), one can derive expressions for P, 1–P, and ∂P/∂V for this gating scheme and substitute them into Eq. 4 to obtain the expression for n_H,

(8)

It may be seen that a Hill coefficient of 2 (or a total gating charge of 2 Z_U) is obtained at infinite negative voltages, as predicted by the limiting probability theorem (Almers, 1978). Usually, however, gating isotherms of voltage-activated channels are parameterized based on the voltage midpoint of the gating transition (V_1/2) where P = 1/2 and on the slope of the gating isotherm around this midpoint (Z). The Hill coefficient at an open probability of half (n_H (V = V_1/2)) may be derived for such a gating model by combining Eq. 8 with a limiting condition derived from P = 1/2 to yield the expression

(9)

where K_A and K_B are the equilibrium constants for the first and second subunit transitions in the absence of voltage (at 0 mV), respectively. It may be seen that, for a channel that gates according to the KNF model, n_H (V = V_1/2) depends only on the Adair-like K_A and K_B model parameters. The quantity K_B/K_A reflects how much the second transition of the channel is facilitated (or inhibited) by the first one and is an intuitive measure of the magnitude of cooperativity in channel gating transitions. In the context of the sequential gating model discussed here, this quantity is directly related to the magnitude of intersubunit interactions (Fig. 1 B). Examining Eq. 9 at the extreme cases yields a logical outcome: At the limits where K_B/K_A is very high, a Hill coefficient of 2 (the total number of subunits or protomers in our model) is obtained, reflecting a complete and concerted gating charge movement. In the case of negative coupling between subunits (or protomers), i.e., where K_B/K_A approaches zero, a value of 1 is obtained for n_H. It is interesting to note that an n_H value of 1.17 is obtained by substituting K_A = K_B in Eq. 9. This outcome addresses the common misconception that Hill coefficient values greater than one are always indicative of positive cooperativity along the reaction pathway (ligand binding or gating). Here, in this particular case, an apparent positive cooperativity is detected for n_H (n_H >1), despite the fact that channel subunits switch from closed to open states in an independent manner. This outcome originates from the fact that the C₂ state is a nonconductive state (see below). This specific outcome underscores the need for a detailed analysis, by means of Eq. 4, to truly capture the meaning of the Hill coefficient.

FIGURE 1.

The KNF allosteric model applied to voltage-dependent gating. (A) Scheme of the different states considered by the KNF model. A homodimeric channel undergoes two sequential voltage-dependent subunit transitions from the closed (square) to open (circle) states. K_A(V) and K_B(V) are the equilibrium constants for the first and second transitions, respectively, and display voltage dependence of the form K_i(V) = K_i exp(Z_iFV/RT), where K_i is the chemical equilibrium constant for the corresponding transitions at 0 mV (i = A, B), Z_i (+++) is the gating charge associated with subunit transition from the closed to open states (it is assumed to be equal for both transitions, Z_A = Z_B = Z), F is Faraday constant, and all other constants have their usual thermodynamic meaning. For this gating scheme, the open probability function is given by (B) Double-mutant cycle representation of the KNF model, above (A). The “mutation” in this cycle is a transition of a subunit from the closed to the open conformation. Cooperativity arises when the free energy associated with this “mutation” depends on the conformational state of the adjacent subunit. Such cooperativity is a function of the magnitude of intersubunit interactions between the monomers in the different conformations and is manifested by K_B/K_A.

The outcome arrived at here, i.e., that only n_H values between 1 and n may be obtained for a channel that gates according to the classical KNF model, further strengthens the analogy between the two Hill equations. It is also points to the generality of the empiric Hill coefficient definition, as given in Eq. 4. This outcome further argues against the strict association of negative cooperativity between protein subunits with Hill values <1. Here, in this particular gating scheme, negative coupling between channel subunits (K_B/K_A ≪ 1) results in a Hill value of 1. This is in contrast with the results of a similar analysis conducted for the same gating scheme, this time assuming a subconductance state for the channel (C₂ state in the scheme of Fig. 1 A for which one subunit is in a permissive open state whereas the second is not). In this case, the following expression for n_H is obtained,

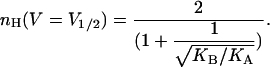(10)

It may be seen that for such a case, a Hill coefficient of 1 is obtained for K_A = K_B (independent subunit transitions) and that Hill values smaller than 1 can be obtained for low K_B/K_A values, reflecting negative cooperativity between channel subunits (or protomers). The Hill analysis applied to these two slight variations on the KNF-type gating model demonstrates that the meaning of the Hill coefficient is context-dependent and, therefore, to capture its true essence a detailed analysis of the channel's gating scheme, using Eq. 4 above, is needed.

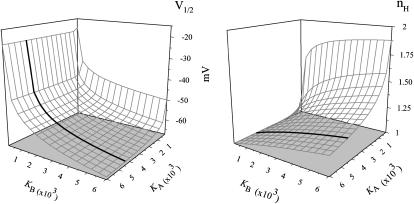
The dependences of both n_H at half-activation and V_1/2 on the Adair-like model parameters, as well as the relation between these two quantities, can be better realized by graphing the three-dimensional surfaces of n_H and V_1/2 as a function of both K_A and K_B, using identical scales (Fig. 2). The main diagonal trajectory in both surfaces, where K_A = K_B, separates the two domains of negative and positive coupling between channel subunits. Upon comparison of n_H and V_1/2 surfaces, it may be seen that the simple sequential KNF-type gating scheme (Fig. 1 A) permits different relations between n_H and V_1/2. For example, increasing K_B alone along the outlined trajectory in Fig. 2 (such as might be achieved upon mutations, for example), would shift the midpoint activation voltage (V_1/2) to more negative potentials (the activation curve is shifted to the left along the voltage axis open-state stabilization effect) and would increase the slope of the activation curve (i.e., n_H increases). Other relations between n_H and V_1/2 are expected for different trajectories crossing these surfaces (see Fig. 2 legend for further discussion).

FIGURE 2.

Three-dimensional surfaces of n_H (V = V_1/2) and V_1/2 as a function of both K_A and K_B using identical scales. The graph for n_H was plotted based on Eq. 9 and that of V_1/2 according to the equation 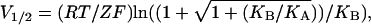derived using the condition of half-activation (P_O = 1/2). Unitary gating charge of 3 was assumed for Z. The main diagonal trajectory where K_A = K_B separates positive ((K_B/K_A) > 1) and negative ((K_B/K_A) < 1) coupling domains to the right and left of this diagonal, respectively. Three extreme scenarios may be envisaged: 1), along the main diagonal trajectory; increasing K_A and K_B upon mutations, for example, would shift the midpoint activation voltage to the left to more negative voltages; however, n_H would not change. 2), The trajectory in bold corresponds to a case in which increasing K_B only would result in a shift of the midpoint activation voltage to the left in parallel with steeper n_H slopes. 3), Opposite dependence is observed between n_H and V_1/2 for a case in which only K_A is changed upon mutations.

n_H for a MWC-type gating model

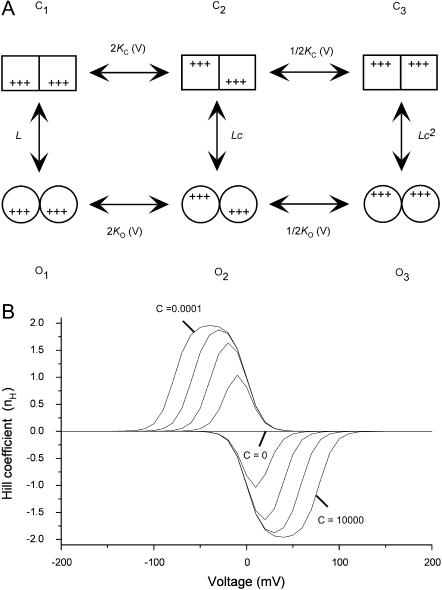
The above definition for the Hill equation for channel gating transitions (Eq. 4) may not be solely restricted to sequential gating schemes. Consider next a dimeric channel which gates according to the classical MWC allosteric model (Monod et al., 1965), described in Fig. 3 A. In this scheme, sequential and independent voltage-dependent transitions, probably reflecting charge movements transitions between closed states and between open states (K_C(V) and K_O(V), respectively), are separated by voltage-independent pore opening transitions (L). We assume, for simplicity, that a similar gating charge moves through both closed and open transitions and that the open probability function for this scheme is given by P_o = (O₁ + O₂ + O₃)/(C₁ + C₂ + C₃+ O₁ + O₂ + O₃). Using the Hill definition outlined in Eq. 4, the following expression is thus obtained for n_H(V)

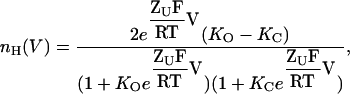(11)

where K_O and K_C are the equilibrium constants for charge movements in the open and closed states in the absence of voltage (i.e., at 0 mV), respectively. Inspection of Eq. 11 reveals the following points: First, the scaled Hill slope for such a gating scheme can be either positive or negative, depending on the relative magnitudes of K_C and K_O. Negative slopes reflect the fact that the probability of the channel to be open is decreased upon membrane depolarization when K_C > K_O. Second, a Hill slope of zero is obtained at both extreme positive or negative voltages, suggesting a bell-shaped dependence of n_H(V) on voltage. Plots of n_H as a function of voltage for different ratios of K_C/K_O values (given as c_, analogous to the binding affinity ratio c of the substrate to the tense (T) and relaxed (R) states of an allosteric enzyme (Monod et al., 1965)) are shown in Fig. 3 B. The extreme points of n_H(V) at any given c can be obtained by taking the partial derivative of Eq. 11 with respect to voltage (∂n_H(V)/∂V). This yields the following expression for 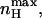the maximal scaled slope of the MWC open probability function obtained at V_max, the activation voltage at this maximal slope:

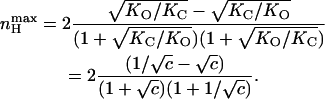(12)

FIGURE 3.

MWC-type allosteric model applied to voltage-dependent gating. (A) Scheme for the different channel states considered by the MWC model. According to this model, voltage-induced charge movement transitions between closed and between open states (horizontal transitions, K_C(V) and K_O(V) transitions, respectively) are separated by concerted voltage-independent subunit conformational changes (vertical transitions, L (= [C₁]/[O₁]) transition). K_C(V) and K_O(V) display Boltzmann-type voltage dependence as specified in Fig. 1 legend. For this MWC gating scheme the open probability function is given by 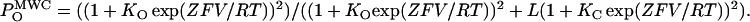It is assumed that identical gating charge Z moves across the membrane electric field in transitions between closed and between open states. (B) Dependence of n_H on voltage at different values of c (= K_C/K_O). Graphs were generated according to Eq. 11 with different c-values ranging from 0.0001 to 10,000 in 10-fold increments and assuming a unitary Z of 3.

It can be seen that 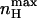depends on the ratio of equilibrium constants for charge movement transitions in the closed and open states and not on the allosteric equilibrium constant L (Karlin, 1967). A Hill value of 2 is obtained for very low values of c (K_O ≫ K_C), whereas a value of −2 is obtained for high c-values (K_O ≪ K_C). Thus, for a channel that gates according to the classical MWC scheme (Fig. 3 A), 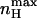reflects the magnitude of cooperativity in channel opening transitions which is solely determined by c. It follows from the above analysis that the maximal slope of the open probability function does not necessarily coincide with the slope at the midpoint of activation (n_H (V = V_1/2)). The direction and magnitude of the departure of 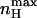from n_H (V = V_1/2) depends on the relative values of L and c. The expression for n_H (V = V_1/2) may be obtained by combining Eq. 11 with the limiting condition derived from P = 1/2 to yield

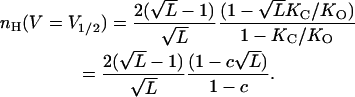(13)

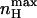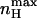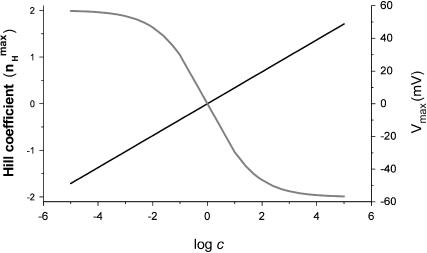
Here, n_H (V = V_1/2) depends on both L and c allosteric parameters of the MWC gating scheme. It can be shown that for any given L, is always greater than n_H at half-activation and that n_H (V = V_1/2) will equal only at the limits where the allosteric constant L is very high and the ratio of charge movement equilibrium constants in the closed and open states, c, is extremely low, in which case a Hill coefficient of 2 is obtained. For the MWC gating scheme analyzed here, 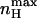rather than n_H (V = V_1/2) is a more natural parameter of homotropic interactions, since the former is a measure of the maximum degree of cooperativity under specific conditions (Rubin and Changeux, 1966). The dependences of 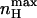and V_max on c are compared in Fig. 4. The symmetry of the graph around K_O = K_C reflects the symmetric nature of the MWC gating scheme. It may be seen that for c-values indicating open state stabilization, i.e., c < 1 (K_O > K_C), 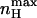is increased, whereas the voltage at this maximal slope is shifted to more negative voltages.

FIGURE 4.

Dependence of the maximal Hill coefficient (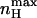) and the activation voltage at this slope (V_max) on c. The graph for 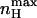was plotted based on Eq. 12 (shaded, left y-axis) and that of V_max (black, right y-axis) according to the equation V_max = (RT/2ZF)ln(1/(K_OK_C)), derived by solving the equation ∂n_H(V)/∂V = 0, which is a normalized second derivative of the MWC open probability expression. In this plot, for convenience, K_C was assigned a value of 1, whereas K_O values range from 10⁻⁵ to 10⁵. See text for further discussion.

It is interesting to note that the MWC gating scheme permits Hill values smaller than 1. Hill values <1 are often interpreted as a reflection of negative cooperativity between subunits or protomers. This outcome is in sharp contrast to similar Hill analysis performed with allosteric enzymes in which negative cooperativity in substrate binding could only be explained by a KNF-type model, whereas both the KNF-type and MWC-type models can account for positive cooperativity (Levitzki, 1978).

Combined MWC and KNF gating model

Sequential KNF-type or concerted MWC-type gating schemes were previously employed to analyze K⁺ and Na⁺ channels activation data. Alternative gating schemes, in which sequential but independent transitions at voltage-sensing domains (K(V) transitions between closed states) are followed by a concerted voltage-independent late pore opening transition (L), are, however, often considered (Sigworth, 1994; Zagotta et al., 1994). The simplest version of such a gating scheme is 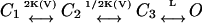(Scheme 3). Assuming that only the end state is conductive, the above analysis can be applied to show that, for high L-values, one obtains the expression for n_H at half-activation of

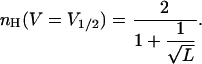(14)

It may be seen that n_H depends only on the allosteric constant L. As for the other gating schemes analyzed, at the limit where L is very large (i.e., cases of extreme positive cooperativity), a Hill coefficient of 2 is obtained, reflecting concerted movement of the total channel gating charge. Interestingly, it can be noted that Eq. 14 is analogous to Eq. 10 above.

The approach presented here, for analyzing cooperativity in channel gating transitions using the empiric Hill coefficient definition (Eq. 4), is general and may be applied to other more realistic or more complicated gating schemes. Such analysis would yield, as demonstrated for the three simple gating schemes considered here, a dependence of the magnitude of cooperativity in gating transitions (n_H) on the equilibrium constants of the specific gating scheme discussed. Such analysis could provide mechanistic insight to account for experimental observations that may complement insight gained from gating currents measurements (Sigg and Bezanilla, 1997; Islas and Sigworth, 1999).

Cooperativity in gating transitions of voltage-dependent potassium channels

The theoretical range of values of n_H for a protein with n subunits exhibiting positive cooperativity is 1 < n_H ≤ n. For many allosteric proteins, however, n_H ≪ n. In the case of the Shaker voltage-gated potassium channel, a Hill coefficient slightly above 1 is obtained, a low value as compared to those obtained with other tetrameric proteins like hemoglobin or glyceraldehyde-3-phosphate dehydrogenase (n_H values of 2.8 and 2.5, respectively; Edelstein, 1971; Kirschner et al., 1971). The low value of n_H for the Shaker channel may reflect the fact that for this channel, gating occurs through many independent transitions. One hint to a functional explanation for the low Hill value for gating transitions of the Shaker channel may be provided by the recently observed correlation between the midpoint (V_1/2) and slope (Z) of gating transitions of wild-type and variants Shaker K⁺ channel proteins (Yifrach and MacKinnon, 2002). It was found that the further the transition midpoint is shifted to the left upon mutation, as compared to the wild-type protein (i.e., an open state stabilization effect), the steeper the slope of the gating transition. At extremely negative V_1/2 values, slope values close to the total number of gating charges of the channel are obtained (n_H approaches n). This relation between V_1/2 and Z (= Z_U n_H (V = V_1/2)) may be generally explained even by simple gating models incorporating cooperativity in different ways (see, for example, analysis of the KNF and MWC gating models in Figs. 2 and 4, respectively). Detailed analysis (Yifrach and MacKinnon, 2002), however, has shown that this observation may be explained within the framework of a well-developed gating model that is a generalized version of Scheme 3, above (Zagotta et al., 1994; Schoppa and Sigworth 1998). It was concluded that such correlation between the midpoint and slope of the gating isotherms is expected if mutations of the Shaker channel primarily affect the late cooperative pore-opening transition (L transition of Scheme 3). This conclusion implies for a possible explanation for the low Hill value obtained for the Shaker K⁺ channel: Tuning the channel to be more cooperative (increased L and n_H values) would shift the activation curve of the channel to the left, thus bringing V_1/2 closer to the resting membrane potential. It would also narrow the voltage range in which transition from the closed to open state occurs. Under such circumstances, potassium channels may be opened even in response to subtle fluctuations (noise) in the resting membrane potential. Uncoordinated opening and closing of K⁺ channels, which reflects the inability to regulate the channel in such an infinitely cooperative case, would have a dramatic effect on the shape of action potentials.

CONCLUDING REMARKS

Here, the two-state Boltzmann equation that is widely used to fit activation data of voltage-activated ion channels has been demonstrated to be analogous to the Hill equation that is commonly used to estimate the magnitude of cooperativity in ligand binding by multisubunit allosteric enzymes. This analogy provides a common ground for the assessment and comparison of the magnitude of steady-state cooperativity in conformational transitions in both channels and enzymes. As such, n_H is an index to cooperativity in either ligand binding by an allosteric protein or in gating transitions of a voltage-gated ion channel. The general empiric definition for n_H derived for channel gating transitions (Eq. 4) provides a useful framework for interpreting the meaning of the Hill coefficient. Following the analysis presented here, one should realize that the comparison between Hill values of different proteins, channels or enzymes, is probably more informative given that the activation mechanisms or ligation pathways of the compared proteins are similar.

The Hill equation was originally deduced in 1910 to account for the sigmoidal kinetics of oxygen binding to hemoglobin. This equation made no assumptions about the molecular mechanisms giving rise to cooperativity. Mechanistic models that account for cooperative phenomena and regulation of enzymes were later suggested by Monod and Koshland and their associates in the early 1960s. In recent years, these allosteric models have been widely employed to analyze the steady-state activation of different kinds of voltage-gated channels. The finding that concepts of classical enzymology are also applicable to the study of channel gating, together with the analogous natures of the Hill and Boltzmann equations demonstrated here, point to a unified conceptual framework for understanding the functional behavior of channels and enzymes.