Effect of ADP on Na⁺-Na⁺ Exchange Reaction Kinetics of Na,K-ATPase

Abstract

The whole-cell voltage-clamp technique was used in rat cardiac myocytes to investigate the kinetics of ADP binding to phosphorylated states of Na,K-ATPase and its effects on presteady-state Na⁺-dependent charge movements by this enzyme. Ouabain-sensitive transient currents generated by Na,K-ATPase functioning in electroneutral Na⁺-Na⁺ exchange mode were measured at 23°C with pipette ADP concentrations ([ADP]) of up to 4.3 mM and extracellular Na⁺ concentrations ([Na]_o) between 36 and 145 mM at membrane potentials (V_M) from −160 to +80 mV. Analysis of charge-V_M curves showed that the midpoint potential of charge distribution was shifted toward more positive V_M both by increasing [ADP] at constant Na⁺_o and by increasing [Na]_o at constant ADP. The total quantity of mobile charge, on the other hand, was found to be independent of changes in [ADP] or [Na]_o. The presence of ADP increased the apparent rate constant for current relaxation at hyperpolarizing V_M but decreased it at depolarizing V_M as compared to control (no added ADP), an indication that ADP binding facilitates backward reaction steps during Na⁺-Na⁺ exchange while slowing forward reactions. Data analysis using a pseudo three-state model yielded an apparent K_d of ∼6 mM for ADP binding to and release from the Na,K-ATPase phosphoenzyme; a value of 130 s⁻¹ for k₂, a rate constant that groups Na⁺ deocclusion/release and the enzyme conformational transition E₁∼P → E₂-P; a value of 162 s⁻¹M⁻¹ for k₋₂, a lumped second-order V_M-independent rate constant describing the reverse reactions; and a Hill coefficient of ∼1 for Na⁺_o binding to E₂-P. The results are consistent with electroneutral release of ADP before Na⁺ is deoccluded and released through an ion well. The same approach can be used to study additional charge-moving reactions and associated electrically silent steps of the Na,K-pump and other transporters.

INTRODUCTION

The Na,K-ATPase or Na,K-pump couples a scalar reaction, the hydrolysis of ATP to ADP and inorganic phosphate, to vectorial transport of Na and K ions against their respective electrochemical gradients (Scheme 1). Besides its normal forward-running mode (3 Na⁺ out/2 K⁺ in), the Na,K-pump can engage, under appropriate conditions, in a noncanonical mode of ion transport, electroneutral Na⁺-Na⁺ exchange (Läuger, 1991). This exchange occurs in the absence of K⁺ and in the presence of ATP and ADP (Glynn, 1985) but without net ATP hydrolysis (Garrahan and Glynn, 1967). In this regard, ADP has been shown to act as an acceptor of the phosphate group in the phosphoenzyme to yield ATP in a reaction called transphosphorylation or ATP/ADP exchange (Glynn, 1985). A crucial intermediate for ATP/ADP exchange that has been extensively included in the formulation of models to describe ion transport by the Na,K-ATPase is (Na₃)E₁∼P·ADP (De Weer, 1970, 1992; Karlish et al., 1978; Cornelius and Skou, 1985; Kennedy et al., 1986; Forbush and Klodos, 1991; Pratap et al., 1991; Keillor and Jencks, 1996; Suzuki and Post, 1997; Campos and Beaugé, 1997). Nevertheless, this phosphorylated intermediate containing occluded Na ions and bound ADP appears to exist in very small amounts during steady-state Na,K-ATPase cycling (Nørby et al., 1983) and, thus, its kinetic characterization has remained elusive. As an approach to solve this problem, Campos and Beaugé (1997) studied ATP/ADP exchange in partially purified Na,K-ATPase subjected to chymotrypsin digestion to estimate the kinetics of ADP binding to and release from the phosphoenzyme. However, proteolytic treatment prevents phosphoenzyme conformational transitions and Na⁺-Na⁺ exchange, so that it remains unclear how these rate constants relate to those of the native enzyme.

SCHEME 1.

Simplified Post-Albers model (Glynn, 1985) describing ATP hydrolysis and ion transport by the Na,K-ATPase. The enzyme exists in two conformations, E₁ and E₂. In its forward (clockwise) direction, the Na,K-pump binds intracellular Na⁺ and MgATP with high affinity to form the complex Na₃E₁ATP (Mg is not shown). The γ-phosphate of ATP is then transferred to the ATPase, and Na ions become occluded (occluded states are depicted by parentheses). The complex (Na₃)E₁∼P·ADP contains a high-energy phosphate bond since this reaction is reversible. After release of ADP, Na ions are deoccluded and released to the extracellular medium along with or after the enzyme conformational change to E₂-P. Extracellular K⁺ binds to E₂-P, favors the release of P_i, and becomes occluded during its transport to the cytoplasm. ATP, acting with low affinity, greatly accelerates K⁺ deocclusion and release. The enzyme experiences a conformational change from E₂ to E₁ to restart the cycle. The left-hand loop represents Na-ATPase activity, i.e., ATP hydrolysis and electrogenic Na⁺ transport in the absence of K⁺. In K⁺-free media, the Na,K-pump can also engage in electroneutral Na⁺-Na⁺ exchange, reversibly moving from E₁ATP to E₂-P through the left branch of the scheme. Under these conditions, the enzyme can move charge through the membrane dielectric in response to changes in cell membrane potential, generating transient currents that can be detected with voltage-clamp techniques. The dashed box comprises the reactions isolated by the experimental conditions in this work.

Vectorial Na⁺ transport is influenced by membrane potential (V_M), and perturbations in V_M produce nonlinear capacitive currents (termed transient charge movements) whose kinetics likely reflect the rate of Na⁺-Na⁺ exchange (Rakowski et al., 1997). The extracellular Na⁺ (Na⁺_o) and V_M dependence of these cardiac glycoside-sensitive transient charge movements have been well characterized (Nakao and Gadsby, 1986; Rakowski, 1993; Holmgren and Rakowski, 1994; Hilgemann, 1994; Friedrich and Nagel, 1997; Holmgren et al., 2000); however, the effect of ADP on V_M-dependent presteady-state kinetics of Na⁺_o-related reactions has not been studied. Such an investigation should yield new mechanistic information about ADP interactions with the Na,K-ATPase phosphoenzyme and how they affect electroneutral Na⁺-Na⁺ exchange.

To kinetically characterize the intermediate (Na₃)E₁∼P·ADP and study the effect of ADP on Na⁺_o-dependent reactions, the Na,K-ATPase can be trapped in phosphorylated conformations that support Na⁺-Na⁺ exchange in the absence of extracellular K⁺. Under these conditions, the right half of Scheme 1 disappears and, since dephosphorylation is very slow (Glynn, 1985; Cornelius and Skou, 1985; Stein, 1986), phosphoenzyme accumulates as E₂-P in the steady state. If, in addition, the level of Na₃E₁ATP is maximized by high concentrations of intracellular Na⁺, ATP, and Mg²⁺, thus favoring enzyme phosphorylation, the Na,K-ATPase will be predominantly confined to reactions in the dashed box of Scheme 1.

Previous works have used the kinetics of transient charge movement to study Na⁺_o release/rebinding reactions by the Na,K-pump (Nakao and Gadsby, 1986; Rakowski, 1993; Holmgren and Rakowski, 1994; Hilgemann, 1994; Friedrich and Nagel, 1997; Holmgren et al., 2000). Unfortunately, apparent rate constants derived from charge movement measurements cannot be directly related to elementary scalar reaction steps without additional information. To circumvent this limitation, this study measured Na⁺_o-dependent charge movements over a wide range of intracellular ADP and extracellular Na⁺ concentrations. Manipulation of intracellular ligands allowed specific physical meanings to be assigned to the estimated rate constants. Thus, the study of ADP effects on Na⁺_o-dependent charge movements generated during Na⁺-Na⁺ exchange permitted determination of the kinetics of ADP binding to the phosphoenzyme and, as a result, kinetic characterization of the intermediate (Na₃)E₁∼P·ADP.

In brief, the results are consistent with a kinetic scheme in which ADP is released from the phosphoenzyme with a k₁ of 404 s⁻¹ and rebound with a k₋₁ = 6.4 × 10⁴ s⁻¹M⁻¹, yielding a K_d = 6.3 mM. ADP binding/release reactions do not move charge within the membrane dielectric, i.e., these reactions represent electrically silent events. In addition, ADP is released from (Na₃)E₁∼P·ADP before deocclusion and electrogenic release of Na⁺_o. Finally, the phosphoenzyme conformational transition and/or sodium deocclusion reaction take place at a rate (k₂ = 130 s⁻¹) that is lower than that of ADP release; however, at least at depolarizing V_M, the rate-limiting step for this sequence of reactions seems to depend on Na⁺_o binding (k₋₂ = 162 s⁻¹M⁻¹). These results also demonstrate the general utility of this approach as a means to gain mechanistic information on electroneutral ligand binding reactions that are closely related to charge-moving reaction steps.

Portions of this work have been previously published in abstract form (Peluffo, 1998, 1999).

GLOSSARY OF SYMBOLS

• [ADP]: intracellular ADP concentration; pipette ADP concentration.

• δ: fractional electrical distance for Na⁺_o binding in an ion well.

• k_min: value of the apparent rate constant for current relaxation at large positive potentials.

• k_tot: apparent rate constant for current relaxation.

• k₁: first-order rate constant describing the release of ADP from (Na₃)E₁∼P·ADP.

• k₋₁: second-order rate constant describing binding of ADP to (Na₃)E₁∼P.

• κ₋₁: pseudo first-order rate constant describing binding of ADP to (Na₃)E₁∼P.

• k₂: lumped first-order rate constant describing Na⁺ deocclusion/release and the enzyme conformational change from E₁∼P to E₂-P.

• k₋₂: lumped second-order voltage-independent rate constant describing Na⁺ binding/occlusion and the enzyme conformational change from E₂-P to E₁∼P.

• κ₋₂: lumped pseudo first-order voltage-dependent rate coefficient describing Na⁺ binding/occlusion and the enzyme conformational change from E₂-P to E₁∼P.

• n: Hill coefficient for extracellular Na⁺ binding to E₂-P; apparent molecularity of the reaction.

• Na⁺_λ: Na ions at the ion binding locus in the Na,K-pump ion well.

• Na⁺_o: extracellular Na ions.

• [Na]_o: bulk extracellular Na⁺ concentration.

• Na_o-TCM: extracellular Na⁺-dependent transient charge movement.

• q: valence of the permeating ion.

• ΔQ: the quantity of charge moved.

• Q_min: minimal amount of charge moved at large negative potentials.

• Q_max: maximal amount of charge moved at large positive potentials.

• Q_tot: total amount of mobile charge (Q_max − Q_min).

• V_M: membrane potential; voltage.

• V_q: midpoint potential for steady-state charge distribution.

• z: apparent valence of the permeating species.

• z_q: apparent valence obtained from steady-state charge distribution measurements.

• z_k: apparent valence for charge translocation obtained from kinetic measurements.

METHODS

Single myocytes, enzymatically isolated from rat cardiac muscle following published methods (Mitra and Morad, 1985), were placed in a superfusion chamber at 23 ± 1°C on the stage of an inverted microscope and superfused with a HEPES-buffered Tyrode's solution (Peluffo and Berlin, 1997). Cells were whole-cell voltage-clamped with low-resistance (0.8–1.3 MΩ) patch electrodes filled with a pipette solution containing (mM): 120 Na⁺, 85 sulfamic acid, 20 tetraethylammonium chloride (TEACl), 15 ATP (magnesium salt), 5 pyruvic acid, 5 Tris₂-creatine phosphate, 10 EGTA/Tris, and 10 HEPES, pH 7.34 (23°C). In those experiments that included ADP, the pipette solution contained (mM): 117–126 Na⁺, 80–85 sulfamic acid, 20 TEACl, variable ATP (magnesium salt), variable ADP (sodium salt), variable MgCl₂, 10 EGTA/Tris, and 10 HEPES, pH 7.38 (23°C). Since complex patterns of current decay were observed in preliminary assays using [Mg] > 2.0 mM, pipette solutions were designed to keep [Mg]_total fairly constant and [Mg]_free below 2 mM. This also required a fixed total concentration of nucleotides. Thus, to prepare ADP-containing solutions, [ADP]_total was increased at the expense of [ATP]_total. Total concentrations of ATP, ADP, and Mg as well as calculated values of [ADP]_free, [MgATP], and [Mg]_free for all six pipette solutions used in this work are shown in Table 1. ADP concentrations referred to throughout this article are “free ADP” concentrations.

TABLE 1.

Nucleotide and magnesium composition of electrode solutions

*[ADP]free (mM)	†[ATP]total (mM)	*[MgATP] (mM)	†[ADP]total (mM)	*[Mg]free (mM)	[Mg]total (mM)
0	15.0	13.2	0	1.0	15.0
0.4	14.3	12.3	0.7	0.9	14.3
0.8	13.4	11.8	1.6	1.1	14.5
1.7	11.0	10.0	4.0	1.3	14.5
3.0	7.0	6.5	8.0	1.7	14.5
4.3	4.0	3.7	11.0	1.6	13.2

[EGTA] = 10 mM was included in the calculations.

The MgATP complex was arbitrarily chosen as the enzyme catalytic substrate.

For experimental evidence supporting the choice of free ADP as the relevant variable in this work, see online supplementary material.

^*Calculated with the program MaxChelator (supplied by Chris Patton, Hopkins Marine Station, Pacific Grove, CA) using the set of constants “CMC1002S.TCM”, pH = 7.4, T = 23°C, ionic strength = 0.2.

^†[ATP]_total + [ADP]_total = 15 mM.

After establishing a gigaohm seal, the superfusion solution was switched to a K⁺-free solution containing (mM): 36.3/72.5/145 NaCl, 2.3 MgCl₂, 2.0 BaCl₂, 0.2 CdCl₂, 5.5 dextrose, and 10 HEPES/NaOH, pH 7.38 (22°C). Na⁺ concentration was changed by equimolar substitution of tetramethylammonium ion with total monovalent cation concentration equal to 148 mM. Ba²⁺, Cd²⁺, and TEA were added to prevent contaminating ohmic ionic currents (McDonald et al., 1994). Control experiments showed that Ba²⁺ and pipette TEA had no effect on either steady-state Na,K-pump current or ouabain-sensitive Na_o-TCM at the concentrations used (R. D. Peluffo and J. R. Berlin, unpublished results), consistent with previous reports (Gadsby et al., 1985, 1992; Gadsby and Nakao, 1989). Cadmium, in concentrations twice as large as those used in this work, had no appreciable effect on steady-state or transient currents by the Na,K-pump (Gadsby et al., 1992). Voltage-clamped myocytes were exposed to these blocking agents for 5 min before further manipulations. Extracellular Na⁺-dependent transient charge movements were measured as 1 mM ouabain-sensitive difference currents as previously described (Peluffo and Berlin, 1997).

Voltage-clamp protocol

Voltage-clamp pulses of 100-ms duration were applied from a holding potential of −40 mV to various potentials over the range −160 to +80 mV at 2 Hz. These voltage jumps were elicited before ouabain application, during superfusion with ouabain-containing solution (1 and 2 min), and again 3 and 6 min after withdrawal of the inhibitor to obtain the respective current-voltage relationships. Since inhibition of the pump was complete in ∼2 min and total recovery of the enzyme was achieved ∼6 min after removal of ouabain, two ouabain-sensitive difference currents were typically calculated for each cell, i.e., traces obtained after 2 min in the presence of ouabain were subtracted from those recorded either before exposure or 6 min after removal of ouabain. Both subtraction procedures yielded similar results, with only small differences in the kinetics of current relaxation. In some cells, ouabain was added and withdrawn more than once. The parameters calculated from kinetic analysis of these current-voltage relationships were averaged for each cell.

Linear cell capacitance was calculated by integrating current elicited by 5-mV depolarizations. Data were sampled at 10 kHz and low-pass filtered at 2.0–2.5 kHz.

Data analysis

Data are displayed as mean ± SE for the indicated number of experiments. Pairwise comparisons were performed using a Student's t-test (p < 0.05). Curve fitting was carried out by nonlinear least-squares routines using commercial software, Clampfit (Axon Instruments, Foster City, CA) or SigmaPlot 2002 for Windows v8.0 (SPSS, Chicago, IL).

Pseudo three-state reaction scheme to account for ADP effects on Na_o-TCM

The pseudo three-state model shown in Scheme 2 is proposed to explain the results that follow and, thus, is tested throughout this article. The general characteristics of the model are: 1), the enzyme is reversibly distributed among three phosphorylated states, i.e., while engaged in electroneutral Na⁺-Na⁺ exchange, the Na,K-ATPase is not cycling through any of the loops in Scheme 1 but rather shuttling back and forth between phosphointermediates; 2), Na⁺-occluded forms contain three Na ions; 3), ADP release from and rebinding to (Na₃)E₁∼P·ADP is V_M-independent; 4), ADP is released from the phosphoenzyme before Na⁺_o; 5), Na⁺_o binds to the enzyme in an ion well; and 6), Na⁺_o is in rapid equilibrium with local Na⁺ (Na⁺_λ) in the ion well.

SCHEME 2.

Pseudo three-state model to characterize ADP effects on 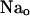-TCM. The scheme features extracellular Na⁺ binding in an ion well, i.e., Na ions travel a certain distance (δ) in the membrane dielectric to reach their binding sites in the Na,K-pump. This feature confers voltage dependence to the rate coefficient κ₋₂. Sodium concentration at the ion binding locus, [Na]_λ, is assumed to be in rapid equilibrium with bulk [Na]_o. Rate constants and coefficients are defined in the text. The intermediate E*-P (Klodos and Nørby, 1987) is not included in this model. Occluded Na ions are represented within parentheses. Magnesium ions are not shown in the scheme.

The intermediate (Na₃)E₁∼P·ADP is a phosphoenzyme containing a high-energy phosphate bond with bound ADP and occluded sodium. The first-order rate constant, k₁, describes the release of ADP from this intermediate. The pseudo first-order rate constant, κ₋₁, describing the reverse process, is defined as:

(1)

where k₋₁ is a second-order rate constant. The V_M-independent forward rate constant, k₂, is a lumped rate constant describing Na⁺ deocclusion, Na⁺ release, and the conformational change E₁∼P → E₂-P. The V_M-dependent pseudo first-order reverse rate coefficient, κ₋₂, which is a function of local Na⁺ concentration ([Na]_λ) at the ion binding locus in the ion well, is described by the equation:

(2)

where n is the Hill coefficient for Na⁺_o and k₋₂ is a second-order V_M-independent rate constant that lumps together Na⁺_o binding and occlusion as well as the phosphoenzyme transition E₂-P → E₁∼P. Taking into account assumption 6 above, [Na]_λ can be related to Na⁺_o bulk concentration ([Na]_o) through a Boltzmann function of V_M:

(3)

where F is Faraday's constant, R is the gas constant, T is absolute temperature, and z is an apparent valence that may be expressed as (Läuger, 1991):

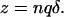(4)

In this equation, n is the apparent molecularity of the charge-moving process, q is the valence of the charged species, and δ, the fractional distance, is the portion of the membrane electric field sensed by the moving charges. Combining Eqs. 2 and 3 gives κ₋₂ as an explicit function of [Na]_o and V_M:

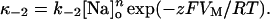(5)

Notice that saturation of the Na,K-pump Na⁺_o binding sites is not included in this formulation.

RESULTS

Ouabain-sensitive transient currents

Given the close association between the release of intracellular ADP and extracellular Na⁺ in the Na,K-ATPase reaction cycle, it seems reasonable to hypothesize that changes in [ADP] will affect extracellular Na⁺-dependent transient charge movements by this enzyme. With this idea in mind, Na_o-TCM can be used to study the kinetics of ADP binding to Na,K-ATPase phosphoenzyme and, reciprocally, the effect of ADP on Na_o-TCM can provide new mechanistic insights on Na⁺-related reactions. Thus, membrane currents were measured in whole-cell voltage-clamped rat cardiac ventricular myocytes internally dialyzed against a 120 mM Na⁺, high MgATP, K⁺-free solution in the presence of various [ADP] from 0 to 4.3 mM. Myocytes were superfused with a 145 mM Na⁺, K⁺-free external solution to promote electroneutral Na⁺-Na⁺ exchange by the Na,K-pump (Glynn, 1985). Upon application of the voltage-clamp protocol (see Methods) in the absence and presence of 1 mM ouabain, ouabain-sensitive difference currents such as those presented in Fig. 1 were obtained. Traces represent “on” transient currents elicited by voltage-clamp pulses to various V_M from a holding potential of −40 mV. Fig. 1 A shows traces from an experiment performed in the presence of 13.2 mM pipette MgATP with no added ADP. Two features are apparent. First, all currents relaxed to a zero steady-state level. Second, current relaxation rates were faster with hyperpolarizing V_M. For example, fitting an exponential function to the decaying portion of current traces obtained in response to V_M jumps to −;140 and +60 mV yielded values for the apparent rate constant, k_tot, of 410 ± 5 s⁻¹ and 149 ± 8 s⁻¹, respectively. In all cases, currents decayed at rates that were much slower than charging of linear membrane capacitance (typical clamp time constants: 160–220 μs).

FIGURE 1.

Effect of ADP on ouabain-sensitive transient currents recorded under Na⁺-Na⁺ exchange conditions. (A) “On” currents measured in a cell voltage-clamped with a patch electrode containing ADP-free solution and superfused with a 145 mM Na⁺-containing solution. Traces were elicited by 100 ms-long voltage-clamp pulses from −40 mV to the values shown in the figure. Although “off” currents were also recorded, large Na⁺ tail currents appearing after repolarization prevented the study of “off” charge movements at potentials ≤−60 mV, similar to previous reports with guinea pig myocytes (Nakao and Gadsby, 1986). Cell capacitance, 149 pF. (B) Currents from a cell voltage-clamped in the presence of 4.3 mM ADP and superfused with 145 mM Na⁺_o. Cell capacitance, 230 pF. Current records were not averaged. Arrows indicate zero current levels.

Transient currents shown in Fig. 1 B were obtained on a cell assayed with 3.7 mM MgATP and 4.3 mM ADP in the pipette solution. The salient feature attributable to the presence of ADP was a significant reduction in the rate of current decay at depolarizing V_M as compared to the control, zero-ADP condition. Accordingly, the value of k_tot at +60 mV was estimated to be 78 ± 5 s⁻¹. Depolarizing potentials should promote Na⁺ release to the extracellular medium, so this twofold decrease in k_tot indicates that binding of ADP slows down forward reactions during electroneutral Na⁺-Na⁺ exchange, consistent with Scheme 2.

In addition to [ADP] and V_M, [Na]_o was experimentally manipulated to study the reactions in Scheme 2. Thus, cells were voltage-clamped with patch electrodes filled with a high Na⁺, high MgATP solution containing various [ADP] and superfused with either 36.3 or 72.5 mM Na⁺-containing, K⁺-free external solutions. After maneuvers similar to those described above for 145 mM Na⁺_o, ouabain-sensitive transient currents were obtained (Fig. 2). Fig. 2 A shows “on” current traces elicited by voltage-clamp pulses from −40 mV to various V_M in the range from −140 to +60 mV for a cell superfused with 72.5 mM Na⁺-containing solution in the absence of pipette ADP. Fig. 2 B exhibits current traces from a cell also superfused with 72.5 mM Na⁺_o but in the presence of 4.3 mM pipette ADP. Comparison of these two panels shows that ADP decreased the rate of current decay at depolarizing potentials, similar to the behavior observed with 145 mM Na⁺_o. The fitted values of k_tot (+60 mV), 128 ± 12 s⁻¹, and 69 ± 5 s⁻¹ with 0 and 4.3 mM ADP, respectively, were not significantly different from those obtained with 145 mM Na⁺_o. A similar pattern was observed for cells superfused with 36.3 mM Na⁺_o in the absence (Fig. 2 C) and presence of 3.0 mM pipette ADP (Fig. 2 D), with values of k_tot at +60 mV of 152 ± 11 s⁻¹ and 95 ± 6 s⁻¹, respectively. The value of k_tot obtained by reducing pipette [ADP] from 4.3 to 3.0 mM increased significantly. On the other hand, a two- to fourfold change in [Na]_o (at a fixed [ADP]) did not affect k_tot at positive V_M.

FIGURE 2.

Effect of varying [Na]_o and [ADP] on transient charge movements recorded during Na⁺-Na⁺ exchange. Rat ventricular myocytes were superfused with 72.5 mM (A and B) or 36.3 mM Na⁺-containing solutions (C and D) and whole-cell voltage-clamped with patch electrodes containing 0 (A and C), 3.0 (D), or 4.3 mM ADP (B). Each panel shows superimposed ouabain-sensitive “on” difference currents. Voltage-clamp pulses as in Fig. 1. Cell capacitances were 140–155 pF. Current records were not averaged. Arrows indicate zero current levels.

Comparison of traces in Fig. 2 is relatively straightforward because of similar cell sizes. Thus, it is obvious from this figure that reducing both [Na]_o (Fig. 2, A and C) and [ADP] (Fig. 2, B and D) can alter the V_M dependence of charge movements. These effects are presented in detail in the next sections.

[ADP], [Na]_o, and V_M dependence of the steady-state charge distribution

The quantity of charge moved (ΔQ), calculated as the time integral of transient currents generated during voltage pulses from −160 to +80 mV (“on” charge) and after voltage pulses from −40 to +80 mV (“off” charge), was characterized as a function of [ADP] and [Na]_o. Fig. 3 A shows ΔQ-V_M relationships for ouabain-sensitive “on” charge at 0 and 4.3 mM ADP in cells superfused with 145 mM Na⁺_o. The value of ΔQ was found to saturate at both large negative (Q_min) and positive potentials (Q_max), suggesting that the partial reactions being studied involve the movement of a finite number of charged particles in the membrane. At least at depolarizing V_M, the value of “off” charge always matched that of “on” charge within experimental error (not shown). Inclusion of 4.3 mM ADP in the electrode solution raised both Q_min and Q_max as compared to the control condition (Fig. 3 A), an effect that can be interpreted as a shift toward more positive V_M in the quantity of charge moved. This ADP-dependent rightward shift of ΔQ along the voltage axis is more clearly seen by normalizing charge with respect to its minimal and maximal values (Fig. 3 B). A similar behavior was observed in the absence of pipette ADP for myocytes superfused with 36.3, 72.5, and 145 mM Na⁺_o (Fig. 3 C), i.e., a rightward shift in the quantity of charge moved along the V_M axis became apparent at increasing [Na]_o (Fig. 3 D).

FIGURE 3.

Effects of ADP and Na⁺_o on steady-state charge distribution. Ouabain-sensitive charge was quantified as the area under transient currents (“on” charge) between t = 0 (defined at the onset of the voltage pulses) and t = 100 ms, using Clampfit software. (A) ΔQ-V_M relationships from experiments performed with 145 mM 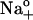and 0 (○) and 4.3 mM pipette ADP (•). Symbols represent the mean ± SE of data from 4–5 cells. Equation 6 was fitted to the data (solid lines) to calculate Q_min, Q_tot, V_q, and z_q. (B) Data from panel A were normalized according to: (ΔQ − Q_min)/Q_tot = {1 + exp[z_qF(V_q − V_M)/RT]}⁻¹. Symbol code as in panel A. Error bars were omitted for clarity. (C) ΔQ-V_M relationships from experiments carried out with 36.3 (▾), 72.5 (○), or 145 mM 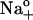(•) in the absence of pipette ADP. Symbols are the mean ± SE of data from 4–5 cells at each [Na]_o and lines represent best fitting of Eq. 6. (D) Data from panel C were normalized to show the rightward shift in ΔQ produced by an increase in [Na]_o. Symbol code as in panel C.

Analysis of the data (solid lines in Fig. 3) was performed by fitting the following Boltzmann equation, derived in the Appendix (Eqs. A11–A12):

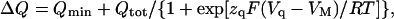(6)

where Q_tot = Q_max − Q_min is the total quantity of mobile charge, z_q represents the apparent valence obtained from steady-state charge distribution measurements, and V_q is the midpoint potential. Best-fit parameters for the entire set of experiments are shown in Fig. 4. The values of V_q increased with [ADP] (Fig. 4 A), showing a shift (ΔV_q) of +16 ± 6 mV between 0 and 4.3 mM ADP, which was independent of [Na]_o. Likewise, V_q values increased by ∼20 mV every time [Na]_o was doubled, regardless of the presence of ADP. Lines in Fig. 4 A represent simultaneous fitting of the following function of [ADP] and [Na]_o derived from Scheme 2:

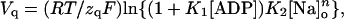(7)

where K₁ = k₋₁/k₁, K₂ = k₋₂/k₂, and n is the Hill coefficient for Na⁺_o binding (see Eq. A13). This analysis yielded z_q = 0.74 ± 0.12, K₁ = 142.1 ± 9.0 M⁻¹, K₂ = 2.73 ± 0.10 M⁻¹, and n = 0.85 ± 0.25.

FIGURE 4.

[ADP] and [Na]_o dependence of Eq. 6 best-fit parameters. (A) Midpoint potential, V_q, as a function of [ADP] with 36.3 (▾), 72.5 (○), and 145 mM 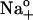(•). Lines represent V_q = f([ADP], [Na]_o) best-fit curves obtained by simultaneous regression of Eq. 7. (B) Effect of [ADP] and [Na]_o on the total amount of mobile charge, Q_tot. The line represents Q_tot = 25.2 fC/pF. (C) Apparent valence of the mobile charge, z_q, as a function of [ADP] for all three [Na]_o tested. The line was set at z_q = 0.91. Data were collected from 50 experiments.

The value of Q_tot was independent of both the presence of ADP and a fourfold increase in [Na]_o (Fig. 4 B). Thus, all best-fit values were averaged to yield Q_tot = 25.2 ± 1.5 fC/pF. The apparent valence of the mobile charges also showed no dependence on [ADP] or on changes in [Na]_o (Fig. 4 C) and, thus, all best-fit values were averaged to give z_q = 0.91 ± 0.12, not statistically significantly different than the value that best fits the data in panel A.

Altogether, the presence of ADP, as well as an increase in [Na]_o, seem to reversibly influence the steady-state distribution of phosphoenzyme intermediates under Na⁺-Na⁺ exchange conditions with no effect on the total quantity of mobile charge or its apparent valence, as expected for a system that behaves according to Scheme 2.

Effect of ADP and Na⁺_o on the V_M-dependent kinetics of current relaxation

A quantitative description of the effect of ADP on electroneutral Na⁺-Na⁺ exchange requires estimation of all four rate constants in Scheme 2. To achieve this goal, the apparent rate constant for current relaxation (k_tot) was obtained at all V_M, [ADP], and [Na]_o tested by fitting single exponential functions to the decaying portion of ouabain-sensitive current traces. The results of this analysis are summarized as k_tot-V_M relationships in Fig. 5. In all cases, k_tot for the relaxation of “on” current became smaller at less negative voltage-clamp pulses and reached a minimum (k_min) at positive V_M, an asymmetry expected for Na⁺_o binding to the Na,K-pump in an ion well (Gadsby et al., 1993).

FIGURE 5.

Effects of ADP and Na⁺_o on the V_M-dependent kinetics of current decay. (A) The apparent rate constant, k_tot, was obtained at each V_M from experiments performed with 145 mM Na⁺_o in the absence (○) and presence of 4.3 mM pipette ADP (•). Values at −40 mV are the average of k_tot for “off” current relaxation. Symbols are the mean ± SE of data from 4–5 cells. Lines were drawn by eye. (Inset) Second derivative of k_tot with respect to V_M, 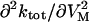, at hyperpolarizing potentials. Values of 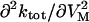were estimated from the experimental data as Δ(Δk_tot)/Δ(ΔV_M) with 0 (○) and 4.3 mM ADP (•). Lines connecting the symbols were drawn by eye. Ordinate, (s⁻¹mV⁻²); abscissa, (mV). (B) k_tot-V_M relationships from cells superfused with 36.3 mM Na⁺-containing solution in the presence of 0.8 (▾), 3.0 (○), and 4.3 mM pipette ADP (•). (C) k_tot-V_M curves from experiments with 72.5 mM Na⁺_o. Symbol code as in panel B. (D) k_tot-V_M relationships from cells superfused with 145 mM Na⁺-containing solution in the presence of 0.8 (▾), 1.7 (○), and 4.3 mM pipette ADP (•). Data at 4.3 mM ADP were redrawn from panel A. Lines in panels B, C, and D are best-fitting curves obtained by simultaneous regression of Eq. 8 to 143 k_tot values (each being the average of 3–5 experiments) that were determined at 13 V_M, 5 [ADP] (zero ADP was not included), and 3 [Na]_o. Best-fit parameters are reported in the text. (E) [ADP] dependence of k_tot at depolarizing V_M. k_tot values obtained at +80 mV with 36.3 (▾), 72.5 (○), and 145 mM 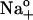(•) were plotted against [ADP]. The curve represents fitting of Eq. 9. Best-fit parameters are listed in the text. (F) V_M-dependent kinetics of current decay as a function of [Na]_o in the absence of added ADP. k_tot-V_M curves were obtained from 14 experiments in cells assayed with 36.3 (∇), 72.5 (•), and 145 mM 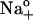(○). Data at 145 mM Na⁺_o were redrawn from panel A. Dotted lines represent k_tot = f(V_M, [Na]_o) as predicted by Scheme 2 using Eq. 10 with k₂ = 130 s⁻¹, k₋₂ = 162 s⁻¹M⁻¹, n = 1.1, and z_k = 0.63 for 36.3 (left), 72.5 (middle), and 145 mM Na⁺_o (right). Solid lines represent fitting of Eq. 8.

Fig. 5 A shows k_tot-V_M curves at 0 and 4.3 mM pipette ADP for cells superfused with 145 mM Na⁺_o. As illustrated in Figs. 1 and 2, addition of ADP changed the kinetics of current decay. The presence of 4.3 mM ADP produced a twofold decrease in the value of k_min as compared to the zero-ADP control. Also apparent is an [ADP]-dependent increase in the rate of current relaxation at test potentials negative to −70 mV that was less obvious in Figs. 1 and 2. Inspection of Fig. 5 A also shows a change in the concavity of k_tot-V_M curves at large negative potentials, particularly evident in the absence of ADP. Mathematical demonstration of this concavity change is presented as a corresponding change in the sign of the second derivative of k_tot with respect to V_M (Fig. 5 A, inset). Addition of ADP shifted the value of the inflexion point toward more negative potentials, closer to the edge of the experimental range of V_M. The change in concavity might suggest that k_tot saturates at large negative potentials, i.e., a V_M-independent reaction becomes rate limiting under those conditions. Unfortunately, saturation of k_tot, if any, would occur outside the experimentally accessible range of V_M.

Panels B, C, and D of Fig. 5 show k_tot-V_M relationships at selected pipette [ADP] with 36.3, 72.5, and 145 mM Na⁺_o, respectively. As judged by the values of k_tot at hyperpolarizing V_M in all three panels, an increase in [Na]_o produced a rightward shift in the k_tot-V_M curves, i.e., the higher the [Na]_o the larger the value of k_tot at any given [ADP]. Analysis of these curves was carried out by fitting the following equation:

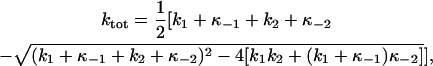(8)

which is an expression for k_tot in terms of the rate constants describing Scheme 2 (see the Appendix for an explanation of this equation). Since κ₋₁ is a function of [ADP] (Eq. 1) and κ₋₂ depends on [Na]_o and V_M (Eq. 5), Eq. 8 was simultaneously fitted to the entire pool of k_tot data obtained at all V_M, [ADP], and [Na]_o tested. This nonlinear regression in three variables yielded the following set of best-fit parameters that was used to draw the curves through the data points in panels B, C, and D: k₁ = 403.6 ± 6.9 s⁻¹, k₋₁ = (6.38 ± 0.54) × 10⁴ s⁻¹M⁻¹, k₂ = 130.1 ± 5.2 s⁻¹, k₋₂ = 162.0 ± 34.0 s⁻¹M⁻¹, n = 0.95 ± 0.20, and z_k = 0.63 ± 0.08. The values of the apparent valence, z_k, the Hill coefficient for Na⁺_o, n, and the ratio k₋₁/k₁ (158.1 ± 13.7 M⁻¹), were not significantly different from those obtained with Eq. 7 when analyzing steady-state charge distribution data. The ratio k₋₂/k₂ (1.25 ± 0.27 M⁻¹), on the other hand, was found to be roughly half the value of K₂ obtained with Eq. 7.

The behavior of the k_tot-V_M relationships at positive potentials is shown in detail in Fig. 5 E, where values of k_tot at +80 mV determined from experiments at all three [Na]_o are plotted against [ADP]. As suggested in Fig. 2, k_tot values were independent of [Na]_o at these depolarizing V_M. Kinetic information can be also extracted from these data by realizing that κ₋₂ approaches zero at large positive V_M. Under these conditions, Eq. 8 becomes

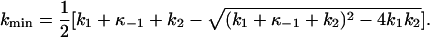(9)

Thus, according to Scheme 2, k_min is a V_M- and [Na]_o-independent, decreasing function of [ADP]. In addition, k_min equals k₂ in the absence of this nucleotide. Fitting Eq. 9 to the k_tot data at +80 mV yielded (curve in Fig. 5 E) k₁ = 386 ± 36 s⁻¹, k₋₁ = (6.89 ± 0.50) × 10⁴ s⁻¹M⁻¹, and k₂ = 145 ± 12 s⁻¹, all within the error of the best-fit parameters reported above.

Scheme 2 reduces to two states in the absence of ADP and, thus, Eq. 8 should no longer provide an adequate description of the k_tot-V_M relationships. For this reason, curves obtained under ADP-free conditions were not included in the previous analysis. Instead, according to Scheme 2, k_tot has the following expression (see Appendix, Eq. A18):

(10)

This equation predicts that the rate of relaxation of Na_o-TCM in the absence of ADP reaches a minimum value at positive V_M equal to k₂ (consistent with Eq. 9), increasing proportionally to and exponentially with V_M as potentials are made more negative.

Experimentally, k_tot-V_M relationships obtained in the presence of 36.3, 72.5, and 145 mM Na⁺_o, with no ADP included in the pipette solution show three distinct features (Fig. 5 F, symbols). First, k_tot converged to a minimum value at positive V_M that was independent of [Na]_o, consistent with the behavior shown in Fig. 5 E and the predictions of Eq. 10. Second, as suggested in panels B, C, and D, curves showed a rightward shift with higher [Na]_o at hyperpolarizing voltage clamp pulses, also in agreement with Eq. 10. Finally, as displayed in Fig. 5 A, k_tot-V_M curves showed a change in concavity, i.e., they did not increase exponentially at hyperpolarizing V_M. As a result, Eq. 10 failed to describe the k_tot-V_M relationships at these potentials, particularly with higher [Na]_o (Fig. 5 F, dotted lines). A simple way to explain this apparent inconsistency is to propose that experiments performed under ADP-free conditions were actually carried out in the presence of residual levels of ADP. In this regard, the activity of cellular adenylate kinase as a source of contaminating ADP was ruled out in control experiments with the competitive inhibitor Ap₅A (see online supplementary material). Nonetheless, since untested sources (cellular or not) could be responsible for such an ADP contamination, the amount of this nucleotide that would account for the shape of k_tot-V_M curves at hyperpolarizing V_M was estimated by fitting Eq. 8 to the data points in Fig. 5 F (solid lines). This analysis gave an average value of 4.4 s⁻¹ for κ₋₁, which, using the best-fit value of k₋₁ calculated above, yielded a residual [ADP] of ∼70 μM.

Ability of the calculated parameters to reproduce experimental results

A test for internal consistency of the best-fit parameters calculated in the previous section was run by solving the expression for time- and V_M-dependent current derived for Scheme 2 (see Appendix, Eq. A17) with these parameter values and a residual [ADP] = 70 μM. Transient currents simulated in this way (Fig. 6) followed [ADP]- and V_M-dependent time courses that resembled those of their experimental counterparts (Fig. 1). Likewise, simulations performed at various [Na]_o were able to reproduce the behavior observed experimentally (not shown). Thus, expressions derived for Scheme 2 can qualitatively reproduce the [Na]_o-, [ADP]-, and V_M-dependent kinetics of ouabain-sensitive transient charge movements with the rate constants, n, and z_k determined experimentally.

FIGURE 6.

Simulated transient currents. Best-fit values of k₁, k₋₁, k₂, k₋₂, n, and z_k were replaced into Eq. A17 and currents were calculated within experimental ranges of time and V_M with 0.070 (A) or 4.3 mM ADP (B) and 145 mM . Simulations were carried out using zF[E]_T = 0.0252 pC/pF.

DISCUSSION

Ouabain-sensitive transient currents were measured in whole-cell voltage-clamped rat cardiac myocytes with a broad range of intracellular ADP and extracellular Na⁺ concentrations to investigate the kinetics of Na,K-ATPase phosphoenzyme-dependent reactions, such as ADP binding and release, that are otherwise difficult to study. The derived reaction kinetics were then used to gain a more detailed understanding of Na⁺ transport steps mediated by this enzyme.

Nature of ouabain-sensitive transient currents

Conditions used in this study's experiments were designed to restrict the Na,K-ATPase to functioning in its Na⁺-Na⁺ exchange mode. Extracellular K⁺-free solutions reduced the rate of E₂-P breakdown to 1–3 s⁻¹ (Glynn, 1985; Cornelius and Skou, 1985; Stein, 1986), thereby diminishing Na,K-pump forward running, and high Na⁺ concentrations and millimolar MgATP ensured maximal rates of phosphorylation (Peluffo et al., 1994a,b), altogether favoring redistribution of enzyme intermediates among phosphorylated forms (Schemes 1 and 2). The absence of ouabain-sensitive steady-state current in experiments with ADP was consistent with the lack of Na,K-pump forward running and the presence of electroneutral Na⁺-Na⁺ exchange. Electrogenic, likely 3 Na⁺-2 Na⁺ (Lee and Blostein, 1980; Apell et al., 1990), exchange is known to require ATP and Na⁺ in the absence of both K⁺ and ADP (Glynn, 1985; Läuger, 1991). However, transient currents measured in the absence of pipette ADP also relaxed to a steady-state level that was indistinguishable from zero. This negligible rate of electrogenic Na⁺-Na⁺ exchange might suggest the presence of residual levels of ADP in the intracellular milieu even with nominally ADP-free electrode solutions (see below).

Therefore, charge movements studied in this work are likely produced by the release and rebinding of Na ions to the Na,K-pump during electroneutral Na⁺-Na⁺ exchange reactions, in agreement with previous reports (Nakao and Gadsby, 1986; Gadsby et al., 1993).

[ADP], [Na]_o, and V_M dependence of the steady-state charge distribution

The total quantity of mobile charge, Q_tot, was independent of the presence of ADP at concentrations up to 4.3 mM (Fig. 4 B). Since Q_tot is proportional to the level of phosphoenzyme, this finding argues against a significant competitive effect of ADP on high-affinity ATP binding. Binding of the nonphosphorylating ADP to the Na,K-ATPase catalytic site should result in a decrease in total levels of phosphoenzyme and, since at least one phosphointermediate must be associated with charge movement, this would produce a decrease in Q_tot. Furthermore, considering that the enzyme binds ADP at the catalytic site with 10-fold lower affinity than ATP (Hegyvary and Post, 1971; Nørby and Jensen, 1971), a competitive model predicts a ratio v/v_max = 0.90 for the inhibitory effect of 4 mM ADP on binding of 3.7 mM MgATP. Thus, competition between ATP and ADP appeared to be negligible in the range of concentrations tested, consistent with the idea that ADP was acting as a low-affinity ligand in these experiments.

Besides being independent of ADP, Q_tot was not affected by changes in [Na]_o between 36.3 and 145 mM. The average value calculated for all conditions tested was 25.2 ± 1.5 fC/pF, in agreement with our previous estimates (Peluffo and Berlin, 1997, 2003). The invariance of Q_tot with [Na]_o was consistent with Na⁺_o binding in an ion well. In fact, inspection of Eq. 3 indicates that [Na]_λ can be made large (by manipulating V_M) to maximize Q_tot with any [Na]_o > 0. Rakowski (1993), on the other hand, found that Q_tot was an increasing function of [Na]_o in Xenopus oocytes. However, this behavior was not observed with squid axons voltage-clamped under conditions promoting electroneutral Na⁺-Na⁺ exchange, where the efflux of ²²Na reached a maximal value at hyperpolarizing V_M that was independent of [Na]_o (Gadsby et al., 1993), consistent with the results of the present work.

The presence of ADP mimicked the effect of increasing Na⁺_o on the ΔQ-V_M relationship. Raising the concentration of either one of these ligands shifted the midpoint potential (V_q) to less negative V_M (Fig. 4 A), suggesting a distribution of phosphointermediates that progressively favored E₁∼P-like conformations, as expected for a system that follows Scheme 2. In fact, the change in V_q values at a fixed [Na]_o, ∼4 mV/mM for the range of [ADP] tested, behaved as anticipated by Scheme 2 (Eq. A14). Likewise, at a fixed [ADP], V_q is expected to shift as a function of [Na]₂/[Na]₁ (Eq. A15) and, in fact, the experimental values of V_q increased by ∼20 mV every time [Na]_o was doubled, at any given [ADP]. This shift in V_q was used to estimate the portion of the membrane electric field, δ, sensed by mobile charges (Eq. A15). For the three [Na]_o tested at each of four [ADP], an average value of 0.85 ± 0.04 (n = 12) was calculated for δ.

[ADP], [Na]_o, and V_M dependence of the kinetics of Na,K-pump current relaxation

The apparent rate constant for current relaxation (k_tot) showed an asymmetric V_M dependence, with faster kinetics at hyperpolarizing potentials and slower kinetics, approaching a constant value, at depolarizing pulses. This behavior, first demonstrated by Nakao and Gadsby (1986), is consistent with an ion well model for Na⁺_o binding and has been reported for Na,K-pumps from different tissues using a variety of techniques (Rakowski, 1993; Fendler et al., 1993; Hilgemann, 1994; Holmgren and Rakowski, 1994; Friedrich and Nagel, 1997; Holmgren et al., 2000). A similar asymmetry in k_tot-V_M curves was demonstrated for extracellular Tl⁺-dependent charge movements under conditions favoring K⁺-K⁺ exchange by the Na,K-pump (Peluffo and Berlin, 1997).

Inclusion of ADP in the electrode solution decreased the values of k_tot at depolarizing potentials and increased them at hyperpolarizing V_M as compared to the control, enhancing even more the asymmetry of k_tot-V_M relationships. The model proposed in Scheme 2, by including one step with measurable V_M dependence (Na⁺_o rebinding) and electroneutral ADP binding/release to/from the phosphoenzyme, was able to account for both the asymmetry and the effects of ADP on k_tot-V_M curves. Accordingly, k_tot-V_M relationships from experiments at various [ADP] and [Na]_o were analyzed with an expression derived from this reaction scheme (Eq. 8) to kinetically describe ADP binding and Na⁺_o-related reaction steps.

Kinetics of ADP binding reactions

The value of the rate constant for ADP release, k₁ (404 s⁻¹), determined under conditions that strongly favor enzyme phosphorylation, is in fair agreement with that reported by Campos and Beaugé (1997) in chymotrypsin-digested enzyme (1067 s⁻¹, 22°C). Both of these values agree with suggestions that (Na₃)E₁∼P·ADP is a short-lived intermediate in the Na,K-ATPase reaction cycle (Mårdh and Post, 1977; Nørby et al., 1983; Hobbs et al., 1985). The second-order rate constant for ADP binding to the phosphoenzyme, k₋₁, was estimated to be 6.4 × 10⁴ s⁻¹M⁻¹, allowing us to calculate an apparent equilibrium constant for the dissociation of ADP from the phosphoenzyme, K_d = 6.3 ± 0.5 mM. The agreement between this value and that obtained from steady-state distribution of charge (1000/K₁ = 7.0 mM) indicates that the model in Scheme 2 can quantitatively describe presteady- and steady-state ADP effects on Na_o-TCM. Our K_d was consistent with the range of 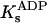values (1–6 mM) reported by Suzuki and Post (1997). Chymotrypsin-modified enzyme, on the other hand, yielded a K_d = 37 μM (Campos and Beaugé, 1997; K_s at 2 mM Mg²⁺). Whether this value represents a true K_d for ADP in the absence of Na⁺-Na⁺ exchange or the proteolytic treatment affected ADP binding sites in E₁∼P, remains to be determined. However, the finding that ADP did not affect Q_tot (Fig. 4 B) argues for a low ADP affinity.

The value of k_min was shown to be a decreasing function of [ADP] (Fig. 5 E), a finding that leads to two mechanistic conclusions. First, since k_min is V_M-independent (Fig. 5 and Eq. 9), it follows that ADP binding to the phosphoenzyme must be an electrically silent event. A similar conclusion was reached from electrical measurements on chymotrypsin-treated Na,K-ATPase after photochemical release of ATP (Borlinghaus et al., 1987). Nonetheless, as judged by the [ADP] dependence of V_q (Fig. 4 A), ADP did modify the V_M dependence of Na_o-TCM, presumably by changing the distribution of phosphointermediates participating in V_M-dependent reactions. Second, according to Scheme 2, ADP decreases k_min by reducing the concentration of the intermediate entering the reactions described by k₂. Thus, ADP must be released before deocclusion/electrogenic release of Na⁺ (and before the phosphoenzyme conformational transition) in the forward running Na,K-ATPase. In support of this view, a reaction scheme in which Na⁺_o is released through an ion well before ADP would lead to an [ADP]-independent value of k_min.

Kinetics of reactions associated with 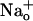release

According to Scheme 2, the rate constant k₂ (130 s⁻¹) lumps together Na⁺ deocclusion and release as well as the transition E₁∼P → E₂-P. Independent of whether the conformational transition takes place before or after Na⁺ release, the value of k₂ represents the rate of the slowest step for charge moving in the forward direction. In this regard, the rate constant for Na⁺ release has been estimated to be several thousands per second (Heyse et al., 1994; Wuddel and Apell, 1995; Hilgemann, 1994, 1997; Holmgren et al., 2000). Therefore, k₂ is likely to be an estimation of the rate of Na⁺ deocclusion or the enzyme conformational change, whichever is slower, assuming they are different microscopic events.

There is no general agreement about the kinetics of the reactions grouped and defined as k₂ in this work. Values fall within a wide range: 20–25 s⁻¹ (20–25°C, Taniguchi et al., 1984; Heyse et al., 1994; Wuddel and Apell, 1995; Sokolov et al., 1998); 60–80 s⁻¹ (20–25°C, Mårdh, 1975; Steinberg and Karlish, 1989; Rakowski, 1993; Klodos et al., 1994; Pintschovius and Fendler, 1999); values similar to that calculated here, 130–200 s⁻¹ (22–24°C, Campos and Beaugé, 1992; Pratap and Robinson, 1993; Kane et al., 1997; Gropp et al., 1998; Clarke et al., 1998); and values ≥300 s⁻¹ (21–24°C, Hobbs et al., 1985; Froehlich and Fendler, 1991; Fendler et al., 1993). Although there is no obvious reason for these differences, possible explanations are the variety of enzyme sources and experimental approaches used to derive these kinetics. An example of the importance of the enzyme source for determining reaction kinetics are the values of k₂ ≥ 300 s⁻¹ that were all derived from experiments with eel electric organ Na,K-ATPase. Likewise, the diversity of experimental approaches led to variations in reaction schemes, some of which lumped together enzyme phosphorylation, Na⁺ occlusion/deocclusion/release, and the transition E₁∼P → E₂-P. As a consequence, the identity of fast and slow steps within this sequence of reactions is uncertain in previous reports.

The results of this study are consistent with fast ADP release followed by a slower conformational change and/or Na⁺ deocclusion step, i.e., k₁ > k₂. It could be argued that the intermediate (Na₃)E₁∼P·ADP might go on to resynthesize ATP and release Na⁺ into the cytoplasm, adding the sequence E₁ ↔ Na₃E₁ATP ↔ (Na₃)E₁∼P·ADP to the left in Scheme 2. In the case of E₁ ↔ Na₃E₁ATP, high-affinity intracellular binding sites in the pump are likely sensing large concentrations of ATP and Na⁺ that drive this reaction forward. Control experiments confirmed that even the lowest pipette [MgATP] delivered enough intracellular MgATP to saturate the Na,K-ATPase (see online supplementary material). Likewise, 120 mM pipette-Na⁺ should supply saturating concentrations of intracellular Na⁺ (Nakao and Gadsby, 1989; Schultz and Apell, 1995). Thus, the reaction(s) E₁ ↔ Na₃E₁ATP will be strongly shifted to the right. With respect to Na₃E₁ATP ↔ (Na₃)E₁∼P·ADP, if enzyme phosphorylation and Na⁺ occlusion contribute to the relaxation kinetics of transient currents, the rate constant describing these reactions would be ≥404 s⁻¹, thus, yielding a fast phosphorylation/Na⁺ occlusion reaction followed by a slow conformational change/Na⁺ deocclusion step.

To complete the kinetic description of Scheme 2, the second-order V_M-independent rate constant, k₋₂, was determined to be 162 s⁻¹M⁻¹. This value agrees with that of 150 s⁻¹M⁻¹ reported by Rakowski (1993). With 145 mM Na⁺_o, κ₋₂ has a value of ∼25 s⁻¹ at 0 mV. The question then arises as to which Na⁺_o-related step (binding, occlusion, or phosphoenzyme conformational transition) becomes rate limiting under these conditions. Again, as with Na⁺ release and k₂, Na⁺_o binding seems to be very fast, with charge movements reaching completion within a few microseconds (Hilgemann, 1994; Holmgren et al., 2000). Thus, the slowest step in Scheme 2 is likely to be Na⁺ reocclusion or the transition E₂-P → E₁∼P.

Unlike k₁ and k₋₁ that describe equally well presteady- and steady-state data, the ratio k₋₂/k₂ was found to be ∼50% of K₂ obtained with steady-state charge distribution. Thus, when k₋₂/k₂ was replaced as K₂ in Eq. 7, V_q values came out ∼20 mV more negative than those that best fit Eq. 6. Since k₂ was also reliably estimated from k_min, which is independent of [Na]_o and V_M, the disagreement seems to reside in k₋₂, i.e., this rate constant must be twice as large to account for steady-state data. Alternatively, a similar correction can be attained by adding to Eq. A13 a surface potential (Hille, 1992), roughly (RT/z_qF)ln 2, generated by fixed charges in the Na,K-pump. Irrespective of these alternatives, the pseudo three-state model seems to describe Na⁺_o effects on charge movements only in a qualitative manner.

The values of n (0.95) and z_k (0.63) obtained with the kinetic analysis provide a second, independent estimate for δ. Thus, replacing these numbers in Eq. 4 (with q = 1), returned a value of δ = 0.66 ± 0.16. Recalling the value of δ calculated above with Eq. A15, these results suggest that Na ions dissipate, on average, 76% of the membrane dielectric to reach their sites in the pump, in agreement with previous estimates (Rakowski, 1993; Gadsby et al., 1993; Hilgemann, 1994; Wuddel and Apell, 1995; Holmgren et al., 2000; De Weer et al., 2001). This value of δ, indicative of a highly electrogenic reaction, has been systematically assigned to release/rebinding of the first Na⁺ from/to an uncharged site in the pump (Heyse et al., 1994; Hilgemann, 1994; Wuddel and Apell, 1995; Holmgren et al., 2000). Thus, the electrogenic reaction studied here might reflect transient release/rebinding of one Na⁺ whereas the other two ions remain bound to the pump, a view that would also agree with a Hill coefficient that is not significantly different from one.

The shape of k_tot-V_M curves in the nominal absence of ADP

The results of this report as well as other reports (Rakowski, 1993; Hilgemann, 1994; Friedrich and Nagel, 1997; Holmgren et al., 2000) show a decrease in the rate of change of k_tot at increasingly negative V_M. According to Scheme 2, this change in concavity of the k_tot-V_M curves at hyperpolarizing potentials suggests that a reaction not lumped within κ₋₂ is becoming slow. The observed [ADP]-dependent increase in k_tot values at hyperpolarizing V_M makes ADP binding an obvious candidate for the new slow reaction step. However, the change in concavity was also apparent in k_tot-V_M curves obtained in the absence of added ADP. The pseudo three-state model does not predict this feature. In fact, in the absence of ADP, Scheme 2 reduces to a pseudo two-state model with k_tot increasing exponentially at hyperpolarizing V_M (Eq. 10).

The presence of residual levels of ADP in what we call “ADP-free conditions” can easily reconcile these observations. In this regard, a residual [ADP] of 70 μM was estimated by fitting Eq. 8 to kinetic data in Fig. 5 F. Since cellular sources did not appear to be responsible for contaminating ADP, the nucleotide might come from the pipette solution. A contamination with ADP of 0.5–1% in the ATP used to prepare the control solution (Table 1) would be enough to account for the estimated residual [ADP]. In addition to explaining the shape of k_tot-V_M curves at hyperpolarizing V_M, this contaminating ADP would prevent the occurrence of electrogenic Na⁺-Na⁺ exchange, thus explaining the zero steady-state current levels shown in Fig. 1 A. In fact, comparable concentrations of ADP have been reported to noncompetitively inhibit forward running (Apell et al., 1990) and block electrogenic Na⁺-Na⁺ exchange (Cornelius and Skou, 1985) by Na,K-ATPase reconstituted in artificial lipid vesicles.

It must be pointed out that this hypothetical contamination would have no impact on the values of most rate constants derived in this work. For example, fitting Eq. 9 to the data in Fig. 5 E after correction by 70 μM residual ADP yielded k₁ = 404 ± 18 s⁻¹, k₋₁ = (6.94 ± 0.39) × 10⁴ s⁻¹M⁻¹, and k₂ = 145 ± 8 s⁻¹, values that were indistinguishable from those reported in Results.

This discussion relies on the premise that experimental k_tot-V_M curves will show no change in concavity under true ADP-free conditions (as anticipated by Eq. 10), i.e., binding of ADP is responsible for decreasing the rate of change of k_tot at hyperpolarizing V_M. An alternative is that a first-order reaction becomes slow at large negative V_M, regardless of the presence of ADP. Since this explanation excludes reaction steps to the left of (Na₃)E₁∼P in Scheme 2, such a first-order reaction must be within κ₋₂, i.e., the transition E₂-P → E₁∼P and/or Na⁺ reocclusion. Thus, modifying Scheme 2 to explicitly include one more step after the release of ADP would also account for the change in concavity observed with k_tot-V_M curves in the absence of ADP as well as the ADP-dependent increase in k_tot values at hyperpolarizing V_M. If such a reaction scheme were valid, it would still support our basic conclusion that ADP is released from the phosphoenzyme before Na⁺ is deoccluded and released in an ion well.

A third way to account for the shape of the k_tot-V_M curve in the absence of added ADP is to include saturation of Na⁺_o binding sites in the formulation of Eq. 5. In this case, although bulk [Na]_o is in rapid equilibrium with [Na]_λ, local Na ions bind to a finite number of sites. As a result, κ₋₂ becomes a saturable function of [Na]_o approaching a maximum equal to k₋₂ at large hyperpolarizing potentials (see online supplementary material).

Irrespective of which alternative is chosen to explain the form of the k_tot-V_M curves at hyperpolarizing V_M in the absence of added ADP, such modifications would affect neither the values of k₁, k₋₁, and k₂ (obtained at positive V_M) nor the mechanistic conclusions in this work.

As a general conclusion, transient currents reported here appear to decay with the kinetics of the phosphoenzyme conformational transition or Na⁺ occlusion/deocclusion steps associated with electrogenic release/rebinding of Na⁺_o. This kinetic and V_M-dependent behavior allows us to match our Na_o-TCM with the slowest component of the multiple exponential relaxation reported by Holmgren et al. (2000) for charge movements generated by sequential Na⁺ deocclusion and release in high-speed voltage-clamped squid axons. It would be mechanistically relevant to know whether the faster kinetic components found by Holmgren and co-workers show ADP sensitivity.

In summary, transient charge movement measurements were used to study the kinetics and V_M dependence of ADP-dependent reactions of native Na,K-ATPase, which have not been determined experimentally in previous studies. Characterization of the proposed reaction scheme allowed new mechanistic insights into the relationship between ADP-related reactions and electroneutral Na⁺-Na⁺ exchange. This approach can also be applied to study additional charge-moving reactions and related electrically silent ligand binding steps of the Na,K-pump and other membrane-bound transporters.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

APPENDIX

Solution of the pseudo three-state reaction scheme

The model in Scheme 2 can be represented in the general form

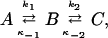where A, B, and C symbolize the three phosphointermediates. The time dependence of a system that reacts according to this scheme is described by the following set of differential equations:

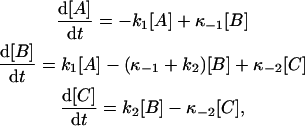(A1)

where [A], [B], and [C] are the concentrations of the respective species at time t. In addition, let us consider mass balance and the following boundary conditions:

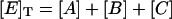(A2a)

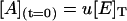(A2b)

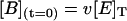(A2c)

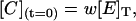(A2d)

where [E]_T is the total concentration of enzyme, and u, v, and w are the initial fractions of A, B, and C with (u + v + w) = 1. Notice that concentrations at t = 0 represent the steady-state distribution of phosphoenzyme intermediates at V_M = −40 mV.

The Laplace transforms method was used to solve Eqs. A1 with conditions A2. In particular, the following expression for species C (E₂-P in Scheme 2) was derived

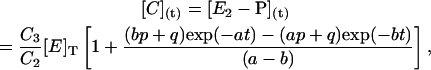(A3)

where

(A4)

Pseudo three-state model expression for steady-state charge distribution

The steady-state quantity of charge moved during Na⁺-translocating steps, ΔQ, can be expressed as

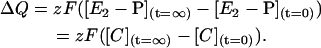(A5)

Solving Eq. A3 under steady-state conditions, recalling Eq. A2d, and replacing in Eq. A5 yields

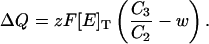(A6)

The steady-state solution of Eqs. A1 gives an expression for the initial fraction of each phosphointermediate:

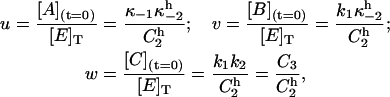(A7)

where the superscript h stands for holding potential and denotes the fact that κ₋₂ and all combinations of rate constants that include κ₋₂ are initially defined at −40 mV. Thus, replacing w in Eq. A6 and rearranging yields

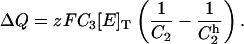(A8)

Using Eq. A8 and recalling Eqs. 1, 5, and A4, the expression for steady-state charge distribution as an explicit function of [ADP], [Na]_o, and V_M, was derived as follows:

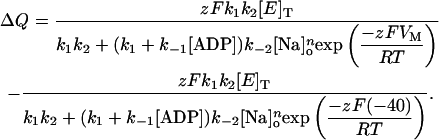(A9)

Rearranging and defining a midpoint voltage V_q such that,

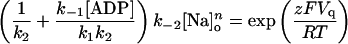(A10)

and knowing that zF[E]_T is the total quantity of mobile charge, Q_tot, Eq. A9 becomes, after further rearrangement

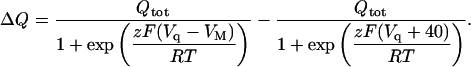(A11)

Note that ΔQ = 0 when V_M = −40 mV. In addition,

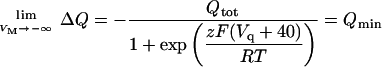and

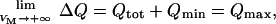(A12)

where Q_tot = Q_max − Q_min. Substitution of Q_min in Eq. A11 leads to Eq. 6 (see main text).

Eq. A10 can be solved for V_q to give

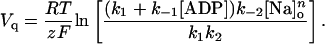(A13)

Note that a midpoint potential is not defined for [Na]_o = 0. When [ADP] = 0, V_q becomes independent of both k₁ and k₋₁.

The change in V_q expected for a change in [ADP] at constant [Na]_o has the form

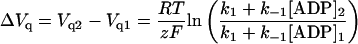(A14)

Likewise, taking into account Eq. 4 with q = 1 (univalent charged species), the change in midpoint voltage expected for a change in [Na]_o at constant [ADP] is

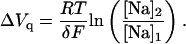(A15)

Pseudo three-state model expression for time- and V_M-dependent current

Differentiating Eq. A3 yields an expression for time- and V_M-dependent current, I = f(t, V_M):

(A16)

Recalling Eqs. A4 and A7, expression A16 becomes, after some algebra

(A17)

Note that, as required by the model and the experimental protocol, I(∞, V_M) = I(t, −40 mV) = 0.

An expression for k_tot in the presence of ADP

The reversible nature of reactions in Scheme 2 (i.e., κ₋₁ > 0) implies that the expression for current is a biexponential function of time (Eq. A17). Since measured currents follow single exponential relaxation kinetics, the question arises as to which rate coefficient in Eq. A17, a or b, describes k_tot in the presence of ADP. A key hint comes from inspection of the conjugated roots in Eq. A4. Recalling that κ₋₁ (Eq. 1) is present in C₁ and C₂ (Eq. A4) and knowing that a and b are real numbers (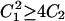), it follows that only rate coefficient b can account for the observed decrease of k_min with [ADP] (Fig. 5). Nevertheless, “component a”, defined as the amplitude term multiplied by the exponential term that contains rate coefficient a, could still significantly contribute to the kinetics of current decay as well as its V_M and [ADP] dependence. To test the contribution of “component a”, Eq. A17 was solved for voltage jumps to −140 and +60 mV using a set of rate constants that included values of κ₋₁ and κ₋₂ calculated with 4 mM ADP and 145 mM Na⁺_o, respectively (Fig. 7 A, solid lines). Alternatively, “component a” was neglected from Eq. A17 and the calculations above were repeated with the resulting “component b” (Fig. 7 A, dotted lines). Except for the first couple of milliseconds after the onset of the voltage pulse, the time course of current decay described by “component b” was practically indistinguishable from that of the complete expression. The same set of rate constants was used to generate values of a and b as a function of V_M according to Eq. A4. Results in Fig. 7 B show that b = f(V_M) resembled the experimental V_M-dependent behavior of k_tot (see Fig. 5), including the change in curve concavity. Rate coefficient a, on the other hand, displayed much larger values, showed no V_M dependence up to −100 mV, and increased exponentially at more negative potentials. Therefore, the V_M- and [ADP]-dependent relaxation kinetics of experimental currents seem to be adequately described by rate coefficient b (Eq. 8).

FIGURE 7.

Predictions of Eq. A17. (A) Current time courses generated by 100 ms-long V_M jumps of ±100 mV. Equation A17 was solved with the following set of parameters and conditions (solid lines): k₁ = 530 s⁻¹, k₋₁ = 4.0 × 10⁵ s⁻¹M⁻¹, k₂ = 180 s⁻¹, k₋₂ = 80 s⁻¹M⁻¹, z = n = 1, zF[E]_T = 0.025 pC/pF, [ADP] = 4 mM, [Na]_o = 145 mM, T = 296 K, V_M = −140 or +60 mV. Similar calculations were performed after neglecting “component a” (defined in the text) from Eq. A17 (dotted lines). (B) V_M dependence of rate coefficients a and b. Values of a (○) and b (•) were generated with Eqs. 1, 5, and A4 for the experimental range of V_M using parameters and conditions from panel A.

Expression for k_tot in the absence of ADP

Scheme 2 reduces to a pseudo two-state model under ADP-free conditions (κ₋₁ = 0). Accordingly, Eq. A17 becomes single exponential

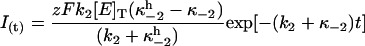(A18)

and the apparent rate constant for current relaxation, k_tot, equals k₂ + κ₋₂.