Determinants of Gating Polarity of a Connexin 32 Hemichannel

Abstract

There is good evidence supporting the view that the transjunctional voltage sensor (V_j-sensor) of Cx32 and other Group 1 connexins is contained within a segment of the N-terminus that contributes to the formation of the channel pore. We have shown that the addition of negatively charged amino acid residues at several positions within the first 10 amino acid residues reverses the polarity of V_j-gating and proposed that channel closure is initiated by the inward movement of this region. Here, we report that positive charge substitutions of the 2nd, 5th, and 8th residues maintain the negative polarity of V_j-gating. These data are consistent with the original gating model. Surprisingly, some channels containing combinations of positive and/or negative charges at the 2nd and 5th positions display bipolar V_j-gating. The appearance of bipolar gating does not correlate with relative orientation of charges at this position. However, the voltage sensitivity of bipolar channels correlates with the sign of the charge at the 2nd residue, suggesting that charges at this position may have a larger role in determining gating polarity. Taken together with previous findings, the results suggest that the polarity V_j-gating is not determined by the sign of the charge lying closest to the cytoplasmic entry of the channel, nor is it likely to result from the reorientation of an electrical dipole contained in the N-terminus. We further explore the mechanism of polarity determination by utilizing the one-dimensional Poisson-Nernst-Plank model to determine the voltage profile of simple model channels containing regions of permanent charge within the channel pore. These considerations demonstrate how local variations in the electric field may influence the polarity and sensitivity of V_j-gating but are unlikely to account for the appearance of bipolar V_j-gating.

INTRODUCTION

Studies of intercellular channels and unapposed conductive hemichannels formed by members of the connexin gene family have established that transjunctional voltage (V_j) dependence is fundamentally a hemichannel property, in that each hemichannel contains a separate set of voltage sensors and gates that function autonomously, but not necessarily independently (see Harris, 2001; Verselis and Bukauskas, 2002). Two separate gating mechanisms, termed V_j-gating and loop gating, have been identified (Trexler et al., 1996; Verselis and Bukauskas, 2002). In single-channel recordings, V_j-gating corresponds to rapid transitions (submicrosecond time course) among a fully open and one of several subconductance states that reduce the conductance of the open state by ∼80%. These transitions underlie the residual conductance (G_min) that is observed in the conductance-transjunctional voltage relations of most intercellular channels obtained with macroscopic recordings. V_j-gating has been termed “fast gating” by some authors to reflect the time course of the gating transitions (see Verselis and Bukauskas, 2002). In single-channel records, loop gating appears as a series of small stepwise changes in conductance that can, but do not always lead, to complete channel closure. Because of the multiple transitions, loop-gating events usually display a noticeable time course (millisecond timescale) and consequently, the mechanism has also been termed “slow gating”. The term “loop gating” was coined by Trexler et al. (1996) to reflect the possibility that this form of voltage gating involved conformational changes of the extracellular loops.

Although the molecular determinants of loop gating are not understood, the opposite polarity of V_j-gating of two closely related connexins, Cx32 and Cx26, has allowed a molecular dissection of this process. Using a chimeric approach, the difference in the gating polarity of the two hemichannels was shown to arise from the electrostatic effect of a charge difference at the 2nd amino acid position (Verselis et al., 1994). Because no other region of either connexin could reverse gating polarity, Verselis et al. (1994) proposed that charged amino acid residues in the amino terminus of Cx26 and Cx32 formed at least a portion of the V_j-sensor. The consistent correlation between charge substitutions at the 2nd amino acid residue and gating polarity led to the suggestion that the Cx32 and Cx26 voltage sensors are oppositely charged. The voltage sensor contained within Cx32 hemichannels would have a net positive charge whereas the voltage sensor in Cx26 hemichannels would have a net negative charge. It was further proposed that the positive valence of the Cx32 sensor arose from the positive charge of the unmodified N-terminal methionine residue and/or the partial positive charge created by a helical dipole in the amino terminus, and that the presence of a negative charge at the 2nd position was sufficient to change the net charge of the voltage sensor from positive to negative.

This view of the composition of the V_j-sensor in the N-terminus was appealing for two reasons: First, it allowed conservation of the gating mechanism; in either case the voltage sensor would move inward, toward the cytoplasm, in response to sufficient polarization of the appropriate polarity, negative for Cx32, positive for Cx26 (see Fig. 9 D). Second, the location of the voltage sensor in the amino terminus would position it in the channel pore near the cytoplasmic surface of each hemichannel (see Oh et al., 1999; Purnick et al., 2000a). The placement of the voltage sensor in this position would account for the observed sensitivity of V_j-dependence of intercellular channels to changes in the relative difference in potential between coupled cells (V_j), the transjunctional voltage, and insensitivity to changes in absolute membrane potential (V_m).

FIGURE 9.

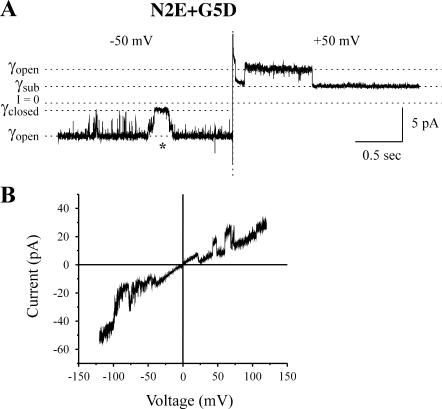
Gating of N2E+G5R hemichannels. (A) A cell-attached record of a single N2E+G5R channel at a holding potential of −50 and +50 mV. The transitions at +50 correspond to V_j-gating, whereas those at negative potentials correspond to loop-gating events. The asterisk marks a loop-gating event, as judged by the slow time course of the transitions between the open and closed states. (B) The current/voltage relation of N2E+G5R recorded in an inside-out patch configuration. Leak current was not subtracted. Loop-gating transitions are observed more frequently at negative potentials, V_j-gating transitions at positive potentials. The open state of the channel rectifies inwardly. Records were obtained in bath and pipette solutions containing 88 mM NaCl, 1 mM KCl, 1 mM MgCl₂, 2 mM EDTA, 2 mM EGTA, and 10 mM HEPES, pH 7.6

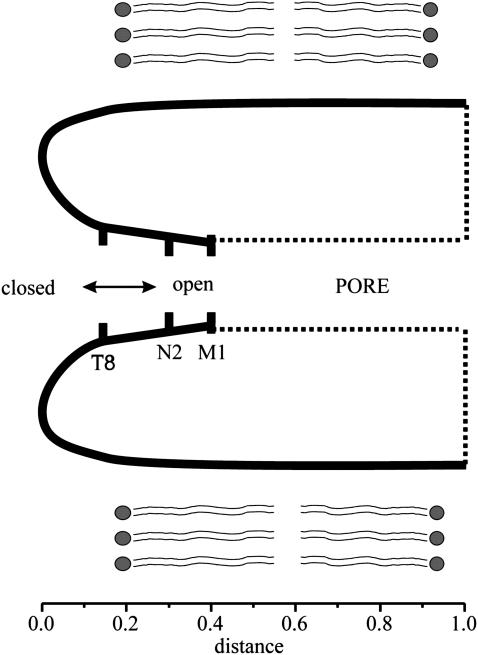
Purnick et al. (2000a) reported that the polarity of V_j-gating in both Cx32 and Cx32*Cx43E1 hemichannels could also be reversed by negative charge substitutions at the 5th, 8th, 9th and 10th positions. It was proposed that at least the first 10 amino acid residues of Cx32 line or lie in close proximity to the aqueous pore and consequently sense changes in the voltage field and that the amino terminus moves as a single unit in response to changes in voltage (see Fig. 1). This model was supported by the solution structure of an N-terminal Cx26 peptide by NMR that provided an atomic resolution model in which the amino terminus formed a vestibule at the cytoplasmic entrance of the channel by virtue of an open turn around the conserved glycine residue at the 12th position. In this structure, the N-terminal methionine residue lies deeper in the pore than the 12th residue, which is closer to the cytoplasmic face of the channel (Purnick et al., 2000b).

FIGURE 1.

Schematic drawing of a longitudinal section of a connexin hemichannel. The N-terminus forms the cytoplasmic entrance of the pore by virtue of a turn in the vicinity of the 12th amino acid residue. The positions of M1, N2, and T8 residues are indicated as a function of the electrical distance along the channel pore. It has been proposed that the inward translocation of charges in the N-terminus initiates channel closure by V_j-gating (see text).

Purnick et al. (2000a) suggested that the mechanism of V_j-gating polarity reversal of the Cx32 hemichannel by negative charge substitutions might involve the reorientation of a dipole whose negative pole was oriented toward the cytoplasm rather than an electrostatic effect that reverses the valence of the voltage sensor. However, the mechanistic interpretation of polarity reversal was complicated by the bipolarity of V_j-gating of homomeric T8D hemichannels, that is, the open probability of the channel decreased at both positive and negative membrane potentials and was maximal at intermediate membrane potentials (Purnick et al., 2000a). The bipolarity of the homomeric T8D channel was explained by postulating the existence of at least two open channel states. In one open channel conformation, the T8D residue would lie within the electric field and closure of the V_j-gate would be initiated by the inward movement of the negative charge at positive potentials. In the second open conformation, T8D would lie outside the electric field and the negative gating polarity would be a consequence of the inward movement of the positive charge associated with the unmodified N-terminal methionine residue (M1) at negative potentials.

In this article, we further explore the determinants of gating polarity, by examining the voltage dependence of channels containing positive charges at the 2nd, 5th, and 8th positions. Positive charges at these positions are expected to maintain the negative polarity of V_j-gating. The possibility that gating polarity is determined by the orientation of a charge dipole is examined by determining the gating polarity of channels in which the relative orientation of positive and negative charges at the 2nd and 5th residues is reversed. A major assumption in the interpretation of our past results has been that the voltage drop across the channel pore is linear and not substantially changed by the substitution of charged residues. Here, we utilize the one dimensional Poisson-Nernst-Plank (PNP) model of Chen and Eisenberg (1993) to determine the voltage profile and resulting electric field of simple cylindrical channels containing regions of fixed permanent charge within the channel pore. The approach illustrates how the original gating model of Verselis et al. (1994), can explain the negative gating polarity and voltage sensitivity of wild-type and positive charge substitutions. It predicts that the reversal of gating polarity by negative charge substitutions requires an asymmetric voltage profile that likely results from the presence of charged residues at other positions and indicates that local asymmetries in the voltage profile are unlikely to account for the appearance of bipolar channels.

MATERIALS AND METHODS

Methods used in the construction of mutations examined in this study, RNA synthesis, Xenopus oocyte injection and electrophysiological recordings are described in Oh et al. (2000). Patch-clamp records were obtained with an Axopatch 200B amplifier and pClamp 7.0 software (Axon Instruments, Union City, CA). Data were acquired at 5 kHz and filtered at 1 kHz with a four-pole low-pass Bessel filter. Unless otherwise noted, records were not further filtered for presentation. In cases where different recording solutions were used to characterize channels in this study, the conditions are provided in figure legends. The antisense oligonucleotide complimentary to Xenopus Cx38 was not used in this study. The Poisson-Nernst-Plank equations were solved with the PNP2 computer program provided by Dr. Duan Chen and recompiled by Dr. Brady Trexler.

RESULTS

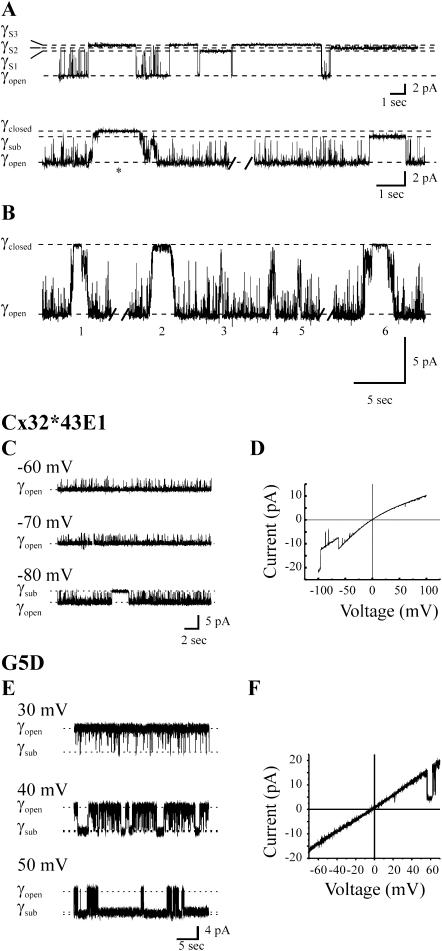
Single-channel records illustrating the two separate voltage-gating mechanisms of Cx32*Cx43E1 and Cx46 hemichannels have been presented in Trexler et al. (1996) and Oh et al. (2000) and are shown in Fig. 2, A and B. V_j- or fast-gating (Verselis and Bukauskas, 2002) events characteristically involve rapid transitions between the fully open state and one of several subconductance states that appear as a single step change in conductance and that occur within the time resolution of the patch clamp. V_j-gating transitions for the parental, Cx32*Cx43E1 channel, are shown in the top panel of Fig. 2 A. The conductance of the substates is ∼20% of the fully open state. The second gating mechanism, termed loop gating or slow gating is characterized by a sequential series of small transitions that give the appearance of a gradual change in conductance and can, but do not always, result in complete closure of the channel. Loop gating is illustrated by the asterisk in the single-channel record of the Cx32*Cx43E1 channel in the bottom panel of Fig. 2 A whereas the second long-lived event in this trace is attributed to V_j-gating. Six additional loop-gating events are illustrated in Fig. 2 B. Note that not all loop-gating events result in full channel closure, but all involve multiple steps, each producing small changes in conductance that together give the appearance of a slow transition. Channel closure by loop gating is observed more frequently at negative holding potentials in all connexin hemichannels examined to date. The negative polarity of loop gating is not reversed by mutations that reverse the polarity of V_j-gating indicating that the two mechanisms are distinct (Oh et al., 2000). The rapid gating transitions that are observed in all traces are too brief to be classified as either loop-gating or V_j-gating events, however, these transitions are usually observed at the same polarity as V_j-gating events and may be brief V_j-closures.

FIGURE 2.

Voltage-gating mechanisms and reversal of V_j-gating polarity by negative charge substitutions. (A) (Top panel) Outside-out recording of a single wild-type, Cx32*Cx43E1 channel illustrating closures by V_j-gating to three substates at a holding potential of −100 mV. (Bottom panel) Cell-attached recording of a single wild-type channel illustrating a loop-gating event (marked by an asterisk) and V_j-gating event at a holding potential of −70 mV. (B) Six additional loop-gating events are shown to illustrate that not all transitions lead to full channel closure. Loop gating is characterized by the appearance of multiple transitions that give the appearance of a slow-gating event. (C) Cell-attached recording of a single wild-type, Cx32*Cx43E1 channel illustrating closures at positive holding potentials. (D) Current-voltage relation obtained by the application of a 3-s ±100-mV voltage ramp to a cell-attached patch containing two Cx32*Cx43E1 hemichannels. (E) Cell-attached recording of a single G5D hemichannel illustrating the reversal of V_j-gating polarity; the channel closes at positive rather than negative potentials. (F) Current-voltage relation of a single G5D channel (outside-out recording configuration) obtained with a 2.1-s duration ±70-mV voltage ramp. Panels A, C, and D were adapted from Oh et al. (2000). The record in panel B was obtained with pipette solutions containing 140 mM KCl, 2 mM EGTA, 2 mM EDTA, and 10 mM HEPES, pH 7.6. The record was digitally filtered at 200 Hz for presentation. In panels D and F, baseline currents were adjusted to zero and records digitally filtered at 200 Hz for presentation. Recordings of Cx32*Cx43E1 and N2E hemichannels were obtained with pipette solutions containing 88 mM NaCl, 1 mM KCl, 1 mM MgCl₂, 2 mM EDTA, 2 mM EGTA, and 10 mM HEPES, pH 7.6. G5D hemichannels were recorded with pipette solutions containing 100 mM KCl, 2 mM EGTA, and 10 mM HEPES, pH 7.6.

Reversal of V_j-gating by negative charge substitutions

Records illustrating the reversal of the polarity of V_j-gating by negative charge substitutions in the N-terminus of Cx32 intercellular channels and Cx32*Cx43E1 unapposed hemichannels have been presented by Purnick et al. (2000a) and Oh et al. (2000). The reversal of the negative V_j-gating polarity of the parental Cx32*Cx43E1 (Fig. 1, C and D) hemichannel by the substitution of a negative charge at the 5th position (G5D) is illustrated in Fig. 2, E and F. In Cx32*Cx43E1 channels, closures attributable to V_j-gating are only observed at negative membrane potentials (Fig. 2 C). At positive membrane potentials, the channel remains in the fully open state. This is illustrated by the I/V relation shown in Fig. 2 D, which was obtained by applying a ±100-mV ramp to a cell-attached patch containing two channels. The open channel I/V relation rectifies inwardly in symmetric salt solutions consistent with the presence of a positive charge within the channel pore near the cytoplasmic end of the channel. Negative charges in the first extracellular loop may also contribute to this rectification of this chimeric hemichannel (see Trexler et al., 2000). The slope conductance of the open state is ∼115 pS in 100 mM KCl determined with excised patches.

The reversal of V_j-gating polarity by G5D is shown in Fig. 2, E and F. Homomeric G5D channels close by V_j-gating only at positive potentials; at negative potentials the channel resides in the fully open state. Loop-gating transitions are rarely observed, but can occur at large negative holding potentials (not shown). The open channel I/V relation of G5D channels is linear in symmetric salt solutions, consistent with the addition of a negative charge at the cytoplasmic end of the channel pore. The slope conductance is increased substantially from that of wild type, to 260 pS in 100 mM KCl.

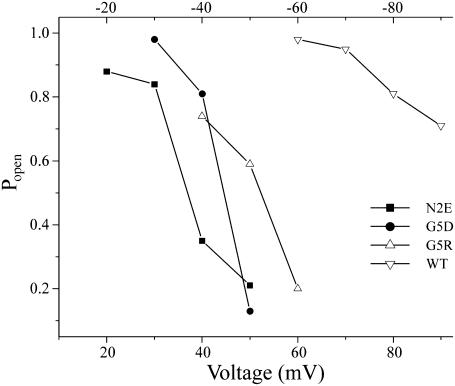
The open probability/voltage relations of WT, N2E, G5R, and G5D channels are shown in Fig. 3. Note that the voltage dependence of the WT and G5R channels are plotted as the absolute value of voltage to facilitate comparison with channels that close with positive polarization. The actual voltages for WT and G5R are provided in the top voltage axis. The N2E and G5D substitutions not only reverse the polarity of V_j-gating but also increase the channels' sensitivity to voltage (i.e., shift the midpoint of the P_open/voltage relation toward 0 mV) and increase their gating charge, as judged by the steepness of the relation. N2E channels appear to be more sensitive to voltage than G5D, in that the open probability of the N2E channel is reduced to a greater extent at comparable positive potentials. The gating charge for both N2E and G5D channels calculated from the slope of the open probability voltage relation is ∼4, suggesting that the movement of charges is equivalent in the two mutations.

FIGURE 3.

P_open/voltage relation of N2E, G5D, G5R, and WT (Cx32*Cx43E1) channels. The P_open/voltage relation for N2E is taken from Oh et al. (2000). The values for G5D and G5R were calculated from longer segments of the traces shown in Figs. 2 and 4, respectively. The open probability of wild-type channels calculated at large positive potentials may include closures by loop-gating events. The absolute value of voltage was used to plot P_open for G5R and WT channels to facilitate comparisons with N2E and G5D. The applied voltage for WT and G5R channels are provided in the axis drawn at the top of the panel.

Maintenance of negative V_j-gating polarity by positive charge substitutions

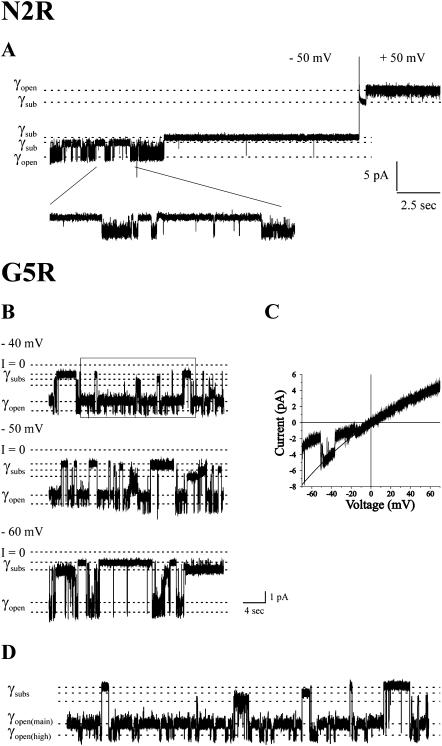
As expected, positive charge substitutions at the 2nd, 5th, and 8th positions maintain the negative polarity of V_j-gating. A cell-attached recording illustrating the negative V_j-gating polarity of the Cx32N2R*Cx43E1 unapposed hemichannel is shown in Fig. 4 A for voltage steps of ±50 mV. The N2R channel transits between an open state and one or more substates in response to the application of negative potentials and then typically enters a long-lived substate from which it opens when the voltage is stepped to positive potentials (Fig. 4 A). The channel resides in the open state at all positive potentials, although partial closures ascribable to loop-gating events are seen occasionally at negative potentials and less frequently at small positive potentials (not shown). The open state of the N2R hemichannel appears “noisy.” As these rapid transitions are observed at both positive and negative holding potentials, they do not appear to be related to the longer-lived V_j-gating events. V_j-gating transitions from the open to “substate” correspond to a change in conductance of ∼55 pS in ND96 recording solutions containing 88 mM NaCl and 1 mM KCl. This would correspond to a conductance change of ∼70 pS in 100 mM KCl solutions, assuming that ionic permeation through N2R channels follows the bulk solution mobility of small metal ions, as has been shown for Cx32 intercellular channels (Oh et al., 1997). The assignment of negative gating V_j-polarity to N2R unapposed Cx32*Cx43E1 hemichannels is consistent with the study of Verselis et al. (1994), which reported that Cx32N2R hemichannels gate at negative potentials in heterotypic pairing assays with Cx32 and Cx26 and by the macroscopic behavior of Cx32N2R*Cx43E1 and Cx32N2K*Cx43E1 hemichannels, which show voltage-dependent current relaxations only at negative membrane potentials (data not shown).

FIGURE 4.

Negative gating polarity of N2R and G5R channels. (A) A cell-attached record of a single N2R channel is shown. At −50 mV the channel transits between an open and one of two subconductance states. The polarity of the holding potential was reversed from −50 mV to +50 mV when the channel resided in a long-lived substate. The channel remained in the substate briefly before entering a fully open state. The channel remained in the fully open state for the duration of the +50-mV voltage step. Similar gating behavior was observed at voltages over the range from ±30 to ±100 mV with the frequency and duration of closures increasing as more negative holding potentials were applied. No closures to substates were observed at positive holding potentials, consistent with the assignment of negative gating polarity to the G5R channel. Bath and pipette solutions contained 88 mM NaCl, 1 mM KCl, 1 mM MgCl₂, 2 mM EDTA, 2 mM EGTA, and 10 mM HEPES, pH 7.6. (B) Segments of current traces of a single G5R channel recorded in a cell-attached configuration illustrating the negative polarity of V_j-gating. The frequency and duration of Vj-gating closures increase as the applied potential is increased from −40 to −60 mV. (C) The current-voltage relation of a single G5R channel obtained in an outside-out configuration obtained with a ±70-mV voltage ramp. Closures ascribable to V_j-gating are observed only at negative potentials. The channel remains open at positive potentials. (D) The boxed segment of the −40-mV trace shown in panel B is expanded to illustrate the main- and high-conductance open states. V_j-gating events appear to occur more frequently when the channel resides in the high-conductance state. Bath and pipettes solutions contained 100 mM KCl, 2 mM EGTA, and 10 mM HEPES, pH 7.6 in all G5R records.

The closure of G5R unapposed hemichannels at negative potentials is illustrated in the current traces shown in Fig. 4 B and in the single channel I/V relation presented in Fig. 4 C. V_j-gating transitions are observed only at negative holding potentials. A plot of the open probability as a function of the absolute value of holding potential is presented for G5R channels in Fig. 3 to facilitate comparison with G5D. G5R channels are slightly less sensitive to voltage than those formed by G5D and the relation between open probability and holding potential is less steep, suggesting a smaller gating charge.

Although the G5R substitution does not change the polarity of V_j-gating it forms channels that exhibit a noisy open state that result from rapid transitions between a main (lower conductance) state and a high-conductance state. This feature is illustrated in Fig. 4 B and in the expanded portion of that −40-mV trace, shown in Fig. 4 D. Similar rapid transitions are observed at positive potentials (not shown) and their frequency does not appear to change substantially as a function of voltage. The transitions between the main and high-conductance state cannot be ascribed to the activity of an endogenous Xenopus oocytes channel, as they are not observed when the G5R channel enters a subconductance state (Fig. 4 B).

Although V_j-gating transitions to subconductance states occur from both the main and high-conductance open states, they appear to occur more frequently from the high-conductance state even though the channel resides primarily in the lower conductance main state. For example, six of the nine resolvable V_j-gating transitions shown in Fig. 4 D originate from and return to the high-conductance state, two originate from and return to the main state, whereas in at least one case, closure from the main state is followed by an opening to the high-conductance state. In contrast, the G5K mutation, which also maintains the negative polarity of V_j-gating, does not display a noisy open state (not shown). This suggests that the effect of the G5R on the open state of the unapposed hemichannel is not simply a consequence of the substitution of a positive charge at the 5th position but also from the difference in the size of the arginine and lysine side chains.

The I/V relation of a single-channel G5R shown in Fig. 4 C was obtained with a 1.2-s voltage ramp and illustrates the behavior of the main state. Transitions between the main and high-conductance open state are not evident in this record most likely as a consequence of the short duration of the ramp protocol. The I/V relations of both G5R and G5K channels rectify inwardly in symmetric salt solutions. The twofold rectification of ionic currents observed with the ±70 mV is somewhat greater than that of the parental Cx32*Cx43E1 channel, which displays a twofold rectification over ±100 mV. The increase is consistent with the expected effect of the addition of a positive charge in the cytoplasmic end of the channel pore. The slope conductance of the main state of the G5R at 0 mV channel is ∼80 pS in symmetric 100 mM KCl.

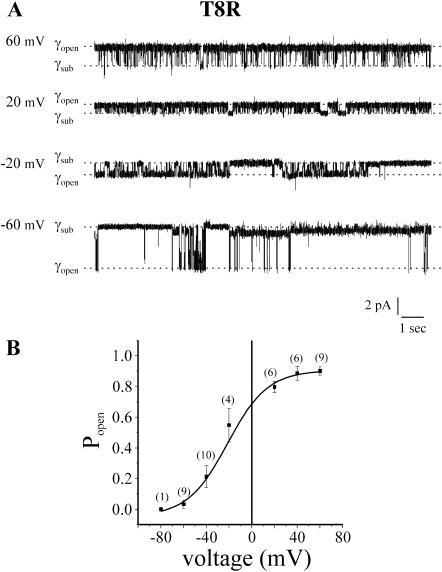
The positive charge substitution, T8R also maintains the negative polarity of V_j-gating but causes a substantial rightward shift in the P_open/voltage relation (Fig. 5, A and B) such that V_j-gating transitions are observed at both negative and positive potentials. V_j-gating of T8R is not bipolar, as the open probability of the channel increases to a maximum as the holding potential becomes positive and decreases to a minimum at negative potentials. In bipolar channels, such as T8D, the open probability is reduced at both positive and negative holding potentials and is maximal at intermediate potentials. The size of the transitions from the fully open to low-conductance substates corresponds to a conductance of ∼95 pS at −60 mV and ∼50 pS at 60 mV in 140 mM KCl recording solutions. These values predict a twofold rectification of open channel currents.

FIGURE 5.

Negative gating polarity of T8R channels. (A) Cell-attached records of a single T8R record at the indicated holding potentials. The open probability of the channel increases as the holding potential becomes more positive. (B) A plot of the P_open/voltage relation of T8R. The number of records used to obtain the mean and standard deviation are in the parentheses. Data were fitted to a sigmoidal function using Origin 6.0 software. Records were obtained with pipette and bath solutions composed of 140 mM KCl, 1 mM EDTA, and 10 mM HEPES, pH 7.6.

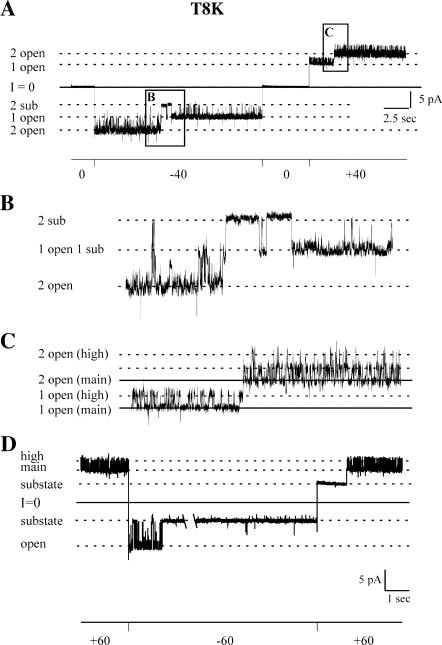
In contrast to T8R, V_j-gating events in channels formed by the T8K substitution are only observed at negative potentials, indicating the positive polarity of V_j-gating. This is illustrated by the current traces obtained at ±40mV and ±60 mV from two different cell-attached patches containing two and one T8K channels, respectively (Fig. 6). The T8K mutation creates a “noisy” open state of the channel but, unlike N2R and G5R, appears to do so only at positive holding potentials. This feature is illustrated in the expanded portions of the trace obtained for two channels at ±40 mV (panel A) that are shown in panels B and C and by the record of a single active channel shown in D. It is unlikely that the rapid transitions observed at positive potentials reflect the activity of an endogenous Xenopus oocyte channel because the number of conductance levels observed always corresponds to the number of connexin channels open. For example, when a single channel resides in a substate at positive potentials, no rapid transitions between the main and high conductance states are observed (panel D). When a single T8K channel is open at positive potentials, the rapid transitions occur between two levels, when two channels are open, the rapid transitions events occur among three levels (see Fig. 6 C) when three channels are open, there are four levels of rapid transitions (not shown).

FIGURE 6.

Negative gating polarity of T8K channels. (A) A cell-attached record of two T8K channels at holding potentials of 0, −40, and +40 mV is shown. Channel closures by V_j-gating are apparent only at negative potentials. (B) An expansion of the boxed region labeled B in panel A to illustrate closures by V_j-gating. (C) An expansion of the boxed region labeled C in panel A to illustrate transitions between a main open state and a high-conductance open state. Channel openings by V_j-gating correspond to transitions between conductance levels marked by solid lines in panel C. The dashed lines in panel C mark transitions between the main state and the high-conductance state. (D) Cell-attached record of a single T8K record at a holding potential of ±60 mV. The channel closes by V_j-gating at negative potentials. Transitions between the high-conductance and main-conductance open states are only seen when the channel is open. Records were obtained with pipette and bath solutions composed of 140 mM KCl, 1 mM EDTA, 1mM EGTA, and 10 mM HEPES, pH 7.6.

Transitions between the lower conductance open state (main state) and higher conductance open state (high state) at positive potentials correspond to a change in conductance of ∼30–35 pS at 40 mV in 140 KCl recording solutions, whereas the difference in conductance resulting from the opening of the V_j-gates is ∼65 pS at this voltage in the same recording solution. V_j-gating transitions at negative potentials correspond to a change in conductance of ∼100 pS in 140 mM KCl (∼75 pS in 100 mM KCl).

We conclude, that channels carrying positive charged substitutions at the 2nd, 5th, and 8th positions maintain the negative V_j-gating polarity of the parental channel.

V_j-gating of double mutations is bipolar

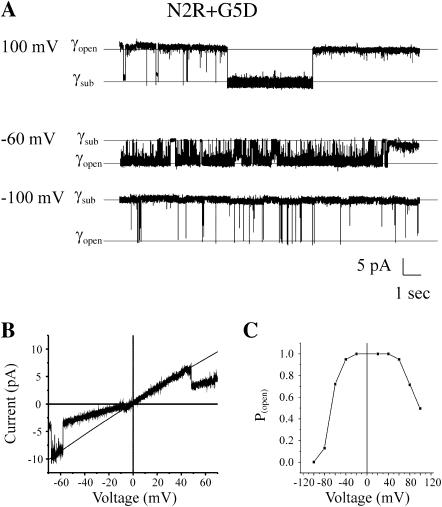
To determine if the polarity of V_j-gating is determined by the relative orientation of positive and negative charges in the N-terminus, three double mutations, N2E+G5K, N2E+G5R and N2R+G5D, were examined. The voltage dependence of the double mutation N2R+G5D is illustrated by the current traces of a single channel obtained in a cell-attached patch configuration (Fig. 7 A). V_j-gating transitions are apparent at holding potentials more negative than −30 mV and more positive than 60 mV but are rarely observed at potentials falling between −30 and +50 mV. The bipolarity of V_j-gating of the N2R+G5D channel is further illustrated by the I/V relation of a single channel that is shown in Fig. 7 B and the open probability/voltage relation plotted in Fig. 7 C. The N2R+G5D channel is more sensitive to the application of negative potentials. This suggests that the sign of the charge at the second amino acid position has a dominant effect in determining the polarity and voltage dependence of V_j-gating. As the I/V relation of the open state of the channel is linear like that of N2E and G5D channels, the sign of the charge lying closest to the entrance of the channel appears to determine the amount and direction of current rectification. The slope conductance of N2R+G5D is similar to WT (∼145 pS at 0 mV in 140 mM KCl, corresponding to ∼105 pS in 100 mM KCl).

FIGURE 7.

Bipolar V_j-gating of N2R+G5D hemichannels. (A) A cell-attached record of a single N2R + G5D channel at voltages ranging over ±100 mV. Closures to substates by V_j-gating are observed at both positive and negative potentials. (B) The current-voltage relation of a single N2R+G5D channel obtained in an outside-out patch configuration illustrating the bipolarity of and increased sensitivity of V_j-gating at negative potentials. The I/V relation of the open state is linear, similar to that of G5D hemichannels. (C) A plot of the P_open/voltage relation illustrating the bipolarity of V_j-gating. The open probability of the channel is reduced at both positive and negative potentials and maximal at intermediate potentials. V_j-gating is more sensitive to negative potentials suggesting a dominant role of the charge at the 2nd position. Data points were obtained from all points histograms after concatenation of voltage traces obtained at each voltage from at least three separate patches. Records were obtained with pipette and bath solutions composed of 140 mM KCl, 1 mM EDTA, 1 mM EGTA, and 10 mM HEPES, pH 7.6.

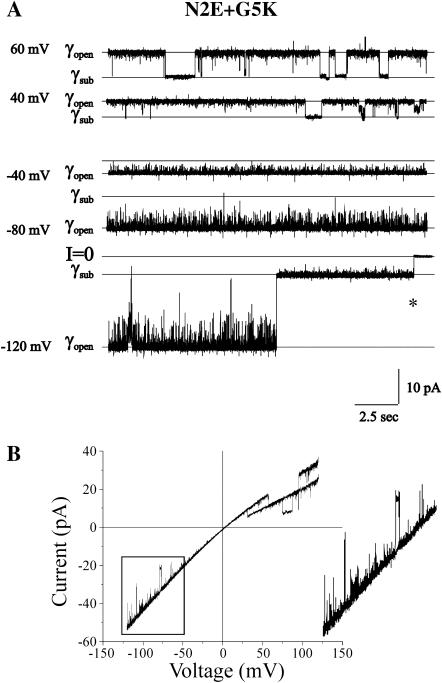
The records shown in Fig. 8 demonstrate that the N2E+G5K channel also displays bipolar V_j-gating. The increased frequency and duration of closures by V_j-gating reduces the open probability of the channel at holding potentials ≥40 mV. At holding potentials between 40 and −80 mV, the channel resides primarily in the open state, although numerous brief transitions are observed. Due to their short duration, these transitions cannot be ascribed to either loop or V_j-gating. However, at negative potentials ≥−80 mV, both loop-gating and V_j-gating transitions are observed. An example of a long-lived V_j-gating transition is shown at the end of the −120 mV trace. The asterisk denotes the time at which the holding voltage was returned from −120 to 0 mV to check the zero current level. The duration of this V_j-gating event is atypical; in most records V_j-gating transitions at large negative potentials are of much shorter duration than the event shown here. As the frequency and duration of channel closures by V_j-gating at negative potentials are much less than at positive membrane potentials, the open channel probability is only slightly reduced at large negative potentials. This is illustrated by the I/V relation of two channels obtained with ±120 mV ramps that is shown in Fig. 8 B. Two sequential ramps are superimposed in this figure. The boxed region of the current traces is expanded to illustrate the presence of V_j-gating transitions at negative membrane potentials. As V_j-gating events are observed at large negative as well as positive membrane potentials but not at intermediate potentials, we conclude that V_j-gating of the N2E+G5K channel is bipolar. However, V_j-gating of the N2E+G5K channel is more sensitive to positive potentials, again suggesting that the charge at the 2nd amino acid positions plays a dominant role in determining the polarity of V_j-gating. Interestingly, the I/V relation rectifies inwardly, suggesting that the sign of the outermost charge (positive K5, in this case) plays a dominant role in shaping the open channel I/V relation. The slope conductance of the N2E+G5K channel is similar to wild type (∼120 pS in 100 mM KCl).

FIGURE 8.

Bipolar V_j-gating of N2E+G5K hemichannels. (A) A cell-attached record of a single N2E+G5K hemichannel at holding potentials ranging from 60 to −120 mV. The channel closes to substates by V_j-gating at positive potentials, with P_open decreasing as the holding potential becomes more positive. Closures attributable to V_j-gating are also observed at negative potentials with their frequency increasing as the holding potential becomes more negative, as exemplified by the trace obtained at a holding potential of −120 mV. The asterisk denotes the time when the applied voltage was stepped to 0 mV to determine the zero current level. (B) The current-voltage relation of two N2E+G5K hemichannels recorded in a cell-attached patch configuration obtained with ±120-mV voltage ramp. Two sequential traces are shown in this panel. Closures attributable to V_j-gating are observed at both positive and negative potentials but occur sooner and are more prevalent positive holding potentials. The boxed region is expanded in the insert to illustrate brief closures ascribable to V_j-gating. The record also illustrates the inward rectification of the N2E + G5K channel. Records were obtained with pipette and bath solutions composed of 140 mM KCl, 1 mM EDTA, and 10 mM HEPES, pH 7.6.

Single-channel records of N2E+G5R channels are presented in Fig. 9. V_j-gating transitions are evident at positive membrane potentials consistent with a dominant effect of a negative charge at the 2nd position in determining the polarity of V_j-gating. At negative potentials, the channel closes primarily by the loop-gating mechanism, as exemplified by the event marked by the asterisk in panel A. The predominance of loop-gating events at negative potentials is further illustrated by the I/V relation obtained with the application of a ±120-mV ramp shown in Fig. 8 B. The high frequency of loop-gating events at all negative voltages prevents the unambiguous assignment of V_j-gating to channel closures at this polarity. Thus, we cannot determine if V_j-gating is bipolar in N2E+G5R channels. The open channel I/V relation of N2E + G5R rectifies inwardly like the G5R and WT channel, again demonstrating that the form of the I/V relation is determined by the charge lying closest to the cytoplasm. The slope conductance is similar to that of wild-type channel (120 pS in symmetric 100 mM KCl solutions at 0 mV).

A summary of the polarity of V_j-gating, unitary conductance, and direction of current rectification for positive and negative substitutions at the 2nd, 5th, and 8th residues are presented in Table 1. Briefly, positive charge substitutions in the N-terminus maintain the negative polarity of V_j-gating and increase the inward rectification of single-channel currents, but substantially reduce unitary conductance and in some cases create a noisy open state. Negative charge substitutions at the 2nd and 5th positions reverse the polarity of V_j-gating from closure at negative to closure at positive holding potentials. Negative substitutions at the 8th positions result in channels that display bipolar V_j-gating but with greater sensitivity to positive than negative voltages (Purnick et al., 2000a). All negative charge substitutions linearize the open channel I-V relation, and markedly increase single-channel conductance. Two of the double mutations, N2R+G5D and N2E+G5K, display bipolar V_j-gating, whereas the high incidence of loop gating at negative potentials precludes the assessment of bipolarity of V_j-gating in the third mutation, N2E+G5R. In all three double mutations, the sign of the 2nd amino acid residue appears to have a dominant effect on V_j-gating, whereas the sign of the charge closest to the cytoplasmic surface of the channel appears to determine the amount and direction of current rectification through the open channel. The effect on conductance appears to be additive in that the unitary conductance of the open state of double mutations is intermediate, falling between that of single negative and single positive charges at the 2nd, 5th, and 8th positions and is similar to that of the wild-type channel. The negative polarity of loop gating is not changed by any mutations.

TABLE 1.

Summary of the properties of WT (Cx32*43E1) and mutant hemichannels

Channel	Vj-gating polarity	Slope conductance in 100 mM KCl	Direction of open-channel current rectification
WT	Negative	115 pS	Inward
N2E	Positive	260 pS	Slightly outward
G5D	Positive	240 pS	Linear
T8D	Bipolar*	180 pS	Linear
N2R/K	Negative	70 pS	Inward
G5R/K	Negative	70 pS	Inward
T8R/K	Negative	80 pS	Inward
N2E+G5K	Bipolar*	120 pS	Inward
N2R+G5D	Bipolar†	105 pS	Linear
N2E+G5R	Bipolar (?)‡	120 pS	Inward

^*V_j-gating more sensitive to positive potentials.

^†V_j-gating more sensitive to negative potentials.

^‡The high incidence of loop gating at negative potentials precludes the assignment of bipolarity to this channel. V_j-gating events are more prevalent at positive potentials.

DISCUSSION

The mutations examined in this study were chosen to further explore the determinants of V_j-gating polarity. Based on previous work, we proposed that charges contained within the first 10 amino acids of the N-terminus constitute at least a portion of the V_j-sensor of Cx32 and other Group 1 connexins, and that the inward movement of this region, toward the cytoplasmic face of the channel, initiates channel closure in response to sufficient polarization. The negative gating polarity of Cx32 and Cx32*Cx43E1 hemichannels was explained by postulating the existence of a positively charged voltage sensor arising from the positive charge of an unmodified N-terminal methionine residue or the partial charge of an N-terminal helical dipole. The reversal of gating polarity by the addition of a negative charge at the 2nd or 5th position was suggested to arise by either an electrostatic mechanism that would reverse the sign of the voltage sensor from positive to negative (Verselis et al., 1994) or alternatively, by the reorientation of a dipole whose negative pole is oriented toward the cytoplasmic surface of the channel (Purnick et al., 2000a).

In this study, we demonstrate that the addition of positive charges at the 2nd, 5th, or 8th positions maintains the negative polarity of V_j-gating of the parental Cx32*Cx43E1 hemichannel. This result is consistent with previous interpretations, as positive charges at any of these positions are expected to lie within the electric field and contribute with the N-terminal methionine residue (M1) to the positive valence of a voltage sensor contained in the N-terminus. The positively charged voltage sensor would move inward in response to adequate hyperpolarization. Unapposed G5R hemichannels display an increased sensitivity to negative voltages and an increased gating charge, as assessed by the steepness of the P_open/voltage relation. The apparent increase in calculated gating charge is consistent with the movement of a greater amount positive charge, presumably reflecting the addition of a positive charge at the 5th position to the already positively charged voltage senor. The steepness of the P_open/voltage relation of G5R channels is, however, less than that of both G5D and N2E channels. This result is surprising, in that one might expect a degree of charge neutralization in channels containing a positive charge at the 1st position and negative charges at either the 2nd or 5th positions. It would be reasonable to expect that the gating charge of N2E and G5D channels would be less than that of either the G5R or the Cx32*Cx43E1 channel if one assumes that the direction and extent of movement of the voltage sensor is conserved in all channels and that the electric field is not appreciably changed by the mutations. The increased sensitivity and steepness of N2E and G5D channels could be explained if the voltage profile of these channels is not linear, but influenced by charges in the pore. This possibility is explored later in the discussion.

The substantial inward shift of the voltage dependence of V_j-gating in T8R channels, which results in the appearance of V_j-gating events at positive as well as negative potentials, can be explained by either of two mechanisms. The mutation may have changed the free energy of the channel such that V_j-gating transitions might occur in the absence of an applied potential. At negative potentials, the force acting on the positively charged voltage sensor would favor its inward movement resulting in an increased frequency and duration of channel closures, whereas at positive potentials, the force would favor the outward movement of the voltage sensor, reducing the frequency and duration of channel closures by V_j-gating. Alternatively, as described later in the discussion, the placement of a positive charge at the 8th positions may alter the voltage profile of the channel providing a net inward force on the voltage sensor, which allows its movement at both positive and negative potentials.

As a means of exploring whether polarity reversal by the addition of negative charges to the N-terminus might involve the formation and reorientation of an electrical dipole in response to changes in membrane potential, we examined the gating polarity of double mutations in which the orientation of positive and negative charges at the 2nd and 5th residues are reversed. Surprisingly, two of the double mutations, N2E+G5K and N2K+G5D, form homomeric channels that display bipolar V_j-gating, whereas the third, N2E+G5R, appears to V_j-gate at only positive potentials. However, the prevalence of loop-gating events at negative potentials may have precluded the detection of bipolar V_j-gating in the N2E+G5R channel. In all three mutations the sensitivity of V_j-gating correlates with the sign of the charge at the 2nd position, but the appearance of bipolar gating does not correlate with the orientation of positive and negative charges at the 2nd and 5th positions. The distribution of charges directed inward from the cytoplasmic surface is (− + +) for the N2K+G5D channel, given that the N-terminal methionine residue is positively charged, whereas that of N2E+G5K is (+ − +). Given these results, it seems unlikely that V_j-gating polarity is simply determined by the sign of the most external charge or by a directionally conserved reorientation of a dipole created by the separation of positive and negative charges in the N-terminus.

The apparent dominance of the 2nd residue in determining the relative sensitivity of V_j-gating in these mutations could be explained by invoking a structural model in which a constriction is placed in the vicinity of the 2nd residue. A constriction in this position could cause a greater proportion of the applied voltage to drop over the 2nd than over either the 1st and 5th residue. Thus, the effective valence of a negative charge substitution at this position would be greater than that of charges at either the 1st or 5th positions. The increased calculated gating charge of N2E hemichannels compared to wild type Cx32 and G5R channels is consistent with this expectation, i.e., a charge at the 2nd position moves through a greater proportion of the electric field for a comparable amount of physical translocation. The slight outward rectification observed for N2E channels compared to the linear I/V relation for G5D and T8D channels also suggests that a negative charge at the 2nd position has a greater effect in determining the voltage profile of the channel. However, this simple structural model is not supported by the similarity in the voltage dependence of N2E and G5D hemichannels. N2E and G5D hemichannels are almost equally sensitive to applied voltage and appear to have comparable gating charge, as assessed by the steepness of the P_open/voltage relation. This suggests that negative charges at the 2nd and 5th positions are equivalent and cross a comparable fraction of the electric field. Although measurements of gating charge and charge selectivity may be less sensitive indicators of structure than the shape of the I/V curve, it seems unlikely that the pore radius differs markedly at the 2nd and 5th positions. However, the channel radius may be larger in the vicinity of the 8th amino acid residue as the cation selectivity and unitary conductance of the T8D channel is less than that of G5D and N2E. The apparent dominance of charges at the 2nd residue can also be explained by invoking changes in the voltage profile of the channel such that a larger proportion of the applied voltage drops over the second residue when charged residues are present at other positions.

Ideally, the consideration of the effects of changes in the voltage profile of the channel in determining the polarity of V_j-gating requires the calculation of the electrostatic potential of the open and closed channel pore that is derived from an atomic resolution structure of the Cx32 hemichannel. This information would permit the derivation of the voltage profile of the open and closed channel and allow the calculation of forces acting on charged residues located in the N-terminus. Unfortunately, an atomic resolution structure of a gap junction channel is not available. Instead, we utilize the one-dimensional Poisson-Nernst-Plank model of Chen and Eisenberg (1993) to examine the effects of permanent charges in determining the voltage profile across the channel pore of mutant and wild-type channels and explore if channel closure could be initiated by the inward movement of a voltage sensor located near the intracellular surface of the pore. We do not attempt to derive a charge distribution model that would simultaneously explain the behavior of all the mutations examined in this and previous studies, but examine if changes in the voltage profile of a channel can account for: 1), the negative gating polarity of the wild-type channel; 2), the maintenance of gating polarity by the addition of positive charges and the shift in the voltage dependence of the T8R mutation; 3), the reversal of V_j-gating polarity by the addition of negative charges; and 4), the bipolarity of some homomeric channels.

Voltage profile of a wild-type channel

We first consider a simple model of a wild-type (Cx32*Cx43E1) channel in which the channel pore is modeled as a right cylinder 60-Å long with a radius of 7 Å and containing six permanent positive charges (one for each connexin subunit). We arbitrarily center the charges at a distance of 0.4 and extend the charged region over the interval, 0.3–0.5 (20% of the channel length). These channel dimensions provide an input parameter of 2 mol/liter of positive charge to the PNP model. Other input parameters are: membrane dielectric 4, pore dielectric 80, bath solutions 100 mM active KCl. Bulk solution ionic mobilities are used. We do not utilize the induced charge term of the PNP model.

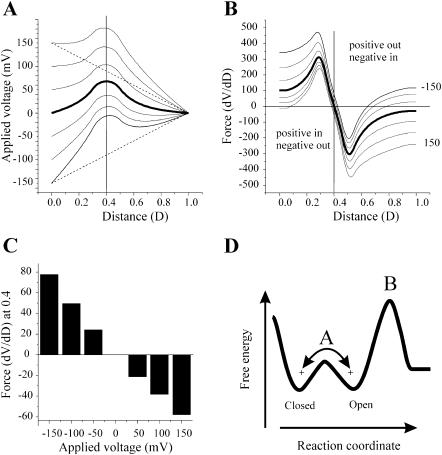
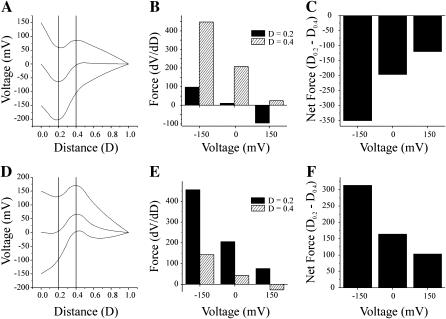
The voltage profiles of the Cx32*Cx43E1 channel, calculated with the PNP model, are shown in Fig. 10 A for applied voltages of 0, ±50, ±100, and ±150 mV. Voltages are applied to the cytoplasmic side of the channel, which corresponds to an outside-out patch configuration. The voltage profiles shown are identical in form to that of an inside-out patch or cell-attached patch, but reversed, as in these configurations the voltage would be applied to the extracellular side of the channel (not shown). Linear voltage gradients at ±150 mV are included for comparison. The force that would be experienced by a charge at any position in the voltage profile is determined by differentiating the voltage/distance relation using a numerical procedure contained in Origin 6.0 (Microcal Software, Northampton, MA). The derivatives of the voltage profiles shown in Fig. 10 A are plotted as smoothed continuous lines as a function of distance in Fig. 10 B. The force acting on the positive charges centered at 0.4 is plotted as a bar diagram in Fig. 10 C. Positive charges at this position would tend to move inward, toward the cytoplasmic surface of the channel (movement toward the left side of the figure) at negative potentials and away from the intracellular surface at positive potentials. If we assume that the intrinsic chemical potential of the open channel at 0 mV is described by the free-energy profile illustrated in Fig. 10 D with two energy minima (open and closed) separated by an energy barrier A, then a positively charged voltage sensor residing in the open position would tend to move to the closed position only at negative potentials. Channel closure would require that the force generated by the applied voltage was sufficient to overcome the intrinsic chemical potential of the channel (energy barrier A). We assume that the height of the energy barrier is sufficient to prevent transitions between the open and closed positions in the absence of an applied potential. Note that the force at a holding potential of 0 mV is zero (Fig. 10 C). At positive potentials, the voltage sensor would remain in the open position, as the height of the energy barrier B would prevent its outward movement away from the cytoplasmic surface of the channel. This gating model corresponds to that proposed by Verselis et al. (1994) for the wild-type channel, in which the inward movement of a positively charged voltage sensor initiates channel closure. Qualitatively similar results are obtained when the position and/or magnitude of the positive charge or when the ionic strength of the bathing solution is changed. Increasing the ionic strength reduces the force acting on the positive charge as a result of charge screening (not shown). It is interesting to note that the force acting on a positively voltage sensor is less than the force obtained if one assumes a linear voltage gradient and that the incremental change in slope as a function of voltage is less. Consequently, the distortion in the voltage profile that results from the presence of the positive charge would reduce the sensitivity of the channel to voltage and decrease the calculated gating charge if the voltage gradient were linear.

FIGURE 10.

A model wild-type channel containing a positively charged voltage sensor. (A) The voltage profile of the pore of a channel calculated with the PNP model of Chen and Eisenberg (1993) using 199 points at holding potentials of 0, ±50, ±100, ±150 mV with a positive charge centered at a distance of 0.4 (see text for details). Linear voltage profiles at ±150 mV are shown as dotted lines for comparison. (B) The first derivative (dV/dD) of each of the voltage profiles shown in A are plotted as a function of distance. The derivative was determined by a numerical procedure contained in Microcal Origin 6.0 software using a second order polynomial smoothing function utilizing 10 points. The uppermost trace in this panel is the derivative of the voltage profile at −150 mV, the lowest trace is that of +150 mV. Values above zero would favor the inward (toward the cytoplasm) movement of a positively charged sensor or outward (away from the cytoplasm) movement of a negatively charged voltage sensor. Values below zero favor the outward movement of a positively charged voltage sensor or inward movement of a negatively charged voltage sensor. (C) Bar graph of the value of each derivative (from −150 to +150 mV voltage range) at a distance of 0.4. (D) A schematic representation of the energy profile of a model channel at 0 mV corresponding to the gating model proposed by Verselis et al. (1994). The inward movement of a voltage sensor (+ at negative voltages, − at positive voltages) would require the crossing of the energy barrier depicted by the peak A. The outward movement of a negatively charged voltage sensor at negative holding potentials from the open state would be prohibited by the size of the energy barrier depicted by the peak B.

The movement of the voltage sensor to the closed position, and the subsequent conformational changes in channel structure would, by necessity, change the voltage profile of the channel. We assert that a voltage profile could be generated for the closed state in which the application of positive potentials would generate a suitable force to favor the outward movement (away from the cytoplasm) of the voltage sensor from the closed to the open position. Furthermore, the above treatment assumes that the six positive charges (one in each connexin subunit) move in concert. If the six connexin subunits move individually, as proposed by Oh et al. (2000), the problem becomes more complex, because the voltage profile and the resulting force experienced by charged residues would change as individual subunits change conformation. Thus, the probability that another charge moves from the open-to-closed position would depend on the position of the charges in other subunits and the corresponding voltage profile. Further considerations of an individual subunit model are beyond the scope of this article and will not be considered.

Voltage profiles of channels adding positive charges

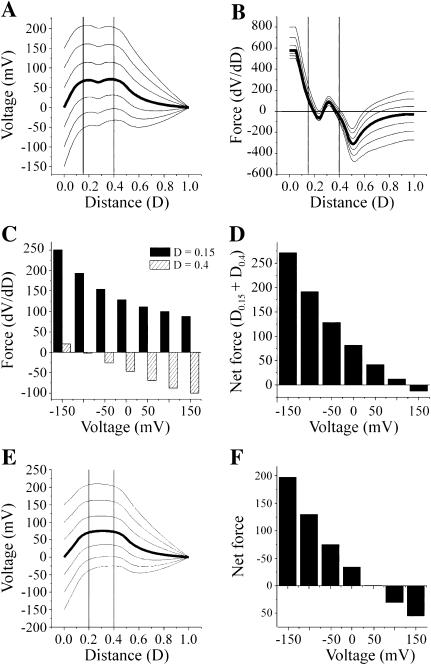
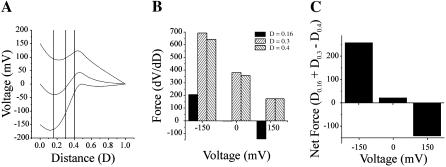
The shift in voltage dependence of the T8R mutation results in the appearance of channel closures by V_j-gating at positive as well as negative holding potentials, but in contrast to T8D channels, V_j-gating is not bipolar. To examine how T8R might alter the voltage profile of the channel and its voltage dependence, we introduce a second region of positive charge lying closer to the cytoplasmic entry, 2 mol/liter, i.e., six charges centered at a distance of 0.15 and extending from .05 to .25, to the model of the wild-type channel. The resulting voltage profiles at 0, ±50, ±100, and ±150 mV are shown in Fig. 11 A. The first derivatives of the voltage profiles (dV/dD) are plotted in Fig. 11 B as a function of electrical distance and the forces acting on permanent positive charges centered 0.15 and 0.4 are plotted in the bar diagram, Fig. 11 C. The positive charges centered at 0.15 experience a force that, according to the original gating model of Verselis et al. (1994), would favor their inward movement at all applied potentials. In contrast, the positive charges centered at 0.4, experience a force that would favor their inward movement only at −150 mV. At all other potentials, the positive charges at 0.4, experience a force that would favor their outward movement. The net force acting on both charges, obtained by the summation of individual forces is plotted as a bar diagram in Fig. 11 D. If we assume that the two charges are physically linked (i.e., the N-terminus moves as a single unit) then the inward movement of both charges is favored at all applied potentials more negative than +150 mV. As the inward force acting on both charges is maximal at a potential of −150 mV and decreases to a minimum at 100 mV, the probability of channel closure would increase as the holding potential becomes more negative; that is, the channel would have negative gating polarity. Closures at positive membrane potentials would occur if the inwardly directed net force acting on the positive charges was sufficient to overcome the chemical potential of the channel. These considerations can account for the observed voltage dependence of T8R channels (Fig. 5 B), where the open probability is maximal at positive potentials and decreases to a minimum as the holding potential becomes more negative, without invoking a reduction in the height of the free-energy barrier that separates the open and closed states.

FIGURE 11.

A model of the wild-type channel with the addition of a second region of positive charge. (A) The voltage profile of the pore of a channel calculated with the PNP model of Chen and Eisenberg (1993) using 199 points at holding potentials of 0, ±50, ±100, ±150 mV with a positive charge centered at a distance of 0.4 and a second region of positive charge centered at 0.15 (see text for details). This corresponds to a simple model of either the T8R or T8K channel. (B) The first derivative (dV/dD) of each of the voltage profiles shown in A are plotted as a function of distance. The uppermost trace is the derivative of the −150-mV voltage profile. The derivative was determined by a numerical procedure contained in Microcal Origin 6.0 software using a second order polynomial smoothing function utilizing 10 points. Plots of derivatives are in descending order from −150 to 150 mV. (C) Bar graph of the values of the derivatives for each curve in B at distances of 0.15 and 0.4. (D) Bar graph of the net force acting on both charged regions, obtained by the summation of forces shown in panel C. (E) The voltage profile of the pore of a channel calculated with the PNP model of Chen and Eisenberg (1993) using 199 points at holding potentials of 0, ±50, ±100, ±150 mV with a positive charge centered at a distance of 0.4 and a second region of positive charge centered at 0.2 (see text for details). This would approximate the G5R channel. (F) Bar graph of the net force acting on both charged regions.

As the T8K channel should have the same voltage profile as T8R, one must invoke a relative reduction in the free energy of the open state of T8K that would effectively raise the height of the barrier separating the open and closed states. Thus, more energy would be required to move the voltage sensor from the open-to-closed position, and channel closures would be observed only at larger negative potentials.

The placement of a positive charge at the 5th position (G5R) can be approximated by moving the positive charge centered at 0.15 in T8K/R channels deeper into the channel, to a distance of 0.2. The resulting voltage profiles are shown in Fig. 11 E and the net force acting on both positive charges is shown in Fig. 11 F. In this case, channel closure could only occur at voltages more negative than +50 mV, as the inward movement of the voltage sensor could occur only at these potentials. A similar result can be obtained for N2R channels if the positive charge is positioned yet deeper into the channel. V_j-gating transitions would only be observed at negative potentials.

The introduction of a second positive charge increases the net force acting on the voltage sensor relative to the wild-type channel (compare Fig. 10 C with Fig. 11, D and F). Thus the simple model correctly predicts that the voltage sensitivity of channels containing two positive charges would be greater than that of the wild-type channel.

Voltage profiles of channels adding negative charges

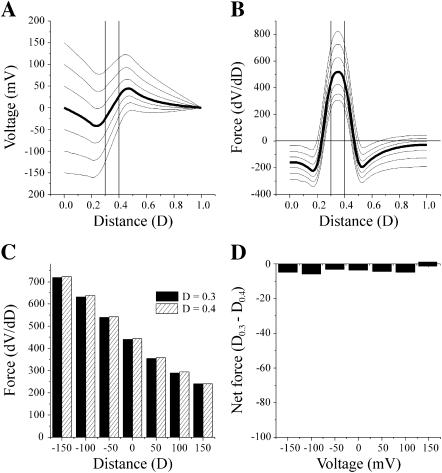
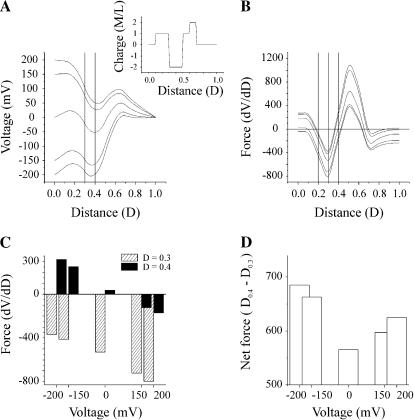
A central and as yet unanswered question is how the addition of negative charges to the N-terminus causes the reversal of V_j-gating polarity. It does not appear to involve the formation and reorientation of a dipole, nor does it seem likely that the addition of a negative charge can reverse the sign of the voltage sensor. We first consider the simple case, in which six negative charges are incorporated into the permanent charge profile of the wild-type channel shown in Fig. 9. The voltage profile of a channel containing six fixed negative charges centered at 0.3 and spanning the interval from 0.2 to 0.4 (2 mol/liter) and six fixed positive charges centered at 0.4 and spanning the interval 0.3–0.4 (2 mol/liter) is illustrated in Fig. 12 A. Notably, the voltage profile of this channel is characterized by a region of negative slope that reverses the orientation of the voltage gradient in the interval extending from ∼0.2 to ∼0.5. As a consequence, positive charges centered at 0.4 would experience a negative voltage gradient oriented toward the cytoplasmic surface of the channel at all potentials, which would favor their inward movement, whereas negative charges centered at 0.3 would lie within a positive voltage gradient and would tend to move outward, away from the cytoplasm. The first derivatives (force) of the voltage profiles are plotted in Fig. 12 B and the values at 0.3 and 0.4 are plotted in the bar diagram Fig. 12 C. As there is little difference in the slopes of the voltage profiles at these positions, the net force acting on the two regions of charge is close to zero at all potentials (Fig. 12 D) and consequently, the channel would not display any voltage dependence. The small differences in net force shown in panel D most likely arise from rounding errors in the numerical procedure used by Origin 6.0 software. The simple model fails to explain the reversal of gating polarity by negative charge substitutions such as N2E and G5D because the voltage profiles are symmetric over the two charges and the resulting forces acting on each charge are equal and opposite. Similar results are obtained if the region of negative charge is positioned at any distance from the positive charge. Evidently, the reversal of gating polarity requires an asymmetry in the voltage profile such that the net force acting on both charges is not zero.

FIGURE 12.

A model of the wild-type channel with the addition of a second region of negative charge. (A) The voltage profile of the pore of a channel calculated with the PNP model of Chen and Eisenberg (1993) using 199 points at holding potentials of 0, ±50, ±100, ±150 mV with a positive charge centered at a distance of 0.4 and a second region of negative charge centered at 0.3 (see text for details). This would approximate a simple model of the N2E channel. (B) The first derivative (dV/dD) of each of the voltage profiles shown in A is plotted as a function of distance. The uppermost trace is the derivative of the voltage profile at −150 mV. The derivative was determined by a numerical procedure contained in Microcal Origin 6.0 software using a second order polynomial smoothing function utilizing 10 points. Plots of derivatives are in descending order from −150 to 150 mV. (C) Bar graph of the values of the derivatives for each curve in B at distances of 0.3 and 0.4. (D) Bar graph of the net force acting on both charged regions. The values in C at each voltage are subtracted because the sign of the charged regions is opposite.

Interestingly, models, which generate asymmetries by changing only the relative magnitude of positive and negative charges in the N-terminus, cannot explain the observed polarity reversal by negative charge additions. These models approximate the condition in which a constriction may exist in the vicinity of one of the charged residues, or in which the channel is formed by heteromeric aggregates of wild-type and mutant subunits (see Oh et al., 2000). Reductions in magnitude of the positive charge in the model shown in Fig. 12 result in a net force that favors the inward movement of charges at negative potentials and consequently, this channel would have the same gating polarity as the parental Cx32*Cx43E1 channel. The reason that polarity is not reversed is that the voltage profile of the channel is altered such that a greater proportion of the voltage falls over the positive charge when a region of negative charge is placed closer to the cytoplasmic surface of the channel. This is illustrated in Fig. 13 A for the case in which positive charges are centered at 0.4 and negative charges at 0.2. The forces acting on these charges are plotted in the bar diagram in Fig. 13 B and the net force acting on both charged regions is plotted in Fig. 13 C. Because the net inward force increases as the applied voltage becomes more negative, the open probability of the channel would, like the parental channel, decrease at negative potentials. Therefore, polarity of V_j-gating would not be reversed by the addition of a dominant negative charge lying deeper in the channel pore.

FIGURE 13.

Model channels in which the magnitude of the positive charge at 0.4 is reduced (panels A–C) or the magnitude of the negative charge at 0.2 is reduced (panels D–F). (A) The voltage profile of the pore of a channel calculated with the PNP model of Chen and Eisenberg (1993) using 199 points at holding potentials of 0, and ±150 mV with a positive charge (1 M/L) centered at a distance of 0.4 and a second region of negative charge (2 M/L) centered at 0.2 (see text for details). (B) Bar graph of the values of the first derivatives at distances of 0.3 and 0.4. (C) Bar graph of the net force acting on both charged regions. The values plotted in panel B are subtracted at each voltage because the sign of the charged regions is opposite. (D) The voltage profile of the pore of a channel calculated with the PNP model of Chen and Eisenberg (1993) using 199 points at holding potentials of 0, and ±150 mV with a positive charge (2 M/L) centered at a distance of 0.4 and a second region of negative charge (1 M/L) centered at 0.2 (see text for details). (E) Bar graph of the values of the first derivatives at distances of 0.3 and 0.4. (F) Bar graph of the net force acting on both charged regions. The values plotted in panel B are subtracted at each voltage because the sign of the charged regions is opposite.

Charge distribution models in which the magnitude of the negative charge is reduced, produce a net outward force at all potentials that increases as the holding potential becomes more negative (Fig. 13, D–F). This would, according to the model presented in Fig. 10, result in a voltage-insensitive channel, as the outward force would favor the positioning of the voltage sensor in the open position. Even if one changed the model, such that channel closure were initiated by the outward movement of the voltage senor, the polarity of V_j-gating, would not be reversed because the outward force acting on the voltage sensor increases as the holding potential becomes more negative. Consequently, the channel would have the same negative gating polarity as the wild-type channel.

There are several charge distribution models that can account for the observed gating of N2E and G5D channels at only positive potentials. These models create asymmetric voltage profiles by considering partial charges that are present in the N-terminus. For example, threonine residues at the 4th and 8th positions, the tyrosine residue at the 7th position, and the serine residue at the 11th position are all expected to contribute partial negative charges. In the model illustrated in Fig. 14, partial negative charges at d = 0.16 and negative charges at d = 0.3 cause a distortion in the voltage profile (Fig. 14 A) such that the force acting on positive charges situated at distance 0.4 would favor their inward movement at all potentials, whereas the force acting on negative charges centered at distance 0.3 would favor their outward movement at all voltages (Fig. 14 B). The forces acting on these charges are opposite and nearly equal in magnitude. However, the force acting on a partial negative situated at a distance of 0.16 would be inward at positive potentials and outward at negative potentials. The net force acting on all three charges, shown in Fig. 14 C, favors the inward movement of the amino terminal voltage sensor at only positive potentials. At negative potentials, an outward movement of the voltage sensor would be favored, but this would be prohibited by the height of the energy barrier depicted as B in Fig. 10 D. Consequently, closure of the channel could occur only at positive potentials, opposite of the wild-type channel. Qualitatively similar results are obtained if the negative charge at 0.3 is placed anywhere between the negative charge at 0.16 and the positive charge at 0.4 (not shown).

FIGURE 14.

A model of a N2E channel with the addition of a partial negative charge. (A) The voltage profile of the pore of a channel calculated with the PNP model of Chen and Eisenberg (1993) using 199 points at holding potentials of 0, and ±150 mV with a positive charge (2 M/L) centered at a distance of 0.4, a second region of negative charge (2 M/L) centered at 0.2, and a third region of negative charge (0.5 M/L) centered at 0.16 (see text for details). (B) Bar graph of the values of the first derivatives at distances of 0.3, 0.4, and 0.16 at 0 and ±120 mV. (C) Bar graph of the net force acting on the three charged regions at each voltage.

Charges located outside the N-terminus can also produce asymmetric voltage profiles across the channel pore, which would favor the inward movement of the voltage sensor (not shown). These charges may include: K22 at the N-terminus/TM1 border, E208 at the TM4/CL border, and the highly conserved charges in transmembrane segments, R22 in TM1 and R142 and E146 in TM3. As the charges at these positions may not move in response to changes in applied voltage, they would not be considered to be part of the voltage sensor. However, they could influence the movements of the voltage sensor by causing distortions in the voltage profile across the channel pore.

Voltage profiles of bipolar channels

An explanation for the existence of bipolar channels that conserves the inward movement of the voltage sensor gating model requires the formulation of a charge distribution model that results in a U-shaped net force/voltage relation, i.e., the net force acting on the voltage sensor at ±150 mV greater than force acting at 0 mV. A charge distribution model that meets this requirement is illustrated in the inset of Fig. 15 A. The resulting voltage profile at 0, ±150, and ±200 mV is shown in Fig. 15 A and the force/distance relation at these voltages is shown in Fig. 15 B. The force acting on a negative charge centered at 0.3 and a positive charge centered at 0.4 is plotted in Fig. 15 C and the net force (inward force–outward force) is plotted in Fig. 15 D. Accordingly, the inward movement of the voltage sensor from the open-to-closed position would be more likely as the holding potential becomes either more positive or more negative. Because the net inward force is minimal at a holding potential of 0 mV, the channel could be bipolar. Similar results are obtained if the negative charge is positioned anywhere in the interval spanning the interval between 0.2 and 0.3.

FIGURE 15.

A charge distribution model that could result in a bipolar channel. (A) The voltage profile of the pore of a channel calculated with the PNP model of Chen and Eisenberg (1993) using 199 points at holding potentials of 0, ±150, and ±200 mV. The distribution of permanent charge used to obtain the voltage profiles is shown in the inset. (B) The first derivative (dV/dD) of each of the voltage profiles shown in A are plotted as a function of distance. The derivative was determined by a numerical procedure contained in Microcal Origin 6.0 software using a second order polynomial smoothing function utilizing 12 points. The uppermost trace is the derivative of the voltage profile at −200 mV. (C) Bar diagram of the value of the first derivative at a distance of 0.3 and 0.4. (D) Bar diagram of the net force acting on a negative charge centered at 0.3 and a positive charge centered at 0.4.

Although the charge distribution shown in Fig. 15 provides the conditions for bipolarity, it is unrealistic in that it requires that the positive charges located at 0.4 lie in a region of the voltage profile that has a net negative charge. To obtain this profile, one must assume that charges located outside the pore have a larger effect in determining the voltage profile of the channel than charges contained within the pore. This does not seem likely. Also, note that the net force on the voltage sensor at 0 mV in the bipolar case presented greatly exceeds that in any other model and is so large that it is unlikely that the open probability of the channel would be close to 1.0 at holding potentials close to 0 mV. Attempts to derive charge distribution models in which pore-lining charges dominate and produce a U-shaped force/voltage relation did not succeed, nor did any models that simultaneously considered three charges to approximate the conditions expected for N2E+G5R and N2R+G5D channels. However, as we cannot prove that charge distribution models resulting in a U-shaped force/voltage relation do not exist, we cannot formally exclude this mechanism as a potential explanation for bipolarity.

Bipolarity could arise by at least two other mechanisms. One could invoke the existence of two open channel states each with different charge distributions, such that the voltage profile of one open state of the channel would favor the inward movement of the voltage sensor at positive potentials, whereas the voltage profiles of the other open state would favor the inward movement of the voltage sensor at negative potentials. This model is essentially a variation of the model originally proposed to explain the bipolarity of T8D homomeric channels but it does not require the repositioning of portions of the N-terminus either inside or outside the electric field nor does it require that transitions between the open states are voltage dependent. The conceptual basis for this model can be illustrated by the behavior of the G5R channel. This channel displays rapid transitions between two open conductance states that do not appear to be voltage dependent and closures at negative potentials appear to be more likely from the high-conductance state. If one envisions a situation in which closures at negative potentials might occur only from the high-conductance state, whereas closures at positive potentials might occur only from the main state, then the channel would exhibit bipolar gating.

Bipolarity could also arise if the voltage sensor behaved as a center open toggle switch, responding with an outward movement to one polarization and an inward movement to the opposite polarization. In this case, mutations that display bipolarity would have to alter the energy profile of the channel such that opposite movements of the voltage sensor would be energetically feasible, i.e., they would reduce the height of energy barrier B, depicted in Fig. 10 D). The model does not require the existence of distinct gating mechanisms, as the opposite movement of the voltage sensor could be coupled to the same downstream mechanism that leads to channel closure, for example, the breaking of a hydrogen bond in another domain that would destabilize the open state, as proposed by Ri et al. (1999).

At this time it is not possible to discriminate between these two possibilities. Further understanding of the mechanism of polarity determination awaits studies that directly determine if the inward movement of N-terminus initiates V_j-gating in response to changes in applied potential. The application of spectroscopic methods that describe conformational changes in proteins, such as those described by Cha et al. (1998), are required to more fully understand the molecular mechanism of V_j-gating and the actions of the mutations described in this study.

In conclusion, most mutations examined in this and in previous studies can be interpreted in terms of a gating model in which the voltage sensor is positioned in the N-terminus and its inward movement initiates V_j-gating. Positive charge substitutions at the 2nd, 5th, and 8th positions maintain the negative polarity of V_j-gating and the shifts in the voltage dependence of these channels can be explained either by invoking changes in the free energy of the open and/or closed states or by changes in the force acting on the voltage sensor due to local distortions in the voltage profile. The appearance of multiple open states in channels carrying additional positive charges may reflect a “gain of function” or may result from the “unmasking” of existing multiple open states. Application of the PNP model predicts that the reversal of gating polarity by the addition of negative charges to the N-terminus is not by itself sufficient to reverse gating polarity but requires asymmetries in the voltage profile of the channel in the vicinity of the voltage sensor that are created by charges at other positions. The bipolarity of V_j-gating observed in homomeric T8D channels, and in homomeric channels with positive and/or negative charge substitutions at both the 2nd and 5th is unlikely to be caused by distortions in the voltage profiles of the channel. Further studies, which determine if the inward movement of the N-terminus is the only translocation that can initiate channel closure by V_j-gating, are required to resolve the origins of bipolarity.