Salting Out the Ionic Selectivity of a Wide Channel: The Asymmetry of OmpF

Abstract

Although the crystallographic structure of the bacterial porin OmpF has been known for a decade, the physical mechanisms of its ionic selectivity are still under investigation. We address this issue in a series of experiments with varied pH, salt concentrations, inverted salt gradient, and charged and uncharged lipids. Measuring reversal potential, we show that OmpF selectivity (traditionally regarded as slightly cationic) depends strongly on pH and salt concentration and is conditionally asymmetric, that is, the calculated selectivity is sensitive to the direction of salt concentration gradient. At neutral pH and subdecimolar salt concentrations the channel exhibits nearly ideal cation selectivity (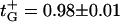). Substituting neutral DPhPC with DPhPS, we demonstrate that the fixed charge of the host lipid has a small but measurable effect on the channel reversal potential. The available structural information allows for a qualitative explanation of our experimental findings. These findings now lead us to re-examine the ionization state of 102 titratable sites of the OmpF channel. Using standard methods of continuum electrostatics tailored to our particular purpose, we find the charge distribution in the channel as a function of solution acidity and relate the pH-dependent asymmetry in channel selectivity to the pH-dependent asymmetry in charge distribution. In an attempt to find a simple phenomenological description of our results, we also discuss different macroscopic models of electrodiffusion through large channels.

INTRODUCTION

Large, highly conductive channels from the bacterial outer membrane are designed by nature to allow exchange of solutes other than halide, alkaline, or alkaline-earth metal ions (see recent reviews by Nikaido, 2003, and Delcour, 2003). The major functional role of these large channels in the cell life-cycle is to support and to regulate the influx of nutrients and the extrusion of waste products. Yet, their selectivity for the small ions may play a certain physiological role too.

However, a much more compelling reason to study the small-ion selectivity of a large channel is to test our understanding of electrostatics at the nanoscale. Questions like the Debye screening in channels that allow one or two counterions only, electric field effects at distances smaller that the Bjerrum length, properties of solvents and solutes in the vicinity of protein surfaces, etc., invariably ignite a researcher's interest and imagination.

For our study we choose OmpF (outer membrane protein F), a channel from the outer bacterial membrane, whose structure is known with 0.24 nm resolution (Cowan et al., 1992). Gram-negative bacteria like Escherichia coli are enclosed in a double membrane cellular envelope. The outer membrane serves as a selective permeability barrier that protects bacteria from harmful components and acts as a passive filter regulating the flow of solutes (Delcour, 2003; Nikaido, 2003; Jap and Walian, 1990). This function is accomplished by a number of membrane channel proteins called porins, which display a wide range of permeability profiles. Among these channels are general diffusion porins (with limited substrate selectivity) and solute-specific channels (with high degree of solute selectivity).

OmpF is one of the general diffusion porins of E. coli. It allows the passage of ions and small neutral solutes up to ∼650 Da. OmpF channels are trimers of identical subunits (Cowan et al., 1992) where each monomer forms a 16-stranded β-barrel, which acts as a water-filled pore with an elliptical cross-section of 2.7 × 3.8 nm² between the main-chain atoms in its walls. The shape of this pore is significantly modified by a polypeptide loop L3 folding into the barrel. The channel is asymmetric: protein structure on the extracellular and periplasmic sides differs significantly not only in the pore dimensions but also in the amount and ionization state of the charged residues facing the pore (Karshikoff et al., 1994).

Because of the presence of loop L3 in the β-barrel, the OmpF pore has an hourglass shape, with a narrow constriction (0.7 × 1.1 nm²) at approximately half the height of the channel. The solute exclusion limit of the channel, as well as its ion selectivity, to a great extent is determined by this constriction. Acidic residues of loop L3 and a cluster of basic residues on the barrel wall opposite the loop give rise to a transverse electrostatic field strong enough to orient water molecules (Tieleman and Berendsen, 1998) and, according to recent molecular dynamics (MD) and Brownian dynamics (BD) simulations (Schirmer and Phale, 1999; Phale et al., 2001; Im and Roux, 2002a), to produce well-separated specific ion pathways.

When reconstituted into planar lipid membranes, OmpF porin forms trimeric channels, whose conductance in 1 M salt solutions is in a nano-Siemens range (Schindler and Rosenbusch, 1978). Recordings of ion currents do not reveal any difference between the monomers of the trimer in regard to their conductance and blockage by water-soluble polymers (Rostovtseva et al., 2002) or antibiotics (Nestorovich et al., 2002). Similar observations have been reported for the specific porin LamB where the time-resolved events of sugar translocation demonstrate mutual independence of the monomers in the trimer (Kullman et al., 2002).

Reconstituted OmpF channels display a cation selectivity at physiological salt concentrations, which decreases at 1-molar concentration (Benz et al., 1979, 1985; Saint et al., 1996). Presently, there is no quantitative explanation for this loss of selectivity at high salt concentration, although it is generally admitted that ions screen both the electrostatic field created by the protein-charged residues and the reaction field from the dielectric environment of the pore. However, the size of the constriction (∼0.7 nm³) and the average ion concentration (∼1.2 ions/nm³ for 1 M KCl) make the application of the Debye screening theory questionable. Recent studies using BD simulations have shown that continuum theories fail in narrow pores because they do not take into account the self-energy contributions (Corry et al., 2000; Im and Roux, 2002a). Alternatively, this behavior could be explained by assuming effective binding of small ions in the vicinity of oppositely charged residues (Miller, 1999).

It has been reported that OmpF selectivity is highly sensitive to the charge state of the channel lining at the constriction (Schirmer, 1998; Nestorovich et al., 2003). OmpF mutants (R42C, R82C, or R132P) after substitution of any of the three arginines by neutral cysteine or proline exhibit an increased cationic selectivity (Saint et al., 1996). Correspondingly, substitution of an acidic group like D113 for a neutral residue reduces considerably the cation preference of the channel (Saint et al., 1996; Bredin et al., 2002).

Despite these straightforward correlations, it appears that channel selectivity cannot be attributed solely to the net charge and geometry of the narrowest region of the channel. In fact, net charge in the constriction is positive whereas the whole channel is cation-selective. Selectivity measurements in OmpF mutants with no charge at the constriction showed significantly higher cation selectivity, close to threefold the selectivity of the wild-type OmpF (Phale et al., 2001). Furthermore, ion trajectories from MD and BD simulations suggest that a number of charged residues distributed over the OmpF aqueous pore also contribute to the channel charge specificity (Im and Roux, 2002a).

The known crystal structure helps to clarify the role of each group in the channel selectivity. However, this information needs to be supplemented by careful estimates of the pK_a values of these groups. This is not an easy task because of the mutual interference between the neighboring residues and the difficulties in estimating the electric potential and the dielectric properties of the solvent in their vicinities. Several studies aimed at the pK_a values determination were using slightly different computational methods and assumptions (Karshikoff et al., 1994; Varma and Jakobsson, 2004). As a result, there is no agreement, for instance, concerning the charge state of some residues at neutral pH.

The exact orientation of the trimer in the bilayer reconstitution experiments is also unknown. Some authors think it is likely that the short periplasmic loops of the porin first insert into the membrane, thus leaving the long extracellular loops on the side of the protein addition (cis side) (Im and Roux, 2002a). What is well established, however, is that under the experimental protocols used in the present study the OmpF channel inserts predominantly in an oriented manner with the error rate of ∼3% (Nestorovich et al., 2003).

Here we discuss experiments on OmpF reversal potential at different lipid membrane composition, salt type, salt concentration gradient, and pH of the surrounding solution. The calculated OmpF selectivity is found to be dependent not only on salt concentration but also on the direction of salt concentration gradient (first reported by Alcaraz et al., 2003). Reversal potential measurements show a substantial asymmetry (of ∼25%) upon inverting the gradient. This asymmetry depends on the bathing solution pH and on the absolute salt concentration. Experiments with charged (DPhPS) and neutral (DPhPC) lipid bilayers show that the fixed charge of the host lipid has a small but measurable effect on the channel reversal potential.

Taking advantage of the known crystal structure of OmpF, we complement our experimental study with numerical calculations of the electric potential all over the protein and electrodiffusion region. To compute the potential it is necessary to have the electric charge distribution, which is not known a priori despite the availability of the three-dimensional structure of the protein. This charge distribution has two main contributions: the fixed partial charges which come from the different electronegativities of the atoms in the molecule and the charges coming from the ionization of the groups. The latter depends on the ionization equilibrium established between the protons of the solution and the titratable residues of the protein. A grossly simplified approach consists in using the amino acid pK_a values in free solution (known as “model pK_a,” 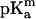) and obtaining the protonation state for a given residue. However, the ionization state of a given residue in the protein will be influenced, among other factors, by the charge distribution in its vicinities and its position in the protein (i.e., whether the residue is buried or not). For this reason, the effective pK_a values are, in some cases, very different from the model pK_a values. Previous work shows that it is possible to estimate these pK_a values in the protein from the model pK_a values by calculating the work (ΔG) necessary to carry the set of amino acids in free solution (unfolded protein) to their actual position in the protein (Antosiewicz et al., 1996; Ullmann and Knapp, 1999). Several alternative methods have been reported for the pK_a calculations (Karshikoff et al., 1994; Varma and Jakobsson, 2004). The common routine is to divide the pK_a shift calculation in two main steps: 1) “single-site titration” ignores the presence of other titratable residues; 2) “multiple-site titration” accounts for the presence of all the remaining titratable groups. We use a Monte Carlo approach for the second step.

Here we use our calculations of the pK_a values of the charged groups in OmpF to obtain the charge distribution in the channel. We find some differences between our results and the pK_a values reported previously by other authors (Karshikoff et al., 1994), but in agreement with the pK_a shifts recently computed using a different method for the “multiple-site titration” (Varma and Jakobsson, 2004). We demonstrate a correlation between the reversal potential asymmetry and the asymmetry in the total charge near the OmpF mouths. We also compare several simple macroscopic models for the reversal potential description identifying a model that accounts best for the reversal potential changes with salt concentration and concentration gradient.

MATERIALS AND METHODS

Experimental

Wild-type OmpF (a generous gift of Dr. Mathias Winterhalter) was isolated and purified from an Escherichia coli culture. Bilayer membranes were formed from two monolayers made from a 5 mg/ml solution of diphytanoylphosphatidylcholine (DPhPC) or diphytanoylphosphatidylserine (DPhPS) (Avanti Polar Lipids, Alabaster, AL) in pentane (Burdick and Jackson, Muskegon, MI) on 70–80-μm diameter orifices in the 15-μm-thick Teflon partition that separated two chambers (Bezrukov and Vodyanoy, 1993; Montal and Mueller, 1972). The orifices were pretreated with a 1% solution of hexadecane in pentane. The total capacitance depended on the actual location of the orifice in the film (and thus area of the film exposed to salt solution), but membrane capacitance was always ∼30–35 pF. Aqueous solutions of KCl were buffered by 5 mM MES at pH values below pH 6, by 5 mM HEPES at pH values (6 ÷ 8), by 5 mM CHES at pH 9, and by 10 mM CAPS at pH values above 9. All measurements were performed on single OmpF channels at room temperature (23.0 ± 1.5)°C. Single-channel insertion was achieved by adding 0.1–0.3 μl of a 1-μg/ml solution of OmpF in the buffer that contained 1 M KCl and 1% (v/v) of Octyl POE (Alexis, Switzerland) to 1 ml aqueous phase at the cis side of the membrane only while stirring.

The membrane potential was applied using Ag/AgCl electrodes in 2 M KCl, 1.5% agarose bridges assembled within standard 200-μl pipette tips (Bezrukov and Vodyanoy, 1993). Potential is defined as positive when it is greater at the side of protein addition (the cis side of the membrane cell). An Axopatch 200B amplifier (Axon Instruments, Foster City, CA) in the voltage-clamp mode was used for measuring the current and applying potential. Data were filtered by a lowpass, eight-pole Butterworth filter (Model 9002, Frequency Devices, Haverhill, MA) at 15 kHz and recorded simultaneously by a VCR operated in a digital mode, and directly saved into the computer memory with a sampling frequency of 50 kHz. The membrane chamber and the headstage were isolated from external noise sources with a double metal screen (Amuneal Manufacturing, Philadelphia, PA).

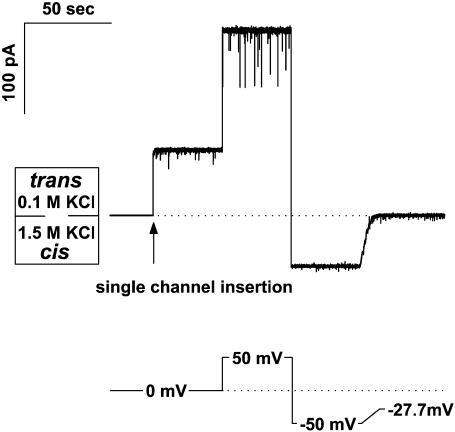
The reversal potential was obtained as follows. First, a lipid membrane was formed at a given concentration gradient. Second, a single OmpF channel was inserted at zero potential and the channel conductance was checked by applying +50 mV and then switching potential polarity (Fig. 1). Third, the ionic current through the channel was manually set to zero by adjusting the applied potential. The potential needed to achieve zero current was read as the “reversal potential.” Each point was measured for at least three different channels in three different experiments to assure reproducibility and to estimate standard deviation. In some experiments negative potentials of −(100 ÷ 200) mV were applied to speed up channel insertion.

FIGURE 1.

A typical recording of transmembrane ion current that illustrates reversal potential measurements. First, spontaneous insertion of a single OmpF channel at zero transmembrane voltage was achieved (arrow). Because of the channel cationic selectivity, the insertion is seen as a non-zero current that flows from the more concentrated 1.5 M KCl solution at the cis side of the membrane to the less concentrated 0.1 M KCl on the trans side. Second, ±50 mV potential was applied to make certain that the number of OmpF channels was equal to 1. Reasonable conductance values determined from the difference in current readings at positive and negative potentials as well as the rare flickering to two-thirds of the total channel conductance at +50 mV provided the evidence for single channel insertion. Finally, ion current was manually set to zero by adjusting the transmembrane potential to −27.7 mV. This potential was read as a “reversal potential.” Time resolution was 1 ms. The DPhPC membrane was bathed by solutions buffered by 5 mM MES at pH 6.

Model calculations: numerical procedure

The entire trimer, built using the Protein Data Bank file (Cowan et al., 1992, 1995) was inserted in a membrane that, for simplicity, was represented by spheres of radius 8 Å spaced at 8 Å. The membrane dimensions were 256 × 296 × 40 ų. Overlapping of spheres ensured that the whole space of the membrane was filled by a low dielectric medium. The University of Houston Brownian Dynamics Program code (Davis et al., 1991; Madura et al., 1995) was used for the calculation of the pK_a of ionizable residues following the procedure described by Antosiewicz et al. (1994). This approach involves the calculation of the interaction energy between the ionizable groups of the protein and of the differences between the ionization energies of each group in the neutral protein and in free solution. All these energies were assumed to be of purely electrostatic nature so that they could be calculated by means of the Poisson-Boltzmann equation. The protein and the membrane were represented by a single region of low dielectric constant.

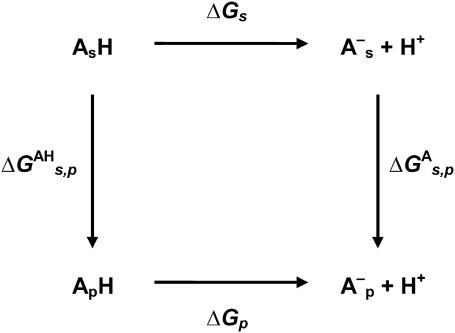
Three energy contributions were considered to be involved in the pK_a shift of the charged groups of the protein: 1), the ion self-energy (Born energy) that takes into account the penalty in free energy for transferring a charged group from solution with a high dielectric constant to the actual position in the protein medium of a low dielectric constant; 2), the background term that includes the electrostatic interaction between residues with the remaining permanent charges of the protein; and 3), the interaction of the charged group with other ionizable charged groups. The first two terms lead to the so-called intrinsic pK_a (pK_int). All three contributions were computed using the linear form of the Poisson-Boltzmann equation. We start from the free energy of ionization of the model compound at each given pH, ΔG_s, then we add the change in free energy of the ionized residue when carried from the free solution to the protein environment, 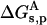. Finally, the change in free energy of the neutral residue when carried from the free solution to the protein environment, 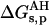, is subtracted. This is summarized in the thermodynamic cycle of Fig. 2.

FIGURE 2.

Thermodynamic cycle used in calculation of pK_a shifts for the dissociation equilibrium of a model residue (A) in solution (subscript s) and in the protein environment (subscript p).

In practice, the calculation of all these energies requires two finite-difference calculations per residue: a first calculation with the charge on the ionizable residue in free solution and another with the charge on the ionizable residue in the neutral protein (but with the permanent partial charges present). To avoid problems coming from the mesh discretization and the self-energy of the charges, all the calculations were carried out with the residue located at exactly the same position on the mesh, which in our calculations has initial dimensions (before “focusing”) 130 × 130 × 60 ų and spacing of 2.5 Å. This treatment allows the exact removal of the mesh-dependent self-energy and the correct finite-difference calculation of Coulombic energy differences when free energies are computed. The calculated potential on the large grid is used to provide boundary conditions for all successive “focusing” steps, where a smaller grid (15 × 15 × 15 and spacing 1.2 Å, 0.75 Å, and 20 × 20 × 20 and spacing 0.25 Å) is built centered on each titratable residue to reach better accuracy. As for the energy due to the interaction between titratable groups, we have used a Monte Carlo method to obtain the statistical distribution of the ionization state for each residue and, from it, the titration curves for all titratable groups. One alternative and most direct possibility, namely calculating all possible ionization states and choosing that of higher Boltzmann probability, is simply unfeasible in our model due to the large number of ionizable residues present in the trimer (3 × 102 = 306, which would give 2³⁰⁶ different states). Nevertheless, this problem can be considerably simplified by introducing a cutoff distance and considering only the residues within this distance (Varma and Jakobsson, 2004).

We use the same dielectric constant, ɛ_m, for the membrane and the protein. The remaining space, corresponding to the membrane-bathing solution, is assigned a dielectric constant of 80. The calculations have been performed both for ɛ_m = 20 and ɛ_m = 4 to check the influence of this parameter on the calculation results. The salt concentration was set in all cases equal to 150 mM and the ionic radius of the permeating ions was set to 2 Å. Typical calculations on a PC (P4, 2.4 GHz processor) took ∼3 h for the energies of all charged residues and 45 min for the Monte Carlo procedure.

RESULTS AND DISCUSSION

To assess OmpF small-ion selectivity, we have measured the channel reversal potential under carefully controlled pH and salt concentrations on both sides of the membrane formed from either neutral or charged lipids. One of the typical measurement protocols is illustrated by Fig. 1. Special care was used to exclude any exchange of electrolyte solutions between the cis and trans cell compartments before the insertion of a single channel. In each new measurement, including those with the same pairs of cis and trans concentrations, a new membrane was formed on fresh salt solutions.

“Salting out” channel selectivity

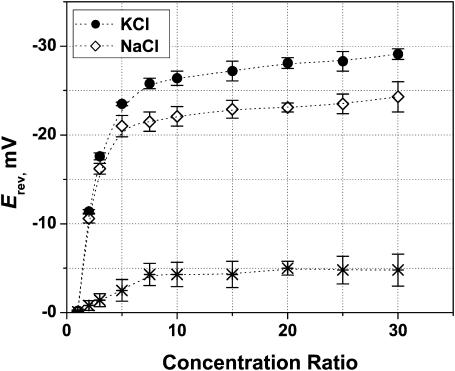
In the main series of experiments the OmpF channel was inserted in a neutral lipid bilayer (DPhPC). The use of an uncharged lipid discards any side effect of counterion accumulation on both sides of the membrane that, in the case of asymmetric lipid compositions or in the case of asymmetric salt concentrations, could contribute to the voltage drop across the channel. First, the salt concentration on the trans side, C_trans, was kept constant (0.1 M), whereas the concentration on the cis side, C_cis, was increased from 0.1 M up to 3 M. Thus, the concentration ratio, r ≡ C_cis/C_trans, was changed between 1 and 30.

As shown in Fig. 3, for both KCl and NaCl, the main change in the OmpF reversal potential occurs at small concentration ratios, mostly up to a fivefold gradient. Only a weak concentration dependence of E_rev is found beyond this gradient. The channel is not equally cation-selective in KCl and in NaCl solutions, although the difference is small (≤5 mV in the reversal potential). Measured values of the reversal potential are similar to those previously reported in the literature (Benz et al., 1979; Saint et al., 1996; Nestorovich et al., 2003), although most of the reported experiments were performed only in a 10-fold salt gradient.

FIGURE 3.

Reversal potential as a function of cis/trans concentration ratio for KCl (solid circles) and NaCl (open diamonds) at pH 6. Bathing solution concentration on the trans side was fixed at 0.1 M, whereas the concentration on the cis side was increased from 0.1 M to 3 M. Membranes were formed from DPhPC. The channel is more permeable to K⁺ ions along the whole range of studied salt gradients. The asterisks represent the difference between the absolute values of E_rev in KCl and NaCl solutions.

Apparently, the channel reversal potential follows the well-known Goldman-Hodgkin-Katz (GHK) equation (Goldman, 1943; Hodgkin and Katz, 1949). For large concentration gradients, GHK equation predicts a limiting value defined by the permeability ratio (see Appendix). The asymptotic behavior seen in the plots for both salts agrees qualitatively with such prediction. However, according to the GHK theory, reversal potential for a given salt is only dependent on the concentration ratio (corrected by activity coefficients), r, and not on the absolute values of salt concentration on both sides of a selective membrane or a pore.

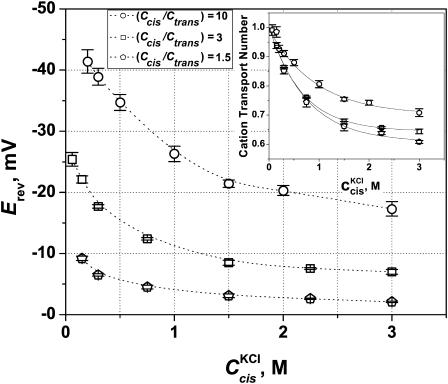
Fig. 4 demonstrates that this is not the case. The reversal potential measurements with KCl performed at a constant concentration ratio, r, but at different concentrations reveal that the reversal potential is also a function of absolute concentrations. In these experiments both C_trans and C_cis were changed to keep their ratio at a particular value specified in the figure. It is seen that the absolute value of the reversal potential decreases as salt concentration increases. Importantly, in the whole concentration range used in these experiments, the KCl activity coefficient changes only by 36% from 0.87 for 0.02 M to 0.56 for 3 M, and, therefore, cannot explain the measured trends.

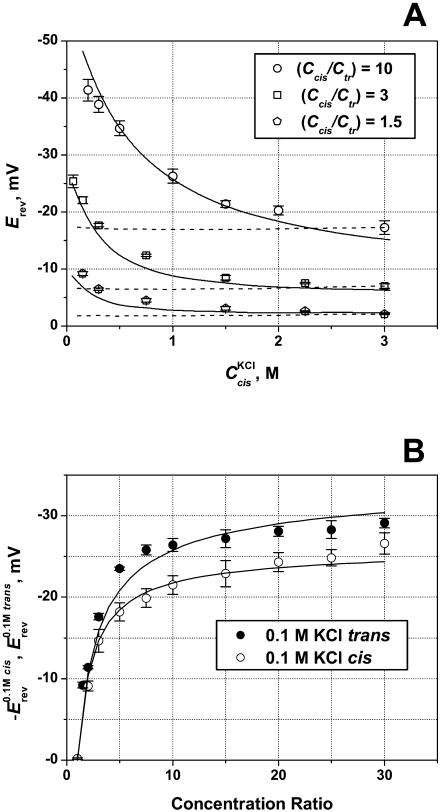
FIGURE 4.

Reversal potential measured at three constant cis/trans KCl concentration ratios (circles, 10; squares, 3; pentagons, 1.5) but different absolute concentrations. Membranes were formed from DPhPC at pH 6. The channel exhibits cationic selectivity: higher salt concentration at the cis side generates negative reversal potential. The absolute value of this potential decreases as salt concentration goes up. (Inset) Cationic transport numbers calculated according to Eq. A5 (Appendix) with salt concentrations corrected with activity coefficients. Solid lines through the data are drawn to guide the eye. It is seen that at C_cis = 3 M cationic selectivity of the channel drops to t⁺ ≈ 0.6 ÷ 0.7.

As might be expected, concentrated solutions screen the channel fixed charges more effectively, and, therefore, the channel cationic preference gets smaller. At C_cis = 3 M, the reversal potential is reduced by more than one-half of its value at the physiological concentration. For a 10-fold gradient (open circles), the change in E_rev in the explored concentration range is greater than 20 mV. It is seen that in contrast with the GHK prediction, the reversal potential changes with salt concentration for all the ratios between cis and trans concentrations (r = 10, 3, and 1.5). Fig. 4 (inset) gives the cation transport numbers calculated using Goldman's constant field approximation (Goldman, 1943; Hodgkin and Katz, 1949; Markin and Chizmadzhev, 1974). It is seen that as both concentrations increase, the selectivity of the channel decreases, from nearly ideal cationic selectivity of 0.98 ± 0.01 to slightly cationic of 0.6 ÷ 0.7 for all concentration ratios. At a given cis side concentration (which is always larger than the trans side concentration), the calculated selectivity also depends on the ratio itself: the higher is the ratio, the higher is the transport number. This observation is in accord with the charge screening idea. Indeed, at a given cis side concentration, higher ratios correspond to smaller trans side concentrations and, therefore, to less pronounced screening.

Reversal potential asymmetry

The structure of the OmpF channel is asymmetric. This concerns both the geometry of the water-filled pore (Cowan et al., 1992) and the fixed charge distribution (Karshikoff et al., 1994). Therefore, because of the difference in salt concentrations at the cis and trans sides of the membrane, the fixed charge is screened differently and we should expect certain a sensitivity of the reversal potential to the direction of the salt gradient.

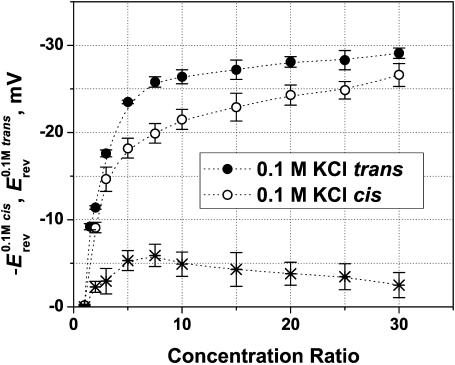
It is known that when OmpF is added from one side of the membrane only, it inserts in a predominantly oriented manner (Rostovtseva et al., 2002; Nestorovich et al., 2002, 2003; Danelon et al., 2003). We made use of this finding to study asymmetry in the reversal potential. Fig. 5 shows results of two series of reversal potential measurements where not only the absolute gradient but also the gradient direction was changed. In the first series, the KCl concentration ratio r is greater than unity (C_cis > C_trans) (same data are compared in Fig. 3 with measurements for NaCl); in the second one, the gradient is inverted, i.e., r < 1 (C_cis < C_trans). Salt concentration in the less concentrated solution was kept constant at 0.1 M in all cases. Indeed, the reversal potential was always negative at the side with the higher salt concentration. However, to facilitate comparison of the two datasets, we plotted −E_rev for the experiments where the cis side concentration was smaller. The channel functional asymmetry manifests itself as a difference reaching ∼25% in the measured reversal potential. The absolute value of E_rev is greater when the more concentrated solution is on the cis side than when the opposite happens. The asymmetry in E_rev (<6 mV) is only slightly concentration-dependent, as shown in the bottom plot of Fig. 5. These results demonstrate once again that OmpF trimer inserts in an oriented manner rather than randomly.

FIGURE 5.

OmpF reversal potential as a function of the concentration ratio for two series of measurements with oppositely directed gradients. (Solid circles) E_rev obtained in the series where C_cis > C_trans = 0.1 M KCl. (Open circles) Plotted as −E_rev for the reversed gradient C_trans > C_cis = 0.1 M KCl. The channel is asymmetric: the absolute value of the reversal potential is greater when the more concentrated solution is on the cis side of the membrane. The asterisks represent the difference. Membranes were formed from the DPhPC at pH 6.

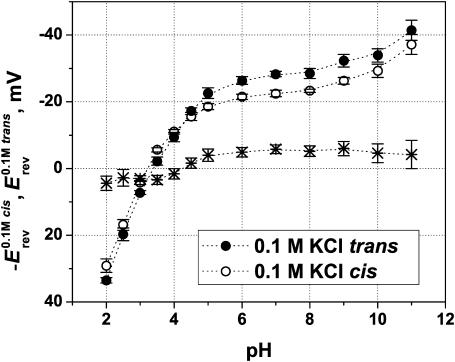
The asymmetry in E_rev is pH-dependent. Fig. 6 shows the change of the reversal potential with pH for a 10-fold concentration ratio. For the ease of comparison, the values of −E_rev have been plotted for r < 1 (less concentrated solution in the cis side). Again, different absolute values of E_rev are found for 0.1 M trans/1 M cis (solid circles) and the opposite gradient, 1 M trans/0.1 M cis (open circles) at every pH except for ∼pH 4.

FIGURE 6.

Dependence of the reversal potential on solution pH at C_cis = 1 M KCl and C_trans = 0.1 M KCl (solid circles) and at the inverted gradient of the same concentrations (open circles). To facilitate comparison, the data for the inverted gradient are plotted as −E_rev. Note that the difference in the reversal potentials (asterisks) changes its sign from high pH to low pH. Thus, Δ|E_rev| ∼5 mV at the wide pH range from 5 to 11 and Δ|E_rev| ∼ (−4 mV) at pH 2. Membranes were formed from DPhPC.

The variation of the reversal potential with pH agrees qualitatively with previously reported measurements (Benz et al.,. 1979; Schirmer and Phale, 1999; Nestorovich et al., 2003). It is seen that the reversal potential changes its sign as pH is decreased below ∼pH 4. Thus, in acidic solutions the OmpF channel becomes anion-selective. At the other extreme, in basic solutions, the cationic selectivity increases beyond its value for neutral pH. Recently, we reported (Nestorovich et al., 2003) that pH-dependent selectivity behavior resembles that of the channel conductance. OmpF conductance in its fully open state displays three characteristic regimes. Under acidic conditions (corresponding to most dramatic selectivity change) conductance strongly depends on solution pH, increasing threefold when pH is increased from pH 1.0 to pH 5. At neutral pH (where channel is slightly selective to cations with 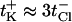), it displays a plateau that extends from pH 5 to pH 9. In basic solutions from pH 9 to pH 12 (corresponding to a slight increase in cationic selectivity), channel conductance is again pH-sensitive and increases by 15–30%, depending on the sign of the applied voltage. Analysis of open channel noise and stepwise time-resolved transients in the open state (Nestorovich et al., 2003) demonstrated that at least three different ionization processes are involved in the pH-dependent modification of the channel transport properties. Noise is minimal in the pH range corresponding to the conductance and selectivity plateaus.

The large amount of titratable residues lining the pore lumen does not allow a simple explanation of selectivity versus pH curves in terms of one or a few pK_a of charged groups. However, it is evident that the asymmetry in E_rev does not remain constant but is also pH-dependent. Moreover, the difference in E_rev between the opposite gradient configurations changes its sign from low to high pH: Δ|E_rev| is ∼−4 mV at pH 2 and Δ|E_rev| is ∼+5 mV at neutral pH.

Interestingly, at ∼pH 3.25 the “sign” of selectivity measured in 1 M/0.1 M KCl gradient depends on the gradient direction. The selectivity is cationic for C_cis > C_trans and anionic for C_cis < C_trans. This inversion of measured selectivity is a consequence of the finite concentration gradient used in experiment. Indeed, as C_cis approaches C_trans the system moves toward equilibrium, so that cis-to-trans and trans-to-cis selectivities have to be equal in order not to violate equilibrium thermodynamics. Once again, the measured inversion demonstrates that the selectivity obtained for a particular concentration gradient is a function of this gradient, its direction, and the absolute salt concentration (Figs. 4 and 5).

Electrostatics versus other interactions

The experimental findings reported above strongly favor electrostatic interactions as the main cause of small-ion selectivity of the large channel formed by OmpF. The decrease in the selectivity with the increasing salt concentration (Fig. 4), selectivity asymmetry (Fig. 5), and its titration at the changing solution acidity (Fig. 6)—all are in perfect agreement with intuitive reasoning based on electrostatic considerations.

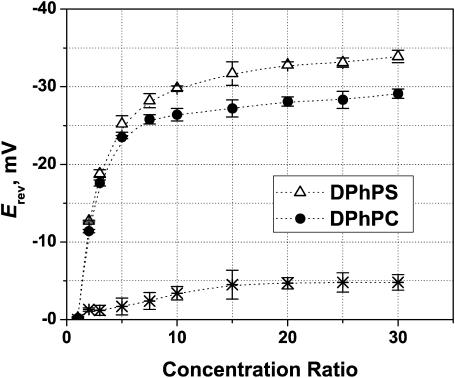
Further support has been found in experiments with charged membranes. The charge of lipid polar groups is able to modify the surface potential significantly (McLaughlin et al., 1970; Ninham and Parsegian, 1971). However, taking into account that the OmpF channel is comprised of three monomers whose size exceeds the typical Debye length of the solutions we use (<1 nm), it is reasonable to expect that the charge on lipid polar groups will have only small influence on the potential near the channel mouths. We have checked this conjecture by carrying out a series of measurements at different concentration gradients in a neutral membrane (DPhPC) and a negatively charged membrane (DPhPS). The results for pH 6 are shown in Fig. 7. The concentration of KCl on the trans side was 0.1 M and the concentration on the cis side was varied from 0.1 M up to 3 M. The reversal potential in the charged lipid is always higher, although the difference in E_rev is small (≤5 mV). This means that the effect of the lipid charge on OmpF selectivity is quite measurable but does not change the channel selectivity drastically.

FIGURE 7.

Reversal potential is sensitive to the lipid charge. It is larger (by the absolute value) for the negatively charged DPhPS membranes (open triangles) than for the neutral DPhPC membranes (solid circles) in the whole range of concentration gradients at pH 6. Salt concentration on the trans side was kept constant at 0.1 M KCl; the cis side concentration increased from 0.1 M KCl to 3 M KCl. The asterisks represent the difference between E_rev in DPhPC and DPhPS.

It is seen that the difference between reversal potentials in DPhPC and DPhPS is constant for the concentration ratio exceeding 10. This is an indication that the Debye length in the cis side is very small and the lipid charge is screened out, so that the major contribution comes from the trans side.

Previously it was shown that the effect of the phosphatidylserine charge on the channel conductance can be “titrated out” by increasing acidity of the membrane-bathing solution (Rostovtseva et al., 1998; Aguilella and Bezrukov, 2001). In a series of experiments we measured the reversal potential of the OmpF channel reconstituted in DPhPS and DPhPC membranes as a function of pH (data not shown). We found that as solution pH was lowered below pH 4, the difference in the reversal potentials began to level off reaching virtual zero at pH 2.

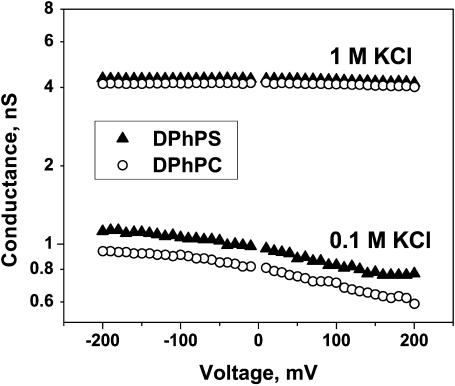
Negative charge of DPhPS headgroups in the vicinity of the channel is expected to accumulate positive ions to an excess of their bulk concentration. Because the OmpF channel is cation-selective at neutral pH, this accumulation may lead to a measurable increase in channel conductance. Fig. 8 compares single channel conductance in a neutral and a negatively charged membrane. The effect is an order-of-magnitude smaller than the effect of charged lipid on gramicidin channels (Apell et al., 1979; Rostovtseva et al., 1998) and is comparable (although still smaller) to the effect on L1 state of alamethicin channels (Aguilella and Bezrukov, 2001). This reduced influence of lipid charge is expected on the basis of electrostatic considerations that account for the channel structural features and the increased distance between the nearest lipid molecules and the water-filled pore of the channel (Apell et al., 1979; Bell and Miller, 1984; Moczydlowski et al., 1985; Rostovtseva et al., 1998; Aguilella and Bezrukov, 2001).

FIGURE 8.

A single open OmpF channel has larger conductance when reconstituted into a negatively charged bilayer at pH 6. At 0.1 M KCl concentration and −100 mV applied voltage the channel conductance in the DPhPS membranes exceeds that in the DPhPC membranes by ∼15%. In 1 M KCl solutions this difference is smaller. In this particular experiment it was ∼4%, which was close to the reproducibility of channel conductance from experiment to experiment (SD was ∼3%). Symmetrical salt solutions were used in these measurements.

Brownian dynamics simulations of the reversal potential in a model OmpF channel that is totally uncharged yielded some residual selectivity: the channel would be 40% more selective to K⁺ than to Cl⁻ ions (Schirmer and Phale, 1999). Within purely electrostatic considerations there is no satisfactory explanation for this residual selectivity. Therefore, other factors like hydrophobic or hydrophilic effects and other short-range interactions cannot be ruled out completely (see also Danelon et al., 2003); however, the results presented above demonstrate that electrostatic interactions dominate.

Charge distribution and reversal potential asymmetry

Table 1 shows the calculated pK_a shifts of the ionizable residues that are presumably most relevant to the channel selectivity: the residues facing the pore lumen and those located in its immediate vicinity. The criterion used for the selection of these 27 residues among the total 102 of one monomer was to pick those lying within some arbitrary distance (0.2 nm) of the solvent-accessible surface of the pore for each axial position in the channel. Also shown is Glu-296 whose ionization properties deserve a special comment. In addition, the residues are divided into three main groups corresponding to those which lie closer to the periplasmic side (toward the inside of the cell), those in the constriction zone (approximately in the center of the channel), and those closer to the extracellular side of the channel. In particular, residues with all their atoms having z-coordinate values between 2.6 nm and 4.0 nm are assigned to the constriction zone, and those with z < 2.6 nm and z > 4.0 nm to the periplasmic region and the extracellular region, respectively. To show the effect of the dielectric constant used to imitate the protein media, pK_a calculations have been performed both for ɛ_m = 4 and ɛ_m = 20. The last column of the table includes the commonly accepted values of 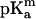in free solution for each group. It is seen that in agreement with a recent study (Varma and Jakobsson, 2004), calculations done with ɛ_m = 20 yield more realistic pK_a values than those obtained with ɛ_m = 4.

TABLE 1.

Comparison of pK_a values of selected residues at different protein dielectric constants

		ɛ = 20			ɛ = 4
Residue	Residue number	pKint	pKa	pKshift	pKint	pKa	pKshift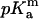
Closer to the periplasmic side
GLU	2	4,9	3,7	−0,7	7,5	7,0	2,6	4,4
LYS	10	10,0	12,5	2,1	8,9	10,2	−0,2	10,4
ASP	12	5,4	3,0	−1,0	12,0	11,2	7,2	4
LYS	46	10,0	13,8	3,4	8,4	9,6	−0,8	10,4
GLU	48	5,5	3,6	−0,8	10,0	9,1	4,7	4,4
LYS	89	9,7	12,5	2,1	7,8	8,9	−1,5	10,4
GLU	181	5,0	4,2	−0,2	7,0	6,0	1,6	4,4
LYS	219	10,0	14,5	4,1	8,5	12,3	1,9	10,4
ASP	221	4,6	3,0	−1,0	5,8	3,8	−0,2	4
LYS	305	10,1	12,6	2,2	9,3	10,6	0,2	10,4
TYR	310	11,6	18,8	9,2	19,3	20,0	10,4	9,6
Constriction zone
LYS	16	10,1	14,2	3,8	8,5	9,2	−1,2	10,4
ARG	42	11,8	16,2	4,2	9,1	9,2	−2,8	12
ARG	82	11,6	15,7	3,7	7,6	5,8	−6,2	12
ASP	113	5,0	3,2	−0,8	6,8	5,6	1,6	4
GLU	117	5,9	6,2	1,8	10,1	15,9	11,5	4,4
ARG	132	10,8	15,5	3,5	3,4	3,7	−8,3	12
TYR	40	11,2	14,3	4,7	15,6	15,1	5,5	9,6
TYR	102	10,7	13,3	3,7	13,7	15,9	6,3	9,6
TYR	106	10,6	16,4	6,8	14,2	19,0	9,4	9,6
Closer to the extracellular side
GLU	29	4,7	4,3	−0,1	6,1	6,2	1,8	4,4
LYS	80	10,3	13,1	2,7	9,3	11,4	1,0	10,4
ARG	167	10,6	14,4	2,4	3,9	4,0	−8,0	12
ARG	168	10,7	14,4	2,4	5,8	4,7	−7,3	12
LYS	243	9,9	13,1	2,7	7,7	9,7	−0,7	10,4
TYR	22	11,0	17,7	8,1	16,0	20,0	10,4	9,6
TYR	32	10,0	17,2	7,6	12,5	20,0	10,4	9,6
Other
GLU	296	5.5	8.9	4.5	11.2	19.2	14.8	4.4

Most of the residues with large pK_a shifts are tyrosines, with positive changes between six and nine units (both for ɛ_m = 20 and ɛ_m = 4), so that tyrosines appear to be stabilized in their protonated state. These tyrosines (only six are shown in the table) are mostly buried between the other residues of the trimer. The significant shift for the tyrosines is not rare since the predicted charge of the protein is huge at high pH (−100e at pH 14.0). This leads to high electrostatic interaction energies, unless dramatic rearrangements in the structure of the protein occur in such an extremely basic environment. The large shifts for tyrosines have been previously reported by Karshikoff et al. (1994), although in our model with ɛ_m = 20 the shifts are generally smaller.

The constriction contains the so-called “cluster of arginines,” which includes Arg-42, Arg-82, and Arg-132, all of them positively charged at neutral pH, and the acidic residues Asp-113 and Glu-117, negatively charged at neutral pH. As already mentioned, the position of these residues, with the arginines at the side close to the axis of the trimer and the aspartic and glutamic residues at the other side, creates a strong transverse field. We also include in the constriction zone three additional groups, which may have some influence on the channel selectivity: Lys-16, Tyr-106, and Tyr-102.

In the physiological pH range most of the residues in our model OmpF channel are in the ionization state corresponding to the so-called “null model,” which assigns the same pK_a to the charged groups in the protein as in free solution. The only exception is Glu-296. According to our calculations, Glu-296 in the protein has an effective pK_a of 8.9, whereas its pK_a in free solution is ∼4.4. This suggests that this residue should be protonated at pH 7. It should be noted that, according to our calculations, Arg-82 should be charged at neutral pH. This is in agreement with previously reported experimental results (Schirmer and Phale, 1999), and in contradiction with calculations by Karshikoff et al. (1994), who used ɛ_m = 4.

Recently Varma and Jakobsson (2004) have reported the protonation states of titratable residues lining the lumen of the wild-type OmpF channel at neutral bulk pH. Their extensive calculations performed under different conditions of protein dielectric constant, solute shielding, and protonation sites yield pK_a shifts that are in close agreement with our results. Particularly, for ɛ_m = 20 we find that at neutral pH the ionization state of the residues lining the pore is the same as in their prediction. The use of a rather unusual dielectric constant of 20 is also supported by an extensive comparison of measured pK_a values of ionizable groups in proteins with the computed values carried out by Antosiewicz et al. (1994).

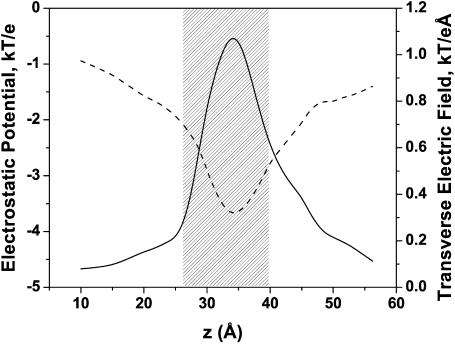
For this reason hereafter we use the results obtained at ɛ_m = 20. We first calculate fields in the pore lumen that are produced by all charges in a monomer. Fig. 9 shows the electrostatic potential (dashed line) sensed by an ion crossing an OmpF monomer at pH 7, following a path approximately along the geometric center of the pore lumen. It also gives the modulus of the transverse electric field (solid line) along the same path. Parameter z is the axial coordinate from the OmpF PDB file; z = 0 refers to the periplasmic side. The shaded region approximately represents the constriction zone. The pore lumen is not exactly perpendicular to the membrane surface and has a rather complex geometry, so that ion trajectories differ considerably from a straight line parallel to z axis.

FIGURE 9.

(Dashed line, left axis) The electrostatic potential felt by a cation crossing an OmpF monomer along the geometric center of the pore lumen. (Solid line, right axis) The modulus of the transverse electric field along the same coordinate in units of force acting on a cation. The shaded part shows the constriction zone of the pore.

It is seen that the electric potential is slightly asymmetric and exhibits a minimum in the constriction zone near z = 3.5 nm. The depth of the potential well at this point exceeds 3.5 kT. Qualitatively, this explains nearly perfect cationic selectivity of the channel measured for the lowest KCl concentrations used in this study (Fig. 4, inset). However, quantitative analysis of the selectivity data based on the electric potential profile illustrated in Fig. 9 is difficult because of the strong transverse field. This field introduces a complex distribution of potential in the channel pore. Indeed, recent MD and BD simulations have shown that cation and anion pathways through the pore are somewhat separated (Im and Roux, 2002a; Schirmer and Phale, 1999). It was also shown (Robertson and Tieleman, 2002) that the transversal field is able to orient dipolar molecules; experiments with ampicillin translocation through OmpF confirmed this prediction (Nestorovich et al., 2002).

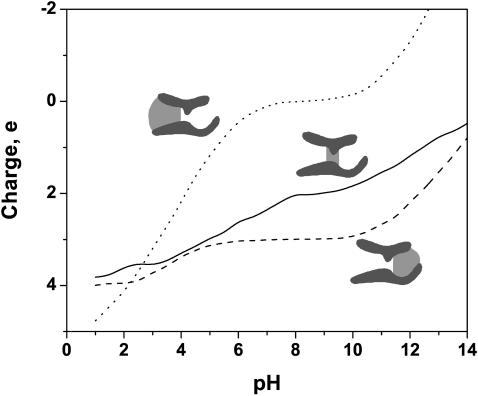
The charge of the ionizable residues located near the lumen of the channel as a function of pH is shown in Fig. 10. Separate plots are presented for the fixed charge of the residues corresponding to the periplasmic region, the con-striction zone, and the extracellular region of the channel. It is seen that, except for the charge in the periplasmic region of the pore at pH > 10, fixed charges lining the pore are positive, which would imply anionic selectivity. However, this conjecture contradicts experimental observations: the results plotted in Fig. 6 show that the channel has cationic selectivity everywhere except for acidic solutions of pH < 3.5.

FIGURE 10.

Charge of the residues that are close to the lumen of OmpF. Residues are divided in three groups corresponding to the constriction (solid line); the part of the channel closer to the periplasmic side (dotted line); and the part closer to the extracellular side (dashed line).

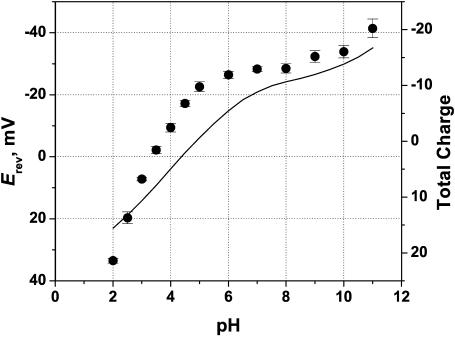
It turns out that the correlation between the total charge of the monomer and the reversal potential is much better. Fig. 11 shows that as pH is decreased, the total charge goes from negative to positive, implying the selectivity transition from cationic to anionic. The solid line represents the sum of all charges in a monomer (i.e., the total charge of the 102 ionizable groups). The discrepancy in the exact pH of the sign change between the calculated total charge and the measured reversal potential can be explained by different influence of different titratable residues on channel selectivity. Residues which are farther from the permeating ion paths influence channel transport properties to a smaller degree. Therefore, such a discrepancy is expected even in the case of purely electrostatic interactions.

FIGURE 11.

Correlation between the total charge of the monomer (solid line, right axis) and the measured reversal potential (points, left axis).

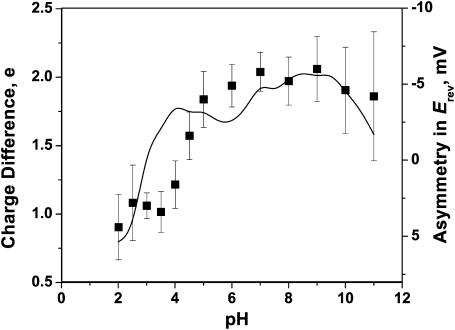
It is interesting to note that not only the pH-dependent total charge correlates with the pH-dependent reversal potential. It is also true for the pH-dependent asymmetry in charge. Indeed, if the asymmetry in E_rev is mainly of electrostatic origin, we expect it to correlate with the difference in the fixed charge in periplasmic and extracellular vestibules of the OmpF channel. Fig. 12 compares the asymmetry in the reversal potential (Fig. 6, asterisks) with the asymmetry in charge defined as net fixed charge of all residues lying on the extracellular side minus net fixed charge of all residues on the periplasmic side.

FIGURE 12.

Correlation between asymmetries in the total charge (solid line, left axis) and the reversal potential (points, right axis).

Because of the wide spread in residues' pK_a (Table 1), changing pH changes not only the total charge but also its asymmetry. Importantly, in this case the direction of the change is not prescribed by the general laws as for the total charge (Fig. 11) where higher acidity always corresponds to a higher total positive charge. Indeed, the rate of change of the total charge with pH can be different (it may sometimes involve cooperativity—Rostovtseva et al., 2000) but its direction is set by thermodynamics. For the charge asymmetry this restriction does not exist. Depending on the residue distribution in the channel, the charge asymmetry can either increase or decrease with solution acidity. Therefore, the correlation illustrated by Fig. 12 can be used to identify channel orientation in the reconstitution experiment.

Macroscopic electrodiffusion models

Reversal potential does not measure ion selectivity directly. The electric potential needed to zero the ion current in the presence of a concentration gradient across the channel is usually regarded as the channel “measurable selectivity.” From this, researchers proceed to different characteristics such as transport numbers, permeability ratios, etc. (see Appendix). None of these quantities is model-free, and, therefore, none of them completely describes the ability to which the channel can discriminate between ion species.

It is well known that surface potentials must be accounted for when addressing selectivity and ion fluxes through biological membranes (Neumcke, 1970; McLaughlin, et al., 1970; Markin and Chizmadzhev, 1974), but very often surface potentials are associated just with the electric double layer on a charged membrane and only seldom with the potential drop arising from the fixed charges of the residues lining the pore mouth. This potential drop depends on the screening by the membrane-bathing solution and, therefore, on its salt concentration. For a pore that is wide enough to discard non-electrostatic interactions between the mobile ions and the pore walls, the reversal potential will be determined not only by the salt concentration gradient but also by the absolute salt concentration on each side of the channel.

An intuitive reasoning based on macroscopic electrodiffusion considerations and ion screening may lead one to predict that for a homogeneously charged channel, the main contribution to the reversal potential comes from the potential drop on the side where the fixed charge screening is weaker. If the effective fixed charge distribution along the electrodiffusion region is symmetric, the largest potential drop occurs on the side of lower concentration, but the system is completely symmetric in respect to concentration gradient inversion. However, if the effective fixed charge distribution is not the same on both sides, one should expect asymmetry effects when the concentration gradient is inversed.

Here we propose a crude description of the small-ion selectivity of the OmpF channel in terms of average properties of three regions of the pore: 1), a vestibule facing the smooth end of the channel (also known as the periplasmic side) with negative net charge; 2), a smaller vestibule facing the rough end of the channel (also known as the extracellular side), also with negative net charge; and 3), a narrow constriction with asymmetric charge distribution and strong transversal field.

We use an approach, which is a modification of Teorell-Meyer-Sievers theory (see Appendix). The zero current potential in Teorell-Meyer-Sievers theory consists of three contributions (which are not independent from each other): Two Donnan potentials at the membrane solution interfaces plus diffusion potential across the membrane itself. Using the features of OmpF channel geometry discussed above, we assume equilibrium ion distributions between the membrane-bathing solution and the channel vestibules and calculate Donnan potentials there. Then, we calculate the diffusion potential generated in the constriction region (region 3) by using Goldman's constant field assumption. Because of the complex structure of this region, we characterize it by the ratio of the effective diffusion coefficients of cations and anions, D₊/D₋.

The resulting expression for the reversal potential (see Appendix for details) is

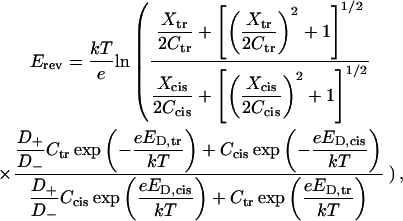(1)

where E_rev is the electric potential difference under open circuit conditions between the cis and trans bulk solutions with concentrations C_cis and C_tr, respectively, corrected with activity coefficients. Constants k, T, and e have their usual meaning. Donnan potentials E_D,cis and E_D,trans are the functions of X_cis and X_tr, effective fixed-charge concentrations in the cis and trans vestibules of the channel.

The reversal potential is thus computed by using three adjustable parameters: the two effective fixed-charge concentrations X_cis and X_tr and the ratio between diffusion coefficients of cations and anions, D₊/D₋ in the constriction zone. Note that in the explanation of the model given above we do not mention periplasmic side or extracellular side but cis side and trans side, because it is not known a priori what is the direction of insertion of the channel in the membrane. The best fit of the E_rev data from Figs. 4 and 5 is shown in Fig. 13, A and B. Both sets of curves were obtained with D₊/D₋ = 1.4, X_cis = −0.11 M, and X_tr = −0.17 M (negative fixed-charge concentration in both vestibules). It is seen that such a simple model for the reversal potential seems to reflect the main trend of its dependence on the concentration gradient as well as on the absolute bulk salt concentration. For comparison, Fig. 13 A gives predictions of Goldman's approximation (dashed lines) that does not take into account the complex structure of the channel. Corrections by activity coefficients introduce certain dependence on salt concentration, but deviations from straight lines are hardly seen. Earlier, the selectivity of a wide uniform channel was addressed by Zambrowicz and Colombini (1993). Their model is able to explain the reduction in the channel selectivity with the increase in salt concentration. However, because it is devised to deal with regular cylindrical pores and homogeneous charge distributions only, it cannot be used to approach the asymmetry in the reversal potential.

FIGURE 13.

Solid lines represent the best fit of the model (Eq. 1) to the measured reversal potential (points) (see Fig. 4 for panel A and Fig. 5 for panel B). Dashed lines in panel A show predictions of the GHK model (Eq. A3) with corrections for the changing salt activity fitted to the 3 M points.

Thus, the asymmetry in the reversal potential measurements shown in Fig. 5 permits a simple qualitative explanation in terms of the structural inhomogeneity of OmpF. Indeed, the “real” concentration gradient over the constriction zone of the channel does not simply invert its sign when bulk solutions are interchanged; it also changes its absolute value. Together with the change in the Donnan potentials on both sides it leads to the observed asymmetry.

Our simple model describes this asymmetry, but only qualitatively. The best fit of experimental data is obtained for both series by using the same values of X_cis; X_tr, and the ratio of ionic diffusivities. Therefore, both sets of measurements (Figs. 4 and 5) can be described using the same effective fixed charge densities. Together with the correlation of the pH dependences for the asymmetries in the reversal potential and the charge distribution (Fig. 12), this may suggest that in our experiments the OmpF channel inserts with its periplasmic end on the trans side of the membrane.

One of the shortcomings of the model is that values of D₊/D₋ could be different for the opposite gradients as an expected consequence of the limitations of the model. Indeed, the central part of the channel, the constriction, exhibits an asymmetric charge distribution; therefore, guided by electrostatic arguments presented above, one could expect a dependence of selectivity on the central part of the channel on the direction of the concentration gradient.

Clearly, any rigorous description of channel transport properties requires detailed and sophisticated accounting for the fine structural features of the channel-forming protein. The exact residue positions from channel atomic structure and their ionization equilibria are now routinely taken as input information in both continuum treatments and MD and BD simulations (Cárdenas et al., 2000; Corry et al., 2000; Kuyucak et al., 2001; Im and Roux, 2002a,b; Gillespie and Eisenberg, 2002; Eisenberg, 2003; Misakian and Kasianowicz, 2003). Nevertheless, our simple electrodiffusion model seems to be a minimal one that still captures the main features of the large-channel reversal potential and, therefore, sheds light on the physics of small-ion selectivity.

CONCLUSIONS

We have studied the small-ion selectivity of a large membrane channel, OmpF. Neutral and charged lipids were used for channel reconstitution. The reversal potential of ionic current was measured as a function of pH, salt gradient, and absolute salt concentrations. Water solutions of KCl were used because of the close mobilities of potassium and chloride ions in the bulk. Our main findings are:

1. The reversal potential and, therefore, channel selectivity are strong functions of absolute salt concentrations. At neutral pH the channel properties change from those of a nearly ideal cation-selective channel at small salt concentration (for example, 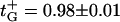at salt gradient of 0.06 M KCl on the cis side versus 0.02 M KCl on the trans side) to those of a poorly cation-selective channel at high salt concentrations.

2. Measured channel selectivity is asymmetric. The reversal potential depends on the direction of the applied salt gradient and, for a 10-fold gradient can be different by ∼5 mV for the opposite directions.

3. Membrane lipid charge has a moderate, but statistically significant effect on channel selectivity. At neutral pH and salt gradients >10, a negatively charged lipid is able to increase the absolute value of the reversal potential by ∼5 mV.

4. Channel selectivity and its asymmetry are functions of the membrane-bathing solution pH. In acidic solutions the channel becomes anion-selective; at a pH value corresponding to the transition between anionic and cationic selectivity the measured selectivity can be either cationic or anionic, depending on the direction of the salt gradient.

We attribute our findings to electrostatic interactions between the charges of ionizable residues and permeating ions. Comparing the pH-dependent selectivity of the channel with the calculated pH-dependent ionization state of the channel residues, we find that selectivity correlates with the total charge of the protein rather than with the charge of the residues only in the vicinity of the pore.

APPENDIX

Macroscopic electrodiffusion models of channel selectivity

Description of membrane ion selectivity usually involves the Nernst-Planck flux equations combined with the Poisson equation, a system of coupled nonlinear differential equations that cannot be solved in closed form even in the case of a homogeneous membrane. Therefore, to obtain analytical solutions for the zero current potential, two main approximations are used (Markin and Chizmadzhev, 1974; Sten-Knudsen, 1978).

First approximation is based on the assumption of net charge neutrality all over the diffusion region, which leads to the classical Planck's expression (Markin and Chizmadzhev, 1974; Sten-Knudsen, 1978; Lakshminarayanaiah, 1984). Straightforward integration of the Nernst-Planck equations with the condition of equal cation and anion concentration for a 1:1 electrolyte and an uncharged membrane gives the following zero-current potential (potential is defined as positive if it is greater at the cis side),

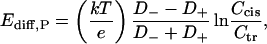(A1)

where k, T, and e have their usual meanings, C_cis and C_tr are salt concentrations corrected with activity coefficients, and D₋ and D₊ are coordinate-independent diffusion coefficients for anions and cations, correspondingly.

Second approximation is based on Goldman's assumption of constant electric field along the diffusion zone (Goldman, 1943), which leads to the well-known Goldman-Hodgkin-Katz equation (Hodgkin and Katz, 1949). In the simplest case of uncharged pores and membranes the integration of Nernst-Planck equation gives

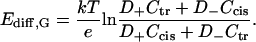(A2)

For a charged membrane or pore, it takes a slightly different form when written in terms of boundary ion concentrations instead of bulk salt concentration,

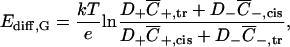(A3)

where overbars denote concentrations at the membrane surfaces to distinguish them from the bulk values.

Ion selectivity is often described in terms of the cation or anion transport numbers, which, in the case of neutral membranes or pores, are represented by t⁺ = D₊/(D₋ + D₊) and t⁻ = 1−t⁺, correspondingly. Planck's approximation (Eq. A1) gives

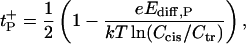(A4)

whereas Goldman's approximation (Eq. A2) leads to

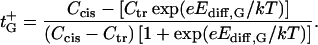(A5)

Thus, at arbitrary concentration gradients the two approximations give different values for the transport numbers even for a homogeneous neutral membrane. A recent discussion concerning applicability of Goldman's approximation to complex molecular pores can be found in Im and Roux (2002a).

In the limit of small gradients, C_cis ≈ C_tr, and, therefore, small diffusion potentials, E_diff ≪ e/kT, both approximations give the same result:

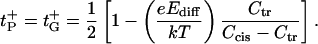(A6)

Both approximations also give identical answers, the Nernst equation, E_diff = ±(kT/e)ln(C_cis/C_tr), for an ideally selective channel with the plus sign corresponding to the anion-selective channel (D₊ = 0).

In an attempt to account for the charge distribution and nonregular geometry of OmpF channel, in this article we use a more elaborate electrodiffusion model (Mafé et al., 1986) by dividing the channel into three domains (see main text). We assume that ionic fluxes are small enough to ensure quasiequilibrium conditions at both channel solution interfaces (similarly to the description of charged surfactant transport through bilayer membranes—Neumcke, 1970; Markin and Chizmadzhev, 1974) and within its relatively large vestibules. Then, to find Donnan potential at the trans interface, E_D,tr, we use the equations (equilibrium and electroneutrality)

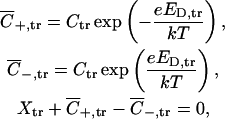(A7)

where X_tr is the effective fixed charge concentration in the trans vestibule of the channel, related to the actual density of charged ionizable groups. Solving these equations we have

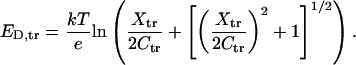(A8)

The corresponding expression for the Donnan potential on the cis side differs only by subscript substitution (cis for trans) and a minus sign at the first term under the logarithm sign.

We calculate the reversal potential as a sum of the diffusion potential of the central constriction (Eq. A3) and the two Donnan potentials,

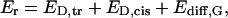(A9)

arriving to Eq. 1 of the main text. This simple approach permits us to describe several important features found in reversal potential experiments including salt-concentration dependence and asymmetry.

The constant field approximation for calculating the diffusion potential in the constriction seems to be a better choice than Planck's approximation. Two reasons can be given. First, the constant field approximation gives better results than the other when the electrodiffusion region is shorter or comparable to Debye length (Syganow and von Kitzing, 1999; Pellicer et al., 1986a; MacGillivray and Hare, 1969). Second, the requirement of constant electric field at the constriction seems not so strict as that of electroneutrality: independence of cation and anion currents (with separate pathways) found in MD and BD simulations (Im and Roux, 2002a) support the constant field assumption, whereas charge neutrality looks a bit unrealistic as a hypothesis for the narrow constriction.

It is interesting to note that both approximations make use of additional assumptions to replace Poisson's equation and to decouple the Nernst-Planck equations. Because the assumptions are different, the outcomes are different too. Although Goldman's approximation leads to a linear profile of the electric potential, the electroneutrality condition results in a nonlinear profile (Sten-Knudsen, 1978). Furthermore, it can be proved that Planck's approximation invariably overestimates the magnitude of the diffusion potential (that is, underestimates transport numbers calculated from the measured reversal potential), whereas the constant field assumption can be “exact” under particular experimental situations (Pellicer et al., 1986b).