NMR Studies of Lipid Lateral Diffusion in the DMPC/Gramicidin D/Water System: Peptide Aggregation and Obstruction Effects

Abstract

The PFG-NMR method has been used in macroscopically oriented bilayers to investigate the effect of the peptide gramicidin D on the lateral diffusion of dimyristoylphosphatidylcholine. By varying both the temperature (21–35°C) and the gramicidin content (0–5 mol %) we have introduced solid obstacles into the lipid liquid crystalline bilayer. It was shown that the obstruction effect exerted by the peptide can be described with several different theoretical models, each based on different premises, and that the fit of the models to experimental data gave reasonable results. We found that each gramicidin molecule was surrounded by approximately one layer of bound lipids and that the obstruction from gel phase patches can be described as small solid obstacles. No evidence of linear aggregates of gramicidin, such as those reported by atomic force microscopy in the gel phase, was found.

INTRODUCTION

The role of lateral organization in membranes composed of synthetic and/or natural lipids has recently received wide interest. Domains formed in biological membranes are thought to be involved in membrane-specific processes, such as signal transduction and membrane trafficking (Simons and van Meer, 1988). In biological systems caveolae (Andersson, 1998) and domains, often referred to as rafts (Simons and Ikonen, 1997) or detergent-resistant membranes (Brown and London, 1998), involve lipids like sphingomyelin, cholesterol, glycosphingolipids, and other saturated phospholipids. In a strategy toward getting an understanding at the molecular level of these biologically important but complex systems interest has been focused on simpler model systems. One important aspect in lateral domain formation is the influence these may have on the lateral mobility of the different membrane constituents. Obstruction and percolation are believed to have a major influence on the reaction yield and kinetics of membrane processes (Saxton, 1999; Vaz and Almeida, 1993), and much effort has been given to describe the influence of domains on the lipid lateral diffusion. For a review of this area, see Saxton (1999) and references cited therein.

Restricted diffusion due to obstacles of gel phase domains has been observed across the gel/liquid crystalline two-phase region with fluorescence recovery after photobleaching (FRAP) (Almeida et al., 1992a), ²H two-dimensional exchange, and fringe-field nuclear magnetic resonance (NMR) spectroscopy (Dolainsky et al., 1997). Domains have also been directly visualized by atomic force microscopy in systems with phosphatidylcholine, sphingomyelin, and cholesterol (Rinia et al., 2001) as well as in model membranes containing small peptides (Rinia et al., 2002, 2000).

In systems of gramicidin A (gA) mixed with dipalmitoylphosphatidylcholine (DPPC) or dimyristoylphosphatidylcholine (DMPC) striated domains have been observed below the gel-to-liquid crystalline phase transition temperature (Ivanova et al., 2003; Mou et al., 1996). Similar structures have also been observed for synthetic peptides in phosphatidylcholine membranes (Rinia et al., 2002, 2000). In the model proposed from these investigations the highly ordered patterns observed are believed to consist of linear aggregates of the peptide surrounded by layers of lipids in a fluid state. These structures would severely restrict the lipid translational motion, and the lipid lateral diffusion coefficient would thus be sensitive to the presence of such aggregates in the lipid bilayer. We have used the pulsed field gradient NMR method (Lindblom and Orädd, 1994) to investigate the influence of gramicidin D (gD) on the lipid lateral diffusion of DMPC in fully hydrated bilayers with 1–5 mol % gD.

MATERIALS AND METHODS

Materials

DMPC and gD were obtained from Sigma (St. Louis, MO). gD is the natural mixture of gramicidin A, B, and C, consisting of ∼85% gA (Killian, 1992). ²H₂O was purchased from Larodan (Malmö, Sweden) and Milli-Q filtered ¹H₂O (Millipore, Billerica, MA) was utilized in the samples for differential scanning calorimetry (DSC).

DSC

Measurements were performed on a MicroCal VP-DCS MicroCalorimeter (Taby, Sweden). Samples for the DSC measurements were prepared by mixing appropriate amounts of DMPC and gD in methanol, followed by evaporation of the solvent. The dry mixtures were hydrated to obtain 2 mg dry material/mL H₂O and thoroughly mixed in a vortex stirrer. The samples were treated with at least five freeze-thaw cycles to obtain a homogenous hydration of the lipid bilayers. DSC thermograms were obtained in heating scans from 0 to 45°C with a heating rate of 25°C/h. Four temperature scans were recorded, where the first scan was discarded to obtain a common thermal history of all samples. The appearance of the following scans were always identical.

NMR

³¹P-NMR spectra were recorded at 162.13 MHz on a Varian/Chemagnetics CMX Infinity spectrometer (Fort Collins, CO) using the Hahn echo sequence with WALTZ-decoupling of the protons (Shaka et al., 1983). The 1024 scans were collected with a recycle time of 1 s and the spectra were Fourier-transformed after a 200-Hz line broadening.

Macroscopically oriented bilayers were prepared as follows. Lipids dissolved in a 1:4 mixture of methanol:1-propanol was deposited onto thoroughly cleaned, but otherwise untreated, glass plates (14 × 2.5 mm², Marienfeldt, Darmstadt, Germany) to a sample mass of ∼4 μg/mm². The solvent was evaporated and the plates were placed into high vacuum for at least 4 h to remove traces of solvent. The choice of solvent mixture gives a good adhesion to the glass surface and results in thin films covering the glass plates. Thirty-five plates were then stacked on top of each other and placed into a glass tube with a 2.5 × 2.5 mm² square cross section.

The tube was placed in a humid atmosphere at 35°C for a minimum of seven days. During this time the lipids became hydrated, and oriented bilayers were formed. Finally, an extra supply of water was added to the test tube, which was then sealed at both ends with wax. The sample was then left another day or two for a final equilibration. This procedure allowed a large part of the sample to be oriented with the bilayers parallel to the glass plates, as determined by ³¹P NMR.

The oriented sample was placed with its long axis horizontally into a Varian/Chemagnetics PFG-diffusion ¹H/BB probe, where a goniometer stage permitted the sample to be rotated along its long axis (Orädd and Lindblom, 2004). A heated air stream passing over the sample controlled the temperature to within ±0.2°C. The sample was oriented with the bilayer normal at an angle of 54.7° by optimizing the proton signal with respect to the line width. At this so-called “magic angle” the dipole broadening of the protons is zero, and the signal from the oriented bilayers then becomes apparently isotropic (Lindblom and Orädd, 1994; Orädd and Lindblom, 2004).

The PFG-NMR diffusion experiments were performed at 400.51 MHz on a Varian/Chemagnetics CMX Infinity spectrometer with the stimulated spin-echo technique (Tanner, 1970). The pulse sequence timing is (90-τ-90-T-90-τ-acquire) with the gradient pulses, of length δ (3 ms) and strength g (0–9 T/m), following immediately after the first and the third 90° RF pulses. In a diffusion experiment typically 20 spectra were recorded with 16 scans/spectrum and a recycle time of 2 s, in which g was varied, keeping all the other parameters constant. The diffusion coefficient, D, was then determined from a nonlinear fit of the signal attenuation of the lipid peaks to the equation of Stejskal and Tanner (1965),

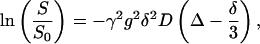(1)

where S and S₀ are the signal amplitudes with and without gradient pulses, γ is the gyromagnetic ratio, and Δ is the separation between the two gradient pulses. The experiment was repeated at least three times, in which Δ was varied between 10 and 500 ms. No variation of the obtained diffusion coefficient on Δ was observed. Finally, to obtain the lateral diffusion coefficient, D_L, the observed diffusion coefficients were multiplied by a factor of 1.5, since diffusion along the z axis is measured while the translational motion actually occurs along the bilayers oriented at the magic angle. Thus, the square of the effective gradient will be and the diffusion coefficient obtained is multiplied by a factor of 1.5 to obtain the lateral diffusion coefficient, D_L = 1.5 × D (Lindblom and Orädd, 1994; Wästerby et al., 2002).

RESULTS

DSC

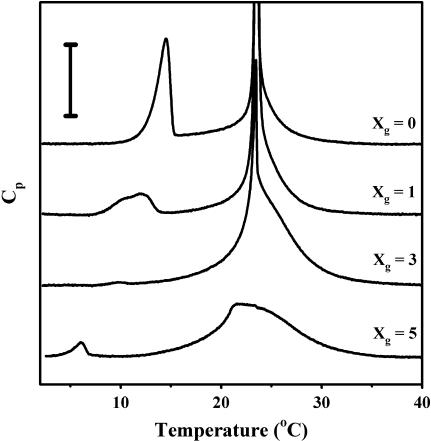
Fig. 1 shows the DSC heating thermograms of the samples with molar percentage of gD with respect to peptide and lipid (X_g) equal to 0, 1, 3, and 5. The two endothermic peaks observed at 15 and 24°C for X_g = 0 correspond to the pre- and main transitions, respectively. The temperatures and transition enthalpies are in good agreement with data from the LIPIDAT database (http://www.lipidat.chemistry.ohio-state.edu) for this sample. As X_g increases the pretransition peak broadens and disappears for X_g = 3 and then reappears again at X_g = 5. The peak gradually shifts to lower temperatures as the gD content is increased. The main transition peak also broadens gradually but the center of the transition stays at approximately the same temperature for all X_g values. These results also agree well with previously obtained data on the similar system of DMPC and gA (Kobayashi and Fukada, 1998). The reappearance of the pretransition peak at X_g = 5 is not observed in the work by Kobayashi and Fukada (1998). One possible explanation for this discrepancy could be that there is a phase separation into gD-rich and gD-poor phases. However, this possibility can be excluded, since that would bring the pretransition peak of the gD-poor phase back to the same temperature as for a sample with X_g = 0. A similar transition has been observed for DMPC bilayers at low water content (Janiak et al., 1979) that was attributed to rearrangements in the hydrocarbon region and/or the interstitial water associated to the polar headgroup of the lipid. At present we cannot say whether the observed low-temperature transition observed by us at X_g = 5 is related to their observation.

FIGURE 1.

Stacked DSC traces obtained on heating scans in samples of DMPC with various fractions of gD. Vertical bar = 0.5 kJ/mol. The traces for X_g = 0, 1, and 3 have been clipped to show the low intensity features.

NMR lineshapes

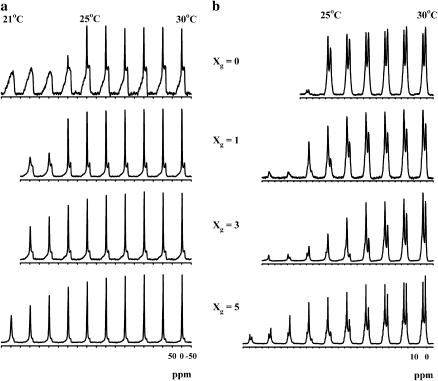
Fig. 2 shows ³¹P- and ¹H-NMR spectra of the samples with X_g = 0, 1, 3, and 5 as a function of temperature. In the ³¹P spectra (a) the phase transition is clearly visible from the broadening of the narrow signal from the oriented part of the samples, whereas the effect on the powder pattern lineshape originating from the unoriented part of the samples is much smaller. For X_g = 0 the signal from the oriented part disappears abruptly between 24 and 25°C, corresponding to the narrow phase transition. The difference of approximately one degree, compared to the DSC results, can be explained by the different water content and the geometrical shape of the lipid bilayers. For the samples containing gD the onset of the broadening of the signal from the oriented part of the sample also coincides with the temperature for the onset of the phase transition according to DSC. In contrast, the unoriented part of these samples looks almost unchanged for all temperatures and no signs of line broadening can be seen in these spectra as the phase transition proceeds. After the completion of the phase transition, as judged by DSC, the powder patterns also exhibit significant line broadening.

FIGURE 2.

³¹P (a) and ¹H (b) NMR spectra of partially oriented samples of DMPC:gD as a function of temperature. All samples are oriented with the glass plate normal at the magic angle with respect to the main magnetic field. The temperature for the rightmost spectrum in each panel is 30°C and it is decreased by 1°C for each spectrum to the left. The observed ³¹P spectra are superpositions of the powder pattern lineshape and the sharp signal from the macroscopically oriented part of the sample. Spectra are deliberately taken from samples that contain a high degree of unoriented sample to be able to observe changes in the signal from both the oriented and unoriented parts. The same features were observed also in samples with a high degree of orientation.

The proton spectra (b) exhibit two peaks originating from the choline methyl groups (3.1 ppm) and the acyl chain methylene groups (1.1 ppm). The spectra are similar in appearance to those obtained from oriented DMPC/gA bilayers by Cornell and co-workers, apart from the missing ¹H₂O peak (Cornell et al., 1988). The reduction of the peak amplitude for the choline headgroup closely follows the behavior of the narrow ³¹P-NMR peak. The peak originating from the acyl chains is, however, more affected by the phase transition and the peak amplitude is significantly reduced even at temperatures slightly above the onset of the phase transition. This indicates that the order and/or dynamics of the lipids in the chain and the headgroup regions are differently affected by the temperature and presence of gD.

Lateral diffusion

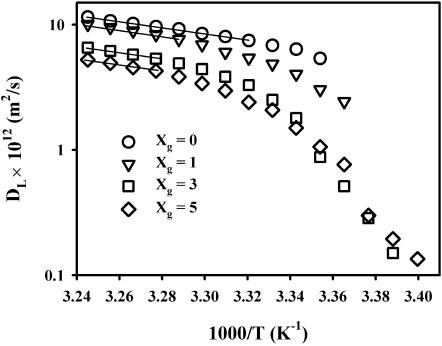
Fig. 3 shows Arrhenius plots of the temperature dependence of D_L for various values of X_g and for decreasing temperatures from 35°C. The low temperature limit for each sample is governed by the disappearance of the proton signal. The obtained D_L values are in good agreement with results obtained by FRAP on lipid fluorescence probes in bilayers of DMPC (Almeida et al., 1992b) and for DMPC bilayers containing gramicidin C (Tank et al., 1982). There is also reasonable agreement with ²H and ³¹P two-dimensional exchange experiments on DMPC bilayers, especially at lower temperatures (Dolainsky et al., 1997; Fenske and Jarrell, 1991). The high temperature behavior is of the Arrhenius type with an apparent activation energy of ∼50 kJ/mol, independent of gD additions up to 5 mol %, indicated by the straight lines in the figure. This is larger than values reported earlier for DMPC/water (Almeida et al., 1992b; Dolainsky et al., 1997; Filippov et al., 2004), and the reason for this seems to be due to a slight curvature of the line at lower temperatures. The values in this work are calculated for temperatures <35°C, whereas the other reported values were calculated for a larger temperature span. A possible reason can be the presence of small amounts of impurities and lipid breakdown products that can broaden the transition. Careful inspection of the trace for X_g = 0 in Fig. 1 reveals a small shoulder that remains up to ∼30°C on the high-temperature side of the main transition peak.

FIGURE 3.

Arrhenius plot of the lateral diffusion of DMPC in samples with various gD content. The straight lines indicate the region, where the diffusion process is well described by an apparent activation energy of 50 kJ/mol. The gD contents are 0 (circle), 1 (down triangle), 3 (square), and 5 mol % (diamond).

The lateral diffusion of DMPC shows a distinct break at the temperature of the onset of the phase transition, as indicated both by DSC (Fig. 1) and the decreasing NMR line intensities (Fig. 2). The translational motion of the lipids is thus clearly influenced by the presence of the second phase.

DISCUSSION

Models for obstructed lateral diffusion

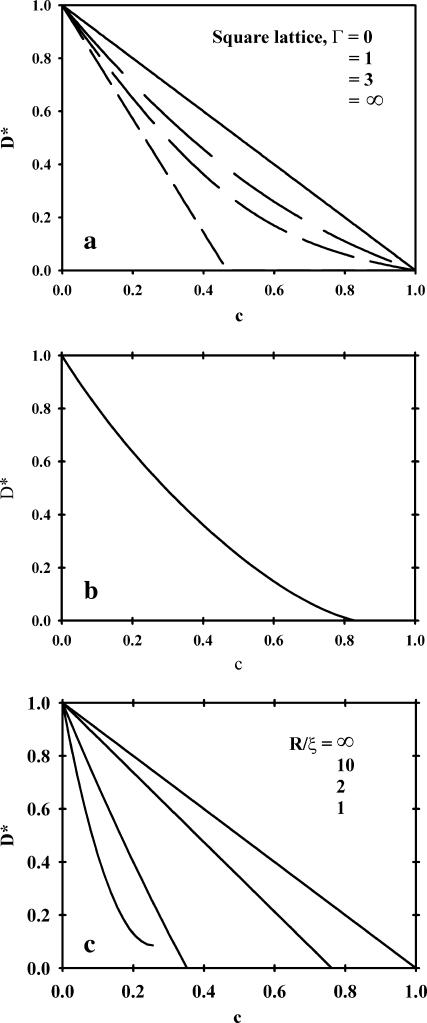
The effect of obstacles on the lipid diffusion is most conveniently studied by forming D^*, the diffusion coefficient normalized to one for zero obstacle concentration. D^* will contain all the effects of obstacles on the diffusion and will in general be a function of the area fraction (c) and shape of the obstacles as well as the ratio of jump rates for the tracer molecules to that of the obstacles (Γ). For a detailed discussion on these topics the review of Saxton (1999) is a good starting point. Here we will restrict ourselves to a limited number of models for which D^* is illustrated in Fig. 4.

FIGURE 4.

Illustration of the dependence on the normalized diffusion of the area fraction of obstacles for the theoretical models described in the text. (a) Eq. 2. The lines correspond to Γ = 0, 1, 3, and ∞, respectively (from top to bottom); (b) Eq. 3; and (c) Eq. 4. The short dashed lines corresponds to R/ξ = ∞, 10, 2, and 1, respectively (from top to bottom).

Tracer diffusion with mobile point obstacles

An expression for a number of different lattices has been derived for D^*(c,Γ) for a system of tracer diffusion with mobile point obstacles (Tahir-Kheli, 1983; Van Beijeren and Kutner, 1985), in which Γ can be varied from zero (obstacles moves much faster than tracers) to infinity (immobile obstacles). The value of D^* in this model is given by

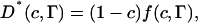(2)

where

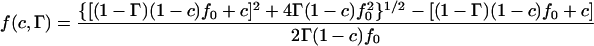and

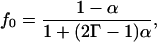and where α is a constant that depends on the lattice. It is equal to 1–2/π for a square lattice, 0.2820 for a triangular lattice, and 0.500 for a honeycomb lattice (Le Claire, 1970). Fig. 4 a gives D^* as a function of c for the square lattice with different values of Γ. Similar curves are obtained for the other two lattices. Note that the shape of the curve D^* vs. c does not change appreciably when Γ is in the range of 1–3.

Monte Carlo simulations of mobile obstacles of variable size

In a Monte Carlo study on a triangular lattice it was found that D^* was largely independent of the obstacle radius for circular objects and D^* was given in a polynomial form as (Saxton, 1987)

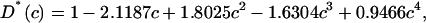(3)

where c is the area fraction of obstacles. This relation holds approximately for hexagonal obstacles of radius 1–16 lattice units. This study was made for equally mobile tracers and obstacles (Γ = 1) and a comparison with Eq. 2 shows that D^* is generally slightly below that for point obstacles (Fig. 4 b). The assumption of Γ = 1 is a simplification, since larger objects move slower. The dependence of D_L on the radius of the obstacles is, however, rather weak (Saffman and Delbrück, 1975), so the ratio between the lipid and obstacle diffusion would not exceed two, even for a 10-fold increase in the obstacle radius, if typical values of R = 6.6 Å and r = 4.5 Å are used for the sizes of gramicidin and lipid (Killian, 1992; Lewis and Engelman, 1983). As seen in Fig. 4 a, the qualitative behavior of D^* is not expected to be strongly dependent on the value of Γ, as long as Γ is in the range of 1–3.

The free volume model with boundary lipids

Almeida and co-workers have used the free-volume model (Cohen and Turnbull, 1959) and its two-dimensional analog (Clegg and Vaz, 1985; Vaz et al., 1985), and they extended it to include a boundary region around the obstacles (Almeida et al., 1992b). In this region the lateral diffusion of the lipids is assumed to decrease due to an increased ordering of the lipids close to the obstacles. The numerical result, valid for 1.17 < R/ξ < 20, for obstacles with a circular cross section is (Almeida et al., 1992b)

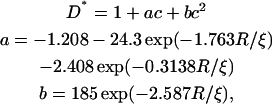(4)

where R is the obstacle radius and ξ is the coherence length of the decay function for the free area. This model is comparable to the two first models without bound lipids if ξ is set to zero. For nonzero values of ξ it gives a similar effect as for bound lipids. The mobility of the obstacles does not explicitly enter this model, but the limiting behavior for ξ = 0, corresponding to hard sphere interactions, gives D^* = 1−c, which resembles the curves of Eqs. 2 and 3 for mobile obstacles. Eq. 4 is illustrated in Fig. 4 c for some values of the dimensionless parameter R/ξ.

Percolation

When the area fraction of the obstacles increases the obstacles must increase in size and/or number. At a certain area fraction of obstacles the surrounding fluid phase will be disconnected and the lateral diffusion can no longer occur over arbitrarily large distances. This happens at the so-called percolation threshold (p_c) and it is accompanied by the absence of long-range diffusion. Although percolation cannot strictly occur in a system with mobile obstacles, the long-range diffusion will also be severely restricted in such systems, as long as the disconnecting structures do not change appreciably on the timescale of the measurement. The percolation threshold is dependent on the obstacle geometry, since elongated objects are more effective in disconnecting the fluid phase. For elliptical objects the interpolation formula 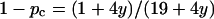gives good agreement with computer simulations (Xia and Thorpe, 1988). Note that p_c is defined as the area fraction of obstacles in this work, whereas it is the area fraction of the conducting (fluid) phase in the work of Xia and Thorpe (1988). The value y is a function of the aspect ratio, ɛ, of the ellipses, y = ɛ + 1/ɛ. The value p_c drops rapidly from 0.67, which is the value for circular objects, to 0.3 for an aspect ratio of 10—i.e., the less compact the shape of the obstacle is, the more effective in obstructing it will be.

Comparison of the models with experimental results

In studies of protein and lipid diffusion in the bacteriorhodopsin/DMPC (Peters and Cherry, 1982) and gramicidin C/DMPC (Tank et al., 1982) the reduction in D^* is found to be larger than expected from Eqs. 2 and 3 (Saxton, 1987). One possible explanation to this is that the effective area of the obstacles is greater than expected due to lipids bound to the obstructing species. For a lipid to be bound it is necessary that the motion of the lipid is restricted by the obstacle for times much longer than the characteristic time between the random lipid movements (jumps). It is, however, not necessary that the lipid stays in contact with the obstacle for the whole diffusion time. The PFG-NMR experiment measures the average diffusion for the whole ensemble of lipids during the diffusion time and, assuming that the same fraction of lipids are bound at all times, exchange of lipids between bound and free sites will not affect the result, as long as this exchange is fast compared to the diffusion time. If we denote the number of bound lipids per gD by n_l, the effective area of obstacles can be written as

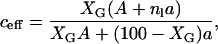(5)

where A and a is the area of gD and the lipid, respectively. This method can be used to obtain the average number of bound lipids per gD molecule if c is replaced by c_eff in Eqs. 2 and 3.

Equation 4 also takes into account the interaction between lipid and peptide through the ξ-parameter. For proteins without bound lipids ξ is expected to be small, whereas a larger ξ indicates a larger lipid-protein interaction. This model has been tested for a variety of integral proteins and gel phase obstacles (Almeida et al., 1992a). In general ξ is found to be slightly above 20 Å for the larger proteins, whereas it is only 1 Å for gD. The different behavior for gramicidin is accounted for by the different size of this peptide.

Percolation over μm-length scales has been observed by FRAP in lipid bilayer systems, in which the fluorescence recovery and the characteristic recovery times change drastically at the percolation threshold (Almeida et al., 1992a, 1993; Vaz et al., 1989). The observed values of the percolation threshold range from 0.2 to 0.8 and this variation is taken as an indication of the presence of different domain shapes.

Obstructed diffusion in the one-phase region

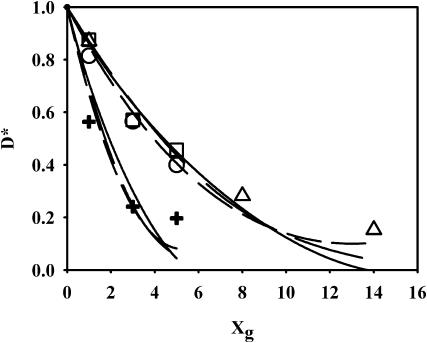
Fig. 5 shows D^* as a function of X_g at 25, 30, and 35°C together with nonlinear fits of the data to Eqs. 2–4. For Eqs. 2 and 3, c_eff calculated according to Eq. 5 has been used to get n_l. The data for 30 and 35°C coincide in this figure (circles and squares). Previously published data of the diffusion of a fluorescence probe at 30°C (Tank et al., 1982) also fall on the same curve (triangles), when normalized with the D_L value obtained by us for X_g = 0 at 30°C. One value of Tank et al. (X_g = 5, D^* = 1.0) deviates significantly from the other values and has been excluded from the analysis. Since all the points for 30 and 35°C lie on the same curve within experimental error, all points are fitted together. The results of the fits give n_l = 5, Γ = 3.4 for Eq. 2, n_l = 4.9 for Eq. 3, and ξ = 6.9 Å for Eq. 4. The values of both n_l and ξ roughly correspond to one layer of bound lipids around each gD molecule. Thus, it seems that all three models presented earlier produce reasonable values for the fitted parameters and although the models rely on different premises, they are each able to describe the obstruction effect in this system. The value of ξ differs from that found in the analysis by Almeida et al. (1992a). One possible reason for this might be that our study was made with saturated DMPC, whereas the system analyzed by Almeida et al. (1992a) contained mainly unsaturated PCs (Blackwell and Withmarsh, 1990).

FIGURE 5.

Normalized diffusion coefficient, D^*, together with best fits to Eqs. 2–4. (Circles) Data at 30°C; (squares) data at 35°C; (triangles) data at 30°C from Tank et al. (1982); and (crosses) data at 25°C. (Long dashed lines) Fit to Eq. 2, modified to include bound lipids; (solid lines) fit to Eq. 3, modified to include bound lipids; and (short dashed lines) fit to Eq. 4. The long dashed lines correspond to n_L = 5, Γ = 3.4 (30 and 35°C); and n_L = 15, Γ = 3.6 (25°C). The solid lines correspond to n_L = 4.9 (30 and 35°C) and 13.5 (25°C). The dashed lines correspond to ξ = 6.9 (30 and 35°C) and 21.6 Å, respectively.

For the data obtained at 25°C the reduction in D^* is much larger and the corresponding fitting parameters are n_l = 15, Γ = 3.6 for Eq. 2, n_l = 13.5 for Eq. 3, and ξ = 21.6 Å for Eq. 4. This increase in the parameters does not necessarily reflect a change in the number of bound lipids, since at higher gD content a single phase is no longer present. According to the DSC data significant amounts of the lipids are in the solid phase for X_g > 0 at 25°C, and therefore, the lipid diffusion will be affected both by obstruction from the peptide and by the gel clusters formed by the lipids. Thus, the data can no longer be interpreted as an obstruction of gD (with bound lipids) alone.

Obstructed diffusion in the two-phase region

To include the effect of the presence of a gel phase on D_L, we make the following assumptions: diffusion is reduced 1), at lower temperatures according to the activated diffusion process; 2), due to the obstacles that gD constitutes, together with the bound lipids; and 3), due to hindered diffusion from the gel clusters that appear at lower temperatures. The influence on D_L from 1 can be accounted for by assuming that the diffusion process can be described with an E_A = 50 kJ/mol in the whole temperature interval. The temperature dependence can thus be reduced to D_L(X_g, T₀) by multiplying each D_L(X_g, T) by the factor exp{(E_A/R) × (1/T−1/T₀)}. The value of T₀ is chosen to be 35°C where no gel phase is present. These reduced data now depend only on the obstructed diffusion by the factors given in 2 and 3, i.e., the area fraction of obstacles produced by gD with bound lipids and gel clusters. The factor in 2 can be calculated from the areas of gD and DMPC, under the assumption that the same number of lipids bind to each gD in the whole temperature interval. To quantify the fraction of gel phase present (f_g), the DSC curves have been integrated. In this integration the pretransition has been removed by interpolating the curve for the main transition across the temperature region of the pretransition. The area fraction of obstacles can now be written as

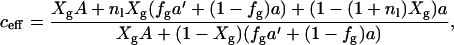(6)

where A, a, and a′ are the areas of gD, and DMPC in the L_α and in the gel phases, respectively. The value f_g is the fraction of the gel phase present. In the derivation both bound and unbound lipids are allowed to enter the gel phase in the same amount. Assuming that bound lipids exclusively are in the liquid phase affects the results only marginally.

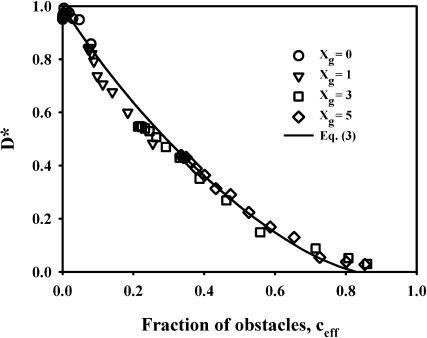
The temperature-corrected D^* values for different X_g and temperature are plotted versus c_eff in Fig. 6. In the calculation of c_eff the following values have been used: A = 137 Ų, a = 65 Ų, a′ = 55 Ų (Killian, 1992; Lewis and Engelman, 1983; Marsh, 1990), and n_l = 4.7. This figure summarizes all the data in a format, where only obstruction effects are present. Here all data fall on the same curve. The line corresponds to Eq. 3 for mobile obstacles. It is obvious that the reduction in D_L can be described by mobile obstacles containing gD with bound lipids and/or gel phase clusters. The adherence of the points to Eq. 3 indicates that no percolation takes place in the system and that the obstructing aggregates can be described as more or less circular in shape, at least as seen on the length scale defined by the diffusion time. For the longest diffusion time, 500 ms, this corresponds to roughly 5 μm. No indications can be seen of linear aggregates on the submicrometer length scale, such as those reported in the gel phase by atomic-force microscopy (Ivanova et al., 2003; Mou et al., 1996; Rinia et al., 2000). If, for example, linear aggregates of the type shown in Fig. 4 in Ivanova et al. (2003) or Fig. 1 in Rinia et al. (2000) are present, a significant fraction of the lipids will be trapped in corrals with dimensions <1 μm and the apparent diffusion coefficient will become dependent on the diffusion time. Furthermore, in the percolated system at 5 mol % gA described in Mou et al. (1996), the lipid motion would be restricted to tens of nanometers and the measured diffusion coefficient would be magnitudes smaller than that for unrestricted diffusion.

FIGURE 6.

Temperature-corrected D^* for DMPC/gD at various gD content and temperatures as a function of the fraction of obstacles present in terms of gD + bound lipids and gel phase. The gD contents are 0 (circle), 1 (down triangle), 3 (square), and 5 mol % (diamond). The expected reduction in diffusion for mobile obstacles (Eq. 3) with n_l = 4.7 is given by the solid line.

The reason for the differing results is most probably that the linear aggregates are only formed in the gel phase. A recent atomic-force microscopy study has shown that gA forms linear aggregates in the gel phase of DPPC, whereas the aggregates formed in the fluid phase of DMPC at the same temperature are small and roughly circular in shape (Ivanova et al., 2003). Another reason might be effects of the solid support on the phase behavior. Solid supported bilayers have different T_m and they lack the pretransition occurring in unsupported systems (Leidy et al., 2002). Results on so called raft-forming lipid bilayer systems also indicate that the oriented bilayer systems have properties more similar to those of giant unilamellar vesicles than to single bilayers on solid support (Filippov et al., 2004).

CONCLUSIONS

This study highlights the benefits of using macroscopically oriented bilayers in the study of phase equilibria and obstruction. We have shown that 1), macroscopically oriented samples can be used in NMR to accurately determine the main phase transition temperature, which is difficult to observe in powder samples; 2), there is no evidence for a linear aggregation of gD in the fluid phase for gD contents up to 5 mol % (the analysis indicates that there is approximately one layer of bound lipids around each gD molecule); and 3), the obstruction in the two-phase area at lower temperatures can also be described by small, mobile obstacles of a gel phase and gD with bound lipids.