Probing Protein Mechanics: Residue-Level Properties and Their Use in Defining Domains

Abstract

It is becoming clear that, in addition to structural properties, the mechanical properties of proteins can play an important role in their biological activity. It nevertheless remains difficult to probe these properties experimentally. Whereas single-molecule experiments give access to overall mechanical behavior, notably the impact of end-to-end stretching, it is currently impossible to directly obtain data on more local properties. We propose a theoretical method for probing the mechanical properties of protein structures at the single-amino acid level. This approach can be applied to both all-atom and simplified protein representations. The probing leads to force constants for local deformations and to deformation vectors indicating the paths of least mechanical resistance. It also reveals the mechanical coupling that exists between residues. Results obtained for a variety of proteins show that the calculated force constants vary over a wide range. An analysis of the induced deformations provides information that is distinct from that obtained with measures of atomic fluctuations and is more easily linked to residue-level properties than normal mode analyses or dynamic trajectories. It is also shown that the mechanical information obtained by residue-level probing opens a new route for defining so-called dynamical domains within protein structures.

INTRODUCTION

Until recently, the mechanical properties of proteins have received relatively little attention. This does not imply that they are of little interest, but rather that, unlike structural studies, the methods for studying the mechanical properties of biological macromolecules are still in their infancy (Bensimon, 1996; Bustamante et al., 2003; Lavery et al., 2002). In addition, there are currently no obvious ways to deduce mechanical properties directly from structure. Despite these difficulties, it seems clear that mechanical properties must play an important role in protein function, not only for those proteins that are subjected to forces at the macroscopic level, for example within muscle fibers, but also for the majority of proteins that must support and react to forces at the microscopic level when they interact with other macromolecules or when they act on target molecules as molecular catalysts.

Although atomic fluctuations, whether obtained experimentally (as in the case of crystallographic B-factors) or theoretically, provide some data on protein mobility, this information is mainly relevant to small, thermally-induced structural changes and is dominated by local structure (Halle, 2002). Molecular dynamics can provide useful information on larger scale movements, although the magnitude of the deformations observed is again limited to thermally induced movements occurring on the nanosecond timescale. It is also more difficult to relate trajectory information to local properties, although techniques exist to locate domain movements and to help to identify critical hinge residues (Hayward et al., 1997). Similar data can be obtained from normal-mode vibrational analyses, where low-frequency modes can also be analyzed in terms of domain movements (Hinsen, 1998; Thomas et al., 1999), or by comparing two or more conformations of the same protein (Gerstein et al., 1994; Lesk and Chothia, 1984; Navizet et al., 2004; Wriggers and Schulten, 1997).

Much larger movements can be investigated via single-molecule experiments, which probe the effect of forces applied to the ends of individual macromolecules using atomic force microscopy or optical, mechanical, and magnetic bead traps. In the case of DNA, such experiments led to the discovery of unexpected force-induced structural transitions (notably, to stretched S-DNA and to stretched and twisted P-DNA) (Allemand et al., 1998; Bryant et al., 2003; Cluzel et al., 1996). These transitions have since been linked to deformations occurring in biological environments under the influence of protein binding (Bertucat et al., 1999; Lebrun and Lavery, 1999; Lebrun et al., 1997). Proteins have also been studied in this manner, with a particular emphasis on muscle proteins such as titin, which, due to their biological role, have evolved to deal with significant applied forces (Kellermayer et al., 1997; Rief et al., 1997; Tskhovrebova et al., 1997; Williams et al., 2003).

Single-molecule experiments generally yield force-extension curves. These data alone cannot be interpreted in structural terms, but with the help of theoretical modeling it has been possible to derive data on the conformational changes that take place under applied traction and/or torsion. Whereas small deformations can be modeled with simple polymer representations such as the worm-like chain model, larger deformations require more detailed atomic simulations, such as those provided by constrained molecular dynamics trajectories or internal coordinate energy minimization (Lavery et al., 2002; Tajkhorshid et al., 2003). Despite their limitations, molecular simulations have made it possible to interpret the features of force-extension curves in terms of detailed molecular deformations. In the case of proteins, advances in both experimental and theoretical studies are beginning to probe the details of force-induced denaturation, revealing domains with distinct mechanical properties, and confirming the vectorial nature of these properties (showing, for example, that the difficulty of unraveling a β-sheet or separating a pair of α-helices depends significantly on the direction of the applied force) (Brockwell et al., 2003; Bryant et al., 2000; Carrion-Vazquez et al., 2003; Rohs et al., 1999).

Despite the progress made with the help of single-molecule techniques, there is still no direct way of probing mechanical properties at the single-residue level. Such data are, however, necessary if we wish to be able to analyze how structures have evolved to exhibit given mechanical behavior. Ideally these data would provide mechanical information for each residue within a macromolecular structure, defining the ease with which the residue can be displaced and the direction in which movement would most easily occur. We have attempted to get access to such data by developing a novel restraint which can be applied to protein structures within either all-atom or simplified bead representations. The results show that mechanical properties can vary widely within a single protein structure. It is also shown that the way a protein responds to our imposed restraints can be used to detect mechanically-coupled regions and to develop a new method for defining domains within the overall structure.

This article presents the approach we propose for the simple test case of a single α-helix and also for a small, soluble protein. The resulting deformations and corresponding force constants are compared with data from molecular simulations and experiments. It is shown that coarse-grain representations with one node per residue (Doruker et al., 2000; Keskin, 2002) yield results close to those obtained with more costly all-atom methods. We then use the results obtained for a variety of proteins to demonstrate how the structural response of a protein to our imposed deformations can be used to define domains.

MATERIALS AND METHODS

In this section we describe the standard simulation methodologies used in this article to study the dynamics and the deformations of protein structure. The new restraint developed to probe local mechanical properties, and the analysis of the deformations produced, are described at the appropriate place in the following section.

Molecular dynamics simulations

Molecular dynamics have been carried out using the AMBER 7.0 program (Case et al., 2002) with the Parm99 force field (Wang et al., 2000). The protein under study, staphylococcal nuclease (PDB code 1EY0) (Chen et al., 2000), hereafter abbreviated as SNase, was constructed using atomic coordinates from the Protein Data Bank (Berman et al., 2002). Although SNase contains 149 amino acids, coordinates were only available for residues 6–141, since both termini show disorder within the crystal. It is, however, remarked that these deletions do not affect the folding of the protein, although they somewhat reduce its stability (Hirano et al., 2002). SNase was solvated using a 10-Å layer of TIP3P water molecules (Jorgensen et al., 1983) and placed inside a truncated octahedral box. This led to a system with 5655 water molecules and a face-to-face box dimension of ∼66 Å. Simulations were carried out using periodic boundary conditions. Electrostatic interactions were treated with the particle mesh-Ewald method (Cheatham et al., 1995; Darden et al., 1993) using a real-space cutoff of 9 Å and a grid spacing of 1 Å. The electroneutrality of the system was ensured by adding 14 randomly positioned chlorine anions to the simulation cell. Dynamics were carried out using a 2-fs time step with SHAKE restraints (Ryckaert et al., 1977) on all bonds involving hydrogen atoms. After energy minimization, the system was heated to 300 K over 10 ps, using quadratic restraints on the protein atoms, and held at this temperature for a further 90 ps. The restraints were then gradually relaxed over a period of 300 ps, after which the trajectory was continued for 4 ns using a constant temperature and pressure ensemble. This led to a stable conformation lying within root mean-square deviation with respect to the crystallographic structure of ∼1.4 Å for the backbone atoms and 1.9 Å for all nonhydrogen atoms.

Restrained energy minimization using an all-atom, internal coordinate model with an implicit treatment of solvent and counterions

Our internal coordinate model of proteins, LIGAND, is derived from the JUMNA program developed for studying nucleic acids (Lavery et al., 1995) and, notably, their deformation under the impact of imposed restraints. In this approach, all bond lengths and most valence angles are taken to be fixed. The remaining variables are all the bond torsions along the peptide backbone and within the amino acid side chains, and also the principle valence angles along the backbone (N-Cα-C′, Cα-C′-N and C′-N-Cα) and within proline rings. Ring closures associated with proline residues and disulphide bonds were treated, as in JUMNA, by replacing a chosen bond (respectively, Cγ-Cδ and S-S) with a quadratic distance restraint, leading to a set of dependent valence and torsion angles. Energy calculations used the AMBER Parm99 force field (Wang et al., 2000), as described in the preceding section. Solvent electrostatic effects are taken into account using the generalized Born model with a salt concentration of 0.1 M (Tsui and Case, 2000). Analytic derivatives of the solute energy and of the solvent electrostatic term were calculated with respect to all internal coordinates and energy minimization is carried out using a quasi-Newton algorithm. This approach reduces the number of variables by roughly an order of magnitude compared to Cartesian coordinate models. It enables large conformational changes to be achieved during energy minimization, as shown by our earlier studies of both nucleic acids and proteins (Lebrun et al., 2001, 1997; Rohs et al., 1999).

Since the molecular mechanics studies we perform require a stable starting conformation, we began by carrying out a short molecular dynamics trajectory with AMBER using the generalized Born solvent model. Conformations separated by 200 ps along this trajectory were then energy-minimized using the AMBER Cartesian coordinate representation, followed by internal coordinate minimization in LIGAND. The resulting lowest energy conformation was used for subsequent mechanical studies (this conformation had a root mean-square deviation with respect to the crystallographic structure of 2.5 Å for all backbone atoms, and of 1.9 Å following the exclusion of the three N- and C-terminal residues and the flexible loop residues 45–53). All mechanical deformations imposed on this conformation led to higher energies and thus to positive force constants for atom displacements.

Restrained energy minimization using a coarse-grained model

In this simple bead representation, each amino acid within a protein structure is represented by a single point, taken as the Cα atom. Interactions between residues are restricted to quadratic springs. Springs are created between those residues which lie closer than a cutoff distance, taken here to be 9 Å. All springs have the same force constant (Tirion, 1996), taken here to be 0.7 nN Å⁻¹, and are assumed to be relaxed in the reference conformation of the protein. Rather than performing normal-mode calculations as in the conventional Gaussian network model (GNM) (Bahar et al., 1997; Haliloglu et al., 1997), we have carried out energy minimizations after deforming the protein structure using the restraint described in the following section. Note that although it is possible to perform energy minimization using the internal coordinates based on the virtual Cα-Cα backbone of the coarse-grained representation, this does not offer any significant gain for this already highly simplified model and we have therefore carried out minimization directly using the Cartesian coordinates of the Cα atoms. Calculations were carried out using protein coordinates drawn from the Protein Data Bank. In the case of SNase, we also made calculations using the lowest energy-minimized conformation described above. This, however, led to only very small changes in the results.

RESULTS AND DISCUSSION

Defining a method for measuring mechanical properties at the residue level

The single-molecule experiments, and the related molecular simulations, discussed in the introduction to this article, are presently limited to studying a single aspect of protein mechanics, namely the impact of end-to-end pulling. Although a number of studies have also looked at smaller peptide fragments, they have also been limited to a single, overall mechanical restraint (Bryant et al., 2000; Idiris et al., 2000; Masugata et al., 2002; Rohs et al., 1999). How can we set about moving from this level to finer data that can describe local mechanical properties, ideally residue by residue, throughout the architecture of a protein?

From the point of view of molecular simulations, various approaches can be considered, but all face one fundamental question: to measure mechanical resistance, it is necessary to be able to push or pull against something. The first way to solve this problem is to consider an extension of the end-to-end pulling experiments and to push (or pull) in turn on the distances separating each pair of residues making up the protein. This approach nevertheless has two disadvantages. First, for a protein containing N amino acids, it is necessary to carry out O(N²) numerical experiments. Second, since the data refers to amino acid pairs rather than to individual amino acids, it is difficult to derive data on the local deformation properties concerning either of the participating residues.

If it were possible to act directly on a single residue, we would reduce the number of numerical experiments to be performed to O(N) and we would be able to derive local data easily. The question is still, however, how do we act on a single residue? One possible choice would be to try and move the residue with respect to the center of mass of the protein under study. Preliminary trials with this approach showed that it is not always easy to relate such results to local mechanical properties of the probed residue. The explanation lies in the fact that a distance restraint between a given residue and the center of mass of the protein can be satisfied by moving either the residue itself or the center of mass. If we consider a protein with a very flexible region or build up from two or more domains joined by flexible hinges, attempts to modify residue-to-center of mass distances within a rigid part of the structure will result mainly in moving the center of mass. This tends to reduce the range of the measured force constants and, notably, means that residues within hinge regions often have force constants similar to those of residues within rigid domains (see below).

It is possible to overcome this difficulty by changing the focus of the restraint to the residue being probed. This implies acting not on a single distance, but on the average of all pair distances linking the probed residue to the other residues in the protein. We first choose the Cα atom as the reference point within each residue. We then define a distance restraint, D_i, which acts on the average of the Cα-Cα distances r_ij between the probed residue i and all other residues j:

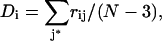(where N is the number of residues in the protein and the sum over j* implies the exclusion of j = I − 1, i, I + 1, since the Cα-Cα distances between neighboring residues along the polypeptide chain are virtually constant).

By constraining D_i to adopt both larger and smaller values than the reference distance found in the native structure, it is possible to obtain mechanical data on the movement of residue i within the overall protein environment. We chose to change D_i over a range of −0.2 Å to +0.2 Å in steps of 0.1 Å. This choice implies carrying out an energy minimization for each residue within the protein and for each value of D_i, to allow the rest of the structure to adapt to the imposed restraint. The range of deformation was initially chosen to be compatible with thermally induced deformations, but it is also possible to study much larger movements and even to partially denature the protein.

After energy minimization, the deformed protein structures can be superposed on the native structure to determine in which direction the probed residue moved. Since our restraint is scalar, this direction provides information on the path of least resistance. Note, in passing, that there is no requirement for the displacements of residue i, which occur as D_i is increased and decreased, to be either linear or to be aligned with one another. From the form of the energy curve as a function of D_i, it is possible to derive a force constant that characterizes the mechanical environment of residue i. We can also analyze how the protein reacts to the imposed restraint by looking at the detailed changes occurring in the r_ij vectors.

All our initial studies were carried out using the all-atom internal coordinate model described in Materials and Methods. We will start by discussing the probing of a simple element of secondary structure, the α-helix. For this purpose, we constructed and energy-minimized a polyalanine helix containing 13 residues. We applied our restraint to each residue in turn using the steps and range of deformation described above. It was found that the energy curves as a function of D_i could be fitted accurately with a simple quadratic function and derived analytically to yield the corresponding force constant. These constants are given in units of nN Å⁻¹ (note that 1 kcal mol⁻¹ Å⁻² ≃ 0.07 nN Å⁻¹). The results for the α-helix are presented in Fig. 1 as a histogram of the measured force constants and a vectorial representation of the backbone displacements produced when the restraint is applied to the central Cα and to a Cα close to the C-terminal of the helix. Although displacements are only shown for D_i = +0.2 Å, we note that for the small displacements studied here all the residues of the α-helix moved linearly and that the deformation vectors obtained by increasing and decreasing D_i were virtually aligned.

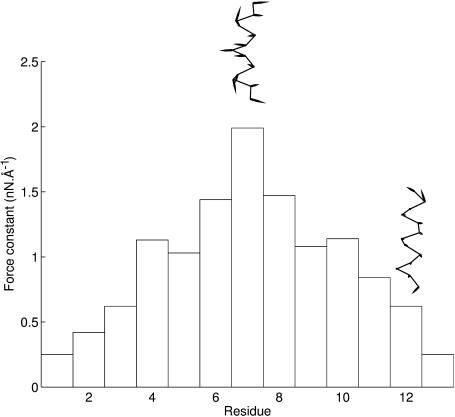
FIGURE 1.

Force constant histogram for the residues of an (Ala)₁₃ α-helix. The inserted schematic graphics show movements of the Cα backbone after an imposed restraint D_i = 0.2 Å on the central residue and on a residue close to the C-terminal. For visibility, the length of the displacement vectors has been increased by an order of magnitude.

The results in Fig. 1 show that the force constants decrease more or less linearly as we move from the center of the α-helix, which has a maximal value of 1.98 nN Å⁻¹, toward the ends. The force constants of the terminal residues, 0.25 nN Å⁻¹, are roughly 8 times smaller than that of the central residue. This shows, not surprisingly, that it is more difficult to perturb the center of a regularly hydrogen-bonded helix. If we look at the way the helix responds to the imposed restraints, we can also see that it prefers to bend when the probing involves the central residue, whereas it prefers to stretch when a residue close to the terminus is probed.

Testing the method on a small protein

It is now interesting to see what data we can extract from a protein using this approach. For our initial study, we chose staphylococcal nuclease, a small (146-residue) soluble protein that is roughly spherical in shape and contains both α-helices and β-sheets (Chen et al., 2000). Calculations of the force constants were again carried out using the all-atom model.

The force constants calculated along the polypeptide backbone of SNase are shown as a histogram in Fig. 2. As for the α-helix test, their values vary significantly, ranging from 0.16 n Å⁻¹ to 10.68 nN Å⁻¹. This variation, by a factor of more than 50, is not correlated with secondary structures as shown by the bars along the abscissa of Fig. 2 which indicate the location of β-sheets (gray) and α-helices (black). The largest force constants are found for residues that lie close to the core region of the protein. Eleven such residues have force constants above 3.4 nN Å⁻¹ (F34, R35, L36, L37, L38, L89, A90, Y91, I92, N100, and L103). These residues are predominantly hydrophobic, and all but two belong to secondary structures; however, they do not obviously fit with the notion of a hydrophobic core. It is nevertheless remarked that the hydrophobic core described earlier for SNase (Chen and Stites, 2001) has four residues in common with those selected on a mechanical basis: F34, L36, I92, and L103. We will return to the sense of the most rigid residues in the following section.

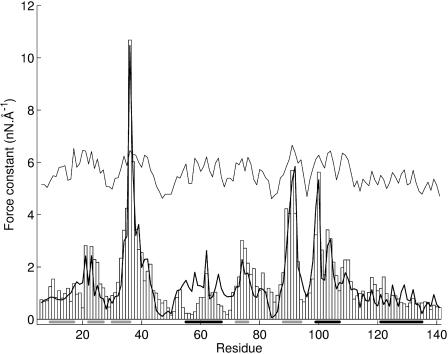
FIGURE 2.

Force constant histogram for the residues of SNase calculated using an all-atom representation. Secondary structures are indicated along the abscissa as gray bars for β-sheets and black bars for α-helices. The bold line shows the force constants calculated using the coarse-grained model. The fine line shows the inverse square fluctuations calculated with the coarse-grained model (fitted using a proportionality constant and then shifted up the ordinate by 4 nN Å⁻¹ for clarity).

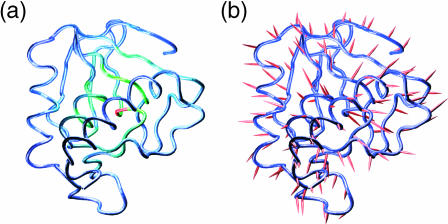
It is possible to get a better idea of the distribution of the rigidity within SNase using a tube model of the protein backbone colored to reflect the calculated force constants. This representation is shown in Fig. 3 a. The blue→green→red color scale, which indicates increasing force constants, clearly shows that the most rigid zones occur where the secondary structures are closely packed together in the heart of the protein. Fig. 3 b shows the movement of the Cα atoms subjected to a restraint of D_i = 0.2 Å. Overall, these vectors tend to point away from the rigid center of the protein. However, this is only approximately true, and the detailed architecture of the protein leads to important deviations in some cases. If we measure the angle formed between the movement vector and the difference vector linking the corresponding residue to the center of mass of the protein, the average deviation is around 20°, but it can exceed 50° for some residues. It is also remarked that, compared to our α-helix test case, SNase shows more deviation from colinearity when we compare the movement vectors for increasing and decreasing D_i. Although the mean deviation is roughly 10°, it reaches 90° for some residues. Both of these aspects of mechanical anisotropy will probably be worth studying in more detail and may signal particularly interesting regions within the protein architecture.

FIGURE 3.

Response of SNase to imposed restraints: (a) a colored backbone representation of the calculated force constants. The blue→green→red scale corresponds to increasing values. (b) Movement of the restrained Cα atoms for D_i = 0.2 Å. For visibility, the length of the movement vectors has been increased by an order of magnitude. The images in figures 3, 5, 6, and 7 were prepared using VMD (Humphrey et al., 1996).

Before leaving SNase, we ask whether a simple coarse-grained model with quadratic springs is capable of providing the same information that we have obtained with an all-atom model and the AMBER force field. If we return to Fig. 2, we can see that the agreement is remarkably good. The bold line in this figure represents the force constants calculated with the coarse-grained model (adjusted to the all-atom results with a single multiplicative factor). The absolute differences are, on average, 0.46 nN Å⁻¹ and the two sets of values show an overall correlation coefficient of 0.91 for 136 data points. The direction of movement vectors also agree well between the two calculations, with an average deviation of only 22°, whether positive or negative values of D_i are considered. It is, however, remarked that finer details, such as the deviation between the positive and negative D_i movement vectors for a single residue, are less well reproduced, with the coarse-grained model understandably showing considerably smaller deviations from colinearity. These results are, however, sufficiently encouraging to justify this computationally much more attractive model.

Although the D_i restraint could in principle have been applied within the molecular dynamics simulation of SNase, this would in practice be computationally prohibitive. We can nevertheless ask whether there is a correlation between the internal coordinate minimization data and the fluctuations that occur naturally within the dynamic trajectory. This can be tested using the thermally driven fluctuations of D_i for each residue seen with molecular dynamics. It is found that the internal coordinate model force constants indeed show a strong linear correlation with the inverse square of the fluctuations in D_i with correlation coefficients ≥0.80 for 136 data points, whether we consider the first or the second half of the dynamic trajectory (suggesting that these fluctuations have effectively converged). In contrast to fluctuations in D_i, there is a relatively poor correlation between our force constants and simple fluctuations in atomic positions. This can be checked using the experimental B-factors, which yield a correlation coefficient of only 0.47, with the B-factors calculated using the coarse-grain model (see the fine line in Fig. 2), or with the atomic fluctuations derived from the molecular dynamics trajectory (correlation coefficient of 0.66). All these results reflect the fact that our restraint probes residue movements with respect to the overall protein structure and not just with respect to the local environment of the residue.

Using mechanical probing to define domains

Although the D_i restraint described above was derived to calculate residue-by-residue force constants, the response of a protein to this restraint can in fact be analyzed in more detail. If we consider a given change D_i applied to the ith residue, we can represent the corresponding deformation as a vector of Δr_ij values that describe the changes in the Cα-Cα distances from residue i to all other residues j, with respect to the relaxed protein structure. Using the deformation restraints applied to all the residues in turn, we can build up a Δr_ij matrix. Note that, in general, Δr_ij ≠ Δr_ji. This matrix reflects the mechanical linkages within the protein, since small Δr_ij values imply that the corresponding residues are strongly coupled and move more or less in unison under the action of the applied restraint. Such residues are therefore likely to belong to a single mechanically coherent domain. In contrast, large Δr_ij values imply weak coupling and the existence of independent domains. This interpretation led us to look for a way of defining domains within a protein structure on the basis of its mechanical response. Note that this type of analysis corresponds to defining what are generally termed “dynamical” domains, rather than “structural” domains, whose definition relies on structural and/or sequence comparisons (Janin and Chothia, 1985; Lesk and Chothia, 1984; Orengo et al., 2003; Swindells, 1995). Our approach is therefore related to methods that define domains on the basis of different experimentally or theoretically derived structures of the same protein (Wriggers and Schulten, 1997), or on the basis of conformational data coming from molecular dynamics simulations (Hayward et al., 1997) or normal mode calculations (Hinsen et al., 1999).

The algorithm we have used for detecting domains is a clustering technique that groups together sets of residues whose absolute Δr values are below a given threshold T (the choice of this threshold will be discussed below). The first domain is constituted by starting with the smallest Δr_ij in the matrix (assuming that this value, and the complementary Δr_ji value, are both below T). This groups the residues i and j into the first domain. We then search along the row i to find the next lowest value and add another residue. This process is repeated until there are no more Δr_ij links below the threshold, which signals the start of a new domain. For each new member added to a domain it is again required that both Δr_kj and Δr_jk are below the chosen threshold, where k represents the set of residues already belonging to the domain in question.

Although searching for the minimal value of Δr_ij at each stage makes this procedure only weakly dependent on the residue order, we complete the clustering by looking again at each residue in turn and asking whether it would be appropriate to move it to another domain. For residue i, the move from domain “A” (containing the set of residues j_A) to domain “B” (containing the set of residues j_B) is accepted if the average value <Δr_ijB> is less than <Δr_ijA>. Note that this question only arises if residue i can effectively become a member of domain “B” (i.e., all Δr_ijB values satisfy the threshold requirements). We repeat this reassignment procedure cyclically for all the residues in the protein until stable domains are obtained. This generally requires less than four cycles.

Since clustering algorithms always run the risk of clustering data that in reality has little internal structure, we test the significance of the domains by constructing a tree structure that describes their hierarchy. The distance between two domains is defined as the maximal value of Δr between the sets of residues belonging to the two domains (from the definitions given above, within a single domain this value will always be less than T). Using this distance, the closest pair of domains is grouped into a superdomain. The procedure is then repeated comparing domains and superdomains pairwise until the overall hierarchy is constructed. In general, the lowest branches of this tree are separated by distances well above the threshold. If this is not the case, we merge the corresponding domains and return to the iterative refinement procedure described in the preceding paragraph, before again building a tree structure. We currently require that independent domains should be separated by a distance of at least 1.3 × T. Note that this procedure also protects against artificial domain separations, which can occasionally occur because of the order of the original domain construction.

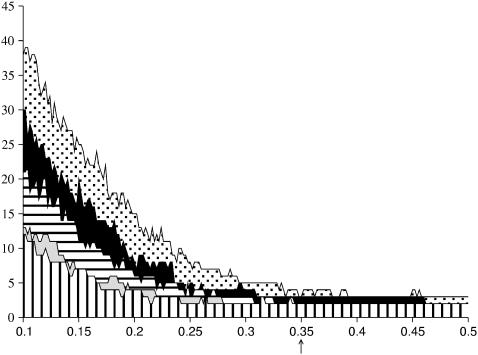
To determine an appropriate value for T we looked at the variation in the number of domains detected as this parameter is modified. Tests on a variety of proteins with different architectures (using a maximum D_i of 0.2 Å) showed that this number is generally stable for T values ranging from roughly 0.34 Å until beyond 0.5 Å (see Fig. 4). Below this value the number of domains increases rapidly, leading to small groups of residues with little apparent physical sense. We consequently set T at 0.35 Å for all subsequent studies. Note that for a few proteins (such as pepsin shown in Fig. 4) the total number of domains can change by 1 for small changes in T. However, such changes have little impact on the interpretation of the resulting mechanical properties.

FIGURE 4.

Number of domains detected as a function of the threshold value T (Å). The curves shown from bottom to top correspond respectively to catenin, cadherin, the D-ribose binding protein (open), the cadherin dimer, and pepsin. The arrow on the abscissa shows the chosen threshold of 0.35 Å.

We will illustrate the results of our approach for SNase, using results from the restraints applied to the coarse-grained model. Fig. 5 a shows that our analysis leads to four domains, three relatively large structures containing respectively 36, 46, and 42 residues, and one small structure with 12 residues. The first domain (shown in blue in Fig. 5 a) begins at the N-terminal and contains half the first β-strand coupled with most of the 4th and 5th strands and the intervening loop. The second domain (red) comprises the rest of the 5-strand β-sheet, with the loop and the α-helix lying between the third and fourth strands. The last large domain (yellow) comprises the two α-helices at the C-terminal end of the protein. The remaining small domain (purple) involves mainly the two short β-strands at the interface between the 2-helix domain and the rest of the protein structure. It should be noted that all residues of SNase were automatically attributed to one of the four domains without any modification of the clustering procedure described above. The secondary structural elements of SNase generally belong completely to a single domain. The only significant exception to this is the splitting of the 5-strand β-sheet between the first and second domains; this, however, corresponds to the hydrogen bonding pattern within this sheet, which is only partially coupled at the interface between the third and fifth strands.

FIGURE 5.

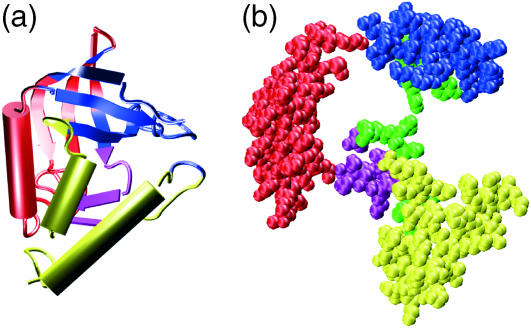
(a) Mechanical domain structure derived for SNase. The secondary-structure cartoon representation shows four domains colored respectively in blue, red, yellow, and purple. (b) An exploded CPK view of the protein domains (colored as in a) showing the residues with the highest force constants in green.

If we return to the eleven residues identified with the all-atom calculations as having the highest force constants, it is interesting to note that these residues all lie at the interface zones between the domains we have described. This can be seen in Fig. 5 b, which shows an exploded CPK view of the SNase domains with the high force-constant residues colored in green. Of the eleven residues in this category, residues 34–38 in the third strand of the principal β-sheet lie at the interface between domains 1 (blue) and 2 (red), residues 89–92 in the fifth strand of the β-sheet lie at the interface between domains 1, 2, and 4 (purple), and residues 100 and 103, which belong to the first α-helix of domain 3 (yellow), lie at the interface with domains 2 and 4. The fact that the most rigid residues lie at domain interfaces has also resulted from the analysis of B-factors obtained with GNM calculations (Bahar and Jernigan, 1999; Isin et al., 2002). We return to this point below.

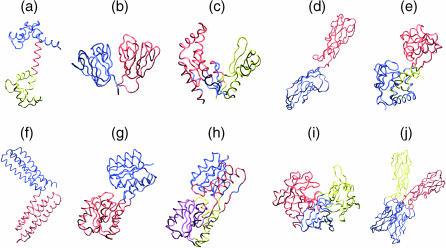
For a more general view of this domain assignment approach, we have analyzed ten proteins whose sizes range from ∼140 to >420 residues (results were again obtained using the coarse-grained model). In order of increasing size the proteins studied were: 1), calmodulin (1CLL), a calcium binding protein (Chattopadhyaya et al., 1992); 2), γB-crystallin (4GCR), a lens-specific protein (Najmudin et al., 1993); 3), guanylate kinase (1EX6), a transferase (Blaszczyk et al., 2001); 4), the two N-terminal extracellular domains of the E-cadherin (1EDH, first chain), hereafter termed cadherin, a cell adhesion protein (Nagar et al., 1996); 5), the lysine/arginine/ornithine-binding protein (2LAO), hereafter termed LAO (Oh et al., 1993); 6), the first chain of the M-fragment of α−catenin (1H6G), hereafter termed α-catenin, a cytoskeleton protein (Yang et al., 2001); 7), the D-ribose binding protein (1URP), a transport protein (Bjorkman and Mowbray, 1998) in its open conformation; 8), the D-ribose binding protein (2DRI) in its closed conformation (Bjorkman et al., 1994); 9) pepsin (5PEP), a hydrolase (Cooper et al., 1990); and 10), the dimer of the N-terminal domains of cadherin (1EDH) (Nagar et al., 1996). The colored zones in Fig. 6 show that we find two to four domains for each of these proteins. All residues are assigned to domains. Domains range in size from 14 residues (the α-helix joining the two calcium binding domains of calmodulin) to 188 residues (the largest domain within the dimer of cadherin), with an average value of 93. Their dimensions range from roughly 20 Å to 40 Å and they are generally composed of contiguous segments of the protein backbone, although a small number of relatively isolated residues occur within some domains. We will not analyze these domains in detail, but it can easily be seen that when visible structural domains exist, these are reflected in the mechanically defined domains. However, there are cases where the structural origins of the mechanical domains are less obvious and these cases merit further study.

FIGURE 6.

Mechanical domain structures of a variety of proteins: (a) calmodulin, (b) γB-crystallin, (c) guanylate kinase, (d) cadherin, (e) LAO, (f) α-catenin, (g) D-ribose binding protein (open), (h) D-ribose binding protein (closed), (i) pepsin, and (j) cadherin dimer. Only the protein backbones are shown.

It is worth examining the residue-by-residue force constants for this set of proteins. If we select the residues associated with the highest force constants for each protein (based on the choice made for SNase, we chose the top 8%), it is again found that these residues mainly lie at the interfaces between the mechanical domains. This can be seen in the exploded CPK graphics of Fig. 7, where the residues with the highest force constants are shown in green. As mentioned above, similar results have been obtained on the basis of GNM calculations (Bahar and Jernigan, 1999; Isin et al., 2002). In the case of our restraint, this result can be explained by noting that lowest energy movements occurring within a protein as a result of our probing are likely to be dominated by more or less rigid domain displacements. If this is true, applying a restraint to a residue imbedded within one domain will mostly result in displacing this domain with respect to the other domains forming the protein. In contrast, applying a restraint to a residue close to a domain interface will be likely to induce more costly intradomain deformations, since simple domain movements (typically rotations) will not significantly change the Cα-Cα distances involving residues in the hinge region.

FIGURE 7.

Exploded CPK views showing that the residues associated with the highest force constants (in green) are principally found at the interface regions between mechanical domains: (a) calmodulin, (b) γB-crystallin, (c) guanylate kinase, (d) cadherin, (e) LAO, (f) α-catenin, (g) D-ribose binding protein (open), (h) D-ribose binding protein (closed), (i) pepsin, and (j) cadherin dimer. The domain colors are the same as in Fig. 6.

CONCLUSIONS

We have developed an index for probing protein mechanics at the residue level. By constraining the average distance between the probed Cα atom and the remaining Cαs in a protein we can deform a structure to yield both scalar and vector information. The scalar information is a force constant that characterizes the ease with which the probed residue i can move in its overall protein environment. This force constant is sensitive to the global structure of the protein and, unlike B-factors, is not dominated by the local packing around the probed residue. The vector information is, first, the preferential direction of movement for residue i indicating the path of least resistance and, second, the vector characterizing the changes that have occurred in the Cαi-Cαj distances to satisfy the restraint. Grouped together, the latter vectors enable us to detect rigid zones within the protein and, using a two-stage clustering algorithm, to define so-called dynamical domains on this basis. In comparison to other algorithms for finding such domains, using experimentally or theoretically derived structures or selected low-frequency normal modes, our approach has the advantage of being based on a homogeneous mechanical probing of all residues within the protein.

The probing and analysis techniques that have been described can be applied to either all-atom or coarse-grained protein representations. Tests on staphylococcal nuclease suggest that most of the information found using all-atom internal coordinate minimization is preserved within a point-per-residue coarse-grained model. It will, however, be necessary to test this result for other proteins. It is also likely that the analysis of finer effects, such as the impact of single point mutations, will require detailed atomic representations.

We have illustrated our technique for locating rigid domains on a number of proteins. These domains generally group together contiguous residue segments and, where structural domains are visually obvious, these elements are reflected in the mechanically defined domains. We are now trying to use this technique to understand how structure and mechanical properties are linked within proteins and whether mechanical properties can indeed help in understanding the detailed deformations which occur during protein function (e.g., changes within enzyme cavities) and interactions (e.g., surface plasticity).