Abstract
Recent atomic force microscopy stretching measurements of single polysaccharide molecules suggest that their elasticity is governed by force-induced conformational transitions of the pyranose ring. However, the mechanism of these transitions and the mechanics of the pyranose ring are not fully understood. Here we use steered molecular dynamics simulations of the stretching process to unravel the mechanism of forced conformational transitions in 1,6 linked polysaccharides. In contrast to most sugars, 1,6 linked polysaccharides have an extra bond in their inter-residue linkage, C5–C6, around which restricted rotations occur and this additional degree of freedom increases the mechanical complexity of these polymers. By comparing the computational results with the atomic force microscopy data we determine that forced rotations around the C5–C6 bond have a significant and different impact on the elasticity of α- and β-linked polysaccharides. β-linkages of a polysaccharide pustulan force the rotation around the C5–C6 bonds and produce a Hookean-like elasticity but do not affect the conformation of the pyranose rings. However, α-linkages of dextran induce compound conformational transitions that include simultaneous rotations around the C5–C6 bonds and chair-boat transitions of the pyranose rings. These previously not-recognized transitions are responsible for the characteristic plateau in the force-extension relationship of dextran.
INTRODUCTION
Sugar rings are the fundamental elements in many biological structures such as the cell wall in plants and bacteria. In higher organisms they have many functions; for example, they serve as lubricants and provide support to cellular elements of tissues and also participate in numerous molecular recognition and adhesive interactions (Rao et al., 1998). They are frequently subjected to various mechanical stresses, which sometimes generate severe deformations of the ring, e.g., during the lysozyme reaction in the cell walls of bacteria, where the enzyme forces the sugar ring into a highly strained conformation. The flexibility of sugar rings in the absence of external forces has been studied for some time already (Pensak and French, 1980; French et al., 1990). However, the response of sugars to external forces has been examined only recently by stretching single polysaccharides in an atomic force microscope (Rief et al., 1997; Marszalek et al., 1998, 1999a, 2001, 2002, 2003; Li et al., 1998, 1999; Brant, 1999). These measurements have expanded the conformational analysis of ring structures (Barton, 1970) to include force-induced chair-boat and chair inversion transitions of the pyranose ring as yet unrecognized biological events (Marszalek et al., 1998, 1999a). For example, Marszalek and co-workers have recently observed force-induced conformational transitions in heparin and they postulated that these conformational changes may finely regulate the affinity of various ligands toward heparin in secretory granules or in the extracellular matrix (Marszalek et al., 2003).
These studies were mainly focused on 1→4 linked polysaccharides such as amylose, cellulose, pectin, or heparin. Axial glycosidic bonds of α-linkages (e.g., amylose) were found to work as “atomic levers,” which produce torque and flip the ring to a boat-like conformation. Equatorial glycosidic bonds of β-linkages (e.g., cellulose), were found to produce minimal torque and therefore no conformational transitions (Marszalek et al., 1999a; Li et al., 1999; O'Donoghue and Luthey-Schulten, 2000). That is why cellulose elasticity faithfully follows the freely jointed chain (FJC) model of polymer elasticity (Flory, 1953), whereas amylose displays large deviations from the FJC model. In contrast to 1→4 linkages, which transmit the stretching forces to the pyranose ring along its axis of symmetry, other linkages attach the force vector to the sides of the ring at various positions and angles. Therefore, such linkages can generate complex deformations of the pyranose ring, which defy simple analysis. Among them 1→6 linkages deserve special attention. They not only attach the aglycone bond to the side of the pyranose ring, at position C6, but they also include an additional bond in the linkage, C5–C6 (Fig. 1, inset), around which restricted rotations occur, increasing the mechanical complexity of 1→6-linked sugars.
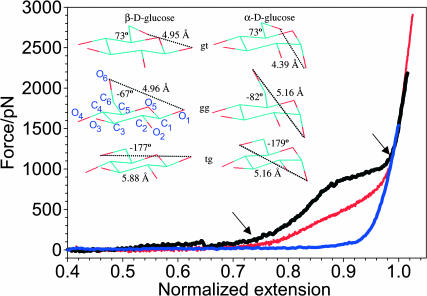
FIGURE 1.
A comparison of normalized force-extension relationships for methylcellulose (blue trace), pustulan (red trace), and dextran (black trace) measured by AFM. The normalization procedure assumed that the extension of the three polysaccharides at the maximum force for the cellulose trace (1538 pN) was equal to 1. The arrows indicate the points on the force spectrogram where the dextran trace separates from the pustulan trace and where both traces join again. They mark the extra extension of both polymers, beyond the extension expected for a simple FJC-like polymer. (Inset) Ab initio optimized rotamers (gt, gg, and tg) of β-D- and α-D-glucose using the B3LYP/6-311++G** method. The O6–O1 distance is shown together with the ω-torsion for all the rotamers. The second ring in the left panel shows the numbering of carbon and oxygen atoms in the glucopyranose ring used to define torsions ω, t1, and t2 (see text).
In this work we expand the conformational analysis of stressed sugar rings by examining in detail the deformations induced by 1→6 linkages using computer modeling tools that include quantum mechanical and steered molecular dynamics (SMD) calculations. SMD is a fairly new method that is particularly well-suited to help the interpretation of AFM stretching measurements on single molecules because it can provide their atomic-scale pictures during forced conformational transitions that are impossible to obtain otherwise. The clear advantage of the SMD method over traditional MD calculations lies in its ability to induce large conformational changes in biopolymers and their complexes, on the nanosecond-to-microsecond timescales which are now accessible to computation. This method was originally developed to model protein-ligand unbinding events measured by AFM (Grubmüller et al., 1996; Izrailev et al., 1997). Later on SMD calculations were instrumental in interpreting AFM stretching measurements on mechanical proteins such as titin and fibronectin, by unraveling the mechanisms of the unfolding of their domains (e.g., Lu et al., 1998; Marszalek et al., 1999b; Lu and Schulten, 1999a,b; Krammer et al., 1999). The details of SMD simulations of mechanical proteins can be found in a recent series of excellent reviews on this topic from the K. Schulten group (Lu and Schulten, 1999a,b; Isralewitz et al., 2001; Gao et al., 2002).
Here we use the SMD approach to analyze two mechanically complementary polysaccharides: pustulan, a β-1→6-linked glucan (Lindberg and McPherson, 1954; Hellerqvist et al., 1968) and dextran, an α-1→6 linked glucan (Whistler and BeMiller, 1993). We find that forced rotations around the C5–C6 bonds govern the elasticity of pustulan, and that previously unrecognized conformational transitions that involve simultaneous C5–C6 rotations and chair-boat transitions govern the elasticity of dextran.
MATERIALS AND METHODS
Polysaccharides
Pustulan, from the lichen Umbilicaria pustulata (Carbomer, San Diego, CA) was dissolved in water at a concentration of 0.001–0.1% (w/v) by heating (∼90°C). A layer of pustulan molecules was created by drying a drop of these solutions onto glass coverslips followed by extensive rinsing which leaves a layer of molecules tightly adsorbed to the glass surface (Li et al., 1998). Similarly, dextran (T500, T2000, Pharmacia/Pfizer, Peapack, NJ) was dissolved in water at a concentration of 0.1–5% and adsorbed to glass from a drop of solution. Typically, the AFM measurements were carried out in water (pustulan, dextran), but some experiments were done in dimethyl carbonate (pustulan) and in ethanol (dextran).
Single-molecule force spectroscopy
Our AFM apparatus consists of a PicoForce AFM (Veeco, Santa Barbara, CA) and a homebuilt instrument similar to that described in Oberhauser et al. (1998). The spring constant of each AFM cantilever (Si3N4, Veeco) was calibrated in solution, using the thermal noise method described in Florin et al. (1995). AFM measurements on single molecules are described in detail in Marszalek et al. (1998, 1999a,b, 2001, 2002).
Steered molecular dynamics simulations
SMD simulations of pustulan and dextran and data analysis were carried out with the programs NAMD2 (Kalé et al., 1999), XPLOR (Brunger, 1992), and VMD (Humphrey et al., 1996) with the new CHARMM-based carbohydrate solution force field (Kuttel et al., 2002). It is significant that this new force field was developed to correctly represent the C5–C6 rotamer populations of D-glucose within the CHARMM framework. The structures, consisting of 10 glucose rings of pustulan or dextran, were generated using the program INSIGHT II (Accelrys, San Diego, CA), and the psfgen module of NAMD. The C6–O6 bonds were positioned in the gt or gg state to mimic the equilibrium distribution of these rotamers (gt/gg/tg/, 40:60:0; see Results and Discussion and Fig. 1, inset, for the definition of these rotamers). The structures were solvated in a box of TIP3P water (pustulan: 38 × 38 × 72 Å, the total of 9309 atoms including 213 atoms of the sugar; dextran: 38 × 37 × 95 Å, the total of 12,198 atoms) with periodic boundary conditions using the program VMD (Humphrey et al., 1996). The boxes were large enough to accommodate the fully extended structures. The structures were first minimized for ∼1000 conjugate gradient steps, then heated from 0 K to 300 K in ∼100 ps and then equilibrated for 1–5 ns at 300 K. The temperature of the system was controlled by the velocity rescaling procedure implemented in NAMD2 (Kalé et al., 1999). SMD simulations were carried out by fixing the O6 atom of the first sugar and applying a force to the O1 atom of the last sugar ring using the SMD protocol within NAMD2 (Kalé et al., 1999). Briefly, SMD simulations of constant velocity stretching are implemented by restraining the pulled end (e.g., O1) harmonically to a point which is translated with constant velocity v in the desired direction. This method is equivalent to attaching one end of a Hookean spring to the end of the molecule being stretched (e.g., O1) and moving the other end of the spring with velocity v. The force applied to the O1 atom is then F=k(vt−x), where x is the displacement of O1 at the time t, from its original position at t = 0 (Lu et al., 1998; Lu and Schulten, 1999a,b). The spring constant, k, used in the simulations was similar to the spring constant of the AFM cantilevers and ranged between 69.5 and 695 pN/nm. The SMD stretching proceeded by moving the end of the spring at a constant velocity of 10−4 Å/fs (simulations in water), and 5 × 10−7 and 1 × 10−7 Å/fs (simulations in vacuum). The simulations adopted a timestep of 1 fs, a uniform dielectric constant ɛ = 1, and a cutoff of Coulomb and vdW interactions with switching function starting at a distance of 8 Å and reaching zero at 12 Å. One-microsecond simulations in implicit solvent were carried out with ɛ = 80. The simulations were done on a Linux cluster with ten 2-GHz AMD CPUs.
Ab initio calculations of α and β-D-glucopyranose rotamers
The gt, gg, and tg rotamers of the 4C1 chair conformation (Rao et al., 1998; Appell et al., 2004) of glucopyranose were generated using the program SPARTAN 02 (Wavefunction, Irvine, CA). The structures were first optimized with the semiempirical method AM1 and then fully optimized with the DFT B3LYP/6-311++G** method using the program PQS on a dedicated Linux cluster with eight processors (Parallel Quantum Solutions, Fayetteville, AK). The optimized dihedral angles ω = O6–C6–C5–O5 and O6–O1 distances are given in Fig. 1 (inset).
RESULTS AND DISCUSSION
Overview of polysaccharide elasticity produced by 1→6 linkages
We begin by comparing the molecular elasticity of three linear glucose-based homopolysaccharides: methylcellulose, pustulan, and dextran (Fig. 1). Methylcellulose (β-1→4 linkages) serves here as a reference polysaccharide. Methylcellulose does not undergo forced conformational transitions upon stretching, and therefore its elasticity is representative of a simple entropic spring, which can be fitted well with the freely rotating chain model, which is an extension of the FJC model (Fig. 1, blue trace, FJC fit not shown) (Li et al., 1999; Marszalek et al., 1998; 1999a; 2002).
Pustulan
Pustulan, like cellulose, has β-linkages, but interestingly, its elasticity measured recently by Lee et al. (2004) clearly deviates from that of methylcellulose (Fig. 1, red trace). This deviation is particularly visible in the force range of 100–700 pN, where the pustulan length increases almost linearly with the force, a feature typical of Hookean springs, not polymers. This observation indicates that the mechanical properties of β-1→6 linkages are significantly different from the “freely rotating” β-1→4 linkages of methylcellulose. It seems that the bonds in pustulan that experience rotational restrictions and higher forces, as compared to cellulose, are needed to fully extend the pustulan chain (see Fig. 1). The extra work done by the external force on extending pustulan must involve the rotation of the aglycone bond (O6–C6) around the C6–C5 bond, because this rotation occurs in pustulan but is absent in methylcellulose. This rotation can be characterized by the torsional (dihedral) angle ω = O6–C6–C5–O5 (Fig. 1, inset). Three stable staggered rotamers are possible: gt, gg, and tg (Fig. 1, inset). However, x-ray and NMR measurements and computations show a significant preference of the glucopyranose monomer toward gt and gg rotamers, which are populated almost equally, with a nearly complete absence of the tg rotamer (gg/gt/tg/, 60:40:0) (Weimar et al., 1999; Barrows et al., 1995; Momany and Willett, 2000; Kirschner and Woods, 2001; Tvaroška et al., 2002; Appell et al., 2004). An inspection of the glucopyranose ring model shows that the distance between the glycosidic oxygen atoms O1–O6 is at the maximum in the tg conformation (Fig. 1, inset), which, in the relaxed state of the glucopyranose is not populated. The results of our ab initio quantum mechanical calculation of the O1–O6 distance (see Methods) in all three relaxed rotamers gt, gg, and tg for β-D-glucopyranose are shown in Fig. 1 (inset, left panel). The O1–O6 distance is the same for gt and gg rotamers (∼4.96 Å) and it increases by ∼0.92 Å (19%) in the tg conformation. The increase in the length of the pustulan chain between 100 and 700 pN measured by AFM is similar (23%; Fig. 1), suggesting that the Hookean elasticity of pustulan is governed by forced gt → tg and gg → tg rotations. Thus, the O6–C6 bond seems to work as an “atomic crank” that swings and rotates between different positions when acted upon by an external force.
Dextran
Dextran is an α-1→6 linked D-glucose polysaccharide and it was among the first polymers studied by single molecule force spectroscopy using AFM (Fig. 1, black trace, this article; see also Rief et al., 1997; Marszalek et al., 1998). However, its elasticity is still not fully understood. Below ∼700 pN dextran behaves as a fairly simple freely rotating chain with extensible segments (Rief et al., 1997). However, at forces >∼700 pN the force extension curve displays a pronounced plateau. Two models have been proposed to explain the elasticity of dextran. Rief et al. (1997) proposed that the plateau is the result of a rotation of the exocyclic C5–C6 bond, whereas Marszalek et al. (1998) proposed that the plateau reports a flip of the pyranose rings to a boat-like conformation. However, neither of these models provided a detailed account of the atomic events that occur during stretching. Ab initio calculations of α-D-glucose indeed show the dependence of the O1–O6 distance on the rotameric state of the C5–C6 bond (Fig. 1, inset, right panel). This distance is at the minimum in the gt state (4.39 Å) and it increases to 5.16 Å in both the gg and tg states. Thus, rotations around the C5–C6 bond to either gg or tg state can in principle increase the length of dextran. In contrast to pustulan, where all the rings can extend through forced rotations (gt → tg and gg → tg), in dextran only ∼50% of all the rings (gt rotamers) can undergo lengthening transitions (gt → tg, 25% and gt → gg, 25%). This is because in equilibrium, half of the rings are already in the extended gg state even before the chain is stretched, and gg → tg transitions are not expected to produce a significant gain in length. One would therefore expect that the overstretching beyond the initial contour length of dextran should be only approximately one-half of that measured for pustulan. However, the comparison of the normalized force-extension curves for pustulan and dextran suggests that both polysaccharides gain approximately the same extra length (compare to the extension indicated by the arrows in Fig. 1). If the forced rotations around C5–C6 bonds were the only overstretching mechanism in dextran, then why are these rotations able to produce a distinct plateau in its force-extension curve, whereas similar rotations in pustulan do not produce any plateau feature? It is also interesting that dextran requires, on average, a much higher force (and therefore a significantly higher work input) than pustulan to reach the same final length. To understand the differences between the mechanism of the extensibility of pustulan and dextran we need to gain insight into atomic-scale events that occur when these polymers are stretched. Such events can be modeled by molecular dynamics simulations of the stretching process.
SMD simulations of pustulan in water: forced rotations around the C5–C6 bond
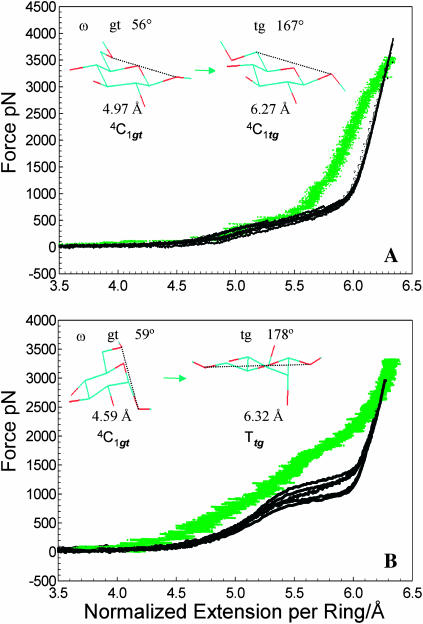
To track the conformational events during the stretching of pustulan and dextran in an atomic force microscope, we carried out steered molecular dynamics (SMD) simulations of this process on a model composed of ten 1→6-linked β-D-glucose rings immersed in a TIP3P water box (see Methods). Fig. 2 A shows the force extension relationship obtained from a 5-ns simulation of pustulan (green trace), together with a set of experimental data (black lines, six different experiments). To compare the simulation result with the experimental data we normalized the latter in such a way that the extension of the chain at a force of 3500 pN equals to 1/10th of the extension of the 10-ring chain, calculated by SMD. We note that the SMD results closely follow the AFM data up to the extension of ∼5.7 Å. However, longer extensions (∼5.7–6.3 Å) required a significantly higher force in silico, as compared to the AFM measurements. We determined that at the end of the stretching process all the rings assumed the tg rotameric state (Fig. 2 A, inset), even though they started as an equilibrium mixture of gt and gg rotamers. All the rings preserved their 4C1 chair conformation throughout the simulation. This is consistent with our understanding of the mechanics of equatorial (β) linkages, which do not trigger conformational transitions of the ring. Gt → tg transitions generated the Hookean-like extension of pustulan, which nicely follows the AFM data, whereas gg → tg transitions occurred at much higher forces and produced that part of the SMD curve that significantly deviates from the experimental data.
FIGURE 2.
A comparison between force-extension curves for pustulan (A) and dextran (B) obtained by AFM (black curves) and by SMD simulations of 10 rings in water (green traces, 5-ns calculations). (A) The AFM extensions for the pustulan traces were normalized at a force of 3500 pN to be equal to 1/10th of the chain extension obtained by SMD (6.3 Å). (Inset) Structures of ring 4 at the beginning and at the end of the SMD stretching process reveal a gt → tg transition with no significant change to the conformation of the ring. (B) The AFM extensions for the dextran traces were normalized at a force of 2900 pN to be equal to 1/10th of the extension obtained by the SMD calculation (6.26 Å). (Inset) Structures of ring 7 at the beginning and at the end of the SMD stretching process reveal a gt → tg transition of the C6–O6 bond and a transition in the ring structure from a chair to a twist-boat conformation.
SMD simulations of dextran in water: forced rotations and chair-boat transitions
Fig. 2 B compares the results of a 5-ns SMD simulation of dextran in water (green trace) with a set of the AFM curves (black traces, five different experiments). We note that the theoretical trace correctly reproduces the general shape of the experimental data including the plateau feature, albeit it deviates at intermediate extensions and the plateau occurs at a significantly higher force than that measured by the AFM (∼1500 pN vs. ∼700–1000 pN). We determined that like pustulan, all the rings in dextran end the stretching process in the tg state. However, in contrast to pustulan, all the rings also flipped from the 4C1 chair conformation to a twist-boat (T) conformation (Rao et al., 1998; Appell et al., 2004; see also this article, Fig. 2 B, inset). Thus, we conclude that the elasticity of dextran is dominated by conformational transitions involving both rotations around the C5–C6 bond and chair-boat transitions. However, the fairly large deviations of the SMD data from the AFM measurements for both pustulan and dextran limit the usefulness of our computational results for developing a detailed mechanistic model of the elasticity of these polymers.
Solvents do not affect the elasticity of pustulan and dextran
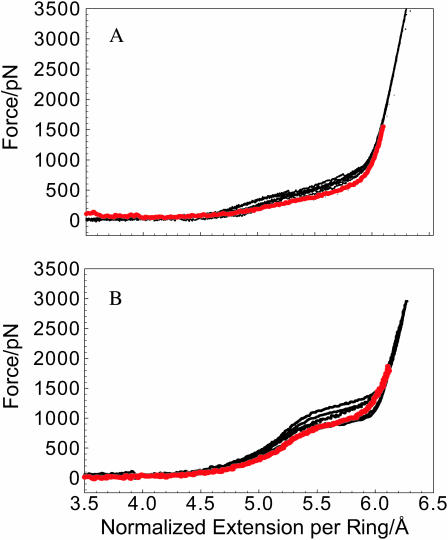
It is possible that the discrepancies between SMD and AFM data indicate the imperfections of the force field used (Kuttel et al., 2002) in our MD simulations and/or the differences between the stretching pathways exercised experimentally and by SMD. AFM measurements proceed at a timescale of 100 ms to several seconds and the stretching process occurs in equilibrium. The SMD stretching is approximately eight orders-of-magnitude faster and therefore is likely not an equilibrium process. The reliable experimental data on the kinetics of various conformational transitions in the glucopyranose ring are scarce. The estimates for the rotational isomerization of the C6–O6 bond vary between 10−10 and 10−3 s (Kuttel et al., 2002, and references cited therein) with the most recent data suggesting the nanosecond-timescale (Stenger et al., 2000). As for the chair-boat or chair inversion exchange of the glucopyranose ring we did not find any recent experimental data, and the available data for cyclohexane place these transitions on an approximately microsecond-timescale (Pickett and Strauss, 1970). If we assume that the parameterization of the carbohydrate solution force field is reasonable and that the timescale of the observed conformational transitions is between nanoseconds and microseconds we need to significantly slow down the stretching process by SMD to approach the equilibrium condition. However, microsecond-scale simulations which are expected to be complete in a reasonable amount of time (month) can only be carried out with no explicit solvent. Such simulations could still be sensible if water plays no critical role in the elasticity of these polysaccharides. To test this assumption we carried out a number of AFM stretching measurements on pustulan and dextran under various solvent conditions. Specifically we were interested in examining the effect of the bulk dielectric constant of the medium on their elasticity. In Fig. 3 A we compare the force curves for pustulan obtained in water (black traces) and in dimethyl carbonate (DMC; red trace) whose dielectric constant is 3.1 (25-times less than water). We see that the AFM data in DMC is within the scatter of the results obtained in water. From this observation we conclude that the characteristic elasticity of pustulan is not solvent-dependent. In Fig. 3 B we show the data for dextran obtained in ethanol whose dielectric constant is 25. We conclude that the solvent does not seem to significantly affect the elasticity of dextran as well. (We failed to carry out similar measurements on dextran in DMC, because in this solvent dextran did not stick to the AFM tip.) It should not be inferred from our experiments that solvents do not have any effect on the behavior of dextran and pustulan and it is possible that our results may not be applicable to other polysaccharides. For example, ethanol is a precipitating solvent for dextran, and dextran tends to aggregate in this solvent. However, as Fig. 3 B suggests, the elasticity of single dextran chains in ethanol is similar to that obtained in water. Based on these results we decided to carry out SMD calculations in the implicit rather than explicit solvent. This reduction of the system (number of atoms decreased from ∼10,000 to 213) and the resulting acceleration of MD calculations allowed us to slow down the stretching process by 200- to 1000-fold as compared to the simulations in water.
FIGURE 3.
The elasticity of dextran and pustulan is not affected by solvents. We compare the experimental force-extension curves for pustulan (A) and dextran (B) obtained in water (black traces) and in solvents with a low dielectric constant (ɛ) (red traces). (A) The red trace represents the force curve for pustulan obtained in dimethyl carbonate (ɛ = 3.1). (B) The red trace represents the force curve for dextran obtained in ethanol (ɛ = 25).
One-μs SMD simulation of pustulan in implicit solvent: gg→ tg transitions are complete during the Hookean phase of the stretch
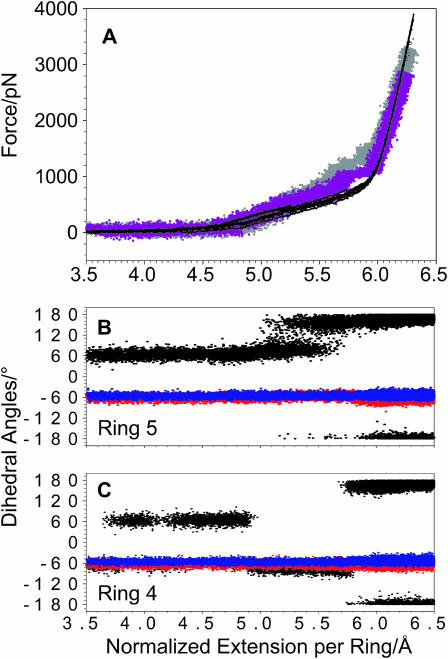
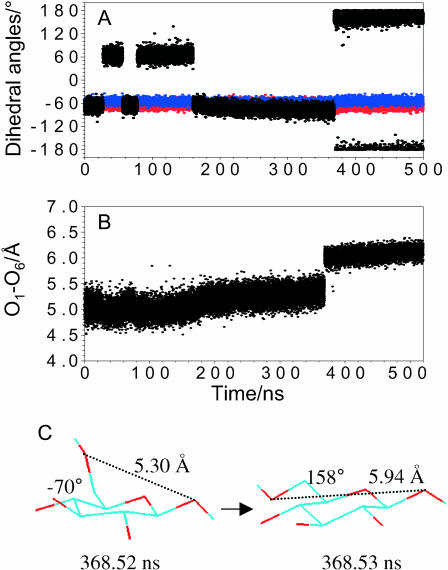
In Fig. 4 A we compare the force extension curves for pustulan obtained with AFM (black curves) and from a 200-ns (gray trace) and a 1-μs (violet trace) SMD simulation carried out in implicit solvent. The results of the 200-ns simulation (stretching speed 5 × 10−7 Å/fs) are much closer to the AFM data than the results of 5-ns simulation in water (Fig. 2 A). However, it took a 1-μs simulation (stretching speed 1 × 10−7 Å/fs) to obtain a very satisfactory agreement between the experiment and the calculation. This observation clearly suggests that the underlying forced rotations in pustulan are fairly slow and must occur at a timescale of tens to hundreds of nanoseconds and that only microsecond-scale calculations can model these processes in quasiequilibrium. To follow the conformational behavior of the pyranose rings and the C6–O6 bonds during the 1-μs simulation we monitored three dihedral angles: ω = O6–C6–C5–O5 reports the rotameric status around the C6–C5 bond, whereas t1 = O1–C1–C2–O2 and t2 = O5–C5–C4–C3 (Fig. 1, inset) report chair-boat transitions. In Fig. 4, B and C, we plot the values of these torsions as a function of the normalized extension of the chain for ring 4, which started in the gg state, and for ring 5, which started as the gt rotamer. First, we note that as in the simulation with explicit water, in the present simulation the torsions t1 and t2 (red and blue traces) also remained constant, indicating no ring transitions. Next, we note that, as before, all the rings end the stretching process as tg rotamers. However, in contrast to the previous simulation, now, not only the gt → tg but also all gg → tg transitions are complete at forces below 1000 pN, and this change results in an excellent fit of the SMD data to the AFM measurements. However, our results do point to a difference between the mechanically driven gt → tg and gg → tg transitions in pustulan. Gt→ tg transitions occur, on average, at lower forces than gg → tg transitions, and are preceded by long phases (∼100 ns) of the gt ↔ tg equilibrium (Fig. 4 B). Gg → tg transitions, on the other hand, occur later during the stretch, and always happen very abruptly. Fig. 5 illustrates this last observation by showing the time sequence of the rotational events for ring 4. In the initial phase of the stretch when the applied force is very small, <100 pN, ring 4, which started as a gg rotamer, spends also a significant amount of time in the gt state, each visit lasting 30–100 ns. These gg ↔ gt transitions must be thermally driven and their occurrence proves that the chain is in equilibrium. At ∼180 ns into the simulation, the ring returns to the gg state and when the stretching force starts to increase (Fig. 4 A) we observe a small but steady increase in the ω-dihedral, which is accompanied by a steady increase in the O1–O6 separation (Fig. 5 B). Then, at 368.52 ns the C6–O6 “crank” flips abruptly to the tg state, increasing the O1–O6 distance in a stepwise fashion (Fig. 5, B and C), and the bond remains in that state until the end of the simulation. We hypothesize that the difference between forced gt → tg and gg → tg transitions in pustulan reflects the differences between the distribution of the forces applied to the C6–O6 bond in both cases.
FIGURE 4.
A 1-μs SMD simulation of pustulan reproduces well the AFM stretching data. (A) A comparison between the normalized force-extension curves for pustulan obtained by AFM (black traces) and by SMD (gray trace, 200-ns simulation; violet trace, 1-μs simulation). (B) The conformational dynamics of ring 5 during the 1-μs simulation as revealed by the three torsions: ω (black trace), t1 (red trace), and t2 (blue trace). (C) The conformational dynamics of ring 4 during the 1-μs simulation: ω = O6–C6–C5–O5 reports the rotameric status around the C6–C5 bond, and t1 = O1–C1–C2–O2 and t2 = O5–C5–C4–C3 report the conformational status of the pyranose ring, e.g., chair-boat transitions.
FIGURE 5.
Analysis of the 1-μs SMD trajectory of ring 4 reveals thermally driven and force driven conformational transitions between gg, gt, and tg states. (A) Time trajectory evolution of the three torsions. The initial gg ↔ gt transitions occur at a minimal stretching force and therefore are driven thermally. The gg → tg transition at 368.52 ns is driven by the external force. (B) Time evolution of the O1–O6 distance reveals a stepwise increase at 368.52 ns due to the gg → tg transition. (C) Two structures of ring 4, separated by 10 ps, immediately before and after the gg → tg transition.
From the analysis of the SMD calculations we conclude that the Hookean elasticity of pustulan is governed by forced rotations of the O6–C6 “crank” around the C5–C6 bond, which shift the distribution of the rotamers from the less energetic and shorter gt and gg conformers to the more energetic and longer tg rotamers. We emphasize that all the rings in pustulan preserve their 4C1 chair conformation during the stretching process.
One-μs SMD simulation of dextran in implicit solvent: C5–C6 rotations are coupled to chair-boat transitions
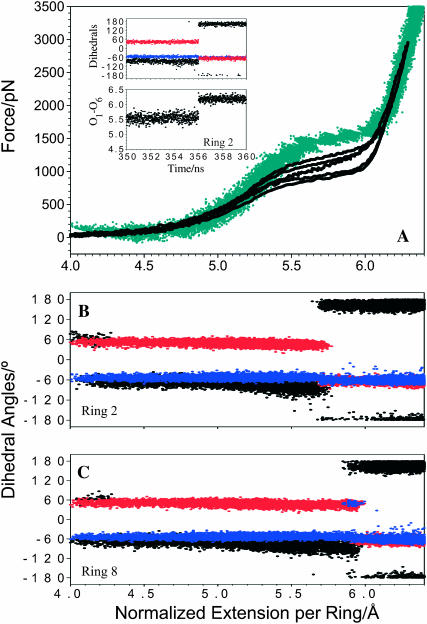
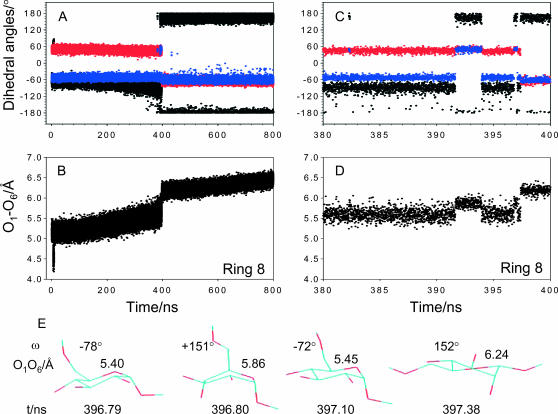
Figs. 6 and 7 show the results of our 1-μs-long SMD simulation of dextran in implicit solvent. Similar to pustulan we see a significant improvement of the fit between the calculation and the AFM data over the 5 ns simulation in water. Good quality of this simulation allows us to propose a detailed model of the stretching process. We determined that, as in the 5-ns simulation, all the rings end the stretching process in a boat-like, tg conformation; however, as discussed in detail below, there are two main differences between the fast and slow stretching. In the 5-ns simulation, gt → gg transitions occurred during the rising phase of the force extension profile, and the gg → tg rotations preceded chair-boat transitions during the plateau phase. The 1-μs simulation reveals that the gt → gg transitions occur at a very early stage of the stretching process, before the force increases above ∼100 pN. Therefore, these low energy transitions do not contribute to the rising phase of the force-extension curve at all; instead, they merely increase the contour length of dextran during the initial phase of the stretch. The second significant difference is that with the slow stretching the final gg → tg rotations occur simultaneously with chair-boat transitions. The temporal analysis of the SMD trajectories suggests that the rings typically undergo compound transformations 4C1,gg → 2,5Btg or 4C1,gg → Ttg, where B represents a boat and T represents a twist-boat, with the C6–O6 bond in the tg orientation (Appell et al., 2004).
FIGURE 6.
A 1-μs SMD simulation of dextran reproduces well the AFM stretching data. (A) A comparison between the normalized force-extension curves for dextran obtained by AFM (black traces) and by SMD (turquoise trace). (Inset) High-resolution time trajectory of the three torsions (upper plot) and the O1–O6 distance (lower plot) for ring 2 reveals a single-step compound conformational transition 4C1gg → Ttg. (B) Conformational dynamics of ring 2 as revealed by the trajectories of the three torsions displayed along the normalized extension of the chain. (C) The conformational dynamics of ring 8. The color-code for the torsions as in Figs. 4 and 5.
FIGURE 7.
Time evolution of the structure of ring 8 reveals ring instabilities and a series of discrete forced conformational transitions involving simultaneous rotations of the C6–O6 bond and transitions to boat-like conformations. (A) Full time trajectory for the three torsions. (B) Full time trajectory for the O1–O6 distance. (C) High-resolution time trajectory of the three torsions during the force-induced ring instability between 380 and 400 ns. (D) High-resolution time trajectory of the O1–O6 distance reveals discrete changes in the separation between the glycosidic oxygens, which accompany the compound conformational transitions involving gg ↔ tg rotations and ring instabilities. (E) Structures of ring 8 during a time window of 396–398 ns, extracted from the SMD simulation, reveal complex force-induced conformational transitions involving simultaneous rotations of the C6–O6 bond and the transitions to an intermediate 2,5B boat structure and the final Ttg twist-boat.
In Fig. 6, B and C, we display the dihedral angles of two representative rings, rings 2 and 8 as a function of the normalized chain extension and in Fig. 7 we follow the conformational behavior of ring 8 in time. We determine that before the extension of the chain per ring reaches 4.6 Å, the rotamer equilibrium is completely shifted to the gg state (compare to Fig. 6, B and C). This behavior is perfectly understandable considering the facts that gg rotamers are longer and their energy is comparable to gt rotamers (Kuttel et al., 2002; Appell et al., 2004). As shown for rings 2 and 8, the C6–O6 bonds, after flipping to the gg state, display a very low rotational mobility and they bend steadily toward the tg state. This process is monitored by the ω-angle, which increases continuously toward the tg state from −60° up to −100° (compare to a declining slope of black traces in Fig. 6, B and C, and Fig. 7, A and B). This continuous bending is accompanied by a similar small movement of the O1–C1 bonds, which are pulled from their axial orientation toward the quasiequatorial orientation (see the small but steady decline of the red traces in Fig. 6, B and C, and Fig. 7, A and B). Combined, these two motions provide a continuous extension of the chain during the rising phase of the force-extension curve that precedes the plateau. A careful analysis of the trajectories indicates that the onset of the plateau feature coincides with the onset of gg → tg rotations and ring instabilities.
Forced conformational transitions in dextran
Two types of forced transitions take place and they are exemplified by the behavior of rings 2 and 8 in Fig. 6, B and C, and in Fig. 7. Ring 2 (Fig. 6 B) flips to its final conformation in a single 4C1,gg → Ttg transformation. This event can be easily identified in the time trajectory of this ring, which, at 356 ns, displays a sharp transition in the dihedrals ω (black trace) and t1 (red trace) and a stepwise increase in the O1–O6 distance (Fig. 6, inset). The conformational behavior of ring 8, which is followed by another 50% of the rings, is somewhat more complex. In Fig. 7, A and B, we show the full time trajectory for this ring, and in Fig. 7, C and D, we follow, at a higher temporal resolution, its behavior during the forced conformational transitions. The O1–O6 distance of this ring increases in a stepwise manner at the beginning of the simulation as a result of the gt→ gg transition. This transition requires very little force (see Fig. 6 A). The O1–O6 distance continues to increase steadily due to a small reorientation of the C6–O6 and C1–O1 bonds (compare to black and red traces in Fig. 7 A and trace in Fig. 7 B). At ∼390 ns (during the plateau phase of the stretching), the ring starts to experience a conformational instability, which is shown in Fig. 7, C–E. At 391.5 ns the C6–O6 bond flips to the tg orientation and at the same time the ring flips to a 2,5B boat (see stepwise changes in ω, black trace, and t2, blue trace in Fig. 7 C). This compound transition produces a step increase in the O1–O6 distance. The ring stays in this conformation for ∼2.5 ns and then returns to the 4C1,gg chair conformation (note that the O1–O6 distance decreases upon this transformation, Fig. 7 D). At 396.79 ns the ring starts a series of rapid conformational transitions that is depicted in Fig. 7 E. This series includes another transition to the intermediate 2,5Btg structure, and it ends when the ring acquires the Ttg twist-boat conformation, which is the final conformation for all the rings in dextran. Ttg seems to work as a ratchet, which locks the ring conformation and secures the gain in the O1–O6 distance. Pure gg → tg rotations in the 4C1 chair conformation also occur and they precede the final compound transition of the ring (Fig. 7, C and D, between 380 and 390 ns). They generate little gain in the O1–O6 distance, and this gain is not permanent because of the reverse transitions O1–O6 averages at ∼5.6 Å. It is the transition to the final Ttg twist boat structure, with the C6–O6 in the tg position and the C1–O1 bond in the quasiequatorial orientation, that provides the maximum gain in the O6–O1 length which is permanent.
From this analysis we conclude that the extensibility of dextran is governed by a series of forced conformational transitions: the initial gt → gg transitions occur at very low forces and are followed by small reorientations of the aglycone and glycosidic bonds. These in turn are followed by the compound chair-boat and gg → tg transitions to the final Ttg conformation of the ring. Our results, by providing many hitherto unknown details, support the earlier results of Marszalek et al. (1998), who proposed that the final conformation of the pyranose ring in the stretched dextran is a boat.
The energetics of atomic cranks and levers
An important result of our 1-μs SMD simulations is the accurate length of the pustulan and dextran decamers as a function of the applied force. This data allowed us to normalize, per ring, the extension of the polysaccharide chains measured by AFM (Figs. 4 and 6). We will now use the renormalized force curves in Fig. 1 to estimate the work per ring (or per bond) necessary to carry out various conformational transitions by comparing the stretching work of pustulan and dextran to that of cellulose. By calculating the areas under the renormalized force curves in Fig. 1, up to the force of 1538 pN (which is the maximum force for cellulose), we find that: wcell = 4.9 kcal/mol/ring, wpust = 10.7 kcal/mol/ring, and wdex = 16.8 kcal/mol/ring. We can now estimate the work to rotate the atomic “crank,” the C6–O6 bond around the C6–C5 bond, as wrot = wpust−wcell = 5.8 kcal/mol/bond. Similarly, the work of the atomic “lever,” the C1–O1 bond and the atomic crank, C6–O6, to flip the ring to the Ttg twist-boat conformation by their common action, can be estimated as wc–b = wdex−;wcell = 11.9 kcal/mol/ring. The significant energy difference between the deformed pyranose ring in dextran and pustulan is, in our opinion, the single most convincing evidence supporting our conjecture that the final conformation of the pyranose ring in the stretched dextran chain must be a (twist) boat.
Can forced conformational transitions in sugar rings play a role in biological systems?
It is tempting to speculate that the types of conformational transitions we described here occur in biological systems during, e.g., interactions between cells where forces amounting to several hundred piconewtons per single ligand/receptor bonds occur (Puri et al., 1998). Similarly, large deforming forces are expected to act on the pyranose ring and the glycosidic linkage during various enzymatic processes. In β-1→6 linked sugar ligands, the forced rotation of the O6–C6 bond to the tg conformation would requires little force, and would result in a significant reorientation of the oxygen atom, O6 to a position where it could engage in, e.g., a hydrogen bonding. Similarly, in α-1→6 linked sugars, a small stretching force would easily shift the gt/gg equilibrium toward the gg state with the similar effect. In extreme cases the adhesive forces would not only rotate the O6–C6 bond but could also flip the pyranose ring to a boat-like conformation with a dramatic reorientation of all the hydroxyl groups. Such a reorientation would have a profound effect on the interaction with a lectin receptor (Drickamer, 1997).
The unique mechanical properties of the pyranose ring with its many discrete conformations may be useful in various nanotechnological applications. For example, many molecular springs with desired lengths and elastic properties (purely entropic, Hookean, mixed) could be constructed with pyranose rings by tailoring different glycosidic linkages. Our results provide the basis for a rational design of such nanosprings.
CONCLUSIONS
By comparing the results of QM and SMD calculations with single molecule force spectroscopy measurements we explained the mechanism of the elasticity of two mechanically complementary glucose polysaccharides with 1 → 6 linkages. Our results strongly suggest that the aglycone cranks and equatorial glycosidic levers force the rotation around the C5–C6 bond but do not change the chair structure of the pyranose ring (pustulan). Aglycone cranks and axial glycosidic levers promote the rotation around the C5–C6 bond and they flip the pyranose ring to a boat-like structure (dextran). Our approach allowed us to correctly interpret the results of single-molecule AFM measurements and to gain insight into the conformational mechanics of the pyranose ring. It is possible that the conformational transitions that we induce in the glucose ring by AFM manipulations mimic the rearrangements that occur in sugars when they carry out their biological functions.
Acknowledgments
This work was supported by a grant from the National Science Foundation (MCB-0243360) and by Duke University funds to P.E.M.
References
- Appell, M., G. Strati, J. L. Willett, and F. A. Momany. 2004. B3LYP/6–311++G** study of α- and β-D-glucopyranose and 1,5-anhydro-D-glucitol: 4C1 and 1C4 chairs, 3,OB and B3,O boats, and skew-boat conformations. Carbohydr. Res. 339:537–551. [DOI] [PubMed] [Google Scholar]
- Barrows, S. E., F. J. Dulles, C. J. Cramer, A. D. French, and D. G. Truhlar. 1995. Relative stability of alternative chair forms and hydroxymethyl conformations of β-D-glucopyranose. Carbohydr. Res. 276:219–251. [Google Scholar]
- Barton, D. H. R. 1970. The principles of conformational analysis. Science. 169:539–544. [DOI] [PubMed] [Google Scholar]
- Brant, D. A. 1999. Novel approaches to the analysis of polysaccharide structures. Curr. Opin. Struct. Biol. 9:556–562. [DOI] [PubMed] [Google Scholar]
- Brunger, A. 1992. X-PLOR, Version 3.1: A System for X-Ray Crystallography and NMR. Yale University, New Haven, CT.
- Drickamer, K. 1997. Making a fitting choice: common aspects of sugar-binding sites in plant and animal lectins. Structure. 5:465–468. [DOI] [PubMed] [Google Scholar]
- Florin, E. L., M. Rief, H. Lehmann, M. Ludwig, C. Dornmair, V. T. Moy, and H. E. Gaub. 1995. Sensing specific molecular interactions with the atomic force microscope. Biosensors Biolelectr. 10:895–901. [Google Scholar]
- Flory, P. J. 1953. Principles of Polymer Chemistry. Cornell University Press, Ithaca, NY .
- French, A. D., R. S. Rowland, and N. L. Allinger. 1990. Modeling of glucopyranose. The flexible monomer of amylose. In Computer Modeling of Carbohydrate Molecules. A. D. French and J. W. Brady, editors. ACS Symposium series, American Chemical Society, Washington, DC. 121–140.
- Gao, M., H. Lu, and K. Schulten. 2002. Unfolding of titin domains studied by molecular dynamics simulations. J. Muscle Res. Cell Motil. 23:513–521. [DOI] [PubMed] [Google Scholar]
- Grubmüller, H., B. Heymann, and P. Tavan. 1996. Ligand binding and molecular mechanics calculation of the streptavidin-biotin rupture force. Science. 271:997–999. [DOI] [PubMed] [Google Scholar]
- Hellerqvist, C. G., B. Lindberg, and K. Samuelsson. 1968. Methylation analysis of pustulan. Acta Chem. Scand. 22:2736–2737. [Google Scholar]
- Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD—visual molecular dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
- Izrailev, S., S. Stepaniants, M. Balsera, Y. Oono, and K. Schulten. 1997. Molecular dynamics study of unbinding of the avidin-biotin complex. Biophys. J. 72:1568–1581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Isralewitz, B., M. Gao, and K. Schulten. 2001. Steered molecular dynamics and mechanical functions of proteins. Curr. Op. Struct. Biol. 11:224–230. [DOI] [PubMed] [Google Scholar]
- Kalé, L., R. Skeel, M. Bhandarkar, R. Brunner, A. Gursoy, N. Krawetz, J. Phillips, A. Shinozaki, K. Varadarajan, and K. Schulten. 1999. NAMD2: greater scalability for parallel molecular dynamics. J. Comput. Phys. 151:283–312. [Google Scholar]
- Kirschner, K. N., and R. J. Woods. 2001. Solvent interaction determine carbohydrate conformation. Proc. Natl. Acad. Sci. USA. 98:10541–10545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krammer, A., H. Lu, B. Isralewitz, K. Schulten, and V. Vogel. 1999. Forced unfolding of the fibronectin type III module reveals a tensile molecular recognition switch. Proc. Natl. Acad. Sci. USA. 96:1351–1356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuttel, M., J. W. Brady, and K. J. Naidoo. 2002. Carbohydrate solution simulations: producing a force field with experimentally consistent primary alcohol rotational frequencies and populations. J. Comput. Chem. 23:1236–1243. [DOI] [PubMed] [Google Scholar]
- Lee, G., W. Nowak, J. Jaroniec, Q. Zhang, and P. E. Marszalek. 2004. Nanomechanical control of glucopyranose rotamers. J. Am. Chem. Soc. 126:6218–6219. [DOI] [PubMed] [Google Scholar]
- Li, H., M. Rief, F. Oesterhelt, and H. E. Gaub. 1998. Single-molecular force spectroscopy on xanthan by AFM. Adv. Mater. 10:316–319. [Google Scholar]
- Li, H., M. Rief, F. Oesterhelt, H. E. Gaub, X. Zhang, and J. Shen. 1999. Single-molecule force spectroscopy on polysaccharides by AFM—nanomechanical fingerprint of α-(1,4)-linked polysaccharides. Chem. Phys. Lett. 305:197–201. [Google Scholar]
- Lindberg, B., and J. McPherson. 1954. Studies on the chemistry of lichens. VI. The structure of pustulan. Acta Chem. Scand. 8:985–988. [Google Scholar]
- Lu, H., B. Isralewitz, A. Krammer, V. Vogel, and K. Schulten. 1998. Unfolding of titin immunoglobulin domains by steered molecular dynamics. Biophys. J. 75:662–671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu, H., and K. Schulten. 1999a. Steered molecular dynamics simulations of force-induced protein domain unfolding. Proteins Struct. Funct. Gen. 35:453–463. [PubMed] [Google Scholar]
- Lu, H., and K. Schulten. 1999b. Steered molecular dynamics simulation of conformational changes of immunoglobulin domain I27 interpret atomic force microscopy observations. Chem. Phys. 247:141–153. [Google Scholar]
- Marszalek, P. E., A. F. Oberhauser, Y.-P. Pang, and J. M. Fernandez. 1998. Polysaccharide elasticity governed by chair-boat transitions of the glucopyranose ring. Nature. 396:661–664. [DOI] [PubMed] [Google Scholar]
- Marszalek, P. E., Y. P. Pang, H. Li, J. E. Yazal, A. F. Oberhauser, and J. M. Fernandez. 1999a. Atomic levers control pyranose ring conformations. Proc. Natl. Acad. Sci. USA. 96:7894–7898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marszalek, P. E., H. Lu, H. Li, M. Carrion-Vazquez, A. F. Oberhauser, K. Schulten, and J. M. Fernandez. 1999b. Mechanical unfolding intermediates in titin modules. Nature. 402:100–103. [DOI] [PubMed] [Google Scholar]
- Marszalek, P. E., A. F. Oberhauser, H. Li, and J. M. Fernandez. 2003. The force-driven conformations of heparin studied with single molecule force microscopy. Biophys. J. 85:2696–2704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marszalek, P. E., H. Li, A. F. Oberhauser, and J. M. Fernandez. 2002. Chair-boat transitions in single polysaccharide molecules observed with force-ramp AFM. Proc. Natl. Acad. Sci. USA. 99:4278–4283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marszalek, P. E., H. Li, and J. M. Fernandez. 2001. Fingerprinting polysaccharides with single molecule AFM. Nat. Biotech. 19:258–262. [DOI] [PubMed] [Google Scholar]
- Momany, F. A., and J. L. Wilett. 2000. Computational studies on carbohydrates: solvation studies on maltose and cyclomaltooligosaccharides (cyclodextrins) using a DFT/ab initio-derived empirical force field, AMB99C. Carbohydr. Res. 326:210–226. [DOI] [PubMed] [Google Scholar]
- Oberhauser, A. F., P. E. Marszalek, H. P. Erickson, and J. M. Fernandez. 1998. The molecular elasticity of the extracellular matrix protein tenascin. Nature. 393:181–185. [DOI] [PubMed] [Google Scholar]
- O'Donoghue, P., and Z. A. Luthey-Schulten. 2000. Barriers to forced transitions in polysaccharides. J. Phys. Chem. B. 104:10398–10405. [Google Scholar]
- Pensak, D. A., and A. D. French. 1980. Conformational differences and steric energies for compounds containing α-D-glucopyranose chairs having a range of O4–O1 distances. Carbohydr. Res. 87:1–10. [Google Scholar]
- Pickett, H. M., and H. L. Strauss. 1970. Conformational structure, energy, and inversion rates of cyclohexane and some related oxanes. J. Am. Chem. Soc. 92:7281–7290. [Google Scholar]
- Puri, K. D., S. Chen, and T. A. Springer. 1998. Modifying the mechanical property and shear threshold of L-selectin adhesion independently of equilibrium properties. Nature. 392:930–933. [DOI] [PubMed] [Google Scholar]
- Rao, V. S. R., P. K. Qasba, P. V. Balaji, and R. Chandrasekaran. 1998. Conformation of Carbohydrates. Harwood Academic Publishers, Amsterdam, The Netherlands.
- Rief, M., F. Oesterhelt, B. Heymann, and H. E. Gaub. 1997. Single molecule force spectroscopy on polysaccharides by atomic force microscopy. Science. 275:1295–1297. [DOI] [PubMed] [Google Scholar]
- Stenger, J., M. C. Cowman, F. Eggers, E. M. Eyring, U. Kaatze, and S. Petrucci. 2000. Molecular dynamics and kinetics of monosaccharides in solution. A broadband ultrasonic relaxation study. J. Phys. Chem. B. 104:4782–4790. [Google Scholar]
- Tvaroška, I., F. R. Taravel, J. P. Utille, and J. P. Carver. 2002. Quantum mechanical and NMR spectroscopy studies on the conformations of the hydroxymethyl groups in aldohexosides. Carbohydr. Res. 337:353–367. [DOI] [PubMed] [Google Scholar]
- Weimar, T., U. C. Kreis, J. S. Andrews, and B. M. Pinto. 1999. Conformational analysis of maltoside heteroanalogues using high-quality NOE data and molecular mechanics calculations. Flexibility as a function of the interglycosidic chacogen atom. Carbohydr. Res. 315:222–233. [Google Scholar]
- Whistler, R. L., and J. N. BeMiller. 1993. Industrial Gums. Polysaccharides and their Derivatives. Academic Press, San Diego, CA.