Kinetics of Target Site Localization of a Protein on DNA: A Stochastic Approach

Abstract

It is widely recognized that the cleaving rate of a restriction enzyme on target DNA sequences is several orders-of-magnitude faster than the maximal one calculated from the diffusion-limited theory. It was therefore commonly assumed that the target site interaction of a restriction enzyme with DNA has to occur via two steps: one-dimensional diffusion along a DNA segment, and long-range jumps coming from association-dissociation events. We propose here a stochastic model for this reaction which comprises a series of one-dimensional diffusions of a restriction enzyme on nonspecific DNA sequences interrupted by three-dimensional excursions in the solution until the target sequence is reached. This model provides an optimal finding strategy which explains the fast association rate. Modeling the excursions by uncorrelated random jumps, we recover the expression of the mean time required for target site association to occur given by Berg et al. in 1981, and we explicitly give several physical quantities describing the stochastic pathway of the enzyme. For competitive target sites we calculate two quantities: processivity and preference. By comparing these theoretical expressions to recent experimental data obtained for EcoRV-DNA interaction, we quantify: 1), the mean residence time per binding event of EcoRV on DNA for a representative one-dimensional diffusion coefficient; 2), the average lengths of DNA scanned during the one-dimensional diffusion (during one binding event and during the overall process); and 3), the mean time and the mean number of visits needed to go from one target site to the other. Further, we evaluate the dynamics of DNA cleavage with regard to the probability for the restriction enzyme to perform another one-dimensional diffusion on the same DNA substrate following a three-dimensional excursion.

INTRODUCTION

Genetic events often depend on the interaction of a restriction enzyme with a target DNA sequence. Indeed, the restriction enzyme has first to find this sequence on DNA. This mechanism has long remained mysterious. The simplest model considers this mechanism as a reaction between two point-like entities, the restriction enzyme and its target DNA sequence, in a solute volume. However, kinetic measurements of reactivity show that the reaction occurs at an extraordinarily rapid rate, far above the three-dimensional diffusion limit rate (Richter and Eigen, 1974; Riggs et al., 1970). To account for this, it was proposed that the reaction occurs via a facilitated diffusion process (Von Hippel and Berg, 1989). The restriction enzyme first binds to DNA on a nonspecific site, then performs a one-dimensional random walk until it reaches the target DNA sequence. Indeed, it is by scanning the DNA and not by diffusing in a three-dimensional volume that the restriction enzyme reaches its target site sequence. However, results from experiments (Szczelkun and Halford, 1996) using two interlinked rings of DNA (plasmid, each containing a target site for the restriction enzyme EcoRV) rule out this possibility: the mechanism of target site localization does not involve a unique one-dimensional diffusion along DNA. If it were the case, the EcoRV enzyme would cleave the DNA of only one of the two rings, as opposed to what is observed. Moreover, it is expected that molecular crowding of in vivo situations must hinder any long one-dimensional scanning process of the DNA (Wenner and Bloomfield, 1999).

To account for the fast association rate, several strategies have been proposed and modeled from experimental data (Berg et al., 1981; Von Hippel and Berg, 1989; Winter et al., 1981). Four major translocation processes were identified (we recall that translocation is the overall process by which a protein goes from one DNA sequence to another). The first, the sliding process, corresponds to the pure one-dimensional diffusion as discussed above. The second, the intersegmental transfer (Milsom et al., 2001), involves dimer proteins having two binding sites. The restriction enzyme bound on DNA at the first site binds its second site to a remote DNA sequence and then dissociates from the first one. The two other translocation processes are induced by several dissociation-reassociation events. According to the rebinding of the enzyme either near the departure site or to an uncorrelated site, the translocation process is called hopping or jumping (Halford and Szczelkun, 2002). Which of these translocation processes or which combination of them describes the mechanism of target site localization on DNA is still an open question.

Understanding the translocation process is of great importance as it governs the kinetics of genetic events (Misteli, 2001). Several experimental investigations were carried out to elucidate the pathway followed by a restriction enzyme to reach a single target site. Some of them quantify the rate of cleavage reactions, by varying the length of the DNA strand (for a review, see Shimamoto, 1999) or the salt concentration (Winter et al., 1981; Lohman, 1996) which affects the binding properties of DNA-affine proteins on nonspecific sequences. These experimental results allow one to reject the possibility of a unique translocation process, but cannot fully describe the structure of the combined process. Berg et al. (1981) had proposed a theoretical approach to quantify the relevant parameters of the localization of a single target site. Their model describes the overall searching process comprising the primary encounter of the enzyme with a DNA domain and the secondary encounter of the enzyme with the target site. Here we deal with the unvisited case of two competitive target sites to quantitatively analyze the physical properties of the second encounter, i.e., the target site localization of a restriction enzyme initially bounded to the DNA. Only the study of such systems gives access to the detailed pathway of secondary encounter with well-defined initial conditions. Related experimental studies with two differentiable target sites located at well-defined positions on the DNA strand (Langowski et al., 1983; Terry et al., 1985; Stanford et al., 2000) allow one to handle two descriptive quantities: the preference and the processivity of the restriction enzymes. The preference is the ratio of the number of enzymes that react with one target site, over the number of enzymes that react with the other target site. The processivity is the fraction of enzymes that will react successively with the two target sites. To extract from these experiments physical parameters of the enzyme pathway such as the proportion of time spent by the enzyme on the DNA, the average number of dissociation-association events and the average DNA length scanned before the target site localization, it is necessary to build a reliable physical model that can mimic the biological situation.

Here, we propose a simple and general stochastic model to describe the kinetics of target site localization of a restriction enzyme on DNA, which explicitly combines any one-dimensional motion along the DNA and three-dimensional excursions in the solution. In the particular case of one-dimensional diffusing motion, our model allows us to recover the analytic expression for the mean time needed for the enzyme to find a single target site on DNA given by Berg et al. (1981). This mean time presents an optimum, corresponding to the quickest finding strategy that can be discussed in the cases of point-like and extended target sites. The model explicitly gives the mean number of enzyme visits on the DNA and the proportion of the DNA visited until the target site is localized. For two target sites, our model provides theoretical expressions for the preference and the processivity factors. These expressions involve two unknown physical parameters: the one-dimensional and three-dimensional residence frequencies λ and λ′. We show that λ is easily evaluated from the confrontation of the theoretical preference to experimental data. The second unknown parameter λ′, of minor physical relevance, is extracted from the assumption that the searching strategy is optimal which will be justified. The comparison of the theoretical processivity factor to experimental data allows us to predict the value of a dynamic-associated parameter: the probability that after an excursion the enzyme will associate to the same DNA substrate it has left, π_r.

The article is constructed as follows: first we give the general background of such an approach and we present the hypothesis of our model. Then we deduce the mean search time from the study of the density of the first time passage, and for the cases of point-like and extended target sites we discuss the optimal strategy for finding the target site as quickly as possible. We give the condition of existence of this optimal strategy as well as its quantitative characteristics. We discuss the value of the optimal one-dimensional frequency and evaluate finite-size effects. Equation 12 gives the mean target site localization time for an enzyme which starts from a random position on the DNA. The complete distribution of the number of visits of the protein on the DNA is explicitly determined. In particular, its mean value is given by Eq. 18. The average number of distinct basepairs (bp) visited on the DNA is given by Eq. 21. Second, the preference and the processivity factors of the restriction enzyme for two target sites, as functions of the distance between the target sites, are obtained (Eqs. 36 and 39) and compared with experimental results concerning EcoRV (Stanford et al., 2000). The comparison gives us the residence time on the DNA per binding event and other related physical quantities. We then numerically obtain the mean time needed for the enzyme to go from the first target site to the second target site (using Eq. 37), and the mean number of visits on the DNA substrate before the two target sites are cleaved. In conclusion, we discuss the predicted value of π_r defined previously.

MODEL

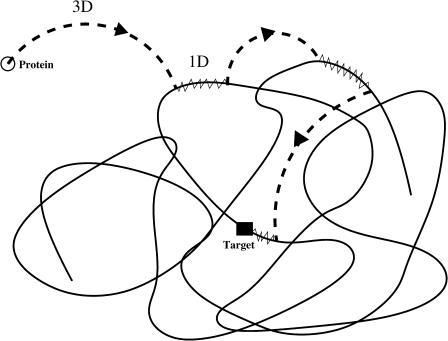
We present our model in the framework of a generic protein searching for its target site on the DNA. The case of dimer proteins which can bind simultaneously to two target sites is not investigated to discard intersegmental transfers. As a first approximation, the hopping translocation process is assumed to be represented effectively in the one-dimensional diffusion of the protein. Then, the pathway followed by the protein, considered as a point-like particle, is a succession of one-dimensional diffusions along the DNA strand and three-dimensional excursions in the surrounding solution (Fig. 1). The time spent by the protein on a DNA strand during each binding event is assumed to follow an exponential law with dissociation frequency λ. This law relies on a Markovian description of the chemical bond which is commonly used. The probability for the protein to still be bound to DNA at a random time t (knowing that it is bound at t = 0) is then P(T > t) = exp(−λt), and the probability that the protein leaves the DNA at a random time T in the interval [t, t + dt] is P(t < T < t + dt) = λ exp(−λt)dt.

FIGURE 1.

A representative path of the restriction enzyme which reaches the target site. Excursions in the solution are represented by dashed lines, one-dimensional diffusion by continuous lines. The solid square is the target site.

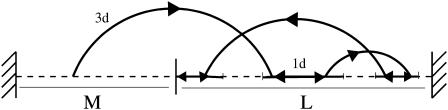
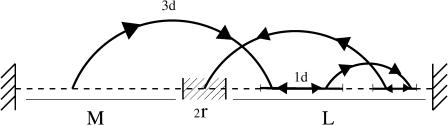
The one-dimensional motion on DNA can be modeled from a continuous Brownian motion with diffusion coefficient D. As it is usually done (see e.g., Jeltsch and Pingoud, 1998), we assume that the extremities of the DNA chain act on the protein as reflecting boundaries. Thus, a protein when reaching an extremity during a binding event is reflected and continues its one-dimensional motion. The target site sequence is a specific sequence of basepairs (e.g., the restriction enzyme, EcoRV, recognizes the sequence GATATC (Taylor and Halford, 1989). The reaction occurs when the reactive domain of the protein matches the target site sequence. To a first approximation, we model the target site sequence as being a perfect reactive point (Fig. 2). The reaction is assumed to be infinitely fast as soon as the protein meets the target site. Note that in this case the protein can find the target site only by diffusing along DNA. The precise mechanism of this elementary act is still subject to discussion. In particular, the profile of the DNA-protein interaction potential is unknown, and could be attractive over an extended area. It is then reasonable also to treat the case where the target site is a zone of finite extension 2r (Fig. 3). In that case the target site can then be reached either by diffusion along the DNA, or by coming directly from a three-dimensional excursion. This second approach, developed further, gives rise to strongly different behavior of the search time.

FIGURE 2.

Representative view of the model. Here the protein executes three excursions before finding the target site.

FIGURE 3.

Extended target site.

As a first approximation, the excursions are assumed to be uncorrelated in space. Hence, when dissociating from DNA, a protein will rebind at a random position. In other words, the probability to reach a site on DNA after an excursion is uniformly distributed along the whole DNA molecule. It has been suggested (Winter et al., 1981) that, for not-excessively concentrated long molecules in solution, the DNA strands form disjoint domains diluted in the medium. A protein which reaches such a DNA domain will be trapped in it. In this case excursions might be correlated due to the geometric configuration of the DNA. As the configuration of a polymer strand in solution is a random coil, even short three-dimensional excursions can lead to a long effective translocation of the linear position of the protein on DNA. Consequently, a small number of long-range transitions is sufficient to uncorrelate the protein position on DNA.

We now introduce three basic quantities used in this work. The first one, P_3D(t), is the probability density that the protein in the solution at time t = 0 will bind DNA at time t at a random position,

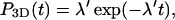(1)

where the distribution of the time spent during an excursion is assumed to follow an exponential law with frequency λ′ corresponding to a mean time spent in the surrounding solution τ′ = 1/λ′. Accounting rigorously for the entire law is beyond the scope of this work. Rather we concentrate here on the characteristic time λ′, which exists and is finite as soon as the system is confined; and the exponential tail of the law, which proves to be valid in most plausible geometries. We will show that this model captures the main relevant characteristics of the problem.

The second quantity, P_1D(t|x), is the conditional probability density that the protein, being on the DNA at position x and at time t = 0, will dissociate at time t without any encounter with the target site. Assuming that the dissociation rate is independent of the state of the protein, one has

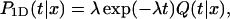(2)

where Q(t|x) is the conditional probability density that the protein, starting from the position x, does not meet the target site during its one-dimensional diffusion. Introducing j(t|x) as the probability density of the first passage to the target site position at time t without dissociation, one gets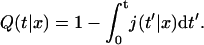

The last quantity, 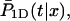is the conditional probability density that the protein, being on DNA at position x and at time t = 0, will find the target site for the first time at time t during its one-dimensional diffusion, without leaving the DNA:

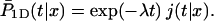(3)

Given these quantities, the first passage density of the protein to the target site can be calculated, first in the case of one target site, and then we will extend it for two target sites.

First passage density

By calculating the first passage density, we obtain the mean time needed for the protein to find its specific target site, as well as all associated moments. We assume that the protein starts at t = 0 linked to the DNA at position x. We consider a generic event (Fig. 2) whose bulk number of excursions is n−1, the residence times on DNA t₁,…,t_n, and the excursion times τ₁,…,τ_n−1. The probability density of such an event, for which the protein finds the target site for the first time (t = time), 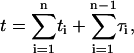is

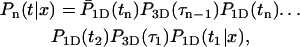(4)

where P_1D(t) and 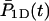are averaged over the initial position of the protein as 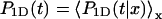and 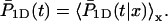We denote by M the DNA length on the “left” side of the target site and by L the length on the “right” side of the target site. The average of a function f over the initial position x is given by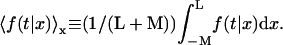

To obtain the density of first passage at the target site, F(t|x), we sum over all possible numbers of excursions and we integrate over all intervals of time, ensuring that The average over the initial position of the protein, can be expressed as

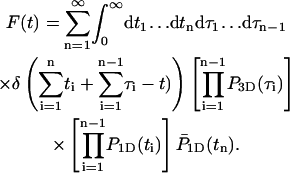(5)

Taking the Laplace transform of 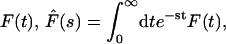we obtain

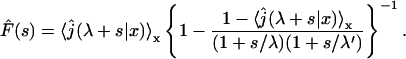(6)

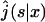being the Laplace transform of j(t|x). This expression completely solves our problem for any one-dimensional motion. We will see in the next section that the main quantities of physical interest can be extracted from this formula.

Optimal search strategy

The relevant quantity to describe the protein/DNA association reaction is the mean time necessary for the protein to find the target site (see above). This mean time is obtained from the derivative of the first passage density by the relation

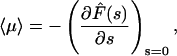(7)

which combined with Eq. 6 gives

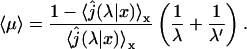(8)

This expression is very general and holds for any one-dimensional motion. Now, we calculate this quantity for a free one-dimensional diffusion. The one-dimensional Laplace transform of the first passage probability density is well known (see the textbooks by Redner, 2001):

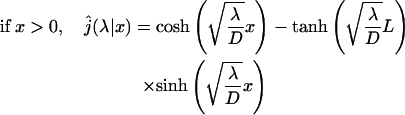(9)

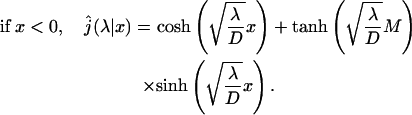(10)

Averaging over x, we finally obtain

(11)

where D is the one-dimensional diffusion coefficient. Then the mean search time takes the form

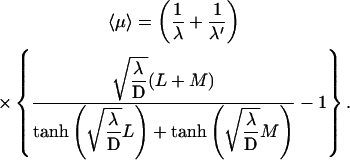(12)

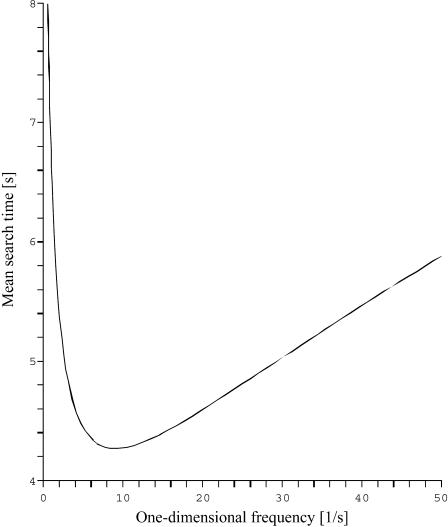
Some comments about this expression (represented in Fig. 4) are appropriate.

1. We recover in a simple and direct way the original result of Berg et al. (1981), obtained from a complete description of the three-dimensional motion (Berg and Blomberg, 1976, 1977, 1978).

2. This quantity is minimum when the target site is centered (as expected for symmetry reasons).

3. As soon as the length of the DNA strand is large enough (more precisely as soon as 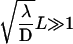or 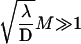), 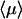grows linearly with the length of the DNA strand. This mirrors the efficiency of the one-dimensional and three-dimensional combined motion when compared to the quadratic growth obtained in the case of pure sliding. In particular, the boundary effects are negligible for this quantity as soon as the overall length is large enough.

4. This expression is valid for a very large class of three-dimensional motions. More precisely, it holds as soon as the mean first return time τ_3D corresponding to the three-dimensional motion is finite and independent of the departure and arrival points. The corresponding expression of the mean first passage time is obtained by replacing λ′ by τ_3D.

FIGURE 4.

The mean search time plotted against the one-dimensional residence frequency λ. The length of DNA is 5000 bp, the three-dimensional residence frequency is 10 s⁻¹, and the one-dimensional diffusion coefficient is 5 × 10⁵ bp²/s.

We now come to an important question, already present in the seminal work of Berg et al. (1981) and recently addressed by Slutsky and Mirny (2004), which concerns the optimum strategy for such a coupled motion. Indeed, it seems reasonable that 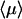is large for both λ very large (in the λ infinite limit, the protein is never on the DNA), and λ very small (pure sliding limit). It has been suggested from qualitative arguments (Slutsky and Mirny, 2004) that the mean search time is minimum when the protein spends equal times bound to the DNA and freely diffusing in the bulk.

Here, we more precisely address this question of minimizing the mean search time with respect to the one-dimensional frequency λ. This is the only specially “adjustable” (depending strongly on the structure of the protein) parameter: λ′ depends on the properties of the environment and will not vary significantly from one protein to another. The one-dimensional diffusion coefficient D is a specific quantity, and optimizing the search time with respect to this parameter is trivial: D should be as large as possible (note that D and λ are assumed to be independent).

The sign of the derivative at λ = 0 of the mean search time gives the criterion for having a minimum as

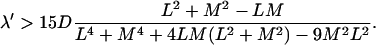(13)

In fact, it can be shown that this sufficient condition is also necessary. If this condition is fulfilled, a careful analysis of the implicit equation satisfied by the frequency at the minimum leads to the expansion for large ℓ = L + M,

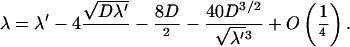(14)

Equations 13 and 14 refine the result of Slutsky—which, however, holds true in the large ℓ limit, or more precisely for 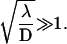For intermediate values of ℓ, boundary effects become important and the minimum can be significantly different.

The 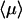value at the minimum is particularly interesting. We compare it to the case of pure sliding where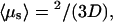

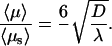(15)

The efficiency of the three-dimensional mediated strategy is therefore much more important when the DNA chain is long. For example, using the λ- and D-values obtained in Results and for a DNA substrate of length 10⁶ bp, the mean target site localization time is given when pure sliding is 1000-fold greater than that predicted by our model.

Further quantitative features of reactive pathways

In this paragraph, we compute two quantities which characterize more precisely the nature of the reactive paths. These quantities are of special interest as they could be experimentally measured using single-molecule techniques.

The first quantity is the distribution p(N) of the number of visits on DNA required before reaching the target site. We recall that in the initial state the protein is bounded to the DNA, therefore N ≥ 1. The distribution can be obtained by slightly modifying the expression of the first passage density Eq. 5:

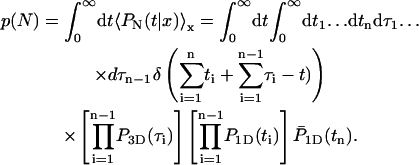(16)

Finally, this distribution happens to be a geometric law with parameter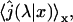

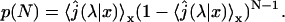(17)

This demonstrates that the mean number of visits before reaching the target site is

(18)

The form holds as

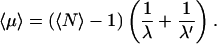(19)

Note that the large N limit is transparent (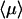 is a succession of approximately N one-dimensional excursions of average duration 1/λ and N three-dimensional excursions of average duration 1/λ′x).

The second interesting quantity is the average number of distinct basepairs visited before the protein reaches its target site. In our continuous description, this corresponds to the average span of the one-dimensional motion. For sake of simplicity, the target is here assumed to be centered on the DNA strand of half-length L. The average span can be expressed as the integral over the position x on the DNA of the probability that x has been visited before reaction. One then obtains

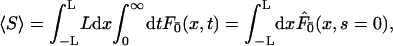(20)

where 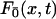is the first passage density at x with adsorbing conditions at x = 0, whose Laplace transform will be explicitly computed in the next section in the context of competitive targets. Anticipating formula Eq. 27, the span finally reads

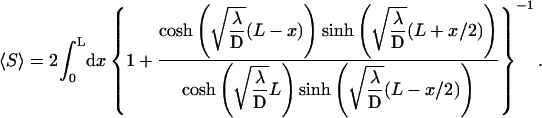(21)

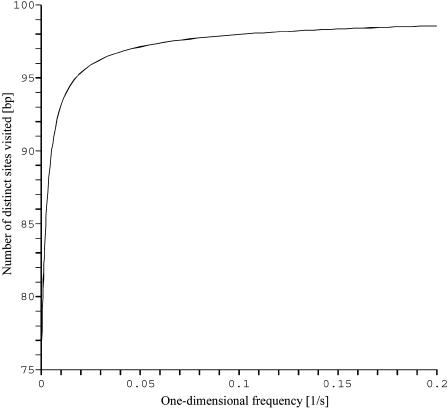
Apparently, this integral form cannot be substantially simplified, but its overall behavior, and in particular the λ-dependence, is easily cleared up. The span appears to grow monotonously from 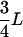at λ = 0 to L for λ → ∞. This monotonicity, as opposed to the existence of a minimum for the mean search time, is a striking feature of this quantity, plotted in Fig. 5.

FIGURE 5.

The average number of distinct DNA sites visited by the enzyme against the one-dimensional residence frequency λ. The half-length of DNA is 100 bp which allows one to also read this number as a percentage.

Extended target site

As mentioned above, the model of a point-like target site disregards the possibility of the protein reaching the target site directly from a three-dimensional excursion. For this reason, we have to study the case where the target site is an area of extension r. We will now show that this new feature significantly changes the behavior of the searching time. The reaction is still assumed to be infinitely fast; it occurs either when the protein reaches the boundary of the reaction area during a sliding round, or when the protein comes on the reaction area directly after a three-dimensional excursion. Following the scheme already developed to derive the density of the first passage time (Eq. 6), one obtains

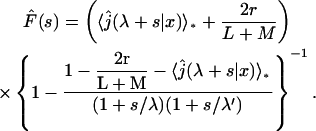(22)

where 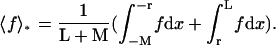The average search time then reads (we only give the case L = M for sake of simplicity),

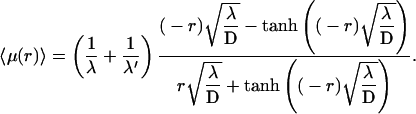(23)

For ℓ large enough, the minimum is obtained for

(24)

It is remarkable that the scaling λ_min ≈ λ′ holds true only for 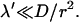For larger frequencies λ′, we have λ_min ≈ 4λ′²r²/D. The value of the search time at the minimum 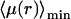is modified. For r small we get

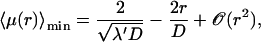(25)

whereas for larger r the expansion reads

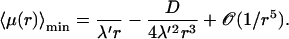(26)

We now consider the case of two target sites to compare the model to experimental results.

Case of two competitive target sites

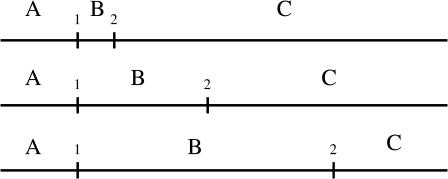
The biological system (Stanford, et al., 2000) consists in integrating two target sites for the restriction enzyme EcoRV on a 690 bp linear DNA substrate. The position along a DNA strand of the first target site, which will be called target 1, is fixed and equals 120 bp. The second target site, which will be called target 2, has been placed at 54 bp, 200 bp, and 387 bp from the first target site. Thus, three substrates (Fig. 6) were used to analyze the kinetics of DNA cleavage. Each assay was carried out at a very low concentration of enzyme with regard to the concentration of DNA. For higher concentration of enzyme, the probability for two—or more—molecules acting on a same DNA strand would be non-negligible. The cleavage of DNA produces different lengths of DNA. An enzyme can cut target 1, target 2, or both, resulting in five lengths of fragments. The authors observed the initial formation of four of these: A, BC, C, and AB types.

FIGURE 6.

Schematic representation of the three substrates of length 690 bp. The position of the second target site relative to the first target equals 54 bp, 200 bp, and 387 bp, respectively.

The advantage of this construction is that the first cleavage process gives a starting point to elucidate how EcoRV will cleave the second target site. In contrast, when using constructions with one target site, the primary pathway of the enzyme to reach the DNA domain can dominate the kinetics of the search process. For example, in highly diluted DNA solutions, the DNA domains are separated by long distances and then the mean time spent by the enzyme in reaching a DNA domain will contribute in a non-negligible manner to the total mean time needed to find the target site. Moreover, our theoretical model supposes that the enzyme starts on the DNA and therefore does not comprise the primary encounter. This assumption agrees with the case of experimental substrates with two target sites.

Conditional search time density

To get a better understanding of this process we first study analytically the distribution of the search time t of one target, for instance 2, knowing that no reaction occurred at target 1. We denote by 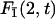this conditional search time density averaged over the initial condition. We make use of the general method developed in the first section to derive this quantity. Indeed, this problem involves a combination of three-dimensional excursions and one-dimensional motions, its peculiarity being that the one-dimensional motion is a constrained diffusion, as reaction with target 1 is excluded. It suffices then to rewrite formula Eq. 6 as

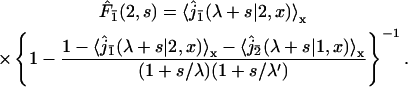(27)

The first factor 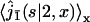is the Laplace transform of the first passage density at 2 avoiding 1 for a standard one-dimensional diffusion, and corresponds to the last excursion before finding the target 2. In turn, the term proportional to 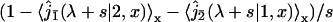is the Laplace transform of the survival probability density, and comes from the succession of nonreactive excursions on DNA. Theses quantities are obtained by standard methods, considering successively the initial condition on fragment A (with mixed boundary conditions), B (with absorbing boundary conditions), and C (with mixed boundary conditions). This finally yields to

(28)

and

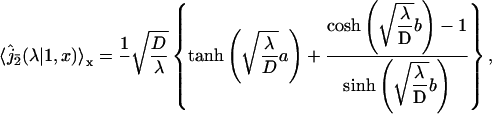(29)

where a,b,c denote the length of fragments A,B,C respectively. This set of equations fully describes the problem, and will be used in next section to analyze experimental data. In particular the mean conditional search time could be deduced straightforwardly from Eq. 27; its explicit form is not given here for sake of simplicity.

Preference and processivity

To get quantitative measurements of the pathway of the enzyme, the authors of Stanford et al. (2000) introduced two concepts: preference and processivity. The value of the preference P quantifies the preferential use of the target 2 by EcoRV. The P-value is experimentally obtained by taking the ratio of the initial formation rate ν_AB of AB substrates (resulting from cleavage at the target site 2), over the initial formation rate ν_BC of BC substrates (resulting from cleavage at the target site 1):

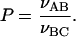(30)

The processivity quantifies the fraction of the cleaved DNA that is cleaved first at one target site, then cleaved at the second target site during the encounter of the DNA substrate with an enzyme. The processivity of the restriction enzyme on the target 2 to the target 1 can be deduced from experimental data by introducing the processivity factor f_p21 = (ν_C − ν_AB)/(ν_C + ν_AB). One can define a symmetric quantity in the same manner, which is the processivity factor of the reaction with the target 1 and then target 2, f_p12 = (ν_A − ν_BC)/(ν_A + ν_BC), and then the total processivity factor which represent the fraction of both processive actions,

(31)

The next sections deal with these two quantities obtained from our model by considering the enzyme-to-target(s) association rate, namely ν₁, ν₂, ν₂₁, and ν₁₂, which are defined by the following elementary reactions, instead of substrate rate production:

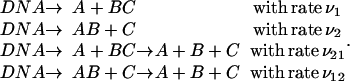(32)

We assume that a restriction enzyme hits a DNA molecule at site x with homogeneous probability per unit time κdx/(L + M). The enzyme concentration is chosen sufficiently small so that multiple encounter events are negligible. Consequently, a fragment BC (or AB) can be cut into B and C (or A and B) only if the enzyme which cleaves the DNA molecule to give BC (or AB) remains on this fragment (the probability of this event, depending in detail on the chemical mechanism, will be denoted p_init) and then finds the site 2 (or 1). The reaction rates are then

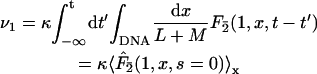(33)

and

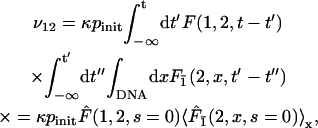(34)

where the quantity F_z(y,x,t) is the first passage density at point y at time t starting from x and avoiding z. This quantity is accessible analytically using Eq. 27. The quantity F(y,x,t) is the first passage density at point y at time t starting from x. The two other rates ν₂ and ν₂₁ are straightforwardly obtained by permutation of symbols 1 and 2. One is now able to derive the processivity and preference factors.

RESULTS

We recall that the lengths of fragments A, B, and C are denoted by the lower-case letters a, b, and c, respectively. First, we evaluate the one-dimensional frequency λ from the comparison of the theoretical preference to experimental data. Then, using the value of λ′ which satisfies the optimal searching time (this assumption is justified below), we deduce several quantities related to the enzyme pathway which links the first target site to the second one. Last, by comparing the analytical expression of the processivity factor to experimental data, we introduce a dynamic-associated parameter: the probability that after an excursion the enzyme will associate to the same DNA substrate it has left, π_r.

Preference

The preference for the target site 1 over site 2 is given by

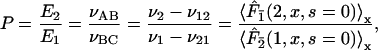(35)

where ν_x = dx/dt is the rate for forming the species x, which can be measured experimentally. Explicitly,

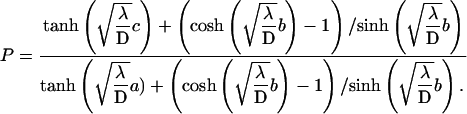(36)

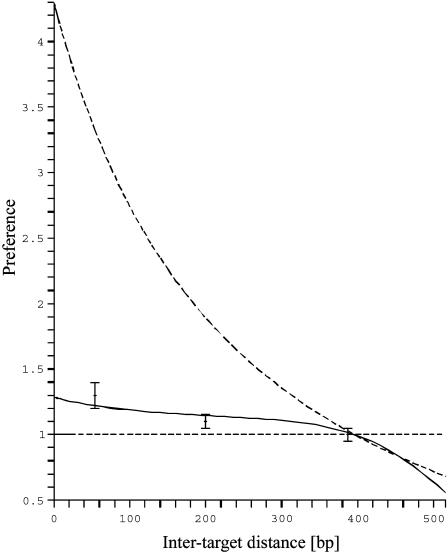
This form which expresses the preference as function of b, and reveals in particular that the preferred target site is the closest to the middle of the molecule, well fits the experimental data (Fig. 7) and allows one to determine the only free parameter 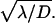The best fit is obtained for bp⁻¹. For a representative fast one-dimensional diffusion coefficient D = 5 × 10⁵ bp²/s (Erskine et al., 1997), the one-dimensional frequency is λ = 37.5 s⁻¹. Then the average time spent by the restriction enzyme on DNA per visit equals 0.027 s and the average distance scanned per visit (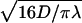) is 260 bp. Using Eq. 21, we obtain a representative average number of distinct sites visited on the DNA during the searching process, 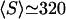bp.

FIGURE 7.

The preference of the protein for the target site 2 over the target site 1. The solid line represents the fitted solution which gives 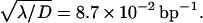The two dashed lines correspond to the limit cases when there is no sliding (straight line, λ = ∞) and when there is only sliding (upper line, λ = 0). The other parameters were drawn from experimental data (ℓ = 690 bp).

Enzyme pathway

A further analysis requires us to know the value of the parameter λ′, which depends strongly on experimental conditions, such as DNA concentration. It could be obtained experimentally as the protein/DNA association rate, and we here choose a typical value corresponding to the optimal search strategy, i.e., λ = λ′. This assumption is supported by the fact that the target site localization is several orders-of-magnitude faster than the diffusion limit. Using the same calculation as from Eqs. 5–12 without averaging on the initial position of the enzyme, we obtain the mean time needed by the restriction enzyme to go from the target 1 to the target 2,

(37)

Then the average search time of the target 2 for a reactive pathway of an enzyme starting from the target 1, with intersite space of 54 bp, is by using the formula from Eq. 37: 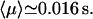The average number of DNA visits before the processive cleaving is, using Eq. 19's formula, 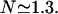The same quantities for the other intertarget site distances, namely 200 bp and 387 bp, are, respectively,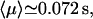 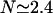; and

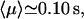
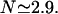
Processivity

Using the previous results, the processivity factor takes the form

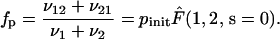(38)

Here we have to refine the derivation of 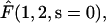i.e., the probability to ever reach 1 starting from 2. The crucial point is about the dilution approximation, hence we treat the case of one single enzyme. We take into account the fact that during each three-dimensional excursion the protein can escape, therefore being definitely lost. We introduce by π_r the probability of return after a three-dimensional excursion. Rigorously this quantity depends on physical parameters such as the DNA length and the typical size of its attractive domain. As the lengths of DNA substrates are constant in the experiments of Stanford et al. (2000) for which b + c = 570 bp, we consider a constant π_r. We finally obtain

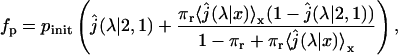(39)

where 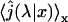is given by the Eq. 11 with L = c and M = b, and 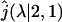is the Laplace transform of the first passage density at 2, starting from 1 which is given by Eq. 10 with x = M = b,

(40)

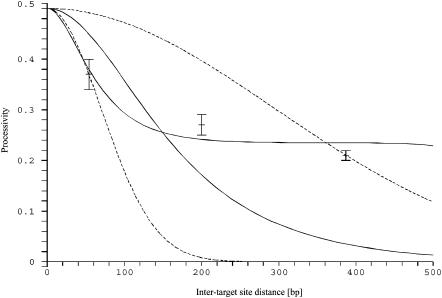
Using the value of λ obtained previously, there are two unknown parameters: p_init and π_r. They can be determined from the experimental data (Fig. 8); the best fit is obtained for p_init = 0.5 and π_r = 0.85. However, these values cannot be very accurate, as used to be the case when estimating two parameters by fitting experimental data with theoretical results.

FIGURE 8.

The processive action of the restriction enzyme. Dashed lines represent two fitted solutions of the model of Stanford, et al. (2000) with pure sliding. The two solid lines represent the solutions of our model for 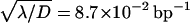and p_init = 0.5: one for π_r = 0, and the other one which passes near experimental points for π_r = 0.85.

We will discuss some possible hypotheses arising from the two last fitted parameters in Conclusion, following.

CONCLUSION

So far, experimental investigations have allowed one to discriminate between two translocation processes, pure sliding or pure jumping. To obtain quantitative measurements for such a compound translocation process, it is necessary to build a physically reliable model, as Berg et al. (1981) did for a single target site. The model presented here permits us to obtain numerous quantities determining the pathway followed by a restriction enzyme in finding one target site or two competitive target sites on DNA, by a series of one-dimensional diffusion periods (sliding) followed by three-dimensional excursions (jumping). The corresponding mean search time shows that such a two-step process is faster than pure sliding or pure three-dimensional diffusion. The existence and the optimization of such a search time is discussed. The length dependence of the optimum was obtained.

Using the preference data from assays on EcoRV (Stanford et al., 2000), we quantify the parameter characterizing the pathway of EcoRV, namely the one-dimensional residence frequency λ. Other quantities were extracted from this parameter: the mean distance scanned by the restriction enzyme during one binding event (260 bp), the distribution of the number of visits on DNA before cleaving the target site, and the average number of distinct DNA sites visited. It should be noticed that the small value of the mean distance scanned might be due to the assumption of a perfect reactive target site which leads to an overestimated λ. In fact, an imperfect reactive target site would decrease the preference. Using the data on processivity for EcoRV, we introduce two secondary parameters characterizing the detailed pathways of the restriction enzyme after DNA cleavage. These parameters come into play when more than one target site is present on the DNA. The first parameter is the probability for the enzyme to stay (after cleavage with a target site) on the DNA strand which harbors the second target site. It was assumed that this probability equals one-half as the DNA sequences which border the target site are almost symmetric. Our best fit suggest that the probability is fairly 0.5, justifying the common assumption. The second parameter π_r is the probability for the enzyme to rebind on the cleaved DNA strand it had left during an excursion. Because of the short length of DNA substrates, it is assumed that the enzyme is “lost” after the dissociation from the DNA. This means that the enzyme rebinds unvisited DNA substrates after each three-dimensional excursion. Therefore, this probability had been previously assumed to be negligible. Our model reveals that this probability is high (0.85) which shows that the enzyme frequently rebinds to the same DNA substrate. The high value of π_r may be explained by the fact that the fragment length ℓ (which is here b + c = 570 bp) is significantly larger than the persistence length (150 bp). The configuration of the DNA is therefore close to a globule, in which the protein can be trapped and hence escape with a rather low probability. However, π_r may be overestimated because of our assumption of neglecting the correlations between the starting and finishing points of the three-dimensional excursions. Indeed, these correlations would result (for small values of the intertarget distance b) in increasing the processivity factor, and therefore lowering π_r. Note that an imperfect reaction would lower the processivity, as in this case the enzyme can pass through the target site without a reaction, therefore increasing the probability of a definitive departure from the DNA strand.

The present model classifies the stochastic pathway followed by a restriction enzyme searching for its target site, by quantifying the dynamical parameters. Our work is in the framework of stochastic dynamics which dictates the biological processes occurring in the highly structured and crowded medium of in vivo systems. Moreover, this model can be helpful for generic situations where a protein has to find a target site on a DNA substrate, e.g., the numerous transcription factors needed to trigger the gene activation.