Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Sep;87(3):1741–1751. doi: 10.1529/biophysj.104.040725

Domains in Binary SOPC/POPE Lipid Mixtures Studied by Pulsed Field Gradient 1H MAS NMR

Ivan V Polozov 1, Klaus Gawrisch 1
PMCID: PMC1304579  PMID: 15345553

Abstract

We studied domain formation in mixtures of the monounsaturated lipids SOPC and POPE as a function of temperature and composition by NMR. Magic angle spinning at kHz frequencies restored resolution of 1H NMR lipid resonances in the fluid phase, whereas the linewidth of gel-phase lipids remained rather broad and spinning frequency dependent. In regions of fluid- and gel-phase coexistence, spectra are a superposition of resonances from fluid and gel domains, as indicated by the existence of isosbestic points. Quantitative determination of the amount of lipid in the coexisting phases is straightforward and permitted construction of a binary phase diagram. Lateral rates of lipid diffusion were determined by 1H MAS NMR with pulsed field gradients. At the onset of the phase transition near 25°C apparent diffusion rates became diffusion time dependent, indicating that lipid movement is obstructed by the formation of gel-phase domains. A percolation threshold at which diffusion of fluid-phase lipid becomes confined to micrometer-size domains was observed when ∼40% of total lipid had entered the gel phase. The results indicate that common phosphatidylethanolamines may trigger domain formation in membranes within a physiologically relevant temperature range. This novel NMR approach may aid the study of lipid rafts.

INTRODUCTION

Phosphatidylcholines (PC) and phosphatidylethanolamines (PE) comprise more than two-thirds of all polar lipids in mammalian plasma membranes. The outer monolayers of plasma bilayers contain more PC than PE whereas inner monolayers are enriched in PE (Devaux, 1991). For example, in membranes of human red blood cells (RBC), 76% of PE is in the inner leaflet of the bilayer (Verkleij et al., 1973). One of the most common, naturally occurring PEs is 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine (POPE). It was reported that 11 mol% of all PEs in RBC are POPE (Knapp et al., 1994). The relative concentration of POPE in the outer leaflet of the bilayer is even higher (18 mol%). A very common monounsaturated PC is 1-stearoyl-2-oleoyl-sn-glycero-3-phosphocholine (SOPC). Therefore, domain formation in SOPC/POPE mixtures is of relevance for RBC and other cell membranes.

The interest in lipid rafts as functional domains in the lipid matrix has revived the research on lipid-phase transitions and lateral domains in the lipid matrix (Anderson and Jacobson, 2002; Brown and London, 1998; Simons and Ikonen, 1997). Rafts are putative lateral domains in the outer monolayer of plasma membranes with elevated cholesterol and glycosphingolipid content that play an important role in cell signaling. Critical questions about raft organization have not been answered, among them raft organization for the inner leaflet of plasma membranes that are low in glycosphingolipid but contain high concentrations of PE (London, 2002). Here we show that membranes with high PE content separate into fluid- and gel-phase domains at physiologically relevant temperatures.

In the past a variety of physicochemical methods have been employed to determine the phase diagrams of saturated DPPC/DPPE or DMPC/DPPE mixtures including differential scanning calorimetry, electron microscopy, fluorescence, Raman, ESR, and 31P, 13C, and 2H NMR spectroscopies (Ahn and Yun, 1999; Arnold et al., 1981; Bagatolli and Gratton, 2000; Blume et al., 1982; Inoue and Nibu, 1999; Petrov et al., 1982; Shimshick and McConnell, 1973; Polozov et al., 1994). A partial phase diagram at high PE concentrations was reported for POPC/POPE (Epand and Bottega, 1988; Cannon et al., 2003). The phase diagram for the SOPC/POPE mixtures was not studied previously (Koynova and Caffrey, 2002).

We used 1H NMR to determine the SOPC/POPE phase diagram as well as rates of lipid lateral diffusion. Despite high proton concentrations in biomembranes and the relatively high sensitivity of proton NMR, until recently application to membrane studies was limited because of the severe broadening of lipid resonances by dipolar interactions that complicate detection of the signals and data analysis (Bloom et al., 1978; Chapman and Oldfield, 1974; Lichtenberg et al., 1975). Those interactions can be averaged out by rapid spinning of the sample about an axis inclined at the magic angle (54° 44′) to the main magnetic field (Andrew et al., 1958). The development of rotors for magic angle spinning (MAS) capable of handling the semiliquid samples was a nontrivial development essential for the successful application of MAS to lipid membranes (Yeagle and Frye, 1987). MAS NMR has been used successfully to improve resolution for lipids in the fluid lamellar phase (Forbes et al., 1988; Oldfield et al., 1987). Further improvement in resolution was achieved recently by using susceptibility-matched coils and rotor inserts that provide a spherical sample volume (see, e.g., Holte and Gawrisch, 1997). Application of 1H MAS NMR to study lateral domains requires careful calibration of the temperature inside the spinning rotor, a low-proton background signal of probes, and exceptional stability of signal intensities and phases. At the appropriate MAS spinning frequency, the linewidth of lipid resonances in fluid and gel phases is distinctly different. We show that differences in the 1H MAS spectra, recorded as a function of temperature, can be used to quantitatively determine the amount of lipids in fluid and gel phases.

A second need addressed is the development of NMR technology to determine the size of lateral domains in the submicrometer range. Recently we developed an approach to determine rates of lipid lateral diffusion in bilayers by pulsed-field gradient 1H MAS NMR spectroscopy (Gaede and Gawrisch, 2003). In this project we observed that gel-phase domains in membranes reduced apparent diffusion rates of lipids in the fluid phase. By conducting experiments as a function of diffusion time we demonstrated that below the percolation threshold diffusion measurements directly reported the size of the fluid-phase domains.

MATERIALS AND METHODS

Sample preparation

SOPC, 1-stearoyl-2-oleoyl-3-sn-phosphatidylcholine, and POPE, 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine were purchased from Avanti Polar Lipids (Alabaster, AL). 2H2O was purchased from Cambridge Isotope Laboratories (Woburn, MA). Lipids were mixed as stock solutions in chloroform/methanol 4:1, and dried as a thin film in a stream of nitrogen, followed by drying in vacuum. Multilamellar vesicles were prepared by adding 1 ml of buffer (10 mM PIPES, pH 7.4, 100 mM NaCl, and 50 μM DTPA in 2H2O) to 10 mg of lipid and homogenization of samples by vortexing, followed by several freeze-thaw cycles. Vesicles were concentrated and separated from extra buffer by centrifugation, resulting in samples containing ∼30 wt% of lipid. From 2 to 4 mg of lipid were transferred to a 4-mm Zirconia rotor with a Kel-F spinner cap and inserts with a spherical volume of 11 μL (Bruker, Billerica, MA).

NMR measurements

Magic angle spinning NMR experiments were carried out on a Bruker DMX500 spectrometer, equipped with a wide-bore 11.7 Tesla magnet, a BVT-2000 variable temperature accessory, a MAS control unit, and a triple resonance, variable temperature CPMAS probe for 4-mm rotors (Bruker). 1H NMR experiments were carried out at a resonance frequency of 500.13 MHz using a spectral width of 25 kHz, which included the spinning center band and one or two side bands, depending on the spinning frequency, 10 or 5 kHz, respectively.

Temperature calibration

The temperature was calibrated by measuring the chemical shift difference between water and choline in a micellar sample of 1,2-dicaproyl-sn-glycero-3-phosphocholine (Avanti Polar Lipids) loaded into an 11-μL spherical MAS rotor insert. For calibration purposes, the same chemical shift difference was measured in a high-resolution probe whose temperature had been calibrated to ±0.1°C with a thermocouple. At MAS spinning frequencies of 5 kHz and lower, the sample temperature was a few degrees lower than the temperature of the bearing gas due to the Joule-Thompson effect of the expanding gas. However, at spinning frequencies >5 kHz, the sample temperature was significantly higher because of friction between the rotor and the bearing gas. Most of the heating takes place at the two bearings at each end of the rotor whereas the center of the rotor is still chilled by the expanding gas, causing significant temperature gradients across the sample. At a spinning frequency of 15 kHz, frictional heating and related temperature gradients severely degrade temperature resolution. A 10-kHz spinning rate was selected as a compromise between acceptable spectral resolution of gel-phase spectra and reliable temperature control. As judged from the apparent width of lipid-phase transitions, temperature gradients across the sample are smaller than 3°C. Spinning of a 4-mm rotor at 10 kHz results in centrifugal forces of the order of 8 × 105 g. This is unlikely to change properties of lipid bilayers much except for minor dehydration that depends on differences in densities between the buffer and the lipid membrane (Nagle et al., 1999; Zhou et al., 1999). Dehydration can be prevented by adjusting the density of the water phase, e.g., by using a proper mixture of H2O and D2O.

PFG NMR measurements

The pulsed field gradient MAS NMR experiments were conducted at a spinning frequency of 10 kHz. The gradient strength was calibrated as described previously (Gaede and Gawrisch, 2003). A stimulated echo sequence with square- or sine-shaped bipolar gradient pulses (Cotts et al., 1989) with a pulse length of 5 ms and an effective gradient strength that varied in 32 increments from 0.01 to 0.61 T/m for square-shaped pulses and 0.01–0.37 T/m for sine-shaped pulses was used. A longitudinal eddy current delay of 5 ms was introduced after the last gradient pulse. Unless stated otherwise, experiments were conducted at a diffusion time Δ = 500 ms. At every gradient strength, eight scans were acquired with a recycle delay of 4 s. Apparent diffusion coefficients (D) were determined from the dependence of peak intensity on gradient strength according to (Gaede and Gawrisch, 2003): 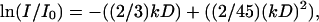Inline graphic where I/I0 is the normalized intensity of the lipid peak and Inline graphic where γ is the gyromagnetic ratio of protons, g the gradient strength, δ the gradient pulse length, and T the time between the gradient pulses sandwiching the 180° pulses (Fordham et al., 1996).

Calorimetry

Differential scanning calorimetry (DSC) experiments were conducted on a CSC 6100 Nano-scan II calorimeter (Calorimetry Sciences, Provo, UT). The SOPC/POPE lipid mixtures (∼3 mg) were dispersed in distilled water by vortexing. Samples were loaded into the calorimeter cell and heating scans recorded at a rate of 0.25°C/min. After the baseline of the cp/T curves was corrected by linear interpolation, the curves were numerically integrated. The temperatures of phase-transition onset and completion correspond to 5% and 95% of integral intensity, respectively.

RESULTS

Previously it was shown that the shape of the lipid 1H MAS NMR spectrum depends on the lipid-phase state (Forbes et al., 1988). For lipids in the fluid phase, spinning at frequencies as low as 500 Hz converts the broad spectra to a well-resolved center band flanked by a series of side bands spaced at multiples of the spinning frequency (Fig. 1). With increasing spinning frequency the spectral density is redistributed from side bands to the center band. At 500 MHz proton resonance frequency and a MAS frequency of higher than 3 kHz the side bands leave the center-band region and spectral resolution becomes similar to high-resolution conditions. At spinning frequencies of 5 kHz and higher signal intensity in the side bands is negligible. For example, for SOPC in the fluid phase at 25°C and 5 kHz MAS frequency 97% of total spectral intensity is in the center band, compared to 99% at 10 kHz. However, the side-band intensities vary between resonances. For SOPC at 25°C the methylene resonances at 1.3 ppm had the strongest side bands, with 90% of intensity in the center band at 5 kHz, and 95% at 10 kHz. The assignment of center-band resonances as well as their integral intensities are provided in Table 1.

FIGURE 1.

FIGURE 1

Open in a new tab

1H MAS NMR spectra of SOPC multilamellar vesicles recorded at 25°C (fluid phase) as a function of MAS frequency. Assignment of peaks in the center band is provided in Table 1. Side bands are separated from the center band by multiples of the spinning frequency (1 ppm corresponds to 500 Hz).

TABLE 1.

1H MAS NMR resonances assignment and comparison of measured integral intensity at a MAS frequency of 10 kHz with the number of protons per resonance

Number of protons
Measured integral intensity
Peak assignment Peak position, ppm POPE SOPC POPE SOPC
-CH3 0.88 6 6 6.4 6.58
(CH2)n 1.3 44 48 39.0 45.5
CH2-CH2-CO 1.6 4 4 4.28 4.24
CH2-CH=CH-CH2 2.05 4 4 4.10 4.01
CH2-CO 2.3–2.4 4 4 3.87 3.93
N(CH3)3 or CH2-NH3 3.28 2 9 2.02 9.02
CH2-N(CH3)3 3.68 0 2 0 1.99
CH2-OP (glycerol) and PO-CH2 (ethanolamine) 4.05 4 2 3.84 1.82
PO-CH2 (choline) 4.3 0 2 0 3.05
OCO-CH2 (glycerol) 4.2 1 1 1.02
4.44 1 1 1.04 0.98
-CH=CH- and OCO-CH in glycerol 5.3 3 3 3 3
Open in a new tab

Fluid-gel transition in POPE and SOPC

We recorded a series of spectra as function of temperature (Fig. 2 A) over the main phase transition of POPE. A rapid decrease in signal intensity from broadening of all POPE resonances was observed at the phase transition. The midpoint of intensity decrease is 24.5°C, in good agreement with previously reported values for the midpoint of the gel-fluid phase transition (Epand and Bottega, 1988). The loss of center-band resolution was accompanied by an increase in the side-band/center-band intensity ratio.

FIGURE 2.

FIGURE 2

Open in a new tab

(A) 1H MAS NMR spectra of POPE multilamellar vesicles recorded at a temperature of 38.5, 29, 28, 26.5, 25.8, 25, 24.3, 23.6, 22.8, 21.5, 20, and 16°C from top to bottom. Assignment of peaks is provided in Table 1. (B) Spectra as in panel A but superimposed. Multiple isosbestic points are visible, indicating superposition of spectra from fluid and gel phases. The inset shows the fraction of fluid lipid as a function of temperature calculated as described in the text.

When the spectra, recorded as a function of temperature, are superimposed they display a series of isosbestic points that are indicative of superposition of resonances from two distinct states (Fig. 2 B). The spectra recorded over the phase transition could be well approximated as a weighted superposition of spectra of fluid- and gel-phase lipids. 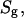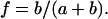The fraction of lipid in the fluid phase, f, as a function of temperature is obtained from the fit of the respective spectrum, S, by a linear combination of spectra of gel, Inline graphic and fluid, Inline graphic states according to Inline graphic and Inline graphic The quality of the fit was evaluated by calculating the mean-square deviation between measured and simulated spectra, as well as by visual inspection of the fit residuals.

The success of the spectral fitting procedure depends heavily on the appearance of gel-phase spectra. Isosbestic points, indicative of signal superposition, were observed for spectra acquired at a spinning frequency of 10 kHz, but not at 5 kHz and lower. The appearance of gel-phase spectra at 10 kHz and 5 kHz is shown in Fig. 3. Spinning at 10 kHz produces somewhat resolved center-band resonances and broad side bands. In contrast, at 5 kHz most of the spectral intensity is in a very broad hump, similar to the proton background signal of the probe. Only the methyl resonance of choline in the center band maintains some resolution.

FIGURE 3.

FIGURE 3

Open in a new tab

Influence of the MAS spinning frequency on the appearance of 1H MAS NMR spectra of SOPC in the gel phase at −12°C (bold lines); top panel, MAS at 5 kHz; bottom panel 10 kHz. The fluid phase spectra (37°C, thin lines) are superimposed for comparison. Spectra are plotted with identical gain settings to enable comparison of baseline intensities. The tops of the well-resolved, fluid-phase resonances are off scale.

This strong dependence of gel-phase spectra on spinning frequency is reflected in the temperature dependence of spectral intensity integrated over the full spectral bandwidth of 25 kHz. Within generous error margins of 10%, integral intensity remained constant at a spinning frequency of 10 kHz, but decreased significantly with formation of gel-phase lipid at a spinning frequency of 5 kHz. This decrease is the result of severe spectral broadening beyond the 25-kHz detection range. All further experiments were conducted at the higher spinning frequency of 10 kHz. The error margins of integral intensity depend on stability of MAS and radio electronics as well as on the intensity of the proton background signal of the probe.

Except for the lower main-phase transition temperature of 6°C, the temperature-dependent changes in the SOPC spectra are similar to POPE with well-resolved resonances in the fluid phase and much broader resonances in the gel state (Fig. 4). However, the gel state spectra of SOPC broaden further at subzero temperatures. Most likely this is the result of lipid dehydration from the formation of ice crystals (Gleeson et al., 1994). At lower temperatures, with increasing dehydration, lipids gradually lose all remaining degrees of motional freedom, and spectra become very broad and unresolved. Freezing of water is also responsible for the intensity loss of the water peak (Fig. 4 B). The resonance of unfrozen water gets weaker and shifts upfield with decreasing temperature, similar to the upfield shift of water resonances with decreasing water content in samples that were prepared by gravimetric addition of water.

FIGURE 4.

FIGURE 4

Open in a new tab

(A) Superimposed 1H MAS NMR spectra of SOPC recorded as a function of temperature from 37 to 2°C. The spectra have isosbestic points, characteristic for superposition of signals from fluid and gel phases. Bold lines are spectra taken at the highest (37°C) and at the lowest (2°C) temperatures. The inset shows the spectral region of the first spinning side band magnified 20-fold. (B) SOPC in the gel state recorded as a function of temperature from 2°C to −12°C. Bold lines show spectra taken at the highest (2°C) and at the lowest (−12°C) temperatures. The inset shows the region of the first side band, magnified 20-fold.

We observed that in the spinning rotor water could be supercooled by several degrees below the freezing point. Supercooling of water permitted the acquisition of spectra over the gel-fluid phase transition of SOPC without interference from dehydration-induced changes in the gel-phase spectra. In contrast to freezing, the melting of ice occurred reproducibly at 3.7°C (2H2O buffer) and was used to calibrate the sample temperature.

SOPC/POPE mixtures

We studied the main-phase transition in binary mixtures of SOPC/POPE at molar ratios of 7:3, 5:5, and 3:7. As in pure POPE and SOPC, multiple isosbestic points were observed in the superimposed 1H MAS spectra recorded as a function of temperature, permitting the determination of fluid- and gel-phase fractions. The temperature dependencies of the fluid-phase fraction, f, in those samples are shown in Fig. 5 A. Compared to the pure lipids, in the mixtures gel and fluid phases coexisted over a much wider temperature range. A higher mol fraction of POPE in the sample corresponded to a higher onset temperature of the phase transition.

FIGURE 5.

FIGURE 5

Open in a new tab

(A) Fluid lipid fraction in binary mixtures of SOPC/POPE as a function of temperature for different lipid ratios. (B) SOPC/POPE phase diagram calculated from the data in panel A. Symbols are: ▪ and ×, onset and completion of the phase transitions directly observed from NMR spectra and DSC, respectively; ▵, calculated by Eq. 2 from overlapping regions of temperature dependence for f0.3 and f0.5; ⋄, calculated by Eq. 2 from overlapping regions of temperature dependence for f0.5 and f0.7; ○ and ♦, calculated by Eq. 3 from nonoverlapping temperature ranges for f0.3 (10–15°C) and f0.7 (22–23°C), respectively, as described in the text. The lines are the fit to the experimental data using regular solution theory with mixing enthalpies of the fluid and gel phases as adjustable parameters (see Discussion and Appendix).

From the temperature dependence of f for the three lipid mixtures we calculated the phase diagram shown in Fig. 5 B using the procedure described below. The composition of a binary lipid system is reported as the mol fraction of POPE, X, in the mixture, plotted as abscissa. The solidus, XS(T), and liquidus, XL(T), curves report the composition of gel- and fluid-phase domains at a given temperature T over the range of phase coexistence. The fraction of fluid phase fX in the system of composition, X, is

graphic file with name M7.gif (1)

where XS(T) is the mol fraction of POPE in gel-phase domains precipitating at the temperature T, and XL(T) the mol fraction of POPE in the fluid phase. It is straightforward to show that at any temperature the fluid phase fractions, fX1(T) and fX2(T), for two different mixtures with the compositions X1 and X2, yield XS(T) and XL(T) via the equations:

graphic file with name M8.gif (2)

The equations have a solution only if both fX1(T) and fX2(T) are within the interval 0 < fX1(T), fX2(T) < 1 over a certain temperature range. The three fX curves shown in Fig. 5 A have two temperature ranges of overlap: f0.3 and f0.5 for 16°C < T < 18°C, and f0.5 and f0.7 for18°C < T < 22°C. Together, the covered temperature range, 16°C < T < 22°C, corresponds to the phase-transition range of the SOPC/POPE, 5:5 sample.

In the range of temperatures where only a single fX measurement is available, the values of XS(T) and XL(T) can be calculated by the equations

graphic file with name M9.gif (3)

assuming a fixed difference between solidus and liquidus curves XS(T) − XL(T). The difference at a given temperature XS(T) − XL(T) is a continuous function of temperature that varies from 0.25 to 0.45 over the temperature range from 16 to 22°C. For fX values close to zero the function XS(T) is less sensitive to the uncertainty in XS(T) − XL(T) whereas at fX(T) values close to one, the values of XL(T) are little affected by this value. The error bars in Fig. 5 B illustrate the effect of a variation of 0.2 < XS(T) − XL(T) < 0.3 on XS(T) and XL(T) calculated from the f0.3 data set over the temperature range 9°C < T < 15°C and for 0.3 < XS(T) − XL(T) < 0.45 on XS(T) and XL(T) calculated from f0.7 at 23°C.

The solid symbols and crosses in the phase diagram (Fig. 5 B) are the phase-transition onset and completion temperatures determined by NMR and calorimetry, respectively. Within small experimental error limits, the agreement between NMR and DSC is excellent. Using the fluid mol fraction of lipid as a function of temperature recorded by NMR almost the entire phase diagram is determined by investigating just three samples with different mol fractions, XE, as well as the pure lipids.

PFG-MAS determination of domain size

The formation of gel-phase domains confines diffusion of lipids to fluid domains whose size and shape varies with temperature. Under conditions of restricted diffusion an apparent diffusion coefficient is determined that reflects diffusion within confined boundaries. We used NMR diffusion measurements to determine the temperature of the percolation threshold in the SOPC/POPE mixtures at which diffusion becomes confined, and we report the mean-square diameter of those domains.

Diffusion was studied using the CH2 peak at 1.3 ppm, which has contributions from the fluid phase both from SOPC and POPE. Diffusion rates determined from other resonances agreed within 10%, which served as a measure of the experimental error.

Upon application of the pulse sequence with pulsed field gradients, signal intensity depends on the magnitude of spatial displacement of the nuclei, z, during the diffusion time, Δ. The stimulated echo attenuation R(G,Δ) may be written as (Callaghan and Söderman, 1983)

graphic file with name M10.gif (4)

where P(z,Δ) is the normalized probability that a spin is displaced by z along the axis of the gradient during the diffusion time Δ, γ is the gyromagnetic ratio of protons, δ the duration of gradient pulses, and G the gradient amplitude. Equation 1 is usually solved assuming that lipid diffusion is controlled by a random walk resulting in a Gaussian distribution

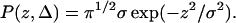graphic file with name M11.gif (5)

The symbol σ is the mean-square displacement of spins from their origins, σ2 = 4DΔ, and D the diffusion constant of the lipid. Integration of Eq. 1 assuming a Gaussian distribution (Eq. 5) yields

graphic file with name M12.gif (6)

The diffusion constant D reports true lipid diffusion if lipid movement is unimpeded by formation of domains. However, in the region of fluid- and gel-phase coexistence, for sufficiently long diffusion times, Δ, and small enough domain size, an apparent diffusion constant, Dapp < D is measured that reports a domain radius according to 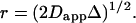Inline graphic The distance r is the mean-square distance that molecules travel during the diffusion time, Δ. We will call this distance “displacement.” It is assumed that displacement is always Gaussian. In the phase-transition region, lipids are confined to fluid- and gel-phase domains. Because the diffusion rate of lipids in the gel phase is orders of magnitude lower, it is safe to assume that apparent diffusion constants are entirely determined by lateral diffusion in the fluid domains. Below the percolation threshold, the fluid domains are discontinuous. If the domains are sufficiently small, lipids will reach the domain boundaries during the diffusion time, Δ. Under those conditions, displacement is reporting the size of fluid domains.

Before conducting experiments over the phase-transition region, we measured the diffusion time dependence of Dapp to determine if the displacement in the SOPC/POPE, 3:7 mixture above the fluid-gel phase coexistence region is confined (Fig. 6). For 0.15 s ≤ Δ ≤ 1 s, the displacement is approximately constant rmax = 1.3 ± 0.1 μm. The observation of a constant value at sufficiently long diffusion times is most likely a reflection of the finite liposome radius rather than a lateral domain size. For example, an average liposome radius of 4.5 μm was determined for POPC liposomes in excess water (Gaede and Gawrisch, 2003). The smaller effective liposome size in these experiments is most likely the result of differences in sample preparation procedures.

FIGURE 6.

FIGURE 6

Open in a new tab

Average lipid displacement in the fluid phase of SOPC/POPE, 3:7 (mol/mol) as a function of diffusion time, Δ, recorded at a temperature of 33.4°C. The solid line is a fit to the data assuming an average liposome radius of 1.3 ± 0.1 μm. The fit yields a curvature-corrected lateral diffusion constant D = 0.8 ± 0.1 × 10−11 m2/s.

The initial part of diffusion time dependence for Δ < 150 ms plotted as r(Δ) allows one to determine a true diffusion constant of fluid SOPC/POPE lipids by fitting the experimentally determined displacement to the equation

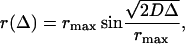graphic file with name M14.gif (7)

using D as an adjustable parameter (Gaede and Gawrisch, 2003). Equation 7 accounts for the curvature of the diffusion pathway assuming the single radius of curvature (rmax) for all liposomes. The fit yields a true diffusion constant D = 0.8 ± 0.1 × 10−11 m2/s at 33°C.

We have no experimental evidence for signal superposition from regions with different values of Dapp within the error limits of the experiment. Furthermore, the decay rate of all resonances is the same. Therefore we assume that Dapp for both SOPC and POPE in the fluid domains is identical.

The temperature dependence of the displacement in SOPC/POPE liposomes was studied at a diffusion time of 0.5 s (Fig. 7, A and B). The displacement had a weak temperature dependence until close to the midpoint of the phase transition where it dropped over a narrow temperature range from values of ∼1.3 μm to <1 μm. At the lower temperatures, experiments conducted at a shorter diffusion time of 0.1 s resulted in identical displacement values (results not shown). We have no evidence for a change in liposome size as demonstrated by repeating lipid displacement experiments at higher temperature. Therefore, the lower displacement values measured over the phase-transition region indicate that displacement now reports the effective radius of the fluid domains.

FIGURE 7.

FIGURE 7

Open in a new tab

(A) Logarithm of normalized methylene resonance (1.3 ppm) intensity of a SOPC/POPE, 3:7 mixture at a diffusion time Δ = 0.5 s recorded as a function of pulsed field gradient strength squared (parameter k) and temperature. From top to bottom are: 33, 29, 22, 21.2, 20.4, 19.6, and 18.8°C. The change in signal intensity at zero gradient strength reflects the decrease in the fluid lipid fraction. The slope of the curves yields an average displacement of lipids along the field gradient axis during diffusion time, Δ, as described in Results. (B) Temperature dependence of the average lipid displacement. Apparent lipid diffusion rates decrease at the onset of the fluid-gel phase transition region. Below the percolation threshold the lipid displacement reflects the average radius of fluid-phase domains.

DISCUSSION

SOPC/POPE phase diagram

Over the gel/fluid phase-transition region, 1H MAS spectra are a superposition of well-resolved spectra of fluid domains and the much broader resonances of gel-phase spectra permitting quantitative determination of the amount of lipid in the coexisting phases (Fig. 5 A). This information was used to construct the SOPC/POPE phase diagram shown in Fig. 5 B. The upward bent in the fluidus and solidus curves indicates some deviation from ideal mixing behavior in both the fluid and gel phases (Lee, 1977). Another indication of nonideality is the insignificant reduction of the high-temperature onset of the phase transition for samples with a composition of 0.5 ≤ XE ≤ 1. At high POPE content our phase diagram has similarities with the previously reported partial POPC/POPE phase diagram (Epand and Bottega, 1988; Cannon et al., 2003).

We quantitatively determined the degree of mixing nonideality by fitting the experimental liquidus and solidus curves to a model based on regular solution theory (Lee, 1977; Arnold et al., 1981). Input parameters are the phase transition temperatures and transition enthalpies of the pure lipids: TSOPC = 279 K (6°C), ΔHSOPC = 24.7 kJ/mol (Vilcheze et al., 1996); TPOPE = 298 K (25°C), ΔHPOPE = 22.8 kJ/mol (Epand, 1985). The fitting (see Appendix) yields an enthalpy of mixing of components, ρol = 3.1 ± 0.2 kJ/mol for the fluid phase, and ρos = 1.9 ± 0.2 kJ/mol for the gel phase. The agreement between the experimental (Fig. 5 B, symbols) and fitted (lines) phase diagram is very good, considering that the theory does not account for the finite width of lipid phase transitions and the broadening of the transition due to temperature gradients of up to 3 K over the sample from MAS. The latter may account for the small deviation between measurement and fit at high POPE content.

The values for nonideal mixing energy yield information about the lateral distribution of lipids in the bilayer. At a 1:1 molar ratio of SOPC and POPE the probability of finding a POPE molecule next to SOPC, XPC,PE, divided by the probability of finding two identical molecules as next neighbors, XPC-PC,PE-PE, is given by the equation

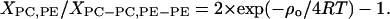graphic file with name M15.gif (8)

We calculated values of 0.46 and 0.66 for the fluidus and solidus curves, respectively. In both phases the probability of having the same type of lipid as next neighbor is higher than the probability of mixed lipid interactions, indicating spontaneous separation of lipid species. Those values can be compared with the previously reported values for DPPC/DPPE that are 0.44 and 0.2, respectively (Arnold et al., 1981). Although the values for the fluidus curve are identical within experimental error, the saturated lipids have a much higher degree of nonideality of mixing at the solidus curve.

The reason for the tendency of SOPC and POPE to demix is related to differences in the capability of both lipids to form hydrogen bonds with water and neighbored lipid molecules. Phosphatidylethanolamines may form intermolecular hydrogen bonds between the amino group of ethanolamine and the phosphate group of a neighbored lipid (Yeagle et al., 1976). Significant differences in hydration properties between phosphatidylcholines and phosphatidylethanolamines have been reported as well (Rand et al., 1988). Phosphatidylethanolamines have a lateral area per molecule that is smaller by 2–3 Å2 compared to phosphatidylcholines with identical hydrocarbon chains, which is reflected by higher-chain order parameters (Separovic and Gawrisch, 1996). The preference for interaction with lipid molecules of the same type must be the result of a complex interplay between differences in energies of H-bond formation, van der Waals attraction, as well as entropy of the fluid lipid molecules and water at the lipid/water interface. Surprisingly those differences are not reflected in lateral diffusion rates of both lipid species in the mixture. At a temperature of 33°C, after correction for influences from liposome curvature, the lateral diffusion rate of lipids in SOPC/POPE mixtures (0.8 ± 0.1 × 10−11 m2/s) is within the range of diffusion rates of other phosphatidylcholines reported earlier (Lindblom and Orädd, 1994; Gaede and Gawrisch, 2003).

In summary, the higher phase-transition temperatures of physiologically relevant PEs result in fluid-gel phase coexistence over a temperature range with physiological relevance. For SOPC/POPE mixtures, at a mol fraction of PE in the membranes of 0.5 or higher, formation of gel-phase domains begins at 25°C. Other biologically relevant PEs may shift this temperature further upwards, e.g., SOPE has a fluid-gel phase transition temperature of 30°C (Huster et al., 1998). Domain formation was observed even at very low PE content albeit at lower temperatures. Perhaps the ordered domains formed by PE in the inner monolayer of plasma membranes interact with ordered structures in the outer monolayer, e.g., rafts rich in sphingomyelin and cholesterol. However, sample preparation procedures for liposomes with asymmetric bilayers would have to be developed to test this hypothesis.

Size of fluid domains

By a novel approach, pulsed field gradient 1H MAS NMR, we determined lipid lateral diffusion rates, average liposome size, and fluid domain size. The liposome radius was within the range from 1.3 μm to 2.1 μm, which is within expectations considering our sample preparation procedures. By NMR and freeze fracture electron microscopy we determined earlier that liposome size in multilamellar dispersions has a distribution that is easily influenced by water content and temperature cycling (Gawrisch et al., 1985). Large multilamellar liposomes are broken up by lateral strain in the bilayers from the reduction in area per molecule when entering the gel state whereas submicrometer size liposomes tend to fuse into larger ones. Therefore samples were carefully equilibrated before the experiments by cycling temperature several times from below the freezing point of water to 50°C.

When conducting experiments over the fluid-gel phase transition, we detected that apparent rates of fluid lipid lateral diffusion are lower and much more temperature dependent than expected from the activation energy of lipid diffusion in the fluid phase. We propose that the rapid onset of diffusional constraints is the result of domain formation. At first the fluid domains remain continuous, but the length of the diffusion pathway for the fluid lipids increases. This is confirmed by the diffusion time dependence of lipid displacement that does not reflect displacement limits from liposome size. When ∼40% of the lipid had entered the gel phase a sudden drop of apparent diffusion constants was observed. We propose that this reflects existence of a percolation threshold where regions of the fluid phase become laterally discontinuous (Almeida et al., 1993). Below the percolation threshold, fluid lipids are truly confined to the smaller domains and displacement is now a reflection of domain radius. Domain radius remained a significant fraction of liposome radius.

Domain size in giant unilamellar liposomes composed of DPPC and DPPE was recently investigated by two-photon fluorescence microscopy (Bagatolli and Gratton, 2000). The authors observed gel-phase domains with shapes such as hexagonal, rhombic, six-cornered star, dumbbell, or dentritic. Gel-phase domains were growing steadily in size with decreasing temperature, restricting fluid areas to irregularly shaped geometries. The authors reported that domain appearance depended on lipid sample composition and liposome size. Although we are uncertain if those results are applicable to the more physiologically relevant unsaturated lipid species investigated in this study, it is tempting to compare those observations with our determination of fluid domain size. Considering that our liposomes are about one order of magnitude smaller, the ratio of fluid domain size to liposome size is comparable in both studies, suggesting that domain size scales with liposome size.

PFG 1H MAS NMR studies on biomembranes

The results are not only important for domain formation in model membranes of biological relevance. They may also serve as a test of the NMR technology to detect phase transitions and fluid domain size in real biomembranes.

Proton NMR spectra of fluid membrane lipids are broadened by proton-proton dipolar interactions (Forbes et al., 1988; Bloom et al., 1978). The resonances are a superposition of spectra from bilayers with different orientation of their normal to the magnetic field. Such inhomogeneously broadened resonances convert into spectra with a well-resolved center band and spinning side bands separated from the center band by multiples of the spinning frequency even at modest MAS frequencies. Side-band intensities depend on lipid order parameters and MAS spinning frequency.

In contrast, resonances of gel-phase lipids are very broad with a linewidth that depends on MAS spinning frequency. The broadening is caused by strong intra- and intermolecular 1H−1H dipolar interactions in combination with slow molecular reorientation that result in homogeneous line broadening that is not averaged out.

We observed that a spinning frequency of 10 kHz partially restores resolution of spectra in the gel state with a typical resonance linewidth of 2–3 kHz. The simultaneous detection of gel and fluid components in one spectrum is an improvement over the previous approach to quantify lipid phase transitions that used a spinning frequency of 5 kHz at which the gel-phase spectra are broadened beyond detection (Polozov et al., 1999). For the region of gel-fluid phase coexistence we observed isosbestic points, indicating that, in first approximation, the superimposed spectra of fluid- and gel-phase lipids are independent of temperature. This was confirmed by a more rigorous fitting procedure using spectra obtained at high and low temperatures as reference.

Recently the first measurements of lipid lateral diffusion by magic angle spinning with application of pulsed field gradients were reported (Gaede and Gawrisch, 2003, 2004). Here we extended the same experimental technology to the detection of domain size in biomembranes. At our current maximal gradient strength of 0.61 T/m we are able to determine fluid domain dimensions down to ∼0.5 μm. By raising gradient strength to 5 T/m, which is technically feasible, this size limit could be lowered by an order of magnitude. For coexisting fluid- and gel-phase domains data analysis is straightforward because gel-phase resonances are much broader and do not perturb data analysis much. Furthermore, it is safe to assume that lipid exchange between fluid- and gel-phase domains is negligible.

It is tempting to explore the usefulness of gradient experiments with MAS for the detection of liquid-ordered domains in biomembranes, so-called lipid rafts. Recently we demonstrated that the 1H MAS NMR technique detects coexistence of liquid-ordered and disordered domains in tertiary DOPC/DPPC/cholesterol mixtures, a model for raft formation (Veatch et al., 2004). The approach was more sensitive than 2H NMR on deuterated lipids. 1H MAS NMR does not require specific labeling of membrane constituents, uses less sample, and signal acquisition is much faster. Detection of raft size may be feasible as well because experiments on oriented samples reported differences in apparent lipid diffusion rates over the region of liquid ordered–liquid disordered phase coexistence (Filippov et al., 2003). Finally, experiments by PFG 1H MAS NMR have sufficient sensitivity to be conducted on very small samples that could be obtained from biopsies of biological tissue.

Acknowledgments

We thank Dr. Holly C. Gaede for stimulating discussions and Kirk Hines for conducting the DSC experiments.

APPENDIX

The binary phase diagram was calculated according to the regular solution theory (Lee, 1977; Arnold et al., 1981). It is assumed that the enthalpy of mixing of the components A and B differs from the ideal solution by an additional enthalpy of mixing:

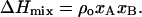graphic file with name M16.gif (1A)

The symbols xA and xB are the mol fractions of components A and B. The nonideality parameter, ρo, is related to the difference in molar enthalpy of A-A, A-B, and B-B pair interactions, UAA, UAB, and UBB, according to

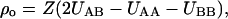graphic file with name M17.gif (2A)

where Z is the number of lipids surrounding each molecule in a first coordination shell. The nonideality of mixing may differ between solid and liquid phases. Therefore separate nonideality parameters for liquidus, ρol, and solidus curves, ρos, must be defined. It is straightforward to show that the assumptions above yield a pair of recursive equations that determine the liquidus, XL(T), and solidus curves, XS(T), of the phase diagram:

graphic file with name M18.gif (3A)
graphic file with name M19.gif (4A)

For temperatures T in the range TA < T < TB, the set of transcendental equations are solved numerically through recursive iterations. The shape of solidus and liquidus curves is very sensitive to small changes of the nonideality parameters ρol and ρos. A unique set of parameters was obtained by minimizing deviations between experimental data points and the calculated curves.

References

  1. Ahn, T., and C. H. Yun. 1999. Phase properties of liquid-crystalline phosphatidylcholine/phosphatidylethanolamine bilayers revealed by fluorescent probes. Arch. Biochem. Biophys. 369:288–294. [DOI] [PubMed] [Google Scholar]
  2. Almeida, P. F. F., W. L. C. Vaz, and T. E. Thompson. 1993. Percolation and diffusion in 3-component lipid bilayers: effect of cholesterol on an equimolar mixture of 2 phosphatidylcholines. Biophys. J. 64:399–412. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Anderson, R. G. W., and K. Jacobson. 2002. Cell biology: a role for lipid shells in targeting proteins to caveolae, rafts, and other lipid domains. Science. 296:1821–1825. [DOI] [PubMed] [Google Scholar]
  4. Andrew, E. R., A. Bradbury, and R. G. Eades. 1958. Nuclear magnetic resonance spectra from a crystal rotated at high speed. Nature. 182:1659. [Google Scholar]
  5. Arnold, K., A. Lösche, and K. Gawrisch. 1981. 31P-NMR investigations of phase separation in phosphatidylcholine/phosphatidylethanolamine mixtures. Biochim. Biophys. Acta. 645:143–148. [DOI] [PubMed] [Google Scholar]
  6. Bagatolli, L. A., and E. Gratton. 2000. Two photon fluorescence microscopy of coexisting lipid domains in giant unilamellar vesicles of binary phospholipid mixtures. Biophys. J. 78:290–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bloom, M., E. E. Burnell, A. L. MacKay, C. P. Nichol, M. I. Valic, and G. Weeks. 1978. Fatty acyl chain order in lecithin model membranes determined from proton magnetic resonance. Biochemistry. 17:5750–5762. [DOI] [PubMed] [Google Scholar]
  8. Blume, A., R. J. Wittebort, S. K. Das Gupta, and R. G. Griffin. 1982. Phase equilibria, molecular conformation, and dynamics in phosphatidylcholine/phosphatidylethanolamine bilayers. Biochemistry. 21:6243–6253. [DOI] [PubMed] [Google Scholar]
  9. Brown, D. A., and E. London. 1998. Functions of lipid rafts in biological membranes. Annu. Rev. Cell Dev. Biol. 14:111–136. [DOI] [PubMed] [Google Scholar]
  10. Callaghan, P. T., and O. Söderman. 1983. Examination of the lamellar phase of aerosol OT/water using pulsed field gradient nuclear magnetic resonance. J. Phys. Chem. 87:1737–1744. [Google Scholar]
  11. Cannon, B., M. Hermansson, S. Gyorke, P. Somerharju, J. A. Virtanen, and K. H. Cheng. 2003. Regulation of calcium channel activity by lipid domain formation in planar lipid bilayers. Biophys. J. 85:933–942. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Chapman, D., and E. Oldfield. 1974. Nuclear magnetic resonance studies of biological and model membrane systems. Methods Enzymol. 32:198–211. [DOI] [PubMed] [Google Scholar]
  13. Cotts, R. M., M. J. R. Hoch, T. Sun, and J. T. Markert. 1989. Pulsed field gradient stimulated echo methods for improved NMR diffusion measurements in heterogeneous systems. J. Magn. Reson. 83:252–266. [Google Scholar]
  14. Devaux, P. F. 1991. Static and dynamic lipid asymmetry in cell membranes. Biochemistry. 30:1163–1173. [DOI] [PubMed] [Google Scholar]
  15. Epand, R. M. 1985. Diacylglycerols, lysolecithin, or hydrocarbons markedly alter the bilayer to hexagonal phase transition temperature of phosphatidylethanolamines. Biochemistry. 24:7092–7095. [DOI] [PubMed] [Google Scholar]
  16. Epand, R. M., and R. Bottega. 1988. Determination of the phase behaviour of phosphatidylethanolamine admixed with other lipids and the effects of calcium chloride: implications for protein kinase C regulation. Biochim. Biophys. Acta. 944:144–154. [DOI] [PubMed] [Google Scholar]
  17. Filippov, A., G. Orädd, and G. Lindblom. 2003. The effect of cholesterol on the lateral diffusion of phospholipids in oriented bilayers. Biophys. J. 84:3079–3086. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Forbes, J., C. Husted, and E. Oldfield. 1988. High-field, high-resolution proton magic-angle sample-spinning nuclear magnetic-resonance spectroscopic studies of gel and liquid-crystalline lipid bilayers and the effects of cholesterol. J. Am. Chem. Soc. 110:1059–1065. [Google Scholar]
  19. Fordham, E. J., P. P. Mitra, and L. L. Latour. 1996. Effective diffusion times in multiple-pulse PFG diffusion measurements in porous media. J. Magn. Reson. 121:187–192. [Google Scholar]
  20. Gaede, H. C., and K. Gawrisch. 2003. Lateral diffusion rates of lipid, water, and a hydrophobic drug in a multilamellar liposome. Biophys. J. 85:1734–1740. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Gaede, H. C., and K. Gawrisch. 2004. Multi-dimensional pulsed field gradient magic angle spinning NMR experiments on membranes. Magn. Reson. Chem. 42:115–122. [DOI] [PubMed] [Google Scholar]
  22. Gawrisch, K., W. Richter, A. Möps, P. Balgavy, K. Arnold, and G. Klose. 1985. The influence of water concentration on the structure of egg yolk phospholipid/water dispersions. Studia Biophysica. 108:5–16. [Google Scholar]
  23. Gleeson, J. T., S. Erramilli, and S. M. Gruner. 1994. Freezing and melting water in lamellar structures. Biophys. J. 67:706–712. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Holte, L. L., and K. Gawrisch. 1997. Determining ethanol distribution in phospholipid multilayers with MAS-NOESY spectra. Biochemistry. 36:4669–4674. [DOI] [PubMed] [Google Scholar]
  25. Huster, D., K. Arnold, and K. Gawrisch. 1998. Influence of docosahexaenoic acid and cholesterol on lateral lipid organization in phospholipid mixtures. Biochemistry. 37:17299–17308. [DOI] [PubMed] [Google Scholar]
  26. Inoue, T., and Y. Nibu. 1999. Phase behavior of hydrated lipid bilayer composed of binary mixture of phospholipids with different head groups. Chem. Phys. Lipids. 100:139–150. [Google Scholar]
  27. Knapp, H. R., F. Hullin, and N. Salem. 1994. Asymmetric incorporation of dietary N-3 fatty-acids into membrane aminophospholipids of human erythrocytes. J. Lipid Res. 35:1283–1291. [PubMed] [Google Scholar]
  28. Koynova, R., and M. Caffrey. 2002. An index of lipid phase diagrams. Chem. Phys. Lipids. 115:107–219. [DOI] [PubMed] [Google Scholar]
  29. Lee, A. G. 1977. Lipid phase transitions and phase diagrams. II. Mixtures involving lipids. Biochim. Biophys. Acta. 472:285–344. [DOI] [PubMed] [Google Scholar]
  30. Lichtenberg, D., N. O. Petersen, J. L. Girardet, M. Kainosho, P. A. Kroon, C. H. A. Seiter, G. W. Feigenson, and S. I. Chan. 1975. The interpretation of proton magnetic resonance linewidths for lecithin dispersions. Effect of particle size and chain packing. Biochim. Biophys. Acta. 382:10–21. [DOI] [PubMed] [Google Scholar]
  31. Lindblom, G., and G. Orädd. 1994. NMR studies of translational diffusion in lyotropic liquid crystals and lipid membranes. Prog. Nucl. Magn. Reson. Spectrosc. 26:483–515. [Google Scholar]
  32. London, E. 2002. Insights into lipid raft structure and formation from experiments in model membranes. Curr. Opin. Struct. Biol. 12:480–486. [DOI] [PubMed] [Google Scholar]
  33. Nagle, J. F., Y. F. Liu, S. Tristram-Nagle, R. M. Epand, and R. E. Stark. 1999. Re-analysis of magic angle spinning nuclear magnetic resonance determination of interlamellar waters in lipid bilayer dispersions. Biophys. J. 77:2062–2065. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Oldfield, E., J. L. Bowers, and J. Forbes. 1987. High-resolution proton and carbon-13 NMR of membranes: why sonicate? Biochemistry. 26:6919–6923. [DOI] [PubMed] [Google Scholar]
  35. Petrov, A. G., K. Gawrisch, G. Brezesinski, G. Klose, and A. Möps. 1982. Optical detection of phase transitions in simple and mixed lipid-water phases. Biochim. Biophys. Acta. 690:1–7. [DOI] [PubMed] [Google Scholar]
  36. Polozov, I. V., A. Krishnamurthy, A. I. Polozova, B. J. Litman, and K. Gawrisch. 1999. MAS-NOESY NMR studies of lateral organization of binary lipid mixtures. Biophys. J. 76:A356. [Google Scholar]
  37. Polozov, I. V., J. G. Molotkovsky, and L. D. Bergelson. 1994. Anthrylvinyl-labeled phospholipids as membrane probes: the phosphatidylcholine-phosphatidylethanolamine system. Chem. Phys. Lipids. 69:209–218. [DOI] [PubMed] [Google Scholar]
  38. Rand, R. P., N. Fuller, V. A. Parsegian, and D. C. Rau. 1988. Variation in hydration forces between neutral phospholipid bilayers: evidence for hydration attraction. Biochemistry. 27:7711–7722. [DOI] [PubMed] [Google Scholar]
  39. Separovic, F., and K. Gawrisch. 1996. Effect of unsaturation on the chain order of phosphatidylcholines in a dioleoylphosphatidylethanolamine matrix. Biophys. J. 71:274–282. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Shimshick, E. J., and H. M. McConnell. 1973. Lateral phase separation in phospholipid membranes. Biochemistry. 12:2351–2360. [DOI] [PubMed] [Google Scholar]
  41. Simons, K., and E. Ikonen. 1997. Functional rafts in cell membranes. Nature. 387:569–572. [DOI] [PubMed] [Google Scholar]
  42. Veatch, S. L., I. V. Polozov, K. Gawrisch, and S. L. Keller. 2004. Liquid domains in vesicles investigated by NMR and fluorescence microscopy. Biophys. J. 86:2910–2922. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Verkleij, A. J., R. F. Zwaal, B. Roelofsen, P. Comfurius, D. Kastelijn, and L. L. van Deenen. 1973. The asymmetric distribution of phospholipids in the human red cell membrane. A combined study using phospholipases and freeze-etch electron microscopy. Biochim. Biophys. Acta. 323:178–193. [DOI] [PubMed] [Google Scholar]
  44. Vilcheze, C., T. P. W. Mcmullen, R. N. McElhaney, and R. Bittman. 1996. The effect of side-chain analogues of cholesterol on the thermotropic phase behavior of 1-stearoyl-2-oleoylphosphatidylcholine bilayers: a differential scanning calorimetric study. Biochim. Biophys. Acta. 1279:235–242. [DOI] [PubMed] [Google Scholar]
  45. Yeagle, P. L., and J. Frye. 1987. Effects of unsaturation on 2H-NMR quadrupole splittings and 13C-NMR relaxation in phospholipid bilayers. Biochim. Biophys. Acta. 899:137–142. [DOI] [PubMed] [Google Scholar]
  46. Yeagle, P. L., W. C. Hutton, C. H. Huang, and R. B. Martin. 1976. Structure in the polar head region of phospholipid bilayers: A 31P-1H nuclear Overhauser effect study. Biochemistry. 15:2121–2124. [DOI] [PubMed] [Google Scholar]
  47. Zhou, Z., B. G. Sayer, D. W. Hughes, R. E. Stark, and R. M. Epand. 1999. Studies of phospholipid hydration by high-resolution magic-angle spinning nuclear magnetic resonance. Biophys. J. 76:387–399. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES