Cardiac Length Dependence of Force and Force Redevelopment Kinetics with Altered Cross-Bridge Cycling

Abstract

We examined the influence of cross-bridge cycling kinetics on the length dependence of steady-state force and the rate of force redevelopment (k_tr) during Ca²⁺-activation at sarcomere lengths (SL) of 2.0 and 2.3 μm in skinned rat cardiac trabeculae. Cross-bridge kinetics were altered by either replacing ATP with 2-deoxy-ATP (dATP) or by reducing [ATP]. At each SL dATP increased maximal force (F_max) and Ca²⁺-sensitivity of force (pCa₅₀) and reduced the cooperativity (n_H) of force-pCa relations, whereas reducing [ATP] to 0.5 mM (low ATP) increased pCa₅₀ and n_H without changing F_max. The difference in pCa₅₀ between SL 2.0 and 2.3 μm (ΔpCa₅₀) was comparable between ATP and dATP, but reduced with low ATP. Maximal k_tr was elevated by dATP and reduced by low ATP. Ca²⁺-sensivity of k_tr increased with both dATP and low ATP and was unaffected by altered SL under all conditions. Significantly, at equivalent levels of submaximal force k_tr was faster at short SL or increased lattice spacing. These data demonstrate that the SL dependence of force depends on cross-bridge kinetics and that the increase of force upon SL extension occurs without increasing the rate of transitions between nonforce and force-generating cross-bridge states, suggesting SL or lattice spacing may modulate preforce cross-bridge transitions.

INTRODUCTION

A fundamental property of cardiac muscle is its ability to increase contractile force when stretched, facilitating the matching of cardiac output with venous return (Frank-Starling's Law of the Heart). The strong length dependence of cardiac contraction manifests as an enhancement of force at all levels of intracellular [Ca²⁺] when sarcomere length (SL) is increased (Gordon et al., 2000; Fuchs, 2002; Konhilas et al., 2002a). It is generally accepted that force in both skeletal and cardiac muscle is a product of the availability of myosin binding sites on thin filament actin (the level of thin filament activation), which is dependent on the position of the dimeric regulatory protein tropomyosin (Tm) on the surface of the two helical actin strands that compose thin filaments. Tm overlays 7 actin monomers along each strand, with head-to-tail overlap between adjacent Tms. Each Tm binds in the overlap region with a troponin complex (Tn), which contains a Ca²⁺-binding subunit (TnC), an actin binding subunit (TnI) and a subunit (TnT) that anchors TnC/TnI to Tm (see Gordon et al., 2000 for review). In the absence of Ca²⁺ TnI binds to actin, holding Tm in a position that inhibits myosin head-actin (cross-bridge) interaction (“blocked” state), and when Ca²⁺ binds to TnC, TnI binding to actin is decreased, allowing Tm to assume a position that is permissive to cross-bridge binding (“closed” state). As cross-bridge binding becomes stronger Tm is further displaced on the thin filaments exposing more strong binding surface on actin, allowing force generation (“open” state) (Lehrer and Geeves, 1998; Geeves and Holmes, 1999; Gordon et al., 2000). Thus in striated muscle the availability of thin filament binding sites for cross-bridges is determined by a balance of the effects of Ca²⁺-binding to troponin and strong cross-bridge formation on the position of Tm. In cardiac muscle, and to a lesser extent in skeletal muscle, the ability of cross-bridges to activate thin filaments is further enhanced by a cross-bridge-dependent increase in the affinity of troponin for Ca²⁺ (Hofmann and Fuchs, 1987; Wang and Fuchs, 1994; Martyn et al., 2001).

It has been suggested that increasing force at longer SL results from the accompanying decrease in lateral myofilament lattice spacing (Fuchs and Wang, 1996; Fuchs, 2002) which increases the proximity of myosin heads to actin in skinned cardiac muscle (Konhilas et al., 2002b; Martyn et al., 2004). When lattice spacing is decreased by osmotic compression, independent of changes in SL, the Ca²⁺-sensitivity of force increases, as it does when SL is increased (McDonald and Moss, 1995; Fuchs and Wang, 1996). Additionally, reduced lattice spacing has been suggested to increase the probability of strong cross-bridge binding and force generation, as evidenced by an increased rate of isometric force redevelopment (k_tr) when SL is stretched in maximally activated skinned skeletal muscle fibers (McDonald et al., 1997). This important hypothesis has not been systematically tested in cardiac muscle. If increasing SL increases force by enhancing the probability of cross-bridge transition from nonforce into force-generating states, then force and k_tr would be likely to have a similar SL or lattice-spacing dependence.

Although there is evidence supporting a role for lattice spacing in force regulation, it has recently been suggested that SL alters force independent of changes in lattice spacing. Konhilas et al. (2002b) found a lack of correlation between the Ca²⁺-sensitivity of force and the lattice spacing of relaxed skinned cardiac muscle. Consistent with this idea, the Ca²⁺ sensitivity of force was found to decrease at longer SL when passive force was reduced by selective digestion of titin, suggesting a role for titin stretch in enhancing cardiac contractile activation (Cazorla et al., 2001; Fukuda et al., 2001). However, recent evidence indicates that titin strain may affect force by altering lattice spacing (Fukuda et al., 2003). Finally, our own observations of an increase in the attached, nonforce-bearing cross-bridge population as lattice spacing is compressed raises the possibility that the SL and lattice-spacing dependence of force may be mediated by altering the probability of the initial, preforce cross-bridge interactions (Martyn et al., 2004). Thus the molecular mechanisms by which changes in SL and lattice-spacing modulate cardiac contractile activation remains poorly understood (Konhilas et al., 2002b; Moss and Fitzsimons, 2002).

To date most evidence suggests that the steep SL dependence of force in cardiac muscle results from the sensitivity of cardiac thin filaments to activation by cross-bridges, coupled with changes in the probability of strong cross-bridge interactions as SL or lattice spacing is altered; decreasing SL or increasing lattice spacing would cause not only a decrease in strong cross-bridge binding but also a corresponding decrease of thin filament activation. A role for strong cross-bridge binding in defining the SL and lattice spacing dependence of contractile activation is emphasized by several observations. For example, inhibition of force during Ca²⁺-activation reduces the SL dependence of Ca²⁺-binding to cardiac thin filaments (Hofmann and Fuchs, 1987; Wang and Fuchs, 1994) and the corresponding conformational changes in cardiac troponin C (cTnC) (Martyn and Gordon, 2001), emphasizing the ability of cross-bridges to not only enhance thin filament activation but also its length dependence. On the other hand when cross-bridge binding was enhanced by elevated MgADP, the Ca²⁺-sensitivity of activation was increased whereas the effects of SL on force-pCa (pCa = −log[Ca²⁺]) relations were diminished (Fukuda et al., 2000). Similarly, the addition of exogenous strong binding, slowly cycling myosin heads eliminated the SL-dependence of force-pCa relations in cardiac myocytes (Fitzsimons and Moss, 1998). The latter two interventions have in common enhanced thin filament activation by slowly cycling cross-bridges, implying that interventions that either inhibit or enhance strong cross-bridge interactions and their contribution to thin filament activation diminish the SL dependence of activation in cardiac muscle. Finally, in addition to cross-bridge binding, the kinetics of cross-bridge cycling could influence the SL dependence of contraction, as implied by observations that the apparent kinetics of cross-bridge and thin filament activation may be coupled in striated muscle (Hancock et al., 1997; Regnier et al., 1998; Adhikari and Wang, 2004).

In this study we tested two hypotheses. First, we tested the hypothesis that increasing SL (and decreasing lattice spacing) enhances force generation by increasing the rate of cross-bridge transitions into strong force producing states. This was done by comparing the steady-state force-pCa and k_tr-pCa relations at 2.0 and 2.3 μm SL over the full range of Ca²⁺-activation. Second, we tested whether the contribution of cross-bridges to the SL or lattice-spacing dependence of force is dependent on actin-myosin cycle kinetics. Cross-bridge kinetics were accelerated by replacement of ATP with 2-deoxy-ATP (dATP) as the contractile substrate (Regnier et al., 2000) or slowed by lowering [ATP] from 5 mM to 0.5 mM. The effects of these interventions on the SL dependence of force-pCa and k_tr-pCa relations were determined. Whereas the Ca²⁺-sensitivity of force and maximal force were increased at both long and short SL by dATP, the SL dependence of force-pCa relations were unaffected. In contrast, lowering [ATP], which slowed cross-bridge cycling, also increased the Ca²⁺-sensitivity of force yet the SL-dependence of force-pCa relations was significantly decreased. Surprisingly, under all nucleotide conditions tested, decreasing SL significantly decreased the maximum Ca²⁺-activated force without a corresponding decrease in maximum k_tr, whereas at equivalent intermediate submaximal forces k_tr was actually higher at the shorter SL. Preliminary reports have been previously published in abstract form (Martyn and Gordon, 2001; Kreutziger et al., 2003; Adhikari et al., 2004).

METHODS

Cardiac trabeculae preparation

Single cardiac trabeculae were prepared from male Sprague-Dawley rats (200–250 gm) as described previously (Martyn and Gordon, 2001). Briefly, rats were anesthetized by an intraperitonial injection of pentobarbital (50 mg/kg) and their hearts were removed rapidly and placed in oxygenated, physiological salt solution (in mM): 100 NaCl, 24 NaHCO₃, 2.5 KCl, 1 MgS0₄.7H₂O, 1 NaHPO₄, and 1 CaCl₂. Small trabeculae (100–200 μm diameter, 1–2 mm length) were dissected from the right ventricle and their surface membranes were rendered permeable to bathing solution constituents by exposing them for 12 h at 4°C to a skinning solution containing (in mM): 100 KCl, 9.0 MgCl₂, 4.0 MgATP, 5.0 K₂EGTA (ethylene glycol-bis-(b-aminoethylether)-N,N,N,N-tetraacetic acid), 10 MOPS (3-(n-morpholino) propane sulfonic acid), 1% (v/v) nonionic detergent Triton X-100, pH 7.0, and 50% (v/v) glycerol and 1% (v/v) protease inhibitor cocktail (P-8340, Sigma). The skinned trabeculae were stored in the same solution without Triton X-100 at −20°C and used for experiments within 1 week. On average, trabeculae dimensions were 1500 ± 50 × 156 ± 10 μm (length × diameter; mean ± SE; n = 20).

Mechanics measurements

The ends of single trabeculae were wrapped in aluminum foil T-clips for attachment to a force transducer (Model 400A, 2.2 kHz resonant frequency, Cambridge Technology, Watertown, MA) and a servomotor (model 300, Cambridge Technology, Watertown, MA) tuned for a 350-μs step response. SL was measured and adjusted under relaxing conditions using laser diffraction techniques as described previously (Chase et al., 1994a). Force, length and SL signals were low pass filtered (f_c = 40% of the sampling rate) with a CyberAmp 380 (Axon Instruments, Foster City, CA) and recorded digitally with a 12-bit resolution. All experiments were done at 15°C.

The rate of force redevelopment after a release-restretch protocol (k_tr), was measured by applying a shortening ramp (∼15% muscle length (L₀) at 4 L₀ s⁻¹) that reduced force to zero, followed by a fast (350 μs) under-damped restretch to the original muscle length. k_tr was calculated from the halftime of force redevelopment (Chase et al., 1994b). Unloaded shortening velocity (V_u) was determined using the slack test method (Edman, 1975).

Solutions

Solutions contained (in mM): 15 phosphocreatine, 15 EGTA, 80 MOPS, 1 Mg²⁺, 135 Na⁺ + K⁺, 1 dithiothreitol (DTT), 250 units/ml⁻¹ creatine kinase (CK, Sigma), and 5 mM ATP, or 0.5 mM ATP, or 5 mM 2 deoxy-ATP (dATP; Sigma) at pH 7.0 and ionic strength 0.17 M. Mg²⁺ affinities of dATP and ATP were assumed to be the same. For activation solutions, [Ca²⁺] (expressed as pCa = −log[Ca²⁺]) was varied by adding Ca²⁺-propionate. In a subset of experiments dextran T500 (4% w/v) was added to all solutions.

Data analysis

Force-pCa data were fit by the Hill equation,

where F_max is the maximally activated force, n_H is the Hill coefficient or slope and pCa₅₀ is the pCa at which force is half-maximal. The reported pCa₅₀ and n_H values represent the means of the values from the individual fits, ± standard error of the means. Means are compared with Student's t-test with significance at the 95% confidence level (P < 0.05). Modeling of k_tr with a six-state cross-bridge cycle was carried out as described previously (Regnier and Homsher, 1998).

RESULTS

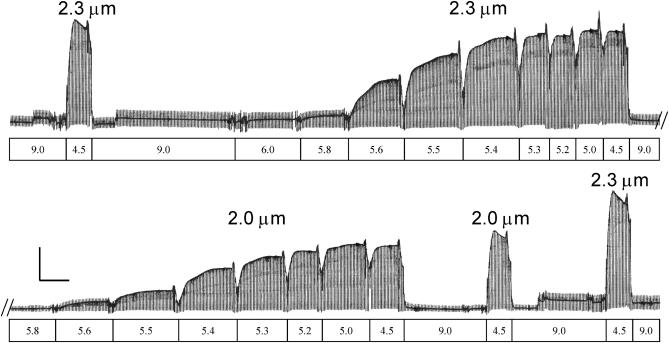
The Ca²⁺-dependence of isometric steady-state force and force redevelopment rate (k_tr) at SL 2.0 and 2.3 μm were determined for single-skinned trabeculae at 15°C using the protocol illustrated in Fig. 1. In this example shown for 5 mM ATP, after an initial maximal activation at SL 2.3 μm the trabecula was activated at SL 2.3 μm step-wise by bathing it in solutions of decreasing pCa. Steady-state force and k_tr were measured at each pCa. Initial SL was then adjusted to 2.0 μm and the protocol was repeated, followed by a final set of maximal activations at SL 2.0 and 2.3 μm (Fig. 1). The order of initial SL was alternated and experimental results were rejected if force at pCa 4.5 (F_max) declined by more than 15% at 2.3 μm SL. Additionally, comparison between dATP or low ATP and corresponding ATP controls were carried out between different sets of trabeculae obtained from the same hearts to avoid excessive F_max decline.

FIGURE 1.

Experimental protocol and example trace of trabecula activation at SL 2.0 and 2.3 μm with 5 mM ATP. SL and solution pCa are indicated above and below the trace. A single trabecula (length 1.4 mm, diameter 198 μm) at SL 2.3 μm was maximally activated (pCa 4.5) and relaxed (pCa 9.0), followed by SL adjustment (2.3 μm) and a series of step-wise activations from submaximal to maximal activations (pCa 6.0–4.5). The trabecula was then relaxed, adjusted to SL 2.0 μm and subjected to another series of step-wise activation and relaxation. Finally, to assess reproducibility, the trabecula was maximally activated (pCa 4.5) at SL 2.0 and 2.3 μm as shown. The periodic transients in the trace are due to a release-restretch protocol. The vertical calibration bar is 10 mN/mm² and the horizontal bar is 100 s.

SL dependence of steady-state force

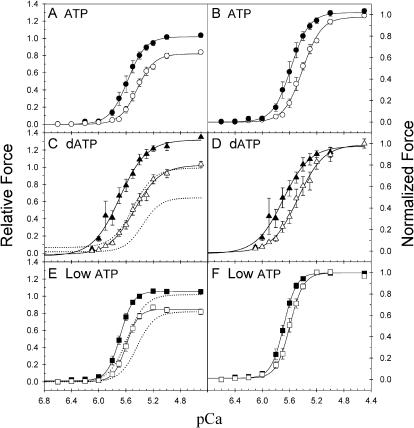
Force-pCa relations obtained with different nucleotide conditions are summarized in Fig. 2. Steady-state isometric force is plotted against pCa at SL 2.0 and 2.3 μm for 5 mM ATP (Fig. 2, A and B), 5 mM dATP (Fig. 2, C and D) and 0.5 mM ATP (Fig. 2, E and F). For comparison the data are normalized either to the F_max in 5 mM ATP at 2.3 μm SL (Fig. 2, A, C, and E) or to the F_max at each SL under each condition (Fig. 2, B, D, and F). The force-pCa data from individual trabeculae were fit with the Hill equation and the mean (± SE) pCa₅₀ and n_H values are given in Table 1. Decreasing SL-reduced steady-state force at all Ca²⁺ concentrations in all three conditions (Fig. 2). In ATP when SL was decreased from 2.3 to 2.0 μm, the F_max decreased by 23 ± 4% (n = 15), the pCa₅₀ decreased by 0.16 (ΔpCa₅₀) and the n_H decreased by 1.0 (Fig. 2, A and B; Table 1).

FIGURE 2.

SL dependence of Ca²⁺-activation of force under differing nucleotide conditions. Force-pCa relations are compared at SL 2.3 (solid symbols) and 2.0 (open symbols) μm for 5.0 mM ATP (A, B; •, ○), 5.0 mM dATP (C, D; ▴, ▵) and 0.5 mM ATP (E, F; ▪, □). Force is scaled to either the F_max in ATP at 2.3 μm SL (left panels) or to the respective F_max for each condition and SL (right panels). The error bars represent mean ± SE from 8, 10, and 13 trabecula for ATP, dATP, and low ATP, respectively. The data was fit with the Hill equation and the corresponding values of pCa₅₀ and n_H are included in Table 1. The dotted curves in C and E are the Hill fit curves for the corresponding sets of control (5.0 mM ATP) experiments.

TABLE 1.

Summary of fitted parameters for force-pCa and k_tr-pCa relations for 5 mM ATP (ATP), 5 mM dATP (dATP), and 0.5 mM ATP (low ATP)

	ATP		dATP		Low ATP
	2.3 μm	2.0 μm	2.3 μm	2.0 μm	2.3 μm	2.0 μm
Fmax	1.0	0.84 ± 0.02	*1.35	1.04 ± 0.03	*1.06	0.82 ± 0.03
pCa50	5.55 ± 0.04	5.39 ± 0.03	5.66 ± 0.04	5.46 ± 0.05	5.70 ± 0.02	5.61 ± 0.02
nH	5.1 ± 0.4	4.1 ± 0.2	3.8 ± 0.5	3.3 ± 0.3	5.5 ± 0.4	5.3 ± 0.5
ktr(max), s−1	10.3 ± 1.5	11.8 ± 1.2	16.7 ± 1.7	18.2 ± 2.0	7.9 ± 0.9	9.8 ± 1.3
pCa50(ktr)	5.26 ± 0.04	5.16 ± 0.05	5.41 ± 0.06	5.35 ± 0.08	5.56 ± 0.03	5.51 ± 0.04

Values shown are averages of 15 (ATP), 10 (dATP), and 13 (low ATP) experiments with errors shown as mean ± SE.

^*The relative values of F_max for dATP and low ATP were determined in separate experiments.

When dATP was substituted for ATP steady-state force increased at all activating pCa at both SL compared to the corresponding controls (Fig. 2 C, dotted lines). We previously reported an increased rate of cross-bridge cycling with dATP, as evidenced by increased k_tr and unloaded shortening velocity (V_u) in skinned cardiac muscle (Regnier et al., 2000). The increase in F_max and pCa₅₀ by dATP was similar at both lengths, so that the difference in pCa₅₀ (ΔpCa₅₀) between the two SLs was comparable to ATP (Fig. 2, C and D; Table 1). In contrast n_H at each SL decreased relative to ATP control (Table 1). The increase in F_max and pCa₅₀ and the decrease in n_H observed with dATP is similar to elevated [ADP] (Fukuda et al., 2000). However, unlike dATP, elevated [ADP] causes a reduction of ΔpCa₅₀ (Fukuda et al., 2000). Thus although the faster cross-bridge cycling with dATP increased the apparent level of thin filament activation (increased F_max and increased pCa₅₀ with respect to ATP), this did not lead to a reduction in the SL-dependence of activation.

When cross-bridge cycling rate was reduced with 0.5 mM ATP (low ATP), there was no significant change in F_max at either SL relative to ATP (Fig. 2 E). Slowed cross-bridge cycling at low ATP was evidenced by a decrease of V_u at maximal activation (pCa 4.5) at SL 2.3 μm from 3.5 ± 0.4 L₀s⁻¹ (n = 10) with ATP to 2.2 ± 0.5 (n = 6) with low ATP (P < 0.05). At SL 2.3 μm pCa₅₀ increased by 0.13 (Table 1) with low ATP, which is similar to that of dATP. However, at SL 2.0 μm low ATP increased pCa₅₀ by 0.2, approximately twice that found for dATP (0.09), leading to a reduction of ΔpCa₅₀ (Fig. 2, E and F; Table 1). At both SL n_H in low ATP was higher than with dATP and either similar to (2.3 μm SL) or greater (2.0 μm) than with ATP (Table 1). A similar increase in the Ca²⁺-sensitivity of force and reduction in ΔpCa₅₀ has been reported with elevated MgADP in skinned cardiac muscle (Fukuda et al., 2000). These results suggest that conditions that slow cross-bridge detachment from strongly bound states lead to a decrease in the SL dependence of the Ca²⁺-sensitivity of force in cardiac muscle.

Ca²⁺ and SL dependence of force redevelopment rate (k_tr)

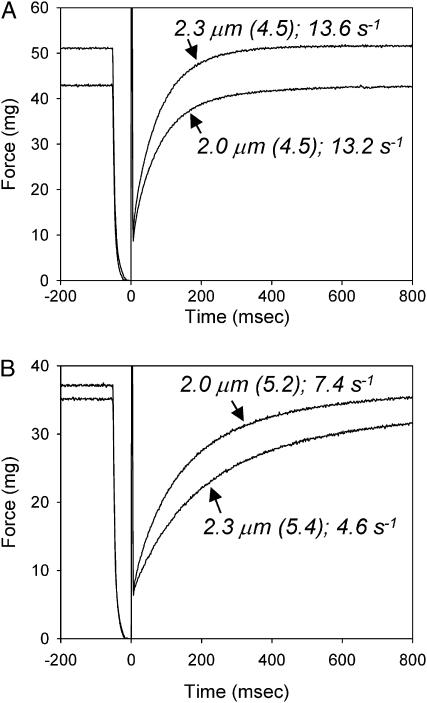
The steady-state data clearly indicate that cross-bridge kinetics can influence the SL-dependence of force-pCa relations in skinned cardiac muscle (Fig. 2; Table 1). To test the idea that elevated force at longer SL results from an increased probability of cross-bridge transition into force-generating states, we measured the Ca²⁺, SL, and nucleotide dependence of k_tr. Although the SL dependence of k_tr has been measured in skeletal fibers, a similar analysis has not yet been reported in cardiac muscle until now. Representative traces of force redevelopment (with ATP) obtained during k_tr measurements at 2.0 and 2.3 μm SL are compared in Fig. 3 at maximal Ca²⁺-activation (Fig. 3 A) and at similar levels of submaximal Ca²⁺-activated force (∼70% F_max at 2.3 μm SL; Fig. 3 B). The k_tr-pCa and k_tr-force data for all nucleotide conditions and both SLs are summarized in Figs. 4 and 5. Maximum values of k_tr at 2.0 μm SL with ATP, dATP, and low ATP were 11.8 ± 1.2 s⁻¹ (n = 15), 18.2 ± 2.1 s⁻¹ (n = 10) and 9.8 ± 1.3 s⁻¹ (n = 13), respectively. Corresponding values at 2.3 μm SL were (ATP) 10.3 ± 1.5 s⁻¹, (dATP) 16.7 ± 1.7 s⁻¹, and (low ATP) 7.9 ± 0.9 s⁻¹. The data demonstrate that during maximal Ca²⁺-activation lowering [ATP] reduces k_tr whereas substitution of dATP for ATP increases k_tr, indicating slower and faster cross-bridge cycling kinetics, respectively, at both SLs (Table 1).

FIGURE 3.

Comparison of example force traces at SL 2.3 and 2.0 μm obtained during k_tr measurements from a single skinned trabecula (length 1.1 mm, diameter 140 μm) during similar levels of submaximal force activation (pCa 5.2 for SL 2.0 μm and pCa 5.4 for SL 2.3 μm) (A) and during maximal activation (pCa 4.5) (B). The SL, pCa (in brackets), and value of k_tr are indicated next to each trace.

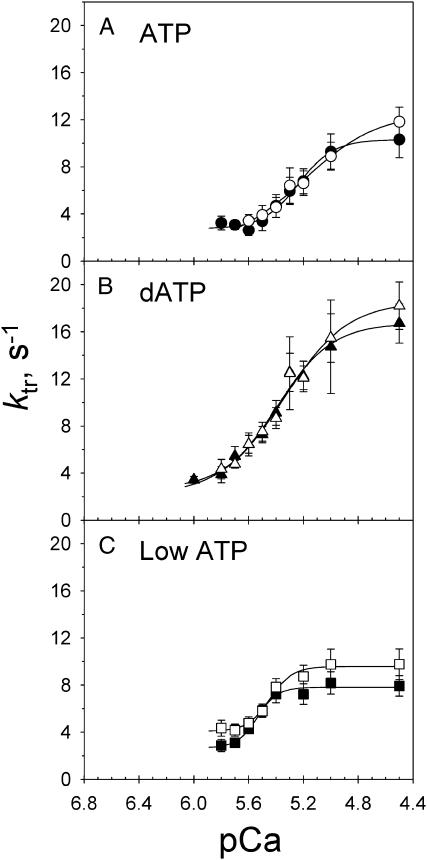
FIGURE 4.

k_tr-pCa relations during Ca²⁺-activation at SL 2.3 (solid symbols) and 2.0 (open symbols) μm in 5 mM ATP (A), 5 mM dATP (B) and 0.5 mM or low ATP (C). Symbols are as in Fig. 2. Data, with error bars representing mean ± SE, were obtained from 8, 10, and 13 trabecula with ATP, dATP, and low ATP, respectively. The solid lines represent fitted curves through the mean data points for each condition.

FIGURE 5.

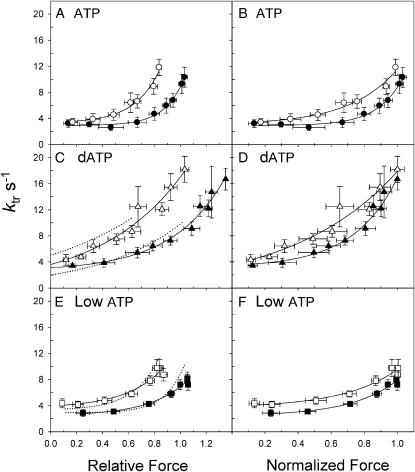
SL dependence of k_tr-force relations for data obtained from fibers shown in Fig. 4. Symbols are as in Figs. 2 and 4. Data are shown with force expressed relative to the F_max in ATP at SL 2.3 μm (left panels) or normalized to the F_max for each condition and SL (right panels). The dotted curves in C and E are from the corresponding sets of control (5.0 mM ATP) experiments.

The Ca²⁺ dependence of k_tr is illustrated in Fig. 4 for control ATP (A), dATP (B), and low ATP (C). The data were fit by the Hill equation to obtain the pCa₅₀ values under the different nucleotide conditions (Table 1). Both dATP and low ATP caused an apparent shift of k_tr-pCa relations to higher pCa relative to ATP, as found for force (Fig. 2). However, in contrast to the force-pCa relations (Fig. 2), the Ca²⁺-dependence of k_tr was unaffected by changes in SL between 2.0 and 2.3 μm with ATP, dATP, or low ATP (Fig. 4). This comparison is important because in cardiac muscle increasing SL increases both force and Ca²⁺-binding to thin filaments (Wang and Fuchs, 1994). The results in Fig. 4 suggest that increased thin filament Ca²⁺-binding at longer SL may not correlate with changes in the kinetics of isometric force redevelopment (k_tr).

To more directly compare the activation dependence of k_tr for each nucleotide condition, k_tr is replotted against the relative force for each pCa, with force expressed either relative to F_max at SL 2.3 μm (Fig. 5, A, C, and E) or normalized to F_max for each SL (Fig. 5, B, D, and F). For each nucleotide condition, a higher [Ca²⁺] was required to obtain the same level of force at SL 2.0 μm compared to SL 2.3 μm (Fig. 2). At the lowest forces k_tr was the same under all three nucleotide conditions and both SLs (∼4 s⁻¹). With increasing force k_tr increased nonlinearly at each SL to an apparent maximum at F_max. The range of k_tr changes during activation at each SL was approximately fourfold for ATP (Fig. 5, A and B), approximately sixfold for dATP (Fig. 5, C and D), and two- to threefold for low ATP (Fig. 5, E and F). As noted above, maximum k_tr was similar at SL 2.0 and 2.3 μm for each condition, whereas at intermediate matched-force levels k_tr was greater at SL 2.0 μm for all three nucleotide conditions, independent of whether force was expressed as relative or normalized values. This and the lack of a significant SL-dependence of maximal k_tr contrasts with a previous report in skinned skeletal fibers, which showed that k_tr was slower at shorter SL than at longer SL during maximal Ca²⁺ activation (McDonald et al., 1997).

When k_tr-force curves are compared between dATP and ATP (Fig. 5 C; solid versus dotted lines, respectively) k_tr is similar over the range of forces common to both conditions at each SL, whereas force and k_tr are both elevated by dATP at the highest Ca²⁺ concentrations. The data in Fig. 5 extend our observations (Regnier et al., 2004) to include shorter SL and supports the idea that dATP may enhance maximal force by increased thin filament activation, even at pCa 4.5. In Fig. 5, B, D, and F, force is normalized to the maximum value at each SL which assumes that activation is independent of SL and is maximal for each nucleotide condition. However, this assumption may not be correct as it has been shown that decreasing SL reduces the amount of Ca²⁺-bound to thin filaments (Wang and Fuchs, 1994). Even so, independent of the method of force normalization, k_tr is faster for equivalent force levels at shorter SL when cross-bridge cycling rate is varied by each nucleotide condition. This idea is discussed in more detail below (see Discussion). Interestingly, at SL 2.0 μm k_tr values at submaximal activation levels are slightly higher in low ATP than the control ATP (Fig. 5 E), reminiscent of our observations in skeletal fibers (Regnier et al., 1998) where we suggested that thin filament activation was elevated at low Ca²⁺ concentrations by slowed cross-bridge cycling.

Effects of lattice compression on force and k_tr at SL 2.0 μm

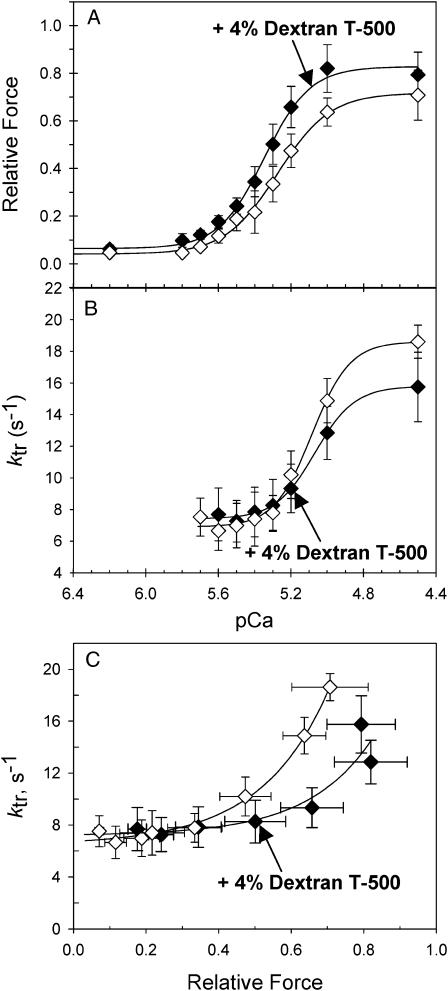
To determine if SL effects on force and k_tr (Figs. 2, 4, and 5) are correlated with accompanying changes in myosin-actin proximity, the myofilament lattice spacing was compressed osmotically using 4% dextran T500 (w/v) at SL 2.0 μm. This level of compression was chosen to produce a small increase in force (12%) to mimic force changes that occur when SL is stretched. The decrease in lattice spacing by this dextran concentration in skinned trabeculae is greater than what occurs by increasing SL from 2.0 to 2.3 μm under relaxing conditions (Konhilas et al., 2002b; Martyn et al., 2004), but is comparable to that occurring in intact trabeculae over the same length range (Irving et al., 2000). Unfortunately, similar comparisons of lattice spacing during active contractions are unavailable. As seen in Fig. 6 A osmotic compression with 4% dextran increased pCa₅₀ from 5.27 ± 0.01 (n = 5) to 5.35 ± 0.02 (n = 5) and F_max by ∼12%. In contrast, Fig. 6 B illustrates that osmotic compression with 4% dextran had no effect on the pCa₅₀ of the k_tr -pCa relationship (5.10 ± 0.04, n = 5 versus 5.07 ± 0.01, n = 5 for 4% dextran), which is similar to the data in Fig. 4 where SL is altered. The corresponding values of k_tr are plotted against the relative level of force (normalized to F_max at SL 2.3 μm) in Fig. 6 C. As with increasing SL (Fig. 5, A and B), k_tr was lower at intermediate and maximally activated matched force levels in the presence of 4% dextran at 2.0 μm SL (Fig. 6 C). These data demonstrate that compression of the lattice spacing at SL 2.0 μm produces similar changes in both force and k_tr as that of increasing SL from 2.0 to 2.3 μm. These observations support the idea (Fuchs and Wang, 1996; Fuchs, 2002; Fukuda et al., 2003) that increased contractile activation at longer SL in cardiac muscle could be due, at least in part, to the accompanying decrease in the distance between thick and thin filaments.

FIGURE 6.

Force-pCa relations (A), k_tr-pCa relations (B), and k_tr-force relations (C) are illustrated for data obtained at SL 2.0 μm with (♦) and without (⋄) the osmotic compression with 4% dextran T500. Data (mean ± SE) were obtained from 5 trabecula. The solid lines are fitted curves through the mean data points.

DISCUSSION

In this study we tested the hypothesis that the kinetics of actin-myosin cross-bridge interactions are important determinants of the steep SL sensitivity of cardiac contractile activation (Frank-Starling effect). In addition we tested whether the rate of isometric force redevelopment (k_tr) covaries with force when SL is changed, as might be expected if SL-dependent changes in the probability of strong cross-bridge interaction were the basis of the SL-dependence of force generation (the Frank-Starling relationship). In the presence of dATP the magnitudes of both force and k_tr at maximal activation increased compared to ATP, as did the Ca²⁺-sensitivity of force and k_tr, whereas the effect of SL on pCa₅₀ (ΔpCa₅₀) was not significantly different from the ATP controls (Table 1). When cross-bridge kinetics were slowed by lowering [ATP] from 5.0 to 0.5 mM, the Ca²⁺-sensitivity of force-pCa and k_tr-pCa relations increased (as for dATP), whereas F_max was unchanged and maximum k_tr decreased. In contrast to both ATP and dATP ΔpCa₅₀ was diminished and n_H was increased with 0.5 mM ATP (Table 1). Importantly we found that at the same level of force, k_tr was faster at the shorter SL over the entire range of submaximal [Ca²⁺] under all tested conditions (Fig. 5). Finally, the compression of myofilament lattice spacing at SL 2.0 μm by 4% dextran led to similar changes in the force and k_tr as that of increasing SL alone (Fig. 6). As discussed below, these results provide important insights into the relationship between the cross-bridge binding and kinetics and the SL dependence of force generation in cardiac muscle.

Effects of cross-bridge cycling kinetics on the SL dependence of Ca²⁺- activation

The hypothesis that the SL dependence of force in cardiac muscle is influenced by the kinetics of actin-myosin interactions is suggested by our observations that submaximal k_tr in skinned skeletal fibers is dependent on the kinetics of Ca²⁺-binding to thin filaments. It also suggests kinetic coupling occurs between thin filament regulatory transitions and cross-bridge cycling (Chase et al., 1994b; Regnier et al., 1996, 1998, 1999). Our current data supports this hypothesis for cardiac muscle because the effect of SL change on force was influenced by cross-bridge kinetics. With dATP cross-bridge binding and cycling kinetics were enhanced, as evidenced by increased F_max (Fig. 2; Table 1) and k_tr (Fig. 5; Table 1), respectively. Both F_max and pCa₅₀ of steady-state force were increased by dATP (relative to ATP) to the same extent at both SL, whereas ΔpCa₅₀ was comparable to ATP. Thus when cross-bridge binding is enhanced with faster kinetics, the SL-dependence of force is unaltered even though Ca²⁺-sensitivity of force increased at each SL. This contrasts with the effects of slower cross-bridge kinetics on the SL and Ca²⁺-dependence of force with low [ATP] (Fig. 2, E and F; Table 1) where ΔpCa₅₀ decreased compared to ATP. Fukuda et al. (2000) reported a similar reduction of ΔpCa₅₀ when cross-bridge cycling was reduced with 0.1 mM MgADP in skinned cardiac muscle. However, although elevated [MgADP] increased F_max, there was also an elevated force in the absence of Ca²⁺ (Fukuda et al., 1998), implying Ca²⁺-independent activation of thin filaments. In our experiments there was no Ca²⁺-independent activation with either dATP or low [ATP] because resting force was not elevated at either SL (data not shown). Interestingly, with low [ATP] pCa₅₀ increased more at the shorter SL, relative to ATP (Fig. 2, E and F; Table 1) causing ΔpCa₅₀ to decrease, as found for elevated [ADP] (Fukuda et al., 2000). Both elevated [ADP] and lowering [ATP] to 0.5 mM reduce the rate of cross-bridge detachment and could therefore affect the apparent cooperativity of the force-pCa relationship. Although F_max did not increase when [ATP] was lowered, as it did with elevated [ADP] (Fukuda et al., 2000), the apparent cooperativity (n_H) of force-pCa relations increased at the shorter SL, indicating enhanced cooperative activation by strong binding cross-bridges. This is consistent with the higher cooperative activation of cardiac versus skeletal muscle by cross-bridges in the rigor state (Metzger, 1995). The effect of low ATP on n_H might be expected to be greatest under conditions where cross-bridge binding is reduced, such as at short SL and lower force, as we observed (Fig. 2, E and F; Table 1).

Our data suggest that increased thin filament activation, as evidenced by increased Ca²⁺-sensitivity of force, does not by itself determine the SL-dependence of force-pCa relations. This is demonstrated by the observation that ΔpCa₅₀ is unaffected by dATP and reduced by low [ATP], even though Ca²⁺-sensitivity of force is increased by both (Fig. 2; Table 1). Thus the question is, “why would the SL-dependence of activation be apparently unaffected by enhanced strong cross-bridge binding (more force and stiffness) with dATP?” The answer may lie in the faster kinetics of cross-bridge cycling with dATP (Regnier et al., 1998, 2000). Kinetic-coupling between thin filament activation processes and cross-bridge cycling has been proposed to explain the lower activation dependence of force redevelopment kinetics in cardiac (Hancock et al., 1997) and skeletal muscle when cross-bridge cycling (Regnier et al., 1998), TnC isoform or structure (Chase et al., 1994b; Regnier et al., 1999) or Ca²⁺-binding properties (Regnier et al., 1996) are altered. Increasing cross-bridge cycling rate with dATP (when thin filament activation kinetics are not altered) could increase coupling between cross-bridge binding and thin filament state (Regnier et al., 2004) thereby reducing or eliminating the effects of SL on thin filament activation mediated through altered cross-bridge binding. The opposite may occur with low ATP, resulting in a reduction of the SL dependence of force.

Does ΔpCa₅₀ accurately describe changes in the Frank-Starling mechanism?

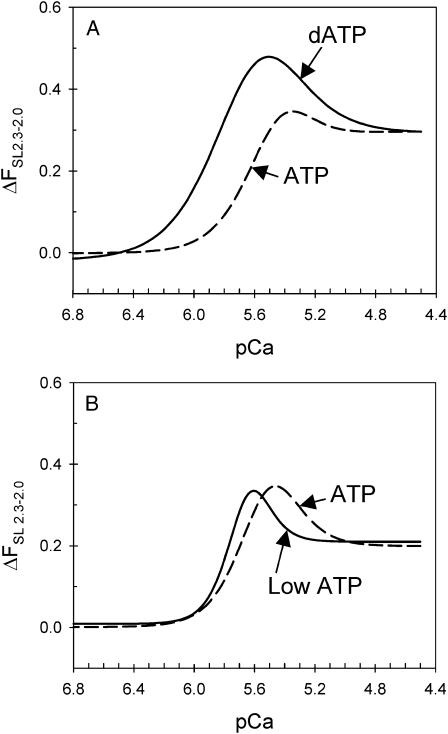
At the cellular level, the Frank-Starling effect in cardiac muscle can be described by the increase in force upon SL extension over the entire range of intracellular Ca²⁺ concentrations experienced under physiological conditions. The ΔpCa₅₀ is therefore a limited indicator of the Frank-Starling effect, because the force difference between SL 2.0 and 2.3 μm depends not only on the respective pCa₅₀ values but also on the respective changes in F_max and slope (n_H) of the individual force-pCa relations. This is illustrated in Fig. 7. Although ΔpCa₅₀ varies little between dATP and ATP (Table 1) the difference in force (ΔF_SL2.3–2.0) between 2.3 versus 2.0 μm is greater with dATP over the entire activation range (pCa 6.4–4.8, Fig. 7 A). Likewise, although low ATP diminished ΔpCa₅₀, ΔF_SL2.3–2.0 illustrates that the Frank-Starling effect is actually enhanced above pCa 5.6 and diminished below pCa 5.6 (Fig. 7 B). This analysis also hints that the cardiac Ca²⁺ regulatory mechanism may be “tuned,” such that a maximal effect of SL on force occurs at or near the peak Ca²⁺ concentration achieved during twitch contractions of intact myocytes (Fabiato, 1981).

FIGURE 7.

The “magnitude” of the Frank-Starling effect (the force difference between SL 2.3 and 2.0 μm) during Ca²⁺-activation for ATP, dATP, and low ATP. The force difference as a function of pCa were obtained by subtracting the corresponding Hill fit curves at SL 2.0 μm from SL 2.3 μm from Fig. 2, and are compared between dATP (A) and low ATP (B) and the corresponding ATP control curves.

The effects of SL and myofilament lattice spacing on k_tr

Although the substitution of dATP for ATP and lowering [ATP] increased the Ca²⁺-sensitivity of k_tr, k_tr-pCa relations were unaffected by changing SL under all three conditions (Fig. 4; Table 1). The lack of an SL-dependence of k_tr-pCa relations is explained by our observations that maximum k_tr is relatively unaffected by changes in SL (Fig. 3 A), whereas at equivalent submaximal levels of force k_tr was faster at SL 2.0 μm compared to SL 2.3 μm (Fig. 3 B). The increase in k_tr at submaximal levels of force, when force was matched at both SL (Fig. 5), can be explained by a higher [Ca²⁺] needed to reach the same level of force at the shorter SL (Fig. 2). Put another way, it appears that [Ca²⁺] is the major determinant of k_tr at both SL under all nucleotide conditions. However, increasing SL causes an enhanced binding of Ca²⁺ to cTnC in cardiac muscle (Wang and Fuchs, 1994; Martyn and Gordon, 2001), and the absence of SL effects on k_tr–pCa relations implies that Ca²⁺-binding to cTnC does not directly modulate cross-bridge steps that are rate limiting to k_tr. Thus the most likely effect of Ca²⁺ on k_tr is via modulation of thin filament activation level.

Our observations that k_tr values were either similar at maximum Ca²⁺-activated force or slightly faster at equivalent submaximal forces for 2.0 vs. 2.3 μm SL, independent of the nucleotide condition (Fig. 5) was surprising because McDonald et al. (1997) reported that maximal k_tr was somewhat slower at shorter SL in skinned skeletal fibers. Furthermore, osmotic compression at SL 2.0 μm increased F_max and pCa₅₀ (Fig. 6 A) but had no effect on the k_tr-pCa relations (Fig. 6 B), which is similar to that found for the SL increase from 2.0 μm to 2.3 μm without osmotic compression (Figs. 2, 4, and 5). These observations are significant because at SL 2.0 μm there was very little passive force and presumably no extension of titin, suggesting that changes in k_tr and force cannot be attributed to a direct effect of titin on cross-bridge binding and that the effects of SL on force and k_tr are, at least in part, a consequence of lattice spacing changes. Thus, at comparable levels of Ca²⁺-activation, increasing SL and decreasing lattice spacing (which increases the proximity of cross-bridge and thin filament binding sites) caused an apparent decrease, rather than increase, of the probability of cross-bridge transition into force generating states in cardiac muscle.

It has been proposed that k_tr reflects the rate at which a new equilibrium is reached in cross-bridge distribution between nonforce and force producing states and is the sum of the apparent forward (f_app) and reverse (g_app) rate constants for these transitions in a two-state cross-bridge model (Brenner and Eisenberg, 1986). The steep dependence of k_tr on [Ca²⁺] and force in skeletal fibers suggested that Ca²⁺ binding to thin filaments controls force redevelopment kinetics by increasing f_app (Brenner and Eisenberg, 1986). However, the regulation and activation dependence of k_tr is likely to be more complicated. For example, thin filament activation kinetics limit k_tr at submaximal forces in skeletal fibers (Chase et al., 1994b; Regnier et al., 1996), indicating that k_tr represents the apparent kinetics of both thin filament activation and inherent cross-bridge cycle kinetics. If this is also true in cardiac muscle the lower activation dependence of k_tr, compared to skeletal fibers, could be explained by a larger influence of thin filament kinetics even at high levels of Ca²⁺ activation (Hancock et al., 1997). It is also possible that cooperative activation of thin filaments by cross-bridges could affect the k_tr-force relationship (Campbell, 1997), especially since the equilibrium activation level appears to be more dependent on strong cross-bridge binding in cardiac muscle (Hofmann and Fuchs, 1987; Wang and Fuchs, 1994; Martyn and Gordon, 2001; Regnier et al., 2004).

Possible explanations for a disproportionate effect of SL or lattice spacing on force and k_tr when SL is extended from 2.0 to 2.3 μm (Fig. 5) or when lattice spacing is compressed at SL 2.0 μm (Fig. 6) are as follows. Cross-bridge binding to thin filaments depends not only on the equilibrium distribution of thin filament states but also on the proximity of thin filament binding sites to cross-bridges. The availability of thin filament sites should increase with decreasing lattice spacing because of increased proximity of the myofilaments, resulting in increased f_app. Our observation that weak cross-bridge binding in relaxed cardiac muscle is elevated when lattice spacing is compressed is consistent with this idea (Martyn et al., 2004). As a result force (proportional to f_app/(f_app+g_app); Brenner, 1988) should increase with increasing SL and reduced lattice spacing, as observed (Fig. 2). However, k_tr (= f_app+g_app) should increase as well if g_app is unaffected by SL extension, as suggested by recent observations that the ratio of ATPase activity (proportional to g_app; Brenner, 1988) to isometric force is independent of SL between 2.0 and 2.2 μm (Wannenburg et al., 1997). This interpretation is contrary to our observations that maximum k_tr is either unaffected by SL or slightly faster at short SL and significantly faster at intermediate levels of force (Fig. 5). The apparent contradiction is resolved if compressed lattice spacing and reduced radial cross-bridge strain at longer SL causes a reduction of g_app (Brenner and Yu, 1985; Goldman and Simmons, 1986) that compensates for the increase of f_app implied by elevated force. Conversely, at shorter SL and expanded lattice spacing the elevated radial cross-bridge strain may cause g_app to increase, compensating for the decrease of f_app (implied by lower force). As a result maximal k_tr would vary little whereas force would be strongly SL dependent, as observed (Figs. 2 and 6). This idea is consistent with the observation that the ratio of ATPase activity to force during isometric contraction at maximal Ca²⁺-activation increases with decreasing SL in skinned cardiac muscle (Kentish and Stienen, 1994) and with the observation of decreased economy and efficiency of oxygen consumption relative to isometric force when muscle length is decreased in intact cardiac muscle (Holmes et al., 2002). We further tested this idea by modeling changes in force and k_tr when the rate of cross-bridge detachment was increased twofold, as might occur at short SL, using a six-state cross-bridge model (Regnier and Homsher, 1998). Simulations predicted a 24% decrease in F_max and an 18% increase in k_tr. When SL was decreased from 2.3 to 2.0 μm, F_max decreased 25% and average k_tr was 14% greater at the short SL, close to the values predicted by the model. Slight decreases in the forward rate of force generation (f_app) coupled with smaller magnitude changes in cross-bridge detachment (g_app) yield quantitatively similar simulation results. Thus in cardiac muscle the steep decrease of force with decreasing SL may result from a simultaneous decrease in the probability of cross-bridge attachment coupled with an increased probability of cross-bridge detachment. These opposing changes in cross-bridge dynamics would result in little change of k_tr, since the sum of f_app + g_app remains relatively constant. This result indicates that the steep decline of force at short SL in cardiac contraction is not accompanied by similar reductions in the rate of force development. Maintenance of the speed of force development with declining force at short length may help maintain rapid ventricular ejection during the later stages of systole in the heart, thus helping to maintain blood flow and ventricular emptying subsequent to the next period of diastole.