Abstract
Dielectrophoretic (DEP) forces have been used extensively to manipulate, separate, and localize biological cells and bioparticles via high-gradient electric fields. However, minimization of DEP exposure time is desirable, because of possible untoward effects on cell behavior. Toward this goal, this article investigates the geometric and material determinants of particle patterning kinetics and efficiency. In particular, the time required to achieve a steady-state pattern is theoretically modeled and experimentally validated for a planar, interdigitated bar electrode array energized in a standing-wave configuration. This measure of patterning efficiency is calculated from an improved Fourier series solution of DEP force, in which realistic boundary conditions and a finite chamber height are imposed to reflect typical microfluidic applications. The chamber height, electrode spacing, and fluid viscosity and conductivity are parameters that profoundly affect patterning efficiency, and optimization can reduce electric field exposure by orders of magnitude. Modeling strategies are generalizable to arbitrary electrode design as well as to conditions where DEP force may not act alone to cause particle motion. This improved understanding of DEP patterning kinetics provides a framework for new advances in the development of DEP-based biological devices and assays with minimal perturbation of cell behavior.
INTRODUCTION
The physical manipulation of biological particles (from DNA to viruses to cells) is a vital component of miniaturized biotechnological platforms such as “lab-on-a-chip” devices and arrays for high-throughput assays (Huang et al., 2001; Kapur et al., 1999; Ozkan et al., 2003; Voldman et al., 2002). To date, cellular arrays have primarily been generated via selective surface modification or micropatterning techniques (Bhatia and Chen, 1999; Folch and Toner, 2000). However, these passive techniques rely on cell adhesion processes that occur over relatively long timescales (hours), are limited to planar surfaces, and cannot be generalized to nonadherent cell types. In the future, “active” patterning techniques that are independent of cell adhesion would be advantageous to decrease patterning time and extend capabilities to the manipulation of nonadherent cell types or cells that alter their behavior when spread against a rigid surface.
Active patterning can arise through the application of a variety of physical forces, including mechanical, fluidic, optical, acoustic, and electromagnetic (Ashkin, 1997; Iwasaka et al., 2001; Jager et al., 2000; Matsue et al., 1997; Ozkan et al., 2003; Wu, 1991). One particularly advantageous strategy utilizes dielectrophoresis (DEP), the translational motion of polarizable matter (neutral or charged) within a spatially nonuniform electric field (Hughes, 2003; Jones, 1995; Pohl, 1978). The DEP force moves particles toward regions of high field intensity (positive DEP or +DEP) or low field intensity (negative DEP or −DEP), depending on electrical properties of the particle and suspending medium. By varying electrode shape and excitation, DEP forces have been used for particle trapping, arraying, levitation, translation, fractionation, filtration, orientation, and characterization based on dielectric properties (Arnold and Zimmermann, 1988; Frenea et al., 2003; Gascoyne and Vykoukal, 2002; Matsue et al., 1997; Voldman et al., 2001). However, the general use of DEP forces for patterning cells to fixed locations has not been extensively pursued since its initial proposal (Matsue et al., 1997), in part because DEP forces are inherently transient and disappear when the field is removed. Because living cells appear to tolerate high electric fields for relatively short times (Archer et al., 1999; Docoslis et al., 1999; Glasser and Fuhr, 1998), long-term biological experimentation requires a method to stabilize cell position in the absence of DEP forces. Recent strategies for restraining cell migration after active DEP localization include the incorporation of cell-adhesive proteins (Gray et al., 2003) or etched microwells (Frenea et al., 2003). Alternatively, encapsulation of patterned cells within hydrogel biomaterials (Elisseeff et al., 2000) would further enable incorporation of cells that are nonadherent or require three-dimensional (3-D) microenvironments to maintain tissue-specific functions (Abbott, 2003; Benya and Shaffer, 1982; Cukierman et al., 2002; Schmeichel and Bissell, 2003). To achieve this goal of positioning cells by DEP and immobilization via hydrogel entrapment, it is desirable to identify experimental parameters that: 1), maximize DEP patterning efficiency, 2), support cell viability without perturbing cell function, and 3), preserve the chemistry of hydrogel formation. These requirements suggest that a model-guided, rather than empirical, determination of experimental parameters is advantageous.
Existing analytical and numerical models of DEP force illustrate spatial variations within a device but historically have been limited to specific geometries or approximate boundary conditions (Chang et al., 2003; Clague and Wheeler, 2001; Green et al., 2002; Heida et al., 2001; Masuda et al., 1987; Morgan et al., 2001; Schnelle et al., 1993; Wang et al., 1993, 1996). Practical applications of these models include predicting levitation height, particle velocity, and selected particle trajectories (Markarian et al., 2003; Morgan et al., 2001; Qiu et al., 2002), although none have integrated these models into a single parameter that describes the overall time for DEP motion or “patterning” to occur.
The purpose of the work, described herein, was to develop and validate a predictive model of DEP patterning efficiency. Toward this goal, an expression was derived for the time at which model particles localize to a parallel line pattern within a thin, rectangular fluid volume. The patterning chamber was bounded by a planar interdigitated bar electrode array that is common to many DEP devices. Patterning kinetics were based on a new analytical solution for electric potential that allowed continuous variation of electrode and chamber geometry. In contrast to previous models, this solution specified a finite, variable chamber height and an improved set of boundary conditions, guided by numerical model data, which resulted in superior accuracy. The variation in particle kinetics was compared for changes in chamber geometry (electrode spacing and width, chamber height), material parameters (particularly viscosity and medium conductivity), patterning configuration (+DEP and −DEP), and particle buoyancy. The model closely predicted experimental kinetics of model particles, even for the unexpectedly slow patterning at very small chamber height. Therefore, the model serves as a useful tool for optimization of materials, geometries, and field conditions for efficient patterning, particularly for the patterning of living cells where viability is crucial.
DIELECTROPHORETIC FORCE MODEL
The parallel, planar, interdigitated electrode array is depicted in Fig. 1 A. When a potential is applied across alternating electrodes, this array establishes a nonuniform electric field dependent on dimensional and material properties. Particles suspended in a fluid experience a spatially varying DEP force that governs particle kinetics. Therefore, we begin with a model of DEP force for any chamber geometry to investigate the geometric determinants of patterning kinetics.
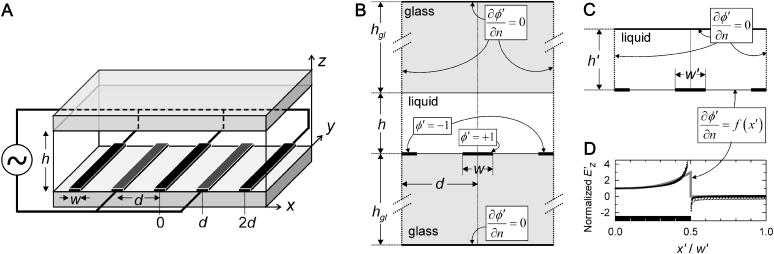
FIGURE 1.
(A) Schematic of the DEP patterning chamber with interdigitating bar electrodes (shaded) at bottom surface. Top and bottom surfaces (shaded) are nonconducting glass. Geometric variables include chamber height (h), electrode spacing (d), and electrode width (w). (B) The 2-D problem space for the numerical model, depicting volume dimensions and boundary conditions in the x-z plane. The rectangular liquid chamber containing water (ɛw = 80 ɛ0; σw = 10−4 S/m) is bounded at the top and bottom by glass (ɛgl = 4.5 ɛ0; σgl = 10−12 S/m; hgl = 1 mm). Potential is specified at the electrode surfaces (solid bars) only. (C) The simplified problem space used for the analytical solution. The boundary condition at the bottom plane is of Neumann type, where function f(x′) is determined from the FEM model (see text). (D) Neumann BC at z′ = 0. Normalized values from 13 FEM models spanning the geometry range of interest (points) are fit to a third-order polynomial f(x′) for analytical solution BC (shaded line). Electrode (solid bar) edge is at x′/w′ = 0.5.
Model theory
Electrokinetic forces are generated by an applied electric field. To determine the electric field characteristics, the electric potential is solved within the model space, using appropriate boundary conditions that represent the electrode array geometry.
The quasielectrostatic form of Maxwell's equations is appropriate for the low currents and high frequencies typical to DEP. For a homogeneous linear dielectric with conductivity σ and permittivity ɛ, the electric potential φ at a sinusoidal steady state is determined by:
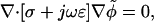 |
(1) |
where ω is oscillation frequency, 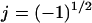 and the tilde (∼) indicates a complex variable (phasor). For a homogeneous medium, this reduces further to Laplace's equation for the real portion of the electric potential,
and the tilde (∼) indicates a complex variable (phasor). For a homogeneous medium, this reduces further to Laplace's equation for the real portion of the electric potential,
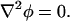 |
(2) |
The time-averaged dipole approximation to the DEP force is given by (Jones, 1995):
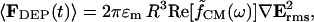 |
(3) |
where Erms is the root-mean-square electric field vector, ɛm is the medium permittivity, R is the particle radius, and 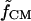 is the Clausius-Mossotti (CM) factor,
is the Clausius-Mossotti (CM) factor,
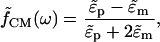 |
(4) |
dependent on complex permittivities 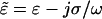 of the particle (p) and medium (m). Equation 3 is valid except where the spatial field nonuniformity is very large, such as at the electrode edges, and higher-order terms are necessary (Voldman et al., 2001).
of the particle (p) and medium (m). Equation 3 is valid except where the spatial field nonuniformity is very large, such as at the electrode edges, and higher-order terms are necessary (Voldman et al., 2001).
Dimensionless equations
The electric field depends on the applied electrode voltage (Vrms), electrode width (w) and spacing (d), and chamber height (h). To reduce the number of model variables, dimensionless variables, denoted by prime (′), are defined as: potential 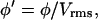 displacement vector
displacement vector 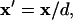 electrode width
electrode width 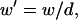 chamber height
chamber height 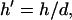 gradient operator
gradient operator 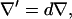 and electric field
and electric field 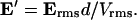 The time-averaged DEP force becomes:
The time-averaged DEP force becomes:
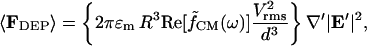 |
(5) |
where the term in braces represents a characteristic force constant, ℑ. Dimensionless DEP force,
 |
(6) |
is obtained by solving Eq. 1 or 2 for potential 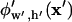 throughout the solution space. As indicated by the subscript notation, this solution needs to be computed only once for a particular nondimensional electrode width w′ and chamber height h′. DEP force is then scaled by the characteristic force constant, according to the applied voltage, electrode spacing, particle radius, and frequency-dependent dielectric properties.
throughout the solution space. As indicated by the subscript notation, this solution needs to be computed only once for a particular nondimensional electrode width w′ and chamber height h′. DEP force is then scaled by the characteristic force constant, according to the applied voltage, electrode spacing, particle radius, and frequency-dependent dielectric properties.
Analytical solution for electric potential
DEP forces throughout the solution space can be predicted readily from the electric potential. Analytical solutions are advantageous because: 1), geometric parameters can be varied continuously and independently to provide physical insight; 2), analytical expressions can be obtained directly for electric field and DEP force; such that 3), errors are not introduced by discretizing the volume and numerically estimating gradients; 4), accurate field and force determinations can be made at volume boundaries; and 5), the approach is computationally more efficient than numerical techniques.
Even for a simple geometry such as the interdigitated planar electrode array, no exact analytical expression exists for the electric potential. A boundary condition (BC) of mixed type (Dirichlet and Neumann) best represents the electrode substrate-fluid interface plane at z′ = 0, hereafter designated as the “electrode substrate.” However, mixed boundary value problems are difficult to solve analytically and solution methods are limited and complex, involving Green's functions or integral transforms (Sneddon, 1966). In contrast, analytical solutions with a single type of BC across each distinct boundary are significantly simpler to obtain. For example, linear approximations to the electric potential at the electrode substrate between interdigitated electrodes were assumed in previous Fourier series (Masuda et al., 1987; Morgan et al., 2001) and Green's function (Clague and Wheeler, 2001; Wang et al., 1996) solutions. These approximate models, which we term “linear BC” solutions, have limited accuracy (Green et al., 2002), prompting the development of complex analytical solutions with improved BCs (Chang et al., 2003; Wang et al., 1996). However, improved solutions to date do not include the effects of a finite top boundary, and are therefore unsuitable for this geometric analysis.
Numerical methods, in contrast, are able to specify the correct mixed BC without difficulty. In this manner, electric field solutions were obtained for several electrode geometries, using point charge, charge density, finite difference, integral equation, and finite element methods (Green et al., 2002; Heida et al., 2001; Schnelle et al., 1993; Wang et al., 1993). However, each geometry requires a separate computation, and general design principles are difficult to extract.
In this article, we employ a hybrid numerical/analytical solution method to obtain Fourier series expressions of both electric potential and DEP force, in which geometric and material properties can be continuously varied. A significant advantage of these solutions is that they do not assume an unbounded half-space and are therefore appropriate for finite upper boundaries. Further, accuracy is greatly improved over linear approximations with only a moderate increase in model complexity. Although this hybrid approach remains an approximation, we demonstrate its suitability in this work and suggest that its simplicity may find further application in other areas.
Modeling approach
The model utilizes a combination of numerical and analytical methods. First, numerical solutions that allow the correct mixed BC definition at the electrode substrate were obtained for a range of chamber geometries. Then, a geometry-independent curve fit to either the electric potential or the electric field provides a single BC type at the entire boundary plane, such that a simple analytical expression of the electric potential can be derived. We found that the latter option, specifying the electric field normal to the wall (a Neumann condition) provides better accuracy, especially for narrow electrodes.
Boundary conditions
Because the electrodes are typically long relative to their width, the problem can be considered two-dimensional (Fig. 1 B). At volume boundaries and symmetry planes, the Neumann condition 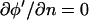 reflects the absence of current conduction across these planes, as described in detail elsewhere (Green et al., 2002). This approximate BC is valid at all frequencies for the potential in the fluid (water; ɛw = 80ɛ0; σw = 10−4 S/m) bounded by an insulating wall with reduced conductivity and permittivity (glass; ɛgl = 4.5ɛ0; σgl = 10−12 S/m). The electrodes are considered infinitely thin, with a constant potential equal to the applied voltage (φ′ = −1 or +1 at z′ = 0).
reflects the absence of current conduction across these planes, as described in detail elsewhere (Green et al., 2002). This approximate BC is valid at all frequencies for the potential in the fluid (water; ɛw = 80ɛ0; σw = 10−4 S/m) bounded by an insulating wall with reduced conductivity and permittivity (glass; ɛgl = 4.5ɛ0; σgl = 10−12 S/m). The electrodes are considered infinitely thin, with a constant potential equal to the applied voltage (φ′ = −1 or +1 at z′ = 0).
For the numerical model, upper and lower glass walls were included (Fig. 1 B). However, because the conductivity of glass is negligible, the solution space for the analytical model is simplified to contain only the liquid volume (Fig. 1 C). By the same argument as above, current conduction normal to the surface is zero at the liquid-glass boundaries, i.e., 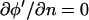 . The numerical model, described below, determines the unknown Neumann BC at the electrode surface.
. The numerical model, described below, determines the unknown Neumann BC at the electrode surface.
Numerical finite element model
The commercially available CFD-ACE+ finite element software suite (CFDRC, Huntsville, AL) was used to solve Eq. 1 for the sinusoidal steady-state electric potential. This package utilized a finite volume method technique and a structured mesh with nodes concentrated near the electrode edges.
Fifteen separate solutions of potential and electric field at the electrode wall (z′ = 0) were obtained for various chamber geometries: h′ = 0.33 − 1.0, and w′ = 0.1 − 0.5. Larger heights were not included because of negligible effects on electrode wall BCs above h′ > 1. Numerical values for electric field normal to the electrode plane for all geometries converge to a single curve upon normalization in the x- and z-directions (Fig. 1 D). A third-order polynomial fit,
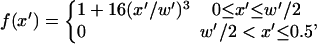 |
(7) |
approximates the Neumann BC across the entire lower boundary for any electrode width and chamber height.
Improved analytical solution
The Fourier series solution for electric potential (Eq. 2) is defined by coefficients:
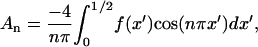 |
(8) |
where 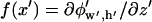 at z′ = 0. For these integral coefficients to have an analytical solution,
at z′ = 0. For these integral coefficients to have an analytical solution, 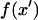 is limited to linear combinations of polynomial, exponential, and sinusoidal functions. These functions may be discontinuous. Power, logarithmic, and inverse functions, for example, would not lead to analytical Fourier coefficients.
is limited to linear combinations of polynomial, exponential, and sinusoidal functions. These functions may be discontinuous. Power, logarithmic, and inverse functions, for example, would not lead to analytical Fourier coefficients.
Using Eq. 7, Fourier coefficients depend on electrode width, w′:
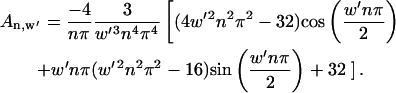 |
(9) |
The electric potential is then described by an infinite series:
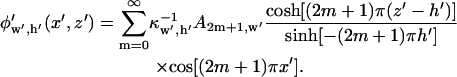 |
(10) |
Here, 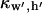 is a scaling function such that potential
is a scaling function such that potential 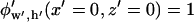 at the electrode center:
at the electrode center:
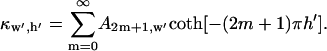 |
(11) |
In this article, the first 250 terms were computed for each series.
Solving Eq. 10, Fig. 2 A illustrates the potential and electric field boundary conditions at the electrode substrate (z′ = 0), for h′ = 2/3, w′ = 0.2. The “improved BC” analytical solution closely matches the numerical model at the boundary, in contrast to the linear BC solution described elsewhere (Morgan et al., 2001).
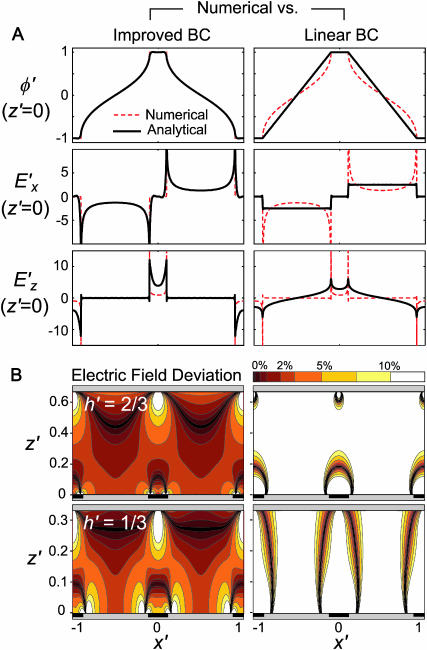
FIGURE 2.
Comparison of analytical solutions using the improved boundary condition (left, “Improved BC”) or a linear approximation between electrodes (right, “Linear BC”) and the numerical solution for w′ = 0.2. (A) Electric potential and field components at the electrode boundary, z′ = 0, demonstrate a closer match between the numerical model and the improved BC analytical model compared to the linear BC model. (B) Comparison between electric field magnitude from numerical solution 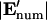 and analytical solutions |E′|, where contour shading indicates relative error:
and analytical solutions |E′|, where contour shading indicates relative error: 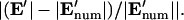 The improved BC solution (left) deviates from the numerical solution by <3% for a majority of the solution space (dark red/orange), whereas the linear solution (right) deviates by >10% throughout most of the volume (white). Similar accuracy is achieved with models of different geometry.
The improved BC solution (left) deviates from the numerical solution by <3% for a majority of the solution space (dark red/orange), whereas the linear solution (right) deviates by >10% throughout most of the volume (white). Similar accuracy is achieved with models of different geometry.
For modeling DEP patterning kinetics, the accuracy of the electric field solution throughout the chamber volume is important. Analytical solutions of electric field magnitude, |E′|, are compared to numerical finite element model (FEM) solutions in Fig. 2 B. Regardless of geometry, the improved BC solution shows <3% error in electric field magnitude for the majority of the solution space, whereas the linear BC solution deviates by >10% throughout most of the volume. The localized inaccuracies in the improved BC solution, at the electrode edges and directly opposite them, were considered acceptable because particle patterning occurs mostly away from these regions; thus, predicted patterning time would not be appreciably affected. In contrast, inaccuracies in the linear BC solution occur throughout the solution space, even far from the electrode array, and significantly influence model results (see “Model validation”).
By employing advantages of both numerical and analytical methods, the improved solution method allows quick computation of the electric potential, 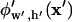 , with greater accuracy than previous analytical solutions. All variables are continuous, including particle position (x′) and chamber geometries (w′ and h′), an important advantage over discrete numerical solutions.
, with greater accuracy than previous analytical solutions. All variables are continuous, including particle position (x′) and chamber geometries (w′ and h′), an important advantage over discrete numerical solutions.
DEP force calculation
Nondimensional DEP force (Eq. 6) is conveniently recast in indicial notation:
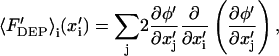 |
(12) |
where i,j represent vector indices. Because electric potential is given by an analytical expression (Eq. 10), gradients of potential are also analytical expressions that are readily computed using symbolic mathematics software, such as Mathematica (Wolfram Research, Champaign, IL). As a result, only a single series calculation is necessary for determining the DEP force vector at a particular position within the solution space.
PATTERNING EFFICIENCY MODEL
The velocity and position of a model particle can be tracked during simulated patterning using the continuous analytical solution of DEP force exerted upon it. The time required for the slowest particle to pattern is a measure of DEP patterning efficiency.
Theory and model
Force balance
Particle motion arises from a balance of applied DEP force, viscous drag, gravity, inertia, surface friction/adhesion, and interparticle attraction, and is further influenced by convection of the suspending fluid due to pressure, electrothermal, or electroosmotic flow. In this analysis, we assume negligible inertia due to low Reynolds number flow (typically, Re < 10−5 in microfluidics), no convection, and no surface forces. Thus, a balance between DEP force (Eq. 5) and drag force defines kinetics of neutrally buoyant particles:
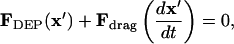 |
(13) |
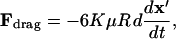 |
(14) |
where μ is fluid viscosity and K(x′) is a scaling factor equal to unity for motion of a rigid particle far from a wall (Stokes drag) but increases near a wall to reflect increased drag force (Goldman et al., 1967; Keh and Chen, 2001; Oseen, 1927).
The particle velocity field,
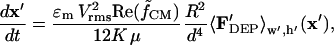 |
(15) |
is nondimensionalized by defining a time constant for DEP,
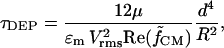 |
(16) |
and a dimensionless time, 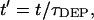 such that:
such that:
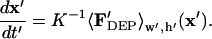 |
(17) |
The position of any particle at any time, 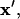 can be determined by solving this system of coupled differential equations with the initial condition
can be determined by solving this system of coupled differential equations with the initial condition 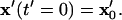 Here, the initial position vector identifies which particle is tracked. A particle reaches its equilibrium patterned location,
Here, the initial position vector identifies which particle is tracked. A particle reaches its equilibrium patterned location, 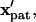 at a dimensionless time,
at a dimensionless time, 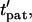 that is dependent on its initial (and final) positions.
that is dependent on its initial (and final) positions.
Patterning kinetics
Patterning kinetics for selected neutrally buoyant particles are demonstrated in Fig. 3. For comparison, the electrode plane is oriented on the bottom for the +DEP case and on top for the −DEP case, such that particles pattern downward to the lower plane in both illustrations. Path lines that track particle centroid over time curve away from the pattern location in the upper portion of the chamber and converge in the lower regions, for both +DEP and −DEP. Also, particle velocity is greatest near the electrodes, as indicated by increased separation between symbol points representing regular time intervals. To understand the evolution of pattern formation over time, consider the contours of dimensionless patterning time, 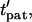 in Fig. 3. At a particular time,
in Fig. 3. At a particular time, 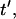 all particles initially within the area where
all particles initially within the area where 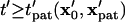 will have translated from their initial locations
will have translated from their initial locations 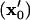 to the final pattern
to the final pattern 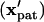 . As
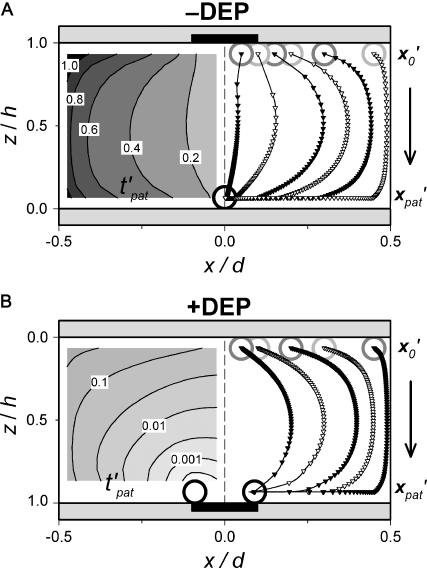
. As 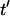 increases, this depleted space will increase until it encompasses the entire chamber area. By −DEP, the center column below the electrode patterns first, and expands over time at a nearly uniform rate. By +DEP, however, particles in a semicircular area surrounding the electrodes pattern initially, and this area grows at an exponentially decreasing rate. These distinct patterning kinetics occur because particles accelerate toward the field maxima by +DEP, whereas they slowly converge to the field minima by −DEP. Patterning time is shorter by +DEP than by −DEP for any initial particle position.
increases, this depleted space will increase until it encompasses the entire chamber area. By −DEP, the center column below the electrode patterns first, and expands over time at a nearly uniform rate. By +DEP, however, particles in a semicircular area surrounding the electrodes pattern initially, and this area grows at an exponentially decreasing rate. These distinct patterning kinetics occur because particles accelerate toward the field maxima by +DEP, whereas they slowly converge to the field minima by −DEP. Patterning time is shorter by +DEP than by −DEP for any initial particle position.
FIGURE 3.
Patterning motion and kinetics by (A) −DEP and (B) +DEP. (Right) The DEP patterning motion varies with initial particle location (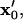 gray open circles), as indicated by centroid pathlines. Symbol points are equally spaced in time, indicating higher particle velocity near the electrode (solid bar). Near the pattern location (
gray open circles), as indicated by centroid pathlines. Symbol points are equally spaced in time, indicating higher particle velocity near the electrode (solid bar). Near the pattern location (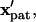 black open circles), motion is slow by −DEP but rapid by +DEP. (Left) Contours of dimensionless patterning time
black open circles), motion is slow by −DEP but rapid by +DEP. (Left) Contours of dimensionless patterning time 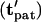 for various initial particle locations. This value is lowest near the pattern location and greatest at the opposite wall in between electrodes.
for various initial particle locations. This value is lowest near the pattern location and greatest at the opposite wall in between electrodes.
Patterning efficiency
The patterning time of the slowest-moving particle represents the total time for all particles to pattern. From Fig. 3, the initial position resulting in the longest 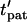 occurs in the upper left corner, i.e., the center of the electrode gap at the upper wall. However, because horizontal force vanishes at this symmetry plane (x′ = 0.5) as well as at the final pattern location, a small distance away from these points must be chosen to obtain a finite solution for patterning time. In this article, we arbitrarily select δ′ = 0.01 or 1% of electrode spacing. The total patterning time for a given geometry is defined as:
occurs in the upper left corner, i.e., the center of the electrode gap at the upper wall. However, because horizontal force vanishes at this symmetry plane (x′ = 0.5) as well as at the final pattern location, a small distance away from these points must be chosen to obtain a finite solution for patterning time. In this article, we arbitrarily select δ′ = 0.01 or 1% of electrode spacing. The total patterning time for a given geometry is defined as:
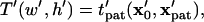 |
(18) |
where initial and final positions are  or
or 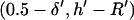 and
and 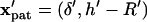 or
or 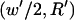 for −DEP or +DEP, respectively, and
for −DEP or +DEP, respectively, and 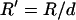 is the dimensionless particle radius.
is the dimensionless particle radius.
The predicted time to achieve complete patterning for any chamber geometry is:
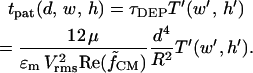 |
(19) |
Effects of geometry on patterning efficiency
Model results are presented below in two forms, based on nondimensionalization of geometric parameters to electrode spacing, d, or chamber height, h. The former case is convenient for choosing an optimal height given a uniform electrode pattern, whereas the latter formulation is ideal for varying pattern dimensions or when a particular height is required.
Constant electrode spacing
In many applications of DEP patterning, control over the dimensions and geometry of the resulting particle pattern is desired. For example, a parallel line pattern is specified by interdigitated electrode spacing, and variations in electrode width and chamber height could be made to accelerate patterning time.
To determine the effects of chamber geometry, the complete nondimensional patterning time, 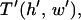 is computed for varying dimensionless chamber height and electrode width. For all geometries, patterning by +DEP (Fig. 4, B and D) is more rapid than by −DEP (Fig. 4, A and C). Increasing electrode width decreases patterning time for both +DEP and −DEP for all chamber heights, although this effect is more pronounced for thinner chambers.
is computed for varying dimensionless chamber height and electrode width. For all geometries, patterning by +DEP (Fig. 4, B and D) is more rapid than by −DEP (Fig. 4, A and C). Increasing electrode width decreases patterning time for both +DEP and −DEP for all chamber heights, although this effect is more pronounced for thinner chambers.
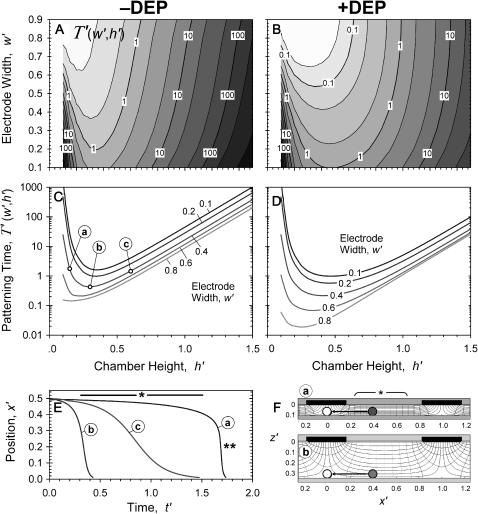
FIGURE 4.
Effects of geometry on patterning efficiency by −DEP (A, C) and +DEP (B, D) for constant electrode spacing. Dimensionless complete patterning time, T′, varies with chamber height h′ and electrode width w′. Model calculations are presented as contour plots (log contours at 1, 2, 5 gradations) above (A, B) and as families of curves below (C, D) for particular electrode widths. To explain the chamber height effect, patterning kinetics (E) and electric field lines (F) are shown for three different chamber heights (a < b < c), where b represents the optimal height with fastest patterning for w′ = 0.4. Particle motion is tracked from x′ = 0.5 to the field minimum at x′ = 0. As chamber height increases beyond optimal (e.g., c), decreased electric field strength increases patterning time. However, at suboptimal chamber heights (a), patterning time increases dramatically due to confinement of the electric field nonuniformity near the electrode. Therefore, patterning is very slow in regions away from the electrodes (*), although it is very fast near the electrodes (**).
Interestingly, the effect of chamber height on patterning time is not monotonic. At large heights, h′ > 1, patterning time increases exponentially with a slope of 2π, i.e., 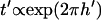 . This is consistent with the exponential decrease in electric field strength with distance from the electrode array by
. This is consistent with the exponential decrease in electric field strength with distance from the electrode array by 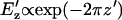 for z′ > 1 (Green et al., 2002; Morgan et al., 2001). However, very small chamber heights also result in long patterning times, due to initially slow kinetics of distant particles (Fig. 4 E, curve a). Under these conditions, electric field lines become more parallel in the electrode gap regions, where both the spatial field nonuniformity and DEP force are reduced (Fig. 4 F). Therefore, a band of particles in the center of the gap region will move very slowly, or not pattern at all. In contrast, field lines near the electrodes are extremely divergent, and particle motion is very rapid. However, the definition of patterning time
for z′ > 1 (Green et al., 2002; Morgan et al., 2001). However, very small chamber heights also result in long patterning times, due to initially slow kinetics of distant particles (Fig. 4 E, curve a). Under these conditions, electric field lines become more parallel in the electrode gap regions, where both the spatial field nonuniformity and DEP force are reduced (Fig. 4 F). Therefore, a band of particles in the center of the gap region will move very slowly, or not pattern at all. In contrast, field lines near the electrodes are extremely divergent, and particle motion is very rapid. However, the definition of patterning time 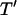 reflects complete patterning, including those particles initially in the gap region, and therefore this value increases greatly for very small chamber heights.
reflects complete patterning, including those particles initially in the gap region, and therefore this value increases greatly for very small chamber heights.
Constant chamber height
Many applications of DEP patterning require a specific chamber height, but allow variable electrode geometry as design parameters. Some examples include microfluidic devices that often contain uniform channel geometry, and the patterning of cells within a gel material whose thickness is defined by the chamber height (Albrecht et al., 2002). Other applications, such as particle depletion from the bulk of a microfluidic channel, would be less concerned with specific pattern dimensions than with chamber height. Finally, optimizing arbitrary particle patterns would require model efficiency information for a variety of relative heights (h′) and widths (w′).
The complete patterning time can be nondimensionalized in terms of chamber height h rather than electrode spacing d:
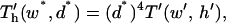 |
(20) |
where dimensionless geometric variables are recast as electrode width, w* = w/h = w′/h′ and electrode spacing, d* = d/h = h′−1. Then,
 |
(21) |
Fig. 5 illustrates the improved analytical model solution for the nondimensional patterning time of a neutrally buoyant particle, for varying nondimensional electrode spacing (d*) and electrode width (w*). Patterning kinetics show similar trends with constant chamber height as with constant electrode spacing. Positive DEP patterning (Fig. 5, B and D) is more rapid than negative DEP (Fig. 5, A and C) for all geometries, and wider electrodes accelerate patterning for all chamber heights and for both +DEP and −DEP. Patterning time is also highly dependent on electrode spacing, increasing above and below optimal values. This variation is due to the balance between: 1), the direct dependence of 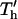 on electrode spacing by (d*)4 (Eq. 20), and 2), the effects of concomitant inverse changes in relative chamber height, h′ = (d*)−1. The former effect dominates at electrode spacing d* > ∼1. However, as spacing is reduced below d* < 1, thereby increasing h′ > 1, the latter effect dominates as patterning time increases exponentially with relative chamber height (Fig. 4). Optimal electrode spacing, which varies with electrode width, occurs when these dependencies are balanced.
on electrode spacing by (d*)4 (Eq. 20), and 2), the effects of concomitant inverse changes in relative chamber height, h′ = (d*)−1. The former effect dominates at electrode spacing d* > ∼1. However, as spacing is reduced below d* < 1, thereby increasing h′ > 1, the latter effect dominates as patterning time increases exponentially with relative chamber height (Fig. 4). Optimal electrode spacing, which varies with electrode width, occurs when these dependencies are balanced.
FIGURE 5.
Effects of geometry on patterning efficiency by −DEP (A, C) and +DEP (B, D) for constant chamber height. The complete patterning time, nondimensionalized to chamber height, 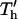 , varies with electrode spacing d* = d/h and electrode width w* = w/h. Model calculations are presented as contour plots (log contours at 1, 2, 5 gradations) above (A, B) and as families of curves below (C, D) for particular electrode widths.
, varies with electrode spacing d* = d/h and electrode width w* = w/h. Model calculations are presented as contour plots (log contours at 1, 2, 5 gradations) above (A, B) and as families of curves below (C, D) for particular electrode widths.
Chamber optimization using model
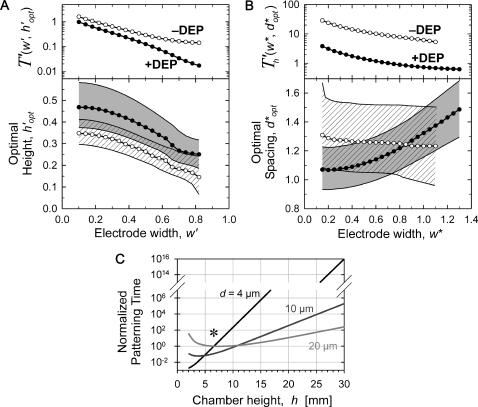
Patterning can be optimized by selecting the chamber height or electrode spacing that minimizes patterning time for a given electrode width. The optimal geometry increases patterning efficiency by maximizing electric field gradients across the chamber relative to the applied field strength. For a constant electrode spacing, optimal chamber height decreases with electrode width from 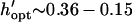 by −DEP, and from
by −DEP, and from 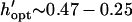 by +DEP (Fig. 6 A). When specifying a constant chamber height, patterning is most rapid with an electrode spacing of about
by +DEP (Fig. 6 A). When specifying a constant chamber height, patterning is most rapid with an electrode spacing of about 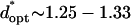 (
(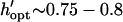 ) by −DEP, and is relatively insensitive to electrode width (Fig. 6 B). By +DEP, optimal electrode spacing increases with electrode width, from
) by −DEP, and is relatively insensitive to electrode width (Fig. 6 B). By +DEP, optimal electrode spacing increases with electrode width, from 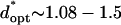 (
(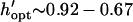 ). To illustrate the sensitivity of optimization, shaded regions indicate the height (or spacing) range where patterning time is within 10% of optimal. By this definition, selecting a dimensionless chamber height or electrode spacing within 0.1–0.2 of the optimal value results in efficient patterning. In all cases, larger electrode widths decrease patterning time, even when considering the optimal geometry for a particular width (top panels). Therefore, the overall optimal geometry would include the widest electrodes and a chamber height or electrode spacing as indicated in Fig. 6, A or B. However, electrode width also affects pattern location for +DEP, but not −DEP (Fig. 3).
). To illustrate the sensitivity of optimization, shaded regions indicate the height (or spacing) range where patterning time is within 10% of optimal. By this definition, selecting a dimensionless chamber height or electrode spacing within 0.1–0.2 of the optimal value results in efficient patterning. In all cases, larger electrode widths decrease patterning time, even when considering the optimal geometry for a particular width (top panels). Therefore, the overall optimal geometry would include the widest electrodes and a chamber height or electrode spacing as indicated in Fig. 6, A or B. However, electrode width also affects pattern location for +DEP, but not −DEP (Fig. 3).
FIGURE 6.
Optimal chamber geometry parameters for −DEP (○) and +DEP (•) determined by minimizing the complete patterning time T′ or 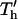 . (A) For a constant electrode spacing (d), the optimal chamber height (h′ = h/d) decreases as electrode width (w′ = w/d) increases. (B) Similarly, for a constant chamber height (h), the optimal electrode spacing (d* = d/h) varies with electrode width (w* = w/h). Shaded or hatched regions indicate parameters resulting in efficiency within 10% of optimal. Overall, patterning time decreases with wider electrodes (top panels). (C) An example of chamber height optimization for +DEP patterning of neutrally buoyant particles within a device containing three distinct electrode geometries: d = 4, 10, and 20 μm, w′ = 0.5. Most rapid patterning for all three geometries occurs at chamber height h ∼ 7 μm (*).
. (A) For a constant electrode spacing (d), the optimal chamber height (h′ = h/d) decreases as electrode width (w′ = w/d) increases. (B) Similarly, for a constant chamber height (h), the optimal electrode spacing (d* = d/h) varies with electrode width (w* = w/h). Shaded or hatched regions indicate parameters resulting in efficiency within 10% of optimal. Overall, patterning time decreases with wider electrodes (top panels). (C) An example of chamber height optimization for +DEP patterning of neutrally buoyant particles within a device containing three distinct electrode geometries: d = 4, 10, and 20 μm, w′ = 0.5. Most rapid patterning for all three geometries occurs at chamber height h ∼ 7 μm (*).
The DEP patterning model is also useful in cases where numerous electrode or chamber geometries exist within a single device. Consider a single chamber of uniform height containing distinct interdigitated electrode arrays with different spacing and width. Patterning time within each array region is expected to vary according to Figs. 5 and 6 B. However, an overall optimal chamber height can be selected for the entire device by plotting dimensional patterning time, tpat (d, w, h), for each geometry. For example, DEP aggregation of negatively buoyant (settling) particles within microfluidic channels was recently analyzed using interdigitated arrays with electrodes either d = 4-, 10-, or 20-μm apart, w′ = 0.5, and a uniform chamber height h = 30 μm (Markarian et al., 2003). In Fig. 6 C, we present as an example model results for +DEP patterning time within this geometry, for the simplified case of neutrally buoyant particles see “Gravitational effects” for the general case). Clearly, a 30-μm chamber height is not optimal for any of the three electrode geometries; in fact, patterning would not be expected to occur at all for the smallest spacing due to the large ratio of chamber height to electrode spacing. Reducing the chamber height to ∼7 μm should not only enable simultaneous patterning at all three electrode geometries, but also result in a 200-fold acceleration compared to the 30-μm height.
A final consideration regarding the chamber height is the limitation imposed by the particle size, requiring for all cases h/2R > 1. Near this limiting case, an increase in drag force due to wall effects may occur, thus increasing the factor K in Eq. 14 and also the predicted patterning time. Remarkably, this effect is minimal for nearly all chamber geometries. For example, drag force on rigid spheres translating along a wall is increased <10% for a chamber height twice that of the particle diameters (h/2R = 2) and ∼80% for the limiting case (h/2R → 1) (Keh and Chen, 2001). Thus, the model conclusions presented in this article are valid even for extremely thin chambers.
Gravitational effects
For particles that are not neutrally buoyant, gravitational force is included in the force balance:
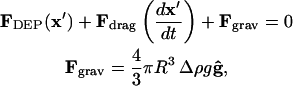 |
(22) |
where 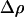 is the difference in density between the particle and the fluid, and g is the gravitational acceleration in the direction of unit vector
is the difference in density between the particle and the fluid, and g is the gravitational acceleration in the direction of unit vector 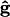 . Then,
. Then,
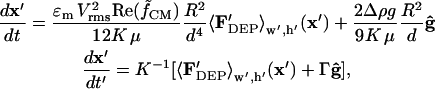 |
(23) |
where the nondimensional gravitational term,
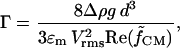 |
(24) |
describes the relative influence of gravitational force to DEP force. Typical values of Γ are of the order 0.01–1 for polymer beads and cells, patterned d = 100 μm apart at 1–10 Vrms. Therefore, DEP force is stronger than gravitational force for most conditions (hence the ability to levitate these particles). In contrast, metal particles may have Γ ∼ 10–1000 under the same conditions.
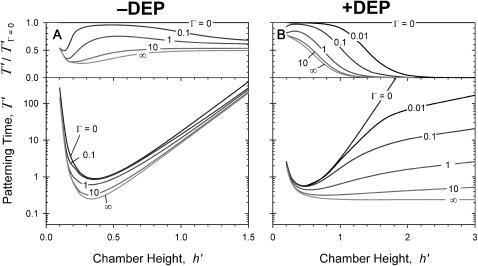
To illustrate the influence of gravitational forces, dimensionless patterning time was computed for varying Γ and chamber height in Fig. 7. Here, the chambers were oriented such that gravity would accelerate patterning. Thus, for particles denser than the fluid, the electrode array was oriented above for −DEP and below for +DEP patterning (as in Fig. 3, gravity acting downward). The greatest potential influence of gravity is illustrated by comparing neutral-bouyancy (Γ = 0) results with the asymptotic case, Γ → ∞, representing maximum gravitation where all particles instantly settle to the bottom wall. This case also characterizes the situation where particles are allowed to settle completely in the absence of an electric field before patterning.
FIGURE 7.
Effects of gravity on patterning efficiency by −DEP (A) and +DEP (B). Nondimensional complete patterning time is calculated for varying gravitational factor, Γ (defined in text), and chamber height. Electrode width is w′ = 0.2. Above, the relative patterning time compared to neutral buoyancy (Γ = 0) indicates that the potential for gravity to assist particle patterning is greater for +DEP than for −DEP.
Fig. 7 demonstrates a consistent, height-dependent decrease in patterning time with increasing Γ, although marked differences between +DEP and −DEP patterning are evident. Importantly, the optimal geometry (Fig. 6) does not change appreciably when gravitational effects are considered. For −DEP, gravitational settling offers at most a two- to threefold patterning acceleration (Fig. 7 A). At larger heights (h′ > 1), the increase in patterning time with chamber height remains exponential with a constant slope of 2π, for all Γ. In contrast, gravitational effects are significantly greater for +DEP (Fig. 7 B). Patterning time increases with chamber height (for h′ > 1) with an exponential slope that decreases with gravitational force from 2π (Γ = 0) to 0 (Γ → ∞). These results are explained by the theoretical limit in patterning time, for +DEP and nonzero Γ, by 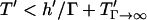 , where
, where 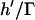 represents the settling time by gravity alone and
represents the settling time by gravity alone and 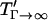 is the DEP patterning time along the bottom wall. The latter term is nearly constant for h′ > 1, and T′ approaches the theoretical limit as h′ and Γ increase.
is the DEP patterning time along the bottom wall. The latter term is nearly constant for h′ > 1, and T′ approaches the theoretical limit as h′ and Γ increase.
To explain these phenomena, it is helpful to refer back to Fig. 3. The arcing pathlines indicate that downward particle motion occurs mainly in the upper half of the chamber, whereas particles converge laterally to the pattern in the lower half of the chamber. Because DEP force and particle velocity are greatest near the electrodes, downward motion is rapid for −DEP and slow for +DEP; conversely, the lateral convergence is slow for −DEP and rapid for +DEP. Because gravity accelerates the downward motion that is already rapid with −DEP but slow with +DEP, it has only a slight effect on patterning by −DEP but a profound effect by +DEP.
MODEL VALIDATION
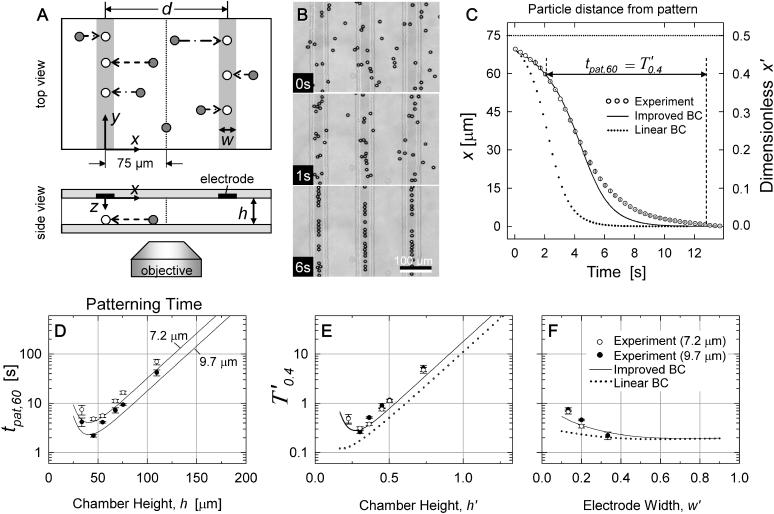
The DEP patterning kinetics model was evaluated using polystyrene microspheres as model particles. Because the polystyrene beads in water experience negative DEP at high frequencies, the patterning chamber was oriented onto the microscope stage such that the upper chamber wall contained the electrode array (Fig. 8 A). The beads were then introduced into the chamber and allowed to settle randomly onto the bottom slide (shaded circles), such that patterning would occur in a single z-plane observable by conventional light microscopy. Upon electrode excitation, particles moved laterally toward field minima located opposite the electrodes (open circles).
FIGURE 8.
(A) Schematic of video microscopy setup for validation of DEP patterning kinetics. Beads initially settle randomly (shaded circles). Application of AC voltage aligns beads (open circles) under the electrodes (solid and vertical shaded bars). Spacing between upper and lower glass slides (h) was adjusted between 34 and 110 μm. Electrode width varied from w = 20–50 μm, whereas electrode spacing was constant at d = 150 μm. Two bead diameters, 2R = 7.2 and 9.7 μm, were utilized. (B) Typical video images (h = 55 μm; w = 50 μm; 2R = 9.7 μm) of patterning beads at time t = 0, 1, and 6 s. Scale bar: 100 μm. (C) Typical patterning kinetics plotted as the distance away from the patterned location (mean ± SD, n ≥ 6) for h = 75 μm; w = 30 μm; 2R = 9.7 μm. (D–F) Summary of validation experiments measuring tpat,60 (or T′0.4), i.e., time for a bead to move from x = 60 μm (or x′ = 0.4) to 1 μm away from the pattern location, for w′ = 0.2. The improved analytical model (solid line) correctly predicts the optimal chamber height and the slower patterning kinetics at greater and smaller heights. Larger beads pattern faster (D; solid symbols and lower lines), and data points converge upon nondimensionalization (E). The improved BC solution results in closer prediction of patterning efficiency than the linear BC (dotted line). (F) Summary of validation experiments varying electrode width for height h = 55 μm and comparison to improved (solid line) and linear (dotted line) analytical models.
To test the spatial effects of the patterning efficiency model, chamber height (h), electrode width (w), and particle radius (R) were varied. Electrode spacing, excitation voltage and frequency, and composition of particles and the surrounding fluid were held constant. Parameters are summarized in Table 1.
TABLE 1.
Validation parameters
| Parameter | Value | Unit | Reference | |
|---|---|---|---|---|
| Medium viscosity | μ | 0.90 | mPa s | Measured |
| Medium conductivity | σm | 0.0001 | S/m | Measured |
| Medium permittivity | ɛm | 80 | ɛ0 | (Murrell and Jenkins, 1994) |
| Particle diameter | 2R | 7.20/9.70* | μm | Measured |
| Particle conductivity | σp | 10−18 | S/m | (Mark, 1999) |
| Particle permittivity | ɛp | 2.5 | ɛ0 | (Mark, 1999) |
| Pattern feature size | d | 150 | μm | Measured |
| Chamber height | h | 34–110 | μm | Measured |
| Electrode width | w | 20–50 | μm | Measured |
| Applied voltage | Vrms | 9.3 | Vrms | Measured |
| AC frequency | ω | 500 | MHz | Measured |
| Clausius-Mossotti factor | Re[fCM] | −0.47 | (Calculated; Eq. 4) | |
| DEP time constant | τDEP | 14.7/8.07* | s | (Calculated; Eq. 16) |
For small/large microspheres.
Materials and methods
Polystyrene microspheres, containing 2% divinyl benzene, density 1.062 g/cm3, were obtained from Bangs Laboratories (Fishers, IN) in two sizes (7.20 μm and 9.70 μm, ±1.0% coefficient of variation). Stock microsphere solutions were washed twice and resuspended in deionized water for validation experiments.
Interdigitated electrodes, spaced d = 150-μm apart and w = 20–50-μm wide, were microfabricated using conventional processes. Glass slides coated with transparent indium tin oxide (ITO) to a sheet resistance of 4–8 Ω per square were purchased from Delta Technologies (Stillwater, MN). Slides were cleaned and photolithographically patterned using S1813 photoresist (Shipley, Marlborough, MA) and ultraviolet exposure through a custom emulsion mask. Next, exposed ITO was etched for 4 min with gentle agitation in a solution of 20% hydrochloric acid and 5% nitric acid, heated to 55°C. Etched slides were then sonicated in acetone to remove photoresist and cleaned. Adhesive copper tape provided electrical contact with the ITO film.
The patterning chamber was formed by sandwiching a thin silicone spacer between the interdigitated electrode array and a bare glass slide drilled with holes for fluidic entry and exit. The spacer thickness determines chamber height, h, and is composed of poly(dimethyl siloxane) (PDMS; Sylgard 184, Dow Corning, Midland, MI) to provide a watertight seal. The resulting fluid chambers were 25-mm long, 5–10-mm wide, and 34–110-μm high. To reduce particle adhesion, chamber walls were treated with poly(ethylene glycol)-disilane (molecular weight of 3400, Shearwater Polymers, Huntsville, AL).
The beads were introduced into the chamber via syringe and allowed to settle randomly onto the electrode array. Electrical excitation (500 kHz sine wave, 9.3 Vrms) generated by an Agilent 33120A signal generator (Agilent, Palo Alto, CA) caused lateral particle motion toward field minima located opposite the electrodes. An oscilloscope connected in parallel measured applied voltage. Particle motion was observed using a Diaphot 300 inverted microscope (Nikon, Melville, NY) with an analog video camera and processor (Dage-MTI VE-1000, Michigan City, IN). Video frames captured at 0.5–5 Hz were calibrated and segmented with Scion Image (Scion, Frederick, MD) to obtain particle centroid data. Particle kinetics were then analyzed with MATLAB (The MathWorks, Natick, MA). Data were nondimensionalized according to Eq. 16, using measured values for most parameters (Table 1) and Eq. 4 to estimate the Clausius-Mossotti factor.
Validation results
In Fig. 8 B, representative video images depict bead patterning behavior by −DEP. For actual validation experiments, fewer beads were introduced into the chamber such that nearby particles would not be encountered during patterning. Approximately six to eight beads per microscope field were selected for analysis based on: 1), their isolation from nearby beads, to prevent disturbances from particle-particle attraction or local fluid flow, and 2), their initial location far from the electrode pattern, to provide the most information on patterning kinetics. Thus, beads located originally at x > 60 μm (x′ > 0.4) were accepted for tracking to obtain sufficient data points.
Typical patterning kinetics are described in Fig. 8 C. Because the electrodes were spaced d = 150-μm apart, no particle was ever more than d/2 = 75 μm away from the nearest field minimum (pattern location), located below the nearest electrode at x = 0. Particles that were initially far (40–75 μm) away accelerated toward this position, but near the pattern (<40 μm away), particle velocity gradually decreased. The “improved BC” analytical model predicts the sigmoidal position versus time curve closely, especially where particles are further away (larger x). Closer to the patterned location, the improved model predicts faster motion and shorter patterning time than experimental measurements. The “linear BC” analytical model predicts velocities about two times higher and patterning time about three times faster.
To demonstrate the effect of chamber geometry on patterning time, experiments were repeated with six chamber heights (h = 34–110 μm; h′ = 0.23–0.73), two bead diameters (2R = 7.2 and 9.7 μm), and three electrode widths (w = 20–50 μm; w′ = 0.13–0.33) (Fig. 8 D). The patterning time was recorded from an initial location at x = 60 μm (x′ = 0.4) and designated tpat,60 (or T′0.4 in dimensionless form) to ensure that sufficient beads were tracked per measurement (n ≥ 6). Larger beads patterned faster for all geometries, and upon nondimensionalization, data points and model curves for different bead sizes converged to a single dimensionless patterning time for a given chamber height (Fig. 8 E). Notably, the model prediction of optimal chamber height (∼40 μm) is consistent with validation data. Heights >∼50 μm (h′ > 0.33) resulted in exponentially longer patterning times, as exhibited in both the improved and linear analytic models. Below h ∼ 40 μm (h′ < 0.27), patterning time also slowed, reflecting the situation predicted by the model wherein a diminished spatial field gradient slows patterning in the central regions between electrodes (Fig. 4, E and F; curve a). In fact, for h = 34 μm (h′ = 0.23), particles >65-μm away from the pattern locations (x′ > 0.43) were not observed to move at all during the experiment. This upturn in patterning time is not reflected in the linear BC analytical model (Fig. 8 E).
Electrode width effects are also consistent with the improved model (Fig. 8 F). Wider electrodes result in faster patterning, although no additional decrease in patterning time is seen for w′ > 0.5. The linear BC model again underestimates patterning time, especially in the range used for validation, w′ = 0.13–0.33.
DISCUSSION
Summary
This report examined the influence of various geometric and material parameters on the speed at which particles pattern by DEP forces. Faster patterning may be important to minimize damage to sensitive particles, especially living biological cells. An expression was derived for the time at which all particles travel to an equilibrium position, by +DEP or −DEP, within an interdigitated electrode array chamber of varying geometry. Particle kinetics were solved by a balance of forces, utilizing a new analytical expression of DEP force.
In contrast to previous solutions for electric potential, the solution presented here: 1), utilized a new method for specifying the BCs at the electrode array plane, and 2), specified a finite chamber height. First, numerical solutions for different geometries were combined into an analytical expression for the Neumann BC at the electrode substrate. The resulting solutions for electric potential, field, and DEP force have significantly greater accuracy than previous analytical solutions. In addition, they are continuous in position throughout the solution space, as well as in geometric parameters.
Variations in these geometric parameters were investigated to determine limitations of DEP patterning and for experiment optimization. The theoretical models were validated using inert microspheres, demonstrating good prediction of both particle kinetics and patterning time (within <50%) without the use of fitted or empirical scaling factors. Improved accuracy in the analytical DEP force solution translated to a twofold better prediction of patterning time compared to previous solutions (Fig. 8, C, E, and F).
Implications for cell patterning
The use of DEP forces for manipulation of living cells requires minimization of potentially cytotoxic physical, chemical, and electrical conditions. In particular, strong electric fields may have a significant physiological impact on a biological cell, due to current-induced Joule heating of the medium and direct field interactions inducing transmembrane potentials (Glasser and Fuhr, 1998). Although these effects can be reduced with low conductivity suspending media and high-frequency fields, respectively, even mild electric field conditions may cause subtle gene upregulation (Archer et al., 1999). Furthermore, electric field-induced damage is dependent on both duration and intensity of exposure (Glasser and Fuhr, 1998). Therefore, selecting the optimal patterning geometry (using Fig. 6) and materials (using Eq. 19) is important to minimize the exposure time (via maximal field gradient and DEP force) for a particular applied field intensity. Alternatively, the optimized chamber geometry may permit a decrease in the electric field strength while maintaining an acceptable patterning rate, again reducing possible cell damage. In general, patterning at the fastest overall velocity (i.e., at the greatest tolerated applied potential) appears to be advantageous, with the following rationale. Transmembrane voltage (Vtm) is proportional to applied voltage (V) but patterning time varies by V−2, such that a linear measure of total exposure, 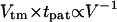 , is minimized at greater applied voltage. However, biological systems rarely display linear responses to stimuli and this analysis offers only a general guideline. Rapid patterning further diminishes the exposure of cells to DEP buffers that often lack standard tissue culture medium components (ions, growth factors, proteins, and serum), and also reduces the relative influence of additional forces (bulk convection, Brownian motion) that may compromise pattern quality.
, is minimized at greater applied voltage. However, biological systems rarely display linear responses to stimuli and this analysis offers only a general guideline. Rapid patterning further diminishes the exposure of cells to DEP buffers that often lack standard tissue culture medium components (ions, growth factors, proteins, and serum), and also reduces the relative influence of additional forces (bulk convection, Brownian motion) that may compromise pattern quality.
The parameters that lead to rapid patterning are summarized in Table 2. From Eq. 19, low viscosity and high permittivity of the suspending medium are desired. Although standard cell culture media meet these requirements, biomaterials for cell encapsulation (e.g., hydrogels) may have significantly greater viscosity and thereby hinder patterning speed. Patterning of polystyrene beads via –DEP and cells by +DEP is accelerated by low conductivity media that also minimize Joule heating. Reducing the characteristic feature length (electrode spacing) greatly speeds patterning, because field strength is increased and particles have less distance to travel, as do larger particles because DEP force is proportional to volume. Increasing the applied voltage accelerates patterning, but also raises potentially detrimental electric field effects. For mammalian cells, a limited range of electric field frequency is ideal, ∼1–10 MHz, that balances the maximal CM factor magnitude (Eq. 4) with minimal induced transmembrane potential at higher frequencies (Gray et al., 2003).
TABLE 2.
Optimal parameters for DEP patterning
| Parameter | Desired value | Scaling | |
|---|---|---|---|
| Medium viscosity | μ | Low | μ |
| Medium conductivity | σm | Low* | |
| Medium permittivity | ɛm | High | 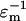 |
| Particle size | R | Large | R−2 |
| Pattern feature size | d | Small | d4 |
| Chamber height | h | (Limited range) | (Fig. 6) |
| Electrode width | w | Wide | |
| Applied voltage | Vrms | High | 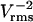 |
| AC frequency | ω | (Limited range) |
For beads by −DEP and cells by +DEP.
For all cases, patterning by +DEP is faster than by −DEP. Not only is the dimensionless patterning time lower for +DEP for a given geometry (Figs. 4 and 5), the maximum magnitude of the CM factor is twice as high for +DEP (1.0) than for −DEP (−0.5). Figs. 4, 5, and 7 demonstrate that patterning time depends greatly on chamber geometry. In general, reducing chamber height accelerates DEP patterning by increasing electric field strength and nonuniformity. However, at very small heights, the strong field gradients become spatially confined (Fig. 4, E and F), such that overall patterning is slow and incomplete. This effect, verified experimentally in this work (Fig. 8), had not been previously described in detail. For all cases, wider electrodes speed patterning (Figs. 4 and 5). However, modulating electrode width also affects the pattern shape by +DEP, because field maxima occur at the electrode edges (Fig. 3 B). In contrast, location of field minima do not change with electrode width (Fig. 3 A), such that this variable can be adjusted more freely in −DEP patterning.
Because geometric variables influence patterning time so greatly, the principal advantage of the efficiency model is optimization of these parameters (Fig. 6). When a particular pattern is desired (such as cells located a uniform distance apart), an optimal height is determined using Eq. 19 and Figs. 4 and 6 A. However, in microfluidic devices, chamber (or channel) height is typically constant, and optimal electrode spacing is determined using Eq. 21 and Figs. 5 and 6 B. Optimal height prediction from Fig. 6 (h′ = 0.28–0.40 for −DEP, w′ = 0.2) was consistent with validation experiments, as the h′ = 0.30 chamber showed the fastest patterning. It must be noted that the optimization figures do not consider particle size, although the model is valid for chamber heights greater than twice the particle diameter (“Chamber optimization using model”). When optimal parameters cannot be chosen exactly due to other system constraints, we found experimentally that it is advantageous to select a larger rather than smaller height. This is because suboptimal chamber heights show increased variation in particle velocity during patterning (curves a versus c in Fig. 4 E), resulting in a zone of poor patterning control with greater susceptibility to other forces (e.g., bulk fluid flow).
When several geometries are incorporated onto a single device, overall optimization is easily achieved by plotting dimensional patterning time and variables for each geometry. In “Gravitational effects”, we chose as an example a set of three geometries previously used for analysis of +DEP-based particle aggregation, and showed that efficiency could be increased over 200-fold for neutrally buoyant particles by a simple reduction in chamber height from 30 μm to ∼7 μm (Fig. 6 C). The actual experiments (Markarian et al., 2003) reported the behavior of nonbuoyant particles (Γ = 0.01–0.16), and showed unsuccessful patterning as feature size decreases, despite the theoretical increase in DEP force as 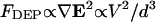 . We attribute these results in part to a chamber that was too tall, as when the reported experimental parameters were applied to the model (including gravity, using Eq. 19 and Fig. 7 B), efficiency improved 15-fold for all array geometries with the same fourfold height reduction. Thus, optimal chamber height can extend the reported lower limit on electrode dimension, although further limitations due to particle or electrical effects may still exist, as discussed below (“Model assumptions and additional forces”).
. We attribute these results in part to a chamber that was too tall, as when the reported experimental parameters were applied to the model (including gravity, using Eq. 19 and Fig. 7 B), efficiency improved 15-fold for all array geometries with the same fourfold height reduction. Thus, optimal chamber height can extend the reported lower limit on electrode dimension, although further limitations due to particle or electrical effects may still exist, as discussed below (“Model assumptions and additional forces”).
Gravitational forces can evidently accelerate DEP patterning, although the improvements are more pronounced for +DEP than −DEP (Fig. 7). By −DEP, patterning time can be reduced by ∼50% with gravitational settling. In contrast, +DEP patterning time is significantly decreased because gravitational settling brings particles toward regions of high field nonuniformity where DEP force is strong. In effect, large chamber heights become feasible for +DEP patterning of particles with significantly different mass density. Also, electric field exposure can be minimized by allowing particles to settle in the absence of the field before DEP patterning. However, biological cells, biomolecules, and biopolymers typically have similar density to that of the suspending aqueous solution (1.0–1.1 g/cm3), such that Γ ≪ 1, settling is relatively slow, and chamber height should be carefully selected.
Using these tools, we have utilized DEP patterning in preliminary biological experiments with a variety of media and hydrogel formulations, several cell types (primary and cultured mammalian fibroblasts, chondrocytes, and hepatocytes), and a number of geometries (parallel lines, planar arrays, arbitrary shapes) (Albrecht et al., 2002), and demonstrated a reduction in patterning time consistent with the model (data not shown).
Model assumptions and additional forces
The patterning efficiency model assumes that particle motion is dominated by DEP forces. Several reports have demonstrated that electric field-derived fluid flow and interparticle effects may contribute significantly to particle motion. To aid in the use of the models for predicting patterning efficiency, the conditions where DEP is the dominating force are briefly discussed below.
Electrical effects
The use of high electric fields in DEP devices with microscale dimensions may give rise to significant temperature gradients, because power generation (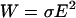 ) is concentrated in a small volume. Electrohydrodynamic forces arise from the spatial variation in fluid permittivity, conductivity, density, and viscosity due to local temperature changes from Joule heating. However, fluid flow by natural convection is generally negligible for microelectrode devices and aqueous solutions (Ramos et al., 1998).
) is concentrated in a small volume. Electrohydrodynamic forces arise from the spatial variation in fluid permittivity, conductivity, density, and viscosity due to local temperature changes from Joule heating. However, fluid flow by natural convection is generally negligible for microelectrode devices and aqueous solutions (Ramos et al., 1998).
The electrical force on a fluid is composed of Coulomb and dielectric forces arising from gradients in conductivity and permittivity, respectively. Coulomb forces dominate at low frequencies and dielectric forces dominate at high frequencies. For aqueous media, the crossover frequency is approximately 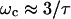 (Ramos et al., 1998), where
(Ramos et al., 1998), where 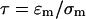 is the charge relaxation time of the liquid. Electrical forces are proportional to medium conductivity and are reduced when dielectric forces dominate, i.e., at frequencies greater than
is the charge relaxation time of the liquid. Electrical forces are proportional to medium conductivity and are reduced when dielectric forces dominate, i.e., at frequencies greater than 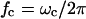 (Ramos et al., 1998). The crossover frequency ranges from 100 kHz for water (σm ∼ 0.1 mS/m) to 1 GHz for standard cell culture medium (σm ∼ 1.5 S/m).
(Ramos et al., 1998). The crossover frequency ranges from 100 kHz for water (σm ∼ 0.1 mS/m) to 1 GHz for standard cell culture medium (σm ∼ 1.5 S/m).
Electroosmotic forces may also contribute to fluid flow, due to the interaction of induced charges appearing at the electrodes and the electric field. Fluid velocity is proportional to surface charge density. The time to establish this charge is on the order of τ, such that it is reduced for frequencies above 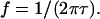
Therefore, the patterning efficiency model as presented is most accurate for low conductivity media and high-frequency electrical excitation. These conditions are desirable for patterning of biological cells by +DEP and polymer beads by −DEP. However, high conductivity media are necessary for −DEP cell patterning, such that estimates of these electrical forces may be important for accurate prediction of kinetics.
Particle effects
Nearby particles subjected to an electric field may interact due to their induced dipoles, forming aggregates or pearl chains (Jones, 1995). The ratio between this interparticle dipole force and the DEP force is given by (Dussaud et al., 2000):
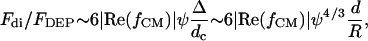 |
(25) |
where ψ is the volume fraction of the particles, 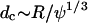 is the characteristic distance between adjacent particles, and Δ is the characteristic length over which the electric field varies (e.g., electrode spacing, d, for the interdigitated array). For 10-μm diameter particles or cells, the DEP force dominates for suspension densities <∼50 million/ml.
is the characteristic distance between adjacent particles, and Δ is the characteristic length over which the electric field varies (e.g., electrode spacing, d, for the interdigitated array). For 10-μm diameter particles or cells, the DEP force dominates for suspension densities <∼50 million/ml.
As patterning progresses, local cell density increases near the pattern locations and aggregates could form over time as interparticle forces strengthen. Aggregate formation typically accelerates patterning. Taking for example two spheres that form a doublet and align parallel to the field gradient, drag force increases by ∼30% (Lee and Leith, 1989), whereas DEP force increases 1.8- to 4.8-fold (Jones, 1995), depending on the Clausius-Mossotti factor. Clearly, velocity of aggregates should be greater than individual particles, and this behavior was observed experimentally (data not shown). Therefore, the model overestimates patterning time when particle aggregation occurs.
Model results may also be affected by changes in effective viscosity, μ, due to high local particle concentrations. Effective viscosity increases with particle volume fraction by 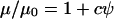 , where constant c = 2.5 for dilute suspensions of spherical particles without interaction (Einstein's formula), or c ∼ 5.5 for more concentrated systems (Happel and Brenner, 1965). As particle volume fraction rises locally during patterning, particle velocity would be expected to decrease due to increased apparent viscosity. However, a relatively dense suspension of 50 million/ml mammalian cells would increase apparent viscosity by only ∼7–14%.
, where constant c = 2.5 for dilute suspensions of spherical particles without interaction (Einstein's formula), or c ∼ 5.5 for more concentrated systems (Happel and Brenner, 1965). As particle volume fraction rises locally during patterning, particle velocity would be expected to decrease due to increased apparent viscosity. However, a relatively dense suspension of 50 million/ml mammalian cells would increase apparent viscosity by only ∼7–14%.
Thus, later stages of patterning may be characterized by kinetics that are accelerated by particle aggregation but slowed by viscosity effects. Because these effects are counteracting and generally small in magnitude, they are unlikely to affect the conclusions of this model for relatively dilute systems.
Electric field simplifications
The electric field and DEP force models included several simplifications. Only the dipole contribution to the DEP force was calculated, although this is known to be a poor approximation at the electrode edges (Voldman et al., 2001). However, the model is valid for particles smaller than the electrode spacing (d > 2R), wherein errors of 1–5% were reported (Schnelle et al., 1999). Inaccuracies in the force calculation near the electrodes have less influence on the patterning efficiency model, because: 1), most patterning time occurs away from the electrode edges (where motion is slower), and 2), electrohydrodynamic effects are concentrated at the electrodes.
The net DEP force on a particle is assumed to be equal to the force at the particle centroid in the absence of particles. Therefore, the particle kinetics model does not account for the possible distortion of the electric field by the presence of particles. These assumptions are also valid where the particles are small relative to the electrode spacing, and for suspensions that are not too dense.
CONCLUSIONS
The kinetic model developed in this article predicts patterning time under conditions where DEP force dominates, i.e., low conductivity media, high-frequency AC excitation, and relatively sparse particles smaller than electrode features. Predicted patterning time was accurate to ∼50%, and predicted optimal geometry was consistent with validation experiments, despite the simplifying assumptions and other driving forces. When DEP force is maximal via optimized geometry, these additional forces will be generally lower because geometric variables affect patterning efficiency more significantly than the electrohydrodynamic forces. In contrast, when DEP forces are weak, forces such as interparticle attractions may dominate, resulting in particle aggregation instead of patterning (Markarian et al., 2003).
The planar parallel interdigitated electrode array geometry modeled here is the most common among DEP devices. However, more complex electrode designs are necessary for creating arbitrary patterns. Nonetheless, order of magnitude calculations from the simplified two-dimensional model can be applied to an arbitrary electrode geometry taking a local characteristic feature size as d. Alternatively, the model strategy outlined here can be generalized to 3-D, from modeling the electric potential to determining 3-D velocity fields. Similarly, the use of numerical FEM data to define the boundary conditions for an analytic solution is a strategy that can improve the accuracy of any model requiring mixed BC types, and could be adapted for geometries more complex than the interdigitated electrode array. Finally, the model formulation can be adapted to incorporate other driving forces where necessary.
The model serves as a predictive tool to determine the geometric and material conditions that minimize exposure to the potentially toxic DEP patterning environment. We have utilized the model to effectively reduce the patterning time of living biological cells within various biomaterials (Albrecht et al., 2002). The ability to reduce patterning time from hours to seconds via a change in chamber height may extend the incorporation of DEP forces into robust and sensitive biological methods, devices, and assays, where perturbation of cell behavior must be avoided. The use of DEP for rapidly positioning cells, without relying on surface chemistry, may become an important tool for future cell biology, tissue engineering, and biotechnology applications.
References
- Abbott, A. 2003. Biology's new dimension. Nature. 424:870–872. [DOI] [PubMed] [Google Scholar]
- Albrecht, D. R., R. L. Sah, and S. N. Bhatia. 2002. Dielectrophoretic cell patterning within tissue engineering scaffolds. IEEE Proceedings of the Second Joint EMBS/BMES Conference 2:1708–1709. [Google Scholar]
- Archer, S., T. T. Li, A. T. Evans, S. T. Britland, and H. Morgan. 1999. Cell reactions to dielectrophoretic manipulation. Biochem. Biophys. Res. Commun. 257:687–698. [DOI] [PubMed] [Google Scholar]
- Arnold, W. M., and U. Zimmermann. 1988. Electro-rotation: development of a technique for dielectric measurements on individual cells and particles. Journal of Electrostatics. 21:151–191. [Google Scholar]
- Ashkin, A. 1997. Optical trapping and manipulation of neutral particles using lasers. Proc. Natl. Acad. Sci. USA. 94:4853–4860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benya, P. D., and J. D. Shaffer. 1982. Dedifferentiated chondrocytes reexpress the differentiated collagen phenotype when cultured in agarose gels. Cell. 30:215–224. [DOI] [PubMed] [Google Scholar]
- Bhatia, S. N., and C. Chen. 1999. Tissue engineering at the micro-scale. Biomedical Microdevices. 2:131–144. [Google Scholar]
- Chang, D. E., S. Loire, and I. Mezic. 2003. Closed-form solutions in the electrical field analysis for dielectrophoretic and travelling wave inter-digitated electrode arrays. J. Phys. D: Appl. Phys. 36:3073–3078. [Google Scholar]
- Clague, D. S., and E. K. Wheeler. 2001. Dielectrophoretic manipulation of macromolecules: the electric field. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 64:026605. [DOI] [PubMed] [Google Scholar]
- Cukierman, E., R. Pankov, and K. M. Yamada. 2002. Cell interactions with three-dimensional matrices. Curr. Opin. Cell Biol. 14:633–639. [DOI] [PubMed] [Google Scholar]
- Docoslis, A., N. Kalogerakis, and L. A. Behie. 1999. Dielectrophoretic forces can be safely used to retain viable cells in perfusion cultures of animal cells. Cytotechnology. 30:133–142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dussaud, A. D., B. Khusid, and A. Acrivos. 2000. Particle segregation in suspensions subject to high-gradient AC electric fields. J. Appl. Phys. 88:5463–5473. [Google Scholar]
- Elisseeff, J., W. McIntosh, K. Anseth, S. Riley, P. Ragan, and R. Langer. 2000. Photoencapsulation of chondrocytes in poly(ethylene oxide)-based semi-interpenetrating networks. J. Biomed. Mater. Res. 51:164–171. [DOI] [PubMed] [Google Scholar]
- Folch, A., and M. Toner. 2000. Microengineering of cellular interactions. Annu. Rev. Biomed. Eng. 2:227–256. [DOI] [PubMed] [Google Scholar]
- Frenea, M., S. P. Faure, B. Le Pioufle, P. Coquet, and H. Fujita. 2003. Positioning living cells on a high-density electrode array by negative dielectrophoresis. Materials Science & Engineering. 23:597–603. [Google Scholar]
- Gascoyne, P. R. C., and J. Vykoukal. 2002. Particle separation by dielectrophoresis. Electrophoresis. 23:1973–1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser, H., and G. Fuhr. 1998. Cultivation of cells under strong AC-electric field: differentiation between heating and trans-membrane potential effects. Bioelectrochem. Bioenerg. 47:301–310. [Google Scholar]
- Goldman, A. J., R. G. Cox, and H. Brenner. 1967. Slow viscous motion of a sphere parallel to a plane wall-I motion through a quiescent fluid. Chemical Engineering Science. 22:637–651. [Google Scholar]
- Gray, D. S., J. L. Tan, J. Voldman, and C. S. Chen. 2003. Dielectrophoretic registration of living cells to a microelectrode array. Biosens. Bioelectron. 19:771–780. [DOI] [PubMed] [Google Scholar]
- Green, N. G., A. Ramos, and H. Morgan. 2002. Numerical solution of the dielectrophoretic and travelling wave forces for interdigitated electrode arrays using the finite element method. Journal of Electrostatics. 56:235–254. [Google Scholar]
- Happel, J., and H. Brenner. 1965. Low Reynolds number hydrodynamics, with special applications to particulate media. Prentice-Hall, Upper Saddle River, NJ.
- Heida, T., W. L. Rutten, and E. Marani. 2001. Dielectrophoretic trapping of dissociated fetal cortical rat neurons. IEEE Trans. Biomed. Eng. 48:921–930. [DOI] [PubMed] [Google Scholar]
- Huang, Y., K. L. Ewalt, M. Tirado, T. R. Haigis, A. Forster, D. Ackley, M. J. Heller, J. P. O'Connell, and M. Krihak. 2001. Electric manipulation of bioparticles and macromolecules on microfabricated electrodes. Anal. Chem. 73:1549–1559. [DOI] [PubMed] [Google Scholar]
- Hughes, M. P. 2003. Nanoelectromechanics in engineering and biology. CRC Press, Boca Raton, FL.
- Iwasaka, M., J. Miyakoshi, and S. Ueno. 2001. Magnetophoresis of diamagnetic cells and microorganisms in a culture medium. IEEE Transactions on Magnetics. 37:2644–2646. [Google Scholar]
- Jager, E. W., O. Inganas, and I. Lundstrom. 2000. Microrobots for micrometer-size objects in aqueous media: potential tools for single-cell manipulation. Science. 288:2335–2338. [DOI] [PubMed] [Google Scholar]
- Jones, T. B. 1995. Electromechanics of Particles. Cambridge University Press, New York.
- Kapur, R., K. A. Giuliano, M. Campana, T. Adams, K. Olson, D. Jung, M. Mrksich, C. Vasudevan, and D. L. Taylor. 1999. Streamlining the drug discovery process by integrating miniaturization, high throughput screening, high content screening, and automation on the CellChip(TM) system. Biomedical Microdevices. 2:99–109. [Google Scholar]
- Keh, H. J., and P. Y. Chen. 2001. Slow motion of a droplet between two parallel plane walls. Chemical Engineering Science. 56:6863–6871. [Google Scholar]
- Lee, C. T., and D. Leith. 1989. Drag force on agglomerated spheres in creeping flow. Journal of Aerosol Science. 20:503–513. [Google Scholar]
- Mark, J. E. 1999. Polymer Data Handbook. Oxford University Press, New York, NY.
- Markarian, N., M. Yeksel, B. Khusid, K. R. Farmer, and A. Acrivos. 2003. Particle motions and segregation in dielectrophoretic microfluidics. J. Appl. Phys. 94:4160–4169. [Google Scholar]
- Masuda, S., M. Washizu, and M. Iwadare. 1987. Separation of small particles suspended in liquid by nonuniform traveling field. IEEE Transactions on Industry Applications. 23:474–480. [Google Scholar]
- Matsue, T., N. Matsumoto, and I. Uchida. 1997. Rapid micropatterning of living cells by repulsive dielectrophoretic force. Electrochimica Acta. 42:3251–3256. [Google Scholar]
- Morgan, H., A. G. Izquierdo, D. Bakewell, N. G. Green, and A. Ramos. 2001. The dielectrophoretic and travelling wave forces generated by interdigitated electrode arrays: analytical solution using Fourier series. J. Phys. D. Appl. Phys. 34:1553–1561. [Google Scholar]
- Murrell, J. N., and A. D. Jenkins. 1994. Properties of Liquids and Solutions. Wiley & Sons, New York, NY.
- Oseen, C. W. 1927. Neuere Methoden und Ergebnisse in der Hydrodynamik. Akademische Verlagsgesellshalt, Leipzig, Germany.
- Ozkan, M., T. Pisanic, J. Scheel, C. Barlow, S. Esener, and S. N. Bhatia. 2003. Electro-optical platform for the manipulation of live cells. Langmuir. 19:1532–1538. [Google Scholar]
- Pohl, H. A. 1978. Dielectrophoresis: The Behavior of Neutral Matter in Nonuniform Electric Fields. Cambridge University Press, New York, NY.
- Qiu, Z. Y., N. Markarian, B. Khusid, and A. Acrivos. 2002. Positive dielectrophoresis and heterogeneous aggregation in high-gradient AC electric fields. Journal of Applied Physics. 92:2829–2843. [Google Scholar]
- Ramos, A., H. Morgan, N. G. Green, and A. Castellanos. 1998. AC electrokinetics: a review of forces in microelectrode structures. J. Phys. D. Appl. Phys. 31:2338–2353. [Google Scholar]
- Schmeichel, K. L., and M. J. Bissell. 2003. Modeling tissue-specific signaling and organ function in three dimensions. J. Cell Sci. 116:2377–2388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnelle, T., R. Hagedorn, G. Fuhr, S. Fiedler, and T. Muller. 1993. 3-Dimensional electric-field traps for manipulation of cells—calculation and experimental verification. Biochim. Biophys. Acta. 1157:127–140. [DOI] [PubMed] [Google Scholar]
- Schnelle, T., T. Muller, S. Fiedler, and G. Fuhr. 1999. The influence of higher moments on particle behaviour in dielectrophoretic field cages. Journal of Electrostatics. 46:13–28. [Google Scholar]
- Sneddon, I. N. 1966. Mixed Boundary Value Problems in Potential Theory. Wiley, New York, NY.
- Voldman, J., R. A. Braff, M. Toner, M. L. Gray, and M. A. Schmidt. 2001. Holding forces of single-particle dielectrophoretic traps. Biophys. J. 80:531–541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Voldman, J., M. L. Gray, M. Toner, and M. A. Schmidt. 2002. A microfabrication-based dynamic array cytometer. Anal. Chem. 74:3984–3990. [DOI] [PubMed] [Google Scholar]
- Wang, X. B., Y. Huang, J. P. H. Burt, G. H. Markx, and R. Pethig. 1993. Selective dielectrophoretic confinement of bioparticles in potential-energy wells. J. Phys. D. Appl. Phys. 26:1278–1285. [Google Scholar]
- Wang, X. J., X. B. Wang, F. F. Becker, and P. R. C. Gascoyne. 1996. A theoretical method of electrical field analysis for dielectrophoretic electrode arrays using Green's theorem. J. Phys. D. Appl. Phys. 29:1649–1660. [Google Scholar]
- Wu, J. 1991. Acoustical tweezers. J. Acoust. Soc. Am. 89:2140–2143. [DOI] [PubMed] [Google Scholar]