Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Oct;87(4):2172–2186. doi: 10.1529/biophysj.104.043000

Uniform Sampling of Steady-State Flux Spaces: Means to Design Experiments and to Interpret Enzymopathies

Nathan D Price 1, Jan Schellenberger 1, Bernhard O Palsson 1
PMCID: PMC1304643  PMID: 15454420

Abstract

Reconstruction of genome-scale metabolic networks is now possible using multiple different data types. Constraint-based modeling is an approach to interrogate capabilities of reconstructed networks by constraining possible cellular behavior through the imposition of physicochemical laws. As a result, a steady-state flux space is defined that contains all possible functional states of the network. Uniform random sampling of the steady-state flux space allows for the unbiased appraisal of its contents. Monte Carlo sampling of the steady-state flux space of the reconstructed human red blood cell metabolic network under simulated physiologic conditions yielded the following key results: 1), probability distributions for the values of individual metabolic fluxes showed a wide variety of shapes that could not have been inferred without computation; 2), pairwise correlation coefficients were calculated between all fluxes, determining the level of independence between the measurement of any two fluxes, and identifying highly correlated reaction sets; and 3), the network-wide effects of the change in one (or a few) variables (i.e., a simulated enzymopathy or fixing a flux range based on measurements) were computed. Mathematical models provide the most compact and informative representation of a hypothesis of how a cell works. Thus, understanding model predictions clearly is vital to driving forward the iterative model-building procedure that is at the heart of systems biology. Taken together, the Monte Carlo sampling procedure provides a broadening of the constraint-based approach by allowing for the unbiased and detailed assessment of the impact of the applied physicochemical constraints on a reconstructed network.

INTRODUCTION

Genome-scale models provide a comprehensive, yet concise representation of biological reaction networks and their functional states (Price et al., 2003a). A growing number of genome-scale reconstructed networks for the model (Famili et al., 2003; Reed and Palsson, 2003; Reed et al., 2003) and infectious (Edwards and Palsson, 1999; Schilling et al., 2002) microorganisms are becoming available. At this scale, it has proven difficult to formulate kinetic models, which have proven to be useful on a small scale (Hasty et al., 2002, 2001) and thus different modeling approaches are needed. One such approach is the constraint-based modeling approach. This approach uses the constraints imposed on network functions by identifiable physicochemical laws to form a solution space which contains all candidate steady-state solutions (Covert et al., 2004; Price et al., 2003a). Previous constraint-based modeling studies have focused on identifying optimal states in steady-state flux spaces (Edwards et al., 2002), potential cellular objectives (Burgard and Maranas, 2003), minimal necessary reaction (or gene) sets (Burgard et al., 2001), and upon enumerating the extreme pathways (Papin et al., 2003; Schilling and Palsson, 2000) (convex basis vectors) or elementary modes (Schuster et al., 2000; Schuster and Hilgetag, 1994) of the solution space. Constraint-based modeling has proven valuable in predicting phenotypes such as optimal growth rates (Edwards et al., 2001), lethality of gene knockouts (Edwards and Palsson, 2000; Forster et al., 2003), effects of gene additions and deletions (Burgard and Maranas, 2001; Segre et al., 2002), and the endpoint of an adaptive evolution (Ibarra et al., 2002).

A recently developed dimension within the constraint-based modeling approach is uniform random sampling of the steady-state flux space (Almaas et al., 2004; Wiback et al., 2004). This approach is used to fully determine the range of possible steady-state fluxes allowed in the network under defined physicochemical constraints. A Monte Carlo sampling procedure was applied to the metabolic network of the human red blood cell, the modeling of which has reached an advanced state (Jamshidi et al., 2001; Kauffman et al., 2002; Lew and Bookchin, 1986; Mulquiney et al., 1999; Mulquiney and Kuchel, 1999, 2003; Price et al., 2003b; Schuster and Holzhutter, 1995; Schuster et al., 1988; Wiback and Palsson, 2002). Monte Carlo sampling has also proven very useful in analyzing the general properties of networks by testing their robustness to parameter variation (Alves and Savageau, 2000a,b,c). The approach utilized herein has the utility to identify the selection of independent measurements to determine the state of a biochemical network and to predict systemic effects from the reduction in a maximal reaction rate to simulate enzymopathies.

MATERIALS AND METHODS

Problem overview

The objectives of the Monte Carlo sampling procedure are: 1), to generate uniform random samples of points in the steady-state flux space and 2), to calculate the hypervolume of this space. To accomplish these objectives the steady-state flux solution space is enclosed by a geometric object in which uniformly distributed random points can be readily generated and that has an easily-calculable volume. Importantly, the shape of the chosen object needs to fit as tightly as possible around the steady-state flux space to have a high fraction of points that are in the geometric object and in the steady-state flux space. A parallelepiped with the same dimension as the rank, r, of the null space of S, is an object that meets these criteria. The parallelepiped is represented as a matrix, B, where each column of B represents a set of spanning edges of the parallelepiped,

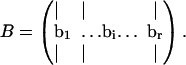graphic file with name M1.gif (1)

The volume of a parallelepiped is simple to compute (Meyer, 2000),

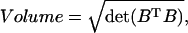graphic file with name M2.gif (2)

where the columns of B are the axes of the enclosing parallelepiped. Uniform random samples can be generated within a parallelepiped simply by generating uniform random weightings on all of the spanning edges between the minimum and maximum allowed values and picking the point inside the space based on the weightings, αi, generated on each of the basis vectors, bi, as

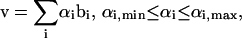graphic file with name M3.gif (3)

where v is a point within the space defined by summing the weightings on each of the basis vectors between the minimum and maximum values allowable in the bounding parallelepiped. The Monte Carlo sampling procedure was applied to a simple flux split to illustrate how this approach works (Fig. 1).

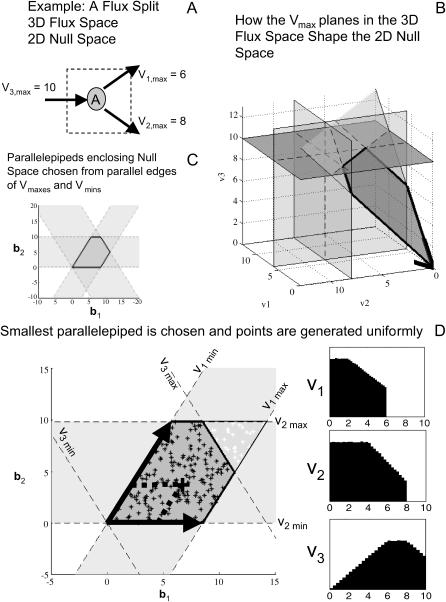
FIGURE 1.

FIGURE 1

Open in a new tab

Algorithm for boxing in solution space with parallelepiped and generating uniform random samples. A simple flux split was used as an example to demonstrate how the Monte Carlo sampling procedure works (A). The two-dimensional null space is constrained by the Vmax planes corresponding to the three reactions in the network (B). Once the null space is capped off by the reaction Vmax values, combinations choosing two of the three sets of parallel constraints leads to forming three potential parallelepipeds (C). The smallest of these parallelepipeds is chosen and uniform random points within the parallelepiped are generated (D) based on uniform weightings on the basis vectors defining the parallelepiped (shown as black arrows). Points within the solution space are kept and those that fall out of the solution space are discarded. The fraction of the points generated inside the parallelepiped that fall within the solution space is called the “hit fraction.” The hit fraction multiplied by the volume of the parallelepiped yields the volume of the solution space. Probability distributions for each of the three fluxes are calculated from the set of points within the solution space (D).

Imposition of constraints: defining the steady-state flux space

The imposition of constraints based on physicochemical principles defines the steady-state flux space. At steady state, a simultaneous mass balance on all compounds in the network requires that (Bonarius et al., 1997; Schilling et al., 1999)

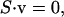graphic file with name M4.gif (4)

where S is the stoichiometric matrix representing all known reactions in the network and v is the flux vector describing the flux through each of these reactions. All solutions to Eq. 4 lie in the null space of S (Fig. 1 B).

The next sets of constraints used to define the steady-state solution space are minimum and maximum flux rates through each of the reactions,

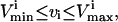graphic file with name M5.gif (5)

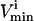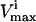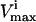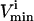where the flux, vi, through each reaction i, must lie between the Inline graphic and the Inline graphic for that reaction. These Inline graphic and Inline graphic constraints thus segment the null space defined by Eq. 4 (Fig. 1 B).

In this article, the elementary forward and reverse reactions are combined into a net reaction. Reactions can thus have a negative 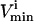Inline graphic to indicate that the reaction is being used in the direction opposite to that defined as positive in S. The 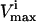Inline graphic values are generally based on experimental measurements. 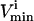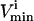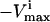For irreversible reactions, the Inline graphic values are set to zero, and for reversible reactions the Inline graphic is set to Inline graphic.

Elimination of redundant constraints

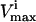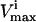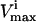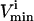Many reaction Inline graphic levels cannot be reached in a steady state because the saturation of other reactions is more constraining upon the reaction flux, vi, than its own saturation state. Thus, many of the Inline graphic constraints are redundant from a systems point of view, and do not affect the size of the solution space. 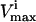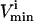Redundant Inline graphic and Inline graphic constraints that were not needed to define the steady-state flux space (i.e., these redundant constraints lay outside of more constraining Inline graphic and Inline graphic constraints) were eliminated and not needed for the generation of the sample points.

Choice of enclosing parallelepiped

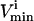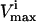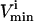Because each pair of Inline graphic and Inline graphic constraints form parallel hyperplanes, the shape of the null space leads naturally to the choice of a high-dimensional parallelepiped in which to enclose it. The set of possible parallelepipeds that could be used to enclose the steady-state flux space was chosen by forming the faces of the parallelepiped along the directions defined by these Inline graphic and Inline graphic constraints. 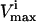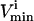Since each parallelepiped is defined by r planes which are chosen from the set of m Inline graphic and Inline graphic planes, the number of such parallelepipeds that could be used enclose the space is

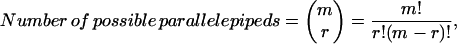graphic file with name M27.gif (6)

where m is the number of Vmax constraints and r is the dimension of the null space (see Fig. 1 C).

Minimizing the volume of the enclosing parallelepiped

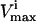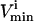Checking the volume of every possible parallelepiped to find the smallest can become prohibitive due to the large number of parallelepipeds (i.e., Eq. 6). Therefore, an alternate approach was used. This algorithm chooses its first direction based on the set of Inline graphic and Inline graphic constraints that are the closest together based on Euclidian distance. 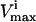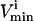Then, the next direction is chosen by determining the smallest parallelogram that can be formed by choosing the next set of Inline graphic and Inline graphic constraints. 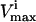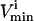The third direction is chosen as the set of constraints that forms the smallest parallelepiped formed using three sets of Inline graphic and Inline graphic constraints and so on until the parallelepiped fully encloses the solution space (Fig. 1 D).

Uniform random sampling of points

Uniform random points were generated within the solution space by randomly sampling within the enclosing parallelepiped. Randomly sampling within the parallelepiped was accomplished by uniformly sampling along each of the edges, bi, defining the parallelepiped and picking the point resulting from the sum of this set of weightings. Each point in the space is uniquely defined by weightings on the edges spanning the parallelepiped (Eq. 3). The weighting, αi, on each basis vector, bi, was uniformly selected by generating a pseudo-random number, f, between 0 and 1 and then assigning each weight as

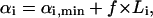graphic file with name M34.gif (7)

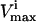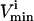where L is the length of the corresponding edge, bi, in the parallelepiped. Points generated uniformly within the parallelepiped were then compared to the set of Inline graphic and Inline graphic constraints to verify whether the point falls in the solution space or not. If the point satisfies all constraints, it is a valid solution and is kept in the set. If the randomly generated point does not satisfy all the necessary constraints, it is excluded. The fraction of total points generated that fall within the space, the “hit” fraction, was used to calculate the absolute volume of the steady-state flux space (see Fig. 1 D).

Volume calculation of steady-state flux space

The volume of the steady-state flux space can be calculated by multiplying the volume of the enclosing parallelepiped by the fraction of generated points that falls within the solution space

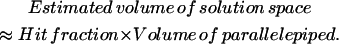graphic file with name M37.gif (8)

The estimated relative error in the volume calculation obtained through the Monte Carlo sampling procedure decreases as the number of points sampled increases. The variance of the estimate, σ2, is given as

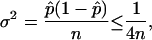graphic file with name M38.gif (9)

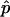where Inline graphic is the ratio of sampled points that fall inside the solution space (hit fraction) and n is the total number of sample points generated. The relative error of the hit fraction estimate, ɛ, is calculated as the ratio of the standard deviation, σ, to the mean, μ,

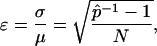graphic file with name M40.gif (10)

showing that the estimate improves with increasing sample size, N, as well as a higher hit fraction, 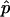Inline graphic, as would be expected.

Red blood cell metabolic network

The red blood cell metabolic network used in this study consists of 48 reactions utilizing 39 metabolites. Reversible reactions were not decoupled into forward and reverse reactions, and thus were allowed to take on negative values as discussed above. The dimension of the null space of this stoichiometric matrix was 11. This red blood cell network differs slightly from the one previously used to study extreme pathways (Wiback and Palsson, 2002) in that the metabolic loads are represented as turnover reactions, rather than as exchange fluxes and also differs from the network studied in Wiback et al. (2004) in that it contains reversible reactions. The 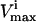Inline graphic values utilized in this study were taken from Wiback and Palsson (2002), with the 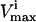Inline graphic of all reactions without a stated 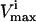Inline graphic in Wiback and Palsson (2002) being set at an arbitrarily high value of 1000 so that none of these reactions was limiting on the system. Thus, all reaction fluxes were limited by either a measured 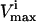Inline graphic value or an uptake rate. The 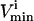Inline graphic values were set to −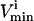Inline graphic for reversible reactions and to zero for all irreversible reactions, unless there was a minimum physiological demand, as detailed in the next section.

Physiologic conditions

In addition to limitations on flux values due to 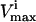Inline graphic values, certain known physiologic demands were used to identify the range of potential flux values. For example, the red blood cell is obligated to produce a basal level of ATP to run the sodium potassium pump to balance against the natural diffusion rate of sodium and potassium that “leaks” through the membrane. Thus, the minimum ATP production rate in this study was set to 1 mM/h to reflect this fact. The maximum ATP production rate was set at 1.5, as a conservative bound, higher than the maximum value observed in a wide range of calculations based on a full-scale kinetic model (Jamshidi et al., 2001). Also, a minimal amount of NADH production is necessary to convert Met-hemoglobin into its functional state. The minimum NADH production rate was set to 0.4 mM/h based on the oxidation rate of iron in hemoglobin. This minimal level of NADPH production was set to 0.05 mM/h for the turnover of GSSG to GSH to combat a minimal level of reactive oxygen species. Lastly, the minimum flux through DPGase was set to 0.3 mM/h, since this flux always operates near saturation levels because of the high intracellular concentration of 23DPG and the slow rate of this reaction (time constant on the order of half a day).

Convergence of statistics with increasing samples

To determine that sufficiently large samples were taken to accurately assess each of the statistical properties computed, samples were taken until the statistics being assessed ceased changing with increased sample size relative to the error deemed appropriate for the property being calculated. At the sample sizes used in this study, completely new sets of random samples were also taken with the results remaining unchanged for the significant figures related, and this resampling was done numerous times. Thus, as should be the case, all results presented herein are independent of the particular set of uniform random samples used, and are generic properties of the metabolic solution space. Specific details on the number of repetitions and the size of the samples are given along with each of the calculated results in the figure captions.

Computation and implementation

Computations for this study were performed on Dell Workstations (either a Dell Precision 340 or Dimension 8200) or on a Linux box (Dual Athlon MP 2400, 2 GB RAM). The program for finding the enclosing parallelepiped and for generating points was performed using MATLAB (The MathWorks, Natick, MA) and an interface with the linear programming package LINDO API (Lindo Systems, Chicago, IL). As an indication of the efficiency of the calculations, the computation of 250,000 uniform random samples within the red blood cell steady-state flux space using the Dell workstations was performed in <30 s. The calculation of 1,000,000 points inside the steady-state flux space was performed on the Linux box in <50 s. The approach herein was very fast compared to the previous sampling approach used in Wiback et al. (2004), which describes the calculation of 250,000 uniform points in the red blood cell metabolic network as taking “over a week” of calculation (Dell Dimension 8200). Thus, the approach presented herein represents an ∼20,000-fold increase in calculation efficiency over the approach used in Wiback et al. (2004). Increased sampling efficiency is important because it allows for more detailed and precise calculations, increased capacity to study improbable regions of the steady-state flux space, and better error assessment.

RESULTS

Uniform random samples were generated within the steady-state flux space of the in silico model of human red blood cell metabolism. The set of candidate solutions can then be further segmented based on additional criteria. The results herein demonstrate how this approach can be used to 1), provide all possible steady-state distributions for unknown metabolic fluxes; 2), guide making informative experimental measurements; and 3), study the systemwide effects of an enzymopathy through lowered enzyme activity.

Distribution of flux values and space segmentation

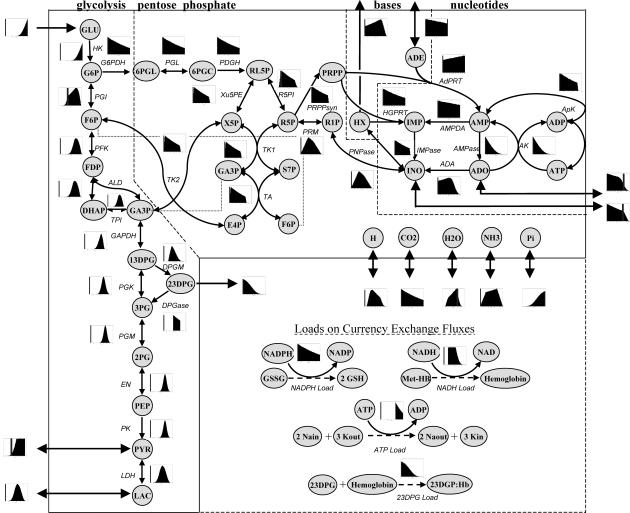
The set of candidate steady-state flux distributions through each reaction in the red blood cell metabolic network were represented as a histogram of all possible flux values and displayed on the metabolic map (Fig. 2). Each histogram presents one-dimensional information on its x axis, in terms of the extent of possible values for that particular flux. The y axis represents the “size” of space in the other r–1 dimensions resulting from slicing the metabolic solution space along a specific value of the flux through the indicated reaction. Thus the “height” of each histogram represents r–1 dimensional data (see illustration in Fig. 1 D).

FIGURE 2.

FIGURE 2

Open in a new tab

Probability flux distributions for human red blood cell. The red blood cell model with imposed maximum and minimum constraints on each flux was sampled using the in silico algorithm. The histograms next to each reaction represent the distribution of solutions with respect to each reaction flux. The vertical shaded line on each plot indicates where the zero flux line is. Several general flux distribution patterns have been identified including right peak (HK), left peak (G6PDH), central peak (PGK), and broad peak (PYR exchange). Due to the convexity of the solution space, no distribution can have more than one peak. The flux distribution shape gives information about the sensitivity of the solution space to each constraint. If a flux distribution has a right peak, decreasing a maximum constraint will eliminate many solutions from the valid space. Reactions that are part of the same pathway with no intermediate branch points (PGM, EM, PK) all have the same flux distributions. Distributions shown are based on 500,000 uniformly distributed points in the steady-state flux space. These details on these distributions can be seen in more detail in Fig. 3 (original distributions). The dotted lines in the load reactions represent the main physiologic function of the specified metabolic load, but are not explicitly accounted for in the stoichiometric matrix.

The histograms of steady-state flux values can be roughly classified into four groups based on their shape:

  1. Left peak, the lowest allowable flux value through the reaction is the most probable, such as the fluxes through AK and AMPase.

  2. Right peak, the highest allowable flux value is most probable such as the flux through reaction HK.

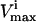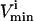  3. Central peak, a point in between the Inline graphic and Inline graphic is the most probable with the upper and lower possible flux values approaching a zero probability, such as the fluxes through reactions PFK, PK, and LD.

  4. Broad peak, a plateau of equally probable flux values exists, such as the fluxes through NADH load and PYR uptake.

Histograms for reactions that do not contain a zero flux value are essential under the conditions examined. None of these histograms can have more than one peak due to the convexity of the steady-state flux space. The shape of these histograms is highly informative about how a reduction in the allowable range of each flux would affect the remaining size of the steady-state flux space. The percentage of the histogram area remaining in the reduced range is the same as the percentage of the remaining steady-state flux space.

Correlation of flux measurements: use in designing experiments

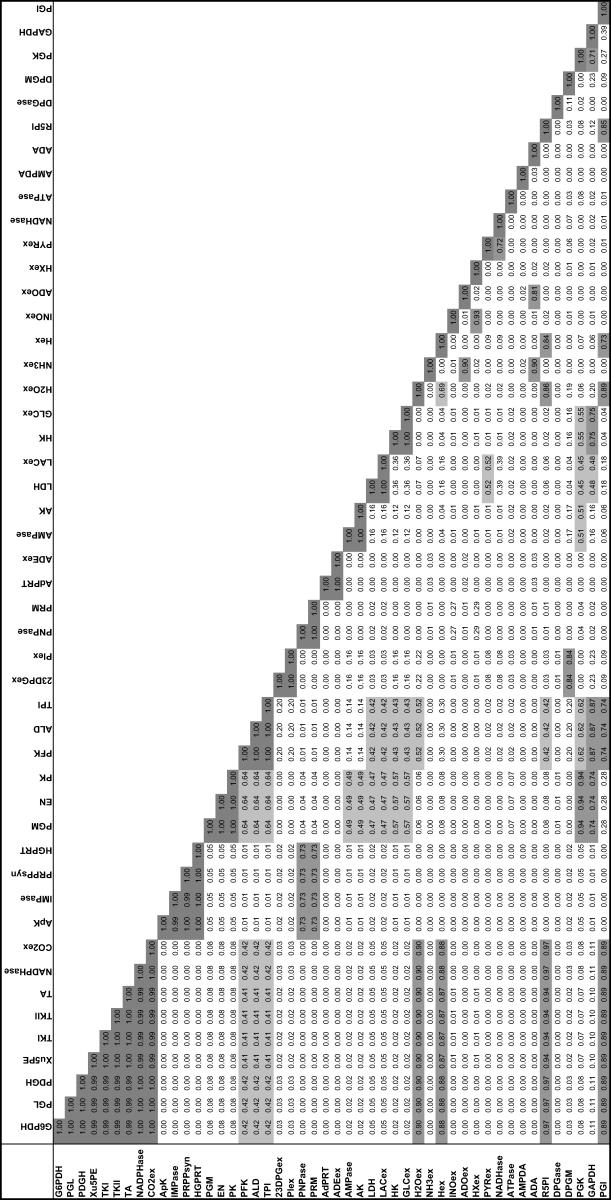
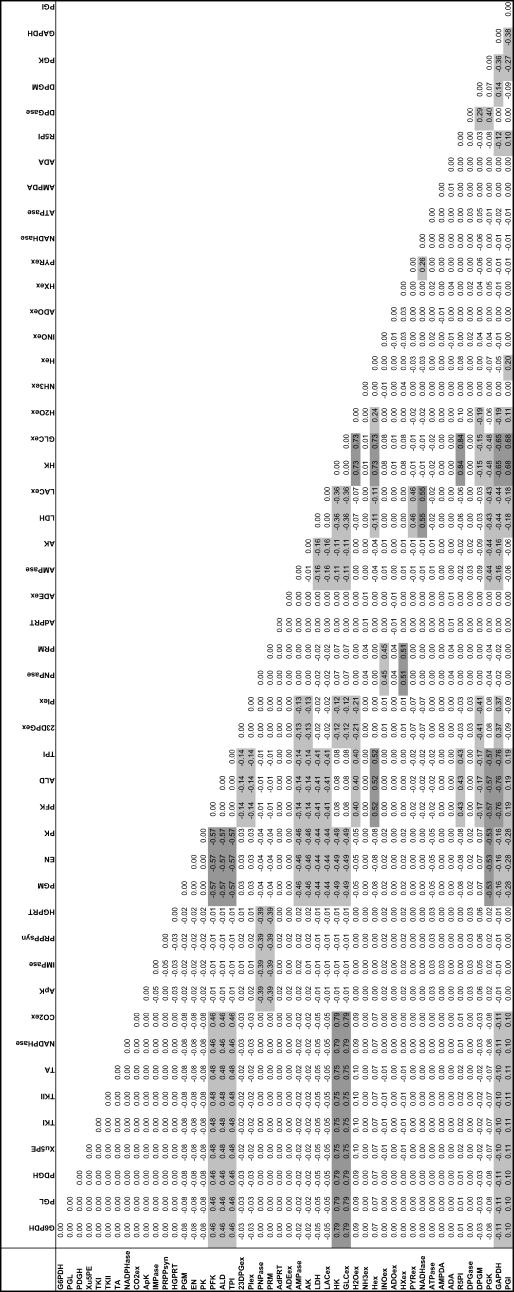
Uniform random sampling of the steady-state flux space allows for the calculation of the correlation coefficient (rij) between any two fluxes (vi and vj) in the network. Thus, sampling provides a straightforward means of not only calculating perfectly correlated subsets (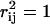Inline graphic), but also of identifying well-correlated, but not perfectly correlated reaction sets. The matrix of squared pairwise correlation coefficients for all the RBC metabolic fluxes was computed. The fluxes can be ordered such that the “correlated reaction sets” (defined here as 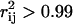Inline graphic) are listed in order of decreasing number of fluxes in each set (Table 1).

TABLE 1.

Correlation between flux values in the solution space

graphic file with name biophysj00043000T01_HT.jpg

Open in a new tab

Correlations were calculated between pairs of reactions in the red blood cell model using 250,000 randomly sampled points. This is used to quantify the degree of similarity between reactions. Perfect correlation (1.00) is exhibited between reactions on the same linear pathway (TK1, TK2, TA, Xu5PE). The correlation coefficients were calculated using 1,000,000 uniform points within the steady-state flux space. The calculation of this correlation matrix was performed three separate times with 1,000,000 points each and the maximum difference between any calculated squared correlation coefficients was 0.002.

The identification of the correlated reaction sets can help guide experimental design. The measurement of any flux in a perfectly correlated reaction set determines the steady-state flux level through all reactions in a set. Therefore, making a measurement of one flux in the largest correlated set, consisting of reactions in the pentose phosphate pathway, essentially determines the steady-state flux distribution through each of the nine reactions in the correlated set. In addition, four other fluxes would also be largely determined, with correlation coefficients >0.88. The same is true with the measurement of any flux in a correlated set.

A second important factor to consider when choosing fluxes for measurement to best determine the flux state of the red blood cell is to measure a set of fluxes that are uncorrelated to each other (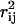Inline graphic values close to zero). Such a set ensures that the flux measurements are not providing duplicate information. Thus, by iteratively choosing to measure fluxes that are uncorrelated to each other and to what has already been measured, the correlation matrix guides the selection of independent flux measurements.

A third factor that determines how informative an experimental measurement will be is where in the solution space the measurement falls. For example, if a flux measurement falls in an improbable region of the histogram, it will be much more constraining for determining the flux state of the system than a measurement taken in a probable region. The numerical range of flux measurement is generally unknown before the measurement is taken, and thus the reduction in the size of the solution space is known only after the experimental measurement is taken. However, this information can be taken into account using previous experience and intuition to evaluate if a flux measurement is likely to occur in a region deemed improbable by, and thus highly informative to, the current status of the model.

Thus, the Monte Carlo sampling procedure provides three important criteria for designing a set of informative measurements to determine the state of the system:

  1. How correlated is a measured flux to unknown fluxes?

  2. Is the measured flux uncorrelated to the information already known?

  3. Is there any basis for expecting that a flux measurement will fall in an improbable region of the flux histogram?

In this manner, the correlation matrix, generated by taking uniform random samples of points in the steady-state flux space, guides which flux measurements will likely provide the most information about the network. Once informative flux measurements are made, the sampling procedure can then be used to fill in all possible steady-state fluxes through all the remaining unmeasured fluxes in the network that are in agreement with the experimental data.

Systemic effects of simulated enzymopathies

The sampling procedure can be used to track the networkwide changes that occur due to changes to a single, or a small number, of individual reactions. For example, a substantial number of single nucleotide polymorphisms (SNPs) have been found in genes of red blood cell enzymes, which significantly decrease the 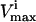Inline graphic values through many reactions in the red blood cell (Jacobasch and Rapoport, 1996; Tanaka and Zerez, 1990). Some of these SNPs have been correlated to chronic and nonchronic anemia (Grimes, 1980; Thorburn and Kuchel, 1985) and the systemic effects of the two most common SNPs in the red blood cell, pyruvate kinase (PK) and glucose-6-phosphate dehydrogenase (G6PDH), have recently been evaluated using a kinetic model of red cell metabolism (Jamshidi et al., 2002).

Defects in glycolytic enzymes were simulated to demonstrate how a 75% reduction in their normal operating range (though a decreased 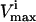Inline graphic) would affect the network. For each reaction, an enzymopathy was simulated by setting a reduced maximum flux for the reaction, Inline graphic as

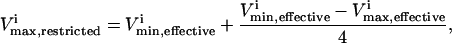graphic file with name M57.gif (11)

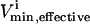where Inline graphic and Inline graphic were the maximum and minimum flux values achievable in the unaltered system. The percentage of the steady-state flux space remaining after restricting each of these reactions to one-quarter their normal operating range is shown in Table 2. As discussed above, the shape of the flux histograms, shown in Fig. 2, are a means for immediately determining the impact of a reduction in the allowable range of any flux. Such impact can be evaluated by comparing the reduction in the size of the steady-state flux space seen in Table 2 with the histograms shown in Fig. 2. A reduction in the 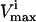Inline graphic of a reaction that has a right peak distribution will reduce the size of the steady-state flux space more than a reduction in the 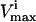Inline graphic of a reaction with a left peak distribution.

TABLE 2.

Effects of simulated enzymopathies in glycolytic enzymes on steady-state flux space

Glycolytic enzymes 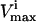Inline graphic Constraining? Systemic 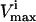Inline graphic Systemic 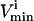Inline graphic Restricted 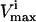Inline graphic Percentage of steady-state flux space remaining Hemolytic anemia?*
Hexokinase (HK) 1.5 Yes 1.50 0.48 0.74 0.02% Yes
Phosphofructokinase (PFK) 250 No 1.58 0.31 0.63 0.21% Variable
Triose phosphate isomerase (TPI) 1000 No 1.58 0.31 0.63 0.21% Yes
Aldolase (ALD) 1000 No 1.58 0.31 0.63 0.21% Yes
Lactate dehydrogenase (LDH) 1000 No 2.81 0.09 0.77 0.56% No
Pyruvate kinase (PK) 250 No 3.21 1.17 1.68 0.83% Yes
Enolase (EN) 1000 No 3.21 1.17 1.68 0.84% Yes
Phosphoglucoisomerase (PGI) 1000 No 1.48 −0.77 −0.21 1.0% Yes
Phosphoglycerate kinase (PGK) 1000 No 2.91 0.87 1.38 2.2% Usually
Diphosphoglycerate phosphatase (DPGase) 0.52 Yes 0.52 0.3 0.36 29% No
Diphosphoglyceromutase (DPGM) 12 No 1.43 0.3 0.58 47% No
Open in a new tab

Several conditions have been identified that decrease the effectiveness of enzymes in the red blood cells. The effect of a reduction in the possible steady-state ranges of fluxes on the steady-state flux space as a whole was simulated by decreasing the maximum allowable reaction flux through the reaction catalyzed by the given enzyme. The columns of the table show: 1), the enzyme defect being simulated; 2), the corresponding 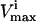Inline graphic; 3), whether the 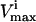Inline graphic is constraining on the system; 4), the actual maximum flux rate for the reaction in the network; 5), the actual minimum flux rate (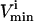Inline graphic) for the reaction in the network; 6), to what extent 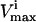Inline graphic is restricted to constrain the allowable flux range for the reaction to one-quarter of its original value; 7), the percentage drop in the volume of the steady-state flux space corresponding to the simulated enzymopathy; and 8), whether defects in an enzyme had been experimentally determined to cause anemia or not.

*

Taken from Tanaka et al. (1990).

The restriction of one reaction flux, such as occurs with an enzymopathy, can have a profound effect on the behavior of the network as a whole, affecting the functioning of many other reactions. Results from a simulated enzymopathy through the PK reaction, the most common enzymopathy in the glycolytic pathway (Tanaka and Zerez, 1990), are shown as an example.

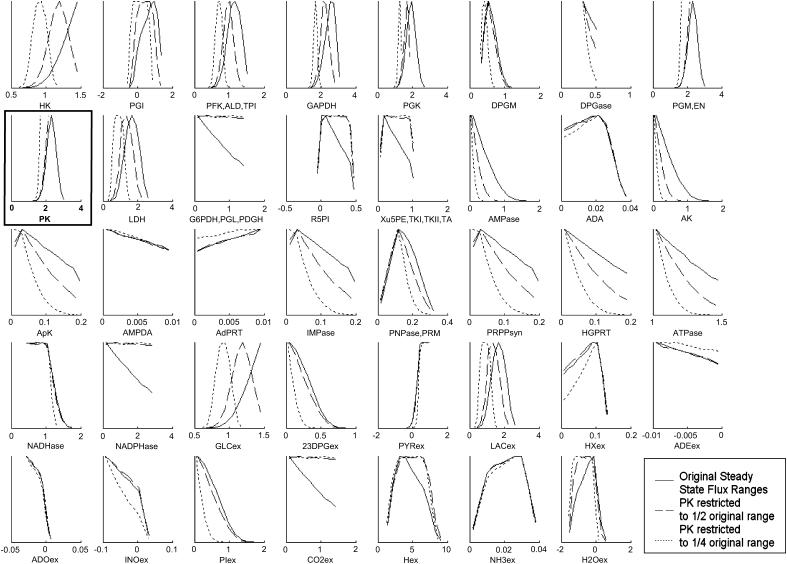
The 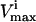Inline graphic through PK was reduced such that the allowable flux range is decreased first to one-half and then to one-quarter of the original range. The systemic effects of the simulated enzymopathy through the PK reaction greatly affected the probability distributions through many reactions in the red blood cell metabolic network (Fig. 3). For example, the probability distribution for glucose uptake changed from being a right peak distribution to being a central peak distribution, meaning that its normal operating range in the red blood cell changed from being in its most probable region to being in an improbable operating region of the steady-state flux space. With the PK range constrained to one-quarter of the original range, the maximum possible value for glucose uptake also decreased, making the previous upper range impossible to the network.

FIGURE 3.

FIGURE 3

Open in a new tab

Systemic effects of simulated enzymopathy in pyruvate kinase. Pyruvate kinase catalyzes the reaction from PEP to pyruvate. Using the Monte Carlo sampling technique, the probability distribution of all fluxes in the red blood cell were shown (solid line). The allowable range of the PK reaction was decreased to 0.5 (dashed line) and 0.25 (dotted line) of its original range by decreasing its effective 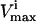Inline graphic. All of the curves were normalized such that the highest point in each of the curves is the same. The actual volume of the steady-state flux space being sampled and represented in each histogram is 6.8 × 10−5 (mM/h)11 for the original solution space, 2.1 × 10−5 (mM/h)11 (31% of original space) for PK range decreased in one-half, and 5.6 · 10−7 (mM/h)11 (0.83% of original solution space) for the PK range decreased to one-fourth. The effect of the simulated PK enzymopathy was different for different reactions, ranging from virtually no change (NH3 exchange) to significant shift in shape and magnitude (HK, PGK). Each distribution shown accounts for 100,000 uniformly distributed points within the steady-state flux space.

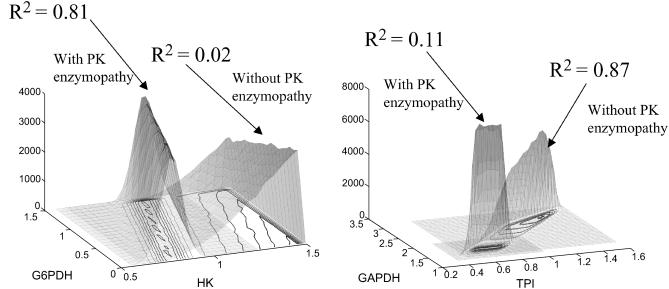
Constraining the range of allowable PK values to one-quarter of the original range significantly changed the correlations between many metabolic fluxes (Table 3). For example, the correlation between glucose uptake and the flux through the pentose phosphate pathway increased dramatically, with the r2 value between HK and G6PDH increasing by 0.79. This change in correlation is due to the limitation on the steady-state flux allowable through glycolysis due to the decreased capacity of PK. The increase in the correlation between two fluxes can be seen in the example of G6PDH versus HK and GAPDH versus TPI (Fig. 4). A high correlation coefficient implies that the shape of the two-dimensional histogram will be narrow, whereas a low correlation coefficient implies that the two-dimensional histogram will be broad. In the case of G6PDH versus HK, the PK enzymopathy causes the r2 value to increase significantly. In the case of GAPDH versus TPI, the r2 value decreases significantly with the simulated PK enzymopathy. Also of interest, the direction of the ridge representing the most probable values with the simulated PK enzymopathy changes direction significantly compared to the dominant direction of the correlation without the PK enzymopathy.

TABLE 3.

Change in flux correlations for simulated PK enzymopathies

graphic file with name biophysj00043000T03_HT.jpg

Open in a new tab

Difference between the new squared correlation coefficient of the steady-state flux space with the 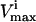Inline graphic of PK decreased so that the flux range of PK was decreased to one-quarter of its initial range. The correlation matrices for each case (full PK flux range and one-quarter PK flux range) were calculated using 1,000,000 uniformly random points in the steady-state flux space. To give an indication of an error in the estimates, the difference matrix was calculated twice from independent samples of 1,000,000 points each. The maximum change in any calculated difference as reported in this table was 0.002.

FIGURE 4.

FIGURE 4

Open in a new tab

Effect of simulated enzymopathy on correlation between other fluxes in network. Decreasing the maximum reaction rate of PK decreases the number of valid steady-state solutions. Solutions for the simulated PK enzymopathy are a subset of those without the simulated PK enzymopathy. Thus, the areas under the curve as shown are not representative. In each case, the size of the solution space with the enzymopathy is 0.83% of the size of the solution space without the enzymopathy. The PK enzymopathy can increase or decrease the correlation between sets of reactions. The correlation between HK and G6PDH goes from 0.06 up to 0.85 when the range of PK values is reduced to 25% (A), whereas the correlation between TPI and GAPDH decreased from 0.83 to 0.07 (B). The plots were generated using 300,000 uniformly distributed points within the steady-state flux space.

DISCUSSION

Uniform random sampling of a constrained steady-state flux space allows for an unbiased appraisal of the effects of the imposed physicochemical constraints on the possible functional states of a reconstructed metabolic network. The computation and analysis of uniform random points for the metabolic network of the red blood cell under the conditions of its nominal physiologic demands yielded the following key results:

  1. Probability distributions were computed for fluxes through all reactions, characterizing the feasible steady-state flux space.

  2. Pairwise correlation coefficients were calculated between all fluxes, determining the level of independence between any two fluxes, and identifying highly correlated reaction sets.

  3. The systemwide effects of the change in one (or a few) variables (i.e., a simulated enzymopathy or setting a flux range based on measurements of physiological considerations) were computed, showing that not only do the ranges of allowed flux values change throughout the network, but also their probability distributions and the correlations between metabolic fluxes.

Uniform random samples were used to calculate probability distributions for every flux in the red blood cell metabolic network. These probability distributions help to quantify the nature of all possible network flux states that satisfy the applied constraints, physiological demands, and experimental data without any additional assumptions (such as optimal behavior), and create a framework in which to place experimental results in the context of total network capabilities. The shape of the distributions are highly informative about:

  1. The impact a lower 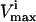Inline graphic will have on the size of the steady-state flux space, and thus on how constraining to the system a reduced flux capacity through a specific reaction would be.

  2. The reduction in the steady-state flux space based on additional experimental measurements.

It may prove to be true that fluxes that are in improbable regions are likely to require other factors than those modeled (such as a high degree of regulation, or additional physicochemical constraints) to maintain them in the experimentally measured operating state of the cell.

The degree of dependence between all of the fluxes in the red blood cell metabolic network was determined by calculating correlation coefficients from the uniform random samples. Different methods have been used to calculate correlated subsets in a metabolic network, including extreme pathway analysis (Papin et al., 2002; Price et al., 2002), elementary mode analysis (Pfeiffer et al., 1999), and the linear programming-based flux-coupling finder (Burgard et al., 2004). The correlated reaction subsets calculated by extreme pathway and elementary modes correspond only to sets that are perfectly correlated. The sets calculated using the flux-coupling finder (Burgard et al., 2004) are more informative and scalable to larger networks. In contrast to previous methods, the direct calculation of correlation coefficients from the Monte Carlo sampling procedure allowed for the stratification of pairwise correlations among all fluxes between 0 and 1 (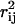Inline graphic) or between −1 and 1 (rij). Thus, the unbiased degree of independence can be determined for any two fluxes under any set of conditions.

Experimental design can be guided from the results of uniform random sampling within a constrained metabolic solution space. Both the probability distributions and the calculated correlation coefficients are condition-dependent, and thus change with the addition of more experimental data. One implication of this fact is that it is best to include as much known information as possible into the model before sampling. Subsequently, the model predicts which combinations of measurements provide independent information and which fluxes are correlated to the highest number of other fluxes under the studied conditions. Since the choice of fluxes to measure providing independent information can change with the experimental conditions, it is important that the Monte Carlo sampling procedure be used iteratively to determine which flux measurements are the most independent at each step. Thus, following the results of one set of experimental measurements, the sampling procedure can be redone to reevaluate the most important measurements given what is already known. Of course, those fluxes that are perfectly correlated (rij = 1) will remain perfectly correlated, regardless of condition. The volume of the solution spaces also changes, giving a quantitative measure for how many potential steady-state fluxes are in agreement with the measured data. As the volume of the steady-state flux space approaches zero, the internal flux distribution inside a cell is determined. Other constraint-based methods also exist for guiding experimental design and could perhaps be used in conjunction with the method proposed herein. One such method enables the calculation of the optimal set of fluxes to measure to minimize the impact of experimental error on the prediction of the steady-state flux state (Savinell and Palsson, 1992a,b).

The effects of enzymopathies on the capabilities of a metabolic network can be studied using the Monte Carlo sampling procedure. Single nucleotide polymorphisms (SNPs) or other genetic defects can impair enzyme function. This impairment can be the result of such factors as an enzyme having a lowered 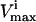Inline graphic or by a lower rate constant which can effectively lower the allowable maximum flux based on the concentration of the substrates in the red blood cell. Importantly, since the probability distributions of individual fluxes and the correlations between them change under differing conditions, the Monte Carlo sampling procedure can be used to study both normal and pathological cases under a variety of different environments. Clinical outcomes of enzymopathies can obviously involve a great many factors outside of those modeled. However, model-driven studies describe the impact of an enzymopathy on the known metabolic network uncoupled from other considerations. Thus, model-driven assessments provide evidence for whether or not a metabolic explanation is sufficient to account for a clinical outcome or not. Indeed, the apparent lack of an explanation for a clinical outcome based on what is known about a metabolic network can lead to novel biological understanding and provide a basis for novel hypotheses. One example of this is the observation that the maximal enzymatic activity of G6PDH vastly exceeds what seems to be needed in the network (Salvador and Savageau, 2003).

Constraining the flux range for the glycolytic enzymes showed a general trend seen that those simulated enzymopathies that severely restricted the steady-state flux space had been shown experimentally to cause anemia, whereas those that were less restrictive did not (Table 2). The exception to this trend was lactate dehydrogenase (LDH), the inhibition of which greatly restricted the steady-state flux space, but which has not been found to lead to anemia (Tanaka and Zerez, 1990). This may be because restriction of LDH does not significantly restrict the glycolytic rate, since pyruvate can leave the cell as the endpoint of glycolysis. However, the restriction of LDH does affect the cell's ability to control NADH levels. Another observation was that, although G6PDH is by far the most common enzymopathy in the red blood cell, only a small fraction of G6PDH enzymopathies lead to anemia. Although fewer in number, a higher fraction of PK enzymopathies than G6PDH enzymopathies lead to anemia. This fact may be attributable, in part, to the fact that restricting PK is generally much more constraining on the metabolism as a whole than is G6PDH.

Strong similarities were seen when comparing the results of the simulated enzymopathies with results from an interesting earlier study using a full-scale kinetic model of glycolysis (Holzhütter et al., 1985). In Holzhütter et al. (1985), a kinetic model of glycolysis was used to study the impact of lowering enzyme activity in a “metabolic homeostasis function.” Of the reactions studied in Holzhütter et al. (1985), one of them, HK, was found using the Monte Carlo sampling procedure to have a right peak distribution, trailing off to zero probability as the flux level through this reaction decreased, and another of the reactions, AK, was left peak, trailing off to zero probability as the flux level through this reaction increased. The kinetic model predicted that constricting HK had the most impact on the homeostasis of the red blood cell and that restrictions of AK had the least, just as predicted with the distributions given with the Monte Carlo sampling procedure. The fluxes shown by the kinetic model to have effects on homeostasis between the extremes of HK and AK, all had either central peak distributions, or were constrained such that the difference in probabilities over the flux range were not highly variable, matching expectations from the sampling procedure. Thus, results of the Monte Carlo sampling procedure corresponded well to results from a kinetic model which requires measurement of a large number of kinetic enzyme data to formulate. The need for few kinetic parameters becomes essential as the Monte Carlo sampling procedure is applied to organisms where kinetic data is much sparser than in the well-characterized red blood cell.

The uniform distribution of points within the solution space used in this study is not meant to imply that the flux steady states of cells in a population are likewise distributed uniformly within the range of allowable steady states. Indeed, it seems highly unlikely that a population of cells would be distributed uniformly in this manner, since certain regions of the solution space are expected to be preferred or excluded based on additional, unmodeled demands and physicochemical constraints under which cells operate. Rather, uniformity is used to clearly grasp the implications of applying the physicochemical constraints to the reconstructed metabolic network. Although not utilized for the purposes of this study, the Monte Carlo sampling procedure could potentially be used to study distributions of populations in cells. The informative aspect of such an approach would be to see how the population density deviated from a uniform distribution within the range of allowable steady states for the in silico cell. By identifying which portions of the steady-state flux space were favored within the population of cells, hypotheses for the preferred states could be formed and the importance of additional physicochemical constraints could be assessed.

Although the present study focused on studying the steady-state flux space, the approach detailed herein can be equally well applied to study concentration or kinetic spaces associated with a reconstructed biochemical network. Also any additional physicochemical law can be used to further confine sets of candidate solutions. If the imposed constraints can be represented as linear equations, they can be easily implemented into this framework and, aside from computational limitations, uniform random sampling can easily be done within the space. Once the set of candidate solutions are generated, any type of nonlinear constraint, such as stemming from regulation or thermodynamics, can be applied as a postprocessing step (as long as dimensionality of the space is not reduced) by eliminating candidate solutions that do not satisfy the imposed constraint. Although “elimination” algorithms such as the one used in this study have certain advantages for sampling smaller networks, it is likely that any “elimination” approach to sampling will be inadequate for sampling genome-scale networks. This difficulty in generating samples in high-dimensional objects occurs because the ratio of the size of an enclosing object to the size of the enclosed object increases rapidly as dimension increases. However, genome-scale networks can be sampled (Almaas et al., 2004) using alternate, but similar, methods for generating the set of candidate solutions, such as Monte Carlo Markov-chain samplers (Chen and Schmeiser, 1993; Kaufman and Smith, 1998; Lovasz, 1999; Zabinsky et al., 1993), and such methods have been well studied and continue to improve. Thus, the methods described herein for analyzing uniform random samples from solution spaces can be utilized for studying genome-scale networks.

Taken together, uniform random sampling provides a broadening of the constraint-based approach by allowing for the unbiased and detailed assessment of the capabilities of reconstructed networks subject to the imposition of physicochemical constraints. Uniform random sampling of solution spaces allows for a detailed framework in which to design experiments to determine the operating state of the cell, a context in which to study the resulting experimental data, as well as detailed insight into what network behaviors are allowed by the imposition of the stated constraints upon the reconstructed network. Clearly understanding model predictions is important because a cell-scale model provides the most compact and quantitative representation of a large-scale hypothesis of how a cell works. Thus, the Monte Carlo sampling procedure coupled with ongoing network reconstruction provides a powerful engine to drive experimental work and the iterative model-building process that is at the heart of systems biology.

Acknowledgments

The authors thank Iman Famili, Harvey Greenberg, Neema Jamshidi, Jason Papin, and Sharon Wiback for helpful discussions.

Support for this research was generously provided by a grant from the National Science Foundation (NSF/BES-01-20363).

APPENDIX: ABBREVIATIONS

TABLE 4.

Metabolites

Abbreviation Metabolite
GLC Glucose
G6P Glucose-6-phosphate
F6P Fructose-6-phosphate
FDP Fructose-1,6-diphosphate
DHAP Dihydroxyacetone phosphate
GA3P Glyceraldehyde-3-phosphate
13DPG 1,3-Diphosphoglycerate
23DPG 2,3-Diphosphoglycerate
3PG 3-Phosphoglycerate
2PG 2-Phosphoglycerate
PEP Phosphoenolpyruvate
PYR Pyruvate
LAC Lactate
6PGL 6-Phosphogluco-lactone
6PGC 6-Phosphogluconate
RL5P Ribulose-5-phosphate
X5P Xylulose-5-phosphate
R5P Ribose-5-phosphate
S7P Sedoheptulose-7-phosphate
E4P Erythrose-4-phosphate
PRPP 5-Phosphoribosyl-1-pyrophosphate
IMP Inosine monophosphate
R1P Ribose-1-phosphate
HX Hypoxanthine
INO Inosine
ADE Adenine
ADO Adenosine
AMP Adenosine monophosphate
ADP Adenosine diphosphate
ATP Adenosine triphosphate
NAD Nicotinamide adenine dinucleotide
NADH Nicotinamide adenine dinucleotide (R)
NADP Nicotinamide adenine dinucleotide phosphate
NADPH Nicotinamide adenine dinucleotide phosphate (R)
H Hydrogen ion
Pi Inorganic phosphate
NH3 Ammonia
CO2 Carbon dioxide
H2O Water
Open in a new tab

TABLE 5.

Reactions

Abbreviation Enzyme Chemical reaction
Glycolysis and Rapoport-Leubering shunt
HK Hexokinase GLU + ATP → G6P + ADP + H
PGI Phosphoglucoisomerase G6P ↔ F6P
PFK Phosphofructokinase F6P + ATP → FDP + ADP + H
ALD Aldolase FDP ↔ GA3P + DHAP
TPI Triose phosphate isomerase DHAP ↔ GA3P
GAPDH Glyceraldehyde phosphate dehydrogenase GA3P + NAD + Pi ↔ 13DPG + NADH + H
PGK Phosphoglycerate kinase 13DPG + ADP ↔ 3PG + ATP
DPGM Diphosphoglyceromutase 13DPG + → 23DPG + H
DPGase Diphosphoglycerate phosphatase 23DPG + H2O → 3PG + Pi
PGM Phosphoglyceromutase 3PG ↔ 2PG
EN Enolase 2PG ↔ PEP + H2O
PK Pyruvate kinase PEP + ADP + H → PYR + ATP
LDH Lactate dehydrogenase PYR + NADH + H ↔ LAC + NAD
Pentose phosphate pathway
G6PDH Glucose-6-phosphate dehydrogenase G6P + NADP → 6PGL + NADPH + H
PGL 6-phosphoglyconolactonase 6PGL + H2O ↔ 6PGC + H
PDGH 6-phosphoglycoconate dehydrogenase 6PGC + NADP → RL5P + NADPH + CO2
R5PI Ribose-5-phosphate isomerase RL5P ↔ R5P
Xu5PE Xylulose-5-phosphate epimerase RL5P ↔ X5P
TKI Transketolase I X5P + R5P ↔ S7P + GA3P
TA Transaldolase GA3P + S7P ↔ E4P + GA3P
TKII Transketolase II X5P + E4P ↔ F6P + GA3P
Adenosine nucleotide metabolism
PRPPsyn Phosphoribosyl pyrophosphate synthetase R5P + ATP → PRPP + AMP
PRM Phosphoribomutase R1P ↔ R5P
HGPRT Hypoxanthine guanine phosphoryl transferase PRPP + HX + H2O → IMP + 2Pi
AdPRT Adenine phosphoribosyl transferase PRPP + ADE + H2O → AMP + 2Pi
PNPase Purine nucleoside phosphorylase INO + Pi ↔ HX + R1P
IMPase Inosine monophosphatase IMP + H2O → ADO + Pi + H
AMPDA Adenosine monophosphate deaminase AMP + H2O → IMP + NH3
AMPase Adenosine monophosphate phosphohydrolase AMP + H2O → ADO + NH3
ADA Adenosine deaminase ADO + H2O → INO + NH3
AK Adenosine kinase ADO + AMP → ADP + AMP
ApK Adenylate kinase 2ADP ↔ ATP + AMP
Open in a new tab

References

  1. Almaas, E., B. Kovacs, T. Vicsek, Z. N. Oltvai, and A. L. Barabasi. 2004. Global organization of metabolic fluxes in the bacterium Escherichia coli. Nature. 427:839–843. [DOI] [PubMed] [Google Scholar]
  2. Alves, R., and M. A. Savageau. 2000a. Comparing systemic properties of ensembles of biological networks by graphical and statistical methods. Bioinformatics. 16:527–533. [DOI] [PubMed] [Google Scholar]
  3. Alves, R., and M. A. Savageau. 2000b. Extending the method of mathematically controlled comparison to include numerical comparisons. Bioinformatics. 16:786–798. [DOI] [PubMed] [Google Scholar]
  4. Alves, R., and M. A. Savageau. 2000c. Systemic properties of ensembles of metabolic networks: application of graphical and statistical methods to simple unbranched pathways. Bioinformatics. 16:534–547. [DOI] [PubMed] [Google Scholar]
  5. Bonarius, H. P. J., G. Schmid, and J. Tramper. 1997. Flux analysis of underdetermined metabolic networks: the quest for the missing constraints. Trends Biotechnol. 15:308–314. [Google Scholar]
  6. Burgard, A. P., and C. D. Maranas. 2001. Probing the performance limits of the Escherichia coli metabolic network subject to gene additions or deletions. Biotechnol. Bioeng. 74:364–375. [DOI] [PubMed] [Google Scholar]
  7. Burgard, A. P., and C. D. Maranas. 2003. Optimization-based framework for inferring and testing hypothesized metabolic objective functions. Biotechnol. Bioeng. 82:670–677. [DOI] [PubMed] [Google Scholar]
  8. Burgard, A. P., E. V. Nikolaev, C. H. Schilling, and C. D. Maranas. 2004. Flux coupling analysis of genome-scale metabolic network reconstructions. Genome Res. 14:301–312. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Burgard, A. P., S. Vaidyaraman, and C. D. Maranas. 2001. Minimal reaction sets for Escherichia coli metabolism under different growth requirements and uptake environments. Biotechnol. Prog. 17:791–797. [DOI] [PubMed] [Google Scholar]
  10. Chen, M. H., and B. Schmeiser. 1993. Performance of the Gibbs, hit-and-run and Metropolis samplers. J. Comput. Graph. Stat. 2:251–272. [Google Scholar]
  11. Covert, M., I. Famili, and B. Palsson. 2003. Identifying the constraints that govern cell behavior: a key to converting conceptual to computational models in biology? Biotechnol. Bioeng. 84:763–772. [DOI] [PubMed] [Google Scholar]
  12. Edwards, J. S., and B. Palsson. O.2000. Metabolic flux balance analysis and the in silico analysis of Escherichia coli K-12 gene deletions. BMC Bioinformat. 1:1. Epub 2000 Jul 27. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Edwards, J. S., M. Covert, and B. Palsson. 2002. Metabolic modelling of microbes: the flux-balance approach. Environ. Microbiol. 4:133–140. [DOI] [PubMed] [Google Scholar]
  14. Edwards, J. S., R. U. Ibarra, and B. O. Palsson. 2001. In silico predictions of Escherichia coli metabolic capabilities are consistent with experimental data. Nat. Biotechnol. 19:125–130. [DOI] [PubMed] [Google Scholar]
  15. Edwards, J. S., and B. O. Palsson. 1999. Systems properties of the Haemophilus influenzae Rd metabolic genotype. J. Biol. Chem. 274:17410–17416. [DOI] [PubMed] [Google Scholar]
  16. Famili, I., J. Forster, J. Nielsen, and B. O. Palsson. 2003. Saccharomyces cerevisiae phenotypes can be predicted by using constraint-based analysis of a genome-scale reconstructed metabolic network. Proc. Natl. Acad. Sci. USA. 100:13134–13139. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Forster, J., I. Famili, B. O. Palsson, and J. Nielsen. 2003. Large-scale evaluation of in silico gene deletions in Saccharomyces cerevisiae. Ohmics. 7:193–202. [DOI] [PubMed] [Google Scholar]
  18. Grimes, A. J. 1980. Human Red Cell Metabolism. Blackwell Scientific Publications, Oxford, UK.
  19. Hasty, J., D. McMillen, and J. J. Collins. 2002. Engineered gene circuits. Nature. 420:224–230. [DOI] [PubMed] [Google Scholar]
  20. Hasty, J., D. McMillen, F. Isaacs, and J. J. Collins. 2001. Computational studies of gene regulatory networks: in numero molecular biology. Nat. Rev. Genet. 2:268–279. [DOI] [PubMed] [Google Scholar]
  21. Holzhütter, H. G., G. Jacobasch, and A. Bisdorff. 1985. Mathematical modelling of metabolic pathways affected by an enzyme deficiency. A mathematical model of glycolysis in normal and pyruvate-kinase-deficient red blood cells. Eur. J. Biochem. 149:101–111. [DOI] [PubMed] [Google Scholar]
  22. Ibarra, R. U., J. S. Edwards, and B. O. Palsson. 2002. Escherichia coli K-12 undergoes adaptive evolution to achieve in silico predicted optimal growth. Nature. 420:186–189. [DOI] [PubMed] [Google Scholar]
  23. Jacobasch, G., and S. M. Rapoport. 1996. Hemolytic anemias due to erythrocyte enzyme deficiencies. Mol. Aspects Med. 17:143–170. [DOI] [PubMed] [Google Scholar]
  24. Jamshidi, N., J. S. Edwards, T. Fahland, G. M. Church, and B. O. Palsson. 2001. Dynamic simulation of the human red blood cell metabolic network. Bioinformatics. 17:286–287. [DOI] [PubMed] [Google Scholar]
  25. Jamshidi, N., S. J. Wiback, and B. O. Palsson. 2002. In silico model-driven assessment of the effects of single nucleotide polymorphisms (SNPs) on human red blood cell metabolism. Genome Res. 12:1687–1692. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kauffman, K. J., J. D. Pajerowski, N. Jamshidi, B. O. Palsson, and J. S. Edwards. 2002. Description and analysis of metabolic connectivity and dynamics in the human red blood cell. Biophys. J. 83:646–662. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kaufman, D. E., and R. L. Smith. 1998. Direction choice for accelerated convergence in hit-and-run sampling. Opt. Res. 46:84–95. [Google Scholar]
  28. Lew, V. L., and R. M. Bookchin. 1986. Volume, pH, and ion-content regulation in human red cells: analysis of transient behavior with an integrated model. J. Membr. Biol. 92:57–74. [DOI] [PubMed] [Google Scholar]
  29. Lovasz, L. 1999. Hit-and-run mixes fast. Math. Program. 86:443–461. [Google Scholar]
  30. Meyer, C. D. 2000. Matrix Analysis and Applied Linear Algebra. Society for Industrial and Applied Mathematics, Philadelphia, PA.
  31. Mulquiney, P. J., W. A. Bubb, and P. W. Kuchel. 1999. Model of 2,3-bisphosphoglycerate metabolism in the human erythrocyte based on detailed enzyme kinetic equations: in vivo kinetic characterization of 2,3-bisphosphoglycerate synthase/phosphatase using 13C and 31P NMR. Biochem. J. 342:567–580. [PMC free article] [PubMed] [Google Scholar]
  32. Mulquiney, P. J., and P. W. Kuchel. 1999. Model of 2,3-bisphosphoglycerate metabolism in the human erythrocyte based on detailed enzyme kinetic equations: computer simulation and metabolic control analysis. Biochem. J. 342:597–604. [PMC free article] [PubMed] [Google Scholar]
  33. Mulquiney, P. J., and P. W. Kuchel. 2003. Modeling Metabolism with Mathematica: Detailed Examples including Erythrocyte Metabolism. CRC Press, Boca Raton, Fl.
  34. Papin, J. A., N. D. Price, and B. O. Palsson. 2002. Extreme pathway lengths and reaction participation in genome-scale metabolic networks. Genome Res. 12:1889–1900. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Papin, J. A., N. D. Price, S. J. Wiback, D. A. Fell, and B. O. Palsson. 2003. Metabolic pathways in the post-genome era. Trends Biochem. Sci. 28:250–258. [DOI] [PubMed] [Google Scholar]
  36. Pfeiffer, T., I. Sanchez-Valdenebro, J. C. Nuno, F. Montero, and S. Schuster. 1999. METATOOL: for studying metabolic networks. Bioinformatics. 15:251–257. [DOI] [PubMed] [Google Scholar]
  37. Price, N. D., J. A. Papin, and B. O. Palsson. 2002. Determination of redundancy and systems properties of Helicobacter pylori's metabolic network using genome-scale extreme pathway analysis. Genome Res. 12:760–769. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Price, N. D., J. A. Papin, C. H. Schilling, and B. O. Palsson. 2003a. Genome-scale microbial in silico models: the constraints-based approach. Trends Biotechnol. 21:162–169. [DOI] [PubMed] [Google Scholar]
  39. Price, N. D., J. L. Reed, J. A. Papin, S. J. Wiback, and B. O. Palsson. 2003b. Network-based analysis of metabolic regulation in the human red blood cell. J. Theor. Biol. 225:185–194. [DOI] [PubMed] [Google Scholar]
  40. Reed, J. L., and B. O. Palsson. 2003. Thirteen years of building constraint-based in silico models of Escherichia coli. J. Bacteriol. 185:2692–2699. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Reed, J. L., T. D. Vo, C. H. Schilling, and B. O. Palsson. 2003. An expanded genome-scale model of Escherichia coli K-12 (iJR904 GSM/GPR). Genome Biol. 4:R54.1–R54.12. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Salvador, A., and M. A. Savageau. 2003. Quantitative evolutionary design of glucose 6-phosphate dehydrogenase expression in human erythrocytes. Proc. Natl. Acad. Sci. USA. 100:14463–14468. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Savinell, J. M., and B. O. Palsson. 1992a. Optimal selection of metabolic fluxes for in vivo measurement. I. Development of mathematical methods. J. Theor. Biol. 155:201–214. [DOI] [PubMed] [Google Scholar]
  44. Savinell, J. M., and B. O. Palsson. 1992b. Optimal selection of metabolic fluxes for in vivo measurement. II. Application to Escherichia coli and hybridoma cell metabolism. J. Theor. Biol. 155:215–242. [DOI] [PubMed] [Google Scholar]
  45. Schilling, C. H., M. W. Covert, I. Famili, G. M. Church, J. S. Edwards, and B. O. Palsson. 2002. Genome-scale metabolic model of Helicobacter pylori 26695. J. Bacteriol. 184:4582–4593. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Schilling, C. H., and B. O. Palsson. 2000. Assessment of the metabolic capabilities of Haemophilus influenzae Rd through a genome-scale pathway analysis. J. Theor. Biol. 203:249–283. [DOI] [PubMed] [Google Scholar]
  47. Schilling, C. H., S. Schuster, B. O. Palsson, and R. Heinrich. 1999. Metabolic pathway analysis: basic concepts and scientific applications in the post-genomic era. Biotechnol. Prog. 15:296–303. [DOI] [PubMed] [Google Scholar]
  48. Schuster, R., and H. G. Holzhutter. 1995. Use of mathematical models for predicting the effect of large scale enzyme activity alterations: application to enzyme deficiencies of red blood cells. Eur. J. Biochem. 229:403–418. [PubMed] [Google Scholar]
  49. Schuster, R., H. G. Holzhütter, and G. Jacobasch. 1988. Interrelations between glycolysis and the hexose monophosphate shunt in erythrocytes as studied on the basis of a mathematical model. Biosystems. 22:19–36. [DOI] [PubMed] [Google Scholar]
  50. Schuster, S., D. A. Fell, and T. Dandekar. 2000. A general definition of metabolic pathways useful for systematic organization and analysis of complex metabolic networks. Nature Biotechnol. 18:326–332. [DOI] [PubMed] [Google Scholar]
  51. Schuster, S., and C. Hilgetag. 1994. On elementary flux modes in biochemical reaction systems at steady state. J. Biol. Sys. 2:165–182. [Google Scholar]
  52. Segre, D., D. Vitkup, and G. M. Church. 2002. Analysis of optimality in natural and perturbed metabolic networks. Proc. Natl. Acad. Sci. USA. 99:15112–15117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Tanaka, K. R., and C. R. Zerez. 1990. Red cell enzymopathies of the glycolytic pathway. Semin. Hematol. 27:165–185. [PubMed] [Google Scholar]
  54. Thorburn, D. R., and P. W. Kuchel. 1985. Regulation of the human-erythrocyte hexose-monophosphate shunt under conditions of oxidative stress. A study using NMR spectroscopy, a kinetic isotope effect, a reconstituted system and computer simulation. Eur. J. Biochem. 150:371–386. [DOI] [PubMed] [Google Scholar]
  55. Wiback, S. J., I. Famili, H. J. Greenberg, and B. O. Palsson. 2004. Monte Carlo sampling can be used to determine the size and shape of the steady-state flux space. J. Theor. Biol. 228:437–447. [DOI] [PubMed] [Google Scholar]
  56. Wiback, S. J., and B. O. Palsson. 2002. Extreme pathway analysis of human red blood cell metabolism. Biophys. J. 83:808–818. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Zabinsky, Z. B., R. L. Smith, J. F. McDonald, H. E. Romeijn, and D. E. Kaufman. 1993. Improving hit-and-run for global optimization. J. Global Optimiz. 3:171–192. [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES