Asymmetry in Membrane Responses to Electric Shocks: Insights from Bidomain Simulations

Abstract

Models of myocardial membrane dynamics have not been able to reproduce the experimentally observed negative bias in the asymmetry of transmembrane potential changes (ΔV_m) induced by strong electric shocks delivered during the action potential plateau. The goal of this study is to determine what membrane model modifications can bridge this gap between simulation and experiment. We conducted simulations of shocks in bidomain fibers and sheets with membrane dynamics represented by the LRd'2000 model. We found that in the fiber, the negative bias in ΔV_m asymmetry could not be reproduced by addition of electroporation only, but by further addition of hypothetical outward current, I_a, activated upon strong shock-induced depolarization. Furthermore, the experimentally observed rectangularly shaped positive ΔV_m, negative-to-positive ΔV_m ratio (asymmetry ratio) = ∼2, electroporation occurring at the anode only, and the increase in positive ΔV_m caused by L-type Ca²⁺-channel blockade were reproduced in the strand only if I_a was assumed to be a part of K⁺ flow through the L-type Ca²⁺-channel. In the sheet, I_a not only contributed to the negative bias in ΔV_m asymmetry at sites polarized by physical and virtual electrodes, but also restricted positive ΔV_m. Inclusion of I_a and electroporation is thus the bridge between experiment and simulation.

INTRODUCTION

Electric shocks are widely used in clinical practice to terminate ventricular tachyarrhythmias. The shock electrodes deliver current into the myocardial extracellular space, leading to the formation of regions of positive and negative membrane polarization in the tissue (Sepulveda et al., 1989; Knisley et al., 1994; Neunlist and Tung, 1995; Wikswo et al., 1995; Trayanova et al., 1998). These shock-induced changes (ΔV_m) in transmembrane potential (V_m) lead to initiation of postshock activations (Kao and Hoffman, 1958; Efimov et al., 1998; Trayanova et al., 2003) and prolongation/shortening of action potential duration (Dillon, 1991; Cheng et al., 1999b; Clark et al., 1999; Gray et al., 2001); both effects are important determinants of shock outcome (Dillon, 1992; Knisley and Hill, 1993; Cheng et al., 1999b). Membrane electroporation resulting from large ΔV_m (Jones et al., 1987; Tovar and Tung, 1991; Tsong, 1991; Knisley and Grant, 1995) has also been implicated in the onset of postshock activations (Yabe et al., 1990; Kodama et al., 1994; Ashihara et al., 2001; Fast and Cheek, 2002; Ohuchi et al., 2002). Therefore, understanding the generation of shock-induced ΔV_m and electroporation is paramount to unraveling the mechanisms of electrical defibrillation.

Research has demonstrated that the delivery of a strong electric shock during the action potential plateau in cultured myocyte strands (Gillis et al., 1996; Cheek et al., 2000; Fast et al., 2000; Fast and Cheek, 2002; Cheek and Fast, 2004), papillary muscles (Zhou et al., 1995b, 1996), and three-dimensional myocardial preparations (Knisley et al., 1994; Zhou et al., 1995a; Fast et al., 2002) leads to asymmetrical membrane polarization in the tissue with the negative ΔV_m being larger than (nearly two times) the positive (negative bias in ΔV_m asymmetry). Furthermore, both positive and negative ΔV_m exhibit a nonlinear behavior as a function of shock strength. However, the mechanisms underlying the asymmetry in membrane responses to electric shocks as well as their nonlinear dependence on shock strength remain incompletely understood.

Several models of ventricular membrane dynamics (Beeler and Reuter, 1977; Luo and Rudy, 1991; Luo and Rudy, 1994a,b) and their modified versions (Drouhard and Roberge, 1982; Roth, 1995; Ashihara et al., 2001) have been used to examine the relationship between shocks and the membrane responses they induce (Jones et al., 1994; Roth, 1995; Fishler and Vepa, 1998; Skouibine et al., 1999, 2000; Ashihara et al., 2001). However, no membrane model, thus far, has been able to reproduce the observed negative bias in the asymmetry of ΔV_m after strong shocks; a match between experiment and model predictions has been achieved for weak shocks only (Clark et al., 1999; Gray et al., 2001). Therefore, the predictive value of simulation results regarding stimulation with strong shocks and defibrillation remains debatable.

A study by Cheng et al. (1999a) suggested that, at the level of a single myocyte, the discrepancy between experiments and simulations could be resolved by the addition, to the total ionic current, of a current through electroporated membranes (I_ep) and a hypothetical outward current (I_a), with both currents activating far outside the range of the normal action potential. Although electroporation is known to occur after strong shocks to the heart (Yabe et al., 1990; Kodama et al., 1994; Al-Khadra et al., 2000) and its contribution to ΔV_m has been clarified over the course of numerous studies (Knisley and Grant, 1995; Neunlist and Tung, 1997; Cheng et al., 1999a; Aguel et al., 1999; Ashihara et al., 2001, 2003; Fast and Cheek, 2002; Cheek and Fast., 2004; Nikolski et al., 2004), the ionic composition of I_a, as well as its role in ΔV_m asymmetry in multicellular cardiac preparations remains unknown. Studies have demonstrated that the inward rectifier potassium current (I_K1) blocker BaCl₂ (Fast et al., 2000; Cheek and Fast, 2004), the rapid delayed rectifier blocker dofetilide (Fast et al., 2000), and the hyperpolarization-activated inward current inhibitor CsCl (Cheek and Fast, 2004) do not significantly change the degree of ΔV_m asymmetry. On the other hand, a study by Cheek et al. (2000) found an increase in positive ΔV_m and a decrease in the negative-to-positive ΔV_m ratio by the L-type Ca²⁺ current (I_Ca(L)) blocker nifedipine. These studies provide evidence that the depolarization-activated outward current I_a might flow through the L-type Ca²⁺ channel.

The I_Ca(L) current has three individual components (Matsuda and Noma, 1984), namely Ca²⁺, K⁺, and Na⁺ currents (I_Ca,Ca, I_Ca,K, and I_Ca,Na, respectively), with the permeability ratio Ca²⁺:K⁺:Na⁺ in the voltage range of the normal action potential being 2800:3.5:1. Therefore, it is reasonable to expect that if the large outward current I_a is a part of I_Ca,Ca, the intracellular Ca²⁺ concentration ([Ca²⁺]_i) should experience, as a consequence of I_a activation, a sudden decrease in the regions of strong shock-induced depolarization. However, in an isolated ventricular myocyte (Sharma and Tung, 2002b), in the region of large positive ΔV_m the change in [Ca²⁺]_i during a shock delivered at the plateau of an action potential was relatively small (≤20% of the magnitude of last pacing-induced change in [Ca²⁺]_i; Sharma and Tung, 2002a). Such finding is supported by the argument that since the Ca²⁺ Nernst potential (E_Ca,N) is 127.5 mV and the peak of I_Ca,Ca occurs ∼0 mV (Luo and Rudy, 1994a), I_Ca,Ca is expected to only be a small contribution to I_Ca(L) as V_m approaches E_Ca,N. Moreover, based on the Goldman-Hodgkin-Katz equation, one can easily estimate that a small [Ca²⁺]_i, of the order of μmol/L, would not result in a large outward current. In contrast, when V_m surpasses the reversal potential of I_Ca(L) (E_Ca = 56 mV; Isenberg and Klockner, 1982; Campbell et al., 1988), I_Ca,K becomes a major outward component of I_Ca(L) (Luo and Rudy, 1994a). However, in the ventricular membrane models used in previous simulation studies of stimulation/defibrillation, I_Ca,K was either not included (Beeler and Reuter, 1977; Luo and Rudy, 1991), or if included, its characteristics for V_m > E_Ca were not based on experimental data (Luo and Rudy, 1994a,b).

Based on the above arguments, we hypothesize that I_a is part of I_Ca,K. We further hypothesize that with the proposed I_Ca,K modification and with the addition of I_ep to the membrane currents, an agreement between experiments and simulations can be achieved. The aim of this study is to test these two hypotheses by investigating, in simulated multicellular fibers and sheets, 1), shock-induced ΔV_m and its dependence on shock strength, and 2), the effects of ionic channel blockade on ΔV_m. This research will thus provide mechanistic insight into the generation of shock-induced ΔV_m, an important factor in the process of cardiac defibrillation.

METHODS

Membrane model and geometry of the preparation

A recent version (Faber and Rudy, 2000) of the Luo-Rudy dynamic model (Luo and Rudy, 1994a,b; Zeng et al., 1995; Viswanathan et al., 1999), referred to here as “LRd” was used. To the LRd model, we then added the electroporation current I_ep (DeBruin and Krassowska, 1998); this membrane model was referred to as “LRd+EP.” Finally, to the original I_Ca,K in the LRd model, we added I_a as formulated by Cheng et al. (1999a), which, together with the addition of I_ep, constituted the “augmented” LRd model, or “aLRd.”

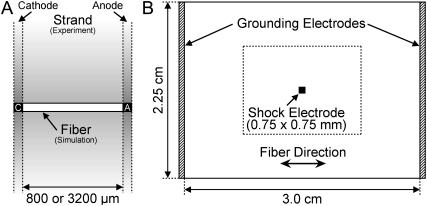
We simulated a homogeneous one-dimensional bidomain myocardial fiber of length either 800 or 3200 μm (Fig. 1 A). Cathodal and anodal shock electrodes (denoted as C and A) were located at fiber ends. The choice of simulation geometry was dictated by the experimental setup in cultured myocyte strand studies (Gillis et al., 1996; Cheek et al., 2000; Fast et al., 2000; Fast and Cheek, 2002; Cheek and Fast, 2004), thus allowing an easy comparison between experimental data and simulation results. The fiber length was equivalent to the cultured myocyte strand width; delivery of shocks through electrodes at fiber ends corresponded to the uniform-field shocks applied via line electrodes across the strand width (Fig. 1 A).

FIGURE 1.

(A) Homogeneous bidomain myocardial fiber, representing the electrical behavior of the cultured myocyte strand in the direction of the applied electric field in the experiment (Gillis et al., 1996; Cheek et al., 2000; Fast et al., 2000; Fast and Cheek, 2002; Cheek and Fast, 2004). Characters C and A at fiber ends denote cathode and anode, respectively. (B) Homogeneous myocardial sheet. Shaded bars at the vertical borders indicate grounding electrodes, whereas the black square in the center of the sheet represents a unipolar shock electrode. The rectangle of size 1.5 × 1.125 cm outlined by the dotted line represents the portion of the sheet shown in Fig. 6.

A homogeneous bidomain myocardial sheet of size 3.0 × 2.25 cm (Fig. 1 B) was also simulated. Myocardial fibers in the sheet were oriented horizontally. Two grounding electrodes (shaded bars) were positioned at the vertical borders of the sheet, whereas a shock electrode of size 0.75 × 0.75 mm was located at the sheet center.

Values of other parameters used in this study included longitudinal and transverse conductivities of 1.74 and 0.19 mS/cm in the intracellular space, and 6.25 and 2.36 mS/cm in the extracellular space, respectively; and surface-to-volume ratio of 1400 cm⁻¹. The one-dimensional simulation studies used the longitudinal conductivities.

Simulation protocol

Eight transmembrane stimuli of 300-ms basic cycle length were applied simultaneously to all myocardial units in the fiber or sheet. Each transmembrane stimulus had duration of 3 ms and strength 15 μA/cm², which was just above the diastolic threshold. The eight transmembrane stimuli were followed by a 10-ms square-wave monophasic shock. Shocks were of various strengths and were delivered extracellularly via the shock electrode(s) at various timings during the eighth stimulus-induced action potential.

Measurements of ΔV_m and asymmetry ratio

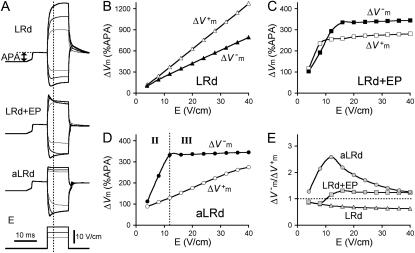
Shock-induced ΔV_m was measured as the difference between the shock-induced V_m at a given time and V_m at the corresponding time in the preceding seventh stimulus-induced action potential. ΔV_m magnitude was then normalized to the amplitude (APA) of the eighth stimulus-induced action potential just before the shock (Fig. 2 A, top). In a preliminary study, we found that the normal action potential shape after the eighth stimulus was identical to the LRd, LRd+EP, and aLRd models; APAs were all 132 mV.

FIGURE 2.

Transmembrane potential responses to 10-ms shocks of various strengths, E, given at a coupling interval of 10 ms in an 800-μm long fiber. Membrane kinetics is represented by the original LRd, LRd with electroporation (LRd+EP), and the augmented LRd (aLRd) models. (A) Superposition of shock-induced positive and negative polarization at the ends of the fiber for the three models. Shock strengths are 8, 12, and 16 V/cm (thin, thicker, and thickest lines, respectively). APA is action potential amplitude. Vertical dotted line indicates 3 ms after shock onset, the time at which ΔV_m is measured. (B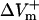–D) and 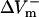(%APA) as functions of shock strength in the LRd (B), LRd+EP (C), and aLRd (D) fibers. (E) Relationship between asymmetry ratio 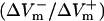and shock strength for the LRd, LRd+EP, and aLRd fibers as calculated from panels B, C, and D, respectively. Horizontal dotted line represents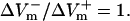

For the myocardial fiber, the asymmetry ratio, defined as 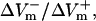was calculated from the absolute values of 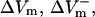and 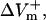measured at the fiber ends 3 ms after shock onset. For the myocardial sheet, two types of asymmetry ratios were calculated, both defined at the end of the 10-ms shock. The first involved recording of ΔV_m at the center of the region directly polarized by the small unipolar electrode (physical electrode); values of 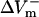and 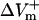were obtained by using opposite shock polarities. The second was calculated from 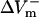and 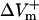at the site of peak polarization in the adjacent virtual electrode after shocks of opposite polarities.

Computation

The numerical approach, including methods for integration and solution of the linear system, has been described elsewhere (Ashihara et al., 2001, 2003). The spatial discretization for the fiber and the sheet was 25 and 75 μm, respectively. The time discretization was varied adaptively between 1.25 and 5.0 μs, depending on the value of the first derivative of V_m.

RESULTS

Dependence of ΔV_m on shock strength

Fig. 2 A presents V_m traces that show positive and negative polarization at opposite ends of a 800-μm fiber with LRd, LRd+EP, and aLRd membrane kinetics; the traces represent responses to 10-ms shocks of strengths 8, 12, and 16 V/cm (thin, thicker, and thickest lines, respectively) delivered at a coupling interval of 10 ms. In the case of a fiber with LRd kinetics (top), the rise of the positive ΔV_m transient was monotonic regardless of shock strength, whereas the rise of the negative ΔV_m transient was monotonic for the 8-V/cm shock but became nonmonotonic for stronger shocks. In the case of a fiber with LRd+EP kinetics (middle), both positive and negative ΔV_m transients had monotonic rises for the 8-V/cm shock and nonmonotonic ones for the 16-V/cm shock. The intermediate 12-V/cm shock resulted in a nonmonotonic rise in the positive ΔV_m transient and monotonic rise in the negative ΔV_m transient. In the case of aLRd kinetics (bottom), all positive ΔV_m transients were rectangular, with monotonic (8-V/cm) or nonmonotonic (all other shock strengths) rises in negative ΔV_m transients.

The dependence of 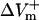and 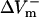on shock strength in the range of 4–40 V/cm in the 800-μm fiber for the three membrane models is shown in Fig. 2, panels B–D. In the case of LRd (Fig. 2 B), both 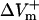and 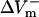were almost linearly dependent on shock strength, whereas in the LRd+EP and aLRd cases (Fig. 2, C and D, respectively), this dependence was nonlinear. Interestingly, in the LRd+EP and aLRd cases, 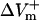and 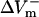were much smaller than those in the LRd case. Furthermore, in the LRd+EP fiber, the 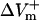curve reached a plateau at a lower shock strength as compared to the 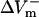curve (Fig. 2 C), whereas in the aLRd case 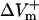continued to gradually increase even when the shock strength was above 30 V/cm.

Fig. 2 E presents the relationship between asymmetry ratio and shock strength, calculated from Fig. 2, panels B–D, for the three types of membrane kinetics in the fiber. The LRd asymmetry ratio was <1 for all shocks; it gradually decreased with increasing shock strengths and reached a value of 0.62 for high strength shocks. Likewise, the LRd+EP asymmetry ratio was <1 for shocks smaller than 8 V/cm but became >1 and reached a plateau level of 1.25 for stronger shocks. In contrast, the aLRd asymmetry ratio was >1 regardless of shock strength; as the shocks became stronger, the asymmetry ratio increased to 2.58 and then decreased to 1.25. The presence of a peak in the aLRd asymmetry ratio dependence on shock strength (Fig. 2 E) was the result of the lower rate of 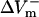increase at higher shock strengths (Fig. 2 D). The shock strength at which the asymmetry ratio reached a peak (Fig. 2 E) corresponded to the transition from monotonic to nonmonotonic rise in negative ΔV_m transient (Fig. 2 A, bottom).

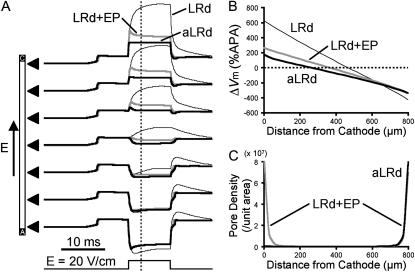
Spatial distribution of ΔV_m and electroporation

Fig. 3 A shows 20-V/cm shock-induced polarization transients at seven recording sites along the 800-μm fiber for the three membrane models. For the LRd, LRd+EP, and aLRd models, at the cathodal fiber end, positive ΔV_m transients of monotonic and nonmonotonic rise as well as of rectangular shape, respectively, were observed (traces as in Fig. 2 A). All three types of traces gradually transitioned into nonmonotonically rising negative ΔV_m transients as the recording site drew closer to the anode.

FIGURE 3.

Spatial distribution of ΔV_m and electroporation induced by 10-ms shocks of strength 20 V/cm in an 800-μm long fiber. (A) Traces of shock-induced polarization transients at seven recording sites along the fiber denoted by black triangles, for the LRd, LRd+EP, and aLRd cases (thin black, thick gray, and thick black traces, respectively). Shock pulse is shown at the bottom. (B) Spatial distribution of ΔV_m (%APA) along the fiber 3 ms after shock onset, denoted as vertical dotted line in panel A, for the three different cases. (C) Spatial distribution of pore density resulting from electroporation at shock end along the LRd+EP and aLRd fibers.

Fig. 3 B presents the spatial distribution of ΔV_m along the fiber length in the three cases. ΔV_m was measured 3 ms after shock onset and normalized to APA. In the LRd case, the portion of the fiber negatively polarized was shorter than the one positively polarized, with 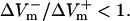For the LRd+EP and aLRd fibers, the distribution of ΔV_m was also asymmetric, however, negative ΔV_m occupied a greater portion of the fiber length than positive ΔV_m; in addition, 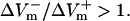Yet, differences between LRd+EP and aLRd cases were also observed: in the aLRd case, the spatial gradient of ΔV_m was lower and the 0-mV location separating positive and negative ΔV_m regions was shifted toward the cathode.

Fig. 3 C portrays the spatial distribution of the density of electroporation pores (as defined by DeBruin and Krassowska, 1998) at shock end along the LRd+EP and aLRd fibers. In the LRd + EP case, electroporation occurred at both fiber ends (pore density 8.66 and 6.97 × 10⁷/unit area, respectively), and the pore density decayed exponentially with the distance from either electrode. In contrast, in the aLRd fiber electroporation took place only near the anode (pore density 7.97 × 10⁷/unit area); this was the region where ΔV_m transients of nonmonotonic rising phases took place (Fig. 3 A).

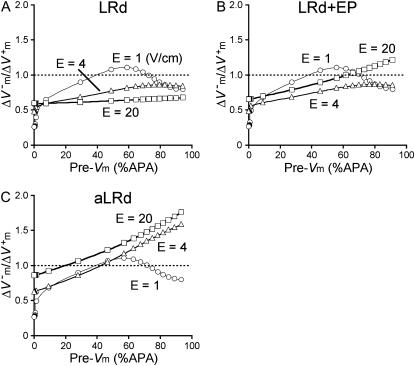
Effects of shock strength on the relationship between asymmetry ratio and preshock V_m

Fig. 4 presents the asymmetry ratio as a function of the fiber preshock V_m (normalized by APA) for shocks of strength 1, 4, and 20 V/cm in the three cases. The figure includes preshock V_m values corresponding to diastole; when the fiber was in diastole, a wave always emanated from the virtual cathode. To prevent this wave from reaching the anode, we used a 3200-μm long fiber in the simulations. For the 1-V/cm shock, the behavior was the same in the three cases: shocks delivered during action potential plateau (Pre-V_m ≈ 60%APA) resulted in a negatively biased ΔV_m asymmetry 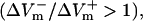whereas shocks delivered during diastole (Pre-V_m = 0) produced a positive asymmetry bias 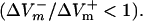For the stronger 4-V/cm shocks, the LRd and LRd+EP curves flattened somewhat and became entirely within the negative asymmetry ratio range. In contrast, in the aLRd fiber, there was a negative bias in ΔV_m asymmetry during action potential plateau, with the ratio increasing as preshock V_m increased. The 20-V/cm shock resulted in a nearly flat 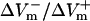curve in the LRd case, whereas in the LRd+EP and aLRd fibers the ratio was strongly dependent on preshock V_m.

FIGURE 4.

Asymmetry ratio 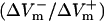as a function of preshock V_m (Pre-V_m) in units %APA for shock strengths of 1, 4, and 20 V/cm in the 3200-μm long fiber for the LRd (A), LRd+EP (B), and aLRd (C) cases.

Effects of ionic channel blockade on shock-induced ΔV_m

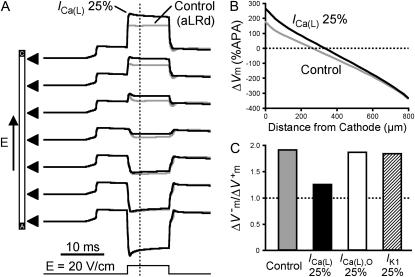
Fig. 5 presents results of simulations regarding the effect of Ca²⁺-channel blockade on V_m responses to shocks of strength 20 V/cm in the 800-μm long aLRd fiber. Reduction of 75% in I_Ca(L) caused a significant increase in the magnitude of the positive ΔV_m at the cathodal end (265.5 vs. 176.4%APA in the aLRd control case as measured 3 ms after shock onset), whereas the magnitude of the negative ΔV_m at the anodal end was not altered (−336.0 vs. −331.2%APA in control as measured 3 ms after shock onset; Fig. 5 A). Blockade of I_Ca(L) reduced the spatial gradient in ΔV_m distribution along the fiber and the degree of asymmetry by causing a significant shift in the location of the 0-mV point toward the cathode (Fig. 5 B). As a result of the increase in positive ΔV_m, the asymmetry ratio was reduced from 1.90 to 1.25 (compare gray and black bars in Fig. 5 C).

FIGURE 5.

Effect of ionic channel blockade on V_m responses to shocks of strength 20 V/cm in the 800-μm long fiber. (A) Shock-induced polarization transients at seven recording sites along the fiber identified by triangles for aLRd (control) and for aLRd with 75% reduction of I_Ca(L) (denoted as I_Ca(L) 25%) models. Shock pulse is shown at the bottom. (B) Spatial distribution of ΔV_m (%APA) along the strand 3 ms after shock onset in the control aLRd case and in the case of I_Ca(L) 25%. (C) Asymmetry ratios 3 ms after shock onset in the cases of control, I_Ca(L) 25%, original LRd I_Ca(L) reduction by 75% (denoted as I_Ca(L),O 25%), and I_K1 reduction by 75% (denoted as I_K1 25%).

In contrast, 75% reduction in the original LRd I_Ca(L) did not result in much of a change in 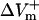(178.9%APA) and did not affect 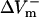much either (−332.5%APA), resulting in an asymmetry ratio of 1.86, which is close to the ratio in the aLRd control case (compare gray and white bars in Fig. 5 C). Further, if I_a was not added to I_Ca,K as in the aLRd model, but instead was added to the LRd I_Ca,Ca current, it then resulted in a rapid decrease in [Ca²⁺]_i that reached 0 μmol/L within 1 ms after shock onset (data not shown). This unrealistic [Ca²⁺]_i response to the shock was not a numerical artifact since decreasing the time discretization step to a half or a quarter of its original value did not alter the result. In addition, we simulated the effect of I_K1 blockade on shock-induced ΔV_m using an aLRd fiber of the same length and found that 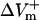and 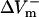were not significantly affected by the 20-V/cm shock (180.6 and −331.6%APA, respectively), resulting in an asymmetry ratio of 1.84, which is, again, close to the ratio in the aLRd control case (compare gray and shaded bars in Fig. 5 C).

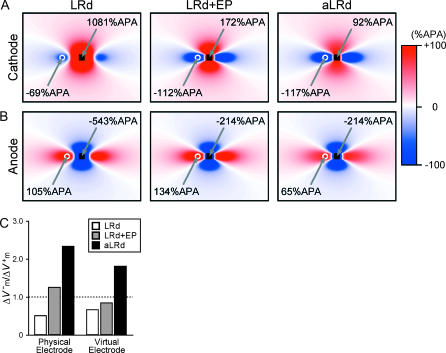
Shock-induced ΔV_m maps in a sheet

Panels A and B in Fig. 6 present ΔV_m maps resulting from 10-ms cathodal (A) and anodal (B) shocks of strength 20 mA delivered via a small unipolar electrode (black square) to the LRd, LRd+EP, and aLRd sheets. Each ΔV_m map corresponds to the end of a shock of either polarity and is normalized to APA. To emphasize the ΔV_m distribution around the shock electrode, each panel represents a quarter of the myocardial sheet; it is the region outlined by the dotted rectangle in Fig. 1 B. As seen in panels A and B, a cloverleaf virtual electrode polarization was induced by the shock in all cases; however, the exact pattern of the polarization and its magnitude were different for the three models. In the LRd sheet, ΔV_m at the center of the region directly polarized by the cathode and the maximum ΔV_m in the virtual anode were 1081 and −69%APA, respectively. In comparison, in the LRd+EP sheet, ΔV_m in the directly polarized region was less positive and ΔV_m in the virtual anode was much more negative (maximum values 172 and −112%APA, respectively); whereas in the aLRd sheet, the corresponding values were 92 and −117%APA, respectively. Responses to anodal shocks, shown in Fig. 6 B, indicated that in the LRd, LRd+EP, and aLRd sheets the maximum ΔV_m values under the anode and in the virtual cathode were −543 and 105%APA, −214 and 134%APA, and −214 and 65%APA, respectively.

FIGURE 6.

ΔV_m maps after 10-ms cathodal (A) and anodal (B) shocks of strength 20 mA in the LRd, LRd+EP, and aLRd sheets. Each ΔV_m map is normalized to APA. Only part of the sheet, the one outlined by the black dotted rectangle in Fig. 1 B, is shown. The black square represents the unipolar shock electrode. The white circle denotes the site of peak ΔV_m magnitude in the virtual electrode. (C) Asymmetry ratios in the three cases at the centers of the black squares (physical electrodes) and the white circles (virtual electrodes) in panels A and B.

Fig. 6 C shows the asymmetry ratios at the center of the region directly polarized by the physical electrode as well as the ratios in the virtual electrode (locations of maximum ΔV_m are indicated by the white circles in Fig. 6, panels A and B). In the LRd sheet, the asymmetry ratios in the physical and the virtual electrodes were significantly below 1 (0.50 and 0.66, respectively). In comparison, in the LRd+EP case both asymmetry ratios increased, but only the former was above 1 (1.24 and 0.84, respectively); whereas in the aLRd sheet, the asymmetry ratios were much larger, both being ∼2 (2.33 and 1.80, respectively).

DISCUSSION

Models of myocardial membrane dynamics have not been able to reproduce the experimentally observed negative bias in the asymmetry of (strong) shock-induced ΔV_m during the plateau of the action potential. The goal of this study is to determine which membrane model modifications could bridge this gap between simulation and experiment. We hypothesize that the experimentally observed negative bias in ΔV_m asymmetry could be reproduced by the addition, to the LRd model, of electroporation and an outward current I_a activated upon strong shock-induced depolarization, the latter suggested by the results of a single-myocyte experimental study by Cheng et al. (1999a). We further hypothesize that I_a is part of the K⁺ flow through the L-type Ca²⁺-channel. This research presents simulation results demonstrating that in multicellular cardiac tissue preparations, I_a and electroporation underlie ΔV_m asymmetry and its nonlinear dependence on shock strength. In the sections below, we present arguments supporting the validity of I_a and the aLRd model. We expect that with the use of the aLRd model, a better agreement between simulations and experiments will be achieved, thus resolving current discrepancies such as activation thresholds for cathodal and anodal stimuli (Roth, 1995; Patel and Roth, 2000; Sambelashvili et al., 2004) and the mechanisms of postshock activation initiation (Efimov et al., 1998; Trayanova et al., 2003). Adequate representation of ΔV_m asymmetry might prove important in the study of the effect of shock polarity reversal on the upper limit of vulnerability and defibrillation threshold, and in the investigation of the mechanisms by which optimal biphasic shocks fail. The faithful reproduction of experimentally observed ΔV_m in bidomain model studies is expected to render computer simulations a powerful tool for the study of electrical fibrillation induction and defibrillation.

Shock-induced polarization transients in a fiber model

Experiments (Fast et al., 2000; Fast and Cheek, 2002; Cheek and Fast, 2004) with cultured myocyte strands of widths 500–2000 μm (the widths are also the distances between shock electrodes) have shown that, for shocks delivered during action potential plateau, the rise of the negative ΔV_m transient changed from monotonic to nonmonotonic as shock strength increased, whereas the shape of the positive ΔV_m transient remained nearly rectangular regardless of shock strength. As shown in Figs. 2 A and 3 A, the shape of the negative and positive ΔV_m transients, recorded at opposite ends of the 800-μm long aLRd fiber, was in all respects identical to the experimentally observed (compare to Figs. 5 and 6 of Fast et al., 2000; Figs. 3–5 of Fast and Cheek, 2002; and Fig. 1 of Cheek and Fast, 2004). In contrast, both LRd and LRd+EP fibers could not reproduce the rectangular positive ΔV_m transient. This indicates that the outward current I_a was responsible for the rectangular shape of the positive ΔV_m transient.

In addition, for high shock strengths, the negative ΔV_m transient in the LRd+EP and aLRd fibers no longer changed with the further increase in shock strength; whereas in the LRd fiber, it continued to increase (Fig. 2 A). This indicates that electroporation contributed to the saturation in the magnitude of the negative ΔV_m transients, which is consistent with experimental findings (Cheng et al., 1999a; Fast and Cheek, 2002; Sharma and Tung, 2002b; Cheek and Fast, 2004; Nikolski et al., 2004).

Electroporation not only contributed to the saturation in the magnitude of the negative ΔV_m transients for strong shocks in the LRd+EP and aLRd fibers, but it was also responsible for the shape of the negative ΔV_m transients, specifically the nonmonotonic rise (Fig. 2 A, middle and bottom traces for 16-V/cm shocks). In the LRd fiber (Fig. 2 A, top trace, 16-V/cm shock), however, the nonmonotonic rise in ΔV_m transient was due to electrotonic interactions between regions of positive and negative polarization at opposite ends of the fiber. In this case, the magnitude of positive ΔV_m was large and the asymmetry ratio small; hence, positive ΔV_m prevailed electrotonically over negative ΔV_m from 2 ms onwards after the shock onset. We conducted simulations with 3200-μm long fibers to diminish the electrotonic interactions between regions of positive and negative ΔV_m at opposite ends of the fiber; the rise of the negative ΔV_m transient remained nonmonotonic for the LRd+EP and aLRd fibers but changed to monotonic for the LRd fiber (data not shown).

ΔV_m asymmetry in the strand preparation

Fast et al. (2000) reported that shock application during action potential plateau in strands produced two types of ΔV_m behavior. The first type was characterized by a monotonic rise in negative ΔV_m transient and a negative bias in ΔV_m asymmetry, with an asymmetry ratio that increased with increasing shock strength (type II behavior as per Fast et al., 2000). Such behavior was observed in various cardiac preparations when relatively low shock strengths were used (Zhou et al., 1995b, 1996; Gillis et al., 1996; Cheek et al., 2000; Fast et al., 2000; Fast and Cheek, 2002; Cheek and Fast, 2004). The other type of behavior (type III) was observed for strong shocks (Fast et al., 2000; Fast and Cheek, 2002; Cheek and Fast, 2004) and was characterized by nonmonotonic rise in negative ΔV_m transient and negative bias in ΔV_m asymmetry, with an asymmetry ratio that decreased with increasing shock strength. In this study, only the aLRd fiber reproduced these two types of ΔV_m behavior (see regions marked with II and III in Fig. 2 D). Furthermore, the dependence of the aLRd asymmetry ratio on shock strength (Fig. 2 E) is in agreement with experimental data in terms of both peak value and shock strength at peak value (i.e., border between types II and III). Indeed, for a 12-V/cm shock delivered to strands wider than 500 μm, the asymmetry ratio curve was found to have a maximum ∼2.5 (Fast et al., 2000). Consistent with experimental results (Knisley et al., 1994; Zhou et al., 1995a,b, 1996; Gillis et al., 1996; Cheek et al., 2000; Fast et al., 2000; Fast and Cheek, 2002; Cheek and Fast, 2004), the aLRd asymmetry ratio was ∼2 for shocks in the range of 8–20 V/cm given during the action potential plateau. In contrast, the asymmetry ratio curve for the LRd+EP fiber exhibited a nonphysiologically small peak value (<1.3). The fact that the asymmetry ratio in the aLRd fiber was higher than the one in the LRd+EP fiber (Fig. 2 E) for all shock strengths was due to the smaller magnitude of the positive ΔV_m in the aLRd case (compare panels C and D in Fig. 2), which, in turn, was due to the contribution of I_a as a large outward current in the strongly depolarized region of the fiber. Further, the asymmetric ΔV_m distribution with the negative ΔV_m fiber region being larger than the positive ΔV_m region in the aLRd case (see thick black solid traces in Fig. 3 A and thick black solid line in Fig. 3 B) is also consistent with experimental results (Gillis et al., 1996; Cheek et al., 2000; Fast et al., 2000; Fast and Cheek, 2002; Cheek and Fast, 2004).

Finally, as shown in Fig. 4, only in the case of an aLRd fiber the relationship between asymmetry ratio and preshock V_m is in agreement with the experiment (Knisley et al., 1994; Zhou et al., 1995a; Gillis et al., 1996; Fast et al., 2002; Sharifov and Fast, 2003) regarding the fact that shocks of intermediate strength (4–23 V/cm) delivered during the plateau (Pre-V_m = 60–90%APA), the relative refractory period (Pre-V_m = 10–40%APA), and in diastole (Pre-V_m = 0–10%APA) result in negatively-biased asymmetry in ΔV_m distribution, nearly symmetric ΔV_m distribution, and positively-biased asymmetry in ΔV_m distribution, respectively. Comparing panels B and C of Fig. 4, there is a significant difference in the asymmetry ratio during the plateau phase but comparatively small difference in diastole, indicating smaller contribution of I_a during the latter phase. This is due to the fact that I_a is a voltage-dependent current; its magnitude, and thus contribution to asymmetry, is small when preshock V_m is low, as in diastole.

Distribution of electroporation in the strand

Experimental studies (Tekle et al., 1990; Knisley and Grant, 1995; Fast and Cheek, 2002) have demonstrated that for a given shock strength, the negative ΔV_m region experiences greater electroporation than the positive ΔV_m region. Examining shock-induced uptake of the dye propidium iodide, Cheek and Fast (2004) recently demonstrated that electroporation was restricted to the anodal edges of the cultured myocyte strands only. We believe that this asymmetry in the occurrence of electroporation is due to the contribution of I_a, resulting in strong negative bias in shock-induced ΔV_m asymmetry 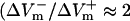); indeed, as shown in Fig. 3 C, in the LRd+EP case electroporation took place at the cathodal end as well, with electroporation pore density there 24% larger than at the anodal end. Furthermore, in previous simulation studies (Skouibine et al., 1999; Ashihara et al., 2001), membrane models (Drouhard and Roberge, 1982; Luo and Rudy, 1991) with an addition of older version of I_ep (without the addition of I_a) (Krassowska, 1995) exhibited a positively-biased ΔV_m asymmetry during action potential plateau, and resulted in a lesser degree of electroporation in the negative ΔV_m region than in the positive. These results indicate that I_a is important in reproducing the physiological distribution of electroporation.

Effect of ionic channel blockade on shock-induced ΔV_m in the strand

Cheek et al. (2000) provided mechanistic insight into ΔV_m asymmetry by demonstrating that blockade of I_Ca(L) modulates ΔV_m. Although I_a remains an unidentified current (or an unidentified component of a known current), the faithful reproduction by the aLRd model of the effect of I_Ca(L) blockade on shock-induced ΔV_m, as shown in Fig. 5, strongly suggests that an I_a-like current should be added to the I_Ca,K component of I_Ca(L). In fact, as already noted in the Results section, we could not reproduce the effect of I_Ca(L) blockade when I_a was instead added to I_Ca,Ca (data not shown) or added to the total ionic current as in Cheng et al. (1999a) (white bar in Fig. 5 C). With the addition of I_a to I_Ca,K, as done in this study, the negative bias in ΔV_m asymmetry and the rectangular shape of the positive ΔV_m transient (Figs. 2 A and 3 A) could be explained. In addition, we found that I_K1 did not contribute to ΔV_m asymmetry because I_K1 blockade did not significantly change the degree of ΔV_m asymmetry in the aLRd fiber (shaded bar in Fig. 5 C), which is consistent with results of experimental studies (Fast et al., 2000; Cheek and Fast, 2004).

Shock-induced ΔV_m in a sheet

Optical mapping studies (Knisley et al., 1994; Neunlist and Tung, 1995) have demonstrated that for shocks delivered during the action potential plateau, the asymmetry ratios in the regions directly polarized by the physical electrode and in the virtual electrodes were ∼2. In this study we show that only the aLRd model (black bars in Fig. 6 C) accurately reproduced the asymmetry ratios documented in the experiment.

Further, optical mapping experiments (Knisley, 1995; Neunlist and Tung, 1995; Wikswo et al., 1995) have typically recorded much smaller values of ΔV_m than the ones predicted numerically (Sepulveda et al., 1989; Neunlist and Tung, 1995; Roth, 1995), especially in the vicinity of the unipolar shock electrode. A possible reason for this discrepancy is the depth-averaging in the optically recorded signal (Janks and Roth, 2002). Another reason could be the lack of both an I_a-like current and I_ep in these bidomain simulations; indeed, in the aLRd sheet (Fig. 6, panels A and B), positive and negative ΔV_m values near the shock electrode were considerably diminished by the inclusion of I_a and I_ep. Faithful reproduction of virtual electrode polarization around a small unipolar electrode is important not only in understanding the basic mechanisms of stimulation with strong shocks; cathode-break excitation ensuing from this polarization has also been implicated in myocardial capture during fibrillation (Ashihara et al., 2004a) and in fibrillation control (Ashihara et al., 2004b).

Comparison with experimental studies of isolated myocytes

The nonmonotonic rise of the negative ΔV_m transient and the negative bias in ΔV_m asymmetry have been previously documented in isolated ventricular myocyte studies (Knisley et al., 1993; Knisley and Grant, 1995; Cheng et al., 1999a; Sharma and Tung, 2002b); however, myocyte responses to shocks are different from those of multicellular preparations. For instance, single myocyte responses exhibit a variety of shapes of the positive ΔV_m transient, rectangular or with monotonic or nonmonotonic rises, and the asymmetry ratio for shocks delivered during the plateau varies between 1.2 and 3.3. This variety in responses might be attributed to the fact that single myocytes come in different sizes and shapes, which could result in different electrotonic interactions between positively and negatively polarized myocyte ends. Another possible reason is that in a single myocyte the intracellular potential gradient during the shock is ∼1/10 of the extracellular potential gradient (Cheng et al., 1999a; Sharma and Tung, 2002b), whereas in a multicellular strand, such as the fiber in this study (Fig. 1 A), the intracellular potential gradient matches macroscopically the extracellular potential gradient (Newton et al., 1999); these differences could result in different V_m in the two cases. In fact, the shape of the shock-induced ΔV_m transient in the single myocyte simulation as documented by Cheng et al. (1999a) differed from that of the multicellular fiber simulations as obtained in both this study (Fig. 2 A) and a study preliminary to this research, in which both I_ep and I_a were added to the total ionic current as implemented by Cheng et al. (data not shown).

Comparison with experimental results in three-dimensional myocardial preparations

Experimental studies of three-dimensional ventricular preparations (Knisley et al., 1994; Zhou et al., 1995a; Fast et al., 2002) have reported that, for intermediate shock strengths (4–23 V/cm), both positive and negative ΔV_m were induced; at a given recording site, upon shock polarity reversal, the magnitude of the negative ΔV_m was about twice that of the positive ΔV_m. However, for very strong shocks (Fast et al., 2002), predominantly negative ΔV_m was observed regardless of shock polarity.

In the isolated rabbit heart preparation, Nikolski et al. (2004) recently documented positive ΔV_m transients, the shape of which was different from that in cultured myocyte strands (Gillis et al., 1996; Cheek et al., 2000; Fast et al., 2000; Fast and Cheek, 2002; Cheek and Fast, 2004). The investigators observed nonmonotonically-rising positive ΔV_m transients instead of rectangularly shaped transients for shocks that caused nonmonotonic rise in negative ΔV_m transient upon shock polarity reversal. Moreover, electroporation effects on the endocardium (Al-Khadra et al., 2000) and epicardium (Nikolski et al., 2004) were found to be independent of shock polarity unlike the findings in single myocyte and cultured myocyte strand studies (Knisley and Grant, 1995; Fast and Cheek, 2002; Cheek and Fast, 2004).

These differences in experimental findings are possibly due to differences in electrotonic interactions between regions of positive and negative ΔV_m arising from different microscopic tissue discontinuities (Fast et al., 2002; Hooks et al., 2002) or macroscopic fiber orientation (Trayanova et al., 1998; Knisley et al., 1999; Roth and Beaudoin, 2003) in the different experiments. Additionally, in the experiment by Fast et al. (2000), for shocks delivered during the action potential plateau, the shape of the positive ΔV_m transient at the cathodal edge changed significantly with the change in the width of the cultured myocyte strand, whereas the negative ΔV_m transient did not; this indicates that negative ΔV_m prevailed electrotonically over positive ΔV_m. Indeed, in preliminary simulations using various fiber lengths (data not shown), similar behavior was observed.

Limitations of the study

The model preparations in this study included horizontal fiber orientation only, which differs from that of cultured myocyte strands (Gillis et al., 1996; Cheek et al., 2000; Fast et al., 2000; Fast and Cheek, 2002; Cheek and Fast, 2004) and could alter, in some degree, the electrotonic interactions between opposite ends of the fiber. Moreover, we did not consider the effects of the three-dimensional myocardial structure with its heterogeneity and the conductive perfusing bath. Different shock waveforms and configurations of the shock electrodes were also not examined; any of these could alter the magnitude and distribution of virtual electrode polarization, and therefore modify the shock-induced ΔV_m asymmetry. In addition, we considered short-term tissue damage (electroporation) only with no consideration of long-term damage effects, such as the decrease in connexin 43 in the vicinity of the shock electrode (Sambelashvili et al., 2004). Experimental data, to which our simulations are compared, might also include important limitations, such as limited bandwidth of the recording systems due to low-pass filtering that could result in a change in the shape of the recorded V_m transients.

Although there is no experimental data to accurately describe the behavior of the various ionic channel blockers at ranges of V_m reached during strong electric shocks, we assumed that the behavior of these blockers remains the same as at physiological ranges of V_m.

The version of the ventricular action potential model utilized here (Luo and Rudy, 1994a,b; Zeng et al., 1995; Viswanathan et al., 1999; Faber and Rudy, 2000) does not include the transient outward K⁺ current (Dumaine et al., 1999) and the chloride current (I_Cl). It is well known that I_Cl does not contribute significantly to the action potential in the absence of adrenergic stimulation (Harvey et al., 1990); however, it remains unknown whether I_Cl plays a role in strong shock-induced ΔV_m. Further, the electroporation expression used (DeBruin and Krassowska, 1998) does not take into account the ion-specific current flow through the membrane pores (DeBruin and Krassowska, 1999; Ohuchi et al., 2002). Finally, the variation between species in repolarizing ionic currents (Varro et al., 1993; Lu et al., 2001) was not considered; it may lead to different tissue responses to electric shocks for different species. Despite these limitations, this study provides mechanistic insight into the asymmetry in both positive versus negative (strong) shock-induced ΔV_m and location of electroporation. Although further experiments are needed to confirm the ionic composition of I_a, the aLRd model appears nonetheless a useful tool in resolving discrepancies between experiments and simulations, and thus, in further elucidating the mechanisms of electrical fibrillation induction and defibrillation.