Structural Calorimetry of Main Transition of Supported DMPC Bilayers by Temperature-Controlled AFM

Abstract

Atomic force microscopy at high temperature resolution () provided a quantitative structural calorimetry of the transition from the fluid (L_α)- to the gel (P_β′)-phase of supported dimyristoylphosphatidylcholine bilayers. Besides a determination of the main transition temperature (T₀) and the van't Hoff transition enthalpy (ΔH_vH), the structural analysis in the nm-scale at T close to T₀ of the ripple phase allowed an experimental estimation of the area of cooperative units from small lipid domains. Thereby, the corresponding transition enthalpy (ΔH) of single molecules could be determined. The lipid organization and the corresponding parameters T₀ and ΔH_vH (ΔH) were modulated by heptanol or external Ca²⁺ and compared with physiological findings. The size of the cooperative unit was not significantly affected by the presence of 1 mM heptanol. The observed linear relationship of ΔH_vH and T₀ was discussed in terms of a change in heat capacity.

INTRODUCTION

It is well accepted that the specific lipid composition and their corresponding phase state in membranes play a crucial role for the activity of embedded membrane proteins. A prominent example represents the potassium channel KcsA (Williamson et al., 2003; Valiyaveetil et al., 2002). The question arises whether regulatory functions of specific agents on membrane proteins can be mediated by induced phase transitions of surrounding lipid domains rather than by binding to specific epitopes (de Kruijff, 1997). Support of this concept is given by the known dependence of protein kinase C on alcohol (Shen et al., 1999) or the finding that long chain alcohols like heptanol or octanol reversibly inhibit gap junctional coupling of neighboring cells (Somogyi and Kolb, 1988; Takens-Kwak et al., 1992). It could be proposed that the addition of hydrophobic components alters the phase state of lipid domains of the membrane which in turn could effect the functional properties of the embedded integral membrane proteins.

A large number of experimental and theoretical studies of thermally induced fluid-gel transitions in phospholipid bilayers have been carried out, using a variety of biophysical methods. A conceived compilation of thermodynamic properties of lipid phases can be found in Koynova and Caffrey (1998) and the associated database LIPIDAT. Scanning calorimetry is used as a direct method to reveal the thermodynamic properties of phase transition like transition temperatures and enthalpies (Hinz, 1972; Mabrey and Sturtevant, 1976; Mabrey et al., 1978). Preferentially the main transition between gel phase and fluid phase has been elucidated. The gel phase is often subdivided into the L_β′- and the P_β′-phases, whereby the latter precedes the first, when the lipid system is cooled down from the fluid L_α-phase. The P_β′-phase plays an emphasized role due to the regular surface pattern, which at first was described by Tardieu et al. (1973). This phase of the bilayer is characterized by a quasiperiodic undulation in one dimension which is called ripple phase. The phase was structurally investigated by electron microscopy preferentially using the freeze fracture technique (Verkleij et al., 1972; Copeland and McConnel, 1980; Meyer, 1996; Meyer et al., 1996), x-ray diffraction using synchrotron radiation (Tardieu et al., 1973; Stamatoff et al., 1982; Mattai et al., 1987; Matuoka et al., 1990, 1993, 1994; Hentschel and Rustichelli, 1991; Cunningham et al., 1998; Sun et al., 1996; Katsaras et al., 2000; Sengupta et al., 2003), or neutron scattering (Mortensen et al., 1988).

The P_β′-phase is subdivided into two substates which differ in their wavelength and shape of ripples as well as in the dependence on the cooling or heating history (Hatta et al., 1994; Matuoka et al., 1993; Meyer, 1996; Cunningham et al., 1998; Sengupta et al., 2003; Kaasgaard et al., 2003). The two substates are denoted as Λ- and Λ/2-ripples, because the ripple wavelength of both states differ by approximately a factor of 2 (Rüppel and Sackmann, 1983). The structure of Λ/2-ripples was studied by x-ray diffraction and scanning tunneling microscopy (STM) techniques. Electron density maps, which were calculated from x-ray diffraction data, indicate for Λ/2-ripples a sawtooth-like shape (Wack and Webb, 1989; Sun et al., 1996; Woodward and Zasadzinski, 1996; Meyer, 1996; Katsaras et al., 2000), whereas the Λ-ripples show a symmetric profile (Katsaras et al., 2000). More recently atomic force microscopy (AFM) was used to reveal information on the morphology of the P_β′-phase of bilayers made of phosphatidylcholines (Mou et al., 1994b; Czajkowsky et al., 1995; Leidy et al., 2002; Kaasgaard et al., 2003). This approach allows us to monitor structural changes of bilayers in buffered aqueous solutions close to real-time (Beckmann et al., 1998; Kolb et al., 1999; Dufrene and Lee, 2000; Giocondi et al., 2001; Tokumasu et al., 2002; Kaasgaard et al., 2003).

In this article the phase transition from the L_α- to P_β′-phase of dimyristoylphosphatidylcholine (DMPC) is studied at high temperature resolution () by AFM. The analysis of the topographies is performed at a lateral resolution in the nm-scale which allows a detailed study of the transition between Λ- and Λ/2-ripples. Besides the main transition temperature (T₀), the van't Hoff transition enthalpy (ΔH_vH) is determined. For the first time the size of cooperative units representing the collective behavior of lipid molecules could be derived from a specific image analysis. With the knowledge of the cooperative unit the enthalpy of transition of single molecules could be calculated from the van't Hoff enthalpy. The modulatory effect of heptanol and by Ca²⁺ in the imaging buffer on the caloric parameters is analyzed and compared with physiological findings. For the observed dependence of ΔH_vH (ΔH) on T₀ a nonvanishing change in heat capacity is introduced and discussed.

MATERIALS AND METHODS

Sample preparation

Supported bilayers were prepared by a vesicle fusion method as described previously (Kolb et al., 1999). 1,2-dimyristoyl-rac-glycero-3-phosphocholine was purchased from Sigma (Munich, Germany) and dissolved in chloroform (Roth, Karlsruhe, Germany). After removing the solvent by a rotary evaporator, the lipid was resuspended in buffer (5 mM K-HEPES at pH 7.2) at a concentration of 10 mg/ml. After dispersing the suspension by a vortex mixer (Model Sonifier VF2, Janke & Kunkel, Staufen, Germany) and ultrasonification in a bath (Model 1200E3, Branson Ultrasonics, Danbury, CT) for 30 min, the suspension was left at 4°C overnight. For the experiments the suspension was diluted 10-fold by an adsorption buffer (1 mM EDTA, 5 mM K-TRIS, pH 9). Freshly cleaved ruby muscovite mica (S & J Trading, Glen Oaks, NY) was glued to a sample holder and a drop of ∼20 μl of the vesicle suspension was placed on the mica surface. The sample holder was placed in a sealed container together with a reservoir of water and incubated at 37°C for ∼30 min. The sample was allowed to cool down to room temperature before removing the excess vesicle suspension. Without allowing the sample to dry the coated mica surface was flushed 3–5 times with the imaging buffer (50 mM KCl, 5 mM MgCl₂, 5 mM K-HEPES, pH 7.2) and mounted to the atomic force microscope (Nanoscope IIIa, Multimode, Veeco Instruments, Mannheim, Germany).

Temperature-controlled atomic force microscope

The atomic force microscope was modified as follows to adjust and to record on-line the temperature of the sample during image acquisition. The head module of the microscope, which houses the deflection detecting optics and electronics were equipped with low-cost Peltier modules (Conrad Elektronik, Hischau, Germany). The Peltier modules were controlled by a LabView System (National Instruments, Austin, TX). To avoid thermal drifts, the driving signal of the Peltier devices was generated by a closed-loop continuous software PI-controller whereby the error signal was delivered from a surface temperature sensor glued to the head module. The hot side of each Peltier device was connected to an aluminum block with a cylindrical cranial open chamber which was filled with water. In each cooling chamber a bar from copper was immersed in a way that the walls were not in contact with the bar. The two bars were fixed with a tripod and connected to an aluminum block, which was placed in an ice-cooled container. In this way the temperature of the hot side of the Peltier devices was kept at sufficiently low temperatures whereas substantial mechanical noise was avoided.

The sample temperature was monitored by a digital thermometer GMH 3230 (Greisinger, Regenstauf, Germany) equipped with a coated miniature probe (Physitemp IT23, Clifton, NJ). Because the viton-seal of the commercial fluid cell was not used, the small temperature probe could be placed directly into the fluid cell in close proximity of the sample surface and in direct contact to the imaging buffer.

Image acquisition and processing

All images were acquired in contact mode using Silicon-Nitride Olympus OMCL-PSA 400 tips with a spring constant of 0.02 N/m (Olympus, Tokyo, Japan) at a scan rate of ∼6 lines/s at minimal loading force. After adjusting the temperature to a new value the setup was allowed to equilibrate for ∼5–10 min until the thermal drift was well below 0.1 K/min.

The topographies were post-processed by a homemade software and the Film GIMP Image Processing System (movieEditor, Beverly Hills, CA). After adding the calibrated error signal images to the topographies, to produce more accurate topographies (Enders et al., 2001), which are in first-order independent of the actual settings of the feedback circuit of the microscope and the scanning speed, each scan line was flattened by subtracting the result of a polynomial fit up to the third order. In general, only those samples were considered for this fit that corresponded to nonelevated domains in the topographies. To remove high frequency noise, the topographies were processed by a Gaussian spatial filter (σ = 1.5, 21 × 21 matrix).

Height histograms were calculated using Film GIMP. For further description of image analysis, see Results.

To determine the size of the cooperative unit, a correlation difference image of two consecutive scans was needed (see Results). The drift vector between the two images in the x,y-plane was calculated by determination of the global maximum of the correlation coefficient function of the two topographical or deflection maps. The difference image was produced by subtracting the second topography from the first one, corrected by the drift vector. The correlation procedure is necessary to compensate for lateral drifts of the scanner, which can be caused by time-dependent temperature gradients. The derived image is called correlation difference image.

Three-dimensional rendering of images was performed using the software package dxopen (IBM, Armonk, NY). Data are given as mean ± SD.

RESULTS

Topography of supported DMPC bilayers in the fluid-crystalline and gel-phases

The topography of mica-supported DMPC bilayers is analyzed in aqueous solution as a function of temperature in contact mode. The imaging is started at temperatures above the main phase-transition of DMPC. At these temperatures the bilayer exhibits a smooth surface without defects within the height of a DMPC bilayer of ∼4.8 nm. A representative image is shown in Fig. 1 a. In the figure, which was recorded at 302.6 K, the membrane surface exhibits an irregular corrugated topography with height differences (peak to bottom) below ∼0.2 nm. At this temperature the DMPC bilayer can be considered to be in the fluid-crystalline- or L_α-phase (Koynova and Caffrey, 1998). The defect-free surface allows repeated scans of the same area without significant contamination of the tip. Before a detailed analysis for the stepwise change of topography during the transition from the fluid-crystalline- to the gel-phase is presented and analyzed, the topography of DMPC at low temperature (T = 295.5 K) is shown in Fig. 1 b and at higher magnification in Fig. 1 c. The bilayer surface exhibits the typical ripple structure. This characteristic structure can be attributed to the gel- or P_β′-phase. The height difference (peak to bottom) is ∼0.3 nm. The ripples run almost equidistant and form regular domains of 10–30 ripples in parallel to each other. From the corresponding Fourier transform of such domains a periodicity of 12.3 ± 0.3 nm is obtained. If a change in direction of the ripples is observed, it occurs predominantly at an angle of 118 ± 9°.

FIGURE 1.

Topography of a supported DMPC bilayer in fluid- (L_α) and gel-phase (P_β′). (a) Topography in L_α-phase at 302.6 K well above the main transition. (b and c) DMPC bilayer surface recorded at 295.5 K at different magnifications. In a the surface appears smooth with an undulating pattern of a height below 0.2 nm. Ripples in b and c are ordered and have a peak-to-bottom value of at least 0.3 nm. The mean distance between neighboring ripples is ∼12 nm. 256 lines per image were scanned with 512 samples per line.

Topography at temperatures of main transition

The image records are started at a temperature above the main transition from the L_α- to the P_β′-phase. The temperature is lowered stepwise and the bilayer surface is imaged respectively. Fig. 2 shows four representative images at temperatures of 297.0–296.1 K, which are within the temperature range of main transition. At the onset of main transition at 297.0 K (Fig. 2 a) the first ripples emerge out of the smooth bilayer surface, which are characteristic for the gel phase (compare Fig. 1 b). At a lower temperature, 296.7 K (Fig. 2 b), the ripple density increases visibly, until the surface becomes almost completely covered by ripples at 296.3 K (Fig. 2 c). Cooling the sample further by 0.2 K causes a sudden and significant change of density and profile of ripples (Fig. 2 d). The ripples are closer to each other and the periodicity of the ripples reflects now those already shown in Fig. 1 b. The profiles of the ripples are given in the insets of Fig. 2, c and d. As can be read from the insets, the corresponding wavelength is reduced by a factor of 2 which can be attributed to a change from the Λ-ripples to the Λ/2-ripples (Rüppel and Sackmann, 1983). The height of the ripples also appears to be significantly reduced. But for the reliability of this change it should be considered that the access of the tip to image the depressions in the nm-scale might be limited by the finite radius of the scanning tip which is of approximately the same order of magnitude.

FIGURE 2.

Topography of a DMPC bilayer at decreasing temperatures as indicated in a–d and the corresponding frequency histogram of height z (lower row). Comparison of c and d shows a transition from Λ- to Λ/2-ripples which is reflected in the corresponding ripple profiles (insets, c and d). The blue line in the frequency histograms indicates the threshold which separates the heights of the L_α- and P_β′-phases For clearer identification of Λ/2-ripples the contrast of d was enhanced. For further explanation, see text. Each image consists of 512 × 256 pixels.

Structural calorimetry of main transition by image analysis

From the acquired images the fraction of the scanned area presenting the P_β′-state of the bilayer () can be estimated. The frequency histogram of heights of the image is calculated, and a suitable threshold of the lower height level is selected to separate the smooth bilayer of the L_α-phase from the ripple structure of the P_β′-phase. Fig. 3 shows an example of this image analysis. The blue area represents the L_α-phase. The corresponding threshold is drawn as a vertical line in the height histogram (inset). The integral of histogram below this threshold reflects the area of L_α-phase, whereas the integral of the height histogram above the threshold corresponds to the area of bilayer in the P_β′-phase. The latter value divided by the total integral yields the fraction Because a high resolution is applied that allows us to identify individual ripples, the intermediate heights along their profile also contribute to the height histogram. Thereby, the height distributions appear to be widened and in many cases two separate Gaussian-like distributions cannot be easily discriminated especially for temperatures below the main transition (compare height distributions in Fig. 2). The derived relation 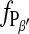as a function of temperature is given in Fig. 6. The data points, especially in the range of main transition, present the mean value of up to three analyzed images at approximately the same temperature within a resolution of 0.1 K.

FIGURE 3.

Post-processing of the topography of a supported DMPC bilayer. The image shows the bilayer at a temperature slightly below the main transition. After selecting a suitable height threshold separating the L_α- and P_β′-phases, the area that corresponds to the L_α-phase is blue. The inset shows the corresponding frequency histogram of heights z. Blue corresponds to the values below the threshold. The values corresponding to the P_β′-phase are in yellow.

FIGURE 6.

Fraction of P_β′-phase () as a function of temperature T. The data were recorded consecutively at increasing concentrations of heptanol and after washout, as indicated. In general, the data were derived by changing T in cooling direction. For the data denoted as 0 mM hept. (heating), the temperature direction was reversed at the lowest value of T. Thereafter 5 mM MgCl₂ was replaced by 5 mM CaCl₂ in the imaging buffer. The drawn curves represent a fit of Eq. 4 to the data. The corresponding values of T₀ and ΔH_vH are included in Table 1. For further details, see text.

For a theoretical description of main transition the two phases are assumed to be in thermodynamic equilibrium at the applied temperature.

If K is the equilibrium constant of the phase transition between the two phases,

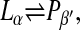(1)

it can be described by the relation

(2)

According to (Mabrey and Sturtevant, 1976) K can be described as a function of T by the integrated form of the van't Hoff equation,

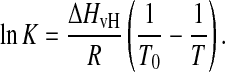(3)

ΔH_vH represents the van't Hoff transition enthalpy, R the gas constant, and T₀ the temperature at K = 1, where half of the bilayer is in P_β′-phase. T₀ is defined as the temperature of main transition. It should be noticed that in Eq. 3 the influence of a change of heat capacity at the transition is neglected (see Discussion). From Eqs. 2 and 3, can be expressed as a function of T,

(4)

Eq. 4 was used to describe the experimental data of Fig. 6, which yields as a result T₀ and ΔH_vH. The corresponding values are included in Table 1.

TABLE 1.

Main transition temperature (T₀) and enthalpy (ΔH, ΔH_vH)

Additives to imaging buffer	T0 (K)	ΔHvH (kJ mol−1)	ΔH (kJ mol−1)
0 mM heptanol	296.5	−2928	−15.0
1 mM heptanol	295.8	−4487	−23.0
2 mM heptanol	294.1	−6087	−31.2
3 mM heptanol	291.3	−8570	−44.0
0 mM hept., washout	296.7	−2439	−12.5
5 mM CaCl2	297.5	−2004	−10.3

T₀ and ΔH_vH were derived from a fit of the data given in Fig. 6 by Eq. 4. Using a cooperative unit n_c = 195 molecules (see text) ΔH of single molecules was calculated by Eq. 5.

Phase transition of DMPC bilayer in the presence of heptanol or Ca²⁺

The phase transition of a DMPC bilayer was analyzed after addition of the long chain alcohol heptanol at different concentration to the imaging buffer. For these experiments the heptanol-free imaging buffer was subsequently replaced by solutions containing 1 mM, 2 mM, and 3 mM heptanol. Without changing the tip or sample, the phase transition was monitored starting at temperatures above the main transition. The corresponding relationship 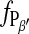versus temperature is included in Fig. 6. From a description of 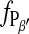vs. T by Eq. 4, the values of T₀ and ΔH_vH could be determined (Table 1). With increasing heptanol concentration T₀ decreases and ΔH_vH increases.

It can be read from Fig. 6 that the temperature-width of phase transition decreases with increasing heptanol concentration. Therefore, within the limit of temperature resolution of ∼0.1 K a comparison of Fig. 5, a and d, as well as of Fig. 5, b and e, shows that a transition from the Λ- to the Λ/2-ripples can be discriminated at lower heptanol concentration. The height of Λ-ripples decreased with increasing heptanol concentration (0 mM heptanol: 0.30 ± 0.05 nm (N = 21), 1 mM heptanol: 0.27 ± 0.05 nm (N = 9), and 2 mM heptanol: 0.18 ± 0.02 nm (N = 15)). But at 3 mM heptanol the phase transition is completed within a small temperature interval of ∼0.4 K, which did not allow a discrimination between Λ- and Λ/2-ripples. Fig. 5 c is recorded at 3 mM heptanol and 291.6 K and shows the L_α-phase and a few ripple-like structures. At 291.3 K the total area is already covered by Λ/2-ripples (Fig. 5 f). After washout of 3 mM heptanol the recorded phase transition (Fig. 6) closely resembles the behavior of the heptanol-free DMPC bilayer which can be seen from the derived values of T₀ and ΔH_vH (Table 1). This finding indicates an almost reversible effect of heptanol on the main transition.

FIGURE 5.

Topographies of a DMPC bilayer at heptanol concentrations of 1 mM (a and d), 2 mM (b and e), and 3 mM (c and f). The pairs of images were consecutively scanned. The upper row of images (a–c) shows the bilayer with Λ-ripples. d–f shows the corresponding images which were recorded thereafter at lower temperatures (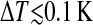). The pattern of the topography changed to Λ/2-ripples. Although the consecutively recorded images a and d as well as b and e were recorded virtually at constant temperature, it cannot be excluded that the temperature changes within the temperature resolution of 0.1 K during the recording time of ∼45 s per image. At 3 mM heptanol (c and f) the phase transition from L_α- to P_β′-phase is completed within ΔT = 0.3 K.

Besides a modification of the bilayer by heptanol, the water-bilayer interface was affected by replacing 5 mM MgCl₂ in the imaging buffer by 5 mM CaCl₂, which yielded a free Ca²⁺-concentration of 4 mM. The corresponding data are included in Fig. 6 and Table 1. The analysis of phase transition shows that T₀ increases by ∼0.8 K and ΔH_vH decreases significantly as compared to the control. Because the temperature-width of phase transition increased by the presence of Ca²⁺ (Fig. 6), Λ- and Λ/2-ripples could be discriminated (data not shown).

Cooperative unit n_c

It is known that the derivation of ΔH_vH strongly depends on the average number of interacting lipid molecules which transit from the L_α-phase to the P_β′-phase (Hinz, 1972). This number is noted as cooperative unit n_c. By correlation analysis, n_c could be determined from pairs of consecutive images. The images (Fig. 4, a and b) were obtained at a time difference of ∼3 min and a temperature decrease of 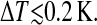Using a correlation algorithm to take into account a possible drift of the position of the scanned area in respect to the tip, the two images could be subtracted from each other. Fig. 4 c shows as a result elevated domains of newly emerged ripples and deeper domains corresponding to ripples which disappeared as well as unchanged lipid areas of intermediate height. For clearer presentation, Fig. 4 d shows the newly emerged ripples and the domains wherein ripples disappeared as different colors. A possible overestimation of the size of the respective domains by lateral aggregation was minimized by selecting pairs of images showing a lower density of domains. The analysis of n_c was performed on the basis of six difference images. The average number of domains per difference image was 164 for emerged domains and 119 for domains wherein ripples disappeared. The two types of domains, those of emerged ripples and of domains wherein ripples disappeared, had a mean area of 239 ± 103 nm² and 117 ± 19 nm², respectively. Both values should be considered as upper-limit. Assuming an average interfacial area of 0.6 nm² per lipid molecule of the bilayer (Kucerka et al., 2003; Nagle and Tristram-Nagle, 2000), cooperative units of 398 ± 172 and 195 ± 32 molecules were obtained, respectively. The two values are comparable within the experimental error. In both cases the size of the cooperative unit was not significantly affected by the presence of heptanol. Within the SD no tendency of a temperature dependence of the cooperative units was observed in the range of but a change of n_c at phase transition cannot be excluded.

FIGURE 4.

Determination of molecules (n_c) in a cooperative unit. a and b are two consecutively scanned images of the bilayer surface at two temperatures below T₀. a was recorded at |T − T₀| = 0.3 K and b was recorded at decreased temperature of 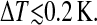After correction for a drift of the scanned area (see Materials and Methods) the difference of images a and b was calculated. The result is shown in c. The domains in d above suitably chosen height levels (threshold), the emerged ripples, are red, and domains below the corresponding threshold (domains wherein ripples disappeared) are blue. For clearer presentation the colored domains are superimposed with b and the result is shown in d. The topographies consist of 256 scan lines at 512 samples per line.

The larger density of domains of emerged ripples could lead to an overestimation of n_c (see above), therefore, n_c for domains wherein ripples disappeared was considered for the following.

Using the value of n_c = 195 molecules (see Discussion), the transition enthalpy of single lipid molecules ΔH could be calculated according to (Hinz, 1972)

(5)

The corresponding values of ΔH are included in Table 1.

DISCUSSION

A temperature-controlled atomic force microscope allows to monitor the different states of phase transition in lipid bilayers (Tokumasu et al., 2002; Kaasgaard et al., 2003). We developed a modified atomic force microscope with a temperature control of high accuracy (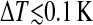), which was applied at a lateral resolution in the nm-range for image analysis of mica-supported DMPC bilayers. Besides the transition temperature (T₀), the van't Hoff transition enthalpy (H_vH) and the as-yet theoretically introduced cooperative unit could be derived from structural data. In addition, the analysis is applied to reveal the effect of the incorporation of the long chain alcohol heptanol on the main transition. Heptanol was used to elucidate the mechanism of electrical uncoupling of gap junctions by long chain alcohols (compare to Somogyi and Kolb, 1988). The results are compared with the effect of Ca²⁺ binding to the bilayer-water interface.

Structural properties of ripple phase

To prepare defect-free smooth DMPC-bilayer surfaces, the image analysis was started above T₀ in the L_α-phase. Cooling to temperatures below T₀ (Fig. 2) exhibited the characteristic topography of ripples as well as the transition from Λ- to Λ/2-ripples of P_β′-phase. Because unilamellar supported bilayers do not exhibit a ripple-like topography (Fang and Yang, 1996; Leidy et al., 2002), we suppose that the applied vesicle fusion method yields defect-free multilamellar bilayers. The observed Λ/2-ripple structure is characterized by a wavelength of 12.3 nm, which is in reasonable agreement with the results of STM (10.7 nm; Woodward and Zasadzinski, 1996), transmission electron microscopy (11 nm; Woodward and Zasadzinski, 1996), x-ray diffraction (12 nm; Janiak et al., 1976, 1979); or 14.3 nm (Wack and Webb, 1989) and AFM (12.5 nm; Leidy et al., 2002). The observed change of direction of ripple structures by ∼118° is comparable to the results of Mou et al. (1994b).

The observed ripple amplitude of ∼0.3 nm is comparable with a value of 0.2 nm as derived from electron density maps (Sengupta et al., 1999), but application of STM yielded 2.4 nm (Woodward and Zasadzinski, 1996).

Structure of the bilayer at main transition

An important structural feature of the transition from the L_α- to P_β′-phase is the gradual appearance of ripples if the bilayer is cooled down (Fig. 2). The ripples are not as ordered as reported in Leidy et al. (2002) and Kaasgaard et al. (2003). However, it has to be taken into account that the main transition is passed in cooling direction in our experiments. Cooling the sample to a temperature of 296.2 K leads to a sudden change of the morphology from Λ- to Λ/2-ripples (see also Fig. 1 b). The profiles of the two ripple morphologies (Fig. 2) exhibit that the width of Λ/2-ripples is approximately one-half the width of Λ-ripples and that the height of Λ/2-ripples is significantly reduced. This is in accordance with the results of Kaasgaard et al. (2003).

If the sample is heated again, the Λ/2-ripples melt directly into L_α-phase without converting to Λ-ripples (data not shown) (compare Hatta et al., 1994; Matuoka et al., 1993; Meyer, 1996; Cunningham et al., 1998; Sengupta et al., 2003; Kaasgaard et al., 2003). The data indicate that Λ-ripples are only generated during the cooling process.

Structural calorimetry and estimation of the cooperative unit n_c

For the performed structural calorimetry it can be assumed that the sample in fluid is close to thermodynamic equilibrium, because the integral temperature rate was well below 0.1 K/min (Mabrey and Sturtevant, 1976).

The image analysis is based on the derivation of suitable frequency histograms of heights as introduced by Tokumasu et al. (2002). Tokumasu and co-workers analyzed supported unilamellar DMPC-patches by an atomic force microscope at μm-scale, which was placed in a temperature-controlled chamber. In the present experiments the upper surface of multilamellar bilayer was analyzed at nm-resolution and the image analysis was focused to T close to T₀.

The obtained value of T₀ = 296.5 K (Fig. 6, Table 1) for DMPC-bilayers is in suitable agreement with values derived from differential scanning calorimetry (Koynova and Caffrey, 1998). The van't Hoff transition enthalpy ΔH_vH of ∼2500 kJ/mol could be determined from Fig. 6 as well. By use of differential scanning calorimetry ΔH_vH values of 35,650 ± 2400 kJ/mol (Sturtevant, 1998), 7456 kJ/mol (Mabrey and Sturtevant, 1976), and 5240 ± 1200 kJ/mol (Hinz, 1972) were reported. But differential scanning calorimetry is applied to vesicle suspensions whereas for image analysis supported planar bilayers are used. It is known that the vesicle diameter also influences the enthalpy of phase transition. Such an influence has been proposed from measurements of the heat capacity (Nagano et al., 1995). Therefore it appears likely that the different values of ΔH_vH could be related to the different geometry of the lipid system under investigation. It has to be noticed that ΔH_vH was determined using the classical van't Hoff equation (Eq. 3). But, the general validity of the van't Hoff equation was questioned (Weber, 1995b) and has been controversially discussed (Holtzer, 1995; Ragone and Colonna, 1995; Weber, 1995a, 1996a,b; Ross, 1996). Weber (1995b) suggested that the different values of the van't Hoff and the calorimetric (true) reaction enthalpy are caused by neglecting a temperature dependence of enthalpy and entropy. The magnitude of the difference will be estimated in the following.

Due to the lack of detailed knowledge about the involved intermolecular interactions, Weber (1995b) describes the temperature dependence by a constant number of intermolecular bonds of the reactants of homogeneous energy E. But a cooperativity is not considered. These bonds are thermally affected during the reaction with an average probability p of transient bond breakage 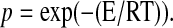Koynova and Caffrey (1998) determined an average calorimetric transition enthalpy of ∼25 kJ/mol for DMPC. If the number of bonds per DMPC molecule ranges from a minimal value of 1–28 (one bond for each CH₂-group of DMPC), E would be in the range of 0.9–25 kJ/mol. Using the formalism of Weber (1995b) the structurally determined values of ΔH_vH (Table 1) could be biased by values in the range of −0.5–14 kJ/mol and possibly account for the difference mentioned above.

For comparison of the structurally derived transition enthalpy of single molecules ΔH_vH with the calorimetric transition enthalpy, the cooperative unit n_c is introduced (see Eq. 5; see also Hinz, 1972). It is proposed that n_c can be estimated from structural data at the temperature range of phase transition by the number of interacting molecules.

The corresponding data were obtained from the difference of pairs of consecutive images (Fig. 4), recorded at approximately the same temperature (see below). The representative Fig. 4 indicates that the molecules of a cooperative unit are organized in small lipid domains. For the two types of domains, emerged ripples and domains wherein ripples disappeared and cooperative units were obtained, respectively, of 398 ± 172 and 195 ± 32 molecules. The larger mean value of n_c for emerged ripples could be caused by the fact that the phase transition (Eq. 1) of the bilayer is not analyzed at true equilibrium. Probably due to the ongoing cooling process of <0.1 K/min the equilibrium is shifted to the P_β′-phase. Such a shift could cause the observed higher density of domains appearing in the P_β′-phase than disappearing from L_α-phase yielding virtually larger domains for the P_β′-phase. A possible dependence of n_c on temperature and/or the phase state cannot be excluded. According to this consideration, a value of n_c = 195 molecules is assumed for the further. The value n_c is of the order of magnitude as theoretically derived (100 ± 50, Hinz, 1972; 330, Mabrey and Sturtevant, 1976; 1720 ± 120, Sturtevant, 1998). Using Eq. 5 a transition enthalpy for single molecules of ΔH = 15.0 kJ/mol is obtained. This value is lower than the average value ΔH = 25.1 ± 10.1 kJ/mol as mainly determined by differential scanning calorimetry (Koynova and Caffrey, 1998), but comparable within the standard deviation.

Effect of heptanol and Ca²⁺ on main transition

At increasing concentration heptanol shifts T₀ to lower values (Table 1). This is in accordance with observations, that alcohols and alcanes (McIntosh et al., 1980) of lower chain length, compared to the acyl chain of lipid, reduce T₀ (Löbbecke and Cevc, 1995; Eliasz et al., 1976). A heptanol-mediated structural change by interdigitation can be ruled out at these low concentrations (Rowe and Campion, 1994). Furthermore, interdigitation should lead to a significant reduction in membrane thickness for the gel phase (Mou et al., 1994a), which was not observed in the experiments.

It is proposed that a decrease of T₀ is responsible for the known regulatory influence of heptanol on the gating of gap junctional coupling. This assumption is supported by the observation that gap junctional coupling is blocked by heptanol or octanol concentrations as low as 1 mM (Somogyi and Kolb, 1988; Takens-Kwak et al., 1992). At this concentration T₀ is reduced by ∼0.7 K (Table 1). Furthermore, the washout of heptanol leads to values of T₀ and ΔH_vH as observed in the absence of heptanol (Table 1). This reversibility is consistent with electrophysiological results, which show that heptanol- or octanol-induced gap junctional uncoupling is reversible in the minute range (Somogyi and Kolb, 1988; Takens-Kwak et al., 1992). Therefore it is proposed that heptanol fluidizes the lipid bilayer adjacent to the head-to-head associated cell-to-cell channels of neighboring cells forming the gap junctional coupling. The observed fluidization of the lipid bilayers could cause closure of the cell-to-cell channels of gap junctions.

After replacement of Mg²⁺ by Ca²⁺ in the imaging buffer an opposite effect is observed on the shift of T₀, which is in agreement with earlier results (Chapman et al., 1977; Sturtevant, 1998). It has been reported that divalent cations Ca²⁺-ions and Mg²⁺-ions bind to the membrane surface of negatively charged and neutral lipids like DMPC, changing the surface potential (Altenbach and Seelig, 1984), the headgroup orientation (Seelig, 1990), and the dipole potential (Clarke and Lüpfert, 1999). Thereby, Ca²⁺ modifies the hydration shell of the headgroup region of the bilayer more effectively according to the Hofmeister series (Chapman et al., 1977). This might explain why Ca²⁺-ions shift the phase-transition temperature compared to Mg²⁺-ions.

Dependence of ΔH on T₀

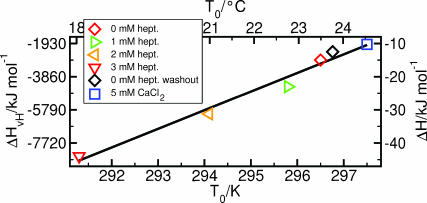
The transition enthalpies ΔH and ΔH_vH show a significant dependence on the concentration of heptanol and on the presence of Ca²⁺-ions. Ca²⁺ leads to a decrease of ΔH (increase of T₀), whereas heptanol increases ΔH (decrease of T₀, Fig. 7).

FIGURE 7.

Transition enthalpy (ΔH) and van't Hoff transition enthalpy (H_vH) as functions of T₀. ΔH, H_vH, and T₀ are given in Table 1. For further explanation, see Discussion.

To explain the observed dependence of transition enthalpy on T₀, a possible heat-capacity change ΔC_p at the transition from L_α- to P_β′-phase is considered. The approach of Naghibi et al. (1995) is based on the well-known equation

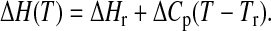(6)

T_r denotes the arbitrary chosen reference temperature and ΔH_r the corresponding transition enthalpy. Taking into account the number of molecules n_c in a cooperative unit as well as Eq. 5, Eq. 3 can be expressed as

(7)

ΔH₀ represents the transition enthalpy at the reference temperature, which is chosen to be T₀. Eq. 7 represents an obvious improvement of the classical van't Hoff equation. But, as already pointed out by Chaires (1997) this approach results in an ill-posed fitting problem, since the phase transitions of Fig. 6 are completed within a narrow temperature range and therefore the shape of the transition curve is not significantly affected by the contribution of the last term of Eq. 7.

Eq. 6 indicates that ΔH depends linearly on T₀ due to a nonvanishing value of ΔC_p. If Eq. 6 is applied to the data of Fig. 7, ΔC_p = 5.6 ± 0.4 kJ/(mol K) is derived. It is proposed that a change of ΔH_vH (ΔH) by heptanol and Ca²⁺-ions is a consequence of a nonvanishing value of ΔC_p and a shift of T₀. A similar relationship of transition enthalpy and transition temperatures with slopes of the same order can be derived from Table 1 in Sturtevant (1998) or the inset of Fig. 1 in Mabrey and Sturtevant (1976), but a contribution of ΔC_p at the main transition was not considered.

Further studies are necessary to evaluate whether the size of observed domains of emerged ripples as well as of domains wherein ripples disappeared change phase at transition. A change could indicate a temperature-dependent cooperativity of lipid molecules in a leaflet of a bilayer.