The Force Exerted by a Muscle Cross-Bridge Depends Directly on the Strength of the Actomyosin Bond

Abstract

Myosin produces force in a cyclic interaction, which involves alternate tight binding to actin and to ATP. We have investigated the energetics associated with force production by measuring the force generated by skinned muscle fibers as the strength of the actomyosin bond is changed. We varied the strength of the actomyosin bond by addition of a polymer that promotes protein-protein association or by changing temperature or ionic strength. We estimated the free energy available to generate force by measuring isometric tension, as the free energy of the states that precede the working stroke are lowered with increasing phosphate. We found that the free energy available to generate force and the force per attached cross-bridge at low [Pi] were both proportional to the free energy available from the formation of the actomyosin bond. We conclude that the formation of the actomyosin bond is involved in providing the free energy driving the production of isometric tension and mechanical work. Because the binding of myosin to actin is an endothermic, entropically driven reaction, work must be performed by a “thermal ratchet” in which a thermal fluctuation in Brownian motion is captured by formation of the actomyosin bond.

INTRODUCTION

The contraction of muscle involves a relative translation of myosin and actin filaments, powered by the heads of myosin (S1), which extend out from the myosin filament, bind to an actin filament, and execute a working stroke in a cyclic manner (Goldman, 1987; Cooke, 1997; Holmes, 1997; Geeves and Holmes, 1999). The structural changes that produce this working stroke and the energetic changes that drive them are the focus of intense investigation. S1 is composed of a large globular catalytic domain, which contains sites for binding both actin and nucleotide, and the light chain (LC) domain, which connects the catalytic domain to the core of the myosin filament. A variety of structural and biochemical results have led to the currently popular hypothesis that the catalytic domain of myosin initially attaches weakly to actin. Subsequent conformational changes in this domain would result in tight binding to actin and a rotation of the LC domain, which would then act as a lever arm to produce force and generate mechanical work (Rayment et al., 1993; Irving et al., 1995; Uyeda et al., 1996; Holmes, 1997; Dominguez et al., 1998; Hopkins et al., 1998; Geeves and Holmes, 1999; Forkey et al., 2003). At the end of the working stroke the myosin is detached from actin by the binding of ATP. The ATP is then hydrolyzed when the myosin is either weakly attached to actin or is detached (Lymn and Taylor, 1971).

To generate force and mechanical work, a myosin head must be attached to actin in a state in which the Gibbs free energy decreases as the actin traverses through some distance, known as the “working stroke.” The amount of mechanical work that can be performed in these states is equal to the change in the Gibbs free energy that occurs in them (for review, see Eisenberg et al., 1980). In this article we investigate the extent of the gradient in free energy that generates force in isometric fibers, but we assume that the same gradients also produce mechanical work during shortening.

Mechanical measurements have shown that force is generated by some compliant element within the actomyosin complex (Huxley and Simmons, 1971). This element has been stretched or bent, trapped in this distorted high-energy state and then released during the working stroke to generate displacement. The force and mechanical work generated in the power stroke is thus provided by this distorted compliant element. How is the energy of ATP hydrolysis used to produce a distorted compliant element? Hydrolysis of the nucleotide on myosin is thought to result in a reorientation of the LC domain relative to the catalytic domain, believed to be a reversal of the conformational changes that lead to force generation (Holmes, 1997; Dominguez et al., 1998). One hypothesis is that a transiently stable conformation of the myosin head, produced during the hydrolysis of ATP, acts as a distorted compliant element that is subsequently released to provide the energy required to drive the working stroke (Huxley and Simmons, 1971). Alternatively the formation of the actomyosin interface, which occurs during the working stroke, liberates more than 30 kJ/mole of free energy (Smith et al., 1984; Rayment et al., 1993; Kurzawa and Geeves, 1996). This is sufficient energy to produce the working stroke, and the high efficiency of muscle would require that a major portion of it is used in performing useful work. It is reasonable to assume that this energy is used to stabilize a distorted compliant element that is subsequently released during the working stroke. The assumption that this energy is used to generate force and produce work has been a major tenet of many theoretical models of the actomyosin interaction (Huxley, 1957; Eisenberg et al., 1980; Pate and Cooke, 1989b), but this assumption has not been previously verified in a quantitative manner.

To investigate the source of free energy leading to force production, we have studied the isometric force generated by skinned skeletal muscle fibers as a function of the strength of the actomyosin bond. The strength of the actomyosin bond in the absence of nucleotides increases with higher temperatures and lower ionic strength and has been determined as a function of both (Highsmith, 1977; Kurzawa and Geeves, 1996). Thus we varied the strength of the actomyosin bond by varying the temperature, the ionic strength, and the concentration of a polymer that promotes protein-protein interaction. Large polymers are excluded from a region surrounding a protein providing an entropic term known as steric exclusion, which favors protein-protein association (Parsegian et al., 1986; Bhat and Timasheff, 1992). One such polymer, polyethylene glycol, molecular weight 4000 (PEG-4000), has been used to potentiate the actomyosin interaction in solution (Chinn et al., 2000). This concentration of PEG also simulates the molecular crowding occurring in vivo (Minton, 2001).

Our previous work has shown that the relationship between force and log[Pi] probes the energetics of force generation (Pate and Cooke, 1989a; Pate et. al., 1998). Following this approach we determined the amount of free energy available to drive force generation by measuring the decrease in force induced by increasing concentrations of phosphate (Pi). In addition we used the slope of the force-log[Pi] relation to estimate the relative numbers of force-generating heads. We measured these parameters in skinned fast skeletal muscle fibers under a variety of conditions that alter the strength of the actomyosin bond. We found that the free energy driving force generation is directly proportional to the strength of the actomyosin bond. In addition, we found that the force generated at low phosphate, normalized by the slope of the force-log[Pi] relation, is also directly proportional to the strength of the actomyosin bond. Both of these results lead to the conclusion that the formation of the actomyosin bond is involved in providing the energy driving the production of force.

METHODS

Measurement of fiber mechanics

Rabbit psoas fibers were harvested and chemically skinned as described previously (Cooke et al., 1988). For mechanical experiments, single fibers were dissected from a bundle of fibers and mounted in a well between a solid-state force transducer and a rapid motor for changing fiber length.

Setup 1

The apparatus, used for all measurements at 2–15°C, has been described more fully in Cooke et al. (1988). The apparatus had two wells to hold solutions, and fibers could be rapidly switched between them in ∼1 s. Data were obtained by protocols described by Chinn et al. (2000). Briefly, the fiber was first immersed in a relaxing solution for ∼5 min to allow complete perfusion of nucleotides and proteins such as creatine kinase. During that time, the fiber's diameter was measured. The fiber was then switched to an activating solution in the other well, and mechanical measurements were made within 20–30 s. After measurements were taken, the fiber was returned to the relaxing solution and the solution in well 2 was replaced by the appropriate experimental buffer. Mechanical measurements were repeated and the fiber returned to the relaxing solution. The solutions in well 2 were changed again and mechanical measurements were repeated under control conditions. The effect of an experimental condition, e.g., PEG, ionic strength, or Pi, was then calculated as the percentage change in the presence of ligand relative to the average of the two control experiments. For half of the experiments, the order was reversed so that the mechanical measurements were made first and third in the presence of PEG and second under control conditions.

Setup 2

Another apparatus was developed that allowed for rapid translation of the mounted fiber between three wells. Due to the ease and rapidity of transferring the fiber between solutions, this apparatus was used for all of the measurements made at 30°C. Three Peltier units were mounted on an aluminum block with drops of solution, 170 μl each, held between the top of the Peltier and a thin glass coverslip. The temperatures for the three Peltier units could be set independently in a range of 2–40°C. The block could be translated on the horizontal plane (right and left) in relation to the fiber, which was held stationary between a force transducer and a motor arm. A modification on the existing software allowed for rapid data collection (10 s⁻¹) during the 2 s in the high-temperature well. The fiber was activated at a low temperature (5 or 10°C), where the fiber sarcomere arrangement is very stable, allowed to reach a plateau of isometric tension, and then rapidly translated to a high-temperature well (30°C), also with activating solution, where force reached its new maximum in 100–300 ms. Force was monitored for 2 s and the fiber returned to a cold relaxing solution. Solutions in the wells could be changed in a manner similar to that used for setup 1. The advantage of setup 2 was that it allowed us to perform rapid temperature jumps with high reproducibility of force at 30°C not previously available using setup 1.

Solutions

The basic rigor buffer contained 120 mM KAc (potassium acetate), 5 mM MgCl₂, 1 mM EGTA, and 50 mM 3-(N-morpholino)propanesulfonic acid (MOPS), pH 7. A relaxing solution was achieved by addition of 20 mM creatine phosphate, 1 mg/ml creatine kinase, and 4 mM ATP. The ionic strength of the standard relaxing solution was ∼0.19 M. Maximal activation was achieved by addition of 1.1 mM CaCl₂ to attain free pCa of 4.3, based on the calculations of Patton et al. (2004) and our own calculations. In the presence of high levels of Pi, it was necessary to increase CaCl₂ by a small amount to achieve full activation. Additional buffers were made with the addition of 5% of PEG-4000 (wt/vol). Data >1 mM [Pi] were obtained by addition of Pi, keeping ionic strength constant by varying the concentration of KAc as described by Pate et al. (1998). Lower concentrations of P_i were obtained using the enzyme nucleoside phosphorylase (NP, 100–200 units/ml) and 8 mM 7-methylguanosine, to serve as a “phosphate mop” to reduce the intrafiber Pi concentration (Webb, 1992; Brune et al., 1994), following the protocols of Pate et al. (1998). The internal level of Pi, which is determined by enzymatic reactions and by diffusion, was estimated using the calculations of Pate et al. (1998). In some of these experiments, the fibers were split, producing diameters of ∼25–30 microns. The split fibers have still lower internal concentrations of Pi, due to faster diffusion of Pi out of the fiber.

Data reduction

The force for each fiber was expressed in mN mm⁻². In some instances, force data were averaged and expressed as mean (± SE), n = 3–10, per condition at a specific [Pi]. Fits (with 95% confidence intervals) to the force-log[Pi] relationships were obtained using Eq. 1 (see Appendix), derived by Pate and Cooke (1989a).

RESULTS

Fiber tension as a function of phosphate for various conditions

For measurements at 2, 10, and 15°C the experimental setup 1 was used. Fibers were mounted between a force transducer and a fast motor, equilibrated in a relaxing solution for 5 min. They were transferred to an activating solution where the isometric tension was measured after force had reached a stable value. The fiber was then returned to the relaxing solution and subsequently reactivated in another solution with a different composition. When titrating force with phosphate, three to five different concentrations of phosphate may be measured, with the last condition the same as the first to monitor fiber deterioration. In this fashion, force was measured as a function of Pi over a large range, as shown in Figs. 1–4.

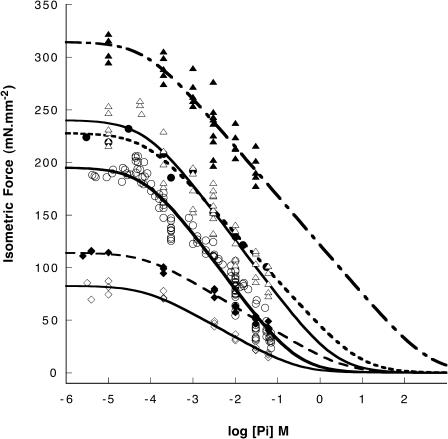
FIGURE 1.

Isometric force of maximally activated psoas muscle fibers is shown as a function of log[Pi] for three temperatures, 2°C (diamonds), 10°C (circles), 15°C (triangles), with or without PEG-4000 (filled or empty symbols, respectively). The lines are fits to the data using Eq. 1, providing estimates of the amount of free energy involved in force-generating states as described in the text. Some data at 10°C are reproduced from Chinn, et al. (2000).

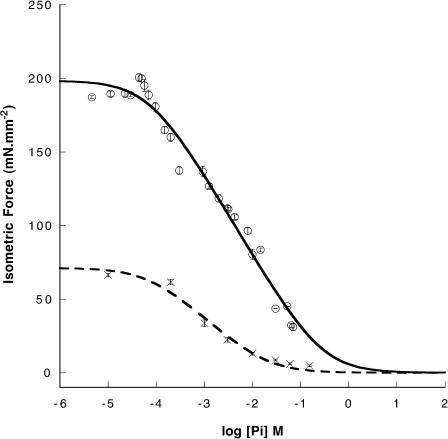
FIGURE 2.

Isometric force is shown as a function of log[Pi] for two values of the ionic strength, 230 mM (circles) or 400 mM (crosses) at 10°C. Values are shown as mean ± SE; n = 3–10. The ionic strength was raised by addition of KCl. The lines are fits to the data using Eq. 1, as described in the text.

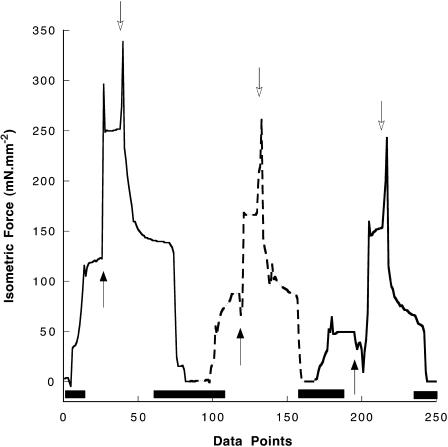
FIGURE 3.

Isometric force traces are shown for one fiber, as the temperature is jumped from 10°C to 30°C (black arrows) and back to 10°C (white arrows), at three different values of [Pi], 3 mM (left trace), 10 mM (middle trace), and 30 mM Pi (right trace). The fiber is initially in a relaxing solution. It is activated at 10°C in 3 mM [Pi], and at the first black arrow it is transferred to 30°C. At the first white arrow it is transferred back to 10°C and then relaxed. It remains relaxed for several minutes. The process is then repeated for 10 mM [Pi], and then again for 30 mM [Pi]. For experimental protocol refer to Methods. Data were collected with setup 2. Data collection was 1 s⁻¹ during the time denoted by the black bars on the x axis and 10 s⁻¹ otherwise.

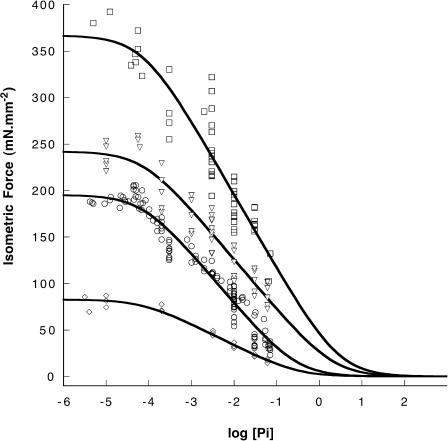
FIGURE 4.

Isometric force is shown as a function of log[Pi] for four values of temperature: 2°C (diamonds), 10 °C (circles), 15°C (triangles), and 30°C (rectangles). Data at 30°C were obtained as shown in Fig. 3. The data at 2 and 10°C are the same as in Fig. 1. The solid lines are fits to the data using Eq. 1, as described in the text.

All of the force-log[Pi] relationships were generally similar. Force was constant for a [Pi] < ∼100 μM. Above this concentration force declined linearly with force-log[Pi] relationship approaching zero at a value that varied with conditions. As shown in Figs. 1 and 4, the force at low Pi concentrations was greater in conditions that favored stronger protein-protein interaction: higher temperatures, lower ionic strength, and the presence of 5% PEG-4000. The slope of the force-log[Pi] relation in the region of linear force decline also varied with conditions, becoming steeper with lower ionic strength and with increasing temperature from 2 to 30°C (but not really different between 10 and 15°C). However, the slope was virtually unchanged by addition of PEG. The slope can be related to the fraction of myosin heads generating tension, as described in the Discussion and previously by Pate and Cooke (1989a). The addition of PEG-4000 generated a constant additive increase in the force-log[Pi] relationship at 2, 10, and 15°C, shown in Fig. 1. The data at 10°C are similar to those seen previously (Chinn et al., 2000). The tension obtained at low Pi and the range of Pi required to titrate force from maximum to zero both increased with temperature or with addition of PEG. The slope of the linear region of the curve also generally increased with increasing temperature but not with addition of PEG. The increase in slope with temperature indicates that the number of force-generating cross-bridges is greater at higher temperatures (see Discussion).

Additional titrations were made at an ionic strength of 400 mM. Although prolonged incubation of the fibers in solutions with these higher ionic strengths irreversibly inhibited tension, the short incubations required to obtain five or more values of tension had no permanent effect, as observed previously (Seow and Ford, 1993; Iwamoto, 2000). Increased ionic strength decreased the isometric force production at low phosphate and decreased the slope of the force-log[Pi] relationship in the region of linear decrease, as shown in Fig. 2.

Fiber mechanics were measured at four different temperatures, 2, 10, 15, and 30°C. Data at 30°C were obtained by temperature jumps in which fibers were first activated at 10°C, and then rapidly switched to the higher temperature for ∼2 s using the experimental setup 2. [Pi] could be changed and the measurements repeated. Force as a function of temperature is shown for such an experiment in Fig. 3. The dependence of force on log[Pi] for the four temperatures is shown in Fig. 4. Our data show that as temperature is raised, force increases and the slope of the force-log[Pi] relationship also increases The greater slope indicates that more myosin heads are generating tension. The increase with temperature is steeper between 2 and 10°C than between 10 and 30°C, which may be due to a “saturation” of the population of force-generating myosin heads with increasing temperature.

Measuring the free energy involved in force production

There are two points where the force-log[Pi] relationship deviates from linearity with a well-defined change in slope, one at a low value of [Pi] where the force first begins to decrease, and the other at the point where force approaches zero. At the lower temperatures or higher ionic strengths the force could be almost completely inhibited by high phosphate. For the other conditions the point where force approaches zero was determined by the fit to Eq. 1, as described below. The difference in the two concentrations, defining the range of phosphate concentrations required to inhibit force completely, also varied with the conditions. The range became greater with conditions that favored stronger protein-protein interactions, as described above. As shown previously and described in the Discussion, the range of Pi concentrations required to titrate force from its maximum value to zero allows one to estimate the free energy available to drive force production (Pate and Cooke, 1989a). This can be made more quantitative by analysis of a simple model, shown in Fig. 8 A (see Fig. 8). Myosin heads attach to actin at the beginning of the working stroke with a high free energy, G₂. Cross-bridges can remain attached to actin until they reach the end of the working stroke, where they have a lower free energy, G₁. The difference between G₁ and G₂ represents the free energy available in the working stroke to perform mechanical work, and also defines the gradient in free energy that generates force in isometric conditions. The values of the two parameters, G₁ and G₂, can be determined by the fit of an equation derived previously (Pate and Cooke, 1989a) and described later (Eq. 1).

FIGURE 8.

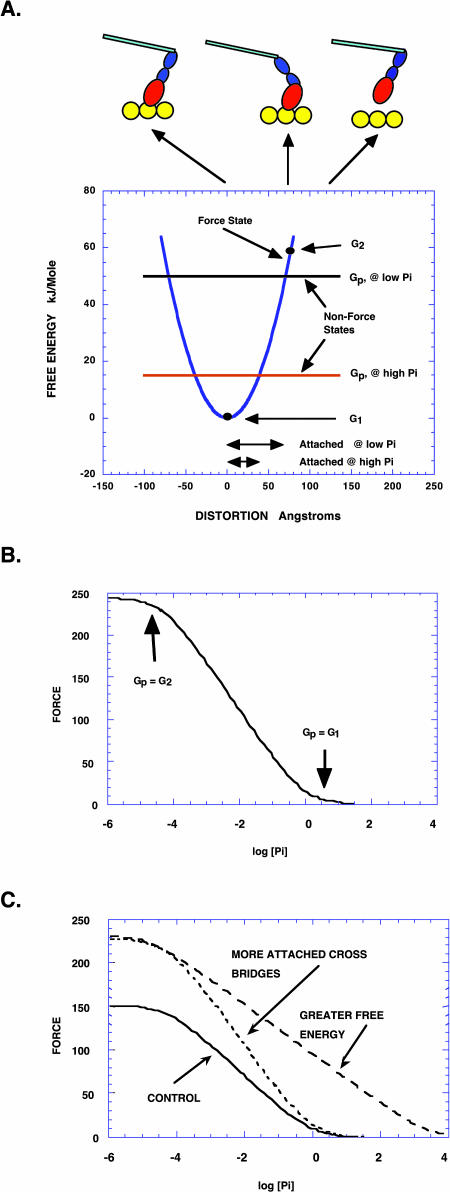
Analysis of the model leading to an interpretation of force-log[Pi] relationships. (A) The free energies of a simple two-state model are shown as a function of the distortion x. The distortion x describes the position of an actin binding site relative to the myosin head. In the force state the myosin head is attached to actin. The generation of force requires that this state has a gradient in free energy as a function of x, as is shown by the blue parabola. A myosin head can make the transition into this state by attaching to actin. The highest free energy at which this transition can occur is at G₂, which thus defines the highest free energy available in the force-generating states. This defines the beginning of the working stroke. The lowest free energy is at G₁, which defines the end of the working stroke. In the nonforce state, myosin heads are detached from actin, are thus not generating force, and have a free energy that is independent of x. Because this state occurs before Pi release the free energy of this state, G_p, varies with [Pi]. As Pi increases the free energy of the nonforce state decreases, as shown for two examples, one with low and one with high [Pi], indicated by the black and red horizontal lines respectively. The inhibition of force by Pi occurs because the force-generating states with free energy greater than G_p are not populated. Force will thus begin to be inhibited as the energy of the nonforce state approaches the actomyosin force-generating state with the highest energy, G₂; and the inhibition will increase with increasing [Pi], with force approaching zero as G_p approaches the actomyosin force-generating state with the lowest free energy, G₁. This relationship can be made more quantitative by integrating over the distribution of cross-bridges leading to Eq. 1. The arrows shown at the bottom indicate the range of distortion over which cross-bridges are attached for low and high [Pi]. As shown, the power stroke at low Pi would begin at a distortion of ∼70 Å and end at 0 Å. The attachment rate, and thus the population of attached cross-bridges in the negative force region, are very low, as has been assumed by all theories, starting with that presented by Huxley (1957). (B) The force versus log[Pi] relationship is shown schematically with the two points defining G₁ and G₂ indicated. (C) The force-log[Pi] relationship responds differently to conditions that increase force by potentiating the number of force-generating cross-bridges and to conditions that potentiate the force per attached cross-bridge. The relationship in a control condition is shown by the solid line. If the number of force-generating cross-bridges increases the control relationship is multiplied by a constant, shown by the dashed curve. If the force per attached cross-bridge increases, the range of Pi required to titrate force from its maximum value to zero increases, as shown by the curve with longer dashes.

Estimating the free energy available from the formation of the actomyosin bond

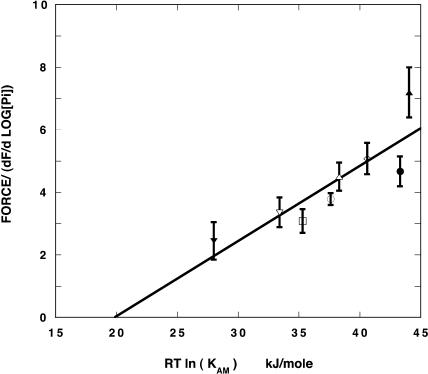
During each force-generating event the myosin head forms a tight bond with actin. Bond formation involves first the formation of a weaker bond, followed by the release of Pi and a transition to a stronger bond. Following the release of ADP the bond reaches its greatest strength in the rigor bond. Our hypothesis is that the free energy driving force production comes from the formation of these bonds between actin and the myosin head. The greatest energy would be released by formation of the strongest bond, the rigor bond. Thus we have related our data on fiber mechanics to the strength of this bond. The free energy available from the formation of the actin-myosin rigor bond depends both on the affinity constant of the reaction and on the concentrations of the products and reactants in the steps involving attachment or detachment from actin. The affinity constant of a myosin head for actin in the absence of nucleotides has been determined by a number of workers. Data for variation of the rigor bond affinity with ionic strength were taken from Kurzawa and Geeves (1996), for variation with temperature from Highsmith (1977), and for variation with PEG from Chinn et al. (2000). Assuming that the concentrations of the reactants and products do not vary by much as conditions change, the free energy for the different conditions will be proportional to RT ln(K_AM), where K_AM is the affinity constant for the binding of a myosin head to actin, R stands for the gas constant per mole, T is absolute temperature, and RT ln(K_AM) is expressed in kJ/mole. In Figs. 5 and 6, the data for available free energy and normalized force are plotted as a function of RT ln(K_AM), with K_AM calculated from the data of Kurzawa and Geeves (1996), Highsmith (1977), and Chinn et al. (2000), as described above.

FIGURE 5.

The free energy available to produce isometric force, as determined by fits of Eq. 1 to the titration of force with Pi, shown in Figs. 1, 2, and 4, is plotted as a function of RT ln(K_AM), where K_AM is the affinity constant for the binding of a single myosin head to actin. RT ln (K_AM) is proportional to the free energy available from the formation of the actomyosin bond as described in the text. The data are fit to a straight line, which shows a direct linear relationship, that extrapolates to zero at a standard free energy, ΔG₀, for formation of the actomyosin complex of 20 kJ/mole. In the Appendix, we estimate the actual free-energy change for the formation of the actomyosin bond and show that it would be close to zero at a ΔG₀ of ∼20 kJ/mole. For the data collected at 15 and 30°C the point of the force-log[Pi] relationship, defining G₁, was assumed to occur at 50 μM [Pi]. The data for each condition are as follows: 10°C, circles; 2°C squares; 15°C, triangles; 30°C, diamond; open symbols = no PEG; solid symbols = 5% PEG; 10°C + 0.6 M KAc, inverted open triangle; 2°C + 0.6 M KAc, inverted solid triangle.

FIGURE 6.

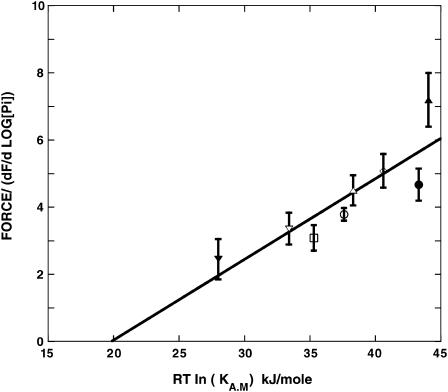
The force generated at a low concentration of Pi, 0.1 mM, normalized by the relative density of force-generating myosin heads, as determined from the slope of the inhibition of force by increasing Pi, is plotted as a function of RT ln(K_AM). The data are fitted to a straight line, which shows a linear relationship, that extrapolates to zero at approximately the point where the free energy associated with formation of the actomyosin bond in the fiber is zero (see legend to Fig. 5 and Appendix). The symbols are the same as in Fig. 5.

The free energy driving force production depends linearly on the free energy of the actomyosin bond

We wished to relate the value of G₂ – G₁, which defines the limits of the free energy gradient that produces tension, to the strength of the actomyosin bond. The difference, G₂ – G₁ is plotted as a function of the standard free energy available from formation of the actomyosin bond, RT ln(K_AM), in Fig. 5. At lower temperatures the internal [Pi] could be reduced to levels sufficient to define the plateau in tension reached at low phosphate. For these conditions it was observed that the change in slope on the left of the force-log[Pi] relationship occurred near the same value of [Pi], ∼50 μM. At the higher temperatures the internal [Pi] could not be reduced sufficiently, and the values of G₂ – G₁ shown for 15 and 30°C assume that the point where the slope changes is the same at these temperatures, indicated by the solid symbols. The data show that G₂− G₁ is directly proportional to RT ln(K_AM) with a slope of 1.3 ± 0.14 (mean ± SE). For the data at temperatures <15°C, where the data are more accurate, the slope is 1.15, close to that expected for an absolute correlation.

Force at low phosphate concentrations

The force exerted by a muscle fiber at low [Pi] varies widely with prevailing conditions. This could indicate either a variable fraction of force-generating heads, or variable force per head as parameters such as temperature or ionic strength are changed. As explained in the Appendix, the relative fractions of force-producing heads found for two different conditions can be determined by measuring the relative change in the slope of the force-log[Pi] relationship in the linear region of force inhibition. In that region, a small change in [Pi] produces a small and well-defined change in the free energy available to do work. In the model considered in the Appendix, this will result in a small fraction of force-generating cross-bridges being transferred into nonforce states. The change in force will be proportional to the fraction detached, which is also proportional to the density of force-generating cross-bridges in the working stroke. Thus the density of force-generating cross-bridges, p(x), is proportional to ΔF/Δ(−RT ln[Pi]), which is proportional to the slopes of Figs. 1, 2, and 4.

Slopes were measured by a fit to the linear portion of the force-log[Pi] curve, over at least one log unit of Pi concentration. Using the slope to normalize for the number of force-generating cross-bridges, the force per attached force-generating cross-bridge (ΔF/Δ(−RT ln[Pi])) was determined. Fig. 6 shows the force at 0.2 mM Pi, normalized to the density of force-generating cross-bridges, as a function of RT ln(K_AM) on the abscissa. As can be seen there is a linear relationship of the normalized force to RT ln(K_AM) and the normalized force approaches zero at approximately the point where the free energy available from the formation of the actomyosin bond in the fiber is also zero (see Appendix for discussion).

The relationship shown in Fig. 6 can be transformed into that shown in Fig. 5, because from geometry, the slope in the linear region of the force-log[Pi] relationship is approximately equal to force at very low phosphate divided by (G₂ – G₁). However, the data shown in Fig. 6 are derived from very different experimental measurements. These measurements do not involve any errors due to determining the points of a well-defined change in slope in the fits to the force-log[Pi] data nor do they require the use of enzymatic methods to insure that Pi internal to the fiber is very low. They rest on two observations, the force at a defined low value of Pi (0.2 mM), and the slope of the force-log[Pi] relationship, evaluated in the linear region. Thus the normalized force can be determined under conditions where G₂ cannot be determined accurately, as occurs at 30°C. Thus Figs. 5 and 6 present two independent experimental correlations, which both show that the free energy of the formation of the actomyosin bond is involved in generating force.

DISCUSSION

Ultimately, the free energy used to produce force is provided by the free energy of ATP hydrolysis. However the actomyosin cycle of interactions that effects this transduction involves a number of steps in which free energy is converted to different forms involving tight bonds between nucleotide and myosin and between myosin and actin (Goldman, 1987; Geeves, 1991; Cooke, 1997). The question investigated in this article concerns how the free energy of ATP hydrolysis is connected to the generation of isometric force. To address this question we measured the inhibition of force by added phosphate. We analyzed these data in terms of a specific model of the actomyosin interaction to determine the amount of free energy available to generate force (see Fig. 8 A and Pate et al. (1998)). Using this approach under a variety of conditions that alter the affinity of myosin for actin, we were able to correlate the strength of the actin-myosin affinity with energy available for force generation. We also found a similar correlation between actin-myosin affinity and the force generated per myosin head at a low level of phosphate. In the sections below we first discuss previous work in this area. We then discuss our conclusions and their implications for the mechanism of force production. The analysis of the force-phosphate data employed to probe the energetics of force generation is described in the Appendix.

Relation to previous work

A number of laboratories have measured force as a function of temperature and some of them have also employed temperature jumps in these measurements (Goldman et al., 1987; Bershitsky and Tsaturyan, 1992; Bershitsky et al., 1997; Coupland et al., 2001). In skinned rabbit psoas fibers previous studies agree that tension increases approximately linearly with temperature from 2° up to ∼20°C, with a more modest increase with temperature >20°C (Goldman et al., 1987; Bershitsky and Tsaturyan, 1992; Coupland et al., 2001; Wang and Kawai, 2001). Our measurements of force as a function of temperature comply with these former studies. Moreover, measurements of fiber stiffness have shown that stiffness increases by only a very modest amount over a similar range of temperatures (Bershitsky et al., 1997). This observation could be explained by a small shift from weakly bound non-force-bearing cross-bridges, which are nonetheless stiff, to strong force-generating cross-bridges, or it could indicate that force-bearing cross-bridges exert greater force at higher temperatures. Our measurements of force as a function of Pi suggest that both of these mechanisms operate, with a portion of force increase due to an increase in the force/cross-bridge and another portion due to an increase in the number of force-bearing cross-bridges.

Other investigators have also concluded that the force generated by each active myosin head increases with temperature. Lombardi and co-workers measured fiber stiffness in frog muscle by rapid length changes and found that the compliance of the force-generating cross-bridges had a greater extension at the higher forces, achieved at higher temperatures (Piazzesi et al., 2003). This observation showed that force-bearing cross-bridges exert more force at the higher temperatures, in agreement with the conclusions drawn here. Kawai and co-workers measured the response of slow muscle fibers to sinusoidal oscillations as a function of temperature (Wang and Kawai, 2001). An analysis of their data led to the conclusion that the force-generating step is an endothermic transition that involves the formation of a large protein interface. The force generated by single myosin molecules has not been measured as a function of temperature due to technical difficulties. However, measurements of the force generated by an ensemble of myosins acting on single actin filaments showed a 24% increase in force between 20 and 30°C with no further increase between 30 and 35°C (Kawai et al., 2000). Although these investigators concluded that force was independent of temperature, their measurement error does not rule out the possibility that force may have increased by the amount found here.

A number of studies agree that added phosphate reduces tension and that the decrease is linear with the logarithm of the phosphate concentration >∼0.2 mM (Tesi et al., 2000; Coupland et al., 2001). Furthermore, added phosphate was reported to have a smaller relative effect on fiber force at higher temperatures. Measurements of the change in force after the photo release of phosphate in fibers found that a 10-fold increase in [Pi] produced a 36% decrease in tension at 10°C and a 27% decrease at 20°C (Dantzig et al., 1992). Phosphate had a reduced effect at higher temperatures based on a rate constant deduced from the response of psoas fibers to sinusoidal oscillations (Kawai and Halvorson, 1991; Zhao and Kawai, 1994). Ranatunga and co-workers also found that phosphate has a decreased effect on tension at higher temperatures (Coupland et al., 2001). Although the negative slope of the tension versus log[Pi] increased with increasing temperatures up to 10°C, it decreased at temperatures >10°C in contrast to the results found here. The observation of increasing negative slope with temperature reported here may be due to the greater stability achieved and thus higher tensions obtained at high temperatures and low [Pi], made possible by the temperature jumps employed in our measurements.

Single myofibrils avoid the buildup of Pi that occurs in the larger fibers. In single myofibrils tension was found to decrease linearly with log[Pi] > 0.5 mM Pi with a slope that was a little greater than those found here (Tesi et al., 2000). Subsequent work measured the effect of temperature on the force-phosphate relationship in myofibrils from both fast and slow muscles (Tesi et al., 2002). Plots of tension as a function of phosphate in slow myofibrils led those authors to conclude that tension reached a plateau at ∼40% of control. Replotting the data as force-log[Pi] reveals that the slope of the relationship for fast myofibrils increased between 5 and 15°C; however, the increase, ×1.3, was less than that found here, ×2.5. Replotting the data for slow myofibrils showed that the tension decreases linearly with log[Pi] with no sign of a plateau, extrapolating to zero at log[Pi] = 0.4. This relationship is not very different from that observed here for fast fibers at a slightly higher temperature (20 vs. 30°C). The slope of the force-log[Pi] relationship is less for the slow myofibrils than for fast myofibrils. The lower slope could indicate a stronger actomyosin bond in the slower muscle. In summary, the linear dependence of force on log[Pi] found in previous investigations is similar to the results reported here.

Phosphate has been thought to play a role in the inhibition of fiber function that occurs during fatigue. However, our results show that the force-depressing effect of Pi declines with increasing temperature, from ∼60% at 10°C to <40% at 30°C, being probably even less at the in vivo physiological temperature of 39°C of the animal. This suggests a smaller role for Pi than what has been previously concluded from studies at low temperatures where the effect of increasing [Pi] is greater (Westerblad et al., 2002).

Models of the actin-myosin interaction

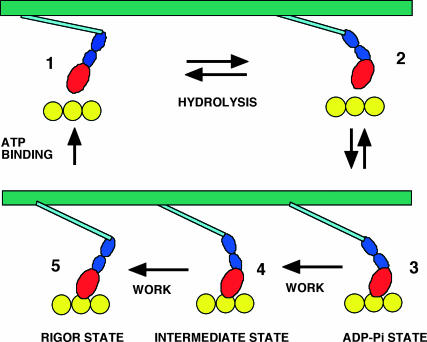
In many current models of force production a myosin head attaches to actin in a high-energy state, state 3 in Fig. 7, traverses down a gradient of free energy, and is detached at some lower free energy in state 5 (Eisenberg et al., 1980; Pate and Cooke, 1989b). The free energy released by this process, which is equal to the difference between the highest free energy of force-generating heads attached in state 3 and the lowest free energy of heads attached in state 5, is used to produce force and work. Here we wished to measure the difference in free energy between the highest and lowest states in the force-producing gradient of free energy.

FIGURE 7.

A schematic of the actomyosin interaction showing the states relevant to the discussion. State 1 occurs with myosin dissociated from actin and with ATP bound to the active site. Hydrolysis of the nucleotide occurs in the transition to state 2, shown to also be accompanied by a change in the orientation of the light chain domain from the postworking stroke to the preworking stroke positions. However the conformational change is not tightly coupled to the state of the nucleotide, and state 1 can probably exist in both conformations. The myosin-ADP-Pi attaches weakly to actin in state 3. Data suggest, as discussed in the text, that force can be generated in this state, shown hypothetically here as the movement of the light chain domain. The properties of state 4 are hypothetical. It is shown with a light chain domain in an orientation between those of states 3 and 5. It represents the end of the working stroke generated with both ADP and Pi bound. Release of Pi in this state leads to a more strongly bound state, and additional work is performed as the light chain region changes orientation to the postworking stroke conformation shown in state 5. States 3, 4, and 5 all generate force.

Measuring the free energy available to generate force

Work in a number of laboratories, including our own, has shown that addition of phosphate to active muscle fibers decreases isometric tension with little or no effect on the maximum shortening velocity (Kawai, 1986; Pate and Cooke, 1989a; Kawai and Halvorson, 1991; Dantzig et al., 1992; Metzger, 1996; Pate et al., 1998). As described in the appendix the relation between force and log[Pi] can be used to estimate the extent of the free-energy gradient, G₂ − G_1, in the force-generating states. As the concentration of Pi is increased, the free energies of those states that precede Pi release decrease linearly with the logarithm of [Pi], as shown in Fig. 8 A. As [Pi] increases the energy available in the force-generating states decreases as the force-generating states with greater energies are depopulated. As shown in Fig. 8 B, the extent of the gradient can be determined from the shape of the force-log[Pi] relationship. This relationship responds differently to an increase in force due to increased numbers of force-generating heads or due to increased force per head, see Fig. 8 C. Thus phosphate can be used in effect to titrate the energies involved in force generation.

Correlation between the strength of the actin-myosin bond and the energetics of force generation

The assumption that we are testing is that the free-energy gradient that generates force comes from the formation of the actomyosin bond. To test this we have measured the free energy used to generate force by titrating force with Pi, and have compared this to the free energy released by formation of the actomyosin bond. The data shown in Fig. 5 demonstrate that the free energy available to generate force varies linearly with the free energy associated with the formation of the actin-myosin bond. Therefore the data suggest that as the affinity of myosin for actin increases, the difference between G₁ and G₂ increases. A greater affinity would lead to an increase in the range of x over which myosin heads can attach, and to an increase in the average force generated.

The data also provide evidence that the initial, weak bond between actin and myosin thought to occur at the beginning of the working stroke is associated with force production. All of the methods used to alter the strength of the actomyosin bond, temperature, ionic strength, PEG, potentiate the formation of both the weak bonds thought to occur at the beginning of the working stroke and the strong bonds thought to occur at the end of the working stroke. If force was only generated in the strong states that occur subsequent to phosphate release one would not expect a large effect of actomyosin affinity on force generation as there would have been no change, or little change, in the difference in free energy between the weak and strong states. Analysis of the models discussed above shows that the force-log[Pi] relationship determines the difference between G₁ and G₂, even when G₂ occurs in a state before Pi release. Thus our data suggest that force is generated both in the strongly bound states and in the weakly bound states that precede them, but not necessarily in equal amounts. There is kinetic evidence that force generation can occur before the release of phosphate (Fortune et al., 1991; Kawai and Halvorson, 1991; Dantzig et al., 1992; Tesi et al., 2002). The fact that so much energy is involved in the formation of the actin-myosin interface also suggests that this energy must be used to generate force and to perform mechanical work. This energy represents a very large fraction of the ∼50–80 kJ/mole released by hydrolysis of ATP (Woledge et al., 1985). If this energy were not used, muscles would be very inefficient. At physiological conditions, with higher temperatures, molecular crowding, etc., the weak bond is stronger, and about half of the energy that would be released by formation of the actomyosin bond would come from the formation of the weak bond.

Force at low phosphate

As described in the appendix, the relative densities of force-generating cross-bridges in two conditions can be estimated by the relative slopes of the force-log[Pi] relationships. Using this to normalize the force generated at a low [Pi], we could separate the effects on force due to changes in the number of force-generating heads. Fig. 6 shows that the normalized force increases linearly with the strength of the actomyosin bond. Because these measurements rely on different experimental observations than do the determination of G₁ and G₂, this provides an independent correlation with force generation and actomyosin affinity. Thus, we have two strong correlations (Figs. 5 and 6) that show that the free energy of the formation of the actomyosin bond is involved in producing isometric tension.

Relation to the cross-bridge cycle

The crystal structures of myosin show that hydrolysis of the nucleotide results in a reorientation of the light chain domain relative to the catalytic domain (Fisher et al., 1995; Smith and Rayment, 1996; Holmes, 1997; Dominguez et al., 1998). This structural change has received wide attention and has suggested the hypothesis that the complete structural changes occurring in the working stroke have now been seen. Does this transition represent the cocking of some spring-like element that is later released to provide the 30–40 kJ/mole required to drive the working stroke? Our data say no. Variation in ionic strength and addition of PEG have known effects on the strength of the actomyosin bond, but are not expected to vary the free energy available from hydrolysis of a bound nucleotide nor to vary the energy stored in a strained conformation of a protein. Thus our observation that these conditions affect force generation in proportion to their effect on actomyosin affinity suggest that the free energy that is transformed into mechanical work in the working stroke does not come from the release of conformational energy stored in the myosin molecule during ATP hydrolysis but from the formation of the actomyosin bond per se. At the end of the working stroke the myosin is bound tightly to actin, the formation of this bond having “paid” for the work performed. This bond is broken when myosin trades one ligand, actin, for a second ligand, ATP, for which it has an even greater affinity (Goody et al., 1977; Kurzawa and Geeves, 1996). Hydrolysis of the ATP then allows myosin to again form a tight bond with actin, and the cycle continues.

The formation of the actomyosin bond is endothermic, i.e., the internal energy of the system is greater after the bond formation than before it (Smith et al., 1984). The formation of this bond is driven primarily by an increase in entropy resulting from the formation of a large hydrophobic interface. Thus if the energy released in bond formation is transduced into mechanical work, either directly in the working stroke or by stretching a compliant element that is released during the working stroke, this work is produced in an entropically driven reaction, not an enthalpically driven reaction. A number of investigators have reached the conclusion that the force-generating step is endothermic (Goldman et al., 1987; Coupland et al., 2001; Kawai, 2003). The second law of thermodynamics states that the work that can be obtained from a reaction is proportional to the change in free energy that occurs during the reaction (Gibbs free energy at constant pressure). This change can involve either a decrease in enthalpy or an increase in entropy. The first law of thermodynamics requires that the net enthalpy in a reaction be unchanged. Thus when work is performed in reactions driven by changes in entropy, the enthalpy required to perform the work is acquired via the absorption of Brownian heat from the medium. This thermal fluctuation is “captured” by formation of the actomyosin bond.

How could the force generated by a muscle depend on the strength of the actomyosin bond? Any model, in which the binding of myosin to actin stabilizes a spring that has been stretched by a thermal fluctuation, such as proposed by Huxley (1957), will produce the data shown in Figs. 5 and 6. In this type of model, the stronger the actomyosin interaction, the greater the strain that can be stabilized, and the greater the energy and the resulting isometric force. The location of the spring is not determined by our data; it could reside in the myosin rod, the light chain domain, or in the actin filament.

The rate at which work can be performed by trapping thermal fluctuations depends strongly on the magnitude of the fluctuation that is trapped. Large fluctuations occur more rarely than small ones. This dependence was considered by Huxley and Simmons (1971), and more recently by Howard (1996), who expanded on an equation by Kramers. The time required for a molecule of the approximate size of the myosin head to diffuse against an elastic load over a barrier of energy E is given by:

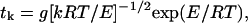where k is the spring constant of the load and g is a constant. This equation estimates t_k = 1–2 ms for E = 25 kJ/mole, and t_k = 15–30 s for E = 50 kJ/mole. The free energy available from ATP in vivo varies with conditions and in an active muscle it is 50–60 kJ/mole. Thus if a large fraction of this energy is devoted to producing work, e.g., 60% (Cooke, 1997), the energy could not be absorbed sufficiently rapidly by capturing a single fluctuation. However, if the working stroke occurred in several steps, each step could be completed in the observed time of a few milliseconds. As discussed above there is evidence that the working stroke occurs in at least two steps in the actomyosin cycle, one associated with the formation of the actin-myosin-ADP-Pi complex and one with the formation of the strong bond after Pi release.

Is this mechanism general to the function of other motor proteins? The structure of the core of the kinesin motor domain resembles that of myosin, but the light chain domain lever arm is replaced by a 15-amino acid polypeptide known as the neck linker. In current models of their mechanism, docking of the neck linker to the motor core positions the unattached head toward the plus end of the microtubule, where it binds to the next site (Rice et al., 1999). The actual translation of the head is produced largely by a thermal fluctuation, which is subsequently captured by the tight binding of the kinesin head to the microtubule. The kinesin cycle also has two force-generating steps. Thus it appears that the mechanisms of force generation by kinesin and myosin share important similarities.

SUMMARY

We conclude that the formation of the actomyosin bond traps thermal fluctuations, which are transformed into force production. Although our results come from measurements of isometric tension, the same mechanism must also be involved in producing mechanical work. This occurs in at least two steps in the actomyosin cycle.

APPENDIX

In this appendix we discuss how the force-phosphate relationship can be used to probe the energetics of the force-generating states. This relationship has been developed in two previous articles, and here we follow the same approach. We first present a simple model of the interaction of a myosin head with actin and with phosphate.

Fig. 8 A shows the free-energy diagram for a very simple cross-bridge cycle consisting of two states, one in which the myosin is not generating force (Non-Force State) and one in which it is attached to actin and generating force (Force State). The free energies of the two states are shown as a function of x, the relative position of the myosin and actin sites. Measurements of the force response to step changes in muscle length have shown that the elements that generate force in muscle act as Hookean springs so that the free energy of the force-generating state is taken to be parabolic (Huxley and Simmons, 1971). The free energy of the highest force-generating state is G₂ and that of the lowest force-generating state is G₁. The free energy of the nonforce state is G_p, and the free energy of this state decreases linearly as −RT ln[Pi] increases.

One major assumption of our model is that the force-generating states are in an effective equilibrium with the non-force-generating states at the beginning of the working stroke. Rapid transitions between these states have been seen experimentally (Brenner, 1991; Karatzaferi et al., 2003). If this assumption is true, then the force-generating states with free energies that are higher than the energy of the nonforce state are not populated. As the concentration of Pi increases, the free energy of the states that precede Pi release (states 1, 2, and 3, Fig. 7) decrease as −RT ln[Pi], relative to the free energy of states after Pi release, shown schematically in Fig. 8 A. With the above assumption the progressive depopulation of the force-generating states (3, 4, and 5) that occurs with increasing Pi can be used to effectively titrate the free energies of the force-generating states. As the free energy of the non-force-producing states decreases below the highest of the force-generating states at the top of the free energy gradient, tension begins to be inhibited. The range of distortion, x, in which force-generating cross-bridges are found is shown by the arrows in Fig. 8 A for two values of [Pi], one low and one high. Thus, as [Pi] increases, tension is inhibited because myosin heads do not attach to actin at high values of x, where they would generate the highest tensions. We note that although state 3 in Fig. 7 is a force-producing state that precedes Pi release, no force will be generated in this state if G₁ is equal to G₂. Thus force decreases as the difference between G₁ and G₂ becomes smaller even when force-generating states precede phosphate release.

A second assumption of the model is that the cross-bridge states are distributed evenly with respect to distortion among these states. This assumption is reasonable because the periodicities of the myosin and actin sites are not equivalent, insuring that all orientations are equally sampled. Ultimately the assumption is supported by the observation that the force-log[Pi] curve is linear in its greatest part, as expected for a uniform distribution. With this assumption, the model predicts that tension is inhibited linearly with log[Pi]. As the free energies of the non-force-generating states go below that of the lowest of the force-generating states, tension approaches zero. Thus the range of RT ln[Pi] required to titrate force from maximum to zero represents the range of free energy available to generate tension (G₂–G₁). In the section below we use this model to derive an expression relating the values of G₁ and G₂ to force generated by this model as a function of [Pi]. The analysis above is compatible with previous models of cross-bridge function in which the addition of phosphate leads reversibly to a non-force-generating state. For example the model proposed by Pate and Cooke in, 1989 was shown to result in a linear dependence of tension on log[Pi] (Pate and Cooke, 1989b).

As described in several previous publications a more quantitative treatment of the force versus log[Pi] relationship can be derived and interpreted to provide information on the energetics of the force-producing states (Pate and Cooke, 1989a; Pate et. al., 1998). The model used to analyze this relationship is described above and in Fig. 8. We assume that the two states shown in Fig. 8 A are in quasiequilibrium with a distribution of populations governed by the energy difference between them. Thus the force-generating states lie approximately between G₁ and G_p. Integrating over all force-generating states one obtains the following equation:

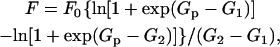(1)

Where F₀ is the force reached at very low concentrations of Pi, G_p is the energy of the nonforce state that precedes phosphate release, and G₂ and G₁ are the highest and lowest available energies of the force-generating state (see Fig. 8). Eq. 1 is also derived by Pate et al,, 1998 (see their Eq. 8). Although the original derivation discussed only a single state, the integral can just as easily be carried out over any number of states. The integral simply involves a sum over the p(x) and ΔG/Δx of all states. Eq. 1 is found to provide an excellent fit to the experimental data obtained previously as well as to that shown in Figs. 1, 2, and 4.

Determining the relative populations of force-generating myosin heads

In this section we discuss how the relative densities of force-generating cross-bridges in two different conditions can be determined, leading to a measure of the relative force generated by an attached cross-bridges in the two conditions. For the simple model shown in Fig. 8 A, force could be raised by increasing the range of x over which force-generating myosin heads can attach, or by increasing the density of force-generating heads attached in this interval. As discussed below, the relative densities of force-producing heads found for two different conditions can be determined by measuring the relative change in the slope of the force-log[Pi] relationship in the linear region of force inhibition. The slope is proportional to the density of force-generating heads because a small increase in [Pi] will produce a small decrease in the free energy available in the working stroke, which will in turn displace a small fraction of force-generating myosin heads. The fraction displaced is proportional to the density, p(x), and thus also to the slope.

The relationship between the slope of the force-log[Pi] relationship and the density of force-generating cross-bridges can be made more exact. The force generated by the cross-bridges found in some interval Δx in the working stroke, can be expressed as:

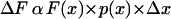(2)

where ΔF is the force generated by these cross-bridges, F(x) is the force generated by each cross-bridge and p(x) is the density of force-generating cross-bridges in the interval. F(x) can also be expressed in terms of the difference in free energy in the interval, ΔG:

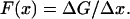(3)

Taking the case where increasing Pi decreases G, ΔG = −ΔRT ln[Pi], and inverting Eq. 3:

(4)

The relative values of p(x) determined from this equation can be used to normalize the force obtained under two different conditions and thus to compare the force generated per attached force-generating cross-bridge under the two conditions.

Determination of the free energy involved in the formation of the actomyosin complex

The affinity of a myosin head for actin has been determined as a function of ionic strength by Kurzawa and Geeves (1996). The affinity decreased with increasing ionic strength, following a relation log Kd = −9.2 + 5.0 IS^−0.5. It has also been determined as a function of temperature by Highsmith (1977), increasing with increasing temperature with a ΔH of 44 kJ/mole. The effect of PEG on the affinity of the actomyosin bond was determined by Chinn et al. (2000). Addition of 5% PEG-4000 increased the affinity of actin for myosin by a factor of 4 ± 0.4 in the absence of nucleotides. In the presence of ADP plus phosphate analogs, AlF4 or vanadate, the effect of PEG was a little stronger, with an eightfold increase in affinity.

In determining the values of RT ln(K_AM) we started with the affinity constant for the actin myosin association at 20°C as a function of ionic strength from the work by Kurzawa and Geeves (1996). We modified this affinity using the effect of a change in temperature, determined by Highsmith, and the effect of PEG, as determined by Chinn et al. (2000). We assumed that the effect of PEG was not a function of temperature or ionic strength, as expected from theory (Parsegian et al., 1986; Timasheff, 1995) and indicated by our results (Fig. 1).

As we argue above, the relative values of the free energy released by formation of the actin-myosin bond is proportional to RT ln(K_AM). However, the absolute value of free energy available from the formation of the actomyosin bond in a fiber depends both on the affinity constant of the reaction and on the concentrations of the products and reactants. If the free energy released by formation of the actin-myosin bond in the fiber is transformed into mechanical work, what is the maximum work that could be performed? At equilibrium the free energy liberated by formation of the bond plus the work done will balance:

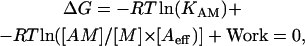(5)

where [M] and [AM] are the concentrations of myosin and actomyosin, and A_eff is the effective concentration of actin seen by a myosin head. At the point where maximum work can be done, [M] and [AM] will be equal. This leads to:

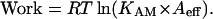(6)

The data shown in Figs. 5 and 6 provide an estimate of A_eff. The intercept on the x axis defines the point where K_AM = 1/A_eff, leading to an estimate for A_eff of ∼0.5 mM, not far from the actual value of 0.6 mM (Woledge, et. al., 1985). Although this is a rather rough estimate, it shows that the absolute free energies measured here are close to those expected for the binding of a myosin head to actin in the filament array of a fiber. Although it may be better to use the affinity of actin for myosin-ADP, this affinity has not been measured over as wide a range of conditions as has the actin-myosin affinity. Those measurements that have been made for skeletal proteins show a difference by a factor of ∼10–30 (Geeves, 1991). The effect of using a weaker affinity would be to shift the values on the x axis of Figs. 5 and 6 to lower values by ∼7.5 kJ/mole.