Tertiary Structure Predictions on a Comprehensive Benchmark of Medium to Large Size Proteins

Abstract

We evaluate tertiary structure predictions on medium to large size proteins by TASSER, a new algorithm that assembles protein structures through rearranging the rigid fragments from threading templates guided by a reduced C_α and side-chain based potential consistent with threading based tertiary restraints. Predictions were generated for 745 proteins 201–300 residues in length that cover the Protein Data Bank (PDB) at the level of 35% sequence identity. With homologous proteins excluded, in 365 cases, the templates identified by our threading program, PROSPECTOR_3, have a root-mean-square deviation (RMSD) to native < 6.5 Å, with >70% alignment coverage. After TASSER assembly, in 408 cases the best of the top five full-length models has a RMSD < 6.5 Å. Among the 745 targets are 18 membrane proteins, with one-third having a predicted RMSD < 5.5 Å. For all representative proteins less than or equal to 300 residues that have corresponding multiple NMR structures in the Protein Data Bank, ≈20% of the models generated by TASSER are closer to the NMR structure centroid than the farthest individual NMR model. These results suggest that reasonable structure predictions for nonhomologous large size proteins can be automatically generated on a proteomic scale, and the application of this approach to structural as well as functional genomics represent promising applications of TASSER.

INTRODUCTION

The protein structure prediction problem, that is, deducing the tertiary structure of a protein from its primary amino acid sequence, has attracted considerable interest in this postgenomic era (Baker and Sali, 2001; Skolnick et al., 2000a). At present, the success rate of structure prediction is dictated by two factors: First, the structure of smaller proteins is easier to predict than those of larger proteins. Given secondary structure assignments (that can be deduced from sequence alone with more than 80% accuracy using state-of-the-art predictors; Jones, 1999; Karplus et al., 1998), the number of ways to assemble the secondary structure blocks into tertiary models increases exponentially with the increasing number of such blocks. Second, since in principle similar sequences have similar folds (Holm and Sander, 1996), solved homologous protein structures can be exploited to greatly increase the accuracy of the predicted models (Marti-Renom et al., 2000). Therefore, in benchmarking tests to establish the applicability of an approach to weakly/nonhomologous proteins, such homologous structures should be carefully excluded.

Until now, most benchmark tests of protein structure prediction algorithms focused on small to medium size proteins. For example, based on an ab initio approach designed to globally optimize their potential energy function, Scheraga et al. could build models of root-mean-square deviation (RMSD) to native below 6 Å for protein fragments of up to 61 residues (Liwo et al., 1999). Using ROSETTA, Baker et al. report 73 successful structure predictions out of 172 target proteins with lengths below 150 residues, with a RMSD < 7 Å in the top five models (Simons et al., 2001). In recent works, we developed a threading template assembly/refinement approach, TASSER, and benchmarked TASSER on a comprehensive benchmark set of 1489 single-domain proteins in the Protein Data Bank (PDB) with length below 200 residues. We find that 990 targets can be folded by the approach; i.e., they have a RMSD < 6.5 Å in at least one of the top five models (Zhang and Skolnick, 2004a). Despite these important efforts, structure prediction on larger proteins with length greater than 200 residues, which is the range of protein lengths adopted by many enzymes and other functionally important proteins, has not previously been systematically explored. Although the Critical Assessment of Techniques for Protein Structure Prediction (CASP) provides a periodic and critical test of all size ranges of proteins (Moult et al., 2001, 2003), because of the relatively small number of targets in various specific categories, a comprehensive general trend still remains to be established.

In this work, we employ a representative benchmark set of all structures in the PDB ranging from 201 to 300 residues in length and present the results of the large-scale testing of TASSER for tertiary structure prediction on these medium to large size proteins. For the first time, folding simulations of multiple-domain proteins and membrane proteins are examined in a series of systematic tests. Finally, a direct comparison of the accuracy of the TASSER predicted models to the spatial uncertainty of NMR experimental structures is made.

METHODS

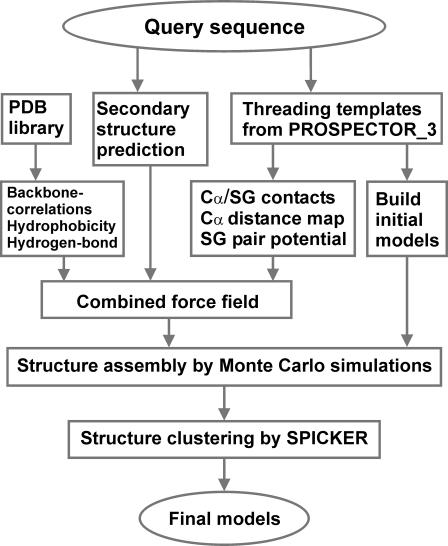
The threading template assembly/refinement procedure, TASSER, consists of threading template identification, fragment assembly, and final model combination (Zhang and Skolnick, 2004a). A flowchart is presented in Fig. 1.

FIGURE 1.

Flowchart of the TASSER structure prediction methodology that consists of template identification by threading, fragment assembly, and fold selection.

Threading

The structure templates for a query sequence are selected from the PDB library (Berman et al., 2000) by our threading program PROSPECTOR_3 (Skolnick et al., 2004). The program is an iterative sequence/structure alignment approach, and all the alignments are generated using a Needleman-Wunsch type of global alignment algorithm (Needleman and Wunsch, 1970). The scoring function of PROSPECTOR_3 consists of close and distant sequence profiles (Skolnick and Kihara, 2001), secondary structure propensities from PSIPRED (Jones, 1999), pair potentials (Skolnick et al., 2000b), and consensus contact predictions generated from the alignments in the previous threading iterations. Depending on the different methods used to generate the pair potentials (quasichemical based, local sequence fragment based, and orientation independent, or local sequence fragment based and orientation dependent) and the ways of calculating the Z-score alignment significance (the energy in standard deviation units relative to mean), there are six classes of alignments returned at the end of PROSPECTOR_3 iterations.

To select the final template alignments for TASSER assembly, we establish two sets of Z-score cutoffs based on benchmarking statistics (Skolnick et al., 2004): Z_struct, above which ∼95% of templates have their best structure alignment with a RMSD to native < 6.5 Å over the aligned regions, and Z_good, above which ∼80% of threading-predicted alignments have a RMSD < 6.5 Å in aligned regions. If a target has a template with a Z-score > Z_good or two templates with consensus alignments both having a Z-score > Z_struct, the target is assigned to the Easy set (note that Easy does not imply the results are trivially found; in a benchmark test, approximately half the proteins in the Easy set are not identified by PSI-BLAST; Frishman et al., 2003; Kawabata et al., 2002; Zhang and Skolnick, 2004a); if a target has a single template (or has multiple templates lacking a consensus structure) where Z_good > Z-score > Z_struct, the target is assigned as to the Medium set; all others are Hard targets.

TASSER force field

A protein's conformation is described by its C_α atoms and side-chain centers of mass (SG), called the CAS model. The force field employed in TASSER modeling consists of three classes of terms: 1), statistical potentials from the PDB database (Kolinski and Skolnick, 1998; Zhang et al., 2003), including long-range SG-pair interactions, local C_α correlations, hydrogen-bond, and hydrophobic burial interactions; 2), propensities for predicted secondary structures from PSIPRED (Jones, 1999); and 3), protein specific SG-pair potentials and tertiary contact restraints extracted from the threading templates by PROSPECTOR_3 (Skolnick et al., 2004).

The combination of all the energy terms was optimized by maximizing the correlation between the CAS energy and RMSD of decoy structures to native, on the basis of 100 training proteins outside the benchmark test set, each with 60,000 structure decoys (Zhang et al., 2003).

Compared with previous energy potential (Zhang et al., 2003; Zhang and Skolnick, 2004a), to increase the hydrogen-bond geometrical specificity, the hydrogen bond used in this work is constructed by including backbone N and CO groups rather than using just the C_α approximation. Protein specific pair interactions are derived on the basis of a freely jointed chain model simulation (our unpublished results) rather than using the quasichemical approximation (Skolnick et al., 2000b). These changes increase the correlation of the energy with RMSD (the average correlation coefficient between energy and RMSD in the decoy structures of 100 training proteins increases from 0.69 to 0.75); this also improved the performance of TASSER simulations.

On- and off-lattice model and structure assembly

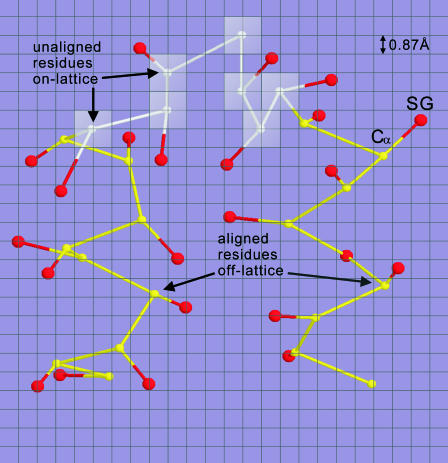
A protein chain in TASSER modeling is divided into aligned and unaligned regions based on its PROSPECTOR_3 alignments, where the aligned regions are modeled off lattice for maximal accuracy and the unaligned regions are simulated on a cubic lattice system for computational efficiency (Fig. 2).

FIGURE 2.

Schematic representation of a piece of polypeptide chain in the combined on- and off-lattice CAS model. Each residue is described by its C_α and side-chain center of mass (SG). Although C_α's of unaligned residues (white) are confined to the underlying cubic lattice system with a lattice space of 0.87 Å, C_α's of aligned residues (yellow) are excised from threading templates and traced off lattice. SGs are always off lattice (red) and determined using a two-rotamer approximation (Zhang et al., 2003).

For a given template, an initial full-length model is built up by connecting the continuous template fragments (greater than or equal to five residues) by a random walk of C_α–C_α bond vectors of variable lengths from 3.26 Å to 4.35 Å. Only excluded volume and geometric constraints of virtual C_α–C_α bond angles (65°–165°) are considered during the initial model building procedure. The side-chain center of mass is determined by a two-rotamer approximation that depends on whether the local backbone configuration is extended or compact. To guarantee that the last step of this random walk can quickly arrive at the first C_α of the next template fragment, the distance l between the current C_α and the first C_α of the next template fragment is checked at each step of the random walk, and only walks with l < 3.54n are allowed, where n is the number of remaining C_α–C_α bonds in the walk. If a template gap is too big to be spanned by a specified number of unaligned residues, a big C_α–C_α bond will remain at the end of the random walk, and a spring-like force that acts to draw sequential fragments close will be applied in subsequent Monte Carlo simulations until a physically reasonable bond length is achieved.

The initial full-length models are submitted to parallel hyperbolic Monte Carlo sampling (Zhang et al., 2002) for assembly/refinement. Two kinds of conformational updates are implemented: Off-lattice movements of the aligned regions involve rigid fragment translations and rotations that are controlled by the three Euler angles. The fragment length normalizes the movement amplitude so that the acceptance rate is approximately constant for different size fragments. The lattice confined residues are subjected to two to six bond movements and multibond sequence shifts (Zhang et al., 2003). Overall, the tertiary topology varies by the rearrangement of the continuously aligned substructures, where the local conformation of the off-lattice substructures remains unchanged during assembly. Both movement of the aligned and the gap regions are guided by the same CAS force field.

Clustering

Forty replicas are employed in the Monte Carlo simulation. Structures generated in the 14 lowest temperature replicas are submitted to an iterative structural clustering program, SPICKER (Zhang and Skolnick, 2004b), for clustering. The final models are combined from the clustered structures and ranked by the structure density D, i.e., 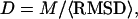where M is the multiplicity of structures in a SPICKER cluster and 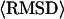denotes the average RMSD of the structures to the cluster centroid.

RESULTS AND DISCUSSION

Benchmark protein set

To construct a benchmark set, we group all protein entries in the PDB having from 201 to 300 residues in length based on their sequence similarity with a pairwise sequence identity cutoff of 35% and randomly select one protein from each group. The resulting representative benchmark set includes 745 proteins: 112, 132, and 501 of them are α-, β-, and αβ-proteins, respectively; 258 of them have more than one domain according to DomainPhaser (Guo et al., 2003); and 18 are transmembrane proteins. The list of target proteins can be found on our website at http://www.bioinformatics.buffalo.edu/abinitio/745.

Threading

After homologous template proteins with sequence identity >30% are excluded from the library, 593 target proteins are assigned by PROSPECTOR_3 as the Easy set. The average coverage of template alignments for these Easy targets is 83%, with an average RMSD to native of 5.9 Å on the aligned regions (see Table 1). There are 418 Easy targets that have a RMSD to native below 6.5 Å; 363 of them have alignment coverage higher than 70%.

TABLE 1.

Summary of threading results from PROSPECTOR_3 and final models by TASSER

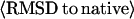				§			Nfold¶
	N*	Template selected†	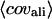‡	Tali	Mali	Mful	Tali	Mali	Mful
Easy set	593 (80%)	Top two plus consensus	83%	5.9 Å	4.7 Å	6.4 Å	418 (363)	481	396 (67%)
Medium set	150 (20%)	Top five	45%	12.4 Å	9.3 Å	15.7 Å	45 (2)	71	12 (8%)
Hard set	2 (0.3%)	Top 20	41%	17.3 Å	13.1 Å	18.1 Å	0 (0)	0	0 (0%)
Single domain	487 (65%)		76%	7.2 Å	5.4 Å	7.7 Å	307 (258)	377	296 (61%)
Multiple domain	258 (35%)		73%	7.4 Å	6.1 Å	9.5 Å	156 (107)	175	112 (43%)
Membrane proteins	18 (2%)		71%	10.7 Å	7.5 Å	12.0 Å	8 (5)	10	6 (33%)
All	745		75%	7.2 Å	5.6 Å	8.3 Å	463 (365)	552	408 (55%)

^*Number of the target proteins in each category and the percentage in whole benchmark.

^†Number of templates used in the TASSER assembly procedure.

^‡Average alignment coverage for the best template that has the lowest RMSD to native.

^§Average RMSD to native: T_ali, the best template with RMSD calculated over aligned regions; M_ali, the best model in top five with RMSD calculated over the same aligned regions as that in the threading template; and M_ful, the best model in top five with RMSD calculated over entire chain.

^¶Number of targets with RMSD to native below 6.5 Å: T_ali, the best template with RMSD calculated over aligned regions. The numbers in parentheses are the templates of the alignment coverage ≥70%; M_ali, the best model in top five with RMSD calculated over the same aligned regions as that in the threading template; and M_ful, the best model in top five with RMSD calculated over entire chain. The value in parentheses is the fraction of targets in the specified category.

There are 150 Medium targets identified by PROSPECTOR_3 where the average sequence identity between target and template is 11.5%. In Medium set targets, the global fold of the identified template (as assessed by structural superposition) is generally correct (Skolnick et al., 2004), but often there are significant alignment errors. As expected, the threading alignments only focus on some local substructures for the targets in this category. The average threading alignment coverage is 45%, and in 45 cases the aligned substructures have a RMSD to native below 6.5 Å (Table 1).

There are only two Hard cases (1hq0A and 1k24A) where PROSPECTOR_3 cannot identify a suitable template. Nevertheless, we still include the alignments of the highest scoring templates in the folding refinement for the Hard set targets. Although the global topology of the threading alignments are often wrong in the Hard set targets, the local fragments are still close to native in most cases, a fact that can be profitably exploited by TASSER (Zhang and Skolnick, 2004a).

Summary of folding results

The threading templates and alignments by PROSPECTOR_3 are taken as the initial inputs in the TASSER reassembly procedure. For the Easy targets, we take the two templates of the highest Z-score as well as their consensus substructure as an independent template. The consensus template is calculated as an average of the commonly aligned residues when their distances are <5 Å after superposition. For Medium and Hard targets, the top five and top 20 templates are taken, respectively.

Table 1 presents a summary of the PROSPECTOR_3 threading results as well as the final models produced by TASSER. If we define a successful prediction as the one where at least one of the top five full-length models has a RMSD to native below 6.5 Å (a statistically significant cutoff (Reva et al., 1998), but other cutoffs could be used as well), there are 396 foldable cases among the 593 Easy set targets (67%) with an average RMSD to native of 3.6 Å. Of the 152 Medium/Hard targets, there are only 12 foldable cases. This unfortunately shows the strong correlation between the final outcome of TASSER modeling and PROSPECTOR_3 threading alignments. Among these 12 foldable cases, 10 of them (all are β- or αβ-proteins, i.e., 1b5tA, 1bwzA, 1cmxA, 1e2tA, 1fs0G, 1g61A, 1gs5A, 1h8vA, 1isfA, and 1jtdB) have initial templates with incorrect alignments (RMSD > 8 Å) or <70% alignment coverage, demonstrating TASSER's ability to assemble big protein models from rather poor and incomplete template alignments.

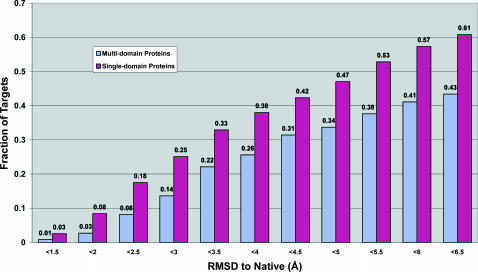
In Fig. 3, we show a histogram of the percentage of foldable targets at different RMSD cutoffs where we categorize the targets into single domain and multiple domain proteins. For the 487 single domain proteins, in ∼61% of targets (296), the best of the top five models has a RMSD to native below 6.5 Å. For the 258 multiple domain proteins, there are 112 targets having RMSD < 6.5 Å in the top five models. However, in 172 cases, there is at least one domain with a RMSD < 6.5 Å and whose average length is 114 residues. This highlights a weak point of TASSER for predicting the mutual orientation of the domains even when the individual domains have correct topology; the solution to this issue is the next major challenge facing TASSER. In the meantime, an enlarged template library including various domain orientations within the same homologous subfamily will certainly be of help for use in TASSER domain assembly (our unpublished results).

FIGURE 3.

Histogram of the percent of foldable targets by TASSER for single-domain and multiple domain proteins.

The overall folding rate for the entire benchmark set is 55% (408/745). If we only count those targets greater than 250 residues in size, the success rate is ∼52%, whereas the success rate for targets less than or equal to 250 residues is 58%. This weak size dependence of model quality is mainly due to the fact that the bigger targets have a higher percentage of multiple domain proteins, (i.e., 40% of the proteins greater than 250 residues in length have multiple domains, and 29% of the proteins less than or equal to 250 residues in length have multiple domains), where TASSER has a lower success rate in predicting the interdomain orientations.

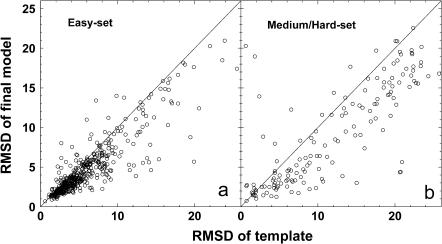
Comparison with the initial template

In Fig. 4, for the threading aligned regions, we show a detailed comparison between the final models and initial template alignments. As expected, the template alignments in the Easy set have much better quality than those in the Medium/Hard set. The majority of the template alignments in the Easy set have a RMSD to native below 6 Å (Fig. 4 a), whereas the alignments in Medium/Hard set have a quite broad RMSD distribution ranging from 1 Å to more than 20 Å. This highlights the threading alignment problems shown by PROSPECTOR_3 on the Medium/Hard targets, even though the majority of templates (∼90%) in this category can have good structure alignments (Skolnick et al., 2004).

FIGURE 4.

RMSD to native of the best models in top five by TASSER versus the RMSD to native of the best initial template by PROSPECTOR_3; both RMSD calculated over the same aligned regions. (a) Easy set targets; (b) Medium/Hard set targets.

In both cases, TASSER refined models show obvious improvements with respect to the initial templates. For example, for the initial template alignments whose RMSD is in the range of 4 ∼ 5 Å, in 53% of the cases, the final models show at least a 1-Å improvement. For those templates that have a higher RMSD to native, there tends to be relatively larger RMSD improvements. This is due to both the requirement of chain connectivity that converts geometrically nonphysical alignments into physical models and the optimized TASSER force field, which is a combination of consensus tertiary restraints from multiple templates and various statistical energy terms (Zhang et al., 2003). This optimal force field can provide better side-chain and backbone packing and is able to drive the template fragments on average closer to native in the Monte Carlo simulations.

Unaligned loops/tails modeling

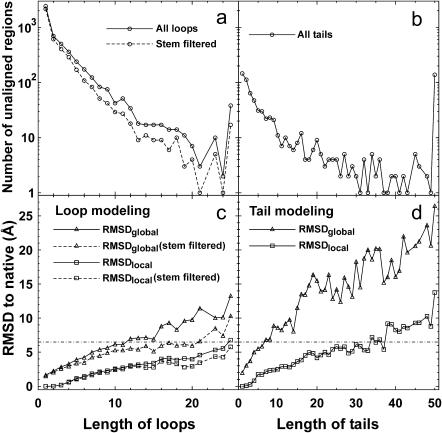
In Fig. 5, we show the results of TASSER modeling for the unaligned loop and tail regions. Here, an unaligned loop (tail) region is defined as a piece of continuous sequence that has no coordinate assignments in the middle (terminus) of a target protein from the PROSPECTOR_3 threading alignments.

FIGURE 5.

(a and b) Size distribution of the unaligned loops and tails, with the last points including all loops (tails) of length above 25 (50) residues. The solid lines connect the data points denoting all loops and tails. The dashed lines signify those loops with good stem backbones having a RMSD to native below 4 Å. (c and d) Average RMSD to native of the unaligned loops and tails by TASSER modeling as a function of the size of the modeled regions. RMSD_local (□) denotes the root-mean-square deviation with direct superposition of native and the modeled regions; RMSD_global (▵) is the root-mean-square deviation after the superposition of up to five neighboring stem residues in both sides of the loops or in a single side of the tails. The dashed-dotted line signifies a RMSD cutoff of 6.5 Å. The solid lines connect the data points denoting the results for all modeled loops/tails; the dashed lines denotes the results for the loops with good stem backbones.

There are in total 4951 unaligned loop regions ranging from 1 to 117 residues in length in all 745 target proteins. In Fig. 5 a, we show the distribution of the unaligned loops as a function of loop length, where the last point includes all the loops of length greater than or equal to 25 residues. For each unaligned loop region, two types of modeling errors are calculated (Fiser et al., 2000): RMSD_local denotes the root-mean-square deviation between the native and the modeled loop with direct superposition of the unaligned region; RMSD_global is the root-mean-square-deviation between native and the modeled loop after superposition of up to five neighboring stem residues on each side of the loop. The value of RMSD_local measures the modeling accuracy of the local conformation, whereas RMSD_global measures both the accuracy of the local conformation and the global orientation of the unaligned loop regions. As shown in Fig. 5 c, TASSER has decreased model accuracy with increasing loop length. If we take a cutoff of 6.5 Å, TASSER can handle the local conformation as assessed by RMSD_local for an unaligned loop region up to at least 25 residues long (here we note that the last point in Fig. 5 c is an average of all the loops having the length above 25 residues). But when considering RMSD_global, TASSER can have an average RMSD below 6.5 Å for the loops under 12 residues.

The accuracy of loop modeling is obviously influenced by the accuracy of the neighboring stem backbone. For example, if the distance between the two stem backbones is much larger than that in the native structure, the loop conformation will tend to be extended because of the constraint of geometric connectivity even if the force field favors a compact loop conformation and vise versa. If we only count those loops where the RMSD of the residues in the stem backbones is below 4 Å, there are 3821 loop regions in total. The modeling results of these loop regions are shown in Fig. 5 c marked as stem filtered. They clearly have higher accuracy than if we count all loops regions, especially for the big loops because the bigger loops have more opportunities to be embedded between distorted stem backbones (see Fig. 5 a). After removing those loops of distorted stem backbones, TASSER can have the average RMSD_global < 6.5Å for the unaligned loop regions up to 20 residues.

There are 785 unaligned regions at the N- or C-termini in the PROSPECTOR_3 alignments, with lengths ranging from 1 to 173 residues. Some of the big tails include an entire individual domain in multidomain proteins. The size distribution of the unaligned tails is presented in Fig. 5 b, with the last point including all tails greater than or equal to 50 residues. In comparison with loop modeling, because of a lack of a second spatial constraint on the free end of the tails, the orientation of the unaligned tails can be seriously misplaced, even though the local conformation can be correct. As shown in Fig. 5 d, TASSER has an average RMSD_global below 6.5 Å for tails under seven residues long. Here, the RMSD_global for tails is defined as the root-mean-square deviation between the modeling region and native after a superposition of five neighboring residues on the stem of the tail. For local tail conformations, TASSER can generate RMSD_local < 6.5 Å for tails up to 35 residues long (Fig. 5 d).

Most of the unaligned loop and tail regions in PROSPECTOR_3 alignments are of small size (see Fig. 5, a and b), which are relatively easier to model because of the limited configuration entropy. If we only focus on the loop/tail regions greater than or equal to four residues in size, there are in total 1345 unaligned loops with an average length of 8.1 residues; there are 464 unaligned tails with an average length of 52.6 residues.

We summarize in Table 2 the RMSD distribution for loops and tails with length greater than or equal to four residues. In ∼42% (561/1345) of the cases, TASSER loop modeling has acceptable accuracy with RMSD_global < 4 Å. The average RMSD_global and RMSD_local for these 1345 loops are, respectively, 5.03 and 1.82 Å. If we consider the loops with good stem backbones, 59% (497/837) of loops have a RMSD_global < 4 Å; and the average RMSD_global and RMSD_local for these 837 loops are 4.03 Å and 1.47 Å, respectively. For the tails, 53% (246/464) of the cases have a RMSD_local below 4 Å. Considering the global conformation of tails, only 11% (50/464) of the tails have RMSD_global below 4 Å. Again, the data show much better control of local conformation than the global orientation for tails in TASSER modeling. This is reminiscent of the problem TASSER has with predicting domain-domain orientations.

TABLE 2.

TASSER modeling result for 1809 unaligned loop/tail regions of length greater than or equal to four residues

	Loops*		Tails†
	RMSDglobal‡	RMSDlocal§	RMSDglobal‡	RMSDlocal§
Total number¶	1345 (837)	1345 (837)	464	464
NRMSD<1Å‖	55 (55)	502 (400)	3	46
NRMSD<2Å	167 (166)	887 (617)	12	133
NRMSD<3Å	338 (327)	1119 (744)	28	194
NRMSD<4Å	561 (497)	1241 (804)	50	246
NRMSD<5Å	810 (670)	1280 (819)	73	279
NRMSD<6Å	990 (773)	1314 (830)	99	304
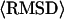**	5.03 (4.03) Å	1.82 (1.47) Å	15.33 Å	6.38 Å

^*Result for unaligned loop regions. The data in parentheses is for the loops with RMSD of the stem residues below four Å.

^†Result for unaligned tail regions.

^‡RMSD between native and the modeling loops (tails) after superposition of up to five neighboring stem residues on both sides (single side) of the modeling regions if applicable.

^§RMSD between native and the modeling loops/tails with direct superposition in the modeling regions.

^¶Total number of the modeling regions.

^‖Number of targets with a RMSD to native below the specific threshold values.

^**Average values of the RMSD to native for all unaligned loop/tail regions with length greater than or equal to four residues.

Membrane proteins

Membrane proteins are usually difficult to crystallize (Baleja, 2001; Levy et al., 2001). In the PDB library (Berman et al., 2000) only <2% of experimental structures belong to membrane proteins, which is much less than the estimated fraction of membrane proteins in a given genome (∼30%) (Ikeda et al., 2003; Stevens and Arkin, 2000). The small number of available solved structures and topologies considerably limit the applicability of traditional comparative modeling techniques to membrane protein structure prediction. On the other hand, the increasing strength of hydrogen bonding (White and Wimley, 1999) in the membrane causes the backbone to form very regular secondary structures (helices or β-sheet). The majority of conformational variances are from the secondary structure arrangements and various loop connections. There structural characteristics are consistent with the TASSER methodology, which was designed for rearranging the well-aligned rigid fragments from threading templates and building the loop regions by CAS ab initio modeling (see Methods).

The folding results of 18 large membrane proteins in current benchmark set are summarized in column 3 of Table 3. In one-third of the cases, TASSER generates at least one model in the top five that has a RMSD to native below 5.5 Å. In column 2 of the table, we also show the TASSER folding results of 20 membrane proteins from the representative benchmark set of smaller proteins (41 ∼ 200 residues), which has a slightly better success rate of 45% because of their smaller size. The overall folding rate in the combined membrane benchmark is ∼40% (15/38).

TABLE 3.

Summary of TASSER predictions for membrane proteins

Protein length	41–200*	201–300†	All
Total number	20	18	38
NRMSD<2.0Ň	2	2	4
NRMSD<2.5Å	2	3	5
NRMSD<3.0Å	2	3	5
NRMSD<3.5Å	4	5	9
NRMSD<4.0Å	5	5	10
NRMSD<4.5Å	5	5	10
NRMSD<5.0Å	6	5	11
NRMSD<5.5Å	8	6	14
NRMSD<6.0Å	9	6	15
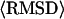§	6.99 Å	12.01 Å	9.37 Å

^*Result taken from previous TASSER performance on the representative benchmark with length from 41 to 200 residues (Zhang and Skolnick, 2004a).

^†Result of current runs for the representative benchmark with length from 201 to 300 residues.

^‡Number of targets that have the best model in top five with RMSD to native below specific threshold values.

^§Average values of the RMSD to native for all membrane proteins.

Among these 15 foldable cases, PROSPECTOR_3 hit at least one other nonhomologous transmembrane template in 10 cases, and in the remaining five cases, PROSPECTOR_3 hit globular proteins but with regular secondary backbone structures consistent with the target structures, which provides the opportunity for TASSER to assemble the global fold. The global alignments in PROSPECTOR_3 are sometimes incorrect. As shown in Table 1, the average RMSD in the PROSPETOR_3 alignments of all 18 membrane proteins with length greater than 200 residues is 10.7 Å. After TASSER refinement, the RMSD for the membrane proteins in the aligned region is reduced to 7.5 Å. For the 20 membrane proteins whose length is below 200 residues, the average RMSD in the aligned regions for initial threading alignments and final refined models are 8.6 Å and 5.0 Å, respectively.

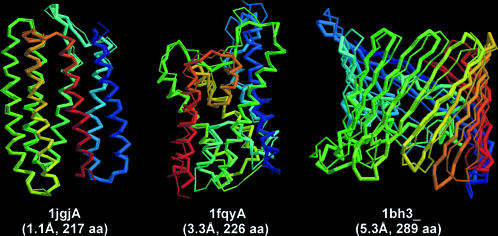
In Fig. 6, we show three typical examples of membrane proteins predictions, 1jgjA, 1fqyA, and 1bh3_, with the well-known GPCR rhodopsin protein 1jgjA having the highest accuracy. The best template hits by PROSPECTOR_3 for 1jgjA, 1fqyA, and 1bh3 are 1ap9_ (1.47 Å over 96% coverage), 1fx8A (5.20 Å over 92% coverage), and 2por_ (13.44 Å over 88% coverage). The final models in these three cases have a RMSD to native of 1.1/0.89 Å, 3.3/3.1 Å, and 5.3/5.2 Å with full-length/aligned regions, respectively. These data show that TASSER has the potential to draw the stem fragments closer to native with respect to the threading templates and build reasonable loops for the membrane proteins as well.

FIGURE 6.

Three representative foldable examples of transmembrane proteins by TASSER. The thin lines denote the C_α-backbone of experimental structures, and the thick lines are the predicted models. Blue to red runs from the N- to C-terminus. Below the structures are the PDB code, RMSD between the model and native structure, and the protein size.

Since the homologous proteins have been exclusively removed from our threading template library, the average sequence identity between targets and templates is low. For the 38 membrane proteins, the average sequence identity between the target and the template of the highest Z-score is 20.2%, below the twilight zone. There is, however, a slight correlation between the sequence identity and the target foldability: For the 15 foldable targets, the average sequence identity is 23.4%; for the 23 nonfoldable cases, the average sequence identity is 18.2%.

There is no significant difference between the loop modeling for membrane proteins and that for nonmembrane proteins. For the 18 big membrane proteins of size from 216 to 299 residues, there are 31 unaligned loops with length greater than or equal to four residues. The average values of RMSD_global and RMSD_local for these loops are 5.36 Å and 2.04 Å, respectively, which are comparable with the values of 5.03 Å and 1.82 Å for all loops including both membrane and nonmembrane proteins (see Table 2). The small difference between the membrane and nonmembrane proteins may be due to the fact that the membrane proteins on average have a worse global quality in comparison with nonmembrane proteins. For example, if we only count the 19 loops with RMSD of stem residues below 4 Å, the average values of RMSD_global and RMSD_local are 4.01 Å and 1.49 Å, respectively, which are almost the same as the corresponding values for all loops in Table 2.

Comparison of TASSER predictions with structures determined by NMR

The structures determined by either x-ray crystallography or NMR experiments are almost always nearly identical (Branden and Tooze, 1999). To compare the accuracy of the models predicted by TASSER to that of protein structures determined by NMR, we calculate the centroid of the set of structures provided by NMR experiments and compare the deviation of the TASSER models to the NMR structure centroid with that of the individual NMR structure located at the maximal distance from the centroid. Since the set of NMR models equally well satisfy the experimental data, the maximal distance between the centroid and the individual structures represents the inherent uncertainty and resolution of the NMR structure. The reason we compare the TASSER models to NMR data rather than x-ray structural data is that three-dimensional structures in NMR are usually derived from distance/contact constraints from their nuclear Overhauser effect (NOE) spectrum, and a collection of models consistent with the experimental restraints is often provided. Thus, there is an envelop of experimental structures to which we can readily compare the quality of our predictions to assess whether or not they are distinguishable.

In our complete benchmark set of 2234 proteins (including 1489 targets between 41 to 200 residues and 745 targets between 201 to 300 residues), there are 503 targets whose experimental structures are determined by NMR; 92% (463) are below 150 residues, a fact due to the difficulty of applying NMR spectroscopy to the structure determination of larger proteins (Branden and Tooze, 1999). Among these 503 NMR targets, there are 363 proteins with 5 ∼ 56 individual models that simultaneously satisfy the NMR spectra (for the other 140, the authors just provide the minimized average structure).

To calculate the structure centroid, for each of the 363 proteins, we superimpose all the NMR models to the first model in the PDB record and average the coordinates of the corresponding residues after superposition. Then, we calculate the maximal root-mean-square deviation of the individual models from the structure centroid, RMSD_NMR. For the 363 NMR targets, the average value of RMSD_NMR = 2.64 Å. For the models predicted by TASSER, we also calculate the RMSD of the theoretical models from the NMR structure centroid. The resultant average value for the TASSER models is 4.84 Å, which is considerably higher than that of NMR experiments. In 72 cases (27 α-proteins, 23 β-proteins, and 22 αβ-proteins), however, the RMSD of the theoretical models from the NMR centroid is smaller than RMSD_NMR. Among the 72 cases, seven cases (i.e., 1cw5A, 1g9pA, 1h9fA, 1i5jA, 1imuA, 2prp_, and 3lriA) are classified by PROSPECTOR_3 as Medium targets, with the best templates having an average RMSD to native 6.9 Å and an average alignment coverage of 60.6%. All other 65 cases are Easy targets, with PROSPECTOR_3 templates having average RMSD to native 4.1 Å and 83.9% alignment coverage.

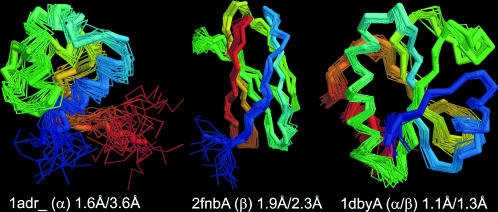
In Fig. 7, we present three typical examples of the superposition of TASSER models on the NMR structures for 1adr_ (an α-protein), 2fnbA (a β-protein), and 1dbyA (an αβ-protein). The maximal RMSD of NMR models from their centroid for the 1adr_, 2fnbA, and 1dbyA are 3.6 Å, 2.3Å, and 1.3 Å, respectively, whereas the RMSD of the TASSER models to the centroids are 1.6 Å, 1.9 Å, and 1.1 Å, respectively. These results show that, in ∼20% of cases, TASSER generates models of accuracy comparable to the NMR experimental methods where the predicted structures are closer to the NMR centroid structure than that of the farthest NMR structure.

FIGURE 7.

Three representative examples of TASSER predicted models that are structurally closer to the NMR structure centroid than some of individual NMR structures. The thick backbone shows the rank-one models predicted by TASSER; the wire frame presents the structures satisfying the NMR distance constraints equally well. Blue to red runs from the N- to C-terminus. The RMSD of TASSER models to the NMR centroid for 1adr_ (α-protein), 2fnbA (β-protein), and 1dbyA (αβ-protein) are 1.6 Å, 1.9 Å, and 1.1 Å, respectively; the maximal RMSD of NMR models to the centroid are 3.6 Å, 2.3 Å, and 1.3 Å, respectively.

CONCLUDING REMARKS

TASSER's ability to fold medium to large size proteins is systematically examined using a comprehensive benchmark protein test set that covers all PDB structures from 201 to 300 residues at the level of 35% sequence identity; including 487 big single domain proteins, 258 multiple domain proteins, and 18 transmembrane proteins.

For approximately three-fifths of larger single domain proteins, TASSER can generate models ranked in the top five that have a RMSD to native below 6.5 Å. For multidomain proteins, the success rate drops to approximately two-fifths; although in two-thirds of the multiple domain proteins, the individual domains of the complex are correctly predicted. Further development of the TASSER force field to control the interdomain orientation is required to improve the quality of the predictions for multiple domain complexes. Keeping in mind that many multidomain proteins with high sequence identity have different domain orientations, an immediate follow-up project will be the construction of an extended multidomain orientation library, which allows TASSER simulations to select suitable domain orientations among the homologous templates. For membrane proteins that have a very limited number of solved template structures, ∼40% of such transmembrane proteins from 41 to 300 residues can be folded to a RMSD below 6 Å. Finally, when TASSER models are compared with the set of experimental structures determined by NMR, ∼20% of the TASSER models are closer to the centroid of the set of NMR structures than the farthest NMR structure consistent with experimental data.

For all the categories of the target proteins, TASSER models show obvious improvement with respect to the initial threading templates from PROSPECTOR_3 (Skolnick et al., 2004). Over the same aligned regions, the average RMSD of all 745 proteins is reduced by TASSER modeling from an initial average RMSD of 7.2 to 5.6 Å, and the number of cases with a RMSD to native < 6.5 Å increases from 463 to 552.

For the unaligned loop regions with good stem backbone conformations (where the RMSD of the stem residues is below 4 Å), the TASSER ab initio modeling approach can generate reasonable loop models with an average RMSD_global < 6.5 Å for loops up to 20 residues long. For the loops of size greater than or equal to four residues (8.1 residues on average), 59% (497/837) have a global RMSD below 4 Å. For the unaligned tail regions with an average length of 52.6 residues, although in most cases the correct global orientation of the tails are not reproduced, TASSER generates tails whose RMSD_local is below 4 Å in 53% (246/464) of the cases.

One purpose of this work is to focus on proteins greater than 200 residues in length, a size range where most enzymes and other functionally important proteins are often found. Although there is still considerable room for improvement of TASSER methodology, especially for multiple domain complexes and membrane proteins, the results of the large-scale benchmark test reported here suggest that reliable predicted structures by automated computational approaches is becoming a reality for at least a subset of non-/weakly homologous large size proteins.