Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Oct;87(4):2818–2827. doi: 10.1529/biophysj.103.037218

Direct Comparison of the Spread Area, Contractility, and Migration of balb/c 3T3 Fibroblasts Adhered to Fibronectin- and RGD-Modified Substrata

Padmavathy Rajagopalan 1, William A Marganski 1, Xin Q Brown 1, Joyce Y Wong 1
PMCID: PMC1304700  PMID: 15454473

Abstract

Native proteins are often substituted by short peptide sequences. These peptides can recapitulate key, but not all biofunctional properties of the native proteins. Here, we quantify the similarities and differences in spread area, contractile activity, and migration speed for balb/c 3T3 fibroblasts adhered to fibronectin- (FN) and Arg-Gly-Asp (RGD)-modified substrata of varying surface density. In both cases spread area has a biphasic dependence on surface ligand density (σ) with a maximum at σ ∼ 200 molecules/μm2, whereas the total traction force increases and reaches a plateau as a function of σ. In addition to these qualitative similarities, there are significant quantitative differences between fibroblasts adhered to FN and RGD. For example, fibroblasts on FN have a spread area that is on average greater by ∼200 μm2 over a ∼40-fold change in σ. In addition, fibroblasts on FN exert ∼3–5 times more total force, which reaches a maximum at a value of σ ∼5 times less than for cells adhered to RGD. The data also indicate that the differences in traction are not simply a function of the degree of spreading. In fact, fibroblasts on FN (σ ∼2000 μm−2) and RGD (σ ∼ 200 μm−2) have both similar spread area (∼600 μm2) and migration speed (∼11 μm/h), yet the total force production is five times higher on FN than RGD (∼0.05 dyn compared to ∼0.01 dyn). Thus, the specific interactions between fibroblasts and FN molecules must inherently allow for higher traction force generation in comparison to the interactions between fibroblasts and RGD.

INTRODUCTION

Specific interactions between cell surface receptors and extracellular matrix (ECM) molecules underlie a wide variety of processes such as cell adhesion, traction force generation, and migration (Akiyama et al., 1985; Zamir et al., 1999; Geiger et al., 2001). These interactions collectively give rise to even more complex physiological phenomena such as tumor metastasis, wound healing, and tissue morphogenesis (Trinkaus, 1969; Harris, 1986; Lauffenburger and Horwitz, 1996). Cells exert tractional forces through adhesive contacts (e.g., focal adhesions), and tractional forces in turn are required for cell migration. However, cell migration is not required for traction force generation. In fact, cells can exhibit low migration rates and yet exert substantial traction forces through contractile proteins. Moreover, both positive and negative correlations between traction and migration have been observed, depending on the cell type (Shreiber et al., 2003).

The relationship between traction and migration also depends on the nature of the ECM, and numerous studies have investigated how cell-ECM interactions control adhesion and migration (Brandley and Schnaar, 1988; Massia and Hubbell, 1990; DiMilla et al., 1993; Garcia et al., 1999; Maheshwari et al., 2000; Hersel et al., 2003). In contrast, there have been relatively few studies that have directly probed the effect of specific cell-ECM interactions on traction force generation (Gaudet et al., 2003; ReinhartKing et al., 2003) or directly compared adhesion, traction, and migration (Gaudet et al., 2003). These types of studies are critical for engineering the cell-biomaterial interface to recapitulate phenomena such as wound healing and tissue morphogenesis. Here, we directly compare cellular response on the well-studied protein fibronectin (FN) and its cell adhesion peptide mimic Arg-Gly-Asp (RGD). Although there have been numerous qualitative studies comparing effects of RGD and FN, to our knowledge, the relationships between cell spreading, migration, and traction force generation on RGD- versus FN-modified substrata have not yet been thoroughly explored.

The cellular response to FN depends not only on the surface density of the molecule, but also its conformation. For example, recent in vitro studies have shown that the conformation of adsorbed FN is not only dependent on the properties of the substrate, but that these changes in FN conformation also lead to differences in cellular response (Garcia et al., 1999). Furthermore, the precise control of the surface conformation of ECM proteins such as FN requires site-specific immobilization and is rather challenging. In contrast, it is much easier to manipulate and preserve the conformation of short synthetic peptide sequences. Therefore, peptide sequences are frequently used in place of the native protein. The best example is RGD, which is found in the cell-binding domain of FN (Pierschbacher and Ruoslahti, 1984; Ruoslahti, 1996) and has been incorporated into a wide variety of otherwise nonadhesive substrata to promote cell adhesion, spreading, and focal contact formation (Massia and Hubbell, 1990, 1991). However, several studies have also shown that RGD-modified substrata do not completely recapitulate the same phenotype and behavior observed in cells adhered to FN-modified substrata. For instance, cells adhered to RGD-modified substrata exhibit significant differences in migration speed (Maheshwari et al., 2000), spreading and focal contact formation (Streeter and Rees, 1987) compared to cells adhered to FN-modified substrata.

Although these studies clearly show differences in cell behavior on FN- versus RGD-modified substrata, they do not give any information regarding the traction stresses exerted by these cells. The lack of quantitative comparisons of cell traction on FN- and RGD-modified substrata can be attributed to the fact that methods to quantify cell traction have only recently been developed (Dembo and Wang, 1999; Balaban et al., 2001; Tan et al., 2003). Because focal contact formation has been linked to traction force generation (Balaban et al., 2001; Tan et al., 2003) and also because cells exert traction forces during migration (Lee et al., 1994; Oliver et al., 1994; Munevar et al., 2001b), we hypothesize that cellular traction force generation will differ on FN- and RGD-modified substrata.

To quantify the differences and similarities between RGD and FN on cellular response, we directly compare the spread area, contractility, and migration of balb/c fibroblasts that are adhered to polyacrylamide substrata modified with varying surface densities of RGD and FN. Polyacrylamide substrata are utilized because they are nontoxic, elastic, and require the covalent attachment of a specific ligand to promote cell adhesion. Thus, we are able to follow the effects of both ligand type and surface density on three different aspects of cellular behavior. Spread area and contractility are measured using traction force microscopy (Dembo and Wang, 1999; Lo et al., 2000; Beningo et al., 2001; Munevar et al., 2001a,b; Wang et al., 2001; Gaudet et al., 2003; Marganski et al., 2003a; Doyle et al., 2004). Cell migration is quantified using a random walk model (Dunn, 1983; DiMilla et al., 1992b). This systematic approach provides a quantitative functional comparison of cellular behavior on RGD- and FN-modified substrata.

MATERIALS AND METHODS

Synthesis of modified polyacrylamide (PAAM) substrata

PAAM substrata are synthesized by copolymerizing acrylamide (BioRad, Hercules, CA), bis-acrylamide (BioRad) and acrylic acid N-hydroxy succinimide (NHS) ester (Sigma-Aldrich, St. Louis, MO) (Brandley and Schnaar, 1988; Brandley et al., 1990). Specifically, the polymerization mixture contains 8% acrylamide, 0.04% bis-acrylamide, 10 μmol/ml acrylic acid NHS ester, 2 ml 0.25 M HEPES (4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid; Sigma-Aldrich), 200 μl 0.75 μm-diameter fluorescent marker beads (Fluoresbrite carboxylate microspheres; Polysciences Inc., Warrington, PA), and 15 μL TEMED (N,N,N′,N′- tetramethylethylenediamine; BioRad). The pH of the solution is adjusted to 6.0 by careful addition of 1 M HCl: it is critical to use a pH of 6.0, since a lower pH can inhibit polymerization whereas a higher pH can hydrolyze the NHS ester. Polymerization is initiated by adding 10% aqueous ammonium persulfate and the solution is cast onto glass cover slips that are activated with 3-aminopropyltrimethoxysilane and glutaraldehyde (Wang and Pelham, 1998).

FN or the hexapeptide GRGDSP (Gly-Arg-Gly-Asp-Ser-Pro) is covalently linked to the substratum through the NHS ester. Various plating concentrations (Table 1) of human plasma FN (Invitrogen, Carlsbad, CA) and the hexapeptide GRGDSP (Invitrogen) are prepared in cold, sterile PBS (phosphate-buffered saline; Invitrogen) and HEPES (pH = 8). The PAAM substrata are incubated in the peptide or protein solution at 4°C for 24 h. After the incubation period, ethanolamine (1 μl/ml in 50 mM HEPES and 10% ethanol) is added to react (15 min) with the remaining hydrolyzed ester groups to prevent nonspecific cell adhesion. Lastly, before cell culture, the substrata are rinsed in cold deionized water for 1 h and sterilized under UV radiation for 30 min.

TABLE 1.

Relationship between plating and surface density for both fibronectin (FN) and GRGDSP (RGD)

Concentration
Number of cells
Substrate Plating σ 〈A〉, 〈|F|〉, 〈|T|〉 〈S〉
(μg/ml) (Molecules/μm2) n n
FN 0.5 10 - 9
FN 1.56 30 - 16
FN 3.13 60 8 -
FN 6.25 120 14 -
FN 12.5 240 15 27
FN 25 475 24 35
FN 50 950 21 37
FN 100 1900 15 40
RGD 25 50 13 23
RGD 50 100 12 25
RGD 100 200 10 25
RGD 250 500 17 27
RGD 500 1000 8 30
RGD 750 1500 6 -
Open in a new tab

Polyacrylamide substrata were modified with indicated plating concentrations of FN or RGD. The immobilized surface density (σ) of FN or RGD on the substratum is given for each plating concentration. The total number of cells for each measurement is indicated by n. 〈|T|〉, 〈|F|〉, 〈A〉, and 〈S〉 are the population-averages of the traction magnitude, total absolute force, projected area, and migration speed, respectively.

Quantification of FN and RGD covalently attached PAAM substrata

The coupling efficiencies of FN and RGD to polyacrylamide substrata are quantified using radioactivity. Briefly, I-125 labeled FN (MP Biomedicals, Irvine, CA) and I-125 labeled YRGDS (Phoenix Pharmaceuticals, Belmont, CA) are added to unlabeled FN and RGD at a ratio of 0.8 μCi/mg FN and 10 μCi/mg GRGDSP. These mixtures are then covalently linked via the NHS ester to the polyacrylamide substrata. Finally, the substrata are rinsed in cold water three times, and the radioactivity of each gel is quantified with a gamma-counter (Cobra Auto-Gamma B5005 Gamma Counter, Packard Instruments, Meriden, CT). These radioactivity values are then converted into mass amounts using a standard curve that is generated by measuring the radioactivity of known amounts of I-125 labeled FN and RGD.

Measurement of the mechanical properties of PAAM substrata

The mechanical properties of PAAM substrata are determined by a bulk tensile measurement (Pelham and Wang, 1997). Briefly, PAAM samples are polymerized to form cylindrical structures with a diameter of ∼1 cm and length ∼10 cm. The Young's modulus is determined by the stress-strain curve obtained by adding known weights to the bottom of a suspended PAAM sample and then measuring the changes in the length of the sample.

Cell culture and microscopy for cell area and traction

Balb/c 3T3 fibroblasts (American Type Culture Collection, Manassas, VA) are maintained at 37°C and 5% CO2 in Dulbecco's Modified Eagle Medium (DMEM; Invitrogen) supplemented with penicillin-streptomycin-L glutamine (Invitrogen) and 10% calf serum (Hyclone, Logan, UT). For cell area and traction measurements, cells are plated on the RGD- and FN-PAAM substrata at a low cell density (∼1000 cells/cm2) in the presence of 10% calf serum. After ∼15 h of incubation, the substratum is mounted on a Zeiss Axiovert S 100 microscope equipped with a 40×, 0.75 N.A. phase objective, a motorized stage (Ludl, Model No. 99D008-Z1, Hawthorne, NY), and a stage incubator that maintains the environment at 37°C and 5% CO2. Phase-contrast images of the cell and fluorescent images of the marker beads within the substratum are collected using a cooled CCD camera (Princeton Instruments, Trenton, NJ) and the Metamorph imaging software (Universal Imaging, Downingtown, PA).

Calculation of cellular traction forces

Traction forces exerted by individual balb/c 3T3 fibroblasts are measured using traction force microscopy (Dembo and Wang, 1999; Lo et al., 2000; Beningo et al., 2001; Munevar et al., 2001a,b; Wang et al., 2001; Gaudet et al., 2003; Marganski et al., 2003a; Doyle et al., 2004). Briefly, an individual cell is identified on the substratum that is isolated from other cells. A phase image of the cell is taken to capture its morphology. In addition, fluorescent images of the marker beads within the substratum are recorded while the cell is adherent (the so-called “strained” image) and after it has been removed using trypsin (the so-called “unstrained” image). The deformation of the substratum due to the activity of the cell is measured using an optical flow-based algorithm that matches patterns of beads between the unstrained and strained fluorescent images (Marganski et al., 2003b). The cellular traction field is then calculated by solving an ill-posed inverse problem based on linear elasticity theory when given the set of substratum deformations, the Young's modulus and Poisson's ratio of the substratum, and the boundary of the cell (Dembo et al., 1996; Dembo and Wang, 1999).

The overall force production of a cell can be determined by computing the magnitude of the total traction force 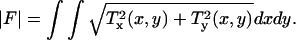Inline graphic In this expression, T(x,y) = [Tx(x,y), Ty(x,y)] represents the continuous field of traction vectors acting at spatial positions (x,y) within the cell boundary. The cell area, A, is determined by integrating the region that is enclosed by the boundary of the cell. Dividing |F| by A yields the average traction magnitude, |T|, a measure of the average absolute force per unit area exerted within the cell.

Quantifying cell migration

Time-lapse microscopy equipped with a motorized stage is used to capture phase-contrast images of single cells at 15 min intervals up to 12 h. Fields are chosen at random and cells that come into contact with each other, undergo mitosis, or leave the field of view are not analyzed. The centroid of each cell is tracked using Metamorph imaging software, and mean-squared displacements (〈d2〉) of the centroid of each cell are calculated. The speed (S) and persistence time (P) of each cell are obtained by fitting 〈d2〉 as a function of time (t) to a random walk model equation 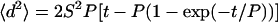Inline graphic (Dunn, 1983; DiMilla et al., 1992b). The Levenberg-Marquandt method for nonlinear least squares fitting is used to obtain S and P. The parameter P represents the mean period of time over which a cell continues to move in a particular direction before changing direction by ∼60°. Here, only values for S are reported.

Cytoskeletal staining

Immunofluorescence co-staining is performed to simultaneously observe actin filaments and focal adhesions containing paxillin. Cells are first fixed for 15 min in a 0.75% glutaraldehyde (Polysciences) solution in PBS. Sodium borohydride is then added to quench autofluorescence and, finally, 0.5% Triton X-100 is added to permeabilize the cell membranes. All solutions used thereafter in the staining protocol are prepared in a 1% BSA in PBS. To prevent nonspecific binding, goat serum (Sigma-Aldrich) is added at room temperature for 1 h. The cells are then incubated at 37°C with a mouse anti-paxillin monoclonal antibody (Chemicon, Temecula, CA) for a total period of 4 h. Rhodamine-phalloidin (Molecular Probes, Eugene, OR) is added 2 h subsequent to the addition of the primary paxillin antibody. Finally, a FITC-conjugated anti-mouse IgG secondary antibody (Sigma-Aldrich) is added to detect the presence of paxillin. The fluorescently-labeled samples are stored in a solution containing 1:3 (v/v) glycerol in PBS. Images are obtained with a Zeiss Axiovert S100 inverted microscope equipped with a cooled CCD digital camera and Metamorph imaging software.

Statistics

All quantitative data are expressed as a mean ± SE. The statistical significance between sets of data was determined using the Student's t-test. A value of p<0.05 was taken as statistically significant.

RESULTS

Substrate characterization

The bulk tensile measurement yields a Young's modulus of ∼30 kdyn-cm−2 for all substrata used in this study. We have also measured the Young's modulus using a Hertzian-based microindentation technique (Landau and Lifshitz, 1986) and find that the values for the Young's modulus obtained from these two different techniques are in good agreement (data not shown). The thickness of the polyacrylamide substrate is estimated to be ∼100 μm and a Poisson ratio of ∼0.3 is assumed (Li et al., 1993).

Quantification of the surface density of FN and RGD

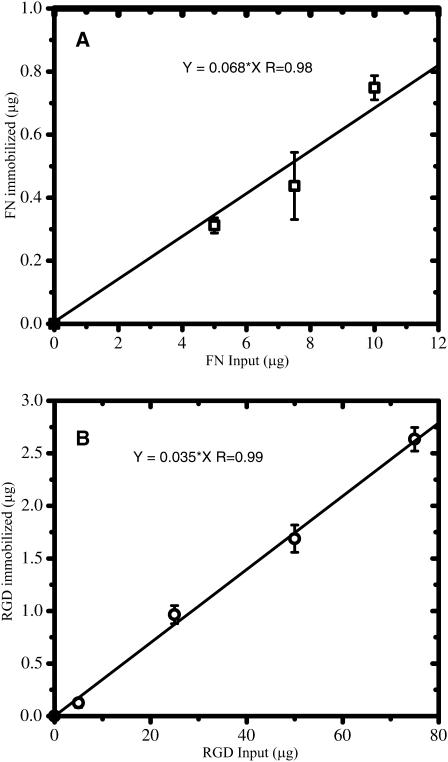
We observe a strong linear correlation between input and immobilized mass for both FN and RGD (Fig. 1). This linearity persists over an ∼10-fold change in input FN and over an ∼80-fold change in input RGD. Fitting each data set with a linear curve illustrates that the binding efficiency is ∼6.8% for FN and ∼3.5% for RGD. One reason for the low coupling efficiency is that the NHS-ester can be hydrolyzed in water (Lomants and Fairbanks, 1976; Brinkley, 1992).

FIGURE 1.

FIGURE 1

Open in a new tab

Quantitation of the coupling efficiency of FN (A) and RGD (B) to polyacrylamide substrata. The relationship between the amount of input ligand and the amount immobilized on the substratum determined by radiolabeling is shown. Linear curve fitting indicates that the coupling efficiency is ∼6.8% (R ∼ 0.98) for FN (A) and ∼3.5% (R ∼ 0.99) for RGD (B). These curves were then used to convert the input concentration of FN or RGD (in μg/ml) into an immobilized surface density (in molecules/μm2).

After determining the coupling efficiencies, the immobilized surface densities of FN (σFN) and RGD (σRGD) were calculated by first converting the immobilized mass amounts into the number of immobilized molecules. The molecular weights used were ∼440 kDa for FN and ∼588 Da for RGD. The number of immobilized molecules of FN and RGD were then normalized by the surface area over which they are distributed. FN is a large molecule and therefore cannot penetrate the surface of the substratum. Evidence supporting low penetration of FN is that we do not observe significant diffusion of FITC-dextran (20 kDa; Stokes radius ∼3.3 nm, Kodama et al., 2000) when it is entrapped in the gel (data not shown). The dimensions of FN have been observed to be 1), an elongated structure (∼150 × 3 nm, H. Erickson, personal communication) on hydrophilic surfaces (Bergkvist et al., 2003; Erickson and Carrell, 1983; Johnson et al., 1999); or 2), cylindrical with 60 nm length and 6 nm base diameter (DiMilla et al., 1992a). Therefore, it is unlikely that FN will penetrate the gel. In contrast, RGD is a small peptide that can penetrate the surface and is therefore distributed throughout the substratum. However, it has been shown that an adherent cell can only access the top ∼10 nm of a polyacrylamide substratum (Brandley and Schnaar, 1988). We therefore calculated the RGD concentration only in the top 10 nm of the gel.

Table 1 provides the immobilized surface densities of FN and RGD for the various input concentrations of ligand used in this study. These values were obtained using Fig. 1 and the calculations discussed in the above paragraph. The units are in molecules-μm−2, and from here on are abbreviated as μm−2.

Traction force microscopy

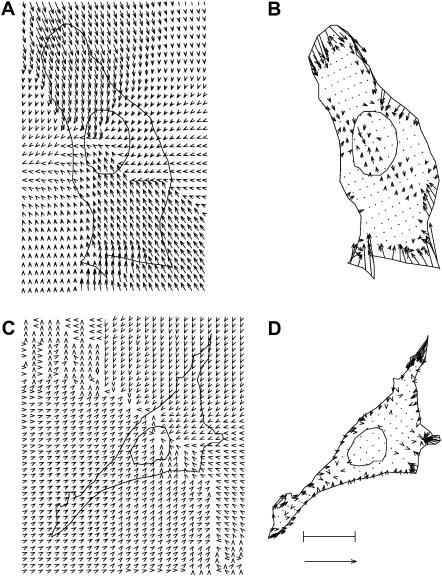
An illustration of the traction force microscopy technique is given in Fig. 2, A and B, for a balb/c 3T3 fibroblast adhered to a FN-modified substratum with a surface density of ∼200 μm−2. The cell shown was selected because it is closest to the population mean (n = 15) in terms of A, |F|, and |T| (denoted as 〈A〉, 〈|F|〉, and 〈|T|〉, respectively). Fig. 2 A displays a vector plot of the substratum displacements overlaid on top of the outline of the cell and its nucleus. Each displacement vector indicates the direction and amount of movement that a particular location within the substratum underwent due to the mechanical activity of the cell. The most-likely traction field that fits the set of substratum displacements is shown in Fig. 2 B. Each vector of the traction field indicates the direction and amount of force exerted at a specific location within the cell. Most of the significant tractions are exerted at the lamellae on the top, bottom, and right side of the cell with very small tractions within the interior in regions near the nucleus. Furthermore, the traction vectors along the edge of the cell tend to be directed toward the cell interior and appear to be contracting the cell inward. Overall, this cell is characterized by A ∼ 900 μm2, |T| ∼ 8.7 kdynes/cm2, and |F| ∼ 0.08 dyn.

FIGURE 2.

FIGURE 2

Open in a new tab

Traction force microscopy of a typical balb/c 3T3 fibroblast adhered to a substratum with σFN ∼ 200 μm−2 (A and B) and σRGD ∼ 200 μm−2 (C and D). The bar equals 9.4 μm and indicates the length scale. The arrow equals 9.4 μm for the experimental substratum displacement fields (A and C) and 96 kdyn/cm2 for the most-likely cellular traction fields (B and D). The cell adhered to the FN-modified substratum is characterized by A ∼ 900 μm2, |T| ∼ 8.7 kdyn/cm2, and |F| ∼ 0.08 dyn, whereas the cell adhered to the RGD-modified substratum is characterized by A ∼ 430 μm2, |T| ∼ 3.8 kdyn/cm2, and |F| ∼ 0.02 dyn.

Similarly, Fig. 2, C and D, show the results of a traction force microscopy experiment for a balb/c 3T3 fibroblast adhered to a RGD-modified substratum with a surface density of ∼200 μm−2. Note that the length scale, displacement vector scale, and traction vector scale are all the same as those illustrated in Fig. 2, A and B, and furthermore, that the cell is closest to the population mean (n = 10) in terms of 〈A〉, 〈|T|〉, and 〈|F|〉. Many aspects of the most typical cell on σRGD ∼ 200 μm−2 are similar to the most typical cell on σFN ∼ 200 μm−2. For instance, the cell on RGD also has three or four lamellae with significant tractions oriented toward the interior. Moreover, tractions near the nucleus are minimal. Although both the morphology and the spatial distribution of the tractions of these two most typical cells are similar, there are quantitative differences. These differences are apparent if one considers that the most typical cell on RGD with σRGD∼ 200 μm−2 is characterized by A ∼ 430 μm2, |T| ∼ 3.8 kdyn/cm2, and |F| ∼ 0.02 dyn. Therefore, even though the ligand density is the same, there are systematic differences in the overall cell properties due to the type of ligand.

Cell-to-cell variability in projected cell area and contractility

To completely characterize the effects of both surface density and ligand type on cellular behavior, experiments such as those depicted in Fig. 2 were carried out on a large sample size of cells at various surface densities of FN and RGD. See Table 1 for the surface densities studied and the sample size at each density. The cell-to-cell variability in the data at a low (∼50 μm−2), medium (∼200 μm−2), and high (∼2000 μm−2) surface density of FN and RGD is illustrated in Table 2. In general, the variance in |F|, A, and |T| is quite large at all three surface densities and both ligand types. For example, A varies ∼3.5-fold, |F| varies ∼25-fold, and |T| varies by ∼10-fold. Despite the large variance in the data, two specific trends are apparent. First, at any particular surface density, the population means 〈|A|〉, 〈|F|〉, and 〈|T|〉 are significantly greater for fibroblasts adhered to FN- compared to RGD-modified substrata (p < 0.05 for six out of nine comparisons). Second, for each ligand type, both 〈|F|〉 and 〈|T|〉 increase as σ increases: 〈|F|〉 increases ∼2.6-fold for FN and ∼4.7-fold for RGD, and 〈|T|〉 increases ∼2.2-fold for FN and ∼3.7-fold for RGD.

TABLE 2.

Cell-to-cell variability in A, |F|, and |T| at a low, medium, and high surface density of FN and RGD

AFN (μm2)
ARGD (μm2)
σ (μm−2) Min Mean ± SE Max Min Mean ± SE Max p-value
Low (∼50) 322 480 ± 55 872 197 359 ± 35 685 0.110
Medium (∼200) 360 860 ± 99 1290 314 595 ± 80 1070 0.048
High (∼2000) 413 640 ± 48 1000 266 423 ± 48 567 0.006
|F|FN (dyn ×10−3)
|F|RGD (dyn ×10−3)
σ (μm−2) Min Mean ± SE Max Min Mean ± SE Max p-value
Low (∼50) 6.0 19.8 ± 7.0 65.0 0.8 4.0 ± 0.7 9.0 0.059
Medium (∼200) 4.5 48.0 ± 9.0 118.0 1.4 12.0 ± 3.1 31.0 0.002
High (∼2000) 12.0 52.0 ± 8.0 141.0 2.3 18.8 ± 6.6 40.0 0.006
|T|FN (kdyn/cm2)
|T|RGD (kdyn/cm2)
σ (μm−2) Min Mean ± SE Max Min Mean ± SE Max p-value
Low (∼50) 1.4 3.7 ± 0.8 7.4 0.4 1.1 ± 0.1 1.9 0.016
Medium (∼200) 1.2 5.7 ± 1.0 12.8 0.5 1.9 ± 0.4 4.0 0.003
High (∼2000) 2.4 8.1 ± 1.3 24.1 0.8 4.1 ± 1.4 9.0 0.056
Open in a new tab

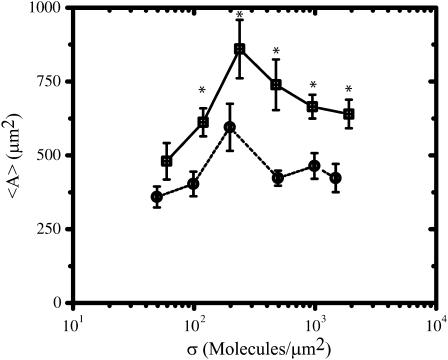
Effect of FN and RGD density on population average projected area

In general, we observe a similar dependence of the population average spread area (〈A〉) on σ for balb/c 3T3 fibroblasts adhered to FN- and RGD-modified substrata (Fig. 3). In both cases, 〈A〉 has a biphasic dependence on σ, reaches a maximum at σ ∼ 200 μm−2, and changes at most by a factor of ∼1.8 as σ is varied ∼40-fold. Despite these similarities there is one significant difference in the average spread area for cells on FN- and RGD-modified substrata. Specifically 〈A〉 is significantly higher by ∼200 μm2 for cells on FN compared to cells on RGD over almost the entire range of surface densities studied (p < 0.05 after σ exceeds ∼50 μm−2). Thus, even if the number of available FN and RGD molecules presented to a cell are equal, there is something inherent in the FN molecule that allows a cell to spread more effectively on FN than on RGD.

FIGURE 3.

FIGURE 3

Open in a new tab

Comparison of FN (□) and RGD (¡) surface densities on the population average spread area 〈A〉. Values are reported as an average ± SE. See Table 1 for the sample size n for each condition. Asterisk indicates that statistically significant differences (p < 0.05) are present between the FN and RGD data at the particular surface density of ligand.

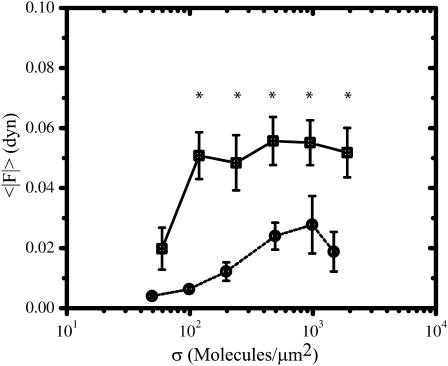
Effect of FN and RGD density on population average contractility

The population average total absolute force (〈|F|〉) increases and reaches a plateau as a function of σ for cells on both FN and RGD (Fig. 4). However, there are significant differences between the two data sets. For the case of RGD, 〈|F|〉 is ∼0.004 dyn at σ ∼ 50 μm−2, increases to ∼0.025 dyn at σ ∼ 500 μm−2, and maintains this value as σ increases to ∼2000 μm−2. In contrast, 〈|F|〉 is significantly higher (∼3–5-fold) for cells on FN compared to cells on RGD when σ exceeds ∼50 μm−2. Furthermore, 〈|F|〉 reaches a plateau at σ ∼ 100 μm−2 for cells on FN, which is ∼5 times less than the surface density needed for 〈|F|〉 to reach a plateau for cells on RGD.

FIGURE 4.

FIGURE 4

Open in a new tab

Comparison of FN (□) and RGD (¡) surface densities on the population average total absolute traction force 〈|F|〉. Values are reported as an average ± SE. See Table 1 for the sample size n for each condition. Asterisk indicates that statistically significant differences (p < 0.05) are present between the FN and RGD data at the particular surface density of ligand.

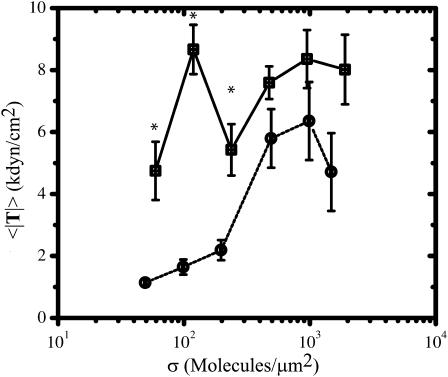
In contrast to the 〈|F|〉 and 〈A〉 data, there are only statistically significant differences in the population average traction magnitude (〈|T|〉) for cells adhered to FN- and RGD-modified substrata at low surface densities (Fig. 5). For instance when σ < ∼500 μm−2, 〈|T|〉 is ∼2–5-fold larger (p < 0.05) for cells adhered to FN-modified substrata. As σ reaches and exceeds ∼500 μm−2, the differences in 〈|T|〉 between cells adhered to FN- and RGD-modified substrata are no longer statistically significant and, therefore, are effectively eliminated. Specifically, as σ reaches ∼2000 μm−2, 〈|T|〉 asymptotes to ∼6–8 kdyn/cm2 for cells on FN and RGD.

FIGURE 5.

FIGURE 5

Open in a new tab

Comparison of FN (□) and RGD (¡) surface densities on the population average traction magnitude 〈|T|〉. Values are reported as an average ± SE. See Table 1 for the sample size n for each condition. Asterisk indicates that statistically significant differences (p < 0.05) are present between the FN and RGD data at the particular surface density of ligand.

Effect of FN and RGD density on population average migration speed

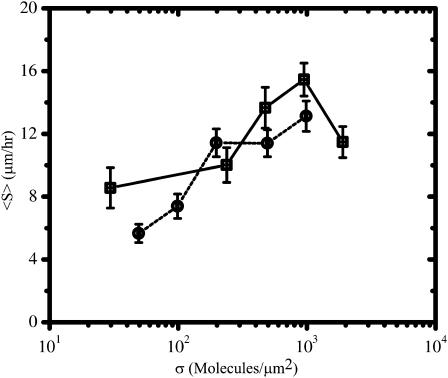
The trends of the population average migration speed (〈S〉) with σ are similar for balb/c 3T3 fibroblasts adhered to FN- and RGD-modified substrata (Fig. 6). In both cases, cells migrate fairly slowly at low surface densities (〈S〉 ∼ 6–8 μm/h at σ ∼ 50 μm−2). However, as σ is increased to ∼1000 μm−2, 〈S〉 rises steadily eventually approaching ∼13–14 μm/h. In the case of cells adhered to FN-modified substrata, 〈S〉 decreases slightly after σ exceeds ∼1000 μm−2.

FIGURE 6.

FIGURE 6

Open in a new tab

Comparison of FN (□) and RGD (¡) surface densities on the population average migration speed 〈S〉. Values are reported as an average ± SE. See Table 1 for the sample size n for each condition.

DISCUSSION

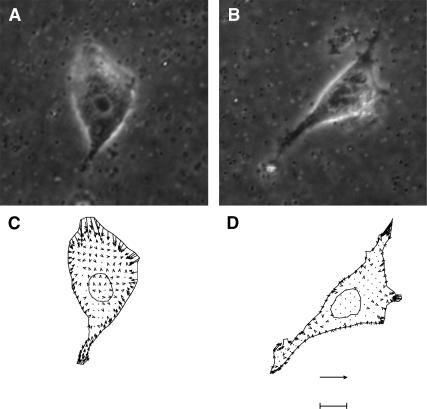
Since a large number of current reports in the literature utilize linear RGD to render surfaces biocompatible, it is important to investigate quantitative differences and similarities in cellular response between linear RGD- and FN-modified surfaces. This study is the first that directly and quantitatively compares the spread area, migration, and contractility for fibroblasts adhered to FN- and RGD-modified substrata. We note that 〈A〉 has a biphasic dependence on σ for both FN and RGD. We reported this biphasic dependence for the same cells on collagen and proposed a receptor-saturation model to explain our results (Gaudet et al., 2003). Our data also indicate that fibroblasts on FN are ∼2–5 times more contractile and have a spread area ∼200 μm2 greater than on RGD over a ∼40-fold change in ligand density. One may expect that the differences in contractility are simply due to the fact that cells on FN are spread to a greater degree. However, there is not a simple correlation between spread area and the amount of force production. As shown in Table 2, 〈|F|〉 is an increasing function of σ, whereas 〈A〉 is a biphasic function of σ for both FN and RGD. Moreover, to remove the influence of spread area on force generation, one could compare the overall force production of fibroblasts at particular surface densities of FN and RGD at which 〈A〉 is equal. This situation occurs at σFN ∼ 2000 and σRGD ∼ 200 μm−2 where 〈A〉 is ∼600 μm2 for both ligand types (see Fig. 3). We can compare the cells closest to the population mean at these two surface densities (Fig. 7). The phase-contrast images (Fig. 7, A and B) indicate that both cells are spread to the same extent and have polarized morphology with a few lamellae. However, the traction fields (Fig. 7, C and D) indicate that there are significant differences in the overall contractile output. Specifically, the cell on the FN-modified substratum generates twice as much total force (∼0.04 dyn) than the cell on the RGD-modified substratum (∼0.02 dyn). Thus, these data show that ligand type directly controls contractile activity and, furthermore, this control is independent of the amount of spreading.

FIGURE 7.

FIGURE 7

Open in a new tab

Contractility differences with equal spread area and migration speed. Phase contrast images and corresponding traction fields of a balb/c 3T3 fibroblast adhered to an FN- (A and C) and RGD- modified (B and D) substratum. The bar is 8 μm for the phase contrast images (A and B) and 120 kdyn/cm2 for the most-likely cellular traction fields (C and D). The surface density is ∼2000 μm−2 for FN and ∼200 μm−2 for RGD. These surface densities were chosen because the population average spread area (〈A〉 ∼ 600 μm2) and speed (〈S〉 ∼ 11.1 μm/h) are similar for cells on FN- and RGD-modified substrata, but the population average contractile output is different. Furthermore, the two cells shown were chosen because they represent the closest to the population mean in terms of 〈A〉, 〈|F|〉, and 〈|T|〉. The contractile output of the cell on FN is characterized by |T| ∼ 8.6 kdyn/cm2 and |F| ∼ 0.04 dyn, whereas the cell on RGD is characterized by |T| ∼ 3.8 kdyn/cm2 and |F| ∼ 0.02 dyn.

One explanation for the observed differences in contractile activity on FN versus RGD concerns additional synergistic sites in the cell-binding domain of FN that have been shown to contribute to binding (Obara et al., 1988; Aota et al., 1991; Redick et al., 2000). The cell binding domain of FN consists of the type III domains 7–10 (denoted as FN III 7–10). In addition to the RGD sequence in the cell binding domain, the peptide sequence Pro-His-Ser-Arg-Asn (PHSRN) on FN III domain 9 (Aota et al., 1994) has also been shown to have a synergistic effect on cell adhesion. More recently, a putative binding site Lys-Asn-Glu-Glu-Asp (KNEED) on FN III domain 8 has been shown to modulate cell spreading (Wong et al., 2002). Finally, recent reports in the literature (Ohashi et al., 1999; Baneyx et al., 2001, 2002; Gao et al., 2003) have shown that FN is a highly extensible molecule and that traction forces exerted by cells can expose additional cryptic binding sites. For instance, NIH 3T3 fibroblasts cultured on FN-coated glass surfaces have been shown to extend and remodel the FN within 1–4 h (Baneyx et al., 2001). In our studies, data on contractility were measured ∼15 h post-cell plating, allowing sufficient time for the fibroblasts to expose additional cryptic binding sites in FN by exerting tractional forces.

Another mechanism that may be responsible for the differences in contractility is the spatial distribution of the ligands on the substratum. For instance, FN molecules can aggregate and assemble at the cell-substratum interface (Magnusson and Mosher, 1998), leading to the presentation of multiple cell-binding sites. In the case of RGD, there is no driving force for ligand clustering on the substratum, and one would expect a random distribution of RGD ligands on the surface. However, Maheshwari et al. (2000) were able to precisely control the spatial distribution of RGD ligands at the nanoscale level, and by increasing the degree of clustering, they were able to enhance cytoskeletal organization and formation of actin stress fibers on clustered RGD to levels close to that found on FN. We point out that they still found significant differences in cell migration, even with clustered RGD: they did not observe a biphasic dependence of cell migration speed on ligand density for clustered RGD. Thus, it is clear that the synergistic sites have a significant role in governing cellular response.

The constrained conformation of the RGD site within the FN molecule has been proposed to account for some differences observed between linear RGD and FN. There are differences in the affinities of ligands to cyclic and linear RGD, and recent studies have also observed differential cellular response (Xiao and Truskey, 1996; Kantlehner et al., 1999). A recent study (Kato and Mrksich, 2004) of 3T3 Swiss Albino cells found twice as many focal adhesions on surfaces modified by cyclic RGD compared to linear RGD. The focal adhesions were smaller in size on cyclic RGD and a higher distribution of focal adhesions was found in the interior of the cell. One would therefore expect to find differences in contractility and migration for cells on cyclic RGD-modified substrata. Such studies that quantify contractility and migration on substrata modified by cyclic RGD would provide valuable insights into the mechanisms of integrin activation and signal transduction.

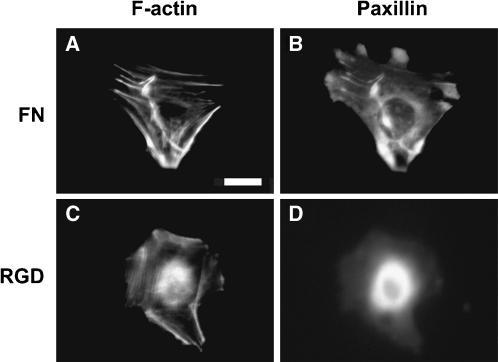
Focal adhesions have also recently been directly related to traction force generation. Traction forces have been shown to be directly correlated to focal adhesion size (Balaban et al., 2001; Tan et al., 2003) as long as the adhesions are greater than 1 μm (Tan et al., 2003). There is clearly a dynamic aspect to this dependency because nascent focal adhesions have been shown to have decreased traction forces when they mature (Beningo et al., 2001). Presumably this change in focal adhesion structure would be reflected in cytoskeletal reorganization events. Thus, co-immunostaining of the cytoskeleton and focal adhesion proteins would give further insight into differences between FN- and RGD-modified substrata. For instance, we can compare the cytoskeletal organization of fibroblasts at particular surface densities of FN and RGD at which 〈A〉 is equal but 〈|T|〉 (or 〈|F|〉) is different. As discussed earlier, this situation occurs at σFN ∼ 2000 and σRGD ∼ 200 μm−2, and cells co-stained for actin and paxillin at these two surface densities are shown in Fig. 8. We find that fibroblasts on FN exhibit well-defined actin stress fibers aligned through the entire interior of the cell (Fig. 8 A). In contrast, fibroblasts adhered to RGD exhibit actin fibers that are extremely fine and located primarily along the periphery of the cell (Fig. 8 C). Punctate regions enriched in paxillin (∼1–3 μm2) are observed on the cell periphery on FN (Fig. 7 B). Such features are not observed for cells on RGD (Fig. 7 D). These findings suggest that cells exert lower tractional forces on RGD because of the difficulty in forming focal adhesions and stress fibers.

FIGURE 8.

FIGURE 8

Open in a new tab

Actin and paxillin distribution for balb/c 3T3 fibroblasts of similar area (|A| ∼ 600 μm2) adhered to FN-PAAM (A and B; σFN ∼ 2000 μm−2), and to GRGDSP-PAAM (C and D; σRGD ∼ 200 μm−2). Scale bar = 10 μm.

In conclusion, our findings show that there are qualitative similarities between fibroblast behaviors on FN- and RGD-modified substrata. However, there are also significant quantitative differences: at any given surface density, traction forces and spread area are consistently higher on FN compared to RGD. These observations can be attributed to possible differences in the organization of the cytoskeleton, which in turn could be due to the presence of additional synergistic binding sites in FN. Importantly, we find that at a given surface density of FN or RGD at which the spread areas and migration speeds are equal, there are still significant differences in the traction stress. Thus, it does not appear that there is a simple relationship between cell area and the magnitude of the traction force. Instead, one must also consider the nature of the interactions between the ECM or ligand and the cell that will ultimately affect the generation of traction forces. These considerations are important to keep in mind in the rational design of biomaterials for applications in tissue engineering and wound healing.

Acknowledgments

Technical assistance from Q. Pham, A. Velasco, and L. Shmuylovich is gratefully acknowledged. We thank M. A. Nugent for assistance with radiolabeling experiments. The authors thank M. L. Burgess and M. Dembo for helpful discussions. We thank J. Leach for critical reading of the manuscript.

This project was supported by the Whitaker Foundation (RG-98-0506; TF-02-0026) and a National Science Foundation CAREER Award (BES-9985338) to J. Y. Wong, and the Computational Science Graduate Fellowship Program of the Office of Scientific Computing and Office of Defense Programs in the Department of Energy under contract DE-FG02-97ER25308 to W. A. Marganski.

Padmavathy Rajagopalan and William A. Marganski contributed equally to this work.

Padmavathy Rajagopalan's present address is Center for Engineering in Medicine, Harvard Medical School, Massachusetts General Hospital, Boston, MA.

References

  1. Akiyama, S. K., E. Hasegawa, T. Hasegawa, and K. M. Yamada. 1985. The interaction of fibronectin fragments with fibroblastic cells. J. Biol. Chem. 260:13256–13260. [PubMed] [Google Scholar]
  2. Aota, S., T. Nagai, and K. M. Yamada. 1991. Characterization of regions of fibronectin besides the arginine-glycine-aspartic acid sequence required for adhesive function of the cell-binding domain using site-directed mutagenesis. J. Biol. Chem. 266:15938–15943. [PubMed] [Google Scholar]
  3. Aota, S., M. Nomizu, and K. M. Yamada. 1994. The short amino acid sequence Pro-His-Ser-Arg-Asn in human fibronectin enhances cell-adhesive function. J. Biol. Chem. 269:24756–24761. [PubMed] [Google Scholar]
  4. Balaban, N. Q., U. S. Schwarz, D. Riveline, P. Goichberg, G. Tzur, I. Sabanay, D. Mahalu, S. Safran, A. Bershadsky, L. Addadi, and B. Geiger. 2001. Force and focal adhesion assembly: a close relationship studied using elastic micropatterned substrates. Nat. Cell. Biol. 3:466–472. [DOI] [PubMed] [Google Scholar]
  5. Baneyx G., L. Baugh, and V. Vogel. 2001. Coexisting conformations of fibronectin in cell culture imaged using fluorescence resonance energy transfer. Proc. Natl. Acad. Sci. USA. 98:14464–14468. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Baneyx G., L. Baugh, and V. Vogel. 2002. Fibronectin extension and unfolding within cell matrix fibrils controlled by cytoskeletal tension. Proc. Natl. Acad. Sci. USA. 99:5139–5143. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Beningo, K. A., M. Dembo, I. Kaverina, J. V. Small, and Y. L. Wang. 2001. Nascent focal adhesions are responsible for the generation of strong propulsive forces in migrating fibroblasts. J. Cell Biol. 153:881–888. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bergkvist M., J. Carlsson, and S. Oscarsson. 2003. Surface-dependent conformations of human plasma fibronectin adsorbed to silica, mica, and hydrophobic surfaces, studied with use of Atomic Force Microscopy. J. Biomed. Mater. Res. 64A:349–356. [DOI] [PubMed] [Google Scholar]
  9. Brandley, B. K., and R. L. Schnaar. 1988. Covalent attachment of an Arg-Gly-Asp sequence peptide to derivatizable polyacrylamide surfaces: support of fibroblast adhesion and long-term growth. Anal. Biochem. 172:270–278. [DOI] [PubMed] [Google Scholar]
  10. Brandley, B. K., J. H. Shaper, and R. L. Schnaar. 1990. Tumor cell haptotaxis on immobilized N-acetylglucosamine gradients. Dev. Biol. 140:161–171. [DOI] [PubMed] [Google Scholar]
  11. Brinkley, M. 1992. A brief survey of methods for preparing protein conjugates with dyes, haptens, and cross-linking reagents. Bioconjug. Chem. 3:2–13. [DOI] [PubMed] [Google Scholar]
  12. Dembo, M., T. Oliver, A. Ishihara, and K. Jacobson. 1996. Imaging the Traction Stresses Exerted By Locomoting Cells With the Elastic Substratum Method. Biophys. J. 70:2008–2022. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Dembo, M., and Y. L. Wang. 1999. Stresses at the cell-to-substrate interface during locomotion of fibroblasts. Biophys. J. 76:2307–2316. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. DiMilla, P. A., S. M. Albelda, and J. A. Quinn. 1992a. Adsorption and elution of extracellular matrix proteins on non-tissue culture polystyrene petri dishes. J. Colloid Interface Sci. 153:212–225. [Google Scholar]
  15. DiMilla, P. A., J. A. Quinn, S. M. Albelda, and D. A. Lauffenburger. 1992b. Measurement of Individual Cell Migration Parameters for Human Tissue Cells. AIChE J. 38:1092–1104. [Google Scholar]
  16. DiMilla, P. A., J. A. Stone, J. A. Quinn, S. M. Albelda, and D. A. Lauffenburger. 1993. Maximal migration of human smooth muscle cells on fibronectin and type IV collagen occurs at an intermediate attachment strength. J. Cell Biol. 122:729–737. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Doyle, A., W. Marganski, and J. Lee. 2004. Calcium transients induce spatially coordinated increases in traction force during the movement of fish keratocytes. J. Cell Sci. 117:2203–2214. [DOI] [PubMed] [Google Scholar]
  18. Dunn, G.A. 1983. Characterizing a kinesis response: time averaged measures of cell speed and directional persistence. Agents and Actions. 12(Suppl.):14–33. [DOI] [PubMed] [Google Scholar]
  19. Erickson, H. P., and N. A. Carrell. 1983. Fibronectin in extended and compact conformations. Electron microscopy and sedimentation analysis. J. Biol. Chem. 258:14539–14544. [PubMed] [Google Scholar]
  20. Gao M., D. Craig, O. Lequin, I. D., Campbell, V. Vogel, and K. Schulten. 2003. Structure and functional significance of mechanically unfolded fibronectin type III1 intermediates. Proc. Natl. Acad. Sci. USA. 100:14784–14789. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Garcia, A. J., M. D. Vega, and D. Boettiger. 1999. Modulation of cell proliferation and differentiation through substrate-dependent changes in fibronectin conformation. Mol. Biol. Cell. 10:785–798. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Gaudet, C., W. A. Marganski, S. Kim, C. T. Brown, V. Gunderia, M. Dembo, and J. Y. Wong. 2003. Influence of type I collagen surface density on fibroblast spreading, motility, and contractility. Biophys. J. 85:3329–3335. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Geiger, B., A. Bershadsky, R. Pankov, and K. M. Yamada. 2001. Transmembrane crosstalk between the extracellular matrix–cytoskeleton crosstalk. Nat. Rev. Mol. Cell Biol. 2:793–805. [DOI] [PubMed] [Google Scholar]
  24. Harris, A. K. 1986. Cell traction in relationship to morphogenesis and malignancy. Dev. Biol. 3:339–357. [DOI] [PubMed] [Google Scholar]
  25. Hersel, U., C. Dahmen, and H. Kessler. 2003. RGD modified polymers: biomaterials for stimulated cell adhesion and beyond. Biomaterials. 24:4385–4415. [DOI] [PubMed] [Google Scholar]
  26. Johnson, K. J., H. Sage, G. Briscoe, and H. P. Erickson. 1999. The compact conformation of fibronectin is determined by intramolecular ionic interactions. J. Biol. Chem. 274:15473–15479. [DOI] [PubMed] [Google Scholar]
  27. Kantlehner, M., D. Finsinger, J. Meyer, P. Schaffner, A. Jonczyk, B. Diefenbach, B. Nies, and H. Kessler. 1999. Selective RGD-mediated adhesion of osteoblasts at surfaces of implants. Angew. Chem. Int. Ed. 38:560–562. [DOI] [PubMed] [Google Scholar]
  28. Kato M., and M. Mrksich. 2004. Using model substrates to study the dependence of focal adhesion formation on the affinity of integrin-ligand complexes. Biochemistry. 43:2699–2707. [DOI] [PubMed] [Google Scholar]
  29. Kodama T., M. R. Hamblin, and A. G. Doukas. 2000. Cytoplasmic molecular delivery with shock waves: importance of impulse. Biophys. J. 79:1821–1832. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Landau, L. D., and E. M. Lifshitz. 1986. Theory of Elasticity, 3rd ed. J. B. Sykes and W. H. Reid, editors. Pergamon Press, Oxford.
  31. Lauffenburger, D. A., and A. F. Horwitz. 1996. Cell migration: a physically integrated molecular process. Cell. 84:359–369. [DOI] [PubMed] [Google Scholar]
  32. Lee, J., M. Leonard, T. Oliver, A. Ishihara, and K. Jacobson. 1994. Traction forces generated by locomoting keratocytes. J. Cell Biol. 127:1957–1964. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Li, Y., Z. Hu, and C. Li. 1993. New method for measuring Poisson's ratio in polymer gels. J. Appl. Polym. Sci. 50:1107–1111. [Google Scholar]
  34. Lo, C. M., H. B. Wang, M. Dembo, and Y. L. Wang. 2000. Cell movement is guided by the rigidity of the substrate. Biophys. J. 79:144–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Lomants, A. J., and G. Fairbanks. 1976. Chemical probes of extended biological structures: synthesis and properties of the cleavable protein cross-linking reagent [35S]dithiobis(succinimidyl propionate). J. Mol. Biol. 104:243. [DOI] [PubMed] [Google Scholar]
  36. Magnusson, M. K., and D. F. Mosher. 1998. Fibronectin: structure, assembly, and cardiovascular implications. Arterioscler. Thromb. Vasc. Biol. 18:1363–1370. [DOI] [PubMed] [Google Scholar]
  37. Maheshwari, G., G. Brown, D. A. Lauffenburger, A. Wells, and L. G. Griffith. 2000. Cell adhesion and motility depend on nanoscale RGD clustering. J. Cell Sci. 113:1677–1686. [DOI] [PubMed] [Google Scholar]
  38. Marganski, W. A., V. M. De Biase, M. L. Burgess, and M. Dembo. 2003a. Demonstration of altered fibroblast contractile activity in hypertensive heart disease. Cardiovasc. Res. 60:547–556. [DOI] [PubMed] [Google Scholar]
  39. Marganski, W. A., M. Dembo, and Y. L. Wang. 2003b. Measurements of cell-generated deformations on flexible substrata using correlation-based optical flow. Methods Enzymol. 361:197–211. [DOI] [PubMed] [Google Scholar]
  40. Massia, S. P., and J. A. Hubbell. 1990. Covalent surface immobilization of Arg-Gly-Asp- and Tyr-Ile-Gly-Ser-Arg-containing peptides to obtain well-defined cell-adhesive substrates. Anal. Biochem. 187:292–301. [DOI] [PubMed] [Google Scholar]
  41. Massia, S. P., and J. A. Hubbell. 1991. An RGD spacing of 440 nm is sufficient for integrin alpha V beta 3-mediated fibroblast spreading and 140 nm for focal contact and stress fiber formation. J. Cell Biol. 114:1089–1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Munevar, S., Y. Wang, and M. Dembo. 2001a. Traction force microscopy of migrating normal and H-ras transformed 3T3 fibroblasts. Biophys. J. 80:1744–1757. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Munevar, S., Y. L. Wang, and M. Dembo. 2001b. Distinct roles of frontal and rear cell-substrate adhesions in fibroblast migration. Mol. Biol. Cell. 12:3947–3954. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Obara, M., M. S. Kang, and K. M. Yamada. 1988. Site-directed mutagenesis of the cell-binding domain of human fibronectin: separable, synergistic sites mediate adhesive function. Cell. 53:649–657. [DOI] [PubMed] [Google Scholar]
  45. Ohashi T., D. P. Kiehart, and H. P. Erickson. 1999. Dynamics and elasticity of the fibronectin matrix in living cell culture visualized by fibronectin-green fluorescent protein. Proc. Natl. Acad. Sci. USA. 96:2153–2158. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Oliver, T., J. Lee, and K. Jacobson. 1994. Forces exerted by locomoting cells. Semin. Cell Biol. 5:139–147. [DOI] [PubMed] [Google Scholar]
  47. Pelham, R. J., and Y. L. Wang. 1997. Cell locomotion and focal adhesions are regulated by substrate flexibility. Proc. Natl. Acad. Sci. USA. 94:13661–13665. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Pierschbacher, M. D., and E. Ruoslahti. 1984. Cell attachment activity of fibronectin can be duplicated by small synthetic fragments of the molecule. Nature. 309:30–33. [DOI] [PubMed] [Google Scholar]
  49. Redick, S. D., D. L. Settles, G. Briscoe, and H. P. Erickson. 2000. Defining fibronectin's cell adhesion synergy site by site-directed mutagenesis. J. Cell Biol. 149:521–527. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Reinhart-King, C. A., M. Dembo, and D. A. Hammer. 2003. Endothelial cell traction forces on RGD-derivatized polyacrylamide substrata. Langmuir. 19:1573–1579. [Google Scholar]
  51. Ruoslahti, E. 1996. RGD and other recognition sequences for integrins. Annu. Rev. Cell Dev. Biol. 12:697–715. [DOI] [PubMed] [Google Scholar]
  52. Shreiber, D. I., V. H. Barocas, and R. T. Tranquillo. 2003. Temporal variations in cell migration and traction during fibroblast-mediated gel conpaction. Biophys. J. 84:4102–4114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Streeter, H. B., and D. A. Rees. 1987. Fibroblast adhesion to RGDS shows novel features compared with fibronectin. J. Cell Biol. 105:507–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Tan, J. L., J. Tien, D. M. Pirone, D. S. Gray, K. Bhadriraju, and C. S. Chen. 2003. Cells lying on a bed of microneedles: an approach to isolate mechanical force. Proc. Natl. Acad. Sci. USA. 100:1484–1489. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Trinkaus, J. P. 1969. Cells into organs: The forces that shape the embryo. C. L. Markert, editor. Prentice-Hall, Englewood Cliffs, NJ.
  56. Wang, H. B., M. Dembo, S. K. Hanks, and Y. Wang. 2001. Focal adhesion kinase is involved in mechanosensing during fibroblast migration. Proc. Natl. Acad. Sci. USA. 98:11295–11300. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Wang, Y. L., and R. J. Pelham. 1998. Preparation of a flexible, porous polyacrylamide substrate for mechanical studies of cultured cells. Methods Enzymol. 298:489–496. [DOI] [PubMed] [Google Scholar]
  58. Wong, J. Y., Z. Weng, S. Moll, S. Kim, and C. T. Brown. 2002. Identification and validation of a novel cell-recognition site (KNEED) on the 8th type III domain of fibronectin. Biomaterials. 23:3865–3870. [DOI] [PubMed] [Google Scholar]
  59. Xiao, Y., and G. A. Truskey. 1996. Effect of receptor-ligand affinity on the strength of endothelial cell adhesion. Biophys. J. 71:2869–2884. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Zamir, E., B. Z. Katz, S. Aota, K. M. Yamada, B. Geiger, and Z. Kam. 1999. Molecular diversity of cell-matrix adhesions. J. Cell Sci. 112:1655–1669. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES