Nicastro, Giuseppe, Paola Margiocco, Barbara Cardinali, Paola Stagnaro, Fabio Cauglia, Carla Cuniberti, Maddalena Collini, David Thomas, Annalisa Pastore, and Mattia Rocco. 2004. The role of unstructured extensions in the rotational diffusion properties of a globular protein: the example of the titin 127 module. Biophys. J. 87:1227–1240.
Due to a typesetting error in the article, a misalignment affected several columns in the last line of Table 4 (page 1233). The corrected version of the table is reprinted below.
TABLE 4.
Prolate axially symmetric (PAS) and fully anisotropic (FA) parameters for the three I27 constructs, corrected to standard conditions (water, 20°C), from the T1/T2 data and Lipari-Szabo analysis
| I27NHT
|
I27SHT
|
I27LHT
|
|||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| *Model MHz (vectors) |
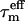 (ns) (ns) |
D|/D⊥ | τa (ns) | τb (ns) | τc (ns) | Model MHz (vectors) |
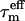 (ns) (ns) |
D|/D⊥ | τa (ns) | τb (ns) | τc (ns) | Model MHz (vectors) |
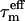 (ns) (ns) |
D|/D⊥ | τa (ns) | τb (ns) | τc (ns) |
| PAS 600 (40) | 5.63 ± 0.24 | 1.51 | 6.59 | 6.07 | 4.93 | PAS 600 (37) | 6.81 ± 0.25 | 1.63 | 8.17 | 7.45 | 5.80 | PAS 600 (38) | 7.66 ± 0.36 | 1.65 | 9.31 | 8.40 | 6.49 |
| PAS 800 (36) | 5.69 ± 0.26 | 1.57 | 6.78 | 6.19 | 4.90 | nd | nd | nd | nd | nd | nd | PAS 800 (36) | 8.13 ± 0.24 | 1.81 | 10.33 | 9.11 | 6.72 |
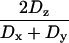 |
τ1 ≈ τ2 (ns) | τ3 ≈ τ4 (ns) | τ5 (ns) | 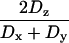 |
τ1 ≈ τ2 (ns) | τ3 ≈ τ4 (ns) | τ5(ns) | 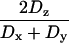 |
τ1 ≈ τ2 (ns) | τ3 ≈ τ4 (ns) | τ5(ns) | ||||||
| FA 600 (40) | 5.63 ± 0.26 | 1.51 | 6.02 | 4.98 | 6.47 | FA‡ 600 (37) | 6.81 ± 0.27 | 1.64 | 7.73 | 5.69 | 8.77 | FA 600 (38) | 7.64 ± 0.41 | 1.64 | 8.35 | 6.59 | 9.09 |
| FA 800 (36) | 5.69 ± 0.17 | 1.57 | 6.10 | 5.04 | 6.56 | nd | nd | nd | nd | nd | nd | FA 800 (36) | 8.08 ± 0.25 | 1.72 | 8.95 | 6.69 | 9.09 |
| Mean value† | 5.66 ± 0.18 | 6.69 | 6.13 | 4.92 | Mean value† | 6.81 ± 0.25 | 8.17 | 7.45 | 5.80 | Mean value† | 7.99 ± 0.20 | 9.10 | 8.11 | 6.14 | |||
 or
or 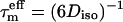 ; for axially symmetric diffusion, D| = Dz and D⊥ = Dx = Dy; τa = (6D⊥)−1, τb = (5D⊥ + D|)−1, τc = (2D⊥ + 4D|)−1; τ1 = (4Dx + Dy + Dz)−1; τ2 = (Dx + 4Dy + Dz)−1; τ3 = (Dx + Dy + 4Dz)−1;
; for axially symmetric diffusion, D| = Dz and D⊥ = Dx = Dy; τa = (6D⊥)−1, τb = (5D⊥ + D|)−1, τc = (2D⊥ + 4D|)−1; τ1 = (4Dx + Dy + Dz)−1; τ2 = (Dx + 4Dy + Dz)−1; τ3 = (Dx + Dy + 4Dz)−1;  ;
; 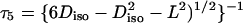 ; Diso = trace{D}/3 = (Dx + Dy + Dz)/3; L2 = (DxDy + DxDz + DyDz)/3; Dx, Dy, and Dz are the principal values of the diffusion tensor D.
; Diso = trace{D}/3 = (Dx + Dy + Dz)/3; L2 = (DxDy + DxDz + DyDz)/3; Dx, Dy, and Dz are the principal values of the diffusion tensor D.
From the PAS model values.
nd, not determined.


