Abstract
A combined total of more than 600.0 ns molecular dynamics simulations with explicit solvent have been carried on systems containing either four peptides or a single peptide to investigate the early-stage aggregation process of an amyloidogenic hexapeptide, NFGAIL (residues 22–27 of the human islet amyloid polypeptide). Direct observation of the aggregation process was made possible by placing four peptides in a box of water with an effective concentration of 158 mg/ml to enhance the rate of aggregation. Partially ordered oligomers containing multistrand β-sheets were observed which could be the precursory structures leading to the amyloid-forming embryonic nuclei. Comparative simulations on a single peptide suggested that the combined effect of higher peptide concentration and periodic boundary condition promoted compact monomers and the short-range interpeptide interactions favored the β-extended conformation. Of particular interest was the persistent fluctuation of the size of the aggregates throughout the simulations, suggesting that dissociation of peptides from the disordered aggregates was an obligatory step toward the formation of ordered oligomers. Although 95% of peptides formed oligomers and 44% were in β-extended conformations, only 16% of peptides formed multistrand β-sheets. The disordered aggregates were mainly stabilized by hydrophobic interactions while cross-strand main-chain hydrogen bonds manifested the ordered oligomers. The transition to the β-extended conformation was mildly cooperative due to short-range interactions between β-extended peptides. Taken together, we propose that the role of hydrophobic interaction in the early stage of aggregation is to promote disordered aggregates and disfavor the formation of ordered nuclei and dissociation of the disordered oligomers could be the rate-limiting step at the initiation stage.
INTRODUCTION
A number of human diseases are associated with a common pathogenic process called amyloidogenesis (Dobson, 1999; Kelly, 1998; Rochet and Lansbury, 2000; Thirumalai et al., 2003), whereby proteins or peptides associate together to form toxic soluble oligomers (Kayed et al., 2003) and insoluble fibrils. The amyloidogenic proteins or peptides do not share any sequence homology or common fold. However, the oligomers and fibrils are structurally similar. Immunologic experiments suggest a common structure of the soluble oligomers (Kayed et al., 2003). X-ray fiber diffraction patterns indicate a general “cross-β” structure of the fibrils in which the β-sheets are parallel to the fibril axis, with the β-strands orientated perpendicular to the fibril axis. Recently, a solid-state NMR study confirmed the β-extended peptide conformation in fibrils and suggests the formation of hydrogen bonds between neighboring β-strands (Jaroniec et al., 2004). The common structural properties of the oligomers and fibrils imply a similar mechanism of amyloidogenesis. This process is believed to be a nucleation process followed by a conformational change into a predominantly β-sheet secondary structure(Dobson, 1999; Kelly, 1998; Rochet and Lansbury, 2000; Thirumalai et al., 2003). Despite the tremendous progress, including the advent of antiamyloid agents (Mason et al., 2003), many important questions on the early stage of the aggregation remain unanswered. These include characterization of the conformation transition to the β-extended structure and peptide association and the relationship between these two important events.
Computational studies have advanced our understanding of protein aggregations. Lattice models were used to describe various scenarios for protein aggregation (Dima and Thirumalai, 2002). Simplified models were also used to search possible aggregating conformations of the SH3 domain where each amino acid was represented by Cα and Cβ atoms (Ding et al., 2002). Discontinuous molecular dynamics (Jang et al., 2004) was used to study the competition between folding and aggregation. Molecular dynamics (MD) simulations with atomic representation of amyloidogenic peptides and the continuum solvent model were performed to investigate the role of side-chain interactions in the early stage of aggregation with the assistance of interstrand harmonic restraining forces (Gsponer et al., 2003). All-atom MD with the explicit solvent has been applied to study the stability of amlyoid fibrils, including the NFGAIL fragment (Li et al., 1999; Zanuy et al., 2003; Zanuy and Nussinov, 2003). The oligomerization mechanism (Klimov and Thirumalai, 2003) was explored by all-atom MD simulations with the assistance of interstrand harmonic restraining forces. Here, we took a step further and applied all-atom MD simulations with the explicit solvent under periodic boundary conditions to study the initial stages of the aggregation process. The novelty of our approach is that the rate of the aggregation was enhanced by elevating the peptide concentration to allow aggregation within affordable simulation time. This allowed observation of the early aggregation process with atomic details without the restraining force. It also allows simple extrapolation of the energetic results back to the physiological concentration to estimate the size of the critical nucleus. The role of short-range interactions was further investigated by comparing multipeptide simulation with single-peptide simulations.
The islet amyloid polypeptide is a 37-amino acid hormone and is the main constituent of the islet amyloid fibrils found in 95% of type II diabetes mellitus (Hoppener et al., 2000; Westermark et al., 1987). It has been established that islet amyloid polypeptide (IAPP) forms amyloid fibrils in vitro that are cytotoxic by inducing islet cell apoptosis (Lorenzo et al., 1994). The peptide NFGAIL is a fragment truncated from human IAPP (residues 22–27). It is one of the shortest fragments that have been shown to form amyloid fibrils similar to those formed by the full polypeptide as characterized by electron microscopy, Congo red staining (Tenidis et al., 2000), and x-ray fibril diffraction (Sunde et al., 1997). Furthermore, the fibrils formed by the hexapeptide were also cytotoxic toward the pancreatic cell line. Thus, the short NFGAIL fragment is a model system useful for studying the formation of the β-sheet, and the amyloid fibril and its cytotoxicity. In this study, the initiation of peptide aggregation and β-sheet formation was investigated by all-atom MD with explicit solvent.
METHOD
Systems
Three sets of simulations have been conducted and each set included 10 simulations of 20 ns in duration, for a combined total of more than 600 ns (Table 1). In the first set of simulations, to accelerate the aggregation process, the peptide concentration was elevated to 158 mg/ml by placing four peptides (NFGAIL) inside a small water box (hereafter referred to as the Quad simulations). The four peptides were assigned as extended conformations, placed 10 Å away from each other in parallel, and separated by waters. In the other two sets, a single peptide (NFGAIL) was placed inside a periodic water box of two different sizes to mimic two different peptide concentrations: 8.8 mg/ml and 42.0 mg/ml (hereafter referred to as the “Single low” and “Single high” simulations, respectively). The minimum water distances to box edge were 15 Å and 5 Å, respectively, in the “Single low” and “Single high” simulations so that the short-range interactions between peptides and their images were not possible.
TABLE 1.
Summary of the three sets of simulations
| Simulation set | No. of peptide | No. of water | Box size (Å)* | C (mg/ml) | No. of simulations | Simulation length (ns) |
|---|---|---|---|---|---|---|
| Quad | 4 | 828 | 33.3 | 157.9 | 10 | 20 |
| Single low | 1 | 4256 | 54.9 | 8.8 | 10 | 20 |
| Single high | 1 | 870 | 32.6 | 42.0 | 10 | 20 |
In the first set (Quad), four peptides were placed in a water box. In the other two sets (Single low and Single high), a single peptide (NFGAIL) was placed inside a water box of two different sizes. All three sets were subjected to periodic boundary condition.
Triclinic box is equivalent to truncated octahedron. Volume = (box size)3 × 0.77.
MD simulation
The AMBER simulation package was used in both simulation and data processing (Case et al., 2002). A recently developed all-atom point-charge force field (Duan et al., 2003) was chosen to represent the peptide. Studies have shown that this force field has a reasonable balance between α-helix and β-sheet regions which appears to be an improvement in comparison to the force fields tested by others (Hu et al., 2003). The solvent was explicitly represented by the TIP3P water model. The peptide-water systems were subjected to periodic boundary conditions. After the initial energy minimization, random velocities were assigned according to Boltzmann's distribution at 278 K, at which NMR measurements are usually taken. A set of 10 simulations was carried out for each peptide-water system with different random number seeds for generating the initial random velocities. The system was equilibrated in the NPT ensemble (constant number of atoms in the box, constant pressure and temperature) for 100 ps to adjust the system size and density and to fully solvate the peptides. Production simulation was carried in the NVT ensemble (constant number of atoms in the box, constant volume and constant temperature) for 20 ns under the periodic boundary conditions. The cumulative simulation time was 200 ns for each peptide system. Particle-mesh Ewald method (Essmann et al., 1995) was used to treat the long-range electrostatic interactions. SHAKE (Ryckaert et al., 1977) was applied to constrain all bonds connecting hydrogen atoms and a time step of 2.0 fs was used. To reduce the computation, nonbonded forces were calculated using a two-stage RESPA approach (Barash et al., 2003) where the forces within a 10-Å radius were updated every step and those beyond 10 Å were updated every two steps. Temperature was controlled at 278 K using Berendsen's algorithm (Berendsen et al., 1984) with a coupling constant of 2.0 ps. The trajectories were saved at 1.0 ps intervals and a total of 201,000 snapshots for each set of simulations were produced for further analysis. The structures at the equilibration phase were also collected and used as a reference for the later snapshots.
Peptide conformation analysis
Main-chain ϕ-ψ torsion angles were calculated for each residue. In this study, the conformational regions were defined as: right-handed helical (−140° < ϕ < −30°, −90° < ψ < 45°), β (−180° < ϕ < −30°, 60° < ψ < 180°, and −180° < ψ < −150°), and coiled regions. A peptide strand was classified as β-extended or α-compact if two consecutive residues were, respectively, in the β- and α-helical regions, and if no two residues were in the α-helical and β-regions, respectively. Otherwise, the peptide was classified as a random coil (Klimov and Thirumalai, 2003). The β-sheet (including isolated β-bridges) was assigned by the STRIDE program of Frishman and Argos (1995). In this program, a β-bridge is defined as two or more pairs of residues that form main-chain hydrogen bonds and are in the β-extended conformation; two consecutive β-bridges form a minimal β-sheet.
Main-chain hydrogen bonds were identified when the heavy atom distances fell below 4.0 Å and the O⋯H-N angle was >120°. Atom-atom contacts were defined when two atoms were closer than their van der Waals (VDW) radii plus 2.8 Å. Interstrand atom contacts were classified as apolar-apolar or polar-polar based on atom types (polar or apolar). The solvent-accessible surface area was calculated using the SURFACE program (Lee and Richards, 1971). The analysis was limited to the nearest images.
Free-energy analysis
- Formation free energy of oligomers: it was assumed that the systems were close to the equilibrium state in the last 5.0 ns of the simulations. The nth formation free energy of the oligomer can be calculated as
and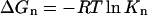
(1)
where R is the gas constant, T is the temperature, Kn is the equilibrium constant of the oligomer with n peptides, [n], [1] , and [n − 1] are the corrected concentrations of the nth oligomers, the monomers, and the (n − 1)th oligomers, respectively.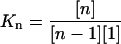
(2) - Folding free energy of a peptide:
where fβ is the fraction of residue/peptide in the β-conformation, R is the gas constant, and T is the temperature.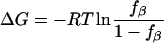
(3)
RESULTS
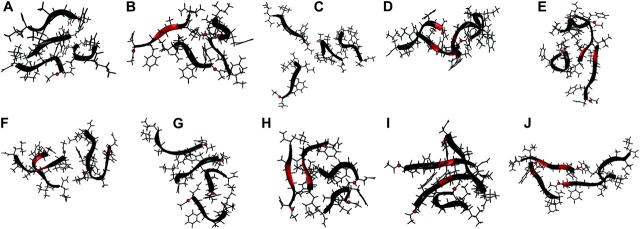
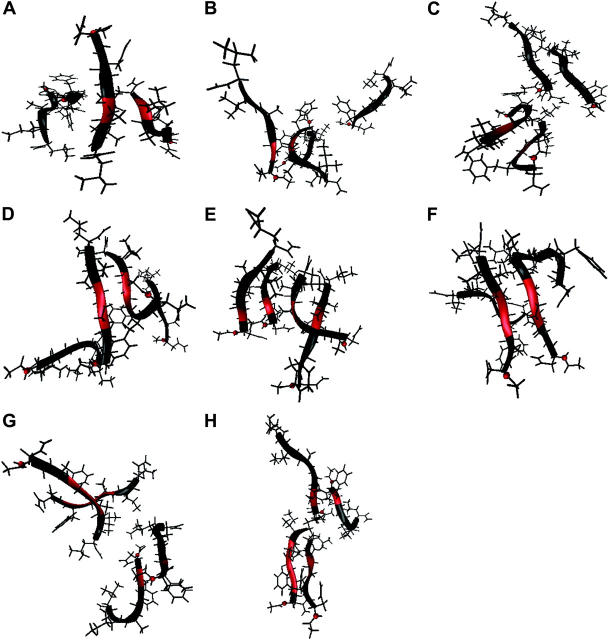
Both disordered and partially ordered aggregates were observed in Quad simulations. The disordered aggregates were highly heterogeneous and the partially ordered ones exhibited high β-sheet content as classified by the STRIDE program based on main-chain cross-strand hydrogen bonds and ϕ-ψ angles. Among the last snapshots of the 10 Quad simulations at 20.0 ns, four formed antiparallel β-bridges (Fig. 1, B, D, H, and J, in red), two formed parallel β-bridges (Fig. 1, D and I, in red), and two formed double-strand antiparallel β-sheets (Fig. 1, B and H). In addition to these, the representative structures of multistrand β-sheets formed in the simulations are shown in Fig. 2. Among them, two-strand antiparallel β-sheets (Fig. 2, A–C, in red), two-strand parallel β-sheets (Fig. 2, D and F–H, in red), and four-strand parallel β-sheets (Fig. 2 E, in red) were observed. To our knowledge, this is the first time that multistrand β-sheets have ever been observed in simulation without the assistance of external forces such as the harmonic restraining forces applied in other studies (Gsponer et al., 2003; Klimov and Thirumalai, 2003).
FIGURE 1.
The last snapshots of the 10 Quad simulation trajectories at 20 ns. Antiparallel β-bridges/sheets (B, D, H, and J) and parallel β-bridges/sheets (D, I) are shown in red ribbons. The N-terminus of each strand is indicated by a red ball.
FIGURE 2.
Representative partially ordered aggregates containing antiparallel and parallel β-sheets (including isolated β-bridges) formed in the Quad simulations. The red ribbon indicates the interstrand hydrogen-bonded residues. The N-terminus of each strand is marked by a red ball.
The atom-atom contacts between peptides were calculated to characterize the peptide associations, which were identified when two atoms were closer than their VDW radii plus 2.8 Å. The atom contacts averaged from the 10 Quad simulations are shown in Fig. 3 A. Overall, peptides 1 and 3 formed contacts with, respectively, peptides 2 and 4 more often than they did between themselves. When the last 10.0 ns of the simulations were considered (averaged over the 10 simulations), there were ∼300 atom-atom contacts between peptides 1 and 2 (247), 1 and 4 (376), 2 and 3 (315), and 3 and 4 (278). These are about twice as many contacts as were formed between peptides 1 and 3 (198), and 2 and 4 (159) during the same period. Thus, the formation pattern was primarily pairwise. It also suggests that the higher-order aggregates were formed by the dimer assembly. Nevertheless, the large fluctuation clearly indicated rather dynamic processes in which atom contacts constantly formed and dissipated (discussed later).
FIGURE 3.
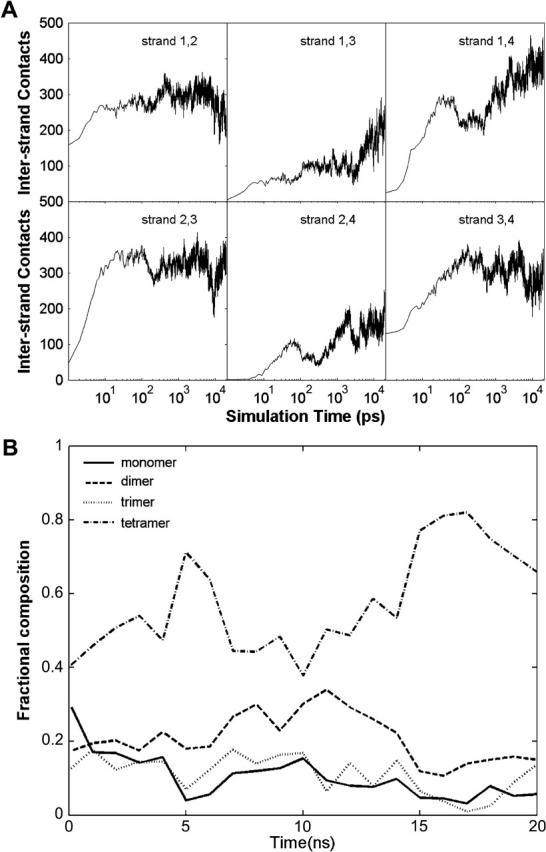
(A) Pairwise cross-peptide atom contacts. (B) The peptide fractions of oligomer species. The fractions were averaged every nanosecond to remove noise.
Oligomeric states were used to characterize the association-dissociation process quantitatively. In this study, the total number of atom contacts between the peptides was utilized to characterize the oligomeric state. Two peptides were considered associated when they had 320 or more atom contacts. Similarly, a peptide was classified as “associated” with an existing oligomer if the total number of atom contacts between the peptide and the oligomer reached the same critical number. When this occurred, the oligomer grew by one peptide. The final oligomeric states of the peptides were defined by the size of the oligomers. As a result, the oligomeric states were assigned to all four peptides in the Quad simulations. The time evolution of the fraction of peptides in each oligomeric state is shown in Fig. 3 B. Again, a rather dynamic process was observed, which indicated that the peptides constantly associated and dissociated.
The compositional fraction of monomers decreased monotonically during the simulation. All oligomers (dimer, trimer, and tetramer) started to form rather early. However, their trends were quite different. The fractions of peptides forming dimers and trimers continued to increase until 10.0 ns, then started to decrease and finally reached 15%, which was caused by the conversion into tetramers as evidenced by the simultaneous increase in the tetramers. As to tetramers, their fraction initially rose to a rather high level, 70%, at 5.0 ns, dropped to 40% at 10.0 ns, then increased again to become the dominant fraction (its fraction reached as high as 80%). This indicates that the early tetramers were an unstable species and underwent dissociation/reassociation.
The fractions averaged in the last 5.0 ns were 5% (monomers), 14% (dimers), 6% (trimers), and 75% (tetramers). Since the simulations were done in a box of 2.84 × 104 Å3 containing four peptides for a total peptide concentration of 234 mM, the concentrations of the species were 12.2 mM (monomers), 16.4 mM (dimers), 4.6 mM (trimers), and 43.7 mM (tetramers). On the other hand, for a system of four peptides, there are six ways to form dimers, four ways to form trimers and monomers, and only one way to form a tetramer. After these combinatorial effects were taken into account, the net concentrations were 3.1 mM (monomer), 2.7 mM (dimer), 1.2 mM (trimer), and 43.7 mM (tetramer). Thus the estimated free energies of formation for the oligomers (at 278 K) are −3.14 (dimer), −5.87 (trimer), and −11.08 kcal/mole (tetramer). One may estimate that the contribution of the free energies from each peptide would be, respectively, −1.57 (dimer), −1.97 (trimer), and −2.77 kcal/mol/peptide (tetramer). These results are summarized in Table 3, which shows that the formation of oligomers is energetically favorable in comparison to monomers at the standard concentration. In fact, tetramer is ∼−5.21 kcal/mole (or −0.87 kcal/mol/peptide) more favorable than trimer. In comparison, trimer is only −2.74 kcal/mole (or −0.40 kcal/mol/peptide) more favorable than dimer. The notable decrease in free energy from trimer to tetramer suggested that the aggregation process was cooperative. Such cooperativity is due to interpeptide interactions and desolvation. The interpeptide interactions would include cross-peptide main-chain hydrogen bonds and side-chain packing. For a highly hydrophobic peptide (such as NFGAIL), the desolvation free energy contributes a rather significant portion to the overall free-energy difference. These are discussed later in more detail.
TABLE 3.
Formation free energies of oligomers
| Oligomeric state | Monomer | Dimer | Trimer | Tetramer |
|---|---|---|---|---|
| Mean fraction* | 0.05 (0.01) | 0.14 (0.01) | 0.06 (0.03) | 0.75 (0.03) |
| Concentration (mM) | 12.2 (0.2) | 16.4 (0.8) | 4.6 (2.0) | 43.7 (2.0) |
| Corrected conc. (mM) | 3.1 (0.1) | 2.7 (0.2) | 1.2 (0.7) | 43.7 (2.0) |
| ΔG (kcal/mol) | 0.00 | −3.1 (0.1) | −5.9 (0.2) | −11.1 (0.1) |
| ΔGp (kcal/mol/peptide) | −1.6 (0.1) | −2.0 (0.2) | −2.8 (0.1) | |
| ΔΔG (kcal/mol) | −3.1 (0.1) | −2.8 (0.2) | −5.2 (0.2) |
Free energies were estimated based on ΔGn = −RT ln Kn where Kn is the nth formation constant, ΔGp is the free energy per peptide, and ΔΔG is the free energy difference between the oligomeric states in the last 5.0 ns. Standard deviations are in parentheses.
Fraction of peptides in respective oligomeric states.
Early aggregates are a mixture of disordered and partially ordered oligomers
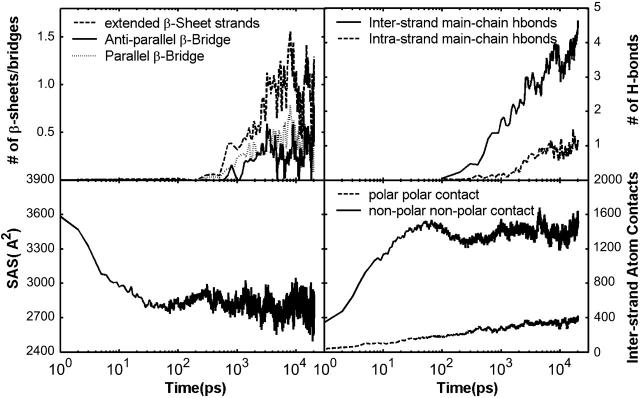
The average number of strands in β-sheets and number of β-bridges are shown in Fig. 4 A. The formation of β-sheets can be divided into three phases. In the first phase, 0–200 ps, there was no formation of β-sheets; in the second phase, 200 ps to 10 ns, isolated β-bridges or β-sheets increased to 32% of the total peptides; in the third phase, 10.0–20.0 ns, β-sheets decreased and varied around 16% of the total peptides. Although these were comparatively rare species observed in our simulations, their significance lies in their potential roles to be the initial nucleus for the formation of the ordered oligomers. The low percentage, 16, of the β-sheets with a moderate percentage, 44, of β-extended strands (Fig. 5) indicated there might be a high kinetic barrier for two β-extended strands to form cross-strand hydrogen bonds (therefore forming β−bridges and β−sheets). In other words, the dissociation of the two β-extended strands which were associated but did not form β−sheets, could be very slow, particularly for hydrophobic peptides. On the other hand, because the stabilization of these species requires simultaneous formation of at least two peptides (in close proximity to each other) in the β-extended conformation, an incorrect association of two compact peptides (after the initial collapse) can significantly hinder the conformational transition to β-extended strands. Thus, cooperative formation would be the key for a rapid conformation transition. Large fluctuations in phase 3 indicate that the β-sheets were marginally stable. This was expected because of the limited number of peptides in the system. More discussions on the conformation transition of individual peptides will be given later.
FIGURE 4.
Physical interactions (hydrophobic interaction, electrostatic interaction) in the Quad simulations averaged over 10 trajectories. (A) Number of strands forming β-sheets and number of antiparallel and parallel β-bridges. (B) Number of interstrand and intrastrand main-chain hydrogen bonds. (C) Solvent-accessible surface area. (D) The interstrand polar and nonpolar atom contacts. The cutoff is 2.8 Å plus VDW radii.
FIGURE 5.
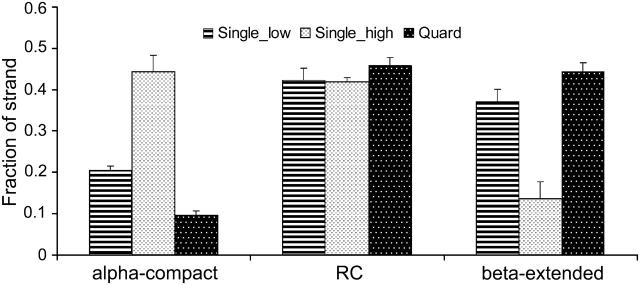
Fractions of peptide strands in α-compact, random coil, and β-extended conformations from three sets of simulations.
Both antiparallel and parallel orientations have been proposed in amyloid fibrils and the orientation has been linked to specific sequences (Li et al., 1999; Zanuy et al., 2003). It is interesting that our simulations showed no significant preference to either antiparallel or parallel orientation at this early stage of aggregation (Fig. 4 A). This suggested that the orientation preference was either determined at the later stage of the amyloid fibril formation or only existed in the full IAPP.
Early β-bridges/β-sheets formed during aggregating process
The aggregation process was further assessed by monitoring interstrand atomic contacts, solvent-accessible surface areas, and formation of main-chain hydrogen bonds (Fig. 4, B–D) of the four-peptide system. The correlation between formation of apolar atomic contacts and the reduction in solvent-accessible surface areas is evident. Both underwent sharp transitions in the early parts of the simulations that were followed by large-scale fluctuations. The close resemblance between the patterns of apolar contacts and that of solvent-accessible surfaces clearly indicated that the collapse process was driven mainly by hydrophobic forces, which is not surprising.
In contrast, the polar-polar contacts increased slowly and monotonically and lacked correlation with the reduction in solvent-accessible surface. In comparison to the apolar contacts, formation of the polar-polar contacts was delayed by ∼2 orders of magnitude. This indicated that these two types of processes took place at two different timescales. Formation of the main-chain hydrogen bonds (and subsequently β-sheets) was after the initial nonspecific hydrophobic collapse and formation of disordered oligomers. This was true in terms of timescales. However, it does not mean that formation of the main-chain hydrogen bonds and β-sheets took place by spontaneous conformational transition from the disordered oligomers. In fact, the oligomers constantly formed and dissolved, which was indicated by the fluctuation of their compositional fractions (Fig. 3) and the solvent-accessible surface area of the peptides (Fig. 5). Such a process enabled the peptides to repack and allowed the individual peptides to undergo conformational changes more easily. In summary, the hydrophobic collapse as nonspecific interaction occurred early. However, most oligomers produced in this early phase were disordered. In contrast, interstrand hydrogen bonds as specific interactions developed more slowly and were responsible for formation of β-bridges and β-sheets. The disordered oligomers could dissolve so that high local monomer concentration was available for subsequent association. Furthermore, the conformational change to β-extended strands occurred during the aggregating process and is correlated with the (re)association process.
Formation of the hydrogen bonds was dominated by interpeptide main-chain hydrogen bonds which were ∼4 times more frequent than intrapeptide ones as shown in Fig. 4 B. Because of the crucial role that the interstrand hydrogen bonds play in the formation of the amyloid fibrils, we speculate that the formation of the interstrand hydrogen bonds were precursory processes leading to the nucleation of ordered aggregates and fibrils.
Concentration effects on conformational change to the β-sheets
Formation of the amyloid oligomers and fibrils as aggregates of high β-sheet content depends on the concentration of the aggregation-prone peptide. Such effects may be attributed to both the crowding effect (Minton, 2000) and the stabilization by close contacts between peptides (e.g., interstrand hydrogen bonds). In the simulations, however, the third possible effect is due to the application of the particle-mesh Ewald method, which imposes periodic boundary conditions in the calculations of long-range interactions. To test these effects, we conducted two additional sets of simulations (“Single low” and “Single high,” 10 simulations of 21.0 ns each) in which a single peptide was immersed in water and was subjected to periodic boundary conditions. The box size was chosen to disallow the short-range interactions (e.g., hydrogen bonds and van der Waals contacts) between the peptide and the periodic images.
An interesting observation was the reduction in the fraction of residues in the β-conformation when the box size was reduced in the single peptide simulations. The effective peptide concentration was increased by ∼5 times from 9.0 mg/ml (“Single low”) to 42.0 mg/ml (“Single high”) when the box size was reduced from 54.9 Å3 to 32.6 Å3. The reduced box size is also expected to enhance the effect due to periodic boundary condition. However, the average fraction of residues in the β-conformation was reduced from 57% to 39% (Table 2) in the last 5.0 ns, corresponding to an increase in free energy by ∼0.21 kcal/mole/residue. This modest decrease (per residue) in β-conformation was accompanied by a modest increase in the α-helical conformation from (on average) 40% to 55% in the last 5.0 ns.
TABLE 2.
Effect of peptide concentration on β-conformation of each residue
| Fraction in β-conformation
|
Folding free energy (kcal/mol)
|
|||||
|---|---|---|---|---|---|---|
| Single low | Single high | Quad | Single low | Single high | Quad | |
| Asn | 0.59 (0.02) | 0.40 (0.01) | 0.65 (0.01) | −0.21 (0.04) | 0.22 (0.03) | −0.35 (0.03) |
| Phe | 0.50 (0.01) | 0.55 (0.01) | 0.67 (0.01) | 0.00 (0.03) | −0.11 (0.03) | −0.38 (0.03) |
| Ala | 0.51 (0.02) | 0.40 (0.01) | 0.63 (0.01) | −0.03 (0.04) | 0.22 (0.03) | −0.29 (0.03) |
| Ile | 0.67 (0.03) | 0.16 (0.02) | 0.55 (0.01) | −0.39 (0.06) | 0.91 (0.04) | −0.12 (0.04) |
| Leu | 0.60 (0.02) | 0.44 (0.03) | 0.55 (0.01) | −0.22 (0.04) | 0.14 (0.06) | −0.11 (0.03) |
| Average | 0.57 (0.02) | 0.39 (0.02) | 0.61 (0.01) | −0.17 (0.04) | 0.25 (0.04) | −0.25 (0.03) |
Free energies were estimated based on 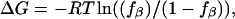 where fβ is the fraction in conformation in the last 5 ns. The Gly residue was excluded from analysis. Standard deviations are shown in parentheses.
where fβ is the fraction in conformation in the last 5 ns. The Gly residue was excluded from analysis. Standard deviations are shown in parentheses.
The effect is not limited to the conformations of individual residues. Rather, the overall conformation of the peptide strand has also been affected. As indicated by the number of residues that are simultaneously in the β-conformations (Fig. 5), the increased concentration also made the peptide less likely to be in the overall β-extended conformations (as defined in the method section). The β-extended species reduced from 37% (at 9 mg/ml, “Single low”) to 14% (at 42 mg/ml, “Single high”). In comparison, the random coil species remained at 42% and the helical/compact species increased from 21% to 44%. Therefore, the peptide becomes more compact at a higher concentration (without short-range forces). This corresponded to the change in the folding free energies (to the β-extended conformation) of 0.54 kcal/mol. Thus, the combined effect of the higher concentration and periodic boundary condition appears to induce marginally more compact peptide strands. Taken together, we found that crowding alone in the absence of short-range interpeptide contacts does not enhance the extended monomers and, in fact, higher concentrations without short-range interpeptide interactions may marginally induce monomers to stay in the relatively compact structures.
In contrast, the above trend was reversed when multiple peptides were placed in a small box that allowed short-range interpeptide interactions (e.g., hydrogen bonding, stacking, etc.). When four peptides were placed in a small box in the Quad simulations, the peptide concentration was increased to 158 mg/ml (234 mM), which was 4 times more concentrated than the “Single high” simulations. One might expect that the crowding effect causes the peptides to be even less extended if the trend observed in “Single low” and “Single high” simulations holds. This was not the case. In fact, the average (per residue) population in the β-conformation increased to 61% (Table 2), the highest among the three cases we studied, compared to the 39% in the “Single high” and 57% in the “Single low” simulations. This lowered the free energy of folding (into β-conformation) to −0.25 kcal/mol/residue. The average fraction in α-helical conformation also decreased to 34%. Thus, the interpeptide short-range interactions, including main-chain hydrogen bonds, had a profound effect on the free-energy landscapes of residue conformations.
Among the amino acids of the peptide, the most dramatic change was the Phe residue. The formation free energy (of β-conformation) changed from 0.00 ∼−0.11 kcal/mol in the single-peptide simulations to −0.38 kcal/mol in the Quad, ∼−0.4 kcal/mol more favorable. The Ala residue also exhibited substantial change from −0.03 ∼0.22 kcal/mol to −0.29 kcal/mol. Both residues were changed from weakly pro-β, as one would expect in a short isolated peptide in solution (Shi et al., 2002), to strong pro-β due to close interpeptide contacts. This is consistent with the notion that Phe plays an important role in fibril formation (Azriel and Gazit, 2001).
Similarly, the overall conformation of the peptides also became more extended in the Quad simulations (Fig. 5). The β-extended peptides were increased to 44% from 37% in “Single low” and 14% in “Single high” simulations, which corresponded to free-energy change (formation of β-extended strands) to 0.12 kcal/mol from 0.29 kcal/mol and 1.02 kcal/mol. Therefore, the short-range interpeptide (close contact) interactions strongly favor the extended conformation and were responsible for the increase of the extended structures. Such interactions compensated for the crowding effect, which tended to make the peptide somewhat compact, as observed in the single-peptide simulations. A similar trend was observed in the simulations on Aβ16_22 peptides by Klimov and Thirumalai (2003).
DISCUSSION
At the simulated peptide concentration (233 mM), the concentration of tetramer was 36 times higher than that of the trimer (Table 3) at 278 K. However, this changes dramatically at typical peptide concentrations in vivo, which are only on the order of 1 nM, ∼4.3 × 107 times more diluted than what we used in this study. If the simulated peptide solution were diluted to that low peptide concentration, the concentration of tetramer would be ∼108 times lower than trimer, making it much less favorable than lower-order oligomers. At such a low peptide concentration, the ratio of the concentration of the tetramer to that of the trimer is equal to the product of the formation constant of tetramer from the trimer and the monomer concentrations ([tetramer]/[trimer] = K4[monomer]), where K4 = exp(−ΔG/RT) (Table 3) and monomer concentration can be approximated by the peptide concentration (1.0 nM). A similar argument would follow for the formation of the higher-order oligomers in a very low peptide concentration. To form higher-order oligomers at low peptide concentration, a critical free energy of association has to be reached such that higher-order oligomers would be more favorable and have higher (equilibrium) concentrations (i.e., [n + 1]/[n] > 1). For the 1-nM concentration at 278 K, this would require a ΔΔG of −11.45 kcal/mol from a lower oligomeric state of n peptides to a higher oligomeric state of n + 1 peptides. Such a level of stabilizing free energy is difficult to obtain from a small peptide in the absence of cooperativity.
For NFGAIL, our calculation indicated that trimer was −2.8 kcal/mol more stable than dimer and tetramer was −5.2 kcal/mole more stable than trimer (Table 3). If this trend continues for higher-order oligomers, we would expect that the critical oligomeric state could be heptamer at physiological peptide concentration (∼1 nM). In addition, since combinatorial effect favors lower-order oligomers by a factor that is proportional to the number of peptides (in terms of association constants), a correction term has to be considered. When such an effect is considered, one would expect that the critical oligomeric state increases to octamer. A similar conclusion was drawn by Zanuy and Nussinov (2003). Obviously, our conclusion was based on the simple extrapolation from the relative free energies of trimers and tetramers and included both ordered and disordered aggregates. On the other hand, the rising trend of stability is expected to diminish and the cooperativity would no longer exist at higher-order oligomers. Thus, a highly cooperative peptide at high concentration would require smaller critical oligomers to form insoluble aggregates. Conversely, a weakly cooperative peptide at a low concentration would require larger critical oligomers, which may not be attainable.
There are two plausible scenarios of fibrillization based on the free-energy landscape theory (Thirumalai et al., 2003). According to scenario I, the assembly-competent state N′ is metastable with respect to the monomeric native state and is formed through partial unfolding induced by denaturation stress. This scenario is not applicable to this study, because high concentration without interpeptide interaction actually marginally stabilizes the compact strands rather than the extended conformation which is an amyloid-prone state. One possible pathway in scenario II is that N′ is formed upon structural conversion triggered by intermolecular interaction. Our results appear to fit this scenario, because the transformation of the compact peptide structure to the extended peptide structure took place upon oligomerization and was facilitated by intermolecular interaction such as interstrand hydrogen bonds. However, we also observed significant deviation from scenario II. Scenario II suggests that disordered oligomers were driven by hydrophobic interactions, then were transformed to ordered oligomers by conformational changes at disordered oligomers to maximize the favorable hydrophobic and electrostatic interactions. In contrast, disordered oligomers in our simulations dissolved and partially ordered oligomers formed during the reassociation by maximizing the favorable hydrophobic and electrostatic interactions and hydrogen bonding. Such a process enables the peptides to repack and allows individual peptides to undergo conformational changes more easily. The coincidence of the reassociation process and the conformational transition process demonstrated a strong but subtle correlation between the two processes. The β-extended structure was not stable without the interpeptide contacts, yet the disordered association may hinder the conformation transition to the β-extended structure.
Although amyloid fibrils share similar overall cross-β superstructures, the proteins and peptides may assume completely different conformations in solution. This is probably also true when they form initial (disordered) aggregates. Among the six amino acids comprising the peptide, Ile has the highest β-propensity (Chou and Fasman, 1977), 1.60, and Leu has the lowest, 0.59. Overall, the average β-propensity of the entire peptide is 1.12, which is only marginally higher than the average helix propensity, 1.01, and turn propensity, 0.91. A secondary structure prediction by PSIPRED (McGuffin et al., 2000) also predicted an overall coiled structure. Thus, the peptide only has marginally higher probability to form β-conformation than either helix or coil. This is consistent with the observations that the average (per residue) population in the β−conformation was 57% in “Single low” and 39% in “Single high” simulations and that the fraction in extended conformation was low in both “Single low” (37%) and “Single high” (14%) simulations (Fig. 5). The notable increase in the β-sheet fraction in the Quad simulations (44%) suggested a cooperative process (Fig. 5). At the molecular level, this cooperativity can be explained by the cross-stabilization between two (or more) β-extended peptides. Furthermore, our analysis suggests that the stabilization effect was attributed primarily to the short-range contacts (i.e., main-chain hydrogen bonds and side-chain packing). Obviously, this requires at least two β-extended peptides to be correctly orientated in close proximity to form the cross-strand hydrogen bonds. Given that the β-extended propensity of this peptide is only marginally higher than those of other conformations, it suffices to argue that the probability to form β-sheets is rather low, which is consistent with our observation. This probability is further reduced by the formation of marginally stable disordered aggregates that are stabilized primarily by the hydrophobic interactions. This is also consistent with our observation that >95% of peptides formed oligomers (Fig. 3) and 44% of peptides were in β-extended conformation, yet only 16% of peptides formed β−sheet (Fig.4 A). Therefore, although hydrophobic interactions could be an important stabilizing factor in the formation of amyloid fibrils, they might significantly reduce the rate of fibril initiation. The dissociation of the disordered aggregate could be the rate-limiting step for the formation of the critical seed. Hydrogen bonds and specific side-chain packing, however, could be the key to facilitate the formation of the amyloid fibrils by promoting formation of highly ordered β-sheets containing multiple peptides. This further implies that high peptide concentration, which promotes disordered aggregates, may actually reduce the initiation rate of the fibrils. Conversely, highly soluble peptides with a high β-sheet propensity can significantly increase the initiation rate but the fibrils formed by such peptides may be unstable due to the lack of hydrophobic interaction. Therefore, (short) amyloidogenic peptides may share common features including 1), reasonable solubility; 2), complementary side chains; and 3), high β-sheet propensity.
We would like to note that this study on a short peptide allowed us to decouple two challenging subjects: conformations of proteins and ordered protein oligomers. The former is analogous to the protein folding problem and the latter is related to the protein assembly problem. However, for a typical amyloidogenic protein, one has to consider both. An additional complexity in the protein aggregation in comparison to aggregation of small peptides is the conformational transition from partially folded states or even the native folded state. These states can have a significant contribution to the kinetic barrier separating the soluble (monomeric) states from aggregated states. Thus, for the aggregation of proteins, one may need to consider protein stability; marginally stable proteins are more likely amyloidogenic than stable proteins. Nevertheless, we would like to suggest the applicability of some of the observations made in this study, particularly the notion that ordered aggregates are formed during the (re)association process and disordered aggregates hinder the formation of an initial nucleus. These observations are consistent with the results of other studies in the context of protein folding (Chowdhury et al., 2003; Southall et al., 2002) and aggregation (Dima and Thirumalai, 2002; Jang et al., 2004; Massi and Straub, 2001).
Much like the purpose of increased concentration in the in vitro experiments relative to in vivo, the increased concentration in our simulations serves to enhance the rate of aggregation to a manageable timescale. Although the simulations were conducted at a concentration that is 100 times higher than the typical concentration found in the in vitro experiments, our quantitative analysis allows simple extrapolation to the physiologically relevant concentrations. Thus, the dissociation/reassociation process can be much slower at the typical experimental concentrations, allowing the peptides to sample the conformational space more thoroughly and, perhaps, to reach a conformational equilibrium when they are dissociated. The quick dissociation/reassociation processes observed in our simulations also suggested that, given reasonable simulation time, the peptide orientation could be randomized, despite the fact that the simulations in each set were started from identical conformations with different random velocities. Judging from the lack of preferred orientations, it appears that the peptide orientation was indeed randomized. This is further corroborated by the observation that the trajectories within each set sampled quite different conformations. This is understandable given that earlier studies indicated that two nearly identical trajectories (identical velocities and nearly identical coordinates) can diverge and produce two quite different trajectories within, typically, 100.0 ps (Zhou and Wang, 1996).
CONCLUSION
We have observed the formation of partially ordered oligomers. These structures are suggested to be the amyloid-forming embryonic nuclei. The underlying association of peptides and the transition to the β-extended conformation is cooperative and strongly correlated. β-sheets form during the reaggregating process rather than after the formation of the disordered oligomers via conformation transition. Furthermore, the combined effect of high concentration and periodic boundary condition enhances the formation of the coiled monomers forming compact structures. The short-range interactions promote β-extended conformations. The short-range interactions include the interpeptide interactions through main-chain hydrogen bonds and the hydrophobic interactions. If β-strands were primarily stabilized by nonspecific hydrophobic interactions, the formation of the hydrogen-bonded β-sheet could be substantially reduced due to a slow dissociation process. If β-strands were primarily stabilized by hydrogen bonds, β-sheets could not be stable in water. Therefore, it is anticipated that amyloidogenic peptides should have reasonably high solubility, should contain complementary side chains, and should have a high β-sheet propensity. Based on the extrapolated free energies of the oligomers, we estimated that for a 1.0-nM peptide concentration, the octamer should be the critical oligometric state beyond which higher-order oligomers would be more stable.
Acknowledgments
This work has been supported by research grants from the National Institutes of Health (RR15588, PI Lenhoff, GM64458 and GM67168 to Y.D.), the state of Delaware, University of Delaware, University of Delaware Research Fund, and Delaware Biotech Institute (to Y.D.). Usage of VMD, WebLab viewer graphics packages are gratefully acknowledged.
References
- Azriel, R., and E. Gazit. 2001. Analysis of the minimal amyloid-forming fragment of the islet amyloid polypeptide - An experimental support for the key role of the phenylalanine residue in amyloid formation. J. Biol. Chem. 276:34156–34161. [DOI] [PubMed] [Google Scholar]
- Barash, D., L. J. Yang, X. L. Qian, and T. Schlick. 2003. Inherent speedup limitations in multiple time step/particle mesh Ewald algorithms. J. Comput. Chem. 24:77–88. [DOI] [PubMed] [Google Scholar]
- Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, A. DiNola, and J. R. Haak. 1984. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 81:3684–3690. [Google Scholar]
- Case, D. A., D. A. Pearlman, and J. W. Caldwell. T. E. Cheatham III, J. Wang, W. S. Ross, C. L. Simmerling, T. A. Darden, K. M. Merz, R. V. Stanton, A. Chang, J. J. Vincent, M. Crowley, V. Tsui, H. Gohlke, R. Radner, Y. Duan, J. Pitera, I. Massova, G. L. Seibel, U. C. Singh, P. Weiner, and P. A. Kollman. 2002. AMBER 7. University of California, San Francisco.
- Chou, P. Y., and G. D. Fasman. 1977. Beta-turns in proteins. J. Mol. Biol. 115:135–175. [DOI] [PubMed] [Google Scholar]
- Chowdhury, S., W. Zhang, C. Wu, G. M. Xiong, and Y. Duan. 2003. Breaking non-native hydrophobic clusters is the rate-limiting step in the folding of an alanine-based peptide. Biopolymers. 68:63–75. [DOI] [PubMed] [Google Scholar]
- Dima, R. I., and D. Thirumalai. 2002. Exploring protein aggregation and self-propagation using lattice models: Phase diagram and kinetics. Protein Sci. 11:1036–1049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding, F., N. V. Dokholyan, S. V. Buldyrev, H. E. Stanley, and E. I. Shakhnovich. 2002. Molecular dynamics simulation of the SH3 domain aggregation suggests a generic amyloidogenesis mechanism. J. Mol. Biol. 324:851–857. [DOI] [PubMed] [Google Scholar]
- Dobson, C. M. 1999. Protein misfolding, evolution and disease. Trends Biochem. Sci. 24:329–332. [DOI] [PubMed] [Google Scholar]
- Duan, Y., C. Wu, S. Chowdhury, M. C. Lee, G. Xiong, W. Zhang, R. Yang, P. Cieplak, R. Luo, T. Lee, J. Caldwell, J. Wang, and P. Kollman. 2003. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase QM calculations. J. Comput. Chem. 24:1999–2012. [DOI] [PubMed] [Google Scholar]
- Essmann, U., L. Perera, M. L. Berkowitz, T. A. Darden, H. Lee, and L. G. Pedersen. 1995. A smooth particle mesh Ewald method. J. Chem. Phys. 103:8577–8593. [Google Scholar]
- Frishman, D., and P. Argos. 1995. Knowledge-based protein secondary structure assignment. Proteins. 23:566–579. [DOI] [PubMed] [Google Scholar]
- Gsponer, J., U. Haberthur, and A. Caflisch. 2003. The role of side-chain interactions in the early steps of aggregation: Molecular dynamics simulations of an amyloid-forming peptide from the yeast prion Sup35. Proc. Natl. Acad. Sci. USA. 100:5154–5159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoppener, J. W. M., B. Ahren, and C. J. M. Lips. 2000. Islet amyloid and type 2 diabetes mellitus. N. Engl. J. Med. 343:411–419. [DOI] [PubMed] [Google Scholar]
- Hu, H., M. Elstner, and J. Hermans. 2003. Comparison of a QM/MM force field and molecular mechanics force fields in simulations of alanine and glycine “dipeptides” (Ace-Ala-Nme and Ace-Gly-Nme) in water in relation to the problem of modeling the unfolded peptide backbone in solution. Proteins. 50:451–463. [DOI] [PubMed] [Google Scholar]
- Jang, H. B., C. K. Hall, and Y. Q. Zhou. 2004. Assembly and kinetic folding pathways of a tetrameric beta-sheet complex: Molecular dynamics simulations on simplified off-lattice protein models. Biophys. J. 86:31–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaroniec, C. P., C. E. MacPhee, V. S. Bajaj, M. T. McMahon, C. M. Dobson, and R. G. Griffin. 2004. High-resolution molecular structure of a peptide in an amyloid fibril determined by magic angle spinning NMR spectroscopy. Proc. Natl. Acad. Sci. USA. 101:711–716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kayed, R., E. Head, J. L. Thompson, T. M. McIntire, S. C. Milton, C. W. Cotman, and C. G. Glabe. 2003. Common structure of soluble amyloid oligomers implies common mechanism of pathogenesis. Science. 300:486–489. [DOI] [PubMed] [Google Scholar]
- Kelly, J. W. 1998. The alternative conformations of amyloidogenic proteins and their multi-step assembly pathways. Curr. Opin. Struct. Biol. 8:101–106. [DOI] [PubMed] [Google Scholar]
- Klimov, D. K., and D. Thirumalai. 2003. Dissecting the assembly of A beta(16–22) amyloid peptides into antiparallel beta sheets. Structure. 11:295–307. [DOI] [PubMed] [Google Scholar]
- Lee, B., and F. M. Richards. 1971. Interpretation of protein structures - estimation of static accessibility. J. Mol. Biol. 55:379–400. [DOI] [PubMed] [Google Scholar]
- Li, L. P., T. A. Darden, L. Bartolotti, D. Kominos, and L. G. Pedersen. 1999. An atomic model for the pleated beta-sheet structure of A beta amyloid protofilaments. Biophys. J. 76:2871–2878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenzo, A., B. Razzaboni, G. C. Weir, and B. A. Yankner. 1994. Pancreatic-islet cell Toxicity of amylin associated with type-2 diabetes-mellitus. Nature. 368:756–760. [DOI] [PubMed] [Google Scholar]
- Mason, J. M., N. Kokkoni, K. Stott, and A. J. Doig. 2003. Design strategies for anti-amyloid agents. Curr. Opin. Struct. Biol. 13:526–532. [DOI] [PubMed] [Google Scholar]
- Massi, F., and J. E. Straub. 2001. Energy landscape theory for Alzheimer's amyloid beta-peptide fibril elongation. Proteins. 42:217–229. [DOI] [PubMed] [Google Scholar]
- McGuffin, L. J., K. Bryson, and D. T. Jones. 2000. The PSIPRED protein structure prediction server. Bioinformatics. 16:404–405. [DOI] [PubMed] [Google Scholar]
- Minton, A. P. 2000. Implications of macromolecular crowding for protein assembly. Curr. Opin. Struct. Biol. 10:34–39. [DOI] [PubMed] [Google Scholar]
- Rochet, J. C., and P. T. Lansbury. 2000. Amyloid fibrillogenesis: themes and variations. Curr. Opin. Struct. Biol. 10:60–68. [DOI] [PubMed] [Google Scholar]
- Ryckaert, J.-P., G. Ciccotti, and H. J. C. Berendsen. 1977. Numerical integration of the Cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 23:327–341. [Google Scholar]
- Shi, Z. S., C. A. Olson, G. D. Rose, R. L. Baldwin, and N. R. Kallenbach. 2002. Polyproline II structure in a sequence of seven alanine residues. Proc. Natl. Acad. Sci. USA. 99:9190–9195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Southall, N. T., K. A. Dill, and A. D. J. Haymet. 2002. A view of the hydrophobic effect. J. Phys. Chem. B. 106:521–533. [Google Scholar]
- Sunde, M., L. C. Serpell, M. Bartlam, P. E. Fraser, M. B. Pepys, and C. C. F. Blake. 1997. Common core structure of amyloid fibrils by synchrotron X-ray diffraction. J. Mol. Biol. 273:729–739. [DOI] [PubMed] [Google Scholar]
- Tenidis, K., M. Waldner, J. Bernhagen, W. Fischle, M. Bergmann, M. Weber, M. L. Merkle, W. Voelter, H. Brunner, and A. Kapurniotu. 2000. Identification of a penta- and hexapeptide of islet amyloid polypeptide (IAPP) with amyloidogenic and cytotoxic properties. J. Mol. Biol. 295:1055–1071. [DOI] [PubMed] [Google Scholar]
- Thirumalai, D., D. K. Klimov, and R. I. Dima. 2003. Emerging ideas on the molecular basis of protein and peptide aggregation. Curr. Opin. Struct. Biol. 13:146–159. [DOI] [PubMed] [Google Scholar]
- Westermark, P., C. Wernstedt, T. D. Obrien, D. W. Hayden, and K. H. Johnson. 1987. Islet amyloid in type-2 human diabetes mellitus and adult diabetic cats contains a novel putative polypeptide hormone. Am. J. Pathol. 127:414–417. [PMC free article] [PubMed] [Google Scholar]
- Zanuy, D., B. Y. Ma, and R. Nussinov. 2003. Short peptide amyloid organization: Stabilities and conformations of the islet amyloid peptide NFGAIL. Biophys. J. 84:1884–1894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zanuy, D., and R. Nussinov. 2003. The sequence dependence of fiber organization. A comparative molecular dynamics study of the islet amyloid polypeptide segments 22–27 and 22–29. J. Mol. Biol. 329:565–584. [DOI] [PubMed] [Google Scholar]
- Zhou, H. B., and L. Wang. 1996. Chaos in biomolecular dynamics. J. Phys. Chem. 100:8101–8105. [Google Scholar]