Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2004 Aug 23;87(5):3010–3022. doi: 10.1529/biophysj.104.047498

Circular Dichroism of Carotenoids in Bacterial Light-Harvesting Complexes: Experiments and Modeling

S Georgakopoulou *, R van Grondelle *, G van der Zwan †
PMCID: PMC1304774  PMID: 15326029

Abstract

In this work we investigate the origin and characteristics of the circular dichroism (CD) spectrum of rhodopin glucoside and lycopene in the light-harvesting 2 complex of Rhodopseudomonas acidophila and Rhodospirillum molischianum, respectively. We successfully model their absorption and CD spectra based on the high-resolution structures. We assume that these spectra originate from seven interacting transition dipole moments: the first corresponds to the 0-0 transition of the carotenoid, whereas the remaining six represent higher vibronic components of the S2 state. From the absorption spectra we get an estimate of the Franck-Condon factors of these transitions. Furthermore, we investigate the broadening mechanisms that lead to the final shape of the spectra and get an insight into the interaction energy between carotenoids. Finally, we examine the consequences of rotations of the carotenoid transition dipole moment and of deformations in the light-harvesting 2 complex rings. Comparison of the modeled carotenoid spectra with modeled spectra of the bacteriochlorophyll QY region leads to a refinement of the modeling procedure and an improvement of all calculated results. We therefore propose that the combined carotenoid and bacteriochlorophyll CD can be used as an accurate reflection of the overall structure of the light-harvesting complexes.

INTRODUCTION

Carotenoids are long polyenes found in all photosynthetic apparatuses of plants, algae, and purple bacteria. They contribute to light harvesting by their strong absorption in the visible part of the spectrum that originates from a long conjugated chain of double bonds. In addition, carotenoids play a very important role in photoprotection (Foote and Denny, 1968; Schrott, 1985; Frank et al., 1991). These two functions have been studied extensively in the light-harvesting 2 complexes (LH2) of purple bacteria: through their singlet states, carotenoids capture the sunlight in the blue-green part of the spectrum, and transfer 25–95% of it to B800 and/or B850 bacteriochlorophyll (BChl) a chromophores (Kramer et al., 1984; Chadwick et al., 1987; Mimuro and Katoh, 1991; Andersson et al., 1996; Scholes et al., 1997); through their triplet states, they quench the BChl excited triplet states which—if long-lived—would lead to formation of singlet oxygen and subsequently to damage of the complex (Nilsson et al., 1972; Cogdell and Frank, 1987). For a thorough review on the spectroscopy of carotenoids, see Polivka and Sundström (2004). Unfortunately, much less is known about their structural role and their contribution in the assembly and stability of the tertiary structures (Gall et al., 2003). Some insight into the matter can be obtained by looking into the highly resolved structures of LH2 complexes. Here, the carotenoids span the lipid membrane, thus connecting the B800 and B850 rings (Cogdell et al., 1996). Furthermore, together with BChls, they maintain the contact between the transmembrane α-helices (McDermott et al., 1995; Cogdell et al., 1996; Prince et al., 1997). As a result, they are likely to play an important role also in the assembly of the complex, particularly in the arrangement of protein α-helices in their native position in the membrane (Paulsen, 1999).

In the LH2 complexes of Rhodopseudomonas acidophila and Rhodospirillum molischianum, two B850 BChls, one B800 BChl, and one carotenoid form the pigment building block that, if rotated a number of times according to the symmetry number, will reproduce the basic, well-known pigment arrangement. The B800 BChls lie with their bacteriochlorin rings almost parallel to the membrane plane at the cytoplasmic side of the complex, and they make contact to carboxyl-α-Met1 through their Mg2+ ions. On the periplasmic side of the complex, the B850 BChls are arranged with their bacteriochlorin rings parallel to the transmembrane α-helices and their Mg2+ ions are liganded to histidine residues. The carotenoids have a sigmoidal-shaped conformation and run through the complex starting on the N-terminal side. They make van der Waals contacts with both the B800 and B850 BChls, while linking two αβ-apoprotein pairs together (Koepke et al., 1996; Prince et al., 1997). In vivo, BChl and carotenoid pigments can be found with a ratio between 3:1 and 2:1, which indicates the existence of more than one carotenoid molecule per αβ-pair (McDermott et al., 1995; Koepke et al., 1996; Papiz et al., 2003). According to the 2.0 Å electron density map from Rps. acidophila LH2, a second carotenoid lies on the outside of each αβ-pair, with its sugar headgroup at the periplasmic side of the complex (Cogdell et al., 2003; Papiz et al., 2003). These carotenoids are not well resolved; they have rather low occupancy and do not appear by the same amount in every complex (McDermott et al., 1995; Koepke et al., 1996; Papiz et al., 2003; R. J. Cogdell, University of Glasgow, personal communication, 2004).

Carotenoid molecules exhibit a broad absorption in the blue-green part of the spectrum, where BChls are not active. Depending on the pigment and on its environment, this band can vary in shape and position (Britton, 1995; Christensen, 1999). In some cases, a very distinct fine structure is observed, originating from transitions from the lowest vibrational level of the electronic ground state S0 (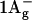Inline graphic) to the lower vibrational levels of the carotenoid's S2 (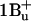Inline graphic) singlet excited state. Transitions to the latter are responsible for the absorption, since transitions to the lower S1 (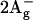Inline graphic) singlet excited state are optically forbidden according to symmetry selection rules (Ritz et al., 2000). Lack of fine structure in the room temperature (RT) absorption spectrum of carotenoids in solution can result from three kinds of inhomogeneity: a), initial-state energy inhomogeneity, arising from thermal population of low frequency ground state vibrations, b), environmental inhomogeneity due to the fact that each solute molecule sees a different microenvironment and therefore experiences a different solvent shift of its excitation energy; and c), inhomogeneity with respect to molecular conformation. The vibrational bands that appear in the carotenoid absorption spectrum involve both the C–C and C=C stretch modes; the latter are generally not well resolved, and the fine structure spacing of ∼1300 cm−1 can be observed between the vibrational bands (Kohler, 1995).

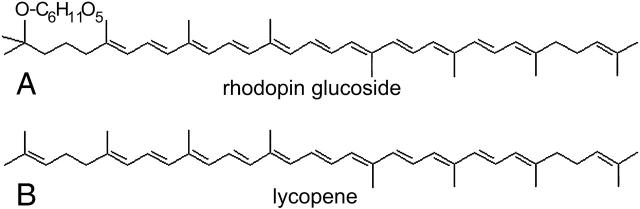
In this work, the issue of the carotenoid arrangement in LH2 complexes in relation to their spectral properties, is approached by studying their circular dichroism (CD) spectra. For this purpose, we concentrate on the carotenoids found in the LH2 antennae discussed above, namely rhodopin (rh.) glucoside of Rps. acidophila and lycopene of Rsp. molischianum. Both are rather long pigments with a conjugated π-electron chain of 11 double bonds each (Fig. 1). The difference between the two carotenoids lies in their headgroups: rh. glucoside has a glucosyl ring at one end, whereas lycopene features no cyclic end groups. The origin of the CD signal of the carotenoids in these complexes is not fully understood. Although many carotenoids are structurally chiral and can thus exhibit intrinsic CD signals (Buchecker and Noak, 1995), the typical intensities of these signals are generally very small (>10 times smaller) compared to the ones arising from the complexes.

FIGURE 1.

FIGURE 1

Open in a new tab

Chemical structures of the carotenoids (A) rh. glucoside and (B) lycopene.

In the following sections, we show that the CD signals of carotenoids in the aforementioned LH2 complexes can be explained on the basis of their atomic structure. Studies relating the structure and spectroscopy of the BChl regions of antenna complexes have been carried out earlier by Koolhaas et al. (1997a,b, 1998, 2000) and Georgakopoulou et al. (2002). Important features of the CD signals were examined, such as the red shift of the CD zero crossing, the sign and nonconservative nature of the CD lines, and the position of the high exciton component of the BChls B850 band. Here, we model the carotenoid CD signals by arranging their transition dipole moments in a ring and calculating the excitonic interactions between them. In the process we get information over the Franck-Condon (FC) factors, the carotenoid-carotenoid interaction energy, and the broadening mechanisms that dominate the spectra. Finally, we compare the modeling results for the carotenoid region with the ones we obtained earlier for the BChl region (Georgakopoulou et al., 2002) and thus acquire a very reliable criterion according to which the calculated spectra are improved.

MATERIALS AND METHODS

Sample preparation and spectroscopic methods

Cells of Rps. acidophila strain 10050 and Rsp. molischianum were grown anaerobically in the light and harvested as previously reported (Cogdell and Thorber, 1979; Cogdell et al., 1983, 1990; Cogdell and Crofts, 1990; Evans et al., 1990; Cogdell and Hawthornthwaite, 1993; Halloren et al., 1995). Isolation and purification of the antenna complexes were performed as described in Cogdell and Hawthornthwaite (1993). For the absorption and CD measurements, the samples were diluted in 20 mM TRIS HCl, pH 7.8, to a final optical density of 0.5 cm−1; 0.1% (v/v) of the detergent N,N-dimethyldodecylamine-N-oxide (LDAO) was added to avoid stacking of the complexes. Glycerol concentrations of 70% (v/v) were necessary in the final solution for creating a transparent glass, and a home-built cuvet with removable windows was used to avoid orientation of the sample upon cooling. The measurements were performed on a home-built setup, consisting of (apart from the relevant optics) a monochromator, frequency regulator, a photoelastic modulator) crystal, a diode detector, and two lock-in amplifiers. To achieve temperatures of 77 K, we used an Oxford Instruments (Gorinchem, The Netherlands) DN1704 liquid nitrogen cryostat.

Spectral deconvolution

The full width at half-maximum (FWHM) of each carotenoid band was calculated by deconvoluting the absorption spectra into a sum of four Gaussians. As initial values, we used the peak positions of the absorption bands to indicate the center of each Gaussian, whereas the width of the bands was given an average estimate.

For the calculation of the FC factors, the same procedure was carried out, but this time the 0–1, 0–2, and 0–3 bands of the absorption spectrum were fitted with two, three, and four Gaussians, respectively, to account for the single and double bond stretches and their combination bands; thus, we arrive to a sum of 10 components instead of four. For the initial positions of the Gaussians in this case, we used, for the 0–0 band, the absorption maximum, whereas for the 0–1 bands we gave two values deviating by ∼150–200 cm−1 from the peak position, according to the expected energy difference between the single and double bond stretches. The positions of the remaining Gaussians can be calculated from the above three values. Initially the width and area of all bands was assigned the same value.

The model

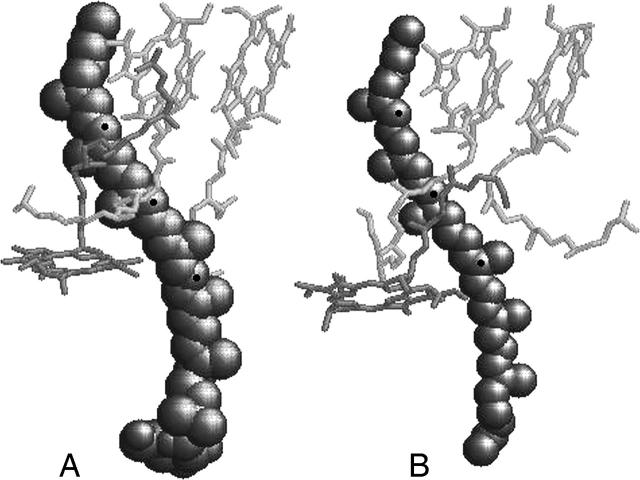
For the calculation of the absorption and CD spectra of carotenoids in LH2 complexes, we start with the known structures of Rps. acidophila and Rsp. molischianum. The ring of carotenoids is then constructed using the positions of three of the carbon atoms on the conjugated chain of each carotenoid. In Fig. 2 the atoms taken into account are shown. The central carbon is used to determine the position of the carotenoid, whereas the other two define the direction of the transition dipole moment. As shown in previous work by Dolan et al. (2001) and Georgakopoulou et al. (2003), the transition dipole moment of carotenoids in LH2 is not oriented along the long axis of the molecule, but is parallel to a line connecting the carbons of the conjugated chain that are situated in the area between the B800 and B850 BChls. For Rps. Acidophila, these are the 11th and 23rd carbon atoms, as they are notated in the Brookhaven Protein Data Bank structure 1KZU, whereas for Rsp. Molischianum, the corresponding carbon atoms are the 17th and 60th (Brookhaven Protein Data Bank structure 1LGH).

FIGURE 2.

FIGURE 2

Open in a new tab

Representation of the carotenoid molecules' positions in the basic building block of (A) Rps. acidophila and (B) Rsp. molischianum LH2 complexes. The carbon atoms that define the beginning, end, and center of the transition dipole moments are marked with black dots.

Once the ring is formed, we calculate the interaction Hamiltonian. For that purpose we take into account four separate vibronic components of the S2 state of the carotenoids, the 0–0, 0–1, 0–2, and 0–3 transitions, and two stretching modes, the C–C and C=C, for the three higher transitions. Therefore, we simulate the transition dipole moment of each carotenoid with seven parallel interacting transition dipole moments: one for the 0–0 transition and two for each of the 0–1, 0–2, and 0–3 transitions. The magnitude of the 0–0 dipole moment, as well as the FC factors on which the remaining transitions are scaled, were calculated for both Rps. acidophila and Rsp. molischianum as described further in this section. The interaction Hamiltonian is then diagonalized and the resulting stick spectrum is dressed with Gaussians to simulate homogeneous broadening. Inhomogeneous broadening is introduced by adding a random contribution to each of the diagonal elements of the Hamiltonian. Another more precise procedure was also carried out, where the site energies of all the transitions belonging to the same carotenoid molecule were distorted by the same amount; this, however, did not cause any significant changes in the resulting spectra. It is important to note here that the calculation of the absorption and CD spectra is simultaneous. A more detailed account of the modeling method, containing some of the mathematical equations used, can be found in the supplemental material on the web.

RESULTS

Experimental results

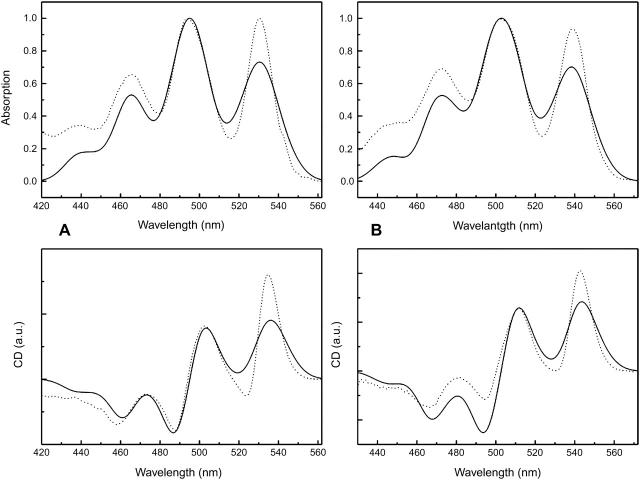
The absorption spectrum of the carotenoid region in both Rps. acidophila and Rsp. molischianum LH2 complexes is illustrated in Figs. 3 and 4. In particular, four bands can clearly be distinguished, which arise from the transition from the ground state to the first (or ground, 0–0), second (0–1), third (0–2), and fourth (0–3) vibronic components (vibrational levels) of the carotenoid's excited state (S2). For Rps. Acidophila, these bands are positioned at 530 nm (18868 cm−1), 494 nm (20243 cm−1), 465 nm (21505 cm−1), and 437 nm (22883 cm−1), with FWHM of 17 nm, 24 nm, 20 nm, and 20 nm, respectively, whereas for Rsp. Molischianum, they are situated at slightly longer wavelengths, specifically at 539 nm (18553 cm−1), 502 nm (19920 cm−1), 472 nm (21186 cm−1), and 445 nm (22472 cm−1), with FWHM of 17 nm, 25 nm, 22 nm, and 21 nm, respectively. The energy gap between these vibrational bands is ∼1300 cm−1 for both complexes. Similar values as the ones mentioned above have been reported earlier by various groups (Polivka et al., 2002). For the 0–1, 0–2, and 0–3 bands, the oscillator strength arises from both the C–C stretch and the C=C stretch of the conjugated chain of the carotenoid. The two vibrations are separated by ∼300–350 cm−1, as seen by Raman studies: the frequencies of the C=C vibration is 1550–1500 cm−1, whereas for the C–C it varies from 1200 to 900 cm−1 (Koyama, 1995). More specifically, for lycopene it has been determined that the frequencies of the C–C and C=C stretches are 1155 cm−1 and 1513 cm−1, respectively, giving an energy difference of 358 cm−1 (Fujii et al., 2001). Raman studies have shown that the frequency of the C=C stretching modes depends on the number of conjugated double bonds in the chain (Koyama, 1995). Since rh. glucoside and lycopene both have the same amount of double bonds in their conjugated chains, we can assume that the energy difference between the single and double bond stretches remains approximately the same.

FIGURE 3.

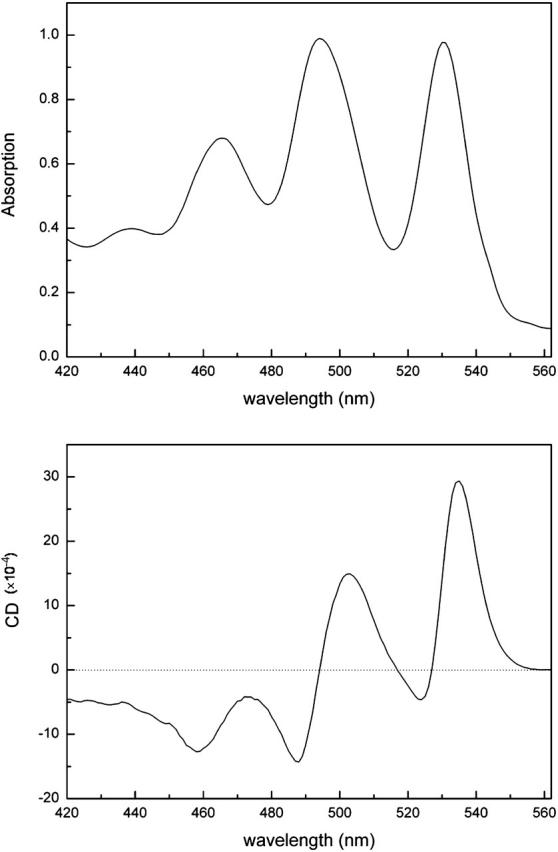
FIGURE 3

Open in a new tab

77 K absorption (top) and CD (bottom) spectra of the carotenoid region of the Rps. acidophila LH2 ring. The absorption is normalized on the 0–1 band and the CD is then scaled on the absorption.

FIGURE 4.

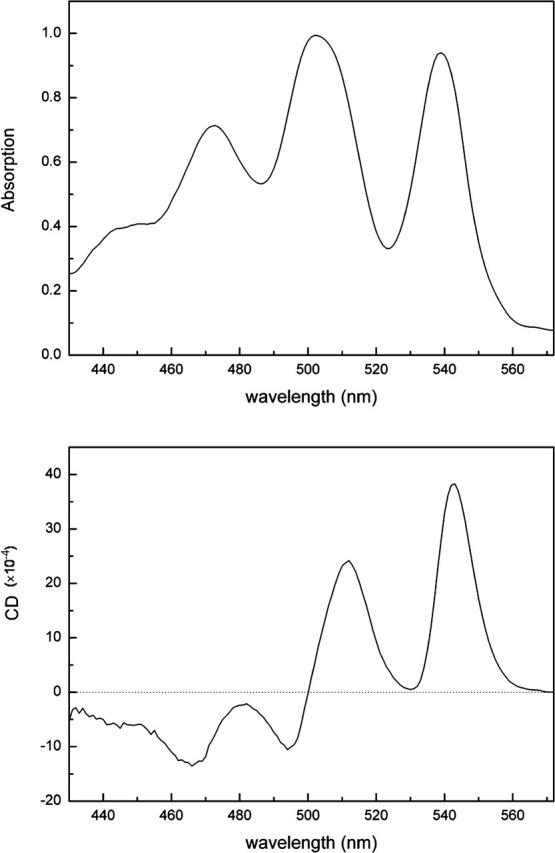
FIGURE 4

Open in a new tab

77 K absorption (top) and CD (bottom) spectra of the carotenoid region of the Rsp. molischianum LH2 ring. The absorption is normalized on the 0–1 band and the CD is then scaled on the absorption.

In the carotenoid region, the CD spectra of these two complexes are also very similar. Four major bands can be distinguished, with signs ++−− from higher to lower wavelengths. The bands arise from the superposition of the CD signal of each absorption band. The intensity ratio of the CD bands of Rps. acidophila is 2.0:1.0:-1.0:-0.9 for the bands situated at 535, 503, 488, and 458 nm, respectively. The Rsp. molischianum CD bands at 543, 512, 494, and 466 nm have intensity ratios of 1.6:1.0:-0.5:-0.6. One small shoulder can be distinguished on the blue side of the carotenoid CD signal, originating from the 0–3 absorption band. However, in this area there is big overlap most likely with CD signal belonging to the BChl's Soret region; therefore no further qualitative or quantitative remarks will be made on this band.

FC factors calculation

The FC factors for the carotenoids in Rps. acidophila and Rsp. molischianum LH2's were estimated by calculating the area covered by the absorption band of each transition dipole that participates in the total absorption of the molecules in the LH2 rings. To derive these values, we fitted the absorption spectra of the carotenoid regions with a number of Gaussians, as described in the Materials and Methods section: the 0–0 bands were fitted with one Gaussian, whereas two Gaussians were used for the 0–1, three for the 0–2, and four for the 0–3 bands (Fig. 5). Thus we account for the two stretching modes and their combinations that contribute to the final shape of the absorption spectra. We can now calculate the oscillator strength

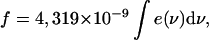graphic file with name M4.gif

where ν is the frequency, e(ν) is the extinction coefficient, and ∫(e(ν)dν) is the total area of the absorption band. The transition dipole moment (in Cm) is found from (Atkins, 1986)

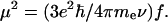graphic file with name M5.gif

FIGURE 5.

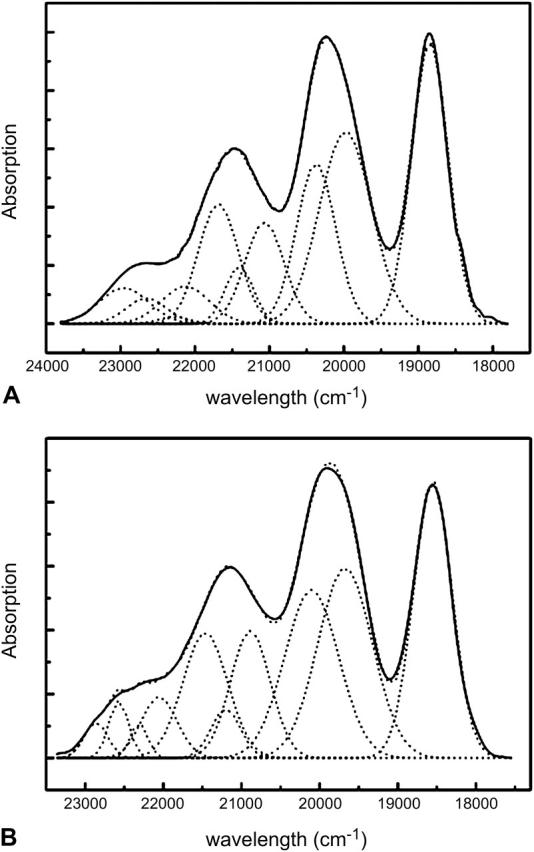
FIGURE 5

Open in a new tab

Deconvolution of the absorption spectra of the LH2 carotenoid region of (A) Rps. acidophila and (B) Rsp. molischianum LH2 rings. The resulting 10 Gaussians represent the two stretching modes and their combinations that are responsible for the final shape of the absorption bands.

Finally, we know from literature that the transition dipole moment for QY is 6.3 D (Georgakopoulou et al., 2002). Therefore, we can estimate the total carotenoid transition dipole moment and FC factors by calculating the area of each band that belongs to a stretching mode and comparing it to that of the B800 BChls absorption. The combination bands are not taken into account because they do not represent a separate transition dipole moment. The comparison is possible since in both cases we deal with N pigments arranged similarly in a ring structure. The results are summarized in Table 1. Previous studies on the 0–1 transition dipole moment of lycopene (Zhang et al., 2000) give a value of 16.377 D for the carotenoid in n-hexane. This value is in reasonable accordance with our result (10.5 D), considering the differences in the pigment's conformation and environment.

TABLE 1.

Transition dipole moments and FC factors for the carotenoid transitions in Rps. acidophila and Rsp. molischianum LH2 rings

Rps. acidophila Rsp. molischianum
μ 5.9 D 5.8 D
0–0 1.0; 18845 1.0; 18553
0–1a 0.96; 19978 0.96; 19673
0–1b 0.75; 20374 0.89; 20103
0–2a 0.59; 21067 0.65; 20886
0–2b 0.63; 21687 0.68; 21464
0–3a 0.38; 22128 0.42; 22053
0–3b 0.38; 22955 0.25; 22862
Open in a new tab

With 0–0 to 0–3, we denote the different transitions from the ground state to the excited (S2) state. a and b distinguish between single and double bond stretches. After the semicolon, we give in cm−1 the position of the Gaussian that corresponds to each transition.

Modeling results

The key parameters that lead to a good agreement between measured and modeled spectra are the site energies for each carotenoid transition, the dielectric constant, and the homogeneous and inhomogeneous broadenings. The values of these parameters can be altered—within reasonable limits—thus providing us with the possibility to control the exact positions and magnitudes of the absorption and CD bands. The fact that these spectra are calculated simultaneously offers a good criterion to decide whether the induced changes on the parameters mentioned above are reasonable or not; thus, a change that would lead to improvement of the shape and size of the CD signal, but would diminish the accuracy of the absorption, is not accepted.

The modeling procedure begins with assigning a site energy for each of the transitions that participate in the formation of the carotenoid absorption spectrum. These site energies should be in accordance with the peak positions of the Gaussians in which the measured absorption spectrum is deconvoluted. In Table 2, we list the values used for simulating the carotenoid spectrum in the rings of Rps. acidophila and Rsp. molischianum. For the energetically higher bands, the deviation of the site energies derived from the modeling with respect to the peak positions of the Gaussians is rather significant. This is understandable if we consider that in the measured spectra there is overlap with higher transitions—for example, the BChls Soret transitions, whereas such effects are not taken into account in our modeling procedure.

TABLE 2.

Final modeling parameters

Rps. acidophila Rsp. molischianum
Site energies (nm; cm−1) 530; 18868 538; 18587
497.5; 20101 507.5; 19704
490; 20408 497; 20121
468; 21368 477; 20964
462.5; 21622 468; 21368
445; 22472 448; 22321
436; 22936 440; 22727
ɛ 1.2 1.5
Δ (cm−1) 480 450
Δ0–0 300 300
σ (cm−1) 680 650
σ0–0 500 500
Open in a new tab

ɛ, dielectric constant.

Δ and σ, homogeneous and inhomogeneous broadening in cm−1.

Δ0–0 and σ0–0, homogeneous and inhomogeneous broadening of the 0–0 band in cm−1.

Subsequently, the value of the high-frequency dielectric constant is estimated. In a previous modeling study (Georgakopoulou et al., 2002) on the BChl rings of various LH2 complexes, we assigned values of 1.2 and 1.5 for the dielectric constants of Rps. acidophila and Rsp. molischianum, respectively. These values give very good results also when applied to the modeling of the carotenoid bands. Here, the dielectric constant does not affect the absorption and CD spectra to the same extent as the equivalent spectra of a strongly coupled ring such as, for instance, the B850 ring. The latter present a large shift to the blue of both absorption and CD bands, whereas the high exciton band shifts to the red for increasing values of the dielectric constant; in other words, the total width of the excitonic manifold decreases. At the same time, the magnitude of both absorption and CD bands decreases gradually (data not shown). In the case of carotenoids, an increase in the dielectric constant—which can be translated to a decrease of the interaction energy—simply leads to a decrease in the magnitude of the CD signal and hardly changes the absorption spectra. The reason for this is that the interaction energy between carotenoids is small, thus minor changes of this small value are not going to substantially change the oscillator strength; they can, however, still affect the much more sensitive rotational strength.

The last parameter that needs to be adjusted to achieve reasonable results is the broadening. As mentioned earlier, in our calculations we take both homogeneous and inhomogeneous broadening into account. Homogeneous broadening accounts for very fast fluctuations in the transition frequencies that are related to the fast component of exciton-phonon coupling. By changing the value of the homogeneous broadening, we can improve the FWHM of the bands; at the same time, we get an insight into the lifetimes of the different transitions. Inhomogeneous broadening, on the other hand, is the slow component of the exciton-phonon coupling, related to very slow dynamics of the protein environment of the pigments. This broadening mechanism, implemented on diagonal disorder, leads to changes in the ground-state energies of the carotenoids; thus, not only the FWHM, but also the position of the bands can be changed slightly. The FWHM of the absorption bands therefore results from the combination of homogeneous and inhomogeneous broadenings.

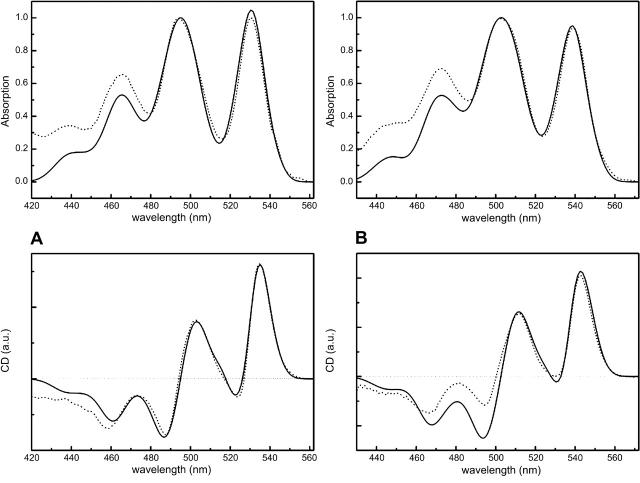
In Fig. 6, we see modeled absorption and CD spectra of the carotenoid rings of Rps. acidophila and Rsp. molischianum, in comparison with the measured spectra. In this example, values of 480 cm−1 and 680 cm−1 are assigned to the homogeneous and inhomogeneous broadenings of Rps. acidophila. For Rsp. Molischianum, the corresponding values are 450 cm−1 and 650 cm−1. This gives rise to absorption bands whose FWHM ratios for Rps. acidophila are 1.07:1.0:0.86:0.86—starting with the 0–0 band—versus the measured 0.71:1.0:0.84:0.85. For Rsp. molischianum and for the same broadening values, we obtain FWHM ratios of 0.93:1.0:0.84:0.7 compared to the measured 0.68:1.0:0.89:0.83. Apparently, the biggest discrepancy between model and experiment lies in the 0–0 band, where the FWHM is increased by ∼30% for both complexes when the aforementioned broadening values are applied. Furthermore, the intensity ratio of the four CD bands, especially at the lower energy side, is far from what we observe in the experimental spectra; this is a direct consequence of the broadening of the 0–0 bands. In principle, we expected that the modeled FWHM of the higher energy bands will be broadened more than that of the 0–0 band due to the overlap of two vibrations—the C–C and the C=C stretches. However, the energetic separation of the two transitions is apparently too small to visibly affect the width of the final absorption band, so a different approach needs to be taken to substantially improve the FWHM ratios. A decrease of the 0–0 band broadening values in the model can be well justified: a longer lifetime for the lowest vibrational mode of the excited state leads to smaller homogeneous broadenings for the 0–0 band; moreover, the lack of conformational freedom of the pigment in the complex can result in smaller inhomogeneity. We therefore reduce these values by 180 cm−1 and 150 cm−1 for Rps. acidophila and Rsp. molischianum, respectively (Fig. 7). This changes the ratios for the two complexes to 0.73:1.0:0.85:0.86 and 0.69:1.0:0.84:0.7. The 0–0 band FWHM is now much closer to the measured value. The CD signals have also improved dramatically, with 0–0 bands that are only a few nanometers wider than the measured and which have an intensity ratio that corresponds to that measured experimentally, specifically 2.0:1.0:-1.0:-0.7 for Rps. acidophila and 1.6:1.0:-0.9:-0.7 for Rsp. molischianum. A summary of the final modeling parameters can be found in Table 2.

FIGURE 6.

FIGURE 6

Open in a new tab

Modeled absorption (top) and CD (bottom) spectra of the carotenoid rings in (A) Rps. acidophila and (B) Rsp. molischianum LH2's for uniform homogeneous and inhomogeneous broadenings. Superimposed, in dotted lines, are the measured spectra.

FIGURE 7.

FIGURE 7

Open in a new tab

Modeled absorption (top) and CD (bottom) spectra of the carotenoid rings in (A) Rps. acidophila and (B) Rsp. molischianum LH2's for reduced homogeneous and inhomogeneous broadenings for the 0–0 bands. Superimposed, in dotted lines, are the measured spectra.

An estimate of the interaction energy between carotenoids arranged in a circular ring can be obtained at this point. For both the carotenoid rings of Rps. acidophila and Rsp. Molischianum, we found interaction energies in the order of 1.0 cm−1 for the 0–0 transitions of neighboring carotenoids, a value that is in accordance with estimates of other groups (Scholes et al., 1997). Compared to the B800 ring, where the interaction energy we derived between the BChls was ∼21 cm−1, the carotenoid value is significantly smaller, even though both the carotenoids and the BChl pigments are arranged radially on the same ring and thus very similar distance from each other. However, the transition dipole moments of the B800 BChls are oriented parallel to the plane of the membrane and in a sort of head-to-tail sequence with each other, whereas the carotenoid dipoles are more or less perpendicular to the plane of the ring and to their connecting vector. The parallel orientation facilitates the interaction between the pigments. By doubling the interaction energy between the carotenoids, we observe no changes in the modeled absorption spectra. The CD signals, on the other hand, increase in size two times but remain very stable in terms of shape (data not shown). The reasons for these changes are of the same nature as the ones that occur when the dielectric constant is decreased.

Rotations and deformations

As mentioned in the previous paragraph, changes in the interaction energy between the carotenoids lead to variations in the intensity of the CD signal without visibly affecting its shape; furthermore, the absorption signal is hardly influenced. In the next paragraph we will show that the shape of the CD signal is also rather insensitive to distortions of the circularity of the ring, or to small rotations of the dipole moments. On the other hand, the magnitude of the signal can be affected significantly.

In Fig. 8, the effect that a rotation of the transition dipole moments of only a few degrees has on the CD spectrum is illustrated. In this case, we orient the transition dipole moment along the long axis S of the carotenoid chain, that is to say 9° off the vector μ that connects the carbon atoms situated between the B800 and B850 BChls. What we observe is an increase of the CD signal to more than double the intensity, similar to the changes in the intensity of the CD bands observed in a previous study by Georgakopoulou et al. (2002). Here, the LH2 BChls were rotated by a few degrees from the pigments' x or z axis causing a decrease of the 800-nm or 850-nm signals, respectively. However, the intensity ratio and positions of the maxima and minima of the carotenoid CD lines change only slightly, so that it is not possible to choose between the two cases in terms of shape. On the other hand, comparing the magnitude of the carotenoid CD signal with the one obtained for the BChl QY region of LH2 (Georgakopoulou et al., 2002) provides a good criterion. Therefore, we construct the visible/near-infrared modeled absorption spectrum by scaling the carotenoid and BChl QY bands on the measured ones. The modeled CD signals of these two regions are then scaled by the same factors as the corresponding absorption bands, and their relative magnitude is compared to that of the measured CD spectra. For Rsp. molischianum, the magnitude ratio of the carotenoid and BChl QY CD is in very good agreement with what is observed experimentally, when the carotenoid transition dipole moment is oriented along μ. The Rps. acidophila CD signals, however, do not give satisfactory ratios. The carotenoid and BChl QY regions differ, approximately, by a factor of two. To explain this discrepancy, we have to reconsider both modeling procedures. In the process, we refine the LH2 modeling program so that the calculated absorption and CD spectra are related to each other not only qualitatively but also quantitatively. We observe, therefore, that the CD signal of the QY region of Rps. acidophila, modeled according to Georgakopoulou et al. (2002), is ∼2 times bigger in magnitude than the one obtained experimentally. The calculated spectrum can be improved by applying different rotations for the BChls; the α-bound B850 BChls are rotated around their z axis by 3° instead of 7°, whereas a rotation of 4° around their x axis is introduced for the B800 BChls. This diminishes the intensity of the CD lines to the desired magnitude, without affecting the shape of the absorption and CD spectra.

FIGURE 8.

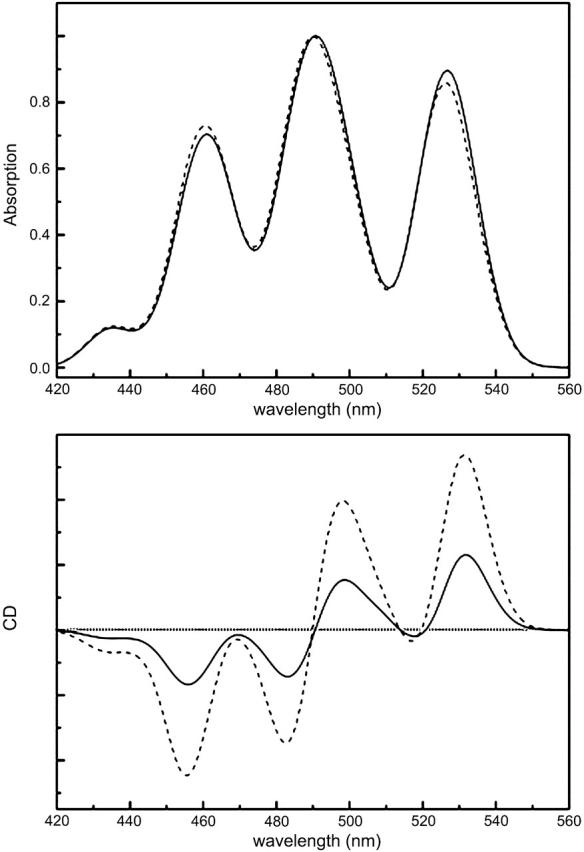
FIGURE 8

Open in a new tab

Absorption (top) and CD (bottom) spectra modeled for two different orientations of the transition dipole moment: parallel to the vector connecting carbon atoms that lie between the B800 and B850 BChl ring (solid curves) or along the carotenoid long π-electron chain (dashed curves).

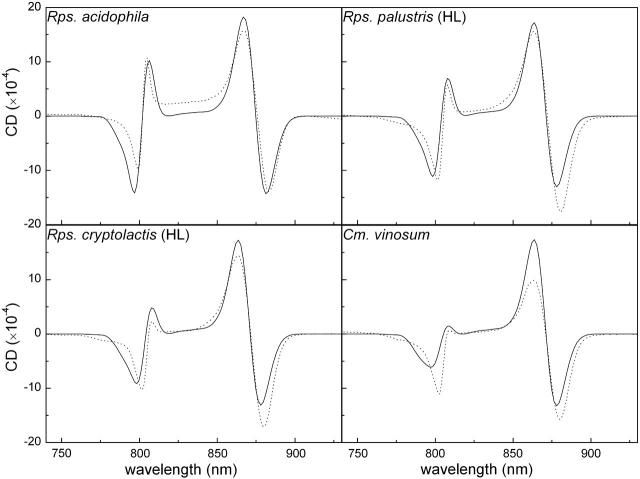
The new results create the need to reexamine also the remaining “acidophila”-type LH2 complexes that were studied in the aforementioned article, namely high-light (HL) Rps. palustris, Rps. cryptolactis (HL), and Chromatium vinosum. These complexes were modeled according to the parameters used for Rps. acidophila. One of the main conclusions deduced from the modeling was that the major difference between them lies in the orientation of their B800 BChls. By rotating the latter a few degrees around their x axis, the CD spectra of these LH2s were reproduced. This conclusion is still valid when the new parameters are employed. In this case, we need to rotate the B800 BChls by 5°, 6°, and 7.5° around their x axis to reproduce the spectra of Rps. palustris (HL), Rps. cryptolactis (HL), and Cm. vinosum, respectively. It is satisfactory to observe that with these improved parameters, the 800-nm CD lines are now nonconservative, and in excellent agreement with the measured spectra (Fig. 9).

FIGURE 9.

FIGURE 9

Open in a new tab

Modeled (solid curves) and measured (dotted curves) CD spectra of the QY region from LH2 complexes of the “acidophila”-type (Georgakopoulou et al., 2002).

Changes in the size of the CD signal are caused also when the circular conformation of the ring is distorted. An example can be seen in Fig. 10, where the carotenoid ring is gradually deformed into an ellipse. In this case, we create the carotenoid transition dipole ring by using the position of only one carotenoid molecule from the known structure. More precisely, we are interested exclusively in the atoms that define the position and orientation of the transition dipole moments, namely the carbons pointed out in Fig. 2. We proceed by rotating these atoms by means of a simple rotation matrix:

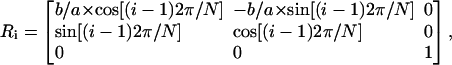graphic file with name M6.gif

where a and b are the long and short axes of the resulting ellipse, N is the symmetry number, and i runs from 1 to N. Thus we create an elliptical ring, whose ellipticity we can control by varying b/α. Consequently, the interaction energies between neighboring carotenoids become nonuniform over the ring, since the relative orientations and positions of the transition dipoles change. What we observe is that the more elliptical the ring becomes, the more the intensity of the CD signal increases. For a b/α ratio up to 0.75, the changes in the position and intensity ratios of the CD signals are insignificant, whereas in the absorption spectrum, only minor shifts and intensity changes are observed. The absolute intensity of the CD signal, however, is increased ∼3 times. For a rather extreme case, where the b/a ratio is increased to 0.5, we observe a clear shift to the blue for the absorption and CD bands and some distinct distortions in the shape of the CD signal.

FIGURE 10.

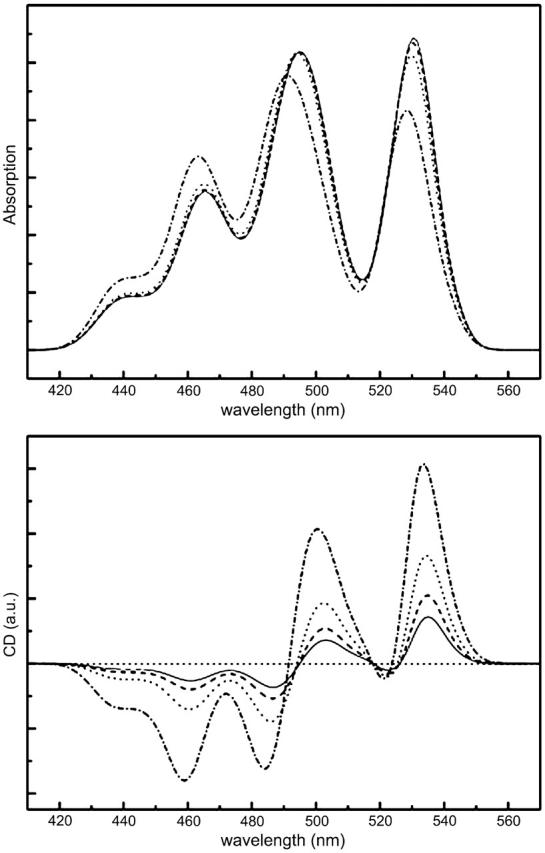
FIGURE 10

Open in a new tab

Modeled absorption (top) and CD (bottom) spectra for different ratios between short (b) and long (a) axes. b/a = 1.0 (solid curves), b/α = 0.9 (dashed curves), b/α = 0.75 (dotted curves), and b/α = 0.5 (dashed-dotted curves).

DISCUSSION

The choice of the site energies and the broadenings assigned for modeling the carotenoid absorption and CD spectra in the LH2 ring needs to be discussed further in this section. In the final set of modeling parameters, the values of the site energies do not coincide with the position of the molecule's absorption bands in solution, as one might expect. This is reasonable considering that, with our model, we are studying a ring comprising solely of carotenoids, omitting any interactions with the protein or the BChls. Such interactions are known to affect the final position of the carotenoid bands by shifting them to the red by ∼30 nm (Polivka and Sundström, 2004). Since these effects are missing here, we have to position the absorption maxima to the correct wavelength by simply assuming from the beginning lower values for the site energies.

After allocating the correct site energies for the bands, and given that the other parameters such as dielectric constant, energy difference between the two stretching modes, and dipole moment magnitudes and orientations have predesignated values—according to previous studies and the experimental results—we still had to adjust the homogeneous and inhomogeneous broadenings to achieve reasonable agreement between theory and experiment. As we mentioned in the results section, using uniform values for the broadenings of all the bands leads to a FWHM of the 0–0 transition that is wider than what we have measured. To obtain satisfactory results, we need to assign smaller values for both the homogeneous and inhomogeneous line widths. Such a reduction of the homogeneous broadening of the lower band with respect to the rest is reasonable, considering that the lowest excited state has a longer lifetime. In particular, a decrease in the homogeneous broadening by 150 cm−1 reflects a rise in the lifetimes by ∼25 fs; taken into account that the higher vibrational bands are known to have higher relaxation rates than the ground state of the S2, such a decrease in the 0–0 band homogeneous broadening is well within the acceptable limits. It is worth noting that the homogeneous broadenings we assign for the higher excited states can be converted to lifetimes of 69 fs and 74 fs for the Rps. acidophila and Rsp. molischianum carotenoid rings, respectively, which are in general agreement with measured results; carotenoids in solution are known to have S2 lifetimes of ∼100 fs, and in the LH complexes this lifetime is even shorter due to energy transfer (Kandori et al., 1994; Ricci et al., 1996; Krueger et al., 1998a,b; Macpherson, 1999).

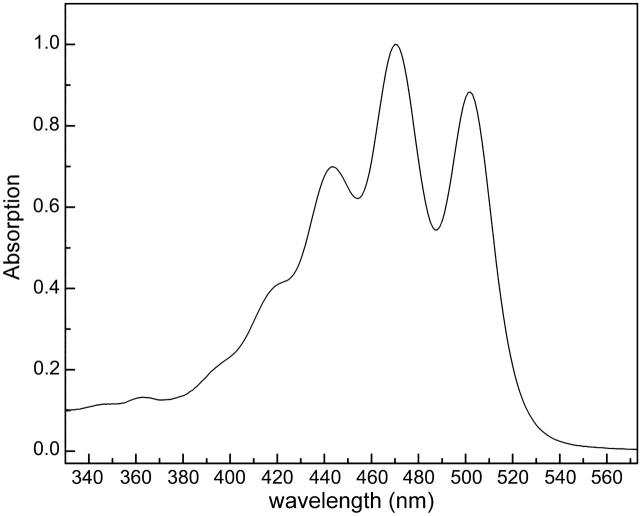
As far as the inhomogeneous broadening is concerned, possible reasons for the discrepancy between values for the 0–0 band and those of the higher vibrational transitions should probably be sought in the conformation of carotenoids in a complex as opposed to that of carotenoids in solution. In the absorption spectrum of lycopene in solution, for example, we can see that the FWHM of the 0–0 band is actually larger than the one of 0–1 transition (Fig. 11), which is in contradiction to what we observe for the carotenoid ring in LH2. This is due to the fact that in solution, the molecules have more freedom to assume different conformations, which causes a dispersion of the site energies; in contrast, when the carotenoid is “locked” in a complex, the number of different conformations the molecule can assume is limited, and therefore the bands are narrower. Specifically, the 0–0 band has been previously reported to be affected even more than the rest by this restriction in the possible conformations of the carotenoid. In a study by Polivka et al. (2002), the authors assign the FWHM differences in the S1→S2 0–0 bands of rh. glucoside in the Rps. acidophila LH2 versus rh. glucoside in solution exactly to lack of freedom in the states' possible conformations. Furthermore, measurements of carotenoids at RT and 77 K have shown a decrease in the FWHM ratio of the 0–0 band with respect to the 0–1 band when going to lower temperatures, which depicts again this difference in the inhomogeneous broadening of the bands due to conformational stability (Frank et al., 2000). In our model the carotenoids are positioned in a specific way—in a circular ring—therefore a decrease of the inhomogeneous broadening of the 0–0 band with respect to the other transitions is justified.

FIGURE 11.

FIGURE 11

Open in a new tab

RT absorption spectrum of lycopene in solution.

After the final assignment of the values for all the parameters involved, there are still small discrepancies between model and experiment, mainly in the blue region of the spectra. However, no effort was made to improve the fit in this area; the overlap with the Soret region of the BChls in the experimental data, which is not accounted for in the model, renders any further assumptions unreliable. As far as the 0–0 band is concerned, we complete our modeling by changing the amount of homogeneity and inhomogeneity by the same value. This does not have to be the case; changes of the two broadening parameters do not have to be uniform, and the resulting spectra can probably be improved slightly by assigning different values for the homogeneous and inhomogeneous broadening of the 0–0 bands; however the broadening mechanisms are introduced in the modeling in such a way that we cannot distinguish which value corresponds to which kind of broadening. Therefore, no additional valuable information can come out of such an effort.

We have to note at this point, that it would be possible to adequately reproduce the measured absorption and CD spectra using a simple model with only three transition dipole moments and a completely intuitive evaluation of the FC factors, however, the parameters derived in that case would not be as meaningful; therefore, less information would be finally deducted from the modeling procedure.

The study of deformations of a circular carotenoid ring can be of great help in identifying the factors that lead to a specific conformation of the LH rings in the membrane. Atomic force microscopy studies on LH1 membranes demonstrate great flexibility in the shape of the LH1 ring, as opposed to the LH2 ring that seems to have a rather rigid circular structure (Bahatyrova et al., 2004). The tight packing of the LH1 complexes in the membrane is thought to lead to elliptical rings, which have been reported to have b/a ratio up to 0.75. As previously suggested (Jungas et al., 1999; Frese et al., 2000), the small PufX protein may be responsible for the orderly arrangement of the complexes in the membrane. In this case, lack of the PufX protein should lead to more circular rings, while in its presence LH1 rings would be, in their majority, elliptical. CD measurements on LH1 membranes from Rb. sphaeroides both in the presence and absence of PufX show a clear increase of the signal for the latter case (to be published) but no further displacement or distortion of the CD bands. The signal becomes ∼3 times bigger, a value that occurs for b/a ratios of ∼0.75, and thus is in agreement with our modeling results and with the atomic force microscopy observations.

In conclusion, the absorption and CD signals of a ring of carotenoids can be well modeled on the basis of its atomic structure. It is therefore possible to relate the structure and spectroscopy in the LH2 complex, not only in the BChl region, as reported earlier (Georgakopoulou et al., 2002), but also in the region of the carotenoids. There is a wide range of information that can be derived by such a modeling. First, an estimate of the FC factors of the carotenoid transitions is given, and their validity is justified by the good correspondence between modeled and experimental bands. Furthermore, we obtain estimates of the interaction energy between carotenoids in a ring, as well as a picture of the broadening mechanisms that contribute to the formation of the final spectra. Finally, a comparison of the results in the carotenoid region with those previously reported for the BChl QY region (Georgakopoulou et al., 2002) offers the opportunity to improve the modeling procedure and verify or even improve the calculated spectra. Modeling the absorption and CD spectra of LH complexes is, therefore, a powerful tool, which we can use to understand their structure in relation with their spectroscopic properties. Thus, we can not only reproduce measured results starting from the well-resolved structures, but also reverse the procedure and use the CD spectra of unknown complexes to speculate over their molecular organization.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

Supplementary Material

[supplemental file]
biophysj_87_5_3010__index.html (780B, html)

References

  1. Andersson, P. O., R. J. Cogdell, and T. Gillbro. 1996. Femtosecond dynamics of carotenoid-to-bacteriochlorophyll a energy transfer in the light-harvesting antenna complexes from the purple bacterium Chromatium purpuratum. Chem. Phys. 210:195–217. [Google Scholar]
  2. Atkins, P. W. 1986. Physical Chemistry. W. H. Freeman, New York.
  3. Bahatyrova, S., R. N. Frese, K. O. van der Werf, C. Otto, C. N. Hunter, and J. D. Olsen. 2004. Flexibility and size heterogeneity of the LH1 light harvesting complex revealed by atomic force microscopy: functional significance for bacterial photosynthesis. J. Biol. Chem. 279:21327–21333. [DOI] [PubMed] [Google Scholar]
  4. Britton, G. 1995. UV/visible spectroscopy. In Carotenoids. G. Britton, S. Liaaen-Jensen, and H. Pfander, editors. Birkhäuser, Basel, Boston, and Berlin. 13–62.
  5. Buchecker, R., and K. Noak. 1995. Circular dichroism. In Carotenoids. G. Britton, S. Liaaen-Jensen, and H. Pfander, editors. Birkhäuser, Basel, Boston, and Berlin. 63–116.
  6. Chadwick, B. W., C. Y. Zhang, R. J. Cogdell, and H. A. Frank. 1987. The effects of lithium dodecyl-sulfate and sodium-borohydride on the absorption spectrum of the B800-850 light-harvesting complex from Rhodopseudomonas acidophila 7750. Biochim. Biophys. Acta. 893:444–451. [Google Scholar]
  7. Christensen, R. L. 1999. The electronic states of carotenoids. In The Photochemistry of Carotenoids. H. A. Frank, A. J. Young, G. Britton, and R. J. Cogdell, editors. Kluwer Academic Publishers, Dordrecht, The Netherlands. 137–159.
  8. Cogdell, R. J., and A. R. Crofts. 1990. Analysis of the pigment content of an antenna pigment/protein complex from three strains of Rhodopseudomonas sphaeroides. Biochim. Biophys. Acta. 502:409–416. [DOI] [PubMed] [Google Scholar]
  9. Cogdell, R. J., I. Durant, J. Valentine, J. G. Lindsay, and K. Schmidt. 1983. The isolation and partial characterization of the light-harvesting pigment-protein complement of Rhodopseudomonas acidophila. Biochim. Biophys. Acta. 722:427–435. [Google Scholar]
  10. Cogdell, R. J., and H. A. Frank. 1987. How carotenoids function in photosynthetic bacteria. Biochim. Biophys. Acta. 895:63–79. [DOI] [PubMed] [Google Scholar]
  11. Cogdell, R. J., P. K. Fyfe, S. J. Barrett, S. M. Prince, A. A. Freer, N. W. Isaacs, P. McGlynn, and C. N. Hunter. 1996. The purple bacterial photosynthetic unit. Photosynth. Res. 48:55–63. [DOI] [PubMed] [Google Scholar]
  12. Cogdell, R. J., and A. M. Hawthornthwaite. 1993. Preparation, purification and crystallization of purple bacterial antenna complexes. In The Photosynthetic Reaction Center. J. R. Norris and J. Deisenhofer, editors. Academic Press, New York. 23–42.
  13. Cogdell, R. J., A. M. Hawthornthwaite, M. B. Evans, L. A. Ferguson, C. Kerfeld, J. P. Thornber, F. van Mourik, and R. van Grondelle. 1990. Isolation and characterization of an unusual antenna complex from the marine purple sulfur photosynthetic bacterium Chromatium purpuratum Bn5500. Biochim. Biophys. Acta. 1019:239–244. [Google Scholar]
  14. Cogdell, R. J., N. W. Isaacs, A. A. Freer, T. D. Howard, A. T. Gardiner, S. M. Prince, and M. Z. Papiz. 2003. The structural basis of light-harvesting in purple bacteria. FEBS Lett. 555:35–39. [DOI] [PubMed] [Google Scholar]
  15. Cogdell, R. J., and J. P. Thorber. 1979. The preparation and characterization of different types of light-harvesting pigment-protein complexes from some purple bacteria. In The CIBA Foundation Symposium 61 (new series) on Chlorophyll Organization and Energy Transfer in Photosynthesis. G. Wolstenholme and D. Fitzsimons, editors. Elsevier, Amsterdam, The Netherlands. 61–79. [DOI] [PubMed]
  16. Dolan, P. M., D. Miller, R. J. Cogdell, R. R. Birge, and H. A. Frank. 2001. Linear dichroism and the transition dipole moment orientation of the carotenoid in the LH2 antenna complex in membranes of Rhodopseudomonas acidophila strain 10050. J. Phys. Chem. B. 105:12134–12142. [Google Scholar]
  17. Evans, M. B., A. M. Hawthornthwaite, and R. J. Cogdell. 1990. Isolation and characterization of the different B800-850 light-harvesting complexes from low-light and high-light grown cells of Rhodopseudomonas palustris, strain 2.1.6. Biochim. Biophys. Acta. 1016:71–76. [Google Scholar]
  18. Foote, C. S., and R. W. Denny. 1968. Chemistry of singlet oxygen. VI. Quenching by β-carotene. J. Am. Chem. Soc. 90:6233–6235. [Google Scholar]
  19. Frank, H. A., J. A. Bautista, J. Josue, Z. Pendon, R. G. Hiller, F. P. Sharples, D. Gosztola, and M. R. Wasielewski. 2000. Effect of the solvent environment on the spectroscopic properties and dynamics of the lowest excited states of carotenoids. J. Phys. Chem. B. 104:4569–4577. [Google Scholar]
  20. Frank, H. A., C. A. Violette, J. K. Trautman, A. P. Shreve, T. G. Owens, and A. C. Albrecht. 1991. Carotenoids in photosynthesis: structure and photochemistry. Pure Appl. Chem. 63:109–114. [Google Scholar]
  21. Frese, R. N., J. D. Olsen, R. Branvall, W. H. J. Westerhuis, C. N. Hunter, and R. van Grondelle. 2000. The long-range supraorganization of the bacterial photosynthetic unit: a key role for PufX. Proc. Natl. Acad. Sci. USA. 97:5197–5202. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Fujii, R., T. Ishikawa, Y. Koyama, M. Taguchi, Y. Isobe, H. Nagae, and Y. Watanabe. 2001. Fluorescence spectroscopy of all-trans-anhydrorhodovibrin and spirilloxanthin: detection of the Inline graphic fluorescence. J. Phys. Chem. A. 105:5348–5355. [Google Scholar]
  23. Gall, A., R. J. Cogdell, and B. Robert. 2003. Influence of carotenoid molecules on the structure of the bacteriochlorophyll binding site in peripheral light-harvesting proteins from Rhodobacter sphaeroides. Biochemistry. 42:7252–7258. [DOI] [PubMed] [Google Scholar]
  24. Georgakopoulou, S., R. J. Cogdell, R. van Grondelle, and H. van Amerongen. 2003. Linear-dichroism measurements on the LH2 antenna complex of Rhodopseudomonas acidophila strain 10050 show that the transition dipole moment of the carotenoid rhodopin glucoside is not collinear with the long molecular axis. J. Phys. Chem. B. 107:655–658. [Google Scholar]
  25. Georgakopoulou, S., R. N. Frese, E. Johnson, M. H. C. Koolhaas, R. J. Cogdell, R. van Grondelle, and G. van der Zwan. 2002. Absorption and CD spectroscopy and modeling of various LH2 complexes from purple bacteria. Biophys. J. 82:2184–2197. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Halloren, E., G. McDermott, J. G. Lindsay, C. Miller, A. A. Freer, N. W. Isaacs, and R. J. Cogdell. 1995. Studies on the light-harvesting complexes from the thermotolerant purple bacterium Rhodopseudomonas cryptolactis. Photosynth. Res. 44:149–155. [DOI] [PubMed] [Google Scholar]
  27. Jungas, C., J. L. Ranck, J. L. Rigaud, P. Joliot, and A. Vermeglio. 1999. Supramolecular organization of the photosynthetic apparatus of Rhodobacter sphaeroides. EMBO J. 18:534–542. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Kandori, H., H. Sasabe, and M. Mimuro. 1994. Direct determination of a lifetime of the S2 state of β-carotene by femtosecond time-resolved fluorescence spectroscopy. J. Am. Chem. Soc. 116:2671–2672. [Google Scholar]
  29. Koepke, J., X. C. Hu, C. Muenke, K. Schulten, and H. Michel. 1996. The crystal structure of the light-harvesting complex II (B800-850) from Rhodospirillum molischianum. Structure. 4:581–597. [DOI] [PubMed] [Google Scholar]
  30. Kohler, B. E. 1995. Electronic structure of carotenoids. In Carotenoids. G. Britton, S. Liaaen-Jensen, and H. Pfander, editors. Birkhäuser, Basel, Boston, and Berlin. 1–12.
  31. Koolhaas, M. H. C., R. N. Frese, G. J. S. Fowler, T. S. Bibby, S. Georgakopoulou, G. van der Zwan, C. N. Hunter, and R. van Grondelle. 1998. Identification of the upper exciton component of the B850 bacteriochlorophylls of the LH2 antenna complex, using a B800-free mutant of Rhodobacter sphaeroides. Biochemistry. 37:4693–4698. [DOI] [PubMed] [Google Scholar]
  32. Koolhaas, M. H. C., G. van der Zwan, R. N. Frese, and R. van Grondelle. 1997a. Red shift of the zero crossing in the CD spectra of the LH2 antenna complex of Rhodopseudomonas acidophila: a structure-based study. J. Phys. Chem. B. 101:7262–7270. [Google Scholar]
  33. Koolhaas, M. H. C., G. van der Zwan, F. van Mourik, and R. van Grondelle. 1997b. Spectroscopy and structure of bacteriochlorophyll dimers. I. Structural consequences of nonconservative circular dichroism spectra. Biophys. J. 72:1828–1841. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Koolhaas, M. H. C., G. van der Zwan, and R. van Grondelle. 2000. Local and nonlocal contributions to the linear spectroscopy of light-harvesting antenna systems. J. Phys. Chem. B. 104:4489–4502. [Google Scholar]
  35. Koyama, Y. 1995. Resonance Raman Spectroscopy. In Carotenoids. G. Britton, S. Liaaen-Jensen, and H. Pfander, editors. Birkhäuser, Basel, Boston, and Berlin. 135–146.
  36. Kramer, H. J. M., R. van Grondelle, C. N. Hunter, W. H. J. Westerhuis, and J. Amesz. 1984. Pigment organization of the B800-850 antenna complex of Rhodopseudomonas sphaeroides. Biochim. Biophys. Acta. 765:156–165. [Google Scholar]
  37. Krueger, B. P., G. D. Scholes, and G. R. Fleming. 1998a. Calculation of couplings and energy-transfer pathways between the pigments of LH2 by the ab initio transition density cube method. J. Phys. Chem. B. 102:5378–5386. [Google Scholar]
  38. Krueger, B. P., G. D. Scholes, R. Jimenez, and G. R. Fleming. 1998b. Electronic excitation transfer from carotenoid to bacteriochlorophyll in the purple bacterium Rhodopseudomonas acidophila. J. Phys. Chem. B. 102:2284–2292. [Google Scholar]
  39. Macpherson, A. N., J. B. Arellano, N. J. Fraser, R. J. Cogdell, and T. Gillbro. 1999. Ultrafast energy transfer from rhodopin glucoside in the light harvesting complex of Rps. acidophila. In Photosynthesis: Mechanisms and Effects. G. Garab, editor. Kluwer Academic Publishers, Dordrecht, The Netherlands. 9–14.
  40. McDermott, G., S. M. Prince, A. A. Freer, A. M. Hawthornthwaite-Lawless, M. Z. Papiz, R. J. Cogdell, and N. W. Isaacs. 1995. Crystal-structure of an integral membrane light-harvesting complex from photosynthetic bacteria. Nature. 374:517–521. [Google Scholar]
  41. Mimuro, M., and T. Katoh. 1991. Carotenoids in photosynthesis: absorption, transfer and dissipation of light energy. Pure Appl. Chem. 63:123–130. [Google Scholar]
  42. Nilsson, R., P. B. Merkel, and D. R. Kearns. 1972. Unambiguous evidence for participation of singlet oxygen (1Δ) in photodynamic oxidation of amino-acids. Photochem. Photobiol. 16:117–124. [DOI] [PubMed] [Google Scholar]
  43. Papiz, M. Z., S. M. Prince, T. Howard, R. J. Cogdell, and N. W. Isaacs. 2003. The structure and thermal motion of the B800-850 LH2 complex from Rps. acidophila at 2.0 Å resolution and 100 K: New structural features and functionally relevant motions. J. Mol. Biol. 326:1523–1538. [DOI] [PubMed] [Google Scholar]
  44. Paulsen, H. 1999. Carotenoids and the assembly of light-harvesting complexes. In The Photochemistry of Carotenoids. H. A. Frank, A. J. Young, G. Britton, and R. J. Cogdell, editors. Kluwer Academic Publishers, Dordrecht, The Netherlands. 123–135.
  45. Polivka, T., and V. Sundström. 2004. Ultrafast dynamics of carotenoid excited states: from solution to natural and artificial systems. Chem. Rev. 104:2021–2072. [DOI] [PubMed] [Google Scholar]
  46. Polivka, T., D. Zigmantas, J. L. Herek, Z. He, T. Pascher, T. Pullerits, R. J. Cogdell, H. A. Frank, and V. Sundström. 2002. The carotenoid S1 state in LH2 complexes from purple bacteria Rhodobacter sphaeroides and Rhodopseudomonas acidophila: S1 energies, dynamics, and carotenoid radical formation. J. Phys. Chem. B. 106:11016–11025. [Google Scholar]
  47. Prince, S. M., M. Z. Papiz, A. A. Freer, G. McDermott, A. M. Hawthornthwaite-Lawless, R. J. Cogdell, and N. W. Isaacs. 1997. Apoprotein structure in the LH2 complex from Rhodopseudomonas acidophila strain 10050: modular assembly and protein pigment interactions. J. Mol. Biol. 268:412–423. [DOI] [PubMed] [Google Scholar]
  48. Ricci, M., S. E. Bradforth, R. Jimenez, and G. R. Fleming. 1996. Internal conversion and energy transfer dynamics of spheroidene in solution and in the LH-1 and LH-2 light-harvesting complexes. Chem. Phys. Lett. 259:381–390. [Google Scholar]
  49. Ritz, T., A. Damjanovic, K. Schulten, J. P. Zhang, and Y. Koyama. 2000. Efficient light harvesting through carotenoids. Photosynth. Res. 66:125–144. [DOI] [PubMed] [Google Scholar]
  50. Scholes, G. D., R. D. Harcourt, and G. R. Fleming. 1997. Electronic interactions in photosynthetic light-harvesting complexes: the role of carotenoids. J. Phys. Chem. B. 101:7302–7312. [Google Scholar]
  51. Schrott, E. L. 1985. Carotenoids in plant photoprotection. Pure Appl. Chem. 57:729–734. [Google Scholar]
  52. Zhang, J. P., R. Fujii, P. Qian, T. Inaba, T. Mizoguchi, Y. Koyama, K. Onaka, Y. Watanabe, and H. Nagae. 2000. Mechanism of the carotenoid-to-bacteriochlorophyll energy transfer via the S1 state in the LH2 complexes from purple bacteria. J. Phys. Chem. B. 104:3683–3691. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[supplemental file]
biophysj_87_5_3010__index.html (780B, html)
biophysj_87_5_3010__1.pdf (84.7KB, pdf)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES