Abstract
The suprachiasmatic nucleus governs daily variations of physiology and behavior in mammals. Within single neurons, interlocked transcriptional/translational feedback loops generate circadian rhythms on the molecular level. We present a mathematical model that reflects the essential features of the mammalian circadian oscillator to characterize the differential roles of negative and positive feedback loops. The oscillations that are obtained have a 24-h period and are robust toward parameter variations even when the positive feedback is replaced by a constantly expressed activator. This demonstrates the crucial role of the negative feedback for rhythm generation. Moreover, it explains the rhythmic phenotype of Rev-erbα−/− mutant mice, where a positive feedback is missing. The interplay of negative and positive feedback reveals a complex dynamics. In particular, the model explains the unexpected rescue of circadian oscillations in Per2Brdm1/Cry2−/− double-mutant mice (Per2Brdm1 single-mutant mice are arrhythmic). Here, a decrease of positive feedback strength associated with mutating the Per2 gene is compensated by the Cry2−/− mutation that simultaneously decreases the negative feedback strength. Finally, this model leads us to a testable prediction of a molecular and behavioral phenotype: circadian oscillations should be rescued when arrhythmic Per2Brdm1 mutant mice are crossed with Rev- erbα −/− mutant mice.
INTRODUCTION
Most organisms have developed endogenous circadian clocks to anticipate daily variations in their environment. In mammals, the master circadian clock is located in the suprachiasmatic nucleus of the hypothalamus, where it orchestrates diurnal changes in physiology and behavior. Circadian oscillations, which have a period of ∼24 h, are generated within single neurons by interlocked transcriptional/translational feedback loops (for a review, see Reppert and Weaver, 2002). In a negative feedback loop, transcription of the period and cryptochrome genes (Per1, Per2, Cry1, and Cry2) is activated by the transcription factor heterodimer BMAL1/CLOCK. After several hours, PER and CRY proteins downregulate their own synthesis by inhibiting BMAL1/CLOCK. Consequently, PER and CRY levels fall, thus, BMAL1/CLOCK is no longer inhibited and restarts the cycle. In a positive feedback loop, Bmal1 mRNA oscillations are caused by the rhythmic inhibition of Bmal1 transcription by REV-ERBα. Rev-erbα is presumably also activated by BMAL1/CLOCK and inhibited by PERs and CRYs. Thus, Bmal1 transcription is essentially positively regulated by PERs and CRYs (Fig. 1).
FIGURE 1.
Schematic view of the mammalian circadian core oscillator (modified from Reppert and Weaver, 2002). The clock mechanism comprises interlocked positive (green) and negative (red) feedback loops. The heterodimer BMAL1/CLOCK (C and B; green ovals) activates transcription of Per, Cry, and Rev-erbα genes. PER proteins (P; red square) are phosphorylated (•−) and form a complex with CRY proteins (C; red diamond) and CKIɛ/δ (ɛ/δ; red circle). In the nucleus this complex inhibits the transactivational activity of BMAL1/CLOCK, thus forming the negative feedback loop. In the positive feedback loop, Bmal1 transcription is activated (derepressed) by PER/CRY/CKIɛ/δ, because this complex also inhibits REV-ERBα synthesis (R, green square), which on its part represses Bmal1 transcription. The action of kinases (?) other than CKIɛ and CKIδ is likely (Sanada et al., 2002).
Experiments in circadian systems of Neurospora, Drosophila, and mammals as well as theoretical studies underline the importance of a delayed negative feedback for the generation of oscillations (Glass and Mackey, 1988). The function of the positive feedback in the circadian clock, however, is much less understood. Interlocked feedback loops potentially allow for multiple inputs and outputs at different phases (Allada, 2003). A contribution of the positive feedback to the robustness of the clock has been deduced from a study with Rev-erbα−/− mutant mice, whose clocks essentially lack the positive feedback (Preitner et al., 2002), and from a study in the Neurospora circadian system (Cheng et al., 2001).
Mathematical models provide insight into properties of the circadian oscillators (Ruoff and Rensing, 1996; Scheper et al., 1999; Smolen et al., 2004; Tyson et al., 1999; Ueda et al., 2001; for a review, see Goldbeter, 2002). In two models (Smolen et al., 2002, 2004) the role of the positive feedback in the Drosophila clock has been discussed. Recently, models of the circadian oscillator were published describing the molecular processes in great detail (Forger and Peskin, 2003; Leloup and Goldbeter, 2003), however, without focusing on the specific function of the positive feedback.
We propose a model for the mammalian circadian oscillator designed for investigating the interdependence of the positive and negative feedback. A reduced but essential set of variables is used to analyze the impact of these feedback loops on the oscillation dynamics. Our model shows sustained oscillations with period and phases in agreement with experimental observations. With and without positive feedback the period, phase, and amplitudes of the oscillations are quite robust in response to varying single parameters. The simultaneous regulation of the two interlocked feedback loops contributes to the maintenance of oscillations and the stability of the period. Using this model, we propose an explanation for the unexpected phenotype of the Per2Brdm1/Cry2−/− double-mutant mice (Oster et al., 2002). In addition, we predict the yet unknown phenotype of the Per2Brdm1/Rev-erbα−/− double-mutant mice to be rhythmic.
Model assumptions
Here, we describe a model of the mammalian circadian core oscillator using a system of ordinary differential equations. The variables of the system represent the concentrations of clock genes' mRNAs and proteins (Fig. 2). We focus specifically on the essential structure of the molecular network to characterize the role of the positive and negative feedback loops.
FIGURE 2.
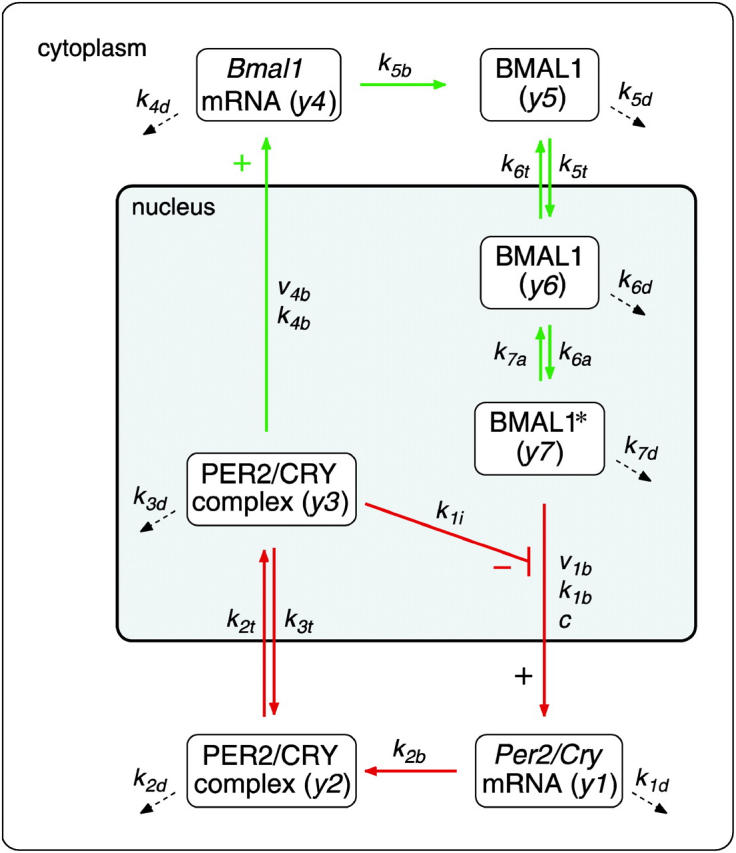
Model of the mammalian circadian core oscillator. An activated form of BMAL1 (BMAL1*) activates the transcription of Per2 and Cry genes resulting in an increase of Per2/Cry mRNA (y1). As the levels of PER2 and CRY proteins increase, they form a complex (y2), which is transported to the nucleus. The nuclear PER2/CRY complex (y3) inhibits Per2/Cry transcription and activates Bmal1 transcription. As a result, Bmal1 mRNA (y4) and protein (y5) increase. Nuclear BMAL1 (y6) in its active form (BMAL1*, y7) restarts transcription of Per2 and Cry genes. Dashed arrows represent degradation of mRNAs and proteins. Reference parameters of the reaction kinetics are given in Table 1.
Clock components oscillate with a period close to 24 h. The delay, which is necessary for oscillations in negative feedback loops (Friesen and Block, 1984; Glass and Mackey, 1988), is caused by processes including posttranslational modification, degradation, complex formation as well as nuclear import and export (Reppert and Weaver, 2002). The transcription factors CLOCK and BMAL1 activate as a heterodimer the transcription of Per, Cry, and Rev-erbα genes. For our model, we only consider the activation by BMAL1, because CLOCK is expressed at a constant level (Maywood et al., 2003) and thus is equivalent to a fixed parameter. PER and CRY proteins downregulate their own synthesis by inhibiting BMAL1/CLOCK transactivation activity. Cry genes are essential components of the clock network, because null mutations in these genes disrupt oscillations (Cry1−/−/Cry2−/− double-mutant mice) or alter their period (Cry1−/− or Cry2−/− single-mutant mice) (van der Horst et al., 1999; Vitaterna et al., 1999). As little is known about the differential functions of the CRY proteins, they are represented by a combined variable in the model. In the case of Per genes we only include Per2, because a null mutation in the Per2 gene causes arrhythmicity (Zheng et al., 2001), whereas different phenotypes have been reported for three Per1−/− mutant mouse strains (Bae et al., 2001; Cermakian et al., 2001; Zheng et al., 2001). However, in principle Per1 could be included into the model (see Discussion). Besides being an inhibitor of BMAL1/CLOCK, PER2 is thought to act positively on Bmal1 transcription (Shearman et al., 2000b). Per2 and Cry mRNAs and proteins are represented by the same variables, respectively, for the following reasons: i), their expression is coregulated by BMAL1/CLOCK; ii), they form a complex that is necessary for nuclear accumulation (Kume et al., 1999); iii), they are both targets of casein kinase Iɛ/δ (CKIδ/ɛ) (Toh et al., 2001; Eide et al., 2002); iv), the phase of their nuclear accumulation is similar (Reppert and Weaver, 2002); v), they both act negatively on BMAL1/CLOCK transactivational activity in vitro (Jin et al., 1999; Shearman et al., 2000b); and vi), details about the exact differential function of Cry and Per genes in the core oscillator are not known.
CKIɛ is considered implicitly by assuming fast phosphorylation of PER2 and CRY. This assumption and a rapid degradation of the monomeric proteins (Akashi et al., 2002; Shearman et al., 2000b) lead to a quasisteady state of the monomeric PER2 and CRY proteins. Here, we assume the same kinetics for PER2 and CRY, as no data exist regarding the stability of monomeric CRY. As a consequence, it is not necessary to consider the monomeric proteins as a separate variable in the model (for a detailed calculation see Supplementary Material). The PER2/CRY complex in the nucleus inhibits BMAL1/CLOCK activation of Per, Cry, and Rev-erbα genes. REV-ERBα has been described to repress Bmal1 transcription (Preitner et al., 2002; Ueda et al., 2002). In the end, this double-negative loop constitutes a positive feedback loop. In our model, REV-ERBα is implicitly taken into account by assuming a positive action of the PER2/CRY complex on Bmal1 transcription. In the model (Fig. 2), the variable y1 represents the concentration of Per2 or Cry mRNA, which are considered to be identical. y2 and y3 represent the concentrations of the PER2/CRY complex in the cytoplasm and the PER2/CRY complex in the nucleus, respectively. The variable y4 represents the concentration of Bmal1 mRNA, y5 of cytoplasmatic BMAL1 protein, and y6 of BMAL1 protein in the nucleus. The variable y7 describes the concentration of a transcriptionally active form BMAL1*, which can be understood as a complex with CLOCK (Gekakis et al., 1998) and/or as a phosphorylated form of BMAL1 (Eide et al., 2002).
The dynamics of these variables is described by the following system of differential equations:
 |
(1) |
 |
(2) |
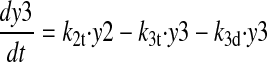 |
(3) |
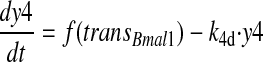 |
(4) |
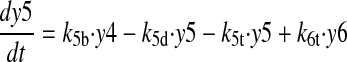 |
(5) |
 |
(6) |
 |
(7) |
Both transcription rates, f(transPer2/Cry) and f(transBmal1), are described by Hill functions implying switch-like behavior of the transcriptional effectors (Yuh et al., 1998) and saturation of transcriptional activity.
The rate of Per2/Cry transcription f(transPer2/Cry)
 |
(8) |
increases with rising BMAL1* concentration (y7) and with decreasing nuclear PER2/CRYconcentration (y3). Moreover, a constitutive transcriptional activator of Per2/Cry transcription is included in the transcription term by the parameter c. This term is a phenomenological representation of the switch-like behavior of this transcriptional regulation rather than a precise description of molecular processes.
The transcription rate of Bmal1 f(transBmal1) is given by:
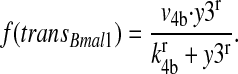 |
(9) |
It increases with rising PER2/CRY concentration (y3).
We use linear and bilinear kinetics for the description of translation, degradation, complex formation, transport across the nuclear membrane, and posttranslational modification, as the molecular details of these processes are not fully characterized. A description of the corresponding parameters is given in Table 1.
TABLE 1.
Model parameters
| Parameter | Value | Description |
|---|---|---|
| v1b | 9 nMh−1 | Maximal rate of Per2/Cry transcription |
| k1b | 1 nM | Michaelis constant of Per2/Cry transcription |
| k1i | 0.56 nM | Inhibition constant of Per2/Cry transcription |
| c | 0.01 nM | Concentration of constitutive activator |
| p | 8 | Hill coefficient of inhibition of Per2/Cry transcription |
| k1d | 0.12 h−1 | Degradation rate of Per2/Cry mRNA |
| k2b | 0.3 nM−1h−1 | Complex formation rate of PER2/CRY |
| q | 2 | No. of PER2/CRY complex forming subunits |
| k2d | 0.05 h−1 | Degradation rate of the cytoplasmatic PER2/CRY |
| k2t | 0.24 h−1 | Nuclear import rate of the PER2/CRY complex |
| k3t | 0.02 h−1 | Nuclear export rate of the PER2/CRY complex |
| k3d | 0.12 h−1 | Degradation rate of the nuclear PER2/CRY complex |
| v4b | 3.6 nMh−1 | Maximal rate of Bmal1 transcription |
| k4b | 2.16 nM | Michaelis constant of Bmal1 transcription |
| r | 3 | Hill coefficient of activation of Bmal1 transcription |
| k4d | 0.75 h−1 | Degradation rate of Bmal1 mRNA |
| k5b | 0.24 h−1 | Translation rate of BMAL1 |
| k5d | 0.06 h−1 | Degradation rate of cytoplasmatic BMAL1 |
| k5t | 0.45 h−1 | Nuclear import rate of BMAL1 |
| k6t | 0.06 h−1 | Nuclear export rate of BMAL1 |
| k6d | 0.12 h−1 | Degradation rate of nuclear BMAL1 |
| k6a | 0.09 h−1 | Activation rate of nuclear BMAL1 |
| k7a | 0.003 h−1 | Deactivation rate of nuclear BMAL1* |
| k7d | 0.09 h−1 | Degradation rate of nuclear BMAL1* |
In negative feedback loops, high Hill coefficients, an explicit delay or Michaelis Menten kinetics can reduce the number of reaction steps that are needed to obtain oscillations. For the purpose of this model, we chose to use a small system based on linear kinetics and with a high Hill coefficient, as this keeps the number of parameters in the system low. This implies a strong nonlinearity of the regulation of Per2/Cry transcription. Indeed, Etchegaray et al. (2003) have recently found that the regulation of CLOCK/BMAL1 activity by CRY proteins is likely to be modulated by histone acetylation and chromatin remodeling in the promoter regions of circadian genes. Multiple histone acetylation events, or other chromatin modifications could contribute to the kinetic nonlinearity, which we modeled by using high Hill coefficients in Eqs. 8 and 9.
The system of differential equations was solved numerically by using a Runge-Kutta algorithm. For the comparison with experimental data and the analysis of robustness the model was implemented in MATLAB (The MathWorks, Natick, MA), the bifurcation analysis was performed with XPP/AUTO (G. Bard Ermentrout; http://www.pitt.edu/phase/).
RESULTS
Dynamics of the model: comparison with experimental observations
For a model of the circadian oscillator, the consistency of its dynamical behavior with experimental observations is a prerequisite for further investigations. Using parameters within a biologically plausible range (Hargrove et al., 1991; Wagner et al., 1990) we were able to reproduce experimentally observed circadian oscillations. Due to their relatively small number the parameters could be optimized by trial and error. Criteria for parameter estimations in the order of their importance were: i), the existence of oscillations with a period close to 24 h; ii), correct phases between various oscillator components; and iii), reasonable peak/trough ratios of the mRNA and protein concentrations. The values of the parameters are listed in Table 1. In the following, the parameters are given without dimensions for ease of reading.
With the given set of parameters, the clock components oscillate with a period of 23.8 h, which is a typical period for mice (Fig. 3 A; Pittendrigh and Daan, 1976). In the model, the peak/trough ratios for Per2/Cry and Bmal1 mRNA are 5.8 and 7.0, respectively, for nuclear PER2/CRY and BMAL1 protein we observe peak/trough ratios of 2.4 and 1.7. Experimentally observed peak/trough ratios of mRNA and protein vary in a wide range from 1.5 to 20, depending on the tissue and the detection method used (Bunger et al., 2000; Okamura et al., 1999; Preitner et al., 2002; Shearman et al., 2000a; Tamaru et al., 2000; Zheng et al., 2001). Most of our values are consistent with these experimental findings. Higher peak/trough ratios as described for PER2 protein in liver tissue (Lee et al., 2001) are not observed; they might be due to additional nonlinear processes or higher nonlinearities in the circadian oscillator, e.g., complex formation with a higher number of PER2 and CRY proteins (e.g., for q = 4) substantially increases the peak/trough ratio (data not shown). In the model, the peak concentration of BMAL1 is about the same as the peak concentration of total (nuclear and cytoplasmatic) PER2/CRY (not shown). Again, this has been found experimentally (Lee et al., 2001).
FIGURE 3.

The model shows sustained circadian oscillations with correct phase relations. (A) Oscillations of clock gene mRNAs and proteins generated by the model (Fig. 2) with parameters as given in Table 1. Per2/Cry mRNA (y1, red, dashed line), nuclear PER2/CRY protein (y3, red, solid line), Bmal1 mRNA (y4, green, dashed line), activated BMAL1* (y7, green, solid line, solid circles), and total BMAL1 protein (y5 + y6 + y7, green, solid line) oscillate with a period of 23.8 h. BMAL1 protein oscillates antiphasic to Per2/Cry mRNA. Nuclear PER2/CRY protein oscillates with a phase delay of 7.5 h compared to Per2/Cry mRNA. (B) The phases between the clock components obtained by the model are in good agreement with experimental data. (Experiment) The circadian times of the maximum concentrations of Per2 mRNA (light red), nuclear PER2/CRY protein (dark red), Bmal1 mRNA (light green), and total BMAL1 protein (dark green) are shown, given as the interval in which the highest concentrations were measured (Reppert and Weaver, 2001; Tamaru et al., 2000). (Model) The phases between the maximum concentrations of the corresponding components are determined and translated into circadian times with the Per2/Cry mRNA peaking at CT7.
Fig. 3 B shows a comparison of the peak phases of clock components observed in experiments (Reppert and Weaver, 2001; Tamaru et al., 2000) and in the model. All phases in the model are in agreement with experimental data. In particular, the delay of several hours between Per2/Cry mRNA and nuclear PER2/CRY protein is reproduced by the model. In the model, this delay is due to the small degradation rates of Per2/Cry mRNA and cytoplasmatic and nuclear PER2/CRY as well as to a slow transport to the nucleus. Moreover, the almost antiphasic phase relation between BMAL1 and Per2/Cry mRNA that is observed experimentally is reproduced in our model. This delay at first glance does not fit to the idea of BMAL1 being the activator of Per2/Cry transcription. In our model, the large delay is only possible if an activated form of BMAL1 exists. Activation may be achieved by various processes, such as complex formation with CLOCK (Gekakis et al., 1998) or posttranslational modification (Eide et al., 2002).
The delay between Per2/Cry mRNA and nuclear PER2/CRY protein is fundamental and cannot be changed considerably without abolishing oscillations in our model. Extreme delays are achieved by variation of k1d (k1d = 0.492; delay 8.8 circadian hours) and k2t (k2t = 0.6; delay 7.2 circadian hours). In the negative feedback loop, oscillations occur if firstly the sum of the delays (Per2/Cry mRNA-cytoplasmic PER2/CRY complex-nuclear PER2/CRY complex) is above one-quarter of the period (Glass and Mackey, 1988; McDonald, 1989) and secondly if the amplitude of the inhibitor (nuclear PER2/CRY) is large enough. With a delay smaller than the observed 7.2 circadian hours (Per2/Cry mRNA versus nuclear PER2/CRY complex) not enough Per/Cry mRNA accumulates before the increasing inhibitor concentration prevents transcription, and the oscillations dampen. On the other hand, a large delay (>8.8 h) between Per2/Cry mRNA and nuclear PER2/CRY protein correlates with lower amplitudes of the inhibitor and thus oscillations are lost as well.
The delay between BMAL1 protein and Per2/Cry mRNA as well as the delay between Bmal1 mRNA and BMAL1 protein are less crucial for the system. They can vary from ∼3 to 12 circadian hours or from ∼3 to 6 circadian hours, respectively, without loss of oscillations. This wide range of possible delays is observed if, e.g., all rate parameters in the positive feedback are multiplied by the same factor. An increase of these rate parameters reduces the delay between Bmal1 mRNA and BMAL1 protein and simultaneously increases the delay between BMAL1 and Per2/Cry mRNA and vice versa. The range of possible delays is limited because: 1), with very high rates in the positive feedback BMAL1 is rapidly degraded, which leads to a complete loss of oscillations, and 2), with decreasing rates the peak/trough ratios in the positive feedback become small and finally oscillations disappear in the positive feedback.
Rhythmic versus constant activation of Per2/Cry transcription
To test whether the positive feedback is essential for the occurrence of oscillations, we compared the dynamics of the model with and without positive feedback for a given strength of the negative feedback. This was done by varying the parameters v4b and c, which reflect the maximal transcription rate of Bmal1 and a constant activator concentration for Per2/Cry transcription, respectively. By varying these parameters, the relative amount of positive feedback dependent and independent activation of Per2/Cry transcription can be controlled.
First, the dynamics of the system was investigated by varying positive feedback strength for a low fixed activator concentration c = 0.01 (Fig. 4 A). For v4b below a threshold of 0.35 the system reaches a steady state indicated by a stable Per2/Cry mRNA concentration, above this threshold the system oscillates. Thus, a positive feedback of a certain strength is necessary for oscillations in the case of low activator concentration. To compare, the concentration of the constitutive activator c was varied in a system without positive feedback (v4b = 0) (Fig. 4 C). With a low concentration of c (<0.02) no oscillations of Per2/Cry mRNA occur, whereas a high value of c leads to oscillations. Thus, the positive feedback can be replaced by a constantly expressed activator to generate oscillations.
FIGURE 4.
Positive feedback and constant activation can both lead to oscillations. (A) Per2/Cry mRNA concentration with varying transcription rate of Bmal1 (v4b). For a low transcription rate of Bmal1, the Per2/Cry concentration reaches a steady state. In the Hopf bifurcation point at v4b = 0.35 the steady state becomes unstable; for higher values of v4b the Per2/Cry mRNA concentration oscillates. Thick lines represent the maximum and minimum of the oscillation. For instance, with the default parameter value v4b = 3.6 the Per2/Cry mRNA concentration oscillates between 0.3 and 1.5 nM (see Fig. 3 A). The dashed line marks the unstable steady state. (C) Per2/Cry mRNA concentration with varying amount of constantly expressed activator c. With low levels of activator the Per2/Cry mRNA concentration reaches a steady state. An activator concentration above the Hopf bifurcation point at c = 0.02 results in Per2/Cry mRNA oscillations. (B and D) Oscillation periods as a function of Bmal1 transcription rate v4b and constantly expressed activator c, respectively. In both cases the period is stable for a broad parameter range and shows a stronger parameter dependence close to the Hopf bifurcation point. (E, F) The positive feedback is gradually replaced by constant activation. The average amount of total activator (y7peak + y7trough)/2 + c is kept constant. Zero-percent positive feedback corresponds to v4b = 0 and c = 1; 100% corresponds to v4b = 3.6 and c = 0.01. Oscillations of Per2/Cry mRNA occur in all cases (E); the period remains stable (F).
In both cases the period is close to 24 h for a wide range of v4b and c, respectively (Fig. 4, B and D). Only close to the Hopf bifurcation point, beyond which oscillations cease to exist, the period shortens in both cases. Therefore, according to our studies a low maximal transcription rate of Bmal1 (e.g., by mutation) as well as a constant low expression of activator should decrease the period.
These dynamical changes are consistent with experimental data from gene knock-out studies. The lack of oscillations for low Bmal1 transcription and low constant activation in the model might reflect the molecular and behavioral arrhythmicity of Bmal1−/− mutant mice, which lack a functional transcriptional activator complex BMAL1/CLOCK (Bunger et al., 2000). The maintenance of oscillations without positive feedback but with high concentration of constitutive activator may correspond to the dynamics observed in Rev-erbα−/− mutant mice. These mice are behaviorally rhythmic, and Per2 and Cry mRNAs and proteins are rhythmically expressed, although Bmal1 mRNA and protein are expressed at a constant high level (Preitner et al., 2002).
To determine how positive feedback and constant activation act together, they were varied simultaneously, while keeping the average concentration of activator (y7 + c) constant. Varying the positive feedback strength hardly affects the dynamics in the negative feedback. The maximum and minimum concentrations of Per2/Cry mRNA remain the same (Fig. 4 E) and the period of the oscillations changes only slightly (Fig. 4 F). However, for other values of the parameters of v4b and c the dynamics may change (Fig. 5). Although a strong positive feedback as well as a high activator concentration result in oscillations (open area), attractors coexist for a low concentration of constant activator c. Oscillations coexist with a stable steady state for low c and high v4b (shaded area). Here, the dynamics of the system depends on the initial conditions (insets; see figure legend).
FIGURE 5.
The positive feedback allows coexisting states in the system. The transcription rate of Bmal1, v4b, and the concentration of the constitutively expressed transcriptional activator, c, are varied simultaneously. The color of the parameter regions encode different types of dynamical behavior. In the white area the system shows oscillations; for parameters of the dark gray area, a stable steady state is reached. Complex dynamics are observed for low values of c. In that case, oscillations may coexist with a stable steady state (light gray area). An example of coexisting states is shown for v4b = 3.6, c = 0.002 (solid circle, insets): The same system (shown is y1) either oscillates or is in a stable steady state depending on the initial conditions (initial conditions 1, all variables initialized at 1; initial conditions 2, all variables initialized at 0). For lower v4b, the coexistence of two steady states (black area) is observed.
Robustness of the system with and without positive feedback
In several studies, an increase of robustness of the circadian oscillator has been proposed as a possible function of the positive feedback (Cheng et al., 2001; Preitner et al., 2002). Here, we compared the robustness of the system with and without positive feedback toward parameter changes. All parameters were varied for a given positive feedback strength or, alternatively, with a given amount of constantly expressed activator. For the system including the positive feedback we use the default parameters (v4b = 3.6 and c = 0.01). In the system without positive feedback we assume v4b = 0 and c = 1 (corresponding to the average amount of BMAL1* with v4b = 3.6). In both cases, each parameter was increased or decreased by a factor of two.
The robustness of the systems was investigated with respect to the existence of oscillations, the period of oscillations and the phases and amplitudes of the oscillator components. Oscillations persist in all cases when we change parameters by a factor of 2. The period and phases (Fig. 6, A–C) tend to be more robust with respect to parameter variations than the peak concentrations (Fig. 6, D and E). This also holds for parameter variations not shown here (see Supplementary Material). The largest changes of the period are caused by the variation of degradation and transport rates in Eqs. 1–3, which form the negative feedback loop (Fig. 6 A, k1d; see Supplementary Material). The inhibitory constant k1i has a pronounced influence on the peak concentrations.
FIGURE 6.

Circadian oscillations are robust toward parameter variations with respect to period, phases, and amplitudes with and without positive feedback. Single parameters are varied systematically (↓, divided by 2, open bars; ↑, multiplied with 2, solid bars) in the system with (left) and without (right) positive feedback. As representatives for all parameters (see Supplementary Material) the variations of v1b (synthesis rate in the negative loop), k1d (degradation rate in the negative loop), k1i (inhibitory constant), v4b (synthesis rate in the positive loop), and k4d (degradation rate in the positive loop) are shown. The relative changes of the period (A), phase differences (B, C), and peak concentrations (D, E) of the oscillations are determined: B, phase difference between y1 and y3; C, phase difference between y4 and y5 + y6 + y7; D, peak concentration of y3; E, peak concentration of y5 + y6 + y7. With and without positive feedback the period only changes significantly when k1d is varied. The relative changes of phase and amplitude are smaller in the negative loop (B, D) than in the positive loop (C, E).
The sensitivity of the period, the phases, and the peak concentrations in the negative loop toward parameter variation differ only slightly with and without positive feedback (Fig. 6, A, B, and D), i.e., the positive feedback has only a minor effect on the negative loop of the oscillator. The phases and peak concentrations in the positive feedback loop (Fig. 6, C and E) are somewhat more sensitive toward parameter variations.
To summarize, the negative feedback loop turns out to be a robust mechanism, whereas the positive feedback itself is more sensitive toward parameter variations. This raises the idea that the negative feedback guarantees undisturbed circadian oscillations, whereas the easily achieved modulation of the components of the positive feedback provides the possibility to change the phase and level of clock-dependent gene transcription.
Interplay of positive and negative feedback
As described in the previous section, the strength of the negative feedback represented by the inhibitory constant k1i particularly influences the peak concentration of the oscillations. Because the nuclear PER2 and CRYs both regulate the positive and the negative feedback, it is interesting to study the interdependence of both feedbacks with respect to the dynamics of the system. To this end, the strength of the positive and the negative feedback was changed simultaneously by varying the Bmal1 transcription rate v4b and the inhibitory constant k1i for various fixed concentrations of activator c (Fig. 7). Note, that the strength of the negative feedback falls with rising k1i.
FIGURE 7.
The state of the system depends on the positive and the negative feedback as well as on the constant activator concentration c. The dynamics of the system is analyzed for varying strengths of the positive (v4b) and negative (k1i) feedback with various concentrations of constantly expressed transcriptional activator c ((A) c = 0.025, (B) c = 0.01, (C) c = 0.008, and (D) c = 0; colored area, oscillations; black area, steady state). Very weak and very strong negative feedback lead to a loss of oscillations. Stronger positive feedback increases the range of oscillations. High values of the activator c support oscillations. The color indicates the period of the oscillations in hours for the reference parameter set and v4b and k1i given in each point (•, reference values of v4b and k1i as given in Table 1). With rising v4b the period increases, with rising k1i it either decreases or increases depending on the position. Note that the strength of the negative feedback falls with rising k1i.
For large values of c, an increasing negative feedback strength as well as an increasing positive feedback strength supports oscillations. For smaller values of c, the positive feedback is still supporting oscillations. Regarding the negative feedback, however, there exists a limited range of oscillations. Here, oscillations only occur if the negative feedback does not exceed an upper and a lower limit. Thus, for small values of c where the positive feedback is the dominant source of activation there exists a complex interplay of positive and negative feedback. Changes in both the positive and the negative feedback strength are accompanied by a change of the period: The period is smaller near the bifurcation line that separates the oscillatory from the nonoscillatory parameter range. The default parameter values, which lead to the best consistency of the model with the experimentally observed oscillatory behavior, are marked by a solid circle (Figs. 7 B and 8, point 1). For these parameters, a loss of oscillations due to a decrease in the positive feedback can be prevented by decreasing negative feedback, i.e., an increase of k1i (Fig. 8; see below).
FIGURE 8.

Variations of the strength of positive and negative feedback lead to dynamical changes observed experimentally in mouse mutants. (A) Loss-of-function mutations of Per2 and Cry are simulated using the assumption that PER2 is mainly activating Bmal1 transcription and CRY is predominantly inhibiting BMAL1/CLOCK transcriptional activity. Compared to the wild-type (wt) mice (point 1, v4b = 3.6, k1i = 0.56) in the Per2Brdm1 mutant mice v4b is decreased, which leads to a loss of oscillations (point 2, v4b = 0.2, k1i = 0.56). The additional mutation of Cry2 is simulated by an increase of k1i (point 3, v4b = 0.2, k1i = 1.5), i.e., a decrease of the strength of the negative feedback. This leads to a rescue of oscillations, as seen in the Per2Brdm1/Cry2−/− double mutant (Oster et al., 2002). Axis units of the insets are as in Fig 3 A. (B) To account for a possible role of PER2 in the negative feedback, the Per2Brdm1 mutant is modeled by a decrease of the complex formation rather than by a decrease of the positive feedback strength v4b (wt, point 1, k2b = 0.3, k1i = 0.56). Again, the Per2Brdm1 mutation leads to a loss of oscillations (point 2, k2b = 0.005, k1i = 0.56), which is rescued by the simultaneous Cry2−/− mutation (point 3, k2b = 0.005, k1i = 1).
We can relate this observation to well-characterized mouse mutants. Reppert and colleagues proposed that PER2 positively regulates Bmal1 transcription as an element of the positive feedback (Shearman et al., 2000b). Assuming that PER2 predominantly activates Bmal1 transcription and CRYs inhibit Per2/Cry transcription, our model can explain the nonintuitive rhythmic phenotype of the Per2Brdm1/Cry2−/− double-mutant mice (Fig. 8). The Per2Brdm1 mutation (functional null mutation) leads to a decrease of the Bmal1 transcription rate, resulting in a loss of oscillations (Fig. 8, point 2). For simulation of the Per2Brdm1 mutation, we assume that PER1 and/or PER3 have some ability to substitute for PER2 in the PER/CRY complex, so that the affected parameter values remain greater than zero. The second mutation Cry2−/− is associated with a decrease of the negative feedback, leading to a rescue of oscillations (Fig. 8, point 3).
The phases of the oscillations are little influenced by this “double mutation”, whereas the amplitudes are not maintained. Interestingly, the period is preserved, when the positive and negative feedback are decreased simultaneously (Fig. 7 B). While a decrease of the positive feedback is accompanied by a shortening of the period, the decrease of the negative feedback lengthens the period. Similar results have been obtained in corresponding mutation experiments: While Per2Brdm1 mutant mice have a shortened period before they get arrhythmic (Zheng et al., 1999), the Cry2−/− mutant mice have a longer period than wild-type mice (van der Horst et al., 1999; Vitaterna et al., 1999). The period of Per2Brdm1/Cry2−/− double-mutant mice is approximately the same compared to that of wild-type mice (Oster et al., 2002).
The role of PER2 is probably far more complex than only being an activator of Bmal1 transcription; e.g., mutation of the Per2 gene might also affect complex formation with CRY proteins, thereby influencing both negative and positive feedback. Considering this dual role of PER2, the Per2Brdm1 mutant has been simulated by reducing the rate of formation of the PER2/CRY complex (k2b). The results of these simulations are qualitatively similar to those described above where we only changed the positive feedback for the Per2Brdm1 mutation. Oscillations disappear in the Per2Brdm1 mutant and reappear in the Per2Brdm1/Cry2−/− double mutant (Fig. 8 B). The rescue of oscillations in the Per2Brdm1/Cry2−/− double mutant is also observed, if, in addition to its function in the positive feedback, PER2 inhibits Per2/Cry transcription to a low extent (i.e., v4b is decreased and k1i is increased in the Per2Brdm1 mutation; e.g., shift of point 2 in Fig. 8 A to k1i = 0.7). In the case of PER2 being a stronger inhibitor of Per2/Cry transcription, the negative feedback would be largely decreased in the Per2Brdm1 mutation, and the loss of oscillations (e.g., v4b = 0.2; k1i = 80) could not be rescued by a further decrease of the negative feedback. Therefore, our simulations only account for the oscillations in the Per2Brdm1/Cry2−/− double mutant if we assume the direct inhibition of Per2/Cry transcription by PER2 to be weak. Experiments indeed suggest that PER2 is a rather weak inhibitor compared to CRY1 and CRY2 (Griffin et al., 1999).
The period of the Cry1−/− mutant mice is shorter than that of wild-type mice (van der Horst et al., 1999, Vitaterna et al., 1999) and this mutation cannot rescue the oscillations in the Per2Brdm1 mice (Oster et al., 2002). The functional difference between the homologs is not known; however, a difference in the inhibitory strength is discussed, CRY1 being the stronger inhibitor (Griffin et al., 1999). Under this assumption, the negative feedback in the Cry1−/− mutant is weaker than in the Cry2−/− mutant. In our model, the period changes for varying negative feedback strength are indeed nontrivial (Fig. 7 B): Depending on how much the strength of the negative feedback is reduced, the period can either become longer or shorter than under default conditions. Close to the default conditions the period increases with decreasing negative feedback (i.e., rising k1i, corresponding to the Cry2−/− mutation). A further decrease of the negative feedback leads to a shortening of the period (k1i > 1.5). A decrease under a certain threshold (k1i > 60) fails to rescue the oscillations in the case of a weak positive feedback (v4b = 0.2). This parameter setting (k1i > 60) might reflect the state observed in the Cry1−/− mutant: This mutation leads to a short period in a wild-type background (v4b = 3.6), and it fails to rescue oscillations in Per2Brdm1 mice (v4b = 0.2). Thus, the persisting arrhythmicity of Per2Brdm1/Cry1−/− mutant mice (Oster et al., 2002) can be reproduced by the model. For a very weak negative feedback (k1i > 756.8) the oscillations disappear (not depicted in the figure) even for a positive feedback strength corresponding to wild type (v4b = 3.6). This is consistent with the loss of rhythmicity in the Cry1−/−/Cry2−/− double mutant (van der Horst et al., 1999).
Taking these considerations together this leads us to a testable prediction. In our model, a loss of oscillations due to a decrease of the positive feedback can be rescued by an increase of the constant activator concentration c (e.g., Fig. 7 A; c = 0.025). A high activator concentration c also supports oscillations if k2b instead of v4b is decreased (c > 0.073 for k2b = 0.005, k1i = 0.56, v4b = 3.6 as in Fig. 8 B, not shown). In Rev-erbα−/− mutant mice the BMAL1 concentration is constantly high, which may be reflected by a high value of c in the model. Therefore, independent of the model representation of the Per2Brdm1 mutation, our model predicts that the simultaneous mutation of the Rev-erbα gene should prevent the loss of oscillations in Per2Brdm1 mutant mice.
DISCUSSION
With the quickly expanding knowledge about the circadian oscillator our view of the clock is getting more and more complex. The model presented here is designed to describe the basic structure of the oscillator, focusing on positive and negative feedback loops. Although a detailed model is useful for examining elementary molecular processes of the mammalian clock (Forger and Peskin, 2003; Leloup and Goldbeter, 2003), for the investigation of the positive feedback a reduced model as presented here is more appropriate. A lower number of variables and parameters is achieved by lumping various variables and by using primarily linear kinetics where appropriate. This facilitates the investigation and understanding of the dynamics. The dynamics of the resulting model is in accordance with experimental data regarding period, phase relations, and peak/trough ratios of the oscillating components.
A motivation of this study was to explore possible functions of the positive feedback within the circadian core oscillator. It turned out that the negative feedback is sufficient for the occurrence of oscillations, i.e., the positive feedback can be replaced by a constantly expressed activator. Similar results have been found in a model for the Drosophila oscillator that is based on delay differential equations (Smolen et al., 2002). This finding suggests that the loss of oscillations in Bmal1−/− mutant mice is due to a lack of transcriptional activator rather than a lack of the positive feedback. This idea is supported by the phenotype of Rev-erbα−/− mutant mice, in which the activator BMAL1 is expressed at a constant high level. These mice are behaviorally rhythmic although they lack a functional positive feedback. The Rev-erbα−/− mice provide an optimal tool to test whether the regulation of output processes (other than locomotor activity) is a function of the positive feedback. If this is the case, at least some circadianly regulated processes should lose their rhythmicity in the Rev-erbα−/− mice, as those mice lack oscillations of BMAL1. A loss of oscillations for an increased Bmal1 transcription rate as described in a detailed model by Leloup and Goldbeter (2003) has not been observed in our model.
Does the positive feedback influence the robustness of the circadian oscillator? It turned out that with and without positive feedback the oscillations of components in the negative feedback loop are quite robust. In contrast, components of the positive feedback loop itself are more sensitive toward parameter variations. This is interesting in the context that the positive feedback and the resulting BMAL1 oscillations might be used to regulate output processes. The higher variability of phases and peak concentrations in the positive feedback principally allows to modulate output pathways without disturbing circadian oscillations. Variations of parameters such as synthesis rates in the positive feedback loop will hardly affect the basic core oscillation, but change the phase and strength of gene expression regulated by components of the positive feedback loop. The period of the oscillations is little affected by changes in the positive feedback.
Positive and negative feedback are not independent from each other. The inhibition of BMAL1/CLOCK by PER and CRY proteins affects both the positive and the negative feedback, because BMAL1/CLOCK activates transcription of Per, Cry, and Rev-erbα genes via binding to E-box elements in their promoters (Fig. 1; Gekakis et al., 1998). Any change of the conditions in the cell that influences the inhibitory strength of PER and CRY proteins on BMAL1/CLOCK therefore leads to simultaneous changes in the positive and the negative feedback. In the model, this corresponds to a coordinated change of v4b and k1i in opposite directions. Compared to a single parameter variation of v4b or k1i the oscillations are maintained for a wider range of v4b and k1i if the parameters are varied simultaneously (Fig. 7 B). The coregulation of positive and negative feedback by PER and CRY proteins, therefore, increases the stability of oscillations toward environmental changes, such as redox potential, nutrient conditions, or metabolic state of the cell (Rutter et al., 2002).
Although a role of PERs and CRYs in the circadian core oscillator is generally accepted, the exact molecular function of these proteins is not fully understood. In the arrhythmic Cry1−/−/Cry2−/− double-mutant mice Per2 mRNA is expressed at a rather high constant level, supporting a role of CRY proteins in the negative feedback (Okamura et al., 1999). In contrast, in Per2Brdm1 mutant mice (loss-of-function mutation) the mRNA concentrations of Bmal1 and Cry1 are severely blunted. This led to the proposal that PER2 positively acts on Bmal1 transcription and is therefore a player in the positive feedback loop (Shearman et al., 2000b).
Although PER2 and CRY proteins are represented by a lumped variable in our model, these considerations allow us to simulate the effect of mutations in those clock genes using parameter variations. The mutations are modeled by changing the features of the lumped variable. The mutation of Per2 is reflected by a decrease of the activating strength of the complex, whereas the mutation of Cry1 or Cry2 is modeled by a decrease of the inhibitory strength to different extents.
Interestingly, in the arrhythmic Per2Brdm1 mutant mice molecular and behavioral oscillations can be rescued with an additional loss-of-function mutation for Cry2 (Oster et al., 2002). This can be explained by our model (see Fig. 8). A decrease of the positive feedback (Per2Brdm1) leads to a loss of oscillations. This is compensated by a simultaneous decrease of the negative feedback (Cry2−/−) resulting in the preservation of oscillations. By knocking out Cry1 rather than Cry2 in a Per2Brdm1 background, oscillations are not rescued (Oster et al., 2002). Although a moderate increase of k1i representing a Cry2 mutation lengthens the period, a shorter period is observed with a strong increase of k1i representing the Cry1 mutation. A difference in the inhibitory strength of the two homologs, therefore, can explain the experimentally observed opposite effect of the mutations on the period.
The function of PER2 is probably more complex than exclusively activating Bmal1 transcription. It forms a complex with CRY proteins (Lee et al., 2001) and thus might play a role in the inhibition of BMAL1/CLOCK (Kume et al., 1999). In our model, however, this role does not seem to be responsible for the loss of oscillations in the Per2Brdm1 mutant, as a moderate decrease of the negative feedback strength rather supports oscillations than prevents them (Figs. 7 and 8). The loss of oscillations in the Per2Brdm1 mutant, therefore, seems to be due to the changes in the positive feedback strength.
For PER2 being a player in the positive feedback loop we can make the following prediction: oscillations in the arrhythmic Per2Brdm1 mutant mice should be rescued by an additional loss-of-function mutation for Rev-erbα. This can be tested by crossing Rev-erbα−/− and Per2Brdm1 mutant mice. In the resulting double-mutant mice a constant high expression of BMAL1 due to the mutation of Rev-erbα should replace the positive feedback. In the model, the Rev-erbα−/− mutant is described by a high concentration of constitutive activator c, which replaces the positive feedback-dependent Bmal1 transcription rate (v4b =0). Therefore the additional mutation of Per2, which is simulated by a decrease of v4b, has no further effect and the oscillations are maintained. Consequently, we predict a rhythmic behavior of those double-mutant mice.
Another important clock gene, Per1, is not explicitly included in the model, because its specific role within the positive or negative feedback loop (in contrast to its function in response to light) is not well understood. As soon as more data accumulate, the role of Per1 can in principle be investigated by varying parameters of the model, as it has been done for differentiating the functions of Cry1, Cry2, and Per2 (Fig. 8).
A characteristic feature of the circadian oscillator is temperature compensation, which guarantees a remarkably stable circadian period over a wide temperature range (Zimmerman et al., 1968). Temperature compensation of circadian oscillators has been addressed in models, assuming either a varying (Ruoff and Rensing, 1996) or the same sensitivity (Leloup and Goldbeter, 1997) of all parameters toward temperature changes. The crucial condition for the first method is the existence of parameters that when changed have the opposite effect on the period. As this condition is fulfilled in our model (Fig. 6 A), temperature compensation can be achieved with the method of Ruoff and Rensing (1996).
In our study, we focus on oscillations generated in a single cell. Although the circadian oscillation in the suprachiasmatic nucleus is generated at the level of individual neurons (Welsh et al., 1995), under natural conditions the cells interact and thereby form whole networks of coupled oscillators. Additional dynamic phenomena can be expected from this more complex system. A molecular model as presented here is a good tool to approach questions of coupling and synchronization, as has been done before for ultradian cellular rhythms (Höfer, 1999; Wolf and Heinrich, 2000) and for a nonmolecular model of the circadian clock (Kunz and Achermann, 2003).
In summary, our model describes well the molecular rhythms observed in the neurons of the suprachiasmatic nucleus and their associated behavioral rhythms. Focusing on modules like negative or positive feedback loops within the transcriptional/translational regulatory network helped to dissect their differential roles in this system. The specific design of the model, taking into account only essential processes, should make it a valuable tool for various additional studies including: i), the entrainment of the oscillator to light-dark cycles (appropriate phase response curves are obtained when “gating” is included; Geier et al., 2004); ii), the incorporation of putative novel components or mechanisms (Becker-Weimann et al., 2004); iii), stochastic simulations for investigating the influence of molecular noise on circadian oscillations (Gonze et al., 2002); iv), output processes for the expression of different phases; v), the coupling of oscillators for the simulation of synchronization events within the suprachiasmatic nuclei as well as between the clock in the brain and in peripheral tissues; and vi), temperature compensation.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
We thank Jean-Christophe Leloup, Didier Gonze, and Florian Geier for helpful comments and discussions.
This work was supported by the Deutsche Forschungsgemeinschaft graduate program grant no. GK268 (S.B.-W.) and Sonderforschungsbereich grant no. 618/A4.
Jana Wolf's present address is Medicines Research Centre, GlaxoSmithKline, Stevenage, UK.
References
- Akashi, M., Y. Tsuchiya, T. Yoshino, and E. Nishida. 2002. Control of intracellular dynamics of mammalian period proteins by casein kinase I epsilon (CKIepsilon) and CKIdelta in cultured cells. Mol. Cell. Biol. 22:1693–1703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allada, R. 2003. Circadian clocks: a tale of two feedback loops. Cell. 112:284–286. [DOI] [PubMed] [Google Scholar]
- Bae, K., X. Jin, E. S. Maywood, M. H. Hastings, S. M. Reppert, and D. R. Weaver. 2001. Differential functions of mPer1, mPer2, and mPer3 in the SCN circadian clock. Neuron. 30:525–536. [DOI] [PubMed] [Google Scholar]
- Becker-Weimann, S., J. Wolf, A. Kramer, and H. Herzel. 2004. A model of the mammalian circadian oscillator including the REV-ERBα module. Genome Informatics. 15:3–12. [PubMed] [Google Scholar]
- Bunger, M. K., L. D. Wilsbacher, S. M. Moran, C. Clendenin, L. A. Radcliffe, J. B. Hogenesch, M. C. Simon, J. S. Takahashi, and C. A. Bradfield. 2000. Mop3 is an essential component of the master circadian pacemaker in mammals. Cell. 103:1009–1017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cermakian, N., L. Monaco, M. P. Pando, A. Dierich, and P. Sassone-Corsi. 2001. Altered behavioral rhythms and clock gene expression in mice with a targeted mutation in the Period1 gene. EMBO J. 20:3967–3974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng, P., Y. Yang, and Y. Liu. 2001. Interlocked feedback loops contribute to the robustness of the Neurospora circadian clock. Proc. Natl. Acad. Sci. USA. 98:7408–7413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eide, E. J., E. L. Vielhaber, W. A. Hinz, and D. M. Virshup. 2002. The circadian regulatory proteins BMAL1 and cryptochromes are substrates of casein kinase Iepsilon. J. Biol. Chem. 277:17248–17254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Etchegaray, J., C. Lee, P. A. Wade, and S. M. Reppert. 2003. Rhythmic histone acetylation underlies transcription in the mammalian circadian clock. Nature. 421:177–182. [DOI] [PubMed] [Google Scholar]
- Forger, D. B., and C. S. Peskin. 2003. A detailed predictive model of the mammalian circadian clock. Proc. Natl. Acad. Sci. USA. 100:14806–14811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friesen, W. O., and G. D. Block. 1984. What is a biological oscillator? Am. J. Physiol. 246:R847–R853. [DOI] [PubMed] [Google Scholar]
- Geier, F., S. Becker-Weimann, A. Kramer, and H. Herzel. 2004. Entrainment in a model of the mammalian circadian oscillator. J. Biol. Rhythms. In press. [DOI] [PubMed]
- Gekakis, N., D. Staknis, H. B. Nguyen, F. C. Davis, L. D. Wilsbacher, D. P. King, J. S. Takahashi, and C. J. Weitz. 1998. Role of the CLOCK protein in the mammalian circadian mechanism. Science. 280:1564–1569. [DOI] [PubMed] [Google Scholar]
- Glass, L., and M. C. Mackey. 1988. From Clocks to Chaos: The Rhythms of Life. Princeton University Press, Princeton, NJ.
- Goldbeter, A. 2002. Computational approaches to cellular rhythms. Nature. 420:238–245. [DOI] [PubMed] [Google Scholar]
- Gonze, D., J. Halloy, and A. Goldbeter. 2002. Robustness of circadian rhythms with respect to molecular noise. Proc. Natl. Acad. Sci. USA. 99:673–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffin, E. A., Jr., D. Staknis, and C. J. Weitz. 1999. Light-independent role of CRY1 and CRY2 in the mammalian circadian clock. Science. 286:768–771. [DOI] [PubMed] [Google Scholar]
- Hargrove, J. L., M. G. Hulsey, and E. G. Beale. 1991. The kinetics of mammalian gene expression. Bioessays. 13:667–674. [DOI] [PubMed] [Google Scholar]
- Höfer, T. 1999. Model of intercellular calcium oscillations in hepatocytes: synchronization of heterogeneous cells. Biophys. J. 77:1244–1256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin, X., L. P. Shearman, D. R. Weaver, M. J. Zylka, G. J. de Vries, and S. M. Reppert. 1999. A molecular mechanism regulating rhythmic output from the suprachiasmatic circadian clock. Cell. 96:57–68. [DOI] [PubMed] [Google Scholar]
- Kume, K., M. J. Zylka, S. Sriram, L. P. Shearman, D. R. Weaver, X. Jin, E. S. Maywood, M. H. Hastings, and S. M. Reppert. 1999. mCRY1 and mCRY2 are essential components of the negative limb of the circadian clock feedback loop. Cell. 98:193–205. [DOI] [PubMed] [Google Scholar]
- Kunz, H., and P. Achermann. 2003. Simulation of circadian rhythm generation in the suprachiasmatic nucleus with locally coupled self-sustained oscillators. J. Theor. Biol. 224:63–78. [DOI] [PubMed] [Google Scholar]
- Lee, C., J. P. Etchegaray, F. R. Cagampang, A. S. Loudon, and S. M. Reppert. 2001. Posttranslational mechanisms regulate the mammalian circadian clock. Cell. 107:855–867. [DOI] [PubMed] [Google Scholar]
- Leloup, J. C., and A. Goldbeter. 1997. Temperature compensation of the circadian rhythms: control of the period in a model for circadian oscillations of the PER protein in Drosophila. Chronobiol. Int. 14:511–520. [DOI] [PubMed] [Google Scholar]
- Leloup, J. C., and A. Goldbeter. 2003. Toward a detailed computational model for the mammalian circadian clock. Proc. Natl. Acad. Sci. USA. 100:7051–7056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maywood, E. S., J. A. O'Brien, and M. H. Hastings. 2003. Expression of mCLOCK and other circadian clock-relevant proteins in the mouse suprachiasmatic nuclei. J. Neuroendocrinol. 15:329–334. [DOI] [PubMed] [Google Scholar]
- McDonald, N. 1989. Delays in Biological Systems: Linear Stability Theory. Cambridge University Press, Cambridge, UK.
- Okamura, H., S. Miyake, Y. Sumi, S. Yamaguchi, A. Yasui, M. Muijtjens, J. H. Hoeijmakers, and G. T. van der Horst. 1999. Photic induction of mPer1 and mPer2 in cry-deficient mice lacking a biological clock. Science. 286:2531–2534. [DOI] [PubMed] [Google Scholar]
- Oster, H., A. Yasui, G. T. van der Horst, and U. Albrecht. 2002. Disruption of mcry2 restores circadian rhythmicity in mper2 mutant mice. Genes Dev. 16:2633–2638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pittendrigh, C. S., and S. Daan. 1976. A functional analysis of circadian pacemakers in nocturnal rodents. J. Comp. Physiol. [A]. 106:223–252. [Google Scholar]
- Preitner, N., F. Damiola, L. Lopez-Molina, J. Zakany, D. Duboule, U. Albrecht, and U. Schibler. 2002. The orphan nuclear receptor REV-ERBalpha controls circadian transcription within the positive limb of the mammalian circadian oscillator. Cell. 110:251–260. [DOI] [PubMed] [Google Scholar]
- Reppert, S. M., and D. R. Weaver. 2001. Molecular analysis of mammalian circadian rhythms. Annu. Rev. Physiol. 63:647–676. [DOI] [PubMed] [Google Scholar]
- Reppert, S. M., and D. R. Weaver. 2002. Coordination of circadian timing in mammals. Nature. 418:935–941. [DOI] [PubMed] [Google Scholar]
- Ruoff, P., and L. Rensing. 1996. The temperature-compensated Goodwin oscillator simulates many circadian clock properties. J. Theor. Biol. 179:275–285. [Google Scholar]
- Rutter, J., M. Reick, and S. L. McKneight. 2002. Metabolism and the control of circadian rhythms. Annu. Rev. Biochem. 71:307–331. [DOI] [PubMed] [Google Scholar]
- Sanada, K., T. Okano, and Y. Fukada. 2002. Mitogen-activated protein kinase phosphorylates and negatively regulates basic helix-loop-helix-PAS transcription factor BMAL1. J. Biol. Chem. 277:267–271. [DOI] [PubMed] [Google Scholar]
- Scheper, T., D. Klinkenberg, C. Pennartz, and J. van Pelt. 1999. A mathematical model for the intracellular circadian rhythm generator. J. Neurosci. 19:40–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shearman, L. P., X. Jin, C. Lee, S. M. Reppert, and D. R. Weaver. 2000a. Targeted disruption of the mPer3 gene: subtle effects on circadian clock function. Mol. Cell. Biol. 20:6269–6275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shearman, L. P., S. Sriram, D. R. Weaver, E. S. Maywood, I. Chaves, B. Zheng, K. Kume, C. C. Lee, G. T. van der Horst, M. H. Hastings, and S. M. Reppert. 2000b. Interacting molecular loops in the mammalian circadian clock. Science. 288:1013–1019. [DOI] [PubMed] [Google Scholar]
- Smolen, P., D. A. Baxter, and J. H. Byrne. 2002. A reduced model clarifies the role of feedback loops and time delays in the Drosophila circadian oscillator. Biophys. J. 83:2349–2359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smolen, P., P. E. Hardin, B. S. Lo, D. A. Baxter, and J. H. Byrne. 2004. Simulation of Drosophila circadian oscillations, mutations, and light responses by a model with VRI, PDP-1, and CLK. Biophys. J. 86:2786–2802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamaru, T., Y. Isojima, T. Yamada, M. Okada, K. Nagai, and K. Takamatsu. 2000. Light and glutamate-induced degradation of the circadian oscillating protein BMAL1 during the mammalian clock resetting. J. Neurosci. 20:7525–7530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toh, K. L., C. R. Jones, Y. He, E. J. Eide, W. A. Hinz, D. M. Virshup, L. J. Ptacek, and Y. H. Fu. 2001. An hPer2 phosphorylation site mutation in familial advanced sleep phase syndrome. Science. 291:1040–1043. [DOI] [PubMed] [Google Scholar]
- Tyson, J. J., C. I. Hong, C. D. Thron, and B. Novak. 1999. A simple model of circadian rhythms based on dimerization and proteolysis of PER and TIM. Biophys. J. 77:2411–2417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ueda, H. R., W. Chen, A. Adachi, H. Wakamatsu, S. Hayashi, T. Takasugi, M. Nagano, K. Nakahama, Y. Suzuki, S. Sugano, M. Iino, Y. Shigeyoshi, and S. Hashimoto. 2002. A transcription factor response element for gene expression during circadian night. Nature. 418:534–539. [DOI] [PubMed] [Google Scholar]
- Ueda, H. R., M. Hagiwara, and H. Kitano. 2001. Robust oscillations within the interlocked feedback model of Drosophila circadian rhythm. J. Theor. Biol. 210:401–406. [DOI] [PubMed] [Google Scholar]
- van der Horst, G. T., M. Muijtjens, K. Kobayashi, R. Takano, S. Kanno, M. Takao, J. de Wit, A. Verkerk, A. P. Eker, D. van Leenen, R. Buijs, D. Bootsma, J. H. Hoeijmakers, and A. Yasui. 1999. Mammalian Cry1 and Cry2 are essential for maintenance of circadian rhythms. Nature. 398:627–630. [DOI] [PubMed] [Google Scholar]
- Vitaterna, M. H., C. P. Selby, T. Todo, H. Niwa, C. Thompson, E. M. Fruechte, K. Hitomi, R. J. Thresher, T. Ishikawa, J. Miyazaki, J. S. Takahashi, and A. Sancar. 1999. Differential regulation of mammalian Period genes and circadian rhythmicity by cryptochromes 1 and 2. Proc. Natl. Acad. Sci. USA. 96:12114–12119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner, P., J. Kunz, A. Koller, and M. N. Hall. 1990. Active transport of proteins into the nucleus. FEBS Lett. 275:1–5. [DOI] [PubMed] [Google Scholar]
- Welsh, D. K., D. E. Logothetis, M. Meister, and S. M. Reppert. 1995. Individual neurons dissociated from rat suprachiasmatic nucleus express independently phased circadian firing rhythms. Neuron. 14:697–706. [DOI] [PubMed] [Google Scholar]
- Wolf, J., and R. Heinrich. 2000. The effect of cellular interaction on glycolytic oscillations in yeast. A theoretical investigation. Biochem. J. 345:321–334. [PMC free article] [PubMed] [Google Scholar]
- Yuh, C. H., H. Bolouri, and E. H. Davidson. 1998. Genomic cis-regulatory logic: experimental and computational analysis of a sea urchin gene. Science. 279:1896–1902. [DOI] [PubMed] [Google Scholar]
- Zheng, B., U. Albrecht, K. Kaasik, M. Sage, W. Lu, S. Vaishnav, Q. Li, Z. S. Sun, G. Eichele, A. Bradley, and C. C. Lee. 2001. Nonredundant roles of the mPer1 and mPer2 genes in the mammalian circadian clock. Cell. 105:683–694. [DOI] [PubMed] [Google Scholar]
- Zheng, B., D. W. Larkin, U. Albrecht, Z. S. Sun, M. Sage, G. Eichele, C. C. Lee, and A. Bradley. 1999. The mPer2 gene encodes a functional component of the mammalian circadian clock. Nature. 400:169–173. [DOI] [PubMed] [Google Scholar]
- Zimmerman, W. F., C. S. Pittendrigh, and T. Pavlidis. 1968. Temperature compensation of the circadian oscillation in Drosophila pseudoobscura and its entrainment by temperature cycles. J. Insect Physiol. 14:669–684. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.






